 Open Access Article
Open Access ArticleLigand design for 227Ac extraction by active learning and molecular topology†
Jeffrey A.
Laub
and
Konstantinos D.
Vogiatzis
 *
*
Department of Chemistry, University of Tennessee, Knoxville, Tennessee 37996-1600, USA. E-mail: kvogiatz@utk.edu
First published on 14th March 2025
Abstract
Targeted α-therapy (TAT) is a promising radiotherapeutic technique for the treatment of various cancers due to the high linear energy transfer and low penetration depth of α-particles. Unfortunately, one of the major hindrances in the use of TAT is the accessibility of acceptable α-emitting radioisotopes. Of the acceptable radioisotopes, 223Ra, 224Ra, 225Ra, and 225Ac can all originate from 227Ac. Being able to selectively isolate 227Ac is crucial for aiding in increasing the accessibility of α-emitting radioisotopes for TAT. Some of the more successful ligands used for the selective separation of trivalent actinides are the 6,6′-bis(1,2,4-triazin-3-yl)-2,2′-bipyridine (BTBP)-based ligand family. Current ligand performance screening is accomplished by using a trial-and-error-based method which is expensive and based primarily on chemical intuition and previous studies. In this study, effective computer-aided ligand screening has been accomplished by generating CyMe4–BTBP-based ligands and predicting stability constants for 227Ac extraction of each using scalar relativistic density functional theory (DFT) followed by supervised machine learning (ML). DFT was used to compute stability constants from a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 stoichiometric ratio of BTBP to 227Ac with three nitrate ions for charge balancing as demonstrated by experimental analysis. The computed stability constants coupled with the vectorized information from the optimized BTBP molecular geometries were used for the training of ML workflows. The performance of each algorithm was determined by the validation set and the outcomes compared to the DFT stability constants. This methodology can aid radiochemists in synthesizing targeted ligands for selective isolation of 227Ac.
1 stoichiometric ratio of BTBP to 227Ac with three nitrate ions for charge balancing as demonstrated by experimental analysis. The computed stability constants coupled with the vectorized information from the optimized BTBP molecular geometries were used for the training of ML workflows. The performance of each algorithm was determined by the validation set and the outcomes compared to the DFT stability constants. This methodology can aid radiochemists in synthesizing targeted ligands for selective isolation of 227Ac.
Introduction
Targeted α-therapy (TAT) is a promising radiotherapeutic technique for the treatment of various cancers.1–8 The effectiveness of TAT is due to the high linear energy transfer (50–230 keV μm−1)1,9 and the short path lengths (50–100 μm)1 of α particles (4He nucleus) allowing for the destruction of cancer cells in a confined region leaving healthy cells relatively unaffected.1,2,5,9 There are, however, only a select few α-emitters that are able to be used for TAT since the α-emitters need a half-life long enough to be effective and cannot contain daughters that emit γ rays but ideally contain daughters that also emit α particles.10 Of the acceptable radioisotopes for radiopharmaceutical applications, 223Ra (t1/2 = 11.4 d),1,5,7,11224Ra (t1/2 = 3.6 d),9,10225Ra (t1/2 = 14.9 d),9 and 225Ac (t1/2 = 9.9 d)1,2,6,9,10 are of interest due to their origination from 227Ac,12 the longest-lived, naturally occurring actinium isotope (t1/2 = 21.77 years) being a great-granddaughter of 235U.3,13 Indeed, the first and only radioisotope currently approved by the FDA is 223Ra in the form of 223RaCl2 (Xofigo, Bayer HealthCare Pharmaceuticals)11 for the treatment of prostate cancer. This radioisotope is known to be produced through the isolation of 227Ac and 227Th.14 There are other methodologies for the production of 225Ac,3,4,6,7,9,15–17 where each of these processes involves the 227Ac radioisotope whether directly from legacy sources or from the transmutation of 226Ra, emphasizing the focus of this study on 227Ac extraction. The radioisotope 225Ac is also a promising α-emitter since the daughters of 225Ac are also all α-emitters, allowing for increased radiation dosage to the cancer cells.1,17,18 However, one of the major hindrances to the implementation of TAT is the supply of α-emitting radioisotopes.4,9,17,18An alternative method for the extraction of actinide(III) radioisotopes is by solvent-based extraction with 6,6′-bis(1,2,4-triazin-3-yl)-2,2′-bipyridine (BTBP, Fig. 1A) ligands.19–24 These ligands were designed for the selective extraction of trivalent actinides over trivalent lanthanides from a nitric acid medium.19,23 They were also designed to be more resistant to radiation degradation than the 2,6-bis(1,2,4-triazin-3-yl)-pyridine (BTP) ligands.19 The BTBP ligands coordinate to trivalent actinides in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (actinide-to-ligand) ratio with instances of extraction in nitric acid solution possessing a coordinated nitrate ligand in the inner coordination sphere with the remaining charge balancing nitrates in the outer solvation sphere of the coordinating complex (Fig. 1B).19,20,25 Extractions with selected BTBP complexes have been shown to be diluent dependent and importantly, structurally dependent. For example, extractions with 6,6′-bis(5,6-dipentyl-[1,2,4]triazin-3-yl)-[2,2′]bipyridine (C5-BTBP) were shown to be dependent upon the utilized diluent showing an increase in the distribution ratios between Am(III) and Eu(III) with an increase in the dielectric constant of the diluent.19,26 Likewise, 6,6′-bis(5,5,8,8-tetramethyl-5,6,7,8-tetrahydro-benzo-1,2,4-triazin-3-yl)-2,2′-bipyridine (or CyMe4–BTBP, in short), the current trivalent actinide/lanthanide extraction European reference ligand,27 when used for extraction in 1-octanol/kerosene and 1-octanol of Am(III) and Eu(III), were shown to indeed selectively extract Am(III) over Eu(III). Unfortunately, the kinetics of these extractions were shown to be inadequate to justify industrial applications.19,28
2 (actinide-to-ligand) ratio with instances of extraction in nitric acid solution possessing a coordinated nitrate ligand in the inner coordination sphere with the remaining charge balancing nitrates in the outer solvation sphere of the coordinating complex (Fig. 1B).19,20,25 Extractions with selected BTBP complexes have been shown to be diluent dependent and importantly, structurally dependent. For example, extractions with 6,6′-bis(5,6-dipentyl-[1,2,4]triazin-3-yl)-[2,2′]bipyridine (C5-BTBP) were shown to be dependent upon the utilized diluent showing an increase in the distribution ratios between Am(III) and Eu(III) with an increase in the dielectric constant of the diluent.19,26 Likewise, 6,6′-bis(5,5,8,8-tetramethyl-5,6,7,8-tetrahydro-benzo-1,2,4-triazin-3-yl)-2,2′-bipyridine (or CyMe4–BTBP, in short), the current trivalent actinide/lanthanide extraction European reference ligand,27 when used for extraction in 1-octanol/kerosene and 1-octanol of Am(III) and Eu(III), were shown to indeed selectively extract Am(III) over Eu(III). Unfortunately, the kinetics of these extractions were shown to be inadequate to justify industrial applications.19,28
Structural modification of BTBP ligands plays an important role in the optimization of actinide extractions.19 As an example, Cm(III) and Eu(III) extractions were evaluated with CyMe4–BTBP in methanol/3.3 mol% water using TRLFS20 which demonstrated conditional stability constants (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β) of 12.4 ± 0.3 and 11.3 ± 0.3, respectively, while C5-BTBP in 1-octanol/water/0.04 M nitrate using TRLFS19,29 was shown to be 10.8 ± 0.6 and 9.4 ± 0.4, respectively. Another study focused on the synthesis of two BTBP molecules (Cl–CyMe4–BTBP and Br–CyMe4–BTBP) with the halogen substituted on the para carbon with respect to the coordinating nitrogen atom on one of the bridging pyridine groups.22 Comparing the behavior of both of these ligands to each other for Am(III) separations from Eu(III) demonstrated a maximum separation factor20,30 of 124 ± 12 and 112 ± 11 at 3 M HNO3 for Cl–CyMe4–BTBP and Br–CyMe4–BTBP, respectively.22 This demonstrates that small structural changes in the functionalization of BTBP ligands can significantly affect the binding affinity of the BTBP ligands to actinides (actinium in this study) and the need to have a protocol for the screening of thousands of different BTBP ligands for evaluation can be vital towards separation optimization and ligand discovery.
β) of 12.4 ± 0.3 and 11.3 ± 0.3, respectively, while C5-BTBP in 1-octanol/water/0.04 M nitrate using TRLFS19,29 was shown to be 10.8 ± 0.6 and 9.4 ± 0.4, respectively. Another study focused on the synthesis of two BTBP molecules (Cl–CyMe4–BTBP and Br–CyMe4–BTBP) with the halogen substituted on the para carbon with respect to the coordinating nitrogen atom on one of the bridging pyridine groups.22 Comparing the behavior of both of these ligands to each other for Am(III) separations from Eu(III) demonstrated a maximum separation factor20,30 of 124 ± 12 and 112 ± 11 at 3 M HNO3 for Cl–CyMe4–BTBP and Br–CyMe4–BTBP, respectively.22 This demonstrates that small structural changes in the functionalization of BTBP ligands can significantly affect the binding affinity of the BTBP ligands to actinides (actinium in this study) and the need to have a protocol for the screening of thousands of different BTBP ligands for evaluation can be vital towards separation optimization and ligand discovery.
Since current industrial processes utilize ligands, in the form of resins, for the selective separation of Ac(III) from a mixture of different isotopic quantities of Th(IV) and Ra(II) dissolved in nitric acid, solvent-based extraction methods have the potential to selectively separate Ac(III) from a mixture of impurities by utilizing highly selective BTBP ligands in the organic phase for Ac(III) separations while utilizing a masking agent that can be used to reduce divalent impurities (such as Ra(II))19 from being extracted or a secondary ligand, such as the hydroxypyridinonate 3,4,3-LI(1,2-HOPO) ligand,31 that can be used to selectively extract tetravalent impurities (such as Th(IV)). Indeed, one such ligand utilized in resin-based extraction is the N,N,N′,N′-tetraoctyl diglycolamide (TODGA)9,18 ligand which has been explored in solvent-based separation processes with CyMe4–BTBP for SANEX applications.19,32 Utilizing solvent-based extractions as an alternative method for the extraction of 227Ac could reduce the number of processes providing a simpler extraction process that can assist in the development of novel methods for extracting trace amounts of Ac found in the ocean,33 uranium ore during the uranium processing stage instead of leaving it to decay, and from nuclear waste.34 This would be advantageous for assisting in an increase in radioisotope supply for applications in targeted radiotherapy.
Artificial intelligence and machine learning (ML) methodologies have shown promise in the analysis and prediction of actinide properties and rare-earth element separations.35–45 A recent study utilized ML to make thermochemical binding predictions from computational data of La(III) and Ac(III) with carboxylic acids.45 More specifically, this study utilized supervised ML methods based on decision tree regression to predict ΔGrxn values for the complexation of La(III) and Ac(III) with carboxylic acids by using Coulomb matrices of the coordinated complexes with inner shell coordination of solvent molecules (water). The most accurate results acquired in this study, in terms of mean absolute error (MAE), derived from the XGBoost46 method resulted in a MAE of 6.93 kcal mol−1.45 Overfitting was observed in all the ML models trained in this study, which was hypothesized to be reduced upon the addition of a larger dataset. Liu and coworkers developed ML models for the prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D, which is the logarithm of the distribution ratio, acquired from experimental analysis for lanthanide separations.43 This study utilized fully connected neural networks with the extended-connectivity fingerprints47 and a descriptor input vector extracted by RDKit48 for the individual ligands and the log
D, which is the logarithm of the distribution ratio, acquired from experimental analysis for lanthanide separations.43 This study utilized fully connected neural networks with the extended-connectivity fingerprints47 and a descriptor input vector extracted by RDKit48 for the individual ligands and the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D values with their respective experimental conditions such as temperature and concentration as examples, as inputs for the neural network. From this study, they were able to acquire a MAE of 0.34 and a root mean square error of 0.53 for their validation set.43 Both studies have specific limitations but are relevant to our study as we aim towards thermochemical predictions based on the structure of the ligand to generate a simple method for screening unexplored ligands for 227Ac extractions.
D values with their respective experimental conditions such as temperature and concentration as examples, as inputs for the neural network. From this study, they were able to acquire a MAE of 0.34 and a root mean square error of 0.53 for their validation set.43 Both studies have specific limitations but are relevant to our study as we aim towards thermochemical predictions based on the structure of the ligand to generate a simple method for screening unexplored ligands for 227Ac extractions.
The present study explores 227Ac extractions using CyMe4–BTBP-based variants as an alternative to current industrial processes and provides a general methodology for BTBP-based ligand discovery and design through scalar relativistic density functional theory (DFT) and ML. We have considered ligand featurization that utilizes information from molecular topology and electronic structure. The workflow for this study is graphically illustrated by Fig. 2 which highlights the three major sections that are presented and discussed: calibration, model development, and impact of the ML results. Application of active learning enabled an extended and reliable screening of thousands of unexplored functionalized BTBP analogs. The interpretability of the ML methodology presented here, as well as its transferability to functionalized CyMe4–BTPhen ligands, is discussed.
Results
Ligand library development
The aim of this study was the effective prediction of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values for more than 350
β values for more than 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 molecular units using only the BTBP ligand geometries and without performing expensive geometry optimization of the full complex (2
000 molecular units using only the BTBP ligand geometries and without performing expensive geometry optimization of the full complex (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between the ligand and actinide cation). This was achieved by using DFT-generated data from a small subset of the full ligand library. In particular, a ligand library of 350
1 ratio between the ligand and actinide cation). This was achieved by using DFT-generated data from a small subset of the full ligand library. In particular, a ligand library of 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 unique molecular structures were generated (see Computational details). Each class of atom size functional groups with respect to SMILES strings has approximately equal amounts of BTBP1–5 generated. Hereafter, when discussing the atom size of a functional group it will be implying the size of the SMILES string which excludes the hydrogen atoms. The five different families that were used for the generation of the ligand library included two families that were symmetrically functionalized and three that were asymmetrically functionalized (Fig. 1A). The two symmetrical families involved the functionalization of the para sites of the 2,2′-bipyridine unit of the CyMe4–BTBP scaffold with respect to the coordinating N atoms (BTBP1), and the functionalization of the lower C atom that is positioned between the tetramethyl substituted cyclohexene unit of the scaffold (BTBP2). The asymmetric functionalization included the single substitution of one side of the 2,2′-bipyridine portion of the CyMe4–BTBP scaffold by substitution of the meta site with respect to the coordinating N atom closest to the other half of the 2,2′-bipyridine group (BTBP3), substitution of the para site (BTBP4), and substitution of the other meta site, which is closest to the 1,2,4-triazine group of the BTBP scaffold (BTBP5).
875 unique molecular structures were generated (see Computational details). Each class of atom size functional groups with respect to SMILES strings has approximately equal amounts of BTBP1–5 generated. Hereafter, when discussing the atom size of a functional group it will be implying the size of the SMILES string which excludes the hydrogen atoms. The five different families that were used for the generation of the ligand library included two families that were symmetrically functionalized and three that were asymmetrically functionalized (Fig. 1A). The two symmetrical families involved the functionalization of the para sites of the 2,2′-bipyridine unit of the CyMe4–BTBP scaffold with respect to the coordinating N atoms (BTBP1), and the functionalization of the lower C atom that is positioned between the tetramethyl substituted cyclohexene unit of the scaffold (BTBP2). The asymmetric functionalization included the single substitution of one side of the 2,2′-bipyridine portion of the CyMe4–BTBP scaffold by substitution of the meta site with respect to the coordinating N atom closest to the other half of the 2,2′-bipyridine group (BTBP3), substitution of the para site (BTBP4), and substitution of the other meta site, which is closest to the 1,2,4-triazine group of the BTBP scaffold (BTBP5).
Ligand orientation and complexation calibration
Before the generation of the necessary data, we first wanted to determine the most stable conformation of the BTBP ligands (ESI, Section S1†) and the Ac(III) complexation with BTBP. The most probable Ac(III) complexation was determined by using La(III) for select ligand complexation analysis due to its chemical similarity to Ac(III).45,49 This was accomplished by taking known experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values of La(III) ligation since, to the best of our knowledge, Ac(III) has no known experimental log
β values of La(III) ligation since, to the best of our knowledge, Ac(III) has no known experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values for these systems. This calibration allowed us to make inferences about the expected performance of Ac(III) ligation with BTBP ligands.
β values for these systems. This calibration allowed us to make inferences about the expected performance of Ac(III) ligation with BTBP ligands.
Table 1 demonstrates experimental log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values for the 1
β values for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio of Cm(III) (from our previous study,50 shown here for comparison) and La(III) using different BTBP ligands. The log
2 ratio of Cm(III) (from our previous study,50 shown here for comparison) and La(III) using different BTBP ligands. The log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values were computationally determined from the chemical reactions (R1) and (R2) for the complexation with Cm(III) and La(III), respectively (L represents the BTBP variants). The coordination complex for La(III) was shown to have an additional nitrate ligand coordinated to the nuclide than Cm(III). Since in our previous study we found agreement between the DFT optimized coordination complex with spectroscopic experimental observations of Cm(III) having a single nitrate ligand coordinated to the complex,19,20,50 we could then imply that due to the larger atomic radius, La(III) could allow for a larger coordination number as determined by DFT. We also note that the predicted log
β values were computationally determined from the chemical reactions (R1) and (R2) for the complexation with Cm(III) and La(III), respectively (L represents the BTBP variants). The coordination complex for La(III) was shown to have an additional nitrate ligand coordinated to the nuclide than Cm(III). Since in our previous study we found agreement between the DFT optimized coordination complex with spectroscopic experimental observations of Cm(III) having a single nitrate ligand coordinated to the complex,19,20,50 we could then imply that due to the larger atomic radius, La(III) could allow for a larger coordination number as determined by DFT. We also note that the predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values for La(III) were overall in better agreement with the experimental values than the Cm(III) values. Thus, we infer that due to the chemical similarity between La(III) and Ac(III), that the log
β values for La(III) were overall in better agreement with the experimental values than the Cm(III) values. Thus, we infer that due to the chemical similarity between La(III) and Ac(III), that the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values from our computational protocol should provide reasonable agreement with the actual value from future experiments.
β values from our computational protocol should provide reasonable agreement with the actual value from future experiments.
| Cm(NO3)3 + 2L → [Cm(L)2(NO3)]2+(NO3)22− | (R1) |
| La(NO3)3 + 2L → [La(L)2(NO3)2]+NO3− | (R2) |
We then used computationally determined stability constants and electronic energies to evaluate the trends from rotations about dihedral angles of CyMe4–BTBP as well as substituted CyMe4–BTBP analogs. The full discussion on dihedral rotation can be found in the ESI (Sections S1 and S2)† and our key findings are summarized here. First, we evaluated the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β associated with Ac(III) ligation with each BTBP analog (Fig. 1A) using methyl as the substituent and then computed the energy barrier between all BTBP conformations of the individual analog to compare thermodynamic favorability with respect to the rotational barriers. Analysis of the computed log
β associated with Ac(III) ligation with each BTBP analog (Fig. 1A) using methyl as the substituent and then computed the energy barrier between all BTBP conformations of the individual analog to compare thermodynamic favorability with respect to the rotational barriers. Analysis of the computed log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β for these analogs demonstrated the following trend from most favorable to least favorable: CyMe4–BTBP > BTBP2 > BTBP4 > BTBP1 > BTBP5 > BTBP3. Comparison of the log
β for these analogs demonstrated the following trend from most favorable to least favorable: CyMe4–BTBP > BTBP2 > BTBP4 > BTBP1 > BTBP5 > BTBP3. Comparison of the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values with respect to the energy barrier of the BTBP analogs demonstrated that the thermodynamic stability constants are dependent upon the coordination complex itself and are not affected by complexation kinetics that are dependent upon the organizational penalty. This phenomenon was observed experimentally when comparing the experimentally determined log
β values with respect to the energy barrier of the BTBP analogs demonstrated that the thermodynamic stability constants are dependent upon the coordination complex itself and are not affected by complexation kinetics that are dependent upon the organizational penalty. This phenomenon was observed experimentally when comparing the experimentally determined log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β for La(III) with the formation rate constant, which was too rapid of a reaction to acquire interpretable results for CyMe4–BTPhen, whereas CyMe4–BTBP was measured to be 70.5 ± 0.8 L mol−1 s−1 with the stability constants for CyMe4–BTBP (8.6 ± 0.2) and CyMe4–BTPhen (8.5 ± 0.2) in acetonitrile showing only a difference of 0.1 for these relatively similar ligands.52
β for La(III) with the formation rate constant, which was too rapid of a reaction to acquire interpretable results for CyMe4–BTPhen, whereas CyMe4–BTBP was measured to be 70.5 ± 0.8 L mol−1 s−1 with the stability constants for CyMe4–BTBP (8.6 ± 0.2) and CyMe4–BTPhen (8.5 ± 0.2) in acetonitrile showing only a difference of 0.1 for these relatively similar ligands.52
To elucidate the solvation effects on the selective complexation between Ac(III) and La(III), the separation factor (SF) for La(III)/Ac(III) ligation using CyMe4–BTBP was evaluated since it has been shown experimentally that the SF increases with decreasing relative permittivity of the solvent when analyzed with Am(III)/Eu(III) separations.23 We also chose to compare Ac(III) with La(III) as the separation between these two radionuclides would be the most challenging if La(III) is present in an analyte with Ac(III). SFLa(III)/Ac(III), the ratio of the βM(III)30 values, was calculated using eqn (1):
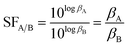 | (1) |
Data collection
We began this study with the consideration of a small subset of 623 ligands evaluated with DFT from this library. We followed a bottom-up procedure where the initial data were collected from molecular geometries of BTBP variants with small functional groups, with the aim of developing ML models that predict properties of larger molecular structures. More precisely, we have utilized all BTBP variants with substituents consisting of 1, 2, 3, and 4 non-hydrogen atoms, together with a small subset of substituents with 5 non-hydrogen atoms. The total number of the selected ligands was 640. DFT computations were performed to determine the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values of each ligand in this subset, but 17 computations were not completed successfully and were returned to the ligand library. Thus, a total of 623 DFT data were used for training a ML algorithm for making predictions on the full ligand library (Fig. 3). A full breakdown on the distribution of the datasets utilized in this study can be found in the ESI (Section S4 and in Fig. S8).†
β values of each ligand in this subset, but 17 computations were not completed successfully and were returned to the ligand library. Thus, a total of 623 DFT data were used for training a ML algorithm for making predictions on the full ligand library (Fig. 3). A full breakdown on the distribution of the datasets utilized in this study can be found in the ESI (Section S4 and in Fig. S8).†
A short analysis was carried out on the 50 molecular complexes with the highest computed log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values (out of the initial 623 examined by means of DFT). We note some common features present in the functional groups of these top 50 ligands, such as 27 of the top 50 contain amine groups, 12 contain a hydroxyl group, 6 contain a cyclic group, and 4 contain a carboxyl group (ESI, Section S3†). These results demonstrated that the addition of polar groups increases the favorability for complexation with Ac(III) since only two ligands out of 50 contain nonpolar functional groups (cyclobutyl). We also identified the symmetrical BTBP1 and the asymmetrical BTBP4 ligand scaffolds as the preferable functionalization sites. In both cases, the substituent is in the para site with respect to the coordinating nitrogen of the 2,2′-bipyridine group within the BTBP analog.
β values (out of the initial 623 examined by means of DFT). We note some common features present in the functional groups of these top 50 ligands, such as 27 of the top 50 contain amine groups, 12 contain a hydroxyl group, 6 contain a cyclic group, and 4 contain a carboxyl group (ESI, Section S3†). These results demonstrated that the addition of polar groups increases the favorability for complexation with Ac(III) since only two ligands out of 50 contain nonpolar functional groups (cyclobutyl). We also identified the symmetrical BTBP1 and the asymmetrical BTBP4 ligand scaffolds as the preferable functionalization sites. In both cases, the substituent is in the para site with respect to the coordinating nitrogen of the 2,2′-bipyridine group within the BTBP analog.
High-throughput virtual screening via active learning
A major objective of this study was to provide the tools necessary for the screening of unexplored BTBP ligands for the prediction of reliable log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values. The computational workflow presented here avoids the explicit computation of each molecular complex (350
β values. The computational workflow presented here avoids the explicit computation of each molecular complex (350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 in total) by means of DFT and active learning, which can provide directions for the targeted synthesis of the next generation of BTBP-based ligands. For that purpose, we utilized the computational data collected from the 623-ligand dataset and progressively increased the size of the ligand dataset in each active learning step (Fig. 3). The active learning process included the following phases: training, database screening, validation, data augmentation, and retraining. The model trained on the 623-ligand dataset was used for screening the unexplored 350
875 in total) by means of DFT and active learning, which can provide directions for the targeted synthesis of the next generation of BTBP-based ligands. For that purpose, we utilized the computational data collected from the 623-ligand dataset and progressively increased the size of the ligand dataset in each active learning step (Fig. 3). The active learning process included the following phases: training, database screening, validation, data augmentation, and retraining. The model trained on the 623-ligand dataset was used for screening the unexplored 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 242 ligand dataset, and predicted log
242 ligand dataset, and predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values were obtained for each molecular unit.
β values were obtained for each molecular unit.
The validation of these predictions was performed by using a validation set composed of 10 randomly selected structures from the remaining 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 252 unexplored molecules. Of these 10 BTBP ligands, six consisted of functional groups with an eight-atom scaffold, two contained seven, and two consisted of functional groups with a five-atom scaffold (see ESI S5† for more details). Three of the BTBP ligands were members of the BTBP1 analog, four were of the BTBP2 analog, one was from the BTBP3 analog, and two were from the BTBP5 analog. We first optimized the geometry of all 10 structures and then determined the log
252 unexplored molecules. Of these 10 BTBP ligands, six consisted of functional groups with an eight-atom scaffold, two contained seven, and two consisted of functional groups with a five-atom scaffold (see ESI S5† for more details). Three of the BTBP ligands were members of the BTBP1 analog, four were of the BTBP2 analog, one was from the BTBP3 analog, and two were from the BTBP5 analog. We first optimized the geometry of all 10 structures and then determined the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values computationally to then be used as comparisons for the predictability of the trained algorithms on new ligands. Note that the validation set was kept unchanged during the active learning steps to track the performance and the increased accuracy of the retrained models (vide infra).
β values computationally to then be used as comparisons for the predictability of the trained algorithms on new ligands. Note that the validation set was kept unchanged during the active learning steps to track the performance and the increased accuracy of the retrained models (vide infra).
Active learning is a machine learning technique that iteratively improves a model by identifying and incorporating new data points where predictions are uncertain. If a model's predictions deviate significantly, new data are added to the training set, the model is retrained, and the process repeats until convergence or predefined criteria are met. In this study, active learning was implemented by selecting 30 ligands with the highest predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values from an extended, unexplored ligand library to augment the dataset. Additional DFT geometry optimizations were performed for the full molecular complexes with these 30 additional ligands, new log
β values from an extended, unexplored ligand library to augment the dataset. Additional DFT geometry optimizations were performed for the full molecular complexes with these 30 additional ligands, new log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values were computed, and comparisons between the ML and DFT log
β values were computed, and comparisons between the ML and DFT log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values were used as an additional control of the models' performance (a detailed discussion on the active learning steps and the collected data is provided in ESI Sections S6–S8†). The predicted log
β values were used as an additional control of the models' performance (a detailed discussion on the active learning steps and the collected data is provided in ESI Sections S6–S8†). The predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values for each of the 10 molecules of the validation set with respect to the actual DFT values are shown in Fig. 4, while the inset demonstrates the improved predictability as the training dataset increased from the initial 623-ligand instances to the 803-ligand dataset, after 6 active learning steps. The grey arrows show the shift of the predicted values during the active learning steps. For example, we identified three outliers that are located in the upper right region of the plot and have significantly higher DFT values (log
β values for each of the 10 molecules of the validation set with respect to the actual DFT values are shown in Fig. 4, while the inset demonstrates the improved predictability as the training dataset increased from the initial 623-ligand instances to the 803-ligand dataset, after 6 active learning steps. The grey arrows show the shift of the predicted values during the active learning steps. For example, we identified three outliers that are located in the upper right region of the plot and have significantly higher DFT values (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β is 10 or higher). These three cases belong to the BTBP1 family of functionalized ligands, and they are shown in ESI S5, Fig. S9.† As the ML models are trained with more data (from 623 to 803), the model's accuracy is increased, as is shown with the value shift towards the diagonal. We also note that similar behavior was found for the rest of the validation set. The drop shown in the inset of Fig. 4 (between dataset 713 and 743) further demonstrates the improvement in the model with a Δlog
β is 10 or higher). These three cases belong to the BTBP1 family of functionalized ligands, and they are shown in ESI S5, Fig. S9.† As the ML models are trained with more data (from 623 to 803), the model's accuracy is increased, as is shown with the value shift towards the diagonal. We also note that similar behavior was found for the rest of the validation set. The drop shown in the inset of Fig. 4 (between dataset 713 and 743) further demonstrates the improvement in the model with a Δlog![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β value of 0.84 which corresponds to 4.79 kcal mol−1 uncertainty. We also quantified the performance of each dataset by calculating the mean absolute error (MAE, which can also be found in the inset of Fig. 4 as previously discussed) and root mean square error (RMSE) for the 623-ligand dataset (MAE of 3.05 and RMSE of 4.23), the 653-ligand dataset (2.99 and 4.04, respectively), the 683-ligand dataset (3.04 and 4.12, respectively), the 713-ligand dataset (3.01 and 3.77, respectively), the 743-ligand dataset (2.17 and 3.06, respectively), the 773-ligand dataset (2.50 and 3.30, respectively), and the 803-ligand dataset with a MAE value of 2.42 and a RMSE value of 3.28.
β value of 0.84 which corresponds to 4.79 kcal mol−1 uncertainty. We also quantified the performance of each dataset by calculating the mean absolute error (MAE, which can also be found in the inset of Fig. 4 as previously discussed) and root mean square error (RMSE) for the 623-ligand dataset (MAE of 3.05 and RMSE of 4.23), the 653-ligand dataset (2.99 and 4.04, respectively), the 683-ligand dataset (3.04 and 4.12, respectively), the 713-ligand dataset (3.01 and 3.77, respectively), the 743-ligand dataset (2.17 and 3.06, respectively), the 773-ligand dataset (2.50 and 3.30, respectively), and the 803-ligand dataset with a MAE value of 2.42 and a RMSE value of 3.28.
To further elucidate the predictability improvement during the active learning steps, we report the evolution of the data distribution, as we augmented the training set from 623 instances (ESI S8 Fig. S11, top†) to 803 instances (ESI S8 Fig. S11, bottom†). The 5 different families of ligands are organized into 5 groups based on their log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values, i.e. below 0, between 0 and 5, between 5 and 10, between 10 and 15, and above 15. We highlight that the distribution associated with the BTBP1 analog demonstrated that before the inclusion of the active learning molecules, there were no reported log
β values, i.e. below 0, between 0 and 5, between 5 and 10, between 10 and 15, and above 15. We highlight that the distribution associated with the BTBP1 analog demonstrated that before the inclusion of the active learning molecules, there were no reported log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values above 15, whereas active learning provided 24 BTBP1 ligands with a log
β values above 15, whereas active learning provided 24 BTBP1 ligands with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β value above 15. This assisted in improving the predictability of the validation set since the two significant outliers were both BTBP1 analogs with stability constants above 15. We also note the increase in ligands with a log
β value above 15. This assisted in improving the predictability of the validation set since the two significant outliers were both BTBP1 analogs with stability constants above 15. We also note the increase in ligands with a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β value in the 10–15 range by 59 during the active learning process for the BTBP1 analog. Thus, active learning helped the model to adapt and be trained on datapoints with higher log
β value in the 10–15 range by 59 during the active learning process for the BTBP1 analog. Thus, active learning helped the model to adapt and be trained on datapoints with higher log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values improving the validation set performance.
β values improving the validation set performance.
The active learning process also identified that symmetrically functionalized BTBP ligands significantly improve 227Ac complexation (BTBP1 and BTBP2 families). From the 623 ligands of our initial dataset, 20 BTBP1 and 3 BTBP2 variants had a log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β value above 10, while after the four active learning steps, these numbers increased to 103 and 7 variants from the BTBP1 and BTBP2 families, respectively. The top-10 performing ligands discovered by active learning are presented in Fig. 5. All ligands are symmetrical, they belong to the BTBP1 family and contain functional groups that are bonded to the BTBP scaffold through a nitrogen atom (with the exception of ligand 664 that is connected through a carbon atom). Additional observations include that these ligands contain (a) cyclic functional groups (ligands 769, 785, and 792 are exceptions), (b) at least one double bond (ligands 774 and 795 are exceptions), and (c) contain polar functional groups. These functional groups are all composed of 8 atom scaffolds (excluding H atoms).
β value above 10, while after the four active learning steps, these numbers increased to 103 and 7 variants from the BTBP1 and BTBP2 families, respectively. The top-10 performing ligands discovered by active learning are presented in Fig. 5. All ligands are symmetrical, they belong to the BTBP1 family and contain functional groups that are bonded to the BTBP scaffold through a nitrogen atom (with the exception of ligand 664 that is connected through a carbon atom). Additional observations include that these ligands contain (a) cyclic functional groups (ligands 769, 785, and 792 are exceptions), (b) at least one double bond (ligands 774 and 795 are exceptions), and (c) contain polar functional groups. These functional groups are all composed of 8 atom scaffolds (excluding H atoms).
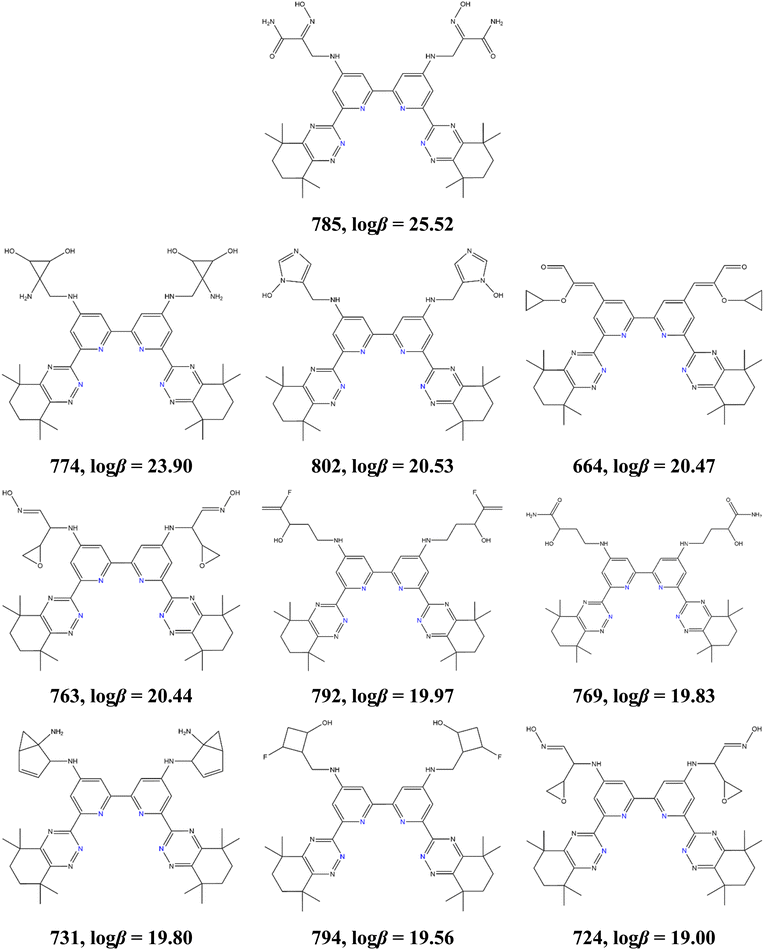 | ||
Fig. 5 The top ten ligands out of the 803 ligands analyzed through this study and their log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values computed by DFT. β values computed by DFT. | ||
Finally, we provide a set of recommendations for the functional groups and functionalization site (Fig. 6) based on analysis of the ligand characteristics that produced high log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values for 227Ac complexation in methanol. We first note the preferred functional site of the BTBP analogs studied in this work. We found that the symmetrical para positions of the coordinating nitrogen atoms of the 2,2′-bipyridine group enhance the ligation with actinium. The recommended R groups providing the largest log
β values for 227Ac complexation in methanol. We first note the preferred functional site of the BTBP analogs studied in this work. We found that the symmetrical para positions of the coordinating nitrogen atoms of the 2,2′-bipyridine group enhance the ligation with actinium. The recommended R groups providing the largest log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values from this study are shown on the right side of Fig. 6 in the magenta box. Our first recommendation is to bridge the BTBP scaffold to the functional group by using an –NH– linker coordinated to the BTBP core. This was a characteristic demonstrated by nine of the top ten ligands. The rest of the functional group branching from the amine bridge has several recommendations for design. The first is the use of cyclic groups such as cyclopentene, cyclopropyl, ethylene oxide, cyclobutane, and imidazole groups. We also recommend minimally branched functional groups, such as a single branch from the linear chain with minimal steric strain. The presence of double bonds was observed to be significant as well, being present in eight of the top ten ligands with a maximum of two double bonds being observed in a functional group. The functional groups should also be polar and contain oxygen and nitrogen groups, especially hydroxyl groups that were in eight of the ten ligands. Finally, we observed that functional groups containing a higher composition of atoms provided stronger favorability for 227Ac complexation than when functionalized with smaller functional groups.
β values from this study are shown on the right side of Fig. 6 in the magenta box. Our first recommendation is to bridge the BTBP scaffold to the functional group by using an –NH– linker coordinated to the BTBP core. This was a characteristic demonstrated by nine of the top ten ligands. The rest of the functional group branching from the amine bridge has several recommendations for design. The first is the use of cyclic groups such as cyclopentene, cyclopropyl, ethylene oxide, cyclobutane, and imidazole groups. We also recommend minimally branched functional groups, such as a single branch from the linear chain with minimal steric strain. The presence of double bonds was observed to be significant as well, being present in eight of the top ten ligands with a maximum of two double bonds being observed in a functional group. The functional groups should also be polar and contain oxygen and nitrogen groups, especially hydroxyl groups that were in eight of the ten ligands. Finally, we observed that functional groups containing a higher composition of atoms provided stronger favorability for 227Ac complexation than when functionalized with smaller functional groups.
Transfer learning
Lastly, we evaluated whether the trained model could make predictions on the structurally similar BTPhen-based ligands on 227Ac complexation. To do so, we used the ML model trained on the DFT optimized 803-ligand dataset to predict log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values of the BTPhen parent ligand together with 10 BTPhen variants using only their molecular structure (and not the full coordination complex) which are shown in ESI S5, Fig. S10.† The resulting absolute differences in log
β values of the BTPhen parent ligand together with 10 BTPhen variants using only their molecular structure (and not the full coordination complex) which are shown in ESI S5, Fig. S10.† The resulting absolute differences in log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values with respect to the DFT computed values and the predicted values from the trained ML algorithms are demonstrated in Fig. 7. To evaluate model performance, the mean absolute error (MAE, 3.22) and the root mean square error (RMSE, 3.79) between the DFT and predicted log
β values with respect to the DFT computed values and the predicted values from the trained ML algorithms are demonstrated in Fig. 7. To evaluate model performance, the mean absolute error (MAE, 3.22) and the root mean square error (RMSE, 3.79) between the DFT and predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β value are also reported. These error values are in good agreement with the final active learning step involving only BTBP ligands (the 803-ligand dataset) which had a MAE of 2.42 and a RMSE of 3.28 and thus, both models have comparable uncertainty. Since DFT-optimized BTBP ligands were used, the DFT optimized BTPhen-based ligands were also used for making predictions. Overall, we found that for the prediction of BTPhen molecules, an algorithm trained on DFT optimized BTBP ligands can provide reasonable agreement for the expected DFT stability constants without the computation of the computationally demanding coordination complexes.
β value are also reported. These error values are in good agreement with the final active learning step involving only BTBP ligands (the 803-ligand dataset) which had a MAE of 2.42 and a RMSE of 3.28 and thus, both models have comparable uncertainty. Since DFT-optimized BTBP ligands were used, the DFT optimized BTPhen-based ligands were also used for making predictions. Overall, we found that for the prediction of BTPhen molecules, an algorithm trained on DFT optimized BTBP ligands can provide reasonable agreement for the expected DFT stability constants without the computation of the computationally demanding coordination complexes.
 | ||
Fig. 7 Transfer learning results using the model trained on 803 BTBP ligands for predicting log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values of 10 + 1 CyMe4–BTPhen analogs (their structures are shown in ESI Section S5 and Fig. S10†). The y-axis shows the absolute difference between the DFT-computed and the predicted log β values of 10 + 1 CyMe4–BTPhen analogs (their structures are shown in ESI Section S5 and Fig. S10†). The y-axis shows the absolute difference between the DFT-computed and the predicted log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values. β values. | ||
Conclusions
The in silico optimization of the tetradentate BTBP ligands for enhancing ligation with 227Ac using active learning and ligand topology was discussed in this article. The study involved three stages: calibration, model development, and chemical interpretation. The calibration included the molecular complex ligation and the consideration of the correct coordination environment between two BTBP units and 227Ac, conformation search of the bare ligand, and solvent effects. These tasks were important for the accurate modeling of the full molecular complexes by DFT.A dataset of 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 unique BTBP variants was generated by considering 5 different functionalization sites, two of which generated symmetrical ligands (BTBP1 and BTBP2 ligand families) and three unsymmetrical (BTBP3, BTBP4, and BTBP5 families). From these, we selected 640 ligands, and we computed their log
875 unique BTBP variants was generated by considering 5 different functionalization sites, two of which generated symmetrical ligands (BTBP1 and BTBP2 ligand families) and three unsymmetrical (BTBP3, BTBP4, and BTBP5 families). From these, we selected 640 ligands, and we computed their log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values by performing DFT geometry optimizations of the full complex (2
β values by performing DFT geometry optimizations of the full complex (2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio between BTBP and 227Ac). A curation step reduced the number of DFT data to 623 to ensure the reliability of the data used for the training of a ML model. In all ML models, we introduced topological information of the molecular ligands together with electronic structure features via a concatenated input vector (PI + SOAP). Then, we utilized active learning to predict log
1 ratio between BTBP and 227Ac). A curation step reduced the number of DFT data to 623 to ensure the reliability of the data used for the training of a ML model. In all ML models, we introduced topological information of the molecular ligands together with electronic structure features via a concatenated input vector (PI + SOAP). Then, we utilized active learning to predict log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values of the unexplored BTBP ligands in a systematic manner. This was accomplished in six active learning steps which were augmenting the ligand set with an additional 30 ligands, followed by extra DFT computations that determined the log
β values of the unexplored BTBP ligands in a systematic manner. This was accomplished in six active learning steps which were augmenting the ligand set with an additional 30 ligands, followed by extra DFT computations that determined the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values. Following this procedure, we increased the dataset from 623 ligands to 803 ligands. The predictability of the trained models was evaluated by comparing the ML-generated log
β values. Following this procedure, we increased the dataset from 623 ligands to 803 ligands. The predictability of the trained models was evaluated by comparing the ML-generated log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values with respect to DFT for a separate set of 10 ligands (validation step). Analysis of the top performers led to the suggestion of ligand design principles. We concluded that the symmetrical BTBP1 analog is the preferred class of ligands for 227Ac extractions, with substituents that are coordinated to the BTBP body via an NH group (secondary amine).
β values with respect to DFT for a separate set of 10 ligands (validation step). Analysis of the top performers led to the suggestion of ligand design principles. We concluded that the symmetrical BTBP1 analog is the preferred class of ligands for 227Ac extractions, with substituents that are coordinated to the BTBP body via an NH group (secondary amine).
We have also explored the transferability of the trained model to a different family of tetradentate ligands. The trained ML model on BTBP data showed good accuracy for a set of 10 + 1 CyMe4–BTPhen derivatives. The importance of this becomes evident when considering that the only input information needed for the log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β predictions is the optimized geometries of the bare ligands, an approach that surpasses the more time-consuming optimization of the larger molecular complexes ligated with 227Ac cations. Therefore, this methodology can be used in the future for a large-scale study for the extraction of 227Ac over Th(IV) and Ra(II) for either the optimization of the current leading extraction process with ion chromatography or for solvent-based methods. The results presented here demonstrate that solvent-based extractions of 227Ac should be feasible, especially with the ligands that have log
β predictions is the optimized geometries of the bare ligands, an approach that surpasses the more time-consuming optimization of the larger molecular complexes ligated with 227Ac cations. Therefore, this methodology can be used in the future for a large-scale study for the extraction of 227Ac over Th(IV) and Ra(II) for either the optimization of the current leading extraction process with ion chromatography or for solvent-based methods. The results presented here demonstrate that solvent-based extractions of 227Ac should be feasible, especially with the ligands that have log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values above 15, and based on the fact that Th(IV) would not favorably complex with BTBP molecules and Ra(II) interactions could be reduced by the use of a masking agent. We conclude that further optimization for the determination of the optimum ligand to use for Ac(III) would still need to be carried out as there is a vast number of unexplored ligands for Ac(III) complexation.
β values above 15, and based on the fact that Th(IV) would not favorably complex with BTBP molecules and Ra(II) interactions could be reduced by the use of a masking agent. We conclude that further optimization for the determination of the optimum ligand to use for Ac(III) would still need to be carried out as there is a vast number of unexplored ligands for Ac(III) complexation.
Computational details
Molecular structure database
A molecular library that includes five BTBP analog ligand classes used for functionalization to use for data generation and machine learning analysis was generated by using molSimplify53 that applies OpenBabel54,55 in the backend to create molecular substitutions. The substitutions were made at symmetrical and asymmetrical positions of a parent structure (CyMe4–BTBP) creating five uniquely substituted BTBP molecule types (Fig. 1A). This was done by using a semi-automated refinement of the GDB8 database (subspace of the GDB11).56,57 Each GDB8 entry is represented as a SMILES string. For example, structures that began with a F atom were excluded, since a terminal fluorine cannot coordinate to the parent structure. Thus, a total of 350![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 875 unique BTBP molecules were generated for this study. The distribution of the composition for the functional groups per molecular scaffold used for ligand substitution of the BTBP analogs is given in Table 2. Note that the sum of these generated ligands is not the sum of the total database by one ligand and that is simply due to the unsubstituted CyMe4–BTBP ligand not being included.
875 unique BTBP molecules were generated for this study. The distribution of the composition for the functional groups per molecular scaffold used for ligand substitution of the BTBP analogs is given in Table 2. Note that the sum of these generated ligands is not the sum of the total database by one ligand and that is simply due to the unsubstituted CyMe4–BTBP ligand not being included.
| Scaffold | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Generated ligands | 20 | 35 | 90 | 340 | 1525 | 7995 | 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 096 096 |
294![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 773 773 |
Since the creation of the coordination complexes for Ac(III) with the individually functionalized BTBP molecules would be an arduous task, the same protocol was utilized for the creation of the Ac(III) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 ratio BTBP complexes but with a pre-optimized [Ac(CyMe4–BTBP)2(NO3)2]+NO3− coordination complex (shown in Fig. 1B). The same molecular substitutions were used for the two BTBP molecules shown in this complex as those from Fig. 1A creating coordination complex counterparts to the individual BTBP molecules for further DFT calculations.
2 ratio BTBP complexes but with a pre-optimized [Ac(CyMe4–BTBP)2(NO3)2]+NO3− coordination complex (shown in Fig. 1B). The same molecular substitutions were used for the two BTBP molecules shown in this complex as those from Fig. 1A creating coordination complex counterparts to the individual BTBP molecules for further DFT calculations.
Ligand orientation – calibration
Dihedral analysis was accomplished by using the built-in scan function in ORCA 5.0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 58–60 to investigate the energy barriers of the different conformers of the CyMe4–BTBP molecule and the BTBP analogs from Fig. 1 using methyl as the substituent. The energy barrier analysis utilized water, methanol, 1-octanol, and kerosene as solvents to show solvation effects on the organization and energy barriers of the BTBP ligands.23,24,61 These energy barriers were calculated with respect to the most stable conformer (lowest electronic energy). Fig. 8A demonstrates the dihedral angles investigated in this study. The dihedral angle φ1 was used for CyMe4–BTBP as well as the methyl substituted BTBP ligands to investigate the steric effects of the transitions between the ctc (cis, trans, cis) and the ccc conformers (Fig. 8B). The dihedral scan was performed with 10° intervals from 0° to 360° making 37 conformers of each ligand. An additional analysis was conducted for CyMe4–BTBP which took each φ1 conformer, fixed the dihedral, and did 37 scans at 10° intervals from 0° to 360° for φ2 producing the cct, ctc, ctt, and ccc conformations, excluding the ttt and tct conformations. Further analysis was conducted by taking the minimum ctt and cct conformers along the path towards the most favorable ccc conformer of each potential energy surface and rotating the previously unrotated 1,2,4-triazine group (φ3) by 180° at 10° intervals starting at 0° to analyze all possible BTBP conformers and acquire the full energy profile of each BTBP ligand.
58–60 to investigate the energy barriers of the different conformers of the CyMe4–BTBP molecule and the BTBP analogs from Fig. 1 using methyl as the substituent. The energy barrier analysis utilized water, methanol, 1-octanol, and kerosene as solvents to show solvation effects on the organization and energy barriers of the BTBP ligands.23,24,61 These energy barriers were calculated with respect to the most stable conformer (lowest electronic energy). Fig. 8A demonstrates the dihedral angles investigated in this study. The dihedral angle φ1 was used for CyMe4–BTBP as well as the methyl substituted BTBP ligands to investigate the steric effects of the transitions between the ctc (cis, trans, cis) and the ccc conformers (Fig. 8B). The dihedral scan was performed with 10° intervals from 0° to 360° making 37 conformers of each ligand. An additional analysis was conducted for CyMe4–BTBP which took each φ1 conformer, fixed the dihedral, and did 37 scans at 10° intervals from 0° to 360° for φ2 producing the cct, ctc, ctt, and ccc conformations, excluding the ttt and tct conformations. Further analysis was conducted by taking the minimum ctt and cct conformers along the path towards the most favorable ccc conformer of each potential energy surface and rotating the previously unrotated 1,2,4-triazine group (φ3) by 180° at 10° intervals starting at 0° to analyze all possible BTBP conformers and acquire the full energy profile of each BTBP ligand.
Quantum chemical calculations
Density functional theory (DFT) computations were performed with the ORCA 5.0 quantum chemistry package58–60 which allows the incorporation of scalar relativistic effects using the zeroth-order regular approximation (ZORA)62 and the segmented all-electron relativistically contracted (SARC)63 basis sets. The conductor-like polarizable continuum model (CPCM)64 was utilized for the incorporation of solvation effects using the built-in solvents methanol, 1-octanol, and water. For kerosene, the dielectric constant and refractive index used were 1.998 and 1.44, respectively.65 All molecular geometry optimizations used the BP86 (ref. 66 and 67) density functional with the SARC-ZORA-TZVP63 basis set for Ac(III)/La(III), both with a closed-shell electronic structure, and the ZORA-def2-SVP68,69 basis set for all other atoms. Each calculation also utilized the resolution of identity for the calculation of the two-electron integrals with the SARC/J auxiliary basis set. The quasi-harmonic approximation was used to compute the Gibbs' free energy at 298.15 K by the addition of the zero-point energy with the thermal vibrational-rotational entropies of the lowest-energy conformers using the same level of theory as the DFT geometry optimizations. This methodology has been used in our previous studies where it provided good agreement between the computed and experimentally determined stability constants of Cm(III) ligation with CyMe4–BTBP and t-Bu–C2–BTBP.50,70Automated data curation was mandatory to screen the large number of calculations performed for this project. Any calculations that failed due to poor starting geometry or that finished but contained imaginary frequencies below −50i cm−1 were filtered out of the useable structures for thermochemical analysis. The Gibbs' free energy values were utilized for the calculation of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β at a specific temperature T using (2).19,71 The reaction used for this study for both Ac(III) as determined by the complexation calibration with La(III) is shown in (R3).
β at a specific temperature T using (2).19,71 The reaction used for this study for both Ac(III) as determined by the complexation calibration with La(III) is shown in (R3).
ΔG = −2.303RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β β | (2) |
| Ac(NO3)3 + 2BTBP → [Ac(BTBP)2(NO3)2]+NO3− | (R3) |
Where![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β is computed as:
β is computed as:
 | (3) |
Machine learning
The machine learning input vectors utilized molecular descriptors of the individual BTBP ligands by using persistence homology72,73 coupled with the smooth overlap of atomic positions (SOAP).74,75 This involved the generation of persistence images (PIs) by the vectorization of persistence diagrams to incorporate ligand topology as the input vectors. Utilizing persistence homology for machine learning in chemistry has been used by previous studies76,77 and shown to be an effective descriptor for regression. This study utilized Ripser78 for the generation of persistence images (PIs) that include connected components, and 1- (holes) and 2-dimensional (voids) homological descriptors by generating 100 × 100 square persistence images with a standard deviation of the Gaussian kernel (spread) of 0.009, an upper boundary of the PIs of 2.5 Å, and a lower boundary of the PIs of −0.1 Å. The SOAP descriptor used the positions of the H, C, N, O, and F atoms present for each individual structure and constructed the descriptor with a local region cutoff value of 4 Å, 6 radial basis functions, a maximum degree of spherical harmonics as 4, and set the output as a dense array as opposed to a sparse matrix. The persistence images coupled with the SOAP (SOAP + PI) for each ligand were used as the input vector with their respective log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values as y for random forest regression as implemented in the Scikit-learn package79 using Python 3.10. The ML model utilized a 5-fold cross validation process with 200 trees, the mean absolute error loss function criteria, and six minimum samples per leaf for the analysis. The root mean square error was also calculated for each fold with the standard deviation of the error. We also investigated the performance of the individual descriptors on the datasets for comparisons with the coupled descriptors (see ESI Section S6†).
β values as y for random forest regression as implemented in the Scikit-learn package79 using Python 3.10. The ML model utilized a 5-fold cross validation process with 200 trees, the mean absolute error loss function criteria, and six minimum samples per leaf for the analysis. The root mean square error was also calculated for each fold with the standard deviation of the error. We also investigated the performance of the individual descriptors on the datasets for comparisons with the coupled descriptors (see ESI Section S6†).
Data availability
The data for the following information are included in the ESI:† the dihedral rotation study, the potential energy surfaces, the top 50 functional groups from DFT optimization in terms of the highest log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values, the distribution of BTBP analogs in the different datasets used in this study, molecular representations of the validation set and the CyMe4–BTPhen-based ligands used for active learning and transfer learning respectively, the active learning molecules, predicted and DFT log
β values, the distribution of BTBP analogs in the different datasets used in this study, molecular representations of the validation set and the CyMe4–BTPhen-based ligands used for active learning and transfer learning respectively, the active learning molecules, predicted and DFT log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β values, and a narrative on the manual correction of some of the generated structures from molSimplify. Cartesian coordinates of all molecular structures and Jupyter Notebook are publicly available at https://zenodo.org/records/14486728, https://10.5281/zenodo.15018297. The code developed for the project that is presented in the submitted paper with the title “Ligand Design for 227Ac Extraction by Active Learning and Molecular Topology” by Laub and Vogiatzis is deposited on GitHub (https://github.com/Jeffrey-107/Code-for-Ligand-Design-for-Ac-227-Extraction-by-Active-Learning-and-Molecular-Topology).
β values, and a narrative on the manual correction of some of the generated structures from molSimplify. Cartesian coordinates of all molecular structures and Jupyter Notebook are publicly available at https://zenodo.org/records/14486728, https://10.5281/zenodo.15018297. The code developed for the project that is presented in the submitted paper with the title “Ligand Design for 227Ac Extraction by Active Learning and Molecular Topology” by Laub and Vogiatzis is deposited on GitHub (https://github.com/Jeffrey-107/Code-for-Ligand-Design-for-Ac-227-Extraction-by-Active-Learning-and-Molecular-Topology).
Author contributions
Jeffrey A. Laub: conceptualization, methodology, data generation, curation and visualization, formal analysis, workflow and ML model development, writing – original draft and editing. Konstantinos D. Vogiatzis: conceptualization, methodology, funding acquisition, project administration, writing – review and editing.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This material is partially based upon work supported by the National Science Foundation under grant no. 2143354 (CAREER: CAS-Climate). The authors acknowledge the Infrastructure for Scientific Applications and Advanced Computing (ISAAC) of the University of Tennessee for computational resources.References
- R. M. Pallares and R. J. Abergel, Front. Med., 2022, 9, 1020188 CrossRef PubMed.
- R. M. Pallares, M. Flick, K. M. Shield, T. A. Bailey, N. Velappan, A. M. Lillo and R. J. Abergel, New J. Chem., 2022, 46, 15795–15798 CAS.
- T. Mastren, V. Radchenko, A. Owens, R. Copping, R. Boll, J. R. Griswold, S. Mirzadeh, L. E. Wyant, M. Brugh, J. W. Engle, F. M. Nortier, E. R. Birnbaum, K. D. John and M. E. Fassbender, Sci. Rep., 2017, 7, 8216 Search PubMed.
- S. Hogle, R. A. Boll, K. Murphy, D. Denton, A. Owens, T. J. Haverlock, M. Garland and S. Mirzadeh, Appl. Radiat. Isot., 2016, 114, 19–27 CAS.
- D. N. Shishkin, S. V. Krupitskii and S. A. Kuznetsov, Radiochemistry, 2011, 53, 404–406 CAS.
- R. A. Boll, D. Malkemus and S. Mirzadeh, Appl. Radiat. Isot., 2005, 62, 667–679 CAS.
- D. S. Abou, J. Pickett, J. E. Mattson and D. L. J. Thorek, Appl. Radiat. Isot., 2017, 119, 36–42 CAS.
- L. Qiu, J. Wu, N. Luo, Q. Xiao, J. Geng, L. Xia, F. Li, J. Liao, Y. Yang, J. Zhang and N. Liu, Ind. Eng. Chem. Res., 2023, 62, 14001–14011 CAS.
- R. Perron, D. Gendron and P. W. Causey, Appl. Radiat. Isot., 2020, 164, 109262 CrossRef CAS PubMed.
- A. A. Kotovskii, N. A. Nerozin, I. V. Prokof'ev, V. V. Shapovaloc, A. Yu, A. S. Bolonkin and A. V. Dunin, Radiochemistry, 2015, 57, 285–291 CrossRef CAS.
- L. Laughhunn, C. Botkin, W. Hubble, D. Hewing, J. Turner, R. Muzaffar, E. Robertson and M. Osman, J. Nucl. Med., 2014, 55, 2707 Search PubMed.
- V. Radchenko, A. Morgenstern, A. R. Jalilian, C. F. Ramogida, C. Cutler, C. Duchemin, C. Hoehr, F. Haddad, F. Bruchertseifer, H. Gausemel, H. Yang, J. A. Osso, K. Washiyama, K. Czerwinski, K. Leufgen, M. Pruszyński, O. Valzdorf, P. Causey, P. Schaffer, R. Perron, S. Maxim, D. S. Wilbur, T. Stora and Y. Li, J. Nucl. Med., 2021, 62, 1495–1503 CrossRef CAS PubMed.
- H. W. Kirby and L. R. Mordd, in The Chemistry of the Actinide and Transactinide Elements, Springer, 3rd edn, 2006, ch. 2, vol. 1, pp. 18–51 Search PubMed.
- R. H. Larsen, G. Henriksen and Ø. S. Brulard, US Pat., US6635234B1, 2003 Search PubMed.
- BWXT, Fusion Pharmaceuticals and BWXT Medical Announce Actinium-225 Partnership to Scale Supply for Developing Targeted Alpha Therapies, accessed January 7, 2024 Search PubMed.
- BWXT, BWXT Medical Expands Collaboration with Fusion Pharmaceuticals Through Strengthened Actinium Supply and Access to Generator Technology, accessed January 7, 2024 Search PubMed.
- W. Yan, ACS Cent. Sci., 2020, 6, 827–829 CAS.
- D. R. McAlister and E. P. Horwitz, Appl. Radiat. Isot., 2018, 140, 18–23 CrossRef CAS PubMed.
- P. J. Panak and A. Geist, Chem. Rev., 2013, 113, 1199–1236 CAS.
- A. Bremer, D. M. Wittaker, C. A. Sharrad, A. Geist and P. J. Panak, Dalton Trans., 2014, 43, 2684–2694 CAS.
- A. Bremer, C. M. Ruff, D. Girnt, U. Müllich, J. Rothe, P. W. Roesky, P. J. Panak, A. Karpov, T. J. J. Müller, M. A. Denecke and A. Geist, Inorg. Chem., 2012, 51, 5199–5207 CAS.
- A. Afsar, P. Distler, L. M. Harwood, J. John and J. Westwood, J. Org. Chem., 2016, 81, 10517–10520 CAS.
- C. Ekberg, E. Löfström-Engdahl, E. Aneheim, M. R. S. Foreman, A. Geist, D. Lundberg, M. Denecke and I. Persson, Dalton Trans., 2015, 44, 18395–18402 CAS.
- M. R. S. Foreman, M. J. Hudson, M. G. B. Drew, C. Hill and C. Madic, Dalton Trans., 2006, 1645–1653 CAS.
- M. Steppert, I. Císařová, T. Fanghänel, A. Geist, P. Lindqvist-Reis, P. Panak, P. Štěpnička, S. Trumm and C. Walther, Inorg. Chem., 2012, 51, 591–600 CAS.
- M. Nilsson, S. Andersson, F. Drouet, C. Ekberg, M. R. S. Foreman, M. Hudson, J.-O. Liljenzin, D. Magnusson and G. Skarnemark, Solvent Extr. Ion Exch., 2006, 24, 299–318 CAS.
- P. Distler, M. Mindova, J. Sebesta, B. Gruner, D. Bavol, R. J. M. Egberink, W. Verboom, V. A. Babain and J. John, ACS Omega, 2021, 6, 26416–26427 CAS.
- A. Geist, C. Hill, G. Modolo, M. R. S. J. Foreman, M. Weigl, K. Gompper and M. J. Hudson, Solvent Extr. Ion Exch., 2006, 24, 463–483 CAS.
- T. Vu, PhD thesis, Université Louis Pasteur (Strasbourg-I), 2008.
- S. Trumm, P. J. Panak, A. Geist and T. Fanghänel, Eur. J. Inorg. Chem., 2010, 2010, 3022–3028 Search PubMed.
- G. J.-P. Deblonde, A. Ricano and R. J. Abergel, Nat. Commun., 2019, 10, 2438 Search PubMed.
- G. Modolo, A. Wilden, H. Daniels, A. Geist, D. Magnusson and R. Malmbeck, Radiochim. Acta, 2013, 101, 155–162 CAS.
- N. Kemnitz, D. E. Hammond, P. Henderson, E. Le Roy, M. Charette, W. Moore, R. F. Anderson, M. Q. Fleisher, A. Leal, E. Black, C. T. Hayes, J. Adkins, W. Berelson and X. Bian, Mar. Chem., 2023, 250, 104180 CAS.
- G. Choppin, J.-O. Liljenzin, J. Rydberg and C. Ekberg, Radiochemistry and Nuclear Chemistry, Academic Press, Oxford, U.K., 4th edn, 2013 Search PubMed.
- S. M. Lyons, C. G. Britt, L. S. Wood, D. L. Duke, B. G. Fulsom, M. E. Moore and L. Snyder, AIP Adv., 2023, 13, 085115 CAS.
- C. Qin, J. Liu, Y. Yu, Z. Xu, J. Du, G. Jiang and L. Zhao, Ceram. Int., 2024, 50, 1220–1230 CAS.
- E. Stippell, L. Alzate-Vargas, K. N. Subedi, R. M. Tutchton, M. W. D. Cooper, S. Tretiak, T. Gibson and R. A. Messerly, Artificial Intelligence Chemistry, 2024, 2, 100042 CrossRef.
- J. Wang, D. B. Ghosh and Z. Zhang, Materials, 2023, 16, 4985 CrossRef CAS PubMed.
- A. Ghosh, F. Ronning, S. M. Nakhmanson and J.-X. Zhu, Phys. Rev. Mater., 2020, 064414 CrossRef CAS.
- E. T. Dubois, J. Tranchida, J. Bouchet and J.-B. Maillet, Phys. Rev. Mater., 2024, 8, 025402 CrossRef CAS.
- K. Zheng, N. Marcella, A. L. Smith and A. I. Frenkel, J. Phys. Chem. C, 2024, 128, 7635–7642 CrossRef CAS.
- M.-T. Nguyen, R. Rousseau, P. D. Paviet and V.-A. Glezakou, ACS Appl. Mater. Interfaces, 2021, 13, 53398–53408 CAS.
- T. Liu, K. R. Johnson, S. Jansone-Popova and D.-e. Jiang, JACS Au, 2022, 2, 1428–1434 CAS.
- M.-T. Nguyen, B. A. Helfrecht, R. Rousseau and V.-A. Glezakou, J. Mol. Liq., 2022, 365, 120115 CrossRef CAS.
- D. A. Penchoff, C. C. Peterson, E. M. Wrancher, G. Bosilca, R. J. Harrison, E. F. Valeev and P. D. Benny, J. Radioanal. Nucl. Chem., 2022, 331, 5469–5485 CAS.
- T. Chen and C. Guestrin, XGBoost: A Scalabale Tree Boosting System, 2016, preprint, arXiv:1603.02754, DOI:10.1145/2939672.2939785.
- D. Rogers and M. Hahn, J. Chem. Inf. Model., 2010, 50, 742–754 CAS.
- G. Landrum, RDKit: Open-Source Cheminformatics, https://www.rdkit.org Search PubMed.
- D. Lundberg and I. Persson, Coord. Chem. Rev., 2016, 318, 131–134 CrossRef CAS.
- J. A. Laub and K. D. Vogiatzis, J. Phys. Chem. A, 2023, 127, 5523–5533 CAS.
- V. Hubscher-Bruder, J. Haddaoui, S. Bouhroum and F. Arnaud-Neu, Inorg. Chem., 2010, 49, 1363–1371 CAS.
- F. W. Lewis, L. M. Harwood, M. J. Hudson, M. G. B. Drew, V. Hubscher-Bruder, V. Videva, F. Arnaud-Neu, K. Stamberg and S. Vyas, Inorg. Chem., 2013, 52, 4993–5005 CAS.
- E. I. Ioannidis, T. Z. Gani and H. J. Kulik, J. Comput. Chem., 2016, 37, 2106–2117 CrossRef CAS PubMed.
- N. M. O'Boyle, C. Morley and G. R. Hutchison, Chem. Cent. J., 2008, 2, 5 CrossRef PubMed.
- N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33 Search PubMed.
- T. Fink, H. Bruggesser and J.-L. Reymond, Angew. Chem., Int. Ed., 2005, 44, 1504–1508 CrossRef CAS PubMed.
- T. Fink and J.-L. Reymond, J. Chem. Inf. Model., 2007, 47, 342–353 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, 1606 Search PubMed.
- K. Lyczko and S. Ostrowski, Nukleonika, 2015, 60, 853–857 CrossRef.
- E. van Lenthe, J. G. Snijders and E. J. Baerends, J. Chem. Phys., 1996, 105, 6505–6516 CrossRef CAS.
- D. A. Pantazis and F. Neese, J. Chem. Theory Comput., 2011, 7, 677–684 CrossRef CAS.
- V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001 CAS.
- P. Panda and S. Mishra, Chem. Phys. Impact, 2024, 8, 100447 Search PubMed.
- J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 8822–8824 Search PubMed.
- A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 CAS.
- D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919 CrossRef CAS PubMed.
- G. A. McCarver, R. J. Hinde and K. D. Vogiatzis, Inorg. Chem., 2020, 59, 10492–10500 CAS.
- A. N. Srivastva, Stability and Application of Coordination Compounds, IntechOpen, London, 2020 Search PubMed.
- H. Adams, T. Emerson, M. Kirby, R. Neville, C. Peterson, P. Shipman, S. Chepushtanova, E. Hanson, F. Motta and L. Ziegelmeier, J. Mach. Learn. Res., 2017, 18, 1–35 Search PubMed.
- G. M. Jones, B. Story, V. Maroulas and K. D. Vogiatzis, Molecular Representations for Machine Learning, Am. Chem. Soc., 2023 Search PubMed.
- L. Himanen, M. O. J. Jäger, E. V. Morooka, F. F. Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CAS.
- J. Laakso, L. Himanen, H. Homm, E. V. Morooka, M. O. J. Jäger, M. Todorović and P. Rinke, J. Chem. Phys., 2023, 158, 234802 CAS.
- G. M. Jones, B. A. Smith, J. K. Kirkland and K. D. Vogiatzis, Inorg. Chem. Front., 2023, 10, 1062–1075 CAS.
- J. Townsend, C. P. Micucci, J. H. Hymel, V. Maroulas and K. D. Vogiatzis, Nat. Commun., 2020, 11, 3230 CAS.
- U. Bauer, J. Appl. Comput. Topol., 2021, 5, 391–423 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher and M. P. É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5dd00007f |
| This journal is © The Royal Society of Chemistry 2025 |






