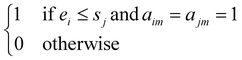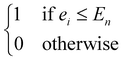Open Access Article
Open Access ArticleSchedule optimization for chemical library synthesis†
Qianxiang
Ai‡
 a,
Fanwang
Meng‡
a,
Fanwang
Meng‡
 a,
Runzhong
Wang
a,
J. Cullen
Klein
b,
Alexander G.
Godfrey
a,
Runzhong
Wang
a,
J. Cullen
Klein
b,
Alexander G.
Godfrey
 b and
Connor W.
Coley
b and
Connor W.
Coley
 *ac
*ac
aDepartment of Chemical Engineering, MIT, Cambridge, MA 02139, USA. E-mail: ccoley@mit.edu
bNational Center for Advancing Translational Sciences, Rockville, MD 20850, USA
cDepartment of Electrical Engineering and Computer Science, MIT, Cambridge, MA 02139, USA
First published on 17th December 2024
Abstract
Automated chemistry platforms hold the potential to enable large-scale organic synthesis campaigns, such as producing a library of compounds for biological evaluation. The efficiency of such platforms will depend on the schedule according to which the synthesis operations are executed. In this work, we study the scheduling problem for chemical library synthesis, where operations from interdependent synthetic routes are scheduled to minimize the makespan—the total duration of the synthesis campaign. We formalize this problem as a flexible job-shop scheduling problem with chemistry-relevant constraints in the form of a mixed integer linear program (MILP), which we then solve in order to design an optimized schedule. The scheduler's ability to produce valid, optimal schedules is demonstrated by 720 simulated scheduling instances for realistically accessible chemical libraries. Reductions in makespan up to 58%, with an average reduction of 20%, are observed compared to the baseline scheduling approach.
1 Introduction
Automated synthetic chemistry has evolved from one-step synthesis of similar targets1,2 to multi-step synthesis with chemically distinct reactions.3–6 Recent studies have demonstrated the potential of automated synthesis modules in synthesis campaigns for a large set of targets, i.e., syntheses of chemical libraries.7–12 Computer-aided synthetic planning with the goal of automated execution must include not only the task of retrosynthetic analysis, but also the subsequent elaboration of abstract routes into specific, actionable hardware operations.13 This elaboration requires high-level considerations such as spatial arrangement/connectivity of devices (hardware orchestration),14 as well as methods to specify operations. The precise timing of these hardware operations directly impacts the total duration of a synthesis campaign. As a simple example, parallel synthesis in reaction vials using a multi-position dry block heater is likely to be more efficient than sequential synthesis if multiple reaction steps can be run with the same temperature setpoint. The impact of optimizing the schedule of operations can be significant as synthetic chemistry laboratories tend to be highly modular and comprise independent hardware modules that allow highly parallel execution. As the size of chemical libraries for synthesis grows, so does the number of requisite hardware operations and interdependencies, motivating the use of formal optimization techniques for time-efficient multi-target synthesis.In examples of automated chemistry platforms, an operation scheduler is typically reported as a component of the overall platform manager rather than as a standalone, reusable module. Most of these schedulers use rule-based, heuristic approximation methods.11,15–19 For example, Canty uses a greedy algorithm to arrange concurrent workflows on a molecular synthesis platform.20 Simple prioritization policies are also popular choices for dynamic scheduling. The platform by Burger et al. uses an oldest-job-first policy,21 and the laboratory automation manager by Delaney et al. adopts a shortest-job-first policy.22 These simple scheduling policies, however, may not provide feasible solutions to comply with constraints that are common to chemical synthesis. A key constraint type is a time lag constraint that restricts the temporal gap between the end of an operation and the start of another. For example, if a stock solution of a homogeneous catalyst is prone to deactivation by oxidation, there is a maximum time lag between the preparation of this solution and its addition to the reactor. A shortest-job-first or an oldest-job-first policy does not guarantee that the shortest/oldest next operation would obey such a maximum time lag constraint. Aarts et al. propose a modified greedy algorithm to address time lag constraints among operations by rejecting infeasible schedules in local searches.18 While these heuristic methods provide solutions with low computational complexity, the obtained solutions can be far from optimal. Few studies describe formal mathematical formulations of laboratory operation schedulers,23–25 and, to the best of our knowledge, only the study by Itoh et al. achieves mathematically optimal solutions.25 However, while Itoh et al. consider constraints on temporal boundaries of operations (time lags) for life science laboratory applications, the formulation still lacks other constraints that are important to generic library synthesis scenarios. For example, module capacity, as illustrated in the case of multi-position heaters, and work shifts, where some operations can only be performed in predefined time slots. It should also be noted that not all of these previous schedulers were designed for the synthesis of chemical libraries.
Chemical production scheduling has become an extensive research area with applications in a variety of industries, such as oil refining,26 polymer production,27 and ceramic production.28 These scheduling problems are posed to optimize a given objective, most often the total execution time (makespan). As a special case of chemical production scheduling, library synthesis deals with small-scale batch reactors due to their flexibility in accommodating different synthetic routes. We identify library synthesis as exhibiting the following characteristics:
(1) Pre-planned batches: while materials merging and splitting are allowed in a generic campaign, the quantities of materials involved in all operations are planned ahead of operation scheduling. This means batch quantities are pre-calculated, and the number of batches/operations is fixed.
(2) Flexible assignment: an operation can be processed by one or more hardware modules in the laboratory, and the assignment of operations to hardware modules is a sub-problem of the scheduling problem.
(3) Interdependent synthetic routes: the reactions to afford a general set of target chemicals can have arbitrary interdependencies. This often originates from shared intermediate products for multiple downstream reactions. Alternative scenarios include precedence relations imposed by functional modules, such as flow systems with fixed operation orders. This thus requires the scheduling algorithm to model arbitrary precedence relations among operations;
(4) Laboratory constraints: the operations are commonly subject to temporal constraints imposed by materials, hardware, and operators. Constraints of this type include time lags, hardware capacity, and operator shifts as mentioned earlier.
Following the classification by Maravelias,29 the library synthesis scheduling problem falls into the category of flexible job-shop scheduling problem (FJSP) due to characteristics 1 and 2. The term “flexible” indicates that a specific operation may be processed by one of many machines. FJSP was first introduced by Brucker and Schlie in 1990 to model linear operation sequences in multipurpose facility environments,30 and is at least as hard as the NP-complete job-shop scheduling problem.31,32 FJSP has since been extended to include arbitrary inter-operation precedence relations,33,34 sometimes referred to as the extended FJSP,35,36 which maps to the dependent synthetic routes issue in library synthesis (characteristics 3). Previous studies have further generalized extended FJSP to include additional hard constraints. For example, Pawar and Bhosale investigated a FJSP in the press working industry with machine capacity constraints.37 Braune and Doerner focus on scheduling workflows in chemical research laboratories with maximum time lag constraints.38 Boyer et al. introduced “generalized FJSP” to include machine setup time and holding time in addition to aforementioned hard constraints.39 While these previous studies include constraints that could partially map onto the constraints in library synthesis, none of these previous studies fully covers the types of constraints that are commonly seen in organic synthesis (Table 1). We found the study by Boyer et al., despite being designed for ring rolling processes, most comprehensive in terms of constraint types, and their formulation is modified to accommodate library synthesis scheduling in this study (Section 2.2).
| Reference | Application | Arbitrary precedence | Module assignment | Module capacity | Time lag | Work shift | Optimal schedule |
|---|---|---|---|---|---|---|---|
| Aarts et al.18 | Chemical synthesis | ✓ | |||||
| Braune and Doerner38 | Molding process | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Itoh et al.25 | Biochemical analysis | ✓ | ✓ | ✓ | |||
| Boyer et al.39 | Ring rolling | ✓ | ✓ | ✓ | ✓ | ✓ | |
| Pawar and Bhosale37 | Press working | ✓ | ✓ | ✓ | |||
| This work | Chemical synthesis | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
In this study, we report an open-source library synthesis scheduler along with visualization modules (Fig. 1). Our formulation optimizes the makespan of arbitrary batch chemistry synthetic routes while respecting common laboratory-relevant constraints, including minimum/maximum lag time, hardware capacity, and work shifts. Our workflow produces optimal schedules for library synthesis by representing synthetic routes (proposed by predictive chemistry models) as reaction and operation networks. We demonstrate the scheduler on exemplary real-world chemical libraries, including a library for cannabinoid receptors40 and a library of FDA-approved drugs.41
2 Methods
2.1 Problem definition
We focus on minimizing the time (makespan) required to synthesize a target chemical library, given the specifications of available hardware units. If the temporal cost of each operation can be reliably estimated, the library synthesis scheduling problem can then be treated as a flexible job-shop scheduling problem (FJSP), where the makespan is optimized as a function of both the operation-to-module assignment and the start times of operations.Each reaction in a reaction network consists of a predetermined set of operations which can be represented by a directed acyclic graph, the operation graph, where the nodes represent the operations of this reaction and edges represent the required precedence relations among the operations. We use the term “required” here to distinguish it from the implied precedence relations in an existing schedule. The required precedence relations of a chemical reaction sometimes lead to a linear sequence of operations (a path graph), such as the additions of reagents with a fixed addition order followed by a heating operation. In other cases, however, an operation can be required to precede, or to be preceded by, multiple other operations. For example, when the addition order of reagents is flexible, there is no required precedence relations among addition operations, and the heating operation becomes a node that has multiple incoming edges from the addition operation nodes in the operation graph of this reaction. Thus, in contrast to previous studies,18 we refrain from making assumptions about the topology of operation graphs and consider them generic directed acyclic graphs.
We further assume that throughout the synthesis campaign, the set of functional modules is fixed, so no modules are added or removed from the laboratory. Given a reaction network and the operation graphs of its reactions, we can generate the operation network of this reaction network by connecting nodes from different operation graphs with directed (precedence) edges. Note these edges still represent required precedence relations among operations, thus the precedence of reaction A over reaction B in the reaction network does not imply all operations of reaction A must precede all operations of reaction B in the operation network. This network can be viewed as a State-Task Network44 where chemicals and operations are states and tasks, respectively.
(1) The operation network  defined by the set of operations
defined by the set of operations  and the required precedence relations among them;
and the required precedence relations among them;
(2) The set of functional modules  ;
;
(3) The processing times
 | (1) |
 includes the ordinary precedence constraints between two operations, i.e., there is a path from Oi to Oj in
includes the ordinary precedence constraints between two operations, i.e., there is a path from Oi to Oj in  ⇔ the end time of Oi must precede the start time of Oj. The term “ordinary” distinguishes these constraints from other precedence constraints (vide infra).
⇔ the end time of Oi must precede the start time of Oj. The term “ordinary” distinguishes these constraints from other precedence constraints (vide infra).
(1) lminij ∈ (−∞, +∞): the minimum lag time between the end of Oi and the start of Oj. This is used when the undetermined delay between two operations has a lower bound. For example, the solution prepared by an exothermic mixing process has to wait for more than a certain time before being used by a subsequent operation;
(2) lmaxij ∈ (−∞, +∞): the maximum lag time between the end of Oi and the start of Oj. This is used when the undetermined delay between two operations has an upper bound, frequently present in reaction input additions. For example, a freshly prepared Grignard reagent must be used within a short period of time before expiring if not stored under fully inert conditions;
(3)  : the module capacity of Mm. This allows efficient usage of functional modules. For example, a heater block with three slots can be used for three independent heating operations with similar set temperatures. For functional modules that can process only one operation at a time, their capacities are set to one;
: the module capacity of Mm. This allows efficient usage of functional modules. For example, a heater block with three slots can be used for three independent heating operations with similar set temperatures. For functional modules that can process only one operation at a time, their capacities are set to one;
(4) Cij ∈ {0, 1}: the compatibility between Oi and Oj. This determines whether two operations can be processed simultaneously by the same functional module. For example, two heating operations cannot be processed concurrently on the same heater block if they require very different set temperatures.
(5) Sn ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +∩{0} and En ∈
+∩{0} and En ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) +: the start time and the end time of the nth work shift
+: the start time and the end time of the nth work shift 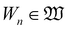 during which the operations in
during which the operations in  are permitted to be processed. This is useful for scheduling operations with safety concerns, e.g., operations involving elevated temperature/pressure would often require human supervision in the laboratory.
are permitted to be processed. This is useful for scheduling operations with safety concerns, e.g., operations involving elevated temperature/pressure would often require human supervision in the laboratory.
By combining lminij and lmaxij, the precedence relations can be described in a more constrained manner than the ordinary precedence constraints in  . For ordinary precedence constraints, we let lminij = 0, lmaxij = +∞ if Oi is required to precede Oj, and lminij = −∞, lmaxij = +∞ otherwise. All input parameters are summarized in Table 2.
. For ordinary precedence constraints, we let lminij = 0, lmaxij = +∞ if Oi is required to precede Oj, and lminij = −∞, lmaxij = +∞ otherwise. All input parameters are summarized in Table 2.
2.2 Mixed-integer linear programming (MILP) formulation
We solve the library synthesis scheduling problem as a mixed-integer linear program (MILP), which includes operation-to-module assignment, arbitrary precedence relations, and common laboratory constraints, as schematically shown in Fig. 2. The variables used in this formulation are defined in Table 3. xijm and yijm are indicators of whether one of {Oi, Oj} precedes another and both are assigned to the Mm. zijm is the indicator of whether there is overlap between Oi and Oj on the same Mm. Yin and Zin are indicators describing temporal positions between the boundary of Wn and the start/end time of Oi. Ain, defined by Yin and Zin, is the indicator of whether Oi is assigned to the work shift Wn.With the variables and the parameters defined in Table 2, we now introduce the MILP formulation of the library synthesis scheduling problem. Eqn (2) and (3) define the optimization objective. Eqn (4) defines ei based on si and the assignment of Oi (aim). Eqn (5) represents the unique assignment constraint for every operation. Eqn (6) and (7) represent the time lag constraints. Eqn (8)–(12) establish zijm as the indicator for overlap between Oi and Oj on the same Mm. Note for the same (i, j, m), xijm + yijm ≤ 1 holds automatically. This mathematical formulation is based on the work by Boyer et al. originally developed for ring rolling processes.39 The choice of indicator zijm is different from the design in Boyer et al. since they assume first-in-first-out (FIFO) policies for all functional modules. This assumption forbids the situation where the duration of Oi on Mm includes the duration of Oj, provided both Oi and Oj are assigned to the same Mm. For example, when two compatible heating operations are assigned to the same heater with time estimates of 1 hour and 3 hours, respectively, the FIFO policy would prevent the 1 hour operation to start until 2 hours after the start of the 3 hours operation. zijm is then used in (13) and (14) to enforce module capacity constraints. Compared to Boyer et al. which does not address work shift constraints, eqn (15)–(21) are included to guarantee work shift-constrained operations  are not scheduled between work shifts. Specifically, eqn (15) ensures that Oi is assigned to exactly one work shift, where Ain, the indicator for assigning Oi to Wn, is established by eqn (16)–(21) through the auxiliary indicators Yin and Zin.
are not scheduled between work shifts. Specifically, eqn (15) ensures that Oi is assigned to exactly one work shift, where Ain, the indicator for assigning Oi to Wn, is established by eqn (16)–(21) through the auxiliary indicators Yin and Zin.
| min emax | (2) |
 | (3) |
 | (4) |
 | (5) |
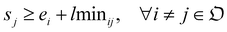 | (6) |
 | (7) |
 | (8) |
 | (9) |
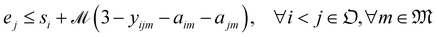 | (10) |
 | (11) |
| xijm + yijm + zijm = 1 | (12) |
 | (13) |
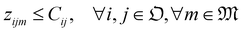 | (14) |
 | (15) |
 | (16) |
 | (17) |
 | (18) |
 | (19) |
 | (20) |
 | (21) |
 used in constraints45 can be estimated as
used in constraints45 can be estimated as | (22) |
 | (23) |
 | (24) |
 | (25) |
It is worthwhile to discuss alternatives of treating laboratory constraints. A computationally equivalent treatment of work shifts is to introduce pre-scheduled “placeholder” operations that occupy gaps between work shifts. While the capacity constraint can be modeled by splitting multi-capacity modules into multiple single-capacity modules, this increases the size of  , thus increases the number of all constraints indexed by m. This is expected to be less computationally efficient than introducing capacity constraints explicitly as in (13). Feasible solutions that comply with lag time constraints can be selected from a set of potential solutions (e.g., the heuristic method by Aarts et al.18), however, it is more computationally efficient to encode these as linear constraints than to select solutions from a less constrained problem in linear programming.
, thus increases the number of all constraints indexed by m. This is expected to be less computationally efficient than introducing capacity constraints explicitly as in (13). Feasible solutions that comply with lag time constraints can be selected from a set of potential solutions (e.g., the heuristic method by Aarts et al.18), however, it is more computationally efficient to encode these as linear constraints than to select solutions from a less constrained problem in linear programming.
2.3 Case study construction
 ,
,  , and
, and  , respectively.
, respectively.
Without loss of generality, we define a fixed set of operation types. For each reaction, an operation graph is constructed by the following steps:
(1) For each solid reactant or reagent, create a  operation for solution preparation;
operation for solution preparation;
(2) For each liquid reactant or reagent, create a  operation for its addition to reaction vessel;
operation for its addition to reaction vessel;
(3) Create a  operation based on the recommended temperature condition of this reaction;
operation based on the recommended temperature condition of this reaction;
(4) Create a  operation for the product mixture.
operation for the product mixture.
Each operation is assigned a unique operation type that can be processed by one or more functional modules. The current list of operation types is shown in Table S1† along with the rules to estimate their processing times. Ordinary precedence relations are added according to the order in the above steps. Specifically, the  operation precedes all
operation precedes all  and
and  operations, and
operations, and  operations for liquid reactant/reagent are preceded by
operations for liquid reactant/reagent are preceded by  operations for solution additions. If a reaction does not include solid reactant/reagent, the
operations for solution additions. If a reaction does not include solid reactant/reagent, the  operation of solvent addition precedes all other
operation of solvent addition precedes all other  operations. Additionally, a maximum lag time constraint is added between each
operations. Additionally, a maximum lag time constraint is added between each  and the
and the  operation to model expiration of stock solutions. A minimum lag time constraint is also added between the
operation to model expiration of stock solutions. A minimum lag time constraint is also added between the  operation and the
operation and the  operation to model the cooling process. Work shift constraints, if included in the formulation, are applied to all operations. The duration of a shift is set as 1.5 × the longest processing time with a gap between shifts set to half the duration of a shift.
operation to model the cooling process. Work shift constraints, if included in the formulation, are applied to all operations. The duration of a shift is set as 1.5 × the longest processing time with a gap between shifts set to half the duration of a shift.
 operations in the same bin are compatible and can be processed on the same heater concurrently if the heater has a capacity higher than one.
operations in the same bin are compatible and can be processed on the same heater concurrently if the heater has a capacity higher than one.
2.4 Baseline scheduler
A heuristic algorithm, as described in Algorithm 1, is implemented to provide baseline schedules for comparison.47 This algorithm approximates optimal schedules by scheduling operations one-by-one in a greedy fashion that considers arbitrarily given precedence relations, operation-to-module assignments, module capacity, and minimum lag time by identifying the operation with the earliest possible end time in each iteration. Schedulers using only greedy iterations, however, may produce solutions that violate maximum lag time constraints. Inspired by Aarts et al.,18 our baseline scheduler constructs feasible solutions by first identifying a reaction sequence that complies with the precedence relations defined in synthetic routes. This sequence is identified by, starting from a zero-precedent reaction, selecting the next reaction which has the fewest unscheduled precedents and does not depend on the last visited reaction. The algorithm further assumes an operation sequence for each reaction by adding artificial precedence relations among operations from the same reaction. This assumption allows adjusting the start times of all operations of a reaction by adding a delay to the first operation of this reaction, and, with a sufficiently large delay, the operations of this reaction can be made temporally close. Since maximum lag time constraints are only defined within a reaction in our case studies, this assumption aids in generating schedules complying with such constraints. We note while the baseline scheduler empirically produces schedules that comply with all constraints for our case studies, it does not guarantee compliance with maximum lag time constraints in general.2.5 Implementation
The scheduling problem is represented by a (version 2.7.4) schema,48 for which an interactive visualization module is developed in
(version 2.7.4) schema,48 for which an interactive visualization module is developed in  (version 1.0.1).49 Sample screenshots of the interface are shown in Fig. S2 and S3.† The MILP solver is implemented using
(version 1.0.1).49 Sample screenshots of the interface are shown in Fig. S2 and S3.† The MILP solver is implemented using  (version 11.0.2) through its
(version 11.0.2) through its  API.50 A thread limit of 12 is imposed for the MILP solver. A time limit of three wall hours is imposed for all scheduling instances. Empirically, we find the primal simplex method often outperforms others for MILP root relaxations in our formulation.
API.50 A thread limit of 12 is imposed for the MILP solver. A time limit of three wall hours is imposed for all scheduling instances. Empirically, we find the primal simplex method often outperforms others for MILP root relaxations in our formulation.
2.6 Chemical libraries
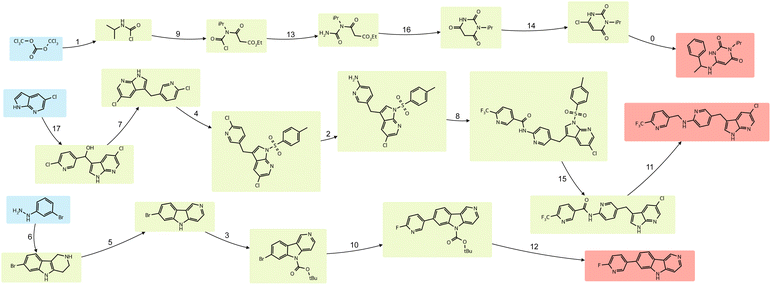
Target compounds from the following compound sets are used to build chemical libraries in case studies:(1) VS-35: a set of 35 previously synthesized compounds from a screening campaign for cannabinoid receptors.40
(2) FDA-20: a set of 20 compounds from FDA-approved drug lists from 2019 to 2022.41
Subsets of VS-35 or FDA-20 are used as test libraries. These test libraries are grouped by the number of target chemicals, indicated by the suffix of the group name. Each group contains ten test libraries constructed by random sampling, e.g., group VS.05 denotes the group of ten randomly selected 5-target libraries that are subsets of VS-35. The parameters of these libraries are summarized in Table S3.†
3 Results and discussion
3.1 Overall results of case studies
is used to evaluate the MILP scheduler. Fig. 4 shows the percentage makespan gap distributions between the baseline schedule and the optimal MILP schedule for all libraries grouped by the number of target chemicals (the groups are listed in Section S3†). Note only optimal schedules are included in Fig. 4 and not all scheduling instances converged to an optimal solution due to the 3 hours scheduler time limit (Section 2.5), as a result, several library groups have fewer than ten percentage gap values shown in Fig. 4; the full set of results including suboptimal MILP schedules can be found in the project repository. The makespan of the optimal MILP schedule tends to be shorter than that of baseline schedule, with a few exceptions for very small libraries (number of targets ≤ 2) where the gap is negligible. This is not surprising as the solution space of small libraries is also small.
For scheduling instances where the MILP scheduler found an optimal schedule (363 instances shown in Fig. 4), the percentage gap ranges from 0% to 57.8% with an average of 20.5%. For instances where at least one feasible solution is found (686 instances including 363 optimal schedules and 323 suboptimal schedules), the average percentage gap becomes 9.8%. The reduction in the average percentage gap is mainly due to 14 of 323 of suboptimal schedules having makespan values higher than baseline schedules, i.e., the percentage gaps are negative for these instances. In general, the percentage gap tends to be larger for larger libraries, which is expected as larger operation graphs tend to have more degrees of freedom and provide greater opportunity for efficient scheduling. Another observation from Fig. 4 is that optimal schedules are hard to find for schedules on LAB-1 compared to LAB-2, e.g., the imbalance of different markers in Fig. 4C and D. Note the only difference between LAB-1 and LAB-2 is the heater modules in the latter have a higher capacity than those in the former.
To seek insights on how to improve heuristic algorithms, we investigate the differences between baseline and optimal MILP schedules are investigated through two metrics. The assignment difference, referring to the operation-to-module assignment, is calculated as the percentage of operations assigned to different modules between two schedules. The sequence difference is the normalized Levenshtein distances between two operation sequences of the same module from two schedules and averaged over all modules. We note that sequence difference is more sensitive than assignment difference, as operation sequences can change on modules without altering the operation-to-module assignment, but the reverse is not true. Fig. S4† shows the makespan gap between baseline and optimal MILP schedules along with corresponding assignment/sequence difference values. The values of assignment difference range from 0 to 25.5%, with 95% of them being lower than 21.5%, indicating the baseline schedule is not very far away from the optimal schedule in terms of operation-to-module assignment even for large libraries. In contrast, the operation sequences on modules from baseline and optimal schedules can differ significantly, as indicated by the high sequence difference values (averaged at 0.43, or 0.53 when libraries of size 1 and 2 are excluded) especially for large libraries. For very small libraries, a strong correlation between assignment and sequence differences is observed, which is weakened and eventually vanishes as the number of targets (library size) increases. These results suggest that the current baseline scheduler can approximate optimal operation-to-module assignments but struggles with approximating optimal operation sequences.
3.2 Illustration of representative schedules
The optimal schedule of FDA.03.09 on LAB-1 produced by the MILP scheduler is shown in Fig. 6A. Compared to its heuristic counterpart (Fig. 6B), the optimal schedule differs in both operation-to-module assignment and processing order (operation sequence) on individual modules. Both schedules follow the precedence relations defined by the three independent routes in Fig. 5. They also share the same initial operations (both start with operations of reaction #1 and #17). However, they differ in terms of the absolute order of reactions (global precedence relations). For example, in the optimal schedule, reaction #9 is scheduled after #7, whereas in the baseline schedule, it precedes #7. As expected, the module utilization is higher for all modules using the optimal schedule. The percentage gap between the two solutions depends on the functional modules. For instance, when this library is scheduled on LAB-2 with other parameters unchanged, the makespan gap increases to 41.2%.
 | ||
| Fig. 6 Comparison of (A) the optimal and (B) the baseline schedules for FDA.03.09 scheduled on LAB-1 with a percentage gap of 51.3%. “H” and “W” represent heaters and workup stations, respectively. Only heaters and workup stations are shown, as the operation duration on these modules is significantly longer than others. Black numerical indices above colored bars are reaction indices indicating to which reaction the process belong. Bars are colored based on the corresponding operations' final target chemicals. The same operation can have different processing time on different functional modules, see Section S2.1† for more details about processing time estimation. | ||
4 Conclusion
In this study, the problem of scheduling chemical library synthesis is formalized as a generalized FJSP. A MILP formulation is proposed to consider common laboratory constraints including lag time, module capacity, and work shifts. Two scheduling algorithms, a greedy heuristic (baseline scheduler) and a MILP formulation, are evaluated for their ability to minimize the total makespan (duration) of a library synthesis campaign. To test the proposed schedulers, 720 scheduling instances are built from hypothetical synthetic routes to realistically accessible chemical libraries involving 3 to 63 reaction steps, or 20 to 402 operations. Within the 3 hours wall time limit, the MILP scheduler is able to produce optimal and suboptimal schedules for 363 and 323 scheduling instances, respectively, leaving 34 instances for which no feasible solution can be found. Compared to the baseline schedules, the optimal MILP schedules show makespan reductions ranging from 0% (very small libraries) to 58% (large libraries) with an average of 20%. We find that the baseline schedule can approximate optimal operation-to-module assignments but fails to approximate optimal operation sequences. Two illustrative case studies show that optimal schedules greatly reduce makespan and improve module utilization for synthesis campaigns of both linear routes and tree routes compared to baseline schedules.There are still opportunities to improve chemical library synthesis scheduling. The current implementation of the MILP formulation suffers from its high time complexity and is thus not ideal for large libraries. An approximation of this formulation with lower time complexity could also enable dynamic scheduling to adapt real-time changes during a synthesis campaign. Additionally, both schedulers require reliable time estimate and pre-planned batches, which could be difficult in real library synthesis scenarios, such as those with large uncertainties in yield. This limitation means that operations with a dynamic end point, such as reaction whose end points are determined by color change, cannot be scheduled. These results provide open-source tools for improving synthesis efficiency and, as a standalone module, could be integrated into automated chemistry platforms in the future.
Data availability
All code and data included in this study are available in the project GitHub repository (https://github.com/qai222/libsyn_tools).Author contributions
Qianxiang Ai: methodology, software, formal analysis, writing – original draft. Fanwang Meng: methodology, software, writing – review & editing. Runzhong Wang: methodology, software, writing – review & editing. J. Cullen Klein: methodology, writing – review & editing. Alexander G. Godfrey: methodology, writing – review & editing, project administration. Connor W. Coley: conceptualization, writing – review & editing, supervision, funding acquisition, project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Research reported in this publication was supported by the National Institutes of Health under award number U18TR004149. This research was supported in part by the Intramural/Extramural research program of the National Center for Advancing Translational Sciences, the National Institutes of Health. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.References
- R. W. Wagner, F. Li, H. Du and J. S. Lindsey, Investigation of Cocatalysis Conditions Using an Automated Microscale Multireactor Workstation: Synthesis of meso-Tetramesitylporphyrin, Org. Process Res. Dev., 1999, 3, 28–37 CrossRef CAS.
- R. B. Merrifield and J. M. Stewart, Automated Peptide Synthesis, Nature, 1965, 207, 522–523 CrossRef CAS PubMed.
- K. Machida, Y. Hirose, S. Fuse, T. Sugawara and T. Takahashi, Development and application of a solution-phase automated synthesizer, ‘ChemKonzert’, Chem. Pharm. Bull., 2010, 58, 87–93 CrossRef CAS PubMed.
- A. Weber, E. Von Roedern and H. U. Stilz, SynCar: an approach to automated synthesis, J. Comb. Chem., 2005, 7, 178–184 CrossRef CAS PubMed.
- T. Jiang, S. Bordi, A. E. McMillan, K.-Y. Chen, F. Saito, P. L. Nichols, B. M. Wanner and J. W. Bode, An integrated console for capsule-based, automated organic synthesis, Chem. Sci., 2021, 12, 6977–6982 RSC.
- S. Steiner, J. Wolf, S. Glatzel, A. Andreou, J. M. Granda, G. Keenan, T. Hinkley, G. Aragon-Camarasa, P. J. Kitson, D. Angelone and L. Cronin, Organic synthesis in a modular robotic system driven by a chemical programming language, Science, 2019, 363, eaav2211 CrossRef CAS PubMed.
- N. Collins, D. Stout, J.-P. Lim, J. P. Malerich, J. D. White, P. B. Madrid, M. Latendresse, D. Krieger, J. Szeto and V.-A. Vu, others Fully automated chemical synthesis: toward the universal synthesizer, Org. Process Res. Dev., 2020, 24, 2064–2077 CrossRef CAS.
- S. Chatterjee, M. Guidi, P. H. Seeberger and K. Gilmore, Automated radial synthesis of organic molecules, Nature, 2020, 579, 379–384 CrossRef CAS PubMed.
- V. Fasano, R. C. Mykura, J. M. Fordham, J. J. Rogers, B. Banecki, A. Noble and V. K. Aggarwal, Automated stereocontrolled assembly-line synthesis of organic molecules, Nat. Synth., 2022, 1, 902–907 CrossRef CAS.
- G. Wang, H. T. Ang, S. R. Dubbaka, P. O'Neill and J. Wu, Multistep automated synthesis of pharmaceuticals, Trends Chem., 2023, 5, 432–445 CrossRef CAS.
- B. A. Koscher, et al., Autonomous, multiproperty-driven molecular discovery: From predictions to measurements and back, Science, 2023, 382, eadi1407 CrossRef CAS PubMed.
- F. Strieth-Kalthoff, et al., Delocalized, asynchronous, closed-loop discovery of organic laser emitters, Science, 2024, 384, eadk9227 CrossRef CAS PubMed.
- W. Gao, P. Raghavan and C. W. Coley, Autonomous platforms for data-driven organic synthesis, Nat. Commun., 2022, 13, 1075 CrossRef CAS PubMed.
- R. Vescovi, T. Ginsburg, K. Hippe, D. Ozgulbas, C. Stone, A. Stroka, R. Butler, B. Blaiszik, T. Brettin and K. Chard, others Towards a modular architecture for science factories, Digital Discovery, 2023, 2, 1980–1998 RSC.
- J. S. Lindsey, L. A. Corkan, D. Erb and G. J. Powers, Robotic work station for microscale synthetic chemistry: On-line absorption spectroscopy, quantitative automated thin-layer chromatography, and multiple reactions in parallel, Rev. Sci. Instrum., 1988, 59, 940–950 CrossRef.
- L. Andrew Corkan and J. S. Lindsey, Experiment manager software for an automated chemistry workstation, including a scheduler for parallel experimentation, Chemom. Intell. Lab. Syst., 1992, 17, 47–74 CrossRef.
- H. Du, L. A. Corkan, K. Yang, P. Y. Kuo and J. S. Lindsey, An automated microscale chemistry workstation capable of parallel, adaptive experimentation, Chemom. Intell. Lab. Syst., 1999, 48, 181–203 CrossRef CAS.
- R. J. Aarts, J. S. Lindsey, L. A. Corkan and S. F. Smith, Flexible protocols improve parallel experimentation throughput, Clin. Chem., 1995, 41, 1004–1010 CrossRef CAS.
- W. S. You, B. J. Choi, H. Moon, J. C. Koo and H. R. Choi, Robotic laboratory automation platform based on mobile agents for clinical chemistry, Intell. Serv. Robot., 2017, 10, 347–362 CrossRef.
- R. B. Canty, Autonomous experimentation for molecular discovery applications, thesis, Massachusetts Institute of Technology, 2024.
- B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Wang, X. Li, B. M. Alston, B. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, A mobile robotic chemist, Nature, 2020, 583, 237–241 CrossRef CAS PubMed.
- N. F. Delaney, J. I. Rojas Echenique and C. J. C. Marx, An Open-Source Manager for Laboratory Automation, SLAS Technol., 2013, 18, 171–177 CrossRef PubMed.
- X. Gu, S. Neubert, N. Stoll and K. Thurow, Intelligent scheduling method for life science automation systems, 2016 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), 2016, pp 156–161 Search PubMed.
- C. Cabrera, M. Fine-Morris, M. Pokross, K. Kish, S. Michalczyk, M. Cahn, H. Klei and M. F. Russo, Dynamically Optimizing Experiment Schedules of a Laboratory Robot System with Simulated Annealing, SLAS Technol., 2014, 19, 517–527 CrossRef PubMed.
- T. D. Itoh, T. Horinouchi, H. Uchida, K. Takahashi and H. Ozaki, Optimal Scheduling for Laboratory Automation of Life Science Experiments with Time Constraints, SLAS Technol., 2021, 26, 650–659 CrossRef CAS PubMed.
- J. M. Pinto, M. Joly and L. F. L. Moro, Planning and scheduling models for refinery operations, Comput. Chem. Eng., 2000, 24, 2259–2276 CrossRef CAS.
- C. Chatzidoukas, S. Pistikopoulos and C. Kiparissides, A hierarchical optimization approach to optimal production scheduling in an industrial continuous olefin polymerization reactor, Macromol. React. Eng., 2009, 3, 36–46 CrossRef CAS.
- S. Wang, X. Wang, F. Chu and J. Yu, An energy-efficient two-stage hybrid flow shop scheduling problem in a glass production, Int. J. Prod. Res., 2020, 58, 2283–2314 CrossRef.
- C. T. Maravelias, General framework and modeling approach classification for chemical production scheduling, AIChE J., 2012, 58, 1812–1828 CrossRef CAS , _eprint: https://onlinelibrary.wiley.com/doi/pdf/10.1002/aic.13801.
- P. Brucker and R. Schlie, Job-shop scheduling with multi-purpose machines, Computing, 1990, 45, 369–375 CrossRef.
- M. R. Garey, D. S. Johnson and R. Sethi, The Complexity of Flowshop and Jobshop Scheduling, Math. Oper. Res., 1976, 1, 117–129 CrossRef.
- Y. N. Sotskov, The complexity of shop-scheduling problems with two or three jobs, Eur. J. Oper. Res., 1991, 53, 326–336 CrossRef.
- R. Alvarez-Valdés, A. Fuertes, J. M. Tamarit, G. Giménez and R. Ramos, A heuristic to schedule flexible job-shop in a glass factory, Eur. J. Oper. Res., 2005, 165, 525–534 CrossRef.
- G. Vilcot and J.-C. Billaut, A tabu search and a genetic algorithm for solving a bicriteria general job shop scheduling problem, Eur. J. Oper. Res., 2008, 190, 398–411 CrossRef.
- E. G. Birgin, P. Feofiloff, C. G. Fernandes, E. L. De Melo, M. T. Oshiro and D. P. Ronconi, A MILP model for an extended version of the flexible job shop problem, Optim. Lett., 2014, 8, 1417–1431 CrossRef.
- G. A. Kasapidis, D. C. Paraskevopoulos, P. P. Repoussis and C. D. Tarantilis, Flexible Job Shop Scheduling Problems with Arbitrary Precedence Graphs, Prod. Oper. Manag., 2021, 30, 4044–4068 CrossRef.
- P. J. Pawar and K. C. Bhosale, Flexible Job Shop Scheduling for Press Working Industries with Operation Precedence Constraint, Process Integr. Optim. Sustain., 2022, 6, 409–430 CrossRef.
- R. Braune and K. F. Doerner, Real-world flexible resource profile scheduling with multiple criteria: learning scalarization functions for MIP and heuristic approaches, J. Oper. Res. Soc., 2017, 68, 952–972, DOI:10.1057/s41274-017-0239-y.
- V. Boyer, J. Vallikavungal, X. C. Rodríguez and M. A. Salazar-Aguilar, The generalized flexible job shop scheduling problem, Comput. Ind. Eng., 2021, 160, 107542 CrossRef.
- A. A. Sadybekov, A. V. Sadybekov, Y. Liu, C. Iliopoulos-Tsoutsouvas, X.-P. Huang, J. Pickett, B. Houser, N. Patel, N. K. Tran and F. Tong, others Synthon-based ligand discovery in virtual libraries of over 11 billion compounds, Nature, 2022, 601, 452–459 CrossRef CAS PubMed.
- Food and Drug Administration, Drug Approvals and Databases, 2024, https://www.fda.gov/drugs/development-approval-process-drugs/drug-approvals-and-databases Search PubMed.
- ASKCOS, 2024, original-date: 2024-30-12, https://gitlab.com/mlpds_mit/askcosv2 Search PubMed.
- J. C. Fromer and C. W. Coley, An algorithmic framework for synthetic cost-aware decision making in molecular design, Nat. Comput. Sci., 2024, 4, 440–450 CrossRef PubMed.
- E. Kondili, C. C. Pantelides and R. W. Sargent, A general algorithm for short-term scheduling of batch operations—I. MILP formulation, Comput. Chem. Eng., 1993, 17, 211–227 CrossRef.
- F. S. Hillier and G. J. Lieberman, Introduction to operations research, McGraw-Hill, 2015 Search PubMed.
- J. C. Fromer and C. W. Coley, An algorithmic framework for synthetic cost-aware decision making in molecular design, Nat. Comput. Sci., 2024, 1–11 Search PubMed.
- R. Wang, Z. Hua, G. Liu, J. Zhang, J. Yan, F. Qi, S. Yang, J. Zhou and X. Yang, A bi-level framework for learning to solve combinatorial optimization on graphs, Adv. Neural Inf. Process. Syst., 2021, 34, 21453–21466 Search PubMed.
- S. Colvin pydantic: Data validation using Python type hints. https://github.com/pydantic/pydantic.
- Team <cytoscape@plotly.com>, T. P. dash-cytoscape, A Component Library for Dash aimed at facilitating network visualization in Python, wrapped around Cytoscape.js. https://dash.plotly.com/cytoscape.
- Gurobi Optimization, LLC, Gurobi Optimizer Reference Manual, 2024, https://www.gurobi.com.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00327f |
| ‡ Authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |





![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)