 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Digital features of chemical elements extracted from local geometries in crystal structures†
Andrij
Vasylenko
 a,
Dmytro
Antypov
a,
Dmytro
Antypov
 a,
Sven
Schewe
a,
Sven
Schewe
 b,
Luke M.
Daniels
b,
Luke M.
Daniels
 a,
John B.
Claridge
a,
Matthew S.
Dyer
a,
John B.
Claridge
a,
Matthew S.
Dyer
 a and
Matthew J.
Rosseinsky
a and
Matthew J.
Rosseinsky
 *a
*a
aDepartment of Chemistry, University of Liverpool, Crown Street, L69 7ZD, UK. E-mail: rossein@liverpool.ac.uk
bDepartment of Computer Science, University of Liverpool, Ashton Building, L69 3DR, UK
First published on 3rd January 2025
Abstract
Computational modelling of materials using machine learning (ML) and historical data has become integral to materials research across physical sciences. The accuracy of predictions for material properties using computational modelling is strongly affected by the choice of the numerical representation that describes a material's composition, crystal structure and constituent chemical elements. Structure, both extended and local, has a controlling effect on properties, but often only the composition of a candidate material is available. However, existing elemental and compositional descriptors lack direct access to structural insights such as the coordination geometry of an element. In this study, we introduce Local Environment-induced Atomic Features (LEAFs), which incorporate information about the statistically preferred local coordination geometry at an element in a crystal structure into descriptors for chemical elements, enabling the modelling of materials solely as compositions without requiring knowledge of their crystal structure. In the crystal structure of a material, each atomic site can be quantitatively described by similarity to common local structural motifs; by aggregating these unique features of similarity from the experimentally verified crystal structures of inorganic materials, LEAFs formulate a set of descriptors for chemical elements and compositions. The direct connection of LEAFs to the local coordination geometry enables the analysis of ML model property predictions, linking compositions to the underlying structure–property relationships. We demonstrate the versatility of LEAFs in structure-informed property predictions for compositions, mapping of chemical space in structural terms, and prioritisation of elemental substitutions. Based on the latter for predicting crystal structures of binary ionic compounds, LEAFs achieve the state-of-the-art accuracy of 86%. These results suggest that the structurally informed description of chemical elements and compositions developed in this work can effectively guide synthetic efforts in discovering new materials.
Introduction
The approaches to description of chemical elements, ranging from historical methods like Döbereiner's Triads, Newlands' Octaves, and Mendeleev's periodic table to modern variations of the Pettifor scale, depending on the criteria employed, offer various insights into relationships between elements and their roles in chemical reactions and compound formation.1–6 More recently, elemental descriptors have evolved into multi-dimensional spaces,7–13 advancing computational modelling of connections between elements, their properties, and the materials they constitute. Detailed numerical descriptions of chemical elements facilitate addressing critical materials science challenges: developing metrics for mapping chemical space,14–21 modelling composition–structure–property relationships22–31 and materials discovery, including through design by similarity.32–40 Quantification of similarity between chemical elements arises from elemental descriptors and drives atomic substitution-based design for novel materials at scale.35,39–41 Incorporating structural insights into representation of chemical elements38 and compounds42 can significantly enhance the efficiency of materials modelling. Materials structure, defined by (i) compositional content, (ii) atomic coordination – interatomic distances, (iii) atomic positions in a unit cell – angles between central atoms and their coordinations, determines stability and properties of materials. Crystal structure is critical for evaluating novel candidates for materials discovery, yet establishing the relationship between candidate chemical composition and optimal structure is a recognised challenge.43–46 The most expressive materials descriptors require crystal structure information as input,47,48 and hence do not afford modelling of materials with unresolved crystal structures solely as compositions. The state-of-the-art elemental descriptors incorporate various aspects of the material structure, such as compositional content (Atom2Vec), atom connectivity in crystal graph (MEGNet, SkipAtom), and implicit structural information learnt through machine learning of scientific literature (Mat2Vec, MatScholar), however, none of the available elemental descriptors offers direct and explicit access to the geometric aspects of materials structure.In this study, we explore a novel approach to explicitly incorporate geometrical local structural information for describing chemical elements and materials compositions, resulting in the creation of Local Environment-induced Atomic Features (LEAFs). The LEAFs maintain a direct and explicit relationship between chemical elements and preferred structural characteristics such as atomic coordination and local structure motifs and we demonstrate how this direct connection can help explain machine learning models for materials property predictions. We further employ this link to address other structure-induced challenges in materials science such as derivation of a metric for mapping chemical space in structural terms, and selecting elemental substitutions for novel materials design.
In the LEAFs approach, we hypothesise that atomic properties, and hence their descriptors, can be deduced from the nature of their local structure environments in crystalline inorganic compounds. To produce LEAFs, we collect statistics of the variations in the local geometries for chemical elements in crystal structures; this element-wise statistics can then be used as the unique identifiers of chemical elements in materials modelling. The determination of these descriptors hinges upon the definition of locality and atomic neighbourhood in coordination environment (CN),49 where each atomic site in a crystal structure of a material can be described in terms of its similarity to the common structural motifs. The atomic site is first described by the interatomic distance-based algorithm for finding CN,34,50 which performs well among other algorithms for near-neighbour finding;51 then for each CN, the geometrical arrangements of the neighbouring atoms can determine similarity to one of the common motifs, e.g., whether a CN2 arrangement is linear or water-like, a CN4 arrangement is tetrahedral or square planar, etc., up to CN12 (Fig. S1 and S2†). Quantification of the similarity between the local structure motifs is performed by comparing interior and dihedral angles for each atomic site in a local structure and the 37 selected common structural motifs presented in ref. 50, using the angle-based similarity metrics34,50 (ESI, eqn (1) and (2)†). Thus, each atomic site can be represented with a set of 37 numbers, each determining similarity to one of the 37 common motifs; this set of numbers is further used as the atomic site's unique vector identifier. In Fig. 1, for the example of a Mg atom in MgO, the local structure environment is compared to the CN6 structural motifs. Concatenation (denoted as ‖ in Fig. 1) of the similarity values s(CN) to all common motifs within different CNs produces a Mg-site identifier in MgO – vector a(Mg | MgO); in this particular vector, for all but three coordination environments in CN6, s = 0.
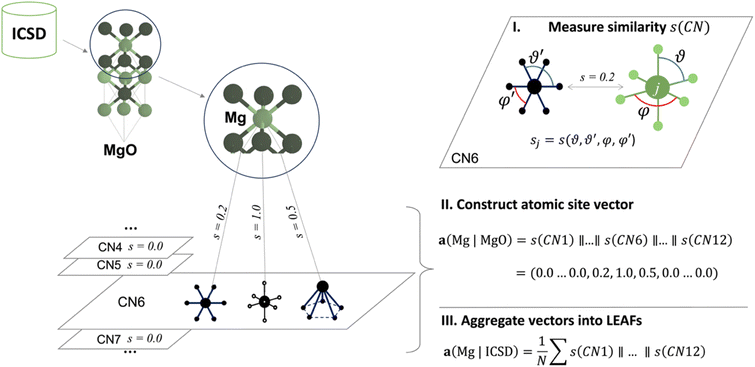 | ||
| Fig. 1 Schematic calculation of local environment-induced atomic features (LEAFs). Similarities of the atomic local structure environments in crystal structures are calculated for the common structural motifs50 within different coordination numbers (CNs), using angle-based similarity metrics.34,41 For the example of the six-coordinate Mg atom in MgO, similarities, s, is zero (s = 0.0) to all common motifs, except for the three structural motifs in CN6: hexagonal (s = 0.2), octahedral (s = 1), and pentagon pyramidal (s = 0.5) motifs. Concatenation (symbol ‖) of the similarity values for all structural motifs in all considered CNs produces a local environment vector for an atom in a crystal structure, e.g., for Mg in MgO, a(Mg | MgO). Collecting these vectors for the 86 most common chemical elements in the crystal structures reported in Inorganic Crystal Structure Database (ICSD),42 and averaging them over the corresponding occurrences, N, of each element produces a set of LEAFs for chemical elements. | ||
Using this approach, we examine the local structure environments for all atomic sites of the 86 most common chemical elements across the experimentally studied materials reported in the Inorganic Crystal Structure Database (ICSD).52 For each element, the 37 similarity values were collated for all individual atomic sites containing that element across all considered structures. The mean was then taken for each of the 37 coordination environments, resulting in 37 values which form a vector-descriptor for that element, e.g., a(Mg | ICSD) in Fig. 1. Carrying out this procedure for all 86 elements produces the LEAFs.
Similarity of chemical elements, compositions and crystal structures
Numerical representation of chemical elements and compositions determine the quality and efficiency of computational modelling of materials. We study the LEAFs' ability to represent chemical elements in comparison to nine other popular elemental descriptors7,9–12,33 and include random representation as a baseline. Using these descriptors, chemical elements can be vectorised and compared via cosine similarity (Fig. S5†). Similarity between elements X, X′ can be associated with the degree of probability of elemental substitution in a chemical compound while retaining its crystal structure: | (1) |
We employ the test for predicting crystal structures of binary compounds proposed in ref. 53 to compare the efficacy of the elemental descriptors. For this test, 494 binary ionic solids reported in Materials Project (MP) were selected, in which metals were excluded to focus on heteropolar bonding and polymorphs were represented with only lowest energy compositions, resulting into a final set of 100 AB ionic solids, matching four structure types: CN8 CsCl (4 compositions), CN6 rock-salt (67 compositions), CN4 zinc blende (20 compositions) and CN4 wurtzite (9 compositions), using labels from Materials Project.54 The uneven distribution of structure types in this dataset impedes evaluation of model performance through accuracy in imbalanced classification tasks.55 To address this, we computed the Matthews correlation coefficient (MCC)56 providing a more balanced evaluation of performance for all elemental characteristics studied in ref. 53. In this task, where for each composition in the test set the structure type is predicted based on the most likely substitution, according to eqn (1), into the remaining 99 compositions in the test set, using the original classifier in ref. 53, LEAFs increase the best values achieved to date (Table 1).
| Features | Origin of descriptors | Acc., % | MCC |
|---|---|---|---|
| LEAFs | Local coordination geometry in ICSD | 86 | 0.72 |
| MatScholar9 | ML-derived from literature | 81 | 0.63 |
| Mat2Vec10 | ML-derived from literature | 80 | 0.60 |
| Atom2Vec13 | ML-derived from compositional content | 79 | 0.59 |
| GNoME40 | Prediction of elemental substitution based on frequency of elements occupying the same atomic sites in GNoME | 79 | 0.58 |
| Magpie7 | Elemental physical characteristics | 78 | 0.54 |
| Oliynyk8 | Elemental physical characteristics | 75 | 0.50 |
| MEGNet11 | ML-derived from atom, bond and graph attributes in MP | 73 | 0.45 |
| SkipAtom12 | ML-derived from atom connectivity graphs in MP | 68 | 0.35 |
| Random | Random numbers | 58 | 0.22 |
| Hautier33 | Prediction of elemental substitution based on frequency of elements occupying the same atomic sites in ICSD | 54 | 0.28 |
The enhanced crystal structure classification suggests LEAFs' capability to capture chemical trends. To illustrate this, we plot t-distributed Stochastic Neighbour Embedding (t-SNE) maps of LEAFs representations for chemical elements Fig. 2a. Noteworthy trends include clustering of the elements belonging to the same group of the periodic table (colour-coding) or to specific families, such as halogens, chalcogens, metals, metalloids, and noble gases (symbols); the size of the markers corresponds to the atomic number.
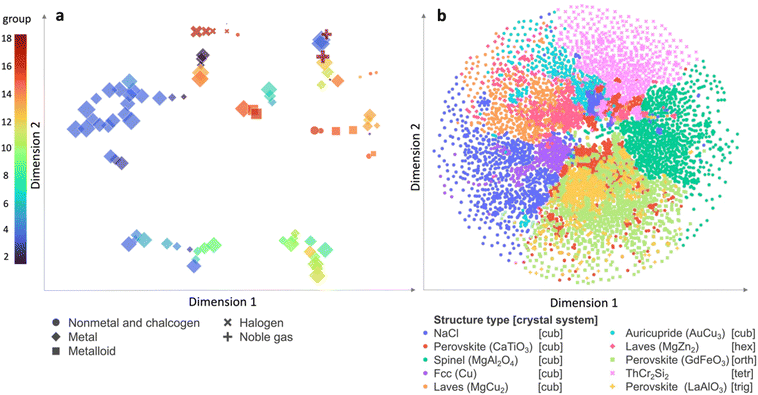 | ||
| Fig. 2 The LEAF representation reveals chemical trends for the elements (a) and for compositions in ICSD (b). (a) t-Distributed Stochastic Neighbour Embedding (t-SNE) map of elements reveal chemical trends: elements belonging to specific families, such as halogens, chalcogens, metals, metalloids, and noble gases (symbols) and different periodic table groups (colour-coding) cluster together; the marker size denotes atomic number; (b) compositions forming the ten most populous structure types in ICSD52 are represented with LEAFs as in eqn (2) and plotted in two principal dimensions of the t-SNE map, displaying clustering patterns based on structure type and crystal system: Cu-like structure type within the fcc system (purple circles), the perovskite (LaAlO3) structure type within the trigonal system (mustard crosses), and the Laves (MgZn2) structure type within the hexagonal system (raspberry diamonds) the ThCr2Si2 structure type in the tetragonal system (pink crosses) and the rock-salt structure type (blue circles) each occupy distinctive areas of the map. The observed patterns suggest that distance in multi-dimensional LEAFs can be used for structural comparison of compositions and design by similarity. | ||
In contrast to the random number descriptors (Fig. S7†), elemental descriptors based on physical and chemical elemental characteristics,7,8 and data-derived vectors9–12 can effectively organise chemical elements,48 offering insights specific to their properties. In the case of LEAFs, the observed grouping of elements based on their local environments implies similarities in element-specific local structures across experimentally realised inorganic materials: similarity of 3d and 4f elements, Li, Mg and 3d metals, Ca, Y and 4f metals, etc. (Fig. S5†).
These qualitative insights into chemical similarity arising from purely geometrical description of local coordination align with the observations derived with ML of local structural topology.38 Furthermore, to confirm the LEAFs' ability to recognise chemical patterns beyond elemental grouping, we represent chemical compositions in ICSD as vectors, by summing the weighted elemental LEAFs according to stoichiometry in a chemical formula, e.g., Li0.375P0.125O0.5 can be represented with a vector:
| aLi0.375P0.125O0.5 = 0.375aLi + 0.125aP + 0.5aO, | (2) |
The t-SNE map of the subset of the ten most common structure types in ICSD with compositions represented with LEAFs as in eqn (2) illustrates the organisational patterns of structure types and crystal systems (Fig. 2b). Notably, distinct densely packed clusters representing various structure types are evident: using notations from ICSD, the clusters include the Cu-like structure type within the fcc system (depicted by purple circles), the perovskite (LaAlO3) structure type within the trigonal system (represented by mustard crosses), and the Laves (MgZn2) structure type within the hexagonal system (depicted by raspberry diamonds). Broader distributions, such as the ThCr2Si2 (CeGa2Al2, BaAl4) structure type in the tetragonal system (marked by pink crosses) and the rock-salt structure type (represented by blue circles) are observed, each occupying distinctive areas of the map. Less represented structure types, omitted in Fig. 2b for clarity, also demonstrate clustering in analogous t-SNE maps, built with LEAFs (Fig. S8†). The observed patterns indicate that the multi-dimensional space distance defined by LEAFs, which can be measured, for example, as Euclidean, Wasserstein or other metric distance between compositions represented with LEAFs, can be a metric for structurally-informed comparison between materials defined only by their composition (eqn (S3†)), complementing other efforts for effective mapping of chemical space.15–17,19–21,57
Connecting properties with structural insights for materials compositions
LEAFs' potential for representing materials compositions in structural terms can be used in predicting materials properties and uncovering the relationships between the properties and local structure environments in materials, described solely by their compositions. We illustrate this in classification of the Li-ion conducting materials by ionic conductivity, which is reported to strongly depend on the local structural coordination of lithium.58,59 In a prior study,60 403 compositions with reported conductivity at room temperature were vectorised via literature-derived elemental descriptors mat2vec,10 and classified into two conductivity classes (below and above σ = 10−4 S cm−1) using a neural-network-based model (CrabNet61), achieving an average accuracy of 81% and MCC of 0.47 over 5-fold cross-validation (Table 2). The underlying elemental descriptors learnt via ML approaches strongly inhibit interpretability of the arising composition–property relationships.62 In contrast, LEAFs structural insights can emphasise the critical aspects of atomic coordination environments in materials' structures that correlate with their properties, such as ionic conductivity. The importance of various structural aspects can be highlighted through feature selection by using LEAFs with methods such as random forest63 or neural networks with feature sparsity.64 The random forest model with LEAFs demonstrates the same average classification accuracy for ionic conductivity of 81% achieved above and MCC of 0.62; by calculating the information entropy gain when selecting different features. In order to highlight the features specific separately to ions of lithium and other species, we expand the compositional representation eqn (2) with concatenation of LEAFs for lithium and a sum of cations, resulting in vectors of double the length, e.g., Li7La3Zr2O12 can be represented as| aLi0.291(6)La0.125Zr0.83(3)O0.5 ∼ 0.292aLi ‖ (0.125aLa + 0.833aZr), | (3) |
| Elemental descriptors | Compositional representation | Model | Accuracy, % | MCC |
|---|---|---|---|---|
| Subset (T = 300 K): 403 entries | ||||
| LEAFs | Eqn (2) | Random forest | 81 | 0.62 |
| LEAFs | Eqn (4) | CrabNet | 81 | 0.60 |
| Mat2Vec | Eqn (2) | CrabNet | 81 | 0.47 |
| LEAFs | Eqn (3) | Random forest | 75 | 0.47 |
| LEAFs | Lithium only | Random forest | 72 | 0.42 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||
| Full dataset (all T): 756 entries | ||||
| LEAFs | Eqn (4) | CrabNet | 77 | 0.52 |
| Mat2Vec | Eqn (2) | CrabNet | 70 | 0.47 |
 | ||
| Fig. 3 Importance of structural environments for classifying materials' ionic conductivity. (a) Structural insights from LEAFs can highlight the local motifs that influence materials properties predictions: feature importance can be calculated using random forest model in supervised classification, considering conductivity of chemical compositions in Li-ion database.60 Inset illustrates the contribution of all local structure environments in comparison to equal contribution (dashed line). (b) In Li-conducting materials, there is a wide distribution of Li local structure environments, demonstrating the absence of a specific preferred Li coordination associated with high Li-ion conductivity. | ||
This may be explained through the feature importance, according to which the majority of top-contributing features are associated with lithium: 29 out of 34 above the equal, uniform contribution line in Fig. 3a, and nine out of top ten. This is consistent with 72% accuracy (MCC, 0.42) achieved for classification of Li-ion-conductivity, based on compositional representation solely with lithium content, i.e., Li7La3Zr2O12 is represented as 0.292aLi, according to fractional Li content. We analyse the crystal structures in the Li-ion conductors database in terms of the similarity of the Li atom sites to the top nine local structure motifs, rendered important for conductivity classification in Fig. 3a. The diverse array of Li site local structure environments in Li-conducting materials (Fig. 3b and S9†) challenges the notion of a specific Li coordination determining Li-ion conductivity, including the widely discussed tetrahedral coordination, as suggested in the literature.58,59 This observation underscores the significance of considering the collective influence of various local environments of the constituent atoms on materials properties.65
Furthermore, LEAFs can be integrated with neural network-based models for predicting properties of materials represented only as compositions, which instead of using a generic set of descriptors for every task, can learn elemental descriptors specific to predicting a particular property of materials from the local structure environments (Fig. 4). This alignment can be achieved through coupling and end-to-end training of the integrated models.29 To implement this, we utilise multi-hot encoding to represent the full information regarding elemental local environments across material structures in ICSD in a format easily interpretable by machine learning algorithms. One-hot encoding can represent real values by discretising continuous range values into predefined bins, where only one bin (hot) is set to 1, and the position of this bin indicates the value, for example, numbers 0.0, 0.5 and 1.0 can be represented as strings (1 0 0), (0 1 0) and (0 0 1), respectively, in the 3-bit one-hot encoding scheme. Similarly, we can represent each of the considered common motifs and each individual similarity value, s, ranging from 0.001 to 1, with three digits of precision as 1000-bit vectors. We note that the exact vector length does not appear to have a major effect on the results and re-doing the experiment with 100-bit vectors yielded similar results. In the considered example of the MgO crystal (Fig. 4a), the similarities of Mg in the octahedral environment to the CN6 motifs, s = 0.2, 0.5, 1, can be represented as 1000-bit binary vectors with 1s in positions 200, 500, and 1000, respectively; for the other 34 motifs, the Mg atom in MgO has similarity s = 0, and hence the corresponding binary vectors will have 1s in the first positions. Concatenating these binary vectors for all 37 motifs results in a sparse 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-bit multi-hot vector with exactly 37 1s in the corresponding positions, encoding the similarity values of Mg in MgO. This representation also affords encoding of those materials where an atom is found in more than one coordination environment; such materials are represented with binary vectors with more than one bit set to 1. We then use the binary vector to collect all occurring similarity values for Mg local environments in all Mg-containing materials reported in ICSD and populate the bins in the corresponding positions with 1s. Doing this for all chemical elements, we encode each element as a 37
000-bit multi-hot vector with exactly 37 1s in the corresponding positions, encoding the similarity values of Mg in MgO. This representation also affords encoding of those materials where an atom is found in more than one coordination environment; such materials are represented with binary vectors with more than one bit set to 1. We then use the binary vector to collect all occurring similarity values for Mg local environments in all Mg-containing materials reported in ICSD and populate the bins in the corresponding positions with 1s. Doing this for all chemical elements, we encode each element as a 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-bit binary string, where 0s denote the absence and 1s the presence of a similarity value to one of the motifs within the corresponding local environment in ICSD. We illustrate this matrix of local elemental environments conceptually by black and white pixels, representing ones and zeros, respectively for the subsets of elements and their similarities to local environments in Fig. 4d and S1–S3,† where more detail is given. The full matrix of local elemental environments is 37
000-bit binary string, where 0s denote the absence and 1s the presence of a similarity value to one of the motifs within the corresponding local environment in ICSD. We illustrate this matrix of local elemental environments conceptually by black and white pixels, representing ones and zeros, respectively for the subsets of elements and their similarities to local environments in Fig. 4d and S1–S3,† where more detail is given. The full matrix of local elemental environments is 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 columns of binary strings by 86 rows of considered elements. This matrix is then pruned to remove all-zero columns and used as a source for nonlinear learning of LEAFs, e.g., with an unsupervised autoencoder12,28,29,38,67 (Fig. S4†), and for integration with the supervised models utilising property-specific elemental descriptors in a variety of downstream tasks for materials property prediction. Such integration can be performed as follows:
000 columns of binary strings by 86 rows of considered elements. This matrix is then pruned to remove all-zero columns and used as a source for nonlinear learning of LEAFs, e.g., with an unsupervised autoencoder12,28,29,38,67 (Fig. S4†), and for integration with the supervised models utilising property-specific elemental descriptors in a variety of downstream tasks for materials property prediction. Such integration can be performed as follows:
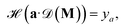 | (4) |
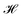 acts on the input of a compositional vector a and the local environments matrix M = (mij)86×21706, connected via a dense layer
acts on the input of a compositional vector a and the local environments matrix M = (mij)86×21706, connected via a dense layer 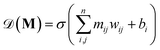 with ReLU activation function68σ, kernel weights wij and biases bi, to predict a property ya. For the considered example of classification of the Li-ion conducting materials ionic conductivity, integration of CrabNet with LEAFs as in eqn (4) results in an equivalent average accuracy of 81% and an increased MCC of 0.60 over 5-fold cross-validation in comparison to the original results of CrabNet used with mat2vec.
with ReLU activation function68σ, kernel weights wij and biases bi, to predict a property ya. For the considered example of classification of the Li-ion conducting materials ionic conductivity, integration of CrabNet with LEAFs as in eqn (4) results in an equivalent average accuracy of 81% and an increased MCC of 0.60 over 5-fold cross-validation in comparison to the original results of CrabNet used with mat2vec.
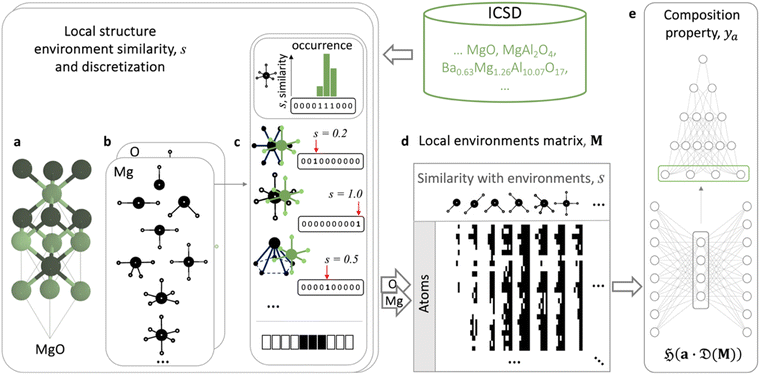 | ||
Fig. 4 Schematic learning of local environment-induced atomic features (LEAFs) aligned with prediction of properties of materials represented solely by their compositions. Similarities of the local structure environments of the atomic sites in a crystal structure, exemplified by MgO (a), to the 37 selected common structural motifs50 (b) are calculated for the atomic sites for experimentally verified structures reported in ICSD. (c) For the example of the six-coordinated Mg octahedral environment in MgO, compared to planar hexagonal (similarity, s = 0.2), octahedral (s = 1), and pentagon pyramidal (s = 0.5) motifs, these similarity values, s, are discretised into a thousand bins spanning from 0.001 to 1, illustrated as 10-digit binary strings for Mg example in (c) for simplicity. Such discretisation and subsequent concatenation of the binary strings for all 37 structural motifs form 37![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000-long vectors of 0s and 1s, denoting the absence or presence of the degrees of similarity to the particular motifs in ICSD for considered chemical elements. The matrix of elemental local environments, M, is represented schematically as black (for ones) and white (for zeros) pixels in (d). Its dimensionality reduction by a single hidden layer neural-network autoencoder, 000-long vectors of 0s and 1s, denoting the absence or presence of the degrees of similarity to the particular motifs in ICSD for considered chemical elements. The matrix of elemental local environments, M, is represented schematically as black (for ones) and white (for zeros) pixels in (d). Its dimensionality reduction by a single hidden layer neural-network autoencoder,  to produce structure-induced elemental vectors, a, is trained end-to-end with a neural network, to produce structure-induced elemental vectors, a, is trained end-to-end with a neural network,  (e.g., CrabNet,61 plotted schematically with NN-SVG66) for prediction materials properties, ya (e). (e.g., CrabNet,61 plotted schematically with NN-SVG66) for prediction materials properties, ya (e). | ||
Notably, such integration trained on the full dataset of 756 entries of conducting materials reported at all temperatures, achieves a higher accuracy of 77% and MCC of 0.53 in comparison to the 70% accuracy and MCC of 0.37 achieved with CrabNet with mat2vec (Table 2), demonstrating enhanced robustness of the proposed approach to noise in the data arising from label ambiguity as the same compounds may have multiple conductivity entries at different temperatures. By employing the integration in eqn (4) to train the models for other properties datasets such as dielectric, elasticity, formation energy, energy band gap, etc.,69 LEAFs demonstrate a comparable performance with the state-of-the-art models for compositions (Table 3), while offering a route for improved interpretability through connection to the prevalent structural features affecting the properties.
| Data set | Number of samples | CrabNet Mat2Vec | CrabNet LEAFs |
|---|---|---|---|
| Mean absolute error | |||
| Perovskites form. energy (eV per unit cell) | 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 928 928 |
0.3473 | 0.3495 |
| Dielectric (unitless) | 4764 | 0.4439 | 0.4254 |
| Elasticity G_VRH (log10(GPa)) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 987 987 |
0.0994 | 0.0973 |
| Elasticity K_VRH (log10(GPa)) | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 987 987 |
0.0741 | 0.0761 |
| JARVIS exfoliation energy (meV per atom) | 636 | 49.8551 | 52.8234 |
| Experimental band gap (eV) | 4604 | 0.3463 | 0.343 |
Conclusion
LEAFs describe chemical elements in terms of the local structural motifs that are likely to form in crystalline inorganic solids. Learning atoms from crystal structures deepens our understanding of the chemical elements and their role in the composition–structure–property relationships. In practical terms, incorporating structural geometry into elemental descriptors enhances modelling of materials described solely as compositions and elucidates the role of particular atomic coordination geometries in determining materials properties. The LEAFs improvement over the state-of-the-art results is especially clear in tasks that are strongly correlated with structural information. In the structure-type classification, based on quantifying elemental similarity and likelihood of elemental substitution, LEAFs increase the state-of-the-art accuracy by 5% and improve the balance of multi-class assignment, as judged by MCC, by 0.09. This suggests the best practice for the popular materials design by substitution, where due to high-throughput approaches, a few per cent change in accuracy can result in thousands of new materials candidates. To facilitate this use of LEAFs, we provide an easy-to-use software tool with simple commands for (1) measuring structure-induced similarity between materials (e.g., reported and hypothetical) described solely by their compositions, and (2) prediction of the most likely elemental substitution to retain structural stability for exploring novel materials. In contrast to other modern multi-dimensional descriptors, machine learnt from literature or materials data, which enable materials property modelling in many tests with accuracy comparable to LEAFs', LEAFs retain the direct links to structural motifs, enabling analysis of the elemental coordination environments underpinning composition–property relationships, e.g., through feature selection, thus making a step towards interpretable results of machine learning of materials. Complemented by the higher robustness to label noise for predicting material properties reported at different temperatures, as demonstrated for the example of Li-ion conductivity data, LEAFs will motivate integration of the proposed structural insights with elemental descriptors focused on other non-structural chemical aspects to further enhance materials modelling.Data availability
The data used in this study is available at https://www.github.com/lrcfmd/LEAF; release (https://doi.org/10.5281/zenodo.14524731).Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the UK Engineering and Physical Sciences Research Council (EPSRC) for funding through grant number EP/V026887.References
- J. W. Döbereiner, Ann. Phys., 1829, 91, 301–307 CrossRef.
- C. Hugh, ‘Newlands, John Alexander Reina’ Encyclopædia Britannica, Cambridge University Press, 11th edn, 1911, vol. 19 Search PubMed.
- D. Mendeleev, J. Chem. Soc., 1871, 3, 25–56 Search PubMed.
- E. R. Scerri, ChemTexts, 2021, 8, 6 CrossRef.
- D. G. Pettifor, Solid State Commun., 1984, 51, 31–34 CrossRef CAS.
- H. Glawe, A. Sanna, E. K. U. Gross and M. A. L. Marques, New J. Phys., 2016, 18, 093011 CrossRef.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2, 16028 CrossRef.
- A. O. Oliynyk, E. Antono, T. D. Sparks, L. Ghadbeigi, M. W. Gaultois, B. Meredig and A. Mar, Chem. Mater., 2016, 28, 7324–7331 CrossRef CAS.
- L. Weston, V. Tshitoyan, J. Dagdelen, O. Kononova, A. Trewartha, K. A. Persson, G. Ceder and A. Jain, J. Chem. Inf. Model., 2019, 59, 3692–3702 CrossRef CAS PubMed.
- V. Tshitoyan, J. Dagdelen, L. Weston, A. Dunn, Z. Rong, O. Kononova, K. A. Persson, G. Ceder and A. Jain, Nature, 2019, 571, 95–98 CrossRef CAS PubMed.
- C. Chen, W. Ye, Y. Zuo, C. Zheng and S. P. Ong, Chem. Mater., 2019, 31, 3564–3572 CrossRef CAS.
- L. M. Antunes, R. Grau-Crespo and K. T. Butler, npj Comput. Mater., 2022, 8, 1–9 CrossRef.
- Q. Zhou, P. Tang, S. Liu, J. Pan, Q. Yan and S.-C. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6411–E6417 CAS.
- N. Nikolova and J. Jaworska, QSAR Comb. Sci., 2003, 22, 1006–1026 CrossRef.
- A. Lin, D. Horvath, V. Afonina, G. Marcou, J.-L. Reymond and A. Varnek, ChemMedChem, 2018, 13, 540–554 CrossRef CAS PubMed.
- C. J. Hargreaves, M. S. Dyer, M. W. Gaultois, V. A. Kurlin and M. J. Rosseinsky, Chem. Mater., 2020, 32, 10610–10620 CrossRef CAS.
- Y. Liu, C. Mathis, M. D. Bajczyk, S. M. Marshall, L. Wilbraham and L. Cronin, Sci. Adv., 2021, 7, eabj2465 CrossRef CAS PubMed.
- J. Yao, Z. Zhang, D. Wang, K. Huang, W. Yang, L. Sun, R. Xie and N. Pradhan, Chem. Mater., 2023, 35, 8745–8757 CrossRef CAS.
- J. Hu, S. Stefanov, Y. Song, S. S. Omee, S.-Y. Louis, E. M. D. Siriwardane, Y. Zhao and L. Wei, npj Comput. Mater., 2022, 8, 1–12 CrossRef.
- R.-Z. Zhang, S. Seth and J. Cumby, Digit. Discov., 2023, 2, 81–90 RSC.
- D. Schwalbe-Koda, D. E. Widdowson, T. A. Pham and V. A. Kurlin, Digit. Discov., 2023, 2, 1911–1924 Search PubMed.
- D. Jha, L. Ward, A. Paul, W. Liao, A. Choudhary, C. Wolverton and A. Agrawal, Sci. Rep., 2018, 8, 17593 CrossRef PubMed.
- Y. Li, R. Dong, W. Yang and J. Hu, Comput. Mater. Sci., 2021, 198, 110686 CrossRef CAS.
- A. Ihalage and Y. Hao, Adv. Sci., 2022, 9, 2200164 CrossRef PubMed.
- K. Choudhary and B. DeCost, npj Comput. Mater., 2021, 7, 1–8 CrossRef.
- T. Xie and J. C. Grossman, Phys. Rev. Lett., 2018, 120, 145301 CrossRef CAS PubMed.
- P.-P. D. Breuck, M. L. Evans and G.-M. Rignanese, J. Phys.: Condens. Matter, 2021, 33, 404002 CrossRef PubMed.
- A. Vasylenko, J. Gamon, B. B. Duff, V. V. Gusev, L. M. Daniels, M. Zanella, J. F. Shin, P. M. Sharp, A. Morscher, R. Chen, A. R. Neale, L. J. Hardwick, J. B. Claridge, F. Blanc, M. W. Gaultois, M. S. Dyer and M. J. Rosseinsky, Nat. Commun., 2021, 12, 5561 CrossRef PubMed.
- A. Vasylenko, D. Antypov, V. V. Gusev, M. W. Gaultois, M. S. Dyer and M. J. Rosseinsky, npj Comput. Mater., 2023, 9, 1–10 CrossRef.
- H. R. Banjade, S. Hauri, S. Zhang, F. Ricci, W. Gong, G. Hautier, S. Vucetic and Q. Yan, Sci. Adv., 2021, 7, eabf1754 CrossRef CAS PubMed.
- L. Ward, R. Liu, A. Krishna, V. I. Hegde, A. Agrawal, A. Choudhary and C. Wolverton, Phys. Rev. B, 2017, 96, 024104 CrossRef.
- S. Curtarolo, G. L. W. Hart, M. B. Nardelli, N. Mingo, S. Sanvito and O. Levy, Nat. Mater., 2013, 12, 191–201 CrossRef CAS PubMed.
- G. Hautier, C. Fischer, V. Ehrlacher, A. Jain and G. Ceder, Inorg. Chem., 2011, 50, 656–663 CrossRef CAS PubMed.
- L. Ward, A. Dunn, A. Faghaninia, N. E. R. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom, M. Dylla, K. Chard, M. Asta, K. A. Persson, G. J. Snyder, I. Foster and A. Jain, Comput. Mater. Sci., 2018, 152, 60–69 CrossRef.
- D. W. Davies, K. T. Butler, J. M. Skelton, C. Xie, A. R. Oganov and A. Walsh, Chem. Sci., 2018, 9, 1022–1030 RSC.
- S. Luo, B. Xing, M. Faizan, J. Xie, K. Zhou, R. Zhao, T. Li, X. Wang, Y. Fu, X. He, J. Lv and L. Zhang, J. Phys. Chem. A, 2022, 126, 4300–4312 CrossRef CAS PubMed.
- H.-C. Wang, S. Botti and M. A. L. Marques, npj Comput. Mater., 2021, 7, 1–9 CrossRef.
- K. Ryan, J. Lengyel and M. Shatruk, J. Am. Chem. Soc., 2018, 140, 10158–10168 CrossRef PubMed.
- A. D. Sendek, E. D. Cubuk, E. R. Antoniuk, G. Cheon, Y. Cui and E. J. Reed, Chem. Mater., 2019, 31, 342–352 CrossRef CAS.
- A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85 CrossRef CAS PubMed.
- M. Kusaba, C. Liu and R. Yoshida, Comput. Mater. Sci., 2022, 211, 111496 CrossRef CAS.
- E. Jaffal, S. Lee, D. Shiryaev, A. Vtorov, N. Barua, H. Kleinke and A. Oliynyk, ChemRxiv, 2024 DOI:10.26434/chemrxiv-2024-rrbhc.
- A. R. Oganov, C. J. Pickard, Q. Zhu and R. J. Needs, Nat. Rev. Mater., 2019, 4, 331–348 CrossRef.
- C. Collins, M. S. Dyer, M. J. Pitcher, G. F. S. Whitehead, M. Zanella, P. Mandal, J. B. Claridge, G. R. Darling and M. J. Rosseinsky, Nature, 2017, 546, 280–284 CrossRef CAS PubMed.
- C. J. Pickard and R. J. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
- J. M. Wynn, P. V. C. Medeiros, A. Vasylenko, J. Sloan, D. Quigley and A. J. Morris, Phys. Rev. Mater., 2017, 1, 073001 CrossRef.
- A. P. Bartók, R. Kondor and G. Csányi, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184115 CrossRef.
- H. Huo and M. Rupp, Int. J. Sci. Math. Technol. Learn., 2022, 3, 045017 Search PubMed.
- D. Waroquiers, X. Gonze, G.-M. Rignanese, C. Welker-Nieuwoudt, F. Rosowski, M. Göbel, S. Schenk, P. Degelmann, R. André, R. Glaum and G. Hautier, Chem. Mater., 2017, 29, 8346–8360 CrossRef CAS.
- N. E. R. Zimmermann and A. Jain, RSC Adv., 2020, 10, 6063–6081 RSC.
- H. Pan, A. M. Ganose, M. Horton, M. Aykol, K. A. Persson, N. E. R. Zimmermann and A. Jain, Inorg. Chem., 2021, 60, 1590–1603 CrossRef CAS PubMed.
- D. Zagorac, H. Müller, S. Ruehl, J. Zagorac and S. Rehme, J. Appl. Crystallogr., 2019, 52, 918–925 CrossRef CAS PubMed.
- A. Onwuli, A. V. Hegde, K. V. T. Nguyen, K. T. Butler and A. Walsh, Element similarity in high-dimensional materials representations, Digit. Discov., 2023, 2, 1558–1564 RSC.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- D. Chicco and G. Jurman, BMC Genomics, 2020, 21, 6 CrossRef PubMed.
- J. P. Guilford, Psychometric Methods, McGraw-Hill, New York, NY, US, 2nd edn, 1954 Search PubMed.
- H. Park, A. Onwuli, K. T. Butler and A. Walsh, ChemRxiv, 2024 DOI:10.26434/chemrxiv-2024-zwkjc.
- R. D. Armstrong, R. S. Bulmer and T. Dickinson, J. Solid State Chem., 1973, 8, 219–228 CrossRef CAS.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- C. J. Hargreaves, M. W. Gaultois, L. M. Daniels, E. J. Watts, V. A. Kurlin, M. Moran, Y. Dang, R. Morris, A. Morscher, K. Thompson, M. A. Wright, B.-E. Prasad, F. Blanc, C. M. Collins, C. A. Crawford, B. B. Duff, J. Evans, J. Gamon, G. Han, B. T. Leube, H. Niu, A. J. Perez, A. Robinson, O. Rogan, P. M. Sharp, E. Shoko, M. Sonni, W. J. Thomas, A. Vasylenko, L. Wang, M. J. Rosseinsky and M. S. Dyer, npj Comput. Mater., 2023, 9, 1–14 CrossRef.
- A. Y.-T. Wang, S. K. Kauwe, R. J. Murdock and T. D. Sparks, npj Comput. Mater., 2021, 7, 1–10 CrossRef.
- J. Schrier, A. J. Norquist, T. Buonassisi and J. Brgoch, J. Am. Chem. Soc., 2023, 145, 21699–21716 CrossRef CAS PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- I. Lemhadri, F. Ruan and R. Tibshirani, in Proceedings of The 24th International Conference on Artificial Intelligence and Statistics, PMLR, 2021, pp. 10–18 Search PubMed.
- G. Han, A. Vasylenko, L. M. Daniels, C. M. Collins, L. Corti, R. Chen, H. Niu, T. D. Manning, D. Antypov, M. S. Dyer, J. Lim, M. Zanella, M. Sonni, M. Bahri, H. Jo, Y. Dang, C. M. Robertson, F. Blanc, L. J. Hardwick, N. D. Browning, J. B. Claridge and M. J. Rosseinsky, Science, 2024, 383, 739–745 CrossRef CAS PubMed.
- A. LeNail, J. Open Source Softw., 2019, 4, 747 CrossRef.
- D. E. Rumelhart, G. E. Hinton and R. J. Williams, in Parallel Distributed Processing: Explorations In The Microstructure Of Cognition, Vol. 1: Foundations, MIT Press, Cambridge, MA, USA, 1986, pp. 318–362 Search PubMed.
- A. F. Agarap, arXiv, 2018, preprint, arXiv:1803.08375, DOI:10.48550/arXiv.1803.08375.
- A. Dunn, Q. Wang, A. Ganose, D. Dopp and A. Jain, npj Comput. Mater., 2020, 6, 1–10 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Details of the data processing, similarity calculations for local structure environments and their discretisation; elemental similarity using LEAFs and LEAFs' distance for comparison of compositions; details of LEAFs' performance in crystal structure prediction – confusion matrices are available at https://www.github.com/lrcfmd/LEAF. See DOI: https://doi.org/10.1039/d4dd00346b |
| This journal is © The Royal Society of Chemistry 2025 |
