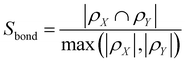A simple similarity metric for comparing synthetic routes

Abstract

Experimentally validated routes to synthetic compounds can be compared to each other by quantitative metrics (step count, yield, atom economy), or by qualitative assessments (strategy, novelty). AI-predicted routes are typically compared to experimental syntheses to check for an exact match among the top-ranked predictions (top-N accuracy). This method is ideal for the evaluation of retrosynthetic algorithms on large datasets (>10⁶ routes), but it cannot assess a degree of similarity between routes, which would be desirable for small datasets (<10² routes). Here, we present a simple method to calculate a similarity score between any two synthetic routes to a given molecule. The score is based on two concepts: which bonds are formed during the synthesis; and how the atoms of the final compound are grouped together throughout the synthesis. As a result, the similarity score overlaps well with chemists' intuition and provides a finer assessment of prediction accuracy.

---

Introduction

In the field of organic synthesis, molecules are synthesized in a stepwise fashion, starting with simple and commercially available building blocks and then carrying out chemical reactions to forge the desired bonds (and break undesired bonds) until the target molecule is in hand. The set of steps used to construct a molecule is known as the synthetic route. Due to the immense size of synthetically accessible chemical space (estimated to encompass >10²⁰ compounds for molecules with ≤36 heavy atoms)¹ and the large number of known chemical reactions,² a given target molecule could theoretically have tens of thousands of plausible routes. Indeed, retrosynthesis algorithms, which predict synthetic routes by iterating backwards from the target molecule until commercial starting materials are achieved, are quite capable of generating >10⁴ routes and are usually explicitly programmed to output a more human-manageable number. In actual practice, even the most intensively studied molecules have on the order of a hundred reported routes.‡

How does a chemist compare one route to another? If both routes in question have been experimentally validated, then a set of practical concerns dominate the comparison: overall yield; cost of goods; and the safety and environmental sustainability of the overall process are all common metrics. This method may establish which route is the most efficient, but it is not well suited to addressing theoretical routes. When assessing theoretical routes, step count, complexity scores, and feasibility predictions can provide rank ordering. This approach is used by AI tools like AiZynthFinder and ASKCOS to present a small set of prioritised routes to the chemist for expert assessment.^3,4 Routes can also be clustered by Tree Edit Distance (TED), which we currently use for AiZynthFinder output.^5,6 This method is best suited to avoiding degeneracy, which arises from the algorithm selecting different versions of the same synthon. Another method is the Retro-BLEU score, which was introduced to estimate the overlap of the predicted sequences of reactions in a route with known sequences of reactions. However, such an approach is naturally limited by the availability of known sequences of reactions.⁷ Finally, when comparing one experimental route with multiple predicted routes, top-N accuracy is routinely used, with the experimental route considered as ground truth.⁸ A relaxed version of this has been suggested, where only the starting material overlap between the predicted route and the experimental route is taken into account.⁹

A more qualitative method of route comparison can be found in the field of total synthesis. Here, complex natural products are obtained in laboratory syntheses, often necessitating numerous steps and the development of new chemistry. When comparing routes to natural products, it is common to consider the “key step(s)” or “strategy” of the routes: which bond-forming step(s) generated the most complexity or provided the most novelty?¹⁰ Cernak et al. have recently described a graph edit distance method to visualize and select the most direct retrosynthetic routes to target molecules; setting up the calculation requires some manual definitions beforehand.¹¹

We found the methods described above to be wanting for several desirable applications in drug discovery. In particular, we sought a similarity metric to compare the predicted routes of a given compound at point-of-design with its subsequent experimental route. Monitoring this score in aggregate for newly synthesized molecules would help to continuously assess the performance of AiZynthFinder. Furthermore, it could be a step on the way to “closing the loop,” on AI-proposed syntheses, making future predictions more accurate. Finally, it could replace our current clustering algorithm to ensure that chemists can quickly access a diverse selection of routes for their expert appraisal. An additional, more challenging goal was to approximate “key step” analysis such that the output concorded with chemist intuition.

Results and discussion

Defining similarity

Similarity calculation. We define the similarity of two routes using a combination of an atom similarity metric and a bond similarity metric. Both are based on atom-to-atom mapping between the reactants and product for each reaction in the route. We use the rxnmapper tool¹² for mapping each reaction in the routes, and we then ensure that the atom-mapping of the reaction forming the target is propagated to the subsequent reactions in the route. The atom similarity of a route is then computed by considering each molecule in the route as a set of atom-mapping numbers that also exists in the target compound:

m_R,i = {a₁, a₂,…,a_n}

where m_R,i is the i:th molecule in route R, and a₁, a₂, etc. are the atom-mapping numbers. We then define the overlap of two molecules in two routes X and Y as the intersection of the two sets of atom-mapping numbers divided by the size of the largest set:

The atom similarity, S_atom is then computed by summing the maximum overlap for each molecule in a route, doing this for both route X and Y, and then normalizing by the total number of molecules (N) in both routes:

It should be noted that the target compound is excluded from these calculations as by definition we ensure that both instances of the target compound are atom-mapped identically.

The bond similarity of a route is based on an analysis of which bonds in the target compound are formed over the course of the route. In particular, we define a reaction as a set of bonds, b_ij:

r_R,i = {b_1,2, b_3,4,…,b_n,m}

where r_R,i is the i:th reaction in route R, and the bonds are atom tuples for which a bond exists in the target compounds between the two atoms and this bond is formed in the i:th reaction. A route ρ is then described as a set of all such bond sets and the bond overlap between route X and Y is computed as a normalized intersection:

ρ_R = {r_R,i|∀_i}

The total similarity is then computed as the geometric mean of the atom and bond similarity:

Benefits and limitations. One straightforward benefit of our algorithm is that it provides a score on a continuous axis from 0 to 1, thereby allowing a finer comparison of routes. For example, consider the experimental vs. the AI-proposed synthesis of benzimidazole 1 (Fig. 1), on which we have previously published.¹³ The key bond-forming strategy between the routes is clearly the same, but the experimental route makes use of a protecting group and a cheaper nitroaniline starting material 2, adding two steps. Out of 20 predicted routes for this compound provided by AiZynthFinder at point-of-design, none were an exact match to the experimental route, so this example would fail to match “ground truth” by even a very generous top-20 analysis. The similarity value provided by our algorithm between these two routes is 0.97, agreeing with chemist assessment.

Fig. 1 (A) Experimental route to benzimidazole 1, using nitroaniline 2 as a cheaper starting material and Boc-protected proline 4 to prevent side reactivity. (B) AiZynthFinder-predicted route to 1. The key cyclization step is the same and S_A,B = 0.97. TED_A,B = 5.25.

The combination of bond and atom similarity is a further advantage. S_bond is rooted in human practice, as numbering atoms and then keeping track of which bonds are formed over the course of a synthesis is a common exercise for students of organic chemistry. S_atom addresses step sequence, another fundamental consideration in the practice of organic synthesis. For example, routes A and B (Fig. 2) differ only in the order of steps. The bond forming events are the same, but intermediates 9 and 12 have different atoms, leading to an S_atom score of 0.90 and an overall S_A,B of 0.95.

Fig. 2 Three syntheses to make hypothetical pyrimidine 11 starting from 7. (A) Buchwald–Hartwig, S_NAr sequence. (B) S_NAr, Buchwald–Hartwig sequence. (C) Chan–Lam, S_NAr sequence. S_A,B = S_B,C = 0.95; S_A,C = 1.0. TED_A,B = 4.62; TED_B,C = 4.63; TED_A,C = 1.04.

There are several limitations that must be considered when using this similarity score. First, if rxnmapper fails to assign atom numberings correctly in any given reaction, then the score will be inaccurate.§ In the case of simple errors like failure to recognize hydroxide as the source of oxygen in an ester hydrolysis, this will not perturb the score greatly, but for larger errors like incorrectly mapped rearrangement reactions the effect is greater. Second, the S_atom component is calculated based on atom groupings but ignores connectivity. Third, stereochemistry is ignored altogether. A more subtle limitation is shared with other methods of comparing synthetic routes: namely, the concept of a “step” is underdefined. Multiple reactions are often carried out in a one-pot or telescoped fashion. Two routes that share the same fundamental transformations in the same sequence but report the individual steps differently will return a score less than unity (see ESI† for an example).

Beyond these “hard” limitations there are also limitations by design. As written, the similarity algorithm does not consider atoms that are absent in the final product. This approach is well suited to our specific interests in AI retrosynthesis and medicinal chemistry, in which synthons and overall strategy are more important than (for example) atom economy or choice of protecting group. Thus, routes A and C in Fig. 2 return S_A,C = 1, because the Buchwald–Hartwig and Chan–Lam couplings—although they would have different conditions, reagents, byproducts, and side products—form the same C–N bond at the same point in the synthesis. Modifying the algorithm to include atoms that are not present in the target could prove useful if comparing many, highly similar routes. Furthermore, the current code can only compare routes that terminate in the same final product; comparing routes to different final compounds for similarity of overall strategy will be the focus of future work.

Case studies

Atorvastatin. First, we sought to perform the similarity analysis on a pharmaceutically relevant molecule. Atorvastatin (14) is a natural choice as it regularly tops the annual list of most prescribed pharmaceuticals in the United States.¹⁴ Furthermore, Warner–Lambert chemists published multiple routes from both the original discovery syntheses and the subsequent development campaigns; we were interested to see if the similarity algorithm could distinguish between them.^15,16 Two medicinal chemistry routes and one patented process were compared (Fig. 3). The medicinal chemistry routes share many steps, including the synthesis of intermediate amino acid 16 and a decarboxylative [3 + 2] cyclization to form pyrroles 15 or 17; they differ in endgame. The process route is substantially different, with a Paal–Knorr cyclization between 18 and 19 to form the pyrrole and a more convergent synthesis overall. As expected, the medicinal chemistry routes were more similar to each other than to the process route (S_A,B = 0.88; S_A,C = 0.59; S_B,C = 0.62).

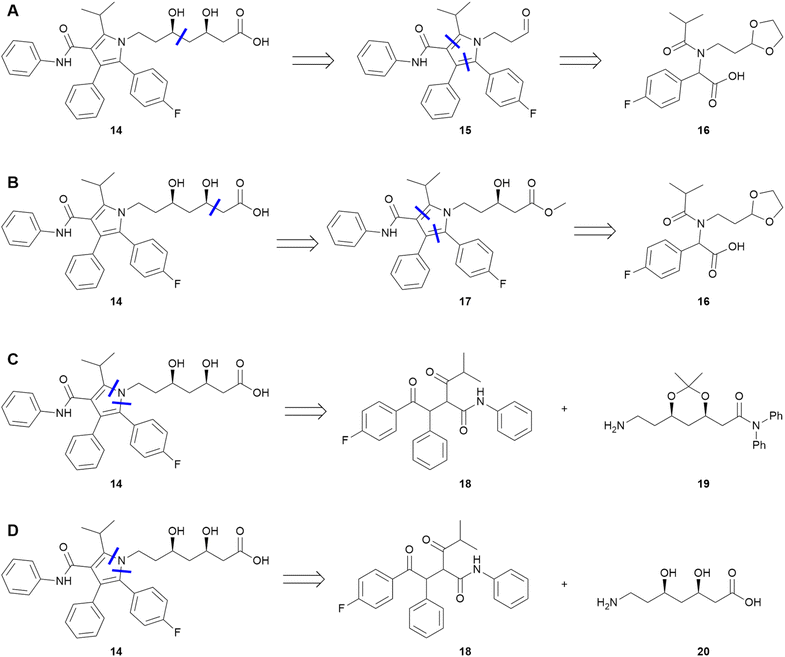Fig. 3 Select key steps and intermediates of the medicinal chemistry routes (A and B), process route (C), and AiZynthFinder route (D) to atorvastatin 14.

As a further test, we used AiZynthFinder to predict a retrosynthesis of atorvastatin.¶ The highest ranked predicted route was compared to the three experimental routes. Simple visual analysis of the key steps suggests high similarity to the process chemistry route: both routes employ a Knoevenagel condensation, a Stetter reaction, and a Paal–Knorr pyrrole cyclization, all in the same sequence (see ESI† for full routes). The similarity algorithm concurs, with S_C,D = 0.74 compared to scores less than 0.5 between both medicinal chemistry routes and the predicted route. It is worth noting that none of the AiZynthFinder results match any of the published routes exactly, demonstrating again that top-N analysis is not fit for small datasets.

In the ESI,† we compare the route similarities to TED. There is a good correlation for these four routes, but TED is unbounded and therefore harder to interpret than the similarity metric.

Strychnine. Following the successful application of the similarity score algorithm to atorvastatin, we sought a complex natural product to test the algorithm more rigorously. Strychnine (21) was selected as an ideal test case: it is highly complex yet has relatively few heavy atoms (twenty-five); it has numerous published total syntheses that nevertheless intercept one of only two penultimate intermediates (isostrychnine 22 or the Weiland-Gumlich aldehyde 23); and it is a longstanding target of interest and testing ground for novel synthetic strategies. We chose to compare the ten syntheses of strychnine reviewed by Overman in 2012: Woodward (1954), Overman (1993), Rawal (1994), Kuehne (1998), Vollhardt (2000), Martin (2001), Fukuyama (2004), Reissig (2010), Vanderwal (2011), and MacMillan (2011).^17–28 Kuehne's racemic synthesis (1993)²⁹ and a proposed biosynthesis of strychnine were also included,³⁰ for a total of twelve routes. Although some routes are racemic and others stereoselective for either (+)- or (−)-strychnine, we considered the final target to be identical for all routes.||

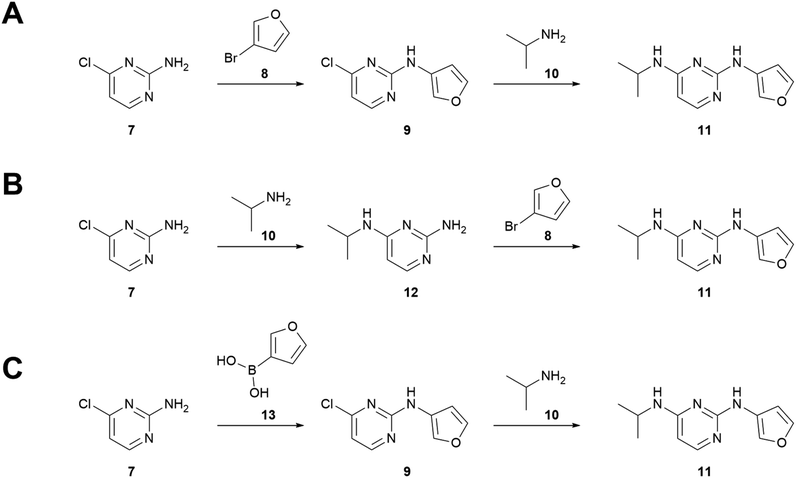
Before running the analysis, we predicted that the routes would split into two clusters based on their penultimate intermediate (Fig. 4). Beyond that, it seemed likely that the two Kuehne syntheses would give the highest similarity scores among all pairwise comparisons, as they intercept complex intermediate 26; and that the Woodward route, being the only exclusively linear sequence, would have the lowest similarity to all other routes. The Martin route is explicitly aimed at mimicking the biosynthesis of strychnos alkaloids via a geissoschizine-like intermediate (29), and we predicted that it would be most similar to the proposed biosynthetic pathway as a result.

Fig. 4 (A) The two penultimate intermediates used to make strychnine 21, isostrychnine 22 and Wieland-Gumlich aldehyde 23. (B) Kuehne's racemic synthesis begins with tryptamine 25 while the enantioselective synthesis begins with methyl L-tryptophanate 27. Both sequences intercept complex intermediate 26, then diverge again. (C) Biosynthetic intermediate geissoschizine 28 and Martin's similar intermediate 29.

These predictions were largely borne out. As expected, the Kuehne enantioselective and racemic syntheses provided the highest pairwise similarity score (0.91). The Woodward route was noticeably dissimilar to the others even by visual inspection using a heat map (Fig. 5), with all S_{Woodward,route} <0.6. The proposed biosynthesis of strychnine was indeed most similar to the Martin synthesis (0.74), although several other syntheses came close. One result highlighting limitations of the similarity algorithm is that the Vanderwal synthesis gave mostly high scores with all other routes, presumably as a consequence of its much lower step count than the others, as S_atom is normalized by number of molecules in both routes. Finally, our prediction that the twelve routes would cluster into two overall groups based on penultimate intermediate was inaccurate (see ESI†); presumably the interception of a very late-stage common intermediate is insignificant compared to the highly variable earlier intermediates across a small dataset.

Fig. 5 Heat map comparing similarity of the 12 routes to strychnine 21. See ESI† for numerical results.

The TED calculations for the twelve strychnine routes return distances that are consistently larger than 30, due to the longer routes. The correlation between the similarity metric and TED is also considerably weaker than in the case of atorvastatin, especially for more dissimilar routes (see ESI†).

Benchmarking predicted routes. The case studies described above gave us confidence to apply the similarity algorithm to large datasets. Previously, we have benchmarked retrosynthesis models and algorithms using both success rate (proportion of routes that terminate in commercial starting materials) and top-N accuracy.^31,32 Here, we extend this analysis by also computing the maximum similarity between a set of reference routes and the corresponding predictions from AiZynthFinder. A high success rate is a minimal requirement for useful retrosynthesis, but does not describe the quality of the routes. The top-N accuracy and the maximum similarity metric introduced here address this aspect of the evaluation. We started by comparing three one-step retrosynthesis models using the n1-set from the PaRoutes benchmark (Table 1; these are routes extracted from the US Patent and Trademark (USPTO) dataset). The models have been described previously and are derived from the USPTO dataset³² or two internal AstraZeneca datasets, one from 2019 (AZ-2019)³³ and one from 2022 (AZ-retrained).³¹ We can see that the success rate of the models vary from 92 to 97% and is not correlated with the N-accuracy. With our new, more refined method of comparing routes, we see that on average the predicted routes with the USPTO-PaRoutes and AZ-retrained are quite similar to the reference routes (0.91), whereas the old AZ-2019 model generates slightly less similar routes (0.85).

Table 1 Benchmarking of three retrosynthesis models on the PaRoutes-n1 dataset

Model	Success rate	Accuracy^a		Similarity
		Top-1	Top-10
a The fraction of targets for which we find the reference route as the first ranked prediction or among the top-10 ranked predictions.
USPTO-PaRoutes^32	97.2%	0.24	0.54	0.91
AZ-2019 (ref. 33)	91.6%	0.10	0.38	0.85
AZ-retrained^31	97.8%	0.11	0.44	0.91

---

We then performed a similar benchmark on 4934 routes extracted from the Journal of Medicinal Chemistry, which is likely a more relevant benchmark set for pharmaceutical applications than PaRoutes. In Table 2, we show the results when employing a stock consisting of only the starting materials in the experimental reference routes. For this benchmark set, the success rate ranges from 69% for USPTO-PaRoutes to 86% for AZ-retrained, although the top-N accuracies are all relatively low. When it comes to similarity, the AZ-retrained model outperforms the other models with an average of 0.84, which is significantly higher than 0.71 for the older AZ-2019 model and 0.75 for USPTO-PaRoutes. Thus we observe a clear effect of training a retrosynthesis model on a combination of literature, patent, and internal data when predicting routes for medicinal chemistry targets. Looking at the distribution of the maximum similarity (see ESI†), we see that for a majority of the targets, the similarity is very high, with only a few targets for which the predictions are far from the reference routes. In the ESI† we outline additional benchmarks of retrosynthesis predictions.

Table 2 Benchmarking of three retrosynthesis model on a dataset of 4934 targets from Journal of Medicinal Chemistry

Model	Success rate	Accuracy		Similarity
		Top-1	Top-10
USPTO-PaRoutes^32	68.6%	0.07	0.16	0.75
AZ-2019 (ref. 33)	72.1%	0.04	0.15	0.71
AZ-retrained^31	86.1%	0.07	0.24	0.84

---

Conclusions

We have presented a simple method for pairwise comparison of any set of routes to a given compound. For small datasets such as might be viewed by a synthetic chemist, it provides a suitably granular metric for route comparison. For large datasets of importance to data scientists, it provides an additional metric that supplements success rate and top-N accuracy. It is important to stress that the resulting similarity score is unrelated to feasibility, although we do speculate that if a theoretical route is similar to a proven experimental route, it is more likely to be feasible. Future research in this area will be to extend similarity comparison to routes for similar compounds, e.g. compounds that share a substructure but vary one portion of the molecule.

Data availability

Routes and processed versions of them for atorvastatin and strychnine, Reaxys IDs for reactions in J. Med. Chem. routes, as well as PaRoutes reference routes for targets also in J. Med. Chem. are available as ESI.† PaRoutes data and code can be downloaded from Github: https://github.com/MolecularAI/paroutes. Code for the route similarity metric is available on Github: https://github.com/MolecularAI/reaction_utils.

Author contributions

Conceptualization, investigation, writing – original draft, writing – review & editing: SG and JDS.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Thanks to Matthew Burns, Mikhail Kabeshov, Christos Kannas, and Per-Ola Norrby for helpful discussions.

Notes and references

1. P. Ertl, J. Chem. Inf. Comput. Sci., 2003, 43, 374–380.
2. S. Szymkuć, T. Badowski and B. A. Grzybowski, Angew. Chem., Int. Ed., 2021, 60, 26226–26232.
3. L. Saigiridharan, A. K. Hassen, H. Lai, P. Torren-Peraire, O. Engkvist and S. Genheden, J. Cheminf., 2024, 16, 57.
4. Y. Mo, Y. Guan, P. Verma, J. Guo, M. E. Fortunato, Z. Lu, C. W. Coley and K. F. Jensen, Chem. Sci., 2021, 12, 1469–1478.
5. S. Genheden, O. Engkvist and E. Bjerrum, J. Chem. Inf. Model., 2021, 61, 3899–3907.
6. S. Genheden, O. Engkvist and E. Bjerrum, Mach. Learn.: Sci. Technol., 2022, 3, 015018.
7. J. Li, L. Fang and J.-G. Lou, Digital Discovery, 2024, 3, 482–490.
8. P. Schwaller, R. Petraglia, V. Zullo, V. H. Nair, R. A. Haeuselmann, R. Pisoni, C. Bekas, A. Iuliano and T. Laino, Chem. Sci., 2020, 11, 3316–3325.
9. P. Torren-Peraire, A. K. Hassen, S. Genheden, J. Verhoeven, D.-A. Clevert, M. Preuss and I. V. Tetko, Digital Discovery, 2024, 3, 558–572.
10. E. J. Corey and X.-M. Cheng, The Logic of Chemical Synthesis, Wiley, 1989.
11. Y. Lin, R. Zhang, D. Wang and T. Cernak, Science, 2023, 379, 453–457.
12. P. Schwaller, B. Hoover, J.-L. Reymond, H. Strobelt and T. Laino, Sci. Adv., 2021, 7(15) DOI:10.1126/sciadv.abe4166.
13. J. D. Shields, R. Howells, G. Lamont, Y. Leilei, A. Madin, C. E. Reimann, H. Rezaei, T. Reuillon, B. Smith, C. Thomson, Y. Zheng and R. E. Ziegler, RSC Med. Chem., 2024, 15, 1085–1095.
14. S. P. Kane, ClinCalc DrugStats Database, Version 2024.01, https://clincalc.com/DrugStats, updated January 1, 2024, accessed July 23, 2024.
15. B. D. Roth, D. F. Ortwine, M. L. Hoefle, C. D. Stratton, D. R. Sliskovic, M. W. Wilson and R. S. Newton, J. Med. Chem., 1990, 33, 21–31.
16. D. E. Butler, T. V. Le and T. N. Nanninga, US Pat., US5298627A, 1993.
17. J. S. Cannon and L. E. Overman, Angew Chem. Int. Ed. Engl., 2012, 51, 4288–4311.
18. R. B. Woodward, M. P. Cava, W. D. Ollis, A. Hunger, H. U. Daeniker and K. Schenker, J. Am. Chem. Soc., 1954, 76, 4749–4751.
19. S. D. Knight, L. E. Overman and G. Pairaudeau, J. Am. Chem. Soc., 1993, 115, 9293–9294.
20. V. H. Rawal, C. Michoud and R. Monestel, J. Am. Chem. Soc., 1993, 115, 3030–3031.
21. V. H. Rawal and S. Iwasa, J. Org. Chem., 1994, 59, 2685–2686.
22. M. E. Kuehne and F. Xu, J. Org. Chem., 1997, 62, 7950–7960.
23. M. J. Eichberg, R. L. Dorta, K. Lamottke and K. P. Vollhardt, Org. Lett., 2000, 2, 2479–2481.
24. M. Ito, C. W. Clark, M. Mortimore, J. B. Goh and S. F. Martin, J. Am. Chem. Soc., 2001, 123, 8003–8010.
25. Y. Kaburagi, H. Tokuyama and T. Fukuyama, J. Am. Chem. Soc., 2004, 126, 10246–10247.
26. C. Beemelmanns and H. U. Reissig, Angew Chem. Int. Ed. Engl., 2010, 49, 8021–8025.
27. D. B. C. Martin and C. D. Vanderwal, Chem. Sci., 2011, 2, 649–651.
28. S. B. Jones, B. Simmons, A. Mastracchio and D. W. MacMillan, Nature, 2011, 475, 183–188.
29. M. E. Kuehne and F. Xu, J. Org. Chem., 1993, 58, 7490–7497.
30. B. Hong, D. Grzech, L. Caputi, P. Sonawane, C. E. R. Lopez, M. O. Kamileen, N. J. Hernandez Lozada, V. Grabe and S. E. O'Connor, Nature, 2022, 607, 617–622.
31. S. Genheden, P.-O. Norrby and O. Engkvist, J. Chem. Inf. Model., 2023, 63, 1841–1846.
32. S. Genheden and E. Bjerrum, Digital Discovery, 2022, 1, 527–539.
33. A. Thakkar, T. Kogej, J.-L. Reymond, O. Engkvist and E. J. Bjerrum, Chem. Sci., 2020, 11, 154–168.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00292j

‡ A Reaxys search for “ibuprofen” conducted on July 23, 2024 provided ∼600 published preparations of ibuprofen, many of which are degenerate; “taxol” ∼400; “aspirin” and “morphine” ∼100. The vast majority of laboratory-synthesized molecules have only one reported route, simply because they were made to test a specific hypothesis and then not pursued. Furthermore, the route in question is often only “reported” in that it exists in a notebook.

§ To ensure correct atom mapping in our case studies, all results with our small datasets were checked by eye. In four cases this led to re-mapping, typically involving either one-atom reactants (e.g. a sulfur ylide in Kuehne's racemic strychnine synthesis) or carbon-centered leaving groups (e.g. Woodward's formal homologation of an acid to a vinyl acetate, which involves a decarboxylation). The more complex the route, the more likely rxnmapper is to misassign atoms and thus propagate errors; strychnine is an extreme example and we do not anticipate the need for manual re-mapping outside of natural products.

¶ Initially AiZynthFinder predicted a one-step synthesis from commercially available atorvastatin lactone. In order to prevent AiZynth from utilizing any commercially available late-stage intermediates, we imposed a 250 Da weight limit on the starting materials, and restricted it to eMolecules stock.

|| Some of these syntheses are “formal” syntheses; that is, they were only carried out experimentally up to a known late-stage intermediate, typically isostrychnine or the Wieland-Gumlich aldehyde. Because the formal syntheses terminate in strychnine itself they are all directly comparable using our algorithm.

---