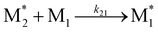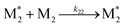Open Access Article
Open Access ArticleCopDDB: a descriptor database for copolymers and its applications to machine learning†
Takayoshi
Yoshimura
a,
Hiromoto
Kato
a,
Shunto
Oikawa
b,
Taichi
Inagaki
a,
Shigehito
Asano
c,
Tetsunori
Sugawara
c,
Tomoyuki
Miyao
 b,
Takamitsu
Matsubara
b,
Hiroharu
Ajiro
b,
Takamitsu
Matsubara
b,
Hiroharu
Ajiro
 b,
Mikiya
Fujii
b,
Mikiya
Fujii
 b,
Yu-ya
Ohnishi
b,
Yu-ya
Ohnishi
 d and
Miho
Hatanaka
d and
Miho
Hatanaka
 *ae
*ae
aGraduate School of Science and Technology, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama, Kanagawa 223-8522, Japan. E-mail: miho_hatanaka@keio.jp
bNara Institute of Science and Technology, 8916-5 Takayama-cho, Ikoma, Nara 630-0192, Japan
cFine Chemical Process Department, JSR Corporation, 100 Kawajiri-cho, Yokkaichi, Mie 510-8552, Japan
dMaterials Informatics Initiative, RD technology and digital transformation center, JSR Corporation, 3-103-9 Tonomachi, Kawasaki-ku, Kawasaki, Kanagawa 210-0821, Japan
eInstitute for Molecular Science, 38 NishigoNaka, Myodaiji, Okazaki, Aichi 444-8585, Japan
First published on 28th November 2024
Abstract
Polymer informatics, which involves applying data-driven science to polymers, has attracted considerable research interest. However, developing adequate descriptors for polymers, particularly copolymers, to facilitate machine learning (ML) models with limited datasets remains a challenge. To address this issue, we computed sets of parameters, including reaction energies and activation barriers of elementary reactions in the early stage of radical polymerization, for 2500 radical–monomer pairs derived from 50 commercially available monomers and constructed an open database named “Copolymer Descriptor Database”. Furthermore, we built ML models using our descriptors as explanatory variables and physical properties such as the reactivity ratio, monomer conversion, monomer composition ratio, and molecular weight as objective variables. These models achieved high predictive accuracy, demonstrating the potential of our descriptors to advance the field of polymer informatics.
Introduction
In recent years, data-driven research on polymers, known as polymer informatics, has been gaining attention, with a rapid increase in the number of reported studies.1–10 Polymers exhibit a wide range of physical properties dictated by various hierarchical parameters, including monomer species, molecular weight distribution, crystal structure, manufacturing process (such as temperature, solvent, and additives), and molding methods (such as film, fiber, and plate). Designing polymers with specific properties is a formidable challenge that often necessitates the exploration of only a subset of these parameters to narrow the vast search space. The availability of high-quality and comprehensive digital polymer databases is essential to facilitate data-driven research in this area. Since 2010, polymer databases such as PoLyInfo,11 Polymer Genome,12–14 NanoMine,15,16 and CoPolDB17 have gradually proliferated. Open-source libraries applicable to polymer informatics, such as RadonPy18 and XenonPy,19 have promoted data-driven research in laboratory settings. Additionally, data-driven research efforts increasingly integrate polymer data obtained from high-throughput20–22 and robot-automated experiments.23Another critical aspect of polymer informatics is the definition of appropriate descriptors. For instance, BIGSMILES24–27 and Polymer Markup Language28 have emerged as string-based descriptors for polymers, serving well in database construction and forming the backbone of data-driven research. However, because string-based descriptors do not directly represent molecular structures or properties, a vast amount of data is typically required to build machine learning (ML) models using these features as explanatory variables. Alternatively, attentive fingerprints of monomers and dimers have been proposed as descriptors for graph attention networks aimed at predicting the physical properties of copolymers.29 However, constructing such networks requires a substantial dataset of up to 4000 data points. Given the difficulties in accumulating extensive data in polymer-synthesis laboratories, even with automated experimental equipment, developing effective descriptors is imperative for constructing ML models capable of predicting the physical properties of polymers, even with limited datasets. In particular, in the search for polymers or copolymers with specific properties obtained by varying monomers or monomer pairs along with process variables (synthesis conditions), selecting appropriate descriptors for monomers or monomer pairs is crucial, because ML models must exhibit high prediction accuracy for untested monomers or monomer pairs to ensure reliable extrapolation accuracy. In our previous study,30 we demonstrated that incorporating density functional theory (DFT) parameters, including the activation barriers and reaction energies of the initial stage of radical polymerization, as descriptors, along with process variables, improved the extrapolation accuracies of copolymer properties (monomer conversion and monomer composition ratio) for monomer pairs not included in the training data. One of the notable achievements of our descriptor was that ML models trained on data from copolymers composed of several monomers could accurately predict the properties of copolymers containing an untested monomer with a different skeleton, a task that conventional descriptors found challenging.30
Therefore, in this study, we computed the descriptors of copolymers, including reaction energies and activation barriers, for 2500 radical–monomer pairs of 50 commercially available monomer species and compiled them into an open database named the “Copolymer Descriptor Database (CopDDB)”. The remainder of this paper is organized as follows: first, the radical–monomer pair descriptors and their calculation methods are described, followed by an explanation of the conversion of radical–monomer pair descriptors to those for copolymers. We then observed the chemical space defined by the descriptors and used them as explanatory variables of ML models in three case studies. In the first and second case studies, we constructed ML models to predict several physical properties using the descriptors in the CopDDB as explanatory variables and validated their predictive abilities. The objective variable in the first case study was the reactivity ratio r1 from the literature, which is an important parameter used to estimate the monomer composition ratio from the monomer ratio to be prepared (i.e., the copolymerization composition curve). The objective variables in the second case study were the physical properties of binary copolymers, such as the monomer conversion, the monomer composition ratio, and the molecular weights, measured under different monomers and process variables in our previous study.30 In the third case study, we applied Bayesian optimization (BO) with only one step, called one-shot BO, to find the appropriate process variables to achieve the desired physical property using an untested monomer. Through these three case studies described, we have demonstrated the usefulness of CopDDB descriptors.
Methodology for constructing a descriptor database
Preprocessing the monomer dataset
We focused on the 50 monomers shown in Fig. S1 and Table S1.† These monomers include commercially available acrylate monomers, methacrylate monomers, and styrene derivatives listed in “17019 Chemical Products”.31 First, we generated the Cartesian coordinates of these 50 monomers from their simplified molecular input line entry system (SMILES) representations using the ETKDGv3 method implemented in the RDKit package. The conformations of each monomer were also generated, and up to five conformers were selected based on the root-mean-square deviations of the heavy atoms, as implemented in RDKit.Calculating descriptors for radical–monomer pairs
CopDDB includes parameters for radical–monomer pairs ( and M2) and consists of four types of parameters: (1) reactivity parameters, (2) electronic parameters, (3) geometrical parameters, and (4) other conventional parameters. Parameters (1)–(3) are based on DFT calculations and are referred to as DFT-based parameters. The details of each parameter are as follows.
and M2) and consists of four types of parameters: (1) reactivity parameters, (2) electronic parameters, (3) geometrical parameters, and (4) other conventional parameters. Parameters (1)–(3) are based on DFT calculations and are referred to as DFT-based parameters. The details of each parameter are as follows.
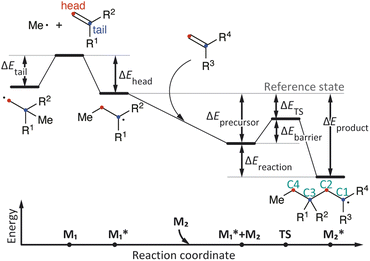
The reactivity parameters represent the relative electronic energies of the elementary reactions at the initial stage of radical polymerization shown in Fig. 1. Polymerization begins with the addition of an initiator radical to a monomer, which is usually a barrierless process, followed by repeated C–C bond formation with another monomer. Therefore, the reaction energies for the addition of a model initiator radical (the methyl radical) to M1 at the head and tail positions (ΔEhead and ΔEtail in Fig. 1, respectively) were calculated. The conformations of the methyl radical adduct to M1 were generated using an automated reaction-path search method called the multicomponent artificial force-induced reaction (MC-AFIR) method.32,33 We randomly selected one of the M1 conformers and placed a methyl radical at a random position, then performed the AFIR calculation with the artificial force between M1 and the methyl radical. This process was repeated until three successive AFIR searches found the already obtained geometries. The most stable geometries of the head- and tail-adducts were used to calculate ΔEhead and ΔEtail. Next, the local minima (LMs) and transition states (TSs) along the C–C bond formation pathway (head-to-tail addition) between the head adduct ( in Fig. 1) and monomer M2 were computed. The reaction pathways for the head-to-tail addition, starting from 20 random initial alignments, were explored using the MC-AFIR method. The obtained pathways (AFIR pathways) were usually close to the real reaction pathways and the energy maximum point on the AFIR pathway could be appropriate for an initial geometry for the geometry optimization of TS. In our case, however, the reaction coordinate was very simple, and the reactive C–C bond distance in a TS was found to be close to 2.28 Å according to our preliminary calculations. Thus, we selected a geometry on the AFIR pathway where the reactive C–C bond distance was close to 2.28 Å, used it as the initial structure for the relaxation calculation by fixing the C–C bond distance, and then carried out the geometry optimization without any constraints (note that the criterion to select an initial geometry was not critical but often affected the computational time). The most stable TS was selected when multiple TSs were obtained. Intrinsic reaction coordinate (IRC) calculations34 were performed to confirm the TS and obtain the structures of the corresponding precursors and products. All precursors, TSs, and products were confirmed by frequency calculations. The energies of the precursor and TS relative to the dissociation limits of
in Fig. 1) and monomer M2 were computed. The reaction pathways for the head-to-tail addition, starting from 20 random initial alignments, were explored using the MC-AFIR method. The obtained pathways (AFIR pathways) were usually close to the real reaction pathways and the energy maximum point on the AFIR pathway could be appropriate for an initial geometry for the geometry optimization of TS. In our case, however, the reaction coordinate was very simple, and the reactive C–C bond distance in a TS was found to be close to 2.28 Å according to our preliminary calculations. Thus, we selected a geometry on the AFIR pathway where the reactive C–C bond distance was close to 2.28 Å, used it as the initial structure for the relaxation calculation by fixing the C–C bond distance, and then carried out the geometry optimization without any constraints (note that the criterion to select an initial geometry was not critical but often affected the computational time). The most stable TS was selected when multiple TSs were obtained. Intrinsic reaction coordinate (IRC) calculations34 were performed to confirm the TS and obtain the structures of the corresponding precursors and products. All precursors, TSs, and products were confirmed by frequency calculations. The energies of the precursor and TS relative to the dissociation limits of  and M2 (ΔEprecursor and ΔETS, respectively) and the activation barrier ΔEbarrier (i.e., the energy difference between the precursor and TS) were collected. All AFIR calculations and geometry optimizations (without constraints) were performed at the GFN2-xTB35 and B3LYP-D3/def2SVP36–39 levels, respectively. The energies and energy gradients were calculated at the GFN2-xTB level using the ORCA program40 and at the B3LYP-D3 level using the Gaussian16 program.41 These computations supported the AFIR calculations and geometry optimizations conducted through the GRRM program.42 The activation energies for subsequent polymer elongation were not collected, as the reactivity of the propagating radical is primarily considered to depend on the identity of the monomer unit at the propagating end rather than the chain length and composition. As shown in Table S2,† the activation barriers for C–C bond formation at the same propagating end (with different chains) were similar.
and M2 (ΔEprecursor and ΔETS, respectively) and the activation barrier ΔEbarrier (i.e., the energy difference between the precursor and TS) were collected. All AFIR calculations and geometry optimizations (without constraints) were performed at the GFN2-xTB35 and B3LYP-D3/def2SVP36–39 levels, respectively. The energies and energy gradients were calculated at the GFN2-xTB level using the ORCA program40 and at the B3LYP-D3 level using the Gaussian16 program.41 These computations supported the AFIR calculations and geometry optimizations conducted through the GRRM program.42 The activation energies for subsequent polymer elongation were not collected, as the reactivity of the propagating radical is primarily considered to depend on the identity of the monomer unit at the propagating end rather than the chain length and composition. As shown in Table S2,† the activation barriers for C–C bond formation at the same propagating end (with different chains) were similar.
The electronic parameters include frontier orbital energies and energy gaps, calculated for the most stable conformers at the B3LYP-D3/def2SVP level.36–39 The singly occupied molecular orbital (SOMO) and lowest unoccupied molecular orbital (LUMO) energy levels of 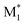 and the highest occupied molecular orbital (HOMO) and LUMO energy levels of M2 were measured. The energy gaps between the SOMO of
and the highest occupied molecular orbital (HOMO) and LUMO energy levels of M2 were measured. The energy gaps between the SOMO of  and the HOMO of M2, and between the SOMO of
and the HOMO of M2, and between the SOMO of 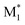 and the LUMO of M2, were determined.
and the LUMO of M2, were determined.
The geometrical parameters include the reactive C–C bond distance and the dihedral angle at the TS of the head-to-tail addition (<C1–C2–C3–C4 in Fig. 1), as well as the volumes and percent buried volumes (%Vbur)43 of the most stable conformers of  and M2. The volume and %Vbur represent the bulkiness of the molecule itself and around the reactive center, respectively. The volume was calculated using the Gaussian16 program, and %Vbur was determined using our own program. In addition, conventional parameters obtained with the ChemDraw program were included, such as the sum of the molecular masses of
and M2. The volume and %Vbur represent the bulkiness of the molecule itself and around the reactive center, respectively. The volume was calculated using the Gaussian16 program, and %Vbur was determined using our own program. In addition, conventional parameters obtained with the ChemDraw program were included, such as the sum of the molecular masses of  and M2, and the partition coefficients (log
and M2, and the partition coefficients (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P) for M1 and M2. In summary, CopDDB includes 24 descriptors: seven reactive parameters, six electronic parameters, eight geometrical parameters, and three conventional parameters, for 2500 radical–monomer pairs.
P) for M1 and M2. In summary, CopDDB includes 24 descriptors: seven reactive parameters, six electronic parameters, eight geometrical parameters, and three conventional parameters, for 2500 radical–monomer pairs.
Converting to descriptors for monomer pairs
To apply the descriptors of radical–monomer pairs for constructing ML models of copolymers, appropriate preprocessing of these descriptors is necessary. When synthesizing copolymers from two monomers, M1 and M2, the following four reactions occur:where
 and
and  represent the radicals with propagating ends M1 and M2, respectively, and kij is the rate constant for the reaction between
represent the radicals with propagating ends M1 and M2, respectively, and kij is the rate constant for the reaction between  and Mj (where i, j = 1, 2) that yields
and Mj (where i, j = 1, 2) that yields  . Therefore, the descriptors for the four types of radical–monomer pairs (
. Therefore, the descriptors for the four types of radical–monomer pairs ( , M1), (
, M1), ( , M2), (
, M2), (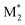 , M1), and (
, M1), and ( , M2) must be used as the descriptors for the monomer pairs of M1 and M2.
, M2) must be used as the descriptors for the monomer pairs of M1 and M2.
In this study, we present three case studies that utilize the ML approach with CopDDB parameters as descriptors. The first case study focused on the reactivity ratio r1, which represents the ratio of the reaction rate constants k11/k12. Thus, the DFT-based parameters (seven reactivity, six electronic, and eight geometrical parameters) for (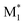 , M1) and (
, M1) and (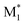 , M2) were used as descriptors for the M1, M2 monomer pairs, resulting in a total of 38 parameter sets. In the second case study, we focused on the physical properties of five binary copolymers synthesized by combining methyl methacrylate (MMA) with five monomers: styrene (St), glycidyl methacrylate (GMA), 4-acetoxystyrene (PACS), tetrahydrofurfuryl methacrylate (THFMA), and cyclohexyl methacrylate (CHMA). By classifying St, GMA, PACS, THFMA, and CHMA as M1 and MMA as M2, the parameter sets for (
, M2) were used as descriptors for the M1, M2 monomer pairs, resulting in a total of 38 parameter sets. In the second case study, we focused on the physical properties of five binary copolymers synthesized by combining methyl methacrylate (MMA) with five monomers: styrene (St), glycidyl methacrylate (GMA), 4-acetoxystyrene (PACS), tetrahydrofurfuryl methacrylate (THFMA), and cyclohexyl methacrylate (CHMA). By classifying St, GMA, PACS, THFMA, and CHMA as M1 and MMA as M2, the parameter sets for (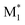 , M1), (
, M1), ( , M2), and (
, M2), and (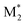 , M1) were utilized as descriptors for the binary copolymers. The same descriptor preprocessing was applied in the third study, which validated the prediction accuracy for another M1, 2-hydroxyethyl methacrylate (HEMA), using one-shot BO.
, M1) were utilized as descriptors for the binary copolymers. The same descriptor preprocessing was applied in the third study, which validated the prediction accuracy for another M1, 2-hydroxyethyl methacrylate (HEMA), using one-shot BO.
Chemical space spanned by the descriptors
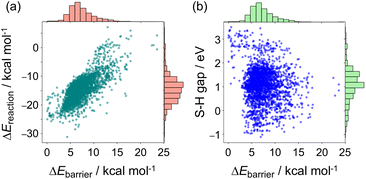
The distribution of each descriptor was examined from various points of view. Fig. 2 shows the scatter plots and histograms of representative radical–monomer pair descriptors, such as the activation barrier (ΔEbarrier in Fig. 1), the reaction energy (ΔEreaction in Fig. 1), and the SOMO–HOMO gap between and M2 (the distributions of other descriptors are shown in Fig. S2–S5†). The activation barriers ΔEbarrier ranged from 0 kcal mol−1 to 25 kcal mol−1, and were positively correlated with the reaction energy ΔEreaction, with a correlation coefficient R of 0.74 (Fig. 2a and S3†). Thus, we can say that the C–C bond formations between radical–monomer pairs roughly followed the Evans–Polanyi principle. The reaction energies were negative for most of the radical–monomer pairs, meaning that they were exothermic reactions, but there were also some endothermic reactions. In addition, there was almost no correlation between activation barriers and other parameters that were calculated from isolated
and M2 (the distributions of other descriptors are shown in Fig. S2–S5†). The activation barriers ΔEbarrier ranged from 0 kcal mol−1 to 25 kcal mol−1, and were positively correlated with the reaction energy ΔEreaction, with a correlation coefficient R of 0.74 (Fig. 2a and S3†). Thus, we can say that the C–C bond formations between radical–monomer pairs roughly followed the Evans–Polanyi principle. The reaction energies were negative for most of the radical–monomer pairs, meaning that they were exothermic reactions, but there were also some endothermic reactions. In addition, there was almost no correlation between activation barriers and other parameters that were calculated from isolated  and M2, such as the SOMO–HOMO and SOMO–LUMO energy gaps (see Fig. 2b, S2, and S3†), thus it can be said that the kinetic and thermodynamic stabilities of radical–monomer pairs could only be represented by the energetics in Fig. 1.
and M2, such as the SOMO–HOMO and SOMO–LUMO energy gaps (see Fig. 2b, S2, and S3†), thus it can be said that the kinetic and thermodynamic stabilities of radical–monomer pairs could only be represented by the energetics in Fig. 1.
Here, a “good” descriptor set is expected to yield similar values for molecules with similar properties. For example, monomers with a styrene skeleton, such as St and PACS, are expected to exhibit similar properties compared to other monomers, such as acrylates and methacrylates. In other words, these monomers should be located close together in the chemical space spanned by the descriptor set. To verify this, we focused on the two-dimensional distribution of 2500 radical–monomer pair data points within the chemical space defined by all the descriptors in the CopDDB. As shown in Fig. 3a, the data points corresponding to St and PACS radicals (i.e., radical–monomer pairs of (St*, M1) and (PACS*, M1); M1 = 50 monomers) were localized in a specific region. Similarly, the data points for their monomers (i.e., ( , St) and (
, St) and (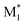 , PACS)) were also located relatively close by. In contrast, within the chemical space defined by a conventional descriptor set (a list of RDKit descriptors for two monomers M1 and M2; see Table S5† for the details), the data points for St and PACS were separated as shown in Fig. 3b. This trend was also observed for alkoxyacrylates (see Fig. S6†). This indicates that the CopDDB descriptors differ significantly from the RDKit descriptors, which were designed to describe the properties of general molecules, and that the CopDDB descriptors effectively capture the specific properties as monomers for radical copolymerization.
, PACS)) were also located relatively close by. In contrast, within the chemical space defined by a conventional descriptor set (a list of RDKit descriptors for two monomers M1 and M2; see Table S5† for the details), the data points for St and PACS were separated as shown in Fig. 3b. This trend was also observed for alkoxyacrylates (see Fig. S6†). This indicates that the CopDDB descriptors differ significantly from the RDKit descriptors, which were designed to describe the properties of general molecules, and that the CopDDB descriptors effectively capture the specific properties as monomers for radical copolymerization.
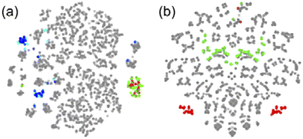 | ||
Fig. 3 Visualization of 2500 radical–monomer pair data points within the chemical space spanned by all the descriptors in the CopDDB (a) and the RDKit descriptors listed in Table S5† (b). The data points were projected into two dimensions using t-distributed stochastic neighbor embedding (t-SNE),44 with standardized descriptors and a perplexity parameter of 50. In panel (a), the data points for (St*, M1), (PACS*, M1), (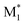 , St), ( , St), ( , PACS), and the others are shown in red, green, blue, light blue, and gray, respectively. In panel (b), the data points for (St, M1) and (M1, St) are in red, (PACS, M1) and (M1, PACS) are in blue, and the others are in gray. Here, M1 and , PACS), and the others are shown in red, green, blue, light blue, and gray, respectively. In panel (b), the data points for (St, M1) and (M1, St) are in red, (PACS, M1) and (M1, PACS) are in blue, and the others are in gray. Here, M1 and 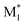 represent 50 monomers in the CopDDB and their corresponding radicals (methyl radical adducts), respectively. represent 50 monomers in the CopDDB and their corresponding radicals (methyl radical adducts), respectively. | ||
Next, we examined the 2500 radical–monomer pair data points in the chemical space defined by the CopDDB descriptors, along with the representative descriptors. As shown in Fig. 4, data points with high or low activation barriers (depicted in red and blue, respectively) were scattered throughout the chemical space. Focusing on the reaction energy, there were some clusters of data corresponding to highly exothermic (in blue), moderately exothermic (in light green), and slightly endothermic reactions (in red). However, data points with different reaction energies were not widely separated. In contrast, for the SOMO–HOMO and SOMO–LUMO orbital energy gaps, the data points with similar gaps tended to be close together, while those with different gaps were generally further apart. These findings suggest that the orbital energy gaps are likely major factors in characterizing the chemical space defined by the CopDDB descriptors. Nonetheless, other descriptors also could contribute to representing the complexity of this multidimensional chemical space.
Applications of the descriptors to ML models
Prediction of reactivity ratios
In the first case study, the reactivity ratio r1 was featured as an objective variable in the ML models. A dataset of r1 values was manually collected from the Polymer Handbook.45 Another reactivity ratio r2 (=k22/k21) also shown in the Handbook was converted to the r1 data because both r1 and r2 represent the ratio of the kinetic constants for homopolymerization (kij, i = 1, 2) and heteropolymerization (kij, j = 1, 2) and their values were identical when the monomer labels 1 and 2 were switched. Although the Handbook includes approximately 4600 data points, only 424 r1 values were available for the 114 radical–monomer pairs recorded in the CopDDB. The r1 data from the literature were obtained under various experimental conditions, resulting in a relatively wide distribution of r1 values for identical radical–monomer pairs. In addition, some radical–monomer pairs had multiple r1 values, while others had only one. The r1 data were preprocessed as follows: (1) negative r1 values, which were physically unrealistic artifacts, were converted to zero, and (2) outliers were deleted manually, as shown in Table S3.† The mean of the remaining r1 data was used as the objective variable. Fig. 5a shows the distribution of the mean r1. Few data points exhibit large r1 values. Considering the composition distribution is crucial, particularly regarding whether r1 approaches 0 or 1, as larger r1 values generally indicate substantial inaccuracy.46 Thus, we extracted r1 values less than 1.5, resulting in 97 data points, as depicted in Fig. 5b. | ||
| Fig. 5 Distributions of mean r1 values: (a) for all 114 datasets and (b) for the 97 datasets after preprocessing. | ||
To evaluate the effectiveness of our descriptors, we constructed ML models to predict r1 values using two different sets of descriptors and compared their prediction accuracies. The first set, obtained from CopDDB, combined DFT-based descriptors for ( , M1) and (
, M1) and (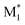 , M2). The second set, derived from the RDKit package, combined descriptors for M1 and M2 (details of the descriptors are shown in Tables S4 and S5†). Before constructing the ML models, the descriptors were preprocessed as follows. Descriptors with a correlation coefficient above 0.9 were reduced to one. For those with a correlation coefficient in the range of 0.8–0.9, we manually selected which descriptor to remove based on scatter plots. As a result, 22 DFT-based and 24 RDKit descriptors were retained. The 97 data points were divided into subsets of 87 (∼90%) for training and 10 (∼10%) for testing. Random forest (RF) regression models were constructed, with hyperparameters optimized through 5-fold cross-validation of the training data using the Optuna package.47 Model performance was validated using R2 scores.
, M2). The second set, derived from the RDKit package, combined descriptors for M1 and M2 (details of the descriptors are shown in Tables S4 and S5†). Before constructing the ML models, the descriptors were preprocessed as follows. Descriptors with a correlation coefficient above 0.9 were reduced to one. For those with a correlation coefficient in the range of 0.8–0.9, we manually selected which descriptor to remove based on scatter plots. As a result, 22 DFT-based and 24 RDKit descriptors were retained. The 97 data points were divided into subsets of 87 (∼90%) for training and 10 (∼10%) for testing. Random forest (RF) regression models were constructed, with hyperparameters optimized through 5-fold cross-validation of the training data using the Optuna package.47 Model performance was validated using R2 scores.
Fig. 6 shows the y–y plots of r1 values predicted by RF models using the two sets of descriptors. The model using DFT-based descriptors achieved higher R2 scores for both training and test data (0.86 and 0.84, respectively) compared to the RDKit descriptors (0.80 and 0.65, respectively). Thus, our descriptors demonstrated excellent performance for ML models, offering better predictive accuracy.
 | ||
| Fig. 6 y–y plots of RF models for r1 values constructed using different descriptor sets: (a) DFT-based descriptors from the CopDDB and (b) RDKit descriptors. y–y plots with different train/test splits are also shown in Fig. S7.† | ||
Prediction of monomer conversion, monomer composition ratio, and molecular weight
In the second case study, we examined the properties of copolymers synthesized via radical copolymerization of two monomers: MMA and M1 that represents one of five other monomers—St, GMA, PACS, THFMA, and CHMA. The target properties include the conversions of MMA and the other monomer (MMA_conv. and M1_conv.), the composition ratio of M1 (M1_CR), number-average molecular weight (Mn), and weight-average molecular weight (Mw). These properties were measured under various process conditions, including temperature, flow rate (reaction time), and the ratio of the two monomers, initiator, and solvent, as reported in our previous study.30 The M1 monomer was also considered a process variable. The list of process variables and corresponding properties is provided in Table S2† of ref. 30.As discussed in our previous study,30 the DFT-based descriptors demonstrated higher extrapolation accuracy than the RDKit descriptors for predicting MMA_conv., M1_conv., and M1_CR. In this study, we extended this approach to predict molecular weights with high accuracy by utilizing the updated CopDDB descriptors and applying additional feature engineering through dimensional compression. We examined two types of descriptors for M1. One set comprised 66 parameters, which were combinations of the CopDDB descriptors ( , M1), (
, M1), ( , MMA), and (MMA*, M1). The other consisted of nine parameters, derived from compressing the CopDDB descriptors (
, MMA), and (MMA*, M1). The other consisted of nine parameters, derived from compressing the CopDDB descriptors (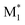 , M1), (
, M1), ( , MMA), and (MMA*, M1) into three dimensions each using principal component analysis (PCA)48 and variational autoencoder (VAE).49 Details of the dimensional compression using the VAE are shown in Fig. S8.† To estimate extrapolation performance, leave-one-monomer (M1)-out cross-validation (LOOCV) was conducted, following the procedure outlined in Examination 2 of Fig. 3 in ref. 30. The ML models were built using Gaussian progress regression (GPR) with the sum of two Matern kernels, with ν values of 0.5 and 1.5.50
, MMA), and (MMA*, M1) into three dimensions each using principal component analysis (PCA)48 and variational autoencoder (VAE).49 Details of the dimensional compression using the VAE are shown in Fig. S8.† To estimate extrapolation performance, leave-one-monomer (M1)-out cross-validation (LOOCV) was conducted, following the procedure outlined in Examination 2 of Fig. 3 in ref. 30. The ML models were built using Gaussian progress regression (GPR) with the sum of two Matern kernels, with ν values of 0.5 and 1.5.50
Table 1 shows the R2 scores of the GPR models built using the three types of parameters mentioned above (see Fig. S9† for the y–y plots). The prediction accuracies for M1_conv., MMA_conv., and M1_CR improved when using the compressed parameters, except for M1_conv. with parameters compressed by PCA. For the molecular weights Mn and Mw, the prediction accuracies were dramatically improved with the compressed parameters. This improvement could be attributed to the reduced number of descriptors, which suppressed overfitting of the training data. Although feature engineering, such as dimensional compression, is sometimes necessary, the descriptors in CopDDB remain valuable for developing ML models of various physical properties of copolymers.
| Descriptors | Original parameters | 9 parameters compressed by PCA | 9 parameters compressed by VAE |
|---|---|---|---|
| a The predicted values were the averages of five values with different random numbers in the GPR model. M1 represents five monomer species: St, GMA, CHMA, PACS, and THFMA. | |||
| MMA conv. | 0.60 | 0.67 | 0.72 |
| M1 conv. | 0.67 | 0.57 | 0.80 |
| M1_CR | 0.72 | 0.87 | 0.82 |
| M n | 0.35 | 0.76 | 0.67 |
| M w | 0.33 | 0.81 | 0.73 |
The three-dimensional latent descriptors compressed using PCA and VAE can be regarded as effective descriptors for improving prediction accuracy by achieving a better balance among all objective variables. To verify the importance of the DFT-based descriptors, the loadings of the compressed DFT-based descriptors obtained through PCA are shown in Fig. S10.† This figure confirms the significance of descriptors related to radical reactivity (SOMO and LUMO of radicals, and ΔEhead), transition state energies (ΔETS and ΔEbarrier), and the partition coefficients (log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P). These factors are indeed crucial in polymer chain elongation reactions and provide information that cannot be obtained from experimental process variables alone. The partition coefficients reflect the hydrophilicity or hydrophobicity of monomers and polymers. The balance between these properties is considered to influence the stability of the copolymer's molecular structure, self-assembly, proton transfer with the solvent, and, ultimately, the molecular weights Mn and Mw.
P). These factors are indeed crucial in polymer chain elongation reactions and provide information that cannot be obtained from experimental process variables alone. The partition coefficients reflect the hydrophilicity or hydrophobicity of monomers and polymers. The balance between these properties is considered to influence the stability of the copolymer's molecular structure, self-assembly, proton transfer with the solvent, and, ultimately, the molecular weights Mn and Mw.
One-shot Bayesian optimization for a novel monomer
As a third case study demonstrating the effectiveness of CopDDB descriptors, we conducted process optimization for the copolymerization of MMA and a new M1 monomer, HEMA, using the GPR models trained in the previous section (the second case study). The initial dataset for the GPR model was the same as that in the second case study, consisting of experimental data30 for the copolymerization of MMA with five M1 monomers (M1 = St, GMA, PACS, THFMA, and CHMA), along with compressed CopDDB descriptors obtained using VAE. Table 1 indicates that PCA-based compression results in better accuracy than VAE-based ones for the target variable “M1_CR”. However, VAE provides more balanced predictions for all target variables compared to PCA, with no specific variables showing poor prediction performance. Since future developments towards multi-objective optimization should also be considered, we chose VAE-based compression rather than PCA. Typically, BO requires an initial training set of target molecules, which entails significant experimental cost. However, our approach overcomes this challenge by using data from previously tested molecules that do not contain the target molecules for the initial dataset.We performed the BO with the target value set to a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 composition ratio (i.e., 50% M1_CR; M1 = HEMA) for the synthesized copolymer. The objective variable for the GPR model was defined as the squared difference between the target M1_CR and the measured M1_CR (note that this BO procedure followed our previous study,51 in which BO was applied for free radical copolymerization using single-molecular datasets). After training with the initial data, four candidate points, each consisting of five process variables, such as initiator concentration, proportion of HEMA (molar ratio of HEMA to HEMA and MMA in the preparation), reaction temperature, solvent-to-monomer (SM) ratio, and reaction time, were generated within the BO design space shown in Table S6.† These candidate points are summarized in Fig. 7, where the predicted objective variable by the GPR model is color-coded in the partial dependence plots (PDPs),52 which confirms that the proposed process variables were sampled within the optimal region (shown in purple in Fig. 7). Focusing on the proposed process variables, three variables such as initiator concentration, HEMA proportion, and reaction temperature were within a narrow range, indicating that only a specific range of these values could achieve the desired HEMA-CR. In particular, the proposed HEMA proportion was limited, ranging from 45.91% to 47.45%, which indicated that the lower proportion of HEMA than MMA in the preparation was required due to their different reactivities. In contrast, a wide range of values was chosen for SM ratio and reaction time.
50 composition ratio (i.e., 50% M1_CR; M1 = HEMA) for the synthesized copolymer. The objective variable for the GPR model was defined as the squared difference between the target M1_CR and the measured M1_CR (note that this BO procedure followed our previous study,51 in which BO was applied for free radical copolymerization using single-molecular datasets). After training with the initial data, four candidate points, each consisting of five process variables, such as initiator concentration, proportion of HEMA (molar ratio of HEMA to HEMA and MMA in the preparation), reaction temperature, solvent-to-monomer (SM) ratio, and reaction time, were generated within the BO design space shown in Table S6.† These candidate points are summarized in Fig. 7, where the predicted objective variable by the GPR model is color-coded in the partial dependence plots (PDPs),52 which confirms that the proposed process variables were sampled within the optimal region (shown in purple in Fig. 7). Focusing on the proposed process variables, three variables such as initiator concentration, HEMA proportion, and reaction temperature were within a narrow range, indicating that only a specific range of these values could achieve the desired HEMA-CR. In particular, the proposed HEMA proportion was limited, ranging from 45.91% to 47.45%, which indicated that the lower proportion of HEMA than MMA in the preparation was required due to their different reactivities. In contrast, a wide range of values was chosen for SM ratio and reaction time.
 | ||
| Fig. 7 Four proposed sets of process variables (shown as white stars) on the PDP color maps for each pair of five process variables within the ranges defined in Table S6.† Color-coded numerical values are the predicted means of the GPR, with colors closer to purple corresponding to values closer to the target HEMA_CR. The detailed process variables are shown in Table S7.† | ||
To validate the proposed process variables (i.e., candidate points), the MMA and HEMA copolymers were synthesized under the four proposed process variable sets. The four observed HEMA_CR values were 49.21%, 49.91%, 47.81%, and 49.21%, all of which were quite close to the desired ratio of 50% (see Table S8† for the detailed results). To validate the effect of reaction time, for which a wide range of values were proposed, we also performed the experiments where only the reaction time was changed to 1/2 and 1/3 of the proposed time. Indeed, the effect of reaction time on the HEMA-CR was quite small, though that on other properties such as the monomer conversions and molecular weights was large as shown in Table S8.† As shown above, we succeeded in proposing process variables to achieve the desired property of copolymers of MMA with an untested M1 monomer (M1 = HEMA) because we were able to transfer the search space of process variables for the tested M1 monomers (M1 = St, GMA, PACS, THFMA, and CHMA) to that for HEMA via CopDDB descriptors.
Conclusions
In this study, we developed a comprehensive database of copolymer descriptors, termed CopDDB, and made it publicly accessible. The database encompasses 24 descriptors across four categories: reactivity, electronic, geometry, and other conventional parameters. These descriptors were compiled for 2500 radical–monomer pairs derived from 50 distinct monomers, including acrylate, methacrylate, and styrene derivatives. To apply these radical–monomer pair descriptors to copolymer development, a preprocessing step is necessary. Specifically, for reactivity ratio analysis, the ratio of kinetic constants for homopolymerization versus heteropolymerization
versus heteropolymerization  is used, with descriptors (
is used, with descriptors ( , M1) and (
, M1) and ( , M2) being relevant input variables for the ML models. In addition, when synthesizing binary copolymers from a specific monomer (e.g., MMA) and other monomers (M1), descriptor sets such as (
, M2) being relevant input variables for the ML models. In addition, when synthesizing binary copolymers from a specific monomer (e.g., MMA) and other monomers (M1), descriptor sets such as ( , M1), (
, M1), ( , MMA), and (MMA*, M1) were used as input variables. Our study demonstrated that these descriptors, combined with process variables, successfully predict monomer conversion, monomer composition ratio, and molecular weight of binary copolymers, and can be effectively applied in one-shot Bayesian optimizations. The high accuracy of the ML models underscores the versatility and applicability of our descriptors for innovative copolymer development.
, MMA), and (MMA*, M1) were used as input variables. Our study demonstrated that these descriptors, combined with process variables, successfully predict monomer conversion, monomer composition ratio, and molecular weight of binary copolymers, and can be effectively applied in one-shot Bayesian optimizations. The high accuracy of the ML models underscores the versatility and applicability of our descriptors for innovative copolymer development.
In our current database, the monomer scope is limited to monofunctional monomers, and the descriptor set includes only the energetics of the early stages of polymerization, without considering the energetics of later stages or variations involving different radical initiators and terminators. Expanding the descriptor set will be essential as we broaden the scope to include polymers with multifunctional monomers and physical properties influenced by the energetics of the later stages of polymerization.
Data availability
The Copolymer Descriptor Database, the Python codes for preprocessing the descriptors, and the Cartesian coordinates used to calculate the descriptors are available at the following URL: https://github.com/hatanaka-lab/CopDDB. The data supporting this article can be found in the ESI.†Author contributions
The manuscript was written with contributions from all authors. All authors approved the final version of the manuscript. The main contributions of each author are as follows: T. Yoshimura: investigation (DB and ML). H. Kato and S. Oikawa: investigation (ML). T. Inagaki: supervision (DB). S. Asano: investigation (EXP). T. Sugawara and H. Ajiro supervised the experimental data (EXP). T. Miyao and T. Matsubara: supervision (ML). M. Fujii and Y. Ohnishi: supervision (DB, ML, EXP). M. Hatanaka: project administration.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study is based on the results obtained from project JPNP14004, subsidized by the New Energy and Industrial Technology Development Organization (NEDO), JSPS KAKENHI Grant No. JP20K05438, JP23H00288, JP24H01094, and JST Grant No. JPMJPF2221. We thank Ms Yuka Uto, Mr Taro Watanabe, Mr Reon Abe, Mr Yugo Osada, Mr Yuki Shimizu, Ms Asano Tsuchiya, Ms Satomi Toguchi, Mr Daichi Mori, Mr Soshi Ikuta, Mr Yu Ikeda, Mr Taiki Inami, Mr Kazuma Hashimoto, Ms Yuka Maeyama, Ms Riho Somaki, and Mr Shunsuke Nakatani for their assistance in extracting bibliographic data from the Polymer Handbook. We also acknowledge the computer resources provided by the Academic Center for Computing and Media Studies (ACCMS) at Kyoto University and the Research Center of Computer Science (RCCS) at the Institute for Molecular Science.References
- N. Adams and P. Murray-Rust, Macromol. Rapid Commun., 2008, 29, 615–632 CrossRef CAS.
- N. Adams, Adv. Polym. Sci., 2010, 225, 107–149 CrossRef CAS.
- D. J. Audus and J. J. de Pablo, ACS Macro Lett., 2017, 6, 1078–1082 CrossRef CAS PubMed.
- L. H. Chen, G. Pilania, R. Batra, T. D. Huan, C. Kim, C. Kuenneth and R. Ramprasad, Mater. Sci. Eng., R, 2021, 144, 100595 CrossRef.
- W. X. Sha, Y. Li, S. Tang, J. Tian, Y. M. Zhao, Y. Q. Guo, W. X. Zhang, X. F. Zhang, S. F. Lu, Y. C. Cao and S. J. Cheng, InfoMat, 2021, 3, 353–361 CrossRef CAS.
- H. Sahu, H. M. Li, L. H. Chen, A. C. Rajan, C. Kim, N. Stingelin and R. Ramprasad, ACS Appl. Mater. Interfaces, 2021, 13, 53314–53322 CrossRef CAS PubMed.
- T. D. Sparks and D. Banerjee, Matter, 2021, 4, 1454–1456 CrossRef CAS.
- K. Hatakeyama-Sato, Polym. J., 2023, 55, 117–131 CrossRef CAS.
- X. L. Liu, C. L. Zhu and B. Z. Tang, Nat. Rev. Chem., 2023, 7, 232–233 CrossRef PubMed.
- S. S. Shukla, C. Kuenneth and R. Ramprasad, Mrs. Bull., 2024, 49, 17–24 CrossRef.
- S. Otsuka, I. Kuwajima, J. Hosoya, Y. Xu, and M. Yamazaki, 2011 International Conference on Emerging Intelligent Data and Web Technologies, Tirana, Albania, 2011, pp. 22–29 Search PubMed.
- T. D. Huan, A. Mannodi-Kanakkithodi, C. Kim, V. Sharma, G. Pilania and R. Ramprasad, Sci. Data, 2016, 3, 160012 CrossRef CAS PubMed.
- C. Kim, A. Chandrasekaran, T. D. Huan, D. Das and R. Ramprasad, J. Phys. Chem. C, 2018, 122, 17575–17585 CrossRef CAS.
- A. Chandrasekaran, C. Kim and R. Ramprasad, Lect. Notes Phys., 2020, 968, 397–412 CAS.
- H. Zhao, X. L. Li, Y. C. Zhang, L. S. Schadler, W. Chen and L. C. Brinson, APL Mater., 2016, 4, 053204 CrossRef.
- H. Zhao, Y. X. Wang, A. Q. Lin, B. Y. Hu, R. Yan, J. McCusker, W. Chen, D. L. McGuinness, L. Schadler and L. C. Brinson, APL Mater., 2018, 6, 111108 CrossRef.
- K. Takahashi, H. Mamitsuka, M. Tosaka, N. Zhu and S. Yamago, Polym. Chem., 2024, 15, 965–971 RSC.
- Y. Hayashi, J. Shiomi, J. Morikawa and R. Yoshida, npj Comput. Mater., 2022, 8, 222 CrossRef CAS.
- S. Wu, Y. Kondo, M. A. Kakimoto, B. Yang, H. Yamada, I. Kuwajima, G. Lambard, K. Hongo, Y. B. Xu, J. Shiomi, C. Schick, J. Morikawa and R. Yoshida, npj Comput. Mater., 2019, 5, 66 CrossRef.
- S. Oliver, L. Zhao, A. J. Gormley, R. Chapman and C. Boyer, Macromolecules, 2019, 52, 3–23 CrossRef CAS.
- M. Reis, F. Gusev, N. G. Taylor, S. H. Chung, M. D. Verber, Y. Z. Lee, O. Isayev and F. A. Leibfarth, J. Am. Chem. Soc., 2021, 143, 17677–17689 CrossRef CAS PubMed.
- E. C. Day, S. S. Chittari, M. P. Bogen and A. S. Knight, ACS Polym. Au, 2023, 3, 406–427 CrossRef CAS PubMed.
- B. Burger, P. M. Maffettone, V. V. Gusev, C. M. Aitchison, Y. Bai, X. Y. Wang, X. B. Li, B. Alston, B. Y. Li, R. Clowes, N. Rankin, B. Harris, R. S. Sprick and A. I. Cooper, Nature, 2020, 583, 237–241 CrossRef CAS PubMed.
- T. S. Lin, C. W. Coley, H. Mochigase, H. K. Beech, W. C. Wang, Z. Wang, E. Woods, S. L. Craig, J. A. Johnson, J. A. Kalow, K. F. Jensen and B. D. Olsen, ACS Cent. Sci., 2019, 5, 1523–1531 CrossRef CAS PubMed.
- T. S. Lin, N. J. Rebello, G. H. Lee, M. A. Morris and B. D. Olsen, ACS Polym. Au, 2022, 2, 486–500 CrossRef CAS PubMed.
- W. Z. Zou, A. M. Monterroza, Y. X. Yao, S. C. Millik, M. M. Cencer, N. J. Rebello, H. K. Beech, M. A. Morris, T. S. Lin, C. S. Castano, J. A. Kalow, S. L. Craig, A. Nelson, J. S. Moore and B. D. Olsen, Chem. Sci., 2022, 13, 12045–12055 RSC.
- L. Schneider, D. Walsh, B. Olsen and J. de Pablo, Digital Discovery, 2024, 3, 51–61 RSC.
- N. Adams, J. Winter, P. Murray-Rust and H. S. Rzepa, J. Chem. Inf. Model., 2008, 48, 2118–2128 CrossRef CAS PubMed.
- T. Nguyen and M. Bavarian, Polymer, 2023, 275, 125866 CrossRef CAS.
- S. Takasuka, S. Oikawa, T. Yoshimura, S. Ito, Y. Harashima, T. Takayama, S. Asano, A. Kurosawa, T. Sugawara, M. Hatanaka, T. Miyao, T. Matsubara, Y. Y. Ohnishi, H. Ajiro and M. Fujii, Digital Discovery, 2023, 2, 809–818 RSC.
- The Chemical Daily Co. Ltd., 17019 Chemical Products, (in Japanese) The Chemical Daily Co., Ltd, 2019 Search PubMed.
- S. Maeda and K. Morokuma, J. Chem. Phys., 2010, 132, 241102 CrossRef PubMed.
- S. Maeda and K. Morokuma, J. Chem. Theory Comput., 2011, 7, 2335–2345 CrossRef CAS PubMed.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theor. Comput., 2019, 15, 1652–1671 CrossRef CAS PubMed.
- A. D. Becke, Phys. Rev. A, 1988, 38, 3098–3100 CrossRef CAS PubMed.
- C. T. Lee, W. T. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16, 2016 Search PubMed.
- S. Maeda, K. Ohno and K. Morokuma, Phys. Chem. Chem. Phys., 2013, 15, 3683–3701 RSC.
- H. Clavier and S. P. Nolan, Chem. Commun., 2010, 46, 841–861 RSC.
- L. J. P. van der Maaten and G. E. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605 Search PubMed.
- J. Brandrup, E. H. Immergut and E. A. Grulke, Polymer Handbook, Wiley, 4th edn, 2003 Search PubMed.
- N. A. Lynd, R. C. Ferrier and B. S. Beckingham, Macromolecules, 2019, 52, 2277–2285 CrossRef CAS.
- T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, Kdd'19: Proceedings of the 25th Acm Sigkdd International Conferencce on Knowledge Discovery and Data Mining, 2019, pp. 2623–2631 Search PubMed.
- I. T. Jolliffe and J. Cadima, Philos. Trans. R. Soc., A, 2016, 374, 20150202 CrossRef PubMed.
- T. Ochiai, T. Inukai, M. Akiyama, K. Furui, M. Ohue, N. Matsumori, S. Inuki, M. Uesugi, T. Sunazuka, K. Kikuchi, H. Kakeya and Y. Sakakibara, Commun. Chem., 2023, 6, 249 CrossRef PubMed.
- C. E. W. Rasmussen and C. K. I. Williams, Gaussian Processes for Machine Learning, MIT Press, 2006 Search PubMed.
- S. Takasuka, S. Ito, S. Oikawa, Y. Harashima, T. Takayama, A. Nag, A. Wakiuchi, T. Ando, T. Sugawara, M. Hatanaka, T. Miyao, T. Matsubara, Y. Phnishi, H. Ajiro and M. Fujii, Sci. Technol. Adv. Mater.: Methods, 2024, 4, 2425178 Search PubMed.
- J. H. Friedman, Ann. Stat., 2001, 29, 1189–1232 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00266k |
| This journal is © The Royal Society of Chemistry 2025 |