Biophysics-guided uncertainty-aware deep learning uncovers high-affinity plastic-binding peptides

Abstract

Plastic pollution, particularly microplastics (MPs), poses a significant global threat to ecosystems and human health, necessitating innovative remediation strategies. Biocompatible and biodegradable plastic-binding peptides (PBPs) offer a potential solution through targeted adsorption and subsequent MP detection or removal from the environment. A challenge in discovering plastic-binding peptides is the vast combinatorial space of possible peptides (i.e., over 10¹⁵ for 12-mer peptides), which far exceeds the sample sizes typically reachable by experiments or biophysics-based computational methods. One step towards addressing this issue is to train deep learning models on experimental or biophysical datasets, permitting faster and cheaper evaluations of peptides. However, deep learning predictions are not always accurate, which could waste time and money due to synthesizing and evaluating false positives. Here, we resolve this issue by combining biophysical modeling data from Peptide Binder Design (PepBD) algorithm, the predictive power and uncertainty quantification of evidential deep learning, and metaheuristic search methods to identify high-affinity PBPs for several common plastics. Molecular dynamics simulations show that the discovered PBPs have greater median adsorption free energies for polyethylene (5%), polypropylene (18%), and polystyrene (34%) relative to PBPs previously designed by PepBD. The impact of including uncertainty quantification in peptide design is demonstrated by the increasing improvement in the median adsorption free energy with decreasing uncertainty. This robust framework accelerates peptide discovery, paving the way for effective, bio-inspired solutions to MP remediation.

---

Introduction

The global proliferation of microplastic (MP) pollution poses a pressing threat to ecosystems and human health.^1–4 With estimates of millions of tons of MPs contaminating marine environments alone,^5,6 these ubiquitous pollutants disrupt ecological balance and can be vectors for harmful contaminants. This contributes to adverse health effects in humans, including inflammation and oxidative stress^7,8 and heart disease.⁹ MPs may also cross the blood–brain barrier.¹⁰ Addressing this crisis necessitates the development of innovative, targeted remediation strategies.

Peptides may be valuable for tackling MP pollution.^1,11,12 The promise of peptides lies in their inherent biocompatibility and biodegradability, strong adsorption to polymeric materials,¹³ and potential ability to bind preferentially to one material over others. Thus, PBPs could offer a sustainable solution to facilitate the detection, capture, and degradation of MPs.¹

Peptide design^14–16 is hampered by the vast combinatorial space of peptide sequences (i.e., over 10¹⁵ for 12-mer peptides).¹⁷ Experimental library screening has successfully identified peptides with affinity for various inorganic substrates^18,19 by sampling up to 10¹⁰ sequences, but this is still only a small fraction of possible sequences and peptide sequences are sampled randomly. This limitation combined with the experimental labor and cost of library screening encourages the use of alternative design strategies. One alternative is biophysics-based design, which reduces the use of experimental resources and can intelligently explore peptide sequence space.¹⁷ Examples include Rosetta surface design,²⁰ iterative procedures combining experimental and computational data,^21,22 and the Peptide Binder Design (PepBD) algorithm.²³ PepBD is especially relevant to this work as it was recently used to design PBPs for four common plastics: polyethylene (PE), polypropylene (PP), polystyrene (PS), and polyethylene terephthalate (PET).¹⁷ However, a major drawback of biophysical methods is that they sample even fewer peptides than library screening due to the computational expense of modeling peptide-plastic interactions. This motivates the adoption of deep learning (DL) models, which can be trained on modeling or library screening datasets to identify relationships between the peptide sequence and the design target,^24,25i.e. peptide affinity to a certain type of plastic. There are many examples of DL having success in this domain, including predictions of whether a peptide will bind polystyrene using PS-Binder,^12,26 discovery of quartz-binding peptides,²⁷ and improvement of binding selectivity of peptides between gold and silver.²⁸

DL's promise in design is often limited by methods that, while powerful, typically do not offer quantified estimations of the reliability of the predictions.²⁹ Thus, a crucial consideration in DL-based peptide design, and in molecular design in general, is uncertainty quantification, which aims to estimate the model's confidence in its predictions.^24,25 Uncertainties in model predictions can preclude sampling of peptides with high affinity and lead to over-sampling in regions where the model lacks confidence and over-generalizes.^30,31 This is particularly relevant to peptide design, where the training data often covers a tiny fraction of possible amino acid sequences, and testing and synthesizing peptides is expensive and time-consuming. It thus is highly desirable to incorporate uncertainty quantification into the peptide design process to strategically navigate the vast combinatorial space and to prioritize candidates based on both predicted affinity and the reliability of predictions derived from biophysics-based calculations.^32,33

Traditional uncertainty quantification methods in deep learning, such as Bayesian neural networks³⁴ and sampling-based³⁵ approaches, although useful, are often computationally intensive for large datasets,^29,36 potentially compromising both efficiency and accuracy.³⁷ These limitations are particularly pronounced in the context of peptide design, where the sheer number of theoretically possible sequences and the different types of peptide–plastic interactions (e.g. hydrogen bonding, pi–pi interactions, hydrophobic forces) pose significant challenges. As an alternative, evidential deep learning (EDL) directly learns and represents uncertainties without the need for extensive sampling.³⁶ Furthermore, EDL's seamless integration with domain-specific architectures amplifies its capacity to quantify uncertainty across peptide–plastic binding affinities and diverse plastic types.³⁸

In this work, we pair biophysical modeling with EDL to discover PBPs for several types of plastic. We hypothesize that quantifying score prediction uncertainty will lead to more effective exploration of peptide sequence space by encouraging the model to ignore sequences for which it cannot confidently predict affinity. To test this hypothesis, we train a convolutional neural network (CNN) with an EDL layer on PepBD data, then combine the trained model with biased random key genetic algorithm (BrKGA) to search for peptides with high affinity for four common plastics: polyethylene, polypropylene, polystyrene, and PET. The trained model accurately predicts affinity calculations from PepBD and generates unique peptides with higher predicted affinity than the best corresponding PepBD designs for all plastics. Validation of EDL peptides using molecular dynamics simulations shows that the EDL peptides have greater affinity than random sequences of amino acid for all plastics, and greater affinity than PepBD peptides for all plastics but PET. For PET, EDL peptides have slightly lower affinity than PepBD peptides, which we attribute to the greater chemical complexity of PET relative to the other plastics. Overall, our results show that uncertainty-aware design can discover and optimize biomaterials for microplastic remediation, and more generally develop solutions to complex environmental and technological problems.

Methods

This section outlines the methodologies employed, including the PepBD method, EDL and optimization framework, and MD simulations. First, the PepBD method¹⁷ is briefly described, which utilizes Metropolis Monte Carlo sampling to calculate scores for amino acid sequences adsorbing to various plastic surfaces. Next, we detail the EDL-based design framework, combining peptide representation, EDL-based binding prediction, design constraints, and the BrKGA method to design high-affinity PBPs. Lastly, we describe the MD simulations performed to validate peptide affinities, using high-temperature simulations and clustering to identify stable adsorbed conformations and then calculating adsorption free energies with the MMGBSA method.³⁹

PepBD method

PepBD was previously used¹⁷ to calculate scores for a large number of amino acid sequences adsorbing to a PE, PP, PS, or PET surface. We provide a brief description of PepBD here, and more details can be found in previous work.⁴⁰ PepBD samples peptide conformations and amino acid sequences using Metropolis Monte Carlo. A random change is made either to the sequence or backbone dihedral angles, the side chains are energy minimized, and the peptide is scored via

Score = ΔG + αU_pep (1)

where ΔG is the binding free energy calculated using the MM/GBSA method,⁴¹U_pep is the peptide internal energy, and α is a scaling factor set to 0.01. U_pep is included to ensure the peptide structure does not have high energy. The likelihood of accepting the change to the peptide is given by the Metropolis criterion,kT is the reference temperature which governs the likelihood of accepting a change that worsens the peptide score. Given a starting peptide sequence and structure provided by the user, tens of thousands of sequence or conformation changes are attempted per design run. The reference temperature is reduced during design per an annealing schedule, resulting in PepBD converging to a local minimum. Since the local minimum is not guaranteed to be the global minimum, peptide design is repeated several times for a given starting conformation over many different starting conformations. For the data set used in this paper, a total of 20 conformations were used for PE designs, and 11 conformations were used for PP, PS, and PET designs, with 5 designs performed for each starting conformation. This gave a total of 939k, 484k, 457k, and 442k unique sequence : score data points for the PE, PP, PS, and PET datasets, respectively.

Evidential deep learning and optimization framework

Our EDL framework combines peptide representation, EDL-based binding prediction, design constraints, and a genetic algorithm to design PBPs. First, peptides are encoded into one-hot vectors. Next, a tailored CNN with an EDL layer³⁶ predicts peptide-plastic binding affinity and associated uncertainty. Design constraints based on hydrophobicity, the PepBD dataset, and predicted uncertainty guide the optimization process. Finally, the BrKGA optimization method is used to explore the search space, utilizing the deep learning model for fitness evaluation to identify promising PBPs. These components are shown in Fig. 1, and the following paragraphs discuss each component in the given order.

Fig. 1 An overall schematic outlining the steps of the deep learning and optimization framework for designing plastic-binding peptides. The framework consists of four steps: (1) peptide representation: peptides are encoded using a one-hot encoding scheme. (2) Deep learning model: a tailored convolutional neural network (CNN) with an Evidential Deep Learning (EDL) output layer is used to predict peptide-plastic binding affinities. (3) Design constraints: identify constraints on hydrophobicity, constraints derived from the PepBD dataset, and uncertainty. (4) Biased random Key Genetic Algorithm (BrKGA): a genetic algorithm-based optimization method is employed to identify plastic-binding candidate peptides with high affinity that meet specific design criteria using the EDL model for evaluating generations of peptides. Figure created with Biorender.

Peptides were represented using a one-hot encoding scheme, transforming each amino acid into a 21-dimensional vector (20 common amino acids plus one placeholder for unknown or other amino acids). The dataset was split into 90% for training, 5% for validation, and 5% for testing. This encoding method preserves the sequential nature of peptide information, enabling direct input into computational models. More complex representations, such as graphs, did not yield performance improvements and performed worse, likely due to the need for spatial and conformational information. This observation aligns with findings from state-of-the-art protein classification and regression models, such as ProtCNN.⁴²

An optimized CNN with an EDL output layer was developed to predict PBPs affinities. Initially trained on PE data, the model was adapted through transfer learning to improve performance for other plastics by approximately 10%. The one-dimensional CNN architecture includes an input layer for one-hot encoded peptide sequences, three convolutional layers with 128, 64, and 32 filters, respectively, and max pooling layers to reduce dimensionality. Two fully connected layers further process the features, with dropout regularization to prevent overfitting. The EDL output layer, specifically a normal gamma layer, performs the regression task, predicting binding affinity and its associated uncertainty. The EDL layer is crucial for providing confidence intervals alongside binding affinity predictions, aiding in the selection of top candidate peptides. The model uses the adam optimizer, EDL-specific loss function, and Mean Absolute Error (MAE) as an evaluation metric, with L2 regularization to mitigate overfitting. Overall, the devised CNN architecture strikes a balance between expressive power and computational efficiency with 81 700 trainable parameters, making it well-suited for the compact representations of peptides featuring 252 integer elements. We observe that more complex models, such as transformers⁴³ and ProtCNN,⁴² yielded slightly worse results likely due to the low dimensionality of peptide data. Additional architectural details and hyperparameters are also available in our models and data repository.

The BrKGA optimization method⁴⁴ on Pymoo⁴⁵ was employed to optimize peptide sequences for binding affinity to plastics, leveraging the predictions from the CNN-EDL model. BrKGA was chosen for its success in solving complex combinatorial problems, efficient search mechanisms, and adaptability to various problem structures.⁴⁶ The algorithm's fast convergence and effective handling of large search spaces make it ideal for peptide design. Initial populations were generated with and without bias towards amino acids known to enhance plastic binding. The fitness function integrated predicted binding affinity, uncertainty magnitude, and constraint violations, guiding the selection of promising candidate peptides. Key operators included tournament selection, simulated binary crossover, and polynomial mutation to maintain diversity. Hyperparameters were fine-tuned using a systematic grid search, optimizing crossover probability, distribution indices, population size, and the number of generations. Because all peptides in the PepBD dataset do not use the amino acids cysteine or proline and allow no more than 3 tryptophan per peptide to maintain peptide solubility in water, these constraints were also enforced by BrKGA. We observe that this combination of BrKGA with EDL predictions enhances the identification of high-affinity PBPs in terms of PepBD scores.

Molecular dynamics simulations

To prepare simulations, the peptide in an extended conformation was placed near the plastic surface by rotating the peptide so its long axis was parallel to the plastic surface, then translated so that the distance between the peptide center of mass and the top of the plastic surface was 4 Å. tLEaP solvated the system by adding TIP3P water 15 Å above the peptide and 10 Å below the bottom of the plastic surface, giving a simulation box size of roughly 50 Å in the direction normal to the plastic surface. The Amber coordinate and parameter files were converted to Gromacs format using Parmed⁴⁷ before running simulations with Gromacs version 2019.6.⁴⁸ The system was energy minimized for up to 1000 steps using steepest descent, heated to 300 K in the NVT ensemble for 100 picoseconds, then equilibrated at 1 bar and 300 K in the NPT ensemble for 200 ps. Different adsorbed conformations were obtained by running a high temperature simulation. The system was heated to 550 K over 200 picoseconds in the NVT ensemble, then simulated for an additional 10 ns. To prevent the peptide from diffusing too far from the surface, the Wall utility in PLUMED⁴⁹ was added to the simulation at a distance of 10 Å from the top of the plastic surface. k-Means clustering with CPPTRAJ⁵⁰ using the peptide alpha carbons extracted 16 representative adsorbed conformations. A representative of each cluster was simulated by first cooling back to 300 K in the NVT ensemble for 100 picoseconds, then simulating for 1 ns at 300 K. Adosrption free energies for each conformation were calculated using Amber's MMGBSA tool.⁵¹ The 8 conformations with the lowest binding free energy were simulated an additional 4 ns, then the adsorption free energy calculation was repeated. The lowest adsorption free energy was selected as representative of the peptide's binding affinity. Simulations used the TIP3P water model,⁵² GAFF⁴⁰ parameters for plastics with partial charges calculated in our previous work,¹⁷ and the ff14SB force field⁵³ for peptides. Atomistic models of plastic surfaces were taken from our previous work.¹⁷ Position restraints were applied to non-hydrogens in the plastic using a force constant of 5000 kJ mol⁻¹ nm⁻². The LINCS algorithm⁵⁴ restrained bonds to hydrogen. Long-range electrostatic interactions were treated using particle mesh Ewald. The simulation time step size was 2 fs. The velocity rescaling algorithm⁵⁵ controlled the system temperature in the NVT and NPT ensembles. The time constant was 0.1 picoseconds, and separate thermostats were applied to water molecules versus the rest of the system. The semi-isotropic Berendsen barostat⁵⁶ controlled the pressure in NPT simulations. The x and y dimensions of the simulation box were allowed to change independently from the z-dimension, the isothermal compressibility was set to 4.5 × 10⁻⁴ for all directions, and the time constant was set to 5 ps.

Results and discussion

In this study, we evaluate the performance of an EDL framework tailored for uncertainty quantification in the computational design of PBPs to estimate uncertainties in binding scores. The framework leverages a convolutional neural network (CNN) architecture with an evidential layer trained on data generated by the PepBD algorithm, a biophysics-based method that has successfully designed peptides that bind to proteins and, more recently, common plastics.¹⁷ The EDL model is trained to predict, for a given sequence, the PepBD score, a measure of the peptide's affinity for the given plastic, along with the uncertainty in the predicted score. We expect that accounting for the uncertainty in the predicted score will help the model avoid sampling sequences for which it cannot confidently predict the affinity. To discover PBPs, we connect the trained EDL model to the Biased Random Key Genetic Algorithm (BRKGA).⁴⁴ This integrated approach allows us to assess the predictive capabilities of the EDL model by comparing the binding affinities and uncertainties of the resulting EDL-designed peptides to those generated by PepBD alone on four common plastics: polyethylene, polypropylene, polystyrene, and polyethylene terephthalate (PET). We further employ MD simulations to validate the binding free energies of the top-ranking PBPs and benchmark their performance against both existing PepBD-designed peptides and randomly generated sequences. This comprehensive evaluation demonstrates that our framework can accelerate PBP discovery which can aid MP remediation efforts.

Evidential deep learning enables enhanced plastic-binding peptide design with biophysical modeling data

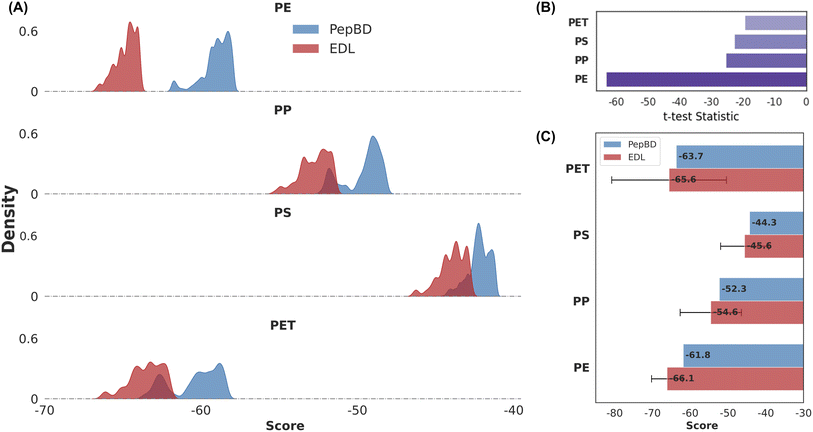
Fig. 2A highlights the capacity of the EDL model to leverage PepBD data and identify PBPs with superior predicted binding affinities compared to the PepBD method alone. Across all four plastics (polyethylene, polypropylene, polystyrene, and PET), the distributions of predicted binding scores for the top EDL candidates are consistently lower (indicating stronger binding) than the scores for PepBD candidates. This suggests that the EDL model effectively identifies peptides within the vast sequence space that were not discovered by PepBD. The degree of improvement varies across plastics, with PE exhibiting the largest enhancement. This material-dependent effect may arise due to differences in the complexity of peptide–plastic interactions, inherent biases in the PepBD data for each plastic type, or differences in the size of the PepBD data set between the plastics.

Fig. 2 Performance comparison of Evidential Deep Learning (EDL) and PepBD for plastic–peptide binding design. (A) Distribution of predicted binding scores for the top 100 EDL candidates and top 1000 PepBD candidates across four plastics: polyethylene (PE), polypropylene (PP), polystyrene (PS), and polyethylene terephthalate (PET). (B) t-Test statistic for each plastic, indicating the statistical significance of the score differences between DL and PepBD candidates (all p-values = 0). The ranking (smallest to largest) reflects the order in which the plastics exhibit the most substantial performance differences between the two methods. (C) Comparison of the top 20 DL and PepBD candidate scores for each plastic, highlighting the effect of uncertainty quantification in DL predictions. The DL ranges represent the mean ± 95% confidence interval for the predicted binding scores using EDL.

The difference in binding score distributions of EDL and PepBD designs, visualized in Fig. 2A, are statistically significant for all plastics. As shown in Fig. 2B, negative t-test statistics⁵⁷ and p-values < 0.001 for all four plastics demonstrate that peptides designed by EDL have much more negative scores than those generated by PepBD. Ranking of the t-values shows polyethylene has the most pronounced difference between the two methods. To address the normality assumption inherent to t-tests, a non-parametric Mann–Whitney U test⁵⁸ was also performed, yielding similarly significant results with all p-values being 0, further corroborating the observed performance gap.⁵⁹ The calculated average mean improvements of EDL over PepBD—9.8% (polyethylene), 6.3% (polypropylene), 4.0% (polystyrene), and 5.1% (PET)—provide a quantitative measure of the EDL model's advantage. However, statistical significance does not equate to practical relevance, so we incorporated uncertainty quantification early in model development to ensure the reliability and applicability of predictions.

Fig. 2C presents an assessment of the uncertainty in EDL-predicted binding affinities. While EDL outperforms PepBD in mean predicted scores, the associated uncertainties, visualized as confidence intervals, vary across plastics and candidates. Average uncertainties range from 4.3 kcal mol⁻¹ (polyethylene) to 14.6 kcal mol⁻¹ (PET), highlighting the model's reduced confidence for certain predictions, especially PET. Material-specific variation in uncertainty may stem from differing complexities in peptide-plastic interactions or biases within the PepBD training data. For example, PET has more functional groups than polyethylene, meaning there are more types of peptide–plastic interactions to consider such as hydrogen bonding and pi–pi stacking. Recognizing this modelling limitation, the EDL framework incorporates uncertainty directly into the objective function in the generation process, prioritizing peptides with lower uncertainties to enhance the confidence and practical relevance of our designs. Although this may yield slightly less favorable mean binding scores compared to a purely score-driven approach, it prioritizes candidates with a higher likelihood of strong binding in simulation and experimental validation. We expand on this topic in the discussion section.

Deep learning identifies novel peptides for plastic binding with enhanced hydrophobicity and selective affinity profiles

EDL peptides are unique relative to the PepBD peptides. This is clearly demonstrated by the difference in the amino acid frequencies between the top 100 PepBD and EDL designs (Fig. 3A). EDL designs are more enriched in bulky and hydrophobic residues methionine (M) and phenylalanine (F), while PepBD designs are enriched in charged or hydrophilic residues arginine (R), asparagine (N), and glutamine (Q). This suggests that EDL's approach for increasing peptide affinity was to increase peptide mass and hydrophobicity, in agreement with physical intuition for this design task. However, EDL's strategy has a more complexity, as reflected by two observations. First, not all bulky or hydrophobic residues are used. Tyrosine (Y), isoleucine (I), and leucine (L) all appear infrequently in EDL designs, a trend likely learned from the PepBD data where these residues were also used infrequently. Second, EDL designs have a greater frequency of lysine (K), a charged residue with a smaller mass than arginine. Thus, EDL appears to have learned a nuanced representation of peptide affinity for plastic.

Fig. 3 Properties of EDL designs. (A) The amino acid frequency in the 100 peptides with the best scores for polyethylene designed by either EDL or PepBD. (B) The amino acid frequency in the 100 peptides with the best scores for polyethylene (PE), polypropylene (PP), polystyrene (PS), and polyethylene terephthalate (PET) designed by EDL.

Comparing the amino acid composition of EDL peptides for all the plastics reveals common peptide features. The same amino acid types appear with high frequency, namely arginine (R), histidine (H), methionine (M), phenylalanine (F), and tryptophan (W) (Fig. 3B). These residues all have bulky side chains, indicating that EDL increases peptide affinity by increasing the number of possible intermolecular interactions or reducing the solvent-accessible surface area of the plastic. We note that the frequency of tryptophan is identical for all plastics due to a limit of 3 or fewer tryptophan per peptide, a constraint also used when generating the PepBD data set. While the amino acid frequencies are general similar between all plastics, there are some differences. Methionine (M) is more frequent in PE designs, perhaps because the crystallinity of the polyethylene surface facilitates interactions with the amino acid. Designs for PET have the greatest frequency of arginine (R), likely because it can form electrostatic interactions with the oxygens in the terephthalic acid group, which carry a partial negative charge. Isoleucine (I) and leucine (L) are more common in designs for polypropylene and polystyrene, respectively. This may be because the models of these plastic surfaces used to collect PepBD data have greater surface roughness, and the greater conformational freedom of leucine and isoleucine permits closer conformation to the plastic surface compared to amino acids with more rigid side chains. A question raised by Fig. 3B is how selective a peptide will be for a given plastic. The similar amino acid compositions suggest there are peptides that can bind strongly to multiple types of plastics. The amino acid composition differences also suggest that there may be peptides that bind selectivity, at least to some degree, to each plastic. However, it should be noted that peptide affinity depends on the arrangement of amino acids rather than just on the amino acid composition,²⁰ and that these hypotheses merit further investigation.

Designed peptides confirmed to have high affinity for plastic in molecular dynamics simulations

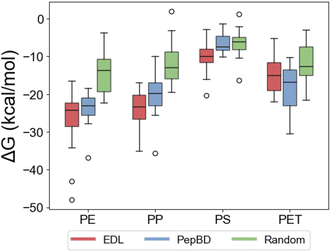
MD simulations show that the EDL peptides consistently have greater affinity for plastic than randomly generated amino acid sequences for all plastics, and greater affinity than PepBD peptides for polystyrene and polypropylene. We validated the EDL peptides by performing MD simulations and comparing the results to peptides from two other design methods: PepBD and random generation of amino acid sequences in which each amino acid was selected randomly and independently of all other residues. Twelve peptides were tested for each plastic: design method combination to enable comparison between the design methods over a large sample size at a reasonable computational cost. A larger sample size of peptides was used for polyethylene: PepBD (20 peptides) and polyethylene: EDL (15 peptides) to evaluate variability in a given design method for the same plastic. The adsorption free energy (ΔG) calculated for each peptide is shown in Fig. 4. Note that affinity increases as ΔG decreases. The percent difference in the median ΔG for EDL designs relative to PepBD designs shows that EDL peptides have higher affinity than PepBD peptides for polypropylene (18%), polystyrene (34%), and polyethylene (5%), but slightly lower affinity for PET (−11%) compared to PepBD designs. EDL peptides have higher affinity than random sequences of amino acids for all plastics. The statistical significance of the difference in affinity was evaluated using a two-sided equivariance t-test. The difference between EDL and PepBD peptides is significant for polystyrene, while the difference between EDL and random peptides is significant for all plastics except PET (Table 1). We thus conclude that pairing EDL with PepBD data can effectively design PBPs, although improvements could be made in designing PBPs for polyethylene and PET. The best three EDL designs for each plastic are provided in Table 2.

Fig. 4 Validation of EDL designs in molecular dynamics simulations. Adsorption free energies (ΔG) of EDL peptides designs, PepBD designs, and randomly generated amino acid sequences to polyethylene (PE), polypropylene (PP), polystyrene (PS), and polyethylene terephthalate (PET). The sample size for each design type with each plastic was 12 peptides, except for PE where 15 EDL peptides and 20 PepBD peptides were tested to evaluate variance between designs over a larger sample size. Results are shown as a box plot for the range of adsorption free energies of each design type.

Table 1 EDL peptides have high affinity for plastic relative to PepBD PBPs and random sequences of amino acid

Plastic	EDL vs. PepBD		EDL vs. random
	p-Value^a	Percent median ΔG improvement^b	p-Value	Percent median ΔG improvement
a Calculated using a two-sided, equivariance t-test. b Median improvement relative to either PepBD or random peptides; a positive improvement corresponds to higher affinity for EDL peptides to the given plastic than either PepBD or random peptides.
Polyethylene	0.140	+5%	2.94 × 10^−4	+78%
Polypropylene	0.126	+18%	−3.86 × 10^−5	+81%
Polystyrene	2.40 × 10^−2	+34%	5.58 × 10^−2	+64%
PET	0.205	−11%	0.196	+18%

---

Table 2 Best peptides found using EDL for all plastics

Plastic	Peptides sequence	ΔG (kcal mol^−1)
Polyethylene	RMHWWMKWFMRR	−48.0
	FFMWHMKWYMRW	−43.0
	SWMHKIHWHMRW	−34.1
Polystyrene	WWMRHMFAWRIF	−35.0
	FWWRTIVWRHIR	−28.3
	YFIWWWRMFFFR	−27.2
Polypropylene	FIFRWWQWHVRM	−20.3
	WWMRWHRLFFIR	−16.0
	WRWIRLIWQGHR	−12.5
PET	FHVWWINIFWFF	−22.0
	FMRWWRMYWFDF	−21.7
	FHEWWRMYWHRY	−19.9

---

The variability in molecular dynamics results emphasizes the need for this screening step prior to using the designed peptides for MP remediation. The values of ΔG span a large range, highlighting the need to evaluate not just the best design but multiple designs. Scores, either from PepBD or EDL, are only predictions of affinity and do not guarantee that high affinity will be observed in MD simulations or experimentally. Thus, MD can screen out false positives to minimize the cost, time, and labor of developing effective peptide-based tools of MP remediation. While the MD protocol can evaluate many peptides (∼150 total) at a reasonable computational cost, its relatively simplistic theoretical basis reduces the accuracy of calculations. It is proper to view the MD results as an initial screen that identifies promising peptides which require more rigorous evaluation, as we describe in detail in the discussion.

Analysis reveals that uncertainty-aware design helps generate better peptides. Ideally, lower uncertainty in score predictions would correspond to better peptide performance. To quantify peptide performance, we can use the percent difference in the median affinity of EDL peptides relative to PepBD or random peptides, as provided in Table 1. We term this quantity “improvement” for the sake of discussion. Noting that uncertainty in score predictions varied greatly between plastics (Fig. 1C), we can determine how score uncertainty relates with peptide performance by plotting improvement versus average uncertainty for all plastics (Fig. 5). The comparison between EDL and random peptides clearly displays the desired trend – as score uncertainty decreases, EDL peptides have greater improvement. The same trend appears to be present when comparing EDL and PepBD peptides, albeit the trend is weaker. We attribute this to PepBD performing better for some plastics (e.g., polyethylene, where PepBD greatly outperforms random peptides) than others (e.g. polystyrene, where PepBD has almost equal performance as random peptides), so possible improvement of EDL designs varies between plastics. Whatever the explanation may be, Fig. 5 shows a strong relationship between lower uncertainty and better peptide performance.

Fig. 5 Lower average uncertainty in EDL score predictions correlates with greater affinity measured by MD simulations. The x-axis is the average uncertainty in the top 100 peptides found by EDL for each plastic. The y-axis is the improvement, or percent difference in the median adsorption free energy between EDL peptides and either random peptides (left) or PepBD peptides (right). Average score uncertainty is taken from Fig. 1c, and improvement is taken from Table 1.

Conclusions

Our research successfully integrates evidential deep learning with PepBD to identify plastic-binding peptides that can be useful for remediating MP pollution. The integrated model finds better-scoring peptides than PepBD for the common plastics polyethylene, polystyrene, polypropylene, and PET. The improvement in peptide scores was statistically validated, and uncertainty quantification allowed us to select peptides that the model predicted to have high affinity with great certainty. Evaluation of the designed peptides in MD simulations showed that EDL peptides had greater affinity than PepBD, enhancing peptide affinity with median binding free energy improvements of 18% for polypropylene, 34% for polystyrene, and 5% for polyethylene. This demonstrates the ability of modeling and uncertainty quantification-based AI tools to develop biologically friendly tools that can help address the pressing environmental issue of MP pollution.

The EDL model possesses useful properties that facilitate peptide design. The model is statistically robust and quantifies uncertainty. This enhances confidence in the predictive power of models and guides the selection of peptides for practical applications. The result is reduced time, labor, and cost during the development of peptide tools for MP remediation as fewer design iterations are required. The EDL model is general - it designed high-affinity peptides for several common plastics, suggesting that the model can be readily transferred to other peptide design tasks previously addressed by PepBD, such as proteins⁶⁰ or RNA.²³ The worse performance of PBP designs for PET indicates that some degree of model tailoring may be needed to capture the complexity of peptide interactions. For example, improved performance for PET could be achieved either by adding more detail to the PepBD dataset or by modifying the architecture or training procedure. The EDL model is flexible. While PepBD data was used in this study to train the model, the PepBD dataset could be complemented with the MD dataset generated in this work to give a richer dataset to train the EDL model. Similarly, if a sufficiently large experimental dataset becomes available for peptide–plastic interactions, such data could be used for model training. This can be useful given the limitations in PepBD modeling including the limited sampling of peptide conformations.

EDL uncertainty varies greatly between plastics and is significantly larger for PET than for the other plastics. We attribute the high uncertainty with PET to two factors that make peptide interactions with PET more complex compared to the other plastics. PET contains polar ester groups and aromatic moieties that interact with the peptide through hydrogen bonding, strong electrostatic interactions, and π–π stacking.⁶¹ The chemical complexity in the PET monomer also leads to a more chemically heterogeneous surface relative to the other plastics. These two factors make PET–peptide interactions complicated and sensitive to system geometry. This differs from peptide interactions with polyethylene and polypropylene, which are driven primarily by hydrophobic and van der Waals interactions. From a deep learning standpoint, it is notable that even though the dataset for PET is only slightly smaller than that used for polypropylene or polystyrene, the greater complexity of peptide–PET interactions results in poorer performance. Resolution of these issues is needed, else model uncertainty will remain elevated and predictions may bias towards simple hydrophobic binding patterns. We see two possible solutions. The first solution is to obtain PepBD data for many more conformations of peptide adsorbed to PET. Increasing the data set size ideally will help the DL model learn a better implicit representation of PET heterogeneity. A second, more complicated solution is to modify our current CNN-based EDL mode, which relies solely on sequence-level features, to include peptide and PET structure in the input representation. This is motivated by work highlighting the importance of capturing specific structural and electrostatic details when modeling interactions between peptides and materials.⁶² This could be achieved using graph neural networks.⁶³

Additional evaluation of the best EDL PBPs will be essential to determine their usefulness for MNP remediation. The MD analysis provided in this work is coarse and preliminary, since the free energy calculations use an implicit solvent model and do not account fully for the peptide's conformation entropy. These simplifications were needed so we could evaluate a large sample of peptides. Having identified the most promising peptides, future work can focus on more rigorously evaluating the best PBPs using simulations methods like metadynamics^64,65 or umbrella sampling.^66,67 Experimental measurements of peptide affinity using methods like atomic force microscopy are also essential. These measurements are underway and will be reported in a future manuscript that evaluates both EDL and PepBD peptides.

The peptides identified in this work can be integrated into many existing technologies and methods developed in recent years for MNP remediation. Examples of these recent developments abound: MNP pollution can be detected using spectroscopy,⁶⁸ chromatography,⁶⁹ image-processing,⁷⁰ liquid crystals sensors,⁷¹ or surface plasmon resonance;⁷² MNP pollution can be captured with magnetic biochar,⁷³ biopolymers,^74,75 fungal mycelium,⁷⁶ carbon-based materials, chemical coagulation,⁷⁷ or lysozyme-based amyloid fibrils;⁷⁸ and MNP pollution can be degraded both chemically⁷⁹ and biologically.^80,81 We believe PBPs can augment many of these technologies. Plastic-degrading microorganisms can be genetically engineered to express PBPs to facilitate biofilm formation and subsequent plastic degradation. PBPs could supplement amyloid fibrils in capturing MNP pollution. PBPs could help improve the sensitivity of the sensors for MNPs. Peptides also possess two properties that are advantageous for MNP remediation. First, peptides are naturally biocompatible, meaning PBPs could help monitor or remove MNP pollution in biological settings. Second, peptides interact with plastic via adsorption, a process driven by surface area, which suggests that PBPs may be particularly helpful in remediating nanoplastics, which have large specific surface area.

Potential limitations of applying PBPs to remediating MNP pollution merit discussion. Perhaps the most significant practical barrier is the cost of peptide synthesis. Two broad routes exist for synthesizing peptides: chemical⁸² and biological.⁸³ Chemical synthesis is well established and several companies offer this service, but purchasing large quantities of peptide is impractical due to the high cost. We thus believe that producing PBPs through chemical synthesis would only be suitable for small scale remediation, method development, and MNP research. Biological synthesis of PBPs can be achieved by engineering microbes to continually produce the PBPs. We think that this could be a promising way to apply PBPs to MNP remediation on a large scale, given the interest and effort in scaling up bioremediation strategies. Another possible issue is the complexity of environmental conditions. MNPs are found in essentially all environment domains that span large ranges of properties like salinity, pH, and temperature. Changes in these properties could influence which PBP should be selected for a given plastic in a given environment. The environment can contain other chemical species that compete with PBPs to adsorb to MNPs. For example, a protein corona⁸⁴ and biofilm⁸⁵ may form on MNPs. Predicting the influence of these environmental factors on PBP adsorption to MNPs is challenging and should be explored in the future.

The designed peptides and our computational framework hold significant potential for the development of peptide-based materials and technologies for MP detection, capture, and degradation. The application of such peptides in environmental safety measures could revolutionize strategies for mitigating MP pollution, particularly in aqueous environments where such pollution is damaging and most pervasive. Our open-source approach to data and methodologies will help advance scientific understanding of peptide–plastic interactions and foster collaborative environment that encourages further research in the application of peptides to MP remediation. This openness is intended to spur innovation across disciplines, leading to more effective solutions to difficult environmental solutions and better functional biomaterials.

Data availability

All data, results, models, and evidential deep learning and biased random key genetic algorithm methods are publicly available for research use and can be accessed at: https://github.com/AbdulelahAlshehri/Biophysics-Guided-Uncertainty-Aware-Deep-Learning-Uncovers-High-Affinity-Plastic-Binding-Peptides. The PepBD code used to generate the data in this work can be accessed at https://github.com/CarolHall-NCSU-CBE/PepBD_Plastics.

Author contributions

Conceptualization: FY, CKH, methodology: ASA, MTB, CKH, FY, investigation: ASA, MTB, FY, visualization: ASA, MTB, supervision: FY, CKH, writing—original draft: ASA, MTB, writing—review & editing: ASA, MTB, CKH, FY.

Conflicts of interest

The authors have no conflicts of interests to disclose.

Acknowledgements

MTB gratefully acknowledges the Expanse Supercomputing Center allocation provided by ACCESS for computational resources needed to conduct molecular dynamics simulations. MTB and CKH were supported by National Science Foundation Grant EFRI E3P-2029327. MTB also received funding from National Institutes of Health grant 1T32GM133366. FY acknowledges the partial support from the Schmidt Sciences.

References

1. R. S. Bang, M. Bergman, T. Li, F. Mukherjee, A. S. Alshehri, N. L. Abbott, N. C. Crook, O. D. Velev, C. K. Hall and F. You, AIChE J., 2023, 69, e18020.
2. H. Kye, J. Kim, S. Ju, J. Lee, C. Lim and Y. Yoon, Heliyon, 2023, 9, e14359.
3. S. O'Brien, C. Rauert, F. Ribeiro, E. D. Okoffo, S. D. Burrows, J. W. O'Brien, X. Wang, S. L. Wright and K. V. Thomas, Sci. Total Environ., 2023, 874, 162193.
4. J. Zhao, R. Lan, Z. Wang, W. Su, D. Song, R. Xue, Z. Liu, X. Liu, Y. Dai and T. Yue, Nat. Nanotechnol., 2024, 19, 406–414.
5. I. A. Kane, M. A. Clare, E. Miramontes, R. Wogelius, J. J. Rothwell, P. Garreau and F. Pohl, Science, 2020, 368, 1140–1145.
6. Y. Pan, S.-H. Gao, C. Ge, Q. Gao, S. Huang, Y. Kang, G. Luo, Z. Zhang, L. Fan and Y. Zhu, Environ. Sci. Ecotechnology, 2023, 13, 100222.
7. K. Yin, Y. Wang, H. Zhao, D. Wang, M. Guo, M. Mu, Y. Liu, X. Nie, B. Li and J. Li, Sci. Total Environ., 2021, 774, 145758.
8. Y. Zhao, S. Liu and H. Xu, Chemosphere, 2023, 138486.
9. R. Marfella, F. Prattichizzo, C. Sardu, G. Fulgenzi, L. Graciotti, T. Spadoni, N. D'Onofrio, L. Scisciola, R. La Grotta and C. Frigé, N. Engl. J. Med., 2024, 390, 900–910.
10. V. Kopatz, K. Wen, T. Kovács, A. S. Keimowitz, V. Pichler, J. Widder, A. D. Vethaak, O. Hollóczki and L. Kenner, Nanomaterials, 2023, 13, 1404.
11. H. Woo, S. H. Kang, Y. Kwon, Y. Choi, J. Kim, D.-H. Ha, M. Tanaka, M. Okochi, J. S. Kim and H. K. Kim, RSC Adv., 2022, 12, 7680–7688.
12. C. Meng, Y. Hu, Y. Zhang and F. Guo, Front. Bioeng. Biotechnol., 2020, 8, 245.
13. D. Walczyk, F. B. Bombelli, M. P. Monopoli, I. Lynch and K. A. Dawson, J. Am. Chem. Soc., 2010, 132, 5761–5768.
14. M. Ansari and A. D. White, Digital Discovery, 2024, 3, 977–986.
15. V. D. Aldas-Bulos and F. Plisson, Digital Discovery, 2023, 2, 981–993.
16. F. Wan, D. Kontogiorgos-Heintz and C. de la Fuente-Nunez, Digital Discovery, 2022, 1, 195–208.
17. M. T. Bergman, X. Xiao and C. K. Hall, J. Phys. Chem. B, 2023, 127, 8370–8381.
18. U. O. S. Seker and H. V. Demir, Molecules, 2011, 16, 1426–1451.
19. A. Care, P. L. Bergquist and A. Sunna, Trends Biotechnol., 2015, 33, 259–268.
20. D. L. Masica, S. B. Schrier, E. A. Specht and J. J. Gray, J. Am. Chem. Soc., 2010, 132, 12252–12262.
21. Z. E. Hughes, M. A. Nguyen, J. Wang, Y. Liu, M. T. Swihart, M. Poloczek, P. I. Frazier, M. R. Knecht and T. R. Walsh, ACS Nano, 2021, 15, 18260–18269.
22. S. P. Schwaminger, P. Anand, M. Borkowska-Panek, S. A. Blank-Shim, P. Fraga-Garcia, K. Fink, S. Berensmeier and W. Wenzel, Langmuir, 2019, 35, 8472–8481.
23. X. Xiao, C. K. Hall and P. F. Agris, J. Biomol. Struct. Dyn., 2014, 32, 1523–1536.
24. B. Sanchez-Lengeling and A. Aspuru-Guzik, Science, 2018, 361, 360–365.
25. B. Decardi-Nelson, A. S. Alshehri, A. Ajagekar and F. You, Comput. Chem. Eng., 2024, 108723.
26. N. Li, J. Kang, L. Jiang, B. He, H. Lin and J. Huang, BioMed Res. Int., 2017, 2017, e5761517.
27. E. E. Oren, C. Tamerler, D. Sahin, M. Hnilova, U. O. S. Seker, M. Sarikaya and R. Samudrala, Bioinformatics, 2007, 23, 2816–2822.
28. Z. E. Hughes, M. A. Nguyen, J. Wang, Y. Liu, M. T. Swihart, M. Poloczek, P. I. Frazier, M. R. Knecht and T. R. Walsh, ACS Nano, 2021, 15, 18260–18269.
29. A. S. Alshehri and F. You, Chem. Eng. J., 2022, 444, 136669.
30. C.-I. Yang and Y.-P. Li, J. Cheminf., 2023, 15, 13.
31. A. S. Alshehri, A. K. Tula, L. Zhang, R. Gani and F. You, in Computer Aided Chemical Engineering, Elsevier, 2021, vol. 50, pp. 227–233.
32. B. Hie, B. D. Bryson and B. Berger, Cell Syst., 2020, 11, 461–477.
33. A. S. Alshehri and F. You, Front. Chem. React. Eng., 2021, 3, 700717.
34. J. M. Hernández-Lobato and R. Adams, Probablistic Backpropagation for Scalable Learning of Bayesian Neural Networks, arXiv, 2015, preprint, arXiv:1502.05336,  DOI:10.48550/arXiv.1502.05336.
35. Y. Gal and Z. Ghahramani, Proceedings of The 33rd International Conference on Machine Learning, PMLR, 2016, vol. 48, pp. 1050–1059.
36. A. Amini, W. Schwarting, A. Soleimany and D. Rus, Advances in neural information processing systems, 2020, vol. 33, pp. 14927–14937.
37. A. S. Alshehri, A. K. Tula, F. You and R. Gani, AIChE J., 2022, 68, e17469.
38. A. P. Soleimany, A. Amini, S. Goldman, D. Rus, S. N. Bhatia and C. W. Coley, ACS Cent. Sci., 2021, 7, 1356–1367.
39. S. Genheden and U. Ryde, Expert Opin. Drug Discovery, 2015, 10, 449–461.
40. X. Xiao, Y. Wang, J. N. Leonard and C. K. Hall, J. Chem. Theory Comput., 2017, 13, 5709–5720.
41. E. Wang, H. Sun, J. Wang, Z. Wang, H. Liu, J. Z. H. Zhang and T. Hou, Chem. Rev., 2019, 119, 9478–9508.
42. M. L. Bileschi, D. Belanger, D. H. Bryant, T. Sanderson, B. Carter, D. Sculley, A. Bateman, M. A. DePristo and L. J. Colwell, Nat. Biotechnol., 2022, 40, 932–937.
43. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser and I. Polosukhin, Advances in neural information processing systems, 2017, vol. 30.
44. J. F. Gonçalves and M. G. Resende, J. Heuristics, 2011, 17, 487–525.
45. J. Blank and K. Deb, IEEE access, 2020, 8, 89497–89509.
46. M. A. Londe, L. S. Pessoa, C. E. Andrade and M. G. Resende, Eur. J. Oper. Res., 2024, 321 DOI:10.1016/j.ejor.2024.03.030.
47. D. A. Case, T. E. Cheatham III, T. Darden, H. Gohlke, R. Luo, K. M. Merz Jr, A. Onufriev, C. Simmerling, B. Wang and R. J. Woods, J. Comput. Chem., 2005, 26, 1668–1688.
48. M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1, 19–25.
49. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, Comput. Phys. Commun., 2014, 185, 604–613.
50. D. R. Roe and T. E. Cheatham III, J. Chem. Theory Comput., 2013, 9, 3084–3095.
51. D. A. Case, H. M. Aktulga, K. Belfon, D. S. Cerutti, G. A. Cisneros, V. W. D. Cruzeiro, N. Forouzesh, T. J. Giese, A. W. Götz and H. Gohlke, J. Chem. Inf. Model., 2023, 63, 6183–6191.
52. W. L. Jorgensen, J. Am. Chem. Soc., 1981, 103, 335–340.
53. J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713.
54. B. Hess, H. Bekker, H. J. Berendsen and J. G. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472.
55. G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101.
56. H. J. Berendsen, J. v. Postma, W. F. Van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690.
57. T. K. Kim, Korean J. Anesthesiol., 2015, 68, 540.
58. T. W. MacFarland, J. M. Yates, T. W. MacFarland and J. M. Yates, Introduction to nonparametric statistics for the biological sciences using R, 2016, pp. 103–132.
59. D. G. Altman and J. M. Bland, Bmj, 2009, 338, a3166.
60. S. Sarma, C. M. Catella, E. T. San Pedro, X. Xiao, D. Durmusoglu, S. Menegatti, N. Crook, S. T. Magness and C. K. Hall, Commun. Biol., 2023, 6, 878.
61. A. Baysal, H. Saygin and A. Soyocak, Environ. Toxicol., 2024, 39, 4899–4926.
62. M. Mao, L. Ahrens, J. Luka, F. Contreras, T. Kurkina, M. Bienstein, M. Sárria Pereira de Passos, G. Schirinzi, D. Mehn, A. Valsesia, C. Desmet, M.-Á. Serra, D. Gilliland and U. Schwaneberg, Chem. Soc. Rev., 2024, 53, 6445–6510.
63. K. Alhamoud, Y. Ghunaim, A. S. Alshehri, G. Li, B. Ghanem and F. You, Comput. Chem. Eng., 2024, 183, 108622.
64. M. Deighan and J. Pfaendtner, Langmuir, 2013, 29, 7999–8009.
65. R. H. Meißner, G. Wei and L. C. Ciacchi, Soft Matter, 2015, 11, 6254–6265.
66. G. D. Degen, K. C. Cunha, Z. A. Levine, J. H. Waite and J.-E. Shea, J. Phys. Chem. B, 2021, 125, 9999–10008.
67. J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 932–942.
68. J. Zhang, M. Peng, E. Lian, L. Xia, A. G. Asimakopoulos, S. Luo and L. Wang, Environ. Sci. Technol., 2023, 57, 8365–8372.
69. Q. Zhang, Y. Liu, Y. Liang, Y. Wu, W. Zhang, D. Zhang, G.-s. Guo, Z. Liu and X. Wang, Anal. Chem., 2023, 95, 9739–9745.
70. M. Giardino, V. Balestra, D. Janner and R. Bellopede, Sci. Total Environ., 2023, 859, 160036.
71. F. Mukherjee, A. Shi, X. Wang, F. You and N. L. Abbott, Small, 2023, 19, 2207802.
72. S. Oh, H. Hur, Y. Kim, S. Shin, H. Woo, J. Choi and H. H. Lee, Nanomaterials, 2021, 11, 2887.
73. N. Singh, N. Khandelwal, Z. A. Ganie, E. Tiwari and G. K. Darbha, Chem. Eng. J., 2021, 418, 129405.
74. Y. Wu, S. Chen, J. Wu, F. Liu, C. Chen, B. Ding, X. Zhou and H. Deng, Sci. Adv., 2024, 10, eadn8662.
75. R. S. Bang, L. Verster, H. Hong, L. Pal and O. D. Velev, Langmuir, 2024, 40, 5923–5933.
76. X. Fu, S. Zhang, X. Zhang, Y. Zhang, B. Li, K. Jin, X. Feng, J. Hong, X. Huang and H. Cao, Adv. Funct. Mater., 2023, 33, 2212570.
77. G. Peng, M. Xiang, W. Wang, Z. Su, H. Liu, Y. Mao, Y. Chen and P. Zhang, J. Hazard. Mater., 2022, 433, 128672.
78. M. Peydayesh, T. Suta, M. Usuelli, S. Handschin, G. Canelli, M. Bagnani and R. Mezzenga, Environ. Sci. Technol., 2021, 55, 8848–8858.
79. K. Hu, P. Zhou, Y. Yang, T. Hall, G. Nie, Y. Yao, X. Duan and S. Wang, ACS ES&T Eng., 2021, 2, 110–120.
80. T. Li, S. Menegatti and N. Crook, AIChE J., 2023, 69, e18228.
81. H. Lu, D. J. Diaz, N. J. Czarnecki, C. Zhu, W. Kim, R. Shroff, D. J. Acosta, B. R. Alexander, H. O. Cole and Y. Zhang, Nature, 2022, 604, 662–667.
82. S. Chandrudu, P. Simerska and I. Toth, Molecules, 2013, 18, 4373–4388.
83. G. Xu and J. Micklefield, Enzymatic Synthesis of Peptide Therapeutics, Nat. Chem. Biol., 2024, 20, 1256–1257.
84. P. C. Ke, S. Lin, W. J. Parak, T. P. Davis and F. Caruso, ACS Nano, 2017, 11, 11773–11776.
85. C. D. Rummel, A. Jahnke, E. Gorokhova, D. Kühnel and M. Schmitt-Jansen, Environ. Sci. Technol. Lett., 2017, 4, 258–267.

---

Footnote

† Contributed equally.

---