Open Access Article
Open Access ArticleCatalytic resonance theory: forecasting the flow of programmable catalytic loops†
Madeline A.
Murphy‡
ab,
Kyle
Noordhoek‡
 b,
Sallye R.
Gathmann
ab,
Paul J.
Dauenhauer
b,
Sallye R.
Gathmann
ab,
Paul J.
Dauenhauer
 *ab and
Christopher J.
Bartel
*ab and
Christopher J.
Bartel
 *b
*b
aCenter for Programmable Energy Catalysis, 421 Washington Ave. SE, Minneapolis, MN 55455, USA
bDepartment of Chemical Engineering & Materials Science, 421 Washington Ave. SE, Minneapolis, MN 55455, USA. E-mail: hauer@umn.edu; cbartel@umn.edu
First published on 30th December 2024
Abstract
Chemical transformations on catalyst surfaces occur through series and parallel reaction pathways. These complex networks and their behavior can be most simply evaluated through a three-species surface reaction loop (A* to B* to C* to A*) that is internal to the overall chemical reaction. Application of an oscillating dynamic catalyst to this reactive loop has been shown to exhibit one of three types of behavior: (1) a positive net flux of molecules about the loop in the clockwise direction, (2) a negative net flux of molecules about the loop in the counterclockwise direction, or (3) negligible flux of molecules about the loop at the limit cycle of reaction. Three-species surface loops were simulated with microkinetic modeling to assess the reaction loop behavior resulting from a catalytic surface oscillating between two or more catalyst surface energy states. Selected input parameters for the simulations spanned an 11-dimensional parameter space using 127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688 different parameter combinations. Their converged limit cycle solutions were analyzed for their loop turnover frequencies, the majority of which were found to be approximately zero. Classification and regression machine learning models were trained to predict the sign and magnitude of the loop turnover frequency and successfully performed above accessible baselines. Notably, the classification models exhibited a baseline weighted F1 score of 0.49, whereas trained models achieved weighted F1 scores of 0.94 and 0.96 when trained on the parameters used to define the simulations and derived rate constants, respectively. The trained models successfully predicted catalytic loop behavior, and interpretation of these models revealed all input parameters to be important for the prediction and performance of each model.
688 different parameter combinations. Their converged limit cycle solutions were analyzed for their loop turnover frequencies, the majority of which were found to be approximately zero. Classification and regression machine learning models were trained to predict the sign and magnitude of the loop turnover frequency and successfully performed above accessible baselines. Notably, the classification models exhibited a baseline weighted F1 score of 0.49, whereas trained models achieved weighted F1 scores of 0.94 and 0.96 when trained on the parameters used to define the simulations and derived rate constants, respectively. The trained models successfully predicted catalytic loop behavior, and interpretation of these models revealed all input parameters to be important for the prediction and performance of each model.
Introduction
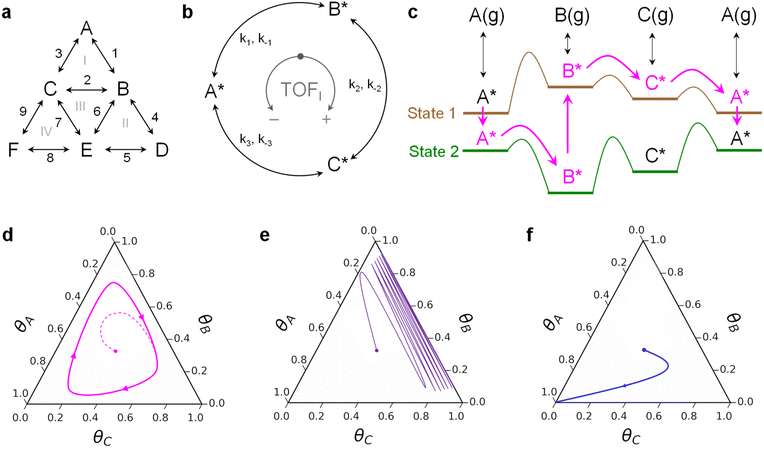
Chemical transformations on surfaces are defined by the sequence of elementary reactions that determine the overall catalytic rate and selection of chemical products.1–3 All elementary steps including adsorption, desorption, bond-breaking and bond-forming reactions together describe the complete decomposition and formation of molecules on the surface.4 Molecules reacting through the entire mechanism can move forwards and backwards along parallel reaction pathways on multiple catalytic active sites.5 Reaction networks also exhibit interconnectedness that creates internal reaction loops (Fig. 1a), such that molecules can react through a sequence of elementary steps to return to original chemical intermediates (e.g., A* to B* to C* to A*, where * indicates a surface species).6,7 Reaction loops exist for many reactions important to energy applications including steam reforming of methane, water gas shift, and methanol synthesis, and these loops can contribute significantly to diminished catalytic rates or altered product selectivity.8–10The concept of a reaction loop was examined by Onsager in the ‘triangle reaction’ of homogeneous reactants shown here (Fig. 1b) for an alternative application as a cyclic surface reaction of A*, B*, and C*.11 Any surface species may react to form any of the others, with the forward direction (A* to B* with rate coefficient k1) defined as clockwise and the reverse reaction direction (A* to C* with rate coefficient k−3) defined as counterclockwise. By the principle of microscopic reversibility, each forward and reverse reaction occurs through the same transition state such that the forward and reverse rates are equal at equilibrium.7,12,13 A detailed balance of the triangle reaction yields the Onsager reciprocal relationship:
 | (1) |
A catalyst that can change with time to promote catalytic reactions away from equilibrium was first described by Jencks in 1969.15 His theoretical enzyme could be forced into two states, E and E′, each exhibiting unique state conformations such that forced enzyme state-to-state changes could catalyze either bond-breaking or bond-forming reactions. The limitation of this concept was the challenge of focusing the energy input to elicit precise changes to the enzyme, resulting in a reaction that could promote reactions away from equilibrium without violating microscopic reversibility.14–16 Enzymes naturally exhibit a range of conformational oscillations, but the mechanistic role of these oscillations attributed to catalysis is debated.17 Instead, other non-biological mechanisms have been developed to force catalysts between electronic and/or physical catalytic states18 with precisely defined temporal transitions (i.e., programmable catalysis) including: periodic illumination of heterogeneous catalysts,19 oscillating catalyst surface strain,20 and oscillating surface charge.21,22 These heterogeneous catalyst perturbation methods forcibly change the free energy of adsorbed molecules as well as their transition state barrier energies.
The implication of forced perturbation of catalysts for catalytic loops is described in Fig. 1c. For the three-species catalytic loop of A* to B* to C* to A*, molecules adsorb to and desorb from the surface with varying binding energy between two catalyst states; state 1 (brown) is weak binding, while state 2 (green) is strong binding. The extent of binding energy change of each intermediate varies with different reaction parameters, catalyst composition and structure, and method of perturbation,23 ultimately requiring four scaling parameters to describe the dynamics of each interconnected elementary reaction and transition state.24 The difference in intermediate binding energy in each state is defined by a linear scaling with slope, γ, and offset, δ, while the linear scaling of the transition state between two intermediates is defined using a Brønsted–Evans–Polanyi relationship with offset, β, and slope, α, proportional to the enthalpy of the surface reaction.23,25–27 With two parameters describing each elementary reaction of species i on the catalyst surface (αi, βi) and two parameters describing the relationship between species i* and species A* (δi–A, γi–A), the energy of each transition state varies uniquely with changes in catalyst state. For example, in the depicted system of Fig. 1c, the A*-to-B* transition state energy decreases significantly between catalyst state 1 and state 2; this also leads to the formation of an ‘energy ratchet’ that prohibits B* from reacting backwards to A* in catalyst state 1.28–30 The result is a sequence of catalytic reactions that enable continuous flow of molecules in a loop of A* to B* to C* to A* as long as the catalyst continues to oscillate between states.31,32
Microkinetic models of three-species loops on heterogeneous catalyst surfaces (e.g., metals) have described the net flux of reactions in loops.32 With four chemistry parameters (α, β, γ, and δ) describing each of the three elementary reactions, there exist several triangle reaction behaviors on oscillating catalyst surfaces. As depicted in Fig. 1d, triangle reaction systems on programmable catalyst surfaces that exhibit a net flux around the reaction loop are described with a limit cycle in catalyst surface coverage. Independent of the initial surface coverage, all reactions of this type converge on a limit cycle that changes shape and extent of surface coverage with different amplitude and frequency of surface oscillation.32 For certain combinations of chemistry parameters, the net flux of the dynamic system can be forced to proceed in either the clockwise or counterclockwise direction.32 Alternatively, some triangle reactions on programmable catalyst surfaces merely oscillate between a surface coverage of two species (Fig. 1e) or terminate in a surface covered in a single chemical species (Fig. 1f). These two distinct behaviors of productive and non-productive loops pose both challenges and opportunities regarding programmable catalysts. Net loop behavior can behave productively, as a catalytic surface pump, to promote cyclic reactions from reactants to products. However, net loops can also be undesirable if they exist amongst surface intermediates, causing the dynamic input energy to the catalyst to be consumed by the continuous flow of molecules about an intermediate loop.
Predicting the non-equilibrium flow of reactions in loops has a basis in the behavior of molecular machines and Brownian ratchets, which use chemical ‘fuel’ to promote non-equilibrium steady-state net circular flux of molecules in loops or in a continuous sequence.33–35 Examples of these systems that operate at non-equilibrium steady state include catenane, a molecular structure of two interlocking rings for which one ring can rotate unidirectionally around the other using chemical energy,36–39 and kinesin, a biological protein motor that moves unidirectionally along intracellular microtubules using chemical energy (ATP to ADP).40,41 The unidirectional motion of these chemically driven systems, rings and protein walkers (and molecular pumps), is predictable via ‘ratchet constants’, which compare the relative magnitude of forward and reverse kinetic rates.34,42–44 However, chemically driven non-equilibrium systems are different from chemical reaction systems such as depicted in Fig. 1c, for which molecules are excited to a higher energy state via mechanisms such as strain, condensed charge, or light.14,42,45,46 One device that could modulate surface energies in this manner is a catalytic condenser;21,47,48 these devices enable pre-determined modulation of catalytic surface energy with time via an input ‘program’ that defines the timescales and extent of binding energy shift of all surface species. As such, existing descriptions of stochastic chemically driven mechanisms cannot predict the non-equilibrium behavior of pre-determined programmable energy-driven catalytic reaction loops.
The type of oscillatory behavior exhibited by a loop triangle reaction on a programmable heterogeneous catalytic surface is determined by the four parameters that describe the chemistry of each elementary step (α, β, γ, and δ). Prediction of loop behavior in programmable triangle reactions remains a challenge due to the multiple possible catalytic behaviors (Fig. 1d–f), the significant number of parameters that describe the chemistry, the complexity of programs that define the transient behavior of catalyst surface states, and the effects of reaction conditions (e.g., temperature).
In this work, we examined the catalytic surface triangle reaction (A* to B* to C* to A*) under surface energy modulation using simulated surface chemistry with microkinetic models and machine learning. In the interest of first understanding the simplest loop scenario, adsorption and desorption were not considered in this analysis. An 11-dimensional parameter space (each describing the chemistry of elementary steps) was uniformly sampled using 177![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147 (311) microkinetic simulations for a specified catalyst program. Machine learning (ML) models were trained to predict the results of a simulation (loop behavior) given these 11 input parameters as features. These models were further interrogated using interpretable ML techniques to understand which parameters govern loop behavior (e.g., change the loop from unproductive to productive). These simulations and the ensuing data analysis help shed insight on the complex interplay between these parameters in governing the productivity of loop reactions on programmable catalytic surfaces.
147 (311) microkinetic simulations for a specified catalyst program. Machine learning (ML) models were trained to predict the results of a simulation (loop behavior) given these 11 input parameters as features. These models were further interrogated using interpretable ML techniques to understand which parameters govern loop behavior (e.g., change the loop from unproductive to productive). These simulations and the ensuing data analysis help shed insight on the complex interplay between these parameters in governing the productivity of loop reactions on programmable catalytic surfaces.
Methods
Kinetic model
The three-species reaction loop was modeled using Julia 1.9.0. This three-species loop simulation was consistent with that of the previous work studying this general loop reaction.32 The model accounts for only the surface conversion of A*, B*, and C*; the adsorption and desorption energies were assumed too large to contribute to the chemical system, such that the molecules remained only on the surface. The microkinetic model included a unimolecular surface reaction for three elementary steps. The binding energy of each species changed in accordance with the dynamic perturbations of the catalyst surface. The mathematical derivation of these perturbations and their effect on the binding energies of surface species through linear scaling relationships and Brønsted–Evans–Polanyi relationships is included in previous work and the ESI.†32With the reaction model, forward integration was performed using Rosenbrock23 in Julia 1.9.0. The maximum number of oscillations was set to 5000, which at the fixed frequency of 50 s−1 allows 100 seconds for the systems to converge on a steady state solution. Periodic checks for steady state, implemented with callbacks, resulted in the termination of the simulation once the time-averaged elementary rate over one oscillation for all three elementary reactions was equal. Following the termination of the solver, the loop turnover frequency (TOF), defined as the time-averaged elementary rate of net reaction about the loop over one period of oscillation, was computed. Using mass action kinetics, the data stored in the simulation for the surface coverage of each species as a function of time was converted into elementary reaction rates as a function of time. The time-averaged rate for each elementary reaction was determined by integrating forward and reverse elementary rates from the start of an oscillation (t1) to the end of an oscillation (t2) and then dividing by the period,
 | (2) |
These simulations always resulted in a non-zero loop TOF (in part, due to floating point precision). As such, loop TOF magnitudes < 10−4 were assigned values of zero. In this way, systems that exhibited a loop TOF > 10−4 s−1 had a positive loop TOF and a clockwise non-equilibrium steady state flux about the loop, and those that exhibited a loop TOF < −10−4 s−1 had a negative loop turnover frequency with counterclockwise non-equilibrium steady-state flux. Systems between those two cutoff values were assigned zero loop TOF, with negligible net flux of surface species at steady state.
To evaluate the full parameter space for the simulation of the three-species catalytic loop, the 11 parameters defining the chemistry of the elementary steps were assigned a high, medium, and low value within ranges of reasonable values, all of which are listed in Table 1. These values and their ranges were chosen such that they span the values recorded in literature for surface reactions.23,27,28,32 Six additional parameters required to perform the simulations were assigned a fixed value: the frequency (f fixed to 50 Hz), catalyst descriptor (binding energy of A in catalyst state 1, BEA, fixed to 0.8 eV), temperature (T fixed to 298.15 K), total surface coverage of bound species (θ fixed to 1.0), duty cycle (D fixed to 0.5), and waveform shape (fixed to a square waveform). Assigning fixed values to these parameters reduced the dimensionality of the parameter space and decreased the number of simulations required to survey the parameter space. As the relationship between the catalyst's oscillation frequency and the resulting loop turnover frequency has already been established, it was not included.32
| Parameter | Low value | Medium value | High value |
|---|---|---|---|
| α [A, B, C] | 0.2 | 0.6 | 0.9 |
| β [A, B, C] (eV) | 0.6 | 0.9 | 1.2 |
| γ [B–A, C–A] | 0.6 | 1.4 | 1.8 |
| δ [B–A, C–A] (eV) | 0.5 | 1.0 | 1.5 |
| ΔBEA (eV) | 0.3 | 0.5 | 0.8 |
With these values, there are 177![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 147 (311) unique combinations of simulation parameters. From each of these combinations, the energy diagram was computed using γi–A and δi–A to compute the binding energies of species B* and C* in each state and αi and βi to compute the activation energy of each surface reaction. For all instances where an elementary step yielded a negative activation energy, the parameter set was excluded. After removing these instances of negative activation energy, 174
147 (311) unique combinations of simulation parameters. From each of these combinations, the energy diagram was computed using γi–A and δi–A to compute the binding energies of species B* and C* in each state and αi and βi to compute the activation energy of each surface reaction. For all instances where an elementary step yielded a negative activation energy, the parameter set was excluded. After removing these instances of negative activation energy, 174![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 312 combinations remained. The microkinetic simulations were performed in parallel using CPU resources provided by the Minnesota Supercomputing Institute. Each parameter set was simulated using the three-species reaction loop simulation. In the loop simulation, integration was performed using Rosenbrock23 with a relative tolerance of 10−8 and an absolute tolerance of 10−10. The callback set implemented in the solver included a periodic check for steady state after every ten oscillations. The check required the time-average of each elementary rate over two oscillations to be less than a set tolerance of 10−5. This analysis effectively checked that each elementary rate was equal within the set tolerance
312 combinations remained. The microkinetic simulations were performed in parallel using CPU resources provided by the Minnesota Supercomputing Institute. Each parameter set was simulated using the three-species reaction loop simulation. In the loop simulation, integration was performed using Rosenbrock23 with a relative tolerance of 10−8 and an absolute tolerance of 10−10. The callback set implemented in the solver included a periodic check for steady state after every ten oscillations. The check required the time-average of each elementary rate over two oscillations to be less than a set tolerance of 10−5. This analysis effectively checked that each elementary rate was equal within the set tolerance  . Upon terminating the integration, the solution was returned. This definition of steady state mitigates the effect of poor integration on the simulation results. Simulations had to achieve steady state with precision to be recorded in the results.
. Upon terminating the integration, the solution was returned. This definition of steady state mitigates the effect of poor integration on the simulation results. Simulations had to achieve steady state with precision to be recorded in the results.
Simulations that failed to converge on a steady-state solution in 5000 oscillations were re-simulated with a new oscillation limit of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. Extending the number of oscillations allowed some simulations to reach convergence; however, for most of these simulations, this extension did not result in convergence of the system, but rather led to issues of solver convergence and memory handling problems. Simulations that failed to converge were discarded, because the loop TOF could not be computed to a steady-state solution. The absence of these data points may remove particular clusters in the sampled parameter space, but these systems are also recognized to encompass many different time scales in the rate equations that may not be present in real systems and lead to stiff equations in the microkinetic model. The remaining 127
000. Extending the number of oscillations allowed some simulations to reach convergence; however, for most of these simulations, this extension did not result in convergence of the system, but rather led to issues of solver convergence and memory handling problems. Simulations that failed to converge were discarded, because the loop TOF could not be computed to a steady-state solution. The absence of these data points may remove particular clusters in the sampled parameter space, but these systems are also recognized to encompass many different time scales in the rate equations that may not be present in real systems and lead to stiff equations in the microkinetic model. The remaining 127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688 converged simulations were used to develop and test machine learning approaches to model and understand the behavior of the three species loop on dynamic catalyst surfaces.
688 converged simulations were used to develop and test machine learning approaches to model and understand the behavior of the three species loop on dynamic catalyst surfaces.
Machine learning models
Three common machine learning architectures – Extreme Gradient Boosting (XGBoost or XGB), Random Forest (RF), and Support Vector Machines (SVM) – were benchmarked against one another to determine which method provided the best performance for the given data. Each method was used to train classification and regression models on the same 90/10 training/test data split, which were implemented using a combination of the XGBoost and scikit-learn packages.49,50XGBoost is an open-source library which provides an efficient implementation of the gradient boosting framework.49,51 Gradient boosting works by training a pool of ‘weak learners,’ decision trees whose predictions are slightly better than an average guess, and generating an ensemble of these learners from the initial pool. Weak learners are added to the ensemble sequentially by a gradient descent algorithm such that the residuals of the ensemble are reduced. RF algorithms train similar models by implementing bagging as opposed to boosting. With bagging, a number of individual decision trees are trained on separate randomized subsections of the available data before all trees are aggregated to form the final model. During prediction for regression tasks, the results of each individual tree are averaged, while for classification tasks, the final class label is determined by a majority vote of the individual decision trees. In addition to tree-based models, regularized linear models with stochastic gradient descent (SGD) were used for the SVM architecture. Additionally, as the parameter space evaluated for the microkinetic simulations resembles a design of experiments approach with 11 features and 3 levels (low, medium, high), a second order surface response model was also fit and compared to the machine learning approaches.
Hyperparameters of each model type were tuned using a randomized grid search and ten-fold cross validation on the training dataset (90% of full dataset). For each architecture, models were trained separately for two objectives: (i) a classification problem to label the loop TOF as positive, negative, or zero, (ii) for non-zero loop TOF simulations, a regression problem to predict the magnitude of loop TOF. For each problem, two feature sets were explored: (a) one relying only on the 11 input parameters, and (b) another that replaces the chemistry features with twelve rate constants derived from the original parameters (see ESI for details†). The chemistry parameters (αi, βi, δi–A, γi–A) were used to describe each elementary reaction. The binding energy of each surface species and the activation energy of each reaction were determined using linear scaling relationships and Brønsted–Evans–Polanyi (BEP) relationships, respectively.23,27,28,32 With the heat of reaction and activation energy for each elementary reaction, the forward and reverse rate constants of each were computed using transition state theory.27,32 Classification models were evaluated primarily using weighted F1 score, while regression models were evaluated primarily on their median absolute error (median AE) due to the many orders of magnitude spanned by the loop TOF. To apply the models for a new set of parameters, one could apply the trained classification model, then the regression model for all samples classified as having non-zero loop TOF (positive or negative) to realize full predictability of the loop TOF.
Permutation feature importances (PFI),52 counterfactual explanations,53 and Shapley additive explanation (SHAP) values54 were used to understand the best performing subset of trained models (see Benchmarking machine learning models). Each interpretable ML approach was applied to the 10% of the data that was not used for model training. PFI was performed with 10 repeats, using the sklearn package. SHAP was performed using the shap package for each target class (positive, negative, and zero TOF).54 Counterfactuals were generated for three transformations – zero to positive loop TOF, positive to negative loop TOF, and negative to positive loop TOF, using the Diverse Counterfactuals Explanations (DiCE) package.53 For each transformation, features were minimally perturbed (as measured by Euclidean distance) to change the class label. For features involved in the perturbations (i.e. those with non-zero change) that resulted in the desired transformation, the mean perturbation was computed and normalized by the range of values simulated for that feature.
Results & discussion
Dataset
174![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 312 microkinetic simulations were performed to determine the steady-state loop TOF as described in Methods. The uniform sampling of parameter combinations yielded certain parameter sets that proved difficult to converge. Of all the parameter combinations, 127
312 microkinetic simulations were performed to determine the steady-state loop TOF as described in Methods. The uniform sampling of parameter combinations yielded certain parameter sets that proved difficult to converge. Of all the parameter combinations, 127![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 688 simulations converged to a steady state, comprising 73% of the total parameter space, while 46
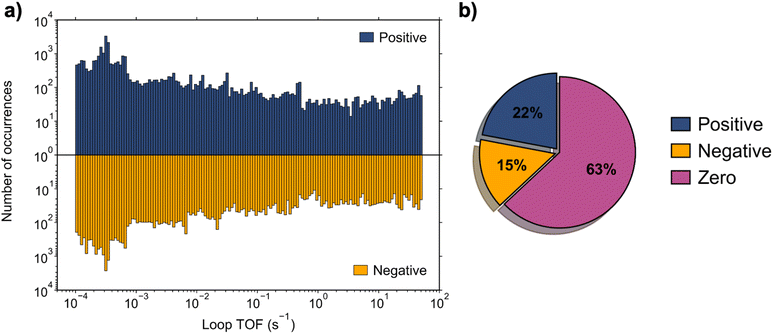
688 simulations converged to a steady state, comprising 73% of the total parameter space, while 46![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 624 simulations failed to converge. For further analysis, only the results of the converged simulation were considered. To classify the behavior of each converged simulation, the loop TOF, defined in eqn (2), quantified the net flux of reacting surface species about the reaction loop at steady state. Simulations were separated into those with a zero loop TOF (|TOF| < 10−4 s−1) and those with a non-zero loop TOF. Of the simulations, 63% had an output of zero loop TOF, while 37% were non-zero. Amongst the data for non-zero loop TOF, ∼60% of the simulations exhibited a positive loop TOF, while ∼40% exhibited negative loop TOF. This distribution of the loop TOF outputs is depicted in Fig. 2.
624 simulations failed to converge. For further analysis, only the results of the converged simulation were considered. To classify the behavior of each converged simulation, the loop TOF, defined in eqn (2), quantified the net flux of reacting surface species about the reaction loop at steady state. Simulations were separated into those with a zero loop TOF (|TOF| < 10−4 s−1) and those with a non-zero loop TOF. Of the simulations, 63% had an output of zero loop TOF, while 37% were non-zero. Amongst the data for non-zero loop TOF, ∼60% of the simulations exhibited a positive loop TOF, while ∼40% exhibited negative loop TOF. This distribution of the loop TOF outputs is depicted in Fig. 2.
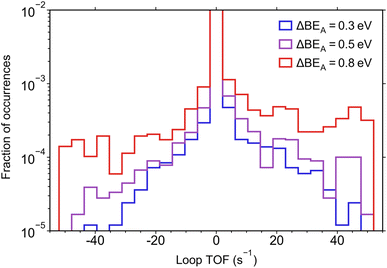
In Fig. 3, we probe how the amplitude of oscillation in the catalyst program (ΔBEA) influences the magnitude of loop TOF, showing that the simulations with higher magnitudes of loop TOF were associated with higher ΔBEA. This is consistent with previous results where higher amplitudes of oscillation were identified to increase the TOF of catalytic loops having the same reaction parameters.32 Despite the increase in high |TOF| simulations associated with larger ΔBEA, the magnitude of ΔBEA did not have an appreciable effect on the number of simulations yielding zero TOF. This indicates that the lack of dynamic behavior in a catalytic loop is not due to the catalyst program (i.e., description of the catalyst surface oscillation) but rather due to the chemistry parameters (αi, βi, δi–A, γi–A) and the resulting reaction coordinate for the sampled amplitudes.
Benchmarking machine learning models
Machine learning (ML) methods were leveraged to understand the three-species dynamic loop and to predict loop behavior without the need for microkinetic simulations. Two feature sets were explored in this work – one making use of the 11 parameters that define each simulation (referred to as the original parameter, OP, dataset) and another that replaces the chemistry parameters with rate constants derived from transition state theory (RC). The behavior of the reaction loop (positive, negative, or zero TOF) was predicted using multi-class classification methods. For classification purposes, the output data was first divided into three classes based on loop turnover frequency with class 0 (|TOF| < 10−4 s−1), class 1 (TOF > 10−4 s−1), and class 2 (TOF < −10−4 s−1). For simulations having non-zero TOF, the TOF magnitude (|TOF|) was predicted using regression models. Due to the distribution of |TOF| in the dataset (Fig. 2a), the data were best interpreted on a log-scale. Models were therefore fit to a dataset that removed all samples with zero TOF and considered ln(|TOF|) for the remaining samples. Model performance was then assessed by mapping the predicted values back to a linear scale (eprediction) for comparison to the |TOF| resulting from the microkinetic simulations.Using the two input datasets, models were trained using the XGBoost, Random Forest, or Support Vector Machine architectures. Model performance was assessed using weighted F1 scoring and accuracy for classification and median absolute error (median AE), mean absolute error (mean AE), root mean squared error (RMSE), and 75th percentile error for regression. This is the first work to predict the dynamic behavior of catalytic loops using ML. As such, there is not an established baseline for comparing the performance of the models trained in this work, so simple baselines were generated for comparison. For the multi-class classification models, the baseline model predicts the most common class (zero TOF) for all samples. For the regression models, the baseline model always predicts the mean or median |TOF| of the regression test dataset, 0.36 s−1 or 2.32 × 10−4 s−1 respectively. If the ML models learn useful information, then their performance on held-out data should yield higher classification metrics and lower regression metrics than the baselines. Benchmark results for each type of model are shown in Tables 2 and 3.
| Regression | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Original parameters | Rate constants | |||||||||
| Random forest | Extreme gradient boosting | Support vector machine | Response surface | Baselineb | Random forest | Extreme gradient boosting | Support vector machine | Response surface | Baselineb | |
| a All metrics are given in units of s−1 and reported for the test set. b Baseline predictions for the RMSE, mean AE, and 75th Percentile metrics are calculated with the mean value of the training set (0.36 s−1) while median AE is calculated with the median value of the training set (2.32 × 10−4 s−1) | ||||||||||
| RMSE | 2.51 | 4.56 | 5.69 | 7.07 | 5.63 | 2.47 | 2.23 | 5.69 | 18.46 | 5.63 |
| Mean AE | 0.44 | 0.60 | 1.11 | 6.66 | 1.39 | 0.41 | 0.35 | 1.11 | 6.95 | 1.39 |
| Median AE | 9.08 × 10−5 | 1.54 × 10−4 | 1.23 × 10−3 | 7.87 | 1.46 × 10− 4 | 5.96 × 10−5 | 8.97 × 10−5 | 1.72 × 10−3 | 7.88 | 1.46 × 10− 4 |
| 75th percentile | 1.75 × 10−3 | 2.22 × 10−3 | 7.01 × 10−3 | 8.22 | 0.36 | 1.34 × 10−3 | 1.41 × 10−3 | 5.35 × 10−3 | 8.22 | 0.36 |
| Classification | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Original parameters | Rate constants | |||||||||
| Random forest | Extreme gradient boosting | Support vector machine | Response surface | Baselineb | Random forest | Extreme gradient boosting | Support vector machine | Response surface | Baselineb | |
| a Performance was assessed on the test set. b Baseline predictions assume the most common class, zero TOF, for all predictions. The response surface was not fit for classification due to the poor regression performance. | ||||||||||
| Accuracy | 0.94 | 0.91 | 0.63 | — | 0.63 | 0.96 | 0.96 | 0.54 | — | 0.63 |
| Weighted F1 score | 0.94 | 0.91 | 0.53 | — | 0.49 | 0.96 | 0.96 | 0.48 | — | 0.49 |
Based on the results of the regression task benchmarking, shown in Table 2, both RF and XGB models outperform the naïve baseline models when trained on OP or RC parameters. The RF regression model trained on RC parameters improves slightly over that trained on OP parameters for all metrics. For the case of XGB, there appears to be significant improvement in the RC model as opposed to the OP model, again for all metrics. The linear SVM models are consistent with the naïve baseline when trained on either dataset, while the traditional second order response surface performs worse than baseline predictions in both cases. These results suggest that the simulation parameters have a strongly nonlinear effect on the resulting loop TOF.
The classification task benchmarking, shown in Table 3, depicts similar trends. RF and XGB models are shown to perform well above baseline metrics and see slight increases in both accuracy and weighted F1 score when trained on RC parameters. The linear SVMs again perform on par with baseline predictions, reinforcing the nonlinear influence of the input parameters on the microkinetic simulations. Due to the overall better performance of the RF models when trained on OP input parameters and the comparable performance of the RF model when trained on RC input parameters, as compared to XGB, the RF models were chosen as the focus of the remaining discussion. “OP/RC classifier/regressor” and “models” will henceforth refer to those with the RF architecture unless otherwise specified. Analogous results for XGB are also provided in the ESI† for comparison.
Classification of zero, positive, or negative TOF
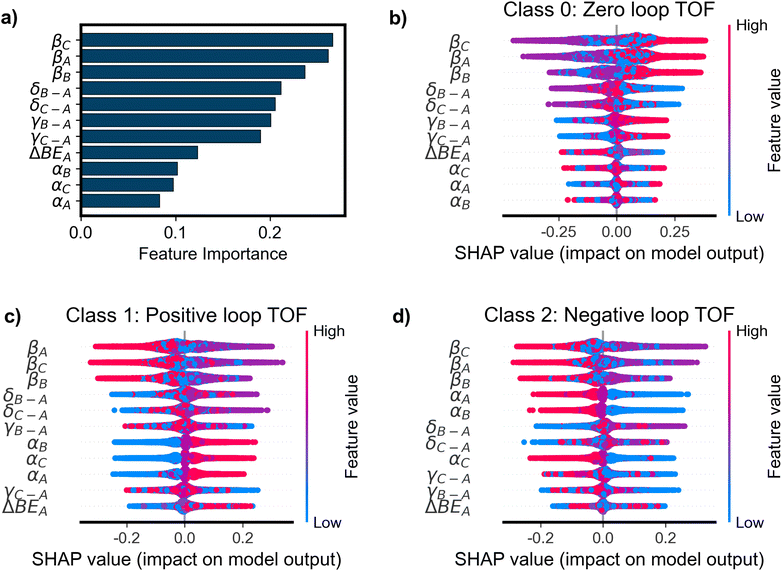
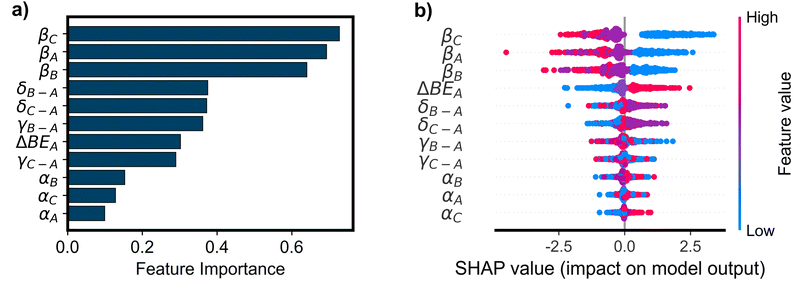
The OP classifier achieved a weighted F1 score of 0.94 on an excluded test set of 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 768 simulations (10% of the total), improving dramatically upon the baseline model that always predicts a loop TOF of zero (F1 = 0.49). The RC classifier improved slightly upon the OP classifier with a weighted F1 score of 0.96 on the test set. Interpretable ML methods (PFI, SHAP, and counterfactual explanations) were applied to the trained models to understand the influence of the input parameters on model predictions and performance on held-out data. While the RC classifier improves upon the OP classifier, rate constant features are much more challenging to interpret than the original parameters used to define the microkinetic simulations. As such, the focus of this analysis will be the OP models. In Fig. 4a, we show the sorted PFI for the OP classifier. The βi features are shown to be the most important for determining the classification performance, followed relatively closely by δi and γi–A features. As βi is the offset in the BEP relationship for each elementary reaction, its value contributes significantly to the activation energies of each reaction. The high values of βi (1.2 eV, see Table 1) result in a barrier to reaction much larger than for small values of βi (0.6 eV). The size of the reaction barrier of each elementary step is predictive of whether a surface species can react about the loop, and therefore permutations of this parameter deteriorate the classification of positive, negative, or zero TOF. δi–A and γi–A define the intermediate linear scaling relationships, determining the binding energies of each surface species. These values determine which species are energetically favored in each catalyst state, dictating the equilibrium coverages of each state. When different species are energetically favored in each state, there is higher or lower probability for a net flux of molecules at dynamic steady-state. In this way, δi–A and γi–A are related to the tendency for a reaction to flux in a loop-like manner when an oscillating stimulus is applied, causing them to be important features for determining the model's performance. Although βi is shown in Fig. 4a to have the highest importance, it is noteworthy that all 11 input parameters have significant importance in determining the performance of the trained classifier. This suggests that the loop behavior is governed by the thermodynamics and kinetics of all elementary steps as well as the amplitude of oscillations in the catalyst program.
768 simulations (10% of the total), improving dramatically upon the baseline model that always predicts a loop TOF of zero (F1 = 0.49). The RC classifier improved slightly upon the OP classifier with a weighted F1 score of 0.96 on the test set. Interpretable ML methods (PFI, SHAP, and counterfactual explanations) were applied to the trained models to understand the influence of the input parameters on model predictions and performance on held-out data. While the RC classifier improves upon the OP classifier, rate constant features are much more challenging to interpret than the original parameters used to define the microkinetic simulations. As such, the focus of this analysis will be the OP models. In Fig. 4a, we show the sorted PFI for the OP classifier. The βi features are shown to be the most important for determining the classification performance, followed relatively closely by δi and γi–A features. As βi is the offset in the BEP relationship for each elementary reaction, its value contributes significantly to the activation energies of each reaction. The high values of βi (1.2 eV, see Table 1) result in a barrier to reaction much larger than for small values of βi (0.6 eV). The size of the reaction barrier of each elementary step is predictive of whether a surface species can react about the loop, and therefore permutations of this parameter deteriorate the classification of positive, negative, or zero TOF. δi–A and γi–A define the intermediate linear scaling relationships, determining the binding energies of each surface species. These values determine which species are energetically favored in each catalyst state, dictating the equilibrium coverages of each state. When different species are energetically favored in each state, there is higher or lower probability for a net flux of molecules at dynamic steady-state. In this way, δi–A and γi–A are related to the tendency for a reaction to flux in a loop-like manner when an oscillating stimulus is applied, causing them to be important features for determining the model's performance. Although βi is shown in Fig. 4a to have the highest importance, it is noteworthy that all 11 input parameters have significant importance in determining the performance of the trained classifier. This suggests that the loop behavior is governed by the thermodynamics and kinetics of all elementary steps as well as the amplitude of oscillations in the catalyst program.
The feature importance analysis suggests species-dependent importances in the models (e.g., the PFI for βC > βA > βB). However, the differences observed across the species-dependent parameters in Fig. 4a are a result of the finite number of simulations that converged and the randomness associated with the method by which each model was trained. Due to the symmetry of the loop reaction that results from rotation of the loop, species dependence should not bring about higher importance; instead, if infinite data was provided, then each parameter for A, B, and C should have identical importance in the model since A, B, and C are equivalent for the purposes of the model systems studied here. In general, the similarity of feature importances within each parameter (e.g., all δi–A importances are similar to one another) suggests generally uniform sampling of the input data with respect to species (A, B, and C).
SHAP (SHapley Additive exPlanations) values were used to interpret the relationship between the values of parameters (features) and the model predictions (positive, negative, or zero loop TOF). For this multi-class classification model, the SHAP values were three-dimensional, where each sample, defined as a unique set of parameter inputs (unique feature values), had a different output SHAP value for each class. For a given sample, the SHAP values reflect how each feature contributes to the (model-predicted) probability of that sample belonging to a given class. In Fig. 4b–d, we show the SHAP values for each class – zero TOF (class 0), TOF > 0 (class 1), and TOF < 0 (class 2), respectively. When the model predicts zero loop TOF (Fig. 4b), the SHAP analysis is consistent with the PFI results, with βi being the most important feature and δi–A and γi–A also holding high importance. For class 0 (zero TOF) in Fig. 4b, high values of βi (up to 1.2 eV, see Table 1) correspond with the highest SHAP values, indicating an increase in the probability that a given sample has zero TOF. For an elementary step, a high value of βi decreases the probability of reaction at that given step, increasing the probability of a zero TOF loop.
Interestingly, when the model predicts the directionality of loops with non-zero loop TOF, αi becomes a more important feature to govern whether the direction is clockwise (positive loop TOF, Fig. 4c) or counterclockwise (negative loop TOF, Fig. 4d). High values of αi (up to 0.9, see Table 1) were found to correspond almost exclusively with a high probability that a given sample is class 1 (positive loop TOF) and low probability that it is class 2 (negative loop TOF). Accordingly, low values of αi were found to correspond almost exclusively with a low probability of a sample being class 1 and a high probability that it is class 2. This is contradictory to the other most important feature, βi, where values on either extreme (high or low) correspond to a moderately low and moderately high impact. The parameter αi is the slope of the BEP relationship and multiplied by the heat of surface reaction (ΔHR) when determining the activation energy of each step. In this way, the value of αi determines how the activation energy scales with respect to ΔHR. High values of αi lead to high barriers to reaction when ΔHR > 0 and lower barriers when ΔHR < 0. As ΔHR is defined in the clockwise direction, the reactions with low barriers are thermodynamically driven in the forward direction, with ΔHR < 0, promoting the clockwise direction of reaction. Conversely, for low value of αi, the dependence of the activation energy on ΔHR is weakened, allowing for more manageable reaction barriers when ΔHR > 0, promoting reactions in the negative, counterclockwise direction.
The feature importance results of Fig. 4a identified δi–A and γi–A to have important influence on the model's performance, while the SHAP analysis in Fig. 4b–d reveals that different values of δi–A and γi–A do not prominently lead to different output predictions. The SHAP values instead reveal that the model uses βi as the key differentiation between loop and no loop behavior, while using αi to differentiate between positive and negative behavior. Similar conclusions can be drawn from SHAP analysis of the XGB models (Fig. S4†) further supporting the importance of βi and αi in classifying loop behavior.
Counterfactual explanations provided further interpretation of the classification model and the mechanism of its decisions. Counterfactuals were generated to find the smallest perturbation to the features of a given sample that resulted in the model predicting a different desired class. In generating counterfactuals, the size of the perturbation was minimized as the Euclidean distance between the original feature values and the counterfactual values within the 11-dimensional feature space. This resulted in simultaneous perturbations to multiple features to realize the change in prediction. In Fig. 5, we show the mean perturbation to each group of features associated with three different class prediction changes – positive TOF to negative TOF (blue), negative TOF to positive TOF (pink), and zero TOF to positive TOF (yellow). The mean perturbation indicates the size of each perturbation normalized to the range of the feature's simulated values (difference between the high and low value for each feature in Table 1), where a small (large) relative perturbation indicates that small (large) changes to the given feature are necessary to change the prediction label. This analysis indicates that perturbations on the order of 10–25% to any of the original parameters (the chemistry parameters or the amplitude of the catalyst program) can alter the direction or productivity of the catalytic loop. As with the SHAP analysis, the counterfactual analysis supports the suggestion that βi is a key parameter in dictating the behavior of the loop TOF, as evident by the small relative perturbations required to change class labels, which indicates the sensitivity of the loop TOF to slight changes in βi. It is also noted that large changes in αi are required to induce a change in prediction from negative to positive loop TOF. This is consistent with the SHAP analysis in which low values of αi strongly correlated to a negative classification and high values with a positive classification. Overall, this counterfactual analysis using the trained models provides useful context for guiding the design of catalyst programs to achieve specific reaction behavior given some fixed inputs (e.g., the chemistry of certain elementary steps). Once again, we find similar results with the XGB models (Fig. S5†) supporting that the observations are robust with respect to model architecture.
Regression models to predict the TOF magnitude
The median AE for the OP regressor was 9.08 × 10−5 s−1 on the test set, which is a ∼38% decrease in median AE from the baseline of 1.46 × 10−4 s−1, where the baseline model always predicts |TOF| to be the median of the training dataset. When evaluating the predictions on a parity plot, Fig. 6a revealed that the predictions generally trended strongly with the actual values resulting from the simulations, with most errors within one order of magnitude of the target. The RC regressor was trained and assessed in the same way as the OP regressor but utilizing the derived rate constant (RC) features instead of the original parameters. The RC regressor performed with a median AE of 5.96 × 10−5 s−1, improving upon the OP regressor by ∼34%. The median AE values of the predictions reveal a moderate increase in performance from the OP regressor to the RC regressor. In Fig. 6b, the parity plot for the RC predictions shows stronger correlation with the target than the OP regressor. Despite the similar median AE's between the two models, the 75th percentile error for the OP model is 1.75 × 10−3 s−1 while that for the RC model is 1.34 × 10−3 s−1. Together these indicate small errors by the RC model for many more samples than the OP model. Similar to the comparison of the OP and RC models for classification, using rate constants as features improves model performance at the detriment of model interpretability. Similar trends can be seen for the XGB models (Fig S6†).PFI for the OP regressor shown in Fig. 7a was consistent with the OP classifier as βi was again identified as the most important feature. However, the regression models show significantly more dependence upon the most important βi features compared with the classification models, which show relatively uniform reliance on several features (Fig. 4a). As with the SHAP values associated with zero TOF predictions made by the OP classifier (Fig. 4b), the SHAP values for the OP regressor shown in Fig. 7b indicate that βi features have the most importance in determining the model prediction. Low values of βi were found to correspond almost exclusively with a high value of loop TOF while high values correspond almost exclusively with low values of loop TOF. Interestingly, and in contrast with any of the classification predictions, the catalyst program amplitude, ΔBEA, is shown to contribute strongly to the magnitude of TOF predicted by the models, as indicated by the large SHAP values and clear trend between high (low) values of ΔBEA and high (low) values of predicted |TOF|. XGB models indicate similar importance in βi features and an increased importance in ΔBEA for the prediction of TOF values (Fig. S7†).
Comparison of random forest machine learning models
ML models trained on high-throughput microkinetic simulations revealed how the inputs to the simulations (the nature of the reaction and catalyst system) determined the behavior of three-species dynamic loops. All ML models also reflected large savings in computational cost relative to the microkinetic simulations. Collection of the dataset required 6 months of running simulations with a typical simulation time ranging from 30 seconds to 96 hours (max time allowed for simulation). The ML models, once trained, require <30 ms to perform the inference, realizing a significant reduction in computational time relative to the microkinetic model. Model training is also comparatively fast, as the final OP models were trained in ∼5 minutes. The classification models exhibited high weighted F1 scores of 0.94 and 0.96 for the OP and RC models, respectively. These scores are near that of a perfect model (weighted F1 score of 1.0) and are drastic improvements from a baseline model that always predicts a loop TOF of zero (F1 of 0.48). Both regression models also exhibited improved performance relative to the baseline median AE (1.46 × 10−4 s−1) realizing a ∼38% and ∼59% decrease in median AE relative to the baseline model, for the OP and RC regressor models, respectively. The separate training and disparate performance of classification and regression models suggests that it is more straightforward to find relationships between the inputs and the direction of the catalytic loop (classification) than to directly predict the magnitude of the loop TOF (regression). Predicting |TOF| may be complicated by the nature of the data, which spans ∼6 orders of magnitude for the diverse parameter combinations explored in this work.The classification model trained on the original chemical parameters (OP) presented interpretable results that emphasized all features to have importance in the trained model. Breakdown of the PFI and SHAP reflected minor differences, where βi was identified as the most important feature to determine whether a loop reaction will have a zero or non-zero loop TOF. Furthermore, γi–A and δi–A were also identified as important features, and αi was isolated as a key feature to determine positive versus negative dynamic behavior. Interpretation of the regression model having the same features showed again that all features inform model prediction and indicated βi to be the most important parameter in dictating the magnitude of the loop TOF. The classification model and regression model trained on the rate constant data (RC classifier and regressor) resulted in higher performance than the models trained on the original chemical parameters (OP classifier and regressor); however, the models trained on the rate constants are difficult to interpret due to the inability to differentiate between each different rate constant in the context of a symmetrical reaction.
The ML models performed consistently on training and tests sets but may not generalize to out of distribution (OOD) data. Since these models have only seen three values of each input parameter, their performance may decrease when assessed on systems that include more varied parameter values. In response to this, there are key takeaways that will help inspire future work in this area. This dataset would have benefitted from exploration of multiple frequencies and a more random parameter selection. Simulating multiple frequencies would have aided in the understanding of cutoff frequencies for each individual elementary reaction; it would also have helped to understand reaction systems that have no loop TOF at low applied frequency but significant loop TOF at high applied frequencies. A more random generation of the input parameter sets would have challenged the models to learn more complex underlying relationships between these parameters and the loop dynamics.
Despite the shortcomings associated with the discrete parameter sampling, the models were found to be effective in predicting the loop behavior and allowed for insight into the relative importance of each parameter in predicting the behavior of a loop reaction. If specific catalytic loop behavior is desired, then the data and models can be leveraged to understand the value of scaling parameters or catalyst programs that would produce that behavior and desired loop turnover frequency. Furthermore, the new understanding of which features are most consequential to each behavior improves our understanding of which scaling parameters should be the focus in designing dynamic catalyst systems. For more complex systems that require more than 11 parameters (accounting for adsorption/desorption, multiple active sites, diffusion, etc.), the brute force sampling used in this paper quickly becomes computational expensive. With the new understanding of which scaling parameters are most consequential, future exploration can collapse the sample space to recognize variation across only those parameters to make these methods more tractable for larger systems.
Conclusions
Applying a dynamic surface to a three-species catalytic reaction loop results in three types of steady state behavior: clockwise reaction flux about the loop (positive loop TOF), counterclockwise reaction flux about the loop (negative loop TOF), and negligible flux (|TOF| < 10−4 s−1). Screening the input parameters for this catalytic system demonstrated that most considered reaction loops yield negligible loop TOF. Machine learning models trained on the generated dataset were successful in predicting the loop behavior and improved further using derived rate constants as input features. However, applying these models to more complex chemistries may require further development of the predictive models and their infrastructure. The ML models also demonstrate that all studied parameters play a role in determining the performance of the models and their predictions of surface behavior. Among the studied parameters, βi (the offset parameter in the BEP relationship, used to determine activation energy of each elementary reaction) was found to be the most consequential parameter, especially for determining the magnitude of the loop TOF. Overall, this work shows how the connection of microkinetic simulation and machine learning can be further integrated with the design of programmable dynamic catalyst systems. The ability to predict system behavior from fundamental reaction parameters or to determine the parameters necessary to achieve a desired catalytic behavior indicates a promising future direction for rational design of programmable catalysts for reactions with complex surface mechanisms.Data availability
Code and data used to generate the presented results are available at https://github.com/Bartel-Group/programmable-loop-directionality. A fully archived version of the code and data can also be found through the Data Repository for the University of Minnesota (DRUM): https://doi.org/10.13020/bh14-3q71. Due to GitHub space limitations, the pre-trained random forest models are only available through DRUM.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported as part of the Center for Programmable Energy Catalysis, an Energy Frontier Research Center funded by the U.S. Department of Energy, Office of Science, Basic Energy Sciences at the University of Minnesota under award #DE-SC0023464. The authors acknowledge the Minnesota Supercomputing Institute (MSI) at the University of Minnesota for providing resources that contributed to the research results reported within this paper.References
- R. Aris, Mathematical aspects of chemical reaction, Ind. Eng. Chem., 1969, 61(6), 17–29, DOI:10.1021/ie50714a005.
- S. Rangarajan, A. Bhan and P. Daoutidis, Language-Oriented Rule-Based Reaction Network Generation and Analysis: Description of RING, Comput. Chem. Eng., 2012, 45, 114–123, DOI:10.1016/j.compchemeng.2012.06.008.
- N. K. Razdan, T. C. Lin and A. Bhan, Concepts Relevant for the Kinetic Analysis of Reversible Reaction Systems, Chem. Rev., 2023, 123(6), 2950–3006, DOI:10.1021/acs.chemrev.2c00510.
- J. A. Dumesic, The Microkinetics of Heterogeneous Catalysis, 1993, vol. 40 Search PubMed.
- A. H. Motagamwala and J. A. Dumesic, Microkinetic Modeling: A Tool for Rational Catalyst Design, Chem. Rev., 2021, 121(2), 1049–1076, DOI:10.1021/acs.chemrev.0c00394.
- A. G. Fredrickson, Stochastic Triangular Reactions, Chem. Eng. Sci., 1966, 21(8), 687–691, DOI:10.1016/0009-2509(66)80018-0.
- R. M. Krupka, H. Kaplan and K. J. Laidler, Kinetic Consequences of the Principle of Microscopic Reversibility, Trans. Faraday Soc., 1966, 62, 2754 RSC.
- B. C. Michael, A. Donazzi and L. D. Schmidt, Effects of H2O and CO2 Addition in Catalytic Partial Oxidation of Methane on Rh, J. Catal., 2009, 265(1), 117–129, DOI:10.1016/j.jcat.2009.04.015.
- B. Lacerda de Oliveira Campos, K. Herrera Delgado, S. Pitter and J. Sauer, Development of Consistent Kinetic Models Derived from a Microkinetic Model of the Methanol Synthesis, Ind. Eng. Chem. Res., 2021, 60(42), 15074–15086, DOI:10.1021/acs.iecr.1c02952.
- L. C. Grabow, A. A. Gokhale, S. T. Evans, J. A. Dumesic and M. Mavrikakis, Mechanism of the Water Gas Shift Reaction on Pt: First Principles, Experiments, and Microkinetic Modeling, J. Phys. Chem. C, 2008, 112(12), 4608–4617, DOI:10.1021/jp7099702.
- L. Onsager, Reciprocal Relations in Irreversible Processes. I, Phys. Rev., 1931, 37(4), 405–426, DOI:10.1103/PhysRev.37.405.
- R. C. Tolman, The Principle of Microscopic Reversibility, Proc. Natl. Acad. Sci. U. S. A., 1925, 11, 436 CrossRef CAS PubMed.
- R. L. Burwell Jr and R. G. Pearson, The Principle of Microscopic Reversibility, J. Phys. Chem., 1966, 70(1), 300–302 CrossRef.
- I. Aprahamian and S. M. Goldup, Non-Equilibrium Steady States in Catalysis, Molecular Motors, and Supramolecular Materials: Why Networks and Language Matter, J. Am. Chem. Soc., 2023, 145(26) DOI:10.1021/jacs.2c12665.
- W. P. Jencks, Catalysis in Chemistry and Enzymology, McGraw-Hill Book Co, New York, NY, 1969, vol. 47, DOI:10.1021/ed047pa860.2.
- R. D. Astumian, P. B. Chock, T. Y. Tsong and H. V. Westerhoff, Effects of Oscillations and Energy-Driven Fluctuations on the Dynamics of Enzyme Catalysis and Free-Energy Transduction, Phys. Rev. A, 1989, 39(12), 6416–6435, DOI:10.1103/PhysRevA.39.6416.
- M. H. M. Olsson, W. W. Parson and A. Warshel, Dynamical Contributions to Enzyme Catalysis: Critical Tests of a Popular Hypothesis, Chem. Rev., 2006, 106(5), 1737–1756, DOI:10.1021/cr040427e.
- M. Shetty, A. Walton, S. R. Gathmann, M. A. Ardagh, J. Gopeesingh, J. Resasco, T. Birol, Q. Zhang, M. Tsapatsis, D. G. Vlachos, P. Christopher, C. D. Frisbie, O. A. Abdelrahman and P. J. Dauenhauer, The Catalytic Mechanics of Dynamic Surfaces: Stimulating Methods for Promoting Catalytic Resonance, ACS Catal., 2020, 12666–12695, DOI:10.1021/acscatal.0c03336.
- J. Qi, J. Resasco, H. Robatjazi, I. B. Alvarez, O. Abdelrahman, P. Dauenhauer and P. Christopher, Dynamic Control of Elementary Step Energetics via Pulsed Illumination Enhances Photocatalysis on Metal Nanoparticles, ACS Energy Lett., 2020, 3518–3525, DOI:10.1021/acsenergylett.0c01978.
- G. R. Wittreich, S. Liu, P. J. Dauenhauer and D. G. Vlachos, Catalytic Resonance of Ammonia Synthesis by Simulated Dynamic Ruthenium Crystal Strain, Sci. Adv., 2022, 8(4), eabl6576, DOI:10.1126/sciadv.abl6576.
- T. M. Onn, S. R. Gathmann, Y. Wang, R. Patel, S. Guo, H. Chen, J. K. Soeherman, P. Christopher, G. Rojas, K. A. Mkhoyan, M. Neurock, O. A. Abdelrahman, C. D. Frisbie and P. J. Dauenhauer, Alumina Graphene Catalytic Condenser for Programmable Solid Acids, JACS Au, 2022, 2(5) DOI:10.1021/jacsau.2c00114.
- T. M. Onn, S. R. Gathmann, S. Guo, S. P. S. Solanki, A. Walton, B. J. Page, G. Rojas, M. Neurock, L. C. Grabow, K. A. Mkhoyan, O. A. Abdelrahman, C. D. Frisbie and P. J. Dauenhauer, Platinum Graphene Catalytic Condenser for Millisecond Programmable Metal Surfaces, J. Am. Chem. Soc., 2022, 144(48), 22113–22127, DOI:10.1021/jacs.2c09481.
- M. A. Ardagh, T. Birol, Q. Zhang, O. A. Abdelrahman and P. J. Dauenhauer, Catalytic Resonance Theory: SuperVolcanoes, Catalytic Molecular Pumps, and Oscillatory Steady State, Catal. Sci. Technol., 2019, 9(18), 5058–5076, 10.1039/c9cy01543d.
- P. J. Dauenhauer, Up up down down Left Right Left Right B A Start for the Catalytic Hackers of Programmable Materials, Matter, 2023, 6(12), 4145–4157, DOI:10.1016/j.matt.2023.11.008.
- T. R. Munter, T. Bligaard, C. H. Christensen and J. K. Nørskov, BEP Relations for N2 Dissociation over Stepped Transition Metal and Alloy Surfaces, Phys. Chem. Chem. Phys., 2008, 10(34), 5202–5206, 10.1039/b720021h.
- J. E. Sutton and D. G. Vlachos, A Theoretical and Computational Analysis of Linear Free Energy Relations for the Estimation of Activation Energies, ACS Catal., 2012, 2(8), 1624–1634, DOI:10.1021/cs3003269.
- S. R. Gathmann, M. A. Ardagh and P. J. Dauenhauer, Catalytic Resonance Theory: Negative Dynamic Surfaces for Programmable Catalysts, Chem Catal., 2022, 2(1), 140–163, DOI:10.1016/j.checat.2021.12.006.
- M. A. Ardagh, O. A. Abdelrahman and P. J. Dauenhauer, Principles of Dynamic Heterogeneous Catalysis: Surface Resonance and Turnover Frequency Response, ACS Catal., 2019, 9(8), 6929–6937, DOI:10.1021/acscatal.9b01606.
- M. A. Ardagh, M. Shetty, A. Kuznetsov, Q. Zhang, P. Christopher, D. Vlachos, O. Abdelrahman and P. Dauenhauer, Catalytic Resonance Theory: Parallel Reaction Pathway Control, Chem. Sci., 2020, 11, 3501–3510, 10.1039/C9SC06140A.
- S. Borsley, J. M. Gallagher, D. A. Leigh and B. M. W. Roberts, Ratcheting Synthesis, Nat. Rev. Chem, 2024, 8(1), 8–29, DOI:10.1038/s41570-023-00558-y.
- O. A. Abdelrahman and P. J. Dauenhauer, Energy Flows in Static and Programmable Catalysts, ACS Energy Lett., 2023, 8(5), 2292–2299, DOI:10.1021/acsenergylett.3c00522.
- M. A. Murphy, S. R. Gathmann, C. J. Bartel, O. A. Abdelrahman and P. J. Dauenhauer, Catalytic Resonance Theory: Circumfluence of Programmable Catalytic Loops, J. Catal., 2024, 430, 115343, DOI:10.1016/j.jcat.2024.115343.
- S. Amano, M. Esposito, E. Kreidt, D. A. Leigh, E. Penocchio and B. M. W. Roberts, Using Catalysis to Drive Chemistry Away from Equilibrium: Relating Kinetic Asymmetry, Power Strokes, and the Curtin-Hammett Principle in Brownian Ratchets, J. Am. Chem. Soc., 2022, 144(44), 20153–20164, DOI:10.1021/jacs.2c08723.
- R. D. Astumian, S. Mukherjee and A. Warshel, The Physics and Physical Chemistry of Molecular Machines, ChemPhysChem, 2016, 1719–1741, DOI:10.1002/cphc.201600184.
- S. Amano, S. Borsley, D. A. Leigh and Z. Sun, Chemical Engines: Driving Systems Away from Equilibrium through Catalyst Reaction Cycles, Nat. Nanotechnol., 2021, 16(10), 1057–1067, DOI:10.1038/s41565-021-00975-4.
- E. R. Kay and D. A. Leigh, Beyond Switches: Rotaxane- and Catenane-Based Synthetic Molecular Motors, Pure Appl. Chem., 2008, 80(1), 17–29, DOI:10.1351/pac200880010017.
- M. R. Wilson, J. Solà, A. Carlone, S. M. Goldup, N. Lebrasseur and D. A. Leigh, An Autonomous Chemically Fuelled Small-Molecule Motor, Nature, 2016, 534(7606), 235–240, DOI:10.1038/nature18013.
- H. Y. Au-Yeung and Y. Deng, Distinctive Features and Challenges in Catenane Chemistry, Chem. Sci., 2022, 13(12), 3315–3334, 10.1039/D1SC05391D.
- S. Amano, S. D. P. Fielden and D. A. Leigh, A Catalysis-Driven Artificial Molecular Pump, Nature, 2021, 594(7864), 529–534, DOI:10.1038/s41586-021-03575-3.
- A. F. Huxley, R. M. Simmons and R. D. Astumian, The Role of Thermal Activation in Motion and Force Generation by Molecular Motors, Philos. Trans. R. Soc., B, 2000, 355(1396), 511–522, DOI:10.1098/rstb.2000.0592.
- R. Dean Astumian, Symmetry Based Mechanism for Hand-over-Hand Molecular Motors, Biosystems, 2008, 93(1), 8–15, DOI:10.1016/j.biosystems.2008.04.005.
- R. D. Astumian, Optical vs. Chemical Driving for Molecular Machines, Faraday Discuss., 2017, 195, 583–597, 10.1039/C6FD00140H.
- G. Ragazzon and L. J. Prins, Energy Consumption in Chemical Fuel-Driven Self-Assembly, Nat. Nanotechnol., 2018, 13(10), 882–889, DOI:10.1038/s41565-018-0250-8.
- K. Das, L. Gabrielli and L. J. Prins, Chemically Fueled Self-Assembly in Biology and Chemistry, Angew. Chem., Int. Ed., 2021, 60(37), 20120–20143, DOI:10.1002/anie.202100274.
- R. D. Astumian, Kinetic Asymmetry and Directionality of Nonequilibrium Molecular Systems, Angew. Chem., 2024, 136(9), e202306569, DOI:10.1002/ange.202306569.
- T. van Leeuwen, A. S. Lubbe, P. Štacko, S. J. Wezenberg and B. L. Feringa, Dynamic Control of Function by Light-Driven Molecular Motors, Nat. Rev. Chem., 2017, 1(12), 1–7, DOI:10.1038/s41570-017-0096.
- T. M. Onn, K.-R. Oh, D. Z. Adrahtas, J. K. Soeherman, J. A. Hopkins, C. D. Frisbie and P. J. Dauenhauer, Flexible and Extensive Platinum Ion Gel Condensers for Programmable Catalysis, ACS Nano, 2024, 18(1), 983–995, DOI:10.1021/acsnano.3c09815.
- K.-R. Oh, T. M. Onn, A. Walton, M. L. Odlyzko, C. D. Frisbie and P. J. Dauenhauer, Fabrication of Large-Area Metal-on-Carbon Catalytic Condensers for Programmable Catalysis, ACS Appl. Mater. Interfaces, 2024, 16(1), 684–694, DOI:10.1021/acsami.3c14623.
- J. H. Friedman, Greedy function approximation: a gradient boosting machine, Ann. Stat., 2001, 29, 1189–1232 Search PubMed.
- F. Pedregosa, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- T. Chen and C. Guestrin, XGBoost: a scalable tree boosting system, in Proc. 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM, New York, NY, USA, 2016, pp. 785–794, DOI:10.1145/2939672.2939785.
- Scikit-learn Developers, Permutation_importance, Scikit-learn Documentation, https://scikit-learn.org/stable/modules/permutation_importance.html Search PubMed.
- R. K. Mothilal, A. Sharma and C. Tan, Explaining machine learning classifiers through diverse counterfactual explanations, Proceedings of the 2020 Conference on Fairness, Accountability, and Transparency (FAT* '20), 2020, pp. 607–617, DOI:10.1145/3351095.3372850.
- S. M. Lundberg and S.-I. Lee, A Unified Approach to Interpreting Model Predictions, in Advances in Neural Information Processing Systems, 2017, vol. 30, https://papers.nips.cc/paper_files/paper/2017/hash/8a20a8621978632d76c43dfd28b67767-Abstract.html Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Binding energies derivation, microkinetic model derivation, code development, block logic diagrams, and XGB feature importance. See DOI: https://doi.org/10.1039/d4dd00216d |
| ‡ These authors contributed equally. |
| This journal is © The Royal Society of Chemistry 2025 |