Open Access Article
Open Access ArticleQuantitative analysis of miniature synaptic calcium transients using positive unlabeled deep learning†
Frédéric
Beaupré‡
 ab,
Anthony
Bilodeau‡
ab,
Anthony
Bilodeau‡
 ab,
Theresa
Wiesner§
a,
Gabriel
Leclerc
ab,
Mado
Lemieux
a,
Gabriel
Nadeau
a,
Katrine
Castonguay
ab,
Bolin
Fan
cd,
Simon
Labrecque
a,
Renée
Hložek
cd,
Paul
De Koninck
ae,
Christian
Gagné
bfg and
Flavie
Lavoie-Cardinal
ab,
Theresa
Wiesner§
a,
Gabriel
Leclerc
ab,
Mado
Lemieux
a,
Gabriel
Nadeau
a,
Katrine
Castonguay
ab,
Bolin
Fan
cd,
Simon
Labrecque
a,
Renée
Hložek
cd,
Paul
De Koninck
ae,
Christian
Gagné
bfg and
Flavie
Lavoie-Cardinal
 *abh
*abh
aCERVO Brain Research Center, Québec, Canada. E-mail: flavie.lavoie-cardinal@cervo.ulaval.ca
bInstitute Intelligence and Data, Université Laval, Québec, Canada
cDunlap Institute for Astronomy and Astrophysics, University of Toronto, Toronto, Canada
dDavid A. Dunlap Department for Astronomy and Astrophysics, University of Toronto, Toronto, Canada
eDepartment of Biochemistry, Microbiology and Bioinformatics, Université Laval, Québec, Canada
fDepartment of Electrical Engineering and Computer Engineering, Université Laval, Québec, Canada
gCanada CIFAR AI Chair, Affiliated to Mila, Canada
hDepartment of Psychiatry and Neuroscience, Université Laval, Québec, Canada
First published on 20th November 2024
Abstract
Ca2+ imaging methods are widely used for studying cellular activity in the brain, allowing detailed analysis of dynamic processes across various scales. Enhanced by high-contrast optical microscopy and fluorescent Ca2+ sensors, this technique can be used to reveal localized Ca2+ fluctuations within neurons, including in sub-cellular structures, such as the dendritic shaft or spines. Despite advances in Ca2+ sensors, the analysis of miniature Synaptic Calcium Transients (mSCTs), characterized by variability in morphology and low signal-to-noise ratios, remains challenging. Traditional threshold-based methods struggle with the detection and segmentation of these small, dynamic events. Deep learning (DL) approaches offer promising solutions but are limited by the need for large annotated datasets. Positive Unlabeled (PU) learning addresses this limitation by leveraging unlabeled instances to increase dataset size and enhance performance. This approach is particularly useful in the case of mSCTs that are scarce and small, associated with a very small proportion of the foreground pixels. PU learning significantly increases the effective size of the training dataset, improving model performance. Here, we present a PU learning-based strategy for detecting and segmenting mSCTs in cultured rat hippocampal neurons. We evaluate the performance of two 3D deep learning models, StarDist-3D and 3D U-Net, which are well established for the segmentation of small volumetric structures in microscopy datasets. By integrating PU learning, we enhance the 3D U-Net's performance, demonstrating significant gains over traditional methods. This work pioneers the application of PU learning in Ca2+ imaging analysis, offering a robust framework for mSCT detection and segmentation. We also demonstrate how this quantitative analysis pipeline can be used for subsequent mSCTs feature analysis. We characterize morphological and kinetic changes of mSCTs associated with the application of chemical long-term potentiation (cLTP) stimulation in cultured rat hippocampal neurons. Our data-driven approach shows that a cLTP-inducing stimulus leads to the emergence of new active dendritic regions and differently affects mSCTs subtypes.
1 Introduction
Ca2+ imaging is widely used for the study of cellular activity modulations in the brain, enabling detailed monitoring and analysis of dynamic processes at various scales: from large neuronal networks down to individual synapses.1,2 Exploiting high-contrast optical microscopy approaches and fluorescent Ca2+ sensors, it offers insights into localized fluctuations of Ca2+ concentration within neurons.3,4 In the last decade, the development of a variety of sensitive Ca2+ sensors with increased brightness and improved detection kinetics has opened up new possibilities for the monitoring of dynamic processes occurring in small cellular compartments such as dendritic spines.5–7 For instance, Ca2+ imaging of miniature Synaptic Calcium Transients (mSCTs) has been studied to monitor the NMDA-receptor driven Ca2+ influxes generated by the spontaneous release of glutamate-containing presynaptic vesicles.3,8–12 mSCTs are characterized by wide variability in their morphology and spatio-temporal propagation, but also by a generally small difference between peak and background intensity fluctuations.3 This makes the task of selecting a robust and general method for automated mSCT analysis very challenging. Spike-inference approaches have been developed to describe the underlying process by which spiking activity leads to fluorescence measurements.13,14 However, such methods do not take into account the spatial extent of calcium events and do not address the problem of event detection from raw videos. Threshold-based methods relying on the extraction of regions of interest (ROIs) have been proposed to segment cell body from whole cell Ca2+ imaging videos.15,16 Such approaches were also applied to detect small events, such as astrocytic calcium events,17,18 which are more similar to the task of mSCT detection. However, the accuracy of the threshold-based methods is reduced for events that propagate or change size and shape over time. Noise-based thresholding was proposed to detect and track sub-cellular events occurring at random locations and propagating over time such as mSCTs.19While user-defined analysis pipelines are still common, the bio-imaging field has seen a shift of paradigm in the tools developed for quantitative analysis. Indeed, further performance gains can be obtained with the use of deep learning (DL) for segmentation,20 small object segmentation21 (Ma et al.22 for a review), or calcium analysis23,24 when compared to user-defined pipelines. DL offers data-driven approaches to automatically learn features and patterns present in a dataset that define the structures or events. Consequently, these networks do not require to make a priori assumptions on either the regions of interest, model-based definitions of spatio-temporal features, or on parameter choices specific to a given task. They have been applied successfully to Ca2+ imaging detection tasks at the cellular level.25–27
One limitation for the broad deployment of supervised DL-based Ca2+ imaging analysis is the need for large annotated datasets28 to train the DL models. In many experimental contexts, including Ca2+ imaging, negative instances, corresponding to pixels that do not contain a Ca2+ event at a given time point, account for a large proportion of the image.29,30 This represents an additional challenge for the development of DL analysis strategies. In cases where Ca2+ transients (positive instances) are small and scarce, a large fraction of the foreground remains without annotation (unlabeled). Positive Unlabeled (PU) learning was proposed to harness unlabeled instances with the intuition that they can be leveraged to train deep neural networks.31,32 It can be used to address challenges associated with the impossibility to annotate all negative instances due to time constraints or subjectivity of the annotation process.33 During PU training, the DL model has access to positive instances and a predefined number of unlabeled instances. This significantly increases the size of the training dataset by providing additional information to the DL models and leveraging the abundance of unlabeled data. In the context of mSCT detection, we reason that unlabeled crops contain information about random Ca2+ fluctuations that can be leveraged by the DL model during training to better differentiate between mSCTs and random fluctuations. PU learning has already been applied with success to several bio-image analysis tasks.34–36
Here, we present a PU learning-based strategy for the analysis of mSCTs in cultured rat hippocampal neurons (Fig. 1). The approach was developed to be applicable for the detection and segmentation of mSCTs characterized by a large diversity of signal amplitudes, frequencies, and spatial distributions. Our algorithm provides both mSCT detection and segmentation through the use of spatio-temporal (2 spatial dimensions + 1 temporal dimension) DL models (3D U-Net37 and StarDist-3D38). We introduce PU learning in the context of mSCTs detection, using foreground intensity fluctuations as unlabeled instances and mSCTs as positive instances. In the absence of unlabeled instances for training, our algorithm is similar to that of Dotti et al.,39 which implements a 3D U-Net for segmentation of low SNR Ca2+ events in full-frame confocal imaging data. The authors tackled a multi-label instance segmentation task to differentiate between types of Ca2+ release in the context of cardiomyocytes. We build upon this work in an instance segmentation task and show that the addition of unlabeled instances to the training procedure leads to significant gains in the performance of the 3D U-Net. To the best of our knowledge, this is the first use of PU learning for Ca2+ imaging analysis. We leverage the trained DL model to create a multidimensional analysis framework, which allows the analysis of mSCT features associated with the application of a chemical long term potentiation (cLTP) inducing stimulus.
2 Methods
2.1 Neuronal cell culture
Dissociated rat hippocampal cultures were prepared as described previously.40,41 In brief, hippocampi were dissected out of P1 rats, following approved protocols from the Université Laval animal care committee, dissociated enzymatically (papain, 12 U/ml; Worthington), and mechanically (trituration through Pasteur pipette). After dissociation, the cells were washed, centrifuged, and plated on poly-D-lysine-coated glass (18 mm) coverslips at a density of ∼67 500 cells per mm2. Growth media consisted of Neurobasal and B27 (50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), supplemented with penicillin/streptomycin (50 U/ml; 50 μg ml−1) and 0.5 mM L-glutamax (Invitrogen). Fetal bovine serum (2%; HyClone) was added at time of plating. After 5 days, half of the media was changed without serum and with Ara-C (5 μM; Sigma-Aldrich) to limit proliferation of non-neuronal cells. After that, half of the growth medium was replaced with serum- and Ara-C-free medium twice a week. For Ca2+ imaging, neurons were transfected with GCaMP6f-expressing plasmid (pGP-CMV-GCaMP6f)6 using Lipofectamine 2000 (Invitrogen). For the plasticity experiments, neurons were transfected at day in vitro (DIV) 9–13 and imaged 24 h later. For the generation of the training dataset for the detection and segmentation of mSCTs, videos from neurons imaged at DIV 7–17 were included.
1), supplemented with penicillin/streptomycin (50 U/ml; 50 μg ml−1) and 0.5 mM L-glutamax (Invitrogen). Fetal bovine serum (2%; HyClone) was added at time of plating. After 5 days, half of the media was changed without serum and with Ara-C (5 μM; Sigma-Aldrich) to limit proliferation of non-neuronal cells. After that, half of the growth medium was replaced with serum- and Ara-C-free medium twice a week. For Ca2+ imaging, neurons were transfected with GCaMP6f-expressing plasmid (pGP-CMV-GCaMP6f)6 using Lipofectamine 2000 (Invitrogen). For the plasticity experiments, neurons were transfected at day in vitro (DIV) 9–13 and imaged 24 h later. For the generation of the training dataset for the detection and segmentation of mSCTs, videos from neurons imaged at DIV 7–17 were included.
2.2 Imaging solutions and pharmacology
The HEPES-buffered aCSF solution used for Ca2+ imaging contained: 104 mM NaCl, 5 mM KCl, 10 mM Na-HEPES, and 10 mM glucose. To initially maintain little or no NMDA receptor activity during the transfer of the coverslip to the microscope, this solution contained 0.6 CaCl2 and 5.0 MgCl2 (high-Mg2+-aCSF). For mSCT measurements, the solution was adjusted to contain no Mg2+, 1.2 mM Ca2+ and 0.5 μM Tetrodotoxin (TTX, Alomone Labs) (0Mg2+/TTX-aCSF). For chemical long term potentiation (cLTP) stimulation, the aCSF solution without Mg2+ was supplemented with 0.2 mM glycine and 0.01 mM bicuculline (0Mg2+/Gly/Bic-aCSF).42 The osmolarity of every solution was maintained around 230 Osm, close to the neurobasal-based growth media value of the neuronal cell cultures.2.3 Live imaging and plasticity protocol
Neurons were imaged using a 100x 1.49NA immersion objective on an inverted Olympus IX-71, equipped with a TIRF illuminator, set on an oblique illumination mode to detect fluorescence with improved contrast.43 The microscope was equipped with a multi-valve perfusion system (VC3-8xG, ALA Scientifics instruments) and an inline heater (SF-28, Warner) so that neurons were continuously perfused with heated (32 °C) solutions. Transfected neurons were imaged with a Toptica iChrome MLE laser at 488 nm. GCaMP6f fluorescence emission was filtered through a Semrock, Brightline 520/35 cube placed before the objective and recorded on a Charge-coupled device (CCD) camera (Princeton ProEm 512B-FT) at a rate of 10 frames per second. The pixel size was 0.16 μm. Image acquisition was performed using a custom written Matlab script in Matlab2007 (ref. 43).For the generalization experiment of the trained model, time-lapse imaging of GCaMP6f was performed at room temperature using an upright microscope (Axioskop FS2; Zeiss) equipped with a 63x 0.95 NA Achroplan water immersion objective (Zeiss) and a multivalve perfusion system (PTR-2000; ALA Scientific Instruments). Fluorescence excitation was achieved using a Lambda DG-4 system with a 175 W Xenon lamp (Sutter Instrument), using a 485/20 nm excitation filter and a LP515 emission filter. Images were acquired in epifluorescence mode with an EMCCD camera (QuantEM:512SC; Photometrics) using an exposure time of 150 ms and a 2 × 2 binning.
For the mSCT plasticity experiments, neurons were transfected at DIV 9–13 and imaged 24 h later. Coverslips were first transferred from the incubator to the perfusion chamber containing fresh high-Mg2+-aCSF, to block the activity and prevent any cellular stress. The perfusion was switched for the imaging session to 0Mg2+/TTX-aCSF and a baseline Ca2+ imaging video of 600 frames (60 seconds) was acquired. Immediately after, the perfusion was changed to 0Mg2+/Gly/Bic-aCSF for 7 minutes for the cLTP stimulation. After the 7 min cLTP stimulation, the perfusion was switched back to 0Mg2+/TTX-aCSF solution. For the control condition, neurons were kept in the 0Mg2+/TTX-aCSF throughout. Neurons were not imaged during the cLTP stimulation to prevent photobleaching of the Ca2+ sensor. Directly after the stimulation, the perfusion was switched back to 0Mg2+/TTX-aCSF. For both conditions a baseline Ca2+ imaging video was first acquired followed by a second video, starting 10 min after the end of the baseline. During the acquisition of both Ca2+ imaging videos the solution was 0Mg2+/TTX-aCSF.
2.4 Intensity-based detection threshold (IDT) annotator
We developed an intensity-based detection threshold (IDT) algorithm to detect and segment mSCTs while recording their temporal and spatial position. IDT is implemented in Matlab 2018 (Mathworks Inc., Natick, USA). It consists of 3 phases: (i) data preprocessing, (ii) automated detection and segmentation of mSCTs, and (iii) manual verification of the detected Ca2+ events.Acquired streams were initially aligned in x and y to the first frame of the video using the custom written Matlab code of Guizar-Sicairos et al.44 Subsequently, the background noise was removed by manually choosing a region of interest in the background and by subtracting its average intensity from each frame. To detect the foreground, a spatial median filter was applied (kernel size of 3) and manual adjustment of an intensity-based threshold was performed. Ca2+ transient detection was performed pixel-wise from the foreground mask. For each pixel the fluorescence intensity was extracted and the baseline was corrected using asymmetric re-weighted penalized least square algorithm (arPLS).45 The fluorescence signal F was normalized to the baseline fluorescence F0 with:46
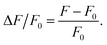 | (1) |
To identify real Ca2+ events from fluorescence foreground fluctuations, we first evaluated the noise of the baseline fluorescence trace. We compared the standard deviation (STD) of the signal while iteratively excluding the time points with the highest values, which correspond to Ca2+ events rather than noise fluctuations. When the STD between 2 consecutive iteration steps becomes similar, indicating that most of the Ca2+ events have been removed, we use the measured STD as an approximation of baseline noise fluctuations for subsequent steps. Ca2+ transients are detected with the Matlab function findpeaks. The first threshold is used to detect peaks in the baseline corrected time traces and set at 4 × STD (detection threshold). A second threshold of 2 × STD is applied subsequently and used for the segmentation of the mSCTs (segmentation threshold). The segmentation threshold is applied within a time window of 1500 ms before and after the peak to determine the length of the mSCTs. Using this approach, events lasting only 1 frame are discarded.
The spatial and temporal properties of the segmented objects are calculated using the regionprops function in Matlab. The events having one of their spatial axis ≤3 pixels are removed. Following this first automated detection step, the user is asked to verify each detected event with the help of a graphical user interface (GUI). The GUI displays a small crop centered around each event (64 by 64 pixels, 12 frames), the corresponding baseline-correction, and detection of the normalized Ca2+ transients. In the GUI, the user inspects the detected events to determine which ones correspond to mSCTs and should be kept for future analysis. To facilitate the analysis, events detected at different time points but with weighted centroids closer than 2.55 μm are given the same region identifier (ID) and can be proofed at the same time. We noted that mSCTs which occur at a high frequency at the same position are often missed by ITD. Additionally those segmented events typically last longer than 4.5 seconds. This issue arises from defining the end of an event as the fluorescence signal dropping below the second threshold, particularly during bursts of events. Hence, the user is asked to inspect these events with another GUI showing the mSCT (64 by 64 pixels, 12 frames) and the overlapped segmentation at the maximal peak intensity frame. This is required to extract the total number of events but does not affect the mask of IDT used to train the DL models. The analysis time of a video strongly depends on the number of Ca2+ transients. On average we can find between 100–800 events and the analysis of such videos can require from 2 to 4 hours (automated and manual steps combined).
2.5 Dataset
The training dataset consisted of 14 Ca2+ imaging videos acquired on different neurons. To account for the very small size of the training dataset, we measured the averaged performance of each model trained with five independent random seeds and five distinct groups of 14 Ca2+ imaging videos annotated using the IDT algorithm. Positive crops (64 × 64 × 64 pixels) were generated for each transient detected by IDT and manually validated by an expert. For each subset, unlabeled crops were sampled from the foreground to obtain the desired PU ratio. Unlabeled crops from a smaller PU ratio are a subset of the next PU ratio, e.g. the set of unlabeled crops used to train the models with a PU ratio of 1–2 is contained in the set of unlabeled crops used to train the models with a PU ratio of 1–4. The validation dataset was kept constant for all training and consisted of 15 independent Ca2+ imaging videos that were annotated with the IDT algorithm.The testing detection dataset consisted of 10 independent Ca2+ imaging videos that were manually annotated by an expert at the peak intensity of the mSCT. The manual detection of mSCTs consisted of point annotations of the event centroids at the maximal ΔF/F0 frame. The segmentation testing dataset consisted of manual segmentation masks obtained from two experts for 69 mSCTs of varied size, shape, and intensity. The masks were drawn on (32 × 32 pixels) pixel crops centered on the frame with maximal ΔF/F0 for each mSCT. This was required to reduce the impact of missed events (false negatives) and the imprecise segmentation masks from the IDT algorithm during the evaluation.
2.6 DL models
All DL models were trained on crops of size (32 × 32 × 32) from the aligned and normalized version of the acquired Ca2+ imaging videos (baseline correction and ΔF/F0, see 2.4) and the corresponding IDT annotations. Training parameters varied for both models and are described below. At inference, tiles of size (64 × 64 × 64) are used to make the final prediction.The model was trained with the Adam optimizer, with default parameters and a learning rate of 0.0002, to minimize the mean quadratic error. The model was trained for 100k steps with a batch size of 128. Every 100 steps, the complete validation dataset was used to assess the generalization performance. Random crops and spatial flip were used during training for data augmentation. The model with the best performance on the validation test was kept for testing.
The model was trained for 400 epochs with a batch size of 64 and 100 batches per epochs. The same data augmentation technique to the 3D U-Net was used during training.
The models were trained with the Adam optimizer, with default parameters and a learning rate of 0.0002. The models were trained with their recommended loss function (DiceCE loss: a weighted sum of the dice loss and the cross-entropy loss) or with the mean squared quadratic loss function. In all cases, the models were trained for 100k steps with a batch size of 128. Every 100 steps, the complete validation dataset was used to assess the generalization performance. Random crops and spatial flips were used during training for data augmentation. The model with the best performance on the validation test was kept for testing.
2.7 Positive unlabeled learning
Typical supervised DL algorithms learn to represent data using raw inputs and their corresponding annotations.52 A binary classification problem consists in training a model to discriminate two classes of events (e.g., positive and negative). Traditionally, supervised machine learning makes use of a dataset {(x0, y0), (x1, y1),…} where is the input and yi, the associated annotation. In the case of the detection task we have yi ∈ {0, 1}, with the sample being positive when y = 1 and negative otherwise (y = 0).
is the input and yi, the associated annotation. In the case of the detection task we have yi ∈ {0, 1}, with the sample being positive when y = 1 and negative otherwise (y = 0).
In Positive Unlabeled (PU) learning,31 a binary variable s ∈ {0, 1} on whether an example was annotated or not is introduced in the training dataset {(x0, y0, s0), (x1, y1, s1),…}. When the annotation process does not make annotation errors, it implies that  . When s = 0, then the example can belong to both classes.
. When s = 0, then the example can belong to both classes.
In some fields, such as biomedical imaging, deep learning algorithms can be difficult to implement due to the scarcity or cost of acquiring data belonging to the positive class, or label.53 In this study, mSCTs account for a very small portion of the training dataset (<0.05% of total pixels, or <0.3% of foreground pixels). In a PU learning framework the network learns from positive (mSCTs detected with IDT) and unlabeled examples (extracted from the foreground). Unlabeled examples differ from negative examples as they could be a positive or negative instance, albeit with a much larger chance of belonging to the negative class for very sparse and small events such as mSCTs. Consequently, PU learning is particularly appealing and efficient when unlabeled examples are available at low cost and in large quantities.31
In our imaging dataset, mSCTs are the positive samples, and to construct a PU learning dataset, we sample regions along dendrites where no mSCTs were detected with IDT. As mSCTs account for such a small portion of the total video pixels, we can acquire unlabeled crops in large quantities. To better study the effect of the number of unlabeled crops on model performance, we first evaluate the performance of a model trained in a positive-only context (PU ratio 1–0). Both StarDist-3D and 3D U-Net are trained in a PU learning setting, with PU ratios ranging from 1–1 to 1–256.
2.8 Evaluation strategies
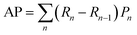 | (2) |
2.9 Multdimensional analysis
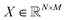 , where N is the number of detected mSCTs and M is the number of features characterizing the mSCTs (note that these are manually defined, ESI Table 2†).58 Each detected mSCT is associated with its closest subtype using the pairwise euclidean distance between the averaged feature vectors of the subtypes and the feature vector of each mSCT.
, where N is the number of detected mSCTs and M is the number of features characterizing the mSCTs (note that these are manually defined, ESI Table 2†).58 Each detected mSCT is associated with its closest subtype using the pairwise euclidean distance between the averaged feature vectors of the subtypes and the feature vector of each mSCT.
We computed the features with the most impact on the classifier's predictions using SHapley Additive exPlanations (SHAP) values, which is a game theory approach used to explain the output of machine learning models.60 SHAP values give information regarding the contribution of each feature of the mSCT to the classifier prediction. The SHAP values predict how the machine learning model would perform with and without each specific feature to discriminate between the different mSCT categories, giving insights into the most important features to distinguish, for example, mSCTs detected only prior (silenced) or after (new) the cLTP simulation.
In Fig. 5h, we plot the SHAP value for each event in the testing dataset, color-coded by their normalized feature values. The grey line corresponds to a SHAP value of 0, indicating no preference towards either class. Higher (or lower) SHAP values correspond to a greater influence on the model's output. The SHAP values are arranged according to their distribution spread, with a larger spread indicating greater importance of this feature in the decision tree prediction. The color-coding of the events highlights the relationship between the value of each feature and its impact on the model's prediction.
The statistical difference between the proportion of subtypes was computed using the χ2 statistical analysis followed by a post-hoc χ2 analysis test.
3 Results
3.1 Intensity threshold-based detection of mSCTs
Ca2+ imaging was performed with video microscopy of cultured rat hippocampal neurons transfected with a genetically-encoded Ca2+ indicator (GCaMP6f),6 using a TIRF microscope set in the oblique illumination mode.43 To reveal mSCTs, the neurons were perfused with HEPES-buffered artificial cerebrospinal fluid (aCSF) lacking Mg2+ and supplemented with 0.5 μM Tetrodotoxin (TTX) to block action potentials. The localized transient changes in Ca2+ concentration, triggered by spontaneous release of glutamate and Ca2+ influx through NMDA receptors were monitored in proximal dendrites (Fig. 2a–c). Videos of 60 s were acquired using a sampling frequency of 10 Hz. Lateral drift and background corrections were first applied to the raw videos (see Methods). The fluorescence signal F was normalized to the baseline F0 (ΔF/F0, see Methods).46We developed an intensity-based detection threshold (IDT) approach for the detection and segmentation of mSCTs in the baseline-corrected dataset. We adopted a two-threshold approach to automatically detect and segment mSCTs in the Ca2+ imaging videos (Fig. 2d), followed by manual inspection of the detected events. The first threshold (4 standard deviations (STD) above the baseline noise) was used to detect transients at their maximal ΔF/F0 value, while the second threshold (2 × STD) was used to generate a segmentation mask covering the entire duration of the mSCT (see Methods). A manual validation step of the detected transients was essential to confirm the detection results, as most mSCTs had a maximal ΔF/F0 < 1, making it difficult to distinguish real events from foreground fluorescence signal fluctuations using a fully-automated threshold-based approach (Fig. 1 – Data preparation). This manual step limited the number of false-positive detected events associated with noise and background fluctuations that were included in the final annotated IDT-dataset.
3.2 Detection of mSCTs with PU-learning
We used the manually curated IDT-annotated dataset of Ca2+ imaging videos as the ground truth to train the DL models in a supervised setting to automatically detect and segment mSCTs. The training sets consisted of 5 sets of 14 videos. The validation set included 15 annotated Ca2+ imaging videos. The detection performance was evaluated on a test set consisting of 10 Ca2+ imaging videos in which the x, y, t coordinates of the brightest point for all mSCTs were manually annotated by an expert. Manual annotation of the test set was necessary to overcome the lower detection accuracy of IDT for transients with a ΔF/F0 ≤ 1. To leverage the spatio-temporal dynamics of mSCTs, we chose 3D deep neural networks that are well established in the field of microscopy: 3D U-Net37 and StarDist-3D.38 The 3D U-Net was implemented in the ZeroCostDL4Mic standard63 and is available for the community.¶ For StarDist-3D, we used the seminal implementation.38,48 Both of these DL models are trained to minimize the squared error (mean squared error loss) between their prediction and the corresponding IDT annotations (see Methods). We also trained two more complex models: the UNetR49 and the Attention-UNet.51 We first used the DiceCE Loss (weighted sum of the dice loss and the cross entropy loss) as in the seminal implementations of those models (from the MONAI library50). We found that the precision of both models was very low due to a large number of false positives (ESI Fig. 1†). Using the mean-squared error, as for the 3D-UNet and StarDist-3D, we improved the precision of UNetR and Attention-UNet but the performance remained significantly lower than that of the 3D U-Net and StarDist-3D (ESI Fig. 1†). We therefore only use the latter two for the PU experiments. To improve the DL models' ability to differentiate between fluorescence signal fluctuations and mSCTs, we included in the training set unlabeled (U) foreground regions in addition to the positive (P) annotations obtained with IDT. We introduced a variable number of unlabeled instances to the training dataset (Fig. 3a) to measure the impact of learning from unlabeled instances and validate the benefit of PU learning for a small data regime.The detection performance of the models trained with different PU ratios is compared using precision-recall (PR) curves (Fig. 3b and c) to quantitatively evaluate the impact of leveraging unlabeled instances during training. For each PU ratio, the DL models were trained with 25 effective folds (5 seeds for 5 different positive-unlabeled training datasets – see Methods) and the averaged performance is reported. We apply the PU learning scheme by sampling unlabeled foreground instances to generate PU ratios ranging from 1–1 to 1–256. With the 3D U-Net, we observe maximal detection performance for a PU ratio of 1–64, after which the performances decreases, albeit remaining higher than the training scheme without unlabeled instances (ratio 1–0) (Fig. 3b). For StarDist-3D, increasing the number of unlabeled instances negatively impacts its performance (Fig. 3c). For PU ratios <1–4, StarDist-3D shows a better performance than the 3D U-Net in terms of average precision (AP – see Methods). However, the 3D U-Net surpasses StarDist-3D for ratios above 1–4. Furthermore, the best 3D U-Net models (1–16, 1–32, 1–64, and 1–256) outperform the best StarDist-3D model in terms of AP, reaching a value of 0.59 for the 3D U-Net trained with a PU ratio of 1–64 (ESI Table 4†).
We then investigated the relationship between detection performance and mSCT fluorescence intensity (Fig. 3d and e). Generally, mSCTs that are most difficult to distinguish from other fluorescence signal fluctuations are small and dim (ΔF/F0 < 1). These account for the majority of the events annotated by the expert in our testing dataset (ESI Fig. 2†). As expected, the performance (accuracy, recall and precision) of the 3D U-Net and StarDist-3D increases with increasing mSCT intensity, stabilizing for ΔF/F0 > 1 for all PU ratios (Fig. 3d and e). The 3D U-Net shows an improved accuracy and recall over StarDist-3D for ΔF/F0 < 1 mSCTs (Fig. 3d and e). For the 3D U-Net, PU learning increases the precision at the cost of a small decrease in recall for PU ratios above 1–64. Training the 3D U-Net with unlabeled crops results in stricter models (better precision/fewer false positives; see ESI Fig. 3†). This could be explained by the capability of the 3D U-Net to leverage information from unlabeled instances to refine its decision boundary between real mSCTs and foreground signal fluctuations. Fig. 3f shows that the 3D U-Net misses fewer ΔF/F0 < 1 events than the IDT annotation method (black horizontal dashed line) and StarDist-3D. Similarly the 3D U-Net performs better than IDT and StarDist-3D in terms of F1-score for the detected mSCTs regardless of their ΔF/F0 (Fig. 3g, see Methods).
As a last experiment, we validated whether the 3D U-Net model would generalize to an out-of-distribution dataset. This dataset consisted of Ca2+ imaging movies of mSCTs in cultured hippocampal neurons but was acquired on a different microscope and using different experimental conditions (Methods, ESI Fig. 4†). The mSCTs detected by the 3D U-Net trained with different PU ratios were compared with manual expert annotations of mSCTs on 5 Ca2+ imaging videos. The detection performance of the 3D U-Net was not impacted when tested on this dataset and improved with the PU ratios up to 1–64, after which the performance slightly decreases. This shows PU learning can be leveraged to detect Ca2+ events in out-of-distribution datasets without fine-tuning of the 3D U-Net model.
3.3 Segmentation of mSCTs
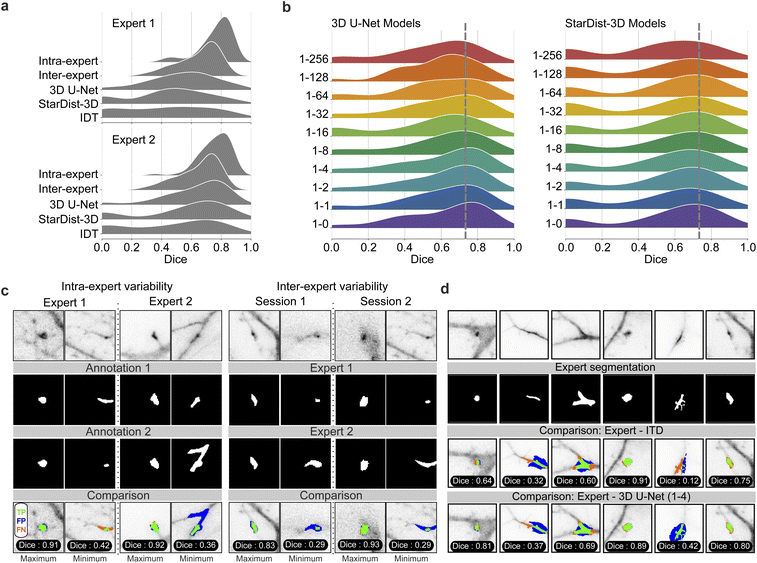
Accurate segmentation of mSCTs is important for the extraction of meaningful morphological (e.g. volume, area, shape) and kinetic (e.g. duration, frequency) features from the segmented fluorescence transients. We therefore evaluated the segmentation performance of our deep neural networks (across the same PU configurations as in Section 3.2) according to the dice similarity score.55 A dice score of zero indicates no overlap and a dice score of unity indicates total overlap. To obtain segmentation ground truths, we asked two experts to manually annotate single frames of 69 mSCTs (see Methods). The type of events that were annotated by the experts varied in form, shape, and intensity. They included synaptic, dendritic, and out-of-focus events. Moreover, the annotation was performed by the same experts at two separate time points, to assess intra- and inter-expert agreement. Fig. 4a shows the agreement results in terms of the dice score as well as the model performance when using either expert as ground truth. We first observe that expert 1 and expert 2 show similar levels of intra-expert agreement, with minimum mSCT segmentation dice scores of 0.42 and 0.36, respectively, means of 0.77 and 0.76, and maximums at 0.91 and 0.92. The inter-expert agreement values are lower, with minimum agreement between the two experts of 0.29, mean of 0.63, and maximum of 0.93. The rather low inter-expert mean dice score highlights the ambiguous nature of ground truths in bio-imaging datasets. These low agreement values suggest that the benchmark performance against which to compare the performance of the deep neural networks is better defined as the inter-expert level of agreement rather than a perfect dice score of 1. When comparing the segmentation performance of the DL models for different PU ratios (Fig. 4b–d), we observe a slightly improved segmentation performance for the 3D U-Net compared to the inter-expert agreement for ratios below 1–64. Notably, ratios between 1–2 and 1–8 decrease the variability compared to the expert annotations: the number of segmentations with low dice scores below 0.5 decreases. As for the detection, PU learning does not improve the segmentation performance of StarDist-3D. Additionally, all StarDist-3D models show a bimodal dice distribution with first mode near zero. This indicates that StarDist-3D is unable to segment a significant number of ground truth events, which is evocative of the large number of missed events with ΔF/F0 < 1 (Fig. 3f).3.4 Multidimensional analysis of detected mSCTs
The presented detection and segmentation pipeline can serve as a valuable tool to extract morphology and kinetic features from mSCTs. We used the 3D U-Net trained with a PU learning ratio of 1–64 as it provides a good trade-off in detection and segmentation performance. The model was applied to the detection and segmentation of mSCTs on an unseen Ca2+ imaging dataset acquired on the same microscope. This dataset consists of paired videos of 600 frames, (see Methods) consisting of a baseline and a second video acquired 17 minutes after the end of the baseline video. In the control condition, the neurons were kept in a 0Mg2+/TTX solution throughout. We tested the effect of a cLTP stimulus on mSCTs using a bath application of a 0Mg2+/Gly/Bic solution during 7 minutes (ref. 64 and 65, see Methods) following the baseline video acquisition. The post-treatment video was acquired 10 minutes after the end of the stimulation, as in the control condition.We observe a significant increase in the number of mSCTs following the cLTP stimulus (Fig. 5a). Seeing the heterogeneous distribution of morphology and kinetic features of mSCTs revealed by our quantitative analysis pipeline, we next extracted those features from the 3D U-Net's mSCT segmentation masks (ESI Table 2†). From all extracted features, we performed a dependency analysis to identify the most relevant features and reduce interdependence between the variables. The segmented mSCTs were clustered using the K-means algorithm to identify mSCT subtypes in the dataset. The number of subtypes K = 5 is determined using the Silhouette score and the Elbow method (ESI Fig. 5†). The median value of the features for each subtype is shown in Fig. 5b. To evaluate the effect of the cLTP treatment, we measured the proportion of mSCTs associated with each subtype before and after the cLTP stimulus (Fig. 5c). We observe that the proportion of the most prevalent subtype (subtype 4), which corresponds to round, short, and small ΔF/F0 Ca2+ events is significantly reduced after the stimulus. Meanwhile, the proportion of high frequency Ca2+ events (subtype 3), as well as of large events associated with a high ΔF/F0 (subtype 1), is significantly increased by the cLTP stimulus. Fig. 5d shows examples of the different mSCT subtypes together with the 3D U-Net's segmentation mask that were used to perform the feature analysis.
 | ||
| Fig. 5 Quantitative analysis of mSCT features in a cLTP paradigm. (a) The fold change in the number of detected mSCTs (FCNum. Events) is significantly increased following a cLTP-inducing stimulus (0Mg2+/Gly/Bic; Wilcoxon Signed Rank Test: p-value = 0.009), while it remains unchanged in the control condition (CTRL; Wilcoxon Signed Rank Test: p-value = 0.644). (b) Median morphological and kinetic normalized feature values for each subtype obtained from K-means clustering (ESI Table 3† for normalization values). (c) The proportion of events belonging to each subtype is modulated by a cLTP inducing stimulus. χ2 statistical analysis is performed (p-value = 1.63 × 10−10) followed by a post-hoc χ2 analysis test (S0: 8.24 × 10−1, S1: 7.70 × 10−4, S2: 5.35 × 10−1, S3: 3.83 × 10−9, S4: 2.13 × 10−4). (d) Fluorescence signal and associated 3D U-Net segmentation for each mSCT subtype. (left) Image of detected transients at their maximal ΔF/F0 and the corresponding segmented borders (green overlay). (right) Segmentation mask predicted by the 3D U-Net for the frame with maximal ΔF/F0. Crops are 10.24 μm × 10.24 μm. (e) The fold change in the number of new (N) events (FCNum. Events) is significantly increased compared to the number of silenced events following the cLTP stimulus (S, Wilcoxon Signed Rank Test: p-value = 0.02). The number of recurrent events is not significantly different before (Rb) and after (Ra) the stimulation (t-test: p-value = 0.30). (f) The proportion of events belonging to each subtype is differently modulated for the silenced (dark) and new events (pale). χ2 statistical analysis is performed (p-value = 1.36 × 10−10) followed by a post-hoc χ2 analysis test (S0: 7.92 × 10−1, S1: 2.15 × 10−2, S2: 1.36 × 10−1, S3: 6.11 × 10−11, S4: 6.24 × 10−3). (g) The subtypes of Rb events are associated with Ra events of different subtypes. Only >20% association are displayed. The raw number of events is shown in parenthesis. (h) SHAP value obtained on the testing dataset from a decision tree classifier trained to differentiate between event categories (Ra vs. S, Rb vs. N, and N vs. S) using the features extracted from the 3D U-Net segmentation mask for each detected mSCT (see Methods). Features are ranked according to their impact on the model's output. Events are color-coded according to their normalized feature value (same normalization as in (b)). | ||
Using the spatial coordinate of the segmentation masks, we can associate mSCTs occurring in the same region at different time points and classify them as: silenced (S) when they are present only in the baseline video, new (N) for events detected only after the stimulus, and recurrent (R) for events detected in the same region before (Rb), and after (Ra) the stimulus. The increase of events following the cLTP stimulus (Fig. 5a) is supported by the emergence of new active regions (Fig. 5e). We next compared the proportion of subtypes between silenced and new events (Fig. 5f). The measured proportions closely follow the overall proportion that was measured when combining all events (Fig. 5c). To measure whether the treatment impacts the features of recurrent events differently, we associated the subtype of each Rb event with that of Ra events. As shown in Fig. 5g, associated mSCTs do not necessarily share the same subtype before and after the stimulus but stronger correspondence between specific subtypes before and after the stimulus indicates that the modulation of recurrent events is dependant on the features of the Ca2+ event before the cLTP treatment.
We next evaluated the importance of each feature to discriminate between the different mSCT classes (S, N, Ra, Rb). We trained a decision tree classifier to differentiate mSCTs according to their classes, and computed the SHAP values to reveal the most important features leading to the predictions. SHAP values are also used to assess the impact that feature values have on the predicted outcome (in this case the classification task). In the SHAP value plot (Fig. 5h), the features are presented in decreasing order of importance (most important = top-most feature), and the feature values (blue data point = low value, red data point = high value) are ordered along the x-axis according to whether they are likely to cause the model to predict that a mSCT belongs to one class or to another class. From Fig. 5h, one can see that silenced mSCTs and new mSCTs are principally differentiated from recurrent mSCTs by their frequency. The second most important feature indicates that smaller events in the baseline videos are generally associated with silenced (S) mSCTs compared to recurrent (Rb) mSCTs. A lower integrated intensity is beneficial to differentiate between new (N) and recurrent (Ra) mSCTs in the videos acquired after the cLTP stimulus. The SHAP values also indicate that the duration of the event is useful in discriminating between S and N events, but has only little impact for the other classes (Fig. 5h). Our automated detection and segmentation approach with the 3D U-Net, combined with a multidimensional feature analysis of mSCTs showed that the increase in the event number measured following a cLTP-inducing stimulus is supported by the appearance of new active regions. Those new regions have distinct features, among which the proportion of events with high frequency is significantly increased, while small and short events are reduced following the stimulus.
4 Discussion
Through the application of PU learning to the quantitative analysis of Ca2+ imaging data, we have provided accurate detection and segmentation of mSCTs in fluorescence microscopy videos. We could extract signal dynamics and meaningful morphological features from these heterogeneous, low density (both spatial and temporal), low intensity, and propagating events. We have demonstrated that the use of unlabeled instances in a PU learning framework can improve the performance for the detection of low intensity Ca2+ that are missed by other approaches, including other DL methods using solely positive examples for training. The improved performance observed with the 3D U-Net models was achieved simply by adding low-cost, quickly-sampled unlabeled instances to the existing positive instances. The training pipeline is implemented in an easy-to-use ZeroCostDL4Mic Jupyter notebook enabling straightforward training and fine-tuning of the models on new datasets, and specific use cases.63We further showed that our approach allows the extraction of features from the segmentation masks to measure the effect of a cLTP stimulus on mSCT morphologies and dynamics. The Ca2+ events extracted from the 3D U-Net detection and segmentation pipeline could be clustered into 5 main subtypes, that are differently modulated by the cLTP protocol. Having access to precise spatio-temporal localization of the mSCTs revealed that such cLTP stimulus leads largely to the emergence of new active regions, rather than an increase in the frequency of events within regions already active prior to the stimulus. This result may reflect a form of plasticity that is part of the mechanisms supporting long term potentiation of synaptic transmission.66,67 This potentiation may reflect changes in release probability in some axonal terminals,68,69 increase recruitment of Ca2+ permeable ion channels in post-synaptic regions,70,71 or an increase coupling between receptor activation and Ca2+ store release.4,72 The ability to identify and analyze localized regions of activity will allow to dissect these various mechanisms and correlate them with molecular trafficking of proteins, such as the Ca2+/Calmodulin–Protein kinase II,73 or cytoskeletal remodelling of dendritic actin filaments.64
Using the segmentation masks, we could also train a decision tree classifier to discriminate between events depending on the moment they were detected (before or after stimulation). SHAP values provided better insights into which features predominantly influence the model's predictions, revealing that different features are used to distinguish recurrent events from new and silenced events.
The robustness and generalization capacities of our method were also highlighted through its application for the detection and segmentation of mSCTs on an unseen Ca2+ imaging dataset acquired with a different microscope. The performance of the 3D U-Net model was maintained on this out-of-distribution dataset. We also showed that the PU learning setting was also beneficial for the generalization. The presented method should be readily applicable to many other small datasets of Ca2+ imaging, in which the events of interest are sparse and heterogeneous, providing insight into different applications and biological inquiries. For instance, this could be applied to the detection of dopamine or norepinephrine dynamics using the GPCR-activation-based (GRAB) sensors74,75 or local glutamate release using the iGluSnFR sensor.76 We also showed that it can be applied to datasets with missing ground truth annotations, and still provide improvement on these annotations through the PU training of the networks, enabling better modeling of the boundaries between real Ca2+ transients and foreground signal fluctuations. While we have considered a simple formulation of PU learning, it could also be of interest to consider more sophisticated definitions such as in Wolny et al.32 on a variety of bio-imaging datasets. Integration of the DL models into an accessible platform such as ZeroCostDL4Mic63 should also facilitate the application of the proposed framework to new datasets or using other annotation methods as ground truths for training.
Code availability
All code used in this manuscript are open source and available at: https://github.com/FLClab/Calcium-Analysis. The ZeroCostDL4Mic notebook allows users to train, finetune, and predict on their own dataset. Optionally, the notebook provides a subset of data from this manuscript.Data availability
All datasets used to train the models and the corresponding acquired images are available for download at https://s3.valeria.science/flclab-calcium/index.html.Author contributions
F. B., A. B., G. L., R. H., C. G., and F. L. C. designed the deep learning analysis strategy. T. W., M. L., and P. D. K. designed the Ca2+ imaging experiments. T. W. performed the Ca2+ imaging experiments. S. L. developed the Ca2+ imaging acquisition software. T. W., M. L., S. L., and G. N. developed the IDT approach. A. B., F. B., and F. L. C. designed the multidimensional analysis approach. T. W. and G. L. designed the user-study. T. W., G. L., and F. L. C. annotated the testing datasets. K. C. and B. L. F. tested implementations of IDT and PU learning strategies. F. B. and A. B. implemented the deep learning models, performed the PU learning experiments, and analyzed the results. F. B., A. B., and F. L. C. wrote the manuscript. R. H., P. D. K., C. G., and F. L. C. co-supervised the project.Conflicts of interest
The authors declare no competing interests.Acknowledgements
We acknowledge the Neuronal Cell Culture Platform of the CERVO Brain Research Center for the preparation of the dissociated hippocampal cultures. We thank Annette Schwerdtfeger for careful proofreading of the manuscript. Funding was provided by grants from the Natural Sciences and Engineering Research Council of Canada (NSERC) (RGPIN-2019-06704 to F.L.C., RGPIN-2017-06171 to P. D. K. RGPIN-2018-05750 to R. H.), Fonds de Recherche Nature et Technologie (FRQNT) Team Grant (2021-PR-284335 to F. L. C, C. G. and P. D. K.), the Canadian Institute for Health Research (CIHR) (471107 to F. L. C. and P. D. K.), a New Frontiers in Research Fund Exploration Grant (NFRFE-2020-00933 to F. L. C., C. G. and R. H.), and the Neuronex Initiative (National Science Foundation 2014862, Fonds de recherche du Québec – Santé 295824 to F. L. C. and P. D. K.). R. H. acknowledges support from CIFAR, the Azrieli and Alfred. P. Sloan foundations and the Connaught Fund. C. G. is a CIFAR AI-Chair and F. L. C. is a Canada Research Chair Tier II. A. B. was supported by a scholarship from NSERC. F. B. was supported by scholarships from FRQNT, NeuroQuébec, and the Québec Bio-Imaging Network. A. B., F. B., and T. W. were awarded an excellence scholarship from the FRQNT strategic cluster UNIQUE.Notes and references
- J. N. Kerr and W. Denk, Nat. Rev. Neurosci., 2008, 9, 195–205 CrossRef CAS.
- C. Grienberger and A. Konnerth, Neuron, 2012, 73, 862–885 CrossRef CAS.
- T. H. Murphy, J. M. Baraban and W. G. Wier, Neuron, 1995, 15, 159–168 CrossRef CAS PubMed.
- K. F. Lee, C. Soares, J.-P. Thivierge and J.-C. Béïque, Neuron, 2016, 89, 784–799 CrossRef CAS.
- Y. Zhang, M. Rózsa, Y. Liang, D. Bushey, Z. Wei, J. Zheng, D. Reep, G. J. Broussard, A. Tsang and G. Tsegaye, et al. , Nature, 2023, 615, 884–891 CrossRef CAS.
- T.-W. Chen, T. J. Wardill, Y. Sun, S. R. Pulver, S. L. Renninger, A. Baohan, E. R. Schreiter, R. A. Kerr, M. B. Orger and V. Jayaraman, et al. , Nature, 2013, 499, 295–300 CrossRef CAS.
- M. Inoue, A. Takeuchi, S. Manita, S.-i. Horigane, M. Sakamoto, R. Kawakami, K. Yamaguchi, K. Otomo, H. Yokoyama and R. Kim, et al. , Cell, 2019, 177, 1346–1360 CrossRef CAS.
- A. L. Reese and E. T. Kavalali, Elife, 2016, 5, e21170 CrossRef PubMed.
- E. T. Kavalali, Nat. Rev. Neurosci., 2015, 16, 5–16 CrossRef CAS PubMed.
- L. C. Andreae and J. Burrone, Cell Rep., 2015, 10, 873–882 CrossRef CAS PubMed.
- A. S. Walker, G. Neves, F. Grillo, R. E. Jackson, M. Rigby, C. O'Donnell, A. S. Lowe, G. Vizcay-Barrena, R. A. Fleck and J. Burrone, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E1986–E1995 CAS.
- V. N. Murthy, T. J. Sejnowski and C. F. Stevens, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 901–906 CrossRef CAS.
- I. J. Park, Y. V. Bobkov, B. W. Ache and J. C. Principe, J. Neurosci. Methods, 2013, 218, 196–205 CrossRef CAS.
- E. Yaksi and R. W. Friedrich, Nat. Methods, 2006, 3, 377–383 CrossRef CAS.
- A. Giovannucci, J. Friedrich, P. Gunn, J. Kalfon, B. L. Brown, S. A. Koay, J. Taxidis, F. Najafi, J. L. Gauthier, P. Zhou, B. S. Khakh, D. W. Tank, D. B. Chklovskii and E. A. Pnevmatikakis, eLife, 2019, 8, e38173 CrossRef PubMed.
- M. Pachitariu, C. Stringer, M. Dipoppa, S. Schröder, L. F. Rossi, H. Dalgleish, M. Carandini and K. D. Harris, Suite2p: Beyond 10,000 Neurons with Standard Two-Photon Microscopy, bioRxiv, 2017, DOI:10.1101/061507.
- A. Agarwal, P.-H. Wu, E. G. Hughes, M. Fukaya, M. A. Tischfield, A. J. Langseth, D. Wirtz and D. E. Bergles, Neuron, 2017, 93, 587–605 CrossRef CAS PubMed.
- R. Srinivasan, B. S. Huang, S. Venugopal, A. D. Johnston, H. Chai, H. Zeng, P. Golshani and B. S. Khakh, Nat. Neurosci., 2015, 18, 708–717 CrossRef CAS.
- Y. Wang, N. V. DelRosso, T. V. Vaidyanathan, M. K. Cahill, M. E. Reitman, S. Pittolo, X. Mi, G. Yu and K. E. Poskanzer, Nat. Neurosci., 2019, 22, 1936–1944 CrossRef CAS.
- O. Ronneberger, P. Fischer and T. Brox, Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015: 18th International Conference, Munich, Germany, October 5-9, 2015, Proceedings, Part III 18, 2015, pp. 234–241 Search PubMed.
- Y. Xu, F. Gao, T. Wu, K. M. Bennett, J. R. Charlton and S. Sarkar, 2019 IEEE 15th International Conference on Automation Science and Engineering (CASE), 2019, pp. 1761–1767 Search PubMed.
- P. Ma, C. Li, M. M. Rahaman, Y. Yao, J. Zhang, S. Zou, X. Zhao and M. Grzegorzek, Artif. Intell. Rev., 2023, 56, 1627–1698 CrossRef PubMed.
- A. Klibisz, D. Rose, M. Eicholtz, J. Blundon and S. Zakharenko, Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: Third International Workshop, DLMIA 2017, and 7th International Workshop, ML-CDS 2017, Held in Conjunction with MICCAI 2017, Québec City, QC, Canada, 2017, pp. 285–293 Search PubMed.
- L. Sità, M. Brondi, P. Lagomarsino de Leon Roig, S. Curreli, M. Panniello, D. Vecchia and T. Fellin, Nat. Commun., 2022, 13, 1529 CrossRef.
- S. Soltanian-Zadeh, K. Sahingur, S. Blau, Y. Gong and S. Farsiu, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8554–8563 CrossRef CAS.
- N. Ruffini, S. Altahini, S. Weißbach, N. Weber, J. Milkovits, A. Wierczeiko, H. Backhaus and A. Stroh, Bioinformatics, 2024, 40, btae177 CrossRef.
- Z. Xu, Y. Wu, J. Guan, S. Liang, J. Pan, M. Wang, Q. Hu, H. Jia, X. Chen and X. Liao, Front. Cell. Neurosci., 2023, 17, 1127847 CrossRef CAS.
- L. Alzubaidi, J. Zhang, A. J. Humaidi, A. Al-Dujaili, Y. Duan, O. Al-Shamma, J. Santamaría, M. A. Fadhel, M. Al-Amidie and L. Farhan, J. Big Data, 2021, 8, 1–74 CrossRef.
- A. Bilodeau, C. V. L. Delmas, M. Parent, P. De Koninck, A. Durand and F. Lavoie-Cardinal, Nat. Mach. Intell., 2022, 4, 455–466 CrossRef.
- E. Gómez-de-Mariscal, M. Maška, A. Kotrbová, V. Pospíchalová, P. Matula and A. Muñoz-Barrutia, Sci. Rep., 2019, 9, 13211 CrossRef PubMed.
- J. Bekker and J. Davis, Mach. Learn., 2020, 109, 719–760 CrossRef.
- A. Wolny, Q. Yu, C. Pape and A. Kreshuk, Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022, pp. 4402–4411 Search PubMed.
- F. Denis, R. Gilleron and F. Letouzey, Theor. Comput. Sci., 2005, 348, 70–83 CrossRef.
- F. Chen, S. Li, C. Wei, Y. Zhang, K. Guo, Y. Zheng, F. Cao and J. Liang, Biomed. Signal Process. Control, 2024, 87, 105473 CrossRef.
- L. Lejeune and R. Sznitman, Med. Image Anal., 2021, 73, 102185 CrossRef PubMed.
- Ö. Çiçek, A. Abdulkadir, S. S. Lienkamp, T. Brox and O. Ronneberger, 3D U-Net: learning dense volumetric segmentation from sparse annotation, in Medical Image Computing and Computer-Assisted Intervention–MICCAI 2016: 19th International Conference, Proceedings, Part II 19, Springer International Publishing, Athens, Greece, 2016, pp. 424–432 Search PubMed.
- Ö. Çiçek, A. Abdulkadir, S. S. Lienkamp, T. Brox and O. Ronneberger, arXiv, preprint, arXiv:1606.06650 cs, 2016 Search PubMed.
- M. Weigert, U. Schmidt, R. Haase, K. Sugawara and G. Myers, 2020 IEEE Winter Conference on Applications of Computer Vision (WACV), Snowmass Village, CO, USA, 2020, pp. 3655–3662 Search PubMed.
- P. Dotti, M. Fernandez-Tenorio, R. Janicek, P. Márquez-Neila, M. Wullschleger, R. Sznitman and M. Egger, Cell Calcium, 2024, 102893 CrossRef CAS PubMed.
- A. Hudmon, E. LeBel, H. Roy, A. Sik, H. Schulman, M. N. Waxham and P. De Koninck, J. Neurosci., 2005, 25, 6971–6983 CrossRef CAS.
- F. Nault and P. De Koninck, Protocols for Neural Cell Culture: Fourth Edition, 2010, pp. 137–159 Search PubMed.
- W.-Y. Lu, H.-Y. Man, W. Ju, W. S. Trimble, J. F. MacDonald and Y. T. Wang, Neuron, 2001, 29, 243–254 CrossRef CAS PubMed.
- M. Gralle, S. Labrecque, C. Salesse and P. De Koninck, J. Neurochem., 2021, 156, 88–105 CrossRef CAS PubMed.
- M. Guizar-Sicairos, S. T. Thurman and J. R. Fienup, Opt. Lett., 2008, 33, 156–158 CrossRef.
- S.-J. Baek, A. Park, Y.-J. Ahn and J. Choo, Analyst, 2015, 140, 250–257 RSC.
- H. Dana, B. Mohar, Y. Sun, S. Narayan, A. Gordus, J. P. Hasseman, G. Tsegaye, G. T. Holt, A. Hu and D. Walpita, et al. , elife, 2016, 5, e12727 CrossRef PubMed.
- A. Paszke, S. Gross, F. Massa, A. Lerer, J. Bradbury, G. Chanan, T. Killeen, Z. Lin, N. Gimelshein, L. Antiga, A. Desmaison, A. Köpf, E. Yang, Z. DeVito, M. Raison, A. Tejani, S. Chilamkurthy, B. Steiner, L. Fang, J. Bai and S. Chintala, PyTorch: An Imperative Style, High-Performance Deep Learning Library, Proceedings of the 33rd International Conference on Neural Information Processing Systems, 2019, pp. 8026–8037 Search PubMed.
- U. Schmidt, M. Weigert, C. Broaddus and G. Myers, Cell detection with star-convex polygons, in Medical Image Computing and Computer Assisted Intervention–MICCAI 2018: 21st International Conference, Proceedings, Part II 11, Springer International Publishing, Granada, Spain, 2018, pp. 265–273 Search PubMed.
- A. Hatamizadeh, D. Yang, H. Roth and D. Xu, CVF Winter Conference on Applications of Computer Vision (WACV), 2021, pp. 1748–1758 Search PubMed.
- M. J. Cardoso, W. Li, R. Brown, N. Ma, E. Kerfoot, Y. Wang, B. Murrey, A. Myronenko, C. Zhao, D. Yang, et al., arXiv, 2022, preprint, arXiv:2211.02701, DOI:10.48550/arXiv.2211.02701.
- O. Oktay, J. Schlemper, L. L. Folgoc, M. Lee, M. Heinrich, K. Misawa, K. Mori, S. McDonagh, N. Y. Hammerla, B. Kainz and B. Glocker, Medical Imaging with Deep Learning 2018 (MIDL2018), 2018 Search PubMed.
- Y. LeCun, Y. Bengio and G. Hinton, Nature, 2015, 521, 436–444 CrossRef CAS PubMed.
- S. Azizi, L. Culp, J. Freyberg, B. Mustafa, S. Baur, S. Kornblith, T. Chen, N. Tomasev, J. Mitrović, P. Strachan, S. S. Mahdavi, E. Wulczyn, B. Babenko, M. Walker, A. Loh, P.-H. C. Chen, Y. Liu, P. Bavishi, S. M. McKinney, J. Winkens, A. G. Roy, Z. Beaver, F. Ryan, J. Krogue, M. Etemadi, U. Telang, Y. Liu, L. Peng, G. S. Corrado, D. R. Webster, D. Fleet, G. Hinton, N. Houlsby, A. Karthikesalingam, M. Norouzi and V. Natarajan, Nat. Biomed. Eng., 2023, 7, 756–779 CrossRef.
- H. W. Kuhn, Nav. Res. Logist. Q., 1955, 2, 83–97 CrossRef.
- L. R. Dice, Ecology, 1945, 26, 297–302 CrossRef.
- P. J. Rousseeuw, J. Comput. Appl. Math., 1987, 20, 53–65 CrossRef.
- R. L. Thorndike, Psychometrika, 1953, 18, 267–276 CrossRef.
- S. van der Walt, J. L. Schönberger, J. Nunez-Iglesias, F. Boulogne, J. D. Warner, N. Yager, E. Gouillart, T. Yu and the scikit-image contributors, PeerJ, 2014, 2, e453 CrossRef PubMed.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- S. M. Lundberg and S.-I. Lee, Advances in Neural Information Processing Systems 30, Curran Associates, Inc., 2017, pp. 4765–4774 Search PubMed.
- F. Wilcoxon, Biom. Bull., 1945, 1, 80–83 CrossRef.
- S. S. Shapiro and M. B. Wilk, Biometrika, 1965, 52, 591–611 CrossRef.
- L. von Chamier, R. F. Laine, J. Jukkala, C. Spahn, D. Krentzel, E. Nehme, M. Lerche, S. Hernández-Pérez, P. K. Mattila and E. Karinou, et al. , Nat. Commun., 2021, 12, 2276 CrossRef CAS PubMed.
- F. Lavoie-Cardinal, A. Bilodeau, M. Lemieux, M.-A. Gardner, T. Wiesner, G. Laramée, C. Gagné and P. De Koninck, Sci. Rep., 2020, 10, 11960 CrossRef CAS.
- T. Wiesner, A. Bilodeau, R. Bernatchez, A. Deschênes, B. Raulier, P. De Koninck and F. Lavoie-Cardinal, Front. Neural Circuits, 2020, 14, 57 CrossRef CAS PubMed.
- E. Edelmann, E. Cepeda-Prado and V. Leßmann, Front. Synaptic Neurosci., 2017, 9, 7 Search PubMed.
- A. Citri and R. C. Malenka, Neuropsychopharmacology, 2008, 33, 18–41 CrossRef PubMed.
- J. H. Jung, L. M. Kirk, J. N. Bourne and K. M. Harris, Proc. Natl. Acad. Sci., 2021, 118, e2018653118 CrossRef CAS PubMed.
- P. E. Castillo, Cold Spring Harbor Perspect. Biol., 2012, 4, a005728 Search PubMed.
- A. J. Watt, M. C. Van Rossum, K. M. MacLeod, S. B. Nelson and G. G. Turrigiano, Neuron, 2000, 26, 659–670 CrossRef CAS PubMed.
- P. Park, H. Kang, T. M. Sanderson, Z. A. Bortolotto, J. Georgiou, M. Zhuo, B.-K. Kaang and G. L. Collingridge, Front. Synaptic Neurosci., 2018, 10, 42 CrossRef CAS PubMed.
- A. L. Reese and E. T. Kavalali, Elife, 2015, 4, e09262 CrossRef PubMed.
- M. Lemieux, S. Labrecque, C. Tardif, É. Labrie-Dion, É. LeBel and P. De Koninck, J. Cell Biol., 2012, 198, 1055–1073 CrossRef CAS PubMed.
- J. Feng, C. Zhang, J. E. Lischinsky, M. Jing, J. Zhou, H. Wang, Y. Zhang, A. Dong, Z. Wu and H. Wu, et al. , Neuron, 2019, 102, 745–761 CrossRef CAS PubMed.
- F. Sun, J. Zhou, B. Dai, T. Qian, J. Zeng, X. Li, Y. Zhuo, Y. Zhang, Y. Wang and C. Qian, et al. , Nat. Methods, 2020, 17, 1156–1166 CrossRef CAS.
- J. S. Marvin, B. G. Borghuis, L. Tian, J. Cichon, M. T. Harnett, J. Akerboom, A. Gordus, S. L. Renninger, T.-W. Chen and C. I. Bargmann, et al. , Nat. Methods, 2013, 10, 162–170 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4dd00197d |
| ‡ These authors contributed equally to this work. |
| § Current address: Aix-Marseille Université, CNRS, INP UMR 7051, NeuroCyto, Marseille, France. |
| ¶ https://github.com/FLClab/Calcium-Analysis. |
| This journal is © The Royal Society of Chemistry 2025 |