Unusually high spin–orbit coupling in the methionine singlet–triplet transition and the role of magnetic perturbations in amino acids

Abstract

Forbidden triplet–singlet transitions (T₁ ← S₀) in a few amino acids (methionine, glycine, tryptophan, cysteine) have been examined for their possible detection. This computational study is based on time-dependent density functional theory (TD-DFT) with spin–orbit coupling (SOC) account. The results of this study indicate that the possibility of detecting the absorption T₁ ← S₀ band is quite high for methionine and cysteine. The results demonstrate that the presence of sulfur in amino acids enhances the SOC effect, increasing the intensity of the singlet–triplet absorptions up to a measurable extinction coefficient. The importance of these SOC effects on the photochemical properties of proteins is emphasized together with the potential role of triplet–singlet transitions in photobiology.

---

Introduction

The term “methionine triplet” is well-known in molecular genetics. In this study, we propose a new additional assonance to “methionine triplet.” We are referring to the triplet excited state of the methionine molecule, which has not been previously reported based on its particular properties, which were revealed using experimental measurements. Methionine, similar to all other amino acids, possesses a singlet ground state (S₀) and a lowest excited molecular triplet (T₁) state. These states are typically associated with the phosphorescence phenomena (radiative T₁ → S₀ transition) usually observed in viscous or solid solutions.¹ The energy of the triplet T₁ state is lower than that of the singlet excited S₁ state, which produces a fast fluorescence emission in the S₁ → S₀ transition after light absorption. The T₁ state is also responsible for the delayed emission, which is known to be of the P and E types according to Parker's discoveries;² the late phenomena are now renamed as thermally activated delayed fluorescence (TADF).¹ Similar to all aliphatic amino acids, the methionine molecule absorbs light in the UV region in the form of a wide absorption band (150–250 nm), with a maximum at the middle of the interval, but never exhibits phosphorescence.^3–5 The present results shed light on the possible role of the methionine triplet in the photo- and radiobiology of proteins.^5–9

Within the field of molecular spectroscopy, the term “triplet” is used to determine the total electronic spin state of a molecule. The electronic wave function Ψ must be an eigenfunction of the S⃑² and S_z operators, where is the total spin operator (eqn (1)).

S⃑²Ψ = S(S + 1)ℏ²Ψ;  S_zΨ = M_SℏΨ (1)

In the triplet state, the total spin quantum number of a molecule is equal to S = 1. This provides three possible spin projections in the external magnetic field direction (z-axis). These correspond to three values of the spin magnetic quantum number M_S, which can be −1, 0, or 1. In the ground state of a diamagnetic molecule, the spin quantum number is zero (S = 0), indicating that all electron spins quench each other by being paired on the occupied molecular orbitals (MO) according to the Pauli principle. This introduction completes our etymological explanation on the genetic term “methionine triplet” and presents a new perspective on its role in photobiology.

Light absorption by molecules typically leads to the observation of the singlet–singlet S₀ → S_n transitions, which are allowed by the spin selection rule in the electric dipole approximation.¹ In contrast, the singlet–triplet S₀ → T_n transitions are spin-forbidden, resulting in their zero intensity, solving the Schrödinger equation without spin–orbit coupling (SOC) account. In fact, the S₀ → T₁ transitions in organic molecules are observed with a long optical path because of their low intensity.¹ To calculate such absorption, the SOC must also be included. In this case, the values of S and M_S in eqn (1) are not good quantum numbers; despite this fact, the full wave function is still antisymmetric with respect to the permutation of any pair of electrons and satisfies Pauli's principle. Consequently, the energies of the S₁ and T₁ states in these cases will be different. S–T splitting occurs even when the potential energy operator does not account for magnetic interactions that depend on spin. The reason is connected to the exchange interaction, which depends on the permutational symmetry of the orbital and spin parts of the wave function.

Since the first excited state of an ordinary organic diamagnetic molecule is always a spin triplet T₁ state, its role in organic photochemistry and spectroscopy is very important, despite the spin-prohibition of the S₀ → T₁ transitions.¹ Such transitions are induced by internal magnetic interaction –spin–orbit coupling (SOC) in molecules, which allows S–T states with different spin multiplicities to mix according to the rule (ΔS = ±1). It is worth noting that SOC effects are much stronger in amino acids than in most typical organic compounds containing no heavy atoms.¹ This is due to the presence of carboxylic and amino groups in proteins, which have n-orbitals of lone pairs and mixed σ–π MO wave functions. SOC depends strongly on the atomic nuclear charge Z (as Z⁴), but the change in orbital angular momentum during an S–T transition is also very important for the spectral manifestations of the SOC effects.

Compounds containing either carbonyl or amino groups individually play an important role in the conceptual understanding of organic photochemistry and spectroscopy because of the typical σ–π and n-orbital separation in many such chromophores, where SOC influences the luminescent properties, it is easily classified by the El-Said rules.^1,9 With particular attention to the excited triplet state behavior, these rules thus explain the luminescence of many organic chromophores with π and n electrons. As far as proteins are concerned, only amino acids that contain aromatic cite groups are mentioned in this context.^1,3–6 We note that the role of SOC perturbations and triplet states properties of aliphatic amino acids are rarely discussed in the photobiology and spectroscopy of proteins.^1,3

Amino acid spectroscopy

The electronic absorption spectra of proteins and individual amino acids in aqueous solutions exhibit broad S₀ → S_n bands within the ultraviolet region (150–280 nm). The longest wavelengths and distinctive absorptions observed in the protein spectra by standard non-vacuum spectrophotometers are attributed mainly to non-saturated chromophores present in the side chains of aromatic amino acids; this concerns tryptophan (absorption peak at approximately 280 nm, molar extinction coefficient of ε = 5600 M⁻¹ cm⁻¹) and tyrosine (peak at 275 nm, ε = 1420 M⁻¹ cm⁻¹).³ The aromatic residues undergo π–π* transitions under UV absorption and then release photons, emitting fluorescence at longer wavelengths (about 360 nm) than the absorption maximum.

Peptide bonds in proteins typically exhibit a strong absorption peak around 190 nm (ε = 7000 M⁻¹ cm⁻¹) and a relatively weak absorption in the region 210–220 nm (ε = 100 M⁻¹ cm⁻¹), with a gradual decrease in intensity at longer wavelengths. A relatively low level of absorption has been reported for protein transitions, with an oscillator strength (f) of approximately f = 10⁻⁵.³ The weak UV absorption of the disulfide bonds in cystine is also well known and can be observed in the wide region of 250–320 nm. Therefore, proteins that do not contain aromatic amino acids or disulphide bonds will be practically transparent at wavelengths above 250 nm.³

Upon UV light illumination and absorption, the amino acid molecule undergoes non-radiative S_n → S₁ transitions (internal conversion, IC) and subsequent S₁ → T₁ intersystem crossing (ISC) processes.^4–8 The ISC relaxation competes with fast fluorescence (S₁ → S₀ radiative transitions), which has been observed for tryptophan, tyrosine and many green fluorescent proteins (GFP).⁵ The fluorescence spectrum and its lifetime are very sensitive to changes in the protein's secondary structure because of the IC and ISC relaxation mechanisms and energy transfer to the nearest nano-environment.⁶

The generation of triplet T₁ states upon illumination of GFP is well known; they are commonly populated via ISC processes.^5–7 The typical quantum yield of triplets in GFP and other organic dyes is about 10⁻³, but they are effectively quenched by the triplet oxygen dissolved in tissues.⁵ The observable lifetimes of triplets in anaerobic conditions are up to milliseconds; however, they are much shorter in the presence of O₂(³Σ⁻).^1,8 Triplet lifetimes of 10–40 μs have been measured at normal aerobic conditions for selected fluorescent proteins (eGFP mutants⁶); such relatively long T₁ state lifetimes are explained by the protective role of transmembrane β-barrel proteins.^5,6 For many organic days and benzene derivatives, the calculated triplet radiative lifetimes are much longer (about 10–100 s).^9,10 Information on fluorescence and phosphorescence of individual aliphatic amino acids is, however, absent. Probably, the S₁ and T₁ excited states of these molecules are effectively quenched by intermolecular energy transfer because their high excitation energy (∼5 eV) can be easily donated to many acceptors (vibronic states of surrounding molecules with lower excited state energies). For amino acid delayed fluorescence, neither P nor E-type² has been reported thus far.

The fate of the ≪dark≫ T₁ state in aliphatic amino acids has not attracted the attention of photobiologists and its role in protein photochemistry remains unknown.^1,3–5 The transient intermediates formed in the IC and ISC radiationless processes are still ≪dark≫ and not amenable to detection by ordinary light absorption or emission.^1,3,4 However, these dark intermediates play critical roles in IC and ISC processes, including fluorescence quenching, and thus are essential for understanding the mechanistic photochemistry of proteins with the standard flash-photolysis methods.

Recently, L-methionine has been used for the determination of Cu²⁺ and Co²⁺ ions based on their quenching effect on the orange fluorescence (580 nm) of methionine-capped gold nanoclusters (Met-AuNCs).¹¹ In the cluster preparation L-methionine was used as a reducing and protecting reagent. It also participates in the interaction with Cu²⁺ and Co²⁺ ions, assisting in the photoinduced electron transfer (PET) and the aggregation-induced quenching of the Met-AuNCs cluster fluorescence (580 nm).¹¹

Looking ahead, it is interesting to note that the present TD-DFT calculation of the optimized T₁ state of methionine predicts a T₁ → S₀ emission with a shorter wavelength of 562.3 nm and a relatively short radiative lifetime of 10 ms.

Fifteen years ago, we calculated the singlet–triplet transition intensity in the long-wave absorption tail of the glycine anion NH₂–CH₂–COO⁻ in an alkaline solvent at high pH > 9.^1,4 Our SOC calculations using the quadratic response method^4,9 provided a relatively high oscillator strength for the S₀ → T₁ transition at 241 nm (f = 0.51 × 10⁻⁶). The T₁ state exhibits ³A′′ spatial symmetry with respect to reflection in the OCO–CN atomic plane of the glycine anion.⁴

The second T₂ triplet in this anion is the totally symmetrical ³A′ state; the calculated wavelength (220 nm) of the S₀ → T₂ transition coincides with the more intense offset of the singlet–singlet absorption of the glycine anion. At the same time, the calculated oscillator strength for the S₀ → T₂ transition (f = 0.44 × 10⁻⁴) is comparable with the spin-allowed singlet–singlet S₀ → S₁ transition. For example, the S₀ → T_n absorption of aromatic hydrocarbons is five-six orders of magnitude weaker.^1,10 These results indicate that relativistic effects are important for near-UV light absorption by the simple amino acids. We cannot exclude the possibility that similar effects may be important for polypeptides and real proteins. Thus, radiation damage to simple amino acids, like glycine, can be induced at longer wavelengths than what has generally been accepted and what is known from their typical absorption spectra detected by standard spectrophotometers.^4–6

Computational details

Time-dependent density functional theory (TD-DFT) is a powerful and widely used approach for quantum chemical calculations of molecular spectra.¹² Decades ago, our research group predicted, on the basis of TD-DFT calculations with SOC account,^1,4 the potential for weak absorption at the low-frequency edge in the region of 240–260 nm of a few simple amino acids associated with the vertical S₀ → T₁ transitions.

In our calculations, we used the TD-DFT method with the B3LYP functional¹³ and the 6-311++G(d,p) basis set,¹⁴ accounting for spin–orbit coupling in the Orca 5.0.4 software package.¹² As noted above, the triplet–singlet transitions are forbidden in the non-relativistic approximation, but the SOC perturbation mixes states with different multiplicities, which gives rise to a non-zero transient dipole moment described by perturbation theory.^1,10 Let us briefly examine the theoretical aspects of such calculations.

The electric dipole S₀–T₁ transition moment, which is associated with the spin sublevel a, is determined by the following equation:

where Ĥ^a_SO is the a-component of the SOC operator (a = x, y, z) and r_i is the radius vector of the i-electron. The a-axes determine the M_S sublevel quantization in the absence of an external magnetic field and the so-called zero-field splitting (ZFS) energy of the T^a sublevel.^15,16 The ZFS energy is determined by the spin–spin coupling of two non-paired electrons and by SOC – in the second order of perturbation theory.¹⁰ In general, the ZFS parameters of a triplet-excited molecule depend on the solvent;¹⁶ however, we neglect this dependence in the present study.

Due to the SOC effect, the triplet states of a molecule have admixtures of singlet state wave functions, which can be described by first-order perturbation theory. Hence, the wave function of the perturbed T̃₁ state can be represented as a zero-order T₁ wave function and an impurity of the n-singlet states S_n.

Thus, the larger the SOC integral and the smaller the energy gap E(T₁) − E(S_n) in the denominator, the greater the value of the singlet impurity. After submission eqn (3) into the transition moment one obtains directly the left part of eqn (2). If we take n = 0 and m = 1 in eqn (2), the simple contribution from the difference in the permanent electric dipole moments of the S₀ and T₁ states occurs as follows:

For the SOC calculation, we used the full form of the Breit–Pauli operator given by the following equation:⁹

where the indices i, j refer to electrons, the index A – to nuclei, Z is the charge of the nucleus, l and s are the orbital and spin angular momentum operators, respectively.⁹

In general, this operator provides very accurate SOC constants for orbitally degenerate L–S states in light atoms and diatomic molecules and determines the energy level splitting of the spin multiplets.⁹ For non-linear polyatomic molecules, the orbital angular momentum is quenched and the expectation value of the SOC operator is zero. Thus, the direct SOC contribution to the zero-field splitting of the molecular triplet sublevels vanishes.⁹ The SOC energy in this case is not measurable; it influences the observable S–T transition intensity through the imaginary SOC matrix elements in eqn (2).

This makes it possible to accurately calculate the energies and probabilities of S–T transitions, which is crucial for understanding the spectral properties and kinetic behavior of such systems. An important characteristic of electronic S–T transitions is the oscillator strength f, which is proportional to the square of the electro-dipole transition moment (M_S–T).

where , M and ΔE values are in atomic units (a.u.), and f – is a dimensionless value.

Knowing the electro-dipole moment of the S–T transition, we can find the radiative lifetime τ_a of the excited triplet state, which is inversely proportional to the radiative rate constant (k_a) of the S₀ ← T₁^a transition:

It is crucial to know the lifetime of an excited triplet state to understand the photochemical behavior of a substance because this can affect the way of possible photochemical reactions and purely physical energy-transfer processes. Given the potential influence of weak S₀ → T₁ transitions on the generation of long-lived triplet states, which may, in turn, affect photochemical transformations (including the decay of individual amino acids) during their lifetimes in proteins, a detailed analysis of the spin–orbit coupling in proteins is required. The results of our quantum chemical calculations of the spectra of a few amino acids accounting for the spin–orbit coupling are presented below.

Results and discussion

As discussed previously, methionine is a vital amino acid essential for the survival of all eukaryotes and their genetic evolution. Methionine exists in two different hirable structures: L and D species. Despite the differing spatial structures, the two forms exhibit identical mirroring of their atomic arrangement.³ In the context of biochemical processes, L-isomers assume a more significant role because of evolutionary adaptations of biological systems that have enabled enzymes to recognize and utilize L-isomers. Conversely, D-isomers are less prevalent in living organisms, largely due to their spatial structure not aligning with the specific configuration of enzyme active sites. Consequently, their involvement in biochemical processes is predominantly limited and, in some cases, deleterious.

Before investigating electronic transitions, the amino acids selected for this study were optimized using the ORCA code¹² by density functional theory (DFT) method with B3LYP functional¹³ and the 6-311++G(d,p) basis set.¹⁴ The optimized geometry of L-methionine in the ground S₀ state illustrated in Fig. 1a, is in good accordance with the experimental data presented in the reference.¹⁷ The triplet T₁ state optimization is obtained by the time-dependent (TD) DFT approach.¹² Tables S1 and S2 (ESI†) provide a comprehensive overview of the geometric parameters of methionine in the ground S₀ and excited T₁ states.

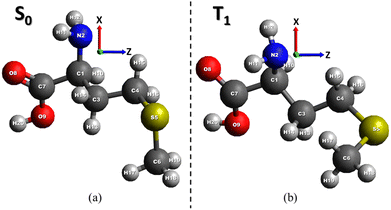Fig. 1 Optimized geometry of the ground S₀ state (a) and the first excited state T₁ (b) of L-methionine.

The general backbone structure of the carboxylic and amino groups attached to the saturated carbon C1 atom (Fig. 1) is reflected in the common features of the gas-phase microwave, IR, UV, and X-ray absorption spectra of many amino acid C edge NEXAFS spectra.^7,17

The obtained geometry was used to calculate the electronic absorption spectra by considering the SOC perturbation and vibrational modes into account. Vibronic analysis of normal coordinates on the potential energy surface (PES) of the L-methionine molecule can be started with the Duschinsky transformation for the electronic S–T transition between two PES varieties:¹ Q_T = JQ_S + D, where Q_T and Q_S are the mass-weighted normal coordinate matrices of the triplet T and singlet S states obtained by DFT gradient minimization and finding vibration frequencies, J is the Duschinsky's rotation matrix determining transformation of the T and S state's coordinate systems, and D is the matrix of displacement vector presenting in detail the geometry changes between T and S states, which are partly shown in Tables S1 and S2 (ESI†). These matrix transformations allow the calculation of the Huang–Rhys parameters and the Franck–Condon factors for vibronic transitions.^18,19 Upon S₀ → T₁ excitation, the whole carboxyl group undergoes strong deformation and prolongation of all chemical bonds (Table S1, ESI†); the C=O and C–OH bond lengths increase by 0.065 and 0.111 Å, respectively. From Table 1, we can see that this excitation is produced simultaneously by two HOMO → LUMO and HOMO → LUMO+2 electronic configurations.

Table 1 Characteristics of the vertical electronic transitions of L-methionine in the ground-state geometry (absorption)

Transition	λ, nm	f	Contribution of orbitals to the transition	ΔEvert, eV
S0 → T1	260.6	2.76 × 10^−6	HOMO → LUMO (36.29%)	4.757
			HOMO → LUMO+2 (35.67%)
S0 → T2	251.7	1.51 × 10^−5	HOMO → LUMO+1 (46.28%)	4.927
			HOMO → LUMO+2 (22.36%)
S0 → S1	249.1	2.07 × 10^−2	HOMO → LUMO (74.45%)	4.976
			HOMO → LUMO+2 (24.55%)
S0 → S2	245.6	1.40 × 10^−2	HOMO → LUMO+1 (90.14%)	5.048
S0 → S3	238.5	1.37 × 10^−2	HOMO → LUMO+2 (57.18%)	5.199
S0 → S4	228.3	1.35 × 10^−2	HOMO → LUMO+3 (66.02%)	5.431
S0 → S6	217.6	3.34 × 10^−2	HOMO → LUMO+4 (80.84%)	5.697

---

The first one corresponds to the charge-transfer (CT) transition from the sulfide to the carboxyl group; moreover, the LUMO is an antibonding orbital with respect to the O=C–O moiety (Fig. 2).

Fig. 2 Some molecular orbitals of L-methionine calculated in the ground-state geometry.

This also explains the drastic change in the carboxyl plane orientation with respect to the quasi-planar carbon zig-zag chain; the dihedral angle ∠(O8=C7–C1–C3) changes by 73.37°. Even larger angular deformation undergoes the sulfide group; see the angle ∠(C3–C4–S5–C6) in Table S2 (ESI†). At the same time, both C–S bonds experience a large reduction (about 0.03 Å) at the S₀ → T₁ transition since the excited electron leaves the C–S–C antibonding HOMO orbital (Fig. 2). The same force-field change supports the second electronic configuration HOMO → LUMO+2, which represents the excitation of the sulfide group. To some extent, this is a local n–σ* transition at the sulfur atom (see HOMO → LUMO+2 in Fig. 2).

Thus, the highest occupied MO of L-methionine represents a typical lone pair of electrons at the 3p_z AO of the sulfur atom, conjugated with the nearest carbon 2p_z orbitals, and the lowest T₁ excited state is produced by a single electron excitation from this lone pair to σ*(C–S) and to π*(C=O) antibonding orbitals. The vertical S₀ → T₁ transition of the L-methionine molecule in the gas phase is expected to be relatively intense (Table 1) in comparison with the aromatic tryptophan counterpart (Table S3, ESI†). A similar SOC approach with a quadratic response calculation predicts for benzene derivatives much weaker S₀ → T₁ absorption.¹⁰ Only Br-benzene has an oscillator strength of about 10⁻⁸, and all other molecules without heavy atoms show f ≈ 10⁻¹⁰; it is interesting that the S₀ → T₂ absorption in the studied benzene derivatives was predicted to be about an order of magnitude more intense than the first S₀ → T₁ transition.¹⁰ The same trend was observed for the L-methionine molecule (Table 1), although its S–T transition intensities were four orders of magnitude higher than those of aniline, styrene and indole.¹⁰ Thus, we propose that the S₀ → T₁ absorption at the long-wavelength wing of L-methionine (260 nm) can be detected by the Zeeman effect and EPR spectra.

According to our DFT calculations of the L-methionine singlet S₀ state geometry optimization, the vertical S₀ → T₁ absorption is predicted at 260.6 nm with an oscillator strength f = 2.76 × 10⁻⁶ (Table 1). In this Table, we present the first two triplet states and the number of singlet transitions of L-methionine. The lowest excited states, T₁ and T₂, lie in the range of 250–260 nm. As illustrated in Table 1, all these excitations can be attributed to the transitions from the highest occupied molecular orbital (HOMO), which is mostly localized as the lone pair of electrons of the sulfur atom at the 3p_z AO (Fig. 2).

The main contribution to the S₀ → T₁ transition intensity in L-methionine is determined by the direct SOC mixing of these states, which follows from eqn (4). Table S3 (ESI†) presents the S₀–T₁ SOC matrix elements (ME) for all studied molecules. For sulfur-containing amino acids, these SOC ME values are unusually high (for methionine, it is equal to 117 cm⁻¹, while the S₀ and T₁ states dipole moment are equal to 2.02 and 16.8 Debye, respectively). The T₁ state of methionine includes a large CT contribution. Accounting for the long chain between the S atom and the COOH group, the great dipole moment is obvious, as well as the large contribution of eqn (4) to the S₀ → T₁ transition intensity in L-methionine.

Usually, the spin-forbidden S₀ → T₁ transition intensity is borrowed from the spin-allowed singlet–singlet S₀ → S_n transitions if the upper singlet state S_n is mixed by SOC ME with the referenced T₁ triplet, eqn (2). Similarly, the ground S₀ state can be perturbed by the highly excited T_m state (m ≠ 1). In this case, the spin-forbidden S₀ → T₁ transition borrows its intensity from the allowed T₁ → T_m transitions, which are measurable in impulse flash-photolysis experiments.² All terms are important in eqn (2) for amino acids because the dense manifold of n–π*, n–σ* and π–π* states with different AO orientations creates an opportunity for intra-atomic orbital angular momentum changes inside carboxyl, amino and sulfide groups, which are important for the SOC ME integrals.¹ The intense SOC mixing between excited S and T states with small energy gaps is important for all amino acids. At the same time, a large energy gap ΔE (S₀, T₁) with the ground state in aliphatic amino acids (about 5 eV, Table S1, ESI†) diminishes the role of the second term in eqn (2), as well as a separate contribution of eqn (4). Nevertheless, the great difference in the permanent dipole moments of the S₀ and T₁ states together with unusually large SOC ME provide the largest contribution of eqn (4) to the S₀ → T₁ transition moment in L-methionine.

All the discussed calculations of the S–T absorption intensity concern the vertical excitations from the optimized ground state, which correspond to the vibrational excited triplet state. Following the Franck–Condon (FC) principle, one can anticipate that the FC factors of such a vibronic band would be close to unity. Account of the large distortion of the carboxyl and sulfide groups upon the S₀ → T₁ transition (Tables S1 and S2, ESI†) together with the calculated vibrational frequencies allows us to estimate the global FC factor for the 0–0 transition as equal to 0.214. The most distortion in the T₁ state refers to the vibrational mode v₂₃ = 688.9 cm⁻¹ (symmetric stretch of the sulfide C–S–C group), and partly – the v₂₄ = 731.6 cm⁻¹ mode (asymmetric sulfide C–S–C stretching). The v₄₈ = 1511.6 cm⁻¹ mode of the C=O valence vibration includes deformation of the COH bending and a few CH₂-bending vibrations. Although the frequency of the corresponding vibrations in the ground state was slightly changed, the forms of the normal modes were similar (Fig. S7, ESI†).

We must note that the T₁ state geometry optimization with the spin unrestricted UB3LYP functional leads to the dissociation of the SCH₃ group and only the TD DFT/B3LYP method provides an equilibrium molecular triplet structure. In any case, the T₁ state is not very stable; the triplet dissociation energy calculated using the UB3LYP method is equal to 1.89 eV, whereas in the ground state, it is almost twice as much (3.75 eV).

To present an idea on possible phosphorescence and its 0–0 band, we calculated the radiative transitions of L-methionine in the T₁-state optimized geometry by TD-DFT (Table 2 and Fig. S2, ESI†). We predict visible emission at 562 nm with a radiative lifetime of 2.3 ms as the most intense phosphorescence red wing. This is the vertical emission from the relaxed T₁ state to the excited vibrational level of the ground S₀ state. The total electronic energy of the S₀ and T₁ optimized states of L-methionine is equal to −800.418395 and −800.276433 a.u., respectively; thus, the electronic transition energy is 3.863 eV, which corresponds to 321 nm. The zero-point energy of vibrations is equal to 0.1650 and 0.1621 a.u., respectively, and we predict the final 0–0 transition energy of 3.782 eV, which corresponds to 328 nm. This should provide an accurate prediction of the 0–0 phosphorescence band. The approximate estimation of the Huang–Rhys (y) and Franck–Condon factors^18,19 for this transition gives τ_r = 350 ms. (For soft modes, we used y factors equal to 0.3).¹⁸ The radiative lifetimes for the most intense vertical emission and the 0–0 band are of the millisecond order. However, the fast non-radiative quenching (NRQ) proceeds thousands of times faster and cannot afford to emit phosphorescent red light. The NRQ rate constant (k_NR) estimation according to the method¹⁸ provides a k_NR value of 5.7 × 10⁶ s⁻¹. A large internal rotation of the SCH₃ group and other distortions between the S₀ and T₁ equilibria (Tables S1 and S2, ESI†) provide effective energy flow to vibrational modes, leading to the phosphorescence quenching of methionine.

Table 2 Characteristics of the vertical electronic transitions of L-methionine in the T₁-state geometry (emission)

State	λ, nm	τ(T1), s	Oscillator strength, f	Contribution of orbitals to the transition	ΔE, eV
T1	562.3	0.0023	2.04 × 10^−6	HOMO−1 ← LUMO (1.58%)	2.205
				HOMO ← LUMO (97.66%)
S1	554.9	0.000038	1.21 × 10^−4	HOMO ← LUMO (99.44%)	2.235
T2	396.1	0.00396	5.94 × 10^−7	HOMO−4 ← LUMO (2.04%)	3.130
				HOMO−3 ← LUMO (39.62%)
				HOMO−2 ← LUMO (30.85%)
				HOMO−1 ← LUMO (24.27%)
				HOMO ← LUMO (1.70%)
S2	341.5	0.000001	2.27 × 10^−3	HOMO−3 ← LUMO (8.04%)	3.631
				HOMO−2 ← LUMO (6.89%)
				HOMO−1 ← LUMO (83.83%)

---

The theoretically calculated electronic spectrum of the vertical S₀ → S_n transitions of L-methionine (Fig. S1a, ESI†) shows a relatively intense first absorption band with a maximum close to 250 nm (ε = 2000 M⁻¹ cm⁻¹) and a series of half-weaker bands in the middle UV region (Table 1). The band half-width in Fig. S1 (ESI†) is equal to 0.61 eV. The same TD-DFT method predicts that L-methionine has a strong absorption band at approximately 217 nm, which corresponds to the S₀ → S₆ transition involving the sulphur-containing side chain. There was no absorption of methionine in the visible region (Fig. S1a, ESI†) according to experimental data.² As can be seen in Table S1 (ESI†), the two S₀ → T_1,2 transitions occurred at the long-wavelength edge of the weak absorption (250–260 nm), which was not contradictory to the experiment.³ Given the width of the bands, it is possible that they can be overlapped by the S₀ → S₁ transition.

Absorption spectrum of glycine

The simplest amino acid was studied for comparison with L-methionine spectra. Glycine, as a natural α-amino acid in the gas phase, exists exclusively in a neutral form and represents a rich conformational landscape^17,20,21 which is determined by various types of intramolecular interactions between carboxyl and amino groups. Their competition through different combinations of hydrogen bonds was carefully studied in theory²¹ and in experiment.¹⁷ The optimized glycine structures in the ground S₀ state and the first excited T₁ state are illustrated in Fig. 3 and Table S4 (ESI†). In the ground state, almost all the heavy atoms in the chain are in one plane. Only nitrogen atoms deviate from the O=C–O–C plane due to the small dihedral angle of 20.14°, which is equal to the ∠N–C–C=O angle. The deviation of the H₁₀ atom is negligible (1.06°); for atom H₆, it is more serious (38.7°). The valence bond angles in the chain were close to 117.5°; only ∠CCN angle deviates to 110.5°. The bond angle ∠H–C–H is equal to 106.4° and the angle ∠H–N–H is 108.9°, which slightly deviates from the sp³ hybridization parameters. We can approximately assign vertical S₀–S_n transitions of glycine in terms of π–π* and n–π*types, though our optimized structure does not contain a symmetry plane.

Fig. 3 Optimized structure of the S₀ ground state (a) and T₁ excited state (b) of glycine.

In the optimized T₁ state at the TD-DFT level, the heavy atoms in the glycine chain deviate far from the planar structure. The main difference from the ground S₀ state structure is determined by a big out-of-plane deviation of the carboxyl group. The dihedral angle ∠N–C–C=O is equal to 173.073° and close to planarity, while the ∠N–C–C–O angle is equal to (−56.55°). In the ground state, these angles are 20.14° and (−161.89°), respectively. Thus, upon the adiabatic S₀ → T₁ excitation, an almost planar zig-zag chain of heavy atoms in glycine experiences out-of-plane zig-zag distortion and inversion of the CH₂–NH₂ group (Fig. 3).

Comparing the vertical S₀ → T₁ transition of methionine with that of glycine (Tables 1 and 3), we can conclude that the former transition is 56 times more intense (in methionine and glycine these transitions possess f = 2.76 × 10⁻⁶ and f = 4.9 × 10⁻⁸, respectively). The two low-lying singlet excited states at about 5.4 and 5.8 eV (Table 3) are in reasonable agreement with experiment and theory (5.6 and 5.8 eV).²⁰ These represent transitions with relatively low intensity from the nitrogen lone pair to the π*(C=O) and Rydberg orbitals, respectively.

Table 3 Characteristics of the vertical electronic transitions from the ground state of glycine

State	λ, nm	Oscillator strength, f	Contribution of orbitals to the transition	ΔE, eV
T1	239.5	4.9 × 10^−8	HOMO → LUMO (81.25%) (nN–π*–transition)	5.176
S1	230.6	6.71 × 10^−3	HOMO → LUMO (93.00%) (nN–π*–transition)	5.375
T2	228.6	3.79 × 10^−7	HOMO−1 → LUMO (40.95%) (nO–π*–transition)	5.423
			HOMO−1 → LUMO+1 (28.19%) (nO–Ry*–transition)
S2	215.5	1.178 × 10^−2	HOMO → LUMO+1 (58.52%)	5.755
			HOMO → LUMO+2 (36.39%) (nN–Ry*–transition)

---

Structural distortions during the S₀–T₁ transition in glycine are rather different from those in the L-methionine molecule. The C=O bond is more strongly prolonged, but the C–O link is compressed (Table S4, ESI†) compared with that in Table S1 (ESI†). The C–C bond becomes weaker and the C–N bond becomes shorter, whereas in L-methionine, the opposite distortions are observed with negligible amplitudes (Table S1, ESI†). Explanations come from Table 3 and Fig. S3 (ESI†); the S₀–T₁ transition in glycine is almost pure HOMO–LUMO excitation with the charge transfer from the amino group to the carboxyl moiety, whereas, in methionine, the local n–σ* excitation of the sulfide group provides an additional contribution to the stronger S₀–T₁ absorption. Such differences are determined by the sulphur atom, which is a component of methionine, which contributes to the SOC matrix elements, increasing the transition probability.

The first vertical S₀ → T₁ transition in a glycine molecule in vacuum represents the n(N) → π_y*(C=O) transition type based on its orbital nature. Both orbitals are oriented along the y-axis, which is approximately perpendicular to the O–C–C–N plane (xz). The singlet S₁ excited state was also of the same HOMO–LUMO type (Table 3). The calculated absorption S₀ → S_n spectrum (Fig. S1, ESI†) corresponds to the observed offset.³ The two vertically excited singlet ππ* states of the peptide group of glycine produce the two most intense absorption bands, known as NV1′ and NV2′ transitions, according to Mulliken's nomenclature.²⁰ Our calculation predicts their energies at 7.92 and 9.98 eV, slightly lower than the results of ref. 20 (8.10 and 10.20 eV, respectively). Our glycine structure does not support an exact C_s symmetry.

The most intense vibronic band of glycine phosphorescence (vertical T₁ → S₀ transition) is predicted to possess a relatively long radiative lifetime (Table 4) with negligible quantum yield at room temperature. The great Stokes shift of 355.4 nm (Tables 3 and 4) and small energy gap for emission readily predict the effective non-radiative quenching of glycine phosphorescence, accounting for the Huang–Rhys parameters of the out-of-plane vibrations (y = 0.57, 0.32 and 0.41) for active modes ν₇ = 556, ν₈ = 590, and ν₁₂ = 1123 cm⁻¹. The zig-zag bending deformation ν₁₆ = 1349 cm⁻¹, strongly mixed with C=O stretching, produces a large contribution to the NRQ rate constant estimated by the method.^18,19 Even the relatively low SOC integral 〈T₁|H_SO|S₀〉 = 16.9 cm⁻¹ (Table S3, ESI†) does not suppress the calculated NRQ rate constant (k_NR = 2.4 × 10⁴ s⁻¹). Thus, the radiative rate of glycine phosphorescence (k_p = 2.86 × 10² s⁻¹) cannot compete with non-radiative quenching. Since the singlet S₁ state is orbitally similar to the lowest triplet (Table 4), their structure and vibronic pattern could also be similar. The fluorescence radiative rate constant (k_f = 4.44 × 10⁶ s⁻¹, Table 4) cannot compete with the spin-allowed non-radiative quenching rate,²² which could be about 10⁹ s⁻¹ by similar vibronic reasons as those in triplet state quenching.^18,22 According to these estimations, glycine cannot produce photoemission and all the absorbed ultraviolet energy (Fig. S1b, ESI†) must be transferred into the mutually hindered rotation of its functional groups.

Table 4 Characteristics of the vertical electronic transitions of glycine in the T₁-state optimized geometry (emission)

State	λ, nm	τ(T1), s	Oscillator strength, f	Contribution of orbitals to the transition	ΔE, eV
T1	584.9	0.035	1.46 × 10^−7	HOMO−2 ← LUMO (1.04%)	2.120
				HOMO−1 ← LUMO (6.46%)
				HOMO ← LUMO (91.04%)
S1	449.0	2.25 × 10^−7	1.35 × 10^−2	HOMO−1 ← LUMO (3.3%)	2.761
				HOMO ← LUMO (95.88%)
T2	332.3	0.00075	2.21 × 10^−6	HOMO−2 ← LUMO (56.48%)	3.731
				HOMO−1 ← LUMO (37.64%)
S2	292.9	5.4 × 10^−7	2.38 × 10^−3	HOMO−1 ← LUMO (95.08%)	4.233
				HOMO ← LUMO (3.40%)

---

Absorption spectrum of cysteine

The optimised cysteine geometry structures in the S₀ and T₁ states obtained using DFT and TD-DFT methods, respectively, are shown in Fig. 4. The ground state structure corresponds to the Ig⁻g isomer detected by microwave spectra; its free energy is slightly higher at room temperature (by 299 cm⁻¹) than that of the most stable IIgg isomer, which is bound by three hydrogen bonds, as calculated by Barone et al.¹⁸ Our structure is more flexible since it includes only two hydrogen bonds (C=O⋯HN⋯HS); thus, it easily relaxes after photoexcitation. The calculated rotational constants of the Ig⁻g isomer¹⁸ coincide with our data, with an accuracy of 0.003 cm⁻¹. The geometrical characteristics of the S₀ → T₁ transition are presented in Table S5 (ESI†). The singlet–triplet transition is accompanied by stretching of the C=O bond by 0.161 Å and by partial mutual rotation of the sulfide and amino groups (Fig. 4).

Fig. 4 Optimized structure of the S₀ ground state (a) and T₁ excited state (b) of cysteine.

The S₀ → T₁ transition is characterised by a 64.4% electron jump from the HOMO to the LUMO and by 15.6% as a HOMO–LUMO+1 transition. The highest occupied MO for cysteine refers to the localization of a lone pair of electrons of the sulfur atom at 4p_y AO (Fig. S5, ESI†). According to Table 5, the vertical S₀ → T₁ transition in the gas phase is intense and has an oscillator strength of f = 4.00 × 10⁻⁶. In addition, the common trend of the tendency that the S₀ → T₂ transition is an order of magnitude more intense than the S₀ → T₁ transition is repeated again, as in previous examples.

Table 5 Characteristics of the vertical electronic transitions of cysteine in the S_o-state optimized geometry (absorption)

State	λ, nm	Oscillator strength, f	Contribution of orbitals to the transition	ΔE, eV
T1	268.3	4.00 × 10^−6	HOMO → LUMO (64.42%)	4.621
			HOMO → LUMO+1 (15.59%)
S1	250.3	6.05 × 10^−3	HOMO → LUMO (89.17%)	4.953
			HOMO → LUMO+1 (4.25%)
T2	248.2	1.10 × 10^−5	HOMO−2 → LUMO+1 (14.2%)	4.996
			HOMO−1 → LUMO (12.12%)
			HOMO−1 → LUMO+1 (15.6%)
			HOMO → LUMO (14.04%)
			HOMO → LUMO+1 (21.36%)
S2	235.7	2.09 × 10^−2	HOMO → LUMO (5.10%)	5.260
			HOMO → LUMO+1 (85.57%)

---

These theoretical calculations indicate that the electronic spectrum of cysteine is located in the same ultraviolet region as that of methionine (Fig. S1c, ESI†). The band half-width in Fig. S1 (ESI†) is equal to 0.61 eV. The spectrum exhibited a peak at 200 nm that subsequently decreased in intensity, reaching 270 nm. At 235.7 nm, a secondary threshold is discernible, which, in theory, corresponds to the S₀ → S₂ transition with an oscillator strength of f = 2.09 × 10⁻².

The probability of the first triplet–singlet transition in sulfur-containing amino acids is influenced by the SOC term in eqn (4). The theoretically determined SOC ME integral 〈T₁|H_SO|S₀〉 for cysteine is equal to 90.87 cm⁻¹. This leads to the mixing of states with different multiplicity, thus mitigating forbidden transitions. In consideration of the spin–orbit coupling for the vertical S₀ → T₁ transition, the theoretical lifetime of the first excited state T₁ of cysteine was determined to be 0.27 ms (Table S1, ESI†). This radiative triplet state parameter in the ground-state geometry has a limited physical meaning, so we calculated the phosphorescence properties at the optimized triplet T₁ state structure for the vertical T₁ → S₀ emission (Table 5 and Fig. S6, ESI†).

We predict visible emission at 661 nm with a radiative lifetime of 5.6 ms for the T₁ → S₀ vertical transition of cysteine in the T₁-state optimized geometry. A great Stokes shift (392.7 nm, Tables 5 and 6) is predicted for this most intense (vertical) phosphorescence band, which produces a return from the v′ = 0 global upper state to the combinations of a few v′′ vibrational quanta of the ground electronic state for the quasi-resonance energy conditions (Fig. S9, ESI†). Such a vertical transition can be accompanied by vibrational quanta excitations. The energy flow to these large nuclear displacements effectively transfers electronic triplet state excitation to the heating of the local environment. Like in other amino acids, a large Stokes shift and a small E(T₁)–E(S₀) energy gap (1.87 eV) lead to fast non-radiative quenching of cysteine phosphorescence, accounting for the great flexibility of the branched σ-core with rather different force fields in the triplet and singlet states. A relatively large 〈T₁|H_SO|S₀〉 matrix element finally provides an intersystem crossing (ISC) rate constant higher than 4.65 × 10⁷ s⁻¹. Comparison with the radiative rate constant (k_p = 1.78 × 10² s⁻¹) predicts complete quenching of cysteine phosphorescence in any biological solvent.

Table 6 Characteristics of the vertical electronic transitions of cysteine in the T₁-state optimized geometry (emission)

State	λ, nm	τ(T1), s	Oscillator strength, f	Contribution of orbitals to the transition	ΔE, eV
T1	661.0	0.0056	1.18 × 10^−6	HOMO−2 ← LUMO (19.24%)	1.876
				HOMO−1 ← LUMO (5.16%)
				HOMO ← LUMO (74.21%)
S1	557.6	1.16 × 10^−5	4.02 × 10^−4	HOMO−2 ← LUMO (6.72%)	2.224
				HOMO−1 ← LUMO (4.65%)
				HOMO ← LUMO (88.31%)
T2	456.9	0.0024	1.30 × 10^−6	HOMO−3 ← LUMO (14.48%)	2.713
				HOMO−2 ← LUMO (42.20%)
				HOMO−1 ← LUMO (22.64%)
				HOMO ← LUMO (18.73%)
S2	403.5	1.09 × 10^−7	2.25 × 10^−2	HOMO−2 ← LUMO (7.17%)	3.073
				HOMO−1 ← LUMO (84.21%)
				HOMO ← LUMO (8.13%)

---

It is interesting to estimate the hypothetical 0–0 phosphorescence band wavelength of cysteine as a possible photophysical reference point (without calculation of its Franck–Condon factor, which is supposed to be close to unity). The total electronic energy of the S₀ and T₁ optimized states of cysteine is equal to −721.82085 and −721.74272 a.u., respectively; thus, the electronic adiabatic transition energy is 2.126 eV, which corresponds to 583.2 nm. The vibrational zero-point energy of the S₀ and T₁ optimized states is 0.10712 and 0.10324 a.u., respectively. It is predicted that the 0–0 phosphorescence transition energy will be 2.02 eV, which is equivalent to a 613.8 nm emission in the dark red region. These parameters can be used as theoretical molecular constants applicable for energy transfer estimation. However, we believe that there is no chance of observing such a weak emission band.

Tryptophan fluorescence and the possible role of the triplet state

Among the three aromatic amino acids that produce fluorescence, tryptophan (TRP) emission is particularly useful because it typically has a large cellular concentration (up to 3% in membranes), intense light absorption and relatively high fluorescence quantum yield (0.2).²³ Tryptophan fluorescence spectroscopy is often used to obtain structural information about intracellular environments by studying solvent quenching effects. However, the involvement of the TRP triplet state in fluorescence quenching via the ISC mechanism has not been reported in the literature.^23–25

In Table 7, we present our TD-DFT results for the vertical absorption spectrum of tryptophan in ground S₀-state geometry for the singlet and triplet excited states while accounting for the SOC perturbation. Table 7 predicts relatively intense S₀ → S₁ absorption and fluorescence, in good agreement with the experimental data.²³ The calculated oscillator strength (f = 0.084) well corresponds to the observed molar extinction coefficient (ε = 5600 L mole⁻¹ cm⁻¹).²⁴ The indole moiety of tryptophan is commonly assumed to be the main source for the ultraviolet absorbance of proteins at 270–280 nm and for their fluorescence at 350 nm.^23–26 The two closely lying states S₁ and S₂ with their different dipole moments can interchange relative energy positions depending on solvent polarity.²⁵ The S₂ state is more stabilized in polar solvents and produces fluorescence, whereas emission originates from the S₁ state in nonpolar environments.²⁵ The S₂ state is determined by the HOMO → LUMO+1 transition (54–56, Table 7), which represents a pure charge transfer from the delocalized indole π-HOMO to the Rydberg orbital at the N₁₁ atom (Fig. S10 and S11, ESI†). The S₁ state represents 79% of the HOMO → LUMO excitation, which is a π → π* transition inside the indole moiety (Fig. S11, ESI†). The permanent dipole moment (4.22 Debye) was similar to that of the ground S₀ state (4.05 Debye). This is the reason for the absence of a strong solvato-chromic effect in the S₀–S₁ transition.

Table 7 TD-DFT results for the vertical absorption spectra of tryptophan in the ground S₀-state geometry

State	λ, nm	f	Configuration state function	E, eV
T1	370.1	2.60 × 10^−8	−0.95(54–55) − 0.15(52–55) − 0.13(53–60)	3.35
T2	276.9	3.74 × 10^−9	−0.94(53–55) + 0.16(53–56)	4.04
T3	269.0	2.56 × 10^−7	0.60(54–56) − 0.32(51–55) − 0.43(54–60)	4.48
S1	266.0	0.0842	0.89(54–55) − 0.26(54–56) + 0.19(53–60)	4.61
S2	266.7	0.0070	0.95(54–56) + 0.24(54–55)	4.65
S3	256.7	0.0317	0.68(53–55) + 0.40(54–57)	4.83
S4	255.1	0.0143	−0.86(54–57) + 0.32(53–55)	4.86
S5	246.0	0.0142	+0.91(54–58) + 0.21(54–59)	5.04
S6	240.8	0.0041	0.96(54–59) + 0.19(54–58) − 0.13(53–56)	5.15
S7	236.6	0.0032	−0.89(53–57) + 0.35(52–55)	5.24
S8	236.2	0.0047	−0.86(52–55) − 0.35(53–56) − 0.21(52–57)	5.25
S9	227.9	0.0069	0.95(54–61) − 0.20(54–58)	5.44

---

The triplet state of tryptophan represents 90% of the same HOMO → LUMO transition; Fig. S10 (ESI†) indicates that this is a π → π* excitation in the aromatic part of the molecule with a very small contribution of charge-transfer from the amino group to the indole moiety. We suspect that the T₁ state of tryptophan could be an intermediate step in energy dissipation because of its long radiative lifetime (0.079 s, Table S3, ESI†) and high flexibility with respect to the mutual internal rotation of carboxyl and amino groups, which is involved through the charge-transfer contribution to electronic-vibrational relaxation. The solvent-dependent energy gap between the S₂ and S₁ states strongly influences the ISC rate constant for the generation of the T₁ state of tryptophan; thus, it governs the efficient rate of fluorescence quenching. The tryptophan fluorescence wavelength (λ_max) and emission intensity are strongly affected by the polarity of the peptide microenvironment.²⁵

The S₁ state is orbitally similar to the triplet T₁ state function; however, there are some differences in the charge-transfer admixtures (Table 7 and Fig. S11, ESI†). A small admixture (2.5%) to the S₀ → T₁ vertical transition of the HOMO–2 → LUMO excitation (52–55) provides a pure charge transfer from the amino group to the indole moiety (Fig. S11, ESI†). The T₁ state of tryptophan, as with other aromatic triplets, has relatively low excitation energy and low oscillator strength (f ≈ 10⁻⁸); its weak absorption must be observed in the near-UV region. Because of the CT admixture from the non-planar peptide fragment with its n-orbitals of lone pairs, tryptophan exhibits more intense S₀ → T₁ absorption than the pure indole molecule.¹⁰ However, it is still predicted to be rather weak and the absence of experimental data about such absorbance indirectly supports our findings: an absorption band with f ≈ 10⁻⁸ is impossible to detect below noise using standard UV spectrometers. However, time-dependent EPR or optically detected magnetic resonance measurements in cold crystals can shed light on triplet tryptophan properties. Accounting for the importance of tryptophan fluorescence as an indicator of protein structure, T₁ detection could open new channels for the regulation of TRP emission and intermolecular energy-transfer mechanisms. The long radiative lifetime of triplet tryptophan (Table S3, ESI†) provides additional opportunities for such regulation, including the ways of studying UV radiation damage in proteins.

The experimentally well-studied fluorescence of tryptophan is a good anchor for the continuation of our study on SOC effects in amino acids and their triplet-state properties.

Conclusions

A detailed analysis of the electronic spectra of a few amino acids was performed in this work, using time-dependent density functional theory with the inclusion of spin–orbit coupling (SOC) perturbation. The electronic vertical absorption and emission spectra were obtained, and the probabilities of forbidden singlet–triplet transitions were predicted. These results offer a novel perspective on the photobiology of amino acids because they predict the important role of the “dark” T₁ excited state in the UV photolysis of proteins. First, the SOC matrix elements in the aliphatic amino acids responsible for promoting the S₀ → T₁ transition intensity are orders of magnitude larger than the SOC parameters in the aromatic counterparts like tryptophan. This SOC contribution influences the ZFS parameters in the EPR spectra and S–T transitions probability of radiative and non-radiative types, including the effective luminescence quenching of aliphatic amino acids through various ISC and IC processes.

For the vertical S₀ → T₁ transition in L-methionine, we predict an absorption maximum at 260 nm with an oscillator strength f = 2.76 × 10⁻⁶. Such molar extinction (about ε ≈ 1–10 M⁻¹ cm⁻¹) could be measurable by spectrometers with a long optical path.

The large torsional and bond-length distortions during the S₀–T₁ transitions in aliphatic amino acids explain the effective quenching of their phosphorescence, under account for a big SOC integral and a small energy gap in the optimized triplet state geometry. The great Stokes shift of 345 nm is predicted for methionine emission supporting its quenching mechanism by energy transfer to intramolecular vibrations, including mutual twisting of all functional groups, rocking and scissoring movements mixed with valence C=O distortions. The orbitally similar S₁ state can form the conical intersection with the ground state, which leads to fluorescence quenching for similar reasons. Glycine differs from sulfur-containing amino acids by a smaller SOC integral (〈T₁|H_SO|S₀〉 = 16.7 cm⁻¹), which is still much higher than that of aromatic molecules. Such SOC estimation is typical for many other aliphatic peptide molecules. One can predict that the onset of protein UV absorption must be determined by the S₀ → T₁ vertical transition of the n(N) → π_y*(C=O) transition type according to its orbital nature; that is, a charge transfer (CT) from the amine lone pair to the carbonyl group. This is a more intense S–T absorption than that of many other organic molecules. This onset corresponds to 260 nm (similar to glycine) and encompasses almost all amino acid residues in the protein scaffold.

UV light absorption in the 250–260 nm range may produce direct excitation of the two lowest triplet excited states T₁ and T₂, which could start radiolysis of amino acids since the T₁ state in all studied molecules is quite unstable (especially in the sulfur-containing amino acids).

Tryptophan, which is the most important UV absorber and emitter in proteins, also does not exhibit triplet-state manifestations. The S₀ → T₁ transition represents π → π* excitation in the aromatic moiety with a small admixture of CT from the amino group to indole; its weak absorption (f ≈ 10⁻⁸) occurs in the near-UV region at 370 nm. A series of low-lying triplet states is important for the quenching mechanism of tryptophan fluorescence.

Author contributions

Boris Minaev: writing – review & editing, writing – original draft, data curation, conceptualization. Maryna Sukhyna: data curation. Pavlo Stakhira: data curation. Valentina A. Minaeva: validation, methodology. Hans Ågren: writing – review & editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors express their sincere congratulatory wishes to Professor Christel Marian in connection with her Birth Day and jubilee and for her longstanding great contributions to Molecular Physics and Quantum Chemistry! The work was supported by the National Research Foundation of Ukraine (Grant No. 0124U003833).

Notes and references

1. G. Baryshnikov, B. Minaev and H. Ågren, Theory and Calculation of the Phosphorescence Phenomenon, Chem. Rev., 2017, 117, 6500–6537.
2. C. A. Parker, Photolumlnescence of Solutions, American Elsevier, New York, 1968.
3. G. D. Fasman, Practical Handbook of Biochemistry and Molecular Biology, CRC Press, 1992.
4. B. Minaev, O. Lut, G. Baryshnikov and V. Minaeva, Calculation of structure and spectra of the glycine radical with dehydrogenated carboxyl group, Ukr. Bioorg. Acta, 2009, 2, 35–41.
5. A. Acharya, A. M. Bogdanov, B. L. Grigorenko, K. B. Bravaya, A. V. Nemukhin, K. A. Lukyanov and A. I. Krylov, Photoinduced Chemistry in Fluorescent Proteins: Curse or Blessing?, Chem. Rev., 2017, 117, 758–795,  DOI:10.1021/acs.chemrev.6b00238.
6. R. B. Vegh, K. M. Solntsev, M. K. Kuimova, S. Cho, Y. Liang, B. L. Loo, L. M. Tolbert and A. S. Bommarius, Reactive oxygen species in photochemistry of the red fluorescent protein “Killer Red”, Chem. Commun., 2011, 47, 4887–4889.
7. V. Carravetta, O. Plashkevich and H. Ågren, A theoretical study of the near-edge x-ray absorption spectra of some larger amino acids, J. Chem. Phys., 1998, 109, 1456–1464,  DOI:10.1063/1.476696.
8. B. F. Minaev, Quantum-chemical investigation of the mechanisms of the photosensitization, luminescence, and quenching of singlet ¹Δ_g oxygen in solutions, J. Appl. Spectrosc., 1985, 42, 518–523.
9. H. Ågren, O. Vahtras and B. Minaev, Advances in Quantum Chemistry, ed. P.-O. Löwdin, J. R. Sabin and M. C. Zerner, Academic Press, 1996, vol. 27, pp. 71–162.
10. Ó. Rubio-Pons, O. Loboda, B. Minaev, B. Schimmelpfennig, O. Vahtras and H. Ågren, CASSCF calculations of triplet state properties: applications to benzene derivatives, Mol. Phys., 2003, 101, 2103–2114.
11. F. Sang, X. Zhang and F. Shen, Fluorescent methionine-capped gold nanoclusters for ultra-sensitive determination of copper(II) and cobalt(II), and their use in a test strip, Microchim. Acta, 2019, 186, 1–9,  DOI:10.1007/s00604-019-3428-3.
12. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
13. A. D. Becke, A new mixing of Hartree–Fock and local density-functional theories, J. Chem. Phys., 1993, 98, 1372–1377.
14. R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, Self-consistent molecular orbital methods, XX. A basis set for correlated wave functions, J. Chem. Phys., 1980, 72, 650–654.
15. M. Kinoshita, N. Iwasaki and N. Nishi, Molecular Spectroscopy of the Triplet State through Optical Detection of Zero-Field Magnetic Resonance, Appl. Spectrosc. Rev., 1981, 17, 1–94.
16. B. Minaev, O. Loboda, O. Vahtras, K. Ruud and H. Ågren, Solvent effects on optically detected magnetic resonance in triplet spin labels, Theor. Chem. Acc., 2004, 111, 168–175.
17. S. Gunasekaran, A. Bright, T. Renuga Devi, R. Arunbalaji and G. Anand, Experimental and Semi-empirical computations of the vibrational spectra of Methionine, Homocysteine and Cysteine, Archiv. Phys. Res., 2010, 1, 12–26.
18. R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, G. V. Baryshnikov and D. Sundholm, et al., First-principles calculations of anharmonic and deuteration effects on the photophysical properties of polyacenes and porphyrinoids, Phys. Chem. Chem. Phys., 2022, 22(39), 22314–22323,  10.1039/d0cp03231j.
19. G. V. Baryshnikov, R. R. Valiev, N. N. Karaush, V. A. Minaeva and A. N. Sinelnikov, et al., Benzoannelated aza-, oxa- and azaoxa[8]circulenes as promising blue organic emitters, Phys. Chem. Chem. Phys., 2016, 18(40), 28040–28051.
20. L. Serrano-Andres and M. P. Fulscher, Theoretical Study of the Electronic Spectroscopy of Peptides. 2. Glycine and N-Acetylglycine, J. Am. Chem. Soc., 1996, 118, 12200–12206,  DOI:10.1021/ja9619972.
21. V. Barone, M. Fusè, F. Lazzari and G. Mancini, Benchmark Structures and Conformational Landscapes of Amino Acids in the Gas Phase: A Joint Venture of Machine Learning, Quantum Chemistry, and Rotational Spectroscopy, J. Chem. Theory Comput., 2023, 19, 1243–1260.
22. L. Shi, X. Xie and A. Troisi, Rapid calculation of internal conversion and intersystem crossing rate for organic materials discovery, J. Chem. Phys., 2022, 157, 134106,  DOI:10.1063/5.0102857.
23. C. J. Fossum, B. O. V. Johnson and S. T. Colde, et al., Insights into the Mechanism of Tryptophan Fluorescence Quenching due to Synthetic Crowding Agents: A Combined Experimental and Computational Study, ACS Omega, 2023, 8, 44820–44830,  DOI:10.3390/ijms151222518.
24. F. W. J. Teale and G. Weber, Ultraviolet fluorescence of the aromatic amino acids, Biochem. J., 1957, 65, 476–482.
25. A. B. T. Ghisaidoobe and S. J. Chung, Intrinsic Tryptophan Fluorescence in the Detection and Analysis of Proteins: A Focus on Förster Resonance Energy Transfer Techniques, Int. J. Mol. Sci., 2014, 15, 22518–22538,  DOI:10.3390/ijms151222518.
26. A. Lindinger, J. P. Toennies and A. F. Vilesov, High resolution vibronic spectra of the amino acids tryptophan and tyrosine in 0.38 K cold helium droplets, J. Chem. Phys., 1999, 110, 1429–1436,  DOI:10.1063/1.478018.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01671a

---