Quantum dynamics of the temporary capture of light atoms by superfluid helium nanodroplets at very low collision energies (≈1–13 meV): the case of the hydrogen atom and its isotopes

Abstract

The capture dynamics of a H atom and isotopic variants [D, T and Q (hypothetical isotope of mass equal to four times the mass of H)] by a superfluid helium nanodroplet (HeND) has been investigated theoretically. The HeND (T = 0.37 K) is (⁴He)_N=400 and a mean field quantum hybrid approach [TDDFT (helium) + quantum wave packet (H, D, T or Q)] at zero angular momentum, is used to explore a rather wide range of very low initial kinetic energies (E_k,0 ≈ 10–150 K). The analysis of the capture mechanism shows the existence of a dynamical barrier and a dynamical minimum that play key roles to understand the time evolution of the capture, especially the former property. In general, the H atom shows a different behavior from the other isotopes, with the behavior of T and Q being very similar to each other and the D atom behaving inbetween H and T. Besides, it is worth noting that, in principle, at the very low initial kinetic energies considered only “short” and “long” lived atom⋯HeND collision complexes are formed, i.e., in the atom-helium nanodroplet collision only the temporary capture of the atom takes place. The different behaviors observed have been interpreted considering the faster motion of the H atom when colliding with (⁴He)_N=400 and the more quantum character of the H behavior both due to its significantly lower mass. As far as we know, this is the first quantum dynamics study carried out on the collision of light atoms with HeNDs at very low energies.

---

1. Introduction

Superfluid helium nanodroplets [(⁴He)_N or HeNDs] are of great interest not only because they allow us to explore finite-size superfluidity but also because of their properties as a solvent.^1–11 The superfluidity, chemically inert character, capability of being doped with almost any atomic or molecular species (neutral or charged), very low temperature (T = 0.37 K) and large heat capacity make these nanodroplets an optimal nanoreactor to investigate a wide variety of chemical processes.^{3–5,7,10,11} Besides, HeNDs are also able to stabilize nanoclusters^12,13 and nanowires.^14,15 that could not be produced by standard chemical synthesis procedures. The stabilization of chemical species is an important issue from a practical perspective and also for the understanding of the impurity (chemical species) relaxation mechanisms.

The first experiments conducted on this topic were centered on the influence of the cage effect in the fragmentation dynamics of photoionized molecules^16–19 and rare-gas clusters^20–23 that were embedded in helium nanodroplets. The energy relaxation caused by these nanodroplets has also been examined experimentally, e.g., in neutral species, where two examples are the photoisomerization of linear and bent isomers of the HCN–HF complex²⁴ and the photodissociation of alkyl iodides (R − I + hν → R + I).^25–27 Most of the experiments indicated that the cooling by the helium environment is not a thermal evaporative process. That is to say, the mean energy per evaporated ⁴He atom is greater than the binding energy per ⁴He atom in liquid helium (approx. 7 K). Furthermore, there are also experiments on femtosecond photoexcitation dynamics inside HeNDs (see, e.g., ref. 28–30).

Thanks to the efforts of the experimentalists a large number of experimental techniques have been adapted and extended so as to make possible the study of processes involving chemical species and helium nanodroplets. Among them in particular we can mention the following: mass spectrometry, Coulomb explosion, spectroscopic techniques (e.g., infrared, fluorescence, Penning ionization, and photoelectron photoion coincidence), electrical deflection, X-rays, pump–probe techniques (e.g., time-resolved photoelectron detection, velocity-map imaging, and time-resolved ion yield detection) and transmission electron microscopy.^{1–5,7,10,11} Furthermore, an experimental technique has been developed recently to detect the primary steps of the Na⁺ ion solvation in HeNDs (see ref. 31, 32 and the related theoretical ref. 33–35); and using a different recent technique multiple ordered helium solvation shells have been observed in Ca₂⁺@HeND.³⁶

In addition to the great interest that the study of the capture of chemical species by HeNDs presents (virtually nearly all species are susceptible to be captured by these nanodroplets), this work has also been stimulated by the experimental advances in this context. Furthermore, the investigation of systems that are prone to show quantum effects (due to their small mass) in very low collision energy situations, where these effects are expected to manifest more clearly, has also been stimulating. To the best of our knowledge this is the first quantum dynamics study carried out on the collision of light atoms with HeNDs at very low energies (quantum studies on the structure and interaction energy of light species, He*⁻ and He₂*⁻, with up to 32 solvating He atoms have been reported previously).³⁷

Thus, here we study theoretically the quantum dynamics of the capture process of a H atom by a HeND of four hundred helium atoms (N = 400), H + (⁴He)_N → H⋯(⁴He)_N′ (collision complex with a given lifetime), at very low collision energies [up to ≈150 K (≈13 meV)], where quantum effects are expected to play a particularly important role. To obtain a deeper insight into the dynamics, we also consider the D and T isotopes and a hypothetical Q (quartium) atom of mass equal to four times the H mass.

The HeND is described by time-dependent density functional theory (TDDFT) and the H atom and isotopes are described quantum-mechanically using a wave packet (WP) approach, i.e., following the same (or a similar) hybrid approach considered by us in previous studies where different physicochemical problems involving HeNDs and atoms or diatomic molecules were analyzed (photodissociation,^38–41 atom capture,^42,43 van der Waals reaction,^44,45 vibrational relaxation,^46,47 rotational relaxation⁴⁸ and helium nanodroplet relaxation⁴⁹). Owing to the high computational resources needed for a quantum description of the present problem, here we have also restricted the investigation to the case of zero total angular momentum (head-on collisions).

Furthermore, considering hypothetical isotopic chemical species interacting with HeNDs in dynamics simulations provides a broader perspective about the dependence of the investigated properties on the mass of the chemical species. Prior to this work, we considered hypothetical isotopic species in the quantum dynamics of the photodissociation,⁴⁰ vibrational relaxation,⁴⁷ and rotational relaxation⁴⁸ of diatomic molecules located inside HeNDs.

This work is related to ref. 42 and 43 where the capture of a Ne atom by a HeND was considered, with the Ne atom described by a WP and by classical mechanics, respectively. It deserves to be highlighted that, differing from the results that will be presented here for H and isotopes, the Ne colliding atom is completely captured by the HeND and remains inside it fully solvated by the helium environment. The different behaviors observed for H and Ne arise from the fact that the H–He interaction is weaker than the Ne–He one. For other systems where atomic capture by HeNDs has been studied previously see, e.g., ref. 50–54 (Cs, Xe, Ar).

This work is organized as follows: the theoretical methods employed are briefly explained in Section 2; the description and analysis of the main results are reported in Section 3; and the summary and conclusions are presented in Section 4. Some useful complementary information is given in the ESI.†

2. Theoretical methods

The capture dynamics is investigated using a quantum approach. The colliding X atom (X: H, D, T or Q) and the HeND are described following the same treatment as that used by us for the capture of a Ne atom by a HeND,⁴² which is analogous to the approach proposed by us to describe the photodissociation of diatomic molecules placed inside HeNDs.³⁸

Thus, for the TDDFT description of the superfluid liquid helium, we use the Orsay–Trento (OT) phenomenological functional,⁵⁵ neglecting the backflow term and the non-local contribution to the helium correlation energy for computational reasons.^38,39,50 This functional is characterized via the ε_c[ρ_He] term in eqn (1a) below, which corresponds to the potential and correlation energy density of superfluid liquid helium. Note that the TDDFT model here concerns the helium atom motions and is not the more familiar electronic TDDFT of quantum chemistry. This approach for superfluid liquid helium has led to a rather good agreement with the experimental findings (see, e.g., ref. 56–58).

In this initial quantum dynamics study on the X + HeND (X = H, D, T, Q) → X⋯HeND capture processes we will consider the situation of zero angular momentum. And in what respects to the X atom only a one-dimensional (z-axis) standard quantum WP dynamics will be considered to account for its time evolution.

The inclusion of angular momentum in quantum dynamics is a really difficult problem to address, even in the case of systems with a small number of atoms,^59,60 and in complex systems as the one we are considering here it is extremely challenging. This results from the large number of coupled differential equations to solve, arising from all possible projections of the angular momentum on the quantization axis. In qualitative terms, as a result of including angular momentum, an additional barrier (centrifugal barrier) will appear in the system that will make harder the approach of the atom to the nanodroplet and the capture process. This barrier grows as J(J + 1), where J is the angular momentum quantum number of the system. Quantum tunneling through this barrier is possible and will be easier the smaller the mass of the atom involved.

A detailed description of the TDDFT+WP method for doped (X₂ diatomic molecules) HeNDs can be found in our previous work,³⁸ and it is also useful to see the reference corresponding to the Ne atom quantum capture.⁴² Here, we will only briefly report the main equations and particularities of the present study.

The mean field equations of motion governing the time evolution of superfluid liquid helium and the X atom, considering here that X=H, correspond to the following pair of coupled non-linear Schrödinger-like equations:

where R_He are the (X, Y, Z) cartesian coordinates of the helium density, z_H is the z-coordinate of the H atom, V_He–H is the interaction potential energy, and the other terms have the usual meaning. In particular, the OT functional is characterized via the ε_c[ρ_He] term in eqn (1a), which here corresponds to the potential and correlation energy density of superfluid liquid helium. In addition, the effective complex wave function of (⁴He)_N satisfies |Ψ_He(R_He,t)|² ≡ ρ_He(R_He,t) (helium density) and the z-axis wave packet of H is specified by ϕ_H(z_H,t). Given the approach of the atom to the nanodroplet along the z axis, the atom–HeND system presents rotational symmetry around this axis.

The He–X diatomic potential energy curve, V_He–X(z_X,R_He), that for all isotopes corresponds to the V_He–H(z_H,R_He) curve, has been taken from the multi-reference configuration interaction ab initio calculations reported in ref. 61. The well depth and interatomic separation in the minimum of the He–H potential energy curve are 7.124 K and 3.524 Å, respectively. While for the 0, 10, 10² and 10³ K interaction energy values of the repulsive part of this curve the corresponding He–H distances are 3.117, 2.975, 2.594 and 2.008 Å, respectively. The helium nanodroplet–X atom interaction potential energy is obtained employing the usual pairwise approach.

Eqn (1a) and (1b) have been discretized using cartesian grids: (a) helium grid for a HeND with 400 He atoms that has 190 × 190 × 256 points for the x, y, and z axes, respectively, with size intervals of 0.4, 0.4 and 0.3 Å, respectively (i.e., total intervals from −38.0 to +38.0 Å for the x and y axes and from −38.4 to +38.4 Å for the z axis); (b) the atomic grid (only z axis) describes the −40.0 to +40.0 Å z-interval and the density of points depends on the initial atomic kinetic energy. For the six kinetic energy values considered (cf. next section) and from the lower to the higher energy, the number of points is 700, 900, 900, 1100, 1300, and 1400, respectively. Thus, the atom grid size interval is between 0.114 and 0.057 Å. On the other hand, it must be considered that the radius of the nanodroplet, defined as r = r₀N^1/3 with r₀ = 2.22 Å, is equal to 16.4 Å for N = 400 (cf. Fig. 1).

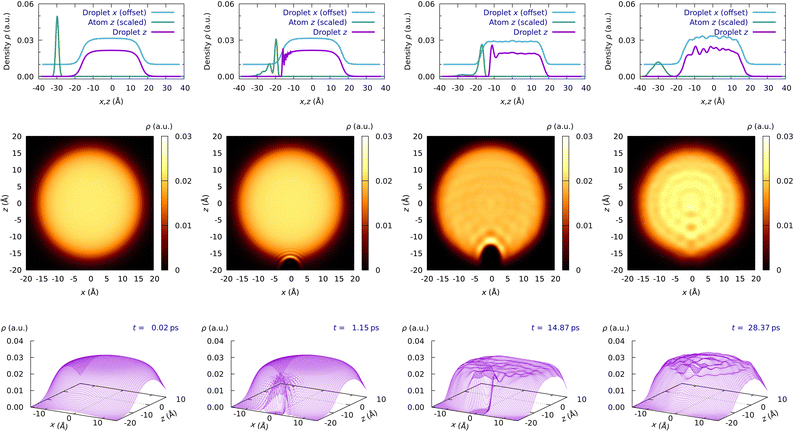Fig. 1 Snapshots of the atomic WP probability density and superfluid helium density for the H atom at E_k,0 = 47.23 K (Movie 2 condition, ESI†) at four representative times (initial, collision with the surface, in the dimple and escape): WP probability density along the z axis and superfluid helium density along the x and z axes (top); superfluid helium density (2D) in the xz plane (middle); superfluid helium density (3D) in the xz plane (bottom). A H⋯HeND collision complex with a lifetime of 3 ps is observed.

The time propagation has been performed using the Adams predictor-corrector-modifier method,⁶² initiated by a fourth order Runge–Kutta method,⁶³ and the time step used varied from 1.0 × 10⁻⁴ to 3.0 × 10⁻⁵ ps from the lower to the higher initial kinetic energy examined. The derivatives for the kinetic energy terms have been calculated in momentum space by means of a Fourier transform.⁶⁴

To absorb the superfluid helium density evaporated from the nanodroplet and thus minimize non-physical reflections from the edges of the grid, a quartic negative imaginary potential (NIP) is placed there.⁶⁵ We also apply a NIP to the edges of the X atom grid so as to account for the possibility of rebound of a fraction of the wave packet due to the collision with the nanodroplet. The NIPs have the following form:

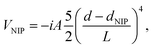where A and L are the absorption strength and length of the NIP. This potential acts for d > d_NIP and A and L are equal to 265.2 K and 5.0 Å for the X atom (z axis), respectively, and 3315.0 K and 1.0 Å for the helium (x, y and z axes). Therefore, the NIPs have been placed 5.0 Å and 1.0 Å before the limits of the system for the X atom and the helium, respectively.

Regarding the initial conditions, we consider a pure (⁴He)_N of 400 ⁴He atoms and a minimum uncertainty wave packet describing the X atom, which corresponds to a Gaussian function. The initial WP is centered on the z-axis at μ = −30 Å and its width is σ = 0.80 Å,

These values are similar to those used in our previous quantum dynamics study on the capture of a Ne atom by a HeND.⁴² The initial expectation values of the kinetic energy of the colliding X atom we have investigated are given in Table 1, where the expectation values of the initial velocity are also shown.

Table 1 Initial kinetic energies, E_k,0 (K), and initial velocities, v_z,₀ (m s⁻¹), of H, D, T and Q^ab

H	D	T	Q
a The velocities are given between parentheses.b Each value really corresponds to the expectation value of the initial kinetic energy or initial velocity of the corresponding atomic WP.
14.86 (300)	10.16 (212.2)	8.59 (173.4)	7.82 (150.6)
27.73 (550)	23.04 (389.1)	21.47 (317.9)	20.71 (276.1)
47.23 (790)	42.52 (558.8)	40.97 (456.7)	40.19 (396.5)
84.07 (1110)	78.04 (778.1)	76.48 (635.9)	75.69 (552.1)
121.50 (1360)	116.79 (962.0)	115.25 (786.2)	114.48 (682.7)
158.79 (1570)	154.10 (1110.6)	152.55 (907.6)	151.77 (788.1)

---

The initial time ground state wave function of the pure HeND is obtained from a static calculation by finding the lowest energy solution of eqn (1a) without the term that describes the atom–HeND interaction. To do this, we follow an analogous strategy to that for dynamic calculations, but applying the imaginary time step propagation method (see, e.g., ref. 38 and 48).

3. Results and discussion

In this section we will consider first the mechanism of formation and breakdown of the atom⋯HeND collision complex and the corresponding dimple in the HeND. For this goal the time evolution of the main properties will be analyzed. After this, the analysis of formation/breakdown of the collision complex will be performed in more quantitative terms in Sections 3.2 and 3.3.

All the properties considered are expectation values but to make things shorter we will refer to them as “properties” instead of “expectation values of properties”, and an analogous simplification is applied to the symbols used for the properties.

The six initial kinetic energies investigated for each one of the atoms, E_k,0, are given in Table 1 (≈10–150 K energy interval) together with the corresponding initial velocities, v_z,0 (300–1570 m s⁻¹ velocity interval for H, and 212–1110, 173–908 and 150–788 m s⁻¹ velocity intervals for D, T and Q, respectively).

In this work we focus on the analysis of the collision complex formation and breakdown process, and we do not analyze the relaxation of the helium nanodroplet that occurs once the atom leaves its surface. This relaxation process requires a substantial amount of time, as it is known from previous works (see, e.g., ref. 41, 43, 45 and 49).

Collision complexes are metastable intermediates in which the chemical species involved remain close to each other for a certain time, X + HeND → X⋯HeND (collision complex; X = H, D, T, Q), and in the end the atom will leave the surface of the nanodroplet and move away from it. The collision complex has a lower interaction potential energy than the X + HeND reactants even though in most cases the H atom (or isotopes) is not fully solvated by the helium environment.

To determine the lifetime of a collision complex we use the following criterion (for a given isotope and initial condition): if the lowest energy dynamical minimum occurs at a given time, t_m, we consider both the previous, t_p, and following, t_f, times at which the atom–HeND interaction potential energy is equal to 3/4 of the corresponding value at the lowest energy dynamical minimum. We then take the lifetime to be the difference t_f − t_p. Similar criteria have been used in the gas phase reaction dynamics context, even though in this case it was applied on minima of the potential energy surface (see, e.g., ref. 66).

It is worth noting that during the existence of the atom⋯HeND collision complex most of the atom WP remains attached to the surface of the HeND, as it will be shown in Section 3.3 when analyzing the atom WP direct reflection probability (i.e., when the system reaches the dynamical minimum) and its dependence with the isotope and initial kinetic energy.

3.1 Microscopic mechanism

From the time evolution plots of the properties (coordinates, velocities, energies, etc.) we have found two of them particularly useful to describe the dynamics of the capture process: the interaction potential energy (V_X–HeND) and the coordinate of the X atom (z_X). Furthermore, the movies showing the time evolution of the probability density of the atomic WP (i.e., its modulus square; ‖WP‖²) and the superfluid helium density along the x (equivalent to y) and z axes, together with the superfluid helium density on the xz plane, have also been very useful to characterize the capture dynamics (cf. Movies 1–4 in the ESI†).

These movies correspond to the collisions of the H atom at E_k,0 = 27.73 and 47.23 K and of the D atom at E_k,0 = 23.04 and 42.52 K, respectively; i.e., to the initial conditions 2 and 3 of both atoms. For the H atom, we can see the formation of a collision complex with a lifetime below 5 ps while for the D atom a collision complex with a lifetime above 40 ps is found.

In addition, Fig. 1 shows snapshots of the time evolution of the four properties mentioned above for the atomic WP and superfluid helium density considering the H atom at E_k,0 = 47.23 K, and in the analogous Fig. S1 (ESI†) the snapshots for the D atom at E_k,0 = 42.52 K are presented; i.e., they correspond to the situations of Movies 2 and 4 (ESI†).

Without considering the atom approach to the nanodroplet, four different steps can be identified in the capture process, where only a small fraction of the atomic WP is reflected during the collision with the HeND (cf. Section 3.3). The first step corresponds to the penetration of the atom through the nanodroplet surface, which acts as a barrier. Once the atom has managed to make a hole in the nanodroplet (second step), generating a dimple in the HeND, it remains there for a certain time (third step), making oscillations but, in general, without being fully solvated by the superfluid helium environment. Finally, the atom begins the process of escaping from the HeND (fourth step) that finishes when the atom and the HeND are well separated.

A temporary full solvation of the atom by the superfluid helium is only observed for the cases of T (conditions 5 and 6) and Q (conditions 4–6). Moreover, it is worth noting that for D, T and Q and some initial kinetic energies, during the simulated time, we do not observe the escaping process indicated above. This occurs for the initial conditions (2, 3), (1–3) and (1–3) of D, T and Q, respectively.

As a result of the collision of the atom with the HeND surface and due to the exchange of energy, oscillatory patterns appear in both the atom WP probability density and the superfluid helium density, cf. Fig. 1 and Movies 1–4 in the ESI.† The intensity of these oscillations increases with the initial kinetic energy due to the higher excitation produced.

Concerning the capture mechanism, for the H atom and all initial conditions a H⋯HeND collision complex with a lifetime in the 1.3–4.7 ps interval is formed (Table 2). For the D atom, a collision complex with a lifetime in the 2.2–6.0 ps interval is produced for the initial conditions 1 and 4–6, while for the initial conditions 2 and 3 the D atom remains attached to the HeND surface during all the simulated time (Table 2). For these two last conditions a collision complex lifetime >40 ps is obtained.

Table 2 Collision complex lifetime (in ps) as a function of the initial kinetic energy (in K) for H, D, T and Q. The first value corresponds to the initial kinetic energy and the second one to the lifetime^ab

H	D	T	Q
a For the criterion to determine the lifetime see the text.b Formation of a long-lived collision complex in the case of D (conditions 2 and 3), T (conditions 1–3) and Q (conditions 1–3).
14.86, 2.1	10.16, 2.2	8.59, ≈160	7.82, >220
27.73, 1.3	23.04, >40	21.47, >90	20.71, >90
47.23, 4.3	42.52, >40	40.97, >40	40.19, >40
84.07, 4.3	78.04, 4.9	76.48, 5.7	75.69, 6.7
121.50, 4.4	116.79, 5.2	115.25, 6.3	114.48, 8.0
158.79, 4.7	154.10, 6.0	152.55, 7.2	151.77, 8.8

---

Regarding the T atom, a collision complex with a lifetime in the 5.7–7.2 ps interval is formed for the initial conditions 4–6, while for the initial conditions 1, 2 and 3 the T atom remains attached to the HeND surface during ≈160 ps and more than 90 and 40 ps, respectively (Table 2). In the case of the Q atom, the situation is similar to that for the T atom, with collision complexes showing a lifetime in the 6.7–8.8 ps interval for initial conditions 4–6, while for the initial conditions 1, 2 and 3 the Q atom remains attached to the HeND surface during more than 220, 90 and 40 ps, respectively (Table 2).

Therefore, from the collision complex lifetime results, we may conclude that the behaviors of T and Q are quite similar to each other (formation of a long-lived atom⋯HeND collision complex for initial conditions 1–3) whereas the behavior of D is in between the behaviors of H (no long-lived H⋯HeND collision complex) and T and Q (Table 2). We use the term “long-lived” in relative terms, i.e., taking as a reference the situations in which the collision complex lasts more than 10 ps. Besides, the shortest duration complexes are those of H, which last less than 5 ps.

At initial kinetic energies higher than those at which long-lived collision complexes are formed, collision complexes of short duration are formed whose lifetime increases moderately with E_k,0 (≈ 80–150 K): 22.4, 26.3 and 31.3% for D, T and Q, respectively. In the case of the H atom, where no long-lived complexes are formed, the corresponding lifetimes increase by 9.0%.

This increase of the lifetime is probably related to the somewhat higher penetration of the atom inside the HeND as E_k,0 increases in that energy interval. This contrasts with what, in general, occurs in the case of gas phase elementary reactions taking place through a minimum of the potential energy surface, where the increase of collision energy is against the duration of the complex.

In strong contrast with the results shown here for the capture of the H and isotopes, the Ne atom is fully captured and solvated by the helium environment of the nanodroplet.^42,43 These results can be interpreted on the basis of the different strength of the H–He and Ne–He interactions. The depth of the minimum of the X–He potential energy curve with respect to the dissociated atoms is equal to 7.124 and 21.02 K for H⁶¹ and Ne,⁶⁷ respectively (the He–He value is 10.63 K⁶⁷), which favors a situation in which the Ne atom is solvated by helium. On the other hand, it is worth noting that at a given collision energy, the velocity of Ne is substantially lower than that of H (v_Ne = 0.225v_H), so that the HeND will have greater ease in adapting appropriately as the Ne colliding atom approaches to it.

Additional and valuable information on the microscopic mechanism of capture can be derived from the time evolution of the atom–HeND interaction potential energy (Fig. 2). Thus, even though there exist some oscillations in the time evolution of this property, the presence of a dynamical potential energy barrier (barrier hereafter) above the potential energy of the X + HeND reactants is evident, where X refers to the colliding atom. This barrier occurs in the early times of the collision process and is followed by the formation of a dynamical minimum (minimum hereafter) that corresponds to the formation of a X⋯HeND collision complex (Fig. 2).

Fig. 2 Time evolution of the atom–HeND interaction potential energy, V_X–HeND, as a function of the initial kinetic energy of the atom, E_k,0, for the four isotopic variants H, D, T and Q, in panels (a), (b), (c) and (d), respectively.

It is important to note that for a number of initial conditions there are, really, several minima of similar relevance (similar potential energy values) that occur for D (conditions 2 and 3), T (conditions 1–3) and Q (conditions 1–3); cf. Fig. 2. These conditions correspond to situations in which a long-lived collision complex is formed, and in these cases when referring to the properties of the minimum we have considered those of the minimum with the lowest atom–HeND interaction potential energy.

For a given atom, the potential energy of the barrier (V_X–HeND at the barrier, V_X–HeND,b) increases with the initial atomic kinetic energy (E_kin X,0) and this energy also increases when evolving from the heaviest atom (Q) to the lightest one (H), being especially important in this last case. The barrier is very small for Q, independently of E_kin X,0, and T presents a similar behavior. The situation for D is in between the behaviors observed for H and T, but closer to this last atom.

In contrast to the case of the potential energy barrier, the depth of the minimum shows on the overall a small dependence with E_kin X,0, with the only exception of what occurs at the lowest E_kin X,0 value region examined for each atom, where a larger dependence is found, particularly for H and D. Besides, the depth of the minimum increases when evolving from the lightest isotope (H) to the heaviest one (Q).

Complementary information about the atom can be obtained when representing the time evolution of the atom kinetic energy (Fig. S2, ESI†). A very important decrease of its initial kinetic energy is observed at the barrier, and at the minimum this decrease is even larger.

In what follows the main properties (atom–HeND potential energy, atom kinetic energy, z-coordinate, etc.) of the barrier and minimum will be examined in greater detail, beginning with the properties of the barrier (Section 3.2) and ending with the properties of the minimum (Section 3.3). Also, some considerations about the dimple formed in the surface of the HeND will be given in Section 3.3.

3.2 Dynamical barrier

When analyzing the dynamical entrance barrier, that is reached at simulated times below ≈1.0 ps, we explore a number of key properties: the atom–HeND interaction energy, the kinetic energy of the atom, the z-coordinate of the atom and the energy of the HeND. In addition, we also consider the norm of the atomic wave packet and of the superfluid helium wavefunction.

The interaction potential energy V_X–HeND at the barrier, V_X–HeND,b, depends on the E_k,0 of the atom in a quite different way for the several isotopes and V_X–HeND,b decreases in an important way when evolving from the H atom to the heavier D, T and Q isotopes (Fig. 3).

Fig. 3 Change in the atom–HeND interaction potential energy, V_X–HeND, at the dynamical barrier, as a function of the initial kinetic energy of the atom, E_k,0, for the four isotopic variants (H, D, T and Q). Changes are relative to the initial reactant state.

The next values of V_X–HeND,b are obtained for the H atom at the six E_k,0 values investigated (14.9, 27.7, 47.2, 84.1, 121.5 and 158.8 K): 0.36, 1.16, 4.43, 15.48, 33.37 and 55.36 K, respectively (Fig. 3). This contrasts with the substantially lower values found for the other isotopes at similar energies. Thus, at the lowest E_k,0 values studied for D, T and Q (10.16, 8.59 and 7.82 K, respectively), a value of 0.023 K is determined for V_X–HeND,b. Whereas, at the highest E_k,0 values examined for these atoms (154.10, 152.55 and 151.77 K, respectively), V_X–HeND,b is equal to 20.10, 6.54 and 0.903 K, respectively (Fig. 3).

The very large differences found in the values of the interaction energy V_X–HeND at the barrier and in the dependence of this property with E_k,0 for the different isotopes can be interpreted, at least in part, considering the faster motion of the atom approaching to the HeND as the mass of the former diminishes for the same kinetic energy. Thus, when the mass of the isotope decreases the nanodroplet will have less time to adapt its structure to the incoming atom, which will not be favorable from an energetic point of view. Moreover, the larger importance of purely quantum effects that is expected when the atomic mass decreases can, of course, play also a role here. However, to determine the importance of these effects on the capture dynamics it would be necessary to compare the present results with those obtained when the H, D, T and Q atoms are described using classical mechanics, but this is out of the scope of the present study.

Based on the above, and in purely qualitative terms, it is reasonable to expect that H, due to its much lighter character, behaves in a particularly different manner with respect to the other isotopic variants.

The kinetic energy of the atom at the barrier, E_k,b, depends on the E_kin,0 of the atom in a rather different way for the several isotopes, and E_k,b increases significantly from the H atom to the heavier D, T and Q atoms, as it can be seen from Fig. 4, where the E_k,b − E_k,0 difference vs. E_k,0 is plotted. Moreover, while the decrease of the kinetic energy of the H atom when reaching the barrier is clearly evident for all the initial kinetic energies examined (and becomes progressively more important as E_k,0 increases), for the D, T and Q atoms the decrease of the kinetic energy becomes clearly evident only at the three, two and one higher initial kinetic energies considered, respectively (Fig. 4).

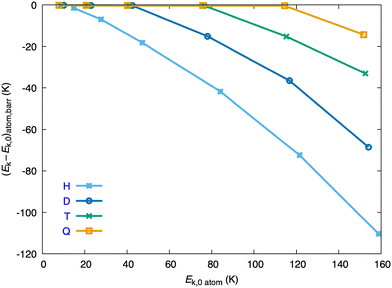Fig. 4 Change in the kinetic energy of the atom at the dynamical barrier, as a function of the initial kinetic energy of the atom, E_k,0, for the four isotopic variants (H, D, T and Q).

For the six E_k,0 values of the H atom (14.9, 27.7, 47.2, 84.1, 121.5 and 158.8 K) the E_k,b values are equal to 89.8, 74.9, 61.4, 50.3, 40.4 and 30.5% of the corresponding E_k,0 values, respectively. Higher or substantially higher percentages are obtained for D, T and Q at similar initial kinetic energies. Thus, at the lowest E_k,0 values of D, T and Q (10.16, 8.59 and 7.82 K, respectively), the E_k,b values are 98.2, 98.1 and 98.0% of their E_k,0 values, respectively. At the highest E_k,0 values of these atoms (154.10, 152.55 and 151.77 K, respectively), the E_k,b values correspond to the 55.5, 78.3 and 90.6% of their E_k,0 values, respectively. These last values are in strong contrast with the substantially smaller percentage that has been found for the H atom (30.5%).

These results correlate with the substantially less attractive character of the atom–HeND interaction that occurs for the H atom in comparison to the other isotopes. This fact is directly related to the substantially higher V_X–HeND,b values that are found in the former case and discussed previously.

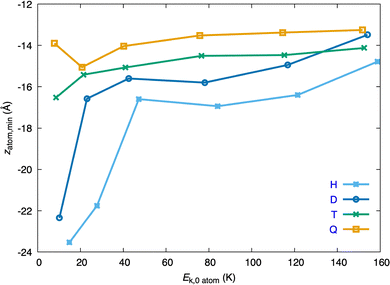
The study of the z-coordinate of the atom at the barrier, z_X,b, helps us to understand somewhat more what happens in the early times of the atom + HeND collision (Fig. 5; z_X,b vs. E_k,0). This coordinate depends on the atomic E_kin,0 in a significant way and at the barrier, on the overall, the atomic WP tends to be closer to the surface of the HeND as E_k,0 increases (i.e., the absolute value of the z-coordinate of the atom takes smaller values). The H atom behaves in a fairly different way as the other atoms in the lower-intermediate E_k,0 region (i.e., in the 75–150 K E_k,0 interval), where z_X,b is almost constant for T and Q; but all atoms show z_X,b values which are not far from each other at the higher E_kin,0. It is worth noting that in the case of this property the D atom behaves quite close to the H atom from the intermediate to the higher E_k,0 region.

Fig. 5 Z-coordinate of the atom at the dynamical barrier, z_X,b, as a function of the initial kinetic energy of the atom, E_k,0, for the four isotopic variants (H, D, T and Q).

Regarding the norm of the atomic wave packet at the barrier, the largest decrease of the norm is observed for the H atom at E_k,0 = 27.73 K and it is equal to 1.92 × 10⁻⁴, while for the D, T and Q atoms the largest decrease of the norm is of the order of 10⁻⁸. With respect to the norm of the superfluid helium wave function, the decrease of the norm at the barrier is of the order of 10⁻⁸. That is to say, at the barrier the norm of the atomic WP and of the superfluid helium wave function are essentially coincident with their initial values (1.0 and 400, respectively; where the superfluid helium wave function is normalized to the number of atoms of the HeND). Therefore, there has not yet been an opportunity for a part of the WP to reach the limits of the system nor for a fraction of the HeND to evaporate and reach these limits.

We have included an additional figure in the ESI† (Fig. S3) of interest for the analysis of the properties at the barrier and that presents the energy change of the HeND at the barrier vs. E_k,0. This change of energy shows approximately a linear dependence with respect to the initial kinetic energy of the atom, and the lines of the different isotopes are approximately parallel to each other with the energy change values following the order H > D > T > Q. This is consistent with the greater decrease in the kinetic energy of the colliding atom at the barrier that follows the same ordering.

3.3 Dynamical minimum (or minima)

In the analysis of the dynamical minimum that is formed once the atom + HeND system overcomes the dynamical barrier, we explore the same key properties as for the dynamical barrier (atom–HeND interaction energy, atom kinetic energy, atom z-coordinate, energy of the HeND and norms of the atomic WP and HeND wave function). Moreover, additional key information on the dynamical minimum has been already reported during the analysis of the capture mechanism carried out in Section 3.1, where the lifetime of the atom⋯HeND collision complex and the existence of several dynamical minima for some isotopes and initial conditions have been shown.

In the present section, for the isotopes and initial conditions (E_k,0 of the atom) that exhibit several dynamical minima in the time evolution of the atom–HeND interaction energy, V_X–HeND, we have considered the properties of the minimum with the lowest value of V_X–HeND (i.e., for the stronger attractive interaction between the atom and the nanodroplet).

The interaction energy V_X–HeND at the minimum, V_X–HeND,m, depends in a smooth way on the E_k,0 of the atom, shows a similar shape for all the isotopes, and the strength of this interaction (given by the absolute value of V_X–HeND,m) evolves according to the following order: Q > T > D > H (Fig. 6). This result anticorrelates with the order of values for the atom–HeND interaction potential energy at the barrier (H > D > T > Q) so that, for a given E_k,0, a higher value of V_X–HeND,b involves a weaker (shallower depth) minimum. This is, in principle, expected, given that a higher barrier makes the atom penetration through the surface of the nanodroplet more difficult. Furthermore, V_X–HeND,m decreases with E_k,0 in an appreciably way in the lower E_k,0 region and presents, in general, a weak decreasing trend for E_k,0 values above 40 K (Fig. 6).

Fig. 6 Change in the atom–HeND interaction potential energy, V_X–HeND, at the dynamical minimum, as a function of the initial kinetic energy of the atom, E_k,0, for the four isotopic variants (H, D, T and Q). In some cases there are more than a single minimum (see the text). Changes are relative to the initial reactant state.

The following values of V_X–HeND,m are found for the H atom at the six E_k,0 values considered in the simulations (14.9, 27.7, 47.2, 84.1, 121.5 and 158.8 K): −3.23, −4.61, −13.95, −16.09, −17.36 and −18.76 K, respectively (Fig. 6). The atom–HeND attractive interaction in the minimum is stronger for the D, T and Q isotopes. So, at the lowest E_k,0 values of D, T and Q (10.16, 8.59 and 7.82 K, respectively), V_X–HeND,m is equal to −5.04, −12.51 and −20.28 K, respectively. And at the highest E_k,0 values of these atoms (154.10, 152.55 and 151.77 K, respectively), V_X–HeND,m is equal to −29.78, −30.25 and −34.10 K, respectively (Fig. 6). The single consideration of the depth of the minimum does not allow us to interpret the lifetime of the collision complexes formed, as can be seen, e.g., in Table 2.

Therefore, the differences found in the values of the atom–HeND interaction energy at the minimum are not so large as the ones we have found in the case of the HeND interaction energy at the barrier. For the former, all isotopic variants present a similar shape although the energies are different. So, for the minimum the H atom is not behaving in a particularly differentiated manner with respect to the other isotopes, differing from what happens for the barrier. Moreover, on the overall, the dependence of V_X–HeND,m with E_k,0 is weaker than in the case of V_X–HeND,b, as previously mentioned.

The change in the kinetic energy of the atom when it evolves from the initial situation (atom + HeND) up to the minimum, E_k,m − E_k,0, depends on E_k,0 in a linear way that is almost identical for H, D, T and Q, as it can be seen from Fig. 7, where the E_k,m − E_k,0 difference vs. E_k,0 is plotted. Moreover, on the overall E_k,m increases smoothly with E_k,0 and takes substantially small values that are even below the lower E_k,0 values considered in this study. More concretely, the E_k,m values obtained for all atoms are within the 3.2–7.5 K interval and so the kinetic energy of the atoms when they are in the minimum is very small.

Fig. 7 Change in the kinetic energy of the atom at the dynamical minimum, as a function of the initial kinetic energy of the atom, E_k,0, for the four isotopic variants (H, D, T and Q). In some cases there are more than a single minimum (see the text).

For the six E_k,0 values of the H atom (14.9, 27.7, 47.2, 84.1, 121.5 and 158.8 K) the E_k,m values are equal to 26.3, 21.5, 10.9, 7.6, 6.1 and 3.5% of the corresponding E_k,0 values, respectively. Comparable percentages are obtained for D, T and Q at similar initial kinetic energies. Thus, at the lowest E_k,0 values of D, T and Q (10.16, 8.59 and 7.82 K, respectively), the E_k,m values are 35.9, 37.6 and 46.8% of their E_k,0 values, respectively. At the highest E_k,0 values of these atoms (154.10, 152.55 and 151.77 K, respectively), the E_k,m values correspond to the 4.1, 4.7 and 4.9% of their E_k,0 values, respectively.

Therefore, when the atom + HeND system reaches the minimum, where an atom⋯HeND collision-complex is formed, most of the initial kinetic energy of the colliding atom has been transferred to the helium nanodroplet, thanks to the highly efficient energy transfer that occurs due to its superfluid character.

We have included an additional figure (Fig. S4) in the ESI† analogous to Fig. S3 (ESI†) that is appropriate for the analysis of the properties at the minimum. This figure shows the energy change of the HeND at the minimum vs. E_k,0, which has a bit more complicated dependence as a function of E_k,0 than in the case of the barrier. The pair H and D behave in a very similar way and the same applies for the pair T and Q and, disregarding what happens at the lower and higher E_k,0 values, in the minimum the increase of HeND energy is larger for T and Q.

The analysis of the z-coordinate of the atom at the minimum, z_X,m, shows that it depends in a significant way on the atomic E_kin,0 only at the lower E_kin,0 and this is particularly clear for H and D (Fig. 8; z_X,m vs. E_k,0). The values of the z-coordinate for the lowest and highest E_kin,0 values investigated for each isotope are, respectively, the following: −23.5 and −14.8 Å (H), −22.3 and −13.5 Å (D), −16.5 and −14.1 Å (T), and −13.9 and −13.3 Å (Q). For this property the behaviors of the H and D atoms are quite similar to each other and the same happens in the case of T and Q, and for these two atoms the dependence of z_X,m with E_kin,0 is particularly smooth (Fig. 8).

Fig. 8 Z-coordinate of the atom at the dynamical minimum, z_X,m, as a function of the initial kinetic energy of the atom, E_k,0, for the four isotopic variants (H, D, T and Q). In some cases there are more than a single minimum (see the text).

The penetration of the atomic WP inside the HeND follows the following order: Q > T > D > H and the results for the different atoms become more similar to each other at the higher E_kin,0 values (the radius of the HeND ends at z = −16.4 Å on the negative part of the z axis; cf. Section 2). This result correlates with the magnitude of the dynamical barrier encountered in the early times of the atom + HeND collision. Thus, the lower the barrier, the deeper the penetration of the atom inside the nanodroplet. A suitable property to account for the size of the dimple generated after the penetration of the atom into the surface of the nanodroplet is the value of the z-atom coordinate (and its oscillations) when it is in the minimum. The lower value of z in absolute value the larger size of the dimple generated by the atom.

The decrease of the norm of the atomic wave packet at the minimum, with respect to the initial value and for the lowest and highest E_kin,0 values are, respectively: −0.0875 and −0.0948 (H), −0.0333 and −0.0168 (D), −0.150 and −0.00476 (T), and −0.105 and −0.000527 (Q). Besides, the changes observed in the norm of the atomic WP are <10% for H, <5% for D and <4% for T and Q, in the case of the two heaviest atoms with exception of result for the lowest E_kin,0. Regarding the norm of the superfluid helium wave function, the maximum decrease of the norm at the minimum is 8.0 × 10⁻⁴, 1.8 × 10⁻³, 4.4 × 10⁻³, and 4.4 × 10⁻³, for H, D, T, and Q, respectively. Therefore, the vast majority of the wave packet reaches the minimum and in this situation the evaporation of helium atoms from the nanodroplet has not yet occurred (recall that the normalization of the atomic WP is taken with respect to unity and in the case of the superfluid helium wavefunction with respect to the number of helium atoms (N = 400 in this case)).

In the ESI† we present an additional figure (Fig. S4) that is also of interest for the analysis of the properties at the minimum and that shows the energy change of the HeND at the barrier vs. E_k,0. This change of energy shows approximately a linear dependence with respect to the initial kinetic energy of the atom, and the lines of the different isotopes are approximately parallel to each other with the energy change values following the order H > D > T > Q. This is consistent with the greater decrease in the kinetic energy of the colliding atom at the barrier that follows the same ordering.

The reflection probability as a function of the initial kinetic energy E_k,0 and for each isotope can be estimated on the basis of the difference between the unity and the norm of the WP while the atom is on the surface of the HeND (i.e., while it is in the dynamic minimum forming a collision complex, atom⋯HeND), that is to say, from the decrease of the WP norm considered above. Although the oscillations of the reflection probability with E_k,0 are clearly evident for H and D, this is not the case for T and Q where this property almost decreases monotonically with E_k,0 (Fig. S5, ESI†). This can be interpreted on the basis of the more quantum character of the behavior that is expected for H and D, in comparison to T and Q, due to their masses.

4. Summary and conclusions

The quantum dynamics of the capture of a H atom (or D, T and Q) by a superfluid helium nanodroplet of 400 ⁴He atoms (T = 0.37 K), with zero angular momentum, has been studied using a TDDFT (helium) + WP (atom) mean field hybrid approach. Very low initial kinetic energies have been considered (≈10–150 K energy interval) in order to try to make more evident the quantum behavior of these systems. To the best of our knowledge these very low energies have not been considered before in this context.

The existence of a dynamical entrance barrier and a dynamical minimum (or minima) during the capture process play a central role in the understanding of this process, especially the former property. In general, the H atom shows a different behavior from the other heavier isotopes, with the behavior of T and Q being very similar to each other and the D atom behaving in between H and T.

Probably, the barrier and minimum are common and important properties in all capture processes, and particularly for systems for which the interaction between helium and the colliding atom is not as attractive as the helium–helium one.

Another key result obtained corresponds to the fact that, in principle, at the very low initial kinetic energies examined only “short” and “long” lived atom⋯HeND collision complexes are formed. Therefore, at the end of the simulations, the atom-helium nanodroplet collision the capture of the atom by the HeND really does not take place. So, we can only refer to the temporary capture of an H atom or isotope by the HeND.

The different behaviors observed for the capture dynamics, i.e., for the capture mechanism and for the properties of the dynamical barrier and dynamical minimum (or minima) have been interpreted in terms of the higher velocity of the H colliding with the (⁴He)_N=400 nanodroplet and the more quantum character of the H behavior due to its significantly lower mass.

In order to identify in a direct way the importance of quantum effects on the different dynamic properties, in the future we expect to investigate these systems considering a classical mechanics description of the colliding atoms, so as to contrast with the quantum mechanics results obtained here.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

The data that support the findings of this study are available from the corresponding author upon a reasonable request.

Acknowledgements

Work performed at the Center for Nanoscale Materials, a U.S. Department of Energy Office of Science User Facility, was supported by the U.S. DOE, Office of Basic Energy Sciences, under Contract No. DE-AC02-06CH11357. Some support has been provided by the Spanish Ministry of Science and Innovation (Excellence MDM CEX2021-001202-M Grant) and the Autonomous Government of Catalonia (2021SGR 354 Project). Thanks are also given to the European Cooperation in Science and Technology (COST Action CA21101). We dedicate this work to Professor Jan Peter Toennies (University of Göttingen) and to the memory of Professor Giacinto Scoles (University of Princeton) for their pioneering contributions on the interaction of chemical species with superfluid helium nanodroplets.

References

1. J. P. Toennies and A. F. Vilesov, Superfluid helium droplets: a uniquely cold nanomatrix for molecules and molecular complexes, Angew. Chem., Int. Ed., 2004, 43, 2622–2648.
2. M. Barranco, R. Guardiola, S. Hernández, R. Mayol, J. Navarro and M. Pi, Helium nanodroplets: an overview, J. Low Temp. Phys., 2006, 142, 1–81.
3. A. Slenczka and J. P. Toennies, Chemical Dynamics Inside Superfluid Helium Nanodroplets at 0.37 K, in Low Temperature and Cold Molecules, ed. I. W. M. Smith, Imperial College Press, London, 2008, pp. 345–392 and references cited therein.
4. S. Yang and A. M. Ellis, Helium droplets: a chemistry perspective, Chem. Soc. Rev., 2013, 42, 472–484.
5. F. Ancilotto, M. Barranco, F. Coppens, J. Eloranta, N. Halberstadt, A. Hernando and M. Pi, Density functional theory of doped superfluid liquid helium and nanodroplets, Int. Rev. Phys. Chem., 2017, 36, 621–707.
6. A. Mauracher, O. Echt, A. M. Ellis, S. Yang, D. K. Bohme, J. Postler, A. Kaiser, S. Denifl and P. Scheier, Cold physics and chemistry: collisions, ionization and reactions inside helium nanodroplets close to zero K, Phys. Rep., 2018, 751, 1.
7. T. González-Lezana, O. Echt, M. Gatchell, M. Bartolomei, J. Campos-Martínez and P. Scheier, Solvation of ions in helium, Int. Rev. Phys. Chem., 2020, 39, 465–516.
8. F. Laimer, F. Zappa, P. Scheier and M. Gatchell, Multiply charged helium droplet anions, Chem. – Eur. J., 2021, 27, 7283–7287.
9. Molecules in Superfluid Helium Nanodroplets. Spectroscopy, Structure and Dynamics, ed. A. Slenczka and J. P. Toennies, Topics in Applied Physics, Springer, Charm, 2022, vol. 145.
10. L. Bruder, M. Koch, M. Mudrich and F. Stienkemeier, Ultrafast Dynamics in Helium Droplets, in Molecules in Superfluid Helium Nanodroplets. Spectroscopy, Structure and Dynamics, ed. A. Slenczka and J. P. Toennies, Topics in Applied Physics, Springer, Charm, 2022, 145, pp. 447–451.
11. F. Lackner, Synthesis of Metallic Nanoparticles in Helium Droplets, in Molecules in Superfluid Helium Nanodroplets. Spectroscopy, Structure and Dynamics, ed. A. Slenczka and J. P. Toennies, Topics in Applied Physics, Springer, Charm, 2022, 145, pp. 513–560.
12. J. Tiggesbäumker and F. Stienkemeier, Formation and properties of metal clusters isolated in helium droplets, Phys. Chem. Chem. Phys., 2007, 9, 4748–4770.
13. S. Yang, A. M. Ellis, D. Spence, C. Feng, A. Boatwright, E. Latimer and C. Binns, Growing metal nanoparticles in superfluid helium, Nanoscale, 2013, 5, 11545–11553.
14. L. F. Gomez, E. Loginov and A. F. Vilesov, Traces of vortices in superfluid helium droplets, Phys. Rev. Lett., 2012, 108, 155302.
15. E. Latimer, D. Spence, C. Feng, A. Boatwright, A. M. Ellis and S. Yang, Preparation of ultrathin nanowires using superfluid helium droplets, Nano Lett., 2014, 14, 2902–2906.
16. A. Scheidemann, B. Schilling and J. P. Toennies, Anomalies in the reactions of He⁺ with SF₆ embedded in large helium-4 clusters, J. Phys. Chem., 1993, 97, 2128–2138.
17. B. E. Callicoatt, D. D. Mar, V. A. Apkarian and K. C. Janda, Charge transfer within He clusters, J. Chem. Phys., 1996, 105, 7872–7875.
18. W. K. Lewis, B. E. Applegate, J. Sztáray, B. Sztáray, T. Baer, R. J. Bemish and R. E. Miller, Electron impact ionization in helium nanodroplets:  controlling fragmentation by active cooling of molecular ions, J. Am. Chem. Soc., 2004, 126, 11283–11292.
19. W. K. Lewis, R. J. Bemish and R. E. Miller, Fragmentation of HCN in optically selected mass spectrometry: nonthermal ion cooling in helium nanodroplets, J. Chem. Phys., 2005, 123, 141103.
20. B. E. Callicoatt, K. Fröde, L. F. Jung, T. Ruchti and K. C. Janda, Fragmentation of ionized liquid helium droplets: a new interpretation, J. Chem. Phys., 1998, 109, 10195–10200.
21. B. E. Callicoatt, K. Fröde, T. Ruchti, L. Jung, K. C. Janda and N. Halberstadt, Capture and ionization of argon within liquid helium droplets, J. Chem. Phys., 1998, 108, 9371–9382.
22. T. Ruchti, K. Fröde, B. E. Callicoatt, H. Ludwigs and K. C. Janda, Charge transfer and fragmentation of liquid helium clusters that contain one or more neon atoms, J. Chem. Phys., 1998, 109, 10679–10687.
23. T. Ruchti, B. E. Callicoatt and K. C. Janda, Charge transfer and fragmentation of liquid helium droplets doped with xenon, Phys. Chem. Chem. Phys., 2000, 2, 4075–4080.
24. G. E. Douberly, J. M. Merritt and R. E. Miller, IR-IR double resonance spectroscopy in helium nanodroplets: photo-induced isomerization, Phys. Chem. Chem. Phys., 2005, 7, 463–468.
25. A. Braun and M. Drabbels, Photodissociation of alkyl iodides in helium nanodroplets. I. Kinetic energy transfer, J. Chem. Phys., 2007, 127, 114303.
26. A. Braun and M. Drabbels, Photodissociation of alkyl iodides in helium nanodroplets. II. Solvation dynamics, J. Chem. Phys., 2007, 127, 114304.
27. A. Braun and M. Drabbels, Photodissociation of alkyl iodides in helium nanodroplets. III. Recombination, J. Chem. Phys., 2007, 127, 114305.
28. B. Thaler, S. Ranftl, P. Heim, S. Cesnik, L. Treiber, R. Meyer, A. W. Hauser, W. E. Ernst and M. Koch, Femtosecond photoexcitation dynamics inside a quantum solvent, Nat. Commun., 2018, 9, 4006.
29. B. Thaler, M. Meyer, P. Heim and M. Koch, Long-lived nuclear coherences inside helium nanodroplets, Phys. Rev. Lett., 2020, 124, 115301.
30. B. Thaler, P. Heim, L. Treiber and M. Koch, Ultrafast photoinduced dynamics of single atoms solvated inside helium nanodroplets, J. Chem. Phys., 2020, 152, 014307.
31. S. H. Albrechtsen, C. A. Schouder, A. Viñas Muñoz, J. K. Christensen, C. Engelbrecht Petersen, M. Pi, M. Barranco and H. Stapelfeldt, Observing the primary steps of ion solvation in helium droplets, Nature, 2023, 623, 319–323.
32. S. H. Albrechtsen, J. K. Christensen, C. E. Petersen, C. A. Schouder, P. J. Carchi-Villalta, I. Sánchez-Pérez, M. Bartolomei, T. González-Lezana, F. Pirani and H. Stapelfeldt, Femtosecond-and-atom-resolved solvation dynamics of a Na⁺ ion in a helium nanodroplet, J. Chem. Phys., 2025, 162, 174309.
33. F. Calvo, Concurrent processes in the time-resolved solvation and Coulomb ejection of sodium ions in helium nanodroplets, J. Chem. Phys., 2024, 161, 121101.
34. E. García-Alfonso, M. Barranco, N. Halberstadt and M. Pi, Time-resolved solvation of alkali ions in superfluid helium nanodroplets, J. Chem. Phys., 2024, 160, 164308.
35. F. Calvo, Time-dependent solvation of potassium ions in helium nanodroplets: interaction fingerprints, Low Temp. Phys., 2025, 51, 453–459.
36. E. Zunzunegui-Bru, E. Gruber, T. Lázaro, M. Bartolomei, M. I. Hernández, J. Campos-Martínez, T. González-Lezana, S. Bergmeister, F. Zappa, P. Scheier, R. Pérez de Tudela, J. Hernández-Rojas and J. Bretón, Observation of multiple ordered solvation shells in doped helium droplets: the case of He_NCa²⁺, J. Phys. Chem. Lett., 2023, 14, 3126–3131.
37. R. Rodríguez-Cantano, T. González-Lezana, P. Villarreal and F. A. Gianturco, A configurational study of helium clusters doped with He*⁻ and He₂*⁻, J. Chem. Phys., 2015, 142, 104303.
38. A. Vilà, M. González and R. Mayol, Photodissociation dynamics of homonuclear diatomic molecules in helium nanodroplets. The case of Cl₂@(⁴He)_N, J. Chem. Theory Comput., 2015, 11, 899–906.
39. A. Vilà, M. González and R. Mayol, Quantum interferences in the photodissociation of Cl₂(B) in superfluid helium nanodroplets (⁴He)_N, Phys. Chem. Chem. Phys., 2015, 17, 32241–32250.
40. A. Vilà and M. González, Mass effects in the photodissociation of homonuclear diatomic molecules in helium nanodroplets: inelastic collision and viscous flow energy exchange regimes, Phys. Chem. Chem. Phys., 2016, 18, 27630–27638.
41. A. Vilà and M. González, Quantum dynamics of the Br₂ (B-excited state) photodissociation in superfluid helium nanodroplets: importance of the recombination process, Phys. Chem. Chem. Phys., 2022, 24, 24353–24361.
42. A. Vilà, M. González and R. Mayol, Quantum dynamics of the pick up process of atoms by superfluid helium nanodroplets: the Ne + (⁴He)₁₀₀₀ system, Phys. Chem. Chem. Phys., 2016, 18, 2006–2014.
43. M. Blancafort-Jorquera, A. Vilà and M. González, Quantum-classical dynamics of the capture of neon atoms by superfluid helium nanodroplets, Phys. Chem. Chem. Phys., 2018, 20, 29737–29753.
44. A. Vilà and M. González, Reaction dynamics inside superfluid helium nanodroplets: the formation of the Ne₂ molecule from Ne + Ne@(⁴He)_N, Phys. Chem. Chem. Phys., 2016, 18, 31869–31880.
45. M. Blancafort-Jorquera, A. Vilà and M. González, Quantum–classical approach to the reaction dynamics in a superfluid helium nanodroplet. The Ne₂ dimer and Ne–Ne adduct formation reaction Ne + Ne-doped nanodroplet, Phys. Chem. Chem. Phys., 2019, 21, 24218–24231.
46. A. Vilà, M. Paniagua and M. González, Vibrational energy relaxation dynamics of diatomic molecules inside superfluid helium nanodroplets. The case of the I₂ molecule, Phys. Chem. Chem. Phys., 2018, 20, 118–130.
47. M. Blancafort-Jorquera and M. González, Vibrational energy relaxation of a diatomic molecule in a superfluid helium nanodroplet: influence of the nanodroplet size, interaction energy and energy gap, Phys. Chem. Chem. Phys., 2021, 23, 25961–25973.
48. M. Blancafort-Jorquera, A. Vilà and M. González, Rotational energy relaxation quantum dynamics of a diatomic molecule in a superfluid helium nanodroplet and study of the hydrogen isotopes case, Phys. Chem. Chem. Phys., 2019, 21, 21007–21021.
49. A. Vilà, M. González and R. Mayol, Relaxation dynamics of helium nanodroplets after photodissociation of a dopant homonuclear diatomic molecule. The case of Cl₂@(⁴He)_N, Phys. Chem. Chem. Phys., 2016, 18, 2409–2416.
50. A. Leal, D. Mateo, A. Hernando, M. Pi and M. Barranco, Capture of heliophobic atoms by ⁴He nanodroplets: the case of cesium, Phys. Chem. Chem. Phys., 2014, 16, 23206–23213.
51. F. Coppens, F. Ancilotto, M. Barranco, N. Halberstadt and M. Pi, Capture of Xe and Ar atoms by quantized vortices in ⁴He nanodroplets, Phys. Chem. Chem. Phys., 2017, 19, 24805–24818.
52. F. Coppens, F. Ancilotto, M. Barranco, N. Halberstadt and M. Pi, Dynamics of impurity clustering in superfluid ⁴He nanodroplets, Phys. Chem. Chem. Phys., 2019, 21, 17423–17432.
53. E. García-Alfonso, M. Barranco, D. A. Bonhommeau, N. Halberstadt, M. Pi and F. Calvo, Clustering, collision, and relaxation dynamics in pure and doped helium nanoclusters: density- vs. particle-based approaches, J. Chem. Phys., 2022, 157, 014106.
54. D. A. Bonhommeau, Collision of cesium atoms on helium nanodroplets: unraveling mechanisms for surface capture at experimental velocities, J. Chem. Phys., 2024, 161, 184302.
55. F. Dalfovo, A. Lastri, L. Pricaupenko, S. Stringari and J. Treiner, Structural and dynamical properties of superfluid helium: a density-functional approach, Phys. Rev. B:Condens. Matter Mater. Phys., 1995, 52, 1193–1209.
56. N. B. Brauer, S. Smolarek, E. Loginov, D. Mateo, A. Hernando, M. Pi, M. Barranco, W. J. Buma and M. Drabbels, Critical Landau Velocity in helium nanodroplets, Phys. Rev. Lett., 2013, 111, 153002.
57. D. Mateo, A. Hernando, M. Barranco, E. Loginov, M. Drabbels and M. Pi, Translational dynamics of photoexcited atoms in ⁴He nanodroplets: the case of silver, Phys. Chem. Chem. Phys., 2013, 15, 18388–18400.
58. D. Mateo, F. Gonzalez and J. Eloranta, Rotational superfluidity in small helium droplets, J. Phys. Chem. A, 2015, 119, 2262–2270.
59. Y. Zhou, Y. Lu, Z. Zhang and D. H. Zhang, An efficient and universal parallel algorithm for high-dimensional quantum dynamics in poly-atomic reactions, J. Chem. Phys., 2024, 160, 202502.
60. X. Zhang, Z. Zhang, F. Gatti and D. H. Zhang, Full-dimensional quantum dynamics study of isotope effects for the H₂ + NH₂/ND₂/NHD and H₂/D₂/HD + NH₂ reactions, J. Chem. Phys., 2021, 154, 074301.
61. W. Meyer and L. Frommhold, Long-range interactions in H–He: ab initio potential, hyperfine pressure shift and collision-induced absorption in the infrared, Theor. Chim. Acta, 1994, 88, 201–216.
62. A. Ralston, Numerical Integration Methods for the Solution of Ordinary Differential Equations, in Mathematical Methods for Digital Computers, ed. A. Ralston and H. S. Wilf, John Wiley & Sons, New York, 1960; vol. 1, pp. 95–109.
63. R. J. Thompson, Improving round-off in Runge-Kutta computations with Gill's Method, Commun. ACM, 1970, 13, 739–740.
64. FFT from the Intel Math Kernel Library, version 2021.4.
65. A. Vibók and G. G. Balint-Kurti, Parametrization of complex absorbing potentials for time-dependent quantum dynamics, J. Phys. Chem., 1992, 96, 8712–8719.
66. M. González, A. Saracibar and E. Garcia, Capture and dissociation in the complex-forming CH + H₂ → CH₂ + H, CH + H₂ reactions, Phys. Chem. Chem. Phys., 2011, 13, 3421–3428.
67. S. M. Cybulski and R. R. Toczyłowski, Ground state potential energy curves for He₂, Ne₂, Ar₂, He-Ne, He-Ar, and Ne-Ar: a coupled-cluster study, J. Chem. Phys., 1999, 111, 10520–10528.

---

Footnote

† Electronic supplementary information (ESI) available: Figures: snapshots of the atomic wave packet (WP) probability density and superfluid helium density for D at E_k,0 = 42.52 K (Fig. S1); time evolution of the change in the kinetic energy of the atom (Fig. S2); change in the energy of the HeND at the barrier (Fig. S3) and at the minimum (Fig. S4); reflection probability of the atomic WP (Fig. S5). Movies: time evolution of the atomic WP probability density and superfluid helium density for H at E_k,0 = 27.73 K (Movie 1); same as Movie 1 but for H at E_k,0 = 47.23 K (Movie 2), D at E_k,0 = 23.04 K (Movie 3) and D at E_k,0 = 42.52 K (Movie 4). See DOI: https://doi.org/10.1039/d5cp01498k

---