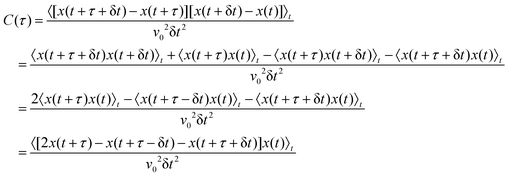Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Discriminating stochastic processes for the assessment of materials properties by diffusion measurements
Ralf
Metzler
 ab and
Matthias
Weiss
ab and
Matthias
Weiss
 *c
*c
aInstitute of Physics & Astronomy, University of Potsdam, Karl-Liebknecht-St 24/25, 14476 Potsdam, Germany
bAsia Pacific Centre for Theoretical Physics, Pohang 37673, Republic of Korea
cExperimental Physics I, University of Bayreuth, Universitätsstr. 30, D-95447 Bayreuth, Germany. E-mail: matthias.weiss@uni-bayreuth.de
First published on 17th June 2025
Abstract
Assessing the materials properties of complex media, e.g. colloidal suspensions or intracellular fluids, frequently relies on quantifying the diffusive motion of tracer particles. In particular, from the particles’ mean squared displacement (MSD) one may infer the complex shear modulus of the medium. Yet, experimentally the same power-law forms of the MSDs emerge for tracer diffusion in very different environments. For example, diffusive motion in a static maze of fractal obstacles (obstructed diffusion, OD) and motion in viscoelastic fluids (often described by fractional Brownian motion, FBM) can show an identical sublinear MSD scaling, but an MSD-derived complex shear modulus is meaningless for OD as the system does not feature any viscoelasticity. Here we show that OD and FBM trajectories are highly similar in many observables, including the MSD and the autocovariance function that reports on the memory of the particle motion. The Gaussianity and/or the asphericity of trajectories, extracted with single-particle tracking, allows for a proper discrimination of OD and FBM, facilitating a meaningful interpretation of the materials properties of the medium. In contrast, techniques that only monitor particle number fluctuations in a region of interest are not capable of discriminating highly similar random processes like FBM and OD as they only rely on the MSD. We therefore highly recommend the use of the more informative tracking of single particles when aiming to asses materials properties of the medium under investigation.
I. Introduction
Quantifying diffusive motion is a versatile and often indispensable tool for determining the (heterogeneous) materials properties of complex fluids, from artificial systems such as liquid crystals, colloidal suspensions, and (semi)dilute polymer solutions to fluids in living cells, e.g., the cytoplasm and nucleoplasm. In the most basic scenario, evaluating the Brownian motion of spherical tracer particles with radius R in an isotropic fluid at thermal equilibrium yields a diffusion constant D, from which the local viscosity η can be retrieved via the Stokes–Einstein relation D = kBT/(6πηR).1 Recent all-atom molecular dynamics simulations demonstrate that a time-local analog of the Stokes–Einstein relation even exists for simple proteins with fluctuating shapes in water.2Considering more complex samples, e.g. viscoelastic fluids, the diffusive transport often features anomalous characteristics in the sense that the mean-squared displacement (MSD) of tracer particles does not increase linearly in time but frequently shows a sublinear power-law scaling 〈r2(τ)〉 ∝ Kτα with α < 1, a phenomenon called “subdiffusion”.3 Several stochastic processes can yield subdiffusive motion, with some processes even showing signatures of weak ergodicity breaking (see ref. 4 for review). For conciseness we will restrict ourselves here to processes with stationary increment statistics that can be linked directly to materials properties at thermal equilibrium. The generalized diffusion coefficient K has units of area per fractional time and only becomes identical to the familiar diffusion constant D for α = 1 (“normal diffusion”). The sublinear MSD scaling and the unconventional units of K reflect the multi-scale nature of the fluid's materials properties that go beyond a simple constant viscosity. In such cases, the complex shear modulus G(ω) = G′(ω) + iG′′(ω) is an informative and more extensive measure that reports on the fluid's elastic (G′) and viscous (G′′) response when shearing it at frequency ω.5
At thermal equilibrium, the MSD of tracer particles may actually be used to determine the complex shear modulus G(ω) via a Laplace transformation and an analytical continuation.6 It is worth noting, however, that this approach tacitly assumes that the particles’ random motion is indeed governed by the fluid's viscoelasticity, hence causing a non-trivial MSD due to the viscoelastic material property. Supposedly the best known stochastic model for describing diffusion in viscoelastic environments is fractional Brownian motion (FBM) in its subdiffusive form.7 FBM is a non-Markovian Gaussian stochastic process with an anti-persisent memory that is set by a single parameter, the Hurst coefficient H (0 < H < 1/2 for subdiffusion). The Hurst coefficient determines the MSD scaling exponent as α = 2H. Translating this MSD into the complex shear modulus yields the non-trivial scaling |G(ω)| ∝ G′(ω) ∝ G′′(ω) ∝ ωα reporting on the viscous and elastic material properties.
However, experimentally acquired trajectories of tracers in a yet uncharacterized fluid may show a sublinear MSD scaling that is not related to viscoelasticity at all, hence jeopardizing a meaningful interpretation in terms of the MSD-derived complex shear modulus. This may already occur for Brownian diffusion, when the (“static”) noise from inaccuracies in determining the particle position effect an apparent subdiffusion at shorter times.8,9 Another prime example is “obstructed diffusion” (OD), when particles move in a fractal maze of (immobile) obstacles: randomly placing immobile obstacles with a density near or at the percolation threshold is known to result in a long-lasting or even asymptotically long subdiffusion of tracers as they can only explore a fractal subset of space.10,11 Although this scenario creates a stationary and subdiffusive random motion, the system contains no viscoelastic medium at all. Therefore, calculating G(ω) from the MSD would erroneously suggest that the particles moved in a viscoelastic fluid, albeit this was not the physical nature of the observed random motion. This situation becomes even more critical in cases when a macroscopic rheological assessment, i.e., an alternative means to assess G(ω), cannot be used to complement the diffusion measurements—as the two approaches probe different length scales. An example is the motion of tracers in a fully polymerized hydrogel that features a typical mesh size, that is similar to the diameter of the tracer particle. While here the tracer may report a sublinear scaling of the MSD due to OD, macroscopic rheology will only report a rubber-like elasticity without any viscosity. It is therefore expedient to extract all necessary information from the diffusion measurement itself when determining the materials properties of a complex fluid—yet without falling into the trap of misinterpreting the data by focusing solely on the MSD.
Here we demonstrate that this may a priori be somewhat delicate, even when dealing with spatiotemporally homogenous systems. Namely, we show that FBM and OD display very similar features in surprisingly many experimentally accessible observables, e.g., a sublinear MSD and a distinct anti-persistent autocovariance function, hence impeding a simple discrimination of the two scenarios. We find, however, that a detailed analysis of an ensemble of trajectories can be used to identify FBM, hence supporting a proper interpretation of an MSD-derived complex shear modulus via single-particle tracking experiments. In contrast, ensemble-based measurement techniques that do not yield individual trajectories basically only exploit the MSD and are hence inadequate for distinguishing scenarios that have very similar properties like FBM and OD. We emphasize this aspect by considering techniques that rely on fluctuating particle numbers in a fixed observation volume. From our data we advocate single-particle tracking as the method of choice if one wishes to arrive at a meaningful interpretation when translating MSDs to complex shear moduli.
II. Methods
To simulate OD random walks, we used two-dimensional random mazes on a square lattice with an obstacle density of ϕ = 40%, close to the percolation threshold of obstacle percolation.11 Specifically, we randomly chose 40% inaccessible sites on a 400 × 400 square lattice with periodic boundary conditions in which ten tracers were allowed to move according to the blind ant algorithm (i.e., 100% probability for nearest-neighbor-hopping attempt, acceptance only if new site is not blocked by an obstacle). Tracers were treated as ghosts that do not see each other but only interact with the impenetrable obstacles. Moreover, tracers were checked to not leave the first unit cell of the lattice on average even in the most mobile case, i.e., finite size effects due to the periodic boundaries were negligible. In total, 100 runs of this setting were performed, yielding a total of M = 1000 trajectories. Each run consisted of 5 × 106 sweeps (all particles try to move once per sweep), and positions were stored every 100th step, i.e., the trajectory length was fixed to N = 5 × 104.To also consider non-static mazes, the same amount of runs were performed with obstacles moving according to the blind ant algorithm every Qth sweep (Q = 103, 104, 105). For a movement attempt of an obstacle, all other obstacles and the tracers were treated as impenetrable to avoid inconsistencies. For comparison, an ensemble of FBM trajectories with the same statistics and a Hurst coefficient H = 0.35 was obtained as described previously.12 FBM trajectories of length N with a scrambled memory kernel were obtained by concatenating independent FBM trajectories with only 50 positions, i.e., every 50 time steps the memory is randomized for the next step increment. For the analysis of these ensembles of trajectories, we used our recently introduced toolbox of Matlab routines.12
Time steps and lattice constants for OD were adjusted to reach experimentally reasonable values. To this end, the time interval between successive positions in the analyzed trajectories was set to Δt = 125 ms and the lattice constant was set in such a way that tracers had a diffusion constant D = 2 μm2 s−1 in the absence of obstacles. Step increments for FBM trajectories were assigned the same time increment and step increments were chosen in such a way that the MSDs of OD and FBM overlapped. Since only stationary stochastic processes are considered, time- and ensemble-averaged quantities were not distinguished but rather ensemble-averages of time-averaged quantities (indicated by 〈·〉t,E) are reported for improved statistics.
III. Results and discussion
Starting from the fact that FBM (with an appropriately chosen Hurst coefficient) and OD in a fractal percolation cluster have the same sublinear scaling of the MSD, we wanted to test by means of simulations in which (experimentally accessible) observables a clear discrimination between the two random motions is possible. For technical simplicity, we restricted our simulations to tracer motion in two dimensions when simulating FBM trajectories and OD tracer motion in random mazes with an obstacle density close to the percolation threshold (see Methods for details).A. Mean-squared displacement
In agreement with the literature on diffusion in static fractal percolation clusters,10,13 we observed a subdiffusive MSD 〈r2(τ)〉t,E ∝ τα with α ≈ 0.7 (Fig. 1) for OD in a maze of immobile obstacles. The same sublinear MSD scaling is obtained for FBM with a Hurst coefficient H = 0.35.7 Hence, if only an experimentally determined MSD is at hand, one cannot decide which of the two processes is underlying the data. | ||
| Fig. 1 MSD of tracers in a static maze (open black circles) shows the anticipated sublinear scaling 〈r2(τ)〉t,E ∝ τα with α = 0.711,13 (indicated by the dash-dotted blue line). Small deviations from the power law are attributed to finite-size effects. As expected, FBM trajectories with Hurst coefficient H = 0.35 also follow this MSD scaling (data not shown for better visibility). When allowing obstacles to move every Qth step (Q = 103: red squares; Q = 104, 105: dark-red and grey lines) a crossover to normal diffusion 〈r2(τ)〉t,E ∝ τ (dashed black line) is observed beyond a crossover time scale tc ∝ Q. Simulating FBM trajectories with Hurst coefficient H = 0.35 and scrambling the memory kernel every 50 time steps (see Methods) results in a highly similar MSD as seen for OD of tracers in a mobile maze with Q = 103 (cf. light-blue line behind the red squares). | ||
Upon mobilizing obstacles, i.e., when updating obstacle positions every Qth step, the subdiffusive scaling of the emerging OD was seen to become transient (Fig. 1): beyond a crossover time tc ∝ Q the trivial scaling of normal diffusion (α = 1) was seen to emerge, in line with previous results.14 On time scales below tc the tracers therefore experienced an effectively immobile maze of obstacles, akin to a static percolation cluster, while on significantly longer time scales the tracers and obstacles were equally mobile, hence yielding the limit of a hard-sphere gas with normal diffusion.
Such a transient subdiffusion can also be obtained when using FBM trajectories with H = 0.35 but intermittently resetting or scrambling the memory kernel (cf. Methods). An example for the resulting transient subdiffusion, being highly similar to OD with Q = 103, is shown in Fig. 1. Therefore, OD and FBM also show highly similar MSDs when being forced to have only a transient subdiffusion characteristics. We note that a similar crossover to normal diffusion can be observed for “tempered FBM”, in which the power-law correlations of the noise include exponential or steeper power-law cut-offs.15
B. Autocovariance function
Given that FBM is a non-Markovian stochastic process by definition, we next probed potential differences of FBM and OD in the (normalized) autocovariance function (ACVF), also known as velocity autocorrelation function, | (1) |
Here, the instantaneous velocity is defined via the spatial increment taken within a time interval δt, v(t) = (r(t + δt) − r(t))/δt, and the lag time τ is rescaled as ξ = τ/δt. As a result, we observed that the ACVF of OD in a static maze shows a pronounced anti-persistent dip at ξ = 1, irrespective of the choice of δt (Fig. 2a). In fact, this signature of an anti-persistent memory matches a previous report.16 More surprising, however, is the fact that the analytical FBM expression for the ACVF,
 | (2) |
 | ||
| Fig. 2 (a) The ACVF for OD in a static maze, as a function of the rescaled lag time ξ = τ/δt, shows a pronounced anti-correlation (negative) dip and follows the same master curve for δt = 3, 5, 7Δt (open black squares, diamonds, circles). The data is, somewhat surprisingly, in very close agreement with the prediction eqn (2) for FBM with H = α/2 = 0.35 (blue dash-dotted line). This suggests that OD in a static maze features a very similar scale-invariant anti-persistent memory as FBM. For OD in a mobile maze (Q = 103, red symbols; shifted upward for better visibility) the FBM prediction still yields a very good description albeit small deviations for ξ > 1 become visible. FBM trajectories with Hurst coefficient H = 0.35 and a scrambled memory kernel follow the OD data for Q = 103 (light-blue triangles). Therefore, the ACVF cannot be used to properly discriminate FBM and OD as both have highly similar properties. (b) For OD in a static maze (open black circles, δt = 7Δt) the asymptotic power-law decay of the ACVF for ξ > 1 also follows the FBM prediction |C(ξ)| ∝ ξα−2 (blue dash-dotted line). For OD in a mobile maze, successively larger deviations are seen (Q = 103: red squares; Q = 104, 105: dark-red, grey lines). FBM trajectories with a scrambled memory kernel show similarly strong deviations (light-blue triangles) from the power law. | ||
ACVFs for OD in a mobilized maze still agree mostly with the analytical FBM expression, but significant deviations become visible for ξ > 1 (see Fig. 2a). The same holds true for FBM trajectories with a scrambled memory kernel. Therefore, the ACVF cannot be used to clearly discriminate OD and FBM, albeit one may have expected this. In Fig. 2b, the correlation decay from the pronounced minimum at ξ = 1 towards zero is highlighted by the double-logarithmic axes. For FBM, |C(ξ)| ∝ ξα−2 is expected. Again, OD in a static maze follows this power law with a remarkable accuracy, whereas OD with mobile obstacles yields deviations that increase with increasing obstacle mobility. Similar deviations from the power-law are also seen for FBM trajectories with a scrambled memory kernel, i.e., losses in the memory kernel for OD and FBM have similar effects on the ACVF in both cases.
The remarkably good agreement of eqn (2) with data for OD in a static maze suggests that the ACVF possesses generic features that are the same for all random motions with stationary increment statistics. Indeed, it was already hypothesized earlier16 that the ACVF decay |C(ξ)| ∝ ξα−2 for ξ > 1 is always observed for (anti-persistent) random motions that feature an MSD scaling 〈r2(τ)〉t,E ∝ τα. An heuristic support of the hypothesis that the ACVF is just the second derivative of the MSD is given in Appendix A for a one-dimensional unbiased random walk process with stationary increments, such as OD or FBM, supplementing a previously discussed integral-based argument.15
C. Power spectral density
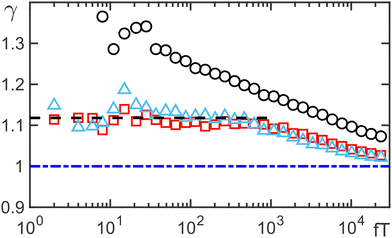
Going beyond the time domain, one might wonder whether the coefficient of variation for the trajectories’ power spectral density (PSD) can be used to discriminate FBM from OD. The time- and ensemble-averaged PSD is known to follow the scaling S(f) ∼ 1/fα+1 for subdiffusive processes with stationary increment statistics.17 For FBM, the PSD of individual trajectories also follows this scaling.17 Fluctuations of single-trajectory PSDs around the ensemble-average are summarized by the coefficient of variation γ, the ratio of the standard deviation and the mean (see also ref. 12). While subdiffusive FBM has been shown to robustly yield γ = 1 for virtually all frequencies f, normal diffusion generically yields .17,18 Using the coefficient of variation, OD in a static maze can indeed be identified via its slow monotonic convergence to γ = 1 for increasing frequencies (Fig. 3). However, OD in mobilized mazes assumes a behavior that is basically indistinguishable from FBM with a scrambled memory kernel: for large frequencies (corresponding to short times), γ → 1 is seen for OD in a maze of mobile obstacles, whereas for small frequencies (long times) a transient plateau with
.17,18 Using the coefficient of variation, OD in a static maze can indeed be identified via its slow monotonic convergence to γ = 1 for increasing frequencies (Fig. 3). However, OD in mobilized mazes assumes a behavior that is basically indistinguishable from FBM with a scrambled memory kernel: for large frequencies (corresponding to short times), γ → 1 is seen for OD in a maze of mobile obstacles, whereas for small frequencies (long times) a transient plateau with  (the normal diffusion case) is observed. This is analogous to the change of the MSD scaling when translating the cross-over time to a frequency fc = 1/tc. Thus, for experimental purposes, also the coefficient of variation of the PSD is not suitable for a reliable discrimination of OD and FBM.
(the normal diffusion case) is observed. This is analogous to the change of the MSD scaling when translating the cross-over time to a frequency fc = 1/tc. Thus, for experimental purposes, also the coefficient of variation of the PSD is not suitable for a reliable discrimination of OD and FBM.
D. Gaussianity and asphericity
Given that MSDs, ACVFs, and PSDs turn out to be inadequate quantities to discriminate subdiffusion in a viscoelastic medium (FBM) from subdiffusion in a fractal percolation maze (OD), one might wonder if there is any better quantity that is able to distinguish the two random motions. In the following, we will highlight deviations between the two processes in two observables, that are readily accessible in single-particle tracking experiments.By construction, FBM is a Gaussian process whereas OD can be expected to show deviations from a Gaussian increment statistics.10,11 A versatile tool to quantify this aspect is the non-Gaussianity parameter (NGP) of the trajectories,
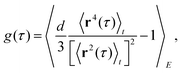 | (3) |
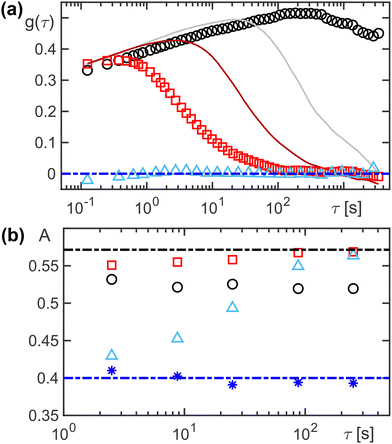 | ||
| Fig. 4 (a) The non-Gaussianity parameter (NGP) for OD in a static maze (black circles) strongly deviates from zero, highlighting that the random walk is not Gaussian on these time scales. For OD with mobile obstacles (Q = 103: red squares, Q = 104, 105 dark-red and grey lines) a successive convergence to g(τ) = 0 is observed for τ > tc ∝ Q, as expected already from the MSD scaling. FBM with a scrambled memory kernel shows a vanishing NGP throughout (light-blue triangles). (b) The asphericity of trajectory segments within a period τ follows the expected AFBM ≈ 0.4 for a pure FBM with Hurst coefficient H = 0.35 (blue dash-dotted line and asterisks) whereas normal Brownian motion features A0 = 4/719 (indicated by black dash-dotted line). For OD (static: open black circles; mobile, Q = 103: red squares) the asphericity remains close to A0, allowing one to discriminate OD from FBM. For FBM with a scrambled memory kernel (light-blue triangles) an interpolation from AFBM to A0 for increasing trajectory length is observed, reflecting the crossover to a Markovian random walk for τ ≫ tc. Concluding, OD and FBM can be discriminated by the values of A. | ||
We finally wondered whether the geometric shape of the acquired trajectories also can provide a robust means to distinguish FBM and OD, hence allowing for a meaningful interpretation of the apparent materials properties of the medium. For two-dimensional trajectories, the trajectory asphericity reads19
 | (4) |
In line with this reasoning, we observed that OD in a static maze but also in the case of mobile obstacles, yielded trajectory asphericities that remained close to A0 = 4/7 (Fig. 3c). In contrast, a pure FBM with Hurst coefficient H = 0.35 yielded A ≈ 0.4. For FBM with a scrambled memory kernel, an interpolation between this value and A0 is observed for increasing length of the trajectory segments (Fig. 4b), reflecting the crossover to a normal, Markovian random motion for τ ≫ tc. In any case, OD and FBM can be discriminated via the asphericity of trajectories in a similarly robust fashion as seen for the NGP (cf.Fig. 4a). Both quantities are readily accessible with single-particle tracking methods. As will be shown in the next paragraph, ensemble-based techniques, that rely on monitoring the fluctuating number of particles in an observation volume, are not suited for revealing these subtle differences.
E. Ensemble-based experimental approaches
There exist several ensemble-based techniques to assess the diffusive motion of tracers in a yet to be characterized medium. Techniques such as fluorescence recovery after photobleaching (FRAP)21 only record the mean number of observable particles in a specified observation volume (region of interest, ROI), i.e., they monitor the relaxation of an observable back to its steady state after a perturbation. In FRAP experiments, this is done by quantifying the recovery of the mean fluorescence in a ROI after having bleached tracer particles in this region. More refined techniques do not require this invasive interaction with the sample but rely on monitoring fluctuating particle numbers in a ROI, an approach that was already utilized by Smoluchowski in his seminal work on diffusing colloids.22 Monitoring particle number fluctuations instead of recording individual trajectories is, for example, a versatile approach when particles are too dense to be tracked properly or trajectories are too short to allow for a meaningful analysis along the lines described above.Supposedly the most prominent and widespread technical implementation to exploit particle number fluctuations in a ROI is fluorescence correlation spectroscopy (FCS).23 Here, stationary fluctuations about a constant fluorescence, F(t) = 〈F〉 + f(t), are monitored with high temporal resolution, allowing to extract the typical residence time τD in the focus (i.e., in the ROI). The fluorescence autocorrelation function is then obtained via spatial averaging and reads (without normalization to the mean fluorescence)
 | (5) |
 . In modern FCS approaches, particle counting is typically performed via the fluorescence signal from a confocal volume, approximating the relevant ROI I(r) as a Gaussian point-spread function. As a result, the fluorescence autocorrelation then decays algebraically with a typical time scale τD, given by the effective area of the ROI divided by the diffusion constant.23 Subdiffusion updates the exponent of the algebraic decay.24–26
. In modern FCS approaches, particle counting is typically performed via the fluorescence signal from a confocal volume, approximating the relevant ROI I(r) as a Gaussian point-spread function. As a result, the fluorescence autocorrelation then decays algebraically with a typical time scale τD, given by the effective area of the ROI divided by the diffusion constant.23 Subdiffusion updates the exponent of the algebraic decay.24–26
In the case that particles can be simply counted without the need to rely on their fluorescence signature, one can replace the ROI I(r) by a step function in every dimension, yielding
| C(τ) = 〈N(t + τ)N(t)〉t. | (6) |
Since this is the only relevant autocorrelation function of the system, also the temporal variation of fluctuations of the squared particle number change is determined by this expression,
| 〈ΔN(τ)2〉t = 〈{N(τ) − N(t)}2〉t = 2〈N2〉t − 2C(τ). | (7) |
The latter quantity has recently been re-invented as “countoscope” and was used for the analysis of diffusive processes in dense colloidal systems.27 For normal Brownian diffusion with diffusion constant D in d dimensions and a cubic box of edge length L, the analytical prediction is
| 〈ΔN2(τ)〉 = 2〈N〉(1 − f(τ)d) | (8) |
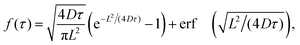 | (9) |
Given the structure of the formula and bearing in mind Smoluchowski's comments that the temporal evolution of 〈ΔN(τ)2〉 is linked to the MSD, one may replace 4Dτ by 2〈r2(τ)〉/d in d dimensions, i.e., counting particles and inspecting the autocorrelator of the fluctuations is completely determined by the MSD. This is confirmed in Fig. 5, where FBM and OD data together with the MSD-determined theoretical curve is shown. Due to their very high similarity in their MSDs, FBM and OD cannot be discriminated—hence a proper assessment whether the medium has indeed a viscoelastic property remains obscure in such setups.
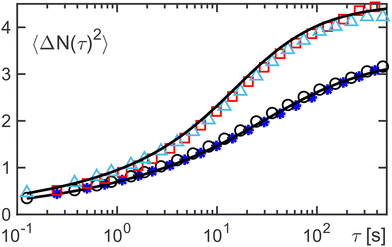 | ||
| Fig. 5 The squared particle number fluctuations 〈ΔN(τ)2〉t for an OD in a static maze (black circles) and for a pure FBM with H = 0.35 (blue asterisks) fully overlap. The same is seen for OD in a maze of mobile obstacles (Q = 103: red squares) and FBM with a scrambled memory kernel (light-blue triangles). In both cases, the MSD-derived theoretical curve [eqn (8)] fits the data (black line). Hence, FBM and OD cannot be discriminated. | ||
IV. Conclusions
In summary, we conclude that monitoring fluctuations of particle numbers will only report on the MSD and hence will not allow one to retrieve the underlying stochastic process, even when dealing with spatiotemporally homogenous systems. Without this knowledge, however, the transfer from MSD to the complex shear modulus is prone to misinterpretations as, for example, OD is not associated with a viscoelastic medium (unlike FBM). In fact, the situation can become even more complicated: when the medium that is explored by the tracer cannot be approximated any more as a homogenous fluid (at thermal equilibrium) no meaningful shear modulus can be defined and extracted from the tracer motion. This is the case, for example, when (intermittent) interactions with filamentous or membraneous structures, non-equilibrium events, and/or spatio-temporal inhomogeneities determine a tracer's trajectory (see ref. 28–35 for a non-exhaustive list of examples and modeling approaches for such cases). Even identifying that the tracer diffusion reports on such a complex scenario is not possible via MSD-based techniques but rather will require the analysis of several observables that are based on trajectory data (see ref. 12 for a short hands-on compendium). We therefore recommend the use of single-particle tracking to allow for a detailed analysis of the tracer motion to eventually arrive at a meaningful interpretation of the materials properties of the medium under investigation. In particular, we have demonstrated here that the Gaussianity and the asphericity of trajectories are promising candidates to properly distinguish viscoelastic from disordered, static environments.Another central result in our study is the remarkable similarity between the ACVF of subdiffusive FBM and that of OD, in particular, the dip to negative (anti-persistent) values. If highly resolved data are available, there is the possibility to evaluate the area under the ACVF. For subdiffusive FBM, this should vanish identically to zero.15 We also note that the ACVF shape, observed here for OD and subdiffusive FBM, also strongly resembles the ACVF of confined subdiffusive continuous time random walks,36 in which subdiffusion is effected by a scale-free probability density function (PDF) of immobilization times with an asymptotic power-law form ψ(τ) ≃ τ−1−α with 0 < α < 1.3 Future studies may also benefit greatly from the statistics of mean-squared increments.37
Our work was aimed at the evaluation of easily accessible observables. This may be complemented by other, more sophisticated data analysis, such as Bayesian methods38,39 or also deep learning-based approaches.40–44 However, these are often not off-the-shelf solutions but rather require detailed knowledge on issues such as data pre-processing. Moreover, many of the available software suites do not contain all relevant stochastic processes, i.e. detailed tests like the one executed here on OD and FBM may require the implementation of such processes.
We finally note that the development of FBM-type processes is still ongoing, even though FBM is by now more than 50 years old. First, there exist different definitions, including Mandelbrot's version in terms of a Weyl fractional integral,7 Lévy's definition via a Riemann–Liouville integral with initial non-stationarity,7,45 and the Langevin equation formulation with fractional Gaussian noise.7,15 While all three lead to the same behavior at longer times, these different definitions give rise to distinct behavior when the parameters are chosen to vary, e.g., for a diffusing diffusivity.46 In that case it can be shown that the associated PDF is also non-Gaussian for times below a typical correlation time. These phenomena will be analyzed in detail in the context of the present work in near future.
Conflicts of interest
There are no conflicts to declare.Data availability
The submitted manuscript is based on simulation data. Data analyses and trajectory calculation for fractional Brownian motion were done with a previously published toolbox of Matlab codes, see Rehfeldt & Weiss, Soft Matter 19, 5206 (2023) and the associated GitHub repository https://github.com/mweisslab/sptanalysis. Fortran90 codes that were used to obtain data for obstructed diffusion are also included and available in this GitHub repository as of April 10, 2025.Appendix A
To obtain a heuristic argument, why an MSD scaling 〈r2(τ)〉t,E ∝ τα may generically yield a ACVF decay |C(ξ)| ∝ ξα−2 for ξ > 1, let us consider a one-dimensional unbiased random walk process with stationary increments and a time-averaged MSD with a power-law scaling| 〈x2(τ)〉t = 〈[x(t + τ) − x(t)]2〉t = 2〈[x(t)]2〉t − 2〈x(t + τ)x(t)〉t ∝ τα |
Mathematical random walk processes like the Wiener process are non-differentiable at every point, yet physical trajectories are continuous on (very) small time scales on which inertial effects and the impact of surrounding particles need to be treated with Newtonian mechanics. Only for sufficiently large time scales a simplified approximate description via an overdamped Langevin equation with uncorrelated noise becomes meaningful, yielding a non-differentiable random walk trajectory. We will therefore assume in the following that there is a small time interval Δτ for which the continuous Newtonian motion of the particle is still differentiable, so that derivatives can be approximated in a meaningful way by difference quotients. The second order derivative of the MSD hence reads
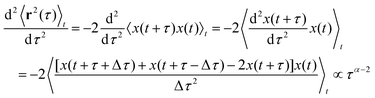 | (A1) |
Using the definition of the ACVF [eqn (1)] and abbreviating its (constant) normalization factor as v02, one can relate C(τ) to 〈r2(τ)〉t:
Despite the lack of full mathematical rigor, this heuristic argument suggests a general validity of the power-law decay observed in the ACVF, irrespective of being a FBM. However, it does not provide any hint on the range ξ ≤ 1 and hence also cannot claim anything on the integral area below the ACVF curve, i.e. these might depend considerably on the random walk process. But at least for the static percolation problem, all FBM features of the ACVF appear to be met.
Acknowledgements
MW gratefully acknowledges financial support by the VolkswagenStiftung (Az. 92738). RM acknowledges funding from the German Research Foundation (DFG, grant ME 1513/22-1).References
- A. Einstein, Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen, Ann. Phys., 1905, 322, 549–560 CrossRef.
- E. Yamamoto, T. Akimoto, A. Mitsutake and R. Metzler, Universal Relation between Instantaneous Diffusivity and Radius of Gyration of Proteins in Aqueous Solution, Phys. Rev. Lett., 2021, 126, 128101 CrossRef CAS PubMed.
- R. Metzler and J. Klafter, The random walk's guide to anomalous diffusion: A fractional dynamics approach, Phys. Rep., 2000, 339, 1–77 CrossRef CAS.
- R. Metzler, J.-H. Jeon, A. G. Cherstvy and E. Barkai, Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking, Phys. Chem. Chem. Phys., 2014, 16, 24128–24164 RSC.
- S. Scott, M. Weiss, C. Selhuber-Unkel, Y. F. Barooji, A. Sabri and J. T. Erler, et al., Extracting, quantifying, and comparing dynamical and biomechanical properties of living matter through single particle tracking, Phys. Chem. Chem. Phys., 2023, 25, 1513–1537 RSC.
- T. G. Mason and D. A. Weitz, Optical Measurements of Frequency-Dependent Linear Viscoelastic Moduli of Complex Fluids, Phys. Rev. Lett., 1995, 74, 1250–1253 CrossRef CAS PubMed.
- B. B. Mandelbrot and J. W. V. Ness, Fractional Brownian Motions, Fractional Noises and Applications, SIAM Rev., 1968, 10, 422–437 CrossRef.
- P. G. Meyer and R. Metzler, Stochastic processes in a confining harmonic potential in the presence of static and dynamic measurement noise, New J. Phys., 2023, 25, 063003 CrossRef.
- M. B. Martin, D. S. Forstner and J. A. Käs, Apparent subdiffusion inherent to single particle tracking, Biophys J., 2002, 83, 2109 CrossRef PubMed.
- S. Havlin and D. Ben-Avraham, Diffusion in disordered media, Adv. Phys., 1987, 36, 695–798 CrossRef CAS.
- Y. Mardoukhi, J.-H. Jeon and R. Metzler, Geometry controlled anomalous diffusion in random fractal geometries: looking beyond the infinite cluster, Phys. Chem. Chem. Phys., 2015, 17, 30134–30147 RSC.
- F. Rehfeldt and M. Weiss, The random walker's toolbox for analyzing single-particle tracking data, Soft Matter, 2023, 19, 5206 RSC.
- J. P. Bouchaud and A. Georges, Anomalous diffusion in disordered media: Statistical mechanisms, models and physical applications, Phys. Rep., 1990, 195(4–5), 127–293 CrossRef.
- N. Malchus and M. Weiss, Anomalous Diffusion Reports on the Interaction of Misfolded Proteins with the Quality Control Machinery in the Endoplasmic Reticulum, Biophys J., 2010, 99, 1321–1328 CrossRef CAS PubMed.
- D. Molina-Garcia, T. Sandev, H. Safdari, G. Pagnini, A. Chechkin and R. Metzler, Crossover from anomalous to normal diffusion: truncated power-law noise correlations and applications to dynamics in lipid bilayers, New J. Phys., 2018, 20, 103027 CrossRef.
- D. Jacobs and H. Nakanishi, Autocorrelation functions for discrete random walks on disordered lattice, Phys. Rev. A, 1990, 41, 706–719 CrossRef CAS PubMed.
- D. Krapf, N. Lukat, E. Marinari, R. Metzler, G. Oshanin and C. Selhuber-Unkel, et al., Spectral Content of a Single Non-Brownian Trajectory, Phys. Rev. X, 2019, 9, 011019 CAS.
- V. Sposini, D. Krapf, E. Marinari, R. Sunyer, F. Ritort and F. Taheri, et al., Towards a robust criterion of anomalous diffusion, Commun. Phys., 2022, 5, 305 CrossRef.
- J. Rudnick and G. Gaspari, The shapes of random walks, Science, 1987, 237, 384–389 CrossRef CAS PubMed.
- D. Ernst, M. Hellmann, J. Köhler and M. Weiss, Fractional Brownian Motion in Crowded Fluids, Soft Matter, 2012, 8, 4886–4889 RSC.
- M. Wachsmuth, Molecular diffusion and binding analyzed with FRAP, Protoplasma, 2014, 251, 373 CrossRef PubMed.
- M. von Smoluchowski, Studien über Kolloidstatistik und den Mechanismus der Diffusion, Kolloid-Z., 1916, 18, 48–54 CrossRef CAS.
- R. Rigler, Fluorescence Correlation Spectroscopy, Springer Verlag, Berlin, 2001 Search PubMed.
- M. Weiss, H. Hashimoto and T. Nilsson, Anomalous protein diffusion in living cells as seen by fluorescence correlation spectroscopy, Biophys J., 2003, 84, 4043–4052 CrossRef CAS PubMed.
- M. Weiss, M. Elsner, F. Kartberg and T. Nilsson, Anomalous subdiffusion is a measure for cytoplasmic crowding in living cells, Biophys. J., 2004, 87, 3518–3524 CrossRef CAS PubMed.
- J. Szymanski and M. Weiss, Elucidating the Origin of Anomalous Diffusion in Crowded Fluids, Phys. Rev. Lett., 2009, 103, 038102 CrossRef PubMed.
- E. K. R. Mackay, S. Marbach, B. Sprinkle and A. L. Thorneywork, The Countoscope: Measuring Self and Collective Dynamics without Trajectories, Phys. Rev. X, 2024, 14, 041016 CAS.
- N. Samanta and R. Chakrabarti, Tracer diffusion in a sea of polymers with binding zones: mobile vs. frozen traps, Soft Matter, 2016, 12, 8554–8563 RSC.
- L. Stadler and M. Weiss, Non-equilibrium forces drive the anomalous diffusion of telomeres in the nucleus of mammalian cells, New J. Phys., 2017, 19, 113048 CrossRef.
- K. Speckner, L. Stadler and M. Weiss, Anomalous dynamics of the endoplasmic reticulum network, Phys. Rev. E, 2018, 98, 012406 CrossRef CAS PubMed.
- P. Kumar, L. Theeyancheri, S. Chaki and R. Chakrabarti, Transport of probe particles in a polymer network: effects of probe size, network rigidity and probe–polymer interaction, Soft Matter, 2019, 15, 8992–9002 RSC.
- A. Sabri, X. Xu, D. Krapf and M. Weiss, Elucidating the Origin of Heterogeneous Anomalous Diffusion in the Cytoplasm of Mammalian Cells, Phys. Rev. Lett., 2020, 125, 058101 CrossRef CAS PubMed.
- M. V. Chubynsky and G. W. Slater, Diffusing Diffusivity: A Model for Anomalous, yet Brownian, Diffusion, Phys. Rev. Lett., 2014, 113, 098302 CrossRef PubMed.
- A. V. Chechkin, F. Seno, R. Metzler and I. M. Sokolov, Brownian yet Non-Gaussian Diffusion: From Superstatistics to Subordination of Diffusing Diffusivities, Phys. Rev. X, 2017, 7, 021002 Search PubMed.
- S. Milster, F. Koch, C. Widder, T. Schilling and J. Dzubiella, Tracer dynamics in polymer networks: Generalized Langevin description, J. Chem. Phys., 2024, 160, 094901 CrossRef CAS PubMed.
- S. Burov, R. Metzler and E. Barkai, Aging and nonergodicity beyond the Khinchin theorem, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 13228–13233 CrossRef CAS PubMed.
- Q. Wei, W. Wang, Y. Tang, R. Metzler and A. Chechkin, Fractional Langevin equation far from equilibrium: Riemann–Liouville fractional Brownian motion, spurious nonergodicity, and aging, Phys. Rev. E, 2025, 111, 014128 CrossRef CAS PubMed.
- A. Robson, K. Burrage and M. C. Leake, Inferring diffusion in single live cells at the single-molecule level, Philos. Trans. R. Soc. London, Ser. B, 2013, 368, 20120029 CrossRef PubMed.
- S. Thapa, M. A. Lomholt, J. Krog, A. G. Cherstvy and R. Metzler, Bayesian analysis of single-particle tracking data using the nested-sampling algorithm: maximum-likelihood model selection applied to stochastic-diffusivity data, Phys. Chem. Chem. Phys., 2018, 20, 29018–29037 RSC.
- G. Munoz-Gil, M. A. Garcia-March, C. Manzo, J. D. Martín-Guerrero and M. Lewenstein, Single trajectory characterization via machine learning, New J. Phys., 2020, 22, 013010 CrossRef.
- G. Munoz-Gil, G. Volpe and M. A. Garcia-March, et al., Objective comparison of methods to decode anomalous diffusion, Nat. Commun., 2021, 12, 6253 CrossRef CAS PubMed.
- P. Kowalek, H. Loch-Olszewska and J. Szwabiński, Classification of diffusion modes in single-particle tracking data: Feature-based versus deep-learning approach, Phys. Rev. E, 2019, 100, 032410 CrossRef CAS PubMed.
- H. Seckler and R. Metzler, Bayesian deep learning for error estimation in the analysis of anomalous diffusion, Nat. Commun., 2022, 13, 6717 CrossRef CAS PubMed.
- H. Seckler, J. Szwabiński and R. Metzler, Machine-learning solutions for the analysis of single-particle diffusion trajectories, J. Phys. Chem. Lett., 2023, 14, 7910 CrossRef CAS PubMed.
- P. Lévy, Random functions: general theory with special reference to Laplacian random functions, University of California Press, Berkeley, 1953 Search PubMed.
- W. Wei, A. V. Chechkin and R. Metzler, Different behaviors of diffusing diffusivity dynamics based on three different definitions of fractional Brownian motion, arXiv, 2025, preprint, arXiv:2504.19190 DOI:10.48550/arXiv.2504.19190.
| This journal is © the Owner Societies 2025 |