Predicting intersystem crossing rate constants of alkoxy-radical pairs with structure-based descriptors and machine learning

Abstract

Peroxy radicals (RO₂) are ubiquitous intermediates in many oxidation processes, especially in the atmospheric gas phase. The recombination reaction of two peroxy radicals (RO₂ + R′O₂) has been demonstrated to lead, via several steps, to a triplet complex of two alkoxy radicals: ³(RO˙⋯R′O˙). The different product channels of RO₂ + R′O₂ reactions thus correspond to different reactions of this triplet complex. Of particular interest to atmospheric chemistry is the intersystem crossing (ISC) to the singlet state, which enables the recombination of the two radicals to an ROOR′ peroxide with considerably lower volatility than the original precursors. These peroxides are believed to be key contributors to the formation of secondary organic aerosol (SOA) particles, which in turn contribute to both air pollution and radiative forcing uncertainties. Developing reliable computational models for, e.g., RO₂ + R′O₂ branching ratios requires accurate estimates of the ISC rate constants, which can currently be obtained only from computationally expensive quantum chemistry calculations. By contrast, machine learning (ML) methods offer a faster alternative for estimating ISC rate constants. In the present work, we create a dataset with 98 082 conformations of radical pairs and their corresponding rate constants. We apply three ML models—random forest (RF), CatBoost (CB), and a neural network (NN)—to predict ISC rate constants from triplet to singlet states. Specifically, the models predict k_ISC(T₁ → S_i) for i = 1–4 and the cumulative k_ISC(T₁ → S_n), in alkoxy radical pairs, using only molecular geometry descriptors as inputs. All ML models achieved a mean absolute error (MAE) on our test set within one order of magnitude and a coefficient of determination R² > 0.82 for all rate constants. Overall, the ML prediction matches the quantum chemical calculations within 1–2 orders of magnitude, providing a fast and scalable alternative for quantum chemical methods for ISC rate estimation.

---

1. Introduction

Atmospheric oxidation of volatile organic compounds, emitted from both biogenic and antropogenic sources, plays an important role in climate change and air pollution. As the dominant atmospheric oxidant, O₂, is a triplet biradical, oxidation proceeds through a cascade of radical intermediates. One of the main classes of radicals in atmospheric chemistry are organic peroxy radicals (RO₂), which are formed whenever carbon-centered radicals (R) created in the initial oxidation steps react with O₂. Due to their relative stability, RO₂ can accumulate to high concentrations compared to other radical classes. The atmospheric chemistry of RO₂ is extremely versatile, as they can react via multiple uni- and bimolecular channels. The branching between different RO₂ reaction channels is one of the central parameters in atmospheric chemistry.¹ For example, bimolecular reactions of RO₂ with nitrogen monoxide (NO) leading to radical propagation are the key driver of tropospheric ozone formation and photochemical smog, while both unimolecular RO₂ H-shifts, RO₂ + HO₂ reactions and possibly also RO₂ + alkene reactions^2,3 often lead to lower-volatility products forming secondary organic aerosol.

Recently, RO₂ reactions with other RO₂ have been identified as sources of very efficiently aerosol-forming accretion products: compounds with more carbon atoms than in the original reactant.⁴ Computational investigations of RO₂ + R′O₂ reactions have revealed that the mechanism for accretion product formation involves an intersystem crossing (ISC; spin–flip).^5–17 While ISCs and other surface hoppings between electronic states are known to play important roles in many fields of chemistry and physics, their involvement in thermal (non-photochemical) atmospheric gas-phase reactions was somewhat surprising. Specifically, RO₂ + R′O₂ reactions inevitably lead to a metastable tetroxide (RO₄R′) intermediate,^5–13 which then decomposes into two alkoxy radicals (RO and R′O) and molecular oxygen (O₂).^9–17 For the reaction to be thermodynamically feasible, the O₂ must be formed in its triplet ground state. Spin conservation then dictates that the alkoxy radical pairs are also coupled as a triplet. For all but the smallest (R=R′=CH₃) system,⁹ the RO⋯R′O interaction is stronger than the RO⋯O₂ interaction, indicating that the O₂ molecule will likely be ejected from the reaction system, leaving a ³(RO⋯R′O) complex, where the upper index 3 indicates the multiplicity. The reaction routes of this complex correspond to different product channels of the overall RO₂ + R′O₂ reaction. For example, dissociation leads to the radical propagating (RO + R′O) channel, a hydrogen shift (H-shift) between the two moieties leads to the molecular (alcohol + carbonyl) channel, while an ISC to the singlet state permits subsequent recombination, leading to peroxide (ROOR′) accretion products. We note that ISCs do not guarantee the formation of a peroxide, as both H-shifts and dissociation are possible also in the singlet state. Furthermore, sufficiently complex (functionalized) alkoxy radicals can undergo a variety of unimolecular reactions within the ³(RO⋯R′O) cluster, potentially leading to an even larger array of possible products.^5,13,14 These reactions can also be either preceded or followed by an ISC. Overall, predictions of branching ratios of RO₂ + R′O₂ reactions, and thus their contribution to, for example, SOA formation, are currently limited by the available methods for estimating ISC rates.

In general, the ISC rate constant (k_ISC) between two electronic states (denoted here S_i and T_f) depends on two parameters: (1) the spin–orbital coupled interaction matrix elements (SOCME) between the states (〈ψ(S_i)|Ĥ_SO|ψ(T_f)〉); (2) the Franck–Condon (FC) factor or overlap between the nuclear wavefunctions of the states.^18–21 The FC factor also depends on the energy gap between the states, which becomes especially important in cases where the final state is higher in energy than the initial state. Both SOCME and the FC factor may depend on the relative orientation of the radical pair. As ³(RO⋯R′O) complexes relevant to atmospheric chemistry are held together by non-covalent interactions that are individually relatively weak, thermal motion will allow them to explore a large variety of orientations. Thus, k_ISC needs to be computed as an ensemble average over all molecular conformations and relative orientations of the radical pair.

A simplified model of ISC rates can be obtained for radical pairs that are characterized by a small energy gap between the S₁ and T₁ states,^18–24 resulting in a dependence primarily on SOCME rather than FC factors. Moreover, in these pairs, each spin is localized on a single atom, making SOCME sensitive to the distance and angular alignment between p-type atomic orbitals (AOs) on these atoms.^6,18–24 This effect was first explained in the pioneering work of Salem and Rowland.²³ Subsequent studies have further investigated SOCME's dependence on structural factors, proposing analytical solutions for simplified cases with the fitting parameters.^2,18–24 However, a comprehensive universal analytical solution that can be applied to radical pairs with any kind of substituents remains elusive.

Quantum chemical calculations have a broad applicability and offer more accurate estimates of ISC rate constants within 1–2 orders of magnitude.⁶ For example, the k_ISC was calculated from the T₁ state to the S₁ state for the first time for minimum-energy geometries of several alkoxy radical pairs by Valiev et al.⁶ The computed rate displays strong variation depending on the structures and the relative orientation of the two radicals. Also, it was shown that the formation of ROOR′ is determined by the total (overall) ISC process, which is more complicated than just the ISC between S₁ and T₁ states, because there are four low-energy singlet excited states with strong SOCME. Thus, the total k_ISC is the sum of k_ISC (T₁ → S₁), k_ISC (T₁ → S₂), k_ISC (T₁ → S₃) and k_ISC (T₁ → S₄) as seen in Fig. 1. Note that after the transition into S₂, S₃, and S₄ states, the internal conversion (IC) process occurs at a high rate, and the final state of the process is still S₁.⁶ Thus, the transition from T₁ to S₁ can take place either in one step (ISC directly to the S₁ state) or through two steps (involving an ISC to an intermediate state – S₂, S₃, or S₄ – followed by IC to S₁). However, obtaining these ISC rate constants is computationally expensive, and not feasible for the vast number of systems of interest to atmospheric chemistry.¹⁰

Fig. 1 The ISC (blue lines) between the T₁ and S₁–S₄ electronic states for ³(CH₃O⋯CH₃O). The overall intersystem crossing rate includes transitions between the triplet (T₁) and four lowest lying singlet states. The IC processes are shown in red arrows.

Here, we explore, if and how machine learning (ML)^24–26 can be used as a tool to accelerate ISC rate constant estimations and to gain chemical insight into the relationship between the radical pair geometry and ISC formation rate. In particular, we apply ML to relate the structural aspects of alkoxy radical pair conformations, to the ISC rate constants for the alkoxy radical clusters.

2. Theory and computational details

2.1. Geometry generation and the ISC rate constant calculations

We consider radical clusters consisting of the following alkoxy radicals: CH₃O˙(MeO), CH₃CH₂O˙(OEt), CH₃(CO)CH₂O˙(OAce) and HOCH₂CH(O˙)CH₂CH₃(HOBuO). The resulting ten cluster types are denoted as ³(MeO)₂, ³(OAce)₂, ³(OEt)₂, ³(HOBuO)₂, ³(MeO⋯OAce), ³(MeO⋯OEt), ³(MeO⋯HOBuO), ³(OAce⋯OEt), ³(OAce⋯HOBuO), ³(OEt⋯HOBuO). We set up 50 000 conformations for each cluster and optimize them. Generation and geometrical optimization of clusters was performed using the semi-empirical GNF-xTB level of theory²⁷ in the ABCluster program.^28,29 All structural optimizations were performed with the system in only the triplet state, and not the singlet. We filtered our final set of cluster conformation ensembles to remove duplicates based if the radius of gyration (R_g) and electronic energy (E) criteria less than 0.01 Å and 0.001 Hartree respectively.⁶ These criteria are used to distinguish between unique structures and remove duplicates.⁶ After removing duplicates, our dataset consists of 98 082 radical pair cluster conformations.

We focus on computing and predicting k_ISC(T₁ → S_i), where i = 1–4, and the total cumulative k_ISC. All five rate constants associated with each radical pair conformation were computed with quantum chemistry. Note that the four singlet and four triplet electronic excited states of RO˙⋯˙OR′ are nearly degenerate (within 10 000 cm⁻¹). In this case, the correct description of energy gaps between them can be obtained using a multireference level of theory accounting for both static and dynamic electronic correlations.^6,30 Therefore, we applied the extended quasi-degenerate 2nd-order multireference perturbation theory (XMC-QDPT2).³⁰ These calculations were carried out using the Firefly software.³¹ Like in our previous work,⁶ we chose an active space consisting of 6 electrons in 4 p-type MOs, for the complete active space self-consistent field (CASSCF) with the stage average over four singlet and four triplet electronic states. The included orbitals are shown in Fig. 2 for a ³(MeO)₂ cluster. The electronic states T₁–T₄ and S₁–S₄ are formed exclusively by electron transitions between the 2p orbitals localized on the oxygen atoms, where the electron spin is also localized. This electronic configuration can be understood within the framework of the topicity of radicals theory proposed by Minaev.¹⁶ For example, the CH₃O radical and other alkoxy radicals are classified as bitopic radicals, featuring two radical centers (2p_x and 2p_y) with an energy splitting of 0.40 eV.^22,32 Consequently, they generate four pairs of singlet and triplet states with similar energy in radical pairs.

Fig. 2 Orbitals corresponding to the active space used for k_ISC rate calculation in state-averaged CASSCF (6,4)/6-311++G(d,p) MOs for a ³(MeO)₂ cluster.

The SOCME between S₁–S₄ and T₁–T₄ were calculated using the CASSCF method, but with the XMC-QDPT2/6-311++G(d,p) energies as the zero-order energies within perturbation theory. GAMESS-US³³ was used for the CASSCF calculations.

The ISC rate constant calculation from T₁ to the S₁, S₂, S₃, and S₄ electronic states was conducted using the method described in ref. 6 and 34. More details can be found in ref. 6, but here we give a short description. The main expression is

k_ISC = 1.6 × 10⁹〈i|Ĥ_SO|f〉²FC, (1)

where 〈i|Ĥ_SO|f〉 (in cm⁻¹) is the matrix element of the spin–orbital coupling interaction operator Ĥ_SO between the initial and final electronic states i and f (SOCME).⁶ The 1.6 × 10⁹ pre-factor has dimension s⁻¹ cm⁻². FC is the Franck–Condon factor calculated according to exp(−y)·yⁿ/n!, where y = 0.3 and n = E_if/1400. Here E_if in cm⁻¹ is the energy gap between the electronic states. This expression (1) is valid for compounds with different kinds of substituents.^34–37 We note that since in this study, the ground state of the studied clusters is a triplet, the process considered here is in principle a thermally activated ISC, as it occurs from the T₁ ground state to S₁ (or to higher singlet states). In this case, the intersystem crossing rate constant (k′_ISC) is calculated using the formula:⁶where k is the Boltzmann constant and E_if is energy gap between the electronic states.

2.2. Dataset

The complete dataset of 98 082 clusters consists of ten different cluster types in the following proportions: 7297 (7.96%) structures for ³(MeO)₂, 7812 (7.96%) for ³(MeO⋯OAce), 8428 (8.59%) for ³(MeO⋯OEt), 14 281 (14.56%) for ³(MeO⋯HOBuO), 6230 (6.35%) for ³(OAce)₂, 8313 (8.48%) for ³(OAce⋯OEt), 14 945 (15.24%) for ³(OAce⋯HOBuO), 5805 (5.92%) for ³(OEt)₂, 12 457 (12.70%) for ³(OEt⋯HOBuO), 12 514 (12.76%) for ³(HOBuO)₂.

We compared the relative size of the four k_ISC(T₁ → S_i) to identify those with largest impact on the overall k_ISC. which we from here on refer to as k_ISC(T₁ → S_n). The number of structures in the full dataset where the T₁ → S₁ process dominates over other ISC processes is 10 049 (10.25%); for T₁ → S₂, it is 85 163 (86.83%); for T₁ → S₃, it is 2866 (2.92%); and for T₁ → S₄, only 3 structures (0.00%). Thus, the rate constant for the T₁ → S_n process is primarily determined by the T₁ → S₁ and T₁ → S₂ transitions.

The rate constant log histograms for T₁ → S₁, T₁ → S₂ and T₁ → S_n transitions are shown in Fig. 3. We observe that the distribution of the T₁ → S_n rate constant order repeats the distribution of the T₁ → S₂ rate constant order. This observation is expected since the number of structures where the T₁ → S₂ process dominates over other ISC processes is larger than T₁ → S₁. We note that there is a slight difference between the shapes of the two distributions near zero values. This is because structures where k_ISC(T₁ → S₂) is zero may have a nonzero k_ISC(T₁ → S₁), and as a result, the cumulative rate constant is mostly nonzero, as seen in the graph (Panel c).

Fig. 3 Histograms of the logarithm of the calculated rate constant (in units of s⁻¹) for T₁ → S₁ (a), T₁ → S₂ (b) and T₁ → S_n (c) transitions.

2.3. Molecular descriptors

In our ML models, we represent the radical clusters using molecular descriptors.^38–44 For this study, we focus specifically on structural descriptors rather than molecular properties or electronic structure to link cluster geometries with rate constants. While predictions based on electronic descriptors are expected to be more accurate, predictions based on structural descriptors do not require additional quantum-chemical calculations and are faster and more computationally cost-effective. Moreover, they directly correlate the molecular structure with the ISC rate constant as seen in Scheme 1.

Scheme 1 The dependence of SOCME values and energy gaps on the angle between C–O˙ bonds of CH₃O⋯CH₃O, at two different distance between the radical O˙ atoms. (a) and (b) illustrate the dependence of SOCME values on the angle at distances of 3.0 Å and 4.5 Å between O˙ atoms, respectively. (c) and (d) illustrate the dependence of the energy gaps on the angle at distances of 3.0 Å and 4.5 Å, respectively.

As shown in Scheme 1, even for the simplest radical pair without large substituents (CH₃O˙⋯CH₃O˙), there is a clear yet quite complex dependence of electronic properties (SOCME and the singlet–triplet energy gap) on the C–O˙⋯C–O˙ angle, with the angular dependence also varying with the O˙⋯O˙ distance. This demonstrates that the electronic parameters governing kISC are sensitive to key structural features of the radical pairs, hence k_ISC depends on those same geometric parameters. Altogether, this again confirms the existence of a nontrivial relationship between k_ISC and structural displacements, that cannot be reduced to simple functions like sine, cosine, or exponential functions, as suggested in some prior works.^2,18–24 At the same time, this dependence guarantees that machine-learning methods can be applied effectively, provided that a sufficiently large and diverse dataset is available.

We trained and tested our models using two types of structural descriptors. The first is a custom descriptor we developed, which combines selected angles and distances within atoms in a cluster. We selected atoms with the localization of MOs responsible for T₁ → S₁, T₁ → S₂, T₁ → S₃ and T₁ → S₄. The second descriptor is the many body tensor representation (MBTR), computed using DScribe v.2.1.0.^38,39 MBTR is a large structural descriptor that captures three-dimensional structures comprehensively. Compared to our custom descriptor, MBTR is computationally intensive and less interpretable. Here, we include MBTR to benchmark the performance of our custom descriptor. Below, we provide further details on the construction of both our custom descriptor and MBTR.

Our optimal custom descriptor consists of 53 structural features, which were constructed considering the atoms denoted in Fig. 4 for one radical pair. The following atoms were selected: spin-carrying oxygen atoms Ou1 and Ou2, the carbon atoms connected to them (C1 and C2), the atoms connected to C1 and C2 – carbon A1, A2, B1, B2, and hydrogens H1 and H2, as well as oxygens Op1 and Op2 without spins and the hydrogens attached to them (H12 and H22). The resulting selected features include 31 distances, 12 angles, 3 torsional angles, 4 minimum atomic distances between radical pair atoms, and 2 hydrogen bond counts. The first hydrogen bond count only includes the hydrogen bonds formed with Ou1 and Ou2, while the second hydrogen bond count represents the total number of hydrogen bonds in the cluster. Certain geometric features were not applicable to all clusters due to missing atom types. In those cases, the missing features were then assigned −1.

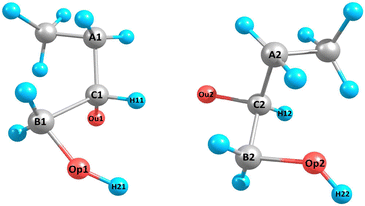Fig. 4 Enumeration of atoms used to create custom geometric features. Here is one example configuration of ³(HOBuO)₂. The molecular descriptors are also given in Tables 4 and 5.

Our second descriptor, MBTR, encodes the geometric properties of molecular structures through a continuous representation of pairwise and angular relationships between all atoms of a molecule at different many-body levels. For level 1, atomic species are represented by Gaussians corresponding to atomic numbers along a designated axis. In level 2, inverse distances between atom pairs are represented by Gaussians along a distance axis, reflecting the geometric structure of the atomic system. Level 3 encodes angular information by Gaussians on an axis corresponding to the cosine of angles between atom triples. To reduce memory requirements, all numerical values in the MBTR computations were converted to float 32 data types.

In this study, we employed only the level 2 and level 3 MBTR kernels to create a concatenated descriptor. For level 2, we used inverse distances within an interval of [0, 1.5] (unit Å⁻¹), while for level 3, we represented interatomic angles by their cosine values over an interval of [−1, 1]. No additional weighting was applied to either kernel. We optimized two MBTR hyperparameters with random search: the smoothing parameter (σ), which affects Gaussian localization, and the number of discretization points (n), which determines resolution. σ was sampled uniformly between 0.005 and 0.015, and n between 40 and 100, for both kernels independently.

2.4. Machine learning techniques

Our goal in this study is to test how accurate ML models can become relative to quantum chemistry models. Such models are known to be within one order of magnitude of true experimental values. Here we focus on predicting quantum chemistry estimates, as obtaining experimental values at large scale is unfeasible (and direct experiments on ISC rates for the specific case of alkoxy–alkoxy cluster are so far impossible). In addition, we are able to explore conformer specific relationships between molecular structure and rate constants which is not possible with experimental values representing the ensemble average. To this end, we tested three different regression models: random forest (RF), CatBoost (CB), and a feed-forward neural network (NN). The last two models, CB and NN, were used only for training on our custom descriptors. We did not test MBTR with the other models due to the computational expense required for model training with MBTR. The three models are based on different philosophies: the RF is easily interpretable, CB offers high accuracy and handles categorical features efficiently, and the NN is more complex but can capture intricate data patterns. To train the models, the dataset was randomly split 80 : 20 into training and testing sets, using five different random states, which are defined in the code provided in the ESI.†

For model performance evaluation, we used a set of metrics including RMSE, the coefficient of determination (R²) and the mean absolute error (MAE). Model performance was evaluated by averaging across five runs and calculating the standard deviations of all performance metrics. All computed average metrics for each model and each predicted feature are provided in the Tables S1–S6 (ESI†). The predicted vs. actual plots presented in the article are based on the identical train-test splits with the random seed number is 339 087.

For each train/test split corresponding to a specific random seed and for each model using the custom descriptor set, hyperparameter optimization was performed using grid search cross-validation on the training set with 3 folds, repeated 3 times. Instead of selecting the hyperparameters that yielded the best metrics, one of the configurations with a MAE differing by no more than 0.01 from the best-performing set was chosen for further analysis. This approach ensures greater model robustness and prevents overfitting to a specific dataset split while maintaining nearly optimal performance, which is particularly important for future applications of the model to molecules that were not included in the training dataset. The hyperparameters that produced the best metrics, as well as those with performance close to the best, along with the corresponding metrics for the selected configuration, are presented in Tables S1–S3 (ESI†) for the RF, NN and CB models, respectively. In contrast, for the MBTR-based model, hyperparameter optimization was conducted using randomized search combined with k-fold cross-validation using 3 folds, sampling 10 parameter configurations with the negative mean squared error as the loss function. The corresponding code is provided in the ESI.†

The first model is a RF regressor from scikit-learn version 1.2.0.⁴⁵ We used RF with both MBTR and our custom descriptor to evaluate the relative performance of the custom descriptor. For the custom descriptor, hyperparameter optimization of the RF model was performed for the number of estimators, tested at 1000, 1250, and 1500, and tree depth, tested at 10, 20, and 30. The optimal values were 1250 estimators and a tree depth of 30. The dependence of the evaluation metrics on hyperparameters is presented in Table S1 (ESI†). For MBTR the RF hyperparameters—number of estimators (50 or 130) and maximum tree depth (10 or 20)—were optimized using random search (MBTR) combined with k-fold cross-validation. The optimal parameters, a tree depth of 20 and 130 estimators, were determined through this process. During model training with MBTR, the random search sampled 10 parameter configurations within the specified intervals, using negative mean squared error (−MSE) as the loss function.

The second model is a NN constructed using Keras.⁴⁶ The network architecture and hyperparameters were optimized for one to four hidden layers, each containing 50, 100, 150, or 200 neurons, with ReLU activation functions and MSE loss function. The output neuron uses a linear activation function to predict the target variable. The batch size was varied between 16 and 32, the number of epochs was either 50 or 100 and learning rate was 0.001, 0.01 and 0.1. The final selection of hyperparameters is two hidden layers each containing 200 neurons with batch size 32, epochs 100 and learning rate 0.001. The hyperparameter optimization results for NN are summarized in Table S2 (ESI†).

The third model is CB regressor,⁴⁷ which is designed for GPU training, enabling faster results. The optimal hyperparameters for CB were found within the following values: the number of trees 1000, 1250 and 1500, the learning rate from 0.05 to 0.25, and the tree depth from 8 to 10. The final optimized values were 1250 trees, a learning rate of 0.1, and a tree depth of 9. The hyperparameter optimization results for CB are summarized in Table S3 (ESI†).

Also, CB was chosen for feature selection as it provided the best performance metrics among the tested models. Feature selection in combination with the CB model was performed using the recursive feature elimination (RFE)⁴⁸ algorithm implemented in the scikit-learn library⁴⁵ for each of considered ISC rate constants. This method was applied exclusively to the custom descriptor set. The RFE process was conducted within a 3-fold cross-validation repeated 3 times, ensuring robust feature ranking. Instead of a single RFE run, feature rankings were obtained across all cross-validation folds, and the final ranking score for each descriptor was determined by averaging the rankings from all iterations.

Following feature ranking, an iterative descriptor evaluation was performed to determine the optimal subset of descriptors to predict any of the considered ISC rate constants. The descriptors were ranked based on their RFE scores, and models were trained sequentially with an increasing number of descriptors, starting from the highest-ranked feature. Performance was assessed with cross-validation performed using 3-fold repeated 3 times. The final optimal descriptor set was obtained by eliminating descriptors that were not informative across all considered ISC rate constants, ensuring a more generalizable and efficient feature representation. The final descriptor rankings are listed in Tables S4–S8 (ESI†) for prediction of T₁ → S_n, T₁ → S₁, T₁ → S₂, T₁ → S₃, T₁ → S₄ correspondingly. The corresponding implementation details and code are provided in the ESI.†

3. Results and discussion

In this section, we present the performance of our trained models for predicting the rate constants k_ISC(T₁ → S₁), k_ISC(T₁ → S₂), k_ISC(T₁ → S₃) k_ISC(T₁ → S₄) and total k_ISC(T₁ → S_n). First, we focus on k_ISC(T₁ → S₁) and k_ISC(T₁ → S₂), which have the largest overall impact on k_ISC(T₁ → S_n) (see Methods).

3.1. Comparison of RF, NN and CB models

Fig. 5 shows results for our RF, NN, and CB models for k_ISC(T₁ → S₁), k_ISC(T₁ → S₂) and k_ISC(T₁ → S_n). The plots for k_ISC(T₁ → S₃) and k_ISC(T₁ → S₄) are shown in Fig. S1 (ESI†). The averaged metrics are provided in the legends of Fig. 5 and Fig. S1 (ESI†) and more detailed in Tables 1–3.

Fig. 5 Ab initio versus predicted k_ISC(T₁ → S_n), k_ISC(T₁ → S₁), and k_ISC(T₁→ S₂) rate constants, denoted as n, 1, and 2, respectively. The predicted values, obtained using random forest, CatBoost, and neural network models, are labeled as a, b, and c, respectively. The solid black line represents y = x, while the dashed line corresponds to the linear regression fit. The legend displays the mean and standard deviation of R², RMSE, and MAE metrics across five runs with different random seeds. The plots are based on the identical train-test splits. The random seed is 339 087.

Table 1 Root mean squared error (RMSE), coefficient of determination (R²), mean absolute error (MAE), and the MAE for each of the 10 considered dimers, comparing ab initio and predicted orders of the ISC rate constants (T₁ → S₁, T₁ → S₂, T₁ → S₃, T₁ → S₄, T₁ → S_n) using Random Forest regressor. The metrics were obtained using the optimal set of custom descriptors

	T1 → S1	T1 → S2	T1 → S3	T1 → S4	T1 → Sn
MSE	0.99 ± 0.010	0.47 ± 0.015	0.80 ± 0.017	1.46 ± 0.023	0.38 ± 0.009
RMSE	0.99 ± 0.005	0.69 ± 0.011	0.89 ± 0.010	1.21 ± 0.010	0.62 ± 0.007
MAE	0.76 ± 0.004	0.46 ± 0.004	0.58 ± 0.005	0.84 ± 0.007	0.42 ± 0.004
R ^2	0.89 ± 0.002	0.83 ± 0.007	0.91 ± 0.002	0.77 ± 0.003	0.83 ± 0.006

---

Table 2 Root mean squared error (RMSE), coefficient of determination (R²), mean absolute error (MAE), and the MAE for each of the 10 considered dimers, comparing ab initio and predicted orders of the ISC rate constants (T₁ → S₁, T₁ → S₂, T₁ → S₃, T₁ → S₄, T₁ → S_n) using CatBoost regressor. The metrics were obtained using the optimal set of custom descriptors

	T1 → S1	T1 → S2	T1 → S3	T1 → S4	T1 → Sn
MSE	0.89 ± 0.008	0.38 ± 0.010	0.63 ± 0.009	1.04 ± 0.010	0.31 ± 0.005
RMSE	0.95 ± 0.004	0.62 ± 0.008	0.79 ± 0.006	1.02 ± 0.005	0.56 ± 0.004
MAE	0.72 ± 0.003	0.42 ± 0.003	0.54 ± 0.003	0.73 ± 0.003	0.38 ± 0.002
R ^2	0.90 ± 0.001	0.87 ± 0.005	0.93 ± 0.002	0.84 ± 0.001	0.86 ± 0.004

---

Table 3 Root mean squared error (RMSE), coefficient of determination (R²), mean absolute error (MAE), and the MAE for each of the 10 considered dimers, comparing ab initio and predicted orders of the ISC rate constants (T₁ → S₁, T₁ → S₂, T₁ → S₃, T₁ → S₄, T₁ → S_n) using feed forward neural network

	T1 → S1	T1 → S2	T1 → S3	T1 → S4	T1 → Sn
MSE	1.11 ± 0.013	0.52 ± 0.018	0.91 ± 0.019	1.52 ± 0.028	0.42 ± 0.005
RMSE	1.05 ± 0.006	0.72 ± 0.013	0.96 ± 0.010	1.23 ± 0.011	0.65 ± 0.004
MAE	0.80 ± 0.002	0.49 ± 0.007	0.65 ± 0.014	0.87 ± 0.008	0.45 ± 0.003
R ^2	0.88 ± 0.002	0.82 ± 0.009	0.90 ± 0.002	0.76 ± 0.003	0.81 ± 0.004

---

The RF model has R² values of 0.89 and 0.82 for k_ISC(T₁ → S₁) and total k_ISC(T₁ → S_n), respectively. The best results are obtained with CB, where the mean MAE across the different runs is 0.90 and 0.86 for k_ISC(T₁ → S₁) and total k_ISC(T₁ → S_n). Also, CB predicts some zero values correctly, unlike RF. This result can be explained by the fact that CB belongs to the family of gradient boosting models. Such models can better adapt to sparse data due to their flexibility and the ability to fine-tune their loss functions. We note that the NN model is also accurate (mean R² = 0.81–0.88) for rate constant predictions, although it is slightly less accurate than CB (mean R² = 0.86–0.90).

In this study, we assess the error of our ML models based on their ability to predict quantum chemistry-derived rate constants. This level of accuracy is comparable to that typically observed in quantum chemical calculations when compared to experimental data.^49,50 The degree of precision is generally sufficient for predicting chemical reaction yields or photophysical processes,⁴⁹ at least in cases where the rates of competing processes are substantially different.

We now consider the ISC from T₁ to S₂, S₃, and S₄. In Fig. 5, Tables 1–3, the best predictions for k_ISC(T₁ → S₂), k_ISC(T₁ → S₃), and k_ISC(T₁ → S₄) are achieved with CB, where the mean R² is 0.87, 0.93 and 0.84, respectively. The prediction of zero values for all rate constants is particularly problematic, as it contributes to the large mean errors in overall predictive accuracy. Additionally, the endothermic nature of the electronic transitions from T₁ to S₂, S₃, and S₄ makes their rate constants highly sensitive to temperature and the energy gap, in contrast to k_ISC(T₁ → S₁).

3.2. The RF based on MBTR descriptors

We next evaluated the performance of our custom molecular descriptor set. To do this, we have used the established MBTR descriptor with RF to predict k_ISC(T₁ → S₁) and total k_ISC(T₁ → S_n). The result is shown in Fig. 6. The R² values for the RF model trained with MBTR are 0.82 and 0.73 for k_ISC(T₁ → S₁) and total k_ISC(T₁ → S_n), respectively. The MAE values are 0.97 and 0.53, indicating that the average prediction errors for k_ISC(T₁ → S₁) and total k_ISC(T₁ → S_n) are within one order of magnitude. As with our custom descriptor, large deviations are observed in regions where either k_ISC(T₁ → S₁) or k_ISC(T₁ → S_n) are zero or close to zero. The results obtained with MBTR (R² = 0.73–0.86) are slightly worse than the simulated result gained by RF based on our custom descriptors (R² = 0.86–0.90). Thus, the MBTR result gives almost similar results as in the case of our custom molecular descriptors. We can conclude our custom molecular descriptor set is comprehensive enough to match MBTR results.

Fig. 6 Ab initio versus predicted values of the k_ISC(S₁ → T₁) (a) and k_ISC(T₁ → S_n) (b) obtained with RF model and MBTR descriptors in one run. The black solid line is y = x, and the dashed line is the linear regression. Legend presents the mean and standard deviation of R², RMSE, and MAE averaged over five runs with different random seeds.

3.3. Feature selection

The feature-selected molecular descriptors used with the CB models are summarized in Tables 4 and 5. R² indicates the accuracy of the rate constant prediction as the number of molecular descriptors increases. For example, using only the C1–C2 descriptor for the k_ISC(T₁ → S₁) constant gives R² = 0.66, while using it together with the min_dist increases R² to 0.755.

Table 4 Custom feature-selected descriptors in descending order of importance for predicting the order of k_ISC(T₁ → S₁), k_ISC(T₁ → S₂), k_ISC(T₁ → S₄), k_ISC(T₁ → S₄) rate constants obtained with CatBoost model, and R² values obtained by using the best ranked descriptors

k ISC(T1 → S1)		k ISC(T1 → S2)		k ISC(T1 → S3)		k ISC(T1 → S4)
Parameter	R ^2	Parameter	R ^2	Parameter	R ^2	Parameter	R ^2
C1–C2	0.663	∠(B1,C1,Ou1)	0.008	∠(A1,C1,Ou1)	0.240	B1–C1	0.134
min_dist	0.755	∠(B2,C2,Ou2)	0.031	∠(B2,C2,Ou2)	0.459	∠(B2,C2,Ou2)	0.289
Ou1–Ou2	0.802	∠(A1,C1,Ou1)	0.066	∠(A2,C2,Ou2)	0.608	∠(A2,C2,Ou2)	0.394
min(C–C)	0.817	∠(A1,C1,B1)	0.077	∠(B1,C1,Ou1)	0.667	B2–C2	0.470
C1–Ou2	0.838	∠(A2,C2,B2)	0.086	C2–Ou2	0.725	min_dist	0.533
C2–Ou1	0.846	C2–Ou2	0.091	∠(Ou1,C1,H11)	0.768	∠(B1,C1,Ou1)	0.577
B1–Ou2	0.855	Ou1–Op1	0.103	C1–Ou1	0.818	∠(A1,C1,Ou1)	0.635
B2–Ou1	0.861	∠(A2,C2,H12)	0.127	∠(A2,C2,H12)	0.831	∠(A1,C1,B1)	0.667
		C1–Ou1	0.142	min_dist	0.850	∠(Ou1,C1,H11)	0.683
		∠(Ou2,C2,H12)	0.397	min(O–O)	0.881	Ou1–Ou2	0.719
		∠(Ou1,C1,H11)	0.500			min(O–O)	0.729
		∠(A1,C1,H11)	0.559			∠(Ou2,C2,H12)	0.744
		min(O–O)	0.663			min(H–H)	0.759
		∠(A2,C2,Ou2)	0.692			C1–C2	0.772
		A2–C2	0.690			Ou1–Op1	0.803
		min_dist	0.711			Ou2–Op2	0.812
		A1–C1	0.711
		Ou2–Op2	0.712

---

Table 5 Custom feature-selected descriptors in descending order of importance for predicting the order of k_ISC(T₁ → S_n) rate constants obtained with CatBoost model

k ISC(T1 → Sn)
Parameter	R ^2
∠(A1,C1,Ou1)	0.132
∠(B2,C2,Ou2)	0.402
∠(B1,C1,Ou1)	0.526
C1–Ou1	0.583
B1–C1	0.628
∠(A2,C2,Ou2)	0.693
C2–Ou2	0.715
∠(A1,C1,B1)	0.743
∠(A2,C2,B2)	0.764
Ou1–H21	0.787
∠(B1,C1,H11)	0.795
∠(B2,C2,H12)	0.803
B2–C2	0.808

---

As shown in Table 4, the primary descriptors with a strong correlation for k_ISC(T₁ → S₁) are the internuclear distances between atoms associated with different radicals. Overall, the most significant general correlated parameter is the internuclear distance between radicals. Interestingly, the angles between C–O˙ bonds with spins do not play an important role here. At the same time, achieving R² = 0.861 requires only 8 descriptors. In contrast, for k_ISC(T₁ → S₂), achieving R² = 0.7112 requires 18 descriptors, most of which are intramolecular distances within one radical. Similarly, for k_ISC(T₁ → S₃) and k_ISC(T₁ → S₄), intramolecular distances serve as key molecular descriptors. For k_ISC(T₁ → S_n), the main descriptors are almost the same as for k_ISC(T₁ → S₂), with the addition of the distance between the radicals.

4. Summary and conclusion

The machine learning (ML) investigation of intersystem crossing (ISC) rate constants of alkoxy radical pairs was conducted using different methods such as CatBoost (CB), random forest (RF), and neural networks (NN), with two different molecular descriptors. The best results were obtained using CB, with R² coefficients exceeding 0.85 and MAE values within one order of magnitude for all rate constants. The absolute maximum error can reach up to 2 orders of magnitude for rate constants at their higher values. The worst results are obtained for the smallest values. with errors of about 4 orders of magnitude. This level of accuracy is typically sufficient for estimating the quantum yield of photophysical processes or chemical reactions.⁴²

Previous studies have shown that k_ISC(T₁ → S₁) mainly depends on the distance between radicals and is only slightly influenced by angles.²⁴ Our ML results confirm this observation. However, the overall ISC rate k_ISC(T₁ → S_n) is actually dominated by k_ISC(T₁ → S₂), which depends on the relative orientation of the two radicals in a more complex manner. Furthermore, the rate constants k_ISC(T₁ → S₂), k_ISC(T₁ → S₃), and k_ISC(T₁ → S₄) correspond to non-spontaneous (reverse) ISCs, i.e., the final state is higher in energy than the initial state. It is worth noting that calculating reverse ISC rate constants is challenging even for quantum chemical methods,⁴⁹ as they strongly depend on the energy gap via the Boltzmann factor. The typical accuracy of quantum chemical calculations for energy gaps, around 0.1–0.3 eV, is often insufficient for rate constant calculations within one order of magnitude, resulting in deviations of 2–3 orders of magnitude.^49,50 Therefore, the ML models give results comparable to quantum chemical calculations but much faster. Although we investigated and confirmed this relationship for alkoxy radical pairs, given the fundamental nature of this dependence, it should also hold for any radical pairs – with the caveat that specific descriptors may be needed to describe ISCs to higher singlet states (e.g. S₂⋯S₄).

Although our ML models do not provide a comprehensive analytical relationship between the ISC rate constant and molecular structure, they can be used to identify important structural features for rate constant prediction and thus improve our understanding of the ISC process. The ML model can also serve as a rapid estimation tool for k_ISC, without the need for quantum chemical calculations, with its generalizability constrained only by the scope of its training data.

While the present model achieving average order-of-magnitude accuracy will already be extremely useful for atmospheric modelling purposes, we anticipate that ongoing ML method development, for example within the SPAINN⁵¹ framework where molecular dynamics is used for data generation, will allow even greater predictive accuracy.

Conflicts of interest

There are no conflicts to declare.

Data availability

Quantum chemical software utilized: (1) generation and geometrical optimization of clusters was performed using ABCluster program [https://www.zhjun-sci.com/index.html], (2) the excitation energies, and matrix elements of spin–orbital coupled interaction operators were computed using FIREFLY [https://classic.chem.msu.su/gran/gamess/index.html] and GAMESS-US [https://www.msg.chem.iastate.edu/gamess/index.html], respectively. All expressions of intersystem crossing rate constants are reported in the main text of the article, with detailed calculations procedures described. All parameters of machine learning methods are reported in the main text of article and are given in the ESI.† The dataset is uploaded to https://zenodo.org/records/15345806.

Acknowledgements

We thank the Research Council of Finland (decision 364226, 346369) and the Jane and Aatos Erkko Foundation (JAES) for funding, and the CSC IT Center for Science in Espoo, Finland, for computing time.

References

1. H. S. Kenagy, C. L. Heald, N. Tahsini, M. B. Goss and J. H. Kroll, Sci. Adv., 2024, 10, eado1482,  DOI:10.1126/sciadv.ado1482.
2. D. Pasik, B. N. Frandsen, M. Meder, S. Iyer, T. Kurtén and N. Myllys, J. Am. Chem. Soc., 2024, 146, 13427–13437,  DOI:10.1021/jacs.4c01972.
3. B. Dong, H. Ding, H. Zhang, H. Zhao, H. Xu, Z. Xu, J. Wang, Y. Li and X. Shi, Atmos. Environ., 2024, 334, 120718,  DOI:10.1016/j.atmosenv.2024.120718.
4. T. Berndt, W. Scholz, B. Mentler, L. Fischer, H. Herrmann, M. Kulmala and A. Hansel, Angew. Chem., Int. Ed., 2018, 57, 3820–3824,  DOI:10.1002/anie.201710989.
5. O. Peräkylä, T. Berndt, L. Franzon, G. Hasan, M. Meder, R. R. Valiev, C. D. Daub, J. G. Varelas, F. M. Geiger, R. J. Thomson, M. Rissanen, T. Kurtén and M. Ehn, J. Am. Chem. Soc., 2023, 145, 7780–7790,  DOI:10.1021/jacs.2c10398.
6. R. R. Valiev, G. Hasan, V.-T. Salo, J. Kubečka and T. Kurtén, J. Phys. Chem. A, 2019, 123, 6596–6604,  DOI:10.1021/acs.jpca.9b02559.
7. G. Hasan, R. R. Valiev, V.-T. Salo and T. Kurtén, J. Phys. Chem. A, 2021, 125, 10632–10639,  DOI:10.1021/acs.jpca.1c08969.
8. G. Hasan, V.-T. Salo, R. R. Valiev, J. Kubečka and T. Kurtén, J. Phys. Chem. A, 2020, 124, 8305–8320,  DOI:10.1021/acs.jpca.0c05960.
9. V.-T. Salo, J. Chen, N. Runeberg, H. G. Kjaergaard and T. Kurtén, J. Phys. Chem. A, 2024, 128, 1825–1836.
10. V.-T. Salo, R. Valiev, S. Lehtola and T. Kurtén, J. Phys. Chem. A, 2022, 126, 4046–4056.
11. C. D. Daub, R. Valiev, V.-T. Salo, I. Zakai, R. B. Gerber and T. Kurtén, ACS Earth Space Chem., 2022, 6, 2446–2452.
12. C. D. Daub, I. Zakai, R. Valiev, V.-T. Salo, R. B. Gerber and T. Kurtén, Phys. Chem. Chem. Phys., 2022, 24, 10033–10043.
13. C. D. Daub, R. Skog and T. Kurtén, Environ. Sci.: Atmos., 2024, 4, 732–739; L. Franzon, M. Camredon, R. Valorso, B. Aumont and T. Kurtén, Atmos. Chem. Phys., 2024, 24, 11679–11699.
14. GECKO-A website, available at https://geckoa.lisa.u-pec.fr.
15. V. A. Belyakov, R. F. Vasil'ev and N. M. Ivanova, Izv. Akad. Nauk SSSR, Ser. Fiz., 1987, 51, 540–547.
16. B. F. Minaev, Russ. Chem. Rev., 2007, 76, 1059–1082,  DOI:10.1070/RC2007v076n11ABEH003732.
17. B. F. Minaev and H. Ågren, EPA Newsletter, 1999, 65, 7–38.
18. J. Michl and Z. Havlas, Pure Appl. Chem., 1997, 69, 785–790,  DOI:10.1351/pac199769040785.
19. M. Klessinger and J. Michl, Excited States and Photochemistry of Organic Molecules, VCH, New York, 1995.
20. J. Michl, J. Am. Chem. Soc., 1996, 118, 3568–3579,  DOI:10.1021/ja9538391.
21. A. G. Kutateladze and W. A. McHale, ARKIVOC, 2005, 4, 88–101.
22. B. F. Minaev and S. Lunell, Z. Phys. Chem., 1993, 182, 263–284.
23. L. Salem and C. Rowland, Angew. Chem., Int. Ed. Engl., 1972, 11, 92–111,  DOI:10.1002/anie.197200921.
24. R. R. Valiev, R. T. Nasibullin, S. Juttula and T. Kurtén, New J. Chem., 2024, 48, 18314–18319.
25. A. Stuke, M. Todorović, M. Rupp, C. Kunkel, K. Ghosh, L. Himanen and P. Rinke, J. Chem. Phys., 2019, 150, 204121,  DOI:10.1063/1.5086105.
26. A. Stuke, C. Kunkel, D. Golze, M. Todorović, J. T. Margraf, K. Reuter, P. Rinke and H. Oberhofer, Sci. Data, 2020, 7, 58,  DOI:10.1038/s41597-020-0385-y.
27. S. Grimme, C. Bannwarth and P. Shuskov, J. Chem. Theory Comput., 2017, 13, 1989–2009.
28. J. Zhang and M. Dolg, Phys. Chem. Chem. Phys., 2016, 18, 3003–3010.
29. J. Zhang and M. Dolg, Chem. Phys., 2015, 17, 24173–24181.
30. A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113,  DOI:10.1063/1.3596699.
31. A. A. Granovsky, Firefly version 8.0.0, available at https://classic.chem.msu.su/gran/firefly/index.html.
32. R. R. Valiev and T. Kurtén, R. Soc. Open Sci., 2020, 7, 200521,  DOI:10.1098/rsos.200521.
33. G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina and E. Guidez, J. Chem. Phys., 2020, 152, 154102.
34. R. R. Valiev, V. N. Cherepanov, G. V. Baryshnikov and D. Sundholm, Phys. Chem. Chem. Phys., 2018, 20, 6121–6133.
35. R. R. Valiev, V. N. Cherepanov, V. Y. Artyukhov and D. Sundholm, Phys. Chem. Chem. Phys., 2012, 14, 11508–11517,  10.1039/c2cp40468k.
36. R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, G. V. Baryshnikov, D. Sundholm, H. Ågren, B. F. Minaev and T. Kurtén, Phys. Chem. Chem. Phys., 2020, 22, 22314–22323.
37. R. R. Valiev, R. T. Nasibullin, V. N. Cherepanov, A. Kurtsevich, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2021, 23, 6344–6348,  10.1039/d1cp00257k.
38. L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949,  DOI:10.1016/j.cpc.2019.106949.
39. J. Laakso, L. Himanen, H. Homm, E. V. Morooka, M. O. Jäger, M. Todorović and P. Rinke, J. Chem. Phys., 2023, 158, 234802.
40. M. F. Langer, A. Goeßmann and M. Rupp, npj Comput. Mater., 2022, 8, 41,  DOI:10.1038/s41524-022-00721-x.
41. G. Landrum, RDKit: Open-Source Cheminformatics Software, available at https://www.rdkit.org (accessed 17 March 2025), 2006.
42. J. L. Durant, B. A. Leland, D. R. Henry and J. G. Nourse, J. Chem. Inf. Comput. Sci., 2002, 42, 1273–1280.
43. M. Rupp, A. Tkatchenko, K.-R. Müller and O. A. von Lilienfeld, Phys. Rev. Lett., 2012, 108, 058301,  DOI:10.1103/PhysRevLett.108.058301.
44. H. Huo and M. Rupp, Mach. Learn.: Sci. Technol., 2022, 3, 045017.
45. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, A. Müller, J. Nothman, G. Louppe, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
46. F. Chollet and others, Keras, 2015, available at https://github.com/fchollet/keras.
47. A. V. Dorogush, V. Ershov and A. Gulin, arXiv, 2018, preprint, arXiv:1810.11363 DOI:10.48550/arXiv.1810.11363.
48. I. Guyon, J. Weston, S. Barnhill and V. Vapnik, Mach. Learn., 2002, 46, 389–422,  DOI:10.1023/A:1012487302797.
49. R. R. Valiev, B. S. Merzlikin, R. T. Nasibullin, A. Kurtzevitch, V. N. Cherepanov, R. R. Ramazanov, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2023, 25, 6406–6415,  10.1039/D2CP05275J.
50. N. K. Ibrayev, R. R. Valiev, E. V. Seliverstova, E. P. Menshova, R. T. Nasibullin and D. Sundholm, Phys. Chem. Chem. Phys., 2024, 26, 14624–14636,  10.1039/D4CP01281J.
51. S. Mausenberger, C. Müller, A. Tkatchenko, P. Marquetand, L. González and J. Westermayr, Chem. Sci., 2024, 15, 15880–15890,  10.1039/D4SC03055C.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp01101a

---