Exploring quantum tunneling in heavy atom reactions using a rigorous theoretical approach to the dynamics: formation of NO + O from the N + O₂ atmospheric reaction

Abstract

This theoretical work is centered on the rigorous study of the importance of quantum effects (tunneling and over the barrier reflection (non-classical reflection)) in heavy atom reactions, considering in this case the elementary gas phase reaction N + O₂(v₀ = 0, j₀ = 1) → NO + O, which is relevant, e.g., in the oxidation mechanism of nitrogen (Zeldovich's mechanism) and air cold plasmas. We have examined the quantum and classical reaction probability, cross-section (E_col: 0.200–0.651 eV) and rate constant (T: 200–1000 K) of this reaction. To do this, we have applied the close-coupling time-dependent real wave packet (CC-TDRWP) method and the quasiclassical trajectory (QCT) method. Even though we are considering a heavy–heavy–heavy atom reactive system, quantum effects are playing a notable role in the low energy region. Thus, for the cross-section they are relevant in the 0.334–0.381 eV E_col interval, while below 0.334 eV reactivity is only possible by tunneling (the minimum energy required for N + O₂(v₀ = 0, j₀ = 1) to overcome the barrier is 0.299 eV). Furthermore, quantum effects are also evident in the rate constant for temperatures between 200 and 500 K. Lastly, we have also made known the limited degree of validity of the J-shifting approximation in the title reaction. From what we know, this work corresponds to the most rigorous theoretical study carried out so far on quantum effects and reactivity for reactions involving only heavy atoms. We expect that it will encourage more investigations of this type in the future, since it is an interesting problem that has been little explored to date.

---

1. Introduction

Around 100 years after the beginning of quantum mechanics, one of the central theories of physics, it continues fascinating both specialists and non-specialists due to the surprising nature of the quantum phenomena, including, e.g., zero-point energy, interferences, resonances and tunneling.^1,2

Here, we will mainly focus on the tunneling effect^3–12 and more specifically on the importance that tunneling presents for the reactivity when a chemical reaction takes place by the transference of a heavy atom (that is, neither a H atom nor one of its isotopes). In this situation, in general, it has been assumed that this effect is of a small relevance. And, according to this, it has been studied almost exclusively in the framework of the transfer of light or very light species, such as a hydrogen atom or an electron, respectively.

Notwithstanding the above, it is worth keeping in mind that reasonable one-dimensional models show that the barrier width has a stronger influence on the tunneling probability than the height of the barrier and the effective mass of the particles involved.

The tunneling effect is almost always important at low temperatures when the reaction under consideration involves the transfer of light atomic species (H, H⁺ and H⁻, mainly). However, this phenomenon can sometimes be also significant in reactions involving the transfer of heavy atomic species (e.g., C, N and O).^11,14 When the rate constant is considered, in general the larger importance of tunneling in light atom transfer reactions can be interpreted based on the greater (imaginary) frequency of the vibrational normal mode of the transition state that connects reactants and products.

The research activity developed during the recent years in organic chemistry in the context of chemical reactions where heavy atoms, such as, e.g., C, N and O, are those that experience the tunneling effect (see, e.g., ref. 13–23), has been an important stimulus for the development of the present work. Thus, the aforementioned research activity has shown that, in a wide variety of reactions (pericyclic reactions, cycloaromatization, rearrangement of radicals, etc.), the tunneling effect involving heavy atoms plays a relevant role.

Given the characteristics (complexity) of these reactions, to estimate theoretically the contribution of the tunneling effect to the reactivity (rate constant) the main approaches used involve one-dimensional models (i.e., those of Wigner, Jeffreys–Wenzel–Kramers–Brillouin (JWKB), Bell, and Truhlar) and the transition state theory (TST) or its variational version (VTST). In the TST or VTST rate constant calculations, carried out using density functional theory (DFT) or ab initio information about the reactants and transition state, multidimensional tunneling corrections have been included by means of the zero curvature tunneling (ZCT) or the small curvature tunneling (SCT) corrections.^10–12 The use of more sophisticated methods is generally not feasible given the significant number of atoms involved in these reactions which, in addition, take place in condensed phase (in solution or in a cryogenic inert gas matrix).

Sometimes the above-mentioned tunneling corrections are confused as being one-dimensional. However, this is not the case as the curvature of the reaction path connecting reactants and products couples the motion along the reaction coordinate with the local vibrational modes that are perpendicular to it (this coupling enters into the Hamiltonian through the kinetic energy term).

It is worth keeping in mind that to determine if a “light atom” or a “heavy atom” tunneling has occurred is not necessarily simple, as light and heavy atoms may be involved simultaneously. In fact, for the barrier defined by the transition state of a given reaction, the normal mode of imaginary frequency usually involves the motion of several atoms. Therefore, the motion of the heavy atom transferred could be accompanied by the motion of one or more light atoms.

Furthermore, it is also worth keeping in mind that while the evolution of the reactants along the minimum energy reaction path (MEP) of the potential energy surface (PES) facilitates the formation of products (after passing over the barrier), this path is not necessarily the best one for reaching products by tunneling.

Concerning the studies of elementary reaction dynamics in which time-independent or time-dependent quantum-mechanical methods have been rigorously applied (i.e., by including the Coriolis coupling (CC)), as far as we know there are only a few cases where reactions with a barrier above reactants and involving a heavy atom transfer have been studied.^24–30 These reactions involve two heavy atoms and a single light atom: H + O₂ → OH + O, H + O₂(a¹Δ_g) → OH + O, O + NH → NO + H, Li + HF → LiF + H, Li + HCl → LiCl + H, and C⁺ + SH → CS⁺ + H. Unfortunately, the influence of tunneling on the reactivity has not been analyzed in any of these six reactions.

Due to the above, here we have focused our attention on the rigorous study of the influence of tunneling on the reactivity of an important heavy atom transfer chemical system. To the best of our knowledge this is the first time that this issue has been considered.

For this purpose, we have selected the N + O₂ → NO + O elementary gas phase reaction (Δ_rH⁰_0K = −32.09 kcal mol⁻¹),³¹ which is an important chemical process. This reaction is relevant in the Earth's atmospheric chemistry, where it is involved in the oxidation mechanism of nitrogen (Zeldovich's mechanism).³² It corresponds to the second reaction of this mechanism, while the related O + N₂ → NO + N reaction corresponds to the first reaction one.

The study of the kinetics and dynamics of these reactions at high temperature is of particular interest in the context of the physicochemical processes occurring during the re-entry of spacecrafts (hypersonic flight) into the Earth's atmosphere, where the strong nonequilibrium thermal conditions produced play an important role.^33,34 Under these hard conditions a fraction of the N₂ and O₂ molecules will dissociate and open the way for the production of NO through the Zeldovich's mechanism.

The N + O₂ reaction is also relevant in shock heated air, supersonic expansion of exhaust gases and combustion processes with hydrocarbon–air mixtures,³⁵ and as a source of infrared chemiluminescence in the upper atmosphere.³⁶ Furthermore, this reaction is also relevant in the context of the air cold plasmas.³⁷

The selected reaction has been the subject of numerous investigations which are mainly of theoretical type. Thus, mostly potential energy surfaces, quasi-classical trajectory and approximate quantum dynamics studies have been developed, considering initially PESs based on a limited number of ab initio points,^38–50 and more recently with higher level PESs.^51–73 On the other hand, the experimental activity has been mainly focused on the measurement of the rate constant of the reaction⁷⁴ and the vibrational distribution of NO.^75–79 Besides, crossed molecular beam experiments at high collision energy (〈E_col〉 = 77.5 kcal mol⁻¹) and with the detection of the NO product have been recently reported.⁷¹

In this work we have carried out a rigorous study on the influence of quantum tunneling on the reaction N + O₂ → NO + O taking place on the ground potential energy surface (1²A′ PES), which is, clearly, the most important one at low/moderate temperatures. Moreover, the O₂ molecule is in its lowest energy vibro-rotational state (i.e., v₀ = 0, j₀ = 1). For this aim the time-dependent quantum dynamic method based on the propagation of real wave packets has been used, including the Coriolis coupling (see refs. in Section 2). Besides, the quasi-classical trajectory method has been also used (see references in Section 2), and the results obtained with both methods for the probabilities, cross-sections and rate constants have been compared. From this comparison it has been possible to determine the importance of the tunneling effect for the selected properties and its dependence on collision energy and translational temperature.

The article has the following structure: Section 2 briefly presents the theoretical methods and describes the main properties of the NO₂ ground potential energy surface; Section 3 reports and discusses the results obtained on the probabilities, cross-sections and rate constants; Section 4 provides the summary and conclusions. Finally, in the ESI,† some useful additional information is given.

2. Theoretical methods

2.1. Potential energy surface

The study of the reaction

N + O₂(v₀ = 0, j₀ = 1) → NO + O (1)

considering as observables the cross-section and the rate constant, has been performed using quantum and classical methods (see below). In both cases, the well-known and accurate analytical expression of the 1²A′ ground PES reported in ref. 52 has been used, which correlates the electronic ground-state of reactants and products. This PES, used together with the first excited 1⁴A′ PES,⁵² has allowed achievement of an excellent agreement with experimental data using quasiclassical calculations in a recent work,⁵⁸ in a wide temperature range. The MEP connecting reactants and products has an exoergicity value of ≈1.4 eV and includes an early transition state (TS1) located ≈0.3 eV above reactants (Table 1). After TS1 there is a shallow minimum (MIN1; ≈1.2 eV below reactants) that allows connecting with NO + O following two different ways: (a) a direct pathway; (b) an indirect pathway that leads to a deep minimum that corresponds to the electronic ground state of the NO₂ molecule [NO₂(X̃); ≈3.3 eV below products] from which products can be formed. This can be seen in Fig. 1.

Table 1 Properties of the barrier height on the NO₂ ground PES^a

a TS1 transition state.^52 b Energy taken with respect to the N + O2 reactants. c (v1, v2, v3) correspond to the vibrational quantum numbers for the N–O stretching (imaginary frequency), ∠NOO bending, and O–O stretching, respectively.
Reactant Jacobi coordinates R, r, γ/a0 and deg	4.123, 2.331, 124.6
Energy/eV^b	0.298
Harmonic vibrational frequencies/cm^−1 ^c	486i, 399, 1221
Energy including ZPE/eV^b	0.299

---

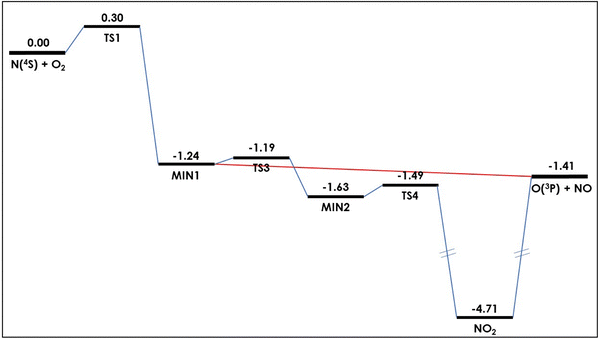Fig. 1 Schematic representation of the minimum energy path of the (analytical) ground potential energy surface of the N + O₂ → NO + O reaction. Energies are given (in eV) relative to reactants. Data taken from ref. 52.

2.2. Quantum mechanical method

We obtain initial-state-resolved quantum mechanics (QM) reaction probabilities, where QM refers to the close-coupling time-dependent real wave packet (CC-TDRWP) method. Thus, we have solved the time dependent Schrödinger equation propagating real wave packets (WPs) up to convergence, and performing a time-to-energy Fourier transform and a flux analysis.^80,81 We employ reactant Jacobi coordinates: the distance R between N and the O₂ center of mass (CM), the distance r between the O nuclei, and the included angle γ (Fig. 2). Jacobi coordinates are frequently used in many-particle systems to make the mathematical description simpler and are commonly employed in chemical reaction dynamics.⁸² Here J and p = ±(−)^J label the total angular momentum and parity quantum numbers respectively, j₀ is the O₂ rotational level, 0 ≤ K₀ ≤ min(J, j₀) is the R-component of both J and j₀ (the body-fixed frame has the z axis pointing along R).

Fig. 2 Reactant Jacobi coordinates of the N + O₂ system, where the different symbols have the usual meaning (see the text).

The present quasiclassical trajectory (QCT) method does not resolve p, while uses orbital angular momentum l instead of K₀; therefore the comparisons will be of 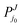(see below for details), that we have quantum-mechanically calculated considering the J-terms of the integral cross-section,

QM probabilities are calculated via the coupled-channel (CC) method⁸² at 0 ≤ J ≤ 40 and J = 50, 60, 70 and 90. Owing to the involved heavy nuclei and the large basis dimensions that are necessary for converging probabilities at high J and E_col, we then employed a J-fitting-interpolation technique at the other Js.⁸³ The validity of this approach is reinforced by the fact that the dependence of the reaction probability with E_col shows very similar shapes when J is large (the curves for different Js are essentially shifted curves; see also comments below).

We have considered all K components of J along R and the initial WP is defined and propagated via the numerical parameters of Table 2. At J = 0, we thus employ 7 312 500 radial-angular basis states, i.e. 112 500 |Rr〉 grid states times 65 associated Legendre polynomials |jK〉, with odd j. These dimensions must be multiplied by J + 1 or J according to the two parity values.

Table 2 Parameters of the QM calculations. Values are in a.u., unless otherwise specified

a The expression used for the damping function that removes the wavepacket when it reaches the edges of the system is the following: exp[−Cabs,R(R − Rabs)^2] for R > Rabs, where Cabs,R and Rabs correspond to the absorption strength and start, respectively. An analogous expression is applied for the r distance.
Initial Gaussian g0(R) [α, E0, R0]	0.15, 0.40 eV, 22
R range and number of grid points	0.0–26 and 450
r range and number of grid points	1.5–10 and 250
Number of |jK〉	65 with j ≤ 129
R and r absorption start at^a	23 and 7
R and r absorption strength^a	0.01
Flux analysis at r∞	7
PES and centrifugal energy cut-off	0.44
Number of propagation steps	40 000

---

The integral cross-section (ICS) for N + O₂(v₀, j₀) → NO + O, as a function of E_col, and the rate constant (k), as a function of the translational temperature T, are obtained from the following expressions (where v₀ is not indicated):

andwhere μ_R is the N + O₂ reduced mass and 1/6 is the ratio of the electronic degeneracy factors of the transition state (2) and reactants (12) of the PES. The ICS has been studied in the 0.200–0.651 eV E_col interval and the rate constant in the 200–1000 K T interval.

2.3. Classical mechanics method

The QCT method was established long ago and is one of the most used theoretical tools for studying chemical reaction dynamics.⁸⁴ The quasiclassical trajectory (QCT) calculations have been performed using standard histogram binning, summing all the final outcomes, i.e. including all the possible product vibrational and rotational states. This is exactly equivalent to doing no final state analysis. We proceed in this way because we are interested in total reactivity comparisons, independently of the final states. However, even though the final state analysis is not relevant in this work, we include at the beginning of the ESI† some considerations about final state analysis and tunneling, and a comparison on the use of Gaussian Binning in this context (Fig. S1, ESI†).

The classical dynamics calculations were performed using a variable time step driven by trajectory error analysis.⁸⁵ The typical integration step size used was around 10⁻¹⁶ s, with a typical variation of one order of magnitude along each trajectory. The accuracy of the numerical integration of Hamilton's differential equations is verified using the same algorithm governing the time step, because at each step a first integration with time step Δt is compared with two successive calculations with half the previous time step, with tolerance limits on both positions and velocities of 10⁻⁹ Å and 10⁻⁹ Å fs⁻¹, respectively. If the test fails, the time step is halved and the cycle is repeated, with a maximum number of attempts equal to 6. This strategy represents an optimal compromise between accuracy and computational load, as tested for different collisional systems (see for example ref. 86).

The trajectories were started at an initial distance of 22 a.u. between the N atom and the center of mass of the O₂ molecule, so that the interaction energy was negligible with respect to the available energy. The same value is adopted for the final distance of interaction. The reaction probability at a given initial condition (v₀, j₀, J, l, and E_col) is determined from the number of reactive trajectories obtained divided by the total number of trajectories calculated. This is obtained at fixed quantized values of total and orbital angular momenta, specified by quantum numbers J and l, respectively (see details in equation 7 of ref. 87). This is important in that it allows a direct comparison with QM probabilities, instead of requiring the comparison of complete cross-section calculation, stressing all the possible QCT-QM differences as a function of J. Using this method of QCT calculation, the cross-section is obtained as in eqn (2) for the quantum results, with the only difference being that there is no parity to consider, while K₀ is replaced by the orbital angular momentum quantum number l, which ranges from |J − j| to J + j. The sum over l is analogous to the sum over K₀ in eqn (3):

As in the case of the QM calculations, the probabilities are determined at 0 ≤ J ≤ 40, J = 50, 60, 70 and 90, and a J-fitting-interpolation technique⁸³ is employed at the other J values.

The total number of trajectories used for the complete calculation of the reaction cross-section from N + O₂(v₀ = 0, j₀ = 1) is about 132 million, distributed over a collision energy range from 0.30 to 0.65 eV, uniformly discretized by 0.01 eV (i.e., on average ≈3.8 million trajectories are calculated for each collision energy). The lower limit is dictated by the classical threshold imposed by the barrier to reaction and accurately checked by preliminary calculations outside this range. In the vicinity of the reaction threshold, the reaction probability is at least five times the value of its standard error (calculated as usual in QCT), with this happening for probabilities which are just above 10⁻³. In addition, the probability/standard error ratio rapidly increases with E_col up to two orders of magnitude.

In all the calculations involved in the present work we have used our own CC-TDRWP and QCT computer programs.

3. Results and discussion

In this section the QM and QCT reaction probabilities, cross-sections and rate constants will be presented and the quantum and classical results will be compared and discussed. The contribution of quantum tunneling to the reactivity will be determined for the three properties indicated above.

3.1. QM and QCT reaction probabilities

The reaction probability P^J₁(E_col) as calculated by the QM and QCT methods at fixed J, weighted by the (2J + 1) multiplicative term, and as a function of collision energy is shown in Fig. 3. The factor (2J + 1) makes it possible to compare the weights of different P(J) values in the cross-section calculation, as is clear from equation 3. The general probability trend rapidly increases for all the J considered. Strictly speaking, the exothermic reaction investigated has no threshold energy as the system can evolve from N + O₂ into NO + O without surmounting the energy requirement (barrier and ZPE) associated with the TS1 transition state,⁵²i.e., by leading to products through tunneling. However, the reactivity of the system is extremely small unless the energy of reactants, E_col + E_vib-rot(O₂), is around/somewhat greater than the energy requirement arising from TS1.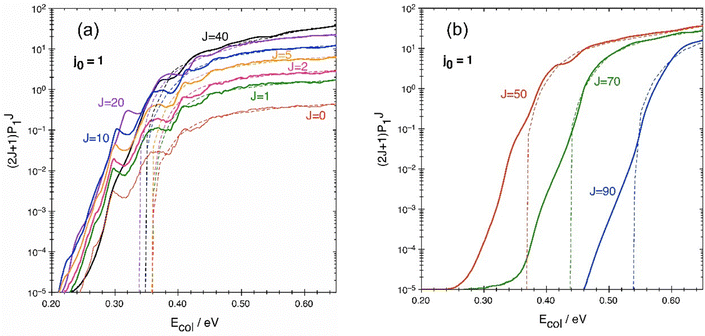

Fig. 3 QM (solid) and QCT (dashed) reaction probabilities for some selected J values between 0 and 40 (a), and between 50 and 90 (b), weighted by the (2J + 1) multiplicative term.

In Fig. 3 it is possible to note the presence of three different regions. In the left panel, the first region is between quantum and classical thresholds (assumed in this figure to be the E_col value at which the term (2J + 1)P(J) is equal to 10⁻⁵), that are slightly different for each value of J but approximately around 0.23 and 0.35 eV respectively, and where there is a clear undulatory trend of the quantum probability. The next region is approximately between 0.35 and 0.45 eV, where QCT and QM probabilities are becoming progressively similar, with QM oscillating around the QCT result, which appears as a sort of average of QM probability. In the third region, for collision energies higher than about 0.45 eV the two probabilities are almost coinciding, with only a very weak residual oscillation as a function of collision energy. Interestingly, the oscillations appear to be “in phase” relative to the collision energy for all the probabilities with 0 ≤ J ≤ 10. For J = 20 the trend is similar but not exactly in phase, while for J = 40 some details of the oscillation are lost, and the trend appears to be much smoother (see in particular the smooth trend between 0.30 and 0.35 eV). Similarly to J = 40 and differently from the lower J values, the other probabilities for J = 50, 70 and 90 in the right panel of Fig. 3 are very smooth, and considering that they are only partially in the second region 0.35–0.45 eV and mostly in the third one, essentially confirm the same features already seen for J values in the left panel, including the level of agreement with QCT results. However, it should be mentioned that the threshold energies for J = 70 and 90 are quite larger compared to those for the lower J values.

The considerations that can be made on these results are the following. In the first region, by definition only quantum tunneling is operating. The QM probability peak at about 0.30 eV, common to all the P(J ≤ 10), appears to be in perfect accord with the barrier height (see Table 1). However, the wavy QM trend is much more extended than just around this classical threshold. In fact, it extends practically to the whole energy range explored in this work, with a sort of “damped” oscillation as a function of collision energy. This is reminiscent of the monodimensional quantum tunneling effect of a wavepacket through a rectangular barrier or a well, where an undulatory trend is observed for the transmission coefficient as a function of collision energy. This effect can be rationalized thinking that along the reaction path the collisional system really encounters a small barrier (TS1; 0.299 eV including ZPE) and then one or more wells of different depth, as already commented (see also ref. 52). Of course, in the present three-dimensional case the observed features are much more complex than in a simple monodimensional barrier and very difficult to be put in precise correspondence with the potential energy surface details.

It is interesting to note that the three main peaks in P(J ≤ 10) are located at about 0.30, 0.36 and 0.41 eV, values that are quite similar to the energies of the transition state TS1 in the three lowest vibrational levels, 0.299, 0.349 and 0.398 eV, respectively. These vibrational levels, (ν₂, ν₃), correspond to (0, 0), (1, 0), and (2, 0), respectively (cf.Table 1), and the quantum numbers v₂ and v₃ are associated with the vibrational modes involving the ∠NOO bending and O–O stretching, respectively. The N–O stretching mode (quantum number v₁) is not mentioned above as it is the vibrational mode of imaginary frequency. So, the influence of the quantized vibrational energy levels of TS1 seems to be evident in the probability curves, producing a stepwise evolution of the probability as a function of collision energy.⁸⁸ A detailed study of the transition state control of the reaction as that reported in ref. 88 for D + H₂ → HD + H is out of the scope of the present work.

Approximate expressions for the wave functions corresponding to the (0, 0), (1, 0), and (2, 0) TS1 vibrational levels can be obtained by multiplying the harmonic oscillator 1D vibrational wavefunction of the bending mode normal coordinate (with quantum number equal to 0, 1 or 2) by the corresponding 1D vibrational wavefunction of the O–O stretching mode normal coordinate (with quantum number equal to 0).

Regarding the (2J + 1)P(J) trends of Fig. 3 as a function of collision energy, they follow essentially three different behaviors w.r.t. J. The first behavior is represented by all the P(J ≤ 10), in which the same trend in the same energy region is reproduced just by using a multiplicative factor (approximately the 2J + 1 factor), while no significant energy shifting is needed to approximate one P(J) with another one in the same group, because thresholds are practically the same. The second group is (2J + 1)P(20 ≤ J ≤ 40), where the trends change significantly with different J values. Some peaks move with J to different positions or disappear. Even in this case, it is quite difficult to see a reliable energy shifting rule in the group. This second group shows the major impact on the cross-section calculation in the second energy region, where (2J + 1)P(J) for lower J are smaller, while higher J contributions are important mainly in the third region. This has significant impact on the QM approximate calculation by J-shifting, as will be clear in the next section. Finally, the third group is (2J + 1)P(J ≥ 50) in which the trends are extremely smooth and an energy shifting can easily be used to approximate one trend with P(J) known at another value in the same group. For all intermediate J values not included in this discussion, (2J + 1)P(J) show intermediate behavior w.r.t. the cited groups.

The QM undulatory trend around the QCT result can be clearly appreciated only if probabilities are compared. The effect is much less evident with cross-sections, as will be clear in the next section. In the sum of eqn (3), in fact, most of the oscillations seen in Fig. 3 disappear because the “in phase” oscillations are limited to P(J ≤ 10), which have the lowest (2J + 1) weight in the cross-section expression.

Some supporting figures are presented on the reaction probability. Fig. S2 (ESI†) presents (2J + 1)P(J) vs. J for a selection of E_col offering a complementary view of the results in Fig. 3. Fig. S3 (ESI†) shows P(J) vs. E_col for a selection of J and also complements Fig. 3 (a similar situation is found in Fig. S4, ESI†). Fig. S5 and S6 (ESI†) give some insights into the influence of K₀ on the reactivity. Based on the N + O₂(v₀ = 0, j₀ = 1) effective potential energy it can be rationalized why K₀ = 1 is more reactive than K₀ = 0 (the barrier in the effective potential energy is smaller in the former case). Finally, Fig. S7 (ESI†) shows P(J) vs. E_col for a selection of j₀ between 1 and 17 (J = 0, K₀ = 0, p = +), where in general reactivity increases with O₂ rotational excitation at E_col below ≈0.4 eV and the results tend to become similar as E_col increases.

3.2. QM and QCT reaction cross-sections

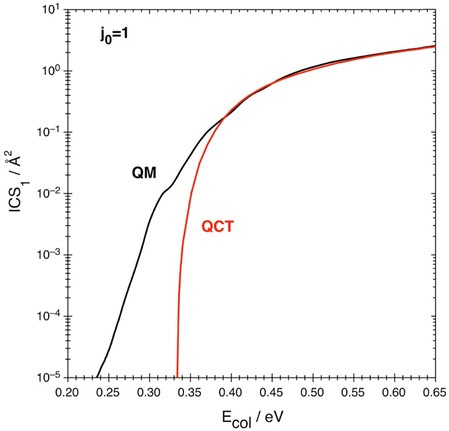
The integral cross-sections ICS(QM) and ICS(QCT) are presented in Fig. 4 and Table 3 at the 0.200–0.651 eV E_col interval. They follow a similar behavior, both increasing with E_col up to maximum values of 2.55 and 2.48 Ų, respectively, but with the QM reactivity starting at lower E_col values. Thus, the lowest value reported here for the ICS (1.0 × 10⁻⁵ Ų) occurs at E_col = 0.235 and 0.334 eV for the ICS(QM) and ICS(QCT), respectively.

Fig. 4 QM (black) and QCT (red) cross-sections as a function of collision energy.

Table 3 QM and QCT cross-sections and contribution of quantum effects to this property

E col/eV	ICS(QM)/Å^2	ICS(QCT)/Å^2	ICS(QM)/ICS(QCT)	Quantum effects contrib./%
a Lowest Ecol at which the QM cross-section is reported (ICS = 1.00 × 10^−5 Å^2). b Lowest Ecol at which the QCT cross-section is reported (ICS = 1.00 × 10^−5 Å^2).
0.235^a	1.00 × 10^−5			100
0.26	7.20 × 10^−5			100
0.28	4.80 × 10^−4			100
0.3	0.0035			100
0.32	0.0111			100
0.334^b	0.0190	1.00 × 10^−5	1900.00	99.95
0.34	0.0262	0.0013	20.15	95.04
0.351	0.0444	0.0101	4.40	77.25
0.361	0.0705	0.0309	2.28	56.17
0.381	0.1341	0.1101	1.22	17.90
0.401	0.2171	0.2365	0.918	-8.94
0.451	0.6359	0.6358	1.00	0.02
0.501	1.1705	1.0770	1.09	7.99
0.551	1.6317	1.5466	1.06	5.22
0.601	2.0773	2.0217	1.03	2.68
0.651	2.5501	2.4756	1.03	2.92

---

These E_col are below and above the ZPE-corrected barrier height (0.299 eV) associated with TS1,⁵² respectively, and point out the importance of quantum effects in this energy region (the rotational energy of O₂ in j₀ = 1 is very small; 3.58 10⁻⁴ eV). Therefore, an important contribution of quantum tunneling to the reactivity is expected to occur below and a little above this energy, justifying the differences observed between the quantum and classical results. We will consider this in detail below.

At the lower E_col values, the ICS(QM)/ICS(QCT) ratio (Table 3) decreases in a very fast way, varying from 1900 at E_col = 0.334 eV to 0.918 at E_col = 0.401 eV, with the last value showing the importance of the over the barrier quantum reflection at that collision energy. At higher collision energies this ratio is close or very close to 1.0.

Among all possible processes (reactive and non-reactive) that may occur starting from N + O₂(v₀ = 0, j₀ = 1), the NO + O reaction channel plays, in general, a minor role in comparison to the inelastic and elastic channels leading to N + O₂. Thus, for instance, the QM J = 0 reaction probability for the NO + O channel is below 10% for E_col ≤ 0.408 eV and reaches values of about 45% only for the higher E_col (0.651 eV). Furthermore, at the low collision energies of, e.g., 0.260, 0.280 and 0.299 eV, the reaction probability is only 5.74 × 10⁻³, 3.68 × 10⁻² and 3.16 × 10⁻¹%, respectively. In spite of these small values, this QM reactivity is essential as at low energies quantum tunneling is the only way to reach the NO + O products, accounting for 100% of the reactivity.

For the analysis of the importance of the quantum behavior, we can express the ICS(QM) as the sum of the ICS(QCT) and a term that accounts for the quantum correction, ICS(QM correction), so that we have

ICS(QM) = ICS(QCT) + ICS(QM correction) (6)

or

ICS(QM correction) = ICS(QM) − ICS(QCT) (7)

Then, the contribution of the quantum effects to the reactivity of the system (in %), expressed in terms of the ICSs, is given by

%quantum effects = 100[ICS(QM correction)/ICS(QM)] = 100{1 − [ICS(QCT)/ICS(QM)]} (8)

Even though, in general, in this context when dealing with quantum effects one often refers to “quantum tunneling”, we have to be aware that the “over the barrier quantum reflection” (non-classical reflection), which leads the system back to the N + O₂ reactants, is also possible when the total energy of the system is above the ZPE-energy corrected barrier.

The contribution of the quantum effects to the cross-section, expressed according to eqn (8), is not monotonic (Fig. 5 and Table 3) and this differs from what happens in the rate constant (cf. Section 3.3), which is a property that involves more averages than the cross-section (cf.eqn (4)). Therefore, after a fast decrease of this contribution from E_col = 0.334 eV to E_col = 0.401 eV (99.95% to −8.94%, respectively), an increase from 0.401 to 0.501 eV (up to 7.99%), a decrease from 0.501 to 0.601 eV (up to 2.68%) and, finally, an increase from the latter collision energy to 0.651 eV (up to 2.92%) follows. With the only exception of the ≈0.39–0.45 eV E_col interval quantum tunneling is more or much more important for the cross-section than the over the barrier quantum reflection. Unfortunately, there is no experimental information available to compare with.

Fig. 5 Contribution of the quantum effects to the cross-section as a function of collision energy.

Of course, if the total energy of the system is below the ZPE-corrected barrier height (0.299 eV), this reaction will take place only by quantum effects, whose contribution to reactivity will then be equal to 100%.

The existence of some (small) quantum contribution to the cross-section when the total energy of reactants, E_col + E_vib-rot[O₂(v₀ = 0, j₀ = 1)], is clearly above the energy of the barrier (including the ZPE), 0.299 eV, seems reasonable. At a more basic level, we can recall the example of the penetration of a particle through a potential barrier, in which even for collision energy values that are five times the value of the barrier, the quantum effects, although small, are very visible (oscillation of the transmission probability with values that in this case are generally smaller than but close to unity).⁸⁹ Furthermore, the careful convergence tests performed before the production runs, both in the QM and QCT calculations, give confidence regarding the results obtained.

A point of interest in the cross-section context is to compare a widely used approximate method with the accurate QM calculations available now for this collisional system. In Fig. 6 we compare the accurate QM and QCT cross-sections with those obtained from the J-shifting approximation,⁹⁰ used for both QM and QCT. This approximation has been applied as usual considering the specific features of the collisional system, as described e.g. in ref. 54 and 64. Therefore, the P(J) values are estimated from the P(J = 0) ones taking into account the rotational energy of the transition state TS1 (described as a nearly prolate symmetric rigid rotor), expressed in terms of J, K₀ and the rotational constants (A = 2.246 cm⁻¹, B = 0.330 cm⁻¹ and C = 0.288 cm⁻¹),

Fig. 6 Quantum (black) and classical (red) cross-sections as obtained without (QCT, QM) and with (QCT JS, QM JS) the J-shifting approximation.

The first observation is that the discrepancy between the accurate and approximate QM calculations is variable but significant along the whole energy axis, with the worst approximation (more than a factor of two) around the energy region between 0.35 and 0.45 eV (the second region in Fig. 3). This coarser approximation is due to the fact that the highest (2J + 1)P(J) values in that region have 20 ≤ J ≤ 40, but the related P(J) are the most difficult to reproduce starting from P(J = 0) (see the discussion in the previous section). In contrast, the quality of the results obtained with QCT, with and without the J-shifting approximation, is excellent w.r.t. the appropriate quantum result if considered after a suitable energy threshold. This threshold is about 0.39 eV for accurate QCT and about 0.44 eV for J-shifting QCT. This displacement towards higher values is due to the overemphasizing of the wavy P(J = 0) trend in J-shifting w.r.t. the complete calculation including all the J values. This result should be considered when only QM J-shifting calculations are available in comparison with QCT results: an approximate QM calculation is not necessarily better than an accurate QCT one.

The second observation is that the accurate QM cross-section is much smoother than the J-shifting QM result. The undulatory trend of P(J = 0) in Fig. 3 heavily reflects in the approximate cross-section curve, but the final effect on the accurate result is just a slight curvature change around E_col = 0.32 eV, and another even weaker effect at 0.38 eV.

Another aspect concerning the J-shifting approximation in the present collisional system can be deduced from Fig. 7, where the classical P(J) results are shown, on a linear scale, as a function of E_col and for various J values ranging from 0 to 100 (on a linear scale the QM-QCT differences just away from thresholds are much less evident, so for clarity only QCT data are shown here). P(J = 0) appears consistently lower than all the other P(1 ≤ J ≤ 20), with all thresholds quite similar, and the P(J = 0) curve shows an opposite curvature w.r.t. any P(J ≥ 30). This means that no energy-shift can be used successfully to reproduce all these P(J > 0) using just P(J = 0). Only for J > 40 this approximation might be applicable starting from P(J = 40), as can be easily seen in the threshold displacement along the energy axis as J increases and the similarity of the P(J > 40) trends.

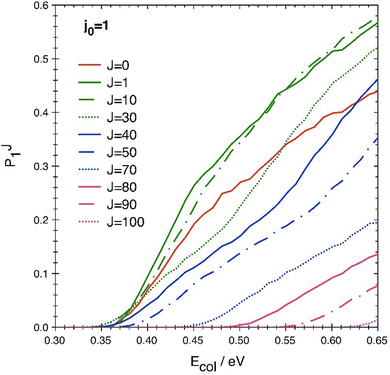Fig. 7 QCT reaction probability as a function of collision energy for some selected values of J in the 0–100 interval.

The present QM and QCT cross-sections for N + O₂(v₀ = 0, j₀ = 1) → NO + O have also been compared with approximate time-dependent (TDRWP)⁵⁵ and time independent⁶⁴ QM results, in which the same analytical expression for the ground PES employed here was used (Fig. S8, ESI†). In these two investigations only the J = 0 case was calculated and the cross-sections and rate constants were estimated using the J-shifting approximation. Consistently with the comparison shown in this section between the rigorous and J-shifting results, there are significant differences between the present results and those based on the J-shifting approximation reported in ref. 55 and 64.

3.3. QM and QCT reaction rate constants

The QM and QCT rate constants, k(QM) and k(QCT), respectively, follow the same behavior with both increasing with T, which really corresponds to the translational temperature, as the initial state of O₂ is fixed at v₀ = 0, j₀ = 1 (Fig. 8 and Table 4). The two results clearly converge at high temperature. The lowest value reported here for the rate constant occurs at T = 200 K, with k(QM) = 1.15 × 10⁻²⁰ cm³ s⁻¹ and k(QCT) = 2.61 × 10⁻²¹ cm³ s⁻¹. Besides, at the higher temperature explored (1000 K) the rate constants are equal to 1.61 × 10⁻¹³ and 1.52 × 10⁻¹³ cm³ s⁻¹ for the quantum and classical results, respectively. Therefore, in the 200–1000 K translational temperature interval studied the QM rate constant increases 1.4 × 10⁷ times, while for the QCT results the increment is of 5.8 × 10⁷ times. The larger differences found between the QM and QCT rate constants are observed at the lower temperatures and this results from the differences observed in the ICS at collision energies below ≈0.40 eV (see also eqn (4)).

Fig. 8 QM (black) and QCT (red) rate constants as a function of translational temperature.

Table 4 QM and QCT rate constants (in cm³ s⁻¹)

T/K	QM	QCT
200	1.15 × 10^−20	2.61 × 10^−21
250	4.39 × 10^−19	1.85 × 10^−19
300	5.73 × 10^−18	3.31 × 10^−18
350	3.89 × 10^−17	2.67 × 10^−17
400	1.71 × 10^−16	1.31 × 10^−16
500	1.49 × 10^−15	1.26 × 10^−15
600	6.65 × 10^−15	5.93 × 10^−15
700	2.01 × 10^−14	1.84 × 10^−14
800	4.72 × 10^−14	4.37 × 10^−14
900	9.29 × 10^−14	8.68 × 10^−14
1000	1.61 × 10^−13	1.52 × 10^−13

---

The Arrhenius’ plot representation (ln k vs. 1/T) of the rate constants shows that both k(QM) and k(QCT) exhibit a good linear dependence, i.e., they show Arrhenius’ behavior in the 200–1000 K temperature interval (Fig. 9). From this representation the pre-exponential factor, A, and the activation energy, E_a, can be determined. They are shown in Table 5 considering: (a) all data points; (b) the five points of higher T; (c) the six points of lower T.

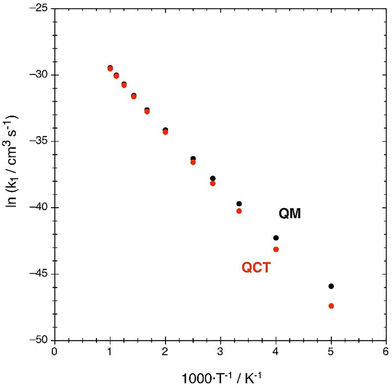Fig. 9 Arrhenius’ plots of the QM (black) and QCT (red) rate constants, with k₁ in cm³ s⁻¹ and T in K.

Table 5 Arrhenius’ parameters A and E_a of the QM and QCT rate constants

T/K		10^11A/cm^3 s^−1	E a/eV
All	QM	0.7399	0.3576
	QCT	1.1057	0.3858
≥600	QM	1.8866	0.4119
	QCT	1.9236	0.4187
≤500	QM	0.3070	0.3372
	QCT	0.7088	0.3754

---

The largest differences between the quantum and classical results occur when we compare the Arrhenius’ parameters at the lower temperatures (200–500 K), where the A(QM)/A(QCT) and E_a(QM)/E_a(QCT) ratios are equal to 0.433 and 0.899, respectively. In contrast, for the temperature interval 600–1000 K the QM and QCT parameters are very close to each other. This can be rationalized on the basis of the influence of tunneling on the reactivity as it diminishes when temperature grows.

Another way to analyze the differences between the QM and QCT results is based on the k(QM)/k(QCT) ratio, which decreases monotonically with T in the 200–1000 K temperature interval; with the stronger changes taking place at the lower temperatures. Thus, in the 200–350 K interval defined by the four lower temperatures investigated, the k(QM)/k(QCT) ratio evolves from 4.41 at 200 K to 1.46 at 350 K. Additionally, from 400 to 1000 K the changes in the ratio are small (from 1.31 to 1.06). The larger k(QM)/k(QCT) ratios at the lower T arise from the relevance of quantum tunneling at these temperatures (see below).

Regarding the importance of the quantum behavior in the rate constant and analogously as for the integral cross-section, we can express k(QM) as the sum of k(QCT) and a term that accounts for the quantum correction, k(QM correction), so that we have

k(QM) = k(QCT) + k(QM correction) (10)

or

k(QM correction) = k(QM) − k(QCT) (11)

Then, the contribution of quantum effects (quantum tunneling and over the barrier reflection (non-classical reflection)) to the reactivity of the system, expressed in terms of the rate constants, will be given, in %, by

%quantum effects = 100[k(QM correction)/k(QM)] = 100{1 − [k(QCT)/k(QM)]} (12)

The dependence of the contribution of quantum effects to the reactivity with respect to temperature, determined from equation 12, is a monotonically decreasing function (Fig. 10). This differs from the ICS that shows a non-monotonic dependence with E_col, as previously indicated. From 200 to 500 K, the contribution of quantum effects (dominated by tunneling) to the reactivity changes from 77.3% to 15.4%, respectively. And at the two higher temperatures reported (900 and 1000 K) the contribution is of 6.6 and 5.6%, respectively. The higher quantum contribution to reactivity at the lower temperatures is expected, since in this situation the lower E_col values have a stronger influence on the rate constant than at higher temperatures.

Fig. 10 Quantum contribution to the rate constant as a function of translational temperature.

As in the case of the integral cross-section, it is not possible to compare with experimental information on the N + O₂(v₀ = 0, j₀ = 1) → NO + O rate constant. However, a variational transition state theory analysis, including an estimation of tunneling using a multidimensional approach (the ICVT/μOMT method), suggested a tunneling contribution of 21.3% (μOMT quantum transmission coefficient = 1.27) for the N + O₂ → NO + O rate constant at T = 300 K.⁵² It should be highlighted that the ICVT/μOMT study mentioned was carried out employing the same analytical expression for the ground potential energy surface of the NO₂ system used in the present work. The first excited (1⁴A′) NO₂ PES, that was also considered in ref. 52, has a completely negligible contribution to the rate constant at 300 K.

At the temperature of 300 K, the N + O₂(v₀ = 0, j₀ = 1) → NO + O state specific reaction investigated presents a quantum contribution (dominated by tunneling) of 42.2% in its rate constant. Even though this value is of the order of magnitude of the value estimated by the ICVT/μOMT method, it must be emphasized that the reaction conditions are different, as in this last calculation⁵² the O₂ molecule presents a 300 K Boltzmann distribution, which mainly consists in v₀ = 0 and several j₀ levels (1, 3, 5,…). For completeness, the logarithmic plots of the k(v₀ = 0, j₀ = 1, T) and k(T) rate constants vs. T are shown in Fig. S9 of the ESI,† where it can be seen that the shapes are similar but the last one presents higher values.

4. Summary and conclusions

This theoretical work has mainly focused on the rigorous study of the importance of quantum effects in heavy atom reactions, considering in this initial investigation the elementary triatomic reaction N + O₂(v₀ = 0, j₀ = 1) → NO + O. This reaction, which involves three heavy atoms, is very relevant in atmospheric chemistry (Zeldovich's mechanism) and is also important in air cold plasmas. We have studied the dynamics at an exact (close coupling) quantum mechanical level, using the time-dependent real WP method, and at the classical mechanics level using the QCT method; and we have determined the reaction probability, cross-section (E_col interval: 0.200–0.651 eV) and rate constant (T interval: 200–1000 K).

The dependence of the reaction probability and reaction cross-section on the collision energy shows the characteristic shape of reactions that present a barrier between reactants and products, both for quantum and classical results. Thus, on the overall, both properties increase with E_col and tend to become constant at high enough E_col values (but not too high E_col so as to open other reaction channels, e.g., the N + O + O dissociation). Regarding the rate constant, it shows a dependence of Arrhenius’ type also in both cases.

For the conditions in which the total energy of reactants, E_col + E_vib-rot[O₂(v₀ = 0, j₀ = 1)], is lower than the energy of the barrier (including the ZPE), 0.299 eV, the NO + O production is only possible thanks to the quantum tunneling effect.

When the total energy of the reactants is slightly higher than the energy requirement indicated above, the contribution to reactivity due to the quantum tunneling effect is dominant. Thus, for example, the ICS(QM)/ICS(QCT) ratio evolves from a value of 1900 at E_col = 0.334 eV to 2.28 at E_col = 0.361 eV, and it is not far from unity for 0.381 eV (1.22). At this point, it is worth keeping in mind that for E_col = 0.361 eV the total energy of the system is only 0.062 eV (1.43 kcal mol⁻¹) above the energy requirement. At higher E_col energies, the minimum value for the ICS(QM)/ICS(QCT) ratio (0.92) is obtained at E_col = 0.401 eV, i.e., at this energy the quantum reflection over the barrier (non-classical reflection) is more important than quantum tunneling. Moreover, in the 0.551–0.651 eV collision energy range the ratio is basically constant and equal to 1.05.

The k(QM)/k(QCT) rate constant ratio evolves from a value of 4.41 at 200 K to a value of 1.31 at 400 K. Quantum effects are very significant in the temperature range 200–400 K with tunneling being the most important one. Besides, this rate constant ratio decreases progressively from 1.18 at 500 K to 1.06 at 1000 K.

Based on the present results, we can conclude that in this heavy–heavy–heavy atom reactive system quantum tunneling is very important for the ICS in the E_col range 0.334–0.381 eV. Besides, below 0.334 eV the reactivity is, essentially, only possible due to the quantum tunneling effect. Quantum effects on the reactivity also manifest significantly in the rate constant between 200 and 500 K.

Finally, we have also shown the limited degree of validity of the J-shifting approximation when applied to determine the cross-section of the selected reaction, from both the quantum and classical perspectives.

To the best of our knowledge, this work is the most rigorous and detailed theoretical study carried out to date on the tunneling effect (and, more generally, on quantum effects and reactivity) in the context of reactions involving only heavy atoms. We hope that this work will be a stimulus for more investigations about this interesting problem to be developed in the future.

Data availability

The data supporting the findings of this study are available from the authors upon reasonable request.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

This work has been supported by the Spanish Ministry of Science and Innovation (Excellence MDM CEX2021-001202-M). Moreover, some support has also been provided by the Autonomous Government of Catalonia (2021SGR 00354 and 2021SGR 00079 Projects). We are also very grateful to A. Bernini and M. Olivucci for invaluable computing resources provided and to R. A. Sultanov and N. Balakrishnan for sharing with us their N + O₂(v₀ = 0, j₀ = 1) reaction probabilities for J = 0. This article is dedicated to Professor Donald G. Truhlar (University of Minnesota) for his very important contributions in reaction dynamics and, in particular, for the study of the tunneling effect in chemical reactions.

References

1. R. P. Feynman, R. B. Leighton and M. Sands, The Feynman Lectures on Physics, (Quantum Mechanics), Basic Books, New York, 2010, vol. 3.
2. C. Cohen-Tannoudji, B. Diu and F. Laloë, Mécanique Quantique, EDP/CNRS, Paris, 2018.
3. C. Eckart, The penetration of a potential barrier by electrons, Phys. Rev., 1930, 35, 1303–1309.
4. E. P. Wigner, Über das überschreiten von potentialschwellen bei chemischen reaktionen, Z. Phys. Chem., 1932, B19, 203–216.
5. R. P. Bell, The tunnel effect correction for parabolic potential barriers, Trans. Faraday Soc., 1959, 55, 1–4.
6. B. C. Garrett and D. G. Truhlar, Accuracy of tunneling corrections to transition state theory for thermal rate constants of atom transfer reactions, J. Phys. Chem., 1979, 83, 200–203.
7. R. P. Bell, The Tunnel Effect in Chemistry, Chapman and Hall, London, 1980.
8. J. Singh, Quantum Mechanics: Fundamentals and Applications to Technology, John-Wiley and Sons, New York, 1997, pp. 126–169.
9. M. Razavy, Quantum Theory of Tunneling, World Scientific, New Jersey, 2003.
10. A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett and D. G. Truhlar, Variational transition state theory with multidimensional tunneling, Rev. Comput. Chem., 2007, 23, 125–232.
11. J. L. Bao and D. G. Truhlar, Variational transition state theory: theoretical framework and recent developments, Chem. Soc. Rev., 2017, 46, 7548–7596.
12. D. G. Truhlar, Semiclassical multidimensional tunneling calculations, in Tunnelling in Molecules: Nuclear Quantum Effects from Bio to Physical Chemistry, ed. J. Kaestner and S. Kozuch, RSC Publishing, Cambridge, 2021, pp. 261–282.
13. W. T. Borden, Reactions that involve tunneling by carbon and the role that calculations have played in their study, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2016, 6, 20–46.
14. J. Meisner and J. Kästner, Atom tunneling in Chemistry, Angew. Chem., Int. Ed., 2016, 55, 5400–5413.
15. T. Schleif, J. Mieres-Perez, S. Henkel, M. Ertelt, W. T. Borden and W. Sander, The Cope rearrangement of 1,5-dimethylsemibullvalene-2(4)-d1: experimental evidence for heavy-atom tunneling, Angew. Chem., Int. Ed., 2017, 56, 10746–10749.
16. C. Doubleday, R. Armas, D. Walker, C. V. Cosgriff and E. M. Greer, Heavy-atom tunneling calculations in thirteen organic reactions: tunneling contributions are substantial, and Bell's formula closely approximates multidimensional tunneling at ≥250 K, Angew. Chem., Int. Ed., 2017, 56, 13099–13102.
17. C. M. Nunes, A. K. Eckhardt, I. Reva, R. Fausto and P. R. Schreiner, Competitive nitrogen versus carbon tunneling, J. Am. Chem. Soc., 2019, 141, 14340–14348.
18. C. Castro and W. L. Karney, Heavy-atom tunneling in organic reactions, Angew. Chem., Int. Ed., 2020, 59, 8355–8366.
19. S. Karkamar and A. Datta, Heavy-atom tunneling in organic transformations, J. Chem. Sci., 2020, 132, 127.
20. T. Schleif, M. Prado Merini, S. Henkel and W. Sander, Solvation effects on quantum tunneling reactions, Acc. Chem. Res., 2022, 55, 2180–2190.
21. T. Schleif, Transformations of strained three-membered rings a common, yet overlooked, motif in heavy-atom tunneling reactions, Chem. – Eur. J., 2022, 28, e202201775.
22. J. F. Rowen, F. Beyer, T. Schleif and W. Sander, Isomer-specific heavy-atom tunneling in the ring expansion of fluorenylazirines, J. Org. Chem., 2023, 88, 7893–7900.
23. W. Guo, E. E. Robinson, R. J. Thomson and D. J. Tantillo, Heavy atom quantum mechanical tunneling in total synthesis, Org. Lett., 2024, 26, 4606–4609.
24. P. Honvault, S. Y. Lin, D. Xie and H. Guo, Differential and integral cross sections for the H + O₂ → OH + O combustion reaction, J. Phys. Chem. A, 2007, 111, 5349–5352.
25. J. Ma, H. Guo, C. Xie, A. Lib and D. Xie, State-to-state quantum dynamics of the H(²S) + O₂(a¹Δ_g) → O(³P) + OH(X²Π) reaction on the first excited state of HO₂(A²A′), Phys. Chem. Chem. Phys., 2011, 13, 8407–8413.
26. A. Li, C. Xie, D. Xie and H. Guo, State-to-state quantum dynamics of the O(³P) + NH(X³Σ⁻) reaction on the three lowest-lying electronic states of HNO/HON, J. Chem. Phys., 2013, 138, 024308.
27. H. Guo, J. Ma and J. Li, Tunneling in unimolecular and bimolecular reactions, in Molecular Quantum Dynamics. From Theory to Applications, ed. F. Gatti, Springer, Berlin, 2014, pp. 59–80.
28. J. Hazra and N. Balakrishnan, Quantum dynamics of tunneling dominated reactions at low temperatures, New J. Phys., 2015, 17, 055027.
29. L. Zhang, J. Zhao, D. Liu, W. Wang, D. Yue, Y. Song and Q. Meng, A new global analytical ab initio potential energy surface for the dynamics of the C⁺(²P) + SH(X²Π) reaction, Phys. Chem. Chem. Phys., 2022, 24, 1007–1015.
30. S. Y. Kumar and R. Padmanaban, Dynamical and mechanical insights into the Li(²S) + HCl(X¹Σ⁺) reaction: a detailed quantum wavepacket study, ChemPhysChem, 2023, 24, e202200747.
31. M. W. Chase, Jr., C. A. Davies, J. R. Downey, Jr., D. J. Frurip, R. A. McDonald and A. N. Syverud, J. Phys. Chem. Ref. Data, 1985, 14(Supplement No. 1).
32. Y. B. Zeldovich, The oxidation of nitrogen in combustion explosions, Acta Physicochim. USSR, 1946, 21, 577–628.
33. S. B. Brooks, M. J. Lewis and R. R. Dickerson, Nitric oxide emissions from the high-temperature viscous boundary layers of hypersonic aircraft within the stratosphere, J. Geophys. Res., 1993, 98, 16755–16760.
34. G. Colonna, F. Bonelli and G. Pascazio, Impact of fundamental molecular kinetics on macroscopic properties of high-enthalpy flows: the case of hypersonic atmospheric entry, Phys. Rev. Fluids, 2019, 4, 033404.
35. A. Burcat, G. Dixon-Lewis, M. Frenklach, W. C. Gardiner, R. K. Hanson, S. Salimian, J. Troe, J. Warnatz and R. Zellner, in Combustion Chemistry, ed. W. C. Gardiner, Jr., Springer-Verlag, New York, 1984.
36. P. Warneck, Chemistry of the Natural Atmosphere, Academic, San Diego, 1998, ch. 3.
37. F. Esposito, On the relevance of accurate input data for vibrational kinetics in air cold plasmas: the case of nitrogen fixation, Plasma Sources Sci. Technol., 2022, 31, 094010.
38. S. P. Walch and R. L. Jaffe, Calculated potential surfaces for the reactions: O + N₂ → NO + N and N + O₂ → NO + O, J. Chem. Phys., 1987, 86, 6946–6956 and references cited therein.
39. R. L. Jaffe, M. D. Pattengill and D. W. Schwenke, Classical trajectory studies of gas phase reaction dynamics and kinetics using ab initio potential energy surfaces, in Supercomputer Algorithms for Reactivity, Dynamics and Kinetics of Small Molecules, ed. A. Laganà, Kluwer, Dordrecht, 1989, pp. 367–382.
40. M. Gilibert, A. Aguilar, M. González and R. Sayós, Quasiclassical trajectory study of the N(⁴S_u) + O₂(X³Σ⁻_g) → NO(X²Π) + O(³P_g) atmospheric reaction on the ²A′ ground potential energy surface employing an analytical Sorbie-Murrell potential, Chem. Phys., 1993, 172, 99–115.
41. M. Gilibert, A. Aguilar, M. González and R. Sayós, A quasiclassical trajectory study of the effect of the initial rovibrational level and relative translational energy of reactants on the dynamics of the N(⁴S_u) + O₂(X³Σ⁻_g) → NO(X²Π) + O(³P_g) atmospheric reaction on the ²A′ ground potential energy surface, Chem. Phys., 1993, 178, 287–303.
42. R. Sayós, A. Aguilar, M. Gilibert and M. González, Orientational dependence of the N(⁴S) + NO(X²Π) and N(⁴S) + O₂(X³Σ⁻_g) reactions: comparison of the angle-dependent line-of-centres model with quasiclassical trajectories, J. Chem. Soc., Faraday Trans., 1993, 89, 3223–3234.
43. M. Gilibert, X. Giménez, M. González, R. Sayós and A. Aguilar, A comparison between experimental, quantum and quasiclassical properties for the N(⁴S_u) + O₂(X³Σ⁻_g) → NO(X²Π) + O(³P_g) reaction, Chem. Phys., 1995, 191, 1–15.
44. R. Sayós, J. Hijazo, M. Gilibert and M. González, Variational transition state calculation of the rate constants for the N(⁴S_u) + O₂(X³Σ⁻_g) → NO(X²Π) + O(³P_g) reaction and its reverse between 300 and 5000 K, Chem. Phys. Lett., 1998, 284, 101–108.
45. R. D. Sharma, Y. Sun and A. Dalgarno, Highly rotationally excited nitric oxide in the terrestrial thermosphere, Geophys. Res. Lett., 1993, 20, 2043–2045.
46. N. Balakrishnan and A. Dalgarno, Rate coefficients for NO formation in energetic N + O₂ collisions, Chem. Phys. Lett., 1999, 302, 485–488.
47. B. Ramachandran, N. Balakrishnan and A. Dalgarno, Vibrational-rotational distributions of NO formed from N + O₂ reactive collision, Chem. Phys. Lett., 2000, 332, 562–568.
48. J. W. Duff, F. Bien and D. E. Paulsen, Classical dynamics of N(⁴S) + O₂(X³Σ⁻_g) → NO(X²Π) + O(³P) reaction, Geophys. Res. Lett., 1994, 21, 2043–2046.
49. G. Suzzi Valli, R. Orrú, E. Clementi, A. Laganà and S. Crocchianti, Rate coefficients for the N + O₂ reaction computed on an ab initio potential energy surface, J. Chem. Phys., 1995, 102, 2825–2832.
50. D. Bose and G. V. Candler, Thermal rate constants of the O₂ + N → NO + O reaction based on the ²A′ and ⁴A′ potential-energy surfaces, J. Chem. Phys., 1997, 107, 6136–6145.
51. R. Sayós, C. Oliva and M. González, The lowest doublet and quartet potential energy surfaces involved in the N(⁴S) + O₂ reaction. I. Ab initio study of the C_s-symmetry (²A′, ⁴A′) abstraction and insertion mechanisms, J. Chem. Phys., 2001, 115, 1287–1297.
52. R. Sayós, C. Oliva and M. González, New analytical ²A′, ⁴A′ surfaces and theoretical rate constants for the N(⁴S) + O₂ reaction, J. Chem. Phys., 2002, 117, 670–679.
53. M. González, C. Oliva and R. Sayós, The lowest doublet and quartet potential energy surfaces involved in the N(⁴S) + O₂ reaction. II. Ab initio study of the C_2v-symmetry insertion mechanism, J. Chem. Phys., 2002, 117, 680–692.
54. P. Defazio, C. Petrongolo, S. K. Gray and C. Oliva, Wave packet dynamics of the N(⁴S_u) + O₂(X³Σ⁻_g) → NO(X²Π) + O(³P_g) reaction on the X²A′ potential energy surface, J. Chem. Phys., 2001, 115, 3208–3214.
55. P. Defazio, C. Petrongolo, C. Oliva, M. González and R. Sayós, Quantum dynamics of the N(⁴S) + O₂ reaction on the X²A′ and a⁴A′ surfaces: reaction probabilities, cross sections, rate constants, and product distributions, J. Chem. Phys., 2002, 117, 3647–3655.
56. P. Defazio, S. Akpinar and C. Petrongolo, Quantum calculations of nonadiabatic ²A₁–²B₂ conical-intersection effects in the reactions N(⁴S) + O₂(X³Σ⁻_g) and N(⁴S) + O₂(A³Δ_u), Chem. Phys., 2010, 375, 46–51.
57. I. Armenise and F. Esposito, N + O₂(v) collisions: reactive, inelastic and dissociation rates for state-to-state vibrational kinetic models, Chem. Phys., 2021, 551, 111325.
58. F. Esposito and I. Armenise, Reactive, inelastic, and dissociation processes in collisions of atomic nitrogen with molecular oxygen, J. Phys. Chem. A, 2021, 125, 3953–3964.
59. I. Armenise, Low temperature state-to-state vibrational kinetics of O + N₂(v) and N + O₂(v) collisions, Chem. Phys., 2023, 571, 111937.
60. A. J. C. Varandas, A realistic multi-sheeted potential energy surface for NO₂(²A′) from the double many-body expansion method and a novel multiple energy-switching scheme, J. Chem. Phys., 2003, 119, 2596–2613.
61. P. J. B. S. Caridade and A. J. C. Varandas, Dynamics study of the N(⁴S) + O₂ reaction and its reverse, J. Phys. Chem. A, 2004, 108, 3556–3564.
62. V. C. Mota, P. J. S. B. Caridade and A. J. C. Varandas, Ab initio-based global double many-body expansion potential energy surface for the first ²A′′ electronic state of NO₂, J. Phys. Chem. A, 2012, 116, 3023–3034.
63. V. Kurkal, P. Fleurat-Lessard and R. Schinke, NO₂: global potential energy surfaces of the ground and the first excited electronic states, J. Chem. Phys., 2003, 119, 1489–1501.
64. R. A. Sultanov and N. Balakrishnan, Quantum mechanical investigations of the N(⁴S) + O₂(X³Σ⁻_g) → NO(X²Π) + O(³P) reaction, J. Chem. Phys., 2006, 124, 124321.
65. J.-J. Ma, M.-D. Chen, S.-L. Cong and K.-L. Han, Stereodynamics study of the N(⁴S) + O₂(X³Σ⁻_g) → O(³P) + NO(X²Π) reaction, Chem. Phys., 2006, 327, 529–535.
66. J. He, F. Chen and J. Li, A quasiclassical trajectory study for the N(⁴S) + O₂(X³Σ⁻_g) → NO(X²Π) + O(³P) reaction on the new ²A’ and ⁴A′ potential-energy surfaces, J. Chem. Phys., 2006, 124, 054303.
67. T. K. Mankodi, U. V. Bhandarkar and B. P. Puranik, Cross-sections for O₂ + N system using the QCT method, Chem. Phys. Lett., 2018, 704, 21–26.
68. Y. Wang and X. Cheng, State-to-state transition study of the exchange reaction for N(⁴S) and O₂(X³Σ⁻_g) collision by quasi-classical trajectory, J. Phys. Chem. A, 2021, 125, 9318–9326.
69. J. C. San Vicente Veliz, D. Koner, M. Schwilk, R. J. Bemish and M. Meuwly, The N(⁴S) + O₂(X³Σ⁻_g) → O(³P) + NO(X²Π) reaction: thermal and vibrational relaxation rates for the ²A′, ⁴A′ and ²A′′ states, Phys. Chem. Chem. Phys., 2020, 22, 3927–3939.
70. Z. Varga, Y. Liu, J. Li, Y. Paukku, H. Guo and D. G. Truhlar, Potential energy surfaces for high-energy N + O₂ collisions, J. Chem. Phys., 2021, 154, 084304.
71. A. Caracciolo, J. C. San Vicente Veliz, D. Lu, H. Guo, M. Meuwly and T. K. Minton, Experimental and theoretical studies of hyperthermal N + O₂ collisions, J. Phys. Chem. A, 2023, 127, 8834–8848.
72. X. Huang, K.-M. Gu, C.-M. Guo and X.-L. Cheng, Dissociation cross sections and rates in O₂ + N collisions: molecular dynamics simulations combined with machine learning, Phys. Chem. Chem. Phys., 2023, 25, 29475–29485.
73. X. Huang and X.-L. Cheng, The role of the sextet potential energy surface in O₂ + N inelastic collision processes, Phys. Chem. Chem. Phys., 2023, 25, 4929–4938.
74. D. L. Baulch, C. J. Cobos, R. A. Cox, G. Hayman, Th Just, J. A. Kerr, T. Murrells, M. J. Pilling, J. Troe, R. W. Walker and J. Warnatz, Evaluated kinetic data for combustion modelling, Supplement I, J. Phys. Chem. Ref. Data, 1994, 23, 847 and references cited therein.
75. M. E. Whitson, Jr., L. A. Darnton and R. J. McNeal, Vibrational energy distribution in the NO produced by the reaction of N(⁴S) with O₂, Chem. Phys. Lett., 1976, 41, 552–556.
76. A. Rahbee and J. J. Gibson, Rate constants for formation of NO in vibrational levels v = 2 through 7 from the reaction N(⁴S) + O₂ → NO^‡ + O, J. Chem. Phys., 1981, 74, 5143–5148.
77. R. R. Herm, B. J. Sullivan and M. E. Whitson, Jr., Nitric oxide vibrational excitation from the N(⁴S) + O₂ reaction, J. Chem. Phys., 1983, 79, 2221–2230.
78. I. C. Winkler, R. A. Stachnik, J. I. Steinfeld and S. M. Miller, Determination of NO (v = 0–7) product distribution from the N(⁴S) + O₂ reaction using two-photon ionization, J. Chem. Phys., 1986, 85, 890–899.
79. G. E. Caledonia, R. H. Krech, D. B. Oakes, S. J. Lipson and W. A. M. Blumberg, Products of the reaction of 8 km s⁻¹ N(⁴S) and O₂, J. Geophys. Res., 2000, 105, 12833–12837.
80. S. K. Gray and G. G. Balint Kurti, Quantum dynamics with real wave packets, including application to three-dimensional (J = 0) D + H₂ → HD + D reactive scattering, J. Chem. Phys., 1998, 108, 950–962.
81. A. J. H. M. Meijer, E. M. Goldfield, S. K. Gray and G. G. Balint Kurti, Flux analysis for calculating reaction probabilities with real wave packets, Chem. Phys. Lett., 1998, 293, 270–276.
82. J. Z. H. Zhang, Theory and Application of Quantum Molecular Dynamics, World Scientific, Singapore, 1999.
83. P. Gamallo, P. Defazio, M. González and C. Petrongolo, Renner-Teller coupled-channel dynamics of the N(²D) + H₂ reaction and the role of the NH₂ A²A₁ electronic state, J. Chem. Phys., 2008, 129, 244307.
84. L. M. Raff and D. L. Thompson, in Theory of Chemical Reaction Dynamics, ed. M. Baer, Boca Raton, 1985, vol. 3, pp. 1–121.
85. S. Akpinar, I. Armenise, P. Defazio, F. Esposito, P. Gamallo, C. Petrongolo and R. Sayós, Quantum mechanical and quasiclassical Born–Oppenheimer dynamics of the reaction N₂(X¹Σ⁺_g) + O(³P) → N(⁴S) + NO(X²Π) on the N₂O a³A′′ and b³A′ surfaces, Chem. Phys., 2012, 398, 81–89.
86. F. Esposito, C. M. Coppola and D. De Fazio, Complementarity between quantum and classical mechanics in chemical modeling. The H + HeH⁺ → H₂⁺ + He reaction: a rigorous test for reaction dynamics methods, J. Phys. Chem. A, 2015, 119, 12615–12626.
87. F. J. Aoiz, V. Sáez-Rábanos, B. Martínez-Haya and T. González-Lezana, Quasiclassical determination of reaction probabilities as a function of the total angular momentum, J. Chem. Phys., 2005, 123, 094101.
88. D. C. Chatfield, S. L. Mielke, T. C. Allison and D. G. Truhlar, Quantized dynamical bottlenecks and transition state control of the reaction of D with H₂. Effect of varying the total angular momentum, J. Chem. Phys., 2000, 112, 8387–8408.
89. N. Zettili, Quantum Mechanics. Concepts and Applications, John Wiley and Sons, Chichester, UK, 2022.
90. J. M. Bowman, Reduced dimensionality theory of quantum reactive scattering, J. Phys. Chem., 1991, 95, 4960–4968.

---

Footnote

† Electronic supplementary information (ESI) available: Auxiliary figures are included in the ESI document, to mainly provide a more complete view of the reaction probability. See DOI: https://doi.org/10.1039/d5cp00539f

---