Intermolecular organization in aqueous mixtures of choline lysinate studied via NMR and molecular dynamics/quantum mechanics

Abstract

Aiming to scrutinize intermolecular organization in aqueous mixtures of the choline lysinate, [Cho][Lys], ionic liquid (IL), the dependence of the ¹H NMR chemical shifts and diffusion coefficients on their composition was measured. To rationalize experimental findings, extensive molecular dynamics (MD) simulations and linear response quantum mechanics/molecular mechanics (QM/MM) computations of NMR shielding constants were performed. Analysis of MD trajectories reveals that the extent of intermolecular contacts between cations and anions intensifies with the increasing content of the IL in the mixture. Moreover, the tendency of choline cations and the side chains of lysinate anions to self-aggregate was observed as well, leading to the formation of a continuous, highly polar domain composed of choline cations and the carboxylate groups of lysinate anions, as well as a less polar domain formed by the side chains of the anions in IL-rich mixtures. Under these circumstances, isolated water pockets are found to be situated at the interface of the polar and nonpolar ionic domains. The dependence of the measured diffusion coefficients on the composition of the mixture reveals the existence of two dynamical regimes – fast and slow regimes below and above molar fraction of the IL of 11%, respectively. Results of MD simulations suggest that – at this specific molar composition of aqueous [Cho][Lys] mixture – continuous water network ceases giving way to the continuous structure of ionic domains being formed. The QM/MM results for the ¹H NMR chemical shifts of aqueous IL mixtures generally agree well with experimental findings and corroborate structural results. The prominent upfield shift of the NMR signal of protons in fast exchange with the rising content of the IL was successfully rationalized.

---

1 Introduction

Ionic liquids (ILs) composed of choline cations and proteinogenic amino acid anions (Cho-AA ILs) have been developed in response to the need for eco-friendlier IL materials,^1–4 as conventional imidazolium or pyridinium ILs, for example, were observed to be harmful and nonbiodegradable.^5,6 Cho-AA ILs can be synthesized from natural precursors without any dangerous byproducts, and the nature of the constituents of the Cho-AA ILs renders these materials virtually nontoxic and readily decomposable by microorganisms.^7,8 Furthermore, structural diversity of natural amino acids assists in tuning various types of intermolecular interactions that can be formed between the ions, including electrostatic, polarization, charge transfer, dispersion as well as specific hydrogen bonding and π–π interactions.⁹ Cho-AA ILs can thus easily dissolve or be mixed with the variety of materials of diverse chemical nature, while problems related to their notoriously high viscosity – which can be higher by a few orders of magnitude than that of imidazolium ILs¹⁰ – can be usually dealt with by dilution with water. These attributes render Cho-AA ILs truly green and versatile in terms of applications in both industry and research laboratories.^4,9,11–13

Like other types of ionic liquids,¹⁴ Cho-AA ILs may exhibit heterogeneous nanosegregation^9,15–20 due to the presence of structural domains of different polarities in the nanometer range within the bulk of the liquid. Structural heterogeneity in the ILs can be detected experimentally by the appearance of a characteristic prepeak at low values of the scattering variable in their X-ray or neutron diffraction profiles.^9,18,21,22 A detailed account by Gontrani⁹ of the energy-dispersive X-ray diffraction measurements carried out on a series of Cho-AA ILs has revealed that the polarity of the side chain of the amino acid anion may be a determining factor governing the formation of polar and nonpolar domains in the Cho-AA ILs. The prepeak in the X-ray diffraction patterns emerged for ILs with nonpolar side chains of AA anions, except for the smallest anions glycinate, alaninate and cysteinate.⁹ The presence of the polar chemical groups in the side chain of the amino acid anion apparently destroys the domain structure within the IL leading to the absence of the prepeak in their X-ray diffraction patterns. This is also the case for the choline lysinate ([Cho][Lys]) IL, see Fig. 1, as its X-ray diffraction pattern does not exhibit the prepeak due to the presence of the polar amino group at position ε of the side chain, despite the side chain also containing an extensive nonpolar moiety of four consecutive methylene groups.

Fig. 1 Molecular structures and atom labeling of a choline cation, Cho⁺, and a lysinate anion, Lys⁻.

Conversely, neutron diffraction measurements on [Cho][Lys] clearly show a prepeak in the diffraction pattern, suggesting the presence of structural nanoorganization in this IL.¹⁸ The empirical potential structure refinement of the neutron diffraction data suggests an extremely heterogeneous morphology of [Cho][Lys] with clearly separated polar and non-polar domains composed of, respectively, charged and non-charged groups of choline and lysinate ions. This strong nanosegregation remains intact even if the [Cho][Lys] IL is mixed with water at a molar ratio of 1 : 5, with the molar fraction of the IL, χ_IL, equal to 0.17. In addition, water molecules were found to be condensed in clusters – the so-called water pockets – the average size of which was estimated to be 8 Å.¹⁸ Interestingly, neutron diffraction measurements on the ternary mixtures of [Cho][Lys], choline arginate and water still indicate structural nanosegregation in the lysinate-rich mixtures, but not in the arginate-rich mixtures.²⁰ Molecular dynamics (MD) simulations performed using the modified OPLS force field do show a degree of nanosegregation in the neat [Cho][Lys] IL and predict the appearance of the prepeak at the low values of the scattering variable.²³

To further scrutinize the structural organization of the aqueous [Cho][Lys] mixtures, we measured the composition dependence of their ¹H nuclear magnetic resonance (NMR) chemical shifts as well as of diffusion coefficients in a systematic manner. The composition of aqueous IL systems has been varied gradually starting from fairly dilute aqueous solutions of [Cho][Lys] with χ_IL values of ∼10⁻⁵ to IL-rich mixtures with χ_IL values of up to 0.66. Because NMR spectra generally include the responses from individual nuclei in the molecular system subject to the perturbation by the external magnetic field, they provide unique information concerning the site-specific intermolecular interactions formed in the sample. NMR has already been fruitfully utilized in the investigation of the structure and dynamics of the IL materials,^24–30 including elucidation of nanostructurization in ILs,^31–34 but – to the best of our knowledge – has not yet been applied to the study of intermolecular organization of Cho-AA ILs.

To resolve our experimental NMR results, we will rely on an integrated computational approach where classical MD simulations are combined with linear-response quantum mechanics/molecular mechanics (QM/MM) approaches for the calculation of NMR isotropic shielding constants. MD simulations is a proven tool for predictions of structural and dynamical properties of IL materials,^14,35–37 and we will use it here to analyze structural organization of aqueous [Cho][Lys] systems as well as to predict the diffusion coefficients. Furthermore, the sampling of the phase spaces of the considered systems will allow evaluating the statistical ensemble-averages of NMR shielding constants computed using the QM/MM approach. According to the QM/MM model, electronic properties of a central molecule are calculated by including the electrostatic interactions with the molecules in its environment which are represented by static multipole expansion, while mutual polarization interactions can be accounted for by using a polarizable potential.^38–40 In this way, discrete nature of the molecules in the environment is preserved, meaning that the QM/MM model should be able to account for inherent local anisotropic distribution of ions of the IL. Furthermore, non-electrostatic intermolecular interactions can be taken into account by including the relevant molecules of the environment to the quantum mechanically treated region of the model.^40–42 Concerning the predictions of ¹H NMR shielding constants for imidazolium ILs, we have recently demonstrated that QM treatment of ions in the first solvation shell is indeed important, especially of those involved in hydrogen bonding.⁴³ The effect of the ions beyond the first shell on the computed values of the ¹H NMR shielding of imidazolium cations was found to be surprisingly small, demonstrating that the ¹H NMR shielding constant is a rather local molecular property.⁴³ The combined MD-QM/MM approach has earlier been shown to be a viable route towards accurate predictions of the NMR spectra of IL materials.^43–47 We believe our large-scale computations will allow elucidating the connection between our experimental ¹H NMR results and structural findings from MD simulations.

2 Methods

2.1 Molecular dynamics simulations

All MD simulations were conducted using the Amber20 suite of programs.⁴⁸ Geometries of choline and lysinate ions in the all-anti conformation were optimised at the HF/6-31G* level of theory^49–51 using the Gaussian16 program.⁵² The point charges were then calculated using restrained electrostatic potential (RESP) procedure⁵³ based on the electrostatic potentials computed at the HF/6-31G* level. Thus, the developed point charges for choline and lysinate ions were scaled by a factor of 0.8. Charge reduction is in fact a common strategy used to account for charge transfer and polarization interactions in the MD simulations of ionic liquid systems, and it often leads to improved accuracy of predicted structural and in particular transport properties.^54–56 The general Amber force field (GAFF)^57,58 was employed to describe van der Waals interactions and intramolecular forces. GAFF atom types and point charges assigned to the choline and lysinate ions are collected in Tables S1 and S2, respectively, of the ESI.† A TIP4P-Ew model⁵⁹ was used for water molecules. Six aqueous mixtures of the [Cho][Lys] IL of different compositions were simulated as detailed in Table 1.

Table 1 Compositions of aqueous mixtures of [Cho][Lys] IL simulated in this work. Molar fractions of the IL and of water, χ_IL and χ_w, respectively, are given in percentage. Quantities N_IL and N_w indicate the numbers of [Cho][Lys] ion pairs and water molecules in each system, respectively

χIL	χw	NIL	Nw
0.025	99.975	1	4000
1	99	40	3960
5	95	150	2850
10	90	300	2700
30	70	450	1050
50	50	450	450

---

The system with χ_IL of 0.025% is rather to be considered as a single [Cho][Lys] ion pair at infinite aqueous dilution. The Packmol program⁶⁰ was employed to construct initial configuration of every system in a cubic simulation box.

MD simulations were performed using the Sander module of the Amber20 suite. Periodic boundary conditions were employed, and the leap-frog algorithm with a time step of 1 fs was used to integrate equations of motion. The SHAKE algorithm⁶¹ was exploited to constrain all bonds involving hydrogen atoms. A cutoff radius of 15 Å was set for short-range electrostatic and van der Waals interactions, and Ewald summation was used to account for long-range non-bonded interactions. A Langevin thermostat and a Berendsen barostat were applied for temperature and pressure control in the MD simulations.

After initial energy minimization, short NVT simulations of 5 ns at the temperature of 298 K were conducted. Then, the ensemble was switched to NPT to simulate every system at an elevated temperature of 400 K for 10 ns, followed by another 10 ns NPT simulations at 350 K. Simulations at high temperatures allow for a more exhaustive sampling of the phase space of the system, and gradual cooling of the system allows reaching a suitable statistical equilibrium. This strategy is useful in simulations of viscous molecular systems such as ILs in general and [Cho][Lys] in particular. Then, the NPT simulations were conducted for another 20 ns at the target temperature of 298 K. The pressure was set to 1 bar in all stages of NPT simulations, and the convergence of the density to a constant value was inspected in all cases. The ensemble was then switched back to NVT, and simulations proceeded for another 20 ns to finalize the equilibration phase. The production run in the NVT ensemble followed for 20 ns, and molecular configurations were sampled in steps of 2 ps to be used in structural analysis. Finally, to sample the trajectories for the calculations of diffusion coefficients, the simulations in the NVT ensemble were extended for another 2 ns for systems with χ_IL ≤ 5% and for 6 ns for systems with χ_IL > 5%, sampling the trajectories every 100 fs. The Einstein expression relating the diffusion coefficient to the slope of the mean-square displacement (MSD) function was employed.⁶²

2.2 QM/MM calculations

The linear-response QM/MM method^39,40 based on the gauge including atomic orbital approach and density functional theory as implemented in the Dalton electronic structure program⁶³ has been employed for the calculations of the ¹H NMR isotropic shielding constants in this work. The PBE0 exchange–correlation functional⁶⁴ and Ahlrichs def2-TZVP basis set⁶⁵ were applied for the QM subsystem of the model. The PBE0 functional has generally been proven to provide reliable results for NMR shielding constants,^41,66,67 and in addition it has been benchmarked against high-level coupled cluster methods for relative ¹H NMR spectra of imidazolium cations, another important cationic constituent of IL materials.⁴⁷ The def2-TZVP basis offers well-converged chemical shifts owing to the well-known error cancellation in computing them as differences of the isotropic shielding constants; see, for example, ref. 42, 43, 47, and 68. The classical subsystem was represented by a point charge distribution, using the same point charges for choline and lysinate ions as in the MD simulations. Point charges from the TIP3P potential⁶⁹ were assigned to classical water molecules. Condensed-phase results for NMR shielding constants are obtained as statistical averages over 100 molecular configurations selected from the MD trajectories at regular intervals of 200 ps. Central molecule in the QM/MM model was chosen randomly in every molecular configuration, except for the case of choline or lysinate at infinite aqueous dilution where only a single [Cho][Lys] ion pair was present in the system. We have applied a spherical cutoff radius of 25 Å centered at the center of mass of the central molecule for every molecular configuration. The QM region of the model was always expanded to include those ions and water molecules that were found in the first coordination shell of the specific site in the central molecule, the shielding constants of which were of interest. Table S3 of the ESI† provides further details concerning the construction and composition of the QM region in all series of QM/MM calculations, while Fig. S2 (ESI†) illustrates some representative structures of the QM region. The def2-TZVP basis set was applied for the entire QM region in all cases. Statistical errors of averaged shielding constants were evaluated according to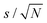 where s is sample standard deviation and N is the sample size.

2.3 NMR experiment

IL [Cho][Lys] was purchased from IoLiTec GmbH (>90% purity, water content 10%) and was used without further purification. Aqueous IL mixtures were prepared using deionized water directly in NMR tubes by weighting the components using KERN ABJ-NM/ABS-N analytical balances (±0.1 mg). The exact concentrations of aqueous IL mixtures were verified by analyzing integral intensities of NMR spectral lines. A capillary insert filled with D₂O and a sodium trimethylsilylpropanesulfonate (DSS) mixture was used for magnetic field stabilization and for chemical shift referencing. All NMR measurements were performed on a Bruker AVANCE Neo 600 MHz NMR spectrometer using a Bruker Ascend 14.1 T superconducting magnet and a 5 mm BB TBI probe, which produces 50 G cm⁻¹ magnetic field gradients. For ¹H NMR measurements, π/3 excitation and 4–200 scans were accumulated. The temperature was stabilized at (25.0 ± 0.1) °C, and the repetition delay was set to 5 s.

For ¹H DOSY measurements, a pulse sequence using stimulated echo, LED and bipolar gradients was used (ledbpgpz). For every measurement, 32 scans were collected for 32 increments with 2–98% of gradient strength, the duration of which was set to 650–4500 μs and diffusion time was 50–100 ms depending on the sample concentration; repetition delay was set to 5 s. The diffusion coefficients were determined from the integral intensities by varying the gradient strength, g, and the data were processed using a well-known equation:

where I₀ is the peak intensity without gradient, D is the diffusion coefficient, γ is the gyromagnetic ratio of the observed nucleus, δ is the duration of the gradient pulse and Δ is the delay between gradient pulses, i.e. the diffusion time.

3 Results and discussion

3.1 Structural analysis of MD trajectories

3.1.1 Conformational equilibrium. Choline cation may acquire either an anti or a gauche conformation with respect to the rotation around its C–C bond. The difference between the electronic energies of the two isolated conformers computed using Gaussian16⁵² at the B3LYP/aug-cc-pVTZ level of theory^70,71 is by 16.1 kJ mol⁻¹ in favour of the gauche conformation, and is thus in good agreement with the conclusions of a previous computational study.⁷² The analysis of the trajectories recorded for all six systems simulated in this work has revealed that choline predominantly adopts the gauche conformation, and its anti conformation occurs rarely. The proton of the hydroxyl group in choline is, on the other hand, mostly found in the anti position with respect to the rotation around the C–O bond, while the gauche conformation is apparently infrequent.

The analysis of the neutron diffraction data using the empirical potential structure refinement procedure suggests that lysinate anions may often adopt the cyclic conformation stabilized by the intramolecular hydrogen bond between the amino group at the ε position and the oxygen atom in the carboxylate moiety, both in neat [Cho][Lys] IL and in its aqueous mixture.¹⁸ In Fig. 2, we show the distribution of the intramolecular distances between the N_ε atoms and oxygen atoms in the carboxylate group computed for our simulated mixtures with χ_IL of 10, 30 and 50%.

Fig. 2 Probability distribution of intramolecular distances between the N_ε atom and oxygen atoms of the carboxylate group of lysinate anion in aqueous mixtures of [Cho][Lys] IL.

In contrast to the findings of ref. 18, lysinate anions are virtually never found to adopt the cyclic conformation. In contrast, they mostly exhibit rather extended conformations having in mind that the distance between N_ε and oxygen atoms of the carboxylate in all-anti conformation of lysinate is around 8 Å.

3.1.2 Radial distribution functions. To study the intermolecular organization of aqueous [Cho][Lys] systems, we first discuss the dependence of the coordination numbers around various sites in choline, lysinate and water molecules on the composition of the mixture. Atom labeling in choline and lysinate ions as presented in Fig. 1 is used throughout this paper. In order for such analysis to be meaningful, the coordination numbers have been calculated by spherical integration of relevant radial distribution functions (RDFs) to systematically chosen limiting values for the interatomic distances. The RDFs we have analyzed are collected in Fig. S3–S31 of the ESI.† The captions of these figures also include information concerning the specific values of the integration limits used to obtain the coordination numbers discussed henceforth.

Fig. 3 shows the coordination numbers of various sites in choline, lysinate and water molecules around the oxygen and nitrogen atoms of the choline cation as functions of the composition of the mixture.

Fig. 3 Coordination numbers, CN, of various sites in choline, lysinate and water molecules around oxygen atom (a) and nitrogen atom (b) in choline cations as a function of the composition of aqueous [Cho][Lys] mixture given in terms of molar fraction of the IL, χ_IL. Refer to Fig. 1 for atom labeling.

While the molar fraction of the IL is low, the hydroxyl group of choline is mostly involved in hydrogen bonding interactions with water molecules in the capacity of both the hydrogen bond donor and acceptor. However, as seen in Fig. 3a, the increasing aggregation of choline cations through intermolecular interactions between the methyl groups of their N–(CH₃)₃ moieties and their hydroxyl groups becomes more pronounced with the rising content of the IL in the mixture. This phenomenon has been also previously observed in the MD simulation study of the aqueous choline glycinate mixture.⁷³ Furthermore, hydrogen bonding interactions between the hydroxyl group of choline and the carboxylate group of lysinate anions have become increasingly more common as well. Considerable qualitative shift in the molecular distribution around the hydroxyl group of choline apparently occurs for χ_IL in-between 10 and 30%. At χ_IL = 10%, there still is, on average, one water molecule forming the hydrogen bond with the OH group of choline. However, as is evidently seen in Fig. 3a, hydrogen bonding between choline and water molecules becomes much less common at χ_IL of 30% and even less so at χ_IL of 50%. The OH group of choline now becomes mainly coordinated by the N–(CH₃)₃ groups of choline and is frequently involved in hydrogen bonding with the carboxylate groups of lysinate anions. Both amino groups of lysinate anions are seen to form hydrogen bonds with the OH group of choline as well, to some extent. The analysis of the RDFs between hydrogen atoms in the amino groups of lysinate and oxygen atoms of choline suggests that the OH group of choline acts more frequently as hydrogen bond acceptor in these situations. We also note that aggregation of choline cations via hydrogen bonding between their hydroxyl groups is never seen as a significant occurrence.

As seen in Fig. 3b, the N–(CH₃)₃ group of choline is predominantly coordinated by water molecules while the content of water is relatively high. With the rising molar fraction of the IL, considerable increase in the coordination of the N–(CH₃)₃ moieties of cholines by the carboxylate groups of lysinate anions is observed. The tendency for the aggregation of choline cations through their N–(CH₃)₃ groups is also evident, as previously observed in the case of choline phenylalaninate IL.⁷⁴ While these particular types of interaction are found to predominate in mixtures with higher values of χ_IL, the presence of a few water molecules around the bulky N–(CH₃)₃ group of choline is still common even at χ_IL of 50%. It is seen that direct interactions between the N–(CH₃)₃ group of choline and amino groups in lysinate as well as the hydroxyl group in choline are relatively rare throughout the entire range of compositions of studied aqueous [Cho][Lys] mixtures.

Due to the presence of two oxygen atoms in the carboxylate group, inspection of the molecular coordination around carboxylate groups of lysinate anions is not straightforward. However, the two oxygen atoms are equivalent as the carboxylate group in lysinate can rotate around the C–C_α bond rather easily. All RDFs computed for the two oxygen atoms of lysinate are essentially identical. Therefore, we show the composition dependence of the molecular coordination only around one of the oxygen atoms of the carboxylate group of the lysinate anion in Fig. 4a.

Fig. 4 Coordination numbers, CN, of various sites in choline, lysinate and water molecules around one of the oxygen atoms of carboxylate group (a) as well as around the nitrogen atoms of the two amino groups (b) and (c) in lysinate anions as a function of the composition of aqueous [Cho][Lys] mixture given in terms of the molar fraction of the IL, χ_IL. Refer to Fig. 1 for atom labeling.

While data shown in Fig. 4 will not account for the changes in the molecular coordination around the entire carboxylate group with the varying composition of the mixture, we believe that recorded trends ought to be sufficiently conclusive.

As expected, the carboxylate moiety of lysinate anions is mostly coordinated by water molecules at χ_IL of 10% and below. With the rising content of the IL, however, rapid increase in pairing of choline and lysinate ions takes place. Previous MD simulation studies have revealed that amino acid anions tend to interact with choline cations by forming hydrogen bonds to their hydroxyl groups and by direct interaction with their N–(CH₃)₃ moieties.^74,75 Our MD simulations show that the carboxylate moiety of lysinate happens to be more intensively coordinated by the N–(CH₃)₃ groups of choline rather than by the hydroxyl moieties. At χ_IL of 30 and 50%, the N–(CH₃)₃ group of choline is apparently the most frequent moiety in the coordination sphere of the carboxylate group. Water molecules are still found in the vicinity of the carboxylate group as well. Even though carboxylate groups of the anions are the most frequent hydrogen bonding partners for the choline cations at χ_IL of 30 and 50%, from the perspective of the lysinate anions, water molecules appear to be more frequent hydrogen bonding partners for their carboxylate groups than choline cations, even in the equimolar mixture. Our results, however, do not support the conclusion drawn in ref. 76 that [Cho][Lys] can completely dissociate into free hydrated ions at χ_IL below 30%. As seen in Fig. 4a, ion pairing is still considerable for χ_IL as low as 5%. Much more dilute aqueous solutions of [Cho][Lys] appear to be required for the complete dissociation of the IL into free ions.

It is evident in Fig. 4a that dimerization of lysinate anions by hydrogen bonds formed between their carboxylate and any of the two amino groups is relatively scarce. As seen in Fig. 4b and c, coordination sphere around both amino groups of lysinate is dominated by water when molar fraction of the IL is below 30%. The tendency of the bulky N–(CH₃)₃ moieties of choline cations to be increasingly more often found within the coordination spheres of the two amino groups of lysinate anions with the rising content of the IL in the mixture is quite evident. The hydrogen bonding of the two amino groups with other potential partners is otherwise more or less equally infrequent for the entire range of χ_IL. The dimerization of the lysinate anions, however rare, occurs more frequently via hydrogen bonding of the carboxylate moiety with the amino group at the ε position rather than with that at the α position.

In Fig. 5, we show the composition dependence of the molecular coordination around water molecules.

Fig. 5 Coordination numbers, CN, of various sites in choline, lysinate and water molecules around the oxygen atom in water molecules as a function of the composition of the aqueous [Cho][Lys] mixture given in terms of molar fraction of the IL, χ_IL. Refer to Fig. 1 for atom labeling.

Naturally, in the systems where water dominates, χ_IL of 10% and below, hydrogen bonding interactions between water molecules are prevalent. For systems where amounts of water molecules and of [Cho][Lys] ion pairs are comparable, the N–(CH₃)₃ groups of choline cations are found to coordinate with water molecules most frequently, apparently due to the bulkiness of this chemical group. On the other hand, the hydroxyl moiety of choline is seen to be the least frequent hydrogen bonding partner of water molecules. As discussed above, hydroxyl groups of choline cations are rather involved in hydrogen bonding with the carboxylates of lysinates, in addition to being often coordinated by the N–(CH₃)₃ groups of neighbouring cholines. The carboxylate groups of anions are also frequently found in the vicinity of water molecules at χ_IL of 30 and 50%. The two amino groups of lysinate anions are observed to coordinate water molecules rather infrequently. Finally, while at χ_IL of 30% the aggregation of water molecules seems to be still a relatively common occurrence, the self-coordination number of water molecules drops to 0.7 at χ_IL of 50%, implying that solitary water molecules may now be likely often found within the matrix of the IL.

3.1.3 Nanostructural organization. The analysis of the local structure of aqueous [Cho][Lys] systems described above suggests a possibility of ionic segregation into domains of higher and lower polarity. The electrostatic potential maps computed for choline and lysinate ions in ref. 76 allow entire choline cation as well as the carboxylate group of the anion to be considered as highly polar, while the side chain of the lysinate including the amino group at ε position is apparently of considerably lower polarity. We have thus first analyzed the propensity of choline cations to self-aggregate. Two choline cations were considered to belong to the same cationic cluster if at least one interatomic distance between any of their heavy atoms is below the cut-off value of 4.5 Å. This specific cut-off value has been chosen as it corresponds to the first minimum in the O2-Cm and Cm-Cm RDFs shown in Fig. S9 and S31 of the ESI,† respectively. The analysis shows that choline cations form a system-wide cationic network that percolates the entire simulation box when χ_IL is 50 and 30%. The enhanced content of water in the mixture leads to the breakdown of the continuous network of choline cations into smaller clusters. Still, clusters consisting of around 100-to-200 choline cations are found to be common in the mixture of χ_IL = 10%. At χ_IL = 5%, solitary cations as well as small clusters of 2–6 choline molecules are most frequently found, yet larger clusters of 10–15 choline cations are not unusual as well.

Similar analysis was performed to inspect the possible aggregation of side chains of the lysinate anions. To be consistent, we consider the side chains of two lysinate anions to be aggregated if the smallest distance between any two heavy atoms in their atomic sequences of C_β to N_ε is smaller than 4.5 Å. As in the case of choline cations, the side chains of lysinate anions are found to be aggregated into a single percolating domain of lower polarity at χ_IL of 50 and 30%. At χ_IL of 10%, the continuous non-polar domain is broken into smaller clusters, yet again they may be composed of as many as 100–170 lysinate anions. Furthermore, at χ_IL of 5%, smaller cluster of lysinate side chains including 2–9 molecules as well as solitary lysinate anions are most common, but larger clusters of 10–20 lysinate anions may occasionally be encountered as well.

To inspect self-aggregation of water molecules, we have performed an analysis of the size distribution of water clusters in our simulated systems. We consider two water molecules to belong to the same cluster if the distance between their oxygen atoms falls within 3.5 Å. The size distribution of water clusters at χ_IL of 50 and 30% is shown in Fig. 6.

Fig. 6 Probability for a randomly selected water molecule to belong to a cluster of N water molecules in aqueous mixtures of [Cho][Lys] at χ_IL of 30 and 50%.

At χ_IL of 50%, solitary water molecules are most likely; however, clusters of a few water molecules may still be commonly encountered. Water clusters of more than 10–12 water molecules are found to be highly unlikely. In the mixture with χ_IL of 30%, larger water clusters become evidently probable, and thus clusters of up to around 40 water molecules can be formed. The analysis of the trajectory recorded for the system with χ_IL = 30% has revealed that water clusters of up to 120 water molecules may be encountered on the course of simulation of 20 ns. At χ_IL of 10%, water molecules are already found to join in a percolating aqueous network which surrounds the ionic aggregates of choline and lysinate molecules.

In Fig. 7, still images of randomly chosen snapshots of simulation boxes from trajectories recorded for the systems with χ_IL of 50, 30 and 10% are illustrated.

Fig. 7 Domains of high and low polarity as well as of water molecules in aqueous mixtures of [Cho][Lys] at molar fractions of the IL, χ_IL, of 50, 30 and 10%. High polarity domain is composed of entire choline cations and carboxylate groups of lysinate anions and is shown in red. Low polarity domain includes side chains as well as C_αH-N_αH₂ fragments of lysinate anions and is colored in grey. The aqueous domain is shown in blue. Thus selected molecular regions are rendered as surfaces with probe radius 1.4 Å using Visual Molecular Dynamics program.⁷⁷

At χ_IL of 50%, continuous networks of high and low polarity are evident, together with small clusters of water composed of mostly a few molecules. Extensive domains of high and low polarity are still persistent at χ_IL of 30%, just the sizes of water aggregates are considerably increased. Qualitative analysis shows that water clusters at χ_IL of 50 and 30% are rather linear in nature and they are mostly found to be situated at the interface of the polar and nonpolar ionic domains. At χ_IL of 10%, water is now seen to form a continuous percolating network with polar and nonpolar ionic domains to be found within.

3.2 Diffusion coefficients

The dependencies of experimental and computational values of diffusion coefficients for choline, lysinate and water molecules on the composition of the aqueous [Cho][Lys] mixture are shown in Fig. 8.

Fig. 8 Diffusion coefficients, D, of choline, lysinate and water molecules as function of the molar fraction of the IL, χ_IL, in aqueous mixtures of [Cho][Lys]. Experimental values based on pulse-gradient ¹H NMR measurements are indicated by open points. Computational values are shown by full points, and they are based on the simulated MSD functions for centers of mass of choline and lysinate as well as for oxygen atoms of water molecules.

Experimental values of diffusion coefficients of choline and lysinate ions are generally found to be fairly independent of the position of the chemical group from which the ¹H NMR signals were selected to derive them. Experimental diffusion coefficients are found to decrease with the increasing molar fraction of the IL, in line with the simultaneously increasing viscosity of the mixture. Magnitudes of the diffusion coefficients of choline, lysinate and water molecules are found to correlate inversely with their molar masses. It is evident in Fig. 8 that diffusion coefficients of all three species given in the log scale are decreasing in the linear fashion with the rising content of the IL in the mixture. However, two dynamical regimes can be identified as linear dependencies of diffusion coefficients exhibit different slopes in water-rich and IL-rich aqueous mixtures of [Cho][Lys]. Based on our structural analysis, we are inclined to conclude that the change in the dynamical regime is due to the disruption of the continuous water network induced by the rising molar fraction of the IL in the mixture. Accordingly, our experimental results suggest that continuous water network ceases at χ_IL of around 11%. Beyond this value of χ_IL, the extent of continuous ionic domain increases with the rising content of the IL, and clusters of water molecules are found to be trapped within this relatively less mobile ionic matrix. Consequently, the mobility of the ions and of water molecules ought to change slower with the increasing χ_IL as compared to the case where ionic aggregates are immersed in the relatively mobile continuous network of water molecules, just as suggested by the experimental data in Fig. 8.

MSD functions simulated in this work are shown in Fig. S32 of the ESI† file. Computed values of diffusion coefficients for choline, lysinate and water molecules are in very good quantitative agreement with the corresponding experimental data at the lowest molar fraction of the IL of 1%. Otherwise, theoretical diffusion coefficients are found to be generally of higher magnitude as compared to corresponding experimental values. In qualitative terms, however, MD simulations confirm the existence of the two dynamical regimes in aqueous mixtures of [Cho][Lys]. Furthermore, just as in the case of experimental data, MD simulations predict linear dependencies of the diffusion coefficients given in the log scale on the molar fraction of the IL for all three species when the content of the IL is relatively low. For IL-rich mixtures, linear dependence of diffusion coefficients on χ_IL of reduced slope compared to that for water-rich mixtures could also be inferred, although this conclusion is only based on two data points for each molecule.

3.3 Experimental ¹H NMR chemical shifts

Fig. 9 illustrates the composition dependencies of the ¹H NMR chemical shifts of aqueous [Cho][Lys] mixtures.

Fig. 9 The dependencies of the ¹H NMR chemical shifts, δ, of choline and water molecules (a) as well as of lysinate anions (b) on the molar fraction of the IL, χ_IL, of aqueous mixtures of [Cho][Lys]. Refer to Fig. 1 for atom labeling.

Samples of the ¹H NMR spectra together with signal assignment for mixtures at χ_IL of 1.3 × 10⁻⁴, 0.11 and 0.40 are shown in Fig. S33 of the ESI.† The dependence of the ¹H NMR chemical shifts of choline and lysinate ions on the molar composition of the aqueous IL mixture could be generally considered to be fairly modest as most chemical shifts vary in the range of only around 0.2 ppm – in contrast, for example, to aqueous mixtures of some imidazolium ILs where chemical shift variations of more than 1 ppm could be observed.^30,43 As seen in Fig. 9a, all three ¹H NMR chemical shifts of choline cations are found to be independent of the composition of the mixture for χ_IL in the range of 10⁻⁵ to 10⁻³. This finding could imply the presence of free fully water-solvated choline cations under these conditions, unless these chemical shifts happen to be insensitive to the formation of contact ion pairs between choline and lysinate via hydrogen bonding between their hydroxyl and carboxylate groups, respectively. Once molar fraction of the IL rises beyond 10⁻³, small upfield shifts of all three signals can be observed. In the cases of protons in the N–(CH₃)₃ group and at position 1 of choline, their chemical shifts are reduced by some 0.10–0.11 ppm until an χ_IL value of around 0.11 is reached. Further increase in the content of the IL in the mixture leads to the downfield shifts of these two signals, eventually increasing by 0.15 ppm at χ_IL of 0.66. The ¹H NMR signal of protons at position 2 in choline exhibits similar dependence, just the character from decreasing to mildly increasing chemical shift is switched at the χ_IL value of around 0.25 in this case.

Unlike for choline cations, ¹H NMR chemical shifts of lysinate anions are clearly not converged with the progressing dilution of the IL even up to an χ_IL value of 1.7 × 10⁻⁵, see Fig. 9b. These findings imply that some degree of self-aggregation of lysinate anions may still take place even in these dilute aqueous solutions of [Cho][Lys]. The strongest dependencies of chemical shifts of lysinate were recorded for protons at positions α and ε in the side chain, i.e. for protons that were closest to the hydrogen bonding capable groups of the anion. These NMR signals exhibit monotonic upfield shifts of around 0.4–0.5 ppm, comparing the corresponding values of chemical shifts at the lowest and highest χ_IL of 1.7 × 10⁻⁵ and 0.66, respectively. The chemical shifts of remaining methylene groups in lysinate exhibit a weaker dependence on the composition of the mixture. The ¹H NMR signals of the two diastereotopic protons at the β position in lysinate could be resolved separately. The difference between their chemical shifts is seen to increase with the rising content of the IL in the mixture, and their composition dependencies are seen to pose different qualitative characters in the range of χ_IL from around 0.11 to 0.66.

In general, most pronounced changes in the ¹H NMR chemical shifts of choline and lysinate ions occur in the range of χ_IL from around 10⁻² to 0.66. Remarkably, some of the chemical shift dependencies of choline and lysinate ions are seen to switch their qualitative character from decreasing to increasing at χ_IL of around 11%, i.e. at the same point where dynamical regimes of the mixtures were observed to change. The dependencies of the chemical shifts shown in Fig. 9 apparently reflect the dramatic intermolecular reorganization of aqueous [Cho][Lys] mixtures taking place in this range of their composition. These restructurings are apparently more complex than a simple picture in which water molecules surrounding choline and lysinate ions at low IL content in the mixture are gradually replaced by ions as χ_IL increases.³⁰ As suggested by present MD simulations, chemical shift trends in Fig. 9 could be a spectroscopic signature of breaking continuous water network and simultaneously forming continuous ionic domains of higher and lower polarity at χ_IL of around 11%.

Because hydrogen bonding interactions between the ions and water molecules in aqueous Cho-AA IL mixtures are extensively formed,^{15,18,20,23,76,78} NMR chemical shifts of protons involved in hydrogen bonds could in principle be excellent spectroscopic probes of the local structure of these materials. However, fast proton exchange between water molecules and polar hydrogen-bonding-capable groups of the ions is expected to take place meaning that only an averaged value of the chemical shift of protons involved in exchange could be measured, as indeed observed for other choline ILs.⁷⁹ Separate ¹H NMR signals from OH groups of choline cations or from the two amino groups of lysinate anions were never resolved in our ¹H NMR spectra of aqueous [Cho][Lys] mixtures, indicating the occurrence of fast proton exchange in the considered range of their molar compositions. In the mixtures where water dominates, the measured chemical shift of 4.78 ppm corresponds to the value of liquid water, as seen in Fig. 9a. The measured chemical shift of fast-exchanging protons is recorded to alter only after the molar fraction of [Cho][Lys] becomes much larger than 10⁻², eventually suffering a considerable monotonic decrease of 0.92 ppm at a χ_IL value of 0.66.

3.4 Computational ¹H NMR results

Attempting to unravel the composition dependence of the chemical shift of protons involved in fast chemical exchange in Fig. 9a, we turn to the linear response QM/MM calculations. Assuming fast chemical exchange of protons in water molecules, hydroxyl groups of choline cations and amino groups of lysinate anions, the observed chemical shift should be related to the averaged value of their ¹H NMR isotropic shielding constants, σ_ave, according to

σ_ave = χ_Hwσ_Hw + χ_HOσ_HO + χ_HNaσ_HNa + χ_HNeσ_HNe. (1)

In this equation, χ_Hw, χ_HO, χ_HNa and χ_HNe are molar parts of protons in, respectively, water molecules, hydroxyl groups of choline cations, and amino groups at positions α and ε in lysinate anions, appropriate for a given composition of the aqueous [Cho][Lys] mixture. Quantities σ_Hw, σ_HO, σ_HNa and σ_HNe are the corresponding isotropic shielding constants. The advantage of present integrated MD-QM/MM computational approach is that it allows for the determination of shielding constants of protons at every site involved in fast chemical exchange – something that is generally difficult to accomplish experimentally. We present the QM/MM-based ensemble averages of the ¹H NMR isotropic shielding constants of protons in water, hydroxyl group of choline and amino groups in lysinate molecules computed for the [Cho][Lys] ion pair at infinite aqueous dilution and for aqueous [Cho][Lys] mixtures at χ_IL of 10 and 50% in Table 2.

Table 2 Computational QM/MM results for ¹H NMR isotropic shielding constants (in ppm) of protons in water, choline and lysinate molecules that are involved in fast exchange. Statistical errors are provided in parentheses. Also given are the averaged values of shielding constants for given composition of the mixture. Calculated and measured changes in averaged chemical shifts of protons in fast exchange with respect to those at infinite dilution, Δδ_calc and Δδ_exp, respectively, are provided in the last two lines

		χIL
		Inf. dil.	0.1	0.5
a Computed value for neat water taken from ref. 43.b Computed using eqn (1) with χHw = 18/23, χHO = 1/23 and χHNα = χHNε = 2/23.c Computed using eqn (1) with χHw = χHNα = χHNε = 2/7 and χHO = 1/7.d Estimated using experimental data shown in Fig. 9a.
H2O	σHw	28.20^a (0.09)	27.87 (0.10)	27.29 (0.08)
Cho^+	σHO	28.03 (0.14)	27.26 (0.14)	26.39 (0.16)
Lys^−	σHNα	30.07 (0.06)	30.10 (0.06)	30.23 (0.06)
	σHNε	30.26 (0.06)	30.19 (0.08)	30.27 (0.09)
σave		28.20	28.24^b	28.85^c
Δδcalc		—	−0.04	−0.65
Δδexp		—	−0.07^d	−0.62^d

---

The ¹H NMR shielding constant of water at infinite dilution of the [Cho][Lys] ion pair in Table 2 corresponds to that of neat TIP4P-Ew water, previously calculated by us using virtually identical computational protocol as in the present work.⁴³

As seen in Table 2, considerable deshielding of protons of water molecules and even more so of those in hydroxyl groups of choline cations with the rising content of the IL in the mixture is predicted. These results are in fact to be expected based on present structural analysis showing that these moieties are increasingly involved in strong hydrogen bonding with the carboxylate groups of lysinate anions with rising content of the IL in the mixture. In contrast, the shielding constants of protons in the two amino groups of lysinate anions are computed to be virtually independent of the molar composition of the mixture. This could have been again anticipated because of the limited capacity of these groups to be involved in hydrogen bonding with the carboxylates of the anions even at highest values of χ_IL. We also note that the thus predicted ¹H NMR chemical shifts of the amino groups would be considerably smaller than those of water molecules or hydroxyl groups of choline cations.

The averaged values of the shielding constants of protons in fast exchange calculated for aqueous [Cho][Lys] mixtures with χ_IL of 10 and 50% are progressively larger than that predicted for neat water, see Table 2. The results imply the lowering of the chemical shift of exchanging protons with the rising content of the IL in the mixture just as recorded experimentally in Fig. 9a, and this effect is predicted rather accurately in quantitative terms as well. In conclusion, the upfield shift of protons in fast exchange observed with the rising molar fraction of [Cho][Lys] in the mixture is due to the presence of the two amino groups in the lysinate anions, the protons of which are shielded considerably more than those of water molecules or hydroxyl groups of choline cations. The relative weight of the amino groups into the averaged value of the shielding constant increases with χ_IL, leading to the overall upfield shift observed experimentally. This joint theoretical and experimental finding shows rather firmly that these amino groups are involved in hydrogen bonding with the carboxylate groups of lysinate anions to a considerably smaller extent than water or choline molecules, in contrast to the conclusion arrived at in ref. 18.

Computational QM/MM results for ¹H NMR isotropic shielding constants of selected sites in choline and lysinate ions at infinite dilution and at χ_IL of 10 and 50% are presented in Table 3.

Table 3 Computational QM/MM results for ¹H NMR isotropic shielding constants (in ppm) of protons of selected groups in choline and lysinate ions for different compositions of aqueous [Cho][Lys] mixture. Statistical errors are given in parentheses. See Fig. 1 for atom labeling

		χIL
		Inf. dil.	0.1	0.5
Cho^+	H1	27.78 (0.04)	27.69 (0.05)	27.53 (0.06)
	H2	27.17 (0.03)	27.22 (0.03)	27.29 (0.03)
Lys^−	Hα	28.14 (0.04)	28.30 (0.04)	28.43 (0.05)
	Hε	28.81 (0.03)	28.81 (0.03)	28.75 (0.04)

---

The computed values for protons at positions 1 and 2 in choline at infinite dilution lead to the difference in their chemical shifts of 0.61 ppm, thus in good qualitative and quantitative agreement with the corresponding experimental value of 0.55 ppm. With the rising molar fraction of the IL, progressive increase in the shielding constant and thus decrease in the chemical shift of protons at position 2 in choline is predicted. These results are in line with the experimental measurements in Fig. 9a, and the computed change in the chemical shift between mixture with χ_IL of 50% and infinite dilution conditions of −0.12 ppm compares fairly well to the corresponding experimental result of −0.19 ppm. For the protons of the methylene group at position 1 in choline, computational model suggests a monotonic upfield shift with the rising content of the IL in the mixture, increasing by 0.25 ppm at χ_IL of 50% compared to the case of free water-solvated choline cations. The computed difference is considerably larger than 0.04 ppm observed experimentally. Furthermore, however, the model fails to predict the recorded change in the character of the composition dependence of this NMR signal from decreasing up until χ_IL of around 11% and increasing beyond that. Arguably, experimentally observed rather subtle variation of this chemical shift by some 0.1 ppm may be beyond the accuracy achievable by present computational scheme.

We have also attempted to compute the dependence of the chemical shifts of protons at positions α and ε in lysinate anions on the composition of the mixture, see Table 3. At infinite dilution, the difference between chemical shifts of protons in these two groups is predicted to be 0.67 ppm, thus considerably larger than experimental value of 0.36 ppm recorded for χ_IL of 1.7 × 10⁻⁵. As discussed above, experimental data in Fig. 9b suggests that lysinate anions may not be at the conditions of infinite dilution even at this low value of χ_IL, and that could be the origin of the quantitative disagreement between computational and measured values. In line with experimental observations, QM/MM calculations predict a monotonic decrease of the chemical shift of the proton at position α in lysinate with increasing χ_IL. At the χ_IL value of 50%, the computed chemical shift is thus by 0.29 ppm smaller than that at infinite dilution. This computational result compares to the corresponding experimental estimate of around 0.40 ppm fairly well. However, QM/MM scheme predicted that chemical shift of protons at position ε is virtually independent on the composition of the mixture, thus in stark disagreement with experimental data in Fig. 9b where this particular chemical shift exhibits largest variation with the content of the IL in the mixture.

Discrepancies between our computational and experimental NMR results suggest the possibility of certain imperfections in the computational model applied in this work. The accuracy of an integrated computational approach that combines classical MD simulations and QM/MM electronic structure calculations of NMR shielding constants depends on an interplay of a few factors, such as the quality of the force field used in the MD simulations as well as the electronic structure method selected for QM/MM calculations. As the ultimate aim here is to investigate the dependence of structural properties of binary aqueous IL mixtures on their composition, the reliability of the effective potential used in the MD simulations is of utmost importance, also because the structure of the molecular system governs its properties, including its NMR spectra. The said discrepancies could be potentially linked to the rather standard pair-wise potential used in the MD simulations in this work. To date, there are no force fields developed specifically for Cho-AA ILs. Furthermore, the force field parametrization for ions of [Cho][Lys] was assumed to be independent of the composition of aqueous IL mixtures, and in particular the point charges developed specifically for different compositions of a binary mixture could lead to improvement of the structural results as demonstrated previously.^80,81 These issues could be partly mitigated by using polarizable potentials, the development of which for the IL systems is currently pursued.⁸² Despite the few discrepancies, the fact that we have obtained reasonable qualitative and quantitative agreement between computed and measured diffusion coefficients – a property that is known to be particularly challenging to model for IL systems using classical simulations⁸³ – lends some support to the validity of the force field parametrization selected for ions of [Cho][Lys] IL and water molecules in this work. Further justification is due to, in most cases, the correctly predicted trends for the ¹H NMR chemical shifts, and in particular due to the qualitatively and quantitatively correctly described behaviour of the ¹H NMR chemical shift of fast-exchanging protons. We are therefore inclined to believe that present study constitutes a substantial contribution to the development of general computational spectroscopy protocols for accurate prediction of NMR properties of ionic liquid materials in bulk phases.⁸⁴

4. Conclusions

In this work, the intermolecular organization of aqueous mixtures of the choline lysinate ionic liquid was scrutinized via complementary ¹H NMR experiments and molecular modelling techniques including classical MD simulations and linear response QM/MM approaches for computing NMR shielding constants. Dependencies of the ¹H NMR chemical shifts on molar composition of aqueous [Cho][Lys] mixtures with molar fraction of the IL in the range of 1.7 × 10⁻⁵ to 0.66 were measured. The ¹H DOSY experiments were performed to obtain diffusion coefficients of choline, lysinate and water molecules in mixtures with χ_IL in the range from 0.01 to 0.25. MD simulations of aqueous [Cho][Lys] mixtures ranging from single ion pair at infinite dilution to equimolar composition were conducted. To rationalize the observed dependencies of ¹H NMR chemical shifts of choline, lysinate and water on the molar composition of aqueous IL mixtures, extensive QM/MM calculations of the ¹H NMR isotropic shielding constants for sets of molecular snapshots taken from the MD trajectories were performed.

Analysis of MD trajectories recorded for aqueous [Cho][Lys] mixtures with χ_IL of 1, 5, 10, 30 and 50% demonstrates clearly that the extent of intermolecular contacts between choline cations and lysinate anions intensifies with the rising content of the IL in the mixture. Counter ions were found to interact in two main ways – hydrogen bonding between hydroxyl group of cations and carboxylate group of anions, and by carobxylates of anions condensing around the bulky N–(CH₃)₃ moieties of cations. In addition, self-aggregation of cations through prolific intermolecular contacts between their N–(CH₃)₃ moieties as well as through interactions between hydroxyl and N–(CH₃)₃ groups were observed. In the case of lysinate anions, progressive aggregation of their side chains was seen with the increasing content of [Cho][Lys] in the mixture as well. Formation of continuous polar domain composed of choline cations and carboxylate groups of anions and continuous nonpolar domain composed of side chains of lysinate anions was confirmed for aqueous mixtures of [Cho][Lys] with χ_IL of 30 and 50%. In these systems, small linear clusters of water molecules situated at the interface of polar and nonpolar domains are formed which become larger with the increasing content of water in the mixture. At χ_IL of 10%, water is already found to form a continuous network that surrounds large clusters of choline and lysinate ions.

Two fast and slow dynamical regimes of aqueous [Cho][Lys] mixtures could be identified based on the ¹H DOSY measured dependencies of the diffusion coefficients of choline, lysinate and water molecules on the composition of the mixture. The two regimes are found to switch at χ_IL of around 11%. Predicted diffusion coefficients show rather good quantitative agreement with experimental data and support the existence of the two dynamical regimes. The results of present study allow proposing that continuous water network breaks at this particular composition of the mixture, leading to the formation of comparatively less mobile water pockets within the matrix of continuous polar and nonpolar ionic domains. Interestingly, measured composition dependencies of the ¹H NMR chemical shifts of some sites in choline and lysinate were found to switch character from decreasing to increasing at χ_IL of exactly 11% as well.

The protons in the hydrogen-bonding-capable groups of choline and lysinate as well as those of water molecules were found to be in the regime of fast exchange within the entire range of molar compositions of aqueous [Cho][Lys] mixtures studied. Even though water molecules and hydroxyl groups of choline cations are progressively involved in strong hydrogen bond interactions with carboxylate moieties of lysinate anions with the rising content of the IL in the mixture, the NMR signal of exchanging protons was measured to exhibit a prominent upfield shift of 0.92 ppm in the range of χ_IL from around 10⁻² to 0.66. Large-scale QM/MM calculations of ¹H NMR isotropic shielding constants confirm that protons of water molecules and of hydroxyl groups in choline become progressively deshielded in the mixtures with higher content of the IL. The observed upfield shift turns out to be due to the protons in the two amino groups of lysinate anions. The ¹H NMR shielding constants of these groups are predicted to be considerably larger than those of water molecules and OH groups in choline cations, and they are virtually independent of the composition of the mixture. The computed dependence of averaged shielding constant of the fast-exchanging protons on the composition of the mixture is thus found to be in very good qualitative and quantitative agreement with experimental results. With one exception, the QM/MM based predictions of the dependencies of ¹H NMR chemical shifts on χ_IL show reasonable agreement with experimental findings, giving support to the validity of present structural results.

Author contributions

E. S.: investigation, data curation, formal analysis, software, validation, writing – original draft, writing – review & editing. L. M.: investigation, formal analysis, writing – review & editing. V. K.: data curation, methodology, validation, resources, supervision, writing – review & editing. K. A.: conceptualization, funding acquisition, methodology, resources, project administration, software, supervision, writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgements

This study was supported by the Research Council of Lithuania, grant no. S-MIP-22-74. Computations were performed on the resources provided by the High Performance Computing Center “HPC Saulėtekis” at Vilnius University, Lithuania. COST Action no. CA21101 is acknowledged. V. K. and L. M. acknowledge the Center of Spectroscopic Characterization of Materials and Electronic/Molecular Processes (SPECTROVERSUM Infrastructure) for the use of NMR spectrometer. The authors kindly thank Prof. Em. Vytautas Balevičius for helpful discussions of experimental NMR results.

References

1. P. Moriel, E. J. García-Suárez, M. Martínez, M. A. Montes-Morán, V. Calvino-Casilda and M. A. Bañares, Tetrahedron Lett., 2010, 51, 4877–4881.
2. Q.-P. Liu, X.-D. Hou, N. Li and M.-H. Zong, Green Chem., 2012, 14, 304–307.
3. X. Chen, R. Hao, W. Chen, H. Jia, S. Qin, Q. Wang, D. Zhang, Z. Han and Y. Li, RSC Adv., 2024, 14, 382–389.
4. S. Miao, R. Atkin and G. Warr, Green Chem., 2022, 24, 7281–7304.
5. A. Romero, A. Santos, J. Tojo and A. Rodríguez, J. Hazard. Mater., 2008, 151, 268–273.
6. K. M. Docherty and C. F. Kulpa, Jr., Green Chem., 2005, 7, 185–189.
7. A. Yazdani, M. Sivapragasam, J.-M. Levêque and M. Moniruzzaman, J. Microb. Biochem. Technol., 2016, 8, 415–421.
8. X.-D. Hou, Q.-P. Liu, T. J. Smith, N. Li and M.-H. Zong, PLoS One, 2013, 8, e59145.
9. L. Gontrani, Biophys. Rev., 2018, 10, 873–880.
10. S. De Santis, G. Masci, F. Casciotta, R. Caminiti, E. Scarpellini, M. Campetella and L. Gontrani, Phys. Chem. Chem. Phys., 2015, 17, 20687–20698.
11. R. Caparica, A. Júlio, A. R. Baby, M. E. Machado Araújo, A. S. Fernandes, J. G. Costa and T. Santos de Almeida, Pharmaceutics, 2018, 10, 288.
12. X. Li, N. Ma, L. Zhang, G. Ling and P. Zhang, Int. J. Pharm., 2022, 612, 121366.
13. X.-D. Hou, T. J. Smith, N. Li and M.-H. Zong, Biotechnol. Bioeng., 2012, 109, 2484–2493.
14. Y.-L. Wang, B. Li, S. Sarman, F. Mocci, Z.-Y. Lu, J. Yuan, A. Laaksonen and M. D. Fayer, Chem. Rev., 2020, 120, 5798–5877.
15. H. S. Dhattarwal and H. K. Kashyap, Chem. Rec., 2023, 23, e202200295.
16. S. Miao, R. Atkin and G. G. Warr, Phys. Chem. Chem. Phys., 2020, 22, 3490–3498.
17. S. Miao, J. Wood, H. J. Jiang, S. Imberti, R. Atkin and G. Warr, J. Mol. Liq., 2020, 319, 114327.
18. H. J. Jiang, S. Miao, S. Imberti, B. A. Simmons, R. Atkin and G. G. Warr, Green Chem., 2021, 23, 856–866.
19. S. Miao, S. Imberti, R. Atkin and G. Warr, J. Mol. Liq., 2022, 351, 118599.
20. L. N. Wong, M. Brunner, S. Imberti, G. Warr and R. Atkin, J. Phys. Chem. B, 2024, 128, 4853–4863.
21. T. L. Greaves, D. F. Kennedy, S. T. Mudie and C. J. Drummond, J. Phys. Chem. B, 2010, 114, 10022–10031.
22. R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Phys. Chem. Chem. Phys., 2011, 13, 3237–3247.
23. D. Ruivo, J. N. Canongia Lopes, F. J. Deive, J. M. S. S. Esperança, L. P. N. Rebelo, A. Rodriguez and K. Shimizu, Phys. Chem. Chem. Phys., 2018, 20, 23864–23872.
24. K. Damodaran, Prog. Nucl. Magn. Reson. Spectrosc., 2022, 129, 1–27.
25. R. Nanda and K. Damodaran, Magn. Reson. Chem., 2018, 56, 62–72.
26. O. Nordness and J. F. Brennecke, Chem. Rev., 2020, 120, 12873–12902.
27. B. A. Marekha, O. N. Kalugin, M. Bria and A. Idrissi, Phys. Chem. Chem. Phys., 2015, 17, 23183–23194.
28. H. Weingärtner, Curr. Opin. Colloid Interface Sci., 2013, 18, 183–189.
29. E. A. Cade, J. Petenuci III and M. M. Hoffmann, ChemPhysChem, 2016, 17, 520–529.
30. S. Cha, M. Ao, W. Sung, B. Moon, B. Ahlström, P. Johansson, Y. Ouchid and D. Kim, Phys. Chem. Chem. Phys., 2014, 16, 9591–9601.
31. V. Balevicius, Z. Gdaniec, K. Aidas and J. Tamuliene, J. Phys. Chem. A, 2010, 114, 5365–5371.
32. S. Miao, A. Sardharwalla and S. Perkin, J. Phys. Chem. Lett., 2024, 15, 11855–11861.
33. B. L. Kuhn, L. Zibetti, V. S. Pereira, C. R. Bender, M. A. Villetti and C. P. Frizzo, Colloids Surf., A, 2024, 702, 135042.
34. W. Silva, M. Zanatta, A. S. Ferreira, M. C. Corvo and E. J. Cabrita, Int. J. Mol. Sci., 2020, 21, 7745.
35. Y. Wang, W. Jiang, T. Yan and G. A. Voth, Acc. Chem. Res., 2007, 40, 1193–1199.
36. D. Bedrov, J.-P. Piquemal, O. Borodin, A. D. MacKerell, Jr., B. Roux and C. Schröder, Chem. Rev., 2019, 119, 7940–7995.
37. B. Kirchner, O. Hollóczki, J. N. Canongia Lopes and A. A. H. Pádua, WIREs Comput. Mol. Sci., 2015, 5, 202–214.
38. J. Kongsted, A. Osted, K. V. Mikkelsen and O. Christiansen, Mol. Phys., 2002, 100, 1813–1828.
39. C. B. Nielsen, O. Christiansen, K. V. Mikkelsen and J. Kongsted, J. Chem. Phys., 2007, 126, 154112.
40. J. Kongsted, C. B. Nielsen, K. V. Mikkelsen, O. Christiansen and K. Ruud, J. Chem. Phys., 2007, 126, 034510.
41. K. Aidas, A. Møgelhøj, H. Kjær, C. B. Nielsen, K. V. Mikkelsen, K. Ruud, O. Christiansen and J. Kongsted, J. Phys. Chem. A, 2007, 111, 4199–4210.
42. K. Aidas, K. V. Mikkelsen and J. Kongsted, Phys. Chem. Chem. Phys., 2010, 12, 761–768.
43. D. Lengvinaite, S. Kvedaraviciute, S. Bielskute, V. Klimavicius, V. Balevicius, F. Mocci, A. Laaksonen and K. Aidas, J. Phys. Chem. B, 2021, 125, 13255–13266.
44. A. Bagno, F. D'Amico and G. Saielli, J. Phys. Chem. B, 2006, 110, 23004–23006.
45. A. Bagno, F. D'Amico and G. Saielli, Chem. Phys. Chem., 2007, 8, 873–881.
46. G. Saielli, Molecules, 2020, 25, 2085.
47. D. Lengvinaite, V. Klimavicius, V. Balevicius and K. Aidas, J. Phys. Chem. B, 2020, 124, 10776–10786.
48. D. A. Case, K. Belfon, I. Y. Ben-Shalom, S. R. Brozell, D. S. Cerutti, T. E. Cheatham, III, V. W. D. Cruzeiro, T. A. Darden, R. E. Duke, G. Giambasu, M. K. Gilson, H. Gohlke, A. W. Goetz, R. Harris, S. Izadi, S. Izmailov, K. Kasavajhala, A. Kovalenko, R. Krasny, T. Kurtzman, T. S. Lee, S. LeGrand, P. Li, C. Lin, J. Liu, T. Luchko, R. Luo, V. Man, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, A. Onufriev, F. Pan, S. Pantano, R. Qi, D. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, L. Wilson, R. M. Wolf, X. Wu, Y. Xiong, Y. Xue, D. M. York and P. A. Kollman, Amber 2020, University of California, San Francisco.
49. C. C. J. Roothaan, Rev. Mod. Phys., 1951, 23, 69–89.
50. W. J. Hehre, R. J. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261.
51. P. C. Hariharan and J. A. Pople, Theor. Chim. Acta, 1973, 28, 213–222.
52. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, 2016, Gaussian Inc., Wallingford CT.
53. C. I. Bayly, P. Cieplak, W. Cornell and P. A. Kollman, J. Phys. Chem., 1993, 97, 10269–10280.
54. F. Dommert, J. Schmidt, C. Krekeler, Y. Y. Zhao, R. Berger, L. Delle Site and C. Holm, J. Mol. Liq., 2010, 152, 2–8.
55. B. Doherty, X. Zhong, S. Gathiaka, B. Li and O. Acevedo, J. Chem. Theory Comput., 2017, 13, 6131–6145.
56. Z. Sun, Z. Gong, L. Zheng, P. Kalhor, Z. Huai and Z. Liu, J. Ion. Liq., 2022, 2, 100043.
57. W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, J. Am. Chem. Soc., 1995, 117, 5179–5197.
58. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174.
59. H. W. Horn, W. C. Swope, J. W. Pitera, J. D. Madura, T. J. Dick, G. L. Hura and T. Head-Gordon, J. Chem. Phys., 2004, 120, 9665–9678.
60. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164.
61. J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
62. M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Clarendon Press, Oxford, 1987.
63. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Salek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, WIREs Comput. Mol. Sci., 2014, 4, 269–284.
64. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
65. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
66. C. Adamo and V. Barone, Chem. Phys. Lett., 1998, 298, 113–119.
67. C. Benzi, O. Crescenzi, M. Pavone and V. Barone, Magn. Reson. Chem., 2004, 42, S57–S67.
68. M. Bursch, T. Gasevic, J. B. Stückrath and S. Grimme, Inorg. Chem., 2021, 60, 272–285.
69. W. L. Jorgensen, J. Am. Chem. Soc., 1981, 103, 335–340.
70. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
71. R. A. Kendall, T. H. Dunning and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806.
72. C. R. Ashworth, R. P. Matthews, T. Welton and P. A. Hunt, Phys. Chem. Chem. Phys., 2016, 18, 18145–18160.
73. F. Khorrami and M. H. Kowsari, J. Phys. Chem. B, 2020, 124, 3770–3783.
74. A. Gupta and H. K. Kashyap, J. Mol. Liq., 2021, 326, 115329.
75. O. Russina, S. De Santis and L. Gontrani, RSC Adv., 2016, 6, 34737–34743.
76. J. Chen, X. Zeng and L. Chen, Phys. Chem. Chem. Phys., 2022, 24, 17792–17808.
77. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
78. A. Le Donne, H. Adenusi, F. Porcelli and E. Bodo, J. Phys. Chem. B, 2019, 123, 5568–5576.
79. E. Veroutis, S. Merz, R. A. Eichel and J. Granwehr, J. Mol. Liq., 2021, 322, 114934.
80. M. Usula, F. Mocci, F. C. Marincola, S. Porcedda, L. Gontrani and R. Caminiti, J. Chem. Phys., 2014, 140, 124503.
81. L. Engelbrecht, F. Mocci, A. Laaksonen and K. R. Koch, Inorg. Chem., 2018, 57, 12025–12037.
82. S. Russo and E. Bodo, Mol. Simul., 2022, 48, 1650–1659.
83. E. J. Maginn, Acc. Chem. Res., 2007, 40, 1200–1207.
84. G. Saielli, Adv. Theory Simul., 2018, 1, 1800084.

---

Footnote

† Electronic supplementary information (ESI) available: Force field data used for the [Cho][Lys] ionic liquid; details of the QM/MM calculations; radial distribution functions recorded in MD simulations; mean square displacement functions; and experimental NMR spectra. See DOI: https://doi.org/10.1039/d5cp00861a

---