High-throughput screening and DFT characterization of bimetallic alloy catalysts for the nitrogen reduction reaction†
Received
20th March 2025
, Accepted 13th June 2025
First published on 8th July 2025
Abstract
The lack of active and selective catalysts hinders transition to the electrochemical nitrogen reduction reaction (NRR) as an environmentally friendly route for on-site ammonia production under ambient conditions. In search of active NRR electrocatalysts, we generated a dataset of surface and ordered intermetallic alloys using density functional theory (DFT) and trained an artificial neural network (ANN) using characteristics of the active-site transition-metal electronic d-states. The electrochemical limiting potential of ∼350 surface alloys with varying surface configurations was predicted using our developed ANN, with a mean absolute error of 0.23 eV comparable to that of DFT. The full energy profiles of Au@Au3Re and Au@Au3Mo as potential candidates were further characterized and compared with those of pure Re(001) and Mo(110) via DFT calculations to understand the enhanced catalytic activity rooted in the electronic structure of the catalyst. Moreover, charge analysis showed significant charge transfer from Re and Mo to Au in these alloys, resulting in a change of their electronic structure, and improvement of their catalytic activity. Finally, the selectivity of the alloys was investigated by comparing the adsorption free energy of nitrogen and hydrogen adatoms, and the resulting theoretical faradaic efficiency. This work further confirms that alloying is an effective approach to enhance the catalytic activity of transition metals and highlights how machine learning algorithms trained with physically intuitive features of the materials can efficiently screen the chemical space of bimetallic alloys and predict the limiting potential for a reaction such as the NRR over these alloys, thereby reducing the computational cost of alloy catalyst design and providing an affordable path to electrocatalytic materials discovery.
1. Introduction
Ammonia (NH3) is one of the most produced chemicals in the world with an annual production of around ∼175 million tons. The main application of NH3 is in agriculture as an ingredient of fertilizers, which has enabled population growth in the 20th century.1 Moreover, NH3 is liquid under compression (10 bar pressure) at room temperature, which makes it a promising candidate as a hydrogen carrier for renewable energy systems.2 Despite significant efforts over the past years to use renewable energies for NH3 production, the industrial synthesis of NH3 is still dominated by the fossil-fuel-based Haber–Bosch process.3 The problem with the latter is that it requires harsh reaction conditions (temperature and pressure in the range of 400–500 °C and 150–200 bar, respectively) due to the sluggish reaction kinetics of nitrogen (N2) with hydrogen (H2).4 As a result, the industrial process is responsible for around 2% of the global annual energy consumption and the emission of a considerable amount of carbon dioxide into the atmosphere.5–8
Interestingly, there is a remarkable contrast between the industrial and natural NH3 production.9,10 Microorganisms use the nitrogenase enzyme to produce NH3 from solvated protons and electrons under ambient conditions.11,12 Inspired by biological NH3 production, the electrochemical nitrogen reduction reaction (NRR) offers a sustainable and localized route toward NH3 production, where electrons are driven to the surface of the catalyst by an applied potential to react with protons and N2 dissolved in the solution.13 However, no heterogeneous catalyst has been able to produce NH3 in significant yields due to two major challenges, (1) the low NRR catalytic activity and (2) the low selectivity toward the NRR. The low catalytic activity is mainly a result of the poor N2 adsorption and activation on the surface of the catalyst, while the second challenge is due to the competing hydrogen evolution reaction (HER) which diverts most of the current from NH3 production and results in low faradaic efficiencies (FE).
The high bond energy of N2 (941 kJ mol−1) limits the activation of this molecule at the surface of the catalyst.14 Moreover, the high ionization energy and non-polar (chemically inert) nature of nitrogen limits the electron/proton transfer during an electrochemical reaction.15 The performance of the NRR depends on the adsorption of N2 on the surface of the electrocatalyst as a crucial non-electrochemical step, via a mechanism that involves σ donation from the N2 bonding orbitals to empty orbitals of the active site and π back donation from the filled orbitals of the catalyst to the N2 anti-bonding orbitals.16–18 The latter mechanism has been unambiguously demonstrated by Lee et al. for N2 adsorption on iron (Fe) and vanadium (V) sites of metal organic frameworks with density functional theory (DFT) and correlated wave function theory, together with natural bond orbital (NBO) analysis, which unveiled the stabilizing interaction between the metal occupied π-type NBOs and the unoccupied N2 π*-type NBOs from second-order perturbation theory.16 A prerequisite of this mechanism is the coexistence of empty and occupied orbitals at the active site. This makes transition metals (TM) promising candidates as NRR catalysts owing to their partially filled d orbitals.18 The acceptance-donation mechanism results in the weakening of the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond and N2 activation at the surface of the catalyst. Thus, the first objective in electrocatalyst design for the NRR is to effectively tune the electronic structure of the active site to enhance this acceptance-donation mechanism and thus N2 activation at the catalyst surface as the most important step.
N bond and N2 activation at the surface of the catalyst. Thus, the first objective in electrocatalyst design for the NRR is to effectively tune the electronic structure of the active site to enhance this acceptance-donation mechanism and thus N2 activation at the catalyst surface as the most important step.
Extensive DFT studies have focused on TM surfaces for the NRR in recent years and have unveiled a linear scaling relationship between the limiting potential (Ulimiting) of the TM surfaces and the adsorption free energy of NRR intermediates.9 This relationship and the interaction of the catalyst surface with the various NRR intermediates can be rationalized on the basis of the catalyst electronic structure. In fact, the electronic factors affecting the interaction of the catalyst with the adsorbate can be described by the d-band model (ESI†),19 which links the activity of a catalyst to the properties of its metal d-band states, and thus manipulating these electronic features of a catalyst would modulate its activity.
Tuning the d-band via alloying proved a simple yet effective approach to control the interactions of the electrocatalyst with NRR intermediates and overcome the NRR activity and selectivity challenges while reducing the cost of the catalyst by limiting the use of expensive elements.20–24 Recently, Shi et al. investigated the activity and selectivity of four different metals (M = Fe, Mo, Ru, and Ni) and their alloys with Au (MxAu) for the NRR via DFT calculations.25 Among 8 different alloys, the Mo3Au ordered intermetallic (OI) alloy with a Ulimiting of −0.66 V performs best for the electrochemical NRR. The selectivity of Mo3Au was then investigated by comparing the adsorption free energy of N2 and that of a hydrogen adatom (H), and Mo3Au was found to adsorb N2 stronger than H (ΔG*N2 < ΔG*H), suggesting high selectivity of the catalyst. Kim et al. investigated a broad range of surface alloys composed of 30 transition metals via DFT, and reported that Ru and Re surface alloy catalysts have lower Ulimiting than their Mn, Mo, Nb, and W counterparts.22 The electronic properties of the catalyst were further investigated on the basis of projected densities of states (PDOS) onto the catalyst d orbitals, showing the changes in electronic structure of the active site due to alloying. On the experimental side, alloying has been shown in many instances to increase the performance of the NRR. Yu et al. used an Ag3Cu porous network to produce NH3 with a production rate of 24.58 μgNH3 h−1 mgcat−1 of catalyst and 13.28% FE at −0.5 V vs. reversible hydrogen electrode (RHE).26 An AuCu nanowire synthesized by Liu et al. showed improved catalytic activity compared to that of AuAg, AuPd, and AuRu bimetallic alloys, with an NH3 production rate of 154.91 μgNH3 h−1 mgcat−1 and 56.96% FE at −0.2 V vs. RHE.27 The high NH3 yield rate and FE of AuCu was mainly attributed to the changes in the electronic properties of the alloy catalyst which resulted in stronger interaction between the NRR intermediates and the catalyst surface.
Despite extensive computational and experimental work, the design of an active and selective catalyst for the NRR remains a challenge as screening the chemical space via conventional computational methods is time consuming, especially for bimetallic alloys with different surface structures and stochiometric ratios. This motivated us to train an artificial neural network (ANN) to predict the overpotential of bimetallic alloys for the NRR on the basis of d-band features obtained from DFT PDOS calculations. Electronic properties of the most promising electrocatalyst candidates and full NRR pathways were further characterized by DFT calculations.
The manuscript is organized as follows: the NRR mechanisms are described in Section 2, the computational details of the simulations used to generate datasets are presented in Section 3, the MLA features and performance in Section 4, while results are presented and discussed in Section 5, with concluding remarks following in Section 6.
2. NRR mechanisms
Two main mechanisms have been proposed for the NRR, based on the characteristics of the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond, namely the associative and dissociative pathways. As the dissociation of N
N bond, namely the associative and dissociative pathways. As the dissociation of N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N requires overcoming a high energy barrier on flat surfaces, the latter pathway was not considered in this study.9 Associative pathways encompass the distal, alternating, and enzymatic routes, which mainly differ in the adsorption configuration and hydrogenation sequence of N2. In the distal and alternating pathway, N2 is adsorbed with an end-on configuration whereas in the enzymatic pathway N2 is adsorbed in a side-on configuration. The hydrogenation step implicates either Tafel-type or Heyrovsky-type mechanisms.9 In the Tafel-type mechanism, the solvated proton is first adsorbed on the surface, where it attaches an electron and reacts as an H adatom with the NRR intermediate. In the Heyrovsky mechanism, the adsorbed intermediate is hydrogenated directly from the solution and electrons from the electrode. Among associative pathways, the distal pathway is the most favourable one on transition metal surfaces, and thus the one considered in this article.9,22,28 In this pathway, through a mechanism detailed in eqn (1), N2 is adsorbed with an end-on configuration as the first and most important step in the NRR (eqn (1a)). This non-electrochemical step is followed by hydrogenation of adsorbed N2 in subsequent electrochemical steps. The first hydrogenation step (eqn (1b)) of the NRR is the potential limiting step for late TMs such as Ni, Pt and Au while the fifth hydrogenation (eqn (1f)) step is the potential limiting step for early TMs such as Sc, Ti and V.9 NH3 ultimately desorbs from the surface of the catalyst (eqn (1h)), making the active site available for another catalytic cycle.
N requires overcoming a high energy barrier on flat surfaces, the latter pathway was not considered in this study.9 Associative pathways encompass the distal, alternating, and enzymatic routes, which mainly differ in the adsorption configuration and hydrogenation sequence of N2. In the distal and alternating pathway, N2 is adsorbed with an end-on configuration whereas in the enzymatic pathway N2 is adsorbed in a side-on configuration. The hydrogenation step implicates either Tafel-type or Heyrovsky-type mechanisms.9 In the Tafel-type mechanism, the solvated proton is first adsorbed on the surface, where it attaches an electron and reacts as an H adatom with the NRR intermediate. In the Heyrovsky mechanism, the adsorbed intermediate is hydrogenated directly from the solution and electrons from the electrode. Among associative pathways, the distal pathway is the most favourable one on transition metal surfaces, and thus the one considered in this article.9,22,28 In this pathway, through a mechanism detailed in eqn (1), N2 is adsorbed with an end-on configuration as the first and most important step in the NRR (eqn (1a)). This non-electrochemical step is followed by hydrogenation of adsorbed N2 in subsequent electrochemical steps. The first hydrogenation step (eqn (1b)) of the NRR is the potential limiting step for late TMs such as Ni, Pt and Au while the fifth hydrogenation (eqn (1f)) step is the potential limiting step for early TMs such as Sc, Ti and V.9 NH3 ultimately desorbs from the surface of the catalyst (eqn (1h)), making the active site available for another catalytic cycle.| | | *N2 + 6(H+ + e−) → *NNH + 5(H+ + e−) | (1b) |
| | | *NNH + 5(H+ + e−) → *NNH2 + 4(H+ + e−) | (1c) |
| | | *NNH2 + 4(H+ + e−) → *N + 3(H+ + e−) + NH3 | (1d) |
| | | *N + 3(H+ + e−) → *NH + 2(H+ + e−) | (1e) |
| | | *NH + 2(H+ + e−) → *NH2 + (H+ + e−) | (1f) |
| | | *NH2 + (H+ + e−) → *NH3 | (1g) |
3. Computational details
3.1 DFT calculations
DFT calculations were performed using GPAW 22.8.0, a Python code based on the projector augmented wave method,29 with the Bayesian error estimation functional with van der Waals correlation (BEEF-vdW).30 The ionic cores were described with pseudopotentials derived from the projector augmented wave (PAW) approach supplied with GPAW.31 The BEEF-vdW exchange–correlation functional, which combines the generalized gradient approximation (GGA) with the Langreth–Lundqvist van der Waals (vdW) functional, was selected given the crucial role of van der Waals interactions in accurately describing adsorption energies. Bulk structures were first cell-optimized, lattice parameters evaluated with a 500 eV plane-wave cutoff and the first Brillouin zone sampled with 6 × 6 × 6 Monkhorst–Pack k-point grids. Closed-packed FCC (111), BCC (110), and HCP (001) with periodically repeated (2 × 2) four-layer supercells were constructed from the BEEF-vdW optimized bulk structures to model the metal surfaces. Periodic images were separated by a 10 Å vacuum in the direction perpendicular to the surface. To aid self-consistent-field (SCF) convergence, the occupations of Kohn–Sham eigenstates were smeared by the Fermi–Dirac function with a width of 0.1 eV typical for metallic systems, and all energies were extrapolated to kBT = 0 eV. 6 × 6 × 1 Monkhorst–Pack k-point sampling was used for surface structure optimization (with the bottom two close-packed layers constrained at their bulk positions) with plane-wave cutoffs similar to those for bulk calculations, while a finer 9 × 9 × 1 grid was used for final electronic structure and density of state calculations. All structural optimizations were considered converged when the force on any position-optimized atom fell below 0.02 eV Å−1. Charge analysis was performed with the quantum theory of atoms in molecules of Richard Bader.32
3.2 Dataset generation
The bimetallic catalysts consist of surface and OI-type alloys composed of the TMs with structures shown in Fig. 1. The binary OI and surface alloy structures were constructed from L12 crystal structures and the most stable crystal structure of the core elements (FCC, BCC, or HCP), respectively. For surface calculations, we considered the (111) surface for FCC metals (Ag, Au, Cu, Ir, Pd, Pt, Rh) and the (001) surface for hcp metals (Re and Ru). As mentioned earlier, among all associative pathways (distal, alternating and enzymatic) for the NRR, the distal pathway is proposed to be the most favourable one at the surface of TMs, with *N2 → *N2H (eqn (1b)) or *NH → *NH2 (eqn (1f)) conversion as the potential determining step (PDS).9,28 One important factor in mechanistic studies for electrochemical reactions is evaluating Ulimiting. The latter is determined as the maximum free energy difference between two electrochemical steps along the free energy profile. For TMs, Ulimiting can be evaluated by comparing the maximum values of (ΔG*N2H − ΔG*N2) and (ΔG*NH2 − ΔG*NH), where ΔG is the adsorption free energy of a given intermediate. It should be noted that multiple adsorption sites exist on the surface of the electrocatalyst, however, we focus here exclusively on the on-top site to isolate and examine the direct influence of alloying on the electronic structure of the guest metal, and consequently, on the Ulimiting.
 |
| | Fig. 1 Bimetallic surface structures considered in the development of the machine learning model. (a) and (c) Side and top view of 111-terminated surface alloy and (b) and (d) side and top view of ordered-intermetallic alloy. A and B (depicted in a) represent metal elements across the periodic table. | |
Using DFT, we generated a database of adsorption free energies of N2, N2H, NH and NH2 for the on-top adsorption site over 220 bimetallic alloy catalysts via:
| |  | (2) |
| | 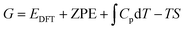 | (3) |
where
x and
y in
eqn (2) are the respective numbers of nitrogen and hydrogen atoms in the NRR intermediates. The Gibbs free energy of NRR intermediates and gas phase molecules were calculated by adding thermal and entropic corrections to the DFT calculated electronic energies in
eqn (3), where
EDFT is the electronic energy calculated by DFT, the zero-point energy (ZPE) and entropy (
S) corrections are calculated using the ASE thermochemistry package under the ideal-gas, harmonic-oscillator, rigid-rotor approximation with information obtained from vibrational frequency analysis at 298.15 K and 1 atm.
33G* refers to the clean adsorbate-free catalyst surface. The ZPE and
S values for gas-phase N
2, H
2 and NH
3 molecules were taken from the NIST web database as per convention of the field;
34 we note that use of experimental data or explicitly calculated properties (Table S1, ESI
†) provides essentially the same results (within at most 0.03 eV).
4. MLA approach
4.1 Feature selection and engineering
Advancements in MLAs prompted the development of massive datasets and made them a popular tool for various applications such as e.g., material discovery and drug design.35,36 The key factor in improving and controlling the accuracy of the algorithms lies in the features that are used to train the model. Thus, exploring new descriptors is crucial for activity prediction and catalyst discovery and synthesis. Choosing the right training features is the most critical step for developing MLAs. In heterogeneous catalysis, the reaction takes place at a well-defined active site, and selected features to estimate Ulimiting of an electrochemical reaction should thus (1) represent structural and electronic properties of the active site uniquely; (2) be available or easily computed; and perhaps most importantly (3) provide chemical insights and be physically intuitive.
As mentioned earlier, the properties of the active site are important factors in heterogeneous catalysis. Therefore, the local geometrical and electronic properties of the active site can be used as input features to train the MLAs. Features derived from the geometrical structure of a system are referred to as structural descriptors. Previous studies have shown that, for example, the active site coordination number is a good structural descriptor that correlates with the catalytic activity.37 Kim et al. developed a slab graph convolutional neural network (SGCNN) using intrinsic properties of the active-site metal such as group number, electron affinity, electronegativity, and periodic number to predict the limiting potential of the NRR for bimetallic alloys.38 The SGCNN was able to predict adsorption energies of intermediates with a 0.23 eV mean absolute error (MAE), which could then be used to estimate the limiting potential. Zafari et al. used a light gradient boosting machine (LGBM) to predict the adsorption energies of N2, N2H, NH2 and NH3 for graphene-based single-atom catalysts and transition metal borides.39 The bond-orientational order parameter (BOP) was used as a local descriptor along with the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond length of adsorbed N2, melting point and atomic number of the active site metal. These approaches only used the geometrical properties of the active site to train the MLAs.
N bond length of adsorbed N2, melting point and atomic number of the active site metal. These approaches only used the geometrical properties of the active site to train the MLAs.
Another category of descriptors, the so-called electronic descriptors, are simply determined from electronic structure calculations. Descriptors like the characteristics of the d-bands/orbitals such as their center, filling and width belong to this family of descriptors, and they have been used to estimate the reactivity of catalysts for other electrochemical reactions such as the CO2 reduction reaction.36,40 The d-band model developed by Hammer and Nørskov states that the interaction between the adsorbate state with the d states of the catalyst (for TMs) determines the interaction strength and is directly related to the properties of the d-band. The first and the second moments of the density of states are the centre  and width (Wd), respectively, defined as:
and width (Wd), respectively, defined as:
| |  | (4) |
| |  | (5) |
where
nd is the PDOS of the active site computed in terms of a single-particle energy
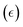
.
19 Also, the filling that is defined as the number of states below the Fermi level affects the center and the width of the d-band.
41–43| |  | (6) |
The model robustness and physical intuition are important factors while choosing the features to train MLAs, thus, the d-band features extracted from the PDOS of the active site ( , Wd, fd) calculated by DFT are used as electronic features to train the MLA. The position of the top edge of the d-band was also included as a training feature since the of filling of the anti-bonding state at the top of the d-band determines the strength of the interaction. Besides electronic structure features, intrinsic properties of the active site available from the periodic table such as electron affinity, Pauli electronegativity, work function, and atomic radius of metal active site were included. We believe that electronic descriptors play a crucial role in modelling actual electrocatalysts with complex structures, such as those exhibiting disorder or phase segregation, as these structural variations result in changes in the electronic structure of the active site that would not be captured by elemental and intrinsic properties of the active site metal alone. Moreover, using the electronic descriptors enhances MLA prediction accuracy compared to that of using only elemental descriptors, as further discussed in the ESI.† In the last step of feature engineering, we standardize MLA features to enhance the accuracy of the model, because of the large variation in the numerical values of the data in the dataset used for training of MLAs, which results in low training efficiency and prediction bias for optimization algorithms. We standardized our training features using the StandardScaler module implemented in scikit-learn44 as:
, Wd, fd) calculated by DFT are used as electronic features to train the MLA. The position of the top edge of the d-band was also included as a training feature since the of filling of the anti-bonding state at the top of the d-band determines the strength of the interaction. Besides electronic structure features, intrinsic properties of the active site available from the periodic table such as electron affinity, Pauli electronegativity, work function, and atomic radius of metal active site were included. We believe that electronic descriptors play a crucial role in modelling actual electrocatalysts with complex structures, such as those exhibiting disorder or phase segregation, as these structural variations result in changes in the electronic structure of the active site that would not be captured by elemental and intrinsic properties of the active site metal alone. Moreover, using the electronic descriptors enhances MLA prediction accuracy compared to that of using only elemental descriptors, as further discussed in the ESI.† In the last step of feature engineering, we standardize MLA features to enhance the accuracy of the model, because of the large variation in the numerical values of the data in the dataset used for training of MLAs, which results in low training efficiency and prediction bias for optimization algorithms. We standardized our training features using the StandardScaler module implemented in scikit-learn44 as:
| |  | (7) |
where
xi is the feature vector, and
μx and
σx are the mean and standard deviation of feature
x, respectively. Features are centered around
μx = 0 with
σx = 1 after standardization.
4.2 MLA performance
To train the MLAs and evaluate their performance for Ulimiting prediction, we randomly divided the dataset into two subsets, with 75% of the data for training and the other 25% for testing the MLA performance. To prevent overfitting, 20% of the training data was used as a validation set, and early stopping was applied during training (Fig. S2, ESI†). The performance of each regression model is quantified by the MAE and root-mean-squared error (RMSE) values as:| | 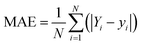 | (8) |
| |  | (9) |
where Yi and yi are the values obtained from DFT calculations and MLA prediction, respectively. To tune the hyperparameters of the ANN, namely the activation function, optimization algorithm, batch size, number of layers, number of neurons, and epochs, the GridSearchCV implemented in the scikit-learn library was used with 10-fold cross-validation (Table S2, ESI†). A feed-forward ANN with two hidden layers of 13 and 11 neurons was designed to understand the correlation of the features and predict Ulimiting of the NRR using Tensorflow.45 The rectified linear activation function (relU) is implemented as the activation function in the input and hidden layers while a linear function is used for the output layer. The GridSearchCV was also used to find the optimal hyperparameters of support vector regressor (SVR) and random forest (RF) algorithms, collated in Table S2, ESI.† Using standardized features and optimized hyperparameters, we trained different regression models, the training/test MAE of which are shown in Fig. 2.
 |
| | Fig. 2 Training and test prediction accuracy (mean absolute error – MAE) of different MLAs for predicting Ulimiting of the NRR at the surface of bimetallic alloy catalysts. | |
The linear regression models (linear, ridge, lasso, and elastic net) give almost similar prediction errors and linear regression has the lowest test error of 0.32 eV, which is significantly larger than the admitted accuracy of DFT calculations (∼0.1 eV). SVR has a similar performance to linear models while RF and ANN feature the lowest MAEs (0.24 and 0.23 eV, respectively). Although SVR, RF, and ANN models yield similar MAEs, the ANN exhibit a lower RMSE on the test set (Table S3, ESI†), indicating greater robustness to outliers. This is critical for model generalization, especially for relatively small datasets. The slightly larger gap between training and test MAEs in ANN reflects reduced overfitting, not poor generalization, and supports its selection as the final model.
While the dataset employed here contains around 220 entries, its small size is balanced by the use of a low-dimensional, physically intuitive feature space of only 10 descriptors. Using physically-sound features like the d-band center allows to decrease model complexity and enhance interpretability without compromising performance, enabling effective learning even with a limited dataset size, as confirmed by results for the cross-validation and test sets. While larger datasets will certainly enhance model stability, it is demonstrated herein that even small, well-designed datasets together with physically informed features yield stable and useful predictions for catalyst design.
4.3 MLA feature correlation
The feature–feature correlation established by Pearson's product moments is shown in Fig. 3. The d-band features are strongly correlated, particularly for the d-band filling, center, and width. The center of the d-band is positively correlated with their width. On the other hand, the center and width are inversely correlated with the filling of the states. As the number of d-orbital electrons increases, the width of the d-state band decreases with a down-shift in energy, as observed in the PDOS of TMs such as e.g., Cu, Ag and Au.43 Based on the d-band model, the down-shift of the d-band center will result in poor interaction between the adsorbate and the metal surface.19
 |
| | Fig. 3 Pearson's pairwise product moment correlation heat map among activity descriptors used as training features in this work. | |
The d-band center shows positive correlation with Ulimiting, while the filling is negatively correlated with Ulimiting (Fig. 3). Feature importance analysis further indicates that the d-band center, filling and upper edge are more influential than other features (Fig. S3, ESI†). We note that the significance of d-band filling in MLA based adsorption predictions has also been reported previously in the context of OH and CO adsorption energy.36 Among the intrinsic properties of the active site, the electronegativity shows the highest correlation with Ulimiting. Incidentally, this correlation was also reported in previous studies where only the catalyst geometrical structure and intrinsic element features of the adsorption site were considered in training the MLA, not including the electronic structure (d-band) features as in this work.46
5. Results and discussion
5.1 MLA prediction of limiting potentials
To design bimetallic alloys with improved catalytic activity, we use the ANN discussed in the previous section to rapidly screen a wide range of (111) terminated bimetallic surface alloys. While such idealized models do not account for disorder, defects or phase segregation often present in actual bimetallic systems, they provide a controlled framework to systematically investigate the influence of composition and geometry on the electronic structure of catalytic active sites and unveil transferable activity descriptors, particularly those based on metal d-band characteristics, that should remain relevant even in more complex environments. By focusing on ordered structures, we aim to establish a foundation for active site prediction and screening, which can later be extended to include non-ideal surfaces. Therefore, this approach enables a proof-of-principle demonstration of how alloying may modulate electrocatalytic behavior and supports rational catalyst design grounded in electronic structure–property relationships.
The ANN is used to predict Ulimiting of the A@A3B, A@A2B2 and A@AB3 surface structures shown in Fig. 4(a)–(c). The structures of the bimetallic (111) alloys consist of a monolayer of A (host) and B (guest) atoms with varying ratios, and three bottom layers of the host metal. We screen the chemical space by substituting the A element with six metals and the B element with 13 transition and noble metals. Fig. 2 shows that the ANN can predict Ulimiting of a wide range of catalysts with different surface compositions with a 0.23 eV MAE. Our ANN can predict, within the confidence level of the model, Ulimiting for pure TM (111) surfaces such as Ag, Cu, Pt and Pd, which have been studied extensively via DFT calculations.32 In Fig. 4(d), we show the volcano plot of Ulimitingvs. d-band center of the alloy for Ulimiting > −1 V predicted by our model for alloys with different surface structures. The top of the volcano plot is occupied by Ag/Re, Au/Re and Au/Mo alloys. These candidates show improved activity compared to pure Re (001) surfaces (Ulimiting = −0.95 V), with e.g. Ulimiting = −0.48 V for Au@Au3Re. The main reason for this improved catalytic activity is the alloy-induced change in the electronic structure of the active site due to charge transfer from Re to the Au substrate. The charge transfer affects the filling of the d-band and thus, the d-band center shifts towards the Fermi level and the anti-bonding state forms above the Fermi level (not filled with electrons). This enhances the interactions between the NRR intermediates, and the catalyst surface as discussed in the following sections.
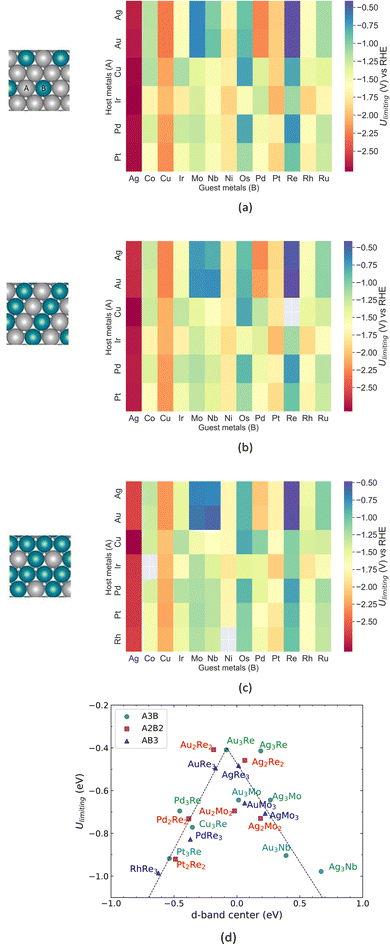 |
| | Fig. 4 Limiting potential of the NRR over alloy catalysts predicted by the ANN model for (a) A3B, (b) A2B2 and (c) AB3 surface alloys; (d) Ulimiting predicted by the ANN model vs. d-band center. | |
5.2 N2 adsorption on Au@Au3M (111) (M = Re, Mo)
DFT calculations were performed for the two potential candidate alloys Au@Au3Re and Au@Au3Mo where the active sites are Re and Mo, respectively, to confirm the ANN predictions and provide further insight regarding the improved catalytic activity of the surface. To investigate the stability of candidate alloys, we calculated the formation energies of Au@Au3Re and Au@Au3Mo (see ESI† for details). Formation energies of −5.37 eV and −3.20 eV for Au@Au3Re and Au@Au3Mo, respectively, demonstrate the stability of these alloys. As the first key step, we investigated the adsorption of N2 on the surface of the alloys and on pure Re (001) and Mo (110) surfaces for comparison. N2 can be adsorbed at the surface of the electrocatalyst with the end-on or the side-on configurations. The adsorption free energies in the end-on configuration on Au@Au3Re and Au@Au3Mo are −0.64 eV and −0.38 eV, respectively, while the adsorption free energies in the side-on configuration are 0.24 eV and 0.28 eV for the same alloys (Fig. S4, ESI†). The positive adsorption free energy for the side-on configuration shows the weak interaction between N2 and the surface of the catalyst and this mode of adsorption is thus not thermodynamically favorable. Accordingly, N2 adsorbs with an end-on configuration at the surface of the catalyst where only one nitrogen atom directly interacts with the surface. The N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond undergoes an elongation from 1.10 Å to 1.13 and 1.12 Å over Au@Au3Re and Au@Au3Mo, respectively. Moreover, Bader charge analysis shows 0.18e− and 0.14e− charge transfer from Re and Mo to the N2 molecule upon adsorption, respectively, confirming N2 activation at the surface of these catalysts.
N bond undergoes an elongation from 1.10 Å to 1.13 and 1.12 Å over Au@Au3Re and Au@Au3Mo, respectively. Moreover, Bader charge analysis shows 0.18e− and 0.14e− charge transfer from Re and Mo to the N2 molecule upon adsorption, respectively, confirming N2 activation at the surface of these catalysts.
The bonding and anti-bonding contributions of each molecular orbital is investigated via crystal orbital Hamilton population (COHP) analysis using the local orbital basis suite toward electronic-structure reconstruction (LOBSTER).47 COHP is a method that partitions the band structure into bonding, anti-bonding and nonbonding contributions. Analogous to integration of the density of states up to the Fermi level, which corresponds to the number of electrons, integration of the COHP (ICOHP) for a pair of atoms up to the Fermi level is related to the bond strength.48,49 The plots of −COHP vs. energy for N2 in the gas phase and adsorbed at the surface of Au@Au3Re and Au@Au3Mo are shown in Fig. 5. The ICOHP for isolated N2 is −23, a low value due to the strong triple-bond character of the N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N molecule. Comparison of the ICOHP between isolated N2 and N2 adsorbed on Au@Au3Re and Au@Au3Mo (Fig. 5(b) and (c)) confirms N2 activation over the catalysts, with an increased ICOHP (reduction in magnitude). The major contribution to the bonding of N2 at the surface of Au@Au3Re arises from the interaction of orbitals aligned with the N2 molecular axis and perpendicular to the surface (Fig. S5, ESI†).
N molecule. Comparison of the ICOHP between isolated N2 and N2 adsorbed on Au@Au3Re and Au@Au3Mo (Fig. 5(b) and (c)) confirms N2 activation over the catalysts, with an increased ICOHP (reduction in magnitude). The major contribution to the bonding of N2 at the surface of Au@Au3Re arises from the interaction of orbitals aligned with the N2 molecular axis and perpendicular to the surface (Fig. S5, ESI†).
 |
| | Fig. 5 Crystal orbital Hamilton population (COHP) plots for (a) isolated N2, (b) N2 adsorbed on the Au@Au3Re catalyst and (c) N2 adsorbed on the Au@Au3Mo catalyst. The increase in ICOHP (reduction of magnitude) indicates the activation of N2 at the surface of the catalyst. The bonding contributions are shown on the right, depicted in blue, and the anti-bonding ones on the left side, depicted in red. The Fermi level (EF) is indicated as a dashed line. | |
5.3 Electrocatalytic N2 reduction to NH3 over Au@Au3M (111) (M = Re, Mo)
In this section, the catalytic activity of Au@Au3Re and Au@Au3Mo is investigated for the reduction of N2 to NH3via the distal pathway and their NRR activity compared to that of pure Re (001) and Mo (110) surfaces. The free energy profiles of the reaction over the alloys and pure surfaces are shown in Fig. 6 (with the adsorption free energies of intermediates collected in Table S6, ESI†). The minimum energy configuration of each intermediate was calculated by considering nine different adsorption sites on the surface of the Au@Au3Re (111) and Au@Au3Mo (111) structures (Fig. S6, ESI†). All NRR pathways involve six proton-coupled electron transfer steps and five possible intermediates. The first electrochemical step of NRR is the hydrogenation of *N2 with an end-on configuration to form *N2H, which is 0.48 eV uphill in free energy over the Au@Au3Re catalyst. The enzymatic mechanism side-on intermediate was also considered for this step. However, the free energy change for the first hydrogenation along the enzymatic pathway ends up 1.25 eV uphill in free energy and thus not favorable compared to that of the distal pathway over Au@Au3Re (Fig. S4b, ESI†). The second hydrogenation step (*N2H2 formation) is uphill in free energy, but to a lesser extent than the first step and is thus not so relevant for evaluating Ulimiting. The proton–electron (H+/e−) pair further attacks *N2H2 to form the intermediate *N by releasing the first NH3 reaction product. The *N is sequentially further hydrogenated to form *NH, *NH2 and *NH3via steps that are all uphill in free energy, but still with lower magnitude than that for the first hydrogenation step (0.48 eV). This makes the first electrochemical step in the NRR (*N2 → *N2H) the PDS for the reduction of N2 to NH3 at the surface of Au@Au3Re, consistent with one of the underlying assumptions of our MLAs. The DFT calculated Ulimiting of −0.48 eV is very close to the MLA predicted value of −0.41 eV for this alloy, demonstrating the reliability of MLAs in predicting Ulimiting with reasonable accuracy. Comparison of the PDS of the NRR over Au@Au3Re catalysts with that at pure Re (001) surfaces (−0.95 eV) demonstrates that the catalytic activity of Re is improved upon alloying with Au.
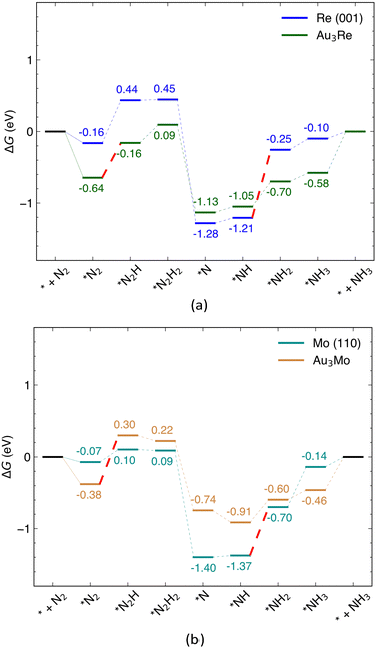 |
| | Fig. 6 Free energy profile of the NRR via the associative distal mechanism at (a) Re (001) and Au@Au3Re (111); (b) Mo (110) and Au@Au3Mo (111) surfaces. The PDS which is *N2 → *N2H for surface alloys and *NH → *NH2 for pure metals surfaces are shown with dashed red lines. | |
To understand the origins of the enhanced catalytic activity for Au@Au3Re, we inspected the PDOS of Re as the metal active site in pure Re and Au@Au3Re, Au@Au2Re2 and Au@AuRe3 alloys, shown in Fig. 7. The PDOS of Re in Au@Au3Re is narrower and the d-band center is closer to the Fermi level compared to that of Re for pure Re (Fig. 7(a)). As the content of Re increases at the surface, e.g. for Au@Au2Re2 (Fig. 7(c)) and Au@AuRe3 (Fig. 7(d)), the d-states become wider, and the d-band center shifts down. The changes in the PDOS of the metal active site are consistent with charge distributions obtained from Bader charge analysis. The latter shows significant electron transfer (0.58e−) from Re to Au in Au@Au3Re (Fig. S7, ESI†), not surprisingly as Au is more electronegative than Re. By increasing Re content (going from Au@Au3Re to Au@Au2Re2 and Au@AuRe3), charge transfer from Re to Au decreases (0.58e−, 0.47e− and 0.39e−, respectively), resulting in a downshift of the d-band center and an increase of the bandwidth compared to that of Au@Au3Re.
 |
| | Fig. 7 PDOS of the Re active site in pure Re (001) surfaces (black) and (111) surface alloys; Au@Au3Re (green), Au@Au2Re2 (red) and Au@AuRe3 (blue); (a) Au@Au3Re and Re, (b) Au@Au3Re and Au@Au2Re2, (c) Au@Au3Re and Au@AuRe3 and (d) Au@AuRe3 and pure Re. | |
As for Au@Au3Mo, the hydrogenation of *N2 to *N2H is the PDS of the NRR over Au@Au3Mo with Ulimiting = −0.67 V, which is incidentally close to the value of −0.64 V predicted by MLAs. Again, the hydrogenation of *N2 to *N2H via the enzymatic pathway is 0.90 eV uphill in free energy and thus not thermodynamically feasible (Fig. S4b, ESI†). The second (*N2H → *N2H2, eqn (1c)), third (*N2H2 → *N, eqn (1d)) and fourth (*N → *NH, eqn (1e)) hydrogenation steps are downhill in free energy over Au@Au3Mo and are thus facile and not pertinent to the evaluation of Ulimiting. All the remaining steps are uphill in free energy over Au@Au3Mo. We note that the *NH → *NH2 step (eqn (1f)) is the PDS over Mo (110), which is 0.67 eV uphill in free energy while the free energy change for this step is reduced to 0.31 eV over Au@Au3Mo. Similarly to the Au–Re alloys discussed above, this is due to the changes in the electronic properties of the Mo active site (PDOS shown in Fig. S8, ESI†), reflected in the Bader charge distributions. According to the latter, almost 1e− is transferred from Mo to Au in Au@Au3Mo. Trends in charge transfer are almost similar to those for Au–Re alloys, where charge transfer from Mo to Au decreases in Au@Au2Mo2 (0.78e−) and Au@AuMo3 (0.59e−). We note that the PDS changes from *NH → *NH2 over pure Mo and Re to the first hydrogenation step (*N2 → *N2H) of the NRR mechanism (eqn (1)) for surface alloys (Fig. S9, ESI†). As discussed earlier, this is due to the changes in the electronic properties of the active site via alloying. Another important factor to consider in electrochemical reactions is the ease of desorption of the products. In the case of Au@Au3Re and Au@Au3Mo, the desorption of NH3 from the active site is ∼0.6 eV uphill in free energy. The endergonic desorption of NH3 is mainly due to the strong interaction of the alloy surface with N2 and the NRR intermediates.50
5.4 NRR vs. HER
The HER is a competing side reaction of the NRR, consuming protons and electrons, and resulting in low FE. Thus, a high selectivity toward the NRR is also essential for a catalyst besides its high catalytic activity. Protons available from aqueous solution at the surface of a catalyst tend to block the active sites and hinder the most important step in the NRR, which is the adsorption of N2 at the surface of the catalyst. This is crucial for the NRR if N2 and H share the same adsorption/active site, which is the case for selected alloys (Fig. S10, ESI†). One approach to measure the selectivity of a catalyst is to compare the free energy of adsorption of N2 and H, and to exploit their difference as a selectivity factor:
The ΔGS (collected in Table S7, ESI†) are positive for Re (0.30 eV) and Mo (0.33 eV), demonstrating the low selectivity of pure surfaces. On the other hand, the ΔGS of −0.38 eV and −0.46 eV for the NRR over Au@Au3Re and Au@Au3Mo catalysts, respectively, suggest that the adsorption of N2 will prevail over that of H, confirming that alloying is an effective approach to increase the selectivity (on top of the activity) of an electrocatalyst.51,52
6. Conclusion
In summary, we used MLAs trained with d-band features extracted from the PDOS along with intrinsic properties of the TM active site to screen the chemical space of bimetallic alloys for the NRR. The ANN was found to outperform the various MLAs developed and tested and was selected as our optimal model. Our trained ANN can predict the electrochemical limiting potential (Ulimiting) of the reaction over alloys with various surface configurations with a MAE of 0.23 eV, which is comparable to the admitted accuracy of DFT calculations. Potential alloy candidates and their role as catalytic supports for the NRR were then investigated via thorough DFT calculations to evaluate the accuracy of the ANN for predicting Ulimiting and characterize the changes in electronic properties responsible for the enhanced activity of the alloys relative to pure metal surfaces. The potential limiting step of the reaction over alloys was found to be the first hydrogenation of *N2 (*N2 → *N2H), as assumed in our MLAs. This work demonstrates that MLAs can be used to effectively screen the chemical space of catalysts upon the availability of a reliable and clean dataset and highlights how these MLAs will help accelerate further research to design and explore even more efficient catalysts for the NRR and other electrochemical processes. Finally, our computational investigations provide further grounds for exploiting alloying as a simple yet effective approach for manipulating the electronic structure of electrocatalysts and optimize both their activity and selectivity.
Conflicts of interest
There are no conflicts to declare.
Data availability
The data supporting this article have been included as part of the ESI.†
Acknowledgements
This work was supported by the Fonds de recherche du Québec – Société et culture (FRQSC) and Fonds de recherche du Québec – Nature et Technologies (FRQNT), through the “Programme intersectoriel Audace” (https://doi.org/10.69777/285517) and “Audace Plus - Volet Visée” (https://doi.org/10.69777/340443). Computational resources were provided by the Digital Research Alliance of Canada, Calcul Quebec and center for research in molecular modelling (CERMM).
Notes and references
- J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, How a century of ammonia synthesis changed the world, Nat. Geosci., 2008, 1, 636–639 CrossRef CAS.
- D. R. MacFarlane, P. V. Cherepanov, J. Choi, B. H. R. Suryanto, R. Y. Hodgetts, J. M. Bakker, F. M. Ferrero Vallana and A. N. Simonov, A Roadmap to the Ammonia Economy, Joule, 2020, 4, 1186–1205 Search PubMed.
- Y. Kojima and M. Yamaguchi, Ammonia as a hydrogen energy carrier, Int. J. Hydrogen Energy, 2022, 47, 22832–22839 Search PubMed.
- T. Brown, Ammonia production causes 1% of total global GHG emissions, Ammonia Ind., 2016 Search PubMed.
- C. Smith, A. K. Hill and L. Torrente-Murciano, Current and future role of Haber–Bosch ammonia in a carbon-free energy landscape, Energy Environ. Sci., 2020, 13, 331–344 RSC.
-
V. Smil, Enriching the earth: Fritz Haber, Carl Bosch, and the transformation of world food production, MIT Press, 2004 Search PubMed.
-
G. Ertl, H. Knözinger, J. Weitkamp, et al., Handbook of heterogeneous catalysis, VCH, Weinheim, 1997, vol. 2 Search PubMed.
- R. Lan, J. T. Irvine and S. Tao, Ammonia and related chemicals as potential indirect hydrogen storage materials, Int. J. Hydrogen Energy, 2012, 37, 1482–1494 CrossRef CAS.
- E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl, F. Abild-Pedersen, T. Vegge, H. Jónsson and J. K. Nørskov, A theoretical evaluation of possible transition metal electro-catalysts for N2 reduction, Phys. Chem. Chem. Phys., 2012, 14, 1235–1245 Search PubMed.
- B. H. Suryanto, H.-L. Du, D. Wang, J. Chen, A. N. Simonov and D. R. MacFarlane, Challenges and prospects in the catalysis of electroreduction of nitrogen to ammonia, Nat. Catal., 2019, 2, 290–296 Search PubMed.
- B. K. Burgess and D. J. Lowe, Mechanism of molybdenum nitrogenase, Chem. Rev., 1996, 96, 2983–3012 CrossRef CAS PubMed.
- L. C. Seefeldt, B. M. Hoffman and D. R. Dean, Mechanism of Mo-dependent nitrogenase, Annu. Rev. Biochem., 2009, 78, 701–722 Search PubMed.
- A. Hellman, E. J. Baerends, M. Biczysko, T. Bligaard, C. H. Christensen, D. C. Clary, S. Dahl, R. van Harrevelt, K. Honkala, H. Jonsson, G. J. Kroes, M. Luppi, U. Manthe, J. K. Nørskov, R. A. Olsen, J. Rossmeisl, E. Skúlason, C. S. Tautermann, A. J. C. Varandas and J. K. Vincent, Predicting Catalysis: Understanding Ammonia Synthesis from First-Principles Calculations, J. Phys. Chem. B, 2006, 110, 17719–17735 CrossRef CAS PubMed.
- X. Yan, D. Liu, H. Cao, F. Hou, J. Liang and S. X. Dou, Nitrogen reduction to ammonia on atomic-scale active sites under mild conditions, Small Methods, 2019, 3, 1800501 CrossRef.
- X.-L. Ma, J.-C. Liu, H. Xiao and J. Li, Surface single-cluster catalyst for N2-to-NH3 thermal conversion, J. Am. Chem. Soc., 2018, 140, 46–49 Search PubMed.
- K. Lee, W. C. Isley III, A. L. Dzubak, P. Verma, S. J. Stoneburner, L.-C. Lin, J. D. Howe, E. D. Bloch, D. A. Reed and M. R. Hudson,
et al., Design of a metal–organic framework with enhanced back bonding for separation of N2 and CH4, J. Am. Chem. Soc., 2014, 136, 698–704 Search PubMed.
- X. Mao, S. Zhou, C. Yan, Z. Zhu and A. Du, A single boron atom doped boron nitride edge as a metal-free catalyst for N2 fixation, Phys. Chem. Chem. Phys., 2019, 21, 1110–1116 RSC.
- C. Ling, X. Niu, Q. Li, A. Du and J. Wang, Metal-free single atom catalyst for N2 fixation driven by visible light, J. Am. Chem. Soc., 2018, 140, 14161–14168 CrossRef CAS PubMed.
- B. Hammer and J. K. Norskov, Why gold is the noblest of all the metals, Nature, 1995, 376, 238–240 CrossRef CAS.
- J. R. Kitchin, J. K. Nørskov, M. A. Barteau and J. Chen, Role of strain and ligand effects in the modification of the electronic and chemical properties of bimetallic surfaces, Phys. Rev. Lett., 2004, 93, 156801 CrossRef CAS PubMed.
- J. Cho, S. Lee, S. P. Yoon, J. Han, S. W. Nam, K.-Y. Lee and H. C. Ham, Role of heteronuclear interactions in selective H2 formation from HCOOH decomposition on bimetallic Pd/M (M = late transition FCC metal) catalysts, ACS Catal., 2017, 7, 2553–2562 Search PubMed.
- S. Kim, M.-C. Kim, B. C. Yeo and S. S. Han, High-throughput design of bimetallic core–shell catalysts for the electrochemical nitrogen reduction reaction, J. Mater. Chem. A, 2023, 11, 24686–24697 RSC.
- P. Wang, W. Nong, Y. Li, H. Cui and C. Wang, Strengthening nitrogen affinity on CuAu@Cu core–shell nanoparticles with ultrathin Cu skin via strain engineering and ligand effect for boosting nitrogen reduction reaction, Appl. Catal., B, 2021, 288, 119999 CrossRef CAS.
- S. Liu, Y. Xu, S. Jiao, W. Tian, T. Zhou, Z. Wang, X. Li, L. Wang and H. Wang, Rational construction of Au 3 Cu@ Cu nanocages with porous core–shell heterostructured walls for enhanced electrocatalytic N2 fixation, J. Mater. Chem. A, 2021, 9, 8372–8377 RSC.
- J.-L. Shi, S.-Q. Xiang, D.-J. Su, X. Liu, W. Zhang and L.-B. Zhao, Theoretical Insights on Au-based Bimetallic Alloy Electrocatalysts for Nitrogen Reduction Reaction with High Selectivity and Activity, ChemSusChem, 2021, 14, 4525–4535 Search PubMed.
- H. Yu, Z. Wang, D. Yang, X. Qian, Y. Xu, X. Li, H. Wang and L. Wang, Bimetallic Ag 3 Cu porous networks for ambient electrolysis of nitrogen to ammonia, J. Mater. Chem. A, 2019, 7, 12526–12531 RSC.
- Y. Liu, L. Huang, X. Zhu, Y. Fang and S. Dong, Coupling Cu with Au for enhanced electrocatalytic activity of nitrogen reduction reaction, Nanoscale, 2020, 12, 1811–1816 Search PubMed.
- J. H. Montoya, C. Tsai, A. Vojvodic and J. K. Nørskov, The Challenge of Electrochemical Ammonia Synthesis: A New Perspective on the Role of Nitrogen Scaling Relations, ChemSusChem, 2015, 8, 2180–2186 CrossRef CAS PubMed.
- J. Enkovaara, N. A. Romero, S. Shende and J. J. Mortensen, GPAW-massively parallel electronic structure calculations with Python-based software, Procedia Comput. Sci., 2011, 4, 17–25 CrossRef.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Density functionals for surface science: Exchange-correlation model development with Bayesian error estimation, Phys. Rev. B:Condens. Matter Mater. Phys., 2012, 85, 235149 Search PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
-
The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, ed. C. F. Matta and R. J. Boyd, Wiley, 1st edn, 2007 Search PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The atomic simulation environment—a Python library for working with atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- N. I. of Standards and Technology, Security Requirements for Cryptographic Modules, U.S. Department of Commerce, Washington, D.C., 2001.
- X. Ma, Z. Li, L. E. K. Achenie and H. Xin, Machine-Learning-Augmented Chemisorption Model for CO2 Electroreduction Catalyst Screening, J. Phys. Chem. Lett., 2015, 6(18), 3528–3533 CrossRef CAS PubMed.
- Z. Li, S. Wang, W. S. Chin, L. E. Achenie and H. Xin, High-throughput screening of bimetallic catalysts enabled by machine learning, J. Mater. Chem. A, 2017, 5, 24131–24138 RSC.
- H. Xu, D. Cheng, Y. Gao and X. C. Zeng, Assessment of catalytic activities of gold nanoclusters with simple structure descriptors, ACS Catal., 2018, 8, 9702–9710 CrossRef CAS.
- M. Kim, B. C. Yeo, Y. Park, H. M. Lee, S. S. Han and D. Kim, Artificial Intelligence to Accelerate the Discovery of N2 Electroreduction Catalysts, Chem. Mater., 2020, 32, 709–720 CrossRef CAS.
- M. Zafari, D. Kumar, M. Umer and K. S. Kim, Machine learning-based high throughput screening for nitrogen fixation on boron-doped single atom catalysts, J. Mater. Chem. A, 2020, 8, 5209–5216 RSC.
- D. Kim, J. Resasco, Y. Yu, A. M. Asiri and P. Yang, Synergistic geometric and electronic effects for electrochemical reduction of carbon dioxide using gold–copper bimetallic nanoparticles, Nat. Commun., 2014, 5, 4948 CrossRef CAS PubMed.
- S. Bhattacharjee, U. V. Waghmare and S.-C. Lee, An improved d-band model of the catalytic activity of magnetic transition metal surfaces, Sci. Rep., 2016, 6, 35916 Search PubMed.
- S. A. Akhade and J. R. Kitchin, Effects of strain, d-band filling, and oxidation state on the surface electronic structure and reactivity of 3d perovskite surfaces, J. Chem. Phys., 2012, 137, 084703 CrossRef PubMed.
- A. Vojvodic, J. K. Nørskov and F. Abild-Pedersen, Electronic Structure Effects in Transition Metal Surface Chemistry, Top. Catal., 2014, 57, 25–32 CrossRef CAS.
-
L. Buitinck, G. Louppe, M. Blondel, F. Pedregosa, A. Mueller, O. Grisel, V. Niculae, P. Prettenhofer, A. Gramfort, J. Grobler, R. Layton, J. Vanderplas, A. Joly, B. Holt and G. Varoquaux, API design for machine learning software: experiences from the scikit-learn project, arXiv, 2013, preprint, arXiv:1309.0238 DOI:10.48550/arXiv.1309.0238.
-
M. Abadi, A. Agarwal, P. Barham, E. Brevdo, Z. Chen, C. Citro, G. S. Corrado, A. Davis, J. Dean, M. Devin, S. Ghemawat, I. Goodfellow, A. Harp, G. Irving, M. Isard, Y. Jia, R. Jozefowicz, L. Kaiser, M. Kudlur, J. Levenberg, D. Mané, R. Monga, S. Moore, D. Murray, C. Olah, M. Schuster, J. Shlens, B. Steiner, I. Sutskever, K. Talwar, P. Tucker, V. Vanhoucke, V. Vasudevan, F. Viégas, O. Vinyals, P. Warden, M. Wattenberg, M. Wicke, Y. Yu and X. Zheng, A System for Large-Scale Machine Learning, 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), USENIX Association, 2016, pp. 265–283.
- M. Zafari, A. S. Nissimagoudar, M. Umer, G. Lee and K. S. Kim, First principles and machine learning based superior catalytic activities and selectivities for N2 reduction in MBenes, defective 2D materials and 2D π-conjugated polymer-supported single atom catalysts, J. Mater. Chem. A, 2021, 9, 9203–9213 RSC.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, LOBSTER: A tool to extract chemical bonding from plane-wave based DFT, J. Comput. Chem., 2016, 37, 1030–1035 Search PubMed.
- M. Küpers, P. M. Konze, S. Maintz, S. Steinberg, A. M. Mio, O. Cojocaru-Mirédin, M. Zhu, M. Müller, M. Luysberg, J. Mayer, M. Wuttig and R. Dronskowski, Unexpected Ge–Ge Contacts in the Two-Dimensional Ge4Se3Te Phase and Analysis of Their Chemical Cause with the Density of Energy (DOE) Function, Angew. Chem., Int. Ed., 2017, 56, 10204–10208 CrossRef PubMed.
- M. Khazaei, J. Wang, M. Estili, A. Ranjbar, S. Suehara, M. Arai, K. Esfarjani and S. Yunoki, Novel MAB phases and insights into their exfoliation into 2D MBenes, Nanoscale, 2019, 11, 11305–11314 RSC.
- G. Kour, X. Mao and A. Du, Computational screening of single-atom alloys TM@Ru(0001) for enhanced electrochemical nitrogen reduction reaction, J. Mater. Chem. A, 2022, 10, 6204–6215 Search PubMed.
- X. Guo, J. Gu, S. Lin, S. Zhang, Z. Chen and S. Huang, Tackling the Activity and Selectivity Challenges of Electrocatalysts toward the Nitrogen Reduction Reaction via Atomically Dispersed Biatom Catalysts, J. Am. Chem. Soc., 2020, 142, 5709–5721 CrossRef CAS PubMed.
- A. Das, S. C. Mandal, A. S. Nair and B. Pathak, Computational Screening of First-Row Transition-Metal Based Alloy Catalysts–Ligand Induced N2 Reduction Reaction Selectivity, ACS Phys. Chem. Au, 2022, 2, 125–135 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Projected density of states, optimized adsorption geometries and hyperparameters of machine learning algorithms and their performances. See DOI: https://doi.org/10.1039/d5cp01094b |
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ab,
Arash
Toghraei
c,
Daniel
Guay
b and
Gilles H.
Peslherbe
ab,
Arash
Toghraei
c,
Daniel
Guay
b and
Gilles H.
Peslherbe
 *abde
*abde
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond and N2 activation at the surface of the catalyst. Thus, the first objective in electrocatalyst design for the NRR is to effectively tune the electronic structure of the active site to enhance this acceptance-donation mechanism and thus N2 activation at the catalyst surface as the most important step.
N bond and N2 activation at the surface of the catalyst. Thus, the first objective in electrocatalyst design for the NRR is to effectively tune the electronic structure of the active site to enhance this acceptance-donation mechanism and thus N2 activation at the catalyst surface as the most important step.![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond, namely the associative and dissociative pathways. As the dissociation of N
N bond, namely the associative and dissociative pathways. As the dissociation of N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N requires overcoming a high energy barrier on flat surfaces, the latter pathway was not considered in this study.9 Associative pathways encompass the distal, alternating, and enzymatic routes, which mainly differ in the adsorption configuration and hydrogenation sequence of N2. In the distal and alternating pathway, N2 is adsorbed with an end-on configuration whereas in the enzymatic pathway N2 is adsorbed in a side-on configuration. The hydrogenation step implicates either Tafel-type or Heyrovsky-type mechanisms.9 In the Tafel-type mechanism, the solvated proton is first adsorbed on the surface, where it attaches an electron and reacts as an H adatom with the NRR intermediate. In the Heyrovsky mechanism, the adsorbed intermediate is hydrogenated directly from the solution and electrons from the electrode. Among associative pathways, the distal pathway is the most favourable one on transition metal surfaces, and thus the one considered in this article.9,22,28 In this pathway, through a mechanism detailed in eqn (1), N2 is adsorbed with an end-on configuration as the first and most important step in the NRR (eqn (1a)). This non-electrochemical step is followed by hydrogenation of adsorbed N2 in subsequent electrochemical steps. The first hydrogenation step (eqn (1b)) of the NRR is the potential limiting step for late TMs such as Ni, Pt and Au while the fifth hydrogenation (eqn (1f)) step is the potential limiting step for early TMs such as Sc, Ti and V.9 NH3 ultimately desorbs from the surface of the catalyst (eqn (1h)), making the active site available for another catalytic cycle.
N requires overcoming a high energy barrier on flat surfaces, the latter pathway was not considered in this study.9 Associative pathways encompass the distal, alternating, and enzymatic routes, which mainly differ in the adsorption configuration and hydrogenation sequence of N2. In the distal and alternating pathway, N2 is adsorbed with an end-on configuration whereas in the enzymatic pathway N2 is adsorbed in a side-on configuration. The hydrogenation step implicates either Tafel-type or Heyrovsky-type mechanisms.9 In the Tafel-type mechanism, the solvated proton is first adsorbed on the surface, where it attaches an electron and reacts as an H adatom with the NRR intermediate. In the Heyrovsky mechanism, the adsorbed intermediate is hydrogenated directly from the solution and electrons from the electrode. Among associative pathways, the distal pathway is the most favourable one on transition metal surfaces, and thus the one considered in this article.9,22,28 In this pathway, through a mechanism detailed in eqn (1), N2 is adsorbed with an end-on configuration as the first and most important step in the NRR (eqn (1a)). This non-electrochemical step is followed by hydrogenation of adsorbed N2 in subsequent electrochemical steps. The first hydrogenation step (eqn (1b)) of the NRR is the potential limiting step for late TMs such as Ni, Pt and Au while the fifth hydrogenation (eqn (1f)) step is the potential limiting step for early TMs such as Sc, Ti and V.9 NH3 ultimately desorbs from the surface of the catalyst (eqn (1h)), making the active site available for another catalytic cycle.
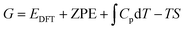
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond length of adsorbed N2, melting point and atomic number of the active site metal. These approaches only used the geometrical properties of the active site to train the MLAs.
N bond length of adsorbed N2, melting point and atomic number of the active site metal. These approaches only used the geometrical properties of the active site to train the MLAs. and width (Wd), respectively, defined as:
and width (Wd), respectively, defined as:

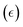 .19 Also, the filling that is defined as the number of states below the Fermi level affects the center and the width of the d-band.41–43
.19 Also, the filling that is defined as the number of states below the Fermi level affects the center and the width of the d-band.41–43
 , Wd, fd) calculated by DFT are used as electronic features to train the MLA. The position of the top edge of the d-band was also included as a training feature since the of filling of the anti-bonding state at the top of the d-band determines the strength of the interaction. Besides electronic structure features, intrinsic properties of the active site available from the periodic table such as electron affinity, Pauli electronegativity, work function, and atomic radius of metal active site were included. We believe that electronic descriptors play a crucial role in modelling actual electrocatalysts with complex structures, such as those exhibiting disorder or phase segregation, as these structural variations result in changes in the electronic structure of the active site that would not be captured by elemental and intrinsic properties of the active site metal alone. Moreover, using the electronic descriptors enhances MLA prediction accuracy compared to that of using only elemental descriptors, as further discussed in the ESI.† In the last step of feature engineering, we standardize MLA features to enhance the accuracy of the model, because of the large variation in the numerical values of the data in the dataset used for training of MLAs, which results in low training efficiency and prediction bias for optimization algorithms. We standardized our training features using the StandardScaler module implemented in scikit-learn44 as:
, Wd, fd) calculated by DFT are used as electronic features to train the MLA. The position of the top edge of the d-band was also included as a training feature since the of filling of the anti-bonding state at the top of the d-band determines the strength of the interaction. Besides electronic structure features, intrinsic properties of the active site available from the periodic table such as electron affinity, Pauli electronegativity, work function, and atomic radius of metal active site were included. We believe that electronic descriptors play a crucial role in modelling actual electrocatalysts with complex structures, such as those exhibiting disorder or phase segregation, as these structural variations result in changes in the electronic structure of the active site that would not be captured by elemental and intrinsic properties of the active site metal alone. Moreover, using the electronic descriptors enhances MLA prediction accuracy compared to that of using only elemental descriptors, as further discussed in the ESI.† In the last step of feature engineering, we standardize MLA features to enhance the accuracy of the model, because of the large variation in the numerical values of the data in the dataset used for training of MLAs, which results in low training efficiency and prediction bias for optimization algorithms. We standardized our training features using the StandardScaler module implemented in scikit-learn44 as:




![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N bond undergoes an elongation from 1.10 Å to 1.13 and 1.12 Å over Au@Au3Re and Au@Au3Mo, respectively. Moreover, Bader charge analysis shows 0.18e− and 0.14e− charge transfer from Re and Mo to the N2 molecule upon adsorption, respectively, confirming N2 activation at the surface of these catalysts.
N bond undergoes an elongation from 1.10 Å to 1.13 and 1.12 Å over Au@Au3Re and Au@Au3Mo, respectively. Moreover, Bader charge analysis shows 0.18e− and 0.14e− charge transfer from Re and Mo to the N2 molecule upon adsorption, respectively, confirming N2 activation at the surface of these catalysts.
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N molecule. Comparison of the ICOHP between isolated N2 and N2 adsorbed on Au@Au3Re and Au@Au3Mo (Fig. 5(b) and (c)) confirms N2 activation over the catalysts, with an increased ICOHP (reduction in magnitude). The major contribution to the bonding of N2 at the surface of Au@Au3Re arises from the interaction of orbitals aligned with the N2 molecular axis and perpendicular to the surface (Fig. S5, ESI†).
N molecule. Comparison of the ICOHP between isolated N2 and N2 adsorbed on Au@Au3Re and Au@Au3Mo (Fig. 5(b) and (c)) confirms N2 activation over the catalysts, with an increased ICOHP (reduction in magnitude). The major contribution to the bonding of N2 at the surface of Au@Au3Re arises from the interaction of orbitals aligned with the N2 molecular axis and perpendicular to the surface (Fig. S5, ESI†).



