Experimental study of the effect of particle collision on bubble dynamics behavior

Abstract

Particle–bubble flows are commonly found in industrial processes such as mineral flotation, catalytic reactors, and fluidized beds. This study reports the behavior of particles colliding with adhered bubbles on surfaces, resulting in their detachment. The effects of particle diameter, particle collision velocity, and bubble height on bubble dynamics were investigated. To connect the three factors together, the Weber number of the particles was fitted with the different heights of bubbles to derive a critical detachment curve for bubbles at varying particle diameters. The results indicate that the detachment height of bubbles is inversely proportional to the collision velocity and diameter of the particles. Additionally, among these three factors, the primary force influencing the bubble detachment time is the capillary force of the particles.

---

1. Introduction

Gases typically disperse in liquids in the form of bubbles, exhibiting various behaviors such as detachment, deformation, and rupture.^1,2 Moreover, the ascent of bubbles creates turbulence and mixing effects. To utilize this principle, in industrial applications such as catalytic reactors, the interaction between bubbles and particles is typically utilized to optimize the contact between gas, liquid, and solid phases, thereby improving the mass transfer efficiency and flow rate of the reactants. Therefore, studying the dynamics of particle–bubble interactions can optimize reactor design and improve reaction efficiency.

The interactions between particles and bubbles are typically categorized into collision, attachment, and detachment, which can alter the size, rise velocity, and residence time of the bubbles, thereby directly influencing the dynamics of gas–liquid flow.^3,4 In order to study the detachment behavior of particles during the collision between bubbles and the air–water interface, Wang et al.⁵ placed hydrophobic particles at the bottom of a water tank and observed their behavior. Bubbles were generated at the capillary tube outlet and attached to the particles, forming mineralized bubbles that rose to the gas–liquid interface. The results showed that the differences in particle hydrophobicity led to inconsistent bubble velocity decay rates. Hydrophilic particles caused a slower decrease in bubble velocity, while hydrophobic particles led to a rapid decline in bubble speed. Mohan et al.⁶ studied the dynamics of rising bubbles containing particles under the influence of surfactants and turbulence, focusing on different bubble surface loads. The experimental data were compared with the behavior of particle-laden bubbles rising in quiescent water without surfactants. In quiescent water, the addition of methyl isobutyl carbinol surfactant reduced the average rise velocity of bubbles with a certain surface load, while turbulence consistently led to an increase in bubble rise velocity under all testing conditions. Wang et al.⁷ studied the effect of particle coverage on the dynamics of rising bubbles. This was done by calculating the buoyancy and drag forces acting on the bubbles, as well as the influence of particles on bubble behavior. The overall velocity of the bubbles is directly related to their aspect ratio and is independent of whether the bubbles are covered by particles. As the shape of the bubbles becomes more spherical, their velocity decreases. Xia et al.⁸ used a three-phase dynamics model of particle–bubble–liquid, this model includes the collision, attachment, and detachment behavior between particles and bubbles. Numerical results indicate that hydrophilic particles can enhance the rise velocity of bubbles, even exceeding that of bubbles rising in pure liquid. However, the attachment behavior significantly hinders bubble rise but enhances particle transport intensity. Particles driven by a higher bubble frequency exhibit greater lift height and a stronger dispersion effect.

However, the dynamic mechanisms underlying the interaction between particles and bubbles leading to bubble detachment are not yet fully understood, as the forces exerted on the bubbles by particle collisions are constantly changing, making the bubble separation process highly complex. Therefore, appropriate experimental setups and correct force theories are crucial for addressing this issue. Mohammadi et al.⁹ designed an experimental setup that allows particles to accurately collide with bubbles every time, using a vacuum pump to secure particles and releasing them at appropriate times for bubble–particle collision experiments. However, they only studied the different forces acting on particles of various sizes during their attachment process to the bubbles, and they did not study the detachment behavior of the bubbles. Chen et al.¹⁰ studied the influence of a single particle on the dynamics of bubble detachment by altering the properties of the liquid as well as the size and position of the particles. The results showed that when the particle is located in the neck region of the bubble, the detachment process is hindered; however, if the particle is positioned above or below the neck of the bubble, it facilitates the detachment process. Nonetheless, the description of the force conditions during bubble detachment is not very clear. Therefore, we can draw on their research theory from the study of Zhu et al.¹¹ They observed the bubble detachment process at the gas nozzle exit using a jet-type microbubble generator device. They established a force balance model that takes into account the fluctuations in the flow field, analyzing the relationship between the bubble detachment size, growth parameters, and forces. This model considers various forces acting on the bubble and categorizes them into separating forces that promote bubble detachment and adhesive forces that hinder it. Wang et al.¹² focused on studying the effect of varying DDA concentrations on the changes in particle contact angle and their influence on the dynamics of bubble neck rupture. By using a high-speed camera to capture the variation in the minimum radius of the bubble neck, they fitted the experimental data with a power law equation that describes the changes in the radius of the bubble neck, thereby determining the surface pressure and surface tension. Ultimately, we can integrate the experimental equipment of the aforementioned scholars and the theory of particle collision with bubbles as the research approach for this paper, which will ultimately allow us to establish our innovative method.

Most of the scholars in the previous section studied the bubble separation mechanisms in bubble-fluid systems or analyzed the sliding of particles on bubbles. However, the mechanism of particles colliding with bubbles and causing detachment remains unclear, and there is relatively little research on the regularity of particle collisions on bubbles in fluid. Therefore, the innovation of this paper lies in the study of the dynamic phenomena of particle collision and bubble separation, including the conditions required for bubble detachment and the detachment time, as well as the proposal of a critical separation curve for bubbles.

2. Experimental methodology

2.1. Experimental apparatus

The experimental setup is shown in Fig. 1. The entire experimental apparatus is mounted on a 500 mm × 500 mm platform, which effectively reduces surrounding vibrations and noise, and also allows for the installation of an aluminum rod to hold the particle-dropping pipe. The liquid used is deionized water, contained in a tank with glass and copper surfaces. The copper base has a 0.8 mm wide channel to allow external air to enter. Air is injected using a micro syringe, with the channel connected by 2 mm inner diameter latex tubes, and air leakage prevention is ensured through multiple tests. Bubbles are generated by injecting pure air through a syringe pump into the channel reserved in the copper base. The high-speed camera operates at 2000 frames per second with a resolution of 1260 × 860, positioned directly in front of the bubble location, and the camera footage is synchronized and displayed on a computer monitor. The spherical brass particles are of model H62, with a density of 8.4 g cm⁻³. The contact angle between the particles and the liquid interface was measured using imaging software. Before the experiment, the particles were ultrasonically cleaned for 5 minutes. For the measurement of the contact angle on the surface of a copper block, we first polished the surface with sandpaper to remove the oxide layer. Subsequently, we used a contact angle measuring instrument to measure the wettability of the surface, and the contact angle was found to be 75°. We employed the traditional static drop method to measure the contact angle of the particles, as shown in Fig. 2, which involves placing the particles directly on a horizontal air–liquid interface.¹³ Once the particles have stabilized, the particle radius R_p and the immersion depth H_p are measured, and the contact angle is calculated using eqn (1). Nine samples of particles with varying diameters were taken and their average contact angle was calculated to be 60°.

Fig. 1 Schematic diagram of the experimental setup.

Fig. 2 Measurement of particle contact angle.

2.2. Experimental procedure

Before the experiment begins, the surface of the copper base is sanded with sandpaper to ensure no water stains are left. Particles are placed in a beaker and immersed in 95% ethanol for cleaning. A glass stirrer is used to agitate the particles, and then the particles are removed and allowed to dry as the alcohol evaporates.

First, a bubble of a certain height is generated using a syringe. Then, particles of a selected diameter are allowed to fall from the top of the tube without any initial velocity. The particles will collide with the bubble along the inner wall of the tube. The entire experiment is recorded by observing the relevant motion of the bubble as it detaches. The images of the particle collision on the bubble are captured using a high-speed camera and stored on a PC (Personal Computer), and then processed and analyzed using image analysis software.

When air is injected from the syringe, a bubble forms that gradually increases in height and width. To facilitate the measurement of the bubble size, the height of the bubble is used as the measurement parameter in this study. Measurement shows that the maximum bubble height before it detaches from the copper surface is 3.8 mm. Therefore, the experiment selects a maximum bubble height of 3.5 mm, with the minimum bubble height being 2.0 mm.

2.3. Experimental schemes

The study explores the effects of various factors on the detachment of bubbles upon collision by particles, including different particle collision velocities u_p (Schemes 1–3), particles colliding with bubbles at different heights H (Schemes 2, 4 and 5), and particles with different diameters D_p colliding with bubbles (Schemes 2, 6 and 7). Detailed schemes are provided in Table 1.

Table 1 Experimental schemes

Scheme	u p (m s^−1)	D p (mm)	H (mm)
1	0.1	1.4	3.5
2	0.2	1.4	3.5
3	0.3	1.4	3.5
4	0.2	1.4	2.5
5	0.2	1.4	3.0
6	0.2	1.0	3.5
7	0.2	1.2	3.5

---

3. Force analysis of particle–bubble collision

Fig. 3 shows the force analysis diagram of particles colliding with bubbles. As articles accelerate towards the bubble surface, they experience gravitational force, buoyancy, resistance, and surface tension. The gravitational force expression for particles, with diameter D_p and density ρ_p iswhere R_p is the radius of the particle, and ρ_p is the density of the brass particles.

Fig. 3 The forces acting on the particle during the particle–bubble collision process: (1) represents the copper particle, (2) the bubble, (3) the bronze base, and (4) the deionized water. φ = 0 (not labeled in the figure).

The buoyancy expression for particles in deionized water is

where ρ_f denotes the fluid density.

According to the relative motion between bubbles and particles, the axial component of the drag prevents the collision process between particles and bubbles. The expression for the drag is¹⁴

C _D is the drag coefficient of the bubble.¹⁴ For rigid spherical particles without wall effects, the drag coefficient is determined using eqn 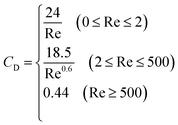(5):

Pressure is expressed as¹⁵

f_p = πR_p² sin²(αK) (6)

where R_b(1 − sin φ) represents the height difference between the top of the bubble and the center of the TPCL, σ is the surface tension coefficient, φ is the particle polar angle, α is the half-fill angle, and the vertical component of force f_p is calculated as

(f_p)_y = πR_p² sin²(αK)sin φ (8)

The particle–bubble attachment to the interface forms a three-phase contact line. For the force analysis illustrated in Fig. 3, the capillary force can be expressed as¹⁵

f_c = 2πR_pσ(sin α sin(θ − α)) (9)

TPCL is the three-phase contact line, representing the distance at which particles come into contact with bubbles at the interface, measurable using image software. Here, R_TPCL is half the length of the three-phase contact line, θ is the contact angle, and R_b is the radius of the bubble.

Regarding the bubble and the base, the solid–liquid surface tension is the horizontal force at the pore edge and naturally does not appear in the vertical capillary force. Thus, the capillary force at the pore edge is the solid–gas surface tension.¹⁶

where D₀ is the diameter of the hole reserved in the brass base.

The expression for the buoyancy of the bubble is

where H is the height of the bubble.

To facilitate analysis, this study focuses exclusively on the forces in the vertical direction. The forces under consideration in Fig. 3 are F_c, F_d, F_p, F_g and F_b.

4. Results and discussion

4.1. Effect of collision velocity on bubble detachment behaviors

Particles are dropped into the liquid pool from pipes of different lengths without any initial velocity, resulting in collisions with varying velocities with the bubbles, causing the bubbles to detach. Through analysis of high-speed camera images, it was observed that the detachment of the bubble could generally be divided into compression and rising stages, based on the force exerted by the particle and changes in the bubble neck. Fig. 4 shows the trajectory images of particles with D_p = 1.4 mm colliding with a bubble of H = 3.5 mm at t = 0 ms with different velocities. To obtain the most accurate collision velocity, multiple measurements were taken using image software, and an average value was calculated. Images in the blue box indicate the bubble compression stage, while those in the adjacent pale orange areas show the bubble rising stage. During the compression stage (t = 0–15 ms), particles accelerate towards the bubble, transferring kinetic energy that compresses and deforms the bubble, reducing its height and elongating its width. Finally, when particles lose kinetic energy, the bubble, no longer affected by particles, begins to rise, marking the critical moment between compression and rising stages. In the rising stage, particles transfer all their kinetic energy to the bubble, which then slides along the bubble's surface under the influence of capillary and pressure forces. As a result of the kinetic energy from the previous stage, the bubble compresses and deforms, while the base exerts an upward reactive force on the bubble. Simultaneously, due to surface tension effects, the bubble stretches and thins, minimizing its surface area within a certain volume, thereby forming a neck, as shown in Fig. 3. For convenience of measurement, the horizontal shortest distance of the bubble neck is defined as R. The variation in R reflects the detachment characteristics of the bubble. At 29 ms in Fig. 4(a), 27 ms in Fig. 4(b), and 27.5 ms in Fig. 4(c), the bubble neck fractures as the bubble continues to rise, causing the neck to contract. According to Rayleigh–Taylor instability, the bubble neck radius decreases, allowing liquid to rush into the bubble membrane, splitting it into two parts, thus completing the entire process of particle collision and bubble detachment.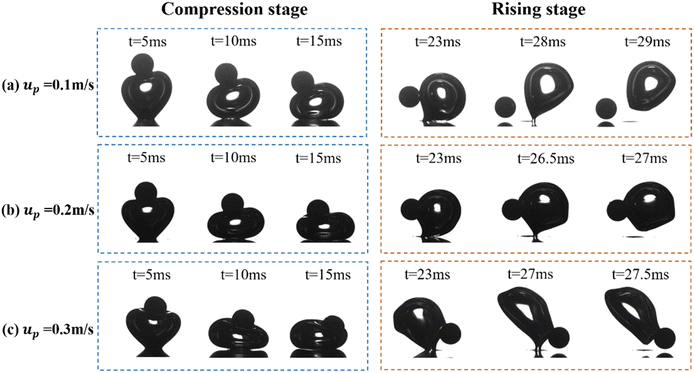

Fig. 4 Trajectory snapshots of a particle colliding with a bubble at different time points under velocities of (a) 0.1 m s⁻¹, (b) 0.2 m s⁻¹, and (c) 0.3 m s⁻¹.

To better analyze quantitatively the detachment characteristics of bubbles, Fig. 5 illustrates the forces acting on the particles in the vertical direction during the bubble compression stage. It can be observed that F_g and F_c are the dominant forces, but they act in opposite directions. F_c increases over time, while F_d decreases. According to eqn (10), F_c is proportional to R_TPCL². During the bubble compression phase, as the particle continually interacts with the bubble, TPCL lengthens until the particle's kinetic energy approaches zero, approximating a critical value. From eqn (4), F_d is proportional to u_p², and in Fig. 4, particle velocity decreases over time during the compression phase. Fig. 5 examines the collision forces of different particle velocities on bubble detachment. Observing these graphs reveals that F_c is proportional to u_p; this relationship arises because greater u_p results in higher particle kinetic energy and more frequent particle-bubble contacts, thus increasing TPCL. Due to the small and relatively constant values of F_p, it does not appear in the graph.

Fig. 5 Forces acting on the bubble during particle-bubble collisions at velocities of (a) 0.1 m s⁻¹, (b) 0.2 m s⁻¹, and (c) 0.3 m s⁻¹ in the compression stage.

Wang et al.¹² studied the influence of different DDA (dodecylamine) concentrations and particle contact angles on the variation of bubble necks. In this study, to investigate whether different particle velocities affect the pinch-off time of bubbles, particles with different collision velocities with the bubble were selected, and the results are shown in Fig. 6. By analyzing the images using software, the length of R at each moment was measured. Upon comparing the images, the detachment times of the bubbles were similar, regardless of the selected particle velocities. However, at higher particle velocities, R started to change earlier. As can be seen from Fig. 5, the capillary force F_c increases with the particle velocity. Therefore, the greater the capillary force of the particles, the earlier the bubble begins to be affected and generates the detachment behavior.

Fig. 6 Change in the bubble neck radius during the rising stage of bubbles.

4.2. Effect of bubble heights on bubble detachment behaviors

To investigate the detachment behavior of particles colliding with bubbles of different heights, bubbles of three different sizes were selected and the bubble heights could be accurately measured using image software. In Fig. 7, when a particle with a diameter of 1.4 mm collides with the bubble at H = 2.5 mm at a velocity of 0.2 m s⁻¹, the bubble initially compresses upon collision. Subsequently, the bubble begins to rise, with the particle sliding along its surface. The bubble deviates to the right but gradually corrects its path and ultimately does not detach. However, when the same diameter particle collides with bubbles at H = 3.0 mm and H = 3.5 mm with the same velocity, detachment occurs. Upon comparison, it was observed that the compression phase of the bubble at H = 2.5 mm lasts only 9 ms. As the bubble height increases, the compression time also increases. It is evident that under the same kinetic energy from the particle collision, longer interaction times between the particle and bubble result in greater energy absorption by the bubble, thus increasing the likelihood of detachment. Additionally, larger bubbles experience greater buoyancy, requiring less force to overcome surface adhesion.

Fig. 7 Snapshots of particle trajectories at different time points during collisions with bubbles of (a) 2.5 mm, (b) 3.0 mm, and (c) 3.5 mm heights.

In Fig. 8, F_c exhibit a trend of initially increasing and then decreasing. Combining this with Fig. 8, it is observed that the increase in F_c is due to the continuous lengthening of the TPCL as particles interact with the bubble. However, F_c is also influenced by φ; as particles begin sliding along the bubble surface, φ increases. When φ reaches , indicating that particles are approaching the equator of the bubble, F_c becomes zero. Moreover, as the bubble size increases, the entire process of F_c variation takes longer, suggesting that the time needed by particles to move from the top to the equator of the bubble also increases. Meanwhile, F_d remains proportional to u_p² overall, showing a trend of initially increasing and then decreasing. Notably, the point at which F_d starts decreasing coincides with the peak of F_c, indicating that particles begin decelerating and reduced contact between particles and the bubble, indirectly verifying the accuracy of F_c.

Fig. 8 The forces acting on bubbles with heights of (a) 2.5 mm, (b) 3.0 mm, and (c) 3.5 mm during the particle-bubble collision process in the bubble compression phase.

In Fig. 9, the variations in neck radius of these three types of bubbles are observed. It is noted that for H = 2.5 mm, R exhibits oscillatory fluctuations and returns to its original length at t = 24 ms, corresponding to the final image in Fig. 6(a). This indicates that particles have moved close to the bottom surface, hence the bubble is no longer influenced by particles. For the other two bubble scenarios, although they detach as well, the time required for detachment is inversely proportional to the height of the bubble. This is primarily attributed to the combined effects of the buoyancy force and the bottom capillary force . is related to D₀, and since capillary force at the bottom does not change, the overall force decreases with larger bubbles. Therefore, larger bubbles detach more quickly due to the reduced combined forces acting on them.

Fig. 9 Change in bubble neck radius during the rising stage of bubbles.

4.3. Effect of particle diameters on bubble detachment behaviors

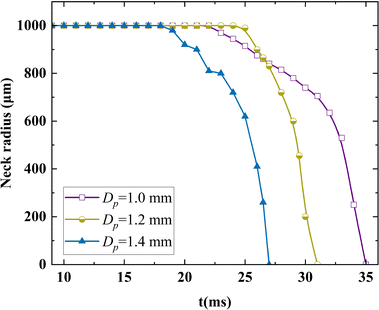
Fig. 10 shows particles of three different diameters (D_p = 1.0 mm, 1.2 mm, 1.4 mm) colliding with bubbles with H = 3.5 mm at a speed of 0.2 m s⁻¹ and the velocity of the particles is also measured multiple times. It is observed that the compression phase of these three cases lasts for 15 ms, similar to the performance of different particle velocity groups in Section 3.1. However, during the bubble's rising phase, larger D_p causes particles to detach earlier. The last frames captured by the high-speed camera before bubble detachment occur at 34 ms, 30 ms, and 26.5 ms respectively, indicating that as D_p increases, so does the mass and kinetic energy of the particles, influencing the detachment timing of the bubble.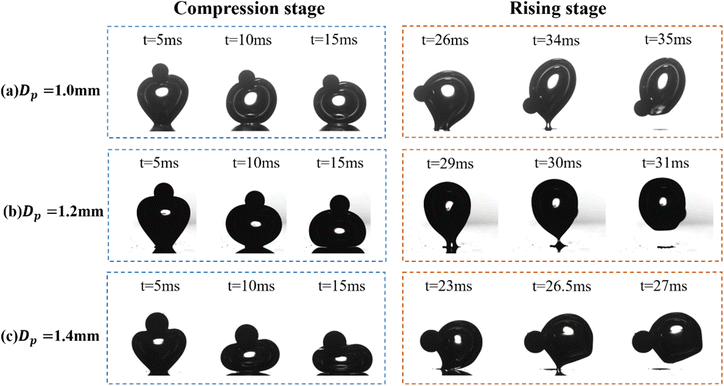

Fig. 10 Trajectory snapshots at different time points for particles with diameters of (a) 1.0 mm, (b) 1.2 mm, and (c) 1.4 mm during collision with a bubble.

In Fig. 11(b) and (c), F_c is significantly greater than in (a), yet the difference between F_c values in the former two cases is not substantial. This is because larger particles, despite having greater kinetic energy upon collision and thereby increasing contact with the bubble to some extent, experience increased upward forces F_d and F_b as well as downward force F_g as D_p increases. Consequently, the variation in F_c may not necessarily correlate linearly with D_p. The trend in F_d still shows an initial increase followed by a decrease, with the key distinction being that initial F_d is directly proportional to D_p.

Fig. 11 Forces acting on the particle during the collision of particles with diameters of (a) 1.0 mm, (b) 1.2 mm, and (c) 1.4 mm in the bubble compression phase.

Fig. 12 illustrates the time taken for bubbles to detach after collision with particles of different diameters, corresponding to the instantaneous detachment moments of bubbles in Fig. 9. This demonstrates that the detachment time of bubbles is inversely proportional to D_p. This is because larger particles generate a greater capillary forc F_c when colliding with bubbles, as shown in Fig. 11, which results in a shorter bubble detachment time.

Fig. 12 Change in the bubble neck radius during the rising stage of bubbles.

4.4. Critical detachment conditions for bubbles

To assess the detachment characteristics of bubbles, the Weber number (We) of the particles was utilized as a metric. During the process of particles colliding with the surface of the bubble, the characteristics of this collision are influenced by properties such as particle size and fluid dynamics. To simplify the analysis, the Weber number was employed to conduct dimensionless analysis of the particle–bubble collision process. The Weber number represents the ratio of inertial forces to surface tension; when We > 1, it indicates that kinetic energy dominates the collision process of the particles.

Fig. 13 represents different motion state diagrams of particles colliding with bubbles. The horizontal axis denotes different bubble sizes, while the vertical axis indicates the particle Weber number at 0 ms. The three graphs in Fig. 13 depict various states of particle–bubble interaction for different D_p values. Experimental data indicate substantial agreement between the boundaries of the two distinct collision behaviors and scaling laws. Our scaling laws suggest that, under identical bubble conditions at the same height, smaller diameter particles exhibit higher inertia forces compared to larger diameter particles, resulting in equivalent behavioral effects. Therefore, extensive experiments were conducted to record the critical We numbers for particle collision leading to bubble detachment or non-detachment, followed by curve fitting of these critical detachment Weber numbers for each bubble at different heights. Smaller particles require a larger We (up to a maximum of 15) to detach bubbles in deionized water, whereas larger particles can detach bubbles with a smaller We (as low as 0.2) when colliding with the same bubbles. The data results indicate that particles colliding with bubbles at higher H require a larger We for detachment, whereas the opposite is true for collisions with bubbles at smaller H. Furthermore, larger D_p particles require a smaller We for bubble detachment, while smaller D_p particles require a larger We for detachment.

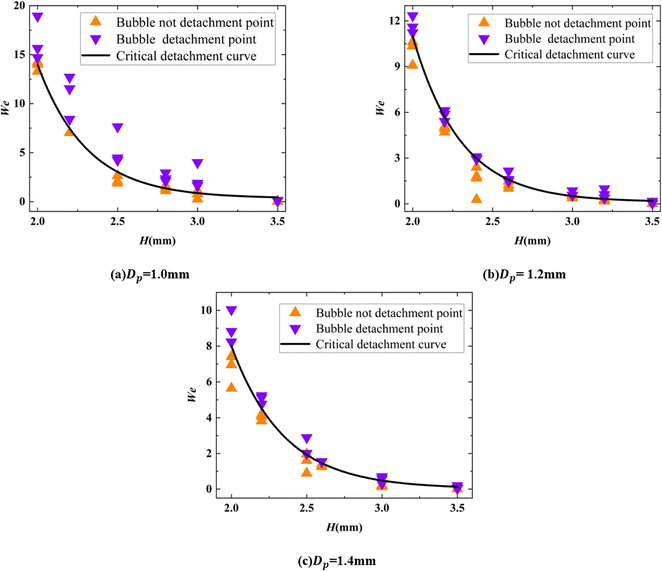Fig. 13 The critical detachment diagram of the bubble illustrates the relationship between the Weber number and bubble height for particles with diameters of (a) 1.0 mm, (b) 1.2 mm, and (c) 1.4 mm.

5. Conclusions

The effects of particle collision velocity, bubble height, and particle diameter on the detachment behavior of bubbles are discussed in this paper. Some research findings are summarized as follows:

(1) Bubble detachment requires the colliding particles to reach a certain kinetic energy, and the conditions for detachment of bubbles of different sizes are provided in the Weber number diagram. The detachment process can be divided into the stages of bubble compression and rising based on the motion and force conditions of particles and bubbles. During the compression stage, the kinetic energy of the particles is transferred to the bubble. In the rising stage, the time taken for R to change from 1000 μm to 0 μm determines the time required for bubble detachment.

(2) The experimental results indicate that the time for the bubbles to detach is inversely proportional to D_p and H. However, an interesting observation is that under the conditions of this study (u_p = 0.1, 0.2, and 0.3 m s⁻¹), the detachment time is not directly related to u_p. When particles collide with larger bubbles at higher u_p, although the generated F_c has increased but this only leads to a rapid change in the bubble neck during the initial rising period (18–25 ms). Finally, the detachment process begins to lag in the subsequent time. The maximum value of F_c is also directly proportional to D_p, as larger D_p has greater kinetic energy, resulting in a larger R_TPCL during collision. In the H factor, the duration of F_c is proportional to H, because more time is required for particles to slide over larger bubbles.

(3) The critical curve relating H and We in bubble detachment is presented in this paper. In the three different D_p factors, the critical detachment curves of the bubbles are all similar inverse proportional curves. Although the We number required for particles with different D_p values to detach from bubbles at H = 2 mm is relatively high (ranging from 8 to 14), the variation in We needed for detachment from bubbles at H = 3.5 mm is minimal (ranging from 0.5 to 1).

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Fundamental Science (Natural Science) Research Project of Higher Education in Jiangsu Province [grant number 22KJA470003], the Postgraduate Research & Practice Innovation Program of Jiangsu Province [grant number SJCX24_2429] and the Postgraduate Research & Practice Innovation Program of Jiangsu Province [grant number KYCX23_3697].

References

1. C. Gong, D. Y. Li and C. Kang, Visualization of the evolution of bubbles in the spray sheet discharged from the air-induction nozzle, Pest Manage. Sci., 2022, 78, 1850–1860.
2. C. Gong, D. Y. Li and C. Kang, Effect of oil-based emulsion on air bubbles in the spray sheet produced through the air-induction nozzle, Pest Manage. Sci., 2022, 78, 5347–5357.
3. F. Z. Chen, H. F. Qiang and W. R. Gao, Numerical simulation of heat transfer in gas particle two-phase flow with smoothed discrete particle hydrodynamics, Acta Phys. Sin., 2014, 63(23), 17.
4. Z. Q. Wu, H. Jin, Y. F. Ren and L. J. Guo, Investigation on drag coefficient of supercritical water cross-flow past cylinder biomass particle at low Reynolds numbers, J. Therm. Sci., 2018, 22(2), 383–389.
5. Y. Wang, Q. Liu, Q. He, S. Ding, W. Shi, X. Gui and Y. Xing, Collision-induced detachment behavior of bubble-particle aggregate at air-water interface, Powder Technol., 2024, 446, 120189.
6. S. M. Murali Mohan, Z. Peng and E. Doroodchi, Rising dynamics of particle-laden bubbles in presence of surfactant and turbulence, Miner. Eng., 2024, 217, 108935.
7. P. Wang, J. J. Cilliers, S. J. Neethling and P. R. Brito-Parada, The behavior of rising bubbles covered by particles, Chem. Eng. J., 2019, 365, 111–120.
8. H. Xia, Z. Zhang, J. Liu, X. Ao, S. Lin and Y. Yang, Modeling and numerical study of particle-bubble-liquid flows using a front-tracking and discrete-element method, Appl. Math. Model., 2023, 114, 525–543.
9. M. Mohammadi, M. Nazari, M. H. Kayhani and G. Ahmadi, Experimental Study And Visualization Of The Particle-Bubble Collision Process, J. Appl. Mech. Tech. Phys., 2022, 63, 903–913.
10. S. Chen, E. Xu, X. Meng, G. Wu and X. Jiang, The effect of a single loaded-particle on bubble pinch-off dynamics in various liquids, Chem. Eng. Sci., 2023, 266, 118239.
11. Y. Zhu, Z. Huang, Y. Shuai, Y. Yang, J. Sun, W. Li, J. Wang and Y. Yang, Experimental and numerical study on the formation and detachment of bubbles at orifices under the impinging jet flow, Chem. Eng. Sci., 2024, 298, 120341.
12. H. Wang and P. R. Brito-Parada, Deformation dynamics of particle-laden bubbles: The effect of surfactant concentration and particle contact angle, Miner. Eng., 2021, 160, 106706.
13. P. S. Raux, H. Cockenpot, M. Ramaioli, D. Quere and C. Clanet, Wicking in a powder, Langmuir, 2013, 29, 3636–3644.
14. A. Bhunia, S. C. Pais, Y. Kamotani and I. H. Kim, Bubble formation in a coflow configuration in normal and reduced gravity, AIChE J., 1998, 44, 1499–1509.
15. G. C. Wang, Y. Gao, S. Mitra, Y. F. Li, S. J. Zhou and G. Evans, Instantaneous bond number for a particle detaching from a bubble, Int. J. Miner. Process., 2015, 142, 22–29.
16. A. V. Nguyen and G. M. Evans, Movement of fine particles on an air bubble surface studied using high-speed video microscopy, J. Colloid Interface Sci., 2004, 273, 271–277.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00938c

---