 Open Access Article
Open Access ArticleCapturing electronic substituent effect with effective atomic orbitals†
Gerard
Comas-Vilà
 and
Pedro
Salvador
and
Pedro
Salvador
 *
*
Institut de Química Computacional i Catàlisi, Departament de Química, Universitat de Girona, c/M Aurelia Capmany 69, 17003, Girona, Catalonia, Spain. E-mail: pedro.salvador@udg.edu
First published on 29th April 2025
Abstract
The occupations of the effective atomic orbitals (eff-AOs) of the carbon atoms in the aromatic ring serve as the basis for deriving accurate descriptors of the inductive (F) and resonance (R) effects exerted by substituents in substituted benzene derivatives. The eff-AOs enable a clear separation of the σ-type electron density into contributions originating from the C–H/X bonds (where X represents a substituent) and those from the C–C bonding framework. Our analysis reveals that the inductive effect of a substituent is effectively captured by the shift in the occupation of the eff-AOs associated with the C–C bonding framework at the meta position. In contrast, the resonance effect is well-described by the shifts in the occupations of the 2pz-type eff-AOs at the ortho and para positions. The two introduced descriptors for inductive and resonant effects, namely IX and RX, are also applied to predict Hammett's σm and σp in meta- and para-substituted benzoic acid derivatives. In the case of the meta-substituted derivatives, the predictions of the σm values are excellent, with a mean average error of just 0.04. This approach provides a robust and systematic framework for quantifying substituent effects in aromatic systems.
Introduction
The substituent effect refers to the influence that a substituent – according to IUPAC,1 an atom or group of bonded atoms that can be considered to have replaced a hydrogen atom (or two hydrogen atoms in the special case of bivalent groups) in a parent molecular entity (real or hypothetical)-has on the physical and chemical properties of the molecule to which it is attached. The substituent effect can alter the reactivity, stability, and electronic distribution within the molecule, influencing reaction mechanisms, reaction rates, and the outcome of chemical reactions.One can distinguish different types of substituent effects. Some effects take place through space, like the steric or field effects. In the steric effect, large substituents can cause steric hindrance, affecting the molecule's shape, reactivity, and ability to undergo certain reactions. In the so-called field effects, it is the local electric field created by a substituent can influence the electron distribution in the rest of the molecule.
Hammett parameters, derived from the pioneering work of Hammett in the 1930s, are fundamental tools for understanding and quantifying the through-bond substituent effects. These parameters, expressed as σ values, provide a quantitative measure of how substituents influence the electron distribution and chemical reactivity. By correlating the rates or equilibrium constants of reactions with these substituent constants, the Hammett equation2,3
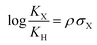 | (1) |
Hammett parameters are an indispensable tool for mechanistic studies in organic chemistry, particularly valuable for rationalizing reaction mechanisms by providing insights into how electronic effects influence the rate-determining steps and intermediates involved in a chemical reaction. In the original ionization reaction of benzoic acid, electron-withdrawing groups (EWG) accelerate the reaction, because they can stabilize (delocalize) the negative charge that is built in the transition state. Conversely, electron-donating groups (EDGs) destabilize the transition state, leading to a decrease in the reaction rate. Consequently, EWGs exhibit a positive substituent constant (σ > 0) while σ < 0 for EDGs. Different reaction mechanisms exhibit distinct ρ values. For example, a nucleophilic aromatic substitution (SNNAr) mechanism typically shows a large positive ρ value because EWGs stabilize the negatively charged Meisenheimer intermediate. In contrast, an electrophilic aromatic substitution (EAS) mechanism might show a negative ρ value, as electron-donating groups stabilize the positively charged arenium ion intermediate. Hammett plots can thus be used to distinguish between competing mechanisms. Also, a linear correlation suggests a consistent mechanism across different substituents, while deviations from linearity (e.g., in cases of steric effects) can indicate a change in mechanism or the involvement of additional factors.
To achieve a comprehensive understanding and rationalization of the σ values, the electronic effect of substituents has historically been factorized into different contributions. In one of the earlier attempts, Taft decomposed the σp and σm parameters into field/inductive (σF) and resonance (σR) contributions as4–6
| σp = σF + σR and σm = σF + ασR, | (2) |
| σp = a·F + R | (3) |
In 1991, Hansch et al.11 justified that field/inductive parameters could indeed be reliably obtained from different sources, provided the data was carefully treated (for instance, Swain and Lupton's F values were not on the same scale as the original Hammett's parameters and had to be rescaled12). In their seminal review, they compiled a comprehensive collection of σp and σm constants for more than 500 substituents. They used the simple linear relationship F = 1.297σm − 0.385σp + 0.033 to derive filed/inductive (F) parameters (also discussing alternative values obtained from several different sources), and from them used the relationship σp = σF + σR to obtain the corresponding reference resonant R (σR) parameter values. This contribution still stands as the main source of data of the field.
The resonance/mesomeric contribution, σR or R, is more difficult to quantify. In some cases, strongly electron-withdrawing or strongly electron-donating substituents don’t fall on the line predicted by the Hammett correlation.13,14 In fact, while Swain and Lupton claimed that a single R value should describe each substituent, Brown15,16 and later Hansch11 advocated for different parametrizations when there is a strong resonance delocalization between the substituent and the reaction center, developing σp+ and σp− constants. These modified Hammett constants in combination with the appropriate F values can be used in eqn (3) to derive the respective R+ and R− constants.
Hammett's σ parameters are typically obtained through experimental measurements, but efforts have been made to estimate the values by computational methods, in particular, to find descriptors to account for the field/inductive and resonance effects. The development of new descriptors to predict σ constants is justified by the need to address the limitations of traditional Hammett parameters. Traditional σ values are derived primarily from benzoic acid ionization or similar reactions, which may not fully capture the electronic effects of substituents in more complex or diverse chemical environments. Also, for new or complex substituents, experimental determination of σ values can be time-consuming and resource-intensive.
Theoretical methods have provided insight into the electronic substituent effects by confronting the original Hammett parameters with various descriptors as validation. For example, good correlations have been observed between descriptors derived from the molecular electrostatic potential (MESP) of substituted benzene and Hammett σ values. Field/inductive effects have been related to the critical points (minima) obtained from the topological analysis of the MESP,17–19 while resonant effects have been rationalized in terms of the difference in the values of the MESP at the meta and para carbon atoms of substituted benzene derivatives.20
Energetic descriptors have also been shown to correlate with σ constants. In particular, the strength of π-conjugation, quantified in the framework of energy decomposition analysis (EDA)21 by the π-type contribution to the orbital interaction term in meta- and para-substituted benzylic cations and anions, exhibited surprisingly good correlations with σm and σp constants,22 despite inductive effects are in principle ignored with such descriptor. Another energy-based descriptor is the so-called substituent effect stabilization energy (SESE), which uses homodesmotic reactions to quantify the energetics between substituent X and reaction site Y in a given framework R23,24
| SESE = E(R − X) + E(R − Y) − E(X − R − Y) − E(R) | (4) |
Several alternative descriptors are rooted in the changes in the charge distribution upon substitution. For instance, Sadlej-Sosnowska29–31 introduced the so-called charge of the substituent active region (cSAR), defined as the sum of partial atomic charges at all atoms of the substituent X and the ipso carbon atom in monosubstituted benzenes
| cSAR(X) = q(X) + q(Cipso) | (5) |
In this work, we introduce charge-density-based descriptors to properly account for inductive and resonant substituent effects separately, making use of Mayer's effective atomic orbitals (eff-AOs) and their occupations.43,44 The eff-AOs are the orbitals of the net atomic density and are obtained straightforwardly from the first-order density, using an atom-in-molecule (AIM) model, as described elsewhere.45 Disregarding the AIM definition and the underlying basis set used in the molecular calculation, one obtains as many significantly occupied eff-AOs as AOs in the classical minimal basis. The formalism can be easily generalized to correlated wavefunctions and also to molecular fragments, leading to the so-called effective fragment orbitals (EFOs).46 We have recently shown how the EFOs can be applied in a general manner to asses Lewis acid/base character47 and also to detect and quantify donor/acceptor interactions in transition metal complexes.48 This prompted us to explore whether descriptors derived from this formalism could be used to quantify inductive/field and resonance effects.
For this purpose, in this work we considered a large set of mono-substituted benzene derivatives, from which descriptors accounting for field/inductive and resonance effects are proposed, supported by excellent correlations with the available σF (F) and σR (R) parameters. In addition, descriptors related directly with Hammett's σm and σp parameters were obtained considering the corresponding meta- and para-substituted benzoic acid derivatives.
Computational details
All DFT calculations were carried out with Gaussian16.49 All geometry optimizations were performed using the BP86 density-functional50,51 coupled with the def2TZVP basis set.52 The spin-resolved EFOs have been obtained with the APOST-3D program.53 The topological fuzzy Voronoi cells (TFVC)54 atomic definition, a fuzzy-atom efficient and robust real-space alternative to QTAIM, has been used.All the substituent constants used in this work and listed in the ESI† are the F and R modified Swain–Lupton parameters and the Hammett constants tabulated in the review of Hansch et al.11 We chose as model rings a series of mono-substituted benzenes and meta- and para-substituted benzoic acid. We have considered 33 different substituents spanning a wide range on both σ and π donor–acceptor properties, depicted in Scheme 1. Indeed, according to the experimentally derived tabulated values, they cover the range from strong π-donating, e.g. NMe2 and OCH(CH3)2, with R = −0.98 and R = −0.79, respectively, to π-electron withdrawing groups like COCH3 (R = +0.17) or CN (R = +0.15).
 | ||
| Scheme 1 Set of studied mono-substituted benzene and meta- and para-substituted benzoic acid derivatives. | ||
Results and discussion
Let us start by considering a diverse set of mono-substituted benzene derivatives. All the systems analyzed have a singlet ground state described by a closed-shell Slater determinant within KS-DFT formalism. This means that the eff-AOs (and their occupations) derived from the alpha and beta spin channels are exactly the same. Henceforth, we refer to eff-AO occupations as the sum of the alpha and beta contributions. Our focus is on the electron density changes induced in the ring by the substituent. For this reason, we consider solely the eff-AOs of the carbon atoms of the ring. For illustrative purposes, Fig. 1 shows an overlay of the relevant eff-AOs of all carbon atoms for iodobenzene (C6H5I). Each carbon atom exhibits five significantly occupied eff-AOS, in line with the concept of minimal basis. There is a core 1s-type eff-AOs with an occupation very close to 2.0 and the remaining eff-AOs are those depicted in Fig. 1. One can easily identify a slightly polarized 2s-type and different 2p-type eff-AOs one each carbon center. Within the latter, one can recognize in-plane 2p-type eff-AOs (Fig. 1(b)) that are involved in the C–C σ-interactions along the ring, clearly separated from other 2p-type eff-AOs (Fig. 1(c)) that reveal the σ polarization along the C–H and C–X bonds. Finally, one can also identify out-of-plane 2pz –type eff-AOs (Fig. 1(d)), which account for the π-type density distribution along the ring. This represents a fundamental difference with the NAO approach, where 2px and 2py AOs with mixed contributions to the C–C and C–H/C–X σ bonding are obtained. Also, contrary to the eff-AOs, a separate out-of-plane 2pz NAO is obtained only if the molecule is placed in the xy plane. Thus, the separation between σ-type and π-type populations is compromised for non-perfectly planar systems.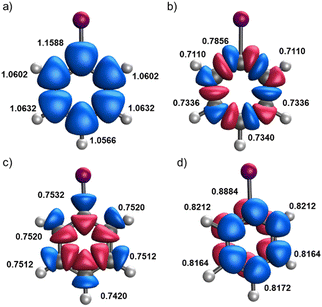 | ||
| Fig. 1 Overlay of carbon's 2s (a), 2pC–C (b), 2pC–H/X (c) and 2pz (d) eff-AO shapes and occupation (alpha plus beta) in the monosubstituted iodobenzene compound. | ||
Fig. 1 reveals a distinct behavior in the occupation numbers of the ipso carbon compared to the other carbon atoms in the ring. However, some eff-AOs, such as the 2s and 2pC–H/X ones, show only minor variations depending on the carbon atom's position in the ring. In this particular example, the occupation numbers of the ipso carbon are not too different from those of the other carbons, as the electronegativities of carbon and iodine are similar. Nonetheless, with most of the studied substituents, these differences are much more pronounced.
The eff-AO occupations that are more sensitive to the carbon position in the ring are the 2pC–C and the 2pz ones, and the former should more selectively account for the inductive effect. The correlation of the 2pC–C eff-AO occupation of each carbon atom position with the available F parameters from Hansch et al.11 for the whole set of mono-substituted benzene derivatives can be found in Fig. S1 of the ESI.† Interestingly, the occupations at the meta position exhibit a very good correlation with the F parameter (r2 = 0.89), while the correlation is inexistent for all other carbon positions (r2 values below 0.08). Also, the negative value of the slope indicates that the larger the inductive effect of the substituent, the smaller the occupation of the 2pC–C eff-AO in meta position. That is, the substituent effectively drains density from the C–C σ bonds involving the carbon in meta position.
In the spirit of the Hammett parameters, we introduce a new descriptor, IX, for the field/inductive effect as the difference of the 2pC–C eff-AO occupations in meta position (average of the two) of the unsubstituted molecule (i.e. benzene) and those of the mono-substituted derivative as
| IX = λ2pC–C(meta,R=H) − λ2pC–C(meta,R=X). | (6) |
We also explored the role of the occupations of the other carbon positions using multilinear regression, but the fitting didn’t improve significantly. These findings are in line with previous observations that the field/inductive effect is more pronounced in meta position.37,55,56 They also show that while eff-AO occupations (and overall partial atomic charge) of the ipso carbon are the ones that are most affected by the substituent, they do not explain the inductive effect on the ring. At this point, it is worth comparing our IX index with the aforementioned sEDA descriptor. Both are defined as differences in atomic orbital populations between the unsubstituted and substituted species. In sEDA, the contributions of the valence NAOs of all carbon atoms of the ring are considered, while in IX we only use one particular eff-AO of one particular carbon position (meta). Since sEDA includes the contributions from the ipso carbon, which is expected to be dominant, it better accounts for the substituent's electronegativity, as shown by the authors, rather than the inductive effect on the ring. We can readily confirm this hypothesis by considering the most appropriate eff-AO for this purpose, namely the occupation of the 2pC–H/X eff-AO of the ipso carbon (see Fig. 1(b)). Fig. S2 and Table S1 of the ESI† show an excellent correlation (r2 = 0.92) with the Boyd group electronegativity. In fact, an even better correlation (r2 = 0.97) is found using the occupations of the σ-type eff-AO of the substituent, which is complementary to the 2pC–H/X eff-AO of the ipso carbon. In recent work,48 we have used this occupation as a measure of σ-donation of ligands, which is revealed here as closely related to the group's electronegativity scale.
There has been a long debate in the literature about whether the field/inductive effect F is transmitted through space (field) or through bonds (inductive). The early calculations and models suggested that the field effect was predominant,57–59 while others advocate for a major role of through-bond transmission.60–62 A more recent study using density-based descriptors (cSAR) revealed a dominant inductive contribution.42 However, quantification of both effects with topological analysis of the electrostatic potential seems to indicate that the ratio of through-space/bonds depends on the nature of the substituent.63 Our present study is not designed to disentangle both effects, but by decomposing the atomic populations in the different eff-AO contributions we identified a unique descriptor that explains the trends in the F parameter and is independent of the electronic structure around the ipso or the ortho carbon in the ring. This observation can only be explained in terms of a through-bond transmission, indicating an inductive effect.
The plot of the reference F values against the IX descriptor is shown in Fig. 2. The relationship obtained from the least-squares fit is
| F = 57.56IX + 0.043 | (7) |
 | ||
| Fig. 2 Experimentally derived F values from Hansch et al.11vs. calculated IX descriptor for the set of monosubstituted benzene derivatives. | ||
| Substituent (X) | F (ref. 11) | I X | R (ref. 11) | R X |
|---|---|---|---|---|
| Sn(CH3)3 | 0.03 | −0.0019 | −0.03 | −0.0024 |
| H | 0.00 | 0.0000 | 0.00 | 0.0000 |
| SiH3 | 0.06 | 0.0008 | 0.04 | 0.0039 |
| CH3 | 0.01 | −0.0010 | −0.18 | −0.0106 |
| CH2CH3 | 0.00 | −0.0010 | −0.15 | −0.0084 |
| CHCH2 | 0.13 | 0.0008 | −0.17 | −0.0017 |
| C6H5 | 0.12 | 0.0010 | −0.13 | −0.0027 |
| C6F5 | 0.27 | 0.0044 | 0.00 | 0.0070 |
| NH2 | 0.08 | 0.0020 | −0.74 | −0.0412 |
| NHCH3 | 0.03 | 0.0022 | −0.73 | −0.0448 |
| NMe2 | 0.15 | 0.0024 | −0.98 | −0.0431 |
| NEt2 | 0.01 | 0.0020 | −0.73 | −0.0432 |
| NHCOCH3 | 0.31 | 0.0043 | −0.31 | −0.0164 |
| SH | 0.30 | 0.0046 | −0.15 | −0.0177 |
| SCH3 | 0.23 | 0.0035 | −0.23 | −0.0193 |
| COOCH3 | 0.34 | 0.0039 | 0.11 | 0.0197 |
| COCH3 | 0.33 | 0.0042 | 0.17 | 0.0190 |
| COOH | 0.34 | 0.0054 | 0.11 | 0.0217 |
| COH | 0.33 | 0.0055 | 0.09 | 0.0219 |
| OH | 0.33 | 0.0050 | −0.70 | −0.0338 |
| OCH3 | 0.29 | 0.0046 | −0.56 | −0.0316 |
| OCH(CH3)2 | 0.34 | 0.0039 | −0.79 | −0.0307 |
| OCH2CH2CH3 | 0.26 | 0.0037 | −0.51 | −0.0301 |
| OC6H5 | 0.37 | 0.0047 | −0.40 | −0.0176 |
| F | 0.45 | 0.0080 | −0.39 | −0.0173 |
| Cl | 0.42 | 0.0056 | −0.19 | −0.0041 |
| Br | 0.45 | 0.0060 | −0.22 | −0.0016 |
| I | 0.42 | 0.0060 | −0.24 | −0.0007 |
| CN | 0.51 | 0.0064 | 0.15 | 0.0147 |
| CF3 | 0.38 | 0.0066 | 0.16 | 0.0125 |
| C(CF3)3 | 0.53 | 0.0076 | 0.02 | 0.0146 |
| COCl | 0.46 | 0.0081 | 0.15 | 0.0281 |
| NO2 | 0.65 | 0.0110 | 0.13 | 0.0253 |
In some cases, the same F parameter is tabulated for chemically similar substituents. For example, F = 0.33 for both X = COH and X = COCH3, and F = 0.34 for both X = COOH and X = COOCH3. However, the IX descriptor can capture the subtle effect of the methyl substitution. As shown in Table 1, there is a slight but meaningful decrease in the IX value for the methylated substituents.
Our results also reveal some rather unexpected reference F data. In the series X = OH, OCH3, OCH2CH2CH3 our calculated IX values show a systematic trend, decreasing from 0.0050 to 0.0046 and 0.0037, respectively, showing again that replacing hydrogen by alkyl groups in the substituent leads to a decrease in the inductive effect. In this case, this trend is captured also by the reference F values, decreasing from 0.33 to 0.29 and 0.26. However, for X = OCH(CH3)2 the IX value (0.0039) is close to that of X = OCH2CH2CH3, while the reference F value is 0.34, even higher than that of the strongest substituent of the series, X = OH. This deviation suggests an anomaly in the reference F data for X = OCH(CH3)2.
The largest discrepancies between the reference F and our calculated IX descriptor are observed for X = NHCH3 and NEt2 substituents. Indeed, by removing these points from the data set the correlation improves significantly to r2 = 0.93. We obtain similar IX values for X = NMe2 (0.0024) and X = NEt2 (0.0020), as could be expected, but the tabulated F values are 0.15 and 0.01, respectively. Similarly, in the X = NH2, NHCH3, N(CH3)2 series, while we observe a slight but monotonic increase of the IX values upon methylation, the tabulated F values are 0.08, 0.03 and 0.15, respectively. Again, the F value for the X = NHCH3 is rather unexpected and does not seem to follow a well-defined trend. It is important to recall that the reference F values from Hansch et al.11 are obtained from the experimentally derived σm and σp Hammett's constants as assuming a common linear relationship. Our results suggest that the IX descriptor may provide a more consistent and reliable measure for certain substituents, especially in cases where the reference F values might be intrinsically unreliable or deviating from expected trends.
On the other hand, the resonant effect involves electron delocalization through the π system. We repeated the same analysis as for the field/inductive effect and checked the correlation of the occupation of the 2pz-type eff-AOs of the different carbon positions on the ring with the reference R parameter from Hansch et al.11 for the set of monosubstituted benzene derivatives. The results are collected in Fig. S4 of the ESI.† Contrary to the inductive effect, we observe some correlation of the R values with the eff-AO occupation of the ipso carbon (r2 = 0.600), and very poor correlation at the meta position (r2 = 0.315). It is well-known the fact that EDGs activate ortho and para positions of the ring.37,55,56 It is not too surprising that we obtain very good correlation (r2 ∼ 0.9) with the eff-AO occupations on either of these positions. Again, a negative slope of the correlation indicates that the larger the resonant effect (+M; R < 0), the higher the occupation of the 2pz eff-AO. To match with the original R scale, we define our new descriptor for resonant effect as (the negative of) the sum of the average of ortho and para 2pz eff-AO occupations in the ring, relative to their value for the unsubstituted system (benzene)
 | (8) |
Fig. 3 (left) shows the correlation of our RX descriptor with the R parameter from Hansch et al.11 The relationship obtained through the fitting is
| R = 14.27RX − 0.125 (r2 = 0.899) | (9) |
 | ||
| Fig. 3 Experimentally derived R values (left) and R* (right, see text) from Hansch et al.11vs. calculated RX descriptor for the set of monosubstituted benzene derivatives. | ||
Although the monosubstituted benzene derivatives considered here are not charged, it appears that the RX descriptor provides a better description of the modified R+ and R− substituent constants for EWGs and EWGs, respectively. In Fig. 3 (right) we plot the RX values against the R* constants, where R* represents R+ for EWGs and R− for EDGs. The range of R* values is significantly wider compared to the original R parameters. The correlation is excellent (r2 = 0.95), although the y-intercept still shows slight deviations from the ideal zero value. The ratio of the slopes of the correlations (ca. 2.4) is not far from the enhancement ratio of ca. 1.9 described by Hansch et al.11 for the R+ and R− values relative to R. In the case of X = SH, the reference R− value is still somewhat too low compared to our prediction. The calculated RX values for X = NMe2 (−0.431) and X = NEt2 (−0.432) are very similar. However, the latter appears to be an outlier, because the reference R− value of −2.08, is much lower than for the chemically similar X = NMe2 (R− = −1.85). This discrepancy, however, is due to the abovementioned unexpectedly different reference F values.
To further test the predictive power of the descriptors derived from the occupations of the eff-AOs, we have also studied meta- and para-substituted benzoic acid derivatives using the same set of 33 substituents. The goal is to test the ability to predict directly the respective Hammett's σm and σp constants. We have obtained the eff-AOs and their occupations for all carbon atoms of the ring in the set of meta- and para-substituted benzoic acid derivatives. The results can be found in the ESI.†
The meta-substituted derivatives have two distinct meta positions relative to the substituent X: the one also in meta relative to the carboxylic group and the ipso carbon relative to the carboxylic group. We have observed that the variations of the 2pC–C eff-AO occupations of the former are very similar to those observed for the monosubstituted benzene derivatives. Indeed, the values of the IX descriptor using only this meta position in the meta-substituted benzoic acids correlate very well (r2 = 0.92, see Fig. S5, ESI†) with the IX values obtained for mono-substituted derivatives using eqn (6). However, the correlation is much worse if including also the contributions from the ipso carbon.
This is not the case of the RX descriptor, where the individual contributions from the ortho and para positions relative to X exhibit a very good correlation between them (r2 = 0.91). In fact, the overall RX values obtained are in almost perfect agreement with those obtained for the mono-substituted benzene derivatives (see Fig. S6, ESI†). Such an excellent transferability of the resonant effect can be ascribed to the fact in the meta-substituted benzoic acid derivatives, the ortho and para positions with respect to substituent X are also in ortho and para with respect to the carboxylic group.
Once we have established that the IX (excluding the ipso carbon) and RX indices derived from the meta-substituted benzoic acid derivatives are proper descriptors for the inductive and resonant effects, respectively, we can attempt the quantification of both effects in the value of Hammett's σm parameter. The correlation of IX against the experimental σm values is significant (r2 = 0.77), but cannot fully explain the trends. Considering also the RX descriptor in a multilinear fit yields the following relationship
| σm = 53.58IX + 5.12RX + 0.053 (r2 = 0.950) | (10) |
The mean unsigned error in the σm values using eqn (10) is just 0.04, incidentally roughly the same uncertainty associated to the expression used by Hansch et al.11 to derive the F parameter from experimental σm and σp values. The worst prediction is for X = SH (0.09 calculated vs. 0.25 experimental), a substituent that already showed significant deviations in the resonant effect.
The slopes of the IX and RX terms in eqn (10) seem to indicate a much larger contribution to the σm value from the former. However, the slopes are misleading because the range of values of the RX parameter is much larger than for the IX one. This is because the σ framework is much more rigid than the delocalized π system, so the shift in the σ-type eff-AO populations is much smaller. But, combining eqn (7) and (9) with eqn (10) we find an expression of the σm values in terms of the modified Swain and Lupton F and R parameters:
| σm = 0.928F + 0.259R + 0.054. | (11) |
On the other hand, it is worth mentioning that the IX values obtained including also the contribution of the ipso carbon show a much better correlation with the experimental σm values (r2 = 0.878, see Fig. S7, ESI†). This relationship is not as good as the one described by eqn (10), but highlights the classical view that the σm values can to a large extent be explained in terms of field/inductive effects.
Analyzing para-substituted benzoic acid derivatives is inherently more complex than their meta-substituted counterparts. This is because the carbon positions that are meta to the X substituent are ortho to the carboxylic group, and vice versa. Furthermore, the para position relative to one substituent corresponds to the ipso position relative to the other. Since both substituents simultaneously exert inductive and resonant effects, their combined influence creates a more intricate interplay, making it difficult to disentangle their individual contributions.
As a result, the changes in the occupations of the 2pC–C eff-AOs at the meta position relative to substituent X do not correlate as well with the F parameter as they do in mono-substituted benzene derivatives. This is reflected in the poor correlation (r2 = 0.61) between the IX parameter calculated for para-substituted derivatives and the reference F values. In contrast, the shifts in the 2pz eff-AO occupations at both ortho and para positions are similar to those observed in mono-substituted benzene derivatives. This similarity allows the RX descriptor, calculated for para-substituted derivatives, to perform equally well, showing a strong correlation (r2 = 0.90) with the R parameter. The correlation further improves (r2 = 0.96) when using the set of R* parameters, partly due to the broader range of R* values. However, as previously noted, the X = SH and X = NEt2 substituents remain outliers, exhibiting significant deviations from the general trend.
In the tables provided by Hansch et al.,11 the σp values are precisely broken down into contributions from F (field/inductive) and R (resonance) effects. However, it is the R contributions that play a more significant role in determining the σp values, ultimately defining whether the substituent is classified as EDG or EWG in nature. Hence, the correlation between the σp values and solely the RX descriptor calculated for the para-substituted benzoic acid derivatives is quite good, too (r2 = 0.88, see Fig. S8, ESI†). To unveil the role of the field/inductive term we have performed a multilinear regression including also the IX descriptor, leading to the relationship
| σp = 10.17IX + 63.36RX + 0.018 (r2 = 0.926) | (12) |
Conclusions
In this study, we have developed a robust and systematic framework for quantifying substituent effects in aromatic systems by leveraging the occupations of the eff-AOs of the carbon atoms in the benzene ring. The key advantage of the eff-AOs lies in their ability to extract the σ-type contributions to the electron density from the C–C bonding framework in the ring. We show that the inductive effect of a substituent is effectively captured by the shift in the occupation of the eff-AOs associated with the C–C bonding framework solely at the meta position. Conversely, the resonance effect is well-captured by the shifts in the occupations of the 2pz-type eff-AOs of the carbon atoms at the ortho and para positions. The introduced descriptors, IX and RX, for inductive and resonance effects, respectively, display excellent correlation against the modified Swain and Lupton F and R (or R+/R−) parameters compiled by Hansch et al.11 for a chemically diverse set of 33 substituents. Our descriptors do not align well with certain F and R reference values, particularly for X = SH and specific amino-type substituents. While the origin of these discrepancies remains unclear, it raises the possibility that some reference values may warrant re-evaluation or could be influenced by experimental or methodological inconsistenciesThe IX and RX descriptors were also applied to predict Hammett's σm and σp constants, considering explicitly meta- and para-substituted benzoic acid derivatives. In the meta-substituted derivatives, the transferability of both descriptors for inductive and resonance effects obtained with the mono-substituted benzene derivatives was excellent. This leads to very accurate predictions of the σm values, with a mean error of just 0.04 units across the set of substituents. The prediction of experimental Hammet's σp values proved to be more challenging, with average errors around 0.08 units.
Overall, this work establishes a clear connection between the electronic structure of aromatic systems and the empirical Hammett parameters, paving the way for more accurate and interpretable models in physical organic chemistry. Our approach not only provides a deeper understanding of the electronic interactions in substituted benzene derivatives but also offers a practical tool for predicting substituent effects in aromatic systems.
Author contributions
G. Comas-Vilà (investigation, data curation, methodology, writing – original draft). P. Salvador (conceptualization, resources, methodology, software, supervision, writing).Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by the Ministerio de Ciencia, Innovación y Universidades (MCIU), grant number PID2022-140666NB-C22, and Generalitat de Catalunya project 2021-SGR1-00487. G. C. also acknowledges support from FPU grant 19/02781.Notes and references
- P. Müller, Glossary of terms used in physical organic chemistry; IUPAC Recommendation, 1994.
- L. P. Hammett, The Effect of Structure upon the Reactions of Organic Compounds. Benzene Derivatives, J. Am. Chem. Soc., 1937, 59, 96–103 CrossRef CAS.
- L. P. Hammett, Physical Organic Chemistry: Reaction Rates, Equilibria, and Mechanisms, McGraw-Hill, New York, 2nd edn, 1970 Search PubMed.
- W. Taft and C. Lewis, The General Applicability of a Fixed Scale of Inductive Effects. II. Inductive Effects of Dipolar Substituents in the Reactivities of m- and p-Substituted Derivatives of Benzene, J. Am. Chem. Soc., 1958, 80, 2436–2443 CrossRef.
- W. Taft and C. Lewis, Evaluation of resonance effects on reactivity by application of the linear inductive energy relationship. V. Concerning a σR scale of resonance effects, J. Am. Chem. Soc., 1959, 81, 5343–5352 CrossRef.
- M. Charton, Electrical Effect Substituent Constants for Correlation Analysis, Prog. Phys. Org. Chem., 1981, 13, 119 CrossRef.
- J. D. Roberts and W. T. Moreland, Electrical Effects of Substituent Groups in Saturated Systems. Reactivities of 4-Substituted Bicyclo [2.2.2]octane-1-carboxylic Acids, J. Am. Chem. Soc., 1953, 75, 2167–2173 CrossRef CAS.
- C. G. Swain and E. C. Lupton, Field and resonance components of substituent effects, J. Am. Chem. Soc., 1968, 90, 4328 CrossRef CAS.
- S. Gutowsky, W. McCall, R. McGarvey and H. Meyer, Electron Distribution in Molecules. I. F19 Nuclear Magnetic Shielding and Substituent Effects in Some Benzene Derivatives, J. Am. Chem. Soc., 1952, 74, 4809–4817 CrossRef.
- W. Taft and A. Precise, Correlation of Nuclear Magnetic Shielding in m- and p-Substituted Fluorobenzenes by Inductive and Resonance Parameters from Reactivity, J. Am. Chem. Soc., 1957, 79, 1045–1049 CrossRef.
- C. Hansch, A. Leo and W. Taft, A survey of Hammet substituent constants and resonance and field parameters, Chem. Rev., 1991, 91, 165–195 CrossRef CAS.
- C. Hansch, A. Leo, S. H. Unger, K. H. Kim, D. Nikaitani and E. J. Lien, Aromatic substituent constants for structure-activity correlations, J. Med. Chem., 1973, 16, 1207–1216 CrossRef CAS.
- H. Jaffé, A Reexamination of the Hammet Equation, Chem. Rev., 1953, 53, 191–261 CrossRef.
- H. Brown and Y. Okamoto, Substituent Constants for Aromatic Substitution, J. Am. Chem. Soc., 1957, 79(8), 1913–1917 CrossRef CAS.
- H. Brown and Y. Okamoto, Electrophilic Substituent Constants, J. Am. Chem. Soc., 1958, 80, 4979–4987 CrossRef CAS.
- Y. Okamoto and H. Brown, A Quantitative Treatment for Electrophilic Reactions of Aromatic Derivatives, J. Org. Chem., 1957, 22, 485–494 CrossRef CAS.
- R. Gadre and C. H. Suresh, Electronic Perturbations of the Aromatic Nucleus: Hammett Constants and Electrostatic Potential Topography, J. Org. Chem., 1997, 62, 2625–2627 CrossRef.
- D. Cheshmedzhieva, S. Ilieva and B. Galabov, Computational evaluation of σI and σR substituent constants, J. Mol. Struct., 2010, 976, 427–430 CrossRef CAS.
- C. H. Suresh, P. Alexander, K. P. Vijayalakshmi., P. K. Sajith and S. R. Gadre, Use of molecular electrostatic potential for quantitative assessment of inductive effect, Phys. Chem. Chem. Phys., 2008, 10, 6492–6499 RSC.
- F. B. Sayyed and C. H. Suresh, An electrostatic scale of substituent resonance effect, Tetrahedron Lett., 2009, 50, 7351–7354 CrossRef CAS.
- G. Te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca-Guerra, S. J. A. Van Gisbergen, J. G. Snijders and T. Ziegler, Chemistry with ADF, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS.
- I. Fernandez and G. Frenking, Correlations between Hammet Substituent Constants and Directly Calculated π-Conjugation Strenght, J. Org. Chem., 2006, 71, 2251–2256 CrossRef CAS PubMed.
- W. J. Hehre, R. Ditchfield, L. Radom and J. A. Pople, H. Molecular orbital theory of the electronic structure of organic compounds. V. Molecular theory of bond separation, J. Am. Chem. Soc., 1970, 92, 4796–4801 CrossRef CAS.
- P. George, M. Trachtman, C. W. Bock and A. M. Brett, Homodesmotic reactions for the assessment of stabilization energies in benzenoid and other conjugated cyclic hydrocarbons, J. Chem. Soc., 1976, 2, 1222–1227 Search PubMed.
- T. Siodla, W. P. Oziminski, M. Hoffmann, H. Koroniak and T. M. Krygowski, Toward a Physical Interpretation of Substituent Effects: The case of Fluorine and Trifluoromethyl Groups, J. Org. Chem., 2014, 79, 7321–7331 CrossRef CAS.
- H. Szatylowicz, T. Siodla, O. A. Stasyuk and T. M. Krygowski, Towards physical interpretation of substituent effects: the case of meta- and para-substituted anilines, Phys. Chem. Chem. Phys., 2016, 18, 11711–11721 RSC.
- M. Jabłoński and T. M. Krygowski, Energetic characteristics of the substituents in para- and meta-substituted derivatives of benzoic acids, Chem. Phys. Lett., 2021, 771, 138464 CrossRef.
- M. Jabłoński and T. M. Krygowski, Dependence of the substituent energy on the level of theory, J. Comput. Chem., 2021, 42(29), 2079–2088 CrossRef.
- N. Sadlej-Sosnowska, Substituent active region-a gate for communication of substituent charge with the rest of a molecule: Monosubstituted benzenes, Chem. Phys. Lett., 2007, 447, 192–196 CrossRef CAS.
- N. Sadlej-Sosnowska, On the way to physical interpretation of Hammett constants: How substituent active space impacts on acidity and electron distribution in p-substituted benzoic acid molecules, Pol. J. Chem., 2007, 81, 1123–1134 CAS.
- T. M. Krygowski and P. Oziminski, Subsituent effects in 1-nitro-4-substituted bicyclo[2,2,2]octane-derivatives: inductive or field effects?, J. Mol. Model., 2014, 20, 2352–2359 CrossRef PubMed.
- O. A. Stasyuk, H. Szatylowicz, C. Fonseca-Guerra and T. M. Krygowski, Theoretical study of electron-attracting ability of the nitro group: classical and reverse substituent effects, Struct. Chem., 2015, 26, 905–913 CrossRef CAS.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- P. Oziminski and J. Cz Dobrowolski, σ- and π-electron contributions to the substituent effect: natural population analysis, J. Phys. Org. Chem., 2009, 22, 769–778 CrossRef.
- R. Boyd and E. Edgecombe, Atomic and group electronegativities from the electron-density distributions of molecules, J. Am. Chem. Soc., 1988, 110, 4182–4186 CrossRef CAS.
- J. Boyd and L. Boyd, Group electronegativities from the bond critical point model, J. Am. Chem. Soc., 1992, 114, 1652–1655 CrossRef.
- P. Oziminski and T. M. Krygowski, Comparison of the substituent effects in tetrazole systems and benzene. A computational study, Tetrahedron, 2011, 67, 6316–6321 CrossRef.
- A. Mazurek and J. Cz Dobrowolski, Heteroatom Incorporation Effect in σ- and π-Electron systems: The sEDA(II) and pEDA(II) Descriptors, J. Org. Chem., 2012, 77(6), 2608–2618 CrossRef CAS PubMed.
- A. Mazurek and J. Cz Dobrowolski, The sEDA(=) and pEDA(=) descriptors of the double bonded substituent effect, Org. Biomol. Chem., 2013, 11, 2997–3013 RSC.
- P. Oziminski and T. M. Krygowski, Natural bond orbital approach to the transmission of substituent effect through the fulvene and benzene ring systems, J. Mol. Model., 2011, 17, 565–572 CrossRef.
- T. M. Krygowski, W. P. Oziminski and M. K. Cyranski, Aromatic Character of heptafulvene and its complexes with halogen atoms, J. Mol. Model., 2012, 18, 2453–2460 CrossRef CAS PubMed.
- H. Szatylowicz, A. Jezuita, K. Ejsmont and T. M. Krygowski, Most of the field/inductive substituent effect works through the bonds, J. Mol. Model., 2019, 25, 350 CrossRef.
- I. Mayer, Relation between the Hilbert space and “fuzzy atoms” analyses, Chem. Phys. Lett., 2013, 585, 198–200 CrossRef CAS.
- E. Ramos-Cordoba, P. Salvador and I. Mayer, The atomic orbitals of the topological atom, J. Chem. Phys., 2013, 138, 214107 CrossRef PubMed.
- I. Mayer, Effective atomic orbitals: A tool for understanding electronic structure molecules, Int. J. Quantum Chem., 2014, 114, 1041–1047 CrossRef CAS.
- E. Ramos-Cordoba, V. Postils and P. Salvador, Oxidation States from Wave Function Analysis, J. Chem. Theory Comput., 2015, 11, 1501–1508 CrossRef CAS PubMed.
- M. Gimferrer, S. Danés, D. M. Andrada and P. Salvador, Unveiling the Electronic Structure of the Bi(+1)/Bi(+3) Redox Couple on NCN and NNN Pincer Complexes, Inorg. Chem., 2021, 60(23), 17657–17668 CrossRef CAS PubMed.
- G. Comas-Vilà and P. Salvador, Quantification of the Donor-Acceptor Character of Ligands by the Effective Fragment Orbitals, ChemPhysChem, 2024, 25, e202400582 CrossRef.
- M. J. Frisch, et al., Gaussian 16 (Revision C.01.), Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- A. D. Becke, Density-Functional exchange-energy approximation with correct asymptotic behaviour, Phys. Rev., 1988, 38, 3098–3100 CAS.
- J. P. Perdew, Density-functional approximation for the correlation energy of the inhomogeneous electron gas, Phys. Rev., 1986, 34, 8822–8824 Search PubMed.
- F. Weigend, Accurate Coulomb-Fitting Basis Sets for H to R, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- P. Salvador, E. Ramos-Cordoba, M. Montilla, L. Pujal and M. Gimferrer, APOST-3D: Chemical concepts from wavefunction analysis, J. Chem. Phys., 2024, 160, 172502 CrossRef CAS PubMed.
- P. Salvador and E. Ramos-Cordoba, Communication: An approximation to Bader's topological atom, J. Chem. Phys., 2013, 139, 071103 CrossRef PubMed.
- C. D. Johnson, The Hammett equation, Cambridge University, Cambridge, 1973 Search PubMed.
- J. Shorter, Correlation Analysis in Organic Chemistry: An Introduction to Linear Free Energy Relationships, Clarendon, Oxford, 1973 Search PubMed.
- S. Marriot and R. D. Topsom, Theoretical studies of the inductive effect. IV. A theoretical scale of substituent field parameters, J. Am. Chem. Soc., 1984, 106, 7–10 CrossRef.
- O. Exner, M. Ingr and P. Cársky, Ab initio calculations of substituent constants: a reinvestigation, J. Mol. Struct., 1997, 397, 231–238 CrossRef CAS.
- K. Sung, Ab initio calculations of field substituent parameters and evaluation of substituent parameters through substituent effects on stability of ketenimines, isocyanides, and nitriles, J. Chem. Soc., Perkin Trans. 2, 2002, 1658–1661 RSC.
- V. I. Galkin, Inductive substituent effects, J. Phys. Org. Chem., 1999, 12, 283–288 CrossRef CAS.
- M. Charton, The nature of electrical effect transmission, J. Phys. Org. Chem., 1999, 12, 275–282 CrossRef CAS.
- O. Exner, The inductive effect: theory and quantitative assessment, J. Phys. Org. Chem., 1999, 12, 265–274 CrossRef CAS.
- F. B. Sayyed, C. H. Suresh and S. R. Gadre, Appraisal of Thorugh-Bond and Through-Space Substituent Effects via Molecular Electrostatic Potential Topography, J. Phys. Chem. A, 2010, 114, 12330–12333 CrossRef CAS PubMed.
- J. E. McMurry, Organic Chemistry, Brooks/Cole Pub Co., Belmont CA, 1995 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Tables with eff-AO occupations and Cartesian coordinates fo all studies systems. See DOI: https://doi.org/10.1039/d5cp01299f |
| This journal is © the Owner Societies 2025 |
