Excited-state methods based on state-averaged long-range CASSCF short-range DFT†
Received
5th March 2025
, Accepted 26th June 2025
First published on 1st July 2025
Abstract
In the present work we propose two distinct state-averaging (SA)-based methodologies for the calculation of excited states, in conjunction with the long-range complete active space self-consistent field (CASSCF) short-range density functional theory (DFT) approach (CAS-srDFT). The state-specific density ansatz, termed SA-CAS-srDFT, initially determines the variational parameters of an approximate srDFT functional that operates with state-averaged densities. Subsequent to convergence, the CAS-srDFT energies of each state are computed from the state-specific one- and two-body densities. The second approach is termed configuration interaction (CI)-srDFT, for which a first-order correction is added to the approximate SA density CAS-srDFT functionals. Unlike the state-specific density approach SA-CAS-srDFT, diagonalisation of the first-order corrected effective Hamiltonian CI matrix yields orthonormal CI solutions for every state. In both approaches, the total one-body and on-top pair density (OTPD) was employed for the final energy evaluation. It was observed that the CI-srDFT approach gives physically correct potential curves for ethylene, in contrast to SA-CAS-srDFT. Moreover, the CI-srDFT approach demonstrates a reduced dependence of excitation energies on the number of states in the average when compared to the SA-CAS-srDFT method. The accuracy of the various CAS-srDFT methods was investigated for 139 singlet excitation energies of 28 typical organic chromophores. The two excited-state approaches in conjunction with multiconfiguration pair-density functional theory (MC-PDFT) were also employed in the benchmark study for comparing the accuracy with CAS-srDFT. It was found that CI-srDFT methods are more accurate than their SA counterparts, giving a mean absolute error of just 0.17 eV when using the sr-ctPBE functional. The accuracy of the new SA-based CAS-srDFT methods was observed to be impressive for organic molecules; however, this was not found to be transferable when investigating excited states of transition-metal complexes. In fact, none of the CASSCF-DFT excited-state methods introduced in this study, and also MC-PDFT, were found to provide a consistent improvement of CASSCF excitation energies.
1 Introduction
The calculation of ground- and excited-state energies at any point on the potential energy surface (PES) remains an active area of research in computational chemistry. In particular, when dealing with points on the PES that are far away from equilibrium, reasonable approximations of the molecular Schrödinger equation must be based on wavefunctions that are expanded in multiple determinants.1 Such so-called multi-reference (MR) or multi-configurational (MC) methods are also needed when dealing with open-shell low-spin systems that are frequently found in transition metal and lanthanide-containing complexes. In such complexes, low-lying excited states are often reached by metal-centered electronic transitions that feature multiplet structures due to their degeneracies. These degeneracies are, in most cases, not properly described by electronic structure methods based on a single Hartree–Fock (HF) or Kohn–Sham (KS) determinant.2
From a computational and conceptual standpoint, the most elementary MC approach is multi-configurational self-consistent field (MCSCF) theory. This theory expands the wavefunction linearly in a multitude of spin-adapted Slater determinants, designated as configuration state functions (CSFs), also known as configuration interaction (CI) expansion. MCSCF minimizes the energy with respect to variations in the molecular orbital and CI expansion coefficients.3 Relevant CSFs can be constructed with the help of an active space that is defined by a preset number of electrons and valence orbitals. For the popular complete active space (CAS) approach, the construction of CSFs is based on all possible occupations of AS orbitals by AS electrons.4 However, the exponential growth in the number of CSFs when employing the CAS expansion necessitates the limitation of the number of active orbitals and electrons to a relatively modest figure, such as 20, in comparison to the total number of electrons and orbitals typically encountered in molecular and even atomic systems. As a result, the accuracy of energies and molecular properties obtained from CASSCF calculations is inherently constrained.
One method by which the accuracy of CASSCF can be enhanced is to incorporate a substantial number of orbitals within the active space, in conjunction with the introduction of approximations to the underlying full configuration interaction (FCI) expansion. Over the past three decades, a multitude of approximate FCI methods have been developed and successfully utilized in larger systems, without substantial compromise to the accuracy. The most popular approaches are based on density matrix renormalization group,5–10 quantum Monte Carlo,11–13 or selected CI algorithms.14–19 Some of these approaches have also been combined with orbital optimization,20–24 a necessity of the CASSCF wavefunction model. However, all of these approximate FCI approaches still feature an exponential scaling with the system size and are rather intended for calculations on strongly correlated systems, in particular those with many spin-coupled centers,25,26 than as a universally applicable, high-level correlation method.
The electronic structure methods with highest accuracy for so called multi-reference situations, we have just elaborated on, are base on coupled cluster (CC) theory. The most general and numerically most stable and affordable MRCC approaches employ the internal contraction (ic) approximation27 for which cluster amplitudes are determined for a CAS-CI state rather than individual CSFs.28–30 Though the scaling of ic MRCC methods with the system size N is still equivalent to their single-reference analogues, e.g. ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N6) for the CC singles and doubles model, the prefactor of state-of-the-art MRCC implementations is enormous due to the huge increase in the number of CC equations to be solved for multi-reference rather than the single-reference case. Even to date, MRCC calculations are usually only performed by specialists using their own implementations.
(N6) for the CC singles and doubles model, the prefactor of state-of-the-art MRCC implementations is enormous due to the huge increase in the number of CC equations to be solved for multi-reference rather than the single-reference case. Even to date, MRCC calculations are usually only performed by specialists using their own implementations.
A much more practical alternative to these highly correlated MRCC methods are the fifth-order scaling internally contracted MR second-order perturbation theory (PT2) approaches CASPT231,32 and n-electron valence (NEV) PT2.33–35 Due to their comparatively small computational prefactor, CASPT2 and NEVPT2 have become popular computational methods that, nowadays, are applied by non-specialists for various types of calculations, almost in a routine fashion. In particular, the non-iterative NEVPT2 method can be efficiently implemented in an integral-direct way without any need to store large multi-dimensional tensors, which unfortunately cannot be avoided for the iterative CASPT2 method unless the locality of electron correlation is exploited.36
Despite their success, molecular property calculations with MRPT2 methods are still to date restricted to nuclear first energy derivatives37–40 for geometry optimization and molecular dynamics simulations.41 This limitation can be attributed, in part, to the inherent complexity of ic MR wavefunction methods. For first-order properties the coupled-perturbed MCSCF equations42,43 must be solved to ensure that the underlying CASSCF solution is preserved in the property calculation by means of Lagrangian multipliers.44,45
Recently, multi-reference density functional theory (DFT) methods have emerged as a potentially viable alternative to MRPT2 theories, particularly those variants that are based on variational energy minimizations. A notable advantage of variational MCSCF-DFT methods is that they do not necessitate the solution of costly coupled-perturbed MCSCF linear equations42,43 for first-order properties such as nuclear gradients. Examples of this category include the long-range (lr) MCSCF short-range (sr) DFT method46 (MC-srDFT) and the variational version47 of multiconfiguration pair-density functional theory (MC-PDFT).48,49
In addition to nuclear gradients, a pivotal quantity that must be calculated by quantum chemical methods is excitation energies. In the context of non-variational MC-PDFT,48 it was demonstrated early on that excitation energies can be readily obtained. This is due to the fact that the MC-PDFT energy functional can be evaluated from state-specific density matrices derived from the state-averaged (SA) MCSCF solution. We follow the notation of the original article48 and denote this method SA-MC-PDFT. A similar approach could have been adopted for MC-srDFT, although the primary focus has been on preserving the variational nature of the method.50,51 MC-srDFT excitation energies were obtained from the linear-response eigenvalue equations52–54 which offer many benefits for computing vertical excitation energies.55 As it is not clear yet how to describe conical intersection with the electronic ground when using linear-response or propagator methods,56 state-averaged or multi-state multi-reference methods57–63 are predominantly used when studying excited-state potential energy surfaces in photochemical investigations.
In this study, we examine a new methodology for computing excitation energies for MC-srDFT when employing a state-averaging formalism. Initially, an averaged MC-srDFT energy functional with fixed, user-defined weights for each state is variationally minimized using the same orbitals for each state. This necessitates an approximate treatment of the srDFT Hartree-exchange (HX) and exchange–correlation (XC) terms since those terms feature a non-linear dependence on the densities which would lead to non-orthogonal configuration interaction solutions. We avoid this issue by computing the HX and XC terms from state-averaged densities when minimizing the state-averaged energy MC-srDFT functional. Following functional minimization, excitation energies are either computed from state-specific densities, as pursued for SA-MC-PDFT,48 or obtained from diagonalizing a first-order corrected linearized CI-srDFT matrix.64 The accuracy of both approaches when computing potential energy surfaces, vertical singlet excitation energies in organic molecules, and also transition-metal complexes is analyzed. Finally, we give a perspective on how to obtain further improvements.
2 Theory
2.1 Long-range CASSCF short-range DFT
The multi-configurational (MC) short-range (sr) DFT method46 combines the long-range (lr) part of the MCSCF energy with the short-range part of the DFT energy| | | = 〈0|Ĥlr|0〉 + Esr-Hx + Esr-xc | (2) |
The MC-srDFT energy for a single state |0〉 is expanded in spin-adapted Slater determinants also referred to as configuration state functions (CSF) |ΦI〉:
| | 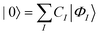 | (3) |
In this work, we will only consider CAS wavefunctions for MC-srDFT, that is, |0〉 is expanded in all possible CSF that are generated by distributing a given number of electrons among a given number of active valence orbitals. Other MC models than CAS for MC-srDFT have been presented previously though.65 For a given MC wavefunction |0〉, the lr MC energy Elr is computed as the expectation value of the lr Hamiltonian
| | 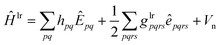 | (4) |
for which we employed the usual spin-summed singlet excitation operators
| | | Êpq = â†pαâqα + â†pβâqβ | (5) |
| | | êpqrs = ÊpqÊrs − δqrÊps | (6) |
The summation indices p, q, r, s label general molecular orbitals (MO) ϕp(r) with r being the position of an electron. The lr Hamiltonian in (4) contains the nuclear repulsion potential Vn, the full part of the one-electron Born–Oppenheimer Hamiltonian but only the lr part of its two-electron Coulomb repulsion integrals
| |  | (7) |
carved out by means of the error function erf.
66,67 The expectation value
| |  | (8) |
can be easily evaluated in terms of one- and two-body densities
The srDFT energy contribution comprises two terms: (i) the Hartree-exchange term
| |  | (11) |
| | 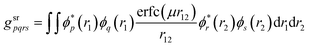 | (12) |
with Becke's adiabatic connection model
68 parameter
a and the short-range part of the two-electron integrals
gsrpqrs, that employs the complementary error function erfc(
x) = 1 − erf(
x), and (ii) a short-range exchange–correlation energy term
Esr-xc that is evaluated from the MC total one-electron density
| | 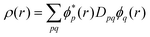 | (13) |
and may also depend on the density gradient invariant,
69 the local kinetic energy density,
70 or the on-top pair density
48,71–74 (
vide infra).
The range-separation parameter, or short-range damping factor, μ controls in which proportion the MC and the DFT energy are added together. Small values of μ favor the srDFT terms and converge to the Kohn-Sham DFT energy as μ approaches zero. Conversely, the lr MCSCF energy becomes the dominating contribution for large μ and the MCSCF energy is restored as μ converges to ∞. A smooth convergence towards the upper and lower boundaries must be ensured when designing sr XC functionals.
In order to treat open-shell systems that have different densities for the α and β electrons, the short-range exchange–correlation energy can be formulated with the MC total density ρ(r) and spin density m(r)75
| | 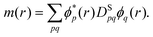 | (14) |
The latter is computed from the one-body spin density
| | DSpq = 〈0|![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) pq|0〉 pq|0〉 | (15) |
that involves the
MS = 0 component of the triplet one-body excitation operator
| | ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) pq = â†pαâqα − â†pβâqβ. pq = â†pαâqα − â†pβâqβ. | (16) |
Employing the total and spin density together for the XC energy gives rise to energy terms originating from different spin multiplicities. This results inevitably in so-called spin contamination, an unpleasant artifact known from spin-unrestricted single-reference theories.
To avoid problems caused by such a spin-density approach, spin polarization can also be described by means of the on-top pair density48,71–73 (OTPD) that reads
| | 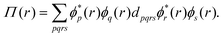 | (17) |
The OTPD contains a product separable and a non-separable part
| |  | (18) |
The latter is known as the two-body density cumulant76,77 of the on-top pair density λ(r). The two-body density cumulant for MCSCF wavefunctions
| |  | (19) |
| |  | (20) |
is only non-zero for active orbitals, denoted by the indices
t,
u,
v,
w, which makes an MO-based evaluation still efficient despite the four active indices.
2.2 On-top pair density functionals
To establish a dependence of existing XC functionals on the OTPD, it is insightful to investigate the relation between the one-body densities for α and β electrons ρα and ρβ, respectively and the total one-body density ρ and on-top pair density Π(r). The following relations holdfor a single-determinant wavefunction but are approximations for MC wavefunctions. When employing eqn (21) and (22), the densities ρα and ρβ can be expressed in terms of ρ(r) and Π(r):| |  | (23) |
| | 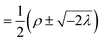 | (24) |
Note that we omitted the position vector dependence for the densities in the equations above and will continue to do so for better readability.
For a single determinant, the radicand of eqn (23) turns into the squared spin density
| | | −2λ = (ρα − ρβ)2 = m2. | (25) |
Note that from eqn (25) the spin density
| |  | (26) |
and spin polarization
ζ =
m/
ρ are readily accessible. The
ρα and
ρβ first derivatives, needed for generalized gradient approximation (GGA) functionals, can also be formulated in terms of the total density and OTPD, though it is customary to drop the dependence on the OTPD first derivatives:
48| |  | (27) |
| |  | (28) |
A consequence of eqn (25) is that the densities ρα and ρβ can never be complex for a single-determinant wavefunction. However, this does not hold anymore when using MC one- and two-body densities for computing ρα and ρβ in eqn (23). For some positions r, ρα and ρβ become complex because the two-body density cumulant matrix (20) is indefinite. For that reason, several authors developed different strategies to handle points with complex densities.48,49,72,78–80
In this work, we adhere to established XC functionals that were developed primarily for being used with single-reference Kohn–Sham determinant methods. Those functionals can still be employed in a MC calculation by using the MC one-body (9) and two-body density (10). For points with a negative OTPD cumulant (19), α and β densities are computed from eqn (23) and the XC energy is readily available when using existing single-reference XC functional implementations. This procedure is often referred to as functional translation in MC pair-density functional theory (MC-PDFT).48 In MC-PDFT the Kohn–Sham DFT energy is evaluated using the one-body density matrix for the one-electron and Hartree term and the one-body density and OTPD for the exchange–correlation energy:
| | 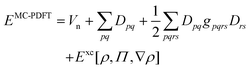 | (29) |
Note that functional derivatives of Exc with respect to ρ and Π are also easily accessible by applying the chain rules.
For points with a positive OTPD cumulant (19), the spin density m and spin polarization
| |  | (30) |
are purely imaginary and the
α and
β densities
| | 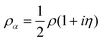 | (31) |
| |  | (32) |
are pairs of complex conjugates. The gradients of the complex
α and
β densities are given in full analogy to
eqn (27) and (28) through
| |  | (33) |
| |  | (34) |
for which the gradient of the OTPD is also neglected in this work.
48,80 In case of complex densities and density derivatives, those complex quantities are substituted into the existing single-reference XC functionals. Then, the energies are reformulated in terms of
ρ and
Π.
Though the densities and their derivatives might be complex, the final X and C energies must be real as already mentioned by Becke et al.72 and also recently Rodrigues et al.80 The exchange energy computed from a complex pair of densities and density derivatives is real, indeed, due to the spin scaling relationship.81
| |  | (35) |
| |  | (36) |
Though, it must be assumed here that X functionals are constructed exclusively from entire functions which is usually the case for established functionals. It is less obvious that the correlation energy computed from a complex pair of densities and density derivatives is real because, to our best knowledge, we assume that there is not such a universal scaling relation for the correlation term. Yet, ρα and the complex partner 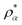 , as well as their corresponding density derivatives, enter Ec in the same manner. Thus, the final correlation energy must be real assuming that Ec is composed of entire functions.
, as well as their corresponding density derivatives, enter Ec in the same manner. Thus, the final correlation energy must be real assuming that Ec is composed of entire functions.
In this work, we have formulated the short-range local density approximation (LDA) and GGA functionals for both the real and the imaginary spin density cases. For srLDA exchange82 and correlation83 and the srGGA correlation functionals,69,84 we tried to minimize the number of operations with complex numbers as much as possible trying reduce to real intermediates as early as possible. We followed the strategies of Rodrigues et al. presented in the ESI† of ref. 80. Only for srGGA exchange,69,84 the number of terms became too involving so that we employed complex alpha density (31) and gradient (33) and used the real component of the final exchange energy intermediate as given in eqn (37).
The srLDA exchange82 and correlation energies83 for a constant density ρ = 1 and sr damping factor μ = 0.4 but varying spin polarization ζ are shown in Fig. 1a and b, respectively. As can be clearly seen, the magnitude of XC energies with complex densities is in the same ballpark as the ones with real densities. We conclude that omitting those complex-density contributions would be a harsh approximation whenever the number of points with a positive OTPD cumulant (negative radicand in rhs of eqn (26)) becomes significant. This will be discussed later in the context of excited-state CASSCF methods.
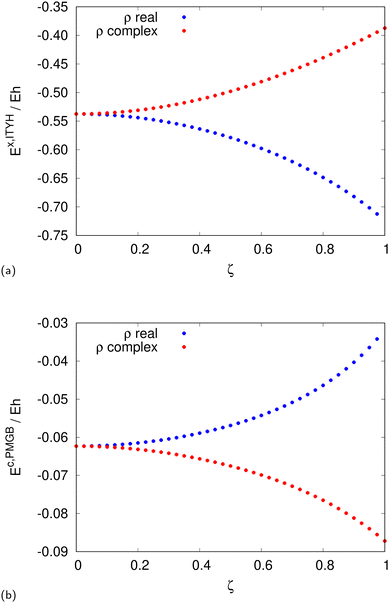 |
| | Fig. 1 The srLDA exchange82 (a) and correlation energies83 (b) for a constant density ρ = 1 and short-range damping factor μ = 0.4 but varying spin polarization ζ. | |
For the XC energies and their functional derivatives, we needed to generate computer code for which we used Python's SymPy module85 for the following functionals with72,80 and without48,71 (complex) functional translation: LDA: Slater exchange,86 VWN correlation;87 PBE: PBE exchange and correlation;88 srLDA: ITYH exchange82 and PMGB correlation;83 srPBE: GWS exchange and correlation.69,84 Note that we follow the convention that acronyms of translated functionals48 are preceded by the letter t, e.g. tPBE, while for complex translated functionals80 ct is used for that purpose, e.g. ctPBE.
As for the original hybrid PBE0 functional,89 the (c)tPBE0, srPBE0, and sr-(c)tPBE0 functionals are trivially obtained by scaling the PBE exchange energy by the factor 3/4 and, as given in eqn (11), by adding the exchange energy scaled by the factor a = 1/4.
The evaluation of those functionals and their derivatives is usually numerically robust if the evaluation is omitted for r with tiny densities ρ(r) and/or density derivatives. The only exception is the ITYH short-range exchange functional82
| |  | (38) |
| | 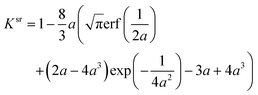 | (39) |
that is part of the srLDA and srPBE functionals. To obtain a numerically stable computer implementation of
Ksr, we had to distinguish between three cases when evaluating the short-range damping factor in
eqn (38) depending on the magnitude of
a =
μ/(2
kF) with
kF = (3π
2ρ)
1/3:
• Low density ρ and/or high sr damping μ: after inserting the series expansions of the erf and exp functions in eqn (39) and simplifying the terms, we arrive at
| |  | (40) |
In our implementation, we use eqn (40) whenever 1/(2a) < tlower and truncate the series at k = 5.
• High density ρ and/or low sr damping μ: if 1/(2a) > tupper, the sr damping factor reduces to
| |  | (41) |
• Moderate density ρ and sr damping μ: the original functional using eqn (39) is employed for all other values of a.
Using eqn (39)–(41) for different regimes of 1/(2a) defined by tlower and tupper avoids the combined evaluation of the erf and exp function for cases they become numerically unstable. We have chosen tlower = 0.1 and tupper = 7.0 which lead to negligible errors in the exchange energy and a seamless transition between the three regions.
2.3 Long-range CASSCF short-range DFT energy first and second derivatives
In this work, the CAS-srDFT energy is minimized with respect to variations in the orbital and CI coefficients using the trust-radius augmented Hessian (TRAH) method – a restricted-step second-order optimization that was recently developed for SCF and CASSCF.90,91 Variations in the orbital space are expressed in terms of orbital rotation operators| |  | (42) |
while variations in the configuration space are expressed through state-transfer operators| |  | (44) |
that perform rotations between the current solution |0〉 and “states” of an orthonormal complement space {|i〉} that includes all CSF of the CAS-CI wavefunction expansion but projects out |0〉.52 For second-order methods as TRAH, the final, minimum energy E is approximated by a truncated Taylor expansion starting from the current solution |0〉| |  | (45) |
and includes also first g and second energy derivatives H while x = {κ,S} being a composite vector containing variational parameters for the orbital (κ) and configurational space (S). More details on how to minimize either the ground-state or the state-average CASSCF energy with TRAH can be found in ref. 91.
At the moment, the variational energy minimization is limited to the spin-density approach.75 Partial energy derivatives with respect to the OTPD are still under development and will be reported elsewhere.
The second-order energy minimization algorithm TRAH and others92–94 require energy first derivatives as well as second derivatives that are transformed by trial vectors also known as sigma vectors. The lrCASSCF energy first derivatives (gradient elements) and sigma vectors are computed in the same way as for CASSCF except for the fact that the lr Coulomb integrals (7) are employed. Those range-separated integrals are generated by the same recursive scheme95 as the regular Coulomb integrals, though use a μ-dependent linear combination of Boys functions.96
The srDFT terms contribute to the orbital and configuration energy gradient with the following terms,
| | 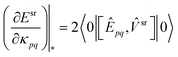 | (46) |
| |  | (47) |
by means of an effective one-electron potential
| |  | (48) |
| | | Vsrpq = Vsr-Hpq + Vsr-xc,ρpq | (49) |
with a short-range Hartree-exchange and short-range XC term
| |  | (50) |
| |  | (51) |
The sr XC potential matrix is only given here and in the following for LDA functionals due to notational convenience. Additional spin-density contributions are given in the Appendix.
Concerning the gradient calculation, the effective one-electron singlet potential matrix Vsrpq of srDFT is processed exactly as the inactive Fock matrix of lrCASSCF
| |  | (52) |
while
i runs over all doubly occupied inactive MO. Thus, in our implementation we simply add
Vsrμν to the inactive Fock matrix giving rise to
| | | fμν = fI,lrμν + Vsrμν | (53) |
when building those two intermediates in the atomic orbital (AO) basis denoted by
μ and
ν. Once such a modified inactive Fock matrix is available in the MO basis, the evaluation of the electronic gradient terms is pursued exactly as for CASSCF.
91
When adding the Vsr matrix to the lr inactive Fock matrix (52), both the Hartree-exchange and the XC potential matrices must be preserved for the energy evaluation as shown in the following. Without the lr/sr joint inactive Fock matrix fpq, the energy reads
| |  | (54) |
while employing the joint intermediate we get
| |  | (55) |
| |  | (56) |
The latter formulation of the lrCASSCF srDFT energy in eqn (55) has been chosen deliberately and will also be relevant for the excited-state CI-srDFT approach discussed in Section 2.4.
The srDFT contributions to the sigma vectors are given below:
| |  | (57) |
| | 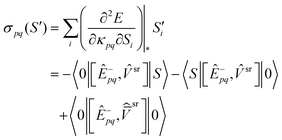 | (58) |
| |  | (59) |
| |  | (60) |
In eqn (57)–(60) the following intermediates were used:
| |  | (61) |
| |  | (62) |
| |  | (63) |
| |  | (64) |
| | ![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) pq = −〈0|Êpq|S〉 − 〈S|Êpq|0〉 pq = −〈0|Êpq|S〉 − 〈S|Êpq|0〉 | (65) |
The last term of eqn (58) can be computed together with the first term of eqn (57) and, likewise, last term of eqn (60) can be computed together with the first term of eqn (59) if a total derivative potential operator is composed
| |  | (66) |
| |  | (67) |
that includes the total derivative density matrix.
| |  | (68) |
With that formulation, the implementation of srDFT sigma vector becomes straightforward since Vpq′sr is processes exactly as the orbital-derivative inactive MO Fock matrix used for (lr) CASSCF.91,93,97 Hence, for the implementation of the srDFT sigma vector we just need to add the sr potential matrix to the lrCASSCF inactive Fock matrix eqn (53), as discussed already earlier for the srDFT gradient part, and the sr total derivative potential matrix to the lrCASSCF orbital-derivative inactive MO Fock matrix is given by
| | | fμν[D′] = fI,lrμν[D′] + Vsrμν[D′] | (69) |
in the AO basis. The Hartree-exchange (HX) and (LDA) XC contribution to the total derivative srDFT potential matrices are given by
| | 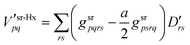 | (70) |
| |  | (71) |
For the XC contribution (71) the total derivative one-electron density
| | 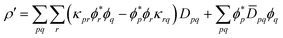 | (72) |
is used.
The sr XC sigma vector terms originating from using the spin-density formalism can be found in the Appendix.
2.4 CASSCF-DFT for excited states
The most popular and most straightforward approach to access CASSCF excitation energies is the so-called state averaging (SA) approximation. The SA-CASSCF energy| |  | (73) |
uses predetermined, user-given state weights wΓ and determines orbital and CI coefficients by minimizing ESA with respect to variations of those wavefunction coefficients. An important feature of the SA approximation is that wavefunctions of multiple states share the same “averaged” orbitals but maintain individual, state-specific CI coefficients. As those CI coefficients are the eigenvectors of the CAS-CI matrix when using SA, they are easily obtained from a full or iterative diagonalization.
In the original, non-variational MC-PDFT ansatz, excited-stated energies are also easily accessible. The SA-CASSCF is obtained first, and then MC-PDFT energies are evaluated with the one- and two-body densities computed from CI solutions of every state. We refer to this state-specific density approaches as SA-MC-PDFT and SA-srDFT. Note that for MC-PDFT also so-called multi-state theories were developed62,63 that are not further discussed here in the present article.
Such an SA ansatz is not compatible with CAS-srDFT with that method because the ground-state functional (2) is variationally minimized.46 It remains to be clarified how the (short-range) DFT functionals Esr-Hx,SA and Esr-xc,SA in
| | | ESA = Elr + Esr-Hx,SA + Esr-xc,SA | (74) |
| |  | (75) |
are determined for an average of states
Γ. Without the loss of generality, we limit the following discussion on the Hartree term which corresponds to a SA CAS-srDFT calculation without XC functionals. The conclusions drawn in the following are equally applicable to both terms because, in contrast to SA-CASSCF, both the Hartree-exchange and XC energy terms are nonlinear in the density.
The most natural way for the Hartree term to enter ESA would be a weighted sum over Hartree energies of every state
| |  | (76) |
| |  | (77) |
For a variational optimization, derivatives of Esr-H,SA with respect to the variational parameters for the orbital κpq and configuration part SΓi are needed.91 When inspecting the electronic gradients, we observe that the state-specific densities DΓpq remain to be apart of the equations
| |  | (78) |
| |  | (79) |
due to the quadratic density dependence of
Esr-H in
eqn (77). Similar observations can be made for the energy second derivatives. For the configuration sigma vectors we get
| |  | (80) |
The dependence on state-specific densities DΓpq is not problematic for a single-state calculation but leads inevitable to non-orthogonal CI solutions for SA calculations, as can seen from eqn (80).
Instead of averaging over the state-specific Hartree energies (76), we evaluate the srDFT functionals from state-averaged densities ρSA and ΠSA, and their derivatives,
| | | Esr-H,SA ≈ Esr-H[ρSA] | (81) |
| | | Esr-xc,SA ≈ Esr-xc[ρSA,∇ρSA,ΠSA], | (82) |
with density matrices computed from
| |  | (83) |
| |  | (84) |
Nevertheless, using averaged densities is obviously a substantial approximation to eqn (76) and the effects on the accuracy need to be carefully investigated. After converging the approximate SA CAS-srDFT energy, the state-specific ground- and excited-state CAS-srDFT energies can be easily evaluated from the state-specific density matrices, in full analogy to the SA-MC-PDFT approach.
An alternative to the SA CAS-srDFT ansatz for excited-state energies is to find a correction to the approximated SA srDFT energy in eqn (81) and (82). For this purpose we introduce difference densities
between the exact
ρ and
Π and the averaged densities
ρSA and
ΠSA. We assume here that the magnitude of the difference densities is comparatively small because the core part of the densities
| |  | (87) |
| |  | (88) |
has usually the largest contribution and, at least, is shared by all exact, state-specific densities.
In order to find a linearized approximation to the DFT terms in eqn (74), Pedersen64 and also Hedegård et al.,65 suggested to expand the srDFT energy in orders of the difference density, around the SA densities:
| |  | (89) |
Note that we limit the discussion here to LDA functionals, in order to avoid an unnecessary elaborate presentation of the concepts and equations. In addition to linearized energy equations in ref. 64 and 65, we also add a first energy derivative with respect to the OTPD as (complex) translated functionals are employed for the final energy evaluation of each state in the average. The linearized CI-srDFT energy for any selected state in the average then reads
| | | ECI-srDFT ≈ Elr + E[ρSA + Δρ, ΠSA + ΔΠ] | (90) |
| |  | (91) |
In analogy to the CAS-srDFT energy in eqn (55), the srDFT one-electron potential matrices are added to the lr CASSCF inactive Fock matrix
| | | ftu = fI,lrtu + Vsr-Hx[DSA]tu + Vsr-xc,ρΠ[DSA]tu | (92) |
| |  | (93) |
though, an effective one-electron potential from the OTPD first energy derivatives arises in
eqn (93). Due to the presence of OTPD first energy derivatives also a sr two-body potential
47,98 is added to the lr two-electron integrals in the CI-srDFT energy in
eqn (91):
| | | gtuvw = glrtuvw + Wsr-xctuvw | (94) |
| |  | (95) |
Interestingly, also the CI-srDFT core energy is closely related to the core energy or the single-state CAS-srDFT in eqn (56):
| |  | (96) |
| |  | (97) |
The only differences are the additional OTPD-related terms and that all active density matrices are replaced by their state-averaged analogues.
With the linearized CI-srDFT energy in (91), the corresponding CI matrix expressed in the basis of CSF is readily available and reads
| |  | (98) |
Diagonalizing H in (98) gives the CI-srDFT energies for every state in the averaged energy functional and the corresponding orthogonal CI wavefunction coefficients which concludes the second excited-state approach that we pursue in this work. It is evident that the same procedure can also be used for MC-PDFT when omitting the two-electron part of the (lr) CASSCF energy terms in (98). Such a linearized CI approach applied to MC-PDFT seems to be closely related to the recently proposed linearized PDFT method.99
Finally, we note the similarity between CI-srDFT and the srDFT linear response method.50,51 If variations in the orbital space are neglected, the only difference between eqn (98) and the electronic configuration–configuration Hessian lies in the choice of CI states used to construct the one- and two-electron RDMs. In srDFT linear-response theory, the RDMs of the electronic ground state are employed, whereas in CI-srDFT, state-averaged RDMs are used in the construction of the effective CI Hamiltonian (98).
3 Computational details
The CASSCF-DFT methods for excited states were implemented in a development version of ORCA100,101 and will be part of the next release version ORCA 6.1. So far, those CASSCF-DFT methods are integrated into the TRAH optimizer for CASSCF91 but are not available for other CASSCF optimizers in ORCA, such as the perturbative super-CI implementation.102 The correctness of the ground-state srDFT implementation without functional translation was confirmed by comparing energies with the implementation in the DALTON program package.46,75,103 The MC-PDFT ground- and excited-state energies of our ORCA implementation agree with the one from OpenMOLCAS104 for the tPBE functional, but differ slightly for tLDA because different sets of VWN parameters87 were used. For ground-state energies, our implementation reproduces the closed-shell KS-DFT LDA in ORCA100,101 and agrees with srLDA in DALTON46,75,103 when setting μ to zero.
The internally contracted (ic) MRCI singles and doubles27 calculations were performed with ORCA's automatically generated code implementation (AutoCI) of correlated wavefunction models.105–107 Also the internally contracted DDCI3+Q implementation in ORCA's AutoCI was employed, though this feature is not released yet. The Davidson correction (Q) was always employed for both ic MRCI-type methods.
Point-group symmetry was never exploited for any calculation. To assign the correct term symbol to each state and make a proper assignment, we visualized active orbitals and natural transition orbitals (NTO).108,109
All CASSCF-DFT calculations used ORCA's tight default grid110 (DefGrid3) for numerical integration of the XC functionals.
For the potential curves of ethylene, we took the planar structure from ref. 111 and left all bond distances and angles fixed while varying only the dihedral angle ∠(H–C–C–H). The structures of the benchmark set of Schreiber et al. were taken from the ESI† of ref. 111. The TZVP orbital basis set112 was employed for those calculations.
The geometries of the three divalent transition-metal hexaquo complexes were taken from ref. 2. For those complexes, the following orbital basis sets were employed in accordance with the calculations in ref. 2: oxygen: TZVPP,112 hydrogen: TZVP,112 transition metal: Wachters+f.113
The choices of active spaces for each MR calculation are explained in Section 4.
4 Results and discussion
4.1 Ethylene twist
We investigate the accuracy of the various CASSCF-DFT methods for the ground state and two lowest excited states in state-averaged calculations of ethylene in its planar (∠(H–C–C–H) = 0°) and twisted conformations. Since ethylene changes its symmetry from D2h to D2 when being twisted, we follow the notation of Merer and Mulliken for the three lowest-lying states,114i.e., N state: 1 1Ag or 1 1A, V state: 1 1B1u or 1 1B1, and Z state: 2 1Ag or 2 1A. At any twisted conformation (0° < ∠(H–C–C–H) < 180°), the three singlet CSF constructed from the π and π* orbital mix strongly up to equal contributions of the |π2(π*)0〉 and |π0(π*)2〉 configurations for the totally symmetric states (N and Z) at 90°. Therefore, we have included the valence π and π* orbitals and their electrons in the active space, i.e. CAS(2,2), and averaged over three singlet roots.
As seen from the srDFT potential curves in Fig. 2, srLDA shows the largest deviation from internally contracted MRCI + Q, which we assume to be a highly accurate reference. The srLDA model just uses the one-electron density for the XC energy and misses for that term any explicit two-electron correlation effects. As a results, we observe a too high rotational barrier around 90° (∠(H–C–C–H)) for the ground state. This is a reminiscence of the well-known cusp of the ground-state energy curve when using restricted single-determinant methods.115
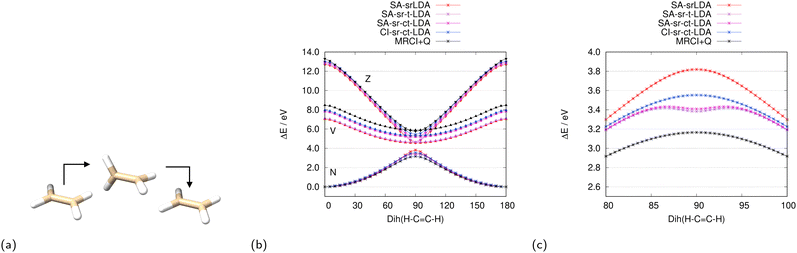 |
| | Fig. 2 Potential energies for the N, V, and Z states114 while twisting ethylene (a) with various srLDA methods (b) and MRCI+Q. The ground (N)-state curves around 90° are shown in (c). | |
The translated XC functional sr-tLDA does include local spin polarization by means of the two-particle density in the XC functional, but only for points r that have a negative on-top two-body density cumulant λ(r). For the three ethylene twist curves, srLDA only changes the energy of the ground (N) state in the vicinity of 90° significantly. This is because the percentage of r for which λ(r) < 0 is more than 70% for the N state but less than 36% for V, and even 0% for the Z state. Thus, complex translation is important, in particular, for the two excited states and the sr-ctLDA curves are in much better agreement with MRCI+Q than the ones of sr-tLDA.
Though improving upon the srLDA curves, the SA approach for the translated XC functionals sr-tLDA and sr-ctLDA have a minimum of ground state curve at 90° when they should have a maximum, as shown in Fig. 2c. This is related to the substantial energy changes in that region when computing state-specific energies with translated functional methods sr-tLDA and sr-ctLDA using state-averaged srLDA solutions. The CI-srDFT approach that accounts for state-specific XC potentials in a linearized fashion remedies this false-minimum artifact in the same way as multi-state theories give improved results close to avoided crossings.57–63
In Tables 1 and 2, all CASSCF-DFT excitation energies of the planar and twisted (∠(H–C–C–H) = 90°) conformer are shown. Those numbers are relative to the ground state of the planar conformer for each of the methods. In the comparison of CASSCF-DFT with MRCI+Q energies, the srDFT methods outperform their corresponding MC-PDFT variants clearly. When looking at the most accurate MC-PDFT variant (CI-ctPBE), the Z-state excitation energy in the planar conformer is still 1.78 eV lower than with MRCI+Q. In contrast to this, the most accurate srDFT variant (CI-sr-ctPBE) is only 0.48 eV below the reference. We attribute the higher accuracy of the srDFT variants mainly to the presence of an exchange-like term in the lr CASSCF part. This argument is supported by the fact that the complex-translated hybrid functional PBE0 with a 25% exchange-like contribution gives a substantial improvement of the ctPBE excitation energies (see Table 1). Furthermore, it is known that Hartree–Fock exchange is an essential ingredient for single-reference XC functionals to perform well for time-dependent (TD) DFT excitation energies.116
Table 1 Relative energies in eV with various MC-PDFT methods and MRCI+Q for planar and twisted ethylene, all based on state-averaged orbital optimizations
| State |
MRCI |
ctLDA |
ctPBE |
ctPBE0 |
| SA |
SA |
CI |
SA |
CI |
SA |
CI |
| Planar |
| 1 1Ag |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
| 1 1B1u |
8.47 |
6.26 |
6.58 |
6.29 |
6.69 |
7.08 |
6.75 |
| 2 1Ag |
13.29 |
11.84 |
12.21 |
11.81 |
12.20 |
12.09 |
12.61 |
|
|
| Twisted |
| 1 1A |
3.17 |
3.28 |
3.61 |
3.33 |
3.49 |
4.48 |
3.91 |
| 1 1B1 |
5.88 |
4.27 |
4.59 |
4.36 |
4.74 |
5.20 |
4.85 |
| 2 1A |
5.76 |
4.42 |
4.74 |
4.53 |
4.95 |
5.31 |
5.01 |
Table 2 Relative energies in eV with various srDFT methods and MRCI+Q for planar and twisted ethylene, all based on state-averaged orbital optimizations
| State |
MRCI+Q |
srLDA |
srPBE |
srPBE0 |
sr-ctLDA |
sr-ctPBE |
sr-ctPBE0 |
| SA |
SA |
SA |
SA |
CI |
SA |
CI |
SA |
CI |
| Planar |
| 1 1Ag |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
| 1 1B1u |
8.47 |
7.03 |
7.03 |
7.28 |
7.82 |
7.95 |
7.86 |
7.99 |
7.83 |
7.85 |
| 2 1Ag |
13.29 |
12.70 |
12.72 |
13.03 |
12.92 |
13.01 |
12.95 |
13.06 |
13.18 |
13.23 |
|
|
| Twisted |
| 1 1A |
3.17 |
3.82 |
3.84 |
4.08 |
3.41 |
3.55 |
3.40 |
3.54 |
3.78 |
3.80 |
| 1 1B1 |
5.88 |
4.56 |
4.59 |
4.84 |
5.17 |
5.31 |
5.24 |
5.37 |
5.30 |
5.31 |
| 2 1A |
5.76 |
4.56 |
4.59 |
4.85 |
5.31 |
5.45 |
5.39 |
5.52 |
5.41 |
5.41 |
For almost all states, the GGA excitation energies are more accurate than the ones computed with the respective LDA functional, though the improvement is rather moderate and ranges from less than 0.01 eV for the V state with srPBE for the planar conformer up to 0.21 eV for the Z state with CI-ctPBE for the twisted conformer.
Finally, we note that our CI-DFT approach leads for both MC-PDFT and srDFT to a better agreement with MRCI+Q than the SA approach. Additionally, as shown for the sr-ctLDA curves, the CI-DFT approach fixes the false-minimum artifact.
4.2 Thiel's benchmark set
To gain more clarity on the accuracy that one can expect from our CASSCF-DFT methods, we computed 139 singlet excitation energies from Thiel's benchmark set using the TZVP basis.111 As in a previous study,55 we have included all valence π/π* and spectroscopically relevant non-bonding and sigma orbitals and electrons in the active space. The active space and number of roots for each molecule are provided in the ESI.† We have compared our CASSCF-DFT excitation energies to the ones111,117,118 obtained primarily from the linear-response, iterative CC with singles, doubles, and perturbative triples119 (CC3) which provides highly accurate results for electronic transitions that are dominated by effective single-electron excitations.119,120 For transitions with a large double-excitation contribution, we chose ic MR second-order coupled cluster linear response121 (icMRCC2) results of ref. 122 as a reference. We had to exclude three high-lying states from the analysis (pyrazine: 1 1B3g, s-tetrazine: 2 1B3g, and p-benzoquinone: 2 1B1u) because for the SA-MC-PDFT methods the underlying SA-CASSCF states could not been found without increasing the number of roots to an undue high value. All other states have been assigned by comparing the natural transition orbitals108,109 (NTO) of CASSCF-DFT with the ones of CC2 states.123,124
The 139 singlet excitation energies for each of the 12 CASSCF-DFT variants, ctLDA, ctPBE, ctPBE0, sr-ctLDA, sr-ctPBE, and sr-ctPBE0 either as SA or CI calculation, are tabulated in the ESI† along with their reference values. According to the histograms of the CASSCF-DFT deviations from Fig. 3 (PBE functionals), and the ESI† (LDA and PBE0 functionals), as well as the error statistics from Table 3, on average, sr-ctDFT is much more accurate (MAE CI-sr-ctPBE: 0.17 eV) than the corresponding ctDFT methods (MAE ctPBE: 0.67 eV).
 |
| | Fig. 3 Histogram of CAS-PBE deviations from the CC3 and icMRCC2 reference for 139 singlet excitation energies from Thiel's benchmark set.111,117,118,122 | |
Table 3 Statistical analysis of CAS-DFT singlet excitation energies. Relative deviation with respect to CC3111,117,118 and icMRCC2122 are given in eV. The following abbreviations were used: ME – mean error; MAE – mean absolute error; SD – standard deviation; MAX(+) – maximum error with positive sign; MAX(−) – maximum error with negative sign
|
|
ctLDA |
ctPBE |
ctPBE0 |
sr-ctLDA |
sr-ctPBE |
sr-ctPBE0 |
| SA |
CI |
SA |
CI |
SA |
CI |
SA |
CI |
SA |
CI |
SA |
CI |
| Count |
139 |
139 |
139 |
139 |
139 |
139 |
139 |
139 |
139 |
139 |
139 |
139 |
| ME |
−0.32 |
−0.99 |
−0.30 |
−0.92 |
1.20 |
0.56 |
−0.02 |
−0.09 |
0.01 |
−0.07 |
0.41 |
0.36 |
| MAE |
0.68 |
0.99 |
0.65 |
0.92 |
1.49 |
0.83 |
0.25 |
0.17 |
0.25 |
0.17 |
0.52 |
0.46 |
| SD |
0.83 |
1.13 |
0.81 |
1.05 |
2.82 |
0.99 |
0.34 |
0.25 |
0.34 |
0.25 |
0.62 |
0.53 |
| MAX(+) |
2.44 |
0.10 |
2.44 |
0.18 |
3.44 |
2.06 |
0.96 |
0.49 |
1.07 |
0.49 |
2.01 |
1.66 |
| MAX(−) |
−2.81 |
−2.38 |
−2.79 |
−2.21 |
−2.38 |
−2.38 |
−1.44 |
−1.34 |
−1.43 |
−1.34 |
−1.37 |
−1.17 |
When considering statistical averages, we also note that GGAs perform, if at all, marginally better than the corresponding LDA functionals (e.g. MAE of CI-sr-ctLDA and CI-sr-ctPBE 0.17 eV). Those trends agree also with our results of the ethylene twist potential curves, except for the fact that the CI-ctDFT excitation energies of are worse than the SA-MC-PDFT results with ct functionals. For the sr functionals, however, the CI-srDFT approach (MAE sr-ctPBE: 0.17 eV) improves the accuracy notably in comparison to SA (MAE sr-ctPBE: 0.25 eV).
Again, we assume that the Hartree–Fock exchange, which is present in lr-CASSCF but not in ctDFT, is a necessary ingredient for obtaining accurate excitation energies. However, we observe that for MC-PDFT the hybrid ctPBE0 functional does not improve upon the ctPBE results. While ctPBE excitation energies are on average red-shifted, excitation energies with ctPBE0 are significantly blue-shifted (ME SA ctPBE0 1.20 eV, CI ctPBE0 0.56 eV) with respect to the accurate CC3 and icMRCC2 reference. This is in contrast to the ethylene curves for which, at least, the ctPBE0 gave significantly more accurate excitation energies than ctPBE. Furthermore, for CAS-srDFT the hybrid sr-ctPBE0 functional feature blue-shifted excitation energies, as well, and deteriorate the satisfying accuracy of the non-hybrid sr-ctPBE functional.
In comparison with other excited-state methods that were employed in previous studies with Thiel's benchmark set,55 our best performing CASSCF-DFT method, CI-sr-ctPBE (MAE 0.17 eV and SD 0.25 eV), is much more accurate than single-reference TD-DFT125 (B3-LYP: MAE 0.37 eV and SD 0.33 eV; BP86: MAE 0.67 eV and SD 0.41 eV) and also untranslated linear-response srPBE126 (MAE 0.26 eV and SD 0.47 eV). CI-sr-ctPBE (MAE 0.17 eV and SD 0.25 eV) also showed a similar accuracy as the second-order correlation MR methods CASPT2111 (MAE 0.21 eV and SD 0.21 eV) and NEVPT2127 (MAE 0.22 eV and SD 0.30 eV) which are, without introducing further approximations, computationally more demanding than CASSCF-DFT due to their inherent ![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N5) scaling with system size N.
(N5) scaling with system size N.
4.3 Low-lying states of imidazole
So far, we have always averaged over a minimum number of roots that are required to find the desired low-lying states, e.g. all π → π* excitations of ethylene or the subset of singlet states in Thiel's benchmark set.111 Here, we investigate the sensitivity of the 2 1A′ and 1 1A′′ states of imidazole towards the number of roots while employing state averaging. We limit ourselves to the different methods based on the srPBE functional for which one approach gave the best performance for Thiel's benchmark set (CI-sr-ctPBE). In Fig. 4, the deviation from the reference is shown for various number of roots in the state averaging.
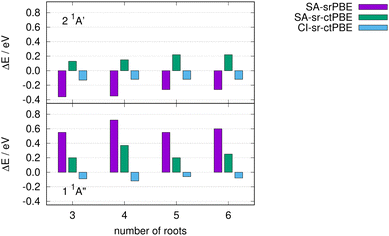 |
| | Fig. 4 Excitation energy differences of various srPBE models from the reference for the lowest n → π* (1 1A′′) and π → π* state (2 1A′) of imidazole. | |
The SA CAS-srDFT approaches with srPBE and sr-ctPBE deviate up to 0.12 eV when comparing the NSA = 4 and NSA = 6 calculations and fluctuate notably when changing the number of SA roots NSA. In contrast to this, the 2 1A′ and 1 1A′′ CI-sr-ctPBE excitation energies only vary by 0.04 eV, at most, when changing the number of SA roots. Thus, CI-sr-ctDFT is not only the most accurate approach but also exhibits the least energy changes while changing the number of SA roots.
4.4 Transition-metal complexes
Finally, we investigate the performance of excited-state CASSCF-DFT methods for a family of transition-metal complexes (TMC). We chose the divalent Th-symmetric first-row transition-metal hexaquo complexes2 with Fe(II), Co(II), and Ni(II) as metal centers. We have employed a minimal active space including only the valence 3d orbitals and electrons in all MR calculations presented here. With that active-space choice the correct multiplet structure for the ground state as well as the low-lying metal-centered (MC) ligand-field excited states is obtained when using CASSCF.2 The frontier orbitals of the three TMC are given as an MO diagram with their ground-state term symbols in Fig. 5. Since the Co(II) and Ni(II) complexes have an open-shell non-singlet ground state, we had to use the spin-density approach75 for srDFT calculations of those complexes. The more consistent variationally optimized sr-(c)tDFT ansatz98 is unfortunately not available yet to study excited states. Though the lowest-energy state is a quintet,2 we have deliberately chosen the singlet-spin states for the Fe(II) complex to detect potential problems that may only occur for the chosen treatment of open-shell systems Co(II) and Ni(II).
 |
| | Fig. 5 Geometric structure of Th-symmetric divalent first-row transition-metal hexaquo complexes and schematic frontier-orbital occupation for the corresponding Fe(II), Co(II), and Ni(II) complexes. | |
We have recomputed highly accurate reference energies employing the internally contracted105–107 difference-dedicated (DD) CI(3) method128 with Davidson correction129 (+Q) in contrast to uncontracted spectroscopy-oriented CI (SORCI) in the original benchmark set of Neese et al.2 Concerning the SORCI calculations in ref. 2, additional states with multiple spin multiplicities were included in the SA-CASSCF calculations and reference energies for the singlet Fe(II) states were not provided. For the Co(II) and Ni(II) complexes the reference energies in Table 4 deviated from the uncontracted SORCI results of ref. 2 only slightly by at most 0.05 eV for 1 4Ag of Co(H2O)62+ and are also in good agreement with most of the experimental results. In our opinion, this supports the assumption that a minimal 3d valence active space should be sufficient to describe the lowest MC transitions.
Table 4 Excitation energies in eV for divalent first-row transition-metal hexaquo complexes with CASSCF, srDFT methods, and DDCI3+Q. For SA methods the average over the multiplet (SAav) is given along with its maximum absolute deviation (|Δav|, in meV)
| State |
DDCIa |
CAS |
srLDA |
srPBE |
srPBE0 |
| SAav |
CI |
SAav |
|Δav| |
SAav |
|Δav| |
SAav |
|Δav| |
|
|Δav| < 3 meV.
|
| FeII(H2O)62+ |
| 1 1Ag |
0.00 |
0.00 |
0.00 |
— |
0.00 |
— |
0.00 |
— |
| 1 1Tg |
0.94 |
0.73 |
0.80 |
11 |
1.02 |
2 |
2.82 |
121 |
| 2 1Tg |
1.78 |
1.41 |
1.79 |
76 |
1.98 |
123 |
4.82 |
44 |
| 3 1Tg |
2.19 |
2.05 |
1.89 |
2 |
2.21 |
13 |
3.07 |
81 |
|
|
| CoII(H2O)62+ |
| 1 4Tg |
0.00 |
0.00 |
0.00 |
5 |
0.00 |
1 |
0.00 |
<1 |
| 2 4Tg |
0.83 |
0.69 |
0.80 |
17 |
1.09 |
134 |
0.62 |
<1 |
| 1 4Ag |
1.80 |
1.52 |
1.83 |
— |
2.02 |
— |
1.56 |
<1 |
| 3 4Tg |
2.44 |
2.86 |
1.87 |
12 |
1.81 |
89 |
1.95 |
<1 |
|
|
| NiII(H2O)62+ |
| 13 Ag |
0.00 |
0.00 |
0.00 |
— |
0.00 |
— |
0.00 |
— |
| 1 3Tg |
0.98 |
0.80 |
1.11 |
1 |
1.31 |
232 |
1.13 |
132 |
| 2 3Tg |
1.68 |
1.40 |
2.27 |
<1 |
2.38 |
77 |
2.34 |
2 |
| 3 3Tg |
3.15 |
3.42 |
2.53 |
<1 |
2.51 |
15 |
2.33 |
2 |
For the lowest excitation energies to the Ag and Tg MC states in Table 4, SA-CASSCF gives already a qualitatively correct picture for the excitation energies. The differences to DDCI3+Q are not larger than 0.42 eV (3 4Tg of Co(H2O)62+). Already CASSCF yields the correct order of states that does not change when the subsequent dynamic correlation method DDCI3+Q is employed. Therefore, it seems those hexaquo TMC should not be a major obstacle for our CASSCF-DFT excited-state methods, but the opposite is true.
Even though these low-lying Ag and Tg MC states are energetically well separated from one another, none of the CASSCF-DFT methods is capable of predicting, at least, the order of states correctly for all three complexes. According to Tables 4 and 5, the order of states is only correct for some of the SA calculations (Fe(II): ctLDA and ctPBE, Co(II): srLDA and srPBE; Ni(II): srLDA, sr-ctLDA, srPBE, sr-ctPBE, ctPBE, and ctPBE0). When inspecting the CI-DFT calculations, there is always a pair of states that collapses to the same or, at least, nearly the same excitation energies (Fe(II): 1 1Tg and 3 1Tg; Co(II): 2 4Tg and 3 4Tg, Ni(II): 1 3Tg and 2 3Tg). The lower-energy state of this pair is always too large with CI-DFT (up to 0.19 eV for 1 1Tg of Fe(II) with CI-sr-ctPBE) while the higher-energy state is always way too small (up to 1.41 eV for 3 4Tg of Co(II) with CI-sr-ctPBE). Furthermore, we could not observe that excitation energies of the singlet Fe(II) complex are more accurate than the open-shell Co(II) and Ni(II) complexes which we assumed to be caused by the spin-density approach.75
Table 5 Excitation energies in eV for divalent first-row transition-metal hexaquo complexes with CASSCF, complex-translated srDFT and MC-PDFT methods, and DDCI3+Q. For SA methods the average over the multiplet (SAav) is given along with its maximum absolute deviation (|Δav|, in meV)
| State |
DDCIa |
CAS |
sr-ctLDA |
sr-ctPBE |
sr-ctPBE0 |
ctLDA |
ctPBE |
ctPBE0 |
| SAav |
CI |
SAav |
|Δav| |
CI |
SAav |
|Δav| |
CI |
SAav |
|Δav| |
CI |
SAav |
|Δav| |
CI |
SAav |
|Δav| |
CI |
SAav |
|Δav| |
CI |
|
|Δav| < 3 meV.
|
| FeII(H2O)62+ |
| 1 1Ag |
0.00 |
0.00 |
0.00 |
— |
0.00 |
0.00 |
— |
0.00 |
0.00 |
— |
0.00 |
0.00 |
— |
0.00 |
0.00 |
— |
0.00 |
0.00 |
— |
0.00 |
| 1 1Tg |
0.94 |
0.73 |
0.98 |
48 |
1.04 |
1.24 |
94 |
1.15 |
2.99 |
159 |
2.53 |
1.04 |
3 |
0.94 |
1.22 |
4 |
1.06 |
3.39 |
5 |
2.65 |
| 2 1Tg |
1.78 |
1.41 |
1.96 |
13 |
2.02 |
2.25 |
35 |
2.24 |
3.24 |
47 |
4.67 |
1.93 |
3 |
1.82 |
2.32 |
14 |
2.04 |
7.01 |
29 |
5.24 |
| 3 1Tg |
2.19 |
2.05 |
1.23 |
118 |
1.07 |
2.06 |
57 |
1.18 |
4.88 |
56 |
2.83 |
2.59 |
4 |
0.95 |
2.94 |
3 |
1.06 |
6.95 |
34 |
2.65 |
|
|
| CoII(H2O)62+ |
| 1 4Tg |
0.00 |
0.00 |
0.00 |
5 |
0.00 |
0.00 |
1 |
0.00 |
0.00 |
<1 |
0.00 |
0.00 |
<1 |
0.00 |
0.00 |
2 |
0.00 |
0.01 |
27 |
0.00 |
| 2 4Tg |
0.83 |
0.69 |
0.80 |
17 |
1.04 |
0.97 |
82 |
1.01 |
0.64 |
<1 |
0.93 |
0.66 |
<1 |
0.98 |
0.57 |
<1 |
0.94 |
0.02 |
9 |
0.88 |
| 1 4Ag |
1.80 |
1.52 |
1.83 |
— |
2.09 |
1.89 |
— |
2.02 |
1.58 |
<1 |
1.85 |
1.65 |
— |
1.97 |
1.52 |
— |
1.88 |
0.89 |
— |
1.76 |
| 3 4Tg |
2.44 |
2.86 |
1.87 |
12 |
1.07 |
1.72 |
26 |
1.03 |
1.85 |
<1 |
0.95 |
1.46 |
<1 |
0.98 |
1.48 |
<1 |
0.94 |
1.50 |
1 |
0.88 |
|
|
| NiII(H2O)62+ |
| 13 Ag |
0.00 |
0.00 |
0.00 |
— |
0.00 |
0.00 |
— |
0.00 |
0.00 |
— |
0.00 |
0.00 |
— |
0.00 |
0.00 |
— |
0.00 |
0.00 |
— |
0.00 |
| 1 3Tg |
0.98 |
0.80 |
1.11 |
1 |
1.12 |
1.22 |
138 |
1.08 |
1.12 |
114 |
1.01 |
1.01 |
<1 |
1.02 |
0.97 |
1 |
0.98 |
0.91 |
<1 |
0.91 |
| 2 3Tg |
1.68 |
1.40 |
2.27 |
<1 |
1.15 |
2.22 |
83 |
1.11 |
2.23 |
2 |
1.03 |
1.87 |
1 |
1.02 |
1.90 |
10 |
0.98 |
3.06 |
27 |
0.91 |
| 3 3Tg |
3.15 |
3.42 |
2.53 |
<1 |
2.25 |
2.47 |
10 |
2.17 |
2.30 |
1 |
2.02 |
1.87 |
3 |
2.04 |
1.94 |
6 |
1.95 |
3.15 |
<1 |
1.82 |
In contrast to our previous findings for organic chromophores, our excited-state CASSCF-DFT methods perform worse than CASSCF for the TMC investigated so far. We assume that a fully variational energy minimization of the (complex) translated functionals47,98 would improve the accuracy. At the moment, only, if at all, the CI coefficients are optimized in the presence of OTPD functionals that incorporate explicit electron correlation in the XC functionals what we refer to as the CI-DFT method. Orbital relaxation for OTPD functionals is still missing for any of our excited-state CASSCF-DFT methods. Note, however, that in a variational state-averaged OTPD function calculation the DFT part would be evaluated still with averaged densities and for those calculations state-specific orbital relaxation is not possible. Therefore, we think that excited states with fully variational (complex) translated CASSCF-DFT methods47,98 should be better computed within the framework of linear response theory.50–52
5 Conclusions
In the present work, we introduced and investigated two different state averaging-based approaches to access excited states either with the multiconfiguration pair-density functional theory (MC-PDFT) method or the long-range CASSCF short-range DFT approach (CAS-srDFT). The so-called SA ansatz for CAS-srDFT first determines the variational parameters of an approximate srDFT functional that operates with state-averaged densities. Then, after convergence, the CAS-srDFT energies of each state are computed from the state-specific one- and two-body densities. An analogous approach termed SA-MC-PDFT is readily applicable to MC-PDFT when executing the corresponding SA-CASSCF calculation in the initial step and, then, utilizing the state-specific one- and two-body CASSCF densities for the state-specific MC-PDFT energy evaluation. The second approach is termed CI-srDFT and originates from the work of Pedersen64 for which a first-order correction is added to the approximate SA-density srDFT functionals. In contrast to the SA-CAS-srDFT approach, diagonalization of the first-order corrected CI matrix yields orthonormal CI solutions for every state.
In both approaches, the total one-body and on-top pair density (OTPD) was employed for the final energy evaluation which avoids the issue of spin contamination and suppressed accuracy associated with the spin-density approach.75 For electronic positions that feature complex densities when employing the OTPD formalism,72,80 we have not introduced further approximations or modified the underlying XC functionals what is referred to as complex functional translation.80 We have applied complex functional translation for the first time also to the dedicated short-range LDA and GGA functionals and reported their superior accuracy when computing excitation energies. For the potential curves of the lowest states of ethylene, we observed that complex translation is highly relevant for the excited-state curves since most of the electronic positions feature complex rather than real density matrices, at least for our excited-state approaches that are based on SA.
It has been demonstrated that the CI-srDFT approach provides potential curves for ethylene that are physically correct, in contrast to the SA-CAS-srDFT method, which features a false minimum at the maximally twisted conformation of ethylene. Furthermore, the dependence of excitation energies on the number of states in the average is reduced when using the CI-srDFT approach as opposed to SA-CAS-srDFT. We investigated the accuracy of the various CASSCF-DFT methods for 139 singlet excitation energies that are part of Thiel's benchmark set of 28 typical organic chromophores.111 We have also found that our CI-srDFT methods are more accurate than the corresponding SA approaches. For instance, the mean absolute error (MAE) of SA sr-ctPBE is 0.24 eV while MAE of CI sr-ctPBE is reduced to 0.17 eV. Furthermore, we have seen in this study that the CAS-srDFT variants outperform their corresponding MC-PDFT analogues clearly. The best MC-PDFT approach, SA ctPBE, exhibit an MAE of 0.65 eV which is four times larger than our best CAS-srDFT method, CI CAS-sr-ctPBE. The enhanced accuracy of CAS-srDFT relative to MC-PDFT for excited states is presumably attributable to the absence of Hartree–Fock (HF)-like exchange terms in the non-hybrid MC-PDFT functionals ctLDA and ctPBE employed in this study. Though, the hybrid ctPBE0 that includes these HF-like exchange terms results in a significant blue shift (ME: SA 1.20 eV, CI 0.56 eV). CAS-srDFT functionals always incorporate HF-like exchange in the long-range CASSCF part. Another potential cause of the accuracy discrepancy between CAS-srDFT and MC-PDFT could be the effectiveness with which double counting of dynamic correlation is handled by either method.79 It is encouraging that our most advanced CASSCF-DFT methods, CI CAS-sr-ctPBE, demonstrate comparable or even superior accuracy to second-order single- or multi-reference perturbation theory methods when applied to Thiel's benchmark set.55
It is unfortunate that the remarkable accuracy observed for organic molecules when employing our most advanced CAS-srDFT methods is not transferable to the investigation of excited states of transition-metal complexes. For three divalent hexaquo complexes of Fe(II), Co(II), and Ni(II), the lowest d-to-d metal-centered transitions are adequately described by the state-averaged CASSCF model already. It is evident that the CASSCF-DFT excited-state methods introduced in this study, despite their potential, have not yielded a consistent improvement of CASSCF excitation energies. However, it is noteworthy that the CI-srDFT approach, despite its limitations, maintains the correct degeneracy of states, i.e. the multiplet structure. It is challenging to draw further conclusions from the results obtained thus far without further advancements in theory and computer implementations.
In the future, we would like to improve the accuracy of our CASSCF-DFT methods by providing a fully variational optimization, also with respect to variations of the on-top pair density.47,98 The effect of state-specific orbital relaxation should also be investigated ideally within the framework of linear-response theory.50–52 In that way, we would try to find a way for also improving the accuracy for transition-metal complexes or other challenging systems. More efficient implementations employing sophisticated integral-decomposition techniques110,130–133 are also important for applications on larger molecules and are currently pursued in our groups.
Author contributions
Benjamin Helmich-Paris: conceptualization (equal); investigation (lead); methodology (lead); software (lead); validation (lead); visualization (lead); writing – original draft (lead); writing – review & editing (equal); funding acquisition (lead); project administration – (lead). Erik Rosendahl Kjellgren: conceptualization (equal); investigation (supporting); methodology (supporting); validation (supporting); writing – original draft (supporting); writing – review & editing (equal). Hans Jørgen Aa. Jensen: conceptualization (equal); investigation (supporting); methodology (supporting); software (supporting); validation (supporting); visualization (supporting); writing – original draft (supporting); writing – review & editing (equal); project administration – (supporting).
Conflicts of interest
There are no conflicts of interest to declare.
Data availability
The data supporting this article have been included as part of the ESI.†
Appendix
In the spin-density approach for open-shell molecules,75 the exchange–correlation energy Exc[ρ,m] depends on the total one-body density ρ(13) and the spin density m(14) and, depending on the functional type, also derivatives of the densities. Following such a spin-density approach necessitates the computation of functional derivatives of Exc with respect the spin density for the srDFT electronic gradients and sigma vectors. A potential term that involves triplet excitation operators (16),| |  | (99) |
| |  | (100) |
is employed for the evaluation of the orbital and configuration gradient equations| |  | (101) |
| |  | (102) |
that are added to (46) and (47), respectively. Note that for the evaluation of CI sigma vectors and density matrices in eqn (101) and (102) coupling coefficients involving ![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) tu are required.134–136
tu are required.134–136
The XC energy derivatives contribute to the sigma vectors with the following terms
| |  | (103) |
In the equations above, x and y correspond to either of the two variational parameters κ and S. The derivative densities are defined as
| |  | (104) |
| |  | (105) |
The additional spin-density terms for the sigma vector can be implemented very conveniently when following the same strategies that were outlined in Section 2 of the main text.
Acknowledgements
The authors would like to express their sincere gratitude to Christel Marian for her invaluable contributions to the field of excited-state electronic structure theory. B. H.-P. would like to thank Frank Neese and Kantharuban Sivalingam for granting access to their internally contracted DDCI3+Q implementation prior to its public release. He is also indebted to Ute Becker for various reviews of the computer code and Kantharuban Sivalingam for invaluable comment on the manuscript. Finally, B. H.-P. gratefully acknowledges financial support from the Max Planck Society. Open Access funding provided by the Max Planck Society.
Notes and references
- H. Lischka, D. Nachtigallová, A. J. Aquino, P. G. Szalay, F. Plasser, F. B. C. Machado and M. Barbatti, Chem. Rev., 2018, 118, 7293–7361 CrossRef CAS PubMed.
- F. Neese, T. Petrenko, D. Ganyushin and G. Olbrich, Coord. Chem. Rev., 2007, 251, 288–327 CrossRef CAS.
- B. Levy and G. Berthier, Int. J. Quantum Chem., 1968, 2, 307–319 CrossRef.
- B. O. Roos, P. R. Taylor and P. E. Siegbahn, Chem. Phys., 1980, 48, 157–173 CrossRef CAS.
- S. R. White, Phys. Rev. Lett., 1992, 69, 2863–2866 CrossRef PubMed.
- S. R. White, Phys. Rev. B:Condens. Matter Mater. Phys., 1993, 48, 10345–10356 CrossRef CAS PubMed.
- G. K.-L. Chan and M. Head-Gordon, J. Chem. Phys., 2002, 116, 4462–4476 CrossRef CAS.
- O. Legeza, J. Röder and B. A. Hess, Phys. Rev. B:Condens. Matter Mater. Phys., 2003, 67, 125114 CrossRef.
- K. H. Marti and M. Reiher, Z. Phys. Chem., 2010, 224, 583 CrossRef CAS.
- Y. Kurashige and T. Yanai, J. Chem. Phys., 2009, 130, 234114 CrossRef PubMed.
- G. H. Booth, A. J. W. Thom and A. Alavi, J. Chem. Phys., 2009, 131, 054106 CrossRef PubMed.
- R. E. Thomas, Q. Sun, A. Alavi and G. H. Booth, J. Chem. Theory Comput., 2015, 11, 5316–5325 CrossRef CAS PubMed.
- N. M. Tubman, J. Lee, T. Y. Takeshita, M. Head-Gordon and K. B. Whaley, J. Chem. Phys., 2016, 145, 044112 CrossRef PubMed.
- B. Huron, J. P. Malrieu and P. Rancurel, J. Chem. Phys., 1973, 58, 5745–5759 CrossRef CAS.
- A. A. Holmes, N. M. Tubman and C. J. Umrigar, J. Chem. Theory Comput., 2016, 12, 3674–3680 CrossRef CAS PubMed.
- P. M. Zimmerman, J. Chem. Phys., 2017, 146, 224104 CrossRef PubMed.
- J. J. Eriksen, F. Lipparini and J. Gauss, J. Phys. Chem. Lett., 2017, 8, 4633–4639 CrossRef CAS PubMed.
- R. Chakraborty, P. Ghosh and D. Ghosh, Int. J. Quantum Chem., 2018, 118, e25509 CrossRef.
- V. G. Chilkuri and F. Neese, J. Comput. Chem., 2021, 42, 982–1005 CrossRef CAS PubMed.
- D. Ghosh, J. Hachmann, T. Yanai and G. K.-L. Chan, J. Chem. Phys., 2008, 128, 144117 CrossRef PubMed.
- G. Li Manni, S. D. Smart and A. Alavi, J. Chem. Theory Comput., 2016, 12, 1245–1258 CrossRef PubMed.
- Y. Ma, S. Knecht, S. Keller and M. Reiher, J. Chem. Theory Comput., 2017, 13, 2533–2549 CrossRef CAS PubMed.
- Q. Sun, J. Yang and G. K.-L. Chan, Chem. Phys. Lett., 2017, 683, 291–299 CrossRef CAS.
- J. Greiner, I. Gianni, T. Nottoli, F. Lipparini, J. J. Eriksen and J. Gauss, J. Chem. Theory Comput., 2024, 20, 4663–4675 CrossRef CAS PubMed.
- Z. Li, J. Li, N. S. Dattani, C. J. Umrigar and G. K.-L. Chan, J. Chem. Phys., 2019, 150, 024302 CrossRef PubMed.
- Z. Li, S. Guo, Q. Sun and G. K.-L. Chan, Nat. Chem., 2019, 11, 1026–1033 CrossRef CAS PubMed.
- H. Werner and P. J. Knowles, J. Chem. Phys., 1988, 89, 5803–5814 CrossRef CAS.
- M. Hanauer and A. Köhn, J. Chem. Phys., 2011, 134, 204111 CrossRef PubMed.
- F. A. Evangelista and J. Gauss, J. Chem. Phys., 2011, 134, 114102 CrossRef PubMed.
- F. A. Evangelista, J. Chem. Phys., 2014, 141, 054109 CrossRef PubMed.
- K. Andersson, P. Å. Malmqvist, B. O. Roos, A. J. Sadlej and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488 CrossRef CAS.
- K. Andersson, P.-Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226 CrossRef CAS.
- C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- F. Menezes, D. Kats and H.-J. Werner, J. Chem. Phys., 2016, 145, 124115 CrossRef PubMed.
- P. Celani and H.-J. Werner, J. Chem. Phys., 2003, 119, 5044–5057 CrossRef CAS.
- W. Györffy, T. Shiozaki, G. Knizia and H.-J. Werner, J. Chem. Phys., 2013, 138, 104104 CrossRef PubMed.
- J. W. Park, J. Chem. Theory Comput., 2019, 15, 5417–5425 CrossRef CAS PubMed.
- Y. Nishimoto, J. Chem. Phys., 2019, 151, 114103 CrossRef PubMed.
- J. W. Park, Phys. Chem. Chem. Phys., 2025, 27, 3531–3551 RSC.
- T. U. Helgaker, J. Almlöf, H. J. A. Jensen and P. Jørgensen, J. Chem. Phys., 1986, 84, 6266–6279 CrossRef CAS.
- A. Bernhardsson, R. Lindh, J. Olsen and M. Fulscher, Mol. Phys., 1999, 96, 617–628 CrossRef CAS.
- N. C. Handy and H. F. Schaefer, J. Chem. Phys., 1984, 81, 5031–5033 CrossRef CAS.
- T. Helgaker and P. Jørgensen, Theor. Chem. Acc., 1989, 75, 111–127 Search PubMed.
- E. Fromager, J. Toulouse and H. J. A. Jensen, J. Chem. Phys., 2007, 126, 074111 CrossRef PubMed.
- M. Scott, G. L. S. Rodrigues, X. Li and M. G. Delcey, J. Chem. Theory Comput., 2024, 20, 2423–2432 CrossRef CAS PubMed.
- G. Li Manni, R. K. Carlson, S. Luo, D. Ma, J. Olsen, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2014, 10, 3669–3680 CrossRef CAS PubMed.
- R. K. Carlson, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2015, 11, 4077–4085 CrossRef CAS PubMed.
- E. Fromager, S. Knecht and H. J. A. Jensen, J. Chem. Phys., 2013, 138, 084101 CrossRef PubMed.
- E. R. Kjellgren, E. D. Hedegård and H. J. A. Jensen, J. Chem. Phys., 2019, 151, 124113 CrossRef PubMed.
- J. Olsen and P. Jørgensen, J. Chem. Phys., 1985, 82, 3235–3264 CrossRef CAS.
- D. L. Yeager and P. Jørgensen, Chem. Phys. Lett., 1979, 65, 77–80 CrossRef CAS.
- P. Jørgensen, H. J. A. Jensen and J. Olsen, J. Chem. Phys., 1988, 89, 3654–3661 CrossRef.
- B. Helmich-Paris, J. Chem. Theory Comput., 2019, 15, 4170–4179 CrossRef CAS PubMed.
- J. T. Taylor, D. J. Tozer and B. F. E. Curchod, J. Chem. Phys., 2023, 159, 214115 CrossRef CAS PubMed.
- F. Spiegelmann and J. P. Malrieu, J. Phys. B: At., Mol. Opt. Phys., 1984, 17, 1235 CrossRef CAS.
- F. Spiegelmann and J. P. Malrieu, J. Phys. B: At., Mol. Opt. Phys., 1984, 17, 1259 CrossRef CAS.
- J. Finley, P.-Å. Malmqvist, B. O. Roos and L. Serrano-Andrés, Chem. Phys. Lett., 1998, 288, 299–306 CrossRef CAS.
- A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113 CrossRef PubMed.
- Y. A. Aoto and A. Köhn, J. Chem. Phys., 2016, 144, 074103 CrossRef PubMed.
- J. J. Bao, C. Zhou, Z. Varga, S. Kanchanakungwankul, L. Gagliardi and D. G. Truhlar, Faraday Discuss., 2020, 224, 348–372 RSC.
- J. J. Bao, C. Zhou and D. G. Truhlar, J. Chem. Theory Comput., 2020, 16, 7444–7452 CrossRef CAS PubMed.
-
J. K. Pedersen, PhD thesis, University of Southern Denmark, 2004.
- E. D. Hedegård, S. Knecht, J. S. Kielberg, H. J. A. Jensen and M. Reiher, J. Chem. Phys., 2015, 142, 224108 CrossRef PubMed.
-
H. Stoll and A. Savin, in Density Functionals for Correlation Energies of Atoms and Molecules, ed. R. M. Dreizler and J. da Providência, Springer US, Boston, MA, 1985, pp. 177–207 Search PubMed.
- T. Leininger, H. Stoll, H.-J. Werner and A. Savin, Chem. Phys. Lett., 1997, 275, 151–160 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 1372–1377 CrossRef CAS.
- E. Goll, H.-J. Werner and H. Stoll, Phys. Chem. Chem. Phys., 2005, 7, 3917–3923 RSC.
- E. Goll, M. Ernst, F. Moegle-Hofacker and H. Stoll, J. Chem. Phys., 2009, 130, 234112 CrossRef PubMed.
- F. Moscardó and E. San-Fabián, Phys. Rev. A:At., Mol., Opt. Phys., 1991, 44, 1549–1553 CrossRef PubMed.
- A. D. Becke, A. Savin and H. Stoll, Theor. Chim. Acta, 1995, 91, 147–156 CrossRef CAS.
- S. Gusarov, P.-Å. Malmqvist and R. Lindh, Mol. Phys., 2004, 102, 2207–2216 CrossRef CAS.
- M. Hapka, E. Pastorczak, A. Krzemińska and K. Pernal, J. Chem. Phys., 2020, 152, 094102 CrossRef CAS PubMed.
- E. D. Hedegård, J. Toulouse and H. J. A. Jensen, J. Chem. Phys., 2018, 148, 214103 CrossRef.
- W. Kutzelnigg and D. Mukherjee, J. Chem. Phys., 1997, 107, 432–449 CrossRef CAS.
- W. Kutzelnigg and D. Mukherjee, Chem. Phys. Lett., 2000, 317, 567–574 CrossRef CAS.
- O. V. Gritsenko, R. van Meer and K. Pernal, Phys. Rev. A, 2018, 98, 062510 CrossRef CAS.
- M. Hapka, K. Pernal and O. V. Gritsenko, J. Phys. Chem. Lett., 2020, 11, 5883–5889 CrossRef CAS PubMed.
- G. L. S. Rodrigues, M. Scott and M. G. Delcey, J. Phys. Chem. A, 2023, 127, 9381–9388 CrossRef CAS PubMed.
- G. L. Oliver and J. P. Perdew, Phys. Rev. A: At., Mol., Opt. Phys., 1979, 20, 397–403 CrossRef CAS.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS.
- S. Paziani, S. Moroni, P. Gori-Giorgi and G. B. Bachelet, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155111 CrossRef.
- E. Goll, H.-J. Werner, H. Stoll, T. Leininger, P. Gori-Giorgi and A. Savin, Chem. Phys., 2006, 329, 276–282 CrossRef CAS.
- A. Meurer, C. P. Smith, M. Paprocki, O. Čertík, S. B. Kirpichev, M. Rocklin, A. Kumar, S. Ivanov, J. K. Moore, S. Singh, T. Rathnayake, S. Vig, B. E. Granger, R. P. Muller, F. Bonazzi, H. Gupta, S. Vats, F. Johansson, F. Pedregosa, M. J. Curry, A. R. Terrel, V. Roučka, A. Saboo, I. Fernando, S. Kulal, R. Cimrman and A. Scopatz, PeerJ Comput. Sci., 2017, 3, e103 CrossRef.
- J. C. Slater, Phys. Rev., 1951, 81, 385–390 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- B. Helmich-Paris, J. Chem. Phys., 2021, 154, 164104 CrossRef CAS PubMed.
- B. Helmich-Paris, J. Chem. Phys., 2022, 156, 204104 CrossRef CAS PubMed.
- H. J. A. Jensen and P. Jørgensen, J. Chem. Phys., 1984, 80, 1204–1214 CrossRef CAS.
- H. J. A. Jensen and H. Ågren, Chem. Phys., 1986, 104, 229–250 CrossRef CAS.
- T. Nottoli, J. Gauss and F. Lipparini, J. Chem. Theory Comput., 2021, 17, 6819–6831 CrossRef CAS PubMed.
- F. Neese, J. Comput. Chem., 2022, 44, 381–396 CrossRef PubMed.
- R. Ahlrichs, Phys. Chem. Chem. Phys., 2006, 8, 3072–3077 RSC.
- B. Helmich-Paris, J. Chem. Phys., 2019, 150, 174121 CrossRef PubMed.
- F. K. Jørgensen, E. R. Kjellgren, H. J. A. Jensen and E. D. Hedegård, J. Chem. Phys., 2025, 162, 034104 CrossRef PubMed.
- M. R. Hennefarth, M. R. Hermes, D. G. Truhlar and L. Gagliardi, J. Chem. Theory Comput., 2023, 19, 3172–3183 CrossRef CAS PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108 CrossRef CAS PubMed.
- C. Kollmar, K. Sivalingam, B. Helmich-Paris, C. Angeli and F. Neese, J. Comput. Chem., 2019, 40, 1463–1470 CrossRef CAS PubMed.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2014, 4, 269–284 CAS.
- G. Li Manni, I. F. Galván, A. Alavi, F. Aleotti, F. Aquilante, J. Autschbach, D. Avagliano, A. Baiardi, J. J. Bao, S. Battaglia, L. Birnoschi, A. Blanco-González, S. I. Bokarev, R. Broer, R. Cacciari, P. B. Calio, R. K. Carlson, R. Carvalho Couto, L. Cerdán, L. F. Chibotaru, N. F. Chilton, J. R. Church, I. Conti, S. Coriani, J. Cuéllar-Zuquin, R. E. Daoud, N. Dattani, P. Decleva, C. de Graaf, M. G. Delcey, L. De Vico, W. Dobrautz, S. S. Dong, R. Feng, N. Ferré, M. Filatov(Gulak), L. Gagliardi, M. Garavelli, L. González, Y. Guan, M. Guo, M. R. Hennefarth, M. R. Hermes, C. E. Hoyer, M. Huix-Rotllant, V. K. Jaiswal, A. Kaiser, D. S. Kaliakin, M. Khamesian, D. S. King, V. Kochetov, M. Krośnicki, A. A. Kumaar, E. D. Larsson, S. Lehtola, M.-B. Lepetit, H. Lischka, P. López Ríos, M. Lundberg, D. Ma, S. Mai, P. Marquetand, I. C. D. Merritt, F. Montorsi, M. Mörchen, A. Nenov, V. H. A. Nguyen, Y. Nishimoto, M. S. Oakley, M. Olivucci, M. Oppel, D. Padula, R. Pandharkar, Q. M. Phung, F. Plasser, G. Raggi, E. Rebolini, M. Reiher, I. Rivalta, D. Roca-Sanjuán, T. Romig, A. A. Safari, A. Sánchez-Mansilla, A. M. Sand, I. Schapiro, T. R. Scott, J. Segarra-Martí, F. Segatta, D.-C. Sergentu, P. Sharma, R. Shepard, Y. Shu, J. K. Staab, T. P. Straatsma, L. K. Sørensen, B. N. C. Tenorio, D. G. Truhlar, L. Ungur, M. Vacher, V. Veryazov, T. A. Voß, O. Weser, D. Wu, X. Yang, D. Yarkony, C. Zhou, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2023, 19, 6933–6991 CrossRef CAS PubMed.
- K. Sivalingam, M. Krupicka, A. A. Auer and F. Neese, J. Chem. Phys., 2016, 145, 054104 CrossRef PubMed.
- M. Krupička, K. Sivalingam, L. Huntington, A. A. Auer and F. Neese, J. Comput. Chem., 2017, 38, 1853–1868 CrossRef PubMed.
- M. H. Lechner, A. Papadopoulos, K. Sivalingam, A. A. Auer, A. Koslowski, U. Becker, F. Wennmohs and F. Neese, Phys. Chem. Chem. Phys., 2024, 26, 15205–15220 RSC.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 024106 CrossRef PubMed.
- B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109 CrossRef CAS.
- M. Schreiber, M. R. Silva-Junior, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 128, 134110 CrossRef PubMed.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- A. J. H. Wachters, J. Chem. Phys., 1970, 52, 1033–1036 CrossRef CAS.
- A. J. Merer and R. S. Mulliken, Chem. Rev., 1969, 69, 639–656 CrossRef CAS.
- U. Kaldor and I. Shavitt, J. Chem. Phys., 1968, 48, 191–203 CrossRef CAS.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009–4037 CrossRef CAS PubMed.
- D. Kánnár and P. G. Szalay, J. Mol. Model., 2014, 20, 2503 CrossRef PubMed.
- D. Kánnár and P. G. Szalay, J. Chem. Theory Comput., 2014, 10, 3757–3765 CrossRef.
- O. Christiansen, H. Koch and P. Jørgensen, J. Chem. Phys., 1995, 103, 7429–7441 CrossRef CAS.
- P.-F. Loos, A. Scemama, A. Blondel, Y. Garniron, M. Caffarel and D. Jacquemin, J. Chem. Theory Comput., 2018, 14, 4360–4379 CrossRef CAS PubMed.
- A. Köhn and A. Bargholz, J. Chem. Phys., 2019, 151, 041106 CrossRef.
- P. Zielinski, J. A. Black and A. Köhn, J. Chem. Theory Comput., 2023, 19(23), 8671–8688 CrossRef CAS PubMed.
- O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154–5161 CrossRef.
- M. R. Silva-Junior, M. Schreiber, S. P. A. Sauer and W. Thiel, J. Chem. Phys., 2008, 129, 104103 CrossRef PubMed.
- M. Hubert, E. D. Hedegård and H. J. A. Jensen, J. Chem. Theory Comput., 2016, 12, 2203–2213 CrossRef CAS PubMed.
- I. Schapiro, K. Sivalingam and F. Neese, J. Chem. Theory Comput., 2013, 9, 3567–3580 CrossRef CAS PubMed.
- V. García, O. Castell, R. Caballol and J. Malrieu, Chem. Phys. Lett., 1995, 238, 222–229 CrossRef.
- S. R. Langhoff and E. R. Davidson, Int. J. Quantum Chem., 1974, 8, 61–72 CrossRef CAS.
- F. Neese, J. Comput. Chem., 2003, 24, 1740–1747 CrossRef CAS PubMed.
- F. Neese, P. Colinet, B. DeSouza, B. Helmich-Paris, F. Wennmohs and U. Becker, J. Phys. Chem. A, 2025, 129(10), 2618–2637 CrossRef CAS PubMed.
- F. Neese, F. Wennmohs, A. Hansen and U. Becker, Chem. Phys., 2009, 356, 98–109 CrossRef CAS.
- R. Izsák and F. Neese, J. Chem. Phys., 2011, 135, 144105 CrossRef PubMed.
- J. Olsen, D. L. Yeager and P. Jørgensen, J. Chem. Phys., 1989, 91, 381–388 CrossRef CAS.
- M. Böckmann, M. Klessinger and M. C. Zerner, J. Phys. Chem., 1996, 100, 10570–10579 CrossRef.
- R. F. K. Spada, M. P. Franco, R. Nieman, A. J. A. Aquino, R. Shepard, F. Plasser and H. Lischka, Mol. Phys., 2022, 0, e2091049 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: For Thiel's benchmark set, we provide information on active-space sizes and number of roots, data on singlet excitation energies including histogram plots for the LDA and PBE0 functionals. See DOI: https://doi.org/10.1039/d5cp00881f |
|
| This journal is © the Owner Societies 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Erik Rosendahl
Kjellgren
b and
Hans Jørgen Aa.
Jensen
*a,
Erik Rosendahl
Kjellgren
b and
Hans Jørgen Aa.
Jensen
 b
b
![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N6) for the CC singles and doubles model, the prefactor of state-of-the-art MRCC implementations is enormous due to the huge increase in the number of CC equations to be solved for multi-reference rather than the single-reference case. Even to date, MRCC calculations are usually only performed by specialists using their own implementations.
(N6) for the CC singles and doubles model, the prefactor of state-of-the-art MRCC implementations is enormous due to the huge increase in the number of CC equations to be solved for multi-reference rather than the single-reference case. Even to date, MRCC calculations are usually only performed by specialists using their own implementations.
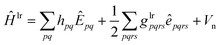



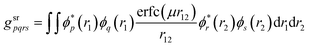
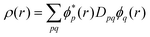
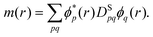
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) pq|0〉
pq|0〉![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) pq = â†pαâqα − â†pβâqβ.
pq = â†pαâqα − â†pβâqβ.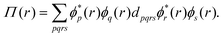




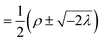



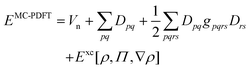

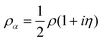





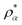 , as well as their corresponding density derivatives, enter Ec in the same manner. Thus, the final correlation energy must be real assuming that Ec is composed of entire functions.
, as well as their corresponding density derivatives, enter Ec in the same manner. Thus, the final correlation energy must be real assuming that Ec is composed of entire functions.

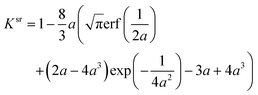





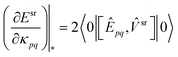















![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) pq = −〈0|Êpq|S〉 − 〈S|Êpq|0〉
pq = −〈0|Êpq|S〉 − 〈S|Êpq|0〉


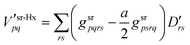

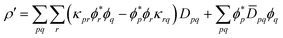














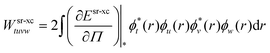





![[scr O, script letter O]](https://www.rsc.org/images/entities/char_e52e.gif) (N5) scaling with system size N.
(N5) scaling with system size N.





![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) tu are required.134–136
tu are required.134–136



