Origins of crystallisation-induced dual emission of terephthalic and isophthalic acid crystals

Abstract

Metal-free organic crystals with room-temperature phosphorescence (RTP) present an innovative alternative to conventional inorganic materials for optoelectronic applications and sensing. Recently, substantial attention has been directed towards the design of new phosphorescent crystals through crystal engineering and functionalisation. In this paper, we investigate the excited-state deactivation mechanisms of two simple organic molecules: terephthalic acid (TPA) and isophthalic acid (IPA) using embedding models based on multiconfigurational MS-CASPT2 calculations. These molecules exhibit prompt and delayed fluorescence and RTP in the solid state. We explore intramolecular internal conversion pathways using high-level quantum chemistry methods in both solution and crystalline phases. We analyse deactivation mechanisms involving singlet and triplet states, quantifying direct and reverse intersystem crossing rates from the lowest triplet states, as well as fluorescence and phosphorescence rates. Additionally, our study examines singlet exciton transport in single crystals of TPA and IPA. Our findings clarify the mechanisms underlying the prompt and delayed fluorescence and RTP of crystalline TPA and IPA, revealing distinct differences in their deactivation processes. Notably, we explain the enhanced fluorescence and phosphorescence in IPA compared to TPA, emphasising how the positioning of the carboxylic group influences electronic delocalisation in excited states, (de)stabilising delocalised ππ* states along the reaction coordinate, thereby significantly impacting deactivation mechanisms.

---

1 Introduction

Room-temperature phosphorescence (RTP) has generated significant interest among experimental and computational scientists due to its wide range of applications, including its use in highly emissive materials for organic light-emitting diodes (OLEDs), anti-counterfeiting, photovoltaic devices, and bioimaging.¹ Since efficient phosphorescence requires a substantial triplet population, these materials have traditionally been designed using inorganic and organometallic compounds that promote intersystem crossing (ISC) via strong spin–orbit coupling (SOC) and charge-transfer mechanisms. In contrast, organic molecules, due to their relatively small triplet populations and competing nonradiative pathways, typically exhibit phosphorescence only at cryogenic temperatures and under inert conditions in solution. However, recently RTP has been achieved in several purely organic crystals composed of molecules with relatively simple structures. These organic materials are significantly more cost-effective and environmentally friendly than their inorganic and organometallic counterparts.

Efficient triplet formation can be achieved in RTP organic crystals in compounds where the presence of heteroatoms facilitates intersystem crossing rates between relevant singlet and triplet states.² A second requirement for organic RTP is to establish a restrictive crystalline environment that suppresses large-amplitude molecular vibrations and reduces the rate of internal conversion to the ground state via conical intersections³ or vibrational wavefunction overlaps.⁴ Depending on the energy gaps and SOCs, RTP can compete with both prompt fluorescence (PF) and delayed fluorescence (DF).⁵ DF can occur through reverse intersystem crossing (rISC), which is crucial in thermally activated delayed fluorescence (TADF) chromophores.⁶

Two of the simplest organic crystals exhibiting RTP are the two isomers of benzenedicarboxylic acid in the crystalline phase: terephthalic acid (TPA) and isophthalic acid (IPA).^7,8 These isomers differ in the relative positions of their substituents (Fig. 1). Transient photoluminescence spectroscopy of TPA and IPA in ethanol solution and disordered amorphous states reveals negligible luminescence quantum yields (below 0.6%). Upon crystallisation, both crystals exhibit dual emission, attributed to fluorescence and phosphorescence. The TPA crystal shows prompt deep blue emission at 388 nm with a lifetime of 〈t〉 = 0.53 ns and an emission efficiency of 8.4%. Additionally, a delayed fluorescence (DF) peak at 392 nm (slightly red-shifted compared to the prompt emission) and a shoulder at 511 nm, attributed to weak RTP, are observed. The experimental RTP lifetime is not determined on the millisecond timescale, suggesting longer lifetimes. The IPA crystal exhibits more efficient crystallisation-induced emission at 380 nm, with a quantum yield of 15.3%, attributed to prompt fluorescence. In addition to fluorescence, a long green afterglow lasting several seconds was observed, with distinct emission peaks at 384 nm and 506 nm, corresponding to DF and RTP, respectively. The measured lifetimes of prompt fluorescence, DF, and RTP in IPA are 1.81 ns, 9.6 ms, and 290 ms, respectively.⁷

Fig. 1 Structures of IPA and TPA molecules (upper panel). The crystal structures of of IPA and TPA crystals, with designated unit cells, are represented in two different perspectives in the bottom panels.

Previous studies have investigated the mechanisms of fluorescence and phosphorescence in TPA and IPA.^7,9 Shuai et al. found the crystalline phase induces a change of ordering of the lowest-lying singlet and triplet states of IPA and TPA in comparison with the vacuum where the S₁ state is a nπ*, the higher ππ* state becomes the lowest according to the CASSCF(8,8)/CASPT2/AMBER level of theory. This change induces higher luminescence yields and larger intersystem crossing rates in the crystal.⁹ Gong et al. performed a similar optimisation of TPA and IPA in both the vacuum and crystalline phases based on QM/MM (TD-M06-2x/UFF) computations. They found that the energy gap between the closest-lying S₁ and T₂ states decreases while the spin–orbit coupling simultaneously increases in the crystal compared to the vacuum, leading to higher populations of the triplet state in the crystalline environment.⁷ Here, we evaluate the impact of using different levels of theory on predicting the ordering of states and consider the competition between various radiative and nonradiative mechanisms.

While some aspects of the luminescence of TPA and IPA have been explored both experimentally and computationally, the precise mechanisms of excited state relaxation in solution and the crystalline phase have yet to be fully understood. There are still many open questions about the competition between different nonradiative and radiative decay pathways and the origin of DF. Our study aims to fill this gap by systematically investigating the molecule-centred excited state relaxation pathways using high-level computational methods. In addition to these pathways, we also analyse the dimer-centred mechanisms and exciton transport mechanisms in both crystal environments. Our calculations provide critical insights into the excited state relaxation mechanisms of TPA and IPA, enhancing the current understanding of their behaviour in solution and crystalline phases.

2 Computational details

We evaluated the performance of several methods for predicting excited states in IPA and TPA across vacuum, solution, and crystal environments. First, we optimised the ground states using the DFT method with B3LYP, PBE0, and ωB97XD functionals, and then computed the vertical excitations of the first five singlet and triplet states with the time-dependent DFT (TD-DFT) method^10–14 at the corresponding ground state minima. We also explored the resolution of identity coupled cluster method to the second order (RI-CC2)^15–18 and the multi-state complete active space second-order perturbation theory^19–21 ((MS-)CASPT2/CASSCF(14,11)) with the aug-cc-pVDZ basis set for describing the lowest-lying singlet and triplet states. For the RI-CC2 calculations, the ground state geometries were optimised at the CC2 level of theory, while for the CASPT2 computations, the ωB97XD/aug-cc-pVDZ ground state geometries were used. Solvent effects were considered by applying the polarisable continuum model (PCM) in the (TD-)DFT and CASPT2/CASSCF calculations, while the conductor-like screening model (COSMO) was used in the RI-CC2 computations. Ethanol was chosen as the solvent to facilitate comparison with available experimental results (dielectric permittivity ε_r = 24.55).

The performance of the excited state methods for the prediction of vertical excitations in the crystal environment was evaluated using QM/MM techniques. To represent the crystal environment, we first refined the experimental crystal structures of TPA and IPA (retrieved from the Cambridge Crystallographic Database, with CCDC codes 1269122 for TPA²² and 1108748 for IPA²³) by performing periodic boundary condition DFT calculations as implemented in Quantum Espresso.²⁴ The PBE-D2 functional, including a dispersion correction, was employed with a plane-wave cutoff of 30 Ry and a Monkhorst–Pack k-point grid of (1 × 2 × 1), chosen based on the unit cell shape. The projector augmented wave (PAW) pseudopotential was used to model the nuclei and core electrons, while the valence electrons were treated explicitly.^25,26 The optimisations were carried out by relaxing the structure within the unit cell while keeping the cell dimensions fixed at their experimental values. Clusters consisting of 123 TPA and 120 IPA molecules (2214 and 2160 atoms, respectively) were extracted from the optimised supercells. The QM/MM simulations included one or two central molecules in the QM region, with the surrounding molecules treated using MM. The QM region was relaxed, while the MM region remained fixed at its optimised lattice positions. For TD-DFT optimisations in the solid state, the ONIOM(QM:MM)method^27,28 was applied, with the QM region treated at the (TD-)ωB97XD/6-311G(d,p) level of theory. For MS-CASPT2/CASSCF(14,11)/aug-cc-pVDZ calculations in the solid state, the QM/MM simulations were performed using the Molcas code for the electrostatic embedding QM calculations and the Tinker code for the MM part considering CM5 point charges. In the (TD-)DFT calculations, the MM region was described using the OPLS-AA force field, with ESP and CM5 charges derived from HF/3-21G calculations on a single molecule. The RI-CC2/aug-cc-pVDZ calculations were done only using electrostatic embedding with CM5 charges. While the calculations with TDDFT and CC2 methods were done using the geometries optimised with the same method, MS-CASPT2 calculations considered the ωB97XD/6-311G(d,p) ground-state structures. All (TD-)DFT computations were performed with the Gaussian 16 program,²⁹ CASSCF and CASPT2 computations with the Molcas code,³⁰ and RI-CC2 computations were performed with the Turbomole v7.0 code.³¹

To investigate the excited state relaxation mechanisms in solution and crystal phase, we optimised the excited states minima (S₁, T₁, T₂) and S₁–S₀ and T₁–S₀ minimum energy crossing points in both environments. The excited states (S₁, T₁, and T₂) were optimised at the CASSCF(14,11)/aug-cc-pVDZ level of theory because the TD-ωB97XD/6-311G(d,p) does not not predict correctly the types and ordering of all excited states of TPA and IPA. The S₁–S₀ minimum energy conical intersections (MECIs) optimisations were first carried out in solution and crystal phase at the SA-2-CASSCF(14,11)/6-31G(d) level of theory, using the branching plane update method³² as implemented in Molcas code. The obtained S₁–S₀ MECI geometries are reoptimised at the extended multistate CASPT2 level (XMS-CASPT2).^33,34 The minimum energy crossing point between the ground and T₁ states was optimised based on T₁ states optimisation and S₀–T₁ energy gap criterion. In the solid state, the optimisations were done at the QM/MM level as described above.³⁰ The active spaces comprised of twelve π orbitals and 2p-orbitals of carboxyl group oxygen atoms for IPA and TPA (Fig. S1, ESI†), were used in all optimisations and single point computations. The single-point CASPT2 computations were based on configuration state functions obtained at the SA-6-CASSCF(14,11)/aug-cc-pVDZ level.³⁵ They were done without an IPEA shift and applying an imaginary shift of 0.1 a.u., which improves the convergence in the case of possible intruder states.³⁶

Linearly interpolated pathways (LIIC) between S₀ and S₁–S₀ MECI geometries in the solution and crystal were created and six lowest-lying singlet and triplet excited states were computed at the MS-6-CASPT2/CASSCF(14,11)/aug-cc-pVDZ level at the obtained geometries. The spin–orbit couplings (SOCs) between relevant singlet and triplet states were computed at the excited states minima in solution and crystal and along the LIIC pathway in the crystal, as implemented in the Molcas code. The method relies on the computation of matrix elements of one-electron spin–orbit part of the Hamiltonian in the atomic mean field approximation^37,38 in the basis of the CASSCF wave functions. The SOCs between singlet and triplet pairs are obtained from the computed components corresponding to transitions between a singlet and three spin triplet components defined with quantum numbers m_l ∈ {−1, 0, 1} as .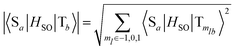

Furthermore, to examine the effect of hyperfine interactions between singlet and triplet states on the excited-state deactivation mechanisms (in particular on the reverse intersystem crossing), we computed the hyperfine Hamiltonian matrix between excited states,³⁹ as implemented in the Q-Chem program package.⁴⁰ The matrix elements of the complete hyperfine Hamiltonian, including spin–spin dipole, Fermi contact, and orbital response term are evaluated in the basis of the TD-DFT excited states.³⁹ The excited-states were computed with the ωB97XD functional and aug-cc-pVDZ basis set.

To investigate the dimer-centred relaxation mechanisms in the crystal phase, we optimised the S₀ and S₁ geometries of the dimers with the shortest centroid distances (π–π stacked dimers) applying the QM/QM′ approach as implemented in the fromage code.^41,42 The QM (dimer) is represented by the algebraic diagrammatic construction ADC(2)^43,44/aug-cc-pVDZ method and QM′ (environment) region was simulated at the second order (SCC-)DFTB method, employing the mio-1-1 set of Slater–Koster parameters parametrised for the tight-binding SCC-DFTB Hamiltonian.^45,46 For the point charges in the environment, we used the ESP charges obtained at ωB97XD/6-31G(d) and PBE/6-31G(d) levels of theory, respectively. The DFTB calculations were performed with the DFTB+ program,⁴⁵ and the ADC(2) computations with the Turbomole program. The lowest lying singlet and triplet states of the optimised dimers were computed at the ADC(2)/aug-cc-pVDZ level of theory.

We estimated the fluorescence and phosphorescence rates in vacuum and crystal applying Fermi's golden rule for the transition between initial (i) and final state (f) states:

where ΔE is the vertical energy difference between states, ε₀ is the vacuum permittivity, ħ is reduced Planck constant, c is the speed of light in vacuum, η is the refractive index of the medium (1.51 for TPA) and [small mu, Greek, circumflex] is the electric transition dipole moment operator. The expectation values of this operator are computed between eigenstates of the Hamiltonian including the spin–orbit term as implemented in Molcas, allowing to estimate the transition dipole moments between the ground state and singlet and triplet excited states.

The rates of the nonradiative electron transport (ET) processes (ISC, rISC and exciton transport) are estimated applying the Marcus semiclassical theory in the Condon approximations as

where T is the absolute temperature, k_B is the Boltzmann constant, λ is the reorganisation energy and ΔG⁰ is the change of the adiabatic Gibbs free energy during the ET process. H_ab is the electronic coupling term between the diabatic states involved in the process. The term represents the vibrational density of states in the final state at the geometry of the initial state weighted by Franck–Condon factors in the limit of high temperatures.⁴⁷

The reorganisation energy for (r)ISC was computed as λ_ab ≈ E_Tb(R_minSa) − E_Tb(R_minTb) for the ISC and λ_ab ≈ E_Sb(R_minTa) − E_Sb(R_minSb) for rISC (for clarification, for example E_Tb(R_minSa) is the energy of the T_b state evaluated at the minimum of the S_a state). The H_ab couplings correspond to the SOCs computed as described above. For the energy difference between the states (ΔE_ab) we used the difference between the energies of adiabatic states at the geometry at which the rates are computed (ΔE_ab = ΔE^ad_ab). The estimation of (r)ISC rates is done based on the MS-6-CASPT2/CASSCF(14,11)/aug-cc-pVDZ energies and CASSCF(14,11)/aug-cc-pVDZ spin–orbit couplings. We note that the energy gaps between singlet and triplet states correlate with the exchange interaction between those states, i.e. stronger exchange correlation induces larger gaps (ESI,† Section S2), and decreases the intersystem crossing rate. For this reason, an adequate treatment of electronic correlation using a high-level multiconfigurational methods, like CASPT2, is often necessary for the reliable prediction of ΔE_ST and consequently of the ISC rates.

In the case of exciton transport, the ΔE^ad_ab = 0 as the exciton hopping occurs between donor and acceptor molecules with identical geometries. The intramolecular reorganisation energy induced by the exciton transfer (λ_ab) is computed considering one molecule (M₁) going from the fully relaxed ground state S₀ to the electronically excited state S₁ and a neighboring molecule (M₂) evolving in the opposite way as

The exciton couplings (H_ab = J_ab) mediate the exciton transport process between the diabatic states (eqn (2)). The exciton transport rates are computed for the dimers with the centroid distances smaller than 10 Å, isolated from the optimised crystal structures. The J_ab of isolated dimers were computed applying a diabatisation method based on the transition dipole moments of S₁ states of isolated molecules and S₁ and S₂ states of dimers,⁴⁸ as implemented in the fromage code.⁴¹ This method takes into account the short-range (exchange, orbital overlap, charge-transfer) and long-range Coulomb interactions. Both reorganisation energies for the exciton transport and exciton couplings are computed based on the TD-ωB97XD/6-311+G(d,p) excited states.

3 Results and discussion

3.1 Light absorption and emission

3.1.1 Vacuum and solution. The performance of several single-reference and multi-reference methods for the description of TPA and IPA excited states in vacuum, ethanol solution, and crystal phase is examined. The five lowest-lying singlet and triplet states of both molecules are computed by applying the TDDFT (with B3LYP, PBE0, and ωB97XD functionals), RI-CC2, and MS-CASPT2 methods at the ground state geometries optimised at the same level of theory. The excitation energies, oscillator strengths and types of states in vacuum/solution and crystal phase are given in Tables 1 and 2, the reported characters correspond to the MS-CASPT2 excited states. The excitations computed at other levels of theory were reordered to match the MS-CASPT2 excited states. In a few cases, the natures of the highest-lying excitations computed with the TD-DFT and RI-CC2 methods differ from the MS-CASPT2 ones, as highlighted in the comments in Tables 1 and 2. The transition densities are shown in the ESI† (Section S3).

Table 1 Vertical excitation energies (eV) and oscillator strengths (in parentheses) of the first five singlet and triplet states of TPA and IPA molecules in vacuum computed at several levels of theory. The 6-311+G(d,p) basis set was used in all DFT calculations, whereas the aug-cc-pVDZ set was used in RI-CC2 and CASPT2(14,11) computations

	B3LYP	PBE0	ωB97XD	ωB97XD/PCM	RI-CC2/COSMO	CASPT2/PCM	Exp.
a S5 states of IPA are predicted as nπ* at the B3LYP and PBE0 level. b T3–T5 states of TPA have different order at the B3LYP and PBE0 level. c Experimental excitation energies taken from ref. 7.
TPA
S1 (ππ*)	4.52 (0.02)	4.67 (0.03)	4.84 (0.04)	4.98 (0.03)	4.56 (0.02)	4.02 (0.04)
S2 (nπ*)	4.51 (0.00)	4.67 (0.00)	5.06 (0.00)	5.30 (0.00)	4.76 (0.00)	4.80 (0.00)
S3 (nπ*)	4.57 (0.00)	4.73 (0.00)	5.11 (0.00)	5.32 (0.00)	4.80 (0.00)	4.88 (0.00)
S4 (ππ*)	5.02 (0.43)	5.16 (0.43)	5.33 (0.41)	5.52 (0.12)	5.39 (0.55)	4.92 (0.44)	5.17^c
S5 (ππ*)	6.20 (0.00)	6.44 (0.00)	6.72 (0.15)	6.01 (0.84)	6.71 (0.14)	6.16 (0.08)	6.20^c
T1 (ππ*)	3.26	3.18	3.33	3.44	3.73	3.36
T2 (ππ*)	3.68	3.75	3.94	4.20	4.24	3.97
T3 (ππ*)^b	4.46	4.46	4.62	4.48	4.78	4.07
T4 (nπ*)^b	4.17	4.27	4.65	4.89	5.63	4.69
T5 (nπ*)^b	4.23	4.33	4.70	4.90	5.82	4.76
IPA
S1 (ππ*)	4.72 (0.02)	4.87 (0.02)	5.01 (0.02)	4.79 (0.05)	4.68 (0.01)	3.94 (0.005)
S2 (nπ*)	4.77 (0.00)	4.91 (0.00)	5.21 (0.00)	5.12 (0.00)	4.92 (0.00)	4.60 (0.00)
S3 (nπ*)	4.80 (0.00)	4.94 (0.00)	5.23 (0.00)	5.18 (0.00)	4.94 (0.00)	4.61 (0.00)
S4 (ππ*)	5.32 (0.09)	5.46 (0.09)	5.60 (0.09)	5.24 (0.50)	5.70 (0.12)	5.20 (0.09)
S5 (ππ*)	5.48^a (0.00)	5.76^a (0.00)	6.20 (0.75)	6.74 (0.00)	6.12 (0.84)	5.34 (0.82)	5.39^c
T1 (ππ*)	3.40	3.29	3.43	3.33	3.88	3.06
T2 (ππ*)	3.99	4.05	4.22	3.91	4.45	3.64
T3 (ππ*)	4.22	4.28	4.50	4.62	4.61	4.04
T4 (nπ*)	4.39	4.47	4.78	4.72	4.68	4.33
T5 (nπ*)	4.41	4.50	4.80	4.78	5.41	4.37

---

Table 2 Vertical excitation energies (eV) and oscillator strengths (in parentheses) of the first five singlet and triplet states of TPA and IPA molecules in crystal computed at several levels of theory. The 6-311+G(d,p) basis set is used in all DFT computations, whereas the aug-cc-pVDZ set is used in RI-CC2 and CASPT2(14,11) computations. the TD-ωB97XD results with the 6-31G(d) basis set are designated by asterix

	ωB97XD*	ωB97XD(CM5)	ωB97XD(ESP)	RI-CC2	CASPT2	Exp.
a S4 and S states of IPA show less nπ*/ππ* mixing according to the ωB97XD and RI-CC2 results, compared to the CASPT2 ones. They are predicted as ππ* at the ωB97XD level, and as nπ* and ππ* at the RI-CC2 level. b S5 states of both IPA and TPA are predicted as nπ* at the RI-CC2 level. c Photon energies used in the photoexcitation spectra for TPA and IPA crystals as reported in ref. 8.
TPA
S1 (ππ*)	4.82 (0.04)	4.72 (0.04)	4.69 (0.04)	4.68 (0.03)	3.97 (0.08)	3.90^c
S2 (nπ*)	5.35 (0.37)	5.23 (0.42)	5.23 (0.42)	5.39 (0.00)	4.74 (0.29)
S3 (nπ*)	5.45 (0.00)	5.46 (0.00)	5.55 (0.00)	5.41 (0.12)	4.80 (0.00)
S4 (ππ*)	5.49 (0.04)	5.50 (0.01)	5.59 (0.01)	5.53 (0.42)	4.83 (0.07)
S5 (ππ*)	6.79 (0.00)	6.68 (0.00)	6.64 (0.00)	7.02^b (0.00)	6.14 (0.38)
T1 (ππ*)	3.31	3.29	3.30	3.88	3.23
T2 (ππ*)	3.86	3.81	3.77	4.32	3.75
T3 (ππ*)	4.67	4.63	4.61	6.01	4.49
T4 (nπ*)	5.04	5.07	5.17	4.95	4.75
T5 (nπ*)	5.06	5.09	5.19	5.44	4.79
IPA
S1 (ππ*)	5.08 (0.02)	4.98 (0.02)	4.96 (0.02)	3.69 (0.00)	3.93 (0.10)	4.00^c
S2 (nπ*)	5.56 (0.00)	5.53 (0.06)	5.52 (0.07)	4.13 (0.00)	4.57 (0.00)
S3 (ππ*)	5.72 (0.08)	5.56 (0.08)	5.56 (0.01)	4.17 (0.00)	5.26 (0.00)
S4 (ππ*/nπ*)	5.60^a (0.01)	5.61^a (0.02)	5.74 (0.01)	4.54 (0.00)	5.72 (0.18)
S5 (ππ*/nπ*)	6.31^a (0.71)	6.10^a (0.73)	6.08 (0.71)	4.66^b (0.02)	5.97 (0.00)
T1 (ππ*)	3.46	3.43	3.44	3.68	3.29
T2 (ππ*)	4.27	4.19	4.20	4.00	3.85
T3 (ππ*)	4.54	4.47	4.46	4.08	3.96
T4 (nπ*)	4.99	4.89	4.88	4.15	4.47
T5 (nπ*)	5.13	5.14	5.26	4.36	5.11

---

We first compare the performance of three functionals, B3LYP, PBE0, and ωB97XD, for the prediction of excited states in vacuum. The bright S₄ state energies in vacuum computed applying these functionals deviate from each other by less than 0.3 eV in both molecules, whereas the energies of other states are predicted to be higher at the TD-ωB97XD level. The calculations with TD-ωB97XD show that, when using the PCM model for ethanol, the energies are shifted by approximately 0.1–0.3 eV, except for the highest singlet state considered (S₅), where the shift exceeds 0.5 eV. In Table 1, the vertical excitations obtained with RI-CC2 and MS-CASPT2 were calculated considering ethanol as the solvent, using the COSMO and PCM approaches, respectively. Comparing the excited state energies in the solution, we notice that the MS-CASPT2 S₁ ππ* state has ∼1 eV and 0.6 eV lower energy compared to the TD-ωB97XD and RI-CC2 energies, respectively. The dark nπ* states (S₂ and S₃) energies are overestimated for ∼0.5 eV at the TD-ωB97XD level, whereas the RI-CC2 predicts their excitation energies closer to the MS-CASPT2 values.

The experimental absorption spectra in ethanol of TPA and IPA featured two bands,⁷ at 200 nm (6.20 eV) and 240 nm (5.17 eV) for TPA and at 210 nm (5.90 eV) and 230 nm (5.39 eV) for IPA. In the case of TPA, the MS-CASPT2/PCM reproduces well the first and second bright excitations at 4.92 eV and 6.16 eV. The TD-ωB97XD/PCM and RI-CC2/COSMO methods overestimate the energies of the bright singlet states and triplet excitations. The MS-CASPT2/PCM method reproduces well the first two bright excitations, the computed vertical excitation energies of bright S₄ and S₅ states are 5.20 eV and 5.34 eV in IPA, assignable to the first peak in the absorption spectrum with the maximum at 5.39 eV. The higher bright states contributing to the second absorption peak at 5.90 eV are not among the first five singlet states. These values are in very good agreement with the positions of the peak maxima (5.39 eV and 5.90 eV).

3.1.2 Crystalline phase. Table 2 presents the excitation energies obtained in the solid state. To assess the impact of using different point charges in the electrostatic embedding with the TD-ωB97XD method, we performed calculations with both CM5 and ESP charges. The energy differences in all cases were smaller than or around 0.1 eV. Given this minor effect, the CASPT2 and CC2 calculations were conducted using only CM5 charges. As observed in solution (Table 1), the absorption energies of singlet states calculated with TD-ωB97XD and RI-CC2 in the crystal significantly deviate from those obtained with MS-CASPT2. For both TPA and IPA, TD-ωB97XD tends to overestimate the singlet energies. In contrast, RI-CC2 overestimates the singlet energies for TPA and underestimates them for IPA. However, the TD-ωB97XD and RI-CC2 energies for the low-lying triplet states are in relatively good agreement with the values from MS-CASPT2.

Table 3 shows the emission energies obtained after relaxation in S₁. While the MS-CASPT2 emission energies are close to the experimental emission maxima, deviating by only 0.3–0.4 eV, the TD-ωB97XD energies are overestimated by more than 1 eV. In contrast to the results reported by Ma et al., we do not observe a change in the S₁ state type from ππ* to nπ* upon crystallisation in the Franck–Condon region.⁹ According to our CASPT2 results, the S₁ states of TPA and IPA in vacuum, solution, and crystal phases possess ππ* character, while the higher S₂ and S₃ states exhibit nπ* character. However, we found that the nπ* state becomes the lowest-lying state along the internal conversion coordinate, as will be discussed below (Section 3.2). These differences from previous works are attributed to the different active spaces employed. Our CASSCF/CASPT2 simulations considered a [14,11] active space (9π and 2n orbitals), while the smaller[8,8] active space used in the work by Ma et al. comprised 6π and 2n orbitals. This suggests that including a larger number of π orbitals in the active space enabled the identification of a lower eigenvalue of the Hamiltonian, corresponding to the ππ* state, whereas the energies of two quasi-degenerate nπ* states are predicted to be very close at both levels of theory (approximately 4.8 eV, ref. 9 and Table 2).

Table 3 Emission energies (eV) of the lowest-lying singlet state (S₁) in TPA and IPA molecules in crystal computed at the TD-ωB97XD/6-311+G(d,p) and CASPT2(14,11)/aug-cc-pVDZ levels of theory. Oscillator strengths are given in parentheses

	ωB97XD(CM5)	ωB97XD(ESP)	CASPT2	Exp.
a Experimental emission energies taken from the ref. 7. b Experimental emission energies taken from the ref. 8.
TPA
S1 (ππ*)	4.40 (0.06)	4.28 (0.05)	3.61 (0.08)	3.20^a, 3.6^b
IPA
S1 (ππ*)	4.70 (0.03)	4.68 (0.03)	2.96 (0.14)	3.26^a, 3.46^b

---

Based on this benchmark, we conclude that the MS-CASPT2 method with the selected active space ([14,11]) reproduces the absorption and emission properties of TPA and IPA well (Table 3). In Section 3.2.1, we will present the deactivation pathways connecting the ground state minimum with the optimised minimal energy conical intersections (S₁–S₀ MECI). These pathways were obtained applying the MS-CASPT2 method, which, apart from the good performance in description of absorption and emission, is suitable for the excited states simulations in the vicinity of the conical intersection, due to multireference character of the wave function.

3.1.3 Crystal structure and exciton transport. The crystal structures of TPA and IPA crystals are given in Fig. 1. Both crystals are characterised by C=O⋯H–O hydrogen bonds between in-plane monomers. In the TPA crystal, each monomer is bonded with two C=O⋯H–O hydrogen bonds with the average length of 1.53 Å, creating linear chains of hydrogen bonded molecules. In the case of IPA, the zig-zag molecular chains are formed by C=O⋯H–O hydrogen bonds, with the average lengths of 1.66 Å. in both crystals, these chains create molecular planes with the distance of ∼3.4 Å, interacting with the adjacent planes through π⋯π interactions between molecules. The other O⋯H interactions between the molecules belonging to adjacent planes, between oxygen atoms from the C=O groups and hydrogen atoms from the C–H and O–H groups, have substantially larger lengths (between 2.5 and 2.7 Å⁷) and are weaker compared to the in-plane hydrogen bonds and π⋯π interactions.

To get an insight into intermolecular interactions and exciton transport mechanisms in TPA and IPA crystals, we isolated dimers from an optimised supercell with centroid distances smaller than 10 Å, and computed the exciton couplings between the lowest-lying bright states of monomers at the TD-ωB97XD/6-311+G(d,p) level. At this level of theory, the S₁ and S₂ states of monomers at the optimised crystal structures are quasi-degenerate and the exciton couplings are very small. The exciton coupling are computed between the bright S₂ (ππ*/nπ*) states, while the close-lying S₁ (nπ*) are dark states. The S₂ pairs of monomers combine in and form S₃ and S₄ states of isolated dimers. The dimers with the largest exciton couplings are the face-to-face slip-stacked dimers with the centroid distances ≈3.75 Å, interacting through π⋯π interactions between the π densities localised on phenyl rings and densities belonging to carboxylic groups (Fig. 2). Their interaction yields relatively weak couplings of 12 meV in both molecules. Other isolated dimers are mainly side-to-side dimers, including the dimers with the intermolecular C=O⋯H–O bonds, and have negligible exciton couplings (<5 meV). The reorganisation energies for the exciton transport computed using eqn (3) is 382 meV for TPA and 277 meV for IPA. Upon reorganisation from the FC region to the excited state minima, the transition density changes from mixed ππ*/nπ* at optimised crystal geometry (Fig. 2) to pure ππ* state in TPA, whereas in IPA the S₁ state has also a mixed ππ*/nπ* at its minimum (Fig. 6).

Fig. 2 TD-ωB97X-D/6-311+G(d,p) transition densities of the S₁ states of IPA and TPA computed at the optimised crystal geometry for an isolated molecule in vacuum (panel a). The isosurfaces corresponding to the 0.001 ų density isovalue are represented. Structures of IPA and TPA dimers with the largest exciton couplings are presented in panel b. The electronic couplings and centre of masses distances between monomers are designated.

The exciton couplings are much smaller than the classical barrier for exciton hopping (λ/4), indicating that the S₁ excitons mostly remain localised on a single site during exciton diffusion in crystals. The exciton diffusion mechanism can be represented as a series of hopping events between isolated molecules. In this context, the exciton hopping rates for this mechanism can be evaluated based on the Marcus theory (eqn (2)). Applying the computed exciton couplings and reorganisation energies for IPA and TPA, the estimated exciton hopping rates for these molecules are 2.7 × 10¹⁰ and 8.3 × 10⁹ s⁻¹, respectively. This will compete with the vibrational relaxation to S₁ in the picosecond scale (rates around 10¹² s⁻¹) followed by other processes such as fluorescence and ISC. Due to a smaller reorganisation energy, the exciton hopping rate in IPA are ∼4 times larger than in TPA. We note that the thermal effects, which can significantly affect the exciton couplings and exciton diffusion rates and mechanism, are neglected here.

3.2 Excited state mechanisms

In this section, we analyse different mechanisms associated with the excited state relaxation of TPA and IPA. Our main focus is understanding the competition of different pathways in the solid state.

3.2.1 S₁–S₀ MECI. To better understand nonradiative decay to the ground state, we examined the internal conversion processes for TPA and IPA molecules in ethanol and crystal phases. To examined the lowest energy internal conversion pathways, we optimised the S₁–S₀ minimum energy conical intersections (MECI) between S₀ and S₁ states in the solution and crystal phase (Fig. 3). All optimised S₁–S₀ MECI geometries correspond to the nπ* type structures with the additional deficiency of electronic density in from the p-orbital of O-atom from the OH-group. The conical intersection structure involves out-of-plane motions of carboxyl group proton and bond alternation of C=O and C_Ph–C_Carb bonds, i.e. the C=O bond elongates by ∼0.25 Å, while the C_Ph–C_Carb bond contracts by ∼0.15 Å with respect to the ground state values. Apart from this, the lone pair orbitals of oxygen atoms in carboxyl group rotate such that their axes lie in the COO-plane, and their interaction decreases their distance (by ∼0.2 Å) with respect to the standard distance. Similarly, ∠O=C–O angle decreases to 80–90° from 120°.

Fig. 3 Structures of conical intersections of IPA and TPA optimised at XMS-CASPT2[14,11]/6-31G(d) level in vacuum and crystal environment. The geometries are represented in top and side views. The lengths of the C–O bonds, distances between O atoms, and ∠HOCO dihedral angles (α) in the carboxyl group are designated.

In the S₁–S₀ MECI structures optimised in the solution, the ∠HOCO is close to 90°, while the rest of the molecule is planar. On the other hand, in the solid state, the more favourable CI structures involve the bending of the COO-plane with respect to the rest of the molecule, while the H-atom dihedral motion is less activated (∠HOCO is 60° in IPA and 53.5° in TPA). A similar type of MECI structure was found in a phenyl-derivative dicarboxylic acid.⁴⁹

The XMS-CASPT2 method is an appropriate choice for the optimisation of conical intersections, due to the multireference character of the wave function near these intersections. We also optimised the S₁–S₀ MECI using less computationally expensive single-reference methods, TD-DFT and ADC(2). These methods predicted the minimal energy crossing structures involving benzene ring puckering, which are much higher in energy compared to the CASPT2-optimised structures. Additionally, we optimised the S₁–S₀ MECI of dimers bonded through C=O⋯H–O hydrogen bonds at the TD-DFT and ADC(2) levels of theory to investigate whether internal conversion occurs through an intermolecular proton transfer mechanism. The obtained S₁–S₀ MECI structures involve geometry changes in only one of the molecules.

3.2.2 Nonradiative decay to S₀. Fig. 4 shows the PES of IPA and TPA along the internal conversion coordinate at CASPT2/SA-6-CASSCF(14,11)/aug-cc-pVDZ level of theory in the solid state. At the FC geometry, the oscillator strengths of S₁ ππ* increase compared to the values in solution (from 0.05 to 0.10 in IPA and from 0.04 to 0.08 for IPA). The second bright state of IPA in the crystal occurs at 5.72 eV, ∼0.4 eV above the bright state in the solution, while in the case of TPA the second bright state can be found at 4.74 eV, ∼0.45 eV below the bright excitation in the solution. The maximum excitation energy used in the experiment for both crystals is ∼3.5 eV (365 nm),⁷ which corresponds to the first excited states (3.93 eV at the CASPT2 level, and 3.69 at the RI-CC2 level in IPA and 3.97 eV at the CASPT2 level in TPA).

Fig. 4 CASPT2/SA-6-CASSCF(14,11)/aug-cc-pVDZ energies of the lowest-lying singlet and triplet states along the LIIC pathway connecting S₀ and MECI geometries in the crystal in IPA (panel a) and TPA (panel b) in a diabatic representation.

The S₁–S₀ MECI for IPA lies at ∼5.2 eV, ∼1.2 eV above the vertical excitation, and for TPA at ∼6.0 eV, ∼2 eV above the vertical excitation, and they are not classically accessible after the excitation to S₁ state. The excitation of the second bright state of TPA at 4.74 eV (S₂) would also not enable the internal conversion to the ground state. The excitation of high-energy bright states of IPA and TPA with energies close to 6 eV (∼200 nm), would enable internal conversion, but that would require the application of vacuum UV radiation, not used in the experiment.⁷ The crystal environment increases the energy barriers to the S₁–S₀ MECI with respect to solution in 0.4 eV for IPA and 0.8 eV for TPA. From the transition state theory, we can obtain that the fractions of nonradiative rates between the solid state and solution are in the order 10⁻⁷ for IPA and 10⁻¹⁴TPA respectively. This is in line with the restricted access to the conical intersection (RACI) model, where the crystal environment blocks the access to the conical intersections associated with the S₁–S₀ nonradiative transitions explaining the enhancement of solid-state luminescence for these systems.^3,50,51 We should notice that for both S₁–S₀ MECI, T₁ gets almost degenerate with S₀ and S₁ providing an additional nonradiative pathway to the ground state, which can be activated by providing larger excitation energies.

The excitation to the S₁ state is followed by a relaxation to its minimum, where fluorescence and intersystem crossing can get activated. According to the PES and the spin–orbit couplings along the reaction coordinate (Fig. 4 and 5), the mechanisms involving triplet states are also possible. In the vicinity of the FC region, up to the (C=O) distance of ∼1.3 Å, where the T₁ and T₂ states are close-lying to the S₁, the S₁/T₁ and S₁/T₂ couplings have small values (below 5 cm⁻¹), indicating the possibility for slow intersystem crossing. The S₁/T₁ and S₁/T₂ SOCs values significantly increase further along the IC coordinate for r_CO > 1.3 Å, but in this region the S₁ state energy is higher than the vertical excitation, and the probability for its population via tunneling is relatively small.

Fig. 5 Spin–orbit coupling matrix elements (SOC in cm⁻¹) between relevant adiabatic singlet/triplet excited states computed along the linearly interpolated pathways for nonradiative relaxation for IPA (left) and TPA (right) in the crystal. The couplings between the states with large energy gaps are not shown.

3.2.3 Prompt fluorescence. A fraction of the population of S₁ can decay to the ground state radiatively and both crystals show PF.⁷ As mentioned in Section 3.1.2, the MS-CASPT2/aug-cc-pVDZ predicts well the values for fluorescence and emission energies. Using the Einstein equation, we estimated fluorescence rates of 1.7 × 10⁸ and 9.9 × 10⁷ s⁻¹ for IPA and TPA corresponding to fluorescence lifetimes of 6 and 10 ns (Table 4). These values, particularly for TPA, are overestimated compared to the experimental values of 2 and 1 ns. This discrepancy might be related to the absence of excitonic effects in the calculations that could affect the oscillator strengths and the lack of consideration of vibrational effects.

Table 4 Fluorescence (Fl), phosphorescence (Ph), most important (reverse) intersystem crossing (rISC) rate constants (k_f and k_P, k_(r)ISC, and k_exc) computed at 300 K in the IPA and TPA crystals. Section S7 in the ESI shows all calculated constants

	k f (s^−1)	k P (s^−1)	k ISC (s^−1)	k rISC (s^−1)
TPA	9.9 × 10^7	0.5	9.1 × 10^6 (S1/T4)	202 (T3/S2)
IPA	1.7 × 10^8	9.9	1.8 × 10^11 (S1/T1)	523 (T2/S1)

---

3.2.4 Role of triplet states. To fully understand the mechanisms operating in these systems, we need to explore the role of triplet states in more detail. Our previous study showed that triplet states can be affected differently than singlet states in a solid-state environment.⁵² Experimentally, in addition to PF, both systems show DF and RTP, which are directly linked with the population of triplet states. Fig. 6 shows the energy of the three lowest-lying singlet and triplet states computed at the optimised S₀, S₁, T₁, and T₂ geometries of TPA and IPA in crystal environment at the MS-CASPT2 level of theory. Possible decay pathways including radiative an nonradiative are highlighted in the figure, the details of the corresponding mechanisms are explained in the next sections. We note that the RI-CC2 method predicts similar excited state transition densities and energies at the (RI-)CC2 optimised geometries (ESI,† Section 8). According to the PES along the reaction coordinate which corresponds mainly to the C=O bond stretching, in both systems the lowest-lying excited states in the FC region are the ππ* states. They cross the higher nπ* singlet and triplet states at r_C=O ∼ 1.3 Å in IPA and r_C=O ∼ 1.35 Å in TPA. For the larger C=O lengths, the nπ* states become more stable (Fig. 5).

Fig. 6 Energy levels of the lowest-lying singlet and triplet states of IPA (panel a) and TPA (panel b) in crystal computed at the S₀, S₁, T₁, T₂, and T₃ (for TPA) states minima at the MS-CASPT2/CASSCF(14,11)/aug-cc-pVDZ level of theory. Possible fluorescence (full line), phosphorescence (dashed line), and (reversed) intersystem crossing (dotted line) transitions are designated. Optimised geometries of IPA (panel c) and TPA (panel d) molecules in S₀, S₁, T₁, T₂, and T₃ states given in two perspectives. The lengths of the C=O bond from the carboxylic group is given as well. The S₁, T₁, and T₂ excited state MS-CASPT2 density differences in the crystal environment are represented for IPA (panel e) and TPA (panel f) at S₀, S₁, T₁, and T₂ minima. In the case of the excited states of TPA at the T₃ minimum, the MS-CASPT2 density differences in the crystal environment are represented for S₂, T₂, and T₃ states.

The most striking difference between TPA and IPA is related to the nature of the most stable excited states. In IPA, the lowest-lying excited states are nπ* states at the S₁ and T₂, and mixed nπ* and ππ* states at the T₁ geometry. Their geometries are non-planar, with signatures of distortions occurring at the conical intersection –C=O bond stretching and out-of-plane bending of carboxyl group with respect to the phenyl ring. In TPA, the lowest-lying S₁, T₁, and T₂ states are ππ* states. The geometries at their minima are planar structures and do not feature C=O elongation.

3.2.4.1 Intersystem crossing. We explore possible intersystem crossing mechanisms from the S₁ minima. In TPA, the energy gaps between S/T pairs (ΔE) at the S₁ geometry are 0.62 eV for the S₁/T₁ and 0.22 eV for the S₁/T₂ pair. Since these states are ππ* states, the spin–orbit couplings between S₁/T₁ is small (∼4 cm⁻¹) and ∼0 cm⁻¹ for S₁/T₂ pair. The estimated ISC rates, based on the eqn (2), are negligible for the S₁/T₁ transition and zero ISC rate for the S₁/T₂ transition (Table 4, parameters used for the computations of all rates are given in the ESI†) at the S₁ geometry. The ISC S₁ (ππ*) and T₁/T₂ (ππ*) states are negligible along the reaction coordinate for the C=O lengths below 1.32 Å, as the gaps between states remain significant and spin–orbit couplings are close to zero. However, there is the possibility for the transition from the S₁ ππ* state to the higher-lying nπ* triplet state along the reaction pathway. The S₁ ππ* state crosses with the 1³nπ* triplet state at r_C=O = 1.32 Å. The minimum of the 1³nπ* state occurs at r_C=O ≈ 1.36 Å (Fig. 6), after the crossing between ππ* and nπ* states along the reaction coordinate (Fig. 4). At this geometry, the 1³nπ* state (T₃) is 0.2 eV above the S₁ vertical excitation. The first two triplet states are ππ* states, whereas the first two singlet states are nπ* and ππ*, respectively. The calculated ISC rate for the S₁/1³nπ* transition at the minimum of the S₁ state is 1.6 × 10⁵ s⁻¹. However, the spin–orbit couplings between these states increase along the reaction coordinate. The ISC rate computed applying the spin–orbit couplings in the vicinity of the crossing point between states (r_C=O ≈ 1.3 Å) is 9 × 10⁵ s⁻¹, indicating that a part of the population can be transferred to the 1³nπ* state, and subsequently to the lower-lying T₁ and T₂ ππ* states.

In IPA, two triplet states are in the vicinity of the S₁ state at its minimum (Fig. 6). The S₁ geometry features significant C=O stretching (r_C=O = 1.44 Å) and out-of-plane motions of carboxylic group (Fig. 6). As a consequence, the S₁, T₁, and T₂ states are nπ* states at this geometry. The S₁ and T₂ states are mostly represented by a single nπ* configuration, while the T₁ state is a linear combination of two nπ* configurations of opposite signs, inducing vanishing density around the C_Ph–C_Carb bond, and the total transition density is localised on C=O oxygen atom. Furthermore, the T₁ transition density is rotated for π/2 around the C=O bond with respect to the S₁ density. The T₂ density is also slightly rotated with respect to the S₁ density. These differences induce significant spin–orbit couplings between S₁/T₁ and S₁/T₂ pairs (32.4 and 27.2 cm⁻¹, respectively). Moreover, relatively small S–T gaps at this geometry (0.27 eV and 0.18 eV) enable significant ISC rates considerably faster than in TPA. The computed rates are 1.8 × 10¹¹ s⁻¹ for the S₁/T₁ transition and 9 × 10⁶ s⁻¹ for the S₁/T₂ transition (Table 4). Since the ISC rates to the T₁ state are larger compared to the fluorescence rates from the S₁ minimum (k_f ≈ 1.7 × 10⁸ s⁻¹), a significant population transfer from the S₁ to T₁ state is expected. According to the reaction pathways (Fig. 4), the lowest-lying ππ* triplet states (T₁ and T₂ in the FC region) can be populated through internal conversion from the nπ* triplet state. This mechanism involves the planarisation of molecule and contraction of the C=O bond.

In both systems, the population transferred to the lowest-lying triplet states could deactivate through phosphorescence, ISC to the ground state, and reversed ISC to the singlet states.⁵ According to the potential energy profiles along the reaction pathways, the ISC to the ground state is hindered in both systems, because the S₀/T₁ crossings, which are in the vicinity of the S₁–S₀ MECI (Fig. 6), are classically inaccessible following the S₁ excitations.

3.2.4.2 Room temperature phosphorescence. Once the T₁ states get populated, a possible relaxation mechanism is phosphorescence in both systems. Similar as fluorescence, the ultralong phosphorescence in IPA is more efficient compared to the TPA, with the computed rates of 9.92 s⁻¹ and 0.5 s⁻¹, respectively. In IPA, according to our results, phosphorescence occurs at 2.91 eV with a lifetime of ∼100 ms. The available experimental phosphorescence energies and lifetimes are in relatively good agreement with our results; RTP is observed at 2.45 eV (506 nm) with a lifetime of 290 ms by Gong et al.,⁷ and in the study by Kuno et al.⁸ at 2.51 eV (501 nm). Our computations predict an ultralong phosphorescence at 2.53 eV for TPA, in good agreement with the experimental weak phosphorescence signal at 2.43 eV (511 nm) by Gong et al.⁷ and at 2.40 eV (516 nm) by Kuno et al.⁸
3.2.4.3 Reverse intersystem crossing. To examine the deactivation pathways from the triplets populated from the singlet states through intersystem crossing, we optimised the geometries of the T₁ and T₂ states in both systems, and the T₃ state in TPA, and computed the reverse ISC rates from the minima of the triplet states. Because these systems experimentally exhibit DF, there must be mechanisms that efficiently populate S₁ from the triplet manifold. However, in both systems, population of singlet states from T₁ seems unlikely due to the significant energy gaps. Nevertheless, we observe that when considering higher triplet states, such as T₂ and T₃, the rates for rISC can be one to two order of magnitudes faster than competing phosphorescence. Previous works highlight the relevant role of the higher-lying triplets in the rISC mechanism in organic systems.^5,6,53–55 In cases where the energy gap between the T/S pair undergoing reverse ISC is substantial, intermediate triplet states can mediate this process. Vibronic interactions between closely spaced triplet states can promote internal conversion between them, effectively lowering the activation energy required for reverse ISC. Our hypothesis is that T₂ in IPA and T₃ in TPA lie very close in energy to T₁ and T₂, respectively, which should facilitate seamless population transfer between these states.

In TPA, the lowest T₁ and T₂ states at their minima are ππ* states. The computed rISC rates from the T₁ and T₂ state minima (the T₂ state is the lowest triplet state at its minimum) to the S₁ state are negligible (10⁻¹⁸ s⁻¹) at the T₁ minimum and zero at the (T₂ minimum), as a consequence of negligible/zero SOCs between (ππ*) states. To explain the rISC mechanism, we take into account the higher-lying 1³nπ* state. At the minimum of this state (T₃), the lower-lying T₁ and T₂ states are ππ* states. The T₃ state can get populated due to excess vibrational energy obtained following the S₁/T₃ ISC. At this geometry, there is a possibility for the rISC to the higher-lying S₂ ππ* state (corresponding to the S₁ state at the FC region) from the T₃ (1³nπ*) state, due to a significant SOC between the states (10 cm⁻¹). The computed rISC rate is ∼200 s⁻¹. The model used to compute the rISC rates (eqn (2)) does not take into account vibrational effects on spin–orbit interaction⁵⁶ and vibronic coupling between triplet states,⁵⁵ which could enhance the rISC rates. Another possible rISC mechanism at the T₃ geometry includes the transition from the ππ* T₁/T₂ states to the close-lying S₁ (nπ*) state. The T₂/S₁ rISC is expected to be efficient, since the ΔE is only ∼0.13 eV, while the T₂/S₁ SOC is 12.4 cm⁻¹. Moreover, the SOCs increase substantially along the reaction coordinate, surpassing 40 cm⁻¹ for the r_C=O > 1.38 Å (Fig. 5), which could further increase the rISC rates.

In IPA, the T₁ state minium has a planar geometry with slightly elongated C=O bond (r_C=O = 1.23 Å) compared to the ground state geometry (r_C=O = 1.21 Å) (Fig. 6). The S₁ state corresponds to the nπ*, whereas lower-lying T₁ and T₂ states correspond to the mixed nπ*/ππ* states at this geometry. The SOCs between the S₁ and T₁ states are 3 cm⁻¹. A significant S₁–T₁ gap at this geometry (0.71 eV), induces negligible rISC rate (Section S7 in the ESI†). The T₂ state features C=O stretching (r_C=O = 1.34 Å) and out-of-plane motion of –COOH group. Similar as at the S₁ geometry, S₁, T₁, and T₂ states are nπ* states at this geometry. We note that the T₂ state is the second triplet state at its minimum. A significant SOC between S₁/T₁ pair (15.4 cm⁻¹) and a relatively small energy gap (0.18 eV) induce more efficient rISC from T₂ to the S₁ state with the rate of 523 s⁻¹, in comparison with the T₁/S₁ rISC. The T₂/S₁ rISC rates can increase along the stretching coordinate, as a results of an increase of the SOCs between them. Similar as for TPA, the T₂/S₁ SOCs significantly increase for r_C=O > 1.3 Å, reaching the values of 50 cm⁻¹ (Fig. 5). Based on this analysis, we can conclude that a part of the population from the triplet states could be transferred back to the S₁ state in both IPA and IPA due to spin–orbit interactions between states.

Previous studies suggest that apart from the spin–orbit interactions, the hyperfine interactions between singlet/triplet pairs could contribute to the rISC mechanism, in particular in intermolecular processes in multi-chromophore systems involving radical-pair charge transfer states.^39,57 For the IPA crystal, Kuno et al.⁸ found that the phosphorescence decreases upon Zeeman splitting of the degenerate triplet state in an external magnetic field and CH-to-CD substitution, but increases in stronger magnetic fields. This was explained by a charge-transfer (CT) state delocalised over two molecules, with spins localised on each, forming nearly degenerate singlet and triplet radical-ion-pair states. Weak hyperfine couplings enable spin exchange between them, accounting for both the suppression (Zeeman effect) and enhancement (Δg mechanism) of phosphorescence. We have explored the effects of hyperfine interactions on intramolecular mechanisms. In the case of the excited states of TPA and IPA, the hyperfine couplings between the singlet and triplet states, calculated using the TD-ωB97XD method, are negligible—less than 10⁻¹⁴ meV (see ESI,† Section S9). Consequently, the influence of hyperfine interactions on singlet–triplet mixing can be considered negligible, suggesting that reverse intersystem crossing (rISC) will be primarily facilitated by spin–orbit interactions. Additionally, our calculations using electrostatic embedded RI-ADC(2)/aug-cc-pVDZ method for the lowest-lying singlet and triplet states (S₁, S₂, T₁–T₄) for the dimers of TPA and IPA (ESI,† Section S10), indicated these states are either localised or delocalised nπ* and ππ* states, without a significant radical-ion pair charge transfer character.

3.2.4.4 Delayed fluorescence. Our results show that the rISC, activated in both systems, enables the transfer of a fraction of the population from triplet manifold to the S₁ states. A fraction of transferred population can undergo delayed fluorescence. In IPA, the delayed fluorescence is observed at 3.23 eV (slightly redshifted compared to the PF at 3.26 eV) with a lifetime of 9.6 ms.⁷ Similarly, in TPA a weak DF signal is recorded at 3.16 eV (392 nm), slightly redshifted compared to the prompt signal (3.20 eV) with the 0.16 ms lifetime. The computed rISC rates in both crystals (k_rISC = 523 s⁻¹ for T₂/S₁ transition in IPA and k_rISC = 202 s⁻¹ for T₃/S₂ transition in TPA) indicate that the delayed fluorescence lifetime is expected on the ms timescale, which is in line with the experiments despite we are not considering the times associated with the transitions between the different triplets.

Kuno et al. attributed the delayed fluorescence observed in IPA to a triple–triplet annihilation (TTA) mechanism, in which two triplet excitons on neighbouring molecules combine to form one S₁ state and one S₀ state, with emission arising from the former.⁸ To assess the thermodynamic feasibility of TTA, we evaluated the energy losses in both the singlet and triplet manifolds (ESI,† Section S11). Efficient TTA requires a small positive energy loss in the singlet states and a significantly negative loss in the triplet states.⁴⁷ However, our calculations reveal that energy losses in the singlet manifold are large and positive (for both S₁ and S₂ excitations), and those in the triplet manifold are also large and positive (ESI,† Section S11). These results suggest that the TTA mechanism is energetically unfavourable in these crystals.

4. Conclusions

Motivated by distinct solid-state luminescence properties of two benzene dicarboxyl acid crystals, TPA and IPA, we have systematically explored their excited-state relaxation mechanisms in solution and crystal environments. Given the weak interactions between π–π stacked dimers, the exciton couplings in both molecules are very small compared to the reorganisation energies associated with exciton transport. As a result, excited-state processes are primarily localised, and exciton transport occurs predominantly through incoherent exciton hopping.

We explore light-activated nonradiative decay mechanisms for both systems, considering multireference methods. We found the conical intersections geometries associated with the decay to the ground state, that involve mainly distortions of a carboxyl group –C=O bond stretching, out-of-plane motions of the carboxyl group with respect to the phenyl ring, and out-of-plane motion of the H-atom with respect to the –COO plane of carboxyl group. In line with the restricted access to the conical intersection (RACI) mechanism, the conical intersections in the crystal environment are not classically accessible. We also explore the intersystem crossing pathways in both systems, enabling relatively efficient populations of triplet states. In general, ISC is more efficient in IPA due to larger SOCs associated with the nature of the excited states involved and smaller energy gaps. We have shown that in both systems, the reverse intersystem crossing could happen through intermediate triplet states, transferring back a part of the population to the singlet manifold, explaining experimentally observed delayed fluorescence. This phenomenon is more efficient in IPA, due to a larger SOC and a smaller energy gap between states involved in the transition. According to our calculations, TTA seems to be energetically unfavourable.

Our results show that for an efficient triplet states population and solid-state phosphorescence in organic crystals, apart from the hindrance of the internal conversion, the positioning of substituents in benzene dicarboxylic acids plays a significant role. In the case of para substitution, the electronic delocalisation over the entire molecule is stabilised in the low-lying singlet and triplet states, resulting in ππ* being the lowest in energy. With meta substitution, electronic delocalisation is less favorable, leading to the stabilisation of mixed nπ*/ππ* or pure nπ* at their respective minima. This electronic effect significantly influences deactivation pathways. Our results indicate that the fluorescence, phosphorescence, and triplet-state population thought intersystem crossing processes are more efficient in IPA, which is in line with experimental observations. We believe this effect can be generalised to other substituents involved in electronic delocalisation with the central ring, as well as to more complex conjugated systems. This result might be of interest for the design of highly efficient room-temperature phosphorescent materials.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the ESI.†

Acknowledgements

This research was supported by the Leverhulme Trust (RPG-2019-122) and EPSRC (EP/R029385/1). We used the Queen Mary's Apocrita HPC facility, supported by QMUL Research-IT and UCL High Performance Computing Facilities Myriad@UCL and Kathleen@UCL. We also acknowledge the use ARCHER UK National Supercomputing Service (EP/X035859/1) via the Materials Chemistry Consortium and the Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/T022213/1). Funding by the UK Research and Innovation under the UK government's Horizon Europe funding guarantee (grant number EP/X020908/2) is acknowledged.

Notes and references

1. W. Zhao, Z. He and B. Z. Tang, Nat. Rev. Mater., 2020, 5, 869–885.
2. J. Zhou, L. Stojanović, A. A. Berezin, T. Battisti, A. Gill, B. M. Kariuki, D. Bonifazi, R. Crespo-Otero, M. R. Wasielewski and Y. L. Wu, Chem. Sci., 2021, 12, 767–773.
3. R. Crespo-Otero, Q. Li and L. Blancafort, Chem. – Asian J., 2019, 14, 700–714.
4. Y. Niu, Q. Peng and Z. Shuai, Sci. China, Ser. B: Chem., 2008, 51, 1153–1158.
5. A. Sidat, F. J. Hernández, L. Stojanović, A. J. Misquitta and R. Crespo-Otero, Phys. Chem. Chem. Phys., 2022, 24, 29437–29450.
6. T. J. Penfold, F. B. Dias and A. P. Monkman, Chem. Commun., 2018, 54, 3926–3935.
7. Y. Gong, L. Zhao, Q. Peng, D. Fan, W. Z. Yuan, Y. Zhang and B. Z. Tang, Chem. Sci., 2015, 6, 4438–4444.
8. S. Kuno, H. Akeno, H. Ohtani and H. Yuasa, Phys. Chem. Chem. Phys., 2015, 17, 15989–15995.
9. H. Ma, W. Shi, J. Ren, W. Li, Q. Peng and Z. Shuai, J. Phys. Chem. Lett., 2016, 7, 2893–2898.
10. R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett., 1996, 256, 454–464.
11. M. E. Casida, C. Jamorski, K. C. Casida and D. R. Salahub, J. Chem. Phys., 1998, 108, 4439–4449.
12. E. R. Stratmann, G. E. Scuseria and M. J. Frisch, J. Chem. Phys., 1998, 109, 8218–8224.
13. C. V. Caillie and R. D. Amos, Chem. Phys. Lett., 1999, 308, 249–255.
14. F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447.
15. O. Christiansen, H. Koch and P. Jørgensen, Chem. Phys. Lett., 1995, 243, 409–418.
16. C. Hättig and A. Köhn, J. Chem. Phys., 2002, 117, 6939–6951.
17. C. Hättig, J. Chem. Phys., 2003, 118, 7751–7761.
18. A. Köhn and C. Hättig, J. Chem. Phys., 2003, 119, 5021–5036.
19. B. O. Roos, A. J. Sadlej, P. Å. Malmqvist, K. Andersson and K. Wolinski, J. Phys. Chem., 1990, 94, 5483–5488.
20. K. Andersson, P. Å. Malmqvist and B. O. Roos, J. Chem. Phys., 1992, 96, 1218–1226.
21. S. Vancoillie, M. G. Delcey, R. Lindh, V. Vysotskiy, P.-Å. Malmqvist and V. Veryazov, J. Comput. Chem., 2013, 34, 1937–1948.
22. M. Bailey and C. J. Brown, Acta Crystallogr., 1967, 22, 387–391.
23. R. Alcala and S. Martnez-Carrera, Acta Crystallogr., Sect. B, 1972, 28, 1671–1677.
24. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395–502.
25. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
26. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
27. S. Dapprich, I. Komaromi, K. Suzie Byun, K. Morokuma and M. J. Frisch, J. Mol. Struct.: THEOCHEM, 1999, 461–462, 121.
28. L. W. Chung, W. M. Sameera, R. Ramozzi, A. J. Page, M. Hatanaka, G. P. Petrova, T. V. Harris, X. Li, Z. Ke, F. Liu, H. B. Li, L. Ding and K. Morokuma, Chem. Rev., 2015, 115, 5678–5796.
29. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision A.03, Gaussian Inc., Wallingford CT, 2016.
30. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez. Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541.
31. TURBOMOLE V7.0 2015, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989-2007, TURBOMOLE GmbH, since 2007; available from https://www.turbomole.com.
32. S. Maeda, K. Ohno and K. Morokuma, J. Chem. Theory Comput., 2010, 6, 1538–1545.
33. A. A. Granovsky, J. Chem. Phys., 2011, 134, 214113.
34. T. Shiozaki, W. Györffy, P. Celani and H.-J. Werner, J. Chem. Phys., 2011, 135, 081106.
35. B. O. Roos, P. R. Taylor and P. E. M. Siegbahn, Chem. Phys., 1980, 48, 157–173.
36. N. Forsberg and P. Å. Malmqvist, Chem. Phys. Lett., 1997, 274, 196–204.
37. P. Åke Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240.
38. B. Schimmelpfennig, Amfi, an atomic mean-field spin–orbit integral program. Computer code, University of Stockholm, 1996.
39. S. R. May, C. Climent, Z. Tao, S. A. Vinogradov and J. E. Subotnik, J. Phys. Chem. A, 2023, 127, 3591–3597.
40. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr., H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. Hanson-Heine, P. H. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O’Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. V. Voorhis, J. M. Herbert, A. I. Krylov, P. M. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215.
41. M. Rivera, M. Dommett and R. Crespo-Otero, J. Chem. Theory Comput., 2019, 15, 2504–2516.
42. M. Rivera, M. Dommett, A. Sidat, W. Rahim and R. Crespo-Otero, J. Comput. Chem., 2020, 41, 1045–1058.
43. J. Schirmer, Phys. Rev. A: At., Mol., Opt. Phys., 1982, 26, 2395–2416.
44. A. B. Trofimov and J. Schirmer, J. Phys. B: At., Mol. Opt. Phys., 1995, 28, 2299.
45. B. Hourahine, B. Aradi, V. Blum, F. Bonafé, A. Buccheri, C. Camacho, C. Cevallos, M. Y. Deshaye, T. Dumitrica, A. Dominguez, S. Ehlert, M. Elstner, T. van der Heide, J. Hermann, S. Irle, J. J. Kranz, C. Köhler, T. Kowalczyk, T. Kubař, I. S. Lee, V. Lutsker, R. J. Maurer, S. K. Min, I. Mitchell, C. Negre, T. A. Niehaus, A. M. N. Niklasson, A. J. Page, A. Pecchia, G. Penazzi, M. P. Persson, J. Řezáč, C. G. Sánchez, M. Sternberg, M. Stöhr, F. Stuckenberg, A. Tkatchenko, V. W.-Z. Yu and T. Frauenheim, J. Chem. Phys., 2020, 152, 124101.
46. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, T. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260–7268.
47. F. J. Hernández and R. Crespo-Otero, Annu. Rev. Phys. Chem., 2023, 74, 547–571.
48. J. Aragó and A. Troisi, Phys. Rev. Lett., 2015, 114, 1–5.
49. Z. Li, C. Roscini, R. Núñez, F. Teixidor, C. Viñas, E. Ruiz and J. G. Planas, J. Mater. Chem. C, 2024, 12, 2101–2109.
50. L. Stojanović and R. Crespo-Otero, ChemPhotoChem, 2019, 3, 907–915.
51. L. Stojanovic and R. Crespo-Otero, Molecules, 2022, 27, 522.
52. L. Stojanović and R. Crespo-Otero, J. Phys. Chem. C, 2020, 124, 17752–17761.
53. T. J. Penfold, F. B. Dias and A. P. Monkman, Chem. Commun., 2018, 54, 3926–3935.
54. J. Gibson and T. J. Penfold, Phys. Chem. Chem. Phys., 2017, 19, 8428–8434.
55. T. J. Penfold, E. Gindensperger, C. Daniel and C. M. Marian, Chem. Rev., 2018, 118, 6975–7025.
56. G. Herzberg and E. Teller, Z. Phys. Chem., 1933, 21B, 410–446.
57. J. M. Dos Santos, D. Hall, B. Basumatary, M. Bryden, D. Chen, P. Choudhary, T. Comerford, E. Crovini, A. Danos, J. De, S. Diesing, M. Fatahi, M. Griffin, A. K. Gupta, H. Hafeez, L. Hämmerling, E. Hanover, J. Haug, T. Heil, D. Karthik, S. Kumar, O. Lee, H. Li, F. Lucas, C. F. R. Mackenzie, A. Mariko, T. Matulaitis, F. Millward, Y. Olivier, Q. Qi, I. D. W. Samuel, N. Sharma, C. Si, L. Spierling, P. Sudhakar, D. Sun, E. Tankelevičiutė, M. Duarte Tonet, J. Wang, T. Wang, S. Wu, Y. Xu, L. Zhang and E. Zysman-Colman, Chem. Rev., 2024, 124, 13736–14110.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00603a

---