 Open Access Article
Open Access ArticleConcerted proton electron transfer or hydrogen atom transfer? an unequivocal strategy to discriminate these mechanisms in model systems†
Davide
Zeppilli
 a and
Laura
Orian
a and
Laura
Orian
 *ab
*ab
aDipartimento di Scienze Chimiche, Università degli Studi di Padova, Via Marzolo 1, 35131 Padova, Italy. E-mail: laura.orian@unipd.it
bIstituto Nazionale di Fisica Nucleare, Laboratori Nazionali di Legnaro (INFN-LNL), 35020 Legnaro (PD), Italy
First published on 3rd March 2025
Abstract
Concerted proton electron transfer (CPET) and hydrogen atom transfer (HAT) are two important mechanisms in many fields of chemistry, which are characterized by the transfer of one proton and one electron. The distinction between these mechanisms may be challenging in several reactions; thus, different computational methods have been developed for this purpose. In this work, we present a computational strategy to distinguish the two mechanisms, rationalizing the factors controlling the reactivity in four different model reactions. Fist, the transition state SOMO (singly occupied molecular orbital) is visualized, presenting all the limits and ambiguities of this analysis. Then, the electron flow along the reaction path is evaluated through the intrinsic bond orbitals (IBOs); this analysis allows to describe correctly the mechanism of each reaction in agreement with previous studies. Furthermore, some structural modifications are applied to the transition state of each system and the energetic differences are rationalized in the framework of the activation strain analysis to understand the geometrical and electronic factors governing the reactivity and the selection of CPET or HAT mechanism. Lastly, the effect of the donor–acceptor distance is evaluated. It emerges that a combined computational analysis is crucial to understand not only the distinction between the two mechanisms, but also the molecular reasons why one mechanism is operative in a specific reaction.
Introduction
Proton-coupled electron transfer (PCET) is a class of reactions involving the transfer of one proton and one electron (H+/e− transfer), which are popular chemical steps in many fields encompassing photochemistry,1 electrochemistry,2,3 redox biology,4 photosynthesis,5 catalysis,6 and medicinal chemistry with applications, for example, in the scavenging of harmful radicals.7 The term PCET was first used in 1981 by the research group of T. J. Meyer to describe a peculiar electron transfer in ruthenium complexes, which was coupled to a proton transfer.8 Later, after more than four decades, the definition of PCET has become very broad.9 It includes stepwise and concerted mechanisms, involving either the same site or separate sites as proton and electron donors/acceptors; multiple reactants may be involved in the process too.10 In detail, in the stepwise pathway, the proton and the electron transfer (or vice versa) are subsequential; conversely, in concerted PCET (cPCET), the proton and the electron are transferred in a single step. This mechanism is also called Concerted Proton Electron Transfer (CPET).11A particular case of CPET is hydrogen atom transfer (HAT), which consists on a single-step mechanism involving the transfer of a hydrogen atom. The different name comes from the previous interest in this kind of reactivity by organic chemists,12,13 who studied hydrogen abstractions before the term PCET was coined. Particularly, the acronym HAT first appeared in the literature in 1941, in a contribution by J. Weiss,14 who studied the mechanism of Cannizzaro reaction (discovered in 1853).15
CPET and HAT mechanisms are identical from a thermodynamic point of view, since a H+/e− transfer or a hydrogen atom transfer from the same reactants leads to the same products; moreover, they both occur in a single step (Scheme 1). Currently, the definitions of the two mechanisms are ambiguous in the literature and, sometimes, chemically imprecise.11 However, a clear and correct definition of these two mechanisms allows to state that when the electron and proton are transferred together at any point of the reaction coordinate, the mechanism is HAT; conversely, CPET occurs when the proton and the electron are transferred separately, usually starting from or arriving at different sites of the molecular species involved in the reaction. This implies that the orbital associated to the transferred electron is not located on the transferred proton in the reactants or in the products; this discrimination is consistent with previous works on this topic.6,16
While thermodynamics is identical, the difference between CPET and HAT lies in the kinetics of these processes. Thus, in the past decades, different computational methods have been employed to rationally discriminate these two mechanisms. In 2002, J. Mayer and co-workers wrote one of the first papers on the topic;17 they studied several model systems and distinguished the mechanisms referring to the set of orbitals involved in the proton and electron transfer. In the same year, S. Hammes–Schiffer presented a different approach to address the topic, based on the adiabaticity of the processes.18 From these pioneering works, two of the most popular methods to understand the H+/e− transfer mechanism have stemmed out and have become widespread in the community, which are based on the analysis of the transition state SOMO (Singly Occupied Molecular Orbital) and the nonadiabaticity of the proton transfer, respectively.
The symmetry of the transition state SOMO may indeed give an idea of the mechanism: a π orbital orthogonal to the proton transfer direction is associated with CPET, while a σ orbital along this direction corresponds to HAT; this straightforward method is commonly used in the scientific community.19–25 However, in some cases, which will be discussed in this work, this approach may lead to ambiguity or inconsistency.
Alternatively, CPET can be described in terms of electronically nonadiabatic proton transfer, while HAT represents the analogous adiabatic mechanism.26–29 This distinction was found in well-known systems and may be rationalized in terms of the distance between the electron donor and acceptor. In detail, the electron transfer distance is relatively short in HAT, while it is generally longer in CPET reactions, which reflects in a higher extent of nonadiabadicity.30 Indeed, this method is quantitatively accurate to calculate the kinetic constants, but is quite elaborate and less chemically intuitive, especially if interested in the chemical modifications influencing the reactivity. This may lead to a scarce applicability of the method by the wide chemistry community (and beyond) interested in this reactivity, as already pointed out in the literature.31
Other approaches have been used to distinguish CPET and HAT, like the analysis of deformation energies proposed by Shaik,6 or the analysis of the charge displacement function proposed by Swart.32 Furthermore, a recent strategy relies on localized orbitals, which represent a powerful tool for orbital analysis.16,33,34 In this context, the Intrinsic Bond Orbital (IBO) approach allows to follow the electron flow along the reaction path.35,36 Thus, it is possible to describe the orbital change during the reaction, evaluating if the proton and the electron are transferred together or separately in a quantum-mechanically accurate but still chemically intuitive procedure.
In this work, we propose an unequivocal computational strategy to discern the nature of the CPET/HAT mechanism and illustrate its application to different model systems. The ability of phenols to quench free radicals,37,38i.e., their scavenging potential, is analyzed first. Indeed, hydrogen abstraction is one of the most relevant paths, allowing the reduction of harmful radicals to less reactive species and plays a crucial role in redox biology.39 The action of many natural substances and drugs consists in maintaining or recovering physiological redox balance via radical quenching.40–42 Phenols represent the chemical motifs of popular scavengers, i.e., the class of polyphenols. Furthermore, the oxidation of phenols plays an important role in sustainable and environmental chemistry, since the pyrolysis of lignin generates phenolic species involved in radical reactions.43,44
Beyond the model scavenging reaction of phenols, the well-known phenoxyl/phenol, benzyl/toluene and methoxyl/methanol systems and their self-exchange reactions are included in the CPET/HAT mechanism study, which is based on electron flow analysis (description) and activation strain analysis (ASA) combined with the energy decomposition analysis–natural orbital for chemical valence (EDA–NOCV) scheme (rationalization) (see Computational details). To perform this latter, selected structural modifications were applied to all systems; the use of suitably constrained geometries allow to understand the mechanistic picture emerging from IBOs.
Results and discussion
The distinction between CPET and HAT is not always straightforward, and it may become very tricky when the proton and electron donors and acceptors are not spatially separated; this critical situation is frequent in the radical scavenging panorama. In this context, hydrogen abstraction is a quite popular mechanistic path, but the distinction between CPET and HAT is usually not specified, generating misinterpretation and ambiguities.45–47 Sometimes, this kind of reactivity is generally referred to as formal HAT (fHAT),48,49 especially if the investigation is focused on the thermodynamics of the process and no mechanistic distinction is required. However, only an accurate description of the radical scavenging mechanism may give insight into the chemical factors controlling the reactivity.A popular class of antioxidants with scavenging activity is represented by polyphenols, which are able to quench also peroxyl radicals.49–51 We used their chemical motif, i.e., the phenol, and a hydroperoxyl radical to assess the CPET/HAT mechanism (Fig. 1(A)).
In gas phase, the reaction proceeds through the initial formation of a reactant complex (RC) due to the stabilizing interaction between the two reactants. Then, upon crossing a transition state (TS), a product complex (PC) is reached, which is also generally more stable than the free products. In the RC, the phenolic hydroxyl group lies in the ring plane resulting in a better orbital overlap between the π system and the O-centered p orbital. As the hydroperoxyl radical approaches, the OH group moves out of the plane and, in the TS, the radical lies almost above the aromatic moiety. This relative position of the reactants suggests a possible involvement of the benzene ring in the mechanism.
To evaluate the effect of the interaction between the two reactants in the geometrical structure of the TS, which will be quantified in the framework of ASA (see below), we applied a structural modification to understand how the relative orientation of the donor and acceptor affects the mechanism. Particularly, an important parameter is the C–C–O–O dihedral angle (Fig. 1(B)), which shows the position of the peroxyl oxygen with respect to the ring plane. In the TS (Fig. 1(C)), its value is 70° implying that the proton transfer direction is nearly orthogonal to the aromatic ring. A partially constrained TS is optimized by keeping fixed the dihedral C–C–O–O angle with a value of 18° (Fig. 1(D)), in which the peroxyl moiety lies closer to the ring plane.
The partially constrained TS is higher in energy by 5.9 kcal mol−1 at M06-2X/6-311+G(d,p)//M06-2X/6-31G(d) level of theory (see Computational details). These relative energy values have been computed also running MP2 as well as highly correlated DLPNO-CCSD(T) calculations. Moreover, different basis sets and functionals were tested to validate the chosen DFT level of theory, which is fully consistent with the frequently used QM-ORSA protocol (see Computational details). These results are included in the ESI† (Tables S1–S3).
Transition state SOMO analysis
To obtain preliminary and qualitative insight into the mechanism, the SOMOs of the two TSs were inspected. As reported in the Introduction, this simple approach is frequently adopted in the literature. Fig. 2(A) shows that the SOMO of the TS is essentially localized on the peroxyl moiety; thus, at this point of the reaction coordinate, the unpaired electron still mostly belongs to the peroxyl radical, which is not ideal to draw assumptions about electron transfer. Moreover, the symmetry of the SOMO is not useful to understand the mechanism; the orbital lobes are neither aligned along the proton transfer direction (which is typically associated to HAT) nor orthogonal to it (which is typically associated to CPET). The SOMO has a pseudo atomic p shape on both the oxygens involved in the proton exchange, which are mutually orthogonal; thus, the proton does not lie in a planar node, since the SOMO partially covers the O–H–O region of space. Nevertheless, the SOMO may be more confidently associated to CPET mechanism rather than to HAT; however, the mechanistic recognition remains ambiguous according to this analysis and the aromatic ring seems to play no significant role in the mechanism.Conversely, the SOMO of the partially constrained TS (Fig. 2(B)) has a strong π contribution from the ring, while, on the oxygen atoms, the lobes are localized mostly along the proton transfer direction, which defines the HAT mechanism. Thus, the imposed geometrical deformation suggests a variation of the mechanism, but the participation of the π system in the reactivity remains still uncertain.
To extend and generalize the analysis of the factors controlling the H+/e− transfer mechanism, the same computational strategy was applied to a series of reference systems used as minimal models for CPET/HAT processes, i.e., phenoxyl/phenol, benzyl/toluene and metoxyl/methanol self-exchange reactions. These symmetric systems were selected to investigate the effect of aromaticity, the presence of heteroatoms as well as their combination. In the literature, hydrogen abstraction is described as CPET for the phenoxyl/phenol system; while the HAT mechanism describes the other two self-exchange reactions.17,22,27,52 However, the rationalization of the observed mechanisms is still lacking.
Starting from the phenoxyl/phenol system, a symmetric TS was found with a π–π stacking configuration and the transferred proton was found equidistant from both oxygen atoms. To assess the effect of the π–π interaction, a geometrical distortion was applied to obtain the opposite configuration. Particularly, the relaxed π–π stacking structure possesses a C–O–O–C dihedral angle of 14°, which was increased to 174° to obtain a partially constrained TS with the two aromatic rings in anti configuration. Fig. 3(A)–(C) show the geometry of the optimized structures highlighting the dihedral angle together with the corresponding SOMOs. Although in the literature there is consensus on a CPET mechanism, the SOMO of the TS (Fig. 3(B)) suggests a HAT mechanism since the orbital has a σ symmetry along the proton transfer (O–H–O) direction. Conversely, the partially constrained TS (Fig. 3(C)) recovers the CPET behavior of the SOMO: π symmetry with a planar node along the proton transfer direction. Hence, the SOMO analysis may indeed lead to a misinterpretation of the mechanism.
Moving from the phenoxyl/phenol to the benzyl/toluene self-exchange reaction, the mechanism becomes HAT. For this system, two fully optimized TSs are found without imposing any constraint: a π–π stacked structure similar to the previous case and the corresponding anti configuration with a dihedral angle of 180°. The former is more stable by 3 kcal mol−1 than the latter, which maintains the benzene rings orthogonal to the plane containing the dihedral angle of 180° rather than an almost planar structure like in the phenoxyl/phenol system.
The SOMO analysis (Fig. 3(E) and (F)) confirms the HAT mechanism for both reaction paths. These MOs represent the π system of each ring assuming the typical shape of HAT due to the geometry of the TSs. Interestingly, the SOMO of the π–π stacking benzyl/toluene structure is perfectly analogous to the corresponding SOMO of the phenoxyl/phenol TS, although the H+/e− transfer mechanisms are reported to be different. Thus, the transition state SOMO may be insightful in some cases, but it can fail the CPET/HAT discrimination even with the simplest minimal model.
Lastly, the methoxyl/methanol self-exchange reaction is briefly presented. A TS was found with a dihedral angle between the two methyl groups of 98°, while a partially constrained structure was optimized with a dihedral angle of 175°, lying 1.6 kcal mol−1 above the relaxed geometry. This structure closely resembles the so-called “hilltop structure” analyzed in a previous study by J. Mayer's group.17
The SOMOs (Fig. S1, ESI†) are consistent with a HAT mechanism for both reaction paths, being similar to those of the benzyl/toluene systems. This finding contrasts with the description of a PCET mechanism for the “hilltop structure” by Mayer et al.17 with an electron transfer occurring between the oxygen lone pairs. Indeed, HAT mechanism is found for the partially constrained structure; this outcome leads us to the conclusion that the oxygen lone pairs are not able to promote a CPET mechanism without the presence of an aromatic moiety.
Electron flow analysis with IBO
Since the result of the SOMO analysis is not consistent with the mechanism established in the literature for the considered systems, a different approach was applied. For the hydrogen abstraction from phenol by ˙OOH, the structure of the TS suggests the involvement of the π system in the mechanism, facilitating some kind of interaction between the two reactants. Thus, we followed the electron flow during the reaction through the IBOs, which are non-empirical localized molecular orbitals, useful to gain insight and to provide intuitive chemical interpretation.Fig. 4(A) shows the change in the main α and β spin IBOs involved in the quenching of ˙OOH from the reactants, through the TS, to the products. The proton is progressively transferred, along the reaction path, from the hydroxyl group of the phenol to the peroxyl radical. Conversely, the description of the electron flow is less straightforward, since the π system of the aromatic ring is involved in the electron transfer, as shown by the blue spin IBO (βπ in Fig. 4(A)). This β spin IBO is initially localized on the ring, as one of the π orbitals of the phenol. Then, it changes during the reaction, evolving in the direction of the phenolic oxygen and the peroxyl moiety, until the TS is reached, covering the proton transfer (O–H–O) region of space. Finally, as the reaction proceeds, this spin IBO remains localized only on the peroxyl moiety, as one spin orbital of the newly formed OH σ bond. While this βπ spin IBO localized on the phenolic ring moves to the peroxyl radical, the corresponding α spin orbital (απ orange IBO in Fig. 4(A)) does not change during the reaction and determines the radical character of the phenoxyl product.
Since the transferred electron comes from a spin orbital which is not localized on the transferred proton, the reaction mechanism is CPET. Indeed, the β spin orbital of the OH σ bond (βOH green IBO in Fig. 4(A)) does not move together with the proton; instead, it remains localized on the phenol as a π C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond orbital. In the case of HAT, this spin IBO would have been transferred to the peroxyl radical, so that the proton and the electron traveled together. Indeed, the early stage of the reaction resembles this situation, since the green spin IBO partially covers the proton transfer region. However, as the blue βπ spin IBO reaches the same region of space, the green βOH spin IBO moves back to the phenolic moiety, while the former spin orbital moves to the peroxyl moiety. Moreover, the corresponding α spin orbital of the OH σ bond (Fig. S2, ESI†) behaves in a similar way, confirming that both electrons of the OH σ bond remain localized on the phenolic system. Lastly, the α unpaired electron of the peroxyl radical belongs to the purple α′ spin IBO as an O-centered orbital (α′ in Fig. 4(A)), which becomes part of the newly formed OH σ bond, pairing to the βπ spin IBO in the closed–shell electronic configuration of hydrogen peroxide, as the reaction product.
O bond orbital. In the case of HAT, this spin IBO would have been transferred to the peroxyl radical, so that the proton and the electron traveled together. Indeed, the early stage of the reaction resembles this situation, since the green spin IBO partially covers the proton transfer region. However, as the blue βπ spin IBO reaches the same region of space, the green βOH spin IBO moves back to the phenolic moiety, while the former spin orbital moves to the peroxyl moiety. Moreover, the corresponding α spin orbital of the OH σ bond (Fig. S2, ESI†) behaves in a similar way, confirming that both electrons of the OH σ bond remain localized on the phenolic system. Lastly, the α unpaired electron of the peroxyl radical belongs to the purple α′ spin IBO as an O-centered orbital (α′ in Fig. 4(A)), which becomes part of the newly formed OH σ bond, pairing to the βπ spin IBO in the closed–shell electronic configuration of hydrogen peroxide, as the reaction product.
The changes of the βπ and βOH spin IBOs (Fig. 4(A)) along the reaction path clearly indicate a CPET mechanism, but the shape of the βπ spin IBO in the proton transfer region at the TS ambiguously suggests a HAT mechanism. However, there is still a non-zero probability of finding the electron on the aromatic ring in the TS, unlike in a canonical HAT mechanism. Therefore, the CPET/HAT distinction relies on the involved orbital, rather than on the absence/presence of a “naked” proton, which is transferred from one molecule to the other. Indeed, no such species really exists since the proton is always surrounded by an orbital: initially the βOH spin IBO, then the βπ one.
The SOMO analysis of the partially constrained TS state suggested a HAT mechanism; however, this picture drastically changes when looking at the spin IBOs along this energetically disfavored reaction path. Fig. 4(B) shows the changes in βπ and βOH spin IBOs involved in the reaction, which allow to discriminate between CPET and HAT mechanisms. As in the previous case, the π system is indeed involved in the reactivity, since one π spin IBO of the ring contributes to the OH σ bond of the peroxide. Meanwhile, the βOH spin IBO is delocalized on the adjacent carbon atom on the phenoxyl radical. Likely in the fully relaxed reaction path, the βOH spin IBO is partially delocalized in the proton transfer region at the early stage of the reaction; then, the βπ spin IBO actually becomes associated to the peroxyl moiety. Interestingly, oxygen lone pairs are not involved in the electronic flow from the donor to the acceptor, not even when forcing the structure to maintain a p orbital orthogonal to the ring plane to promote a better overlap with the aromatic π system. Therefore, the mechanism is described with confidence as a CPET from the aromatic ring and the limits of the SOMO analysis clearly emerge.
The same strategy was applied to the phenoxyl/phenol, benzyl/toluene and methoxyl/methanol self-exchange reactions to assess if the analysis based on IBOs might reproduce the established mechanisms of these well-known systems. Starting with the phenoxyl/phenol reaction, the electron flow was evaluated along the reaction path, highlighting the main spin IBOs involved. Fig. 5 shows that the electron associated with the βπ spin IBO (blue) is transferred from one phenol ring to the other via a direct π–π interaction. The oxygen atoms and the proton transfer region are hardly involved in the process, resulting in a CPET mechanism with an electron transfer between the two aromatic moieties. The OH σ spin IBO (green) does not change following the proton transfer but is rather delocalized on the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group of the same system. Similar results are also found in the absence of the π–π interaction, along the reaction path via the partially constrained TS in the anti configuration (Fig. S3, ESI†). The process prefers to maintain the CPET mechanism characterized by an electron transfer between the π systems of the aromatic rings, rather than involving the oxygen lone pairs and switching to HAT.
O group of the same system. Similar results are also found in the absence of the π–π interaction, along the reaction path via the partially constrained TS in the anti configuration (Fig. S3, ESI†). The process prefers to maintain the CPET mechanism characterized by an electron transfer between the π systems of the aromatic rings, rather than involving the oxygen lone pairs and switching to HAT.
The CPET mechanisms of the systems above described involve their π aromatic moieties, but their presence does not necessarily imply a mechanistic preference. Conversely, the role of the heteroatom (oxygen in our case) is crucial in this context; indeed, the electron flow analysis revealed a change of mechanism when moving from the phenoxyl/phenol to the benzyl/toluene self-exchange reaction. Particularly, the spin IBOs (Fig. S4, ESI†) clearly show a HAT process along both reaction paths; the CH σ bond orbital progressively moves to the other molecule following the proton at each step, until the new CH bond is formed and the spin IBO maintains the same σ symmetry.
Lastly, the methoxyl/methanol self-exchange reaction is described by a HAT mechanism according to our IBO-based analysis (Fig. S5, ESI†) for each reaction path, as found in the SOMO analysis. Indeed, no differences can be found when compared to the benzyl/toluene system looking at the spin IBOs involved in both reaction paths.
Table 1 summarizes the outcomes of the SOMO and IBO analysis for all the reactions studied, i.e., whether the mechanism is CPET or HAT according to the specific method. Overall, the HAT mechanism is well reproduced by the established SOMO analysis, while the CPET is not always correctly assigned by this method. Particularly, the SOMO analysis is intrinsically limited since it is focused on a single point along the PES, i.e. the transition state. Although it may lead to the correct assessment of the mechanism, it is not a guarantee of success. Conversely, the IBO-based analysis correctly assigns the mechanism of each system in a chemically intuitive way, by following the electron flow during the whole reaction path. Moreover, the IBO analysis gives information about the molecular moiety involved in electron transfer, providing a complete picture of the phenomena; however, no general rationalization can be drawn. Therefore, we propose to combine the IBO-based analysis with ASA to understand the determining factors that control the reactivity.
| Reaction | Path | SOMO | IBO | Literature |
|---|---|---|---|---|
| a The recognition is uncertain due to SOMO ambiguity. | ||||
| Phenol + ˙OOH | Relaxed | CPETa | CPET | — |
| Partially constrained | HAT | CPET | ||
| Phenoxyl/phenol | Relaxed | HAT | CPET | CPET |
| Partially constrained | CPET | CPET | ||
| Benzyl/toluene | Relaxed | HAT | HAT | HAT |
| Partially constrained | HAT | HAT | ||
| Methoxyl/methanol | Relaxed | HAT | HAT | HAT |
| Partially constrained | HAT | HAT | ||
Mechanistic insights through ASA
In all systems, the IBO-based analysis revealed that the mechanism does not change when comparing the relaxed and partially constrained reaction paths; however, the relative orientation of the two reactants affects the energy of the TSs. Thus, ASA (see Computational details) was employed to accurately evaluate the structure–reactivity relation, particularly the factors controlling the preferential geometry of the approaching reactants, highlighting the differences between CPET and HAT mechanisms.First, the hydrogen abstraction from phenol by ˙OOH was evaluated. ΔEstrain and ΔEint were calculated along a reaction coordinate, which is the distance between the peroxyl radical's oxygen accepting the proton and the transferred proton itself; that is, the reaction coordinate is the O–H bond formation with respect to the initial O–H distance at the beginning of the reaction, i.e., in the reactant complex.
Fig. 6(A) shows the energy profiles for the CPET of phenol with ˙OOH and, as expected, the energy path crossing the partially constrained TS lies at higher energies than the relaxed path. ΔEstrain is not responsible for the energy difference between the two paths; the lines are superimposed, revealing that the same strain destabilizes the two systems at each step of the reaction coordinate. In contrast, ΔEint reproduces the observed trend, with much favorable interaction energy computed along the relaxed reaction path.
A different reaction coordinate could be used for the analysis without significant difference in the interpretation (Fig. S6, ESI†). Particularly, the distance between the phenol oxygen and hydrogen represents the complementary O–H breaking coordinate, with respect to the initial O–H distance. With this reaction coordinate, the reactivity is still interaction-controlled; however, ΔEstrain curves are no longer superimposed, following the opposite trend compared to the total energy. This indicates that the relaxed path is characterized by a slightly higher ΔEstrain, which is probably due to the shift of the hydroxyl group out of the ring plane. Conversely, along the partially constrained path, this deformation is less pronounced since the proton transfer occurs closer to the ring plane. Since the energy trend is ruled by ΔEint, EDA scheme was applied. ΔEPauli (Fig. 6(B)) and ΔVelstat (Fig. 6(C)) curves are superimposed for the two reaction paths at any point of the reaction coordinate; in contrast, ΔEOI (Fig. 6(D)) reproduces the energy trend. Thus, a more stabilizing orbital interaction is computed for the relaxed path, justifying why the relaxed geometry of the TS is preferred.
Finally, to gain insight on the nature of the orbital interaction, the EDA–NOCV scheme was applied to further decompose ΔEOI. The reaction coordinate corresponding to the TSs was selected (r.c. = 0.54) and one main contribution to the energy was found for specific α and β NOCV pairs in both selected points. Fig. 6(E) and (F) shows the α and β deformation densities associated to the main ΔEkOI for each species. In both cases, the α densities correspond to the charge flow of the peroxyl O–H bond formation and the phenolic O–H bond cleavage. The β densities are more interesting since they show a net charge flow from the aromatic moiety to the peroxyl one. This finding nicely agrees with the IBO-based analysis, supporting the outcome that the π system is indeed involved in the electron transfer in a CPET mechanism.
The energy difference in ΔEOI for the two TSs can be rationalized by the ΔEkOI contribution associated to the NOCV pairs. Particularly, similar ΔEkOI are computed for the two α densities of the relaxed and the partially constrained TSs (−20.5 and −21.0 kcal mol−1, respectively). Conversely, a larger energy difference is computed for the β densities, i.e., −40.3 and −30.7 kcal mol−1, respectively; indicating a better orbital interaction associated with the β charge flow in the relaxed TS. Thus, overall, the π system acts as a better electron donor to the peroxyl radical in the relaxed structure. In the end, the reduced orbital stabilization associated to the charge transfer in the partially constrained TS is responsible for its reduced stability.
The same approach was also employed in the phenoxyl/phenol case to evaluate the origin of the preferential transition state geometry and, thus, the reaction path. To remain consistent with the previous analysis, the chosen reaction coordinate is the formation of the O–H bond. Fig. 7(A) shows the energy profiles of the two reaction paths; particularly, an additional energy of 4 kcal mol−1 is required to cross the barrier via the partially constrained TS. This overall energy amount is due to ΔEint, which is highly more stabilizing for the fully relaxed path. Conversely, ΔEstrain is lower in the partially constrained reaction path, since it occurs without any significant distortion of the hydroxyl group out of the ring plan. However, the higher ΔEstrain leading to the π–π stacking configuration is not sufficient to compensate for the ΔEint difference, which represents the key contribution for the path preference.
The TSs fall at similar points of the reaction coordinate. Particularly, a slightly later transition state characterizes the partially constrained path along the chosen reaction coordinate. Actually, if the curves are projected along the O–H bond breaking coordinate (Fig. S7, ESI†), the relaxed TS becomes slightly later. However, the same conclusions can be drawn.
The decomposition of ΔEint shows ΔEOI (Fig. 7(B)) as the sole contribution consistent with the observed trend, while ΔEPauli and ΔVelstat (Fig. S8, ESI†) do not support the ΔEint energy order, consistently with the previous CPET reaction analyzed. Thus, since ΔEOI is responsible for the preference of one configuration of the TS, the EDA–NOCV scheme was applied to understand quantitatively the orbital interaction. The α deformation densities associated to the main ΔEkOI (Fig. 7(C) and (D)) correspond to the charge flow of the O–H bond formation and breaking; while the corresponding β densities show a net charge flow between the two aromatic moieties. As found for CPET with ˙OOH, the α densities do not affect the reaction path, since ΔEkOI are very similar in both cases (−22.1 and −21.7 kcal mol−1, respectively). Indeed, the β deformation density for the π–π stacking system is associated with a ΔEkOI value of −28.9 kcal mol−1, while a value of −16.1 kcal mol−1 is computed for the anti configuration. Thus, a better orbital interaction is observed in the former, justifying the relaxed reaction path as the most favored for the CPET mechanism with electron transfer between the π systems of the aromatic moieties.
A different picture is observed for the benzyl/toluene self-exchange reaction, which represents a HAT process without the participation of the π system of the aromatic moieties to the electron transfer. However, also in this case, two TSs are found with different energies; therefore, ASA helped to understand why one is preferred over the other (Fig. 8(A)). As in the previous cases, the degree of C–H bond formation was chosen as the reaction coordinate. Once again, ΔEint explains the energy trend, since it is more stabilizing for the lower energy path. As result of ΔEint decomposition, both ΔVelstat (Fig. 8(C)) and ΔEOI (Fig. 8(D)) are equally responsible for the energy difference of the two reaction paths. The orbital contribution is still partially significant due to the presence of aromatic moieties, which stabilize the π–π stacking configuration, although they are not directly involved in the electron transfer process. Interestingly, ΔVelstat arises as a dominant contribution for this HAT process, while only ΔEOI affects the CPET mechanisms previously analyzed.
To confirm that the aromatic moieties are not involved in the electron transfer, the β deformation densities were computed (Fig. S9, ESI†). Indeed, they show a net charge flow confined in the hydrogen atom transfer region between the methylene groups of the two molecules.
Lastly, Fig. S10 (ESI†) shows ASA/EDA results for the methoxyl/methanol self-exchange reactions. ΔEint and particularly ΔVelstat are responsible for the reaction path selection, while ΔEOI has no role in explaining the lowest energy one. This confirms that in HAT mechanisms, unlike in CPET, the orbital interaction does not impact the structure of the transition state and the reaction path choice, but rather the electrostatic effects seem to dominate the reactivity. Thus, the effect of donor–acceptor distance is evaluated to understand how the CPET mechanism responds to a decreased orbital interaction.
Donor–acceptor distance effects
The CPET mechanism requires the transfer of an electron and a proton as separate processes; however, as above described, a naked proton is not observed since it is always surrounded by electron density, making the distinction between hydrogen atom or proton transfer difficult to detect even experimentally.4 Thus, a computational experiment was set up by increasing the reaction distance between the phenol and the ˙OOH radical, in order to facilitate the separation of the two transfer processes.A TS was found by increasing the distance, from 2.3 Å to 3.3 Å, between the two oxygen atoms donating and accepting the proton. Indeed, this transition state is highly destabilized by 56.4 kcal mol−1 with respect to the relaxed one. To evaluate the effect of this distance on the mechanism, the spin IBO (Fig. 9) associated with the transferred β electron was analyzed along the new reaction path. Instead of obtaining a better separation of the electron and proton transfers, the IBO-based analysis reveals a change in the mechanism, which becomes HAT. The β spin IBO of the OH σ bond progressively follows the proton, becoming part of the new OH σ bond on the peroxide. Moreover, the same spin IBO covered the whole proton transfer region at the TS and this shape clearly indicates a HAT mechanism. Thus, at higher donor–acceptor distance the orbital interaction is no longer efficient to allow a CPET mechanism and, in order to avoid the presence of a naked proton, the mechanism switches to HAT, maintaining the electron density on the proton itself.
The same experiment was performed for the phenoxyl/phenol system; thus, the distance between the two molecules was increased to assess how the electron transfer mechanism changes. In this case, the increase in the TS O–O distance by 1 Å (from 2.4 Å to 3.4 Å) is not sufficient to switch the mechanism, which remains CPET (Fig. S11A, ESI†). However, the proton transfer character of the process is reduced since the spin IBO is also delocalized on the proton in the transition state to avoid the presence of a naked traveling proton. Again, a proper HAT mechanism is found when the O–O distance is further increased to 4.4 Å (Fig. S11B, ESI†), since the aromatic moieties are too far to interact and HAT is the only possible mechanism to occur.
Conclusions
A computational strategy is presented to distinguish CPET and HAT mechanisms and to evaluate the factors controlling the reactivity of four model reactions: hydrogen abstraction from phenol by a hydroperoxyl radical and the well-known phenoxyl/phenol, benzyl/toluene and methoxyl/methanol self-exchange reactions.The analysis of the SOMO of the transition state shows some ambiguities for the hydrogen abstraction form phenol and inconsistencies for the phenoxyl/phenol system, if compared to the mechanism established in the literature. Thus, this approach, focused on a single point along the reaction path, seems limited and although it works nicely in some cases, it may fail in others. Conversely, the electron flow along the reaction path computed by following the change of the main spin IBOs involved in each reaction allows the correct identification of the mechanism. The results clearly show the distinction between CPET and HAT; particularly, the hydrogen abstraction form phenol and the phenoxyl/phenol self-exchange reaction are associated with the CPET mechanism with electron transfer from the π system of the aromatic moieties. Conversely, the benzyl/toluene and methoxyl/methanol systems are associated with the HAT mechanism.
The rationalization of the mechanistic picture of IBOs is evaluated in the framework of ASA/EDA, through a comparison with partially constrained structures selected according to chemical intuition. According to this decomposition scheme, the energy trend of the different reaction paths for the CPET mechanism is ruled by orbital interaction, while the electrostatic contribution becomes significant in the HAT mechanism. These results suggest that the orbital and electrostatic contributions determine the geometrical structure of the transition state for CPET and HAT mechanisms, respectively.
Lastly, the effect of the donor–acceptor distance is evaluated for CPET reactions by increasing the O–O distance in the transition state of the considered systems. At a sufficiently large distance the CPET mechanism switches to HAT, since the orbital interaction is no longer efficient to allow the electron transfer involving the π system of the aromatic moieties. Thus, HAT is the only possibility to perform a H+/e− transfer under these conditions.
Overall, we recommend that due to the intrinsic difficulties in discriminating between CPET and HAT, a combination of the illustrated approaches should be used. The SOMO analysis is qualitative and must be taken with caution; the IBO-based study in principle provides a correct identification of the mechanism but does not offer a thorough explanation especially if a comparison between similar substrates is considered; particularly useful, in this case, is ASA which helps to rationalize also the mechanistic changes occurring upon deformations or atom variations in series of analogous compounds.
Computational methods
All density functional theory (DFT) calculations were carried out using Gaussian16.53 For all geometry optimizations, the M06-2X54 functional was used combined with the 6-31G(d) basis set. Frequency calculations were performed for all optimized structures to assess the nature of each stationary point. Particularly, it was ascertained that all minima have real frequencies, whereas transition states have one imaginary frequency associated with the correct normal mode along the reaction coordinate. The reaction paths were calculated using the intrinsic reaction coordinate (IRC) method.55 To obtain more accurate estimates of the electronic energies, single-point calculations were carried out, using the same functional combined with the extended 6-311+G(d,p) basis set (level of theory: M06-2X/6-311+G(d,p)//M06-2X/6-31G(d)), in agreement with hydrogen abstraction reactions performed on small organic molecules and the QM-ORSA protocol applied to quantify their scavenging potential.7,56–61 Electron flow was analyzed along the reaction path using the intrinsic bond orbital (IBO) formalism,35,36 as implemented in IboView software. Since this software does not support the 6-31G basis set family, single point calculations were performed using the def2TZVP basis set. Spin contamination was checked for all doublet species and was found to be negligible; also, each wave function stability was assessed.Partially constrained transition states were optimized by imposing a frozen dihedral angle for each species during the optimization; by relaxing the constraints, the optimization of these transition states leads to the structures obtained by the full optimization. The values of the frozen dihedral angles are different and depend on the system since they were selected by performing an initial scan of the potential energy surface (PES) along a specific coordinate. This scan was conducted with the initial purpose of obtaining the energetically disfavored path without imposing any constraint. When not possible (the relaxation lead to the fully optimized transition state structure), the computed dihedral angle was maintained frozen and a partially constrained structure was optimized.
For the sake of comparison and completeness, highly correlated CCSD(T) energies were calculated, starting from the previously optimized structures, through the DLPNO-CCSD(T) method,62 as implemented in the Orca 4.2.1 package.63,64 The all-electron relativistic contracted basis set cc-pVTZ-DK with Douglas–Kroll–Hess (DKH) scalar relativistic Hamiltonian was used for all atoms.65,66 This level of theory is denoted as DLPNO-CCSD(T)/cc-pVTZ-DK//M06-2X/6-31G(d). Moreover, the second-order Moller–Plesset (MP2)67 method was tested in single point calculations, combined with the aug-cc-pVTZ basis set. Finally, in the DFT framework, different functionals (BLYP, BLYP-D3(BJ), M06L, PBE1PBE, PBE1PBE-D3(BJ), M06 and M05-2X) and different basis sets combined to M06-2X (cc-pVTZ, def2TZVP and 6-311+G(d,p)) were tested in the geometry optimizations for the methoxyl/methanol self-exchange reaction.
Activation strain analysis (ASA) and energy decomposition analysis (EDA) were performed along a selected reaction coordinate,68–71 using IRC profiles and the program PyFrag.72 Therefore, single point calculations along the energy profiles were performed using amsterdam density functional (ADF) 2019.307.73,74 Zeroth-order regular approximation (ZORA) was employed to include scalar relativistic effects.75 The same functional used for the optimization procedure was employed together with the all electron TZ2P basis set for all atoms (level of theory: ZORA-M06-2X/TZ2P//M06-2X/6-31G(d)).
ASA is an approach based on the definition of chemically meaningful fragments, in which the total energy is expressed as the sum of two contributions at any point along the reaction coordinate (ζ):
| ΔE(ζ) = ΔEstrain(ζ) + ΔEint(ζ) | (1) |
| ΔEint(ζ) = ΔVelstat(ζ) + ΔEOI(ζ) + ΔEPauli(ζ) + ΔEdisp(ζ) | (2) |
The orbital contribution ΔEOI was further decomposed according to EDA–NOCV (energy decomposition analysis–natural orbital for chemical valence) scheme:76,77
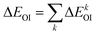 | (3) |
 | (4) |
However, since M06-2X functional was used, a meta-hybrid correction term is included in ΔEOI of EDA in eqn (2); this correction term is not decomposed in this framework according to eqn (3), thus generating a discrepancy between the ΔEOI of the two schemes. In our systems, this term is positive and smaller than the dominating ΔEkOI (in absolute value); most importantly, this term remains approximately constant in the analyzed systems. Thus, the meta-hybrid correction is not fundamental for this orbital analysis.
Data availability
All data generated or analyzed during this study are included in the ESI.†Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This research was supported by Università degli Studi di Padova. The authors are grateful to CINECA for the generous allocation of computational resources (Project ISCRA C SIM-2, HP10C9J8UJ P.I. Laura Orian) and to Legnaro National Laboratories of the Italian Institute of Nuclear Physics (INFN) for access to cloud facilities (CloudVeneto). The authors are grateful to Dr Andrea Madabeni for scientific discussion.References
- B. Pettersson Rimgard, Z. Tao, G. A. Parada, L. F. Cotter, S. Hammes-Schiffer, J. M. Mayer and L. Hammarström, Science, 2022,(377), 742–747 CrossRef PubMed
.
- P. R. D. Murray, J. H. Cox, N. D. Chiappini, C. B. Roos, E. A. McLoughlin, B. G. Hejna, S. T. Nguyen, H. H. Ripberger, J. M. Ganley, E. Tsui, N. Y. Shin, B. Koronkiewicz, G. Qiu and R. R. Knowles, Chem. Rev., 2022, 122, 2017–2291 CrossRef CAS PubMed
.
- G. A. Parada, Z. K. Goldsmith, S. Kolmar, B. Pettersson Rimgard, B. Q. Mercado, L. Hammarström, S. Hammes-Schiffer and J. M. Mayer, Science, 2019, 364(6439), 471–475 CrossRef CAS PubMed
.
- J. J. Warren and J. M. Mayer, Biochemistry, 2015, 54, 1863–1878 CrossRef CAS PubMed
.
- T. J. Meyer, M. H. V. Huynh and H. H. Thorp, Angew. Chem., Int. Ed., 2007, 46, 5284–5304 CrossRef CAS PubMed
.
- D. Usharani, D. C. Lacy, A. S. Borovik and S. Shaik, J. Am. Chem. Soc., 2013, 135, 17090–17104 CrossRef CAS
.
- A. Galano and J. Raúl Alvarez-Idaboy, Int. J. Quantum. Chem., 2019, 119, 1–23 CrossRef
.
- R. A. Binstead, B. A. Moyer, G. J. Samuels and T. J. Meyer, J. Am. Chem. Soc., 1981, 103, 2897–2899 CrossRef CAS
.
- J. M. Mayer, Annu. Rev. Phys. Chem., 2004, 55, 363–390 CrossRef CAS
.
- J. W. Darcy, B. Koronkiewicz, G. A. Parada and J. M. Mayer, Acc. Chem. Res., 2018, 51, 2391–2399 Search PubMed
.
- J. J. Warren, T. A. Tronic and J. M. Mayer, Chem. Rev., 2010, 110, 6961–7001 Search PubMed
.
-
J. Perkins, Radical chemistry, Ellis Horwood, 1994 Search PubMed
.
-
L. Feray, N. Kuznetsov and P. Renaud, in Radicals in Organic Synthesis, Wiley, 2001, pp. 246–278 Search PubMed
.
- J. Weiss, Trans. Faraday Soc., 1941, 37, 782 Search PubMed
.
- S. Cannizzaro, Justus Liebigs Ann. Chem., 1853, 88, 129–130 CrossRef CAS
.
- J. E. M. N. Klein and G. Knizia, Angew. Chem., Int. Ed., 2018, 57, 11913–11917 CrossRef CAS PubMed
.
- J. M. Mayer, D. A. Hrovat, J. L. Thomas and W. T. Borden, J. Am. Chem. Soc., 2002, 124, 11142–11147 CrossRef CAS PubMed
.
- S. Hammes-Schiffer, ChemPhysChem, 2002, 3, 33–42 CrossRef CAS
.
- M. Lingwood, J. R. Hammond, D. A. Hrovat, J. M. Mayer and W. T. Borden, J. Chem. Theory Comput., 2006, 2, 740–745 CrossRef CAS PubMed
.
- A. Galano, Phys. Chem. Chem. Phys., 2011, 13, 7178 RSC
.
- P. D. Maldonado, J. R. Alvarez-Idaboy, A. Aguilar-González, A. Lira-Rocha, H. Jung-Cook, O. N. Medina-Campos, J. Pedraza-Chaverrí and A. Galano, J. Phys. Chem. B, 2011, 115, 13408–13417 CrossRef CAS PubMed
.
- G. A. DiLabio and E. R. Johnson, J. Am. Chem. Soc., 2007, 129, 6199–6203 CrossRef CAS PubMed
.
- C. Isborn, D. A. Hrovat, W. T. Borden, J. M. Mayer and B. K. Carpenter, J. Am. Chem. Soc., 2005, 127, 5794–5795 CrossRef CAS PubMed
.
- D. Milenković, J. Đorović, V. Petrović, E. Avdović and Z. Marković, React. Kinet., Mech. Catal., 2018, 123, 215–230 CrossRef
.
- A. Martínez, A. Galano and R. Vargas, J. Phys. Chem. B, 2011, 115, 12591–12598 CrossRef
.
- S. Hammes-Schiffer, Acc. Chem. Res., 2001, 34, 273–281 CrossRef CAS PubMed
.
- A. Sirjoosingh and S. Hammes-Schiffer, J. Phys. Chem. A, 2011, 115, 2367–2377 CrossRef CAS PubMed
.
- O. Tishchenko, D. G. Truhlar, A. Ceulemans and M. T. Nguyen, J. Am. Chem. Soc., 2008, 130, 7000–7010 CrossRef CAS
.
- J. H. Skone, A. V. Soudackov and S. Hammes-Schiffer, J. Am. Chem. Soc., 2006, 128, 16655–16663 CrossRef CAS
.
- E. Hatcher, A. Soudackov and S. Hammes-Schiffer, J. Phys. Chem. B, 2005, 109, 18565–18574 CrossRef CAS PubMed
.
- J. M. Mayer, J. Phys. Chem. Lett., 2011, 2, 1481–1489 CrossRef CAS PubMed
.
- L. D’Amore, L. Belpassi, J. E. M. N. Klein and M. Swart, Chem. Commun., 2020, 56, 12146–12149 RSC
.
- K. M. Hess, I. F. Leach, L. Wijtenhorst, H. Lee and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2024, 63, e202318916 CrossRef CAS PubMed
.
- L. D. Mena and M. T. Baumgartner, J. Am. Chem. Soc., 2022, 144, 15922–15927 Search PubMed
.
- G. Knizia and J. E. M. N. Klein, Angew. Chem., Int. Ed., 2015, 54, 5518–5522 CrossRef CAS PubMed
.
- G. Knizia, J. Chem. Theory Comput., 2013, 9, 4834–4843 CrossRef CAS
.
- I. Kruk, H. Y. Aboul-Enein, T. Michalska, K. Lichszteld and A. Kładna, Luminescence, 2005, 20, 81–89 CrossRef CAS PubMed
.
- M. Platzer, S. Kiese, T. Tybussek, T. Herfellner, F. Schneider, U. Schweiggert-Weisz and P. Eisner, Front. Nutr., 2022, 9, 882458 CrossRef PubMed
.
- K. Neha, M. R. Haider, A. Pathak and M. S. Yar, Eur. J. Med. Chem., 2019, 178, 687–704 CrossRef CAS
.
- G. Ribaudo, M. Bortoli, C. Pavan, G. Zagotto and L. Orian, Antioxidants, 2020, 9, 714 CrossRef CAS
.
- Md. M. Rahaman, R. Hossain, J. Herrera-Bravo, M. T. Islam, O. Atolani, O. S. Adeyemi, O. A. Owolodun, L. Kambizi, S. D. Daştan, D. Calina and J. Sharifi-Rad, Food Sci. Nutr., 2023, 00, 1–14 CAS
.
- A. Galano, D. X. Tan and R. J. Reiter, J. Pineal Res., 2011, 51, 1–16 CrossRef CAS PubMed
.
- J. Kibet, L. Khachatryan and B. Dellinger, Environ. Sci. Technol., 2012, 46, 12994–13001 CrossRef CAS PubMed
.
- S. V. Patil and D. S. Argyropoulos, ChemSusChem, 2017, 10, 3284–3303 CrossRef CAS
.
- M. Navarrete, C. Rangel, J. Espinosa-García and J. C. Corchado, J. Chem. Theory Comput., 2005, 1, 337–344 Search PubMed
.
- Y.-Z. Li, X.-L. Zhou, B.-Q. Huo, D.-Z. Chen, Z.-H. Liu and X.-H. Sheng, Front. Chem., 2019, 7, 498611 Search PubMed
.
- A. Galano, R. Álvarez-Diduk, M. T. Ramírez-Silva, G. Alarcón-Ángeles and A. Rojas-Hernández, Chem. Phys., 2009, 363, 13–23 CrossRef CAS
.
- R. Castañeda-Arriaga, T. Marino, N. Russo, J. R. Alvarez-Idaboy and A. Galano, New J. Chem., 2020, 44, 9073–9082 RSC
.
- M. Spiegel, K. Cel and Z. Sroka, Food Chem., 2023, 407, 134677 CrossRef CAS
.
- W. Bors and C. Michel, Ann. N. Y. Acad. Sci., 2002, 957, 57–69 CrossRef CAS PubMed
.
- F. Di Meo, V. Lemaur, J. Cornil, R. Lazzaroni, J.-L. Duroux, Y. Olivier and P. Trouillas, J. Phys. Chem. A, 2013, 117, 2082–2092 CrossRef CAS PubMed
.
- G. Litwinienko and K. U. Ingold, Acc. Chem. Res., 2007, 40, 222–230 CrossRef CAS PubMed
.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed
.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed
.
- Y. Zhang, M. Sayama, M. Luo, Y. Lu and D. J. Tantillo, J. Chem. Educ., 2022, 99, 2721–2725 CrossRef CAS
.
- G. Ribaudo, M. Bortoli, A. Ongaro, E. Oselladore, A. Gianoncelli, G. Zagotto and L. Orian, RSC Adv., 2020, 10, 18583–18593 RSC
.
- D. Zeppilli, G. Ribaudo, N. Pompermaier, A. Madabeni, M. Bortoli and L. Orian, Antioxidants, 2023, 12, 525 CrossRef CAS PubMed
.
- D. Zeppilli, A. Aldinio-Colbachini, G. Ribaudo, C. Tubaro, M. Dalla Tiezza, M. Bortoli, G. Zagotto and L. Orian, Int. J. Mol. Sci., 2023, 24, 11797 CrossRef CAS
.
- M. Spiegel, J. Chem. Inf. Model., 2022, 62, 2639–2658 CrossRef CAS
.
- D. Zeppilli, G. Grolla, V. Di Marco, G. Ribaudo and L. Orian, Inorg. Chem., 2024, 63, 21856–21867 CrossRef CAS PubMed
.
- G. Ribaudo, M. Bortoli, C. E. Witt, B. Parke, S. Mena, E. Oselladore, G. Zagotto, P. Hashemi and L. Orian, ACS Omega, 2022, 7, 8314–8322 CrossRef CAS PubMed
.
- D. G. Liakos, Y. Guo and F. Neese, J. Phys. Chem. A, 2020, 124, 90–100 CrossRef CAS PubMed
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, 1–6 Search PubMed
.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS
.
- D. A. Pantazis and F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 363–374 CAS
.
- F. Neese, A. Wolf, T. Fleig, M. Reiher and B. A. Hess, J. Chem. Phys., 2005, 122, 204107 CrossRef PubMed
.
- Chr Møller and M. S. Plesset, Phys. Rev., 1934, 46, 618–622 CrossRef
.
- L. P. Wolters and F. M. Bickelhaupt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 324–343 CAS
.
- F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070–10086 Search PubMed
.
-
F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley, Indianapolis, 2000, vol. 15, pp. 1–86 Search PubMed
.
- P. Vermeeren, S. C. C. van der Lubbe, C. Fonseca Guerra, F. M. Bickelhaupt and T. A. Hamlin, Nat. Protoc., 2020, 15, 649–667 CrossRef CAS
.
- W.-J. van Zeist, C. F. Guerra and F. M. Bickelhaupt, J. Comput. Chem., 2008, 29, 312–315 CrossRef CAS
.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967 CrossRef CAS
.
- ADF2019, AMS2020, SCM. Theoretical Chemistry, Vrije Universiteit, Amsterdam: The Netherlands., https://www.scm.com/, (accessed 10 January 2025).
- E. van Lenthe, E. J. Baerends and J. G. Snijders, J. Chem. Phys., 1994, 101, 9783–9792 CrossRef CAS
.
- A. Michalak, M. Mitoraj and T. Ziegler, J. Phys. Chem. A, 2008, 112, 1933–1939 CrossRef CAS PubMed
.
- M. P. Mitoraj, A. Michalak and T. Ziegler, J. Chem. Theory Comput., 2009, 5, 962–975 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available: Reaction and activation energies computed using MP2 and DLPNO-CCSD(T) levels of theory; reaction and activation energies computed using different functionals and basis sets for the methoxyl/methanol systems; transition state SOMOs for the methoxyl/methanol systems; additional IBOs along reaction paths; additional ASA/EDA with a different reaction coordinate; EDA–NOCV scheme for the benzyl/toluene systems; coordinates, energies and imaginary frequencies of the stationary points. See DOI: https://doi.org/10.1039/d5cp00690b |
| This journal is © the Owner Societies 2025 |










