Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Development of a force field for ATP – how charge scaling controls self-association†
Tuan Minh
Do
 *ab,
Nobuyuki
Matubayasi
*ab,
Nobuyuki
Matubayasi
 b and
Dominik
Horinek
b and
Dominik
Horinek
 *a
*a
aInstitute of Physical and Theoretical Chemistry, University of Regensburg, 93040 Regensburg, Germany. E-mail: dominik.horinek@ur.de
bDivision of Chemical Engineering, Graduate School of Engineering Science, Osaka University, 560-8531 Toyonaka, Osaka, Japan. E-mail: do.minh@cheng.es.osaka-u.ac.jp
First published on 19th February 2025
Abstract
The discovery that ATP can prevent the aggregation of proteins and enhance their stability sparked significant interest in understanding the interactions between ATP and proteins. All-atom molecular dynamics simulations provide detailed insight into the underlying mechanism, while an appropriate force field must be developed. Existing force fields accurately describe the conformations of polyphosphates, but are not suitable for simulations at high ATP concentrations, because excessive self-aggregation occurs. We address this issue by scaling the atomic charges of the ATP anion and its counterions. The experimentally observed aggregation can be reproduced by using a scaling factor of 0.7 applied to the phosphate moiety of ATP and its counterions. This charge scaling is in line with a physically motivated implicit account of polarization effects, which is increasingly applied in simulations of ionic systems.
1. Introduction
Adenosine triphosphate (ATP) is an amphiphilic molecule composed of a ribose sugar, an adenosine base, and a highly negatively charged triphosphate. It is mainly known through its ubiquitous role as an energy source in biology. Recent experiments have revealed that ATP has an additional function: it can suppress the malicious aggregation of peptides.1 Hence, another presumed function of ATP is the maintenance of proteins inside cells in solution. Due to this finding, numerous studies both experimentally and computationally have been carried out to analyze how ATP suppresses fibril formation.2–9Computational studies using all-atom molecular dynamics simulations are especially valuable to obtain molecular-level insight into the underlying mechanism with atomic resolution. It has been revealed that ATP binds to protein surfaces through unspecific interactions with both hydrophilic and hydrophobic residues thanks to the amphiphilic and flexible structure of ATP.3–5,7,9 Several mechanisms based on this finding have been proposed to explain the suppression of fibril formation by ATP.3–5,7,9 For computational studies with molecular dynamics simulations, it is important that suitable force field parameters are used. For ATP, the polyphosphate parameters of Meagher et al. based on AMBER parameters have been widely adopted.2–5,10 However, it is also known that the original force field parameters of Meagher et al. lead to strong aggregation of ATP at concentrations of 10 mM, in contradiction to experiments.3,11 As the ATP concentration in molecular dynamics simulations typically range between 10 mM and 100 mM,2–4,7,9 it might be necessary to adjust the force field parameters. While it has been reported that the TIP4P-D and OPC water models greatly improve the aggregation of ATP compared to the TIP3P water model, the oligomeric state is still over-represented.11
To counteract the overestimated aggregation tendency of ATP, we proposed to scale the charges of the phosphate moiety of ATP by a factor of 0.7.3 The motivation to scale the charges is to account for the error in the description of electronic screening which arises when non-polarizable force fields are used.12,13 It has been shown that this approach reduces the amount of aggregation to experimentally close values.3,14
While screening effects can also be described by explicitly incorporating polarization into force fields,15–17 a major drawback is the increased computational cost, which is particularly limiting for simulations of complex systems such as ATP–protein solutions. As a result, polarizable force fields are not as refined as non-polarizable ones, which can lead to lower accuracy.18–20
An alternative approach for addressing the exaggerated aggregation tendency of solvated molecules is the adjustment of the Lennard-Jones potential parameters or combination rules in an ad hoc manner.21–24 However, adapting this heuristic method for ATP is challenging due to its structural complexity, and the parameters are not transferable to other systems, making the approach both unphysical and impractical. Another option is to parameterize the force field using Kirkwood–Buff theory.25–28 This approach should be used with finite-size corrections29 and requires well-converged radial distribution functions, which are challenging to obtain for complex systems like ATP solutions.
Compared to these alternative options, charge scaling appears to be the most feasible solution. While our approach to scale the atomic charges is physically motivated, the procedure can be in principle conducted arbitrarily. This means that the charge scaling procedure does not need to be limited to the phosphate moiety and the value of the charge scaling factor can be set as needed. In this work, we analyze in detail how the charge scaling approach improves the self-aggregation of ATP quantitatively by scaling the atomic charges of different moieties in various combinations and varying the scaling factor from 1.0 to 0.1.
2. Theory and computational methods
The GROMACS software package version 2022.1 was used to perform all molecular dynamics simulations.30 The leap-frog algorithm was adopted to integrate the equations of motion with a time step of 2 fs. Periodic boundary conditions with the minimum image convention were employed. The simulations were carried out in the isothermal–isobaric (NPT) ensemble at a pressure of 1 bar and a temperature of 300 K by coupling the systems to a Parrinello–Rahman barostat31 and a v-rescale thermostat,32 respectively, each with a coupling time of 0.1 ps. Temperature coupling groups were used to couple ATP, Na+, and water separately to the thermostat. Electrostatic interactions were computed with a cut-off distance of 1.4 nm and the smooth particle-mesh Ewald summation method33 using a Fourier spacing of 0.12 nm, a relative tolerance of 10−5, and an interpolation order of 4. Van der Waals interactions were computed using Lennard-Jones potentials with a cut-off radius of 1.4 nm and long-range dispersion corrections for energy and pressure as implemented in GROMACS. The potentials were shifted such that their value at the cut-off distance is zero. The lengths of all bonds of all ATP anions and water molecules were fixed by employing the LINCS (LINear Constraint Solver)34 and SETTLE35 algorithms, respectively.The Na+ counterions and water molecules were described using the force field parameters of the Amber ff03w force field36 and the TIP4P/200537 water model, respectively. The force field of the ATP anions was constructed by combining the Amber force field parameters of Meagher et al.10 with the phosphate parameters of Steinbrecher et al.38 Leontyev et al. pointed out that an effective screening factor of approximately 0.7 should be applied to charged species to account for the electronic screening in non-polarizable forcefields.12,13 The effect of this charge scaling approach on the self-aggregation of the ATP anions was studied by scaling the atom charges of either the phosphate moiety, the phosphate and the ribose moieties, the phosphate and the adenine moieties, or the whole ATP anion by a factor between 0.1 and 0.9. The charges of the Na+ counterions were also scaled by the same factor to maintain charge neutrality for the whole system. The force field parameters are provided in the ESI.†
Fig. 1 illustrates the atom labels, and Table 1 lists the unscaled charges for each atom of ATP. The table also provides the adjusted charges, where only the charges of the phosphate moiety have been scaled by a factor of 0.7, while the charges of the other moieties remain unchanged. The phosphate moiety, ribose moiety, and adenine moiety of ATP correspond to atoms 1 to 13, 14 to 21 and 36 to 43, and 22 to 35, respectively. When the charges of the entire ATP are not scaled with a factor f, but only parts of it, the total charge of the ATP qATP is not exactly equal to qscaled = f·qATP. Therefore, the charge of the oxygen atom connecting the phosphate and the ribose moieties (O5*) was adjusted such that the total net charge of ATP equals exactly qscaled.
 | ||
| Fig. 1 Visual representation of the atom names of ATP. Double bonds and charges of the phosphate moiety are not shown. Atoms of the phosphate, ribose, and adenine moieties are colored orange, turquoise, and blue, respectively. The names of the atoms depicted here are also listed in Table 1 along with their corresponding charges. | ||
| Nr. | Atom name | Unscaled charge | Scaled charge | Moiety |
|---|---|---|---|---|
| 1 | O1G | −0.95260 | −0.66682 | Phosphate |
| 2 | PG | 1.26500 | 0.88550 | Phosphate |
| 3 | O2G | −0.95260 | −0.66682 | Phosphate |
| 4 | O3G | −0.95260 | −0.66682 | Phosphate |
| 5 | O3B | −0.53220 | −0.37254 | Phosphate |
| 6 | PB | 1.38520 | 0.96964 | Phosphate |
| 7 | O1B | −0.88940 | −0.62258 | Phosphate |
| 8 | O2B | −0.88940 | −0.62258 | Phosphate |
| 9 | O3A | −0.56890 | −0.39823 | Phosphate |
| 10 | PA | 1.25320 | 0.87724 | Phosphate |
| 11 | O1A | −0.87990 | −0.61593 | Phosphate |
| 12 | O2A | −0.87990 | −0.61593 | Phosphate |
| 13 | O5* | −0.59870 | −0.47693 | Phosphate |
| 14 | C5* | 0.05580 | 0.05580 | Ribose |
| 15 | H50 | 0.06790 | 0.06790 | Ribose |
| 16 | H51 | 0.06790 | 0.06790 | Ribose |
| 17 | C4* | 0.10650 | 0.10650 | Ribose |
| 18 | H40 | 0.11740 | 0.11740 | Ribose |
| 19 | O4* | −0.35480 | −0.35480 | Ribose |
| 20 | C1* | 0.03940 | 0.03940 | Ribose |
| 21 | H10 | 0.20070 | 0.20070 | Ribose |
| 22 | N9 | −0.02510 | −0.02510 | Adenine |
| 23 | C8 | −0.20060 | 0.20060 | Adenine |
| 24 | H80 | 0.15530 | 0.15530 | Adenine |
| 25 | N7 | −0.60730 | −0.60730 | Adenine |
| 26 | C5 | 0.05150 | 0.05150 | Adenine |
| 27 | C6 | 0.70090 | 0.70090 | Adenine |
| 28 | N6 | −0.90190 | −0.90190 | Adenine |
| 29 | H60 | 0.41150 | 0.41150 | Adenine |
| 30 | H61 | 0.41150 | 0.41150 | Adenine |
| 31 | N1 | −0.76150 | −0.76150 | Adenine |
| 32 | C2 | 0.58750 | 0.58750 | Adenine |
| 33 | H2 | 0.04730 | 0.04730 | Adenine |
| 34 | N3 | −0.69970 | −0.69970 | Adenine |
| 35 | C4 | 0.30530 | 0.30530 | Adenine |
| 36 | C3* | 0.20220 | 0.20220 | Ribose |
| 37 | H30 | 0.06150 | 0.06150 | Ribose |
| 38 | O3* | −0.65410 | −0.65410 | Ribose |
| 39 | H3′ | 0.43760 | 0.43760 | Ribose |
| 40 | C2* | 0.06700 | 0.06700 | Ribose |
| 41 | H20 | 0.09720 | 0.09720 | Ribose |
| 42 | O2* | −0.61390 | −0.61390 | Ribose |
| 43 | H2′ | 0.41860 | 0.41860 | Ribose |
The simulation systems with ATP concentrations of 50 mM, 100 mM, 200 mM, 300 mM, and 400 mM consisted of 30, 60, 120, 180, and 240 ATP anions, respectively. Corresponding numbers of Na+ counterions—120, 240, 480, 720, and 960—were included to maintain charge neutrality. For each system, the number of water molecules was adjusted so that the total number of ATP anions, Na+ counterions, and water molecules was 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000.
000.
The systems were energy minimized with the steepest descent method with a threshold for the maximum force of 1000 kJ mol−1 nm−1. The temperature was then equilibrated to 300 K by performing a short 100 ps NVT simulation and using a Berendsen thermostat. This was followed by a short 100 ps NPT simulation by coupling the systems to a Berendsen barostat to set the pressure to 1 bar. The simulation time of the production run was 150 ns. If not mentioned otherwise, the first 75 ns were discarded and only the last 75 ns were used for analysis. The ATP clusters were identified using the gmx clustsize tool of GROMACS.30 ATP anions were considered to belong to the same cluster if the minimum distance between atoms in different molecules was smaller than 0.34 nm. For each charge scaling setting, five simulations with different starting configurations were conducted and the results were averaged if not mentioned otherwise. The errors shown are the standard errors resulting from the averaging without taking the errors from the individual simulations into account.
3. Results and discussion
The effect of charge scaling on the ATP self-aggregation is illustrated in Fig. 2. It shows snapshots of the simulation box after a simulation time of 150 ns with the original (left) and scaled (right) atom charges for ATP concentrations between 50 mM and 400 mM. During simulations where the charges of the ATP molecules were not scaled, excessive aggregation of the ATP anions occurred. Large ATP clusters were found even at the lowest studied concentrations of 50 mM and 100 mM, and all ATP molecules essentially aggregated into one cluster at ATP concentrations of 200 mM, 300 mM, and 400 mM. This corresponds to a phase separation and suggests that ATP is not soluble in water within this concentration range. However, this is in contradiction with experiments as it has been demonstrated that ATP is soluble at a concentration of 400 mM.39–41 Therefore, we suggest that the force field parameters of ATP should be modified before simulations with ATP in this concentration range are performed. To counteract the excessive clustering behavior, we applied the charge scaling approach suggested by Leontyev et al.12,13 as explained in detail in the Methods section. After scaling the charges of the phosphate moiety by 0.7, the ATP anions do not aggregate into a single cluster anymore. Instead, they are distributed evenly throughout the whole simulation box and form several smaller clusters of different sizes. | ||
| Fig. 2 Snapshots of the simulation box. Snapshots of the simulation box are compared for simulations conducted with the original charge parameters of Meagher et al.10 (unscaled charges, left half) and for simulations where the atom charges of the phosphate moiety were scaled by a factor of 0.7 (right half). The simulations were conducted at ATP concentrations of 50 mM, 100 mM, 200 mM, 300 mM, and 400 mM with a simulation time of 150 ns. An overemphasized tendency of the ATP anions to cluster with each other is observed when the charges are not scaled. Water and Na+ counterions are omitted. | ||
3.1. Analysis of the size and number of ATP clusters
Fig. 3 shows the effect of charge scaling on the average aggregation number, the maximum aggregation number, and number of ATP clusters as a function of simulation time (upper half: unmodified atomic charges, lower half: atomic charges of the phosphate moiety and Na+ counterions scaled by a factor of 0.7) for ATP concentrations of 50 mM, 100 mM, 200 mM, 300 mM, and 400 mM. All quantities shown in Fig. 3 relax within 75 ns. When the unscaled charges are used, fluctuating aggregates are observed for the simulations with ATP concentrations of 50 mM and 100 mM, whereas for concentrations of 200 mM, 300 mM, and 400 mM one aggregate with all ATP molecules is formed, which becomes increasingly stable as the simulation progresses.Using a scaling factor of 0.7 for the atomic charges of the phosphate moiety, the average cluster size increases until saturation is achieved in less than 75 ns for all concentrations, but the average cluster size is much smaller compared to the unscaled charges. Table 2 lists the time-averaged values of the average cluster size between 75 ns and 150 ns for all concentrations, the values for the maximum cluster size, and number of clusters. The average cluster size ranges from 1.6 to 8.4, which is ∼5% of the total number of ATP anions of the system, and fluctuates around its mean value after saturation is reached for all studied concentrations. The scaling of the charges also results in a decrease of the maximum cluster sizes to ∼10% of the total number of ATP anions for all concentrations. Although larger clusters are formed for the simulation with 400 mM ATP at 35 ns and 125 ns, they quickly dissolve into smaller ones within one nanosecond. Regarding the number of clusters, the time-averaged equilibrium values range from 20 to 36, indicating the formation of numerous small clusters. In conclusion, the exaggerated aggregation tendency of the ATP anions is significantly reduced after the atom charges of the phosphate moiety are scaled.
| Concentration in mM | Average cluster size | Maximum cluster size | Number of clusters |
|---|---|---|---|
| 50 | 1.6 | 3.7 | 20 |
| 100 | 2.1 | 5.1 | 29 |
| 200 | 3.5 | 10 | 34 |
| 300 | 5.1 | 18 | 36 |
| 400 | 8.4 | 33 | 29 |
3.2. Distribution of the ATP cluster size
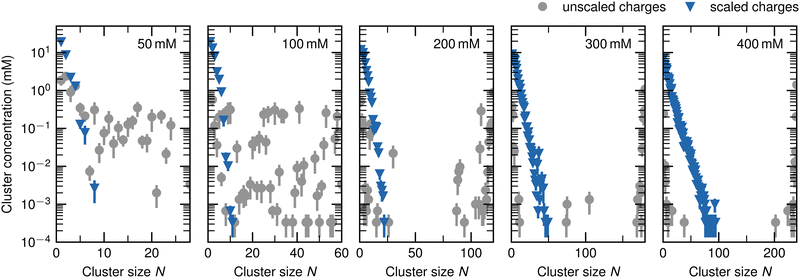
The distribution of the ATP cluster size is quantified in Fig. 4. It shows the concentration of all clusters as a function of the cluster size N for the simulations with the original and the scaled charges. In the following, they are denoted as cluster concentration, while the concentration of all ATP anions inside the system is referred to as total ATP concentration.The gray circles show the results for unscaled charges. For a total ATP concentration of 50 mM, the cluster concentration amounts to ∼1 mM when N is smaller than 4 and decreases to roughly 0.1 mM for larger N. For a total ATP concentration of 100 mM, the cluster concentration amounts to ∼1 mM only for N ≤ 2, and is in the order of 10−4 mM to 10−1 mM for N > 2. At higher total ATP concentrations, a decrease of the cluster concentration with increasing N can be observed. However, once N approaches the total number of ATP in the box, the cluster concentration increases. Note that with higher total ATP concentration, the rate of decrease also becomes higher, and the threshold value for the increase is at larger values of N. Further note that at total ATP concentrations of 200 mM, 300 mM, and 400 mM, the cluster concentration is highest when N values are 120, 180, and 240, respectively, i.e., when N equals the total number of ATP anions inside the system.
The blue triangles show the results when a scaling factor of 0.7 is applied to the phosphate moiety. The aggregate concentration decreases exponentially with increasing N. No clusters with more than 20% to 30% of all ATP anions inside the system are observed.
3.3. Self-aggregation constant and comparison with experimental data
The self-association equilibrium of ATP can be described by| ATPN−1 + ATP1 ⇌ ATPN, | (1) |
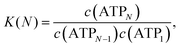 | (2) |
As shown in the ESI,†K(N) exhibits strong fluctuations when plotted against N, making the direct application of eqn (2) infeasible for comparison with experimental values. To address this, the determination of K was simplified by assuming the isodesmic model above, which implies that c(ATPN) decreases exponentially with N, as confirmed by Fig. 4. Consequently, c(ATPN) follows a geometric progression
| c(ATPN) = c(ATP1)qN−1, | (3) |
 . The total ATP concentration c0 can thus be rewritten as
. The total ATP concentration c0 can thus be rewritten as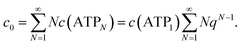 | (4) |
The geometric series converges for q < 1 to
 | (5) |
 | (6) |
Using eqn (6), eqn (4) reduces to
 | (7) |
Applying eqn (5) and (7), the average cluster size 〈N〉 is given by
 | (8) |
 | (9) |
From eqn (2), (7), and (9), K is expressed as
 | (10) |
The assumption of an isodesmic model therefore simplifies the analysis by implying that K depends only on the total ATP concentration and the number of clusters. Since the clusters are defined based on a distance criterion, it is crucial to select an appropriate cluster cutoff radius. Fig. 5 illustrates how this cutoff radius was determined.
 | ||
| Fig. 5 Determination of the cluster cutoff radius from the local density and self-association constant K. The peak at 0.33 nm in the local density for both whole ATP anions (top) and the adenine moieties (center) is associated with aromatic ring stacking, as illustrated by the snapshot of an ATP cluster (right). The minimum of this peak occurs at 0.34 nm, and this value was therefore used as the cutoff radius throughout this work. Around this value, the change in K (bottom) remains nearly constant as the cluster cutoff radius increases for all concentrations, further supporting this choice. Using this cutoff radius, K amounts to 19 ± 2 M−1, 25 ± 2 M−1, 48 ± 2 M−1, 79 ± 3 M−1, and 142 ± 7 M−1 at 50 mM, 100 mM, 200 mM, 300 mM, and 400 mM, respectively. The experimental value is 1.3 ± 0.2 M−1 and it increases to ∼17 ± 0.5 M−1 when Cd2+ is the counterion.40,41 Scaling the atom charges of the phosphate moiety by 0.7 therefore ensures that the self-aggregation of the ATP anions is adjusted to a reasonable extent. | ||
The local density of the whole ATP anions (top) and their adenine moieties (center) were obtained from the RDFs between all atoms of the whole ATP anions and between all atoms of the adenine moieties, respectively. The peaks observed at distances smaller than 0.3 nm are independent of the total ATP concentration, indicating that they correspond to intramolecular atom distances. The first peak showing a pronounced concentration dependence appears at 0.33 nm. Since this peak is also present in the local atomic density of the adenine moieties, it is attributed to aromatic ring stacking, as illustrated by the snapshot of an ATP cluster on the right. Consequently, the cluster cutoff should be set to a value greater than 0.33 nm. The bottom panel shows that K increases with a larger cluster cutoff radius for all ATP concentrations. As the cutoff radius approaches 0.3 nm, the slope decreases. While the slope of K remains nearly constant up to a cutoff radius of 0.5 nm for ATP concentrations up to 100 mM, it becomes steeper at higher concentrations as the cutoff radius increases. Specifically, at a total ATP concentration of 400 mM, the slope starts increasing around 0.37 nm, whereas for lower concentrations, this increase occurs at larger cutoff radii. Throughout this work, a cutoff radius of 0.34 nm (gray dashed line) was used, as it corresponds to the first minimum in the local densities after the peak at 0.33 nm.
With this choice of cutoff radius, K amounts to 19 ± 2 M−1 and 25 ± 2 M−1 at 50 mM and 100 mM, respectively, whereas at the higher concentrations of 200 mM, 300 mM, and 400 mM, it increases to 48 ± 2 M−1, 79 ± 3 M−1, and 142 ± 7 M−1, respectively. Compared with the experimental value, the simulated values of K are one to two orders of magnitude higher. However, it has been demonstrated by experiments that the value of K depends on the counterion. It increases by a factor of 3 to 4 ± 0.5 M−1 with Mg2+, and by one order of magnitude with Zn2+ and Cd2+, reaching 11.1 ± 4.5 M−1 and ∼17 ± 0.5 M−1, respectively.40,41 Hence, the self-aggregation of the ATP anions can be decreased to an experimentally reasonable degree by scaling the charges of the phosphate moiety by a factor of 0.7 for concentrations up to 100 mM. In the following, we analyze if additional scaling of the atom charges of the other moieties or a different scaling factor can further improve the self-aggregation of ATP.
3.4. Effect of additional charge-scaled moieties
The average cluster size, the maximum cluster size, the number of clusters, and the self-association constant K are presented in Fig. 6 when the charges of only the phosphate moiety, the phosphate and the ribose moieties, the phosphate and the adenine moieties, or the whole ATP anions are scaled by a factor of 0.7. The ATP concentration ranges from 50 mM to 400 mM. Scaling solely the atom charges of the phosphate moiety yields the smallest average cluster size across all investigated concentrations. The average cluster size increases when the atom charges of the ribose or adenine moiety are scaled in addition, with a larger increase observed for the adenine moiety. When all atom charges of the entire ATP anion are scaled, the average cluster size increases the most. These effects are observed across all concentrations and are more pronounced at higher concentrations. Consequently, the highest number of clusters is obtained when only the atom charges of the phosphate moiety are scaled. When charge scaling is also applied to the ribose or adenine moiety, the number of clusters decreases, with the decrease being more pronounced for the adenine moiety. The smallest number of clusters is observed when all atom charges of the entire ATP anion are scaled. The extent of the decrease is similar for concentrations of 100 mM and higher, while it is less pronounced for 50 mM. The maximum cluster size is smallest when the charge scaling is applied only to the atom charges of the phosphate at concentrations of 200 mM or lower, and it is largest when the atom charges of the entire ATP are scaled. While this trend reverses for ATP concentrations of 300 mM and 400 mM, the presence of larger error bars suggests that longer simulation times might be necessary for the simulations at higher concentrations. Regarding the self-association constant K, the smallest value, and thus closest to the experimental result, is obtained when the charge scaling is only applied to the phosphate moiety. The deviation of K from the experimental value increases when the atom charges of the ribose moiety are scaled in addition, and further increases when the additional charge scaling is applied to the adenine moiety instead when the ATP concentration is 200 mM and higher. The largest deviation occurs when the atom charges of the entire ATP anion are scaled, especially at higher concentrations.This analysis reveals that the optimal result is obtained when the charge scaling is applied only to the phosphate moiety, irrespective of the concentration. An explanation for this observation is the reduction of the dipole moments of the ribose and adenine moieties when the charges of their atoms are scaled. From a chemical point of view, their polarities are reduced, making them more hydrophobic. This results in a stronger tendency of the ribose and adenine moieties to aggregate with those of the other ATP anions in a polar solvent such as water. Next, the atom charges of the phosphate moiety are scaled between 0.1 and 0.9, which reveals the optimal charge scaling factor.
3.5. Effect of the scaling factor
The dependences of the average cluster size, the maximum cluster size, the number of clusters, and the self-association constant K on the value of the scaling factor are depicted in Fig. 7. It shows their values as a function of the scaling factor ranging from 1.0 (no scaling) to 0.1 (strongest scaling) for concentrations between 50 mM and 400 mM.A decrease of the average cluster size with increasing charge scaling can be observed at all concentrations. After a minimum is reached at 0.7, the average cluster size increases monotonically. The origin of this minimum is related to two different mechanisms for self-aggregation of ATP in water: at high charges, strong ion–ion interactions favor the clustering of the ATP anions with the Na+ counterions, resulting in the formation of ionic solids. At low charges, the aggregate formation is driven by the increasingly low solubility of ATP.
Accordingly, the number of clusters first increases and subsequently decreases with stronger charge scaling once it surpasses a maximum at a scaling factor of 0.7. The maximum cluster size exhibits a similar trend, with a minimum observed at a scaling factor of 0.6 across all concentrations. Regarding the self-association constant K, an initial decrease followed by the subsequent increase with stronger charge scaling is also observed, with the minimum located at a scaling factor of 0.7 for all concentrations. Note the steep decrease and increase of K as the scaling factor is reduced from 1.0 to 0.9 and 0.4 to 0.3, respectively. This implies that the charge-scaling method is only effective in correcting the excessive tendency of the ATP anions to aggregate with each other when the atom charges are scaled by a factor between 0.9 and 0.4.
In summary, this analysis demonstrates that the optimal value for the scaling factor is 0.7. Note that the influence of the scaling factor on the results is more pronounced for higher concentrations, in particular above 100 mM. Thus, a deviation from 0.7 by ∼0.1 will be only notable when the ATP concentration exceeds ∼100 mM.
4. Conclusions
Our study demonstrates that the commonly used force field parameters of Meagher et al. result in an overemphasized tendency of the ATP anions to aggregate with each other for concentrations between 50 mM and 400 mM, which is in contradiction to experimental findings. This discrepancy occurs due to the high negative charge of the phosphate moiety of −4 which leads to overestimated electrostatic interactions in non-polarizable force fields. The strong ionic interactions with the Na+ counterions lead to the formation of ionic solids, which in turn favors the aggregation of the ATP anions.Our findings reveal that scaling the atomic charges of ATP effectively reduces its excessive self-aggregation tendency to a reasonable degree for concentrations up to 100 mM, as confirmed by experimental data. The optimal results are achieved when only the atom charges of the phosphate moiety and counterions are scaled by a factor of 0.7. This finding is consistent with the analysis of Leontyev et al., who noted that the charge screening for ionized groups and ions in non-polarizable force fields like AMBER and CHARMM is treated inconsistently and suggested that their charges should be scaled by a factor of approximately 0.7. Therefore, our work demonstrates that a consistent treatment of the charge screening yields the best agreement with experimental results.
In contrast to other approaches that account for polarization effects, such as incorporating polarization explicitly or adjusting the Lennard-Jones potential, charge scaling is straightforward to integrate into existing force fields. It requires no further adjustments to other parameters and does not increase the computational cost, making it an appealing method for simulating ionic systems. This approach, also known as the electronic continuum correction (ECC), is not an arbitrary adjustment of parameters but is physically justified, and has been widely adopted to simulate ions at interfaces, in biological systems, and for studying salt effects and ion solvation.20,42–46 Our work shows that ECC is not only crucial for consistently describing the interactions in ATP solutions but also leads to the most accurate reproduction of their aggregation behavior when the Lennard-Jones parameters remain unmodified.
Author contributions
The study was conceived by T. M. D., N. M., and D. H. and supervised by N. M. and D. H. T. M. D. carried out the simulations and analysis. All authors discussed the results and contributed to the writing of the manuscript.Data availability
The force field parameters have been included as part of the ESI,† and are available at Zenodo at https://doi.org/10.5281/zenodo.14981715.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work is supported by the Grants-in-Aid for Scientific Research (No. JP23K27313) from the Japan Society for the Promotion of Science, by the Fugaku Supercomputer Project (No. JPMXP1020230325 and JPMXP1020230327) and the Data-Driven Material Research Project (No. JPMXP1122714694) from the Ministry of Education, Culture, Sports, Science, and Technology, and by the Maruho Collaborative Project for Theoretical Pharmaceutics. The simulations were conducted partly using Flow at Nagoya University, ITO at Kyushu University, ohtaka at the University of Tokyo, the supercomputer resources of the Research Center for Computational Science, and Fugaku at RIKEN Advanced Institute for Computational Science through the HPCI System Research Project (Project IDs: hp240223 and hp240224). T. M. D. is grateful to the Postdoctoral Fellowship for Research in Japan (No. PE21718) from the Japan Society for the Promotion of Science.References
- A. Patel, L. Malinovska, S. Saha, J. Wang, S. Alberti, Y. Krishnan and A. A. Hyman, Science, 2017, 356, 753–756 CrossRef CAS
.
- S. Pal and S. Paul, J. Phys. Chem. B, 2020, 124, 210–223 Search PubMed
.
- J. Mehringer, T.-M. Do, D. Touraud, M. Hohenschutz, A. Khoshsima, D. Horinek and W. Kunz, Cell Rep. Phys. Sci., 2021, 2, 100343 Search PubMed
.
- M. Nishizawa, E. Walinda, D. Morimoto, B. Kohn, U. Scheler, M. Shirakawa and K. Sugase, J. Am. Chem. Soc., 2021, 143, 11982–11993 Search PubMed
.
- R. Roy and S. Paul, J. Phys. Chem. B, 2021, 125, 3510–3526 CrossRef CAS PubMed
.
- J. Song, Protein Sci., 2021, 30, 1277–1293 CrossRef CAS PubMed
.
- G. Hu, X. Ou and J. Li, J. Phys. Chem. B, 2022, 126, 4647–4658 CrossRef CAS PubMed
.
- M. Zalar, J. Bye and R. Curtis, J. Am. Chem. Soc., 2023, 145, 929–943 CrossRef CAS PubMed
.
- T. M. Do, D. Horinek and N. Matubayasi, Phys. Chem. Chem. Phys., 2024, 26, 11880–11892 RSC
.
- K. L. Meagher, L. T. Redman and H. A. Carlson, J. Comput. Chem., 2003, 24, 1016–1025 CrossRef CAS PubMed
.
- T. Mori and N. Yoshida, J. Chem. Phys., 2023, 159, 035102 CrossRef CAS
.
- I. V. Leontyev and A. A. Stuchebrukhov, J. Chem. Theory Comput., 2010, 6, 1498–1508 CrossRef CAS PubMed
.
- I. Leontyev and A. Stuchebrukhov, Phys. Chem. Chem. Phys., 2011, 13, 2613–2626 RSC
.
- M. P. Pandey, S. Sasidharan, V. A. Raghunathan and H. Khandelia, J. Phys. Chem. B, 2022, 126, 8486–8494 CrossRef CAS
.
- G. Lamoureux and B. Roux, J. Chem. Phys., 2003, 119, 3025–3039 CrossRef CAS
.
- J. W. Ponder, C. Wu, P. Ren, V. S. Pande, J. D. Chodera, M. J. Schnieders, I. Haque, D. L. Mobley, D. S. Lambrecht, R. A. J. DiStasio, M. Head-Gordon, G. N. I. Clark, M. E. Johnson and T. Head-Gordon, J. Phys. Chem. B, 2010, 114, 2549–2564 CrossRef CAS
.
- S. Patel and C. L. Brooks III, Mol. Simul., 2006, 32, 231–249 CrossRef CAS
.
- H. Li, J. Chowdhary, L. Huang, X. He, A. D. J. MacKerell and B. Roux, J. Chem. Theory Comput., 2017, 13, 4535–4552 CrossRef CAS PubMed
.
- H. S. Antila, S. Dixit, B. Kav, J. J. Madsen, M. S. Miettinen and O. H. S. Ollila, J. Chem. Theory Comput., 2024, 20, 4325–4337 CrossRef CAS
.
- R. Nencini, C. Tempra, D. Biriukov, M. Riopedre-Fernandez, V. Cruces Chamorro, J. Polák, P. E. Mason, D. Ondo, J. Heyda, O. H. S. Ollila, P. Jungwirth, M. Javanainen and H. Martinez-Seara, J. Chem. Theory Comput., 2024, 20, 7546–7559 CrossRef CAS
.
- S. Bernèche and B. Roux, Nature, 2001, 414, 73–77 CrossRef
.
- K. Han, R. M. Venable, A.-M. Bryant, C. J. Legacy, R. Shen, H. Li, B. Roux, A. Gericke and R. W. Pastor, J. Phys. Chem. B, 2018, 122, 1484–1494 CrossRef CAS PubMed
.
- J. Yoo and A. Aksimentiev, Phys. Chem. Chem. Phys., 2018, 20, 8432–8449 RSC
.
- D. A. Tolmachev, O. S. Boyko, N. V. Lukasheva, H. Martinez-Seara and M. Karttunen, J. Chem. Theory Comput., 2020, 16, 677–687 CrossRef CAS PubMed
.
- S. Weerasinghe and P. E. Smith, J. Phys. Chem. B, 2003, 107, 3891–3898 CrossRef CAS
.
- S. Weerasinghe and P. E. Smith, J. Chem. Phys., 2003, 119, 11342–11349 CrossRef CAS
.
- B. Hess and N. F. A. van der Vegt, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 13296–13300 CrossRef CAS PubMed
.
- N. F. A. van der Vegt, K. Haldrup, S. Roke, J. Zheng, M. Lund and H. J. Bakker, Chem. Rev., 2016, 116, 7626–7641 CrossRef CAS PubMed
.
- P. Ganguly and N. F. A. van der Vegt, J. Chem. Theory Comput., 2013, 9, 1347–1355 CrossRef CAS PubMed
.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19–25 CrossRef
.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS
.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed
.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS
.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef CAS
.
- S. Miyamoto and P. A. Kollman, J. Comput. Chem., 1992, 13, 952–962 CrossRef CAS
.
- R. B. Best and J. Mittal, J. Phys. Chem. B, 2010, 114, 8790–8798 CrossRef CAS
.
- J. L. F. Abascal and C. Vega, J. Chem. Phys., 2005, 123, 234505 CrossRef CAS PubMed
.
- T. Steinbrecher, J. Latzer and D. A. Case, J. Chem. Theory Comput., 2012, 8, 4405–4412 CrossRef CAS PubMed
.
- M. P. Heyn and R. Bretz, Biophys. Chem., 1975, 3, 35–45 CrossRef CAS PubMed
.
- K. H. Scheller, F. Hofstetter, P. R. Mitchell, B. Prijs and H. Sigel, J. Am. Chem. Soc., 1981, 103, 247–260 CrossRef CAS
.
- H. Sigel and R. Griesser, Chem. Soc. Rev., 2005, 34, 875–900 RSC
.
- B. J. Kirby and P. Jungwirth, J. Phys. Chem. Lett., 2019, 10, 7531–7536 CrossRef CAS PubMed
.
- E. Pluhařová, H. E. Fischer, P. E. Mason and P. Jungwirth, Mol. Phys., 2014, 112, 1230–1240 CrossRef
.
- M. Kohagen, P. E. Mason and P. Jungwirth, J. Phys. Chem. B, 2016, 120, 1454–1460 CrossRef CAS PubMed
.
- E. Duboué-Dijon, P. E. Mason, H. E. Fischer and P. Jungwirth, J. Phys. Chem. B, 2018, 122, 3296–3306 CrossRef PubMed
.
- P. E. Mason, P. Jungwirth and E. Duboué-Dijon, J. Phys. Chem. Lett., 2019, 10, 3254–3259 CrossRef CAS PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04270k |
| This journal is © the Owner Societies 2025 |