Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fitting ambiguities mask deficiencies of the Debye–Hückel theory: revealing inconsistencies of the Poisson–Boltzmann framework and permittivity†
Benjamin
Janotta
 *a,
Maximilian
Schalenbach
*a,
Maximilian
Schalenbach
 *a,
Hermann
Tempel
*a,
Hermann
Tempel
 a and
Rüdiger-A.
Eichel
a and
Rüdiger-A.
Eichel
 abc
abc
aFundamental Electrochemistry (IET-1), Institute of Energy Technologies, Forschungszentrum Jülich, Wilhelm-Johnen-Straße, 52425 Jülich, Germany. E-mail: b.janotta@fz-juelich.de; m.schalenbach@fz-juelich.de
bInstitute of Physical Chemistry, RWTH Aachen University, 52062 Aachen, Germany
cFaculty of Mechanical Engineering, RWTH Aachen University, Aachen, Germany
First published on 28th March 2025
Abstract
The more than 100-year-old Debye–Hückel theory displays the most widely used approach for modeling ionic activities in electrolytes. The Debye–Hückel theory finds widespread application, such as in equations of state and Onsager's theory for conductivities. Here, a theoretical inconsistency of the Debye–Hückel theory is discussed, which originates from the employed Poisson–Boltzmann framework that violates the statistical independence of states presumed for the Boltzmann statistics. Furthermore, the static permittivity of electrolytic solutions is discussed as not directly measurable, while common methods for its extraction from experimental data are assessed as erroneous. A sensitivity analysis of modeled activity coefficients with respect to the permittivity and ionic radii as input parameters is conducted, showing that their influences overshadow physicochemical differences of common variations of Debye–Hückel models. Eventually, this study points out that the justification of the traditional and still often used Debye–Hückel models by experimental validation is affected by fitting ambiguities that eventually impede its predictive capabilities.
1 Introduction
In ideal solutions, colligative properties like the boiling-point elevation, freezing-point depression, and lowering of the vapour pressure are proportional to the concentration of the solute. The activity coefficient quantifies the deviations between real and ideal solutions by relating the real properties of solutes to their theoretical ideal values.1 Debye and Hückel developed the first widely accepted model for the activity coefficient of dissolved ions, assuming electrostatic interactions between ions distributed in a dielectric continuum, with their distribution governed by the Poisson–Boltzmann (PB) equation.2 In the Debye–Hückel (DH) theory, the ionic radii serve as input parameters to model the activity coefficient, while the impact of concentration dependence of the relative permittivity (also often referred to as dielectric constant) is still being investigated.3 The modeled activity coefficients can be accurately matched to those measured of strong electrolytes (completely or almost completely dissociated ions) at low concentrations using ionic radii as fitting parameters and a constant permittivity.2 This agreement of model and experiment reasoned the success of the original DH theory and its rise to a standard model.4 The DH theory displays the foundation for many electrolyte models, such as thermodynamic equations of state5,6 and the conductivity.7 However, the validity of the DH theory is restricted to low-molar electrolytes with monovalent ions.8–11 This restricted validity is often ascribed to the linearization of the PB equation, the mean-field character of the electrostatic potential, and neglected physicochemical effects.Although Arrhenius addressed the role of association in his 1903 Nobel Prize lecture, moderating his award-winning theory of electrolytic dissociation,12,13 ion pairing was largely overlooked in the formulation of the DH theory in 1923 and in numerous subsequent extensions of the theory.14 To extend the good match between the DH theory and experimental data to higher salt concentrations and to include physicochemical effects that are not incorporated in the original DH theory, a variety of extensions were proposed that can be categorized into:
(1) (Semi-) empirical models with parametrized concentration-dependent terms (like Hückel's model for the concentration-dependence of the permittivity,15 and the Davies equation16,17).
(2) Virial expansions of the thermodynamic potentials (like Mayer's and Pitzers models18–21), which enable a parameterization of interactions between electrolyte components using virial coefficients.
(3) Models for physicochemical effects of ions in solution (such as ion–solvent interaction,14,22,23 short-range repulsion,24 association25) that affect the thermodynamic potentials of the ions.
All these extensions come at the cost of an increased amount of parameters, as the parameters of one electrolyte are usually not transferable to other electrolytes or mixtures.14 Although models of the third category aim to overcome the restricted applicability of parameters, the accuracy and validity of the used physicochemical models are debated11,26–29 because isolating individual contributions to the activity coefficient from a single measurement technique is not possible.
The mean ionic activity coefficient of all ions in solution can be measured accurately by physicochemical properties such as electrochemical potentials, freezing point depression, and vapor pressure.30 To better understand the individual contributions of the physiochemical effects (third category), other (macroscopic) properties such as the conductivity or vibrational spectra are often investigated.31 The inferred contributions (such as the fraction of associated ions) are obtained by comparing the measurement with models for the measured property. A drawback of using models like Onsager's conductivity models7 is their foundation in the DH theory or comparable theories for the ion distribution around a central ion and their dependence on several parameters.
In the DH theory, the ion radii and the electrostatic interactions between the ions determine the ion distribution around the central ion. Three DH models with different assumptions regarding the parameterization of the distance of closest approach (the sum of ionic radii ai) between ions and the central ion are commonly used in the literature: (i) the full DH model (denoted as “DHFULL”), which accounts for different radii of the ions; (ii) the extended DH model (introduced by Hückel15 and denoted as “EDH”), where a mean distance of closest approach for all ions is assumed; and (iii) the DH limiting law (denoted as “DHLL”) for low concentrations, where the effects of the finite ion radius approach zero and are thus neglected. Repulsive interactions between ions around the central ion due to the finite volume (hard sphere) of the ions and the concentration dependence of parameters like the permittivity are not considered in the derivation of DH theory.
These shortcomings are reasons for the ongoing discussion on the validity and applicability of the DH models.32–46 Consequently, adaptations42,47–50 of and alternatives51–53 to the DH theory were developed aiming to overcome these intrinsic shortcomings. Refined derivations of the DH theory starting with the PB equation such as the one by Shilov et al.54,55 and Valiskó et al.22,56 enable incorporating measurement data of the concentration dependent permittivity and predicting the activity coefficients over a larger range of concentrations without the introduction of new parameters. The non-monotonic behaviour of ionic activity coefficients of ions is explained by ion–solvent interaction. Alternative theories like the hypernetted chain theory,51 and the Mean Spherical Approximation (MSA)52 intrinsically account for hard-sphere repulsion (and association), showing significant theoretical improvements compared to the DH theory. Unlike the explanation of Hückel15 and Shilov et al.,54,55 the non-monotonic increase of the activity coefficient is (largely) attributed to hard-sphere repulsion. By developing a modified PB theory based on thermodynamic perturbation theory, Budkov et al.57,58 developed a model that intrinsically accounts for the local permittivity of the solvent and explicitly accounts for the dipole moment of the solvent and ions. Nevertheless, to date, theoretical models and foundations for electrolytes still lack a wide range of applicability, and improvements in electrolyte theories are regarded as the most crucial research area for applied thermodynamics.59
In this study, the assumptions underlying the derivation of the DH theory are examined and its parametrizability is critically investigated. First, the PB framework is discussed to violate the statistical independence of states presumed for the Boltzmann theory. Then, the measurement and calculation of the permittivity and its concentration dependence are critically discussed, showcasing the uncertainty of a property that is usually assumed to be known exactly. To assess the impact of parameter uncertainties, a sensitivity analysis is conducted comparing the three DH models with the MSA. Furthermore, contributions due to hard sphere repulsion of the ions, hydration, and association are compared which are used as physicochemical model extensions. The activity coefficient is calculated using the four named model contributions on presumed parameter intervals to mimic a predictive input of uncertain physical parameters. Additionally, the impact of the parameterization on the calculated conductivity is discussed, as transport properties are often used to determine thermodynamic properties like the degree of association. The uncertainty of the input parameters is shown to significantly impact the model results. Consequently, the good agreement between measurement data and models based on the DH theory are found to be a result of overfitting rather than a rigorous physicochemical modeling. With this approach, a critical discussion on the parameterization and physicochemical assumptions of the DH theory is presented, motivating the further development of modern models for electrolytic solutions as well as experimental techniques and atomistic modeling60–64 for detailed validations.
2 Results and discussion
2.1 Conceptual inconsistencies of the Debye–Hückel theory
The qualitative and quantitative description of ion–ion and ion–solvent interactions for macroscopic models is intensely debated in the contemporary literature.14,65 A key characteristic for models of (dilute) electrolytes is the propagation of the electrical field inside the electrolyte for which the Debye–Hückel (DH) theory displays the most widely used theory regarding macroscopic modeling.4 In the following, the suitability of the DH theory as foundation for predictive electrolyte theories (in contrast to merely fitting available data) is discussed. Detailed analyses of mathematical assumptions (like the linearization of the Poisson–Boltzmann equation) during the derivation and further discussions (charging process) that often take the Poisson–Boltzmann framework as starting point can be found in the literature.4,8,50,66The Boltzmann distribution is derived for the assumption that the probability ps to observe a system in a microstate (namely that a well-defined subsystem has the energy ws) is proportional to the number of possible states M for a system with total energy W: p ∝ M(W − ws).67,68 Here, M is a function of (W − ws). The probability ps for the microstate is
 | (1) |
 | (2) |
To avoid the necessity to calculate all microstates, the DH theory compares the probabilities to find an ion k in the two specific states denoted with superscripts ∞ and s. The superscript s denotes the state of interest with a specified energy wsk of k near a central ion, and ∞ a well known (reference) state far away from the central ion. By dividing one probability by another, Z gets eliminated and their relation can be expressed as
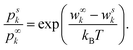 | (3) |
The probability psk manifests as the concentration ck of the macroscopic system. Using the electrostatic potential energy wk = zkeΦk, where Φk, and zk are the potential acting on k and the valence of k, and assuming that the potential far away from the central ion is negligible (Φ∞k = 0) reveals the starting point of the derivation of the DH theory
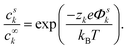 | (4) |
Since eqn (4) describes the distribution of a species k around the central ion j based on the mean concentration of the solution c∞k (assuming radial symmetry), it is often written as the radial distribution function gkj(d) = csk(d)/c∞k. The potential at a distance d from the central ion is determined by the Poisson equation
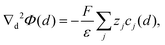 | (5) |
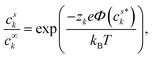 | (6) |
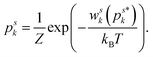 | (7) |
Hence, the energy wsk and the associated probability psk depend on the probability for other states. Therefore, the microstates are not independent and the proportionality between the probability and the number of possible state M is violated. This dependence violates the statistical independence of the microstates presumed for Boltzmann statistics.
Fig. 1 illustrates the dependence of the probability for a state on the probability for a different state. The propagation of the electrostatic potential in Fig. 1(B) is determined by the probabilities for the states (by means of the concentrations, eqn (5)) in Fig. 1(A). Therefore, the probability to find an ion at a distance d from a central ion is calculated based on the potential energy (by means of the potential field) of different states, which, however are not simultaneously occupied.
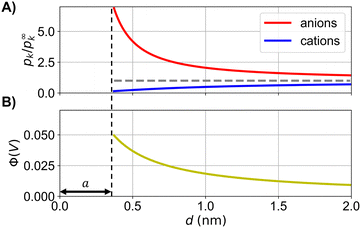 | ||
| Fig. 1 (A) Calculated probability distributions of cations and anions, and (B) electrostatic potential around a central cation for a one-one electrolyte (solution of Debye and Hückel, see ESI† for equations), where a is the distance of closest approach. The probability for an ion to occupy a state in (A) affects the propagation of the electrostatic potential in (B) (see eqn (5)). Hence, the electrostatic potential energy of the same ion at a distance d is affected by the probability for the states with a smaller distance that d (which are not occupied at that time). | ||
The critique on the intrinsic approximation of the employed Poisson–Boltzmann equation discussed in this work is in contrast to statements in contemporary literature4 claiming that the only approximation in the Poisson–Boltzmann equation is the used potential of mean force Φ (before linearization of the exponential). Importantly, even the DH limiting law is not free of the approximation discussed so far.
The approximate nature of the potential of mean force was criticised by Onsager who showed that eqn (4) is not self-consistent because the reciprocal relations (Onsager's Nobel prize in 1968) for two ions k and m are in general not fulfilled: zkeΦm(d) ≠ zmeΦk(d).69 The inconsistency found by Onsager (and Fowler70) stems from the mean-field approximation, because the mean-field does not coincide with the potential of mean force (for the virtual displacement of the ion). The potential of mean force near a central ion calculated via the static Poisson–Boltzmann framework does not include the thermal ion movement by Brownian motion. Hence, the radial distribution function around the central ion derived in the static Poisson–Boltzmann framework does not portray the physical ion dynamics, leading to an intrinsic inaccuracy of the static fundament. In the presence of localized ions, the electrostatic potential field deviates significantly from the mean electrostatic potential field (DH theory) due to the de-localized (smeared) ion distribution. Furthermore, the average (mean) field due to localized ions does not coincide with the field due to smeared ions because of the non-linearity of the electric field strength as a function of the distance:  . The bar over a variable denotes local averaging. Therefore, a localized ion at a distance d from a central ion is subjected to a different field and electrostatic potential energy than calculated in the DH theory. This argumentation coincides with the simulation results by Lyubartsev et al.71 who used a reverse Monte Carlo approach for a NaCl solution. The Mean Spherical Approximation (MSA) is affected by similar mean-field assumptions, but the ion distribution is modeled based on a more realistic function for the potential of mean force.
. The bar over a variable denotes local averaging. Therefore, a localized ion at a distance d from a central ion is subjected to a different field and electrostatic potential energy than calculated in the DH theory. This argumentation coincides with the simulation results by Lyubartsev et al.71 who used a reverse Monte Carlo approach for a NaCl solution. The Mean Spherical Approximation (MSA) is affected by similar mean-field assumptions, but the ion distribution is modeled based on a more realistic function for the potential of mean force.
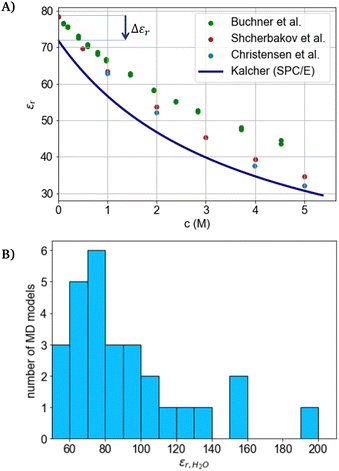 | ||
| Fig. 2 (A) Measurement data and simulation results for aqueous NaCl solutions from literature.72–75 (B) Simulation results from molecular dynamics simulations for water by Kadaoluwa et al.77 | ||
The permittivity ε is typically measured by dielectric spectroscopy, in which a sinusoidal perturbation is applied and the sinusoidal response in terms of phase angle and amplitude is measured (like in impedance spectroscopy). For the dielectric spectroscopy of aqueous solutions, microwave-frequencies between 108 and 1010 Hz are typically employed.78 Lower frequencies increase the measurement challenges as the capacitive impedance diverges to infinity towards low frequencies. Hence, the permittivity obtained in the high-frequency regime are typically applied in the DH-theory, where they describe a static system without a perturbation (0 Hz). In the case of an ideal dielectric, which is purely capacitive and non-conducting, the permittivity is mostly frequency independent and can be extrapolated to that at zero frequency. Resonance phenoma in real dielectrics are described by the Debye relaxation model79 in which the complex permittivity approaches a static value with decreasing frequency. Using the Debye model,80,81 measurement data for water (a bad conductor) from measurement frequencies between 1 GHz and 40 GHz may be represented with an accuracy of 1% in this range.82 However, for conducting electrolytes, the real and imaginary part of the permittivities typically diverge with power-law-dependencies towards low frequencies.83,84 The power-law can be ascribed to the many-body interactions of strongly interacting bodies (such as water molecules), while weak interactions lead to the Debye characteristic.84–87 Therefore, the static relative permittivity of water and especially electrolytes is not directly measurable and its estimation by fits80 can be erroneous, while its real values might be significantly larger than the commonly measured values obtained at microwave-frequencies. Such larger values of the static permittivity of pure water were reported by some authors based on molecular dynamics simulations (see Fig. 2(B)). Here, the static permittivity of a conducting medium is proposed to be undefined, as in electrostatics (at zero frequency) a conductor is electric field-free (Gauss law). Therefore, the permittivity of a conducting medium is only defined for the electrodynamic probing with alternating voltages. Thus, the static permittivity is considered inaccessible from measured data (also referring to the described diverging power-law-dependence towards zero frequency). Hence, the use of the static relative permittivity of conducting electrolytes displays a thus far unrecognized and unquantified source of error for the DH theory.
Additional arguments regarding the uncertainty of measured permittivities of electrolytes were discussed by Shilov et al.54 (see their introduction), who incorporated the possibility to integrate an arbitrary function for the concentration dependent permittivity in the DH theory. Using concentration dependent literature data of the static relative permittivity (which are subjected to the discussed uncertainties), their model shows a qualitatively correct trend of the activity coefficients of solvent and solutes for one-one electrolytes.
The influence of the permittivity on the activity coefficient, especially the electrostatic contribution is still debated in the literature.3,5,88–90 In the DH theory, the ions are assumed to be dispersed inside a dielectric continuum (primitive model), which allows for the derivation of analytical solutions of the models.91 However, the permittivity is a heterogeneous property in electrolytes.92 Molecular dynamics simulations support the conception of a heterogeneous permittivity as the dielectric response changes from bulk to confined fluids93,94 and emphasize the anisotropy of the permittivity of water near charged surfaces.95 Due to the preferred orientation of dipoles close to ions, the permittivity of the solvent close to the ion is smaller than that of the pure solvent which ultimately leads to the dielectric decrement for the bulk electrolyte.46,92,96 The dielectric decrement affects the permittivity of the bulk electrolyte upon external excitation because less water molecules react to the excitation as depicted in Fig. 3. This explanation implies that the water molecules close to a central ion have more robust orientations to the ion than those of more distant ones. However, as long as the orientation of water molecules in the (first) hydration shell is not affected by the increased ion concentration, the electric field propagating from a central ion should also not be affected by the decrease of the (dynamically measured) bulk permittivity. Therefore, the electrostatic contribution (DH theory) is affected differently by the dielectric decrement than the bulk electrolyte. In other words, the concentration dependence of the static permittivity measured for the bulk electrolyte (Fig. 2(A)) is probably not directly integrable for the electrostatic contribution (as exemplary done in Fig. 4(A), (C), and (D)).
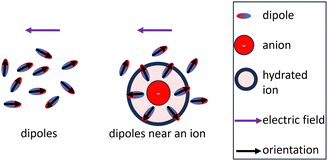 | ||
| Fig. 3 Common explanation for the dielectric decrement: dipoles that are part of the hydration shell keep their orientation with respect to the ion upon external excitation.46,92,96 | ||
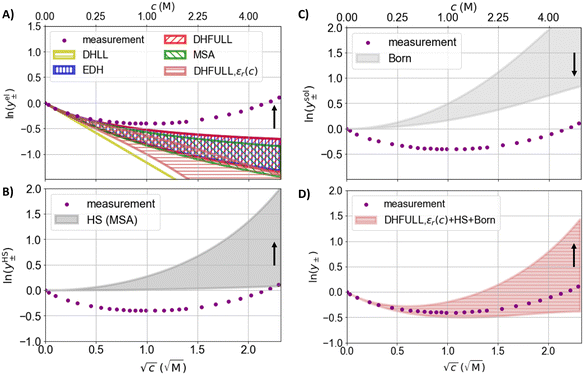 | ||
| Fig. 4 Logarithmic activity coefficient as a function of the square root of the concentration. Dots: measured activity coefficients for NaCl at 25 °C from the literature.97,98 Coloured areas: activity coefficients between the lower and upper margins of the span of assumed ion radii calculated with different models. (A) The electrostatic contribution to the activity coefficient. (B) The hard sphere (HS) contribution to the activity coefficient. (C) The contribution due to Born hydration to the activity coefficient. (D) Sum of the logarithmic activity coefficients of the HS, Born hydration, and the electrostatic term of DHFULL including the concentration dependence of the permittivity. The black arrows indicate the direction the activity coefficients change towards larger ion radius/distance of closest approach. | ||
The effect of ion solvation on the activity coefficient is often modeled using the Born term or derivations of it.3 To evaluate the Born term, the dependence of the permittivity on the concentration is intrinsically required. Therefore, the uncertainty of the local dielectric properties also affects the Born term. The approach to calculate the contribution of the ion–solvent interaction using the Born term was criticized in general in a study by Simonin,101 as the solution permittivity is probably irrelevant for the ion–solvent interaction it was meant to describe.
2.2 Sensitivity analysis
In the following sensitivity analysis, the impact of the uncertain value of the (concentration dependent) permittivity is compared to the impact of the usual parameters, the ionic radii. The three DH models (DHLL, EDH, DHFULL) introduced in Sections 1 and 4.1.1 are applied to calculate activity coefficients and are (exemplary) compared to the MSA. Additionally, selected models for contributions that account for the hard sphere (HS) repulsion, ion hydration (Born term), and association are evaluated regarding their impact on the activity coefficient. For the variation of the distance of closest approach, intervals of 0.95 to 3.84 Å for Na+ and 1.81 to 3.60 Å for Cl− were chosen, corresponding to the Pauling radii and a hydration number of up to 7.9, and 6, respectively.105 The static relative permittivity is varied between literature values of 78.14 and 95 as exemplary significantly higher value.Fig. 4(B) shows the distribution of the hard sphere (HS) contribution for the given radius intervals. The HS contribution is more sensitive to the specified ion radii than the electrostatic contribution and is always positive. The spread of the HS contribution increases significantly with concentration. Fig. 4(C) shows the Born term accounting for the hydration of ions. Like the HS contribution, the activity coefficient calculated from the Born term is always positive, but the dependence on the ion radius is smaller. For the Born term, the same radii are assumed as for the other contributions (to reduce the degrees of freedom). Fig. 4(D) shows the summation of the three contributions in Fig. 4(A)–(C) combined using “DHFULL, εr(c)” from Fig. 4(A). For c ≤ 0.25 M, the predicted activity coefficient fits the measurement data well for the whole intervals of radii, while the spread around the measurement data is large for c ≥ 0.25 M and increases.
Fig. 5 shows the measured activity coefficient of NaCl97,98 at 25 °C and models for the electrostatic contribution to the activity coefficient calculated with the variation of the static permittivity. The magnitude of the electrostatic contributions (Fig. 5(A)) are inversely proportional to the static relative permittivity (the Pauling radii are used). The effect of the changed permittivity increases with increasing concentrations. Below c = 0.04 M, the static relative permittivity of 95 leads to a small positive deviation of the models from the measurement data. For higher concentrations, the prediction using ε = 95 is closer to the measurement data than 78.14. Fig. 5(B) shows the impact of assuming the static relative permittivity of water to be 95 on the Born term for concentrations up to the solubility limit (in contrast to Fig. 5(A)) assuming the same variation with concentration (eqn (18)). The absolute value of the activity coefficient decreases assuming a higher static relative permittivity for water and becomes significant above about 0.25 M.
To compare models for association, Fig. 6(A) shows the fraction of free ions α in a NaCl solution at 25 °C as a function of the concentration. In Bjerrum's model (based on the DH theory), the cutoff distance q between two ions for association for NaCl is smaller than the distance of closest approach of Na+ and Cl− necessary to fit measured activity coefficients (for all considered relative permittivities). Therefore, NaCl does not show association in this model and the fraction of free ions α equals 1 for all concentrations.25 Hence, NaCl is considered a strong electrolyte. The binding mean spherical approximation (BiMSA) predicts association even at low concentrations (≤0.25 M, Fig. 6(A)). The data of molecular dynamics (MD) using a SPC model in simulations for 1 m (molal) NaCl by Driesner et al.99 indicate that incomplete dissociation needs to be considered even for a strong electrolyte like NaCl as only about 63% of the ions are completely dissociated. The simulation at 25 °C shows the formation of various aggregates besides the fully dissociated ions such as the species NaCl(aq), Na2Cl+, NaCl2−, and Na2Cl2(aq). The resulting fraction of free ions is shown for all ions and only the fully dissociated Na+ and Cl−, respectively. Data from MD calculations by Alejandre et al.107 using SPC/E, TIP4P/2005, and SPCE-FH force fields indicate negligable association for a concentration of 0.494 M, but a reduction of α to 0.55 at 2.375 M. Based on the concentrations given by Driesner et al.,99 the fraction of free ions is calculated for all concentrations using the mass-action-law (MAL) assuming DHLL, and EDH-H for the activity coefficient, respectively. The MAL based on DHLL predicts increasing fractions of free ions above 1 M which is counterintuitive. Using the data of Driesner et al. as fix points for the mass action law leads to negligible dependence of α on the distance of closest approach (for EDH-H). Nevertheless, the data indicate the significance of ion association even for a strong electrolyte like NaCl in water, but also shows that the degree of association deviates strongly between the models. The arbitrariness of the parameterizations is exemplified in Table 1, where the equilibrium constants based on DHLL and EDH-H deviate up to a factor of ten for the same reaction.
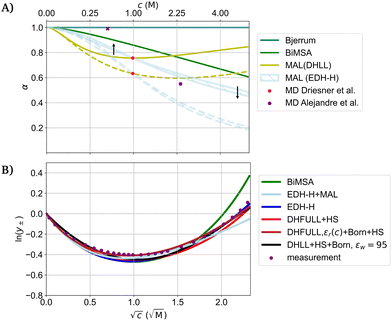 | ||
| Fig. 6 (A) Fraction of free ions of NaCl at 25 °C as a function of the concentration for different models. The Bjerrum length at 25 °C in water for a 1-1 electrolyte is 3.55 Å which is smaller than the distance of closest approach for the radii considered for the fits in (B). Data by Alejandre et al.107 using SPC/E, TIP4P/2005, and SPCE-FH force fields with similar results, the x denotes little association (without a given value). MD: molecular dynamics; BiMSA: binding means spherical approximation; MAL: mass action law (based on the MD by Driesner et al.99 (pink points)). (B) Models with different physical interpretation fitted to measured activity coefficients of NaCl at 25 °C. The parameterization is summarized in the ESI.† EDH-H: DH theory as extended by Hückel; DHFULL: full DH theory; HS: hard sphere contribution; Born: Born term. BiMSA and EDH-H + MAL (upper limit of a) depict the same models in (A) and (B), respectively. | ||
| m + n | 2 | 3 | 4 |
|---|---|---|---|
| DHLL | 3.09510−3 | 1.87810−6 | 3.47810−9 |
| EDH-H | 0.96810−3 | 0.58810−6 | 0.34010−9 |
The outcome of the models for the individual contributions for electrostatic interaction, hard sphere repulsion, solvation, and association (Fig. 4, 5, and 6(A)) show a significant dependence on their parameterization and model assumptions. Combining different contributions with an appropriate parameterization allows to match all the different models with measurement data as exemplified in Fig. 6(B). The four selected contributions here are combined to six different models for the activity coefficient of NaCl. Hückel's extension of the DH theory (EDH-H) accounting for the semi-empirical concentration dependence of the permittivity (denoted by C) is parametrized with C = 0.1. In combination with the MAL to account for association (EDH-H + MAL) it is parameterized by C = 0.2. The activity coefficients shown in Fig. 6(B) using EDH-H + MAL and BiMSA correspond to the graphs in Fig. 6(A). The BiMSA includes contributions due to electrostatics, hard sphere repulsion and association. Lastly, a model using DHLL, the hard sphere contribution and the Born term is shown assuming εw = 95 (eqn (18)). All models shown above describe different physicochemical assumptions, but (unsurprisingly) match the measurement data reasonably.
Importantly, Fig. 4–6 show that variation of the parameterization of the permittivity (be it the static value or the concentration dependence) can be compensated by fitting the ionic radii. The ionic radii used for the models depicted in Fig. 6(B) span over the complete intervals given in the Introduction.
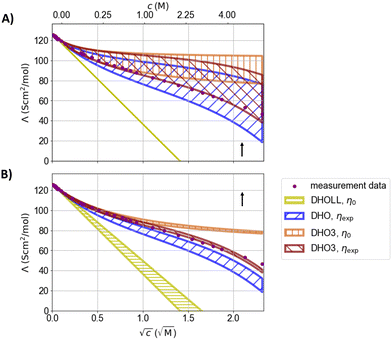 | ||
| Fig. 7 Parameter variation of (A) the distance of closest approach from 2.76 to 7.44 Å (with εr = 78.14) and (B) the relative static permittivity of water from 78.14 to 95 (using Pauling radii) for conductivity models. The arrows indicate the impact of increasing the respective varied values. DHO-LL: Debye–Hückel–Onsager limiting law. DHO denoting the extension of the DHOLL from ref. 108 and DHO3 from ref. 109. | ||
2.3 Interdependence of properties, measurements, and models
For the development of predictive electrolyte theories (especially with a focus on multi-ion models), the microscopic interactions in electrolytes must be described by precise physicochemical models.110 As shown above, almost arbitrary model combinations can be used to precisely describe experimental data; however, it confines the model to the domain of the data used for fitting, making extrapolations beyond this range generally unreliable.14 Hence, this interchangeability of the contributions including their physicochemical parameterization prohibits the assessment of the validity of individual contributions based on fitting accuracies.65 Furthermore, a challenge for the development of models and their parameterization is the interdependence and interaction of physical contributions as exemplary illustrated in Fig. 8. With changing concentration, the effect of one contribution (like the association) on the other contribution changes. This interdependence is seldom displayed in the models. As stated by Onsager111 in 1968 with reference to association parameterization: “in a complete theory this [arbitrary definition of associated ions] would not matter; what we remove from one page of the ledger would be entered elsewhere with the same effect.” To develop validate such models, a variety of independent measurement data is essential. Besides thermodynamic properties and their thermodynamic entanglement (e.g. by the Gibbs–Duhem equation), data based on non-equilibrium thermodynamics and transport models can help to develop and validate models but require a rigorous foundation.The DH theory predicts the electrostatic contribution to the activity coefficient, while other contributions like association, hard sphere repulsion and hydration are neglected during its derivation. Although these contributions can be added explicitly to improve the alignment with measured electrolyte properties, the interdependence between the electrostatic contribution and these other contributions is not considered in the DH theory (see Fig. 8). Introducing for example the hard sphere contribution during the derivation of the electric field, changes it and the outcome of the activity coefficient (compare DH theory to MSA). It is also shown above that the parametrizability of the DH theory in combination with other contributions allows to model a wide range of possible trends for measurement data up to their solubility limit. However, if the electrostatic contribution is modeled incorrectly at moderate to high concentrations (as key assumptions are violated) while the measurement data is fitted well, then the other contributions are inevitably also modeled incorrectly. The uncertainty of the DH theory at moderate concentrations is transferred into other model contributions, while these contributions are being studied. Therefore, a good match between model and measurement does not necessitate a physically accurate model. Since modern theories aim to predict electrolyte properties based on detailed, quantitative physical understanding in contrast to just describing them, it is questionable whether the DH theory is the proper basis for such theories, especially since more physically detailed models exist. For now, the enduring success of the Debye–Hückel theory, spanning more than a century, is attributed in part to its high degree of parametrizability, rather than to its physical rigor.
3 Conclusions
This work has explored physicochemical assumptions, simplifications, and fitting ambiguities of the Debye–Hückel theory. In detail, the solution of the Poisson–Boltzmann equation as it is employed in the Debye–Hückel theory is shown to violate assumptions necessary for its derivation. Furthermore, the uncertainty of the static permittivity due to measurement challenges and its impact on exemplary model contributions are discussed. For that purpose, the influence of the uncertainty of the permittivity is compared to the parametrizability of the distance of closest approach (linked to the ionic radius) for the Debye–Hückel models, as well as the mean spherical approximation, hard sphere repulsion, Born term, and ion association. The analysis demonstrates that the ability of these models to fit experimental data does not necessitate an accurate physical representation of the system. In particular, uncertainties for the value and the concentration dependence of the permittivity can be compensated by the parameterization and model selection. Therefore, an assessment of any contribution and its parameterization without a fundamentally rigorous background is ambiguous. The interdependence of the DH theory and theories for other contributions is discussed, revealing that the complexity of physiochemical interactions in electrolytes cannot be easily displayed by non-interacting models.4 Methods
The activity coefficient of a species describes the (energetic) deviation of a compound from ideal behavior in a mixture. The non-ideality of ions in solution consists of multiple dominant contributions. Here, the electrostatic (el) contribution, the hard sphere (HS) contribution, the solvation (sol) and the association (asso) are discussed. The activity coefficient yi of ion i is related to the individual contribution112 by eqn (8)| ln(yi) = ln(yeli) + ln(yHSi) + ln(ysoli) + ln(yassoi) + … | (8) |
The mean molar activity coefficient y± of a binary salt is defined as the average of the single ion activity coefficients46eqn (9)
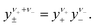 | (9) |
4.1 The electrostatic contribution
The first model for ions in solution to be successfully matched with experimental data (for activity coefficients, and for the conductivity) was the Debye–Hückel (DH) theory.2,113 The primary distinction between electrolytes and non-electrolytes in terms of their contributions to the activity coefficient stems from the electrostatic interactions between ions. The DH theory aims to describe this contribution but is restricted to low concentrations.8 In the literature, different equations for the DH theory (based on different simplifications) are used.114 The three most important ones,114 namely the Debye–Hückel limiting law (DHLL), the extended Debye–Hückel theory (EDH) and the full Debye–Hückel theory (DHFULL) are briefly discussed in the following.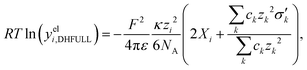 | (10) |
 are defined by
are defined by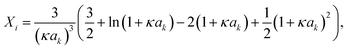 | (11) |
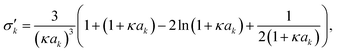 | (12) |
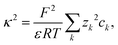 | (13) |
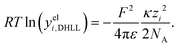 | (14) |
Hückel15 assumed a common mean distance of closest approach a for both ions in binary electrolytes during the derivation of the influence of the permittivity. This model is called extended DH theory (EDH), leading to:
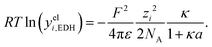 | (15) |
4.2 The hard sphere contribution
The hard sphere contribution yHSi accounts for the repulsive short-range interactions by treating ions as impenetrable spheres that cannot overlap.10 The hard sphere contribution is assumed to account for the contribution to the free energy by volume exclusion due to the ions and the hydration shell.116 The equations for the hard sphere contribution used in this work are available in the literature.1154.3 Hydration and changing relative permittivity
Besides the volume exclusion, the solvation (hydration) of ions also affects the solution permittivity.15 To account for the hydration, Hückel15 extended the DH theory with the semi-empirical extension for the concentration dependence of the permittivity (EDH-H) using a constant parameter C. The activity coefficient of the EDH-H is calculated by: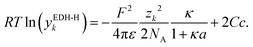 | (16) |
If association is neglected, C is set to C = 0.1 here, while C = 0.2 is used in combination with models for association (for better fits). Another model accounting for the hydration by means of the changing permittivity is the Born term, which is a semi-empirical expression inspired by the model for the Gibbs solvation energy. Eqn (17) shows a simplified model for the Born term which is discussed in detail by Silva et al.3 (being denoted as ‘Born-0’ there)
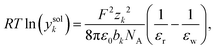 | (17) |
| εr(c) = εw − 15.2c + 3.64c3/2. | (18) |
4.4 Association
Association has a substantial impact on electrolyte properties as it decreases the fraction of free ions α (number of ions in solution divided by number of ions assuming complete dissociation) in solution, directly affecting other contributions such as the electric contribution, or properties like the conductivity.31 Therefore, an accurate association model is vital for modeling electrolytes. Three models for the association are briefly compared within this study: the Bjerrum model,25 a mass action law (MAL) based on results from molecular dynamics simulations,99 and an association model based on MSA.116 The first extension of the DH theory for association was proposed by Bjerrum.25 Bjerrum defined ions as associated when their distance is smaller than a cutoff distance q where the probability of to find an ion near a central ion has a minimum: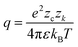 | (19) |
The association is described by the fraction of free ions α, which can be calculated based on the energy to separate the ions.25 As a compensation for a lack of reliable measurement data, results from molecular dynamics simulations for a NaCl solution from Driesner et al.99 are shown for comparison with the models. Based on these results, equilibrium constants are derived in this work to show results for a simplified mass action law,117 assuming an equilibrium constant K for each associated species:
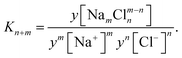 | (20) |
The simulation data of Driesner et al.99 shows that at 25 °C only n,m ∈ [0,1,2] are relevant. Here, the activity coefficient of all anions and cations is assumed to equal the mean activity coefficient for this equation, whereas the activity coefficient of neutral species is assumed to equal 1.
The last association model is based on the Binding Mean Spherical Aapproximation (BiMSA) which extends the MSA to explicitly account for the equilibrium between free ions and ion pairs. Details on and the derivation of the BiMSA can be found in the literature.103,116 For the simulation, the published code of Crothers et al.116 was adapted for aqueous NaCl and used. In a 1-1 electrolyte, α can be calculated based on an equilibrium constant, the activity coefficient and geometrical data of the ions in solution.116
4.5 Conductivity models
Conductivity measurements are often used to investigate electrolyte properties such as the degree of association of the ions in solution.109,118,119 In detail, the difference between model and measurement is typically explained with association.31 Here, three different conductivity models are compared, starting with the most important one: the Debye–Hückel–Onsager limiting law (DHOLL). The DHOLL reads120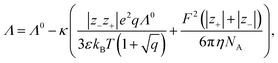 | (21) |
Author contributions
Benjamin Janotta: conceptualization, methodology, software, writing – original draft preparation, visualization. Dr Maximilian Schalenbach: conceptualization, methodology, writing – original draft preparation, visualization, funding acquisition, supervision. Dr Hermann Tempel: writing – reviewing and editing, project administration, funding acquisition. Prof. Dr Rüdiger-A. Eichel: project administration, funding acquisition.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the German Federal Ministry of Education and Research (BMBF) within the Project PRELUDE (03SF0650A).Notes and references
- J.-L. Burgot, The Notion of Activity in Chemistry, Springer International Publishing, Cham, 2016 Search PubMed.
- P. Debye and E. Hückel, Phys. Z., 1923, 24, 185–206 CAS.
- G. M. Silva, X. Liang and G. M. Kontogeorgis, Fluid Phase Equilib., 2023, 566, 113671 CAS.
- G. M. Kontogeorgis, B. Maribo-Mogensen and K. Thomsen, Fluid Phase Equilib., 2018, 462, 130–152 CrossRef CAS.
- L. Rueben, P. Rehner, J. Gross and A. Bardow, J. Chem. Eng. Data, 2024, 69, 3044–3054 CrossRef.
- B. Maribo-Mogensen, Development of an electrolyte CPA equation of state for applications in the petroleum and chemical industries, DTU Chemical Engineering, Department of Chemical and Biochemical Engineering, Kgs. Lyngby, 2014 Search PubMed.
- L. Onsager and R. M. Fuoss, J. Phys. Chem., 1932, 36, 2689–2778 CrossRef CAS.
- J. S. Newman and N. P. Balsara, Electrochemical systems, John Wiley & Sons, Inc, Hoboken, 4th edn, 2021 Search PubMed.
- O. Redlich, Chem. Rev., 1946, 39, 333–356 CrossRef CAS.
- J.-P. Simonin and O. Bernard, Fluid Phase Equilib., 2023, 571, 113805 CrossRef CAS.
- E. A. Guggenheim, London, Edinburgh Dublin Philos. Mag. J. Sci., 1935, 19, 588–643 CAS.
- S. Arrhenius, Dissertation, Academy of Sciences, Stockholm, 1884 Search PubMed.
- S. Arrhenius, Z. Phys. Chem., 1887, 1U, 631–648 Search PubMed.
- G. M. Kontogeorgis, A. Schlaikjer, M. D. Olsen, B. Maribo-Mogensen, K. Thomsen, N. von Solms and X. Liang, Int. J. Thermophys., 2022, 43, 1–68 CrossRef.
- E. Hückel, Phys. Z., 1925, 1925, 93–147 Search PubMed.
- C. W. Davies, J. Chem. Soc., 1938, 2093 CAS.
- C. W. Davies and T. Shedlovsky, J. Electrochem. Soc., 1964, 111, 85C Search PubMed.
- J. E. Mayer, J. Chem. Phys., 1950, 18, 1426–1436 CAS.
- K. S. Pitzer, Thermodynamics, McGraw-Hill, New York, 3rd edn, 1995 Search PubMed.
- D. G. Archer, J. Phys. Chem. Ref. Data, 1991, 20, 509–555 CAS.
- F. Pérez-Villaseñor, G. A. Iglesias-Silva and K. R. Hall, Ind. Eng. Chem. Res., 2002, 41, 1031–1037 Search PubMed.
- J. Vincze, M. Valiskó and D. Boda, J. Chem. Phys., 2010, 133, 154507 CrossRef.
- J.-P. Simonin, J. Mol. Liq., 2023, 380, 121713 CrossRef CAS.
- R. Triolo, J. R. Grigera and L. Blum, J. Phys. Chem., 1976, 80, 1858–1861 CrossRef CAS.
- N. Bjerrum, K. Dan. Vidensk., 1926, 7, 1 CAS.
- L. Onsager, Ann. N. Y. Acad. Sci., 1945, 46, 241–265 CrossRef CAS PubMed.
- J. Prausnitz, R. Lichtenthaler and E. G. de Azevedo, Molecular Thermodynamics of Fluid-Phase Equilibria, Pearson Education, Limited, Hoboken, 3rd edn, 1998 Search PubMed.
- P. M. V. Résibois, Electrolyte theory. An elementary introduction to a microscopic approach, Harper & Row, New York, 1968, p. 29 Search PubMed.
- D. Fraenkel, J. Phys. Chem. B, 2011, 115, 14634–14647 CAS.
- G. N. Lewis and M. Randall, J. Am. Chem. Soc., 1921, 43, 1112–1154 CAS.
- Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 CAS.
- D. Fraenkel, Mol. Phys., 2010, 108, 1435–1466 CAS.
- D. Fraenkel, J. Comput. Chem., 2015, 36, 2302–2316 CAS.
- D. Fraenkel, J. Chem. Theory Comput., 2018, 14, 6434–6442 CAS.
- D. Fraenkel, J. Chem. Theory Comput., 2018, 14, 2609–2620 CrossRef CAS.
- P. van der Weg, Am. J. Anal. Chem., 2018, 09, 406–422 CrossRef CAS.
- E. A. Guggenheim, Trans. Faraday Soc., 1959, 55, 1714 RSC.
- E. A. Guggenheim, Trans. Faraday Soc., 1960, 56, 1152 RSC.
- T. Biver and F. Malatesta, J. Chem. Theory Comput., 2018, 14, 6427–6433 CrossRef CAS PubMed.
- C. W. Outhwaite, M. Molero and L. B. Bhuiyan, J. Chem. Soc., Faraday Trans., 1993, 89, 1315–1320 RSC.
- K. S. Pitzer, J. Chem. Soc., Faraday Trans. 2, 1972, 68, 101 CAS.
- J.-L. Liu and C.-L. Li, AIP Adv., 2019, 9, 1–6 Search PubMed.
- D. L. Bowers and E. E. Salpeter, Phys. Rev., 1960, 119, 1180–1186 Search PubMed.
- Z. Abbas, M. Gunnarsson, E. Ahlberg and S. Nordholm, J. Phys. Chem. B, 2002, 106, 1403–1420 CAS.
- T. S. Sørensen, J. Chem. Soc., Faraday Trans., 1990, 86, 1815–1843 Search PubMed.
- R. A. Robinson, Electrolyte solutions: Robinson RA, Stokes RH (2002) Electrolyte solutions, Dover, Mineola, 2002 Search PubMed.
- P. Vieillefosse, J. Phys., 1981, 42, 723–733 CAS.
- T. Xiao and X. Song, J. Chem. Phys., 2011, 135, 104104 Search PubMed.
- M. Costa Reis, ChemTexts, 2021, 7, 1–17 CrossRef.
- P. B. van der Weg, J. Colloid Interface Sci., 2009, 339, 542–544 CrossRef CAS PubMed.
- J. Rasaiah, Chem. Phys. Lett., 1970, 7, 260–264 CrossRef CAS.
- L. Blum, Mol. Phys., 1975, 30, 1529–1535 CAS.
- A. O. Quiñones, L. B. Bhuiyan and C. W. Outhwaite, Condens. Matter Phys., 2018, 21, 23802 Search PubMed.
- I. Y. Shilov and A. K. Lyashchenko, J. Phys. Chem. B, 2015, 119, 10087–10095 CAS.
- I. Y. Shilov and A. K. Lyashchenko, J. Solution Chem., 2019, 48, 234–247 CAS.
- M. Valiskó and D. Boda, J. Phys. Chem. B, 2015, 119, 14332–14336 Search PubMed.
- Y. A. Budkov, A. L. Kolesnikov and M. G. Kiselev, EPL, 2015, 111, 28002 Search PubMed.
- Y. A. Budkov and A. L. Kolesnikov, J. Stat. Mech.:Theory Exp., 2022, 2022, 053205 Search PubMed.
- E. Hendriks, G. M. Kontogeorgis, R. Dohrn, J.-C. de Hemptinne, I. G. Economou, L. F. Žilnik and V. Vesovic, Ind. Eng. Chem. Res., 2010, 49, 11131–11141 CAS.
- K. A. Maerzke, T. J. Yoon and R. P. Currier, J. Chem. Eng. Data, 2022, 67, 3661–3671 CrossRef CAS.
- J.-C. Chen, B. Reischl, P. Spijker, N. Holmberg, K. Laasonen and A. S. Foster, Phys. Chem. Chem. Phys., 2014, 16, 22545–22554 CAS.
- P. Habibi, P. Dey, T. J. H. Vlugt and O. A. Moultos, J. Chem. Phys., 2024, 161, 1–10 Search PubMed.
- L. C. Kröger, S. Müller, I. Smirnova and K. Leonhard, J. Phys. Chem. A, 2020, 124, 4171–4181 Search PubMed.
- B. Svensson and B. Jönsson, Chem. Phys. Lett., 1984, 108, 580–584 CAS.
- N. Novak, F. Yang, M. D. Olsen, X. Liang, N. von Solms, I. G. Economou, M. Castier, J.-C. de Hemptinne, A. Z. Panagiotopoulos and G. M. Kontogeorgis, Fluid Phase Equilib., 2025, 594, 114339 CrossRef CAS.
- J. G. Kirkwood and J. C. Poirier, J. Phys. Chem., 1954, 58, 591–596 CrossRef CAS.
- L. Boltzmann, 1877, pp. 373–435.
- J. Williard Gibbs, Elementary principles in statistical mechanics: developed with especial reference to the rational foundations of thermodynamics, Charles Scribner's Sons, 1902 Search PubMed.
- L. Onsager, Chem. Rev., 1933, 13, 73–89 CrossRef CAS.
- R. H. Fowler, Trans. Faraday Soc., 1927, 23, 434 CAS.
- A. P. Lyubartsev and A. Laaksonen, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 3730–3737 CrossRef CAS PubMed.
- R. Buchner, G. T. Hefter and P. M. May, J. Phys. Chem. A, 1999, 103, 1–9 CAS.
- V. V. Shcherbakov, Y. M. Artemkina and E. N. Korotkova, Russ. J. Inorg. Chem., 2014, 59, 922–926 CAS.
- J. H. Christensen, A. J. Smith, R. B. Reed and K. L. Elmore, J. Chem. Eng. Data, 1966, 11, 60–63 CAS.
- I. Kalcher, Aqueous Electrolytes: Ion-Specific Structure and Thermodynamics (Dissertation), 2011 Search PubMed.
- R. D. Mountain and A. Wallqvist, A collection of results for the SPCE water model Search PubMed.
- S. P. Kadaoluwa Pathirannahalage, N. Meftahi, A. Elbourne, A. C. G. Weiss, C. F. McConville, A. Padua, D. A. Winkler, M. Costa Gomes, T. L. Greaves, T. C. Le, Q. A. Besford and A. J. Christofferson, J. Chem. Inf. Model., 2021, 61, 4521–4536 CrossRef CAS.
- Microwave and Radio-Frequency Technologies in Agriculture: An Introduction for Agriculturalists and Engineers, ed. G. Brodie, M. V. Jacob and P. Farrell, De Gruyter, Warschau/Berlin, 2016 Search PubMed.
- P. Debye, Polar molecules, Dover Publications, INC, 1929, vol. 48 Search PubMed.
- R. Gulich, M. Köhler, P. Lunkenheimer and A. Loidl, Radiat. Environ. Biophys., 2009, 48, 107–114 CrossRef CAS.
- A. de Ninno, E. Nikollari, M. Missori and F. Frezza, Phys. Lett. A, 2020, 384, 126865 CAS.
- D. P. Fernández, Y. Mulev, A. R. H. Goodwin and J. M. H. L. Sengers, J. Phys. Chem. Ref. Data, 1995, 24, 33–70 Search PubMed.
- A. K. Jonscher, Nature, 1977, 267, 673–679 CAS.
- A. K. Jonscher, IEEE Trans. Electr. Insul., 1992, 27, 407–423 Search PubMed.
- L. A. Dissado, Phys. Scr., 1982, T1, 110–114 CAS.
- L. A. Dissado and R. M. Hill, Proc. R. Soc. London, Ser. A, 1983, 390, 131–180 CAS.
- L. A. Dissado, Chem. Phys., 1984, 91, 183–199 CAS.
- N. Yao, X. Chen, X. Shen, R. Zhang, Z.-H. Fu, X.-X. Ma, X.-Q. Zhang, B.-Q. Li and Q. Zhang, Angew. Chem., 2021, 60, 21473–21478 CrossRef CAS.
- Q. Lei, B. Peng, L. Sun, J. Luo, Y. Chen, G. M. Kontogeorgis and X. Liang, AIChE J., 2020, 66, 1–13 CrossRef.
- C. Zhang, S. Yue, A. Z. Panagiotopoulos, M. L. Klein and X. Wu, Phys. Rev. Lett., 2023, 131, 076801 CrossRef CAS.
- D. Zuckerman, M. Fisher and B. Lee, Phys. Rev. E:Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 6569–6580 CrossRef CAS.
- N. Gavish and K. Promislow, Phys. Rev. E, 2016, 94, 012611 CrossRef PubMed.
- M. H. Motevaselian and N. R. Aluru, ACS Nano, 2020, 14, 12761–12770 CrossRef.
- Y. Mao, T. Zhou, L. Xu, W. Wu, R. Wang, Z. Xiong, D. Wu and H. Shi, Chem. Eng. J., 2022, 435, 134750 CrossRef CAS.
- A. Limaye, D. Suvlu and A. P. Willard, Faraday Discuss., 2024, 249, 267–288 RSC.
- J. B. Hasted, D. M. Ritson and C. H. Collie, J. Chem. Phys., 1948, 16, 1–21 CAS.
- R. A. Robinson, Electrolyte Solutions, Butterworths Scientific Publication, 1959 Search PubMed.
- T. W. Chapman and J. Newman, A compilation of selected thermodynamic and transport properties of binary electrolytes in aqueous solution, 1968 Search PubMed.
- T. Driesner, T. M. Seward and I. G. Tironi, Geochim. Cosmochim. Acta, 1998, 62, 3095–3107 CAS.
- P. Kumar, M. D. Bharadwaj and S. Yashonath, RSC Adv., 2016, 6, 114666–114675 CAS.
- J.-P. Simonin, J. Chem. Phys., 2019, 150, 244503 CrossRef PubMed.
- D. D. Perrin, Ionisation constants of inorganic acids and bases in aqueous solution, Pergamon Press, Oxford, 2nd edn, 1982, vol. 29 Search PubMed.
- H. Krienke, J. Barthel, M. Holovko, I. Protsykevich and Y. Kalyushnyi, J. Mol. Liq., 2000, 87, 191–216 CrossRef CAS.
- P. Wang and A. Anderko, Fluid Phase Equilib., 2001, 186, 103–122 CrossRef CAS.
- D. H. Powell, A. C. Barnes, J. E. Enderby, G. W. Neilson and P. S. Salmon, Faraday Discuss. Chem. Soc., 1988, 85, 137 CAS.
- B. Maribo-Mogensen, G. M. Kontogeorgis and K. Thomsen, Ind. Eng. Chem. Res., 2012, 51, 5353–5363 CrossRef CAS.
- J. Alejandre, G. A. Chapela, F. Bresme and J.-P. Hansen, J. Chem. Phys., 2009, 130, 1–10 CrossRef PubMed.
- R. A. Robinson and R. H. Stokes, J. Am. Chem. Soc., 1954, 76, 1991–1994 CrossRef CAS.
- S. Naseri Boroujeni, B. Maribo-Mogensen, X. Liang and G. M. Kontogeorgis, J. Phys. Chem. B, 2023, 127, 9954–9975 CAS.
- P. M. May and D. Rowland, J. Chem. Eng. Data, 2017, 62, 2481–2495 CAS.
- The collected works of Lars Onsager: (with commentary), ed. L. Onsager and P. C. Hemmer, World Scientific, Singapore, Repr edn, 1998, vol. 17 Search PubMed.
- C. Held, L. F. Cameretti and G. Sadowski, Fluid Phase Equilib., 2008, 270, 87–96 CAS.
- P. Debye and E. Hückel, Phys. Z., 1923, 24, 305 CAS.
- G. M. Silva, X. Liang and G. M. Kontogeorgis, Mol. Phys., 2022, 120, 1–22 Search PubMed.
- W. Verweij and J.-P. Simonin, J. Solution Chem., 2020, 49, 1319–1327 Search PubMed.
- A. R. Crothers, C. J. Radke and J. M. Prausnitz, Ind. Eng. Chem. Res., 2019, 58, 18367–18377 CrossRef CAS.
- J. H. Hoff, Études de dynamique chimique, Frederik Muller & Company, 1884 Search PubMed.
- R. J. Lemire and M. W. Lister, J. Solution Chem., 1976, 5, 171–181 CrossRef CAS.
- S. Katayama, J. Solution Chem., 1976, 5, 241–248 CrossRef CAS.
- L. Onsager, Trans. Faraday Soc., 1927, 23, 341 RSC.
- S. Naseri Boroujeni, B. Maribo-Mogensen, X. Liang and G. M. Kontogeorgis, Fluid Phase Equilib., 2023, 567, 113698 CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00646e |
| This journal is © the Owner Societies 2025 |