Sodium and potassium mixed effect on thermal conductivity in a borosilicate glass

Abstract

To investigate the combined effects of sodium and potassium on thermal conductivity, a series of borosilicate glasses with precise compositions (65.0SiO₂·5.0B₂O₃ (17.6 − x)Na₂O·xK₂O·7.5CaO·4.9MgO) was synthesized, where R = [K₂O]/([Na₂O] + [K₂O]). As R increased systematically, a pronounced nonlinear variation in thermal conductivity, characteristic of the mixed alkali effect, was observed. Within the phonon gas model framework, the thermal conductivity was primarily governed by changes in sound velocity, as both volumetric heat capacity and phonon mean free path remained nearly constant across the glass series. NMR and Raman spectra revealed nonlinear evolution in the local coordination environment of silicon cations with increasing R. These structural changes, coupled with anomalous variations in atomic packing fractions, provided atomic-scale evidence for the observed thermal conductivity trends. This study not only deepens the understanding of the physical mechanisms governing thermal properties in borosilicate glasses but also provides valuable insights for designing advanced materials with precisely tailored thermal performance.

---

1. Introduction

Oxide glasses have found widespread applications in diverse fields, including electrical devices and building materials. Among their critical properties, thermal conductivity has garnered significant attention due to its potential to address pressing challenges in energy storage, renewable energy production, and energy efficiency.^1–3 This has spurred interest in developing novel glass compositions with tailored thermal conductivity, ranging from extremely high to low values, to meet specific application requirements.^4–6

Significant progress has been made in understanding the thermal conductivity of oxide glasses through extensive research. A well-established finding is that thermal conductivity decreases with network depolymerization,⁷ with the extent of this reduction influenced by both network-forming cations (e.g., Si and B)⁸ and modifying cations (e.g., alkali and alkaline earth metals).⁹ Kim et al.^7,10 demonstrated that thermal conductivity in Na₂O–SiO₂ glasses is primarily governed by structural changes in the silicate network, while in the Na₂O–B₂O₃ system, it can be expressed as a function of the relative fraction of 4-coordinated boron within the tetraborate-dominated region. In addition, their work further evaluated the effects of ionization potential variations for different cations on thermal conductivity in alkali borate glasses. Using the ionization potential parameter, defined as the ratio of cation charge (Z) to the square of the cation radius (r), i.e., Z/r², the impact of cation types on the structure and thermal conductivity of oxide glasses was assessed.¹⁰ The higher the Z/r² value, the stronger the structural rigidity and bond strength will be, leading to an increment in thermal conductivity.^11,12 Therefore, the ionization potential parameter can be used to evaluate the thermal conductivity of oxide glasses.

Furthermore, the influence of network modifier ions on thermal conductivity has been investigated by Rasmussen et al.,¹³ who employed the quasi-harmonic Green Kubo method to investigate modified sodium silicate glasses, demonstrating that the increase of Na₂O content induces vibrational localization and reduces the contribution of mid-high frequency modes to thermal conductivity, ultimately resulting in a decrease in thermal conductivity. Interestingly, Sukenaga et al.¹⁴ discovered that lead ions can partially act as framework cations in binary silicate glasses. They further demonstrated that the phonon mean free path (MFP) serves as a useful parameter to distinguish framework cations (e.g., Pb²⁺) from non-framework cations (e.g., Li⁺, Na⁺, Ca²⁺, Sr²⁺) in silicate glasses. Lead cations partly act as framework species and exhibit higher MFP due to reduced phonon scattering, while non-framework cations disrupt the silicate network and enhance scattering. In thermal management strategies for electronic devices, Kirchner et al.¹⁵ reveals that a large and systematic decrease in thermal conductivity can be obtained by shorter intermediate ordering distances controlled by stronger constraints from the substrate surface atoms. The largest effect on thermal conductivity is observed for SiO_x films on Si substrates, which can reach one-third of the bulk value. Recently, our group¹² reported the dual-regime thermal conductivity behavior in magnesium–calcium mixed borosilicate glasses. The atomic-scale structural origins of these phenomena were elucidated by the complementary Raman and NMR spectra.

To understand the thermal transport in glass materials, it is essential to understand the scattering mechanisms of phonons. Noguchi¹⁶ showed that the thermal conductivity estimated by molecular dynamics simulations was closer to the experimental value of the laser flash method than those of the hot wire method above 1200 K. The decrease of thermal conductivity measured in the range of 1250–1550 K was attributed to the decrease in the bulk modulus of 33.3Na₂O·66.7SiO₂ melt. Furthermore, Hiroshima¹⁷ investigated alkali silicate glasses, revealing that reduced sound velocity is the primary factor driving thermal conductivity reduction at room temperature, although phonon mean free path dependencies also play a significant role. Complementing these findings, Sørensen et al.⁹ established a strong positive correlation between sound velocity and thermal conductivity in modified silicate and borate glasses. Their analysis of diffuson-mediated heat transport mechanisms revealed distinct behaviors: borate glasses exhibit heat transport dominated by diffusive vibrational modes, while silicate glasses demonstrate contributions from both diffusive and propagative modes. These differences stem from variations in low-frequency phonon mean free paths, which are intrinsically linked to differences in atomic rigidity between silicate and borate networks. Such fundamental understanding of thermal conductivity is essential for designing advanced materials with optimized thermal properties.^18,19

While numerous studies have focused on simple binary glass systems, such as borosilicate and alkali metal silicate glasses, research on industrially relevant and complex glass compositions remains limited. To address this gap, we selected an industrially significant borosilicate glass composition-glass wool (65.0SiO₂·5.0B₂O₃·17.1Na₂O·0.5K₂O·7.5CaO·4.9MgO)-as the base composition. A series of borosilicate glasses with various R (R refers to the molar ratio of [K₂O]/([Na₂O] + [K₂O])) were prepared using the melt-quenching method to investigate the effects of sodium–potassium mixing on thermal conductivity. Using the phonon gas model, we analyzed the relationships between thermal conductivity, sound velocity, and phonon mean free path. Furthermore, the atomic-scale structural origins of these effects were elucidated through Raman spectroscopy and nuclear magnetic resonance (NMR) analysis.

2. Experimental procedure

2.1. Sample preparation

Through a conventional melt-quenching method, a series of borosilicate glasses with the molar composition of 65.0SiO₂·5.0B₂O₃ (17.6 − x)·Na₂O·xK₂O·7.5CaO·4.9MgO were prepared, corresponding to R (R refers to the molar ratio of [K₂O]/([Na₂O] + [K₂O])) = 0.0, 0.2, 0.4, 0.5, 0.6, 0.8 and 1.0. Using 99.9% pure SiO₂, B₂O₃, Na₂CO₃, K₂CO₃, CaCO₃, and MgCO₃ as raw materials, for each glass composition, a 150 g bulk glass was prepared. To ensure chemical homogeneity, they were thoroughly mixed by an agate mortar and a pestle for about 2 h. The mixed powder was then transferred into a Pt90Rh10 crucible, and introduced into the furnace at 1200 °C to minimize boron volatilization and prevent spraying due to rapid decomposition of carbonate. Then the melt was held at 1470 °C for 40 min to homogenize the melt and to release the bubbles trapped inside. Subsequently, the melt was cast onto the graphite mold in air to form a bulk glass. To release the stress, the obtained glass was annealed for about 2 h near the respective glass transition temperature (T_g). Finally, the annealed bulk glass was cut into appropriate blocks for different characterizations. Based on the inductively coupled plasma atomic emission spectroscopy (ICP-AES), only a minor discrepancy (±0.5 mol%) compared to their nominal compositions exists.

2.2. Characterizations of thermal and physical properties

By using a standard calorimetric method, T_gs were evaluated under Ar according to a differential scanning calorimetry (DSC) instrument (STA 449 F1, Netzsch) with an accuracy of ±2%. To obtain the standard T_g, two runs of DSC up- and down-scans at 20 °C min⁻¹ were conducted. The DSC output of the first up-scan reflected the enthalpy response of a sample with unknown thermal history (i.e., an unknown quenching rate), whereas that of the second up-scan exhibited the enthalpy response of the sample with a well-defined thermal history (the cooling rate of 20 °C min⁻¹).

Thermal expansion coefficients (CTE), and dilatometric softening temperatures (T_d) were conducted using a horizontal dilatometer (Netzsch DIL 402PC, Germany). And the dilatometric run was made from room temperature to 700 °C at 5 °C min⁻¹ according to a polished bulk glass with the dimensions of 5 mm × 5 mm × 25 mm. Silica glass was used as the reference material.

Using the transient plane source (TPS) method, thermal constants, i.e., thermal conductivity (k) and the volumetric heat capacity (C), can be obtained by using the thermal constant analyzer (TPS-2500 S, Sweden).^20,21 During the measurements, the polished glass was cut into two plates with a size of 25 mm × 25 mm × 8 mm. Selecting the 5465 probe as the detector, based on the repeatability of measured thermal constants at room temperature we chose the appropriate heating time (10 s) and power (50 mW). By averaging the values of measured thermal constants for at least ten times, the values of thermal constants were obtained within an accuracy of ±2%.

The density (ρ) of these glasses was determined using the Archimedes method, with measurements taken in air and deionized water at 25 °C (density of water = 0.998 g cm⁻³). Each glass sample was weighed ten times to ensure accuracy, and the final density was reported as the average of the ten measurements.

Young's modulus, shear modulus and bulk modulus of these glasses were determined by an ultrasonic measurement gauge. The ultrasonic wave propagated in the polished glasses with the dimensions of 15 mm × 15 mm × 6 mm includes the longitudinal wave and the transversal one. These velocities of the sound waves were measured using ultrasonic pulse-echo techniques (45MG, Olympus, USA). The test was performed using two transducers; one was M208 for longitudinal wave (10 MHz) and another was M110 for the transverse wave (5 MHz). Glycerin and burnt honey were used as bonding materials between samples and transducers. Each glass sample was weighed ten times to ensure accuracy, and the final velocities were reported as the average of the ten measurements. Elastic parameters such as Young's modulus (E), shear modulus (G) bulk modulus (K) and Poisson's ratio (σ) was obtained using the following standard equations:

G = ρV_T² (2)

where ρ is density, ν_L and ν_T are the velocities of longitudinal and transversal waves, respectively.

2.3. Structural characterizations

Using a HORIBA Lab RAM HR Evolution Raman microscope, Raman scattering measurements were performed with a backscattering geometry at room temperature. A semiconductor (λ = 532 nm) green laser with 100 mW power as the probing light source was used to collect the Raman spectra for an acquisition time of 15 s, where Raman scattering signals can be acquired and averaged by hundreds of scans (>200). The range of the Raman spectrum was from 200 to 1600 cm⁻¹ and the resolution was better than ±1 cm⁻¹.

In addition, to probe the coordinated surroundings of B and Si in the present glasses, ¹¹B and ²⁹Si NMR spectra of the glasses were obtained at 9.4 T on a Bruker Advance DSX 500 spectrometer. ¹¹B and ²⁹Si chemical shifts are referenced to a 1 M aqueous solution of boric acid (19.6 ppm) and tetrakis(trimethylsilyl)silane (−9.8 ppm), respectively.

3. Results and discussion

In good agreement with those from the literature,^22,23 as shown in Fig. 1, here we also observed a clear mixed alkali effects on the glass transition temperature (T_g), the dilatometric softening temperature (T_d), and the coefficient of thermal expansion (CTE). That's to say, for the 65.0SiO₂·5.0B₂O₃ (17.6 − x)·Na₂O·xK₂O·7.5CaO·4.9MgO glasses investigated in this work, T_g and T_d exhibit a negative deviation from additivity with a maximum drop of 44 °C in T_g and 52 °C in T_d at the nearly equal-molar composition, respectively; while the CTE indicates a positive divergence from linearity with a maximum rise of 0.92 × 10⁻⁶ K⁻¹ at a similar equal-molar composition R = 0.5. Although complete consistency was not arrived at in the glassy community, several models has been given to explain the related physical mechanism.^24–27 Recently, based on the topological constraint theory, a structural model was presented to elucidated the origin of these mixed alkali effects. Due to the difference in alkali radii, the thus induced network strain is considered to be the structural origin of mixed alkali effects.²²

Fig. 1 Thermal performances. (A) Temperature dependence of calorimetric curves obtained at 20 °C min⁻¹ under argon and (B) dilatometric curves measured at 5 °C min⁻¹ for the 65.0SiO₂·5.0B₂O₃ (17.6 − x)·Na₂O·xK₂O·7.5CaO·4.9MgO glasses with different molar ratios R, where R is equal to the molar ratio of [K₂O]/([Na₂O] + [K₂O]). Taking the glass with R = 1.0 as an example, inset in B indicates how to determine the values of the dilatometric softening temperature (T_d). (C) Variation of T_g from A and T_d from B as a function of the molar ratio R. (D) Dependence of CTE from B on R, where CTE is taken as the average value between 50 and 500 °C. Dashed line: the linear correlation between the two endmembers.

Similar to the above observed mixed alkali effect on CTE, here the thermal conductivity (k) also exhibits a positive deviation from linearity. As shown in Fig. 2A, with the increase of R, a decrease of 0.11 W m⁻¹ K⁻¹ in thermal conductivity occurs from 0.9185 W m⁻¹ K⁻¹ at R = 0.0 to 0.8120 W m⁻¹ K⁻¹ at R = 1.0, representing an overall reduction of 12%. And the maximum deviation, 0.02 W m⁻¹ K⁻¹, also appears at about the equal-molar composition R = 0.5. That's to say, within the present investigated glassy system, mixed alkali effect on thermal conductivity appears.

Fig. 2 Compositional dependence of (A) thermal conductivity (k) and (C) volumetric heat capacity (C) at room temperature of the 65.0SiO₂·5.0B₂O₃ (17.6 − x)·Na₂O·xK₂O·7.5CaO·4.9MgO glasses as a function of different molar ratios R, where R is equal to the molar ratio of [K₂O]/([Na₂O] + [K₂O]). (B) Debye sound velocity (ν_D) at room temperature plotted as a function of different molar ratios R. (D) Compositional dependence of the phonon mean free path (l) on R. Dashed line: the linear correlation between the two endmembers.

3.1. Physical mechanism of mixed alkali effects on thermal conductivity

Thermal conductivity refers to the ability of a material to conduct heat, which is defined as the quantity of heat that passes in unit time through a plate of particular area and thickness when its opposite faces differ in temperature by one kelvin.

The phonon gas model (PGM), which treats transport of phonons as quasiparticles that can be modeled like gas molecules, has been successfully used to understand heat conduction in crystalline solids.^10,28–30 Moreover, it is also applicable to the calculation of thermal conductivity in oxide glasses and remains an important tool for understanding the behavior of thermal conductivity in amorphous solids.^8,31 With this assumption, the phonon gas model offers an intuitive way to understand the variables that influence thermal conductivity in oxide glasses.

In order to explore the physical mechanism about the compositional dependence on thermal conductivity in the present oxide glasses, PGM was used to quantitatively evaluate the impacts of sound velocity, volumetric heat capacity and phonon mean free path on thermal conductivity. Within the phonon gas model framework,^17,32 thermal conductivity and be calculated as the product of three physical parameters according to the following equation,

where k is the thermal conductivity, C is the volumetric heat capacity, ν_D is the Debye sound velocity and l is the phonon mean free path. This formula offers an intuitive way to link thermal conductivity with changes in these three parameters (Table 1).

Table 1 Density (ρ), longitudinal sound velocity (ν_L), transversal sound velocity (ν_T), Debye sound velocity (ν_D), thermal conductivity (κ), phonon mean free path (l) and volumetric heat capacity (C) of the as-prepared glasses with R = 0.0–1.0 in this work

R	ρ	ν L	ν T	ν D	κ	l	C
	(g cm^−3)	(m s^−1)	(m s^−1)	(m s^−1)	(W m^−1 K^−1)	(10^−10 m)	(J cm^−3 K^−1)
0.0	2.5298	6240	3430	3823	0.9185	3.7298	1.9186
0.2	2.5219	6230	3420	3813	0.9119	4.1256	1.7516
0.4	2.5171	6160	3390	3778	0.8976	4.1965	1.6984
0.5	2.5139	6130	3370	3756	0.8832	4.2036	1.6782
0.6	2.5107	6100	3340	3724	0.8736	4.2269	1.6650
0.8	2.5012	5990	3290	3668	0.8430	4.2493	1.6226
1.0	2.4754	5780	3180	3544	0.8120	4.2496	1.6174

---

In addition, ν_D can be obtained according to the following equation,³²

where ν_L and ν_T are the longitudinal and transversal sound velocities, respectively.^33,34

As shown in Fig. 4A, both the longitudinal and transversal sound velocities decrease as the R value increases. And the ν_D calculated using eqn (5) also exhibits a positive deviation from linearity as shown in Fig. 2B. With increasing the K₂O content, it drops from 3823 m s⁻¹ at R = 0.0 to 3544 m s⁻¹ at R = 1.0, representing an overall reduction of approximately 7.30%. And the maximum deviation of 70 m s⁻¹ appears at about the equal-molar composition R = 0.5. These reductions in Debye sound velocity may be likely related to the drop in thermal conductivity. And this positive correlation between ν_D and k was further confirmed by the near-linear relationship throughout the entire compositional range from R = 0.0 to 1.0 as shown in Fig. 3A. In addition, Lorösch et al.³⁵ also observed a similar compositional trend of thermal conductivity on sound velocities for the binary alkali borate glasses. Additionally, similar relationship between sound velocity and thermal conductivity have been also observed in other series of glasses.³⁶

Fig. 3 Relationship between thermal conductivity (k) and (A) Debye sound velocity (ν_D), (B) volumetric heat capacity (C) and (C) phonon mean free path (l) for the glasses with different R investigated in this work. The dashed line is a guide for the eye.

Furthermore, as shown in Fig. 2C, different from the dependence of ν_D and k on R, with the increase in R, the volumetric heat capacity C exhibits a negative deviation from additivity. C first steeply decreases from 1.9186 J cm⁻³ K⁻¹ at R = 0.0 to 1.7195 J cm⁻³ K⁻¹ at R = 0.3. And at R = 0.3, there is a maximum deviation of 0.11 J cm⁻³ K⁻¹ from linearity. Then a slower drop in C appears up to 1.6174 J cm⁻³ K⁻¹ at R = 1.0, indicating that the volumetric heat capacity change less at high potassium compositions. And the maximum change of about 0.3 J cm⁻³ K⁻¹ in C is very small. Finally, as shown in Fig. 3B, there is a clear nonlinear relationship between k and C. And the dependence of thermal conductivity on volumetric heat capacity is not so strong.

In addition, by combining the measured thermal conductivity, volumetric heat capacity, and Debye sound velocity, the phonon mean free path can be calculated using eqn (5). Even though this can’t give correctly absolute values of l, the compositional dependence on l can be valid (Fig. 2D). In contrary to the compositional dependence of k and ν_D on R, the phonon mean free path exhibits a non-linear increase from 3.73 × 10⁻¹⁰ m at R = 0.0 to 4.25 × 10⁻¹⁰ m at R = 1.0. Certainly, the maximum change of 0.52 × 10⁻¹⁰ in l is also very small. In addition, the maximum positive deviation of 0.27 × 10⁻¹⁰m from linearity occurs also at R = 0.3. Finally, as shown in Fig. 3C, the dependence of thermal conductivity on the phonon mean free path is also very weak, indicating a nonlinear relationship.

In summary, the Debye sound velocity and thermal conductivity exhibit a strong positive correlation, with a near-linear relationship as shown in Fig. 3A. In addition, the changes in the volumetric heat capacity and the phonon mean free path are both minimal. The phonon mean free path for this series of glasses is expected to be relatively small and changes less, which is consistent with previous literature.^9,17,32 Therefore, the variation in Debye sound velocity for this series of glasses can be the dominant factor contributing to the evolution in thermal conductivity. Certainly, composition dependence of the phonon mean free path and volumetric heat capacity also affect the thermal conductivity. At the same time, the different nonlinear behavior of Debye sound velocity, volumetric heat capacity and phonon mean free path results in the nonlinear evolution of thermal conductivity for the investigated glasses.

3.2. Structural origin of mixed alkali effect on thermal conductivity

Firstly, similar to the previous reports,^37,38 with the gradual substitution of Na by K, here we also observed an abnormal drop in density or a clear enhancement in molar volume as shown in Fig. 5. Considering the larger atomic weight of K cations than that of Na cations, given that no atomic packing fraction (C_g) alters the present borosilicate glasses can exhibit an increase in density with increasing the molar ratio R. Therefore, with the gradual substitution of Na cations by K cations, there may induce a clear drop in C_g. That's to say, atomic-scale pores increase with adding more content of K cations,³⁹ which can be helpful to reduce the phonon scattering. This increase in atomic-scale pores may be the cause why the phonon mean free path exhibits an abnormal rise with increasing R as shown in Fig. 2D.

Furthermore, compared to Na⁺ cations, K⁺ cations own a slightly less FS (field strength) due to their relatively larger ionic radius; and thus have a lower I (ionization potential), together with a weaker cation–oxygen bond strength, as listed in Table 2. Considering its simplicity, the ionization potential is often used for describing the systematic relationship between a metal cation and its field strength in oxide systems.¹⁰ Usually, a lower I means a weaker linkage, and thus a softer structure, further leading to a lower modulus.⁴⁰ As verified by the evolution of moduli on R (Fig. 4B–D), with adding the content of K⁺ cations, E, G and K all exhibit a positive deviation from the linear reduction. Similarly, based on the above-mentioned eqn (1)–(4), longitudinal sound velocity ν_L and transversal sound velocity ν_T also exhibit a similar evolution as shown in Fig. 4A, that can play a key role to control the variance of thermal conductivity on the molar ratio R for the studied glasses.

Table 2 Physical and chemical properties of related cations

Cations M	CN^a/—	r ion /Å	FS^c/Å^−2	E M–O /kJ mol^−1	I /—
a Coordination number (CN). b Ionic radius (rion) reported by Shannon.^48 c Cation field strength (FS) is calculated based on cations in different coordination numbers.^49 The equation is as follows: FS = ZM^2+/(rM^2+ + rO^2+)^2. Here, ZM^2+ represents the charge carried by the cation M^2+, while rM^2+ and rO^2+ denote the ionic radius of the M^2+ cation and the O^2− anion, respectively, as reported by Shannon.^48 d Bond strength of M−O single-bond linkage (EM–O).^50 e Ioization potential (I) is a function of the charge (Z) and ionic radius (r) of the cation,^45I = Z/r^2.
Na	6	1.02	0.178	84	0.961
	7	1.12	0.164	72	0.797
	8	1.18	0.156	63	0.718
K	6	1.39	0.134	80	0.518
	7	1.46	0.127	69	0.469
	8	1.51	0.122	60	0.439

---

Fig. 4 Compositional dependence of (A) longitudinal sound velocity (ν_L) and transversal sound velocity (ν_T), (B) Young's modulus E, (C) Bulk modulus K and (D) Shear modulus G at room temperature as a function of the molar ratio R (R is equal to the molar ratio of [K₂O]/([Na₂O] + [K₂O])).

In addition, to further probe the atomic-scale structural origin of mixed alkali effect on thermal conductivity, ¹¹B, and ²⁹Si NMR spectra (Fig. 6), together with the corresponding Raman spectra (Fig. 7) for the present borosilicate glasses, were obtained in detail.

Fig. 5 Compositional dependence of the density (ρ) and molar volume of the 65.0SiO₂·5.0B₂O₃ (17.6 − x)·Na₂O·xK₂O·7.5CaO·4.9MgO glasses as a function of different molar ratios R, where R is equal to the molar ratio of [K₂O]/([Na₂O] + [K₂O]). The dashed line is a guide for the eye.

Fig. 6 (A) ¹¹B NMR spectra of the 65.0SiO₂·5.0B₂O₃ (17.6 − x)·Na₂O·xK₂O·7.5CaO·4.9MgO glasses, where R is equal to the molar ratio of [K₂O]/([Na₂O] + [K₂O]). (B) ²⁹Si NMR spectra of the glasses with different R. (C) Dependence of the peak position (ν) near −91 ppm as a function of the molar ratio R. Dashed line: the linear correlation between the two endmembers.

Fig. 7 Structural characterizations. (A) Raman spectra of the 65.0SiO₂·5.0B₂O₃ (17.6 − x)·Na₂O·xK₂O·7.5CaO·4.9MgO glasses with different R, where R is equal to the molar ratio of [K₂O]/([Na₂O] + [K₂O]). For clarity, the spectra are shifted vertically. (B) Dependence of the peak position (ν) near 1090 cm⁻¹ as a function of the molar ratio R. Dashed line: the linear correlation between the two endmembers.

With the gradual substitution of Na cations by K cations, no clear change can be observed about the characteristic peaks ascribed to B_III (three coordinated B, near 10 ppm) and B_IV (four coordinated B, near 0 ppm)^41,42 as shown in Fig. 6A, indicating that B cations mainly exist as B_IV and no observable transformation between B_III and B_IV occurs. According to the previous reports,⁴¹ this can be ascribed to the characteristics of excess network modifiers (alkali cations and alkali earth cations) within the present borosilicate glassy system. Based on the widely adopted structural model,^43,44 the alkali cation can act as a charge balancer and/or network modifier in the glass structure. In this work, the fraction of [BO_4/2]⁻ species is predominant in the glass structure as shown in Fig. 6A. This identified that the corresponding part of alkali ions should act as charge balancers, compensating the negative charge of [BO_4/2]⁻ units.

However, we observed a clear shift about the characteristic peak ascribed to ²⁹Si (Fig. 6B), revealing the subtle variance about the local coordinated surroundings of Si cations with increasing R. More precisely, for the pure Na endmember, the NMR peak of ²⁹Si is located at −91 ppm. While for the pure K endmember, a shift of about 3 ppm in peak location appears toward the more negative chemical shift. Particularly, similar to the evolution of thermal conductivity with increasing R shown in Fig. 2A, the shift in the characteristic NMR peak location of ²⁹Si also exhibits a positive deviation from additivity (Fig. 6C).

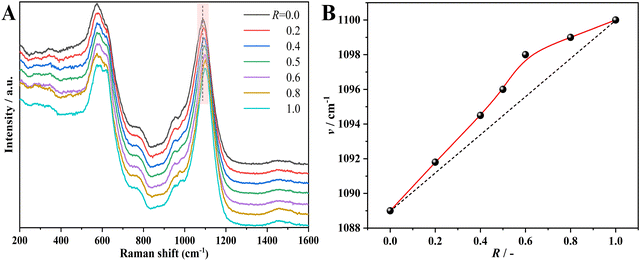
Further structural information about the atomic-scale structural evolution comes from Raman spectra (Fig. 7). Except for the peak located at about 1100 cm⁻¹ within the region of 1000 to 1200 cm⁻¹, no other clear evolution in Raman spectra can be observed. According to the previous reports,^45,46 this peak could be ascribed to the stretching vibration of [SiO₄] related structural units. According to previous work,⁴⁷ the increase in Si–O stretching force in the network structure ought to induce this peak to shift toward the higher wavenumber, thereby strengthening the rigidity of the glass network. For the pure Na endmember, this peak locates at 1089 cm⁻¹; when it comes to the pure K endmember, this peak shifts to 1100 cm⁻¹. Similar to the evolution of thermal conductivity on R, the dependence of this peak site on R also exhibits a positive deviation from linearity.

For xR₂O·(1 − x)SiO₂ (R = Li, Na, K) binary glasses, the addition of alkali ions will cause the formation of non-bridging oxygens to break the network structure.¹⁶ This ultimately leads to a reduction in thermal conductivity. The observed trend in thermal conductivity, i.e., Li₂O·2SiO₂ > Na₂O·2SiO₂ > K₂O·2SiO₂ glasses, can be attributed to the combined differences in volumetric specific heat capacity, sound velocity and mean free path. Moreover, compared to single-cation systems, mixed alkali cations could induce a further reduction in thermal conductivity due to the well-known mixed alkali effects. This further reduction in thermal conductivity for the mixed alkali silicate glasses was ascribed to their shorter phonon mean free path compared to the single alkali glasses.¹⁷ Recently, our group¹² observed that the thermal conductivity of mixed alkaline-earth (i.e., Ca–Mg) borosilicate glasses only exhibited a partial non-linear variation on compositional change in thermal conductivity. This phenomenon was attributed to atomic-scale structural transition, which likely modifies network connectivity and cation field strength distribution, thereby influencing phonon propagation characteristics through changes in interatomic bonding configurations. Therefore, for the present mixed alkali glasses, the observed non-linear evolution on R in thermal conductivity should be attributed to the mixed alkali (i.e., Na–K) effect. Considering the similar positive deviation behavior observed on Raman, NMR spectra and thermal conductivity with the gradual substitution of Na cations by K cations, the subtle evolution in the local coordinated surroundings of Si cations within the glassy network can also be a main atomic-scale structural origin of the mixed alkali effect on thermal conductivity.

4. Conclusions

Through systematic compositional adjustment of R (R = molar ratio of [K₂O]/([Na₂O] + [K₂O])) from 0.0 to 1.0, a series of borosilicate glasses were successfully fabricated to investigate the effects of sodium–potassium mixing. The thermal conductivity, along with other thermal properties such as glass transition temperature (T_g), dilatometric softening temperature (T_d), and coefficient of thermal expansion (CTE), exhibited a distinct nonlinear variation characteristic of the “mixed alkali effect” as the R value increased. Within the framework of the phonon gas model, the observed changes in thermal conductivity were primarily attributed to variations in Debye sound velocity, as both volumetric heat capacity and phonon mean free path showed minimal alterations. Notably, the phonon mean free path demonstrated a positive deviation from additivity, which can be explained by the abnormal increase in atomic-scale pores manifested as an unusual density reduction with increasing K₂O content. Structural characterization through NMR and Raman spectroscopy revealed that the evolution of thermal conductivity with increasing R was closely correlated with atomic-scale structural changes. Both the ²⁹Si NMR peak shifts and Raman spectral features exhibited positive deviations from additivity, mirroring the trend observed in thermal conductivity. These findings provide atomic-scale insights into the structural origins of the mixed sodium–potassium effect on thermal conductivity. This study offers valuable guidance for tailoring the thermal properties of borosilicate glasses through strategic compositional design, paving the way for optimized material performance in specific applications.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by National Natural Science Foundation of China (No. 52172007), Wuhan Natural Science Foundation Exploration Program (Chen Guang Program) (No. 2024040801020267), the Fundamental Research Funds for the Central Universities (WUT: 2023IVA003), The Young Top-notch Talent Cultivation Program of Hubei Province. The authors also thank Tanaka Atsuhiro and Ozaki Hitoshi from Panasonic Group for valuable discussions.

References

1. Z. Ke, X. Cao, C. Shan, L. Shi, P. Wang, Y. Yang, F. Zhao, J. Cui, J. Li and G. Zhou, Ceram. Int., 2021, 47, 19605–19613,  DOI:10.1016/j.ceramint.2021.03.298.
2. M. Hubert and A. J. Faber, Phys. Chem. Glasses: Eur. J. Glass Sci. Technol., Part B, 2014, 55, 136–158,  DOI:10.13036/17533562.55.1.
3. B. P. Jelle, Energy Build., 2011, 43, 2549–2563,  DOI:10.1016/j.enbuild.2011.05.015.
4. M. B. Østergaard, M. Zhang, X. Shen, R. R. Petersen, J. König, P. D. Lee, Y. Yue and B. Cai, Acta Mater., 2020, 189, 85–92,  DOI:10.1016/j.actamat.2020.02.060.
5. F. Hu, L. An, C. Li, J. Liu, G. Ma, Y. Hu, Y. Huang, Y. Liu, T. Thundat and S. Ren, Cell Rep. Phys. Sci., 2020, 1, 100140,  DOI:10.1016/j.xcrp.2020.100140.
6. J. C. Mauro, C. S. Philip, D. J. Vaughn and M. S. Pambianchi, Int. J. Appl. Glass Sci., 2014, 5, 2–15,  DOI:10.1111/ijag.12058.
7. Y. Kim and K. Morita, J. Am. Ceram. Soc., 2015, 98, 1588–1595,  DOI:10.1111/jace.13490.
8. Y. Kim, Y. Yanaba and K. Morita, J. Non-Cryst. Solids, 2015, 415, 1–8,  DOI:10.1016/j.jnoncrysol.2015.02.008.
9. S. S. Sørensen, E. J. Pedersen, F. K. Paulsen, I. H. Adamsen, J. L. Laursen, S. Christensen, H. Johra, L. R. Jensen and M. M. Smedskjaer, Appl. Phys. Lett., 2020, 117, 031901,  DOI:10.1063/5.0013400.
10. Y. Kim and K. Morita, J. Am. Ceram. Soc., 2015, 98, 3996–4002,  DOI:10.1111/jace.13820.
11. Y. Kim and K. Morita, J. Non-Cryst. Solids, 2017, 471, 187–194,  DOI:10.1016/j.jnoncrysol.2017.05.034.
12. S. Chen, Q. Zhang, Y. Cai, C. Huang, A. Qiao and H. Tao, J. Non-Cryst. Solids, 2025, 658, 123522,  DOI:10.1016/j.jnoncrysol.2025.123522.
13. P. Rasmussen and S. S. Sørensen, J. Chem. Phys., 2024, 161(15), 154506,  DOI:10.1063/5.0230354.
14. S. Sukenaga, B. Ozato, Y. Onodera, S. Kohara, M. Shimizu, T. Nishi, R. Endo, T. Tomai, A. Yoko and S. Kawanishi, ISIJ Int., 2024, 64, 2245–2252,  DOI:10.2355/isijinternational.isijint-2024-141.
15. K. A. Kirchner, S. Ogasawara, M. Jeem, H. Ohta, A. Suzuki, H. Tajiri, T. Koganezawa, L. S. R. Kumara, J. Nishii and J. C. Mauro, Nano Lett., 2025, 25, 7748–7753,  DOI:10.1021/acs.nanolett.5c00646.
16. Y. Noguchi, M. Shimizu, S. Sukenaga, R. Endo, T. Nishi, Y. Shimotsuma and K. Miura, J. Am. Ceram. Soc., 2025, 108, e20288,  DOI:10.1111/jace.20288.
17. Y. Hiroshima, Y. Hamamoto, S. Yoshida and J. Matsuoka, J. Non-Cryst. Solids, 2008, 354, 341–344,  DOI:10.1016/j.jnoncrysol.2007.08.082.
18. Z. Zhang, Y. Guo, M. Bescond, J. Chen, M. Nomura and S. Volz, Phys. Rev. Lett., 2022, 128, 015901,  DOI:10.1103/physrevlett.128.015901.
19. X. Qian, J. Zhou and G. Chen, Nat. Mater., 2021, 20, 1188–1202,  DOI:10.1038/s41563-021-00918-3.
20. Z. Zeng, C. Müller and B. Mihiretie, Thermochim. Acta, 2024, 742, 179883,  DOI:10.1016/j.tca.2024.179883.
21. D. Hume, A. Sizov, B. M. Mihiretie, D. Cederkrantz, S. E. Gustafsson and M. K. Gustavsson, Thermal Conductivity Thermal Expansion, 2019, 21 DOI:10.12783/tc33-te21/30333.
22. C. J. Wilkinson, A. R. Potter, R. S. Welch, C. Bragatto, Q. Zheng, M. Bauchy, M. Affatigato, S. A. Feller and J. C. Mauro, J. Phys. Chem. B, 2019, 123, 7482–7489,  DOI:10.1021/acs.jpcb.9b06512.
23. J. Shelby, J. Appl. Phys., 1976, 47, 4489–4496,  DOI:10.1063/1.322418.
24. C. Le Losq and D. R. Neuville, J. Non-Cryst. Solids, 2017, 463, 175–188,  DOI:10.1016/j.jnoncrysol.2017.02.010.
25. P. Richet, Geochim. Cosmochim. Acta, 1984, 48, 471–483,  DOI:10.1016/0016-7037(84)90275-8.
26. J. Lu, Z. Shan, J. Zhang, Y. Su, K. Yi, Y. Zhang and Q. Zheng, J. Non-Cryst. Solids: X, 2022, 16, 100125,  DOI:10.1016/j.nocx.2022.100125.
27. J. Shelby, J. Appl. Phys., 1975, 46, 193–196,  DOI:10.1063/1.321318.
28. R. Peierls, Ann. Phys., 1929, 395, 1055–1101,  DOI:10.1002/andp.19293950803.
29. C. Kittel, Phys. Rev., 1949, 75, 972,  DOI:10.1103/physrev.75.972.
30. W. Kingery, J. Am. Ceram. Soc., 1955, 38, 251–255,  DOI:10.1111/j.1151-2916.1955.tb14940.x.
31. S. Park and I. Sohn, J. Am. Ceram. Soc., 2016, 99, 612–618,  DOI:10.1111/jace.14013.
32. S. S. Sørensen, H. Johra, J. C. Mauro, M. Bauchy and M. M. Smedskjaer, Phys. Rev. Mater., 2019, 3, 075601,  DOI:10.1103/physrevmaterials.3.075601.
33. A. K. Varshneya, Fundamentals of Inorganic Glasses, Elsevier, 2013.  DOI:10.1016/b978-0-08-057150-8.50025-2.
34. R. Zeller and R. Pohl, Phys. Rev. B, 1971, 4, 2029,  DOI:10.1103/physrevb.4.2029.
35. J. Lorösch, M. Couzi, J. Pelous, R. Vacher and A. Levasseur, J. Non-Cryst. Solids, 1984, 69, 1–25,  DOI:10.1016/0022-3093(84)90119-4.
36. D. G. Cahill, S. K. Watson and R. O. Pohl, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6131,  DOI:10.1103/physrevb.46.6131.
37. H. Doweidar, J. Non-Cryst. Solids, 1996, 194, 155–162,  DOI:10.1016/0022-3093(95)00489-0.
38. I. M. Matos and N. M. Balzaretti, Results Mater., 2024, 21, 100517,  DOI:10.1016/j.rinma.2023.100517.
39. H. Doweidar, J. Phys. Chem. Solids, 1992, 53, 807–814,  DOI:10.1016/0022-3697(92)90194-i.
40. Y. Kim and K. Morita, J. Non-Cryst. Solids, 2017, 471, 187–194,  DOI:10.1016/j.jnoncrysol.2017.05.034.
41. R. Martens and W. Müller-Warmuth, J. Non-Cryst. Solids, 2000, 265, 167–175,  DOI:10.1016/s0022-3093(99)00693-6.
42. T. Nanba, M. Nishimura and Y. Miura, Geochim. Cosmochim. Acta, 2004, 68, 5103–5111,  DOI:10.1016/j.gca.2004.05.042.
43. Y. Yun and P. Bray, J. Non-Cryst. Solids, 1978, 27, 363–380,  DOI:10.1016/0022-3093(78)90020-0.
44. Z. Du, Z. Shan, A. Qiao, H. Tao and Y. Yue, J. Non-Cryst. Solids, 2025, 650, 123340,  DOI:10.1016/j.jnoncrysol.2024.123340.
45. B. Mysen and P. Richet, Silicate glasses and melts, Elsevier, 2018 DOI:10.1016/b978-0-444-63708-6.00010-7.
46. N. Ollier, T. Charpentier, B. Boizot, G. Wallez and D. Ghaleb, J. Non-Cryst. Solids, 2004, 341, 26–34,  DOI:10.1016/j.jnoncrysol.2004.05.010.
47. T. Furukawa and W. B. White, J. Am. Ceram. Soc., 1981, 64, 443–447,  DOI:10.1111/j.1151-2916.1981.tb09893.x.
48. R. D. Shannon, Found. Crystallogr., 1976, 32, 751–767,  DOI:10.1107/s0567739476001551.
49. A. Dietzel, Z. Elektrochem. und Ang. Phys. Chem., 1942, 48, 9–23,  DOI:10.1002/bbpc.19420480104.
50. K. H. Sun, J. Am. Ceram. Soc., 1947, 30, 277–281,  DOI:10.1111/j.1151-2916.1947.tb19654.x.

---