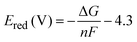Systematic improvement of redox potential calculation of Fe(III)/Fe(II) complexes using a three-layer micro-solvation model

Abstract

Electrochemical transformations of metal ions in aqueous media are challenging to model accurately due to the dynamic solvation structure surrounding ions at different charge states. Predictive modeling at the atomistic scale is essential for understanding these solvation architectures but is often computationally prohibitive. In this contribution, we present a simple, fast, and accurate three-layer micro-solvation model to evaluate the redox potential of metal ions in aqueous solutions. Our model, developed and validated for Fe³⁺/Fe²⁺ redox potentials, combines the DFT-based geometry optimizations of the octahedral Fe complex with two layers of explicit water molecules to capture solute–solvent interactions and an implicit solvation model to account for bulk solvent effects. This approach yields accurate predictions for Fe³⁺/Fe²⁺ redox potentials in water, achieving errors of 0.02 V with ωB97X-V, 0.01 V with ωB97X-D3, 0.04 V with ωB97M-V, and 0.02 V with B3LYP-D3 functionals. We further demonstrate the generality of our model by applying it to additional metal complexes, including the challenging Fe(CN)₆^3−/4− system, where our model successfully achieves close agreement with experimental values, with an error of 0.07 V and an average error of 0.21 V for all five systems. In summary, the presented simple solvation model has broad applicability and potential for enhancing computational efficiency in redox potential predictions across various chemical and industrial processes of metal ions.

---

Introduction

The standard redox potential of iron (Fe) and other transition metals is a fundamental property dictating their reactivity, providing essential insights into the likelihood of electron transfer reactions in corrosion studies,^1–3 electrochemical applications,^4–6 advanced industrial processes,^7–10 and aqueous chemistry.^11–18 In energy storage science, for example, knowledge of iron's redox behavior is crucial for designing efficient and durable iron-based redox flow batteries and components.^19–23 In emerging chemical process design, the discovery of alternative routes to conventional pathways, such as electrocatalysis (such as water-splitting²⁴) and electrochemical separations (such as electrochemical lithium extraction²⁵ and heavy metals recovery²⁶),^7,8 necessitates accurate and efficient calculations of redox potentials to allow for accelerated in silico discovery of new environmentally friendly processes.^27–29

Solvation models are essential for accurately representing solute–solvent interactions and can be categorized as either implicit or explicit.^30–32 Implicit models, such as the polarizable continuum model (PCM),³³ conductor-like PCM (C-PCM),^34,35 conductor-like screening model (COSMO),^36,37 and the solvation model based on density (SMD),³⁸ treat the solvent as a continuous polarizable medium surrounding the solute, significantly reducing computational costs.^30,31 However, these models lack the precision needed to capture specific solute–solvent interactions, which can strongly influence the representation of solvation structure of chemical reactions in solution.^39–41 This limitation is particularly relevant for metal ions like Fe^2+/3+, which coordinate with water molecules to form stable octahedral complexes, and for cases where solvents interact directly with ligands, potentially undergoing ligand substitution reactions.^42–44 Explicit solvation models, in contrast, incorporate individual solvent molecules into the quantum mechanical framework, enabling a more accurate description of electrostatic and non-bonded interactions, especially when the solvent participates directly in chemical or physical processes.^40,45,46 Despite their advantages, explicit models introduce challenges such as increased computational demand, complex optimization processes due to numerous local minima, and prolonged calculations.⁴⁷ Hybrid approaches that combine implicit and explicit solvation, often referred to as micro-solvation models, also been explored to balance accuracy and efficiency and have shown success in modeling solvated organic molecules.^48–58

In modeling the redox potential of iron-based complexes, several approaches have been previously considered.^19,28,59,60 In one study, Hughes et al. used a database of experimental single-electron reduction potentials for 95 octahedral fourth-row transition metal complexes, employing a localized orbital correction (LOC) scheme for transition metal complexes, known as the d-block LOC (DBLOC).⁶¹ Their twelve-parameter model effectively predicted the redox potential of Fe(III) at 0.67 V.⁶¹ In another study, Masliy and coworkers adopted a different approach, referred to as the cluster-continuum method, to calculate the redox potential of Fe(III).⁵⁹ They used density functional theory (DFT) to optimize a structure that included two solvation shells: the first with six water molecules and the second with twelve water molecules, achieving a calculated redox potential of 0.786 V, closely matching the experimental value of 0.77 V.^59,62 However, Masliy's model, while adding explicit calculations, can be computationally expensive as the size of ligands increases, adding geometric degrees of freedom that complicate the geometry optimization process. In a third study, Rahbani and co-workers developed a DFT-based protocol for predicting redox potentials of first-row transition metal complexes in aqueous redox-targeting flow batteries.¹⁹ Their model combined solvation models, including the COSMO-RS model for enhanced accuracy, with linear regression corrections, and predicted the redox potential of Fe(III) as 0.65 V.¹⁹ Both Hughes and Rahbani's approaches are based on data extrapolation and parameterized models to correct for limitations in current solvation models, but this approach may lack generalizability across diverse chemical systems.^63,64

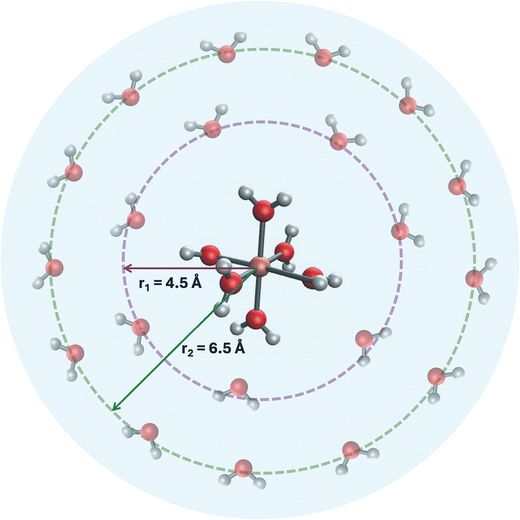
In this study, we developed a three-layer micro-solvation model designed to enhance the accuracy of implicit solvation models while simplifying the computational demands of explicit solvation approaches (Fig. 1). This model involves spherical additions of water molecules around the Fe²⁺/Fe³⁺ core, tailored to capture crucial solute–solvent interactions. We clarify that our “first layer” consists of the strongly bound octahedral coordination sphere, [Fe(H₂O)₆]^2+/3+, forming the Fe-aqua cation, which we still term a solvation layer because its water molecules derive from the solvent. To distinguish these strongly coordinated water molecules from loosely bound ones, we use the notation Fe^2+/3+[H₂O]₆·(12H₂O)·(18H₂O), where the square brackets denote the six waters covalently bound to Fe, and the parentheses denote additional solvation shells of 12 and 18 water molecules, respectively. In this way, our three-layer model captures three distinct types of solute–solvent interaction: direct coordination (first layer), immediate solvation shell (second layer), and extended solvation shell (third layer). For non-spherical systems, such as Fe complexes with ligands, we incorporated an additional step of semiempirical optimization of the surrounding water molecules while keeping the DFT-optimized complex frozen. We validated the model by testing it against five experimental Fe-complexes, demonstrating its reliability, and then applied it to the challenging Fe(CN)₆^3−/4− complex to further assess its robustness (described in Table 5). These challenges arise from the strong-field cyanide ligands, which induce significant crystal field splitting, the high charge polarization, and strong hydrogen bonding between CN⁻ and water.

Fig. 1 Schematic representation of the three-layer micro-solvation model used for calculating Fe³⁺/Fe²⁺ redox potentials. The model consists of: (a) the core octahedral Fe^2+/3+[H₂O]₆ complex, optimized using DFT in the gas phase; (b) two layers of explicit water molecules positioned at radii r₁ = 4.5 Å and r₂ = 6.5 Å, respectively, which account for specific solute–solvent interactions; and (c) an implicit solvation model (depicted by the blue sphere) that approximates bulk solvent dielectric effects with a dielectric constant ε = 78 for water.

Computational methods

DFT calculations were performed using Gaussian 16 software.⁶⁵ The geometry optimizations were carried out on Fe^2+/3+[H₂O]₆ complexes in the gas phase using a limited list of popular DFT functionals. Results from the best performing functionals (B3LYP,^66,67 BLYP,^68–70 and PBE^71,72) are discussed later in this manuscript, namely those that exhibit errors less than 0.25 V relative to experiment. Detailed results regarding the performance of all functionals used, including the redox potentials and errors in redox potential calculations, are provided in the ESI.† The 6-31+G(2df,p) Pople-style basis set was used for all systems.⁷³ Frequency calculations confirmed that all optimized structures are minima, as indicated by the absence of imaginary frequencies.⁷⁴ To account for dispersion corrections, Grimme's D3 empirical dispersion (DFT-D3(0)) was used.⁷⁵ Since the Fe ions form an octahedral complex, six water molecules around the Fe center are considered as the first solvation layer. All semiempirical GFN2-xTB calculations were performed using xTB version 6.6.1. More details on the convergence criteria, optimization thresholds, and additional methodological clarifications (including all DFT calculations, discussion on functionals and dispersion corrections, B3LYP implementation, and spin-entropy considerations) are provided in the ESI† (Table S1 and Text S2).^76–90

To evaluate modern functionals and dispersion corrections not available in Gaussian, we performed single-point energy calculations in ORCA 6.0 using geometries optimized at the B3LYP/6-31+G(2df,p) level. This ensured consistent structural input while isolating electronic energy differences. The tested combinations include B3LYP-D3BJ, B3LYP-D4, ωB97X-D3, ωB97X-D3BJ, ωB97X-D4, ωB97X-V, ωB97M-D3BJ, ωB97M-D4, and ωB97M-V.^67,91–100 In these calculations, D3BJ^75,93 and D4^96,97 dispersion corrections were applied. For functionals incorporating the VV10¹⁰¹ kernel (ωB97X-V⁸⁴ and ωB97M-V⁸²), the nonlocal correlation component was included self-consistently as part of the functional. Single-point energies were calculated with the CPCM implicit solvation model (water as the solvent) and the 6-31+G(2df,2p) basis set.

To model the second solvation layer, additional solvation shells were added to the gas-phase optimized octahedral complexes using an in-house code (more details in Text S1 in ESI†).¹⁰² The radius r for each shell was approximated at 4.5 Å for the first shell and 6.5 Å for the second shell. The choice of 4.5 Å as the radius for the first shell was guided by the Fe-outer water distance in Masliy et al.,⁵⁹ which is in the range of 4.0–4.3 Å. Setting it to 4.5 Å provided an upper limit to ensure that the interaction between the inner and outer water molecules would not become covalent. We used the 12 water molecules consistent with Masliy et al.⁵⁹ and estimated this count by using 3× the rounded-down value of r: 3× (round down of 4.5 to 4) = 12.

To further simulate bulk solvation, we added a second shell at a radius of 6.5 Å, providing an additional 2 Å distance from the first shell to account for extended solvation effects. Using the same estimation method, we rounded down 6.5 to 6, and applied 3 × 6 = 18, resulting in 18 water molecules in the second shell. Altogether, this approach yielded a model with 36 water molecules surrounding the Fe complex. To ensure uniform distribution, spherical coordinates were used to position the oxygen atoms equidistantly on the surface of each solvation sphere. These solvation layers were generated programmatically using Hydration_shell_radius.py for shell placement and run_multiple_xtb.py for xTB-based optimization. Both scripts are available at https://github.com/HassanHarb92/solvation_shells/tree/main/paper_materials/web_app/xyz_files.

The third solvation layer consists of accounting for implicit solvation effects. This was done by performing single point energy calculations using the conductor-like polarizable continuum model (C-PCM)³⁶ on the Fe^2+/3+[H₂O]₆·(12H₂O)·(18H₂O) clusters. These calculations provided the electronic energies needed for redox potential estimation.

For Fe^2+/3+ complexes with multiple ligands, where the solute–solvent interaction is not uniformly spherical, we employ a slightly modified approach. First, we optimize the Fe complex using density functional theory (DFT) at the B3LYP/6-31+G(2df,p) level in the gas phase. Following this, we add a layer of explicit water molecules surrounding the complex in a manner similar to the approach used for solvated Fe ions. However, in this case, we re-optimize the water molecules using the tight binding semiempirical GFN2-xTB method,¹⁰³ freezing the coordinates of the Fe complex itself to maintain its optimized structure. This procedure is repeated with second and third solvation layers, each time re-optimizing only the added water molecules. This approach allows us to account for solute–solvent interactions while preserving the geometry of the Fe complex. A summary of the steps, actions denoted as action, and description involved in this approach is given in Table 1 and a pictorial overview is given in Scheme 1.

Table 1 Description of solvation architectures used in redox potential calculations for iron complexes. Each step progressively incorporates additional explicit solvation layers and optimizations to better model solute–solvent interactions. In this context, spheres refer to layers of explicit H₂O molecules arranged around the Fe complex to mimic solvation effects. Acronyms: DFT: density functional theory, SPE: single-point energy calculation, CPCM: conductor-like polarizable continuum model (implicit solvation), H₂O: explicit water molecules, Fe: iron complex, xTB: semiempirical tight-binding method used for optimizing solvent molecules

Step	Action	Description
1	Gas-phase OPT + CPCM	Gas-phase DFT optimization followed by an SPE calculation using CPCM.
2	1-Sphere SPE	One sphere of H2O molecules added around the DFT-optimized geometry, followed by an SPE with CPCM.
3	1-Sphere OPT	Based on step 2, with the Fe complex frozen. H2O molecules are optimized using xTB followed by an SPE with CPCM.
4	2-Sphere SPE	A second sphere of H2O molecules is added, followed by an SPE with CPCM.
5	2-Sphere OPT	Based on step 4, with the Fe complex frozen. H2O molecules are optimized using xTB, followed by an SPE with CPCM.
6	3-Sphere SPE	A third sphere of H2O molecules is added, followed by an SPE with CPCM.
7	3-Sphere OPT	Based on step 6, with the Fe complex frozen. H2O molecules are optimized using xTB, followed by an SPE with CPCM.

---

Scheme 1 Schematic overview of the three-layer micro-solvation model. Each step corresponds to the solvation procedure described in Table 1, where successive layers of explicit water molecules are added around the Fe complex. Optimization (OPT) and single-point energy (SPE) calculations are performed at each stage (1,2,3) to refine solute–solvent interactions.

The difference in free energies (ΔG) is estimated as the difference between the single point energy (SPE) calculations of the Fe(III) and Fe(II) clusters:

ΔG ∼ SPE_III − SPE_II

where SPE_III and SPE_II are the single point calculations of Fe(III) and Fe(II), respectively.

The reduction potential, E_red is then calculated using the following equation:

where n = 1 (the number of electrons) and F is the Faraday constant. The factor −4.3 is used to convert the reduction potential to the standard hydrogen electrode (SHE).¹⁰⁴ This value of 4.3 V, known as the Trasatti potential, is widely accepted and has an uncertainty of ±0.02 V, as discussed in various ref. 59 and 104–106.

Results and discussion

Benchmarking DFT functionals

Table 2 provides a comparison of calculated redox potentials of Fe³⁺ using selected DFT functionals (B3LYP, BLYP, and PBE) with various solvation environments, alongside the experimental value of 0.77 V⁶² and theoretical values from the literature.^19,59,61 The results show that calculated redox potentials improve as additional water layers are introduced to the solvation model. For example, using B3LYP with only the octahedral Fe^2+/3+[H₂O]₆ complex yields a redox potential of 2.79 V, which deviates significantly from the experimental value. With the inclusion of additional water shells, the calculated values approach experimental results, reaching 0.86 V with 18 waters and 0.75 V with 36 water molecules, aligning closely with the experimental reference (0.77 V).⁶² Similar trends are observed with the other functionals, though the absolute values vary. The micro-solvation model with 36 waters (Table 2, E = 0.75 V) achieves similar agreement with experimental values as other models that require explicit DFT-level solvation such as the approach by Masliy et al., or rely on parameterized methods, such as the d-block localized orbital correction model by Hughes et al. or COSMO-RS with regression correction by Rahbani et al. This demonstrates the effectiveness of our approach in balancing computational efficiency and accuracy in redox potential predictions.

Table 2 Calculated redox potentials (E) of Fe³⁺/Fe²⁺ (in V, vs. SHE) using selected DFT functionals (B3LYP, BLYP, PBE) and the 6-31+G(2df,p) basis set with various solvation models (implicit and explicit water layers). Experimental values and theoretical values from the literature are included for comparison along with brief descriptions of methods from previous studies

Entry	DFT functionals	E (V/SHE) water models				Experiment (V/SHE)
		0H2O implicit	6H2O	18H2O	36H2O
1	B3LYP	5.28	2.79	0.86	0.75	0.77 V^62
2	BLYP	5.49	2.33	1.39	0.74
3	PBE	5.38	2.30	1.26	0.64

---

	Theory values from literature
	Method	E (V)	Method description
5	Rahbani^19	0.65	COSMO-RS with regression correction
6	Masliy^59	0.79	Cluster-continuum with solvation shells
7	Hughes^61	0.67	d-Block LOC correction model

---

Additionally, calculations performed with only implicit solvent effects (i.e., Fe ions without added water layers) show very high error values ranging from 4.15 V (HSE06) to 4.72 V (BLYP) (Table 2, entries 1–4: 0H₂O, implicit). The significant reduction in error observed with the inclusion of explicit water layers highlights the importance of accounting for solvation effects in accurately modeling redox potentials. Specifically, the inclusion of three solvation layers generally yields the most accurate results, as evidenced by the lower absolute errors across all tested functionals. This outcome emphasizes that the explicit treatment of solvent molecules is crucial for achieving experimentally consistent redox potential predictions in transition metal complexes.

Fig. 2 shows the absolute error associated with the calculation of the reduction potential of Fe(III) across the four density functionals and different solvation models. The column labeled “6H₂O” refers to the Fe^2+/3+[H₂O]₆ complex, while “18H₂O” and “36H₂O” correspond to Fe^2+/3+[H₂O]₆·(12H₂O) and Fe^2+/3+[H₂O]₆·(12H₂O)·(18H₂O), respectively. The histogram demonstrates that redox potential predictions improve significantly with the addition of the second solvation layer and further improve with the third layer. The absolute error decreases from a range of 1.53–2.02 V with only 6H₂O to 0.09–0.62 V with 18H₂O and further to 0.02–0.13 V with 36H₂O. Among the functionals, B3LYP exhibits the lowest error (0.02 V) when using three solvation layers.

Fig. 2 Absolute errors (V) in redox potential calculations of Fe(III) complexes using B3LYP, BLYP, and PBE functionals compared with experimental values (0.77 V).⁶² The orange bars show values for Fe^2+/3+[H₂O]₆ structures optimized in gas phase with corrected single point calculations in implicit water continuum. Blue (18H₂0) and green bars (36H₂O) show results from our model with the inclusion of additional 12 waters (Fe^2+/3+[H₂O]₆·(12H₂O)), and 30 water molecules (Fe^2+/3+[H₂O]₆·(12H₂O)·(18H₂O)), respectively.

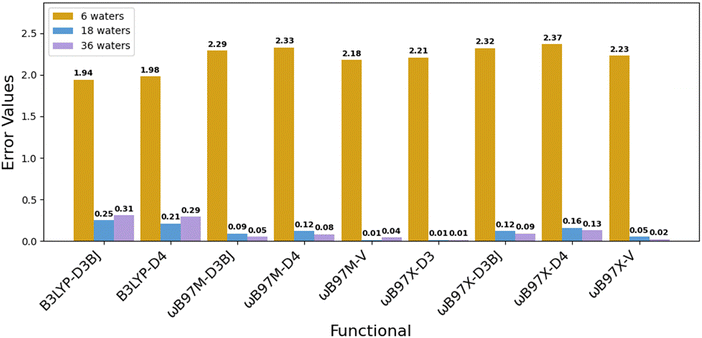
We further evaluated the performance of modern functionals by benchmarking the ωB97X and ωB97M families paired with advanced dispersion corrections, D3BJ, D4, and nonlocal “–V”, within our three-layer solvation framework (Fig. 1). As shown in Fig. 3, the computed redox potential errors reduced as solvation increased: from >2.0 V with 6 waters, to <0.3 V with 36 waters. Among all tested combinations, ωB97M-V and ωB97X-V yielded the lowest final errors (0.01–0.02 V), with other variants such as ωB97M-D3BJ and ωB97X-D4 also achieving errors below 0.13 V. These results highlight the effectiveness of range-separated hybrid functionals with robust dispersion corrections for capturing redox energetics in Fe(II)/Fe(III) complexes. By comparison, B3LYP-D3BJ and B3LYP-D4 improved modestly with added solvent shells but consistently exhibited higher errors (∼0.29–0.31 V), indicating limitations in B3LYP's exchange–correlation treatment for high-spin d-electron systems. Results from the two sets of benchmarking demonstrate two key insights: (1) incorporating multiple explicit solvation layers is essential to reduce redox errors; and (2) modern dispersion-corrected functionals, particularly the ωB97X/M family, perform exceptionally well within our solvation framework. These approaches offer a promising balance between computational efficiency and predictive reliability for transition metal redox modeling.

Fig. 3 Absolute errors in redox potential calculations of Fe(III) using different combinations of exchange–correlation functionals and dispersion methods as implemented in Orca 6.0. We note here that these are single-point calculations performed starting from Fe^2+/3+[H₂O]₆ optimized geometry in Gaussian 16 (B3LYP/6-31+G(2df,p)).

The comparison of Fe–O bond lengths calculated using DFT models with experimental values and those reported by Masliy et al. demonstrates consistency across different functionals (Table 3). For Fe²⁺, the average bond lengths from our models deviate by no more than 0.03 Å, with a standard deviation of 0.02 Å, from the experimental value of 2.12 Å. For Fe³⁺, the deviation remains within 0.07 Å, with a standard deviation of 0.00 Å, from the experimental value of 2.00 Å. The results from Masliy et al. also show close agreement,⁵⁹ with a slightly larger deviation, overestimating the Fe²⁺–O bond length by 0.07 Å and the Fe³⁺–O bond length by 0.06 Å.

Table 3 Comparison of calculated bond lengths. Averages and standard deviations of the six Fe–OH₂ are reported as x̄ and σ, respectively. Experimental values are from ref. 107. All bond lengths are given in angstroms

	Expt.	Our model						Masliy et al.^60
		B3LYP		BLYP		PBE		PBE/TZVP
		x̄	σ	x̄	σ	x̄	σ	x̄	σ
Fe^2+	2.12	2.14	0.02	2.15	0.02	2.14	0.02	2.19	0.08
Fe^3+	2.00	2.04	0.00	2.07	0.00	2.06	0.00	2.06	0.05

---

Although Fe[H₂O]₆²⁺ (a high-spin d⁶ complex) can, in principle, undergo a small Jahn–Teller distortion, experimental results report nearly octahedral geometries with minimal splitting between axial and equatorial bond lengths.¹⁰⁷ Fe-aqua complexes are known to be octahedral, with experimental Fe–O bond lengths of 2.12 Å for Fe²⁺ and average bond length of 2.00 Å for Fe³⁺. To identify potential structural distortions in the DFT calculations, we evaluated the standard deviation (σ) of the six Fe–O bond lengths. In a perfect octahedral arrangement, all bond lengths should be equal, resulting in a σ of zero. Our models consistently show lower σ values compared to those reported by Masliy et al., indicating fewer distortions in the calculated structures. For instance, with the B3LYP functional, σ for Fe[H₂O]₆³⁺ is 0.02 Å, reflecting a minimal Jahn–Teller distortion, whereas σ for Fe[H₂O]₆²⁺ is 0.00 Å, corresponding to a perfectly octahedral geometry. This suggests that the DFT methods we used can achieve accurate structures even without additional solvation shells. This suggests that the DFT-optimized geometries of the iron complexes provide a reliable starting point by accurately capturing the coordination environment. The addition of explicit water molecules then refines the local solvation effects, while implicit solvation further accounts for bulk solvent interactions, ultimately enabling a computationally efficient yet comprehensive description of the solvated structures.

The higher σ values reported by Masliy et al. may indicate artificial distortions in their optimized structures, potentially due to the absence of a third solvation shell. The lack of this additional solvation shell could lead to increased interactions between water molecules in the first and second shells, affecting the Fe–O bond lengths, while on the other hand, adding a third solvation shell will increase the geometric degrees of freedom which further complicates the optimization process.

Redox potentials of Fe-complexes

As shown in Table 4, the redox potentials for Fe–L₃ complexes reveal notable sensitivity to the solvation model applied. In gas-phase optimized calculations followed by CPCM implicit solvation, the computed redox potentials are not accurate, showing significant deviation (error > 0.85 V) from experimental values, particularly for ligands such as maltolate (error = 0.85 V) and catecholate (error = 1.98 V). These deviations underscore the limitations of relying solely on implicit solvation models, as they fail to capture the complex solute–solvent interactions.

Table 4 Calculated redox potentials (V/SHE) of Fe–L₃ complexes (see Fig. 4 for the structures of ligand, L). Experimental data (V) were retrieved from literature.¹⁹ The bold values in the table reflect the values closest to the experimental values and are used to calculate errors relative to experimental redox potentials. g.s.: gas phase, L: ligands, S: sphere

Entry	L	g.s. OPT + CPCM	1-S SPE	1-S OPT	2-S SPE	2-S OPT	3-S SPE	3-S OPT	Expt.	Error
1	Maltolate	−1.08	−0.71	−0.57	−0.57	−0.57	−0.57	−0.57	−0.23	0.34
2	Deferiprone	−1.59	−0.86	−0.76	−0.76	−0.76	−0.76	−0.76	−0.58	0.18
3	Kojate	−1.02	−0.53	−0.52	−0.52	−0.27	−0.27	−0.28	−0.13	0.14
4	Catecholate	−2.80	−2.80	−1.39	−1.39	−1.23	−1.24	−0.99	−0.83	0.16
5	Salicylate	−1.98	−1.32	−1.09	−1.09	−0.84	−0.84	−0.84	−0.66	0.18

---

Adding explicit water molecules in successive solvation layers improves the calculated redox potentials, bringing them closer to experimental values. For example, the redox potential for catecholate shows a substantial shift from −2.80 V in the gas-phase CPCM calculation to −0.99 V after incorporating three optimized solvation layers, aligning closely with the experimental value of −0.83 V. Notably, some ligands, such as kojate and salicylate, exhibit smaller shifts with additional solvation layers, suggesting that a single- or two-layer solvation model may suffice for these systems. However, the overall trend across most ligands indicates that optimized three-layer models are more reliable for capturing explicit complex solvation environments in multivalent ions. This trend highlights the importance of including explicit solvation layers, as it allows for accurate simulation of electrochemical properties by accounting for critical solute–solvent interactions.

In all cases, the 1-sphere SPE model (step 2, Table 1) displays higher errors than the 1-sphere OPT (step 3, Table 1) model, indicating that the interactions between water molecules and the complexes are not purely electrostatic. These interactions extend to noncovalent interactions, particularly hydrogen bonding between water and hydrogen donor/acceptor sites on the ligands and were captured by performing semiempirical geometry optimizations of water molecules around a frozen complex. This is evident from the fact that all ligands (see Fig. 4) contain oxygen and/or nitrogen atoms, which can act as hydrogen bond acceptors or donors, thereby enhancing the solvation environment through hydrogen bonding.

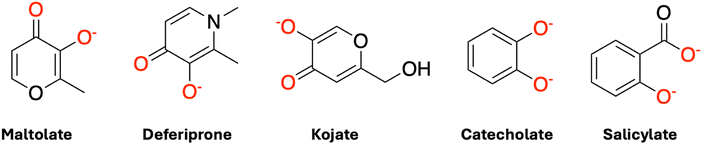Fig. 4 Schematic structures of the five ligands (L) considered in this study. Red color on atoms (predominantly on oxygen atoms) indicates the sites of coordination with the metal ion.

We note here that, while the initial placement of water molecules follows a spherical distribution, these solvent molecules undergo a semiempirical optimization step while keeping the core complex frozen. This refinement process ensures that the water molecules are not arbitrarily positioned but instead adopt configurations that better capture solute–solvent interactions. By optimizing only the solvent positions, our approach reduces the randomness in solvation shell placement while maintaining computational efficiency. This step is particularly important for achieving a balance between accurate representation of hydrogen bonding interactions and minimizing computational overhead.

Resolving the challenging redox potential of Fe(CN)₆^3−/4−

The redox potential of the Fe(CN)₆^3−/4− complex has posed significant challenges in computational chemistry, leading to discrepancies between experimental and calculated values reported by various research groups.^{19,61,108–110} Cyanide, recognized as a strong field ligand, generates a high crystal field splitting energy, favoring a low-spin configuration where the t_2g orbitals are filled before the e_g orbitals.¹⁹ This stabilization, coupled with the complex's high negative charge, contributes to the difficulties in accurate modeling. Liang et al. noted that while incorporating diffuse functions could reduce computational errors, larger basis sets did not yield significant improvements for the Fe(CN)₆ complex compared to other systems.^19,108 Liang et al. also highlighted the limitations of B3LYP in capturing the substantial crystal field stabilization energy associated with cyanide ligands, suggesting that π-back bonding between iron and the cyanide ligand might further complicate the electron configuration of the complex.¹⁰⁸ The experimental redox potential is reported at +0.37 V,¹¹⁰ while computational results have varied widely, with Rahbani et al. calculating −0.56 V,¹⁹ Liang et al. −0.34 V,¹⁰⁸ Hughes et al. −0.33 V,⁶¹ and Baik et al. −0.172 V,¹⁰⁹ illustrating the ongoing challenges in accurately modeling this system.

Table 5 shows previously reported redox potentials of for Fe(CN)₆^3−/4− alongside computed values using various model introduced in this study (Table 2 and Scheme 1). This demonstrates that the model introduced in this work (entry 11 of Table 5) is able to predict the redox potential of Fe(CN)₆^3−/4− (0.30 V) in a good agreement with the experimental value (0.37 V). This high level of accuracy highlights the importance of including direct water–ligand interactions to properly model the redox potential of iron complexes.

Table 5 Comparison of calculated redox potentials (E_red) in V, vs. SHE and absolute errors relative to the experimental value (0.37 V) for Fe(CN)₆^3−/4−. Previous studies report significant discrepancies in computing redox potentials, with errors between 0.542 V and 0.93 V.^{19,61,108,109} Our model, using up to three explicit solvation layers, reduces this error progressively, achieving the closest match (0.30 V, error of 0.07 V) with the three spheres – optimized CPCM approach

Entry	Method	Ered (V)	Error (V)
	Previous work
1	Rahbani^19	−0.56	0.93
2	Liang^108	−0.34	0.71
3	Hughes^61	−0.33	0.7
4	Baik^109	−0.172	0.542
	This work
5	Gas-phase OPT + CPCM	−0.60	0.97
6	1-Sphere SPE	−1.19	1.56
7	1-Sphere OPT	0.21	0.16
8	2-Sphere SPE	0.21	0.16
9	2-Sphere OPT	0.28	0.09
10	3-Sphere SPE	0.28	0.09
11	3-Sphere OPT	0.30	0.07
	Experiment^110	0.37

---

By optimizing the metal–solvent complexes in explicit solvent molecules, our model ensures the inclusion of hydrogen bonding at the terminal nitrogen atoms significantly enhances the accuracy of redox potential predictions. These hydrogen bonds cause the polarization of electron density away from the iron center, causing nitrogen atoms to share a portion of their cyanide electron density with the hydrogen atoms of water, slightly destabilizing the Fe(CN)₆ complex with the effect being more pronounced for Fe(CN)₆⁴⁻ than Fe(CN)₆³⁻, leading to an increased redox potential. This example illustrates the impact of hydrogen bonding on redox potentials in transition metal complexes, emphasizing the need to carefully consider specific solute–solvent interactions. Moving forward, such interactions, especially hydrogen bonding, should be routinely considered in modeling, as they are easier to handle and simulate than other complex interactions, like oxo-complex formation and metal–ligand interactions.

Conclusion

We present computationally efficient and accurate methods to calculate the redox potential of Fe³⁺, consistent with experiments, achieving minimal errors with density functionals; 0.01 V with ωB97X-D3, 0.02 V with both ωB97X-V and B3LYP/D3, and 0.04 V with ωB97M-V. Based on the simulations, the best performing computational model is a three-solvent layer micro-solvation architecture. In this model, we perform DFT optimization of an octahedral Fe^2+/3+[H₂O]₆ complex in the gas phase, followed by the addition of two layers of explicit water molecules (12 in layer 1 and 18 in layer 2) to capture critical electronic effects. An implicit solvation model is also incorporated, and single-point calculations are carried out to determine the reduction potentials.

We validated this model on five different Fe–L₃ ligand systems, demonstrating that the inclusion of explicit solvent layers not only reduces error but also provides insights into the specific interactions between water molecules and the ligand. These explicit solute–solvent interactions polarize the electron density of the ligand, significantly influencing the redox potential. Additionally, our model successfully resolves the long-standing issue of accurately modeling the Fe(CN)₆^3−/4− redox potential, achieving close agreement with experimental values—unlike previous approaches that exhibited substantial deviation.

Our findings demonstrate that it is possible to capture explicit solvent–solute interactions effectively with a cost-efficient approach, using semiempirical methods to optimize outer water layers while retaining the DFT-optimized geometry of the inner solvation shell. This approach enables the calculation of redox potentials across a wide range of Fe–ligand complexes with computational efficiency, making it suitable for exploring large chemical spaces of organometallic complexes.

This model reveals three critical ways in which the solvent can interact with the complex: (a) direct coordination, as in the formation of Fe–[H₂O]₆, (b) hydrogen bonding, particularly with electronegative atoms on ligands, and (c) electrostatic interactions, which are captured by combining explicit water molecules with implicit solvation models. This framework opens avenues for extending the model to a broader range of chemical environments and further enhancing the accuracy and efficiency of redox potential predictions in complex systems.

Data availability

The density functional theory (DFT) results from selected functionals, Cartesian coordinates of all structures, and all scripts used in this study are available on the GitHub repository: https://github.com/HassanHarb92/solvation_shells/paper_materials. A web application featuring interactive 3D structures from this work, built using the POPPY platform,^111,112 is available at https://solvationshells-fe.streamlit.app/.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This material is based upon work supported by the U.S. Department of Energy, Office of Science Energy Earthshot™ Initiative as part of the Center for Steel Electrification by Electrosynthesis (C-STEEL) at Argonne National Laboratory under Contract Number DE-AC02-06CH11357. We acknowledge the computing resources provided on “Improv” and “BEBOP”, two computing clusters operated by the Laboratory Computing Resource Center at Argonne National Laboratory. We thank Dr Alvaro Vazquez Mayagoitia, Dr Hieu Anh Doan, and Dr Yunkai Sun (Argonne National Laboratory) for their valuable insights and discussions.

References

1. E.-J. Kim, J.-H. Kim, Y.-S. Chang, D. Turcio-Ortega and P. G. Tratnyek, Effects of Metal Ions on the Reactivity and Corrosion Electrochemistry of Fe/FeS Nanoparticles, Environ. Sci. Technol., 2014, 48(7), 4002–4011,  DOI:10.1021/es405622d.
2. H. W. Pickering and R. P. Frankenthal, On the Mechanism of Localized Corrosion of Iron and Stainless Steel, J. Electrochem. Soc., 1972, 119(10), 1297,  DOI:10.1149/1.2403982.
3. S. S. Mahmoud, Electrochemical Studies of Pitting Corrosion of Cu–Fe Alloy in Sodium Chloride Solutions, J. Alloys Compd., 2008, 457(1–2), 587–592,  DOI:10.1016/j.jallcom.2008.01.029.
4. Y. Tian, G. Zeng, A. Rutt, T. Shi, H. Kim, J. Wang, J. Koettgen, Y. Sun, B. Ouyang, T. Chen, Z. Lun, Z. Rong, K. Persson and G. Ceder, Promises and Challenges of Next-Generation “Beyond Li-Ion” Batteries for Electric Vehicles and Grid Decarbonization, Chem. Rev., 2021, 121(3), 1623–1669,  DOI:10.1021/acs.chemrev.0c00767.
5. D. G. Kwabi, Y. Ji and M. J. Aziz, Electrolyte Lifetime in Aqueous Organic Redox Flow Batteries: A Critical Review, Chem. Rev., 2020, 120(14), 6467–6489,  DOI:10.1021/acs.chemrev.9b00599.
6. A. Van Der Ven, Z. Deng, S. Banerjee and S. P. Ong, Rechargeable Alkali-Ion Battery Materials: Theory and Computation, Chem. Rev., 2020, 120(14), 6977–7019,  DOI:10.1021/acs.chemrev.9b00601.
7. J. Cabana, T. Alaan, G. W. Crabtree, P.-W. Huang, A. Jain, M. Murphy, J. N’Diaye, K. Ojha, G. Agbeworvi, H. Bergstrom, S. Gersib, H. Harb, A. Stejer, G. Quiles-Galarza, O. Rodriguez, I. Caruso, J. M. Gonçalves, G. Y. Chen, C. A. Fernández, H. Pan, K. Ritter, Y. Yang, H. Zhang, A. C. García-Álvarez, S. Ilic, K. Kumar, R. Silcox, Y. Yao, H. Song, S. Stoyanov, M. Saraf, C. H. Chen, S. M. S. Subasinghe, R. Gomes, S. Lang, E. Murphy, A. S. Thind and Y. Zheng, NGenE 2022: Electrochemistry for Decarbonization, ACS Energy Lett., 2023, 8(1), 740–747,  DOI:10.1021/acsenergylett.2c02587.
8. J. Cabana, T. Alaan, G. W. Crabtree, M. C. Hatzell, K. Manthiram, D. A. Steingart, I. Zenyuk, F. Jiao, A. Vojvodic, J. Y. Yang, N. P. Balsara, K. A. Persson, D. J. Siegel, C. L. Haynes, J. Mauzeroll, M. Shen, B. J. Venton, N. Balke, J. Rodríguez-López, D. R. Rolison, R. Shahbazian-Yassar, V. Srinivasan, S. Chaudhuri, A. Couet and J. Hattrick-Simpers, NGenE 2021: Electrochemistry Is Everywhere, ACS Energy Lett., 2022, 7(1), 368–374,  DOI:10.1021/acsenergylett.1c02608.
9. R. Xia, S. Overa and F. Jiao, Emerging Electrochemical Processes to Decarbonize the Chemical Industry, JACS Au, 2022, 2(5), 1054–1070,  DOI:10.1021/jacsau.2c00138.
10. N. C. Kani, S. Olusegun, R. Chauhan, J. A. Gauthier and M. R. Singh, High-Pressure Electrochemistry: A New Frontier in Decarbonization, EES Catal., 2024, 2(2), 507–521,  10.1039/D3EY00284E.
11. K. G. Taylor and K. O. Konhauser, Iron in Earth Surface Systems: A Major Player in Chemical and Biological Processes, Elements, 2011, 7(2), 83–88,  DOI:10.2113/gselements.7.2.83.
12. F. J. Millero, Solubility of Fe(III) in Seawater, Earth Planet. Sci. Lett., 1998, 154(1–4), 323–329,  DOI:10.1016/S0012-821X(97)00179-9.
13. F. J. Millero, W. Yao and J. Aicher, The Speciation of Fe(II) and Fe(III) in Natural Waters, Mar. Chem., 1995, 50(1–4), 21–39,  DOI:10.1016/0304-4203(95)00024-L.
14. R. G. Burns, Rates and Mechanisms of Chemical Weathering of Ferromagnesian Silicate Minerals on Mars, Geochim. Cosmochim. Acta, 1993, 57(19), 4555–4574,  DOI:10.1016/0016-7037(93)90182-V.
15. S. Balzano, P. Statham, R. Pancost and J. Lloyd, Role of Microbial Populations in the Release of Reduced Iron to the Water Column from Marine Aggregates, Aquat. Microb. Ecol., 2009, 54, 291–303,  DOI:10.3354/ame01278.
16. Z. Wang, C. Liu, X. Wang, M. J. Marshall, J. M. Zachara, K. M. Rosso, M. Dupuis, J. K. Fredrickson, S. Heald and L. Shi, Kinetics of Reduction of Fe(III) Complexes by Outer Membrane Cytochromes MtrC and OmcA of Shewanella Oneidensis MR-1, Appl. Environ. Microbiol., 2008, 74(21), 6746–6755,  DOI:10.1128/AEM.01454-08.
17. J. K. Fredrickson and Y. A. Gorby, Environmental Processes Mediated by Iron-Reducing Bacteria, Curr. Opin. Biotechnol, 1996, 7(3), 287–294,  DOI:10.1016/S0958-1669(96)80032-2.
18. M. M. Urrutia, E. E. Roden, J. K. Fredrickson and J. M. Zachara, Microbial and Surface Chemistry Controls on Reduction of Synthetic Fe(III) Oxide Minerals by the Dissimilatory Iron-reducing Bacterium Shewanella Alga, Geomicrobiol. J., 1998, 15(4), 269–291,  DOI:10.1080/01490459809378083.
19. N. Rahbani, P. De Silva and E. Baudrin, Density Functional Theory-Based Protocol to Calculate the Redox Potentials of First-row Transition Metal Complexes for Aqueous Redox Targeting Flow Batteries, ChemSusChem, 2023, 16(18), e202300482,  DOI:10.1002/cssc.202300482.
20. K. Gong, F. Xu, J. B. Grunewald, X. Ma, Y. Zhao, S. Gu and Y. Yan, All-Soluble All-Iron Aqueous Redox-Flow Battery, ACS Energy Lett., 2016, 1(1), 89–93,  DOI:10.1021/acsenergylett.6b00049.
21. C. Sun and H. Zhang, Review of the Development of First-Generation Redox Flow Batteries: Iron-Chromium System, ChemSusChem, 2022, 15(1), e202101798,  DOI:10.1002/cssc.202101798.
22. B. S. Jayathilake, E. J. Plichta, M. A. Hendrickson and S. R. Narayanan, Improvements to the Coulombic Efficiency of the Iron Electrode for an All-Iron Redox-Flow Battery, J. Electrochem. Soc., 2018, 165(9), A1630–A1638,  DOI:10.1149/2.0451809jes.
23. M. C. Tucker, A. Phillips and A. Z. Weber, All-Iron Redox Flow Battery Tailored for Off-Grid Portable Applications, ChemSusChem, 2015, 8(23), 3996–4004,  DOI:10.1002/cssc.201500845.
24. Z. Li, L. Sun, Y. Zhang, Y. Han, W. Zhuang, L. Tian and W. Tan, Coupled and Decoupled Electrochemical Water Splitting for Boosting Hydrogen Evolution: A Review and Perspective, Coord. Chem. Rev., 2024, 510, 215837,  DOI:10.1016/j.ccr.2024.215837.
25. D. Jiang, R. Xu, L. Bai, W. Wu, D. Luo, Z. Li, T. Asahi, Y. Mai, Z. Liu, Y. Yamauchi and X. Xu, Insights into Electrochemical Paradigms for Lithium Extraction: Electrodialysis versus Capacitive Deionization, Coord. Chem. Rev., 2024, 516, 215923,  DOI:10.1016/j.ccr.2024.215923.
26. M. Li, N. Chen, H. Shang, C. Ling, K. Wei, S. Zhao, B. Zhou, F. Jia, Z. Ai and L. Zhang, An Electrochemical Strategy for Simultaneous Heavy Metal Complexes Wastewater Treatment and Resource Recovery, Environ. Sci. Technol., 2022, 56(15), 10945–10953,  DOI:10.1021/acs.est.2c02363.
27. L. X. Sepulveda-Montaño, J. F. Galindo and D. G. Kuroda, Infrared Spectroscopy of Liquid Solutions as a Benchmarking Tool of Semiempirical QM Methods: The Case of GFN2-xTB, J. Phys. Chem. B, 2023, 127(37), 7955–7963,  DOI:10.1021/acs.jpcb.3c03174.
28. H. Neugebauer, F. Bohle, M. Bursch, A. Hansen and S. Grimme, Benchmark Study of Electrochemical Redox Potentials Calculated with Semiempirical and DFT Methods, J. Phys. Chem. A, 2020, 124(35), 7166–7176,  DOI:10.1021/acs.jpca.0c05052.
29. K. D. Vogiatzis, M. V. Polynski, J. K. Kirkland, J. Townsend, A. Hashemi, C. Liu and E. A. Pidko, Computational Approach to Molecular Catalysis by 3d Transition Metals: Challenges and Opportunities, Chem. Rev., 2019, 119(4), 2453–2523,  DOI:10.1021/acs.chemrev.8b00361.
30. J. Tomasi, B. Mennucci and R. Cammi, Quantum Mechanical Continuum Solvation Models, Chem. Rev., 2005, 105(8), 2999–3094,  DOI:10.1021/cr9904009.
31. C. J. Cramer and D. G. Truhlar, A Universal Approach to Solvation Modeling, Acc. Chem. Res., 2008, 41(6), 760–768,  DOI:10.1021/ar800019z.
32. C. J. Stein, J. M. Herbert and M. Head-Gordon, The Poisson–Boltzmann Model for Implicit Solvation of Electrolyte Solutions: Quantum Chemical Implementation and Assessment via Sechenov Coefficients, J. Chem. Phys., 2019, 151(22), 224111,  DOI:10.1063/1.5131020.
33. G. Scalmani and M. J. Frisch, Continuous Surface Charge Polarizable Continuum Models of Solvation. I. General Formalism, J. Chem. Phys., 2010, 132(11), 114110,  DOI:10.1063/1.3359469.
34. M. Cossi, N. Rega, G. Scalmani and V. Barone, Energies, Structures, and Electronic Properties of Molecules in Solution with the C-PCM Solvation Model, J. Comput. Chem., 2003, 24(6), 669–681,  DOI:10.1002/jcc.10189.
35. V. Barone and M. Cossi, Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model, J. Phys. Chem. A, 1998, 102(11), 1995–2001,  DOI:10.1021/jp9716997.
36. A. Klamt, Conductor-like Screening Model for Real Solvents: A New Approach to the Quantitative Calculation of Solvation Phenomena, J. Phys. Chem., 1995, 99(7), 2224–2235,  DOI:10.1021/j100007a062.
37. C. C. Pye and T. Ziegler, An Implementation of the Conductor-like Screening Model of Solvation within the Amsterdam Density Functional Package, Theor. Chim. Acta, 1999, 101(6), 396–408,  DOI:10.1007/s002140050457.
38. A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396,  DOI:10.1021/jp810292n.
39. S. N. Steinmann, P. Sautet and C. Michel, Solvation Free Energies for Periodic Surfaces: Comparison of Implicit and Explicit Solvation Models, Phys. Chem. Chem. Phys., 2016, 18(46), 31850–31861,  10.1039/C6CP04094B.
40. J. M. Boereboom, P. Fleurat-Lessard and R. E. Bulo, Explicit Solvation Matters: Performance of QM/MM Solvation Models in Nucleophilic Addition, J. Chem. Theory Comput., 2018, 14(4), 1841–1852,  DOI:10.1021/acs.jctc.7b01206.
41. A. Okur, L. Wickstrom, M. Layten, R. Geney, K. Song, V. Hornak and C. Simmerling, Improved Efficiency of Replica Exchange Simulations through Use of a Hybrid Explicit/Implicit Solvation Model, J. Chem. Theory Comput., 2006, 2(2), 420–433,  DOI:10.1021/ct050196z.
42. M. Grant and R. B. Jordan, Kinetics of Solvent Water Exchange on Iron(III), Inorg. Chem., 1981, 20(1), 55–60,  DOI:10.1021/ic50215a014.
43. T. K. Sham, J. B. Hastings and M. L. Perlman, Structure and Dynamic Behavior of Transition-Metal Ions in Aqueous Solution: An EXAFS Study of Electron-Exchange Reactions, J. Am. Chem. Soc., 1980, 102(18), 5904–5906,  DOI:10.1021/ja00538a033.
44. D. T. Richens, Ligand Substitution Reactions at Inorganic Centers, Chem. Rev., 2005, 105(6), 1961–2002,  DOI:10.1021/cr030705u.
45. M. C. Groenenboom and J. A. Keith, Explicitly Unraveling the Roles of Counterions, Solvent Molecules, and Electron Correlation in Solution Phase Reaction Pathways, J. Phys. Chem. B, 2016, 120(41), 10797–10807,  DOI:10.1021/acs.jpcb.6b07606.
46. C. M. Sterling and R. Bjornsson, Multistep Explicit Solvation Protocol for Calculation of Redox Potentials, J. Chem. Theory Comput., 2019, 15(1), 52–67,  DOI:10.1021/acs.jctc.8b00982.
47. M. Bursch, J. Mewes, A. Hansen and S. Grimme, Best-Practice DFT Protocols for Basic Molecular Computational Chemistry, Angew. Chem., Int. Ed., 2022, 61(42), e202205735,  DOI:10.1002/anie.202205735.
48. R. Sure, M. El Mahdali, A. Plajer and P. Deglmann, Towards a Converged Strategy for Including Microsolvation in Reaction Mechanism Calculations, J. Comput.-Aided Mol. Des., 2021, 35(4), 473–492,  DOI:10.1007/s10822-020-00366-2.
49. D. Sicinska, P. Paneth and D. G. Truhlar, How Well Does Microsolvation Represent Macrosolvation? A Test Case: Dynamics of Decarboxylation of 4-Pyridylacetic Acid Zwitterion, J. Phys. Chem. B, 2002, 106(10), 2708–2713,  DOI:10.1021/jp013252a.
50. S. Spicher, C. Plett, P. Pracht, A. Hansen and S. Grimme, Automated Molecular Cluster Growing for Explicit Solvation by Efficient Force Field and Tight Binding Methods, J. Chem. Theory Comput., 2022, 18(5), 3174–3189,  DOI:10.1021/acs.jctc.2c00239.
51. M. Steiner, T. Holzknecht, M. Schauperl and M. Podewitz, Quantum Chemical Microsolvation by Automated Water Placement, Molecules, 2021, 26(6), 1793,  DOI:10.3390/molecules26061793.
52. S. A. Katsyuba, S. Spicher, T. P. Gerasimova and S. Grimme, Fast and Accurate Quantum Chemical Modeling of Infrared Spectra of Condensed-Phase Systems, J. Phys. Chem. B, 2020, 124(30), 6664–6670,  DOI:10.1021/acs.jpcb.0c05857.
53. G. N. Simm, P. L. Türtscher and M. Reiher, Systematic Microsolvation Approach with a Cluster-continuum Scheme and Conformational Sampling, J. Comput. Chem., 2020, 41(12), 1144–1155,  DOI:10.1002/jcc.26161.
54. Y. Basdogan and J. A. Keith, A Paramedic Treatment for Modeling Explicitly Solvated Chemical Reaction Mechanisms, Chem. Sci., 2018, 9(24), 5341–5346,  10.1039/C8SC01424H.
55. M. Rahbar and C. J. Stein, A Statistical Perspective on Microsolvation, J. Phys. Chem. A, 2023, 127(9), 2176–2193,  DOI:10.1021/acs.jpca.2c08763.
56. R. Sure, M. El Mahdali, A. Plajer and P. Deglmann, Towards a Converged Strategy for Including Microsolvation in Reaction Mechanism Calculations, J. Comput.-Aided Mol. Des., 2021, 35(4), 473–492,  DOI:10.1007/s10822-020-00366-2.
57. U. Farooq, S. M. Bukhari, S. Khan, X.-L. Xu, H.-G. Xu and W.-J. Zheng, Microsolvation of Salts in Water: A Comprehensive Overview of the Experimental and Computational Approaches, Coord. Chem. Rev., 2024, 517, 216041,  DOI:10.1016/j.ccr.2024.216041.
58. Y. Chamorro, E. Flórez, A. Maldonado, G. Aucar and A. Restrepo, Microsolvation of Heavy Halides, Int. J. Quantum Chem., 2021, 121(7), e26571,  DOI:10.1002/qua.26571.
59. A. N. Masliy, T. N. Grishaeva and A. M. Kuznetsov, Standard Redox Potentials of Fe(III) Aqua Complexes Included into the Cavities of Cucurbit[ n]Urils (n = 6–8): A DFT Forecast, J. Phys. Chem. A, 2019, 123(25), 5341–5346,  DOI:10.1021/acs.jpca.9b04053.
60. S. J. Konezny, M. D. Doherty, O. R. Luca, R. H. Crabtree, G. L. Soloveichik and V. S. Batista, Reduction of Systematic Uncertainty in DFT Redox Potentials of Transition-Metal Complexes, J. Phys. Chem. C, 2012, 116(10), 6349–6356,  DOI:10.1021/jp300485t.
61. T. F. Hughes and R. A. Friesner, Development of Accurate DFT Methods for Computing Redox Potentials of Transition Metal Complexes: Results for Model Complexes and Application to Cytochrome P450, J. Chem. Theory Comput., 2012, 8(2), 442–459,  DOI:10.1021/ct2006693.
62. A. J. Bard; R. Parsons and J. Jordan Standard Potentials in Aqueous Solution, CRC Press, 1985.
63. K. Hansen, G. Montavon, F. Biegler, S. Fazli, M. Rupp, M. Scheffler, O. A. Von Lilienfeld, A. Tkatchenko and K.-R. Müller, Assessment and Validation of Machine Learning Methods for Predicting Molecular Atomization Energies, J. Chem. Theory Comput., 2013, 9(8), 3404–3419,  DOI:10.1021/ct400195d.
64. O. A. von Lilienfeld, Quantum Machine Learning in Chemical Compound Space, Angew. Chem., Int. Ed., 2018, 57(16), 4164–4169,  DOI:10.1002/anie.201709686.
65. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox Gaussian 16, Gaussian, Inc., Wallingford CT, 2016.
66. A. D. Becke, Density-Functional Thermochemistry. III. The Role of Exact Exchange, J. Chem. Phys., 1993, 98(7), 5648–5652,  DOI:10.1063/1.464913.
67. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98(45), 11623–11627,  DOI:10.1021/j100096a001.
68. A. D. Becke, Density-Functional Exchange-Energy Approximation with Correct Asymptotic Behavior, Phys. Rev. A:At., Mol., Opt. Phys., 1988, 38(6), 3098–3100,  DOI:10.1103/PhysRevA.38.3098.
69. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37(2), 785–789,  DOI:10.1103/PhysRevB.37.785.
70. B. Miehlich, A. Savin, H. Stoll and H. Preuss, Results Obtained with the Correlation Energy Density Functionals of Becke and Lee, Yang and Parr, Chem. Phys. Lett., 1989, 157(3), 200–206,  DOI:10.1016/0009-2614(89)87234-3.
71. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple [Phys. Rev. Lett. 77, 3865 (1996)], Phys. Rev. Lett., 1997, 78(7), 1396,  DOI:10.1103/PhysRevLett.78.1396.
72. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
73. M. J. Frisch, J. A. Pople and J. S. Binkley, Self-consistent Molecular Orbital Methods 25. Supplementary Functions for Gaussian Basis Sets, J. Chem. Phys., 1984, 80(7), 3265–3269,  DOI:10.1063/1.447079.
74. H. P. Hratchian and H. B. Schlegel Finding Minima, Transition States, and Following Reaction Pathways on Ab Initio Potential Energy Surfaces, Theory and Applications of Computational Chemistry, Elsevier, 2005, pp. 195–249 DOI:10.1016/B978-044451719-7/50053-6.
75. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132(15), 154104,  DOI:10.1063/1.3382344.
76. S. H. Vosko, L. Wilk and M. Nusair, Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin Density Calculations: A Critical Analysis, Can. J. Phys., 1980, 58(8), 1200–1211,  DOI:10.1139/p80-159.
77. T. P. Veshohilova, [Effect of combined use of steroid preparations with pyrroxane on the gonadotropic function of the hypophysis], Akush. Ginekol., 1975, 10, 10–12.
78. R. R. Baker, M. J. Dowdall and V. P. Whittaker, The Involvement of Lysophosphoglycerides in Neurotransmitter Release; the Composition and Turnover of Phospholipids of Synaptic Vesicles of Guinea-Pig Cerebral Cortex and Torpedo Electric Organ and the Effect of Stimulation, Brain Res., 1975, 100(3), 629–644,  DOI:10.1016/0006-8993(75)90162-6.
79. B. Tian, Z. Fan, H. Tao, Z. Liu and Z. Zhang, Exploring Elemental Sulfur-Solvent Interactions via Density Functional Theory, ChemistrySelect, 2025, 10(6), e202405654,  DOI:10.1002/slct.202405654.
80. X. Liu, H. Yang, H. Harb, R. Samajdar, T. J. Woods, O. Lin, Q. Chen, A. I. B. Romo, J. Rodríguez-López, R. S. Assary, J. S. Moore and C. M. Schroeder, Shape-Persistent Ladder Molecules Exhibit Nanogap-Independent Conductance in Single-Molecule Junctions, Nat. Chem., 2024, 16(11), 1772–1780,  DOI:10.1038/s41557-024-01619-5.
81. M. R. Dooley and S. Vyas, Role of Explicit Solvation and Level of Theory in Predicting the Aqueous Reduction Potential of Carbonate Radical Anion by DFT, Phys. Chem. Chem. Phys., 2025, 27, 6867,  10.1039/D4CP04487H.
82. N. Mardirossian and M. Head-Gordon, ωB97M-V: A Combinatorially Optimized, Range-Separated Hybrid, Meta-GGA Density Functional with VV10 Nonlocal Correlation, J. Chem. Phys., 2016, 144(21), 214110,  DOI:10.1063/1.4952647.
83. F. Z. M. Zahir, M. A. Hay, J. T. Janetzki, R. W. Gable, L. Goerigk and C. Boskovic, Predicting Valence Tautomerism in Diverse Cobalt–Dioxolene Complexes: Elucidation of the Role of Ligands and Solvent, Chem. Sci., 2024, 15(15), 5694–5710,  10.1039/D3SC04493A.
84. N. Mardirossian and M. Head-Gordon, ωB97X-V: A 10-Parameter, Range-Separated Hybrid, Generalized Gradient Approximation Density Functional with Nonlocal Correlation, Designed by a Survival-of-the-Fittest Strategy, Phys. Chem. Chem. Phys., 2014, 16(21), 9904,  10.1039/c3cp54374a.
85. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, A Look at the Density Functional Theory Zoo with the Advanced GMTKN55 Database for General Main Group Thermochemistry, Kinetics and Noncovalent Interactions, Phys. Chem. Chem. Phys., 2017, 19(48), 32184–32215,  10.1039/C7CP04913G.
86. F. Neese, The ORCA Program System, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2(1), 73–78,  DOI:10.1002/wcms.81.
87. E. Caldeweyher, J.-M. Mewes, S. Ehlert and S. Grimme, Extension and Evaluation of the D4 London-Dispersion Model for Periodic Systems, Phys. Chem. Chem. Phys., 2020, 22(16), 8499–8512,  10.1039/D0CP00502A.
88. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, A Generally Applicable Atomic-Charge Dependent London Dispersion Correction, J. Chem. Phys., 2019, 150(15), 154122,  DOI:10.1063/1.5090222.
89. E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 Dispersion Coefficient Model, J. Chem. Phys., 2017, 147(3), 034112,  DOI:10.1063/1.4993215.
90. F. Neese, Software Update: The ORCA Program System—Version 5.0, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12(5), e1606,  DOI:10.1002/wcms.1606.
91. A. Najibi and L. Goerigk, The Nonlocal Kernel in van der Waals Density Functionals as an Additive Correction: An Extensive Analysis with Special Emphasis on the B97M-V and ωB97M-V Approaches, J. Chem. Theory Comput., 2018, 14(11), 5725–5738,  DOI:10.1021/acs.jctc.8b00842.
92. H. Schröder, A. Creon and T. Schwabe, Reformulation of the D3(Becke–Johnson) Dispersion Correction without Resorting to Higher than C₆ Dispersion Coefficients, J. Chem. Theory Comput., 2015, 11(7), 3163–3170,  DOI:10.1021/acs.jctc.5b00400.
93. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32(7), 1456–1465,  DOI:10.1002/jcc.21759.
94. E. R. Johnson and A. D. Becke, A Post-Hartree-Fock Model of Intermolecular Interactions: Inclusion of Higher-Order Corrections, J. Chem. Phys., 2006, 124(17), 174104,  DOI:10.1063/1.2190220.
95. E. Caldeweyher, S. Ehlert, A. Hansen, H. Neugebauer, S. Spicher, C. Bannwarth and S. Grimme, A Generally Applicable Atomic-Charge Dependent London Dispersion Correction, J. Chem. Phys., 2019, 150(15), 154122,  DOI:10.1063/1.5090222.
96. E. Caldeweyher, C. Bannwarth and S. Grimme, Extension of the D3 Dispersion Coefficient Model, J. Chem. Phys., 2017, 147(3), 034112,  DOI:10.1063/1.4993215.
97. E. Caldeweyher, J.-M. Mewes, S. Ehlert and S. Grimme, Extension and Evaluation of the D4 London-Dispersion Model for Periodic Systems, Phys. Chem. Chem. Phys., 2020, 22(16), 8499–8512,  10.1039/D0CP00502A.
98. N. V. Tkachenko, L. B. Dittmer, R. Tomann and M. Head-Gordon, Smooth Dispersion Is Physically Appropriate: Assessing and Amending the D4 Dispersion Model, J. Phys. Chem. Lett., 2024, 15(42), 10629–10637,  DOI:10.1021/acs.jpclett.4c02653.
99. M. Friede, S. Ehlert, S. Grimme and J.-M. Mewes, Do Optimally Tuned Range-Separated Hybrid Functionals Require a Reparametrization of the Dispersion Correction? It Depends, J. Chem. Theory Comput., 2023, 19(22), 8097–8107,  DOI:10.1021/acs.jctc.3c00717.
100. L. Wittmann, I. Gordiy, M. Friede, B. Helmich-Paris, S. Grimme, A. Hansen and M. Bursch, Extension of the D3 and D4 London Dispersion Corrections to the Full Actinides Series, Phys. Chem. Chem. Phys., 2024, 26(32), 21379–21394,  10.1039/D4CP01514B.
101. O. A. Vydrov and T. Van Voorhis, Nonlocal van der Waals Density Functional: The Simpler the Better, J. Chem. Phys., 2010, 133(24), 244103,  DOI:10.1063/1.3521275.
102. Https://Github.Com/HassanHarb92/Solvation_shells (https://Https://Github.Com/HassanHarb92/Solvation_shells).
103. C. Bannwarth, S. Ehlert and S. Grimme, GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions, J. Chem. Theory Comput., 2019, 15(3), 1652–1671,  DOI:10.1021/acs.jctc.8b01176.
104. An. M. Kuznetsov, A. N. Maslii and L. I. Krishtalik, Quantum Chemical Model of Solvation for Calculation of Electrode Potentials of Redox Processes Involving Ferrocene, Cobaltocene, and Their Ions, Russ. J. Electrochem., 2008, 44(1), 34–42,  DOI:10.1134/S1023193508010060.
105. A. Frumkin and B. Damaskin, Remark on the Paper of S. Trasatti: The Concept of Absolute Electrode Potential. An Attempt at a Calculation, J. Electroanal. Chem. Interfacial Electrochem., 1975, 66(2), 150–154,  DOI:10.1016/S0022-0728(75)80222-1.
106. S. Trasatti, The Concept of Absolute Electrode Potential an Attempt at a Calculation, J. Electroanal. Chem. Interfacial Electrochem., 1974, 52(3), 313–329,  DOI:10.1016/S0022-0728(74)80446-8.
107. I. Persson, Hydrated Metal Ions in Aqueous Solution: How Regular Are Their Structures?, Pure Appl. Chem., 2010, 82(10), 1901–1917,  DOI:10.1351/PAC-CON-09-10-22.
108. G. Liang, N. J. DeYonker, X. Zhao and C. E. Webster, Prediction of the Reduction Potential in Transition-metal Containing Complexes: How Expensive? For What Accuracy?, J. Comput. Chem., 2017, 38(28), 2430–2438,  DOI:10.1002/jcc.24894.
109. M.-H. Baik and R. A. Friesner, Computing Redox Potentials in Solution: Density Functional Theory as A Tool for Rational Design of Redox Agents, J. Phys. Chem. A, 2002, 106(32), 7407–7412,  DOI:10.1021/jp025853n.
110. P. A. Rock, The Standard Oxidation Potential of the Ferrocyanide-Ferricyanide Electrode at 25° and the Entropy of Ferrocyanide Ion, J. Phys. Chem., 1966, 70(2), 576–580,  DOI:10.1021/j100874a042.
111. H. Harb and R. S. Assary, POPPY: Python-Based Tool for Visualizing and Sharing Computational Chemistry Data via Web Applications, J. Mol. Graphics Modell. , in press.
112. H. Harb HassanHarb92/SI_create_web_app, 2024. https://github.com/HassanHarb92/SI_create_web_app (accessed 2025-01-22).

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00454c

---