Theoretical understanding and prediction of metal-doped CeO₂ catalysts for ammonia dissociation

Abstract

Ammonia plays a critical role in energy and environmental catalysis, particularly in ammonia dissociation reactions. Understanding the adsorption and dissociation of ammonia-related species on catalysts is essential for the development of new chemical reactions and high-performance catalysts. However, establishing the relationship between catalyst properties and the adsorption of dissociated species remains challenging, particularly for metal oxide catalysts. This study employs density functional theory calculations to investigate the adsorption properties of ammonia and dissociated intermediate species on metal-doped CeO₂. Through a feature correlation heat map, certain descriptors, such as single atom formation energy, gaseous atom formation heat, valence band maximum, and work function, were determined to exhibit a strong linear relationship with the adsorption properties of NH_x species. As deduced from the density of states properties and orbital theory, it is also found that the energy difference between the lowest unoccupied orbital of the metal and the highest occupied orbital of ammonia, has a good relationship with the adsorption energy of NH₃.

---

1. Introduction

Ammonia (NH₃) has attracted considerable attention in the fields of energy and environmental catalysis owing to its high hydrogen content and energy density, making it a promising renewable energy source.^1–4 The synthesis of NH₃ from N₂ and H₂ has been extensively studied for a century, tracing back to the development of the Haber–Bosch reaction.^5–7 Additionally, recent advancements in NH₃ decomposition technology for hydrogen production have demonstrated significant potential for hydrogen energy storage and transportation.^8–10 In the field of environmental catalysis, NH₃ selective catalytic reduction (NH₃-SCR)^11–13 and NH₃ selective catalytic oxidation (NH₃-SCO)^14–16 technologies are widely employed as key measures to address exhaust emissions from industrial and mobile sources. In response to the escalating energy crisis and environmental challenges, researchers have explored the electrochemical reduction of nitrate (NO₃⁻) in solution^17–19 to produce NH₃, as well as the electrochemical coupling of C–N bonds in CO₂ and NH₃ to synthesize chemicals with industrial value.^20–22 These technologies involve NH₃ adsorption and dissociation reactions (NH₃ ↔ NH₂–H ↔ NH–2H ↔ N–3H) on catalysts, which are crucial in determining the reaction rate and have become the focus research in this field.

Analysis of the adsorption and dissociation properties of catalysts for NH₃-related species was conducted using temperature-programmed desorption (TPD),²³in situ diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS),²⁴ and adsorption penetration²⁵ tests for NH₃. Hahn et al. demonstrated that Fe species enhanced the adsorption of NH₃ over H⁺-exchanged beta zeolite molecular sieves through TPD experiments.²⁶ Zhang et al. used in situ DRIFTS to show that Cu sites on TiO₂ promoted the conversion of NH₃ into NO₂ species, which is an important participant in the fast SCR reaction.²⁷ They also proved that S doping enhances the NH₃ adsorption capacity of the Fe₂O₃/TiO₂ catalyst through adsorption penetration testing.²⁸ Although various characterization methods exist, most of them primarily examine the NH₃ adsorption properties of the catalyst, making it challenging to clarify the adsorption effects of intermediate reaction species on the catalyst surface. Additionally, experimental screening of catalysts for high activity is typically costly and time-consuming. Conversely, screening the adsorption properties of catalysts and reaction intermediates with theoretical calculations can greatly reduce these costs.

Theoretical calculations are commonly used to complement experimental findings in NH₃ catalytic reactions.^29–34 Zhang et al. performed theoretical calculations to compare the adsorption sites of NH₃ on Ag/CeSnO_x catalysts and discovered that NH₃ is more readily adsorbed on Ag as a Lewis acid site.³⁵ Using theoretical calculation, Jiang et al. demonstrated that K species reduce the adsorption energy of NH₃ on the catalyst surface.³⁶ Liu et al. compared the reaction paths of NH₃ decomposing into N₂ and H₂ on Ni(111) and Ni/CeO₂ catalysts and confirmed that CeO₂ enhances the dispersion of Ni clusters, thereby reducing the reaction activation energy.³⁷ With the advancement of computational power, theoretical calculations are increasingly utilized to screen catalysts and identify factors that influence catalytic efficiency.^38–44 Hansgen et al. screened bimetallic alloy catalysts using the adsorption energy of N atoms and alloys as descriptors. They predicted that catalysts with Ni–Pt–Pt surface chemistry exhibit excellent catalytic performance for hydrogen production by NH₃ decompostion.⁴⁵ Similarly, Yang et al. employed high-throughput theoretical calculations to screen metal catalysts for high activity in the NH₃-SCO reaction. They found that the binding energy of N and O on metals serves as a descriptor for catalytic performance, and predicted that Cu(100) and Pt(111) catalysts possess the highest activity.⁴⁶ Zheng et al. investigated the factors influencing the activation energy of transition metal-doped TiO₂ catalysts to dissociate NH₃ into NH₂ and H species, as well as the subsequent activation energy of reaction with NO to form N₂O, and found that the activity of surface oxygen has a significant impact.⁴⁷ Currently, establishing the relationship between catalyst properties and dissociated species adsorption through a single descriptor is challenging for low-cost and readily available metal oxide catalysts in NH₃ dissociation reactions. Therefore, exploring the factors influencing the interaction between metal oxide catalysts and NH₃-related species is crucial to facilitate more effective catalyst screening.

In this study, the effects of transition metal doping on cerium dioxide (CeO₂) and on NH₃ dissociation in gas–solid interface thermal catalytic reaction were theoretically investigated. CeO₂ is commonly used in NH₃ catalytic reactions owing to its affordability, widespread availability, excellent dispersibility of active sites, and high oxygen storage capacity.^48–50 The impact of metal doping on the local distortion and chemical properties of the CeO₂ structure was explored. The adsorption positions and energies of species that participate in NH₃ dissociation on the catalyst surface were examined. A feature correlation heat map was employed to scrutinize the relationship between the adsorption energies of NH₃-related species and the physicochemical properties of the catalyst. The projected density of states (PDOS) was used to further analyze the electronic interactions between the adsorption sites on the catalyst surface and the NH_x species. This work will offer valuable insights for the design and comprehension of metal oxide catalysts in NH₃ dissociation reactions.

2. Computational methods

Density functional theory (DFT) calculations were performed using the Vienna ab initio simulation package (VASP 6.4.2).⁵¹ The projector augmented wave method was used to describe the electronic structure of atoms.⁵² The exchange correlation energy functional is described by the Perdew–Burke–Ernzerhof (PBE) functional in generalized gradient approximation.⁵³ Hubbard U was used to rationalize the Coulomb repulsion between electrons in local orbitals. Therefore, PBE+U was adopted to improve the processing of strongly correlated electron systems.⁵⁴ The U(U_eff) was used to represent the U–J parameters. All metallic elements containing d and f orbitals were assigned U_eff values (Table S1, ESI†). The plane wave cutoff energy was set to 500 eV. The force convergence criterion for the structure was −0.02 eV Å⁻¹. The DFT-D3 method was used to improve the treatment of van der Waals interactions.⁵⁵ The K-point convergence tests were conducted (Fig. S1, ESI†). The energies of the structures converged by (1 × 1 × 1), (2 × 2 × 1), and (4 × 4 × 1) k-point meshes were compared. All variations are very small and do not affect the conclusions. Hence, the Brillouin zone integration⁵⁶ was performed using a k-point grid (1 × 1 × 1). All electronic structure calculations were performed using Monkhorst–Pack (3 × 3 × 1).

The lattice parameter of the optimized CeO₂ bulk structure was 5.47 Å, which is close to the experimental value of 5.41 Å.⁵⁷ The unit cell of the CeO₂(111) plane was used as the surface model as this plane is the most thermodynamically stable surface. The surface structure of CeO₂(111) and metal-doped CeO₂(111) was composed of a supercell (3 × 2) with 9 atomic layers and surface terminals of O–Ce–O (Fig. 1). The replacement of a surface Ce atom by another metal atom constitutes a doped structure. The adsorption of NH₃, NH₂–H, NH–2H, and N–3H species was performed on the surface model. During structural optimization, the six atomic layers at the bottom of the supercell were fixed.

Fig. 1 Structural diagrams of pure CeO₂ and metal-doped CeO₂.

The energy of a single metal atom (E_{single metal atom}) was calculated using the following formula:

E_{single metal atom} = E_M-bulk/n (1)

where E_M-bulk is the total energy of the bulk metal and n is the total number of atoms in the bulk metal.

The formation energy (E_doped) of metal-doped CeO₂ was calculated by the following formula:

E_doped = E_M–CeO2 − E_CeO2 − (E_M-bulk/n) + (E_Ce-bulk/n) (2)

where E_M–CeO2, E_CeO2 and E_Ce-bulk are the total energies of the metal-doped CeO₂ surface, pure CeO₂ surface, and bulk Ce, respectively.

The oxygen vacancy formation energies (E_Ov) were obtained by the following calculation formula:

E_Ov = E_{M–CeO2–Ov} − E_M–CeO2 + E_O2/2 (3)

where E_{M–CeO2–Ov}, E_M–CeO2, and E_O2 are the energies of the metal-doped CeO₂ structure with oxygen vacancies, the metal-doped CeO₂ structure without oxygen vacancies, and the oxygen molecule, respectively.

The adsorption energies (E_ads(species)) of NH₃, NH₂–H, NH–2H, and N–3H species are calculated using the following formula:

E_ads(species) = E_{species/surface} − E_surface − E_NH3 (4)

where E_{species/surface}, E_surface, and E_NH3 are the total energies of the species (NH₃, NH₂–H, NH–2H and N–3H) adsorbed on the catalyst surface, the catalyst surface, and the NH₃ molecule, respectively. NH₃ was used as a reference for the relevant adsorption structures of all NH₃ species to calculate the adsorption energies.

The adsorption energy of a single H atom (E_ads(H)) was calculated using the following formula:

E_ads(H) = E_H/surface − E_surface − (E_H2/2) (5)

where E_H/surface and E_H2 are the total energies of H adsorbed on the catalyst surface and H₂ molecules, respectively.

The d-band center (ξ_d) of metal doped CeO₂ was calculated by the following formula:⁵⁸

where ξ is the energy and n_d(ξ) is the number of electrons in the ξ energy state.

The valence band maximum (VBM), conduction band minimum (CBM), band gap, d-band center and work function were obtained through the calculation of the density of states and the work function.

3. Result and discussion

3.1. Structure filtered by distortion

In the dissociation reaction of NH₃, the presence of active surface oxygen species and oxygen vacancies plays a crucial role in facilitating hydrogen extraction. Metal doping can modulate the local lattice distortion in metal oxides, thereby affecting the presence of active surface oxygen species and oxygen vacancies.⁵⁹ Metal oxides with higher lattice distortions exhibit higher concentrations of surface oxygen species and oxygen vacancies. By combining the structure and distance between the metal dopant and oxygen (Fig. S2 and Table S2, ESI†), the local lattice distortion⁵⁸ (Δ) of CeO₂ doped with various metals was calculated using the following formula:where R_i represents the distance between the dopant element and the adjacent O atom and R_av denotes the average of all R_i values. Fig. 2a illustrates the correlation between the dopant element and the local lattice distortion in metal-doped CeO₂.

Fig. 2 (a) Scatter plot of local structural distortion of Ce and metal dopant sites. Schematic of structures that are (b) prone to structural distortion and (c) not prone to structural distortion.

As depicted in Fig. 2b and c, the structures of metal-doped CeO₂ can be divided into two categories based on the lattice distortion. One category exhibits a higher tendency for local structural distortion (Δ > 0.01), which promotes the formation of active surface oxygen species and oxygen vacancies. The other category exhibits a lower tendency for local structural distortion (Δ < 0.01), rendering these structures more stable and less likely to generate active surface oxygen species and oxygen vacancies. The structures that were susceptible to distortion were selected for further adsorption of species in the NH₃ dissociation reaction.

3.2. Adsorption of reaction species

The adsorption strength of reactants and intermediates significantly impacts reaction activity and selectivity. The NH₃ dissociation reaction primarily follows the following steps:

NH₃ + * → NH₃* (8)

NH₃* + * → NH₂* + H* (9)

NH₂* + H* + * → NH* + 2H* (10)

NH* + 2H* + * → N* + 3H* (11)

The adsorption properties of the above species were studied on all metal-doped CeO₂ surfaces (*). As illustrated in Fig. 3 and Fig. S3, S4 in the ESI,† NH₃ adsorbs onto the catalyst surface, where the N lone pairs of electrons interact and bonds with the empty orbitals of the metal dopant. The H atoms of NH₃ undergo hydrogen bonding interactions with neighboring surface lattice oxygen. Through interactions between the metal dopant and the adjacent surface lattice oxygen, NH₃ progressively dissociates as the N–H bonds break and the three H atoms are adsorbed onto the adjacent lattice oxygen. The metal dopant not only directly influences the adsorption energies of NH₃ and intermediate species, but also indirectly impacts the chemical activity of the neighboring O atoms, thus affecting the adsorption energy of H atoms. Therefore, it is essential to investigate the correlation between the chemical properties of metal dopants and the adsorption energies of dissociated species.

Fig. 3 Adsorption structure diagram of NH₃ and its dissociated intermediate species on the catalysts.

3.3. Descriptor screening for elucidating adsorption

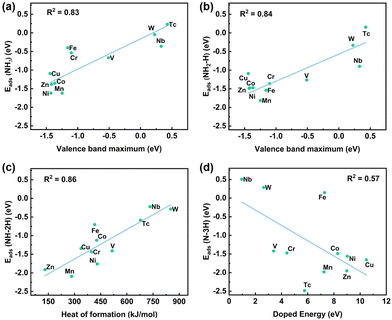
The feature correlation heat map depicts the strength of the correlation between the chemical properties of metal dopants and the adsorption energies of species. Fig. 4 and Tables S3, S4 in the ESI,† present various chemical properties of the metal dopants. The Pearson correlation coefficient was employed as a statistical measure to analyze the relationship between two variables. The value in each cell of the figure represents the correlation strength between each pair of variables, which ranges from −1 to 1. Positive values indicate a positive correlation between the variables, while negative values indicate a negative correlation. The darkness of the cell's color signifies the strength of the correlation, with darker colors indicating stronger correlations. Evidently, the analysis shows that the VBM (0.83), CBM (0.83), and work function (−0.81) of metal dopants are strongly correlated with the adsorption energies of NH₃. Additionally, the VBM (0.84), work function (−0.76), and heat of formation (0.76) are strongly correlated with the adsorption energies of NH₂–H species. Furthermore, the heat of formation (0.86), VBM (0.79), and work function (−0.75) are strongly correlated with the adsorption energies of NH–2H species. Lastly, the doping formation energy (−0.57), heat of formation (0.55), and covalent radius (0.53) exhibit some correlation with the adsorption energy of N–3H species.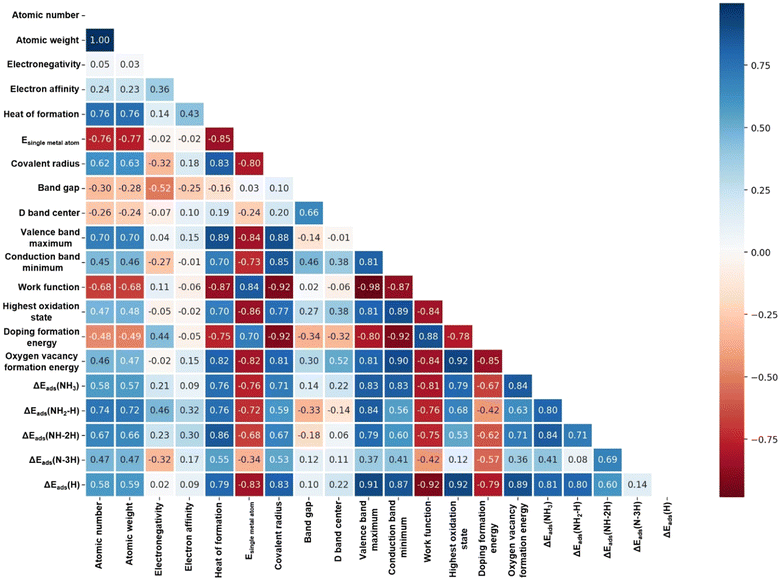

Fig. 4 Feature correlation heat map. The correlation between individual descriptors and adsorption energies of species in NH₃ dissociation. (Correlation coefficient is Pearson).

Plots exhibiting the strongest linear correlation with the adsorption of the four intermediate species are presented in Fig. 5, along with Fig. S5 in the ESI,† which demonstrate that the adsorption energies of the NH₃, NH₂–H, and NH–2H species on various metal-doped catalysts are all highly linearly correlated with the VBM. The dissociation of a single H atom has a minimal impact on the adsorption energy and linearity, suggesting that the adsorption intensity is primarily governed by the interaction between the N atoms and the metal dopants. As further dissociation of H atoms occurs, the overall adsorption energy of the species is influenced by the adsorption of both N and H atoms on the metal dopant and adjacent O atoms, respectively. Additionally, the VBM has a good linear relationship with the heat of formation of the metal (0.89), the energy of a single metal atom (−0.84), and the atomic radius (0.88). However, the linear correlation between the above three metal properties and the adsorption energies of NH₃-related species is not as strong as the VBM, except for the heat of formation and NH–2H. This may be because the three metal properties jointly affect the VBM, and further affect the adsorption energies of NH₃-related species. Additionally, Ni-doped CeO₂ exhibits strong adsorption for NH₃-related species, aligning with the excellent performance of Ni-based catalysts in NH₃ dissociation reaction experiments.^60–63 Meanwhile, Zn-, Cu-, Co-, and Mn-doped CeO₂ catalysts also demonstrate strong adsorption of NH₃-related species, warranting further study.

Fig. 5 (a) and (b) Valence band maximum, (c) heat of formation, and (d) doped energy of metal dopant as functions of the adsorption energies of (a) NH₃, (b) NH₂–H, (c) NH–2H and (d) N–3H species in NH₃ dissociation.

Oxygen vacancies play an important role in the reaction process. The linear correlation between the adsorption energies (E_ads) of NH₃-related species and the oxygen vacancy formation energies (E_Ov) is shown in Fig. S6 (ESI†). The linear correlation between E_ads and E_Ov of NH₃, NH₂–H, NH–2H, and N–3H species is 0.84, 0.63, 0.71, and 0.36 respectively. The linearity (0.84) between E_ads and E_Ov of NH₃ shows that the lower the formation energies of the oxygen vacancy, the more favorable it is for the oxygen atom (adsorbed on the oxygen vacancy) to bind to the first H atom of NH₃. The oxygen atom that has already bound to the first H atom has little effect on the binding of the remaining H atoms with other oxygen atoms, so the linear correlation between oxygen vacancy formation energies and NH₃ adsorption energies is high, and other correlations are low.

Meanwhile, the activation energies of the gradual dissociation of NH₃ on Ni, V, and Nb doped CeO₂ surfaces were also obtained by DFT calculation, and its relationship with the valence band maximum of the catalyst is shown in Fig. S7 (ESI†). There is no obvious linear relationship between the valence band maximum and the activation energies of NH dissociation. This may be because the activation energy of NH dissociation is affected by both the properties of the doped metal and the adsorption ability of H by different surrounding oxygen atoms.

The density of states (Fig. 6) of Ni-, V-, and Nb-doped catalysts with NH₃ adsorbed on the surface were studied to further elucidate the effect of metal dopants on adsorption species from the electronic structure level. As shown in Fig. 6a, d, and g, the valence band of the catalyst is primarily composed of atomic orbital energy levels occupied by O and Ce electrons. Owing to the presence of only one metal dopant atom, its contribution to the valence band is relatively small. Nevertheless, the VBM values of Ce, O, and the metal dopant are all equal. This equality arises from the strong interaction between the atomic orbitals of the metal dopant and the surrounding O atoms, resulting in the hybridization of atomic orbital and subsequently impacting the overall valence band. Consequently, the adsorption of NH₃ on the catalyst largely originates the interaction between N atoms and metal dopant atoms. Therefore, the adsorption effect of NH₃ can be elucidated by studying the orbital properties of metal dopant and N orbitals.

Fig. 6 Partial density of electronic state for N of NH₃ and metal-doped CeO₂ before and after NH₃ adsorption. (a)–(c) Ni-doped, (d)–(f) V-doped and (g)–(i) Nb-doped CeO₂. The Fermi level (dashed line) has been set at 0 eV.

Before NH₃ adsorption, based on Frontier molecular orbital theory,⁶⁴ the energy difference (ΔE_LUMO–HOMO) between the LUMO of the metal atom at the adsorption site and the HOMO of the N atom in NH₃ can be used to predict the ease of adsorption (Scheme 1 and Fig. S8, ESI†). A smaller ΔE_LUMO–HOMO indicates that adsorption occurs more easily. As shown in Fig. 6b, e, and h, the density of state for the metal dopant is predominantly contributed by the d orbital, while the density of state for N is predominantly contributed by the p orbital. Therefore, the minimum value of the metal d orbital energy level above the Fermi level is regarded as E_LUMO, and the maximum value of the N p orbital energy level below the Fermi level is regarded as E_HOMO. It was found that ΔE_LUMO–HOMO(Ni) = 0.18 eV < ΔE_LUMO–HOMO(V) = 0.53 eV < ΔE_LUMO–HOMO(Nb) = 1.43 eV. This suggests that NH₃ is easily adsorbed on Ni-doped CeO₂, but less readily adsorbed onto Nb-doped CeO₂. This is consistent with the conclusion in Fig. 5a that the adsorption of NH₃ on Ni doped CeO₂ is stronger than that of NH₃ on Nb-doped CeO₂. Moreover, ΔE_LUMO–HOMO has a good linear correlation (R² = 0.85) with the NH₃ adsorption energy (Fig. S9, ESI†). From the density of states after NH₃ adsorption, it can be observed that for Ni-doped CeO₂, the Ni d orbitals and N p orbitals exhibit significant overlap both above and below the Fermi level. In contrast, for V- and Nb-doped CeO₂, the overlap between the metal (V, Nb) d orbitals and N p orbitals is primarily below the Fermi level, with only a slight overlap occurring above the Fermi level. This indicates that the interaction strength between Ni and N is higher than that of the other two, which also indicates that the adsorption of NH₃ on Ni-doped CeO₂ is stronger than on the other two metal dopants. Therefore, the interaction between metal orbitals and N orbitals can also be analyzed by the HOMO and LUMO energy difference.

Scheme 1 Orbital interaction between isolated NH₃ orbitals and a metal dopant in the CeO₂ surface.

3.4. Discussion

In Fig. 4 and Fig. S10 in the ESI,† the work function, as the VBM, has a good linear relationship with the adsorption energies of NH₃, NH₂–H and NH–2H species, but the linearity is opposite. The work function is strongly linearly correlated (−0.98) with the VBM (Fig. S11, ESI†). The work function is equal to the difference between the vacuum level and the Fermi level of the catalyst. The vacuum energy levels of the catalysts are nearly equal, and the transition metal-doped CeO₂ predominantly exhibits acceptor-type doping, which shifts the Fermi level closer to the valence band. Therefore, the correlation between work function and adsorption energy are affected by the position of the valence band. Additionally, the adsorption energy of a single H atom has a good linear correlation with various properties of the catalyst (Fig. S12, ESI†). This can be attributed to the fact that the adsorption sites of H atoms are surface lattice O atoms adjacent to the metal dopant. The chemical properties of the adjacent O atom are directly affected by the doping metal.

The reason for the good linear correlation shown in Fig. 5c between the heat of formation and the adsorption energy of NH–2H species remains unclear. The heat of formation data is obtained from the enthalpy of formation of gaseous atoms for each element. The formation enthalpy of gaseous atoms is significantly influenced by the atomic radius and the energy of a single metal atom. As shown in Fig. 4, the heat of formation has a good linear relationship with the radius of the metal atom and the energy of a single metal atom, at 0.83 and −0.85, respectively. Therefore, the relationship between the heat of formation and the adsorption energy of NH–2H species might be associated with the atomic radius and the energy of a single metal atom. Additionally, a weak linear correlation exists between the adsorption energy of N–3H species and the catalyst properties, with only a low correlation coefficient of 0.57 observed with the doping formation energy (as shown in Fig. 5d). This may be because the adsorption of species by the catalyst during the NH₃ dissociation process is influenced not only by the adsorption of N by metal dopant sites, but also by the adsorption of three H atoms by three different surface lattice oxygens surrounding the metal. In general, the process of complete dissociation of NH₃ is not considered, because in related reactions involving NH₃ (such as NH₃-SCO and NH₃-SCR), the dissociation of NH₃ typically does not progress to form a co-adsorbed N and three H atoms.

4. Conclusions

In summary, density functional theory calculations were used to study the chemical properties and adsorption of NH₃-related species on different metal-doped CeO₂ catalysts. According to the degree of local distortion, the metal-doped CeO₂ structures are divided into two categories: structures that are easily distorted and those that are not easily distorted. For catalysts whose structures are easily distorted, the VBM, work function, heat of formation, and metal atom energy can be used as descriptors with good linear relationships with the adsorption energies of NH₃, NH₂–H and NH–2H species in the feature correlation heat map. Ni-, Zn-, Cu-, Mn-, and Co-doped CeO₂ catalysts all strongly adsorb NH₃-related species. Through the HOMO and LUMO theories, it is found that NH₃ adsorption is also affected by the difference between the LUMO of the metal dopant d orbital and the HOMO of the N p orbital in NH₃. Although some well-correlated relationships cannot be explained at the chemical level, the phenomena and conclusions of this study offer valuable insights for designing metal oxide catalysts for NH₃ dissociation reactions.

Author contributions

M. G. and Y. S. designed, performed, and conceived this study. S. Y., M. G., and K. W. analyzed the data. All authors read and agreed to the published version of the manuscript.

Data availability

The data supporting this article has been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by JSPS KAKENHI Grant Numbers JP24H02219 (M. G.) in Transformative Research Areas (A) JP24A202 Integrated Science of Synthesis by Chemical Structure Reprogramming (SReP). The results were computed at the Computer Center of Kyoto University and the Research Center for Computational Science, Okazaki, Japan (Project Number 22-IMS-C002).

References

1. K. Nakajima, H. Toda, K. Sakata and Y. Nishibayashi, Nat. Chem., 2019, 11, 702–709.
2. P. L. Dunn, B. J. Cook, S. I. Johnson, A. M. Appel and R. M. Bullock, J. Am. Chem. Soc., 2020, 142, 17845–17858.
3. Q. Li, G.-h Liu, S. Chen, L. Qi and H. Wang, Chem. Eng. J., 2023, 473, 145120.
4. S. Li, Y. Zhou, X. Fu, J. B. Pedersen, M. Saccoccio, S. Z. Andersen, K. Enemark-Rasmussen, P. J. Kempen, C. D. Damsgaard, A. Xu, R. Sazinas, J. B. V. Mygind, N. H. Deissler, J. Kibsgaard, P. C. K. Vesborg, J. K. Norskov and I. Chorkendorff, Nature, 2024, 629, 92–97.
5. M. Kitano, J. Kujirai, K. Ogasawara, S. Matsuishi, T. Tada, H. Abe, Y. Niwa and H. Hosono, J. Am. Chem. Soc., 2019, 141, 20344–20353.
6. S. Feng, W. Gao, Q. Wang, Y. Guan, H. Yan, H. Wu, H. Cao, J. Guo and P. Chen, J. Mater. Chem. A, 2021, 9, 1039–1047.
7. T. Wu, B. Chang, Y. Li, X. Zhang, X. Zhao, Z. Liu, G. Zhang, X. Liu, L. Zhao, Y. Zhang, H. Zhang, H. Liu and W. Zhou, Nano Energy, 2023, 116, 108855.
8. K. Nagaoka, T. Eboshi, Y. Takeishi, R. Tasaki, K. Honda, K. Imamura and K. Sato, Sci. Adv., 2017, 3, e1602747.
9. H. Fang, S. Wu, T. Ayvali, J. Zheng, J. Fellowes, P. L. Ho, K. C. Leung, A. Large, G. Held, R. Kato, K. Suenaga, Y. I. A. Reyes, H. V. Thang, H. T. Chen and S. C. E. Tsang, Nat. Commun., 2023, 14, 647.
10. M. Asif, S. Sidra Bibi, S. Ahmed, M. Irshad, M. Shakir Hussain, H. Zeb, M. Kashif Khan and J. Kim, Chem. Eng. J., 2023, 473, 145381.
11. G. Yang, J. Ran, X. Du, X. Wang, Z. Ran, Y. Chen, L. Zhang and J. Crittenden, Phys. Chem. Chem. Phys., 2021, 23, 4700–4710.
12. Y. Shan, G. He, J. Du, Y. Sun, Z. Liu, Y. Fu, F. Liu, X. Shi, Y. Yu and H. He, Nat. Commun., 2022, 13, 4606.
13. Y. Fu, W. Ding, H. Lei, Y. Sun, J. Du, Y. Yu, U. Simon, P. Chen, Y. Shan, G. He and H. He, J. Am. Chem. Soc., 2024, 146, 11141–11151.
14. G. Jiang, F. Zhang, Z. Wei, Z. Wang, Y. Sun, Y. Zhang, C. Lin, X. Zhang and Z. Hao, Catal. Sci. Technol., 2020, 10, 1477–1491.
15. Y. Guo, L. Ma, Z. Li, Z. Liu, H. Chang, X. Zhao and N. Yan, Catal. Sci. Technol., 2022, 12, 6507–6517.
16. H. S. Pillai, Y. Li, S. H. Wang, N. Omidvar, Q. Mu, L. E. K. Achenie, F. Abild-Pedersen, J. Yang, G. Wu and H. Xin, Nat. Commun., 2023, 14, 792.
17. J. Hu, A. Ma, X. Wu, Y. Yin, D. Liu, A. T. Kuvarega, B. B. Mamba and J. Gui, Chem. Commun., 2023, 59, 7232–7235.
18. F. Zhao, G. Li, Q. Hua, J. Cao, J. Song, L. Gao, T. Ma, X. Ren and A. Liu, Catal. Sci. Technol., 2023, 13, 5543–5548.
19. K. Liu, H. Li, M. Xie, P. Wang, Z. Jin, Y. Liu, M. Zhou, P. Li and G. Yu, J. Am. Chem. Soc., 2024, 146, 7779–7790.
20. H. Wang, Y. Dong, C. Zheng, C. A. Sandoval, X. Wang, M. Makha and Y. Li, Chemistry, 2018, 4, 2883–2893.
21. R. Wu, F. Li, X. Cui, Z. Li, C. Ma, H. Jiang, L. Zhang, Y. P. J. Zhang, T. Zhao, Y. Zhang, Y. Li, H. Chen and Z. Zhu, Angew. Chem., Int. Ed., 2023, 62, e202218387.
22. P. Li, Z. Zhang, X. Yang, Y. Zhu, Z. Zhou, X. Jiang, Q. Wang, X. Gao, X. Yang, Y. Shen and M. Wang, ChemCatChem, 2023, 16, e202301302.
23. K. T. Wang, S. Nachimuthu and J. C. Jiang, Phys. Chem. Chem. Phys., 2018, 20, 24201–24209.
24. W. Yang, H. He, Q. Ma, J. Ma, Y. Liu, P. Liu and Y. Mu, Phys. Chem. Chem. Phys., 2016, 18, 956–964.
25. J. W. Lee, G. Barin, G. W. Peterson, J. Xu, K. A. Colwell and J. R. Long, ACS Appl. Mater. Interfaces, 2017, 9, 33504–33510.
26. C. Hahn, J. Seidel, F. Mertens and S. Kureti, Phys. Chem. Chem. Phys., 2022, 24, 7493–7504.
27. T. Lan, M. Gao, J.-Y. Hasegawa, Y. Shen, W. Qu, Q. Hu, J. Deng, D. Cheng and D. Zhang, ACS Catal., 2023, 13, 14070–14079.
28. X. Liu, P. Wang, Y. Shen, L. Zheng, L. Han, J. Deng, J. Zhang, A. Wang, W. Ren, F. Gao and D. Zhang, Environ. Sci. Technol., 2022, 56, 11646–11656.
29. L. Huang, K. Zha, S. Namuangruk, A. Junkaew, X. Zhao, H. Li, L. Shi and D. Zhang, Catal. Sci. Technol., 2016, 6, 8516–8524.
30. H. Zheng, W. Song, Y. Zhou, S. Ma, J. Deng, Y. Li, J. Liu and Z. Zhao, J. Phys. Chem. C, 2017, 121, 19859–19871.
31. H. Ma and W. F. Schneider, J. Catal., 2020, 383, 322–330.
32. H. Liu, C. You and H. Wang, Chem. Eng. J., 2020, 382, 122756.
33. D. Fang, S. Hou, Y. Ye, Q. Jin, F. He and J. Xie, Appl. Surf. Sci., 2022, 599, 153998.
34. L. Yang, J. Fan and W. Zhu, Phys. Chem. Chem. Phys., 2023, 25, 26659–26665.
35. Y. Zhang, M. Zhang, Y. Zang, H. Wang, C. Liu, L. Wei, Y. Wang, L. He, W. Wang, Z. Zhang, R. Han, N. Ji, C. Song, X. Lu, D. Ma, Y. Sun and Q. Liu, ACS Catal., 2023, 13, 1449–1461.
36. Y. Jiang, T. Liu, C. Lai, Z. Yang, R. Lin, X. Wang and X. Zhu, Appl. Surf. Sci., 2021, 547, 149196.
37. H. Liu, Y. Zhang, S. Liu, S. Li and G. Liu, Chem. Eng. J., 2023, 473, 145371.
38. Q. An, Y. Shen, A. Fortunelli and W. A. Goddard III, J. Am. Chem. Soc., 2018, 140, 17702–17710.
39. A. R. Singh, J. H. Montoya, B. A. Rohr, C. Tsai, A. Vojvodic and J. K. Nørskov, ACS Catal., 2018, 8, 4017–4024.
40. H. Zhang, S. Wang, H. Wang, B. Huang, S. Dong, Y. Dai and W. Wei, Nanoscale, 2021, 13, 17331–17339.
41. Y. Li, G. Zheng, L. Li, X. Zhang, Z. Tian and L. Chen, Phys. Chem. Chem. Phys., 2022, 24, 29112–29119.
42. Y. Wang and M. Shao, ACS Catal., 2022, 12, 5407–5415.
43. Z. Li, R. Dong, X. Liu, C. Lin, Y. Li, X. Feng, Z. W. Seh and Q. Zhang, Surf. Sci., 2023, 730, 122238.
44. M. Chen, Z. Zhu, J. Chen, L. Xia, L. Gan and Y. Zhou, J. Mater. Chem. A, 2024, 12, 14035–14044.
45. D. A. Hansgen, D. G. Vlachos and J. G. Chen, Nat. Chem., 2010, 2, 484–489.
46. J. Yang, X. Chen, Z. Liu, Q. Wang, Y. Wen, A. Zhang, R. Chen and B. Shan, J. Mater. Chem. A, 2022, 10, 12447–12457.
47. H. Zheng, R. Li, C. Zhong, Z. Li, Y. Kang, J. Deng, W. Song and Z. Zhao, Catal. Sci. Technol., 2022, 12, 1429–1440.
48. I. Lucentini, G. García Colli, C. D. Luzi, I. Serrano, O. M. Martínez and J. Llorca, Appl. Catal., B, 2021, 286, 119896.
49. J. Zhang, Y. Fan, L. Chen, L. Yang, L. Zhou, X. Luo, J. Zou and W. Dai, Chem. Eng. J., 2023, 473, 145272.
50. H. Sun, H. Wang and Z. Qu, ACS Catal., 2023, 13, 1077–1088.
51. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
52. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
54. A. I. Liechtenstein, V. V. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470.
55. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
56. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192.
57. S. Colis, A. Bouaine, G. Schmerber, C. Ulhaq-Bouillet, A. Dinia, S. Choua and P. Turek, Phys. Chem. Chem. Phys., 2012, 14, 7256–7263.
58. B. Hammer and J. K. Nørskov, Adv. Catal., 2000, 45, 71–129.
59. X. Zhang, C. Pei, X. Chang, S. Chen, R. Liu, Z. J. Zhao, R. Mu and J. Gong, J. Am. Chem. Soc., 2020, 142, 11540–11549.
60. J.-L. Cao, Z.-L. Yan, Q.-F. Deng, Z.-Y. Yuan, Y. Wang, G. Sun, X.-D. Wang, B. Hari and Z.-Y. Zhang, Catal. Sci. Technol., 2014, 4, 361–368.
61. R. Wang, H. Liu, K. Zhang, G. Zhang, H. Lan and J. Qu, Chem. Eng. J., 2021, 404, 126795.
62. Y. Jin, Y. Liu, R. Wu and J. Wang, Chem. Commun., 2024, 60, 1104–1107.
63. I. Nakamura and T. Fujitani, Appl. Catal., A, 2016, 524, 45–49.
64. K. Fukui, T. Yonezawa and H. Shingu, J. Chem. Phys., 1952, 20, 722–725.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00430f

---