An inductively coupled plasma tandem mass spectrometry investigation of the activation of methane by lanthanide cations

Abstract

The activation of C–H and C–C bonds by atomic metal cations remains a profitable area of research to utilize environmentally abundant methane and produce useful hydrocarbon fuel. Although methane activation by transition metal cations has been the focus of catalysis research for decades, less is known about the catalytic capabilities of lanthanide cations. Here we employ inductively coupled plasma tandem mass spectrometry to examine the kinetic energy dependences of the reactions of lanthanide cations Ce⁺, Pr⁺, Nd⁺, Sm⁺, and Eu⁺ with methane. The resulting energy-dependent reaction cross sections enable a measurement of the reaction thermochemistry and provide fundamental insight into the physical characteristics that enable Ln⁺ reactivity. We report values for the Ln⁺–D bond dissociation energies, D₀(Ln⁺–D), and the first experimentally obtained values for D₀(Ln⁺–CD₃) and D₀(Ln⁺–CD). We find that the observed reaction efficiencies correlate to the promotion energies (E_p) from the Ln⁺ ground state electronic configurations to the 5d² or 5d6s electronic configuration. This indicates that the Ln⁺ requires an electron configuration with two unpaired valence electrons in non-f orbitals to effectively insert into C–H bonds.

---

Introduction

Ongoing technological developments seek to produce useful hydrocarbon fuels from environmentally abundant methane to satisfy increasing energy demands while reducing atmospheric content of greenhouse gases as part of the methane emissions reduction program. Because environmental abundance of methane is problematic from a global climate perspective, it is becoming an increasingly profitable target for new technologies that reduce its environmental burden by increasing its use in the production of alternative fuels or other useful polymers. The use of metal-based catalysts to mediate C–H bond activation and C–C coupling has been explored previously;^1,2 however, a detailed understanding of the fundamental role of the metal involved remains elusive. Gas-phase studies are advantageous because they possess the unique ability to isolate and closely examine the elementary steps within large-scale catalytic processes without perturbations like solvent effects.³

Armentrout previously reviewed gas-phase studies of the reactions of 5d transition metal cations with methane; the review also includes references to 3d and 4d transition metal results.⁴ Notably, 3d (first row) transition metals do not activate methane at room temperature, 4d (second row) transition metals do not activate methane at room temperature (except for Zr⁺ which will form ZrCH₂⁺ at room temperature, although the reaction is slightly endothermic, and ZrCH₂⁺ therefore forms very inefficiently), and a number of 5d (third row) transition metals do activate methane at room temperature (specifically, Ta⁺, W⁺, Os⁺, Ir⁺, and Pt⁺). In compiling and assessing the MH⁺, MCH₂⁺, MCH₃⁺, and MCH⁺ (M = La, Lu, Hf, Ta, W, Re, Os, Ir, Pt, Au) bond dissociation energies (BDEs) it was noted that Lu⁺ forms relatively weaker bonds, La⁺ forms relatively stronger bonds, and neither Lu⁺ nor La⁺ form the MCH⁺ species because they lack the three bonding electrons required to form a triple bond. These observations are all explained by examining the ground state configurations of Lu⁺, 4f¹⁴6s² (¹S), which is closed shell and therefore requires an energy input of 1.63 eV to enable covalent bond formation, whereas La⁺ has a 5d² (³F) ground state configuration and can readily form covalent bonds.

Reactions between atomic lanthanide cations and methane have not been studied as extensively as the transition metals, still a body of work has provided valuable insight into the role of Ln⁺ electronic structure in product formation. An early ion beam study by Schilling and Beauchamp⁵ examined the reactions of Pr⁺ (4f³6s¹) and Eu⁺ (4f⁷6s¹), both with the “typical” lanthanide configuration (4fⁿ6s¹), and Gd⁺ (4f⁷5d¹6s¹), which has two valence electrons in non-f orbitals, with alkanes, cycloalkanes, and alkenes to evaluate the role of 4f electrons. Pr⁺ and Eu⁺ are unreactive towards alkanes and cycloalkanes. Schilling and Beauchamp explain that ion–molecule reactions begin with an ion-induced dipole association to form the ion–molecule association complex, M⁺–CH₄. If the energy of the ion–molecule association complex is sufficiently lower than that of the reactants, then the reaction proceeds as though there is no barrier to bond insertion by M⁺. They relate the reaction barrier height to the energy required to achieve an electronic configuration where there are two unpaired valence electrons in non-f orbitals and use this guide to predict the relative reactivities of other Ln⁺. Schwarz and coworkers⁶ systematically studied the reactions of Ln⁺ (La–Lu, except for Pm) with alkanes, cyclopropane, and alkenes using a Fourier transform ion cyclotron resonance (FT-ICR) mass spectrometer. None of the Ln⁺ studied were reactive towards methane; however, in monitoring the reactions of each Ln⁺ with progressively more reactive hydrocarbons, relative reactivities of the Ln⁺ could be determined. Their results provide additional support for the ion beam study by Schilling and Beauchamp and enable them to build upon a curve-crossing model, defined by a crossing between the potential energy surface evolving from the ground state reactants and one leading to the ground state products, to qualitatively describe the promotion of Tb⁺ from its unreactive ground state configuration (4f⁹6s¹) to an electronically excited and reactive state (4f⁸5d¹6s¹).

Although the use of FT-ICR mass spectrometers is advantageous for high mass resolution and mass accuracy, the energy range accessible in an FT-ICR mass spectrometer is limited; therefore, only products resulting from exothermic or thermoneutral reactions are typically observed. Inductively coupled plasma selected-ion flow tube (ICP-SIFT) mass spectrometry experiments by Bohme and coworkers⁷ indicate that La⁺, Ce⁺, and Gd⁺ will form the association complex M(CH₄)⁺ but with very low reaction efficiency, k/k_col = 0.001. ICP-SIFT utilizes a flow tube at ≈0.5 Torr where ions thermalize under many collisions with the carrier gas, so the accessible energy range in ICP-SIFT experiments is a select range of temperatures that also limits observable processes to primarily exothermic and thermoneutral reactions. MarÇalo et al. have noted the inability of Ln⁺, and even Ln²⁺, to activate methane;⁸ however, the ability of the more reactive lanthanides, La⁺, Ce⁺, Gd⁺, and Tb⁺, to activate other hydrocarbons has been attributed to their ground state or low-lying electronic configurations of the form 4fⁿ⁻¹5d¹6s¹.^5,6

Because of radioactivity concerns, Ln⁺ have also been used as surrogates for the actinides (An⁺).^9,10 Gibson noted similarities in the importance of the nd electrons to MO⁺ bond formation (n = 5, 6, M = Ln, An).⁹ These similarities have also been reported in Ln⁺ and An⁺ oxidation reaction rates.^11,12 Nevertheless, a key difference between Ln⁺ and An⁺ is that the 4f orbitals are unlikely to contribute to Ln⁺ reactivity but the 5f orbitals may have a role in An⁺ reactivity. Thus, understanding the differences between Ln⁺ and An⁺ reactivity may elucidate when the 5f orbitals are active. This concept of comparison has been recently applied to the reactions of Nd⁺, Sm⁺, and Pu⁺ with NO to suggest that the 5f orbitals are active participants in NO bond activation by Pu⁺.¹³

Here, we provide the first report of the kinetic energy dependences of the reactions of Ln⁺ (Ln = Ce, Pr, Nd, Sm, Eu) with perdeuterated methane over an extended energy range using inductively coupled plasma tandem mass spectrometry (ICP-MS/MS) and derive values for D₀(Ln⁺–D), D₀(Ln⁺–CD₃), and D₀(Ln⁺–CD). We find that our values for D₀(Ln⁺–D) are comparable to those obtained by guided ion beam tandem mass spectrometry (GIBMS) experiments determined using D₂,^14–17 while our values for D₀(Ln⁺–CD₃) and D₀(Ln⁺–CD) are the first experimental determinations. Unlike the previous experiments, LnCD₂⁺ was observed as an exothermic product; however, this is attributed to the higher starting electronic energy of the ICP-MS/MS. Nevertheless, the observed reaction efficiencies of this process correlate with the promotion energy of Ln⁺ to a reactive electronic configuration with two valence electrons in non-f orbitals (5d² or 5d6s). We also compare the correlations of reaction efficiencies and LnD⁺ BDEs obtained in the present study with those obtained from the reactions of An⁺ with CD₄ presented in recent work.¹⁸ A comparison of the LnCD₂⁺ and AnCD₂⁺ cross section magnitudes and reaction efficiencies suggests that the An⁺ are more reactive towards CD₄ than their Ln⁺ congeners. A closer examination of the correlations of Ln⁺ and An⁺ reaction efficiencies with promotion energies to nd² and nd(n + 1)s (n = 5, 6) reactive electronic configurations presents the opportunity to gain insight on 5f orbital activity. Because the 4f orbitals are not expected to contribute to the chemical behavior observed for the Ln⁺, results from Ln⁺ reactions can be used to define the “zero” of f orbital participation in comparison with results from An⁺ reactions. The increased reactivity observed for the An⁺ may be attributable to participation of the 5f orbitals in formation of the insertion intermediate (HAnCD₃⁺). The correlations of LnD⁺ and AnD⁺ BDEs with promotion energies to nd² and nd(n + 1)s (n = 5, 6) reactive electronic configurations suggest that the d orbitals are the primary contributors to bonding for both the Ln⁺ and An⁺.

Methods

Experiments were conducted using an Agilent 8900 ICP-MS/MS at Pacific Northwest National Laboratory. Operation of this instrument has been detailed previously.^12,19 Briefly, the instrument consists of two quadrupole mass filters with a collision reaction cell (CRC) that contains an octopole ion guide between the mass filters. Ions are generated within an inductively coupled plasma (ICP) source. Ions are focused through the first mass filter where the reactant ion is mass selected and subsequently directed into the CRC. The reaction cell holds the neutral reactant, CD₄. Adjustment of the octopole bias allows the kinetic energy of the reactant ion to be set. In the reaction cell, product and reactant ions are radially constrained by the octopole ion guide and focused through the second quadrupole mass filter to a standard electron multiplier detector.

A stock multi-element standard solution containing 1 ng g⁻¹ of Ce, Pr, Nd, Sm, and Eu in 2% HNO₃ was prepared. This solution was introduced to the ICP ion source using a quartz double-pass spray chamber and a 100 μL min⁻¹ perfluoroalkyl alkane (PFA) nebulizer. Table 1 lists the isotopes used for each M⁺. Nominally pure, perdeuterated methane (CD₄) obtained from Sigma Aldrich was used as the neutral reactant gas. The flow rates ranged from 0.06–0.13 mL min⁻¹, corresponding to estimated pressures of 1.4 (187) and 2.8 (373) mTorr (Pa). The instrument settings to note are: octopole rf peak-to-peak voltage of 180 V, axial acceleration of 2.0 V, and a kinetic energy discrimination (KED, the voltage difference between the octopole bias in the CRC and the second quadrupole) of −10.0 V. The octopole bias was adjusted from +7 V to −78 V while keeping other cell parameters constant. Data were acquired in triplicate using 1 s acquisition times.

Table 1 Average electronic energy (in eV) of Ln⁺ from the ICP source assuming a Boltzmann distribution^a

M^+ (isotope)	Mass (amu)	300 K	700 K	1000 K	5000 K	8000 K	10 000 K
a Masses and electronic states taken from ref. 20 (https://physics.nist.gov/PhysRefData/Handbook/periodictable.htm).
^140Ce^+	139.90	0.00	0.04	0.10	0.58	0.69	0.74
^141Pr^+	140.91	0.01	0.03	0.05	0.42	0.54	0.61
^146Nd^+	145.91	0.01	0.03	0.06	0.57	0.79	0.90
^149Sm^+	148.92	0.02	0.06	0.10	0.43	0.59	0.69
^153Eu^+	152.92	0.00	0.01	0.01	0.28	0.68	0.93

---

Absolute reaction cross sections (σ) are calculated from the raw signal intensities using eqn (1),²¹

I = I₀e^−ρσl (1)

where I is the intensity of the precursor ion exiting the collision cell, I₀ is the intensity of the precursor ion entering the collision cell, ρ is the number density of the neutral reagent, CD₄, in the collision cell, and l is the effective length of the collision cell. Because the instrument operates at a low ion current to prevent excessive backgrounds, I₀ is estimated from the sum of reactant and product ion intensities observed. l is estimated as the physical length of the collision cell, 10 cm, but is not strictly correct because the pressure gradient extends beyond the reaction cell. The uncertainty in l is expected to be ≤20% and is included in the absolute uncertainty of the cross section. Individual product ion cross sections (e.g., MD⁺) are calculated as percentages of the total reaction cross section. The cross sections observed at 1.4 and 2.8 mTorr were extrapolated to zero pressure (i.e. single collision conditions) to remove pressure dependencies. Absolute uncertainties in the cross sections are estimated to be ±50% with relative uncertainties of ±10%.

The laboratory frame energy is estimated based on the octopole bias using eqn (2),²²

where V_p is the plasma potential (∼2 V), M is the mass of the reactant ion, M⁺, m_Ar is the mass of argon, k_B is Boltzmann's constant, T_p is the ion temperature entering the octopole, and V_oct is the octopole bias. The temperature of the ions exiting the plasma is expected to be the plasma temperature, 8000–10 000 K. Some collisional cooling is anticipated to occur in the differentially pumped region between the ion source and first quadrupole. Recent work suggests that T_p is within the range of 1000–10 000 K. At higher temperatures, the average electronic energy of the reactant ions can be significant; therefore, the average electronic energy is included in the energy available for reaction. Table 1 lists the average electronic energy for a Boltzmann distribution for the given temperatures within the 1000–10 000 K temperature range. The energy in the center-of-mass (E_CM) frame represents the kinetic energy available for a chemical reaction. The relationship between E_LAB and E_CM is described by eqn (3):²¹

E_CM = E_LAB × m/(m + M) (3)

where m is the mass of the neutral reactant partner, CD₄ = 20.04 amu and M is the mass of the metal ion, M⁺ found in Table 1. All subsequent mention or discussion of energy refers to energy in the center-of-mass frame, E_CM unless stated otherwise.

Data analysis

GIBMS studies have successfully utilized a modified line-of-centers model (mLOC) to determine the BDEs of many ML⁺ from absolute reaction cross sections.^21,23 The mLOC model is described by eqn (4),²⁴

σ(E) = σ₀Σg_i(E + E_el + E_i − E₀)ⁿ/E (4)

where σ₀ is an energy-independent scaling factor, E is the relative (E_CM) kinetic energy of the reactants, E_el is the electronic energy of the M⁺ reactant (defined above), E_i is the energy of the neutral reactant rovibrational states having populations of g_i (Σg_i = 1), n is an adjustable parameter, and E₀ is the 0 K reaction threshold. Eqn (4) can also be used to model the ICP-MS/MS cross sections. When using eqn (4) to model the cross sections from the ICP-MS/MS experiments, it is important to understand the key differences in the experimental conditions in GIBMS compared to the ICP-MS/MS. GIBMS experiments collisionally cool reactant ions in a 1 m flow tube (∼0.5 Torr of buffer gas) prior to precursor selection by a magnetic sector mass spectrometer.²¹ A conservative estimate of the electronic energy distribution of ions in a GIBMS is 700 ± 400 K.^25–27 In contrast, the electronic distribution of ions in the ICP-MS/MS is not well characterized and the extent of collisional cooling prior to entering the first mass filter is unclear. Comparison between GIBMS and ICP-MS/MS cross sections indicate an elevated electronic energy distribution for ions generated in the ICP-MS/MS.¹² We have previously modified eqn (4) to include E_el as an adjustable variable. Internal energy (rotational and vibrational) of the CD₄ reactant at 300 K is calculated as 0.07 eV using the Beyer–Swinehart algorithm²⁸ in CRUNCH²⁹ and is also included in models of the cross sections using eqn (4). We find that inclusion of the average electronic energy, E_el, for the precursor ion at 8000 K reproduces the data with high fidelity. Additionally, GIBMS operates at extremely low pressures (0.05–0.4 mTorr)²¹ to promote single collision conditions whereas the ICP-MS/MS operates at higher pressures where the probability of multiple collisions cannot be mitigated. Because the product kinetic energy is a distribution after any ion–molecule collision, the energy after multiple collisions is difficult to delineate, resulting in a poorly defined kinetic energy distribution.²¹ Our best effort to account for multiple collision conditions is extrapolation of the ICP-MS/MS cross sections to zero pressure so that the cross sections correspond to near-single collision processes. Note that this is a two-point extrapolation. Although more pressures may be ideal to ensure that a linear extrapolation is the best approximation, two points were used because of the need to balance instrument time with the objective of the experiment. Previous work suggests that this is an acceptable approach within the uncertainty of the ICP-MS/MS work.^12,13,18,30

Eqn (4) is fit to the experimental cross section using a non-linear least squares method. Uncertainties in n and σ₀ are calculated as the standard deviation (1σ) of the acceptable fits. Uncertainty in E₀ is calculated by propagating the standard deviation of the acceptable fits and the standard deviation of the average E_el. The uncertainty in E_el over the range of 5000–8000 K is ≈0.25 eV, as detailed in Table 1.

Results

Product ion cross sections for the reactions of Ln⁺ + CD₄ for Ln = Ce, Pr, Nd, Sm, and Eu are shown below. The processes observed include reactions (5)–(8):

Ln⁺ + CD₄ → LnD⁺ + CD₃ (5)

→ LnCD₂⁺ + D₂ (6)

→ LnCD₃⁺ + D (7)

→ LnCD⁺ + D₂ + D (8)

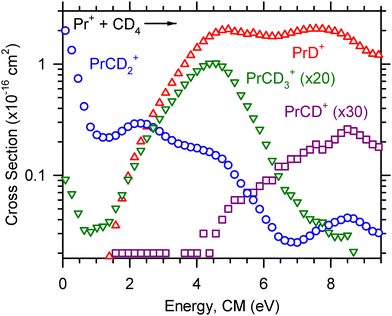
Reactions (5)–(8) were observed for Ce⁺, Pr⁺, and Nd⁺ and are shown in Fig. 1–3, respectively. For Ce⁺, Pr⁺, and Nd⁺, the LnCD₂⁺ product is observed at the lowest energy, and the cross section decreases with increasing energy until ∼0.5 eV for Ce⁺ and ∼1 eV for Pr⁺ before increasing with increasing energy, suggesting that higher energy pathways to CeCD₂⁺ and PrCD₂⁺ formation become available. The NdCD₂⁺ cross section levels out near 2 eV. The LnD⁺ cross section corresponding to reaction (5) increases with increasing energy, and the kinetic energy dependence of the LnD⁺ cross section is indicative of an endothermic process. Small amounts of the LnCD₃⁺ products are observed at the lowest energy because these cross sections possess low-lying exothermic tails. We suspect that the observation of the LnCD₃⁺ product at the lowest energy is an artifact of excited state Ln⁺ generated at the elevated temperatures of the ICP ion source. The LnCD₃⁺ and LnCD⁺ product ion cross sections ultimately increase with increasing energy and correspond to endothermic processes, although there may be a minor exothermic feature from some excited state contributions to CeCH₃⁺. Note that reaction (7) is magnified in Fig. 1, so the peak magnitude of this early feature is 0.006 × 10⁻¹⁶ cm² and is likely insignificant. For Pr⁺ and Nd⁺, the LnCD⁺ cross section begins to rise as the LnCD₃⁺ cross section begins to decline, suggesting that the LnCD⁺ product forms by dehydrogenation of the LnCD₃⁺ product.

Fig. 1 Product ion cross sections for the reaction of Ce⁺ + CD₄ as a function of ion kinetic energy in the center-of-mass frame, E_CM. The dominant product at low energies is CeCD₂⁺ (blue circle). At higher energies the dominant product is CeD⁺ (red triangle). Minor products CeCD₃⁺ (green inverted triangle) and CeCD⁺ (purple square) are also observed. These channels have been magnified as indicated.

Fig. 2 Product ion cross sections for the reaction of Pr⁺ + CD₄ as a function of ion kinetic energy in the center-of-mass frame, E_CM. The dominant product at low energies is PrCD₂⁺ (blue circle). At higher energies the dominant product is PrD⁺ (red triangle). Minor products PrCD₃⁺ (green inverted triangle) and PrCD⁺ (purple square) are also observed. These channels have been magnified as indicated.

Fig. 3 Product ion cross sections for the reaction of Nd⁺ + CD₄ as a function of ion kinetic energy in the center-of-mass frame, E_CM. The dominant product at low energies is NdCD₂⁺ (blue circle). At higher energies the dominant product is NdD⁺ (red triangle). Minor product CeCD₃⁺ (green inverted triangle) is also observed. This channel has been magnified as indicated.

Reactions (5) and (6) were observed for Sm⁺ and are shown in Fig. 4. The SmCD₂⁺ cross section is present at the lowest energy and declines with increasing energy which indicates that SmCD₂⁺ forms through an exothermic, barrierless process. The SmD⁺ cross section increases with increasing energy, consistent with an endothermic process. Only reaction (5) was observed for Eu⁺, as shown in Fig. 5, and the EuD⁺ cross section increases with increasing energy which is consistent with the behavior of a cross section for an endothermic reaction. Note that in some cases product channels were magnified in Fig. 1–5 so that they display more clearly.

Fig. 4 Product ion cross sections for the reaction of Sm⁺ + CD₄ as a function of ion kinetic energy in the center-of-mass frame, E_CM. The dominant product at low energies is SmCD₂⁺ (blue circle). At higher energies the dominant product is SmD⁺ (red triangle).

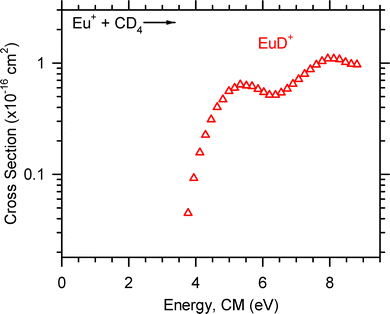Fig. 5 Product ion cross section for the reaction of Eu⁺ + CD₄ as a function of ion kinetic energy in the center-of-mass frame, E_CM.

The optimized parameters used in eqn (4) to model endothermic cross sections and obtain threshold energies, E₀, are detailed in Table 2. The measured threshold energies were used to derive the bond dissociation energies listed in Table 3. The LnD⁺ and LnCD₂⁺ product ion cross sections for all Ln⁺ studied here are displayed in Fig. 6 and 7, respectively. As can be seen in Fig. 6, the CeD⁺, PrD⁺, and NdD⁺ cross sections are similar in magnitude. The CeD⁺ cross section possesses a threshold energy of 2.32 ± 0.34 eV, the PrD⁺ cross section possesses a threshold energy of 2.01 ± 0.32 eV, and the rises in these cross sections are followed closely by the rise in the NdD⁺ cross section with E₀ = 2.52 ± 0.36 eV. The onset of the SmD⁺ cross section is higher in energy and rises at 3.10 ± 0.40 eV and is followed by the onset of the EuD⁺ cross section at 3.72 ± 0.45 eV.

Table 2 Modeling parameters using eqn (4)

Reaction	Ln^+	n	σ	E 0 (eV)
Ln^+ + CD4 → LnD^+ + CD3	Ce^+	2.5 ± 0.3	0.56 ± 0.06	2.32 ± 0.34
	Pr^+	2.5 ± 0.3	0.50 ± 0.05	2.01 ± 0.32
	Nd^+	2.5 ± 0.3	0.58 ± 0.06	2.52 ± 0.36
	Sm^+	2.5 ± 0.3	0.55 ± 0.06	3.10 ± 0.40
	Eu^+	2.5 ± 0.3	0.47 ± 0.05	3.72 ± 0.45
Ln^+ + CD4 → LnCD^+ + D + D2	Ce^+	2.5 ± 0.3	0.03 ± 0.01	3.20 ± 0.41
	Pr^+	2.5 ± 0.3	0.007 ± 0.001	2.96 ± 0.39
	Nd^+	2.5 ± 0.3	0.0004 ± 0.0001	3.31 ± 0.42
Ln^+ + CD4 → LnCD3^+ + D	Ce^+	2.5 ± 0.3	0.04 ± 0.01	2.38 ± 0.35
	Pr^+	2.5 ± 0.3	0.012 ± 0.001	1.73 ± 0.30
	Nd^+	2.5 ± 0.3	0.012 ± 0.001	2.02 ± 0.32

---

Table 3 Derived bond dissociation energies

	D 0(Ln^+–D)^a (eV)		D 0(Ln^+–CD) (eV)		D 0(Ln^+–CD3) (eV)
	This work	Literature	This work	Literature	This work	Literature
a Adjusted from published D0(Ln^+–H) to D0(Ln^+–D) by the zero point energy difference between LnH^+ and LnD^+. b Ref. 14. c Ref. 16. d Ref. 15. e Ref. 17.
Ce^+	2.26 ± 0.34	2.15 ± 0.10^b	6.05 ± 0.41		2.20 ± 0.35
Pr^+	2.56 ± 0.32	2.09 ± 0.06^c	6.29 ± 0.39		2.85 ± 0.30
Nd^+	2.05 ± 0.36	2.02 ± 0.06^d	5.93 ± 0.42		2.55 ± 0.32
Sm^+	1.47 ± 0.40	2.06 ± 0.12^e
Eu^+	0.86 ± 0.45

---

Fig. 6 LnD⁺ product ion cross sections for the reaction of Ln⁺ + CD₄ → LnD⁺ + CD₃ as a function of ion kinetic energy in the center-of-mass frame, E_CM. The observed apparent thresholds are CeD⁺ (red circle) ≥ PrD⁺ (dark red hexagon) > NdD⁺ (blue triangle) > SmD⁺ (purple square) > EuD⁺ (teal diamond).

Fig. 7 LnCD₂⁺ product ion cross sections for the reaction of Ln⁺ + CD₄ → LnCD₂⁺ + D₂ as a function of ion kinetic energy in the center-of-mass frame, E_CM. The observed reaction efficiencies are CeCD₂⁺ (red circle) ≥ PrCD₂⁺ (dark red hexagon) > NdCD₂⁺ (blue triangle) > SmCD₂⁺ (purple square) > EuCD₂⁺ (not observed).

The LnCD₂⁺ cross sections decrease with increasing energy, which is characteristic for species formed through exothermic processes. The LnCD₂⁺ cross sections of Ce⁺, Pr⁺, Nd⁺, and Sm⁺ are observed at the lowest energy, where the magnitude of the CeCD₂⁺ cross section is the greatest (∼3 × 10⁻¹⁶ cm²) and the magnitude of the SmCD₂⁺ cross section is the lowest of those observed (∼1.5 × 10⁻¹⁶ cm², roughly half of the CeCD₂⁺ cross section at the lowest energy). The SmCD₂⁺ cross section displays a more rapid falloff than the other LnCD₂⁺ cross sections observed, which may suggest that the SmCD₂⁺ product is not as stable as those for the other Ln⁺ studied here. The EuCD₂⁺ cross section is not observed, presumably because of the energy required for Eu⁺ to achieve a reactive 5d² or 5d6s electronic configuration. Note that this early exothermic behavior for Ce⁺, Pr⁺, Nd⁺, and Sm⁺ can likely be attributed to the electronic energy distribution. Ce⁺ is the most reactive Ln⁺ of those included in the present study and has a ground state electronic configuration of 4f5d², in contrast to the other Ln⁺ included which have ground state electronic configurations of the form 4fⁿ⁻¹6s¹.²⁰

Discussion

Comparison to other methods

The threshold energies reported in Table 2 were used to derive the Ln⁺–D, Ln⁺–CD₃, and Ln⁺–CD bond dissociation energies (BDEs) listed in Table 3. Previous GIBMS experiments have provided values for D₀(Ln⁺–D),^14–17 and those values are included in Table 3 for comparison. To make a fair comparison between the BDEs provided by ICP-MS/MS and those provided by GIBMS, it is important to remember that GIBMS collisionally cools ions to 700 ± 400 K prior to reaction.^25–27 By contrast, the ions generated by the ICP source exit the source with expected temperatures of 8000–10 000 K, although a more conservative estimate is 1000–10 000 K. Excited states are expected to be significantly populated at these temperatures and complicate characterization of the electronic energy distribution. Nonetheless, inclusion of the average electronic energy of Ln⁺ at 8000 K in our model reproduces the experimental data reasonably well, and the estimated 0.25 eV uncertainty in E_el is included in the uncertainty in the reported threshold measurements. Another important difference to note is that in GIBMS, the true zero of energy is routinely determined before each experiment so that the energy scale is well defined.³¹ Our experiment lacks the capability to explicitly determine the true zero of energy, therefore uncertainties in the energy scale are estimated as ∼10% and are included in the overall uncertainty in the resulting threshold measurements. GIBMS also operates under extremely low pressures (0.05–0.4 mTorr) such that multiple collisions with the reactant neutral are improbable. Nevertheless, GIBMS cross sections are extrapolated to zero pressure when pressure dependences are observed so that product formation corresponds to single collision conditions.²¹ Our instrument operates at much higher pressures, (∼1.4–2.8 mTorr), and our cross sections are also extrapolated to zero pressure in our best attempt to provide data that reflect single collision processes. Still, the LnD⁺ BDEs provided here are comparable to those provided by GIBMS experiments,^14–17 and we anticipate that the LnCD₃⁺ and LnCD⁺ BDEs reported here are reasonably accurate, though analogous GIBMS values are not currently available for comparison and a more thorough assessment of accuracy. Previous comparison between GIBMS and ICP-MS/MS cross sections indicate that overall cross section magnitudes are within experimental uncertainties.¹⁸

Anticipated reaction coordinate

To the best of our knowledge, the reaction coordinate of Ln⁺ + CH₄ have not been published. Nevertheless, there have been many reports of third row transition metal cation reaction coordinates^32–39 and Th⁺ and U⁺ reaction coordinates.^40–43 In general, the reactants form an association complex M⁺–CH₄ (I) where the stabilization energy is characteristic of the ion-induced dipole interaction between the reactants. M⁺ then begins to insert into the C–H bond to form the global intermediate H–M⁺–CH₃ (II). Hybridized s–d orbitals are the anticipated participants in bonding in the inserted H–M⁺–CH₃ intermediate, which can go on to dissociate to either LnH⁺ or LnCH₃⁺ at higher energies. At lower energies, M⁺ abstracts a second hydrogen from the C to form H₂–M⁺–CH₂ (III) that readily dissociates to M⁺–CH₂⁺ + H₂ when the energetics have been satisfied.

Because of the stabilization of I by the ion-induced dipole interaction between M⁺ and CH₄, the transition state (TSI/II) between I and II is typically submerged below the energies of the reactants so that observed reaction threshold energies are usually the reaction enthalpy. Nevertheless, electronic configurations of M⁺ can cause a barrier to be observed at TSI/II. This was observed experimentally in GIBMS reactions of Th⁺ and CH₄ when a threshold energy was observed for an otherwise exothermic reaction.⁴³ Subsequent collision induced dissociation reactions of [Th,C,H₄]⁺ with Xe confirmed that the observed threshold was a barrier at TSI/II. This barrier was attributed the mixed ground state²⁰ of Th⁺ [²D–⁴F, (6d7s²/6d²7s)] that drives up the cost of activating the H–CH₃ bond. Alternatively, when the ground state does not have the correct electronic configuration to activate a bond, the rate limiting step may be the crossing (C_p) between the surface originating from the ground state reactants and the surface leading to the ground state products (curve crossing model). An⁺ and Ln⁺ oxidation rates have been tied to this crossing point.^{11–13,44,45} Recent ICP-MS/MS work also indicates that there is a correlation to AnCH₂⁺ formation and the promotion energy to the first state with two unpaired 6d electrons, E_p(6d²) suggesting a curve crossing model.¹⁸

Schilling and Beauchamp explored the gas-phase reactions of Pr⁺, Eu⁺, and Gd⁺ with methane and other hydrocarbons to examine the role of f orbitals in Ln⁺ reactivity.⁵ Pr⁺ (4f³6s¹) and Eu⁺ (4f⁷6s¹) were selected for this study because their ground state electronic configurations are representative of the electronic configurations of most other members of the lanthanide series. Gd⁺ (4f⁷5d¹6s¹) was selected because the ground state configuration includes two unpaired electrons in non-f orbitals and resembles that of the more widely studied transition metal cations. Results obtained by Schilling and Beauchamp reveal that Pr⁺ and Eu⁺ are unreactive towards alkanes while Gd⁺ is reactive. They attribute the observed reactivity of each metal to the strength of the bonds in the ion-induced dipole association and insertion complexes. For Pr⁺ and Eu⁺, the 4f and 6s orbitals are available for bonding; however, due to the spatial contraction of the 4f orbitals, bonds involving the 4f electrons are weak. The increased reactivity of Gd⁺ is afforded by the availability of two non-f electrons (5d6s) to form two strong σ bonds in the intermediate, H–Gd⁺–R. Strong bonding in the activated intermediate decreases its overall energy such that the activation barrier to product formation lies below the energy of the ground state reactants, and product formation becomes energetically favorable. Schilling and Beauchamp note that the ground state electronic configuration of Ce⁺ includes two 5d electrons and extend their present observations to predict that Ce⁺ will be reactive.

Dehydrogenation

The relative magnitudes of the observed cross sections for reaction (6) can be used to assess the relative reactivities of Ce⁺, Pr⁺, Nd⁺, Sm⁺, and Eu⁺:

Ce⁺ > Pr⁺ > Nd⁺ > Sm⁺ > Eu⁺

Notably, the exothermic features observed in reaction (6) are likely caused by excited states. In principle, excited states may be more or less reactive than the ground state; however, assuming that a pathway exists between the excited state and ground state potential energy surfaces, presumably this energy is available for reaction. Previous ICP-MS/MS work suggests that this is likely for the Ln⁺ and An⁺.¹² The temperature of the plasma is expected to be within the range of 8000 to 10 000 K, with some collisional cooling anticipated in the region between the ion source and the first quadrupole. Our recent work¹⁸ suggests that the effective ion temperature is within the range of 1000 to 10 000 K. Table 1 includes the average electronic energy of each Ln⁺ at several temperatures within the specified range, and Table 4 includes the ground state configuration of the respective Ln⁺ along with the promotion energies from the ground state configuration to the 5d², 5d6s, and 5d configurations for each Ln⁺. Combining information from Tables 1 and 4, specifically the average electronic energy of each Ln⁺ at a given temperature and the respective promotion energies for that cation, the accessible electronic configurations can be inferred. Overall, the promotion energy for each Ln⁺ to a reactive configuration increases across the series, justifying the reduced reactivity observed moving from Ce⁺ to Eu⁺. Previous work has established a correlation between reaction efficiencies (k/k_col) and E_p(5d²) for Ln⁺ oxidation reactions with O₂, CO₂, and H₂O.^11,12 A similar correlation has been made for An⁺ reaction threshold energies with E_p(6d²).^12,46 This comparison is also made using k/k_col and E_p(5d²) listed in Table 4 and shown in Fig. 8 where an excellent correlation (r² = 0.998) is observed.

Table 4 Reaction (6) efficiencies (k/k_col) with Ln⁺ ground state electron configurations and selected promotion energies (eV)

Ln^+	E p(5d^2)^a	E p(5d6s)^b	E p(5d)^b	Ave E k/kcol^c	Low E k/kcol^d
a Ref. 11 and references therein. b Kramida, A., Ralchenko, Yu., Reader, J. and NIST ASD Team (2023). NIST Atomic Spectra Database (version 5.11), [Online]. Available: https://physics.nist.gov/asd [Thu Jun 27 2024]. National Institute of Standards and Technology, Gaithersburg, MD. DOI: https://doi.org/10.18434/T4W30F10. c Average k/kcol for energies less than 1 eV. d k/kcol at the lowest energy (0.08–0.10 eV).
Ce (4f5d^2)	0.00	0.295	0.00	0.012 ± 0.006	0.016 ± 0.008
Pr (4f^36s)	0.73	0.97	0.65	0.009 ± 0.004	0.012 ± 0.006
Nd (4f^46s)	1.14	1.25	0.63	0.008 ± 0.004	0.012 ± 0.006
Sm (4f^66s)	2.35	2.67	0.95	0.004 ± 0.002	0.009 ± 0.004
Eu (4f^76s)	4.54	3.74	1.23

---

Fig. 8 Correlation of k/k_col with promotion energies of Ln⁺ to a 5d² electronic configuration (r² = 0.998) on the left and 5d6s electronic configuration (r² = 0.988) on the right.

Schilling and Beauchamp previously noted the increased reactivity of Gd⁺(4f⁷5d¹6s¹) compared to Pr⁺(4f³6s¹) and Eu⁺(4f⁷6s¹) attributing the increase in reactivity to the two unpaired non-f electrons in the ground state of Gd⁺.⁵ The 4f orbitals of the Ln⁺ are not expected to significantly participate in bond activation or formation due to the spatial contraction of the 4f orbitals, which limits their accessibility. Additionally, 4f orbitals do not contribute sufficient electron density to form strong σ bonds. As a result, Bohme and coworkers⁷ have also attributed Ln⁺ reactivity to a 5d6s electronic configuration. Fig. 8 also shows the correlation of k/k_col to E_p(5d6s). The correlation (r² = 0.988) is slightly worse than the correlation of k/k_col to E_p(5d²); however, given experimental uncertainties the present work is not sufficient to determine which correlation is more appropriate. Nevertheless, Fig. 8 further supports the notion that two unpaired non-f electrons are necessary for bond activation.

Ln⁺ thermochemistry

The relative LnD⁺ and LnCD₂⁺ cross section magnitudes, respective threshold energies, and observed reactivities of Ln⁺ show comparable correlation with both E_p(5d²) and E_p(5d6s) to achieve a reactive state with two valence electrons in non-f orbitals as postulated by Schilling and Beauchamp⁵ and Schwarz and coworkers.⁶ For LnD⁺, only one electron is necessary for bond formation; nevertheless, the correlation to promotion energy of the first electronic state with one 5d electron [E_p(5d)] with D₀(Ln⁺–D) is poor (r² = 0.59); however, the correlation of D₀(Ln⁺–D) with E_p(5d6s) is reasonably good (r² = 0.89) and is shown in Fig. 9. Theoretical work with third row transition metals by Ohanessian et al. suggests that the 5d and 6s orbitals are comparable in size.⁴⁷ Consequently, the 5d and 6s orbitals hybridize when forming covalent σ bonds. Armentrout and coworkers have made similar conclusions.⁴ Because of the positioning of the lanthanide series in the periodic table, they can be thought of as early third row transition metals; thus, D₀(Ln⁺–D) is correlated to E_p(5d6s) which facilitates sd hybridization. Notably, BDEs of LnD⁺ determined by Armentrout and coworkers are CeD⁺ ≈ PrD⁺ ≈ NdD⁺ ≈ SmD⁺ with no apparent correlation to a promotion energy; however, the correlation is observed in the associated theoretical calculations within these works at the CCSD(T) level of theory.^14–17,23 The discrepancy between the present ICP-MS/MS results and the GIBMS values is not understood, but it may suggest that the true value of D₀(Sm⁺–H) is at the higher end of the range listed in Table 3. This may occur in part because of competition of reaction (5) with the energetically more favorable reaction (6). Such competition would likely shift the observed reaction (5) threshold higher in energy resulting in a lower BDE than that measured from the reaction with H₂. The potential for competition between reaction channels was not accounted for in the model used to provide E₀. Table 4 indicates that most of these Ln⁺ have a 4fⁿ⁻¹6s¹ ground state configuration, which may suggest that the 6s orbital is sufficient to form the metal hydride bond; however, Ce⁺ has a 4f¹5d² ground state. Notably, a suggestion of bonding between the Ln⁺ 6s and H 1s orbital is inconsistent with previous conclusions regarding third row transition metals.²³ The measured threshold may also represent a barrier in excess of the reaction enthalpy. Such barriers have been observed in several Ln⁺ reactions.^12,13,44,45 A barrier in excess of the reaction enthalpy is unlikely in the present case because reaction (5) probably occurs through dissociation of the intermediate II to LnD⁺ + CD₃ without additional barriers.

Fig. 9 Correlation of LnD⁺ BDEs determined by ICP-MS/MS (open squares) with promotion energies of Ln⁺ to a 5d electronic configuration (left) and 5d6s electronic configuration (right). The least squares linear regression detailing the correlations of the values of D₀(Ln⁺–D) with E_p(5d) and E_p(5d6s) are shown by the solid lines (r² = 0.59 for 5d and 0.89 for 5d6s). Values of D₀(Ln⁺–D) from GIBMS are indicated by the filled circles. Models of the ICP-MS/MS cross sections using eqn (4) provide threshold energies used to derive D₀(Ln⁺–D) indicated by the open squares.

For the actinides, there is a stronger correlation of An⁺–L BDEs with E_p(6d) for singly bound species and E_p(6d²) for multiply bound species than with E_p(6d7s) based on work by our group and others.^12,30,48,49 For the lanthanides, the s orbital may be much more important for MD⁺ bond formation than for the actinides. The restricted reactivity observed for Sm⁺ and Eu⁺ compared to Ce⁺, Pr⁺, and Nd⁺ can likely be attributed to the significant energy required for Sm⁺ and Eu⁺ to achieve a reactive 5d² or 5d6s electronic configuration (2.35/2.67 eV and 4.54/3.74 eV, respectively) to enable insertion into the C–D bonds of CD₄. It is also important to consider that LnD⁺ formation may also occur by a direct abstraction mechanism, though reactions that were assumed to proceed by direct atom abstraction were inefficient and largely dependent upon precise alignment of the reactants.⁵⁰ Such a requirement instead imparts a dynamic or kinetic rather than energetic restriction on the observed reactivity.

Comparison to actinide reactions

Comparison between the f block reactions can be useful to understand which orbitals are active during bond activation and chemical bonding. The 4f orbitals are not expected to contribute significantly to chemical bonding, but the 5f orbitals may. The actinide reactions with methane have been recently published.¹⁸ Notably, no exothermic reaction was observed for the An⁺ reaction with the exception of Th⁺ where ThCH₂⁺ was observed at the lowest energies. This is consistent with previous FT-ICR MS^51,52 and GIBMS⁴³ experiments. By contrast, previous SIFT-MS⁷ and FT-ICR MS⁶ experiments observed no reaction for the Ln⁺ at nominally 300 K. The observation of LnCD₂⁺ in the present work suggests that the electronic distribution of the Ln⁺ is higher than that observed for the An⁺ in previous work. Similarly, the same overall trend of decreasing cross section magnitudes moving across the series is observed for the Ln⁺ as well as for the An⁺. This includes not observing reaction (6) for Eu⁺, the congener of Am⁺ where AmCD₂⁺ was also not observed.

The previous ICP-MS/MS work showed a correlation of D₀(An–CH₂⁺) to E_p(6d²).¹⁸ Because AnCH₂⁺ is the lowest energy product (except for Am⁺), this is presumably similar to the correlation to k/k_col. In the present work, Fig. 8, a slightly better correlation (r² = 0.998 vs. 0.988) to E_p(5d²) than E_p(5d6s) was observed, although experimental uncertainty makes a definitive conclusion difficult. Similarly, Gibson observed that D₀(Ln⁺–O) vs. E_p(5d²) is a slightly better correlation than D₀(Ln⁺–O) vs. E_p(5d6s).⁹ Cox et al. have also tied k/k_col for several SIFT-MS, GIBMS, and FT-ICR MS Ln⁺ oxidation reactions to E_p(5d²).¹² While this analysis does not preclude 4f orbital participation, it does suggest that the 5d orbitals are the primary driver to bond activation for the Ln⁺. This is similar to the observation that the 6d orbitals are the primary drivers of An⁺ bond activation.^{9,11,12,18,53}

The recent ICP-MS/MS investigation of the reactions of An⁺ with methane¹⁸ does not provide definitive evidence that the 5f orbitals are active during C–D bond activation; nevertheless, the AnCD₂⁺ cross sections are systematically higher than their LnCD₂⁺ congeners. Because cross section (σ) is related to rate (k = σv, where v is the reactants’ relative velocity), this may suggest 5f orbital participation in formation of the insertion intermediate (HAnCD₃⁺). This is far from conclusive but does warrant additional investigation. Notably, the theoretical potential energy surface of a related reaction, An⁺ + NH₃ → AnNH⁺ + H₂ indicates 5f orbital participation in HAnNH₂⁺.⁵⁴

It is also useful to identify and compare trends in AnD⁺ and LnD⁺ bonding. For the AnD⁺, a good correlation between D₀(An⁺–D) and E_p(6d) was observed. In the present work, the correlation between D₀(Ln⁺–D) and E_p(5d) is poor (r² = 0.59); however, the correlation with E_p(5d6s) is good (r² = 0.89). This indicates that for the Ln⁺ both the 5d and 6s orbitals are necessary to form the σ bond. This has also been observed for the third row transition metals.^4,23 Consequently, the LnD⁺ σ bond is likely a sd hybrid. An interesting aspect of the AnD⁺ BDEs, though, is that there is a minimal difference between D₀(Pu⁺–D) and D₀(Am⁺–D). This is not observed for the Ln⁺ analogs, D₀(Sm⁺–D) and D₀(Eu⁺–D), in Fig. 9. For the AnD⁺, it was speculated that there may be a change in bonding that occurs starting at PuD⁺ that may include contributions from 5f orbitals. This is substantiated by a similar observation in unpublished work reporting D₀(An⁺–N).⁴⁶ In the case of AnN⁺, the experimental BDE trend is replicated by CCSD(T) calculations of AnN⁺ BDEs. Additional work with transplutonic elements is necessary to establish this trend. Failure to observe a similar deviation in the D₀(Ln⁺–D) trend between SmD⁺ and EuD⁺, where the 4f orbitals are not expected to contribute to bonding may offer evidence that the deviation between PuD⁺ and AmD⁺ is caused by participation of the 5f orbitals beyond Pu⁺.

Extended perspective on catalysis

The primary focus of the present study is the activation of methane by atomic lanthanide cations, which at most corresponds to a single step within a larger catalytic cycle. A brief discussion of C–H bond activation mechanisms facilitated by metal catalysts may offer a greater context in which information obtained in the present study is of interest. Catalysts are required in the activation of methane due to its inert nature and chemical stability afforded by the strength of C–H bonds. Two mechanisms governing the catalytic activation of the C–H bonds in methane have been identified.⁵⁵ One pathway proceeds by the formation and stabilization of the methyl radical utilizing the transition metal (surface stabilization) whereas the alternative pathway proceeds by direct H abstraction, stabilization on an oxygen atom of the support, and reduction of the metal support.⁵⁶ Single atom catalysts incorporate a single atom bound to a reducible oxide support structure and stabilize the atom through exchangeable charge transfer throughout the catalytic reaction.^57–59 Cerium oxide possesses catalytic capabilities serving as the support structure for transition metal catalysts.^60,61 Moraes et al. utilized theoretical calculations to evaluate the energetic barriers to the dehydrogenation of methane by Fe, Co, Ni, and Cu on cerium oxide clusters.⁶² The preliminary step is the adsorption of CH₄ onto the transition metal (TM) doped cluster. The interaction of CH₄ with the TM is weak and results in the transfer of an electron to the CeO₂ cluster support. Adsorption of CH₄ by the TM is followed by distortion of the H–C–H bond angle, where Co and Ni induce a greater variance of the HCH angle than Fe and Cu. For each of the clusters investigated, splitting of CH₄ into CH₃ + H results in adsorption of CH₃ to the TM site and adsorption of H to Ce. At the atomic level, our results offer quantitative evidence that supports the requirement for Ln⁺ to possess two valence electrons in non-f orbitals to enable effective C–H bond insertion.

Conclusions

Catalysis research continues to be fueled by the persistent challenge to activate C–H and C–C bonds to produce fuel. Methane activation by transition metals has been thoroughly explored on the fundamental level. The catalytic capabilities of lanthanide cations have not previously been extensively explored. ICP-MS/MS was used to examine the kinetic energy dependences of the reactions of lanthanide cations Ce⁺, Pr⁺, Nd⁺, Sm⁺, and Eu⁺ with methane. Models of the energy-dependent reaction cross sections provided thermodynamic information and bond dissociation energies for Ln⁺–D, and the first measurements of the Ln⁺–CD₃ and Ln⁺–CD bond dissociation energies. Values for the Ln⁺–D BDEs, D₀(Ln⁺–D), are comparable to those obtained from previous GIBMS experiments. The observed reaction efficiencies correlate with the E_p(5d²) and E_p(5d6s) for each Ln⁺ and offer quantitative evidence for the requirement of Ln⁺ to possess two valence electrons in non-f orbitals for effective C–H bond insertion. A closer examination of the correlations of Ln⁺ and An⁺ reaction efficiencies and BDEs with promotion energies to nd² and nd(n + 1)s (n = 5, 6) electronic configurations enables an assessment of 5f orbital contributions, where the Ln⁺ serve as the baseline for no f orbital contributions. The increased reactivity observed for the An⁺ may be the result of 5f orbital activity in formation of the insertion intermediate (HAnCD₃⁺). The correlations of LnD⁺ and AnD⁺ BDEs with promotion energies to nd² and nd(n + 1)s (n = 5, 6) configurations suggest that the d orbitals drive bonding in the Ln⁺ and An⁺.

Data availability

The primary data used to support the claims in this paper are included in the primary manuscript. Fig. 1–5 contain the reported absolute reaction cross sections observed in this work. Fig. 6–9 are derived from Fig. 1–5. Table 1 contains isotopes used and average electronic energy used in eqn (4). Table 2 contains all the modelling parameters used in eqn (4). Table 3 contains the thermochemistry derived from the eqn (4) model. Table 4 contains reaction efficiencies calculated from Fig. 1–5. All other data is publicly available through the associated citations.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the Open Call Initiative under the Laboratory Directed Research and Development (LDRD) Program at Pacific Northwest National Laboratory (PNNL). PNNL is a multi-program national laboratory operated for the U.S. Department of Energy (DOE) by Battelle Memorial Institute under Contract No. DE-AC05-76RL01830.

References

1. D. Hasenberg and L. Schmidt, HCN synthesis from CH4 and NH3 on platinum, J. Catal., 1986, 97(1), 156–168.
2. J. Leduc, M. Frank, L. Jürgensen, D. Graf, A. Raauf and S. Mathur, Chemistry of Actinide Centers in Heterogeneous Catalytic Transformations of Small Molecules, ACS Catal., 2019, 9(6), 4719–4741.
3. J. Roithova and D. Schroder, Selective activation of alkanes by gas-phase metal ions, Chem. Rev., 2010, 110(2), 1170–1211.
4. P. B. Armentrout, Methane Activation by 5 d Transition Metals: Energetics, Mechanisms, and Periodic Trends, Chem. – Eur. J., 2017, 23(1), 10–18.
5. J. B. Schilling and J. Beauchamp, Hydrocarbon activation by gas-phase lanthanide cations: interaction of praseodymium (Pr⁺), europium (Eu⁺), and gadolinium (Gd⁺) with small alkanes, cycloalkanes, and alkenes, J. Am. Chem. Soc., 1988, 110(1), 15–24.
6. H. H. Cornehl, C. Heinemann, D. Schroeder and H. Schwarz, Gas-phase reactivity of lanthanide cations with hydrocarbons, Organometallics, 1995, 14(2), 992–999.
7. A. Shayesteh, V. V. Lavrov, G. K. Koyanagi and D. K. Bohme, Reactions of atomic cations with methane: gas phase room-temperature kinetics and periodicities in reactivity, J. Phys. Chem. A, 2009, 113(19), 5602–5611.
8. J. Marcalo, M. Santos, A. N. P. D. Matos, J. K. Gibson and R. G. Haire, Gas-phase reactions of doubly charged lanthanide cations with alkanes and alkenes. Trends in metal (2+) reactivity, J. Phys. Chem. A, 2008, 112(49), 12647–12656.
9. J. K. Gibson, Role of Atomic Electronics in f-Element Bond Formation: Bond Energies of Lanthanide and Actinide Oxide Molecules, J. Phys. Chem. A, 2003, 107, 7891–7899.
10. H. H. Cornehl, R. Wesendrup, M. Diefenbach and H. Schwarz, A Comparative Study of Oxo-Ligand Effects in the Gas-Phase Chemistry of Atomic Lanthanide and Actinide Cations, Chem. – Eur. J., 1997, 3(7), 1083–1090.
11. R. M. Cox, K. Harouaka, M. Citir and P. B. Armentrout, Activation of CO₂ by Actinide Cations (Th⁺, U⁺, Pu⁺, and Am⁺) as Studied by Guided Ion Beam and Triple Quadrupole Mass Spectrometry, Inorg. Chem., 2022, 8168–8181.
12. R. M. Cox, K. M. Melby, A. D. French and M. J. Rodriguez, f-Block Reactions of Metal Cations with Carbon Dioxide Studied by Inductively Coupled Plasma Tandem Mass Spectrometry, Phys. Chem. Chem. Phys., 2024, 26, 209–218.
13. R. M. Cox, A. R. Bubas, K. M. Melby, A. D. French, M. J. Rodriguez, M. P. Prange and N. Govind, The Curious Case of Pu+: Insight on 5f Orbital Activity from Inductively Coupled Plasma Tandem Mass Spectrometry (ICP-MS/MS) Reactions, Inorg. Chem., 2024, 63(43), 20617–20624.
14. M. Ghiassee and P. B. Armentrout, Cerium Cation (Ce⁺) Reactions with H₂, D₂, and HD: CeH⁺ Bond Energy and Mechanistic Insights from Guided Ion Beam and Theoretical Studies, J. Phys. Chem. A, 2020, 124(13), 2560–2572.
15. M. Ghiassee and P. B. Armentrout, Activation of D₂ by Neodymium Cation (Nd⁺): Bond Energy of NdH⁺ and Mechanistic Insights through Experimental and Theoretical Studies, J. Phys. Chem. A, 2021, 125(14), 2999–3008.
16. M. Ghiassee, J. Ewigleben and P. B. Armentrout, Praseodymium Cation (Pr+) Reactions with H₂, D₂, and HD: PrH⁺ Bond Energy and Mechanistic Insights from Guided Ion Beam and Theoretical Studies, J. Chem. Phys., 2020, 153(14), 144304.
17. M. Demireva and P. B. Armentrout, Samarium Cation (Sm⁺) Reactions with H₂, D₂, and HD: SmH⁺ Bond Energy and Mechanistic Insights from Guided Ion Beam and Theoretical Studies, J. Chem. Phys., 2018, 149(16), 164304.
18. A. R. Bubas, A. D. French, K. M. Melby, M. J. Rodriguez and R. M. Cox, The Balance of Orbital Overlap and Orbital Energy in the Activation of Methane by Actinide Cations; Insights from Inductively Coupled Plasma Tandem Mass Spectrometry, Inorg. Chem. Front., 2025, 12, 1503–1516.
19. K. Harouaka, C. Allen, E. Bylaska, R. M. Cox, G. C. Eiden, M. L. D. Vacri, E. W. Hoppe and I. J. Arnquist, Gas-Phase Ion-Molecule Interactions in a Collision Reaction Cell with Triple Quadrupole-Inductively Coupled Plasma Mass Spectrometry: Investigations with N₂O as the Reaction Gas, Spectrochim. Acta, Part B, 2021, 186, 106309.
20. J. E. Sansonetti and W. C. Martin, NIST Standard Reference Database 108. https://www.nist.gov/pml/handbook-basic-atomic-spectroscopic-data (accessed 03/02/2023).
21. P. B. Armentrout, Mass Spectrometry – Not Just a Structural Tool: The Use of Guided Ion Beam Tandem Mass Spectrometry to Determine Thermochemistry, J. Am. Soc. Mass Spectrom., 2002, 13(5), 419–434.
22. N. Yamada, Kinetic Energy Discrimination in Collision/Reaction Cell ICP-MS: Theoretical Review of Principles and Limitations, Spectrochim. Acta, Part B, 2015, 110, 31–44.
23. P. B. Armentrout, Periodic Trends in Gas-Phase Oxidation and Hydrogenation Reactions of Lanthanides and 5d Transition Metal Cations, Mass Spectrom. Rev., 2022, 41, 606–626.
24. P. B. Armentrout, The Kinetic Energy Dependence of Ion-Molecule Reactions: Guided Ion Beams and Threshold Measurements, Int. J. Mass Spectrom., 2000, 200, 219–241.
25. M. R. Sievers, Y.-M. Chen, J. L. Elkind and P. B. Armentrout, Reactions of Y⁺, Zr⁺, Nb⁺, and Mo⁺ with H₂, HD, and D2, J. Phys. Chem., 1996, 100, 54–62.
26. C. L. Haynes and P. B. Armentrout, Thermochemistry and Structures of CoC₃H₆⁺: Metallacycle and Metal-Alkene Isomers, Organomettalics, 1994, 13, 3480–3490.
27. B. L. Kickel and P. B. Armentrout, Guided Ion Beam Studies of the Reactions of Group 3 Metal Ions (Sc⁺, Y⁺, La⁺, and Lu⁺) with Silane. Electronic State Effects, Comparison to Reactions with Methane, and M⁺-SiH_x (x = 0–3) Bond Energies, J. Am. Chem. Soc., 1995, 117, 4057–4070.
28. T. Beyer and D. Swinehart, Algorithm 448: Number of multiply-restricted partitions, ASSOC Computing Machinery 2 Penn Plaza, STE 701 New York, NY 10121-0701 USA, 1973, vol. 16, p. 379.
29. N. Dalleska, K. Honma, L. Sunderlin and P. Armentrout, Solvation of transition metal ions by water. Sequential binding energies of M⁺ (H₂O) x (x = 1–4) for M = Ti to Cu determined by collision-induced dissociation, J. Am. Chem. Soc., 1994, 116(8), 3519–3528.
30. A. R. Bubas, A. Kafle, B. C. Stevenson and P. B. Armentrout, The Bond Energy of UN⁺: Guided Ion Beam Studies of the Reactions of U⁺ with N2 and NO, J. Chem. Phys., 2024, 160, 164305.
31. K. M. Ervin and P. B. Armentrout, Translational Energy Dependence of Ar⁺ + XY → ArX⁺ + Y (XY = H₂, D₂, HD) from Thermal to 30 eV c.m, J. Chem. Phys., 1985, 83(1), 166–189.
32. F.-X. Li and P. Armentrout, Activation of methane by gold cations: Guided ion beam and theoretical studies, J. Chem. Phys., 2006, 125(13), 133114.
33. X.-G. Zhang, R. Liyanage and P. Armentrout, Potential energy surface for activation of methane by Pt⁺: a combined guided ion beam and DFT study, J. Am. Chem. Soc., 2001, 123(23), 5563–5575.
34. F.-X. Li, X.-G. Zhang and P. Armentrout, The most reactive third-row transition metal: Guided ion beam and theoretical studies of the activation of methane by Ir⁺, Int. J. Mass Spectrom., 2006, 255, 279–300.
35. P. Armentrout, L. Parke, C. Hinton and M. Citir, Activation of Methane by Os⁺: Guided-Ion-Beam and Theoretical Studies, ChemPlusChem, 2013, 78(9), 1157–1173.
36. M. M. Armentrout, F.-X. Li and P. Armentrout, Is spin conserved in heavy metal systems? Experimental and theoretical studies of the reaction of Re⁺ with methane, J. Phys. Chem. A, 2004, 108(45), 9660–9672.
37. P. Armentrout, S. Shin and R. Liyanage, Guided-ion beam and theoretical study of the potential energy surface for activation of methane by W⁺, J. Phys. Chem. A, 2006, 110(4), 1242–1260.
38. L. G. Parke, C. S. Hinton and P. Armentrout, Experimental and theoretical studies of the activation of methane by Ta⁺, J. Phys. Chem. C, 2007, 111(48), 17773–17787.
39. L. G. Parke, C. S. Hinton and P. Armentrout, Why is hafnium so unreactive?: Experimental and theoretical studies of the reaction of Hf⁺ with methane, Int. J. Mass Spectrom., 2006, 254(3), 168–182.
40. E. di Santo, M. D. C. Michelini and N. Russo, Methane C–H Bond Activation by Gas-Phase Th⁺ and U⁺: Reaction Mechanisms and Bonding Analysis, Organometallics, 2009, 28(13), 3716–3726.
41. K. De Almeida and H. Duarte, Gas-phase methane activation by the Ac + − Pu+ Ions: Theoretical insights into the role of 5f electrons/orbitals in early actinide chemistry, Organometallics, 2009, 28(11), 3203–3211.
42. K. J. de Almeida and H. A. Duarte, Dehydrogenation of Methane by Gas-Phase Th, Th⁺, and Th²⁺: Theoretical Insights into Actinide Chemistry, Organometallics, 2010, 29, 3735–3745.
43. R. M. Cox, P. B. Armentrout and W. A. de Jong, Activation of CH₄ by Th⁺ as Studied by Guided Ion Beam Mass Spectrometry and Quantum Chemistry, Inorg. Chem., 2015, 54(7), 3584–3599.
44. P. B. Armentrout and R. M. Cox, Potential Energy Surface for Reaction of Sm⁺ + CO₂ → SmO⁺ + CO: Guided Ion Beam and Theoretical Studies, Phys. Chem. Chem. Phys., 2017, 19, 11075–11088.
45. P. B. Armentrout, R. M. Cox, B. C. Sweeny, S. G. Ard, N. S. Shuman and A. A. Viggiano, Lanthanides as Catalysts: Guided Ion Beam and Theoretical Studies of Sm⁺ + COS, J. Phys. Chem. A, 2018, 122(3), 737–749.
46. R. M. Cox, A. R. Bubas, K. M. Melby, A. D. French, M. J. Rodriguez, M. P. Prange, N. Govind, K. A. Peterson and P. B. Armentrout, The Reactions of An⁺ (An⁺ = Th⁺, U⁺ - Am⁺) + NO Reactions Observed by Inductively Coupled Plasma Tandem Mass Spectrometry In Progress, 2025.
47. G. Ohanessian, M. J. Brusich and W. A. Goddard III, Theoretical study of transition-metal hydrides. 5. Hafnium to mercury (HfH⁺ through HgH⁺), barium and lanthanum (BaH⁺ and LaH⁺), J. Am. Chem. Soc., 1990, 112(20), 7179–7189.
48. J. Marçalo and J. K. Gibson, Gas-Phase Energetics of Actinide Oxides: An Assessment of Neutral and Cationic Monoxides and Dioxides from Thorium to Curium, J. Phys. Chem. A, 2009, 113(45), 12599–12606.
49. R. M. Cox, A. Kafle, P. B. Armentrout and K. A. Peterson, Bond Energy of ThN⁺: A Guided Ion Beam and Quantum Chemical Investigation of the Reactions of Thorium Cation with N₂ and NO, J. Chem. Phys., 2019, 151(3), 034304.
50. A. R. Bubas, C. J. Owen and P. B. Armentrout, Reactions of Atomic Thorium and Uranium Cations with CF₄ Studied by Guided Ion Beam Tandem Mass Spectrometry, Int. J. Mass Spectrom., 2022, 472, 116778.
51. J. K. Gibson, R. G. Haire, J. Marçalo, M. Santos, A. Pires de Matos, M. K. Mrozik, R. M. Pitzer and B. E. Bursten, Gas-Phase Reactions of Hydrocarbons with An⁺ and AnO⁺ (An = Th, Pa, U, Np, Pu, Am, Cm): The Active Role of 5f Electrons in Organoprotactinium Chemistry, Organometallics, 2007, 26(16), 3947–3956.
52. J. Marçalo, J. P. Leal and A. P. de Matos, Gas Phase Actinide Ion Chemistry: Activation of Alkanes and Alkenes by Thorium Cations, Int. J. Mass Spectrom. Ion Processes, 1996, 157–158, 265–274.
53. M. Santos, J. Marçalo, A. P. D. Matos, J. K. Gibson and R. G. Haire, Gas-Phase Oxidation Reactions of Neptunium and Plutonium Ions Investigated via Fourier Transform Ion Cyclotron Resonance Mass Spectrometry, J. Phys. Chem. A, 2002, 106, 7190–7194.
54. M. Goujet, A. Quemet and D. Guillaumont, Gas-Phase Reactivity of Actinides Monocations with NH3: ICP-MS Experiments Combined with a DFT Study, Inorg. Chem., 2024, 63(45), 21430–21440.
55. G. Kumar, S. L. J. Lau, M. D. Krcha and M. J. Janik, Correlation of methane activation and oxide catalyst reducibility and its implications for oxidative coupling, ACS Catal., 2016, 6(3), 1812–1821.
56. A. A. Latimer, H. Aljama, A. Kakekhani, J. S. Yoo, A. Kulkarni, C. Tsai, M. Garcia-Melchor, F. Abild-Pedersen and J. K. Nørskov, Mechanistic insights into heterogeneous methane activation, Phys. Chem. Chem. Phys., 2017, 19(5), 3575–3581.
57. X.-F. Yang, A. Wang, B. Qiao, J. Li, J. Liu and T. Zhang, Single-atom catalysts: a new frontier in heterogeneous catalysis, Acc. Chem. Res., 2013, 46(8), 1740–1748.
58. B. B. Sarma, F. Maurer, D. E. Doronkin and J.-D. Grunwaldt, Design of single-atom catalysts and tracking their fate using operando and advanced X-ray spectroscopic tools, Chem. Rev., 2022, 123(1), 379–444.
59. J.-C. Liu, Y.-G. Wang and J. Li, Toward rational design of oxide-supported single-atom catalysts: atomic dispersion of gold on ceria, J. Am. Chem. Soc., 2017, 139(17), 6190–6199.
60. A. Trovarelli, Catalytic properties of ceria and CeO₂-containing materials, Catal. Rev., 1996, 38(4), 439–520.
61. D. R. Mullins, The surface chemistry of cerium oxide, Surf. Sci. Rep., 2015, 70(1), 42–85.
62. P. I. R. Moraes, C. S. Peraça and J. L. Da Silva, Single-atom catalysts on ceria substrates: Exploring cluster and surface effects on methane activation, Mol. Catal., 2024, 564, 114318.

---