 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Determinants of hydrogen bond distances in proteins†
Masaki
Tsujimura
 *a,
Hiroshi
Ishikita
*a,
Hiroshi
Ishikita
 bc and
Keisuke
Saito
bc and
Keisuke
Saito
 *bc
*bc
aDepartment of Advanced Interdisciplinary Studies, The University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8904, Japan. E-mail: masaki.tsujimura@riken.jp; Fax: +81-3-5452-5083; Tel: +81-3-5452-5056
bDepartment of Applied Chemistry, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo 113-8654, Japan. E-mail: ksaito@appchem.t.u-tokyo.ac.jp
cResearch Center for Advanced Science and Technology, The University of Tokyo, 4-6-1 Komaba, Meguro-ku, Tokyo 153-8904, Japan
First published on 25th April 2025
Abstract
Hydrogen bonds (H-bonds) between oxygen atoms, with the O–H bond donated to the acceptor O atom (Odonor–H⋯Oacceptor), are essential for stabilizing protein structures and facilitating enzymatic reactions. The dielectric and electrostatic environment of proteins, as well as structural constraints imposed by protein folding, influence the nature of H-bonds. In this study, we investigated how these factors affect H-bond distances in proteins. Analysis of 906 high-resolution protein structures (≤1.2 Å) from the Protein Data Bank revealed that H-bond distances for H-bonds with the same donor and acceptor groups are distributed around a value primarily determined by the pKa difference between these groups (ΔpKa) in water, with lower ΔpKa values leading to shorter distances. This correlation arises from enhanced electron redistribution from the H-bond acceptor to the donor in lower ΔpKa H-bonds, which increases the covalent character of the H-bond and decreases the H⋯Oacceptor distance. In contrast, H-bond distances are largely unaffected by whether the H-bond is buried in the protein interior or exposed to bulk water, as the strength of the electrostatic interaction between the donor and acceptor groups plays a minor role in determining distances. Furthermore, analysis of H-bonds in microbial rhodopsins using a quantum mechanical/molecular mechanical approach demonstrates that the protein environment primarily influences H-bond distances electrostatically by altering the ΔpKa of the H-bond, while structural constraints impose a secondary influence by altering Odonor–H⋯Oacceptor angles or H⋯Oacceptor distances without changing ΔpKa.
Introduction
Hydrogen bonds (H-bonds) are abundant in proteins and play a crucial role in stabilizing protein structures and facilitating enzymatic reactions.1 The H-bond donor and acceptor can be defined as the groups donating and accepting the O–H bond (or the N–H bond), respectively (e.g., Odonor–H⋯Oacceptor). H-bonds are characterized by properties such as distances, stretching vibrational frequencies, and 1H NMR chemical shifts. Over 200![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 structures in the Protein Data Bank (PDB)2 provide extensive information about H-bond distances.3–9 These distances reflect the chemical properties of the donor and acceptor groups as well as the influence of the protein environment on the nature of the H-bond.
000 structures in the Protein Data Bank (PDB)2 provide extensive information about H-bond distances.3–9 These distances reflect the chemical properties of the donor and acceptor groups as well as the influence of the protein environment on the nature of the H-bond.
An H-bond can be considered an interaction between a Brønsted acid (H-bond donor) and a Brønsted base (H-bond acceptor).10 pKa is an indicator of the Brønsted acidity. Therefore, the pKa difference between the donor and acceptor groups (ΔpKa)10 reflects the characteristics of the H-bond. A lower ΔpKa leads to a higher binding enthalpy,11 a lower Odonor–H stretching vibrational frequency,12,13 and a higher 1H NMR chemical shift.12–16
A positive correlation between O⋯O distances and ΔpKa values was reported for 68 H-bonds of small compounds in neutron diffraction structures, with a coefficient of determination R2 = 0.86.16,17 Similarly, positive correlations between N⋯O or N⋯N distances and ΔpKa values were reported (R2 = 0.74 and 0.69 for 86 and 29 H-bonds, respectively).17 Deviations from these correlations mainly arise from additional H-bonds of the donor and acceptor groups,17,18 as well as geometric constraints in crystals.17 O⋯O distances are almost independent of the solvent dielectric environment, as the 1H NMR chemical shift for the same H-bond remains largely unchanged across different solvents (chloroform, acetone, or water), and the calculated equilibrium O⋯O distance of the [HOH⋯−OH] H-bond remains nearly constant among solvents with dielectric constants ranging from 5 to 78.16,17
The present study aims to elucidate the determinants of H-bond distances in proteins, focusing primarily on O⋯O H-bonds, but also examining N⋯O and N⋯N H-bonds. We begin by investigating small-compound H-bonds relevant to those in proteins to clarify the basis for the correlation between H-bond distances and ΔpKa in the absence of the protein environment.
However, in contrast to H-bonds in solution under comparable conditions, systematic analysis of H-bond distances in protein environments remains limited. A major challenge lies in the heterogeneity of the PDB, which contains structures determined under inconsistent conditions and resolutions. For instance, many structures resolved at >2.5 Å lack sufficient clarity to assign side-chain orientations or identify interacting water molecules. This heterogeneity has hindered meaningful comparisons of H-bond properties among proteins.
To overcome these limitations, we next focus exclusively on 906 high-resolution protein crystal structures (≤1.2 Å), in which both side chains and interacting water molecules can be reliably modeled based on electron density. By limiting our dataset to these high-resolution structures, we are able to clarify which factors in the protein environment determine H-bond distances. This classification further enables us to compare buried and solvent-exposed H-bonds and to elucidate how the dielectric properties of the protein environment influence H-bond distances. Finally, based on the insights obtained, we analyze H-bonds in microbial rhodopsins using a quantum mechanical/molecular mechanical (QM/MM) approach.
Methods
Quantum chemical calculations of small-compound H-bonds
H-bonds involving water (pKa = 15.74), methanol (15.519), phenol (9.9919), and protonated acetic acid (4.7619) as donors, and water (−1.74), methanol (−220), phenol (−620), deprotonated acetic acid (4.7619), protonated acetic acid (−620), and N-methylacetamide (−120) as acceptors, were analyzed. H-bond donors and acceptors were solvated with explicit water molecules, and additional solvent effects were modeled using the polarizable continuum model (PCM) (Fig. S1, ESI†). This approach, which solvates H-bonded compounds using several explicit water molecules and an implicit solvent model, has been shown to reproduce the experimentally observed vibrational21 and excitation22 energies of H-bonded compounds in aqueous solutions. Geometries were optimized using the second-order Møller–Plesset perturbation theory (MP2) method. H-bond interaction energies were calculated using the two-body fragment molecular orbital (FMO) method23 combined with MP2,24 and decomposed into electrostatic, exchange, charge-transfer, and dispersion terms using pair interaction energy decomposition analysis (PIEDA).25 Although the FMO method is commonly applied to large molecular systems, it was specifically used here due to its capability to calculate and decompose H-bond interaction energies in the presence of explicit solvent water molecules. To ensure meaningful fragmentation, each molecule in the system was treated as a separate fragment. Dimer corrections were included in the electrostatic potential calculations in PCM (i.e., PCM[2]).26 The electron redistribution amount was obtained from the Mulliken charge distribution in the dimer. The 6-31G* basis set was used. All calculations were performed using the GAMESS program.27Natural bond orbital (NBO)28,29 energies were calculated for (i) water, methanol, phenol, and protonated acetic acid molecules donating an H-bond to a water molecule, and (ii) water, methanol, phenol, deprotonated acetic acid, protonated acetic acid, and N-methylacetamide molecules accepting an H-bond from a water molecule (Fig. S2, ESI†). NBO energies were obtained following geometry optimization using the density functional theory (DFT) method. To include long-range corrections in the DFT functional,30,31 the CAM-B3LYP functional32 was employed with the 6-31G**+ basis set. The CAM-B3LYP-related parameters α, β, and μ were set to the standard values of 0.19, 0.46, and 0.33, respectively.32 All calculations were performed using the NBO 5.0 program33 implemented in Jaguar.34
Distributions of H-bond distances in high-resolution protein structures
A dataset of 906 protein structures was obtained from ref. 9. This dataset comprises X-ray crystal structures of proteins with resolutions of ≤1.2 Å, sequence identities of ≤90%, and R-factors of ≤0.20.9 PDB IDs of the structures included in the dataset are listed in Supporting Data 1 (ESI†). For structures with several models, the first model was analyzed. Distances for all O⋯O, N⋯O, and N⋯N atom pairs satisfying the following criteria were obtained, excluding pairs within the same residue: (i) O⋯O distance <3.0 Å, N⋯O or N⋯N distance <3.2 Å; (ii) B-factor values for both atoms <40 Å2; and (iii) occupancies for both atoms equal to 1.00. For sp2-hybridized N atoms in the backbone and in the side-chains of Arg, His, and Trp, a dihedral angle criterion was applied to exclude N⋯O and N⋯N atom pairs that are closer than 3.2 Å but do not form H-bonds (Fig. S3, ESI†). H-bonds involving Asn and Gln side-chains were excluded due to difficulties in unambiguously assigning the O and N atoms in these side-chains, even in high-resolution structures. The analysis was conducted using the Biopython package35,36 in Python.H-bonds with relative solvent accessibilities of <16% and ≥16% were classified as buried and exposed, respectively.37 Solvent accessibilities were calculated in the absence of crystal water molecules, using the DSSP program.38,39 Therefore, the absence of water molecules that are difficult to capture by crystallography does not affect this classification. Asymmetric units, the smallest portions of crystal structures, are deposited in the PDB. The entire crystal can be reconstructed by applying symmetry operations to the asymmetric unit. In the absence of neighboring asymmetric units, ∼10% of H-bonds that are buried in the entire crystal are calculated as exposed (Fig. S4 and Table S1, ESI†). Therefore, solvent accessibilities were calculated in the presence of neighboring asymmetric units. Residues of neighboring asymmetric units within 7 Å of the focusing asymmetric unit were included in the calculation of solvent accessibility. The 7 Å threshold was set to be longer than the sum of the longest atomic diameter (3.74 Å for the Cα atom) and the water probe diameter (2.80 Å) used in the DSSP program.38
QM/MM calculations of microbial rhodopsins
Atomic coordinates were obtained from the X-ray crystal structures of (i) ground-state bacteriorhodopsin from Halobacterium salinarum (BR) (PDB ID: 5ZIM40), (ii) N′-state V49A mutant BR (1P8U41), (iii) halorhodopsin from Natromononas pharaonis (pHR) (3A7K42), (iv) sodium-pumping rhodopsin KR2 from Krokinobacter eikastus (6YC343), and (v) sodium-pumping rhodopsin ErNaR from Erythrobacter sp. HL-111 (8QLF44). Hydrogen atom positions were optimized with the heavy atom positions fixed, using the CHARMM program.45 Atomic charges and force field parameters were obtained from the CHARMM22 parameter set.46The protonation pattern was determined using the electrostatic continuum model by solving the linear Poisson–Boltzmann equation with the MEAD program.47 The experimentally measured pKa values employed as references were 12.0 for Arg, 4.0 for Asp, 9.5 for Cys, 4.4 for Glu, 10.4 for Lys, 9.6 for Tyr,48 and 7.0 and 6.6 for the Nε and Nδ atoms of His, respectively.49–51 Dielectric constants were set to 4 for the protein interior and 80 for water. All calculations were performed at 300 K, pH 7.0, and with an ionic strength of 100 mM. The linear Poisson–Boltzmann equation was solved using a three-step grid-focusing procedure at resolutions of 2.5, 1.0, and 0.3 Å. Protonation patterns were sampled using the Monte Carlo method with the Karlsberg program.52
Geometries were optimized using a QM/MM approach. The restricted DFT method was employed with the B3LYP functional and the LACVP**+ basis set, using the QSite program.53,54 The QM region was defined as follows: (i) ground-state BR: retinal, side-chains of Lys216, Tyr57, Arg82, Asp85, Trp86, Thr89, Tyr185, and Asp212, and H2O-402, 401, and 406. (ii) N′-state BR: side-chains of Tyr57, Asp85, and Asp212, and H2O-401, 406, and 407. (iii) pHR: retinal, side-chains of Lys256, Ser78, Ser81, Tyr82, Arg123, Thr126, Trp127, Ser130, Tyr225, Asp252, and Tyr257, H2O-502, 503, and 504, and Cl−-401. (iv) KR2: retinal, side-chains of Lys255, Ser70, Arg109, Asn112, Trp113, Asp116, Tyr218, Asp251, and Ser254, and H2O-434, 437, 501, and 512. (v) ErNaR: retinal, side-chains of Lys246, Ser25, Ser60, Glu64, Arg98, Trp102, Asp105, Tyr215, Thr239, and Asp242, and H2O-503, 504, 532, and 542. All atomic coordinates were relaxed in the QM region. In the MM region, hydrogen atom positions were optimized using the OPLS2005 force field,55 while heavy atom positions were fixed. The protonation pattern of titratable residues in the MM region was implemented in the atomic partial charges. Vibrational frequencies were calculated at the same level of theory as the geometry optimizations. The calculated frequencies were scaled using a standard factor of 0.9614 for the B3LYP functional.56
Results and discussion
In this study, we classified the donors and acceptors of Odonor–H⋯Oacceptor H-bonds in proteins (excluding ligand molecules) into the following five groups (Table 1): (i) water molecules; (ii) Ser and Thr side-chains, which have hydroxyl OH groups (denoted as C–OH in this study); (iii) Tyr side-chains (denoted as PhOH); (iv) Asp and Glu side-chains, which have carboxyl COOH groups (denoted as COOH); and (v) backbone and Asn/Gln side-chains, which have amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups (denoted as C
O groups (denoted as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O). Relevant H-bonds involving (i) water molecules, (ii) alcohols (denoted as C–OH), (iii) phenols (denoted as PhOH), (iv) carboxylic acids (denoted as COOH), and (v) amide C
O). Relevant H-bonds involving (i) water molecules, (ii) alcohols (denoted as C–OH), (iii) phenols (denoted as PhOH), (iv) carboxylic acids (denoted as COOH), and (v) amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups (denoted as C
O groups (denoted as C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) are abundant in the crystal structures of small compounds (Table 1).6,57,58
O) are abundant in the crystal structures of small compounds (Table 1).6,57,58
| Small compounds | In proteins | pKa as a donor (acid/conjugated base) | pKa as an acceptor (base/conjugated acid) | |
|---|---|---|---|---|
| a pKa value of methanol.19 b Ref. 48. c Ref. 20. | ||||
| (i) | Water | Water | 16 (H2O/OH−) | −2 (H2O/H3O+) |
| (ii) | Alcohol | Ser, Thr | 16 (C–OH/C–O−)a | −2 (C–OH/C–OH2+)c |
| (iii) | Phenol | Tyr | 10 (PhOH/PhO−)b | −6 (PhOH/PhOH2+)c |
| (iv) | Carboxylic acid | Asp, Glu | 4 (COOH/COO−)b | 4 (COO−/COOH)b, −6 (COOH/COOH2+)c |
| (v) | Amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
Backbone, Asn, Gln | — | −1 (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O/C O/C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) OH+)c OH+)c |
Even when the groups forming an H-bond are the same, several H-bond types can exist depending on (i) which group serves as the donor and (ii) the protonation states of the donor and acceptor groups. For instance, the donor/acceptor of an H-bond between water and a carboxyl group can be COOH/H2O, H2O/COO−, or H2O/COOH. Different H-bond types for the same pair can be distinguished for crystal structures of small compounds obtained from the Cambridge Structural Database (CSD).59 This is not the case for H-bonds in proteins, where the hydrogen atom positions are mostly unidentified. To clarify why H-bond distances are primarily determined by ΔpKa, we first investigate small-compound H-bonds relevant to those in proteins.
Basis for the correlation between H-bond distances and ΔpKa
H-bonds with H2O, C–OH, PhOH, and COOH groups as donors are investigated. Similarly, H-bonds with H2O, C–OH, PhOH, COO−, COOH, and C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups as acceptors are investigated (Table 1). To confirm the correlation between O⋯O distances and ΔpKa, the average O⋯O distance was compared with ΔpKa for 23 out of the 24 possible H-bond types involving these donor and acceptor groups (Table 2 and Fig. 1). Average O⋯O distances were obtained from small-compound H-bonds in the CSD, with each group containing from 18 to 4931 H-bonds.6,57,58 The average O⋯O distance is highly correlated with ΔpKa for each H-bond type (Fig. 1, R2 = 0.89), confirming that O⋯O distances are primarily determined by ΔpKa.
O groups as acceptors are investigated (Table 1). To confirm the correlation between O⋯O distances and ΔpKa, the average O⋯O distance was compared with ΔpKa for 23 out of the 24 possible H-bond types involving these donor and acceptor groups (Table 2 and Fig. 1). Average O⋯O distances were obtained from small-compound H-bonds in the CSD, with each group containing from 18 to 4931 H-bonds.6,57,58 The average O⋯O distance is highly correlated with ΔpKa for each H-bond type (Fig. 1, R2 = 0.89), confirming that O⋯O distances are primarily determined by ΔpKa.
| H-bond pair | Donor | Acceptor | ΔpKa (in water) | (Å) |
|---|---|---|---|---|
| a Average O⋯O distances. Values for [water⋯water], [water⋯alcohol], and [water⋯phenol] pairs were taken from ref. 57. Values for the [water⋯carboxylic acid] pair were taken from ref. 58. Other values were taken from ref. 6. | ||||
| Water⋯Water | H2O | H2O | 18 | 2.83 |
| Water⋯Alcohol | H2O | C–OH | 18 | 2.83 |
| C–OH | H2O | 18 | 2.75 | |
| Water⋯Phenol | PhOH | H2O | 12 | 2.68 |
| H2O | PhOH | 22 | 2.89 | |
| Water⋯Carboxylic acid | COOH | H2O | 6 | 2.59 |
| H2O | COO− | 12 | 2.77 | |
| H2O | COOH | 22 | 2.82 | |
| Alcohol⋯Alcohol | C–OH | C–OH | 18 | 2.78 |
| Alcohol⋯Phenol | PhOH | C–OH | 12 | 2.73 |
| C–OH | PhOH | 22 | 2.82 | |
| Alcohol⋯Carboxylic acid | COOH | C–OH | 6 | 2.65 |
| C–OH | COO− | 12 | 2.74 | |
| C–OH | COOH | 22 | 2.81 | |
Alcohol⋯Amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
C–OH | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
17 | 2.77 |
| Phenol⋯Phenol | PhOH | PhOH | 16 | 2.80 |
| Phenol⋯Carboxylic acid | PhOH | COO− | 6 | 2.64 |
| COOH | PhOH | 10 | 2.67 | |
| PhOH | COOH | 16 | 2.74 | |
Phenol⋯Amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
PhOH | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
11 | 2.70 |
| Carboxylic acid⋯Carboxylic acid | COOH | COO− | 0 | 2.54 |
| COOH | COOH | 10 | 2.65 | |
Carboxylic acid⋯Amide C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
COOH | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
5 | 2.60 |
 | ||
| Fig. 1 Correlation between average O⋯O distances6,57,58 and ΔpKa for each H-bond type in small-compound crystal structures from the CSD (R2 = 0.89). Orange crosses, blue squares, and black triangles indicate H-bonds involving COOH, PhOH, and H2O/C–OH groups as donors, respectively. H-bonds involving the COO− group as acceptors are surrounded by open circles. | ||
To clarify the basis for the correlation between O⋯O distances and ΔpKa, we performed quantum chemical calculations of small-compound H-bonds. The O⋯O distance is correlated with ΔpKa for quantum-chemically optimized H-bonds in water solvent (Fig. S5a, R2 = 0.73, ESI†), which aligns with the correlation between the average O⋯O distance from the CSD and ΔpKa (Fig. 1).
A lower ΔpKa leads to a shorter O⋯O distance because as ΔpKa decreases, (i) the Odonor–H distance increases, and (ii) the H⋯Oacceptor distance decreases more significantly than the increase in the Odonor–H distance (Fig. 2a). Thus, the H⋯Oacceptor distance serves as the primary limiting factor for the O⋯O distance. For example, the O⋯O distances for the H-bond between water and protonated acetic acid (ΔpKa = 22, Fig. 2b), and between protonated acetic acid and deprotonated acetic acid (ΔpKa = 0, Fig. 2c), are 2.91 and 2.59 Å, respectively. Odonor–H distances are 0.98 and 1.04 Å, with the latter being 0.06 Å longer than the former. In contrast, H⋯Oacceptor distances are 1.97 and 1.55 Å, with the latter being 0.42 Å shorter than the former.
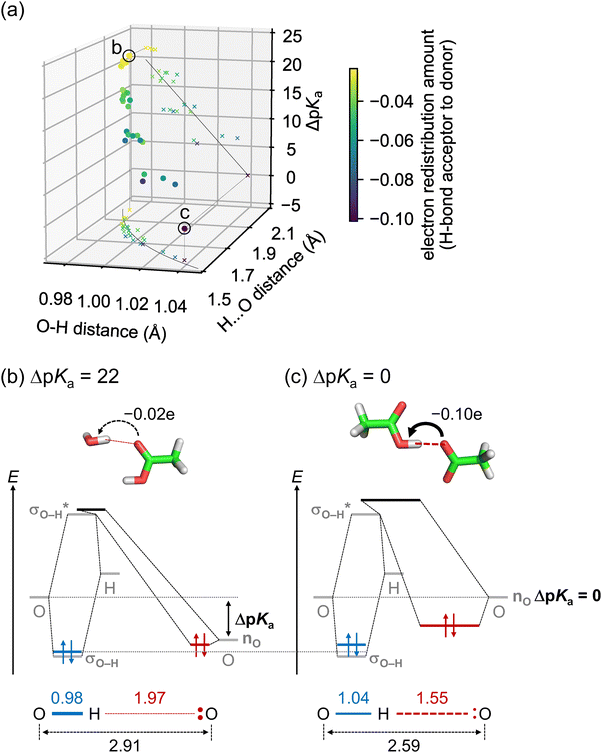 | ||
Fig. 2 Relationships among H-bond geometries and ΔpKa. (a) Odonor–H distance (rO–H), H⋯Oacceptor distance (rH⋯O), and ΔpKa for quantum-chemically optimized H-bonds in water solvent (circles). Relationships between rO–H and rH⋯O, and between rO–H and ΔpKa, are shown as crosses on the rO–H–rH⋯O plane and the rO–H–ΔpKa plane, respectively. Circles and crosses are color-scaled according to the electron redistribution amount from the H-bond acceptor to donor, calculated from the change in Mulliken charges due to H-bond formation. The curve on the rO–H–rH⋯O plane indicates the correlation derived from the bond order model.60–64 The parameters r0OH and b in the model were set to 0.95 Å and 0.38 Å, respectively, to best fit the rO–Hversus rH⋯O relationship (see the discussion in ESI†). The line on the rO–H–ΔpKa plane indicates the linear fit line (R2 = 0.76). (b) and (c) Energy diagrams of molecular orbitals for the H-bond: (b) between water and protonated acetic acid (ΔpKa = 22), and (c) between protonated acetic acid and deprotonated acetic acid (ΔpKa = 0). Gray bars indicate energies of the donor O atom and H atom orbitals forming the Odonor–H bond, as well as of the Odonor–H bonding (σO–H), Odonor–H antibonding ( ), and Oacceptor lone pair (nO) NBOs. Blue, black, and red bars indicate localized molecular orbitals formed by the three NBOs, which roughly correspond to the Odonor–H bonding orbital, the Odonor–H antibonding orbital, and the lone pair orbital of the acceptor O atom, respectively. Values in the lower panels indicate distances in Å. ), and Oacceptor lone pair (nO) NBOs. Blue, black, and red bars indicate localized molecular orbitals formed by the three NBOs, which roughly correspond to the Odonor–H bonding orbital, the Odonor–H antibonding orbital, and the lone pair orbital of the acceptor O atom, respectively. Values in the lower panels indicate distances in Å. | ||
Since pKa is an indicator of proton affinity (Brønsted acidity), a lower ΔpKa indicates a closer proton affinity between the H-bond donor and acceptor. In low ΔpKa H-bonds, the proton is strongly attracted to the H-bond acceptor, resulting in an increased Odonor–H distance and a significantly decreased H⋯Oacceptor distance.
Relationships among H-bond geometries and ΔpKa can also be explained in terms of electron redistribution induced by H-bond formation. A lower ΔpKa leads to pronounced electron redistribution from the H-bond acceptor to the donor (Fig. 2a). For example, electron redistribution amounts for the H-bond between water and protonated acetic acid (ΔpKa = 22, Fig. 2b), and between protonated acetic acid and deprotonated acetic acid (ΔpKa = 0, Fig. 2c), are 0.02e and 0.10e, respectively. Analysis of NBO28 showed that this electron redistribution arises from the hybridization between the lone pair orbital of the H-bond acceptor (nO) and the Odonor–H antibonding orbital of the H-bond donor 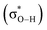 .29
.29
ΔpKa is related to the energy difference between (i) the orbital of the donor O atom forming the Odonor–H bond, and (ii) the orbital of the acceptor O atom accepting the Odonor–H bond (i.e., the nO orbital) (Fig. 2b and c). When ΔpKa is high, the orbital energy of the donor O atom is much higher than that of the acceptor O atom (Fig. 2b), resulting in the H atom forming a bond with the donor O atom. As ΔpKa decreases, the energy difference between these orbitals decreases. In the extreme case where ΔpKa ∼ 0, the energies of these orbitals are nearly equal (Fig. 2c). In this case, the H atom can bind to either the donor or acceptor O atom with almost no energy difference (a low-barrier H-bond, LBHB65,66). In LBHBs, the O⋯O distances are as short as ∼2.5 Å.67
Therefore, a lower ΔpKa leads to a decreased energy difference between the nO orbital of the H-bond acceptor and the 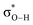 orbital of the H-bond donor, which enhances their hybridization (Fig. 2b and c). Indeed, pKa values are correlated with the nO and
orbital of the H-bond donor, which enhances their hybridization (Fig. 2b and c). Indeed, pKa values are correlated with the nO and  orbital energies (Lewis acidity, Fig. S2, ESI†). This enhanced hybridization increases the
orbital energies (Lewis acidity, Fig. S2, ESI†). This enhanced hybridization increases the  electron redistribution, leading to an increased
electron redistribution, leading to an increased  orbital occupancy, a decreased Odonor–H bond order, and an increased Odonor–H distance. These correspond to the destabilization of the Odonor–H bonding orbital, resulting in a weaker Odonor–H bond (Fig. 2b and c). Furthermore, the enhanced hybridization between the nO and
orbital occupancy, a decreased Odonor–H bond order, and an increased Odonor–H distance. These correspond to the destabilization of the Odonor–H bonding orbital, resulting in a weaker Odonor–H bond (Fig. 2b and c). Furthermore, the enhanced hybridization between the nO and  orbitals, corresponding to the increased covalent character of the H⋯Oacceptor “bond”,64 decreases the H⋯Oacceptor distance more significantly than the Odonor–H distance increases. Thus, a lower ΔpKa results in a shorter O⋯O distance.
orbitals, corresponding to the increased covalent character of the H⋯Oacceptor “bond”,64 decreases the H⋯Oacceptor distance more significantly than the Odonor–H distance increases. Thus, a lower ΔpKa results in a shorter O⋯O distance.
Notably, the correlation between the O⋯O distance and ΔpKa is mostly unaffected by the total charge of the H-bond (0 or −1) (Fig. 1 and Fig. S5a, ESI†). Asp and Glu side-chains are frequently involved in short H-bonds (O⋯O distances <2.7 Å).4,8,9 This is due to their tendency to form low ΔpKa H-bonds not only when (i) the deprotonated COO− group serves as an acceptor, but also when (ii) the protonated COOH group serves as a donor (Fig. 1). The shorter O⋯O distances are not caused by the stronger Odonor–H⋯−Oacceptor electrostatic interactions resulting from the negative charge of the deprotonated COO− group. Indeed, the average O⋯O distance of the charge-neutral [COOH⋯OH2] H-bonds with ΔpKa of ∼6 (2.59 Å) is shorter than that of the negatively charged [HOH⋯−OOC] H-bonds with ΔpKa of ∼12 (2.77 Å) for small compound H-bonds from the CSD (Table 2).58 Although Asp/Glu side-chains are often assumed to be deprotonated,4,8 the possibility of Asp/Glu side-chains serving as H-bond donors in their protonated forms should be considered, especially for short H-bonds.
Distributions of H-bond distances involving the same donor/acceptor groups
Next, we analyze H-bonds in proteins to elucidate how the protein environment affects distances. O⋯O distances for 313![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680 O atom pairs with distances <3.0 Å were obtained from 906 X-ray crystal structures. These structures were selected based on resolutions (≤1.2 Å), sequence identities (≤90%), and R-factors (≤0.20).9 Among the 15 possible pairs of the five groups (Table 1), O⋯O distance distributions for 14 pairs were analyzed, excluding the [backbone⋯backbone] pair. Average O⋯O distances for each pair were determined by fitting the distribution histograms (Fig. S6, ESI†) using a Gaussian function (Table 3).
680 O atom pairs with distances <3.0 Å were obtained from 906 X-ray crystal structures. These structures were selected based on resolutions (≤1.2 Å), sequence identities (≤90%), and R-factors (≤0.20).9 Among the 15 possible pairs of the five groups (Table 1), O⋯O distance distributions for 14 pairs were analyzed, excluding the [backbone⋯backbone] pair. Average O⋯O distances for each pair were determined by fitting the distribution histograms (Fig. S6, ESI†) using a Gaussian function (Table 3).
| H-Bond pair | Donor | Acceptor | ΔpKa (in water) | (Å) | N |
|---|---|---|---|---|---|
| a Average O⋯O distance and standard deviation, obtained by fitting the distribution histogram (Fig. S6, ESI) using a Gaussian function. b Total number of O atom pairs. c Obtained from distributions of O⋯O distances shorter than 2.75 Å, as many of the O atom pairs with distances longer than 2.75 Å are unlikely forming H-bonds (Fig. S6, ESI). | |||||
| Water⋯Water | H2O | H2O | 18 | 2.77 ± 0.12 | 149![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 940 940 |
| Water⋯Ser/Thr | H2O | C–OH | 18 | 2.76 ± 0.09 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 411 411 |
| C–OH | H2O | 18 | |||
| Water⋯Tyr | PhOH | H2O | 12 | 2.72 ± 0.11 | 5924 |
| H2O | PhOH | 22 | |||
| Water⋯Asp/Glu | COOH | H2O | 6 | 2.73 ± 0.10 | 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 151 151 |
| H2O | COO− | 12 | |||
| H2O | COOH | 22 | |||
| Water⋯Backbone | H2O | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
17 | 2.79 ± 0.09 | 92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 415 |
| Ser/Thr⋯Ser/Thr | C–OH | C–OH | 18 | 2.75 ± 0.08 | 635 |
| Ser/Thr⋯Tyr | PhOH | C–OH | 12 | 2.74 ± 0.07 | 329 |
| C–OH | PhOH | 22 | |||
| Ser/Thr⋯Asp/Glu | COOH | C–OH | 6 | 2.68 ± 0.07 | 2675 |
| C–OH | COO− | 12 | |||
| C–OH | COOH | 22 | |||
| Ser/Thr⋯Backbone | C–OH | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
17 | 2.75 ± 0.09 | 6220 |
| Tyr⋯Tyr | PhOH | PhOH | 16 | 2.73 ± 0.07 | 72 |
| Tyr⋯Asp/Glu | PhOH | COO− | 6 | 2.63 ± 0.06 | 1359 |
| COOH | PhOH | 10 | |||
| PhOH | COOH | 16 | |||
| Tyr⋯Backbone | PhOH | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
11 | 2.69 ± 0.06 | 1313 |
| Asp/Glu⋯Asp/Glu | COOH | COO− | 0 | 2.52 ± 0.05c | 254 |
| COOH | COOH | 10 | |||
| Asp/Glu⋯Backbone | COOH | C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O O |
5 | 2.64 ± 0.05c | 173 |
The distributions of O⋯O distances were compared with the ΔpKa values in water for each H-bond pair (Fig. 3). A lower ΔpKa leads to a shorter O⋯O distance distribution. The O⋯O distance distributions exhibit certain widths, with standard deviations ranging from 0.05 to 0.12 Å (Table 3).
Several H-bond types with different ΔpKa values are possible for the [Asp/Glu⋯Asp/Glu], [Tyr⋯Asp/Glu], [Ser/Thr⋯Asp/Glu], [water⋯Asp/Glu], [Ser/Thr⋯Tyr], and [water⋯Tyr] pairs (Fig. 3). Among these six pairs, the predominant H-bond types for the [Asp/Glu⋯Asp/Glu] and [water⋯Asp/Glu] pairs can be deduced from their O⋯O distance distributions. For the [Asp/Glu⋯Asp/Glu] pair, the [COOH⋯−OOC] type with ΔpKa ∼ 0 is likely predominant. For the [water⋯Asp/Glu] pair, the [HOH⋯−OOC] type with ΔpKa ∼ 12 is likely predominant (see the discussion in ESI†).
Average O⋯O distances in proteins were compared with ΔpKa values in water. We compared the values of H-bond pairs whose ΔpKa values of the predominant H-bond types were inferred (indicated by the dotted squares in Fig. 3). The average O⋯O distance  is highly correlated with ΔpKa (Fig. 4a, R2 = 0.91), which is best described by the following equation:
is highly correlated with ΔpKa (Fig. 4a, R2 = 0.91), which is best described by the following equation:
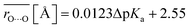 | (1) |
 | ||
| Fig. 4 Average O⋯O distances for each H-bond type in proteins. (a) Correlation between average O⋯O distances in proteins and ΔpKa in water (R2 = 0.91). Solid and open circles indicate H-bonds with total charges of 0 and −1, respectively. (b) Average O⋯O distances for buried and exposed H-bonds (RMSD = 0.03 Å). The black diagonal line indicates perfect correspondence (i.e., identity line). (a) and (b) Labels indicate donor/acceptor groups. (c) Representative structures of buried (PDB ID: 4KQP68) and exposed (PDB ID: 3CLM, unpublished) H-bonds (dotted lines). | ||
This high correlation indicates that O⋯O distances with the same donor and acceptor groups are distributed around a value primarily determined by ΔpKa in water. This ΔpKa value does not account for the influence of the protein environment. Therefore, deviations in O⋯O distances from their average values, corresponding to the width of the O⋯O distance distribution (Fig. 3), reflect the influence of the protein environment on the characteristics of the H-bond.
H-Bond distances for buried and solvent-exposed H-bonds
For small compound H-bonds, the distances are largely unaffected by differences in solvent dielectric constants.16,17 The environment of H-bonds buried in the protein interior is low-dielectric, whereas that of H-bonds exposed to bulk water is high-dielectric.69,70 To investigate the influence of the dielectric properties of the protein environment on O⋯O distances, we compared the average O⋯O distances of buried and exposed H-bonds. H-bonds were classified as buried or exposed according to their relative solvent accessibility values.37The average O⋯O distances of buried and exposed H-bonds are nearly identical for H-bond pairs with inferred predominant types (Fig. 4b and c, root mean square distance [RMSD] = 0.03 Å). This result indicates that O⋯O distances are unaffected by whether the H-bond is buried in the protein interior or exposed to bulk water. This suggests that differences in the dielectric properties of the protein environment do not influence O⋯O distances, consistent with the previous reports for small compounds.16,17
Water solvent weakens the electrostatic interaction between the Odonor–H and Oacceptor groups due to electrostatic shielding. This electrostatic interaction is the major stabilizing factor of an H-bond.71 On the other hand, the strength of the Odonor–H⋯Oacceptor electrostatic interaction plays a minor role in determining the O⋯O distance. When comparing H-bonds with similar O⋯O distances, the electrostatic interaction energy is higher for H-bonds with total charges of −1 than for charge-neutral H-bonds (Fig. S5b, ESI†). This indicates that a strong Odonor–H⋯Oacceptor electrostatic interaction does not necessarily result in a shorter H-bond. This is because the stabilization provided by the electrostatic interaction is largely compensated by the destabilization due to exchange repulsion at short O⋯O distances (Fig. S5c, ESI†).62,64 In contrast, a lower ΔpKa leads to an enhanced electron redistribution from the H-bond acceptor to the donor, which decreases the O⋯O distance (Fig. 2). Therefore, O⋯O distances are predominantly determined by the ΔpKa of the H-bond without being affected by whether the H-bond is buried in the protein interior or exposed to bulk water.
N⋯O and N⋯N distances
H-bonds between N and O atoms (N⋯O) and between N atoms (N⋯N) are also crucial in the H-bond network of proteins. From the same dataset of 906 protein structures, distances for 144![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 464 N⋯O atom pairs and 247 N⋯N atom pairs with distances <3.2 Å were obtained (see the discussion in ESI,† for details).
464 N⋯O atom pairs and 247 N⋯N atom pairs with distances <3.2 Å were obtained (see the discussion in ESI,† for details).
The average N⋯O distance in proteins is highly correlated with ΔpKa in water for each H-bond type (Fig. 5a, R2 = 0.71). Similarly, the average N⋯N distance in proteins is highly correlated with ΔpKa in water (Fig. 5b, R2 = 0.93). These are consistent with the high correlations between N⋯O or N⋯N distances and ΔpKa observed for small-compound H-bonds.17 The strength of the electrostatic interaction between the donor and acceptor groups differs among H-bonds formed between (i) charge-neutral donor and acceptor (e.g., backbone-N–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C-backbone), (ii) a positively charged donor and a negatively charged acceptor (salt-bridges, e.g., Lys-NH3+⋯−OOC-Asp), (iii) a positively charged donor and a charge-neutral acceptor (e.g., Lys-NH3+⋯OH2), and (iv) a charge-neutral donor and a negatively charged acceptor (backbone-N–H⋯−OOC-Asp). The correlations between average N⋯O or N⋯N distances and ΔpKa are largely unaffected by these differences (Fig. 5a and b), indicating that the ΔpKa of the H-bond, rather than the electrostatic interaction strength between the donor and acceptor groups, is the primary determinant of N⋯O and N⋯N distances, as well as O⋯O distances. Indeed, average N⋯O and N⋯N distances for buried H-bonds (with low electrostatic shielding) and solvent-exposed H-bonds (with high electrostatic shielding) are nearly identical (Fig. 5c and d).
C-backbone), (ii) a positively charged donor and a negatively charged acceptor (salt-bridges, e.g., Lys-NH3+⋯−OOC-Asp), (iii) a positively charged donor and a charge-neutral acceptor (e.g., Lys-NH3+⋯OH2), and (iv) a charge-neutral donor and a negatively charged acceptor (backbone-N–H⋯−OOC-Asp). The correlations between average N⋯O or N⋯N distances and ΔpKa are largely unaffected by these differences (Fig. 5a and b), indicating that the ΔpKa of the H-bond, rather than the electrostatic interaction strength between the donor and acceptor groups, is the primary determinant of N⋯O and N⋯N distances, as well as O⋯O distances. Indeed, average N⋯O and N⋯N distances for buried H-bonds (with low electrostatic shielding) and solvent-exposed H-bonds (with high electrostatic shielding) are nearly identical (Fig. 5c and d).
 | ||
| Fig. 5 Average N⋯O and N⋯N distances for each H-bond type in proteins. (a) Correlation between average N⋯O distances in proteins and ΔpKa in water (R2 = 0.71). (b) Correlation between average N⋯N distances in proteins and ΔpKa in water (R2 = 0.93). (a) and (b) Black closed circles, orange crosses, blue plus signs, and black open circles indicate H-bonds formed between (i) charge-neutral donor and acceptor, (ii) positively charged donor and negatively charged acceptor (salt-bridges), (iii) positively charged donor and charge-neutral acceptor, and (iv) charge-neutral donor and negatively charged acceptor, respectively. For H-bond pairs involving His side-chains, H-bond types with the lowest ΔpKa values are assumed (see the discussion in ESI†). (c) Average N⋯O distances for buried and exposed H-bonds (RMSD = 0.02 Å). (d) Average N⋯N distances for buried and exposed H-bonds (RMSD = 0.06 Å). (c) and (d) The black diagonal lines indicate perfect correspondence (i.e., identity line). Data points for Trp⋯Ser/Thr, Trp⋯Tyr, Arg⋯His, Lys⋯His, and Trp⋯His pairs were excluded due to an insufficient number of exposed H-bonds (<10). | ||
Electrostatic and structural effects
H-bond distances with the same donor and acceptor groups are distributed around a value primarily determined by ΔpKa in water, regardless of whether the H-bond is buried in the protein interior or exposed to bulk water (Fig. 4 and 5). Deviations in H-bond distances from their average values reflect the influence of the protein environment. To investigate the influence of the protein environment in detail, we analyzed H-bonds between water and deprotonated Asp/Glu side-chains using a QM/MM approach. This [HOH⋯−OOC] H-bond, with medium ΔpKa (∼12) and average O⋯O distance (2.73 Å) values, is abundant in proteins (Table 3). Because [HOH⋯−OOC] H-bonds are frequently found near the active site (retinal Schiff base) of microbial rhodopsins, we analyzed 12 [HOH⋯−OOC] H-bonds in H+-pump (ground-state40 and N′-state41 BR), Cl−-pump (pHR42), and Na+-pump (KR243 and ErNaR44) rhodopsins.Odonor–H stretching vibrational frequencies of H-bonds in proteins are predominantly determined by the ΔpKa of the H-bond.72 Here, ΔpKa values were estimated from the calculated Odonor–D stretching vibrational frequencies (νO–D) using the following equation:72
| ΔpKa = 0.019 νO–D [cm−1] − 32 | (2) |
Note that this ΔpKa value, obtained from the Odonor–D stretching vibrational frequency, represents the ΔpKa value of the H-bond in the protein environment, not the ΔpKa value of ∼12 in water. O⋯O distances were obtained from the QM/MM-optimized structures. O⋯O distances and ΔpKa values were compared for the 12 [HOH⋯−OOC] H-bonds (Fig. 6a and Table S2, ESI†).
 | ||
Fig. 6 O⋯O distances for [HOH⋯−OOC] H-bonds in microbial rhodopsins. (a) O⋯O distances and ΔpKa for 12 [HOH⋯−OOC] H-bonds. The open square, the cross, and circles indicate O⋯O distances and ΔpKa values of the [H2O-406⋯Asp212] H-bond in the N′-state BR, [H2O-402⋯Asp212] H-bond in the ground-state BR, and the other 10 H-bonds, respectively. The solid line indicates the correlation between  and ΔpKa (eqn (1)). The vertical dotted line indicates the average O⋯O distance for the [HOH⋯−OOC] H-bonds in proteins (Table 3). The solid arrow indicates the shift in O⋯O distance due to the ΔpKa shift. The dotted arrows indicate the shift in O⋯O distance due to structural constraints in proteins. (b) [H2O (w)-406⋯Asp212] H-bond in the N′-state BR. (c) [H2O (w)-402⋯Asp212] H-bond in the ground-state BR. (b) and (c) Dotted lines indicate H-bonds. Arrows indicate deviations in O⋯O distances from the average value in proteins. and ΔpKa (eqn (1)). The vertical dotted line indicates the average O⋯O distance for the [HOH⋯−OOC] H-bonds in proteins (Table 3). The solid arrow indicates the shift in O⋯O distance due to the ΔpKa shift. The dotted arrows indicate the shift in O⋯O distance due to structural constraints in proteins. (b) [H2O (w)-406⋯Asp212] H-bond in the N′-state BR. (c) [H2O (w)-402⋯Asp212] H-bond in the ground-state BR. (b) and (c) Dotted lines indicate H-bonds. Arrows indicate deviations in O⋯O distances from the average value in proteins. | ||
The O⋯O distance is correlated with ΔpKa for 12 H-bonds (Fig. 6a, R2 = 0.79). This relatively high correlation suggests that deviations in O⋯O distances from their average values primarily arise from ΔpKa shifts induced by the protein electrostatic environment.
Although Odonor–H stretching vibrational frequencies are mostly determined by the ΔpKa of the H-bond,72 O⋯O distances are influenced more significantly by factors other than the ΔpKa of the H-bond. The correlation between 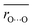 and ΔpKa for each H-bond type in proteins (eqn (1), the solid line in Fig. 6a) likely represents the relationship between the O⋯O distance and ΔpKa. While O⋯O distances and ΔpKa values for many H-bonds align with this
and ΔpKa for each H-bond type in proteins (eqn (1), the solid line in Fig. 6a) likely represents the relationship between the O⋯O distance and ΔpKa. While O⋯O distances and ΔpKa values for many H-bonds align with this 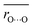 versus ΔpKa relationship, some H-bonds significantly deviate from this trend (Fig. 6a). These deviations arise from factors other than the ΔpKa of the H-bond. Among these, we focus on the [H2O-406⋯Asp212] H-bond in the N′-state BR with a short O⋯O distance of 2.57 Å (Fig. 6b), and the [H2O-402⋯Asp212] H-bond in the ground-state BR with a long O⋯O distance of 2.92 Å (Fig. 6c).
versus ΔpKa relationship, some H-bonds significantly deviate from this trend (Fig. 6a). These deviations arise from factors other than the ΔpKa of the H-bond. Among these, we focus on the [H2O-406⋯Asp212] H-bond in the N′-state BR with a short O⋯O distance of 2.57 Å (Fig. 6b), and the [H2O-402⋯Asp212] H-bond in the ground-state BR with a long O⋯O distance of 2.92 Å (Fig. 6c).
The O⋯O distance of the [H2O-406⋯Asp212] H-bond in the N′-state BR is 2.57 Å, which is 0.16 Å shorter than the average O⋯O distance for [HOH⋯−OOC] H-bonds in proteins (2.73 Å) (Fig. 6b). The calculated ΔpKa value of this H-bond is 13, nearly identical to the ΔpKa value of the [HOH⋯−OOC] H-bond in the absence of the protein environment (∼12) (Fig. 6a). Therefore, the short O⋯O distance of this H-bond is not caused by a decreased ΔpKa due to the protein electrostatic environment, but rather by structural constraints in the protein environment.
In the absence of the protein environment, a lower ΔpKa tends to result in a higher binding enthalpy,11 a shorter O⋯O distance, and a larger Odonor–H⋯Oacceptor angle approaching 180°.16,17 On the other hand, the Odonor–H⋯Oacceptor angle of this short H-bond is 149° (Fig. 6b). Short H-bonds with decreased Odonor–H⋯Oacceptor angles, despite high ΔpKa values, are frequently observed in intramolecular H-bonds, where structural constraints are significant.17 Such short H-bonds with small Odonor–H⋯Oacceptor angles result from rigid anchoring in the protein matrix, which causes deviations from the equilibrium O⋯O distance. In the case of the [H2O-406⋯Asp212] H-bond in the N′-state BR, the formation of the H-bond network involving protonated Asp85, H2O-401, H2O-406, and Asp212 decreases the O⋯O distance (Fig. 6b). Indeed, when the structure is QM/MM-optimized in the absence of H2O-401, the O⋯O distance of the [H2O-406⋯Asp212] H-bond increases to 2.79 Å (Fig. S7, ESI†).
The O⋯O distance of the [H2O-402⋯Asp212] H-bond in the ground-state BR is 2.92 Å, which is 0.19 Å longer than the average O⋯O distance for [HOH⋯−OOC] H-bonds in proteins (2.73 Å) (Fig. 6c). The calculated ΔpKa value of this H-bond is 19, indicating that ΔpKa is increased from ∼12 due to the protein electrostatic environment (Fig. 6a). However, a ΔpKa of 19 corresponds to an O⋯O distance of 2.78 Å based on eqn (1), which is shorter than 2.92 Å. Therefore, the long O⋯O distance of 2.92 Å cannot be solely attributed to the increased ΔpKa. Instead, it results from both (i) the increased ΔpKa due to the protein environment, and (ii) structural constraints in the protein environment (Fig. 6a). The increase in ΔpKa is due to the decrease in pKa of Asp212, caused by H-bond donations from Tyr57 and Tyr185 to Asp21273 (Fig. 6c). The structural constraints likely arise from the H-bond formations between H2O-402 and Asp85/Lys216, and between Asp212 and Tyr57/Tyr185, which may increase the H⋯Oacceptor distance (Fig. 6c).
To summarize, H-bond distances are influenced by the following two factors of the protein environment: (i) the protein electrostatic environment that shifts the ΔpKa of the H-bond. This ΔpKa shift alters the covalent character of the H⋯Oacceptor bond (Fig. 2), thereby altering the O⋯O distances. (ii) Structural constraints imposed by protein folding. These constraints alter the Odonor–H⋯Oacceptor angle (Fig. 6b) or the H⋯Oacceptor distance (Fig. 6c) without affecting ΔpKa (or the corresponding Odonor–H distance), thereby altering the O⋯O distance. Such constraints destabilize the H-bond, which is likely compensated by stabilization through other interactions and H-bonds (e.g., H-bonds between H2O-402 and Asp85/Lys216, and between Asp212 and Tyr57/Tyr185 in the ground-state BR, Fig. 6c).
Conclusions
In H-bonds, while the Odonor–H distance remains around ∼1 Å, the H⋯Oacceptor distance is significantly longer and serves as the primary limiting factor for the O⋯O distance. Thus, minimizing the H⋯Oacceptor distance decreases the overall H-bond distance. The present study demonstrates that electron redistribution counteracts proton migration from the H-bond donor to the acceptor upon H-bond formation. This electron redistribution increases as ΔpKa decreases, introducing a covalent character to the H⋯Oacceptor “bond”, thereby significantly decreasing the overall O⋯O distance (Fig. 2). In contrast, the strength of the electrostatic interaction between the donor and acceptor groups plays a minor role in determining H-bond distances, as indicated by the small dependence of H-bond distances on the total charges of the donor and acceptor groups (Fig. 1, 4 and 5). Therefore, the protein electrostatic environment influences H-bond distances primarily by altering the ΔpKa of the H-bond (Fig. 6a), whereas differences in the dielectric properties of the protein environment do not affect H-bond distances (Fig. 4 and 5).Beyond this primary determinant of H-bond distance, structural constraints in the protein environment impose a secondary influence. Odonor–H⋯Oacceptor angles (Fig. 6b) and H⋯Oacceptor distances (Fig. 6c) are often restricted by rigid anchoring in the protein matrix, causing deviations in the O⋯O distance from the equilibrium value determined by ΔpKa. While the effect of structural constraints on H-bond distances is weaker than the covalent-bond-like electronic effect, it enables the formation of unique H-bond geometries that are inaccessible in bulk solvent (Fig. 6a). These protein-specific H-bond geometries may play a crucial role in shaping the functional properties of proteins.
Data availability
The data supporting the findings of this study are available in the main article and the ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research was supported by JSPS KAKENHI (JP22KJ1109 to M. T.; JP23H04963 and JP24K01986 to K. S.; JP23H02444 to H. I.) and the Interdisciplinary Computational Science Program in CCS, University of Tsukuba (K. S.).References
- L. Pauling, The nature of the chemical bond and the structure of molecules and crystals: an introduction to modern structural chemistry, Cornell University Press, Ithaca, NY, 1960 Search PubMed.
- H. M. Berman, J. Westbrook, Z. Feng, G. Gilliland, T. N. Bhat, H. Weissig, I. N. Shindyalov and P. E. Bourne, Nucleic Acids Res., 2000, 28, 235–242 CrossRef CAS PubMed.
- M. M. Flocco and S. L. Mowbray, J. Mol. Biol., 1995, 254, 96–105 CrossRef CAS PubMed.
- S. Rajagopal and S. Vishveshwara, FEBS J., 2005, 272, 1819–1832 CrossRef CAS PubMed.
- G. Wohlfahrt, Proteins, 2005, 58, 396–406 CrossRef CAS PubMed.
- A. Langkilde, S. M. Kristensen, L. Lo Leggio, A. Mølgaard, J. H. Jensen, A. R. Houk, J.-C. N. Poulsen, S. Kauppinen and S. Larsen, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2008, 64, 851–863 CrossRef CAS PubMed.
- J. Lin, E. Pozharski and M. A. Wilson, Biochemistry, 2017, 56, 391–402 CrossRef CAS PubMed.
- S. Zhou and L. Wang, Chem. Sci., 2019, 10, 7734–7745 RSC.
- H. W. Qi and H. J. Kulik, J. Chem. Inf. Model., 2019, 59, 2199–2211 CrossRef CAS PubMed.
- P. Huyskens and T. Zeegers-Huyskens, J. Chem. Phys., 1964, 61, 81–86 CAS.
- P. Gilli, L. Pretto, V. Bertolasi and G. Gilli, Acc. Chem. Res., 2009, 42, 33–44 CrossRef CAS PubMed.
- B. Brycki and M. Szafran, J. Chem. Soc., Perkin Trans. 2, 1984, 223–226 RSC.
- P. Huyskens, L. Sobczyk and I. Majerz, J. Mol. Struct., 2002, 615, 61–72 CrossRef CAS.
- B. Brycki, B. Brzezinski, G. Zundel and T. Keil, Magn. Reson. Chem., 1992, 30, 507–510 CrossRef CAS.
- J. B. Tobin, S. A. Whitt, C. S. Cassidy and P. A. Frey, Biochemistry, 1995, 34, 6919–6924 CrossRef CAS PubMed.
- P. A. Sigala, E. A. Ruben, C. W. Liu, P. M. Piccoli, E. G. Hohenstein, T. J. Martinez, A. J. Schultz and D. Herschlag, J. Am. Chem. Soc., 2015, 137, 5730–5740 CrossRef CAS PubMed.
- D. Herschlag and M. M. Pinney, Biochemistry, 2018, 57, 3338–3352 CrossRef CAS PubMed.
- M. M. Pinney, A. Natarajan, F. Yabukarski, D. M. Sanchez, F. Liu, R. B. Liang, T. Doukov, J. P. Schwans, T. J. Martinez and D. Herschlag, J. Am. Chem. Soc., 2018, 140, 9827–9843 CrossRef CAS PubMed.
- J. R. Rumble, CRC handbook of chemistry and physics, CRC Press, Boca Raton, FL, 103rd edn, 2022 Search PubMed.
- M. B. Smith and J. March, March's advanced organic chemistry, John Wiley & Sons, Inc., Hoboken, NJ, 5th edn, 2001 Search PubMed.
- M. Śmiechowski, E. Gojlo and J. Stangret, J. Phys. Chem. B, 2011, 115, 4834–4842 CrossRef PubMed.
- M. A. Brown, F. Vila, M. Sterrer, S. Thürmer, B. Winter, M. Ammann, J. J. Rehr and J. A. van Bokhoven, J. Phys. Chem. Lett., 2012, 3, 1754–1759 CrossRef CAS PubMed.
- K. Kitaura, E. Ikeo, T. Asada, T. Nakano and M. Uebayasi, Chem. Phys. Lett., 1999, 313, 701–706 CrossRef CAS.
- D. G. Fedorov and K. Kitaura, J. Chem. Phys., 2004, 121, 2483–2490 CrossRef CAS PubMed.
- D. G. Fedorov and K. Kitaura, J. Comput. Chem., 2007, 28, 222–237 CrossRef CAS PubMed.
- D. G. Fedorov, K. Kitaura, H. Li, J. H. Jensen and M. S. Gordon, J. Comput. Chem., 2006, 27, 976–985 CrossRef CAS PubMed.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, J. Comput. Chem., 1993, 14, 1347–1363 CrossRef CAS.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS.
- F. Weinhold and C. Landis, Valency and bonding. A natural bond orbital donor–acceptor perspective, Cambridge University Press, Cambridge, 2005 Search PubMed.
- J. S. Arey, P. C. Aeberhard, I.-C. Lin and U. Rothlisberger, J. Phys. Chem. B, 2009, 113, 4726–4732 CrossRef CAS PubMed.
- R. Misra, D. K. Maity and S. P. Bhattacharyya, Chem. Phys., 2012, 402, 96–104 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales and F. Weinhold, NBO 5.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2001 Search PubMed.
- A. D. Bochevarov, E. Harder, T. F. Hughes, J. R. Greenwood, D. A. Braden, D. M. Philipp, D. Rinaldo, M. D. Halls, J. Zhang and R. A. Friesner, Int. J. Quantum Chem., 2013, 113, 2110–2142 CrossRef CAS.
- T. Hamelryck and B. Manderick, Bioinformatics, 2003, 19, 2308–2310 CrossRef CAS PubMed.
- P. J. A. Cock, T. Antao, J. T. Chang, B. A. Chapman, C. J. Cox, A. Dalke, I. Friedberg, T. Hamelryck, F. Kauff, B. Wilczynski and M. J. L. de Hoon, Bioinformatics, 2009, 25, 1422–1423 CrossRef CAS PubMed.
- B. Rost and C. Sander, Proteins, 1994, 20, 216–226 CrossRef CAS PubMed.
- W. Kabsch and C. Sander, Biopolymers, 1983, 22, 2577–2637 CrossRef CAS PubMed.
- W. G. Touw, C. Baakman, J. Black, T. A. H. te Beek, E. Krieger, R. P. Joosten and G. Vriend, Nucleic Acids Res., 2015, 43, D364–D368 CrossRef CAS PubMed.
- N. Hasegawa, H. Jonotsuka, K. Miki and K. Takeda, Sci. Rep., 2018, 8, 13123 CrossRef PubMed.
- B. Schobert, L. S. Brown and J. K. Lanyi, J. Mol. Biol., 2003, 330, 553–570 CrossRef CAS PubMed.
- T. Kouyama, S. Kanada, Y. Takeguchi, A. Narusawa, M. Murakami and K. Ihara, J. Mol. Biol., 2010, 396, 564–579 CrossRef CAS PubMed.
- K. Kovalev, R. Astashkin, I. Gushchin, P. Orekhov, D. Volkov, E. Zinovev, E. Marin, M. Rulev, A. Alekseev, A. Royant, P. Carpentier, S. Vaganova, D. Zabelskii, C. Baeken, I. Sergeev, T. Balandin, G. Bourenkov, X. Carpena, R. Boer, N. Maliar, V. Borshchevskiy, G. Buldt, E. Bamberg and V. Gordeliy, Nat. Commun., 2020, 11, 2137 CrossRef CAS PubMed.
- E. Podoliak, G. H. U. Lamm, E. Marin, A. V. Schellbach, D. A. Fedotov, A. Stetsenko, M. Asido, N. Maliar, G. Bourenkov, T. Balandin, C. Baeken, R. Astashkin, T. R. Schneider, A. Bateman, J. Wachtveitl, I. Schapiro, V. Busskamp, A. Guskov, V. Gordeliy, A. Alekseev and K. Kovalev, Nat. Commun., 2024, 15, 3119 CrossRef CAS PubMed.
- B. R. Brooks, R. E. Bruccoleri, B. D. Olafson, D. J. States, S. Swaminathan and M. Karplus, J. Comput. Chem., 1983, 4, 187–217 CrossRef CAS.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiorkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- D. Bashford and M. Karplus, Biochemistry, 1990, 29, 10219–10225 CrossRef CAS PubMed.
- Y. Nozaki and C. Tanford, Methods Enzymol., 1967, 11, 715–734 CAS.
- M. Tanokura, Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol., 1983, 742, 576–585 CrossRef CAS PubMed.
- M. Tanokura, Biochim. Biophys. Acta, Protein Struct. Mol. Enzymol., 1983, 742, 586–596 CrossRef CAS PubMed.
- M. Tanokura, J. Biochem., 1983, 94, 51–62 CrossRef CAS PubMed.
- B. Rabenstein and E.-W. Knapp, Biophys. J., 2001, 80, 1141–1150 CrossRef CAS PubMed.
- D. M. Philipp and R. A. Friesner, J. Comput. Chem., 1999, 20, 1468–1494 CrossRef CAS.
- R. B. Murphy, D. M. Philipp and R. A. Friesner, J. Comput. Chem., 2000, 21, 1442–1457 CrossRef CAS.
- W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236 CrossRef CAS.
- A. P. Scott and L. Radom, J. Phys. Chem., 1996, 100, 16502–16513 CrossRef CAS.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- L. D'Ascenzo and P. Auffinger, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 164–175 CrossRef PubMed.
- C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179 CrossRef CAS PubMed.
- L. Pauling, J. Am. Chem. Soc., 1947, 69, 542–553 CrossRef CAS.
- T. Steiner and W. Saenger, Acta Crystallogr., Sect. B:Struct. Sci., Cryst. Eng. Mater., 1994, 50, 348–357 CrossRef.
- P. Gilli, V. Bertolasi, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 1994, 116, 909–915 CrossRef CAS.
- H.-H. Limbach, P. M. Tolstoy, N. Pérez-Hernández, J. Guo, I. G. Shenderovich and G. S. Denisov, Isr. J. Chem., 2009, 49, 199–216 CrossRef CAS.
- S. J. Grabowski, Chem. Rev., 2011, 111, 2597–2625 CrossRef CAS PubMed.
- W. W. Cleland, Biochemistry, 1992, 31, 317–319 CrossRef CAS PubMed.
- C. N. Schutz and A. Warshel, Proteins, 2004, 55, 711–723 CrossRef CAS PubMed.
- W. W. Cleland, Arch. Biochem. Biophys., 2000, 382, 1–5 CrossRef CAS PubMed.
- F. Fulyani, G. K. Schuurman-Wolters, A. V. Zagar, A. Guskov, D.-J. Slotboom and B. Poolman, Structure, 2013, 21, 1879–1888 CrossRef CAS PubMed.
- G. M. Ullmann and E.-W. Knapp, Eur. Biophys. J., 1999, 28, 533–551 CrossRef CAS PubMed.
- C. N. Schutz and A. Warshel, Proteins, 2001, 44, 400–417 CrossRef CAS PubMed.
- K. Morokuma, Acc. Chem. Res., 1977, 10, 294–300 CrossRef CAS.
- M. Tsujimura, K. Saito and H. Ishikita, Biophys. J., 2023, 122, 4336–4347 CrossRef CAS PubMed.
- K. Saito, H. Kandori and H. Ishikita, J. Biol. Chem., 2012, 287, 34009–34018 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00511f |
| This journal is © the Owner Societies 2025 |



