Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The universal vibrational dynamics of water bound to tertiary amines: more than just Fermi resonance†
Eaindra
Lwin
 ,
Nils O. B.
Lüttschwager
,
Nils O. B.
Lüttschwager
 and
Martin A.
Suhm
and
Martin A.
Suhm
 *
*
Institute of Physical Chemistry, University of Göttingen, Tammannstr. 6, 37077 Göttingen, Germany. E-mail: msuhm@gwdg.de
First published on 24th February 2025
Abstract
Amines with three alkyl substituents are shown to be strongly microsolvated by water molecules, unless the steric hindrance of the alkyl groups overcompensates the increase in basicity of the N atom by alkylation. The hydrogen bond interaction of the first water molecule is so strong that the softened OH vibration shares its intensity with up to three largely dark states involving quanta of intramolecular bending or stretching and intermolecular stretching vibration. A combination of FTIR, Raman, isotope and chemical substitution spectroscopy in supersonic jet expansions establishes the existence, character and extent of the underlying anharmonic coupling. The observed resonance pattern is remarkably systematic and allows to extract physically plausible, effective normal mode coupling constants which are relevant for the initial energy flow out of the excited OH oscillator. A remaining ambiguity in the coupling pattern for the weakest transition invites detailed anharmonic quantum dynamics studies, but it still allows for robust deperturbed positions of the uncoupled oscillators for 8 amine monohydrates, which are valuable as experimental benchmarks for databases and for the training phase of theory blind challenges on microhydration. The more isolated hydrogen-bonded OH stretching vibration of a second water molecule is also assigned to widen the scope of a future theory challenge addressing the wavenumber of hydrogen-bonded OH groups. Such blind challenges thus remain accessible not only to fully anharmonic, but also to scaled harmonic and machine learning approaches which may try to average over the anharmonic details.
1 Introduction
Hydrogen bonds are mediators of energy dissipation in protic solvents.1–4 Being able to model the primary processes of this energy flow is of fundamental importance in fields as diverse as heat conductivity and reaction dynamics. Stationary vibrational spectroscopy can provide important constraints for realistic models of anharmonic energy flow,5 but not so much in the condensed phase, where the protic vibrations are typically broad and structureless. The situation is more favourable in the gas phase at low temperature, where microsolvation environments can be created and studied in much detail by action6 or by linear spectroscopy.7 The obtained frequency and intensity information can be translated into dynamical phenomena, such as anharmonic resonances. For water molecules, the most prominent feature is a strong Fermi resonance between the OH stretching fundamental and the HOH bending overtone, reflecting sub-picosecond energy flow between stretching and bending amplitudes of the hydrogen atoms. It is activated if at least one OH bond of the water molecule is weakened by strong hydrogen bonding, such as in liquid water, in water clusters,8 or in monohydrates of strong bases like tertiary amines.9 Remarkably little is known about the underlying vibrational spectra in cryomatrix isolation or in the cold gas phase. Two studies for the trimethylamine–water prototype10,11 were interpreted controversially and the room temperature gas phase spectrum12 is quite broad, making any interpretation beyond the basic Fermi resonance pattern difficult. We have recently set out to address the problem with FTIR spectroscopy in supersonic expansions and found a remarkably robust pattern of three narrow bands across several tertiary amine monohydrates,9 where the harmonic approximation would predict a single transition. We were not able to firmly decide between different vibrational coupling models due to the limited experimental evidence, but we could already demonstrate that the coupling is far from accidental. Although the complex of phenol with ammonia falls in a similar spectral range,13 it does not exhibit the same spectral complexity. The intra- and intermolecular modes of water must be responsible for the observed features. In this work, we extend our study to further tertiary amines with systematically tuned water binding affinity, to isotope substitution, and to spontaneous Raman scattering. In this way we are able to derive two variants of a generic coupling pattern among up to four, rather than three states – the expected Fermi resonance couple and two dark two- to four-quantum states involving overall stretching motion of the water molecule against the amine on top of water bending or stretching motion. We reconstruct and validate the zero-order (deperturbed) position of the spectrally bright OH stretching mode based on experimental data only and on the assumption that intrinsic intensity of the dark states is negligible.9,14 This is important for theory benchmarking purposes,15 including quantum-chemical and machine-learning approaches which neglect the anharmonic resonances but still aim to reproduce the local OH stretching environment for water near an amine base. We are not aware of another strong hydrogen bonding scenario across different neutral compounds which provides such a detailed and uniform, vibrational state-resolved anharmonic picture involving coupled intra- and intermolecular motions. It goes far beyond what is currently possible for carboxylic acid dimers, where the vibrational OH stretching signature is uniform in shape but seemingly random in detail.16 For charged systems, which often have enhanced interactions, related coupling situations have been analyzed successfully.17,18 However, it can be more challenging to extract reliable spectral intensities in ion- and generally any action spectroscopy. Therefore, we postulate that amine monohydrates as studied by linear FTIR and Raman spectroscopy are particularly well suited for the multidimensional anharmonic modeling of proton dynamics in neutral hydrogen-bonded complexes. The simplest case of trimethylamine will be published separately, as it requires matrix isolation and gas phase spectroscopy at different temperatures to connect to previous studies which came to other conclusions.10,112 Experimental
The experimental spectra reported in this work were obtained in a gas recycling FTIR jet spectrometer, for details see Table S2 in the ESI,† and ref. 9. In selected cases, complementary gas recycling Raman jet spectra were also obtained, as described in ref. 19 (Table S3 in the ESI†). Band integration and centroid determination were carried out using a numerical approach which includes the noise characteristics of the spectrometer,20 all the values are described in Tables S4 and S5 in the ESI.† Due to the close vicinity of the resonance partners, the linear dependence of the band integrals on the wavenumber was not corrected for.3 Nomenclature and modeling
We continue the molecule nomenclature used before,9 which is designed to be elementary, yet flexible enough to accomodate the large number of cases demanded by the designated benchmarking purpose of this work. The letter N stands for a tertiary amine. It is preceded by letters representing linear substituents and followed by numbers representing rings which include N as a heterocycle. If the heterocycle has n methyl groups attached to the ring, these are added as n letters M. The systems presented in this work include the heterocycles N-methyl pyrrolidine (MN4),9N-methyl piperidine (MN5),9 quinuclidine (N555)9 and 1,2,2,6,6-pentamethylpiperidine (MN5MMMM) as well as the dimethylalkylamines MMEN, MMIN, MMCN (see ref. 9) and MMTN, where E stands for ethyl, I for isopropyl, C for cyclohexyl and T for tert-butyl, see also Fig. 12 at the end of the paper and Table S1 in the ESI.† The predictive power of the coupling models developed in this work is further tested for the multiconformational triethylamine (EEEN) and the sterically most crowded triisopropylamine (IIIN) is also briefly addressed.In terms of vibrational state nomenclature, we use an in-line notation which includes OHb (the hydrogen-bonded OH stretching fundamental of water) as the intensity carrier, b2 (the bending overtone of a water molecule) and ON (as the dimer stretching fundamental which moves the water periodically away from and towards the amine binding partner). These are combined in the order of decreasing fundamental frequency (i.e. b2ON, b2ON2, OHbON), when two different modes are simultaneously excited. An unclear combination band assignment involving ON is denoted xONn, where x could stand for OHb or b2 and n could be (implicitly) 1 or (explicitly) 2. Any combination band involving a high-frequency component (OHb, b2) and a low frequency component (ON) can derive IR intensity from its vibrational Franck–Condon factor due to a vertical transition with respect to the slow mode in an adiabatic channel picture21 or from wavefunction mixing with the bright carrier state OHb. For b2ON, Franck–Condon effects can at best be secondary because of the weak intrinsic IR strength of b2, whereas for OHbON both effects can contribute independently.
A technique to obtain effective coupling constants between two to four resonance partners based on a single bright-state model is described in the ESI,† part 2 and 3. It goes beyond the sequential coupling models applied before9 by solving an inverse eigenvalue problem derived from experimental band positions and band integrals as well as additional plausible coupling constraints.
Although there is a strong emphasis on purely experimental evidence in this work, some auxiliary harmonic quantum-chemical calculations at the B3LYP-D3(BJ,abc)/def2-TZVP22–26 level were carried out using Orca 5.0.327–30 to provide structural information and substitution trends in harmonic wavenumbers, shown in Table S6 in the ESI.†
4 Results
4.1 Monohydrates of heterocyclic tertiary amines
Fig. 1 shows the infrared OH stretching spectrum of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex of N-methylpiperidine (MN5) with H2O9 for a highly diluted expansion, which minimises larger clusters (top trace). It exhibits four bands labelled b2, OHb, b2ON and xONn. The first three have been introduced before9 and the fourth, provisional label xONn indicates a much weaker second band involving ON stretching excitation, which will be discussed in detail below. In the double-harmonic approximation (linear restoring force and linear dipole moment change as a function of atomic displacement), one would just expect a single signal from the hydrogen-bonded OH stretching mode of the 1
1 complex of N-methylpiperidine (MN5) with H2O9 for a highly diluted expansion, which minimises larger clusters (top trace). It exhibits four bands labelled b2, OHb, b2ON and xONn. The first three have been introduced before9 and the fourth, provisional label xONn indicates a much weaker second band involving ON stretching excitation, which will be discussed in detail below. In the double-harmonic approximation (linear restoring force and linear dipole moment change as a function of atomic displacement), one would just expect a single signal from the hydrogen-bonded OH stretching mode of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex in this region, whose position is very sensitive to the strength of the hydrogen bond. The bending overtone b2 of the complex is much less sensitive to hydrogen bonding and expected to be very weak in the IR spectrum (see the two weak lines marked M due to monomer bending overtone signals from a large excess of water monomers over complexes) even upon inclusion of some diagonal anharmonicity. However, anharmonic coupling between the OHb stretching fundamental and neighbouring modes in the complex can redistribute the OH stretching intensity to further transitions, while conserving the total intensity and the center or centroid of this intensity distribution in a simple model of one bright and several dark states. The arrows labelled A, B, C mark this experimental centroid for the coupling of b2 and OHb only (model A, classical Fermi resonance), for b2, OHb and b2ON (model B, a triad of states) and for all four absorptions (model C, a tetrad of interacting states), shown in Fig. S3–S6 in the ESI.†
1 complex in this region, whose position is very sensitive to the strength of the hydrogen bond. The bending overtone b2 of the complex is much less sensitive to hydrogen bonding and expected to be very weak in the IR spectrum (see the two weak lines marked M due to monomer bending overtone signals from a large excess of water monomers over complexes) even upon inclusion of some diagonal anharmonicity. However, anharmonic coupling between the OHb stretching fundamental and neighbouring modes in the complex can redistribute the OH stretching intensity to further transitions, while conserving the total intensity and the center or centroid of this intensity distribution in a simple model of one bright and several dark states. The arrows labelled A, B, C mark this experimental centroid for the coupling of b2 and OHb only (model A, classical Fermi resonance), for b2, OHb and b2ON (model B, a triad of states) and for all four absorptions (model C, a tetrad of interacting states), shown in Fig. S3–S6 in the ESI.†
 | ||
Fig. 1 The good agreement of the 4-transition intensity centroid of the OH stretching spectrum of the N-methylpiperidine–H2O complex (upper orange trace, arrow C) with the OH stretching spectrum of the corresponding HOD complex (lower trace, grey) after (unscaled) harmonic correction for kinematic effects (Δω = 8 cm−1, middle trace, black) suggests that all four 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex transitions in the orange trace are likely to derive their intensity from the OH stretching mode. Arrows mark centroid positions and are labelled according to models A, B, C (see text), the horizontal bar crossing these arrows indicates the uncertainty (more than 1σ, see Tables S9–S12 in the ESI†). 1 complex transitions in the orange trace are likely to derive their intensity from the OH stretching mode. Arrows mark centroid positions and are labelled according to models A, B, C (see text), the horizontal bar crossing these arrows indicates the uncertainty (more than 1σ, see Tables S9–S12 in the ESI†). | ||
To support that indeed all four absorptions derive most of their intensity from the OH stretching fundamental, the bottom spectrum shows the OH stretching spectrum of MN5 with D2O, containing a small amount of H and thus DOH. Some of the DOH will form a hydrogen bond with the amine, although the competing deuterium bond is more stable and can be reached by internal rotation of the DOH unit. Apart from traces of H2O, which give rise to weak transitions strictly corresponding to those in the upper trace, there is a single relatively broad band, very likely due to the DOH⋯MN5 complex. Apparently, the jet expansion is able to suppress the isomerisation to HOD⋯MN5 sufficiently well to allow for some metastable population. Single deuteration of water moves the b2 state down by several 100 cm−1. The disappearance of b2ON thus suggests that this state also involves b2 character. For xONn, this is less clear, due to the limited signal-to-noise ratio. If it also disappears, b2ON2 (continuing the sequence of b2, b2ON) would be a plausible interpretation, whereas if it only becomes weaker, it is perhaps better described as OHbON (potentially gaining intensity from OHb through vibrational Franck–Condon effects). b2ON is easier to analyse on the basis of the DOH experiment. There is a small and largely kinematic effect on the harmonic bound OH wavenumber when the free H in water is replaced by D. This shift Δω can be roughly estimated from a harmonic DFT calculation (about +8 cm−1 for the amines investigated here, at B3LYP-D3/def2-TZVP level, shown in Table S13 in the ESI†) and the central spectrum in Fig. 1 is backshifted by this calculated amount. It is unlikely that anharmonic effects will change the sign of this isotope shift or increase it substantially. A conservative uncertainty for the kinematic isotope shift is ±5 cm−1. It has been argued that the bright state approximation could be a more critical assumption14 for strongly bound water molecules, but the diagnosed errors are of a similar magnitude and it is not trivial to obtain purely energy-based deperturbation values for complex systems. Therefore we rely on the intensities, which evolve in a rather systematic way. The resulting isotopically reconstructed OHb band position is thus somewhere in between the observed dominant OHb position and the intensity centroid C of the upper trace. These two reference values are within the uncertainty of the isotopic procedure, as is the intensity centroid B, whereas a simple Fermi resonance between OHb and b2 (centroid A) appears incompatible with the isotope substitution experiment. The discrepancy is even larger if one adds the b2ON intensity to b2 before carrying out the Fermi resonance analysis (assuming that b2ON steals intensity from b2 by a vibrational Franck–Condon effect rather than directly from OHb by wave function mixing).
This suggests that at least three or even all four transitions observed in the monohydrate of N-methyl piperidine (MN5) derive most of their intensity from OHb. If b2ON and xONn had their own significant intensity, the DOH extrapolation should fall closer to the centroid A. This hypothesis, that the OHb transition in the MN5 monohydrate is affected by two to three IR-dark states through anharmonic coupling, shall be confirmed in the following by a number of arguments. Note that because the resonating states are at higher and lower wavenumber than OHb, the actual shift of the dominant transition from the zeroth order position (arrow C) is rather small. This was not the case for ketone hydrates,31 where a single dark state caused a unidirectional shift of up to 10 cm−1.
A first confirmation for our coupling hypothesis comes from the introduction of four methyl groups at the α-carbons of the N-heterocycle. This substitution pattern is reminiscent of the one in TEMPO32 and leads to two opposing effects for the N-docking water molecule – steric hindrance and increased proton affinity. As the upper trace spectrum in Fig. 2 shows, the latter effect wins for water and the Fermi resonance centroid (A) would be about midway between OHb and b2, if it were not for the compensating effect of the higher order resonances involving ON stretching excitation. The centroids B and even more so C are much closer to the OHb signal and deuteration of the free OH (lower trace) confirms that centroid C (and not so much B) is likely the correct interpretation, in particular after introducing a harmonic correction of the kinematic effect (central trace).
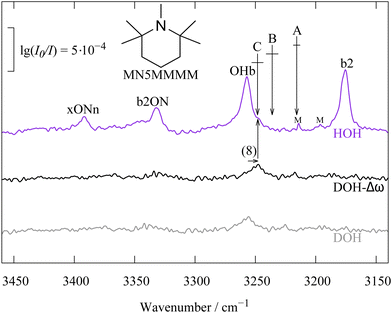 | ||
| Fig. 2 Same as Fig. 1 but with four additional methyl groups at the heterocyclic carbon atoms next to N, strengthening the hydrogen bond and shifting the resonance pattern. Similar trend is shown in other systems (see Fig. S7–S9 in the ESI†). | ||
So far, the assignment still relies on a small piece of theoretical input, namely the approximate spectral shift from DOH to HOH hydrogen bonding. This can be further minimised by looking at the corresponding spectra in the OD stretching range (Fig. S12 in the ESI†). Two of the four spectra shown correspond exactly to the upper trace spectra shown in Fig. 1 and 2, the other two involve even less H (i.e. a higher degree of deuteration). For the latter, a Fermi resonance is again assumed between the peaks labeled ODb and b2, as they correspond to the positions in the non-deuterated spectra. The resulting centroid (A) of the deperturbed ODb stretch is marked with an arrow. For MN5, where the effect of deperturbation is very small, one can nicely see that the shift from DOD to HOD for the main peak is small, and it corresponds reasonably well to the harmonic prediction (in parentheses), as expected for a resonance-free case. Therefore, the procedure to shift the DOH spectrum by the harmonic shift prediction between the HOH and the DOH complex is experimentally justified. Note that there is a common pattern of weak transitions to the right and to the left of the ODb and b2 signals, which we cannot assign unambiguously at this stage. They could be explained by sum and difference transitions around both ODb and b2 with modulation wavenumbers between 150 and 200 cm−1, which might be due to dimer stretching or methyl torsion modes.
Another purely experimental way to investigate which of the transitions of the monohydrate are involved in the wavefunction mixing is to plot the different HOH centroids against the observed DOH wavenumber for a number of substituted amines (all wavenumbers are described in Table S14 in the ESI†). This is done in Fig. 3 for five amines, two of which are heterocyclic and span the extremes (for the other three with intermediate band positions, see below). Linear relationships are found for the most intense HOH transition, for the centroid A obtained from OHb and b2, for the centroid B where b2ON is added, and for the centroid C where the weak xONn transition is included. The standard deviation of the slope is largest for model C, because of the large experimental uncertainty of the weakest transition. This slope of the linear correlation should be close to 1.0, if partial deuteration does not affect the structure of the complex, if the kinematic effect is uniform across the amines, and if all mixed states for HOH are included in the centroid determination. This is not the case if one just correlates the most intense HOH transition (0.89 ± 0.04) or determines the centroid from OHb and b2 only (1.25 ± 0.08). Centroids B and C yield correlations with slopes reasonably close to 1 (1.10 ± 0.07, 0.99 ± 0.12), suggesting that the three strongest or all four signals in the OH stretching spectrum have partial OHb character in all four investigated amine hydrates.
Further support for the centroid-conserving resonance hypothesis comes from Raman jet spectroscopy. Normally, the selection rules and thus intensities strongly differ between linear IR and Raman spectroscopy, but in the absence of inversion symmetry and for truly dark states interacting with a single bright state, any wavefunction mixing due to anharmonic resonance should lead to the same relative intensity pattern in the IR and Raman spectra. This neglects minor issues such as residual intrinsic intensity of the dark states, differences in depolarisation ratio in combination with polarisation-selective gratings or detectors, different cooling efficiencies etc.Fig. 4 compares the FTIR (upper) and Raman (middle trace) spectra for MN4 and indeed shows a rather analogous quartet of states. The Raman transitions are somewhat broader, mainly because for technical reasons they were recorded closer to the (much shorter) slit nozzle. This weakens in particular the most intense OHb transition, but otherwise, the Raman pattern is remarkably analogous to the one found in the IR spectrum. Note that the Raman spectrum contains additional bands due to (CH)-based combination transitions of the amine, because the CH bond has a much higher Raman than IR intensity. This is illustrated by showing a Raman spectrum at very low water content (lowest trace), scaled to match the CH bands of the central trace. One can see that while the OH-derived signals of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex decrease in intensity, the CH monomer transitions persist uniformly. The band marked T which is visible in IR and Raman spectra is due to the OHb vibration of a second water attaching to the first solvating water. This can be shown by concentration variation9 and is elaborated in the ESI,† Fig. S17–S20.
1 complex decrease in intensity, the CH monomer transitions persist uniformly. The band marked T which is visible in IR and Raman spectra is due to the OHb vibration of a second water attaching to the first solvating water. This can be shown by concentration variation9 and is elaborated in the ESI,† Fig. S17–S20.
 | ||
| Fig. 4 Demonstration of wave function mixing of the OHb state in the MN4 monohydrate by observing largely the same relative intensity pattern in IR (top) and Raman (middle) spectroscopy, apart from CH combination bands in the Raman spectrum which persist at much lower water concentration (bottom trace). Analogous to Fig. S11 in the ESI.† | ||
A final validation of the robust coupling scenario for N-heterocyclic monohydrates comes from quinuclidine (N555), which has particularly narrow transitions and a higher mass than the other two N-heterocycles. It thus lends itself to 18O substitution of the water. The isotope effect shown in Fig. 5 progressively increases from OHb over b2ON to xONn. This is consistent with combination band assignments for the latter two states, because the isotope effect on the ON stretching vibration is combined with that of b2 or OHb. Actually, the increment of the isotope shift from b2 to b2ON (5 cm−1) is about the same as the increment from OHb to xONn (6 cm−1), which suggests the interpretation of xONn as OHbON (hydrogen-bonded OH stretching combined with dimer ON stretching). For a b2ON2 (water bending overtone combined with dimer ON stretching overtone) interpretation, one would expect a doubling of the increment, but it only increases from 5 to 7 cm−1. While the underlying band positions are clearly affected by resonances, it appears plausible to assume that this influence is similar for both isotopologues. Indeed, the intensity pattern remains quite similar when the oxygen isotope is changed. Also, the analogous experiment with N-methyl piperidine (MN5, see Fig. S13 in the ESI†) shows the same trend. Therefore, the isotope exchange at O provides a first piece of evidence for the nature of the weakest of the four transitions.
 | ||
| Fig. 5 Comparison of the OH stretching spectrum of N555 with 16OH2 (bottom, inverted) to the same spectrum enriched in 18OH2. The 16-18-isotope shifts in cm−1 are clarified by arrows (see Table S15 in the ESI,† for details). | ||
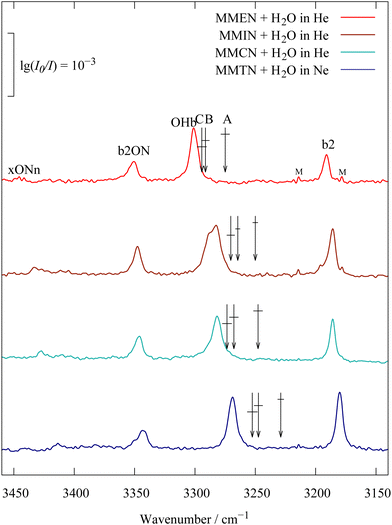
4.2 Dimethylalkylamine monohydrates
While heterocyclic amines are potentially affected by ring strain effects on the hydrogen bond acceptor quality of the amine, amines with three unconnected substituents lend themselves better to the study of substitution trends. If all substituents are bulky, they may block the approach of the water molecule, but if two of them are methyl groups, the acceptor quality should increase with the number of substituents in α position of the third one. It is interesting to see whether this trend can already be recognised from the dominant OHb transition or whether it needs deperturbation by correlating the model B or C centroids. Fig. 6 compares the spectra for 1 (MMEN), 2 (MMIN, MMCN, see ref. 9) and 3 (MMTN) methyl groups attached in α-position of the third substituent. They all show the same resonance pattern, underscoring its robustness. For dimethylisopropylamine (MMIN) there is some spectral evidence for two coexistent conformations (shoulder of the main signal), but for simplicity we treat the two conformations together. Details on the isomerism in MMIN and also MMCN are described in Tables S7, S8 and Fig. S1, S2 in the ESI.† For dimethylcyclohexylamine (MMCN), it also plays a role in molecular recognition within trace amine-associated sensory receptors.33 The main central peak moves progressively to lower wavenumber with the number of methyl groups, but the steps are significantly more pronounced after deperturbation of two (model B) or three (model C) perturber states. The error bars for the deperturbation (horizontal lines crossing the arrows) for models B and C overlap, such that the effect of the weak xONn perturber is only weakly significant, but of course systematic in its direction. MMTN is relatively close to the crossover, where the largest intensity peak moves to the lowest wavenumber. This does not necessarily mean that the deperturbed positions of b2 and OHb swap, because of the influence of the ON-containing resonance partners. The HOD control experiment in analogy to Fig. 1 and 2 for MMTN (see ESI,† Fig. S9 and S10) again confirms that model B or C deperturbation is in best agreement with the prediction from isotope-edited spectra.4.3 8 new monohydrate entries for the HyDRA database
This work is part of a major effort to collect and compile reliable hydrogen-bonded OH stretching band positions of gas phase mono- and dihydrates of small molecules for benchmarking purposes (HyDRA, standing for Hydrate Donor Redshift Anticipation). The corresponding database34 currently does not contain aliphatic amine monohydrates. Based on the present work and its largely experiment-based reasonings, Table 1 contains raw (dominant intensity) positions and deperturbed estimates based on two (centroid B) or three (centroid C) perturbers for the monohydrate OHb position of 8 tertiary amine monohydrates. In most cases, centroid B and C results overlap within their added uncertainties. Even for Gaussian error propagation (last column), the difference is hardly significant (except for MN5MMMM). Therefore, the weakest of the transitions (labelled xONn) is not decisive for the benchmarking of theoretical predictions. We thus propose to use the average of models B and C for the benchmarking of theoretical approaches to the OHb position on the wavenumber scale, if the theoretical approach is ignorant of the underlying anharmonic resonance. Obviously, for theoretical approaches which include the possibilty of anharmonic resonance, direct comparison to experiment at the level of the individual band positions can be made.| Amine | OHb (raw) | Centroid B up to 3 quanta | Centroid C up to 4 quanta | C–B |
|---|---|---|---|---|
| MN4 | 3299(1) | 3287(4) | 3292(5) | 5(7) |
| MN5 | 3289(1) | 3274(5) | 3281(5) | 8(7) |
| MN5MMMM | 3257(1) | 3236(5) | 3248(5) | 12(7) |
| N555 | 3297(1) | 3278(3) | 3284(4) | 6(5) |
| MMEN | 3301(1) | 3291(3) | 3294(4) | 3(5) |
| MMIN | 3285(1) | 3265(2) | 3270(3) | 6(4) |
| MMCN | 3282(1) | 3268(4) | 3273(4) | 6(5) |
| MMTN | 3269(1) | 3247(4) | 3252(4) | 5(5) |
4.4 Quantitative analysis of the coupling patterns
In particular for those future advanced theoretical studies, we shall explore an effective Hamiltonian approach in normal coordinates, to provide some guidance from experiment. Depending on the system, the OHb stretching mode is visibly split into 3 or 4 components. While it is straightforward to reconstruct the deperturbed OHb position based on the assumption that it is the only spectrally bright state, a localisation of the original (deperturbed) perturber states requires further approximations. Here, we assume that there is only pairwise coupling between these dark states and OHb and no coupling among the perturber states themselves. A similar assumption has been proposed for the case of decorated H3O+.35 This allows for an easily interpretable solution of the coupling problem (apart from the sign of the effective coupling constants Wi, which is uniformly chosen to be positive). It consists in transforming the 3 × 3 or 4 × 4 Hamiltonian matrices from diagonal form F = diag(EOHb, Eb2, Eb2ON) and F = diag(EOHb, Eb2, Eb2ON, ExONn) into the forms | (1) |
 | (2) |
 and
and 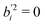 otherwise, thus
otherwise, thus 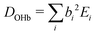 (for the centroid) which the coupling constants Wj mix into the observed pattern. The matrices D in eqn (1) and (2) are derived by solving the inverse eigenvalue problem D = LFLT. The orthonormal transformation matrix (L) contains the eigenvectors, the OHb vector with components bi being directly known from the spectral intensities. Solving the inverse eigenvalue problem is done using an iterative algorithm36 implemented in the Julia programming language, see ESI,† part 2 and 3 for further information.
(for the centroid) which the coupling constants Wj mix into the observed pattern. The matrices D in eqn (1) and (2) are derived by solving the inverse eigenvalue problem D = LFLT. The orthonormal transformation matrix (L) contains the eigenvectors, the OHb vector with components bi being directly known from the spectral intensities. Solving the inverse eigenvalue problem is done using an iterative algorithm36 implemented in the Julia programming language, see ESI,† part 2 and 3 for further information.
The magnitude of Wi provides information across the different amines on how strong the coupling between the individual perturbers and the deperturbed OHb state is. The Wi constants are expected to be rather similar across the amines, the spectral variation coming mainly from the position of the deperturbed states, rather than their coupling strength. If this is observed for the 8 amines under investigation, it provides additional evidence for the plausibility of the coupling model. As Table 2 shows, W2 is very uniform, as expected for a robust Fermi resonance between OHb and the bending overtone. For the higher order coupling W3 involving the 3-quantum state b2ON, this is also the case except for the bulky MN5MMMM case, which may well have a different potential shape for relative motion of the solvating water against the amine. Expectedly, W4 shows the largest variations, as it depends sensitively on the weakest intensity transition and does not lead to significant variations in the intensity centroid.
| Amine | W 2(B) | W 2(C) | W 3(B) | W 3(C) | W 4 |
|---|---|---|---|---|---|
| MN4 | 46(3) | 46(3) | 22(1) | 23(1) | 24(8) |
| MN5 | 44(3) | 44(3) | 21(1) | 22(1) | 30(5) |
| MN5MMMM | 44(1) | 45(1) | 37(4) | 41(3) | 33(3) |
| N555 | 50(1) | 51(1) | 26(1) | 27(1) | 27(7) |
| MMEN | 46(3) | 46(3) | 24(1) | 24(1) | 17(9) |
| MMIN | 48(1) | 48(1) | 28(1) | 29(1) | 26(7) |
| MMCN | 48(2) | 48(2) | 32(2) | 33(2) | 25(3) |
| MMTN | 46(1) | 47(1) | 35(2) | 37(2) | 23(7) |
The associated original perturber positions are summarised in Table 3. For the bending overtone, the symmetric N555 (quinuclidine) case stands out, but otherwise, the position is expectedly uniform, much more so than the original OHb position summarised in Table 1. It is also hardly dependent on the choice between model B or C. The variation of the original b2ON position is larger, because the ON stretching frequency obviously depends on the mass of the amine and one can see that it generally increases with decreasing mass, as expected. The largest scatter is observed in the position of the xONn state and ideally, this scatter can tell us something about the physical nature of this least prominent perturber state within the tetrad. The structure of eqn (2) would suggest that xONn is actually b2ON2, adding a further quantum of ON to b2ON.
| Amine | D b2(B) | D b2(C) | D b2ON(B) | D b2ON(C) | D xONn |
|---|---|---|---|---|---|
| MN4 | 3214(4) | 3214(4) | 3337(1) | 3337(1) | 3437(3) |
| MN5 | 3213(4) | 3212(4) | 3334(1) | 3334(1) | 3423(3) |
| MN5MMMM | 3215(3) | 3214(3) | 3317(4) | 3315(4) | 3383(2) |
| N555 | 3225(3) | 3225(3) | 3338(1) | 3338(1) | 3435(3) |
| MMEN | 3214(3) | 3213(3) | 3339(1) | 3339(1) | 3444(3) |
| MMIN | 3219(2) | 3218(2) | 3336(1) | 3336(1) | 3426(3) |
| MMCN | 3217(3) | 3216(3) | 3331(2) | 3331(2) | 3422(1) |
| MMTN | 3217(2) | 3217(2) | 3329(2) | 3328(3) | 3409(2) |
One could design other 4 × 4 coupling scenarios than the one in eqn (2), such as the following tridiagonal one, in which the fourth state is not directly coupled to OHb, but rather indirectly via b2ON
 | (3) |
We thus consider two variants of model C (eqn (2)) in which xONn is either interpreted as OHbON (C′) or as b2ON2 (C). Evidently, one will need anharmonic theory to decide between these simplified coupling schemes or to find that several of them combined provide the best description. However, we will continue our empirical strategy to see whether we can already adjudicate between the two variants of model C by following some substitution trends on the resulting deperturbed states.
4.5 Mass trends for perturbed and deperturbed ON stretching states in model C
We start with the interpretation of xONn as b2ON2, i.e. the assumption that OHb lights up a whole ladder of ON excitations built on b2. It is instructive to analyse the resulting deperturbed ON stretching fundamental and overtone of the monohydrate complexes in combination with the b2 bending overtone, obtained by subtracting b2 from the observed and deperturbed positions.In a simplified harmonic pseudo-diatomic picture, these ON stretching modes should scale inversely with the square root of the reduced mass between water (18 u) and the amine. Superimposed on this kinematic scaling, which is indicated by dashed curves in Fig. 7, there could be changes in the force constant due to varying hydrogen bond strength, caused by inductive effects of the N lone pair electron density and steric hindrance of the substituents. The filled symbols in Fig. 7 provide the raw results, obtained from the experimental differences between b2ON and b2 (ON fundamental around 160 cm−1) and between b2ON2 and b2 (ON overtone between 220 and 260 cm−1). While the fundamental appears to be nearly mass-independent, the overtone exhibits a strong mass dependence. Such a discrepancy would be difficult to rationalise without resonance effects and indeed the situation improves if the raw band positions are replaced by deperturbed band positions for b2 and b2ON, b2ON2, based on the model C deperturbation (empty symbols at different shades, model B gives nearly indistinguishable results). Now, the fundamental and overtone values behave more consistently. Both drop with increasing amine mass. They do so more steeply than the harmonic prediction (dashed curves), possibly due to anharmonic effects and due to an increasing steric hindrance of the water docking, which weakens the interaction. However, in view of the OHb trend observed for dimethylalkylamine monohydrates, one would have expected a less steep decrease with increasing mass. The drop is particularly pronounced for the most sterically hindered amine 1,2,2,6,6-pentamethylpiperidine (MN5MMMM) and for the overtone. Because this amine has the lowest OHb stretching frequency and thus strongest hydrogen bond, the strong drop is somewhat counterintuitive and may also point to some mode mixing among the intermolecular motions.
From the deperturbed ON (intermolecular stretching fundamental) and ON2 (intermolecular stretching overtone) values, one can extract pseudo-diatomic harmonic wavenumbers and anharmonicity constants by assuming a Morse oscillator. With about 140 and 10 cm−1, respectively, they fall in an expected range for the dimer stretching motion, and again the most sterically hindered MN5MMMM shows the lowest frequency and most anharmonic hydrogen bond stretching motion (ESI,† Tables S16–S18).
4.6 Alternative interpretation of the fourth member of the tetrad (model C′)
Despite the reasonable success of this coupling model, where the OHb intensity is redistributed among b2, b2ON and b2ON2, we consider an alternative interpretation, where the highest energy state actually builds on OHb instead of b2.9 In this case, xONn would be interpreted as OHbON. Due to the increase in dipole moment upon OH stretch excitation, the hydrogen bond typically strengthens and shortens, which can lead to significant vibrational Franck–Condon intensity redistribution and thus resonance-independent intensity for such an OHbON combination band. The absence of significant intensity in the decoupled DOH experiments would have to be explained by limited signal-to-noise ratio. Alternatively, the OHbON combination band could gain intensity from mode mixing with resonance partners, without having to invoke transition moment redistribution. This is formally subsumed in a proposed effective W4 coupling constant to OHb. A way to test the plausibility of such an assignment is to adapt the analysis in Fig. 7 to the new situation. Fig. 8 thus compares the ON stretching fundamental on top of b2 for the raw (filled) and deperturbed (empty symbols) difference b2ON–b2 (blue, as in Fig. 7) with the same ON stretching fundamental on top of OHb for the raw (filled) and deperturbed (empty symbols) difference OHbON–OHb (green). One can see that the deperturbation effect for ON superimposed on OHb is now almost negligible. More importantly, the deperturbed values for ON on top of OHb and on top of b2 are physically meaningful, because they are systematically higher for the stronger hydrogen bond upon OHb excitation and lower for the weaker hydrogen bond upon b2 excitation. Without deperturbation, this is clearly not the case. The same is true for the mass trend, which follows the kinematic prediction (dashed lines) rather closely for ON in combination with b2. In combination with OHb, the drop with increasing mass is compensated by the increased strengthening of the hydrogen bond by OHb excitation for more highly substituted amines (with the exception of MN5MMMM, where steric hindrance affects the strengthening). Thus, the assumption that OHbON mainly gains visibility upon resonance (model C′) turns a counterintuitive assignment of the raw experimental data (ON stretching would have a higher frequency when coupled with b2 excitation than when coupled with OHb excitation) into an expected trend. Any resonance-independent vibrational Franck–Condon contribution to the OHbON intensity is neglected in this model, but anyway appears to be low.Ultimately, ab initio potential energy hypersurface + anharmonic dynamics calculations will have to show which of the empirical models (C with b2ON2 as the fourth state, or C′ with OHbON as the fourth state) is more realistic, but here, we continue testing and ranking the models empirically, now supported by simple harmonic DFT calculations.
4.7 Quantum-chemical bridging
To see whether the insights into the coupling mechanism allow for some predictive power, the case of triethylamine38 (EEEN) shall be explored. Based on quantum-chemical calculations including isomerisation barriers (Tables S27 and S28 in the ESI†), it may consist of several energetically close conformers. This is illustrated in Fig. 9. The experimental IR spectrum (Fig. 10) indeed indicates that at least two are populated in the jet expansion. The decoupled harmonic OHb position predicted for all three conformers at B3LYP-D3(BJ,abc)/def2-TZVP level can be adjusted based on experimental values for all 8 amine monohydrates which have been experimentally explored and assigned in this work (see Fig. S14 and Tables S19–S21 and S23 in the ESI†). The same procedure is followed for the perturber states. With the empirically refined harmonic positions and average empirical coupling constants for these 8 reference systems, synthetic spectra for the two conformers are calculated and compared to the experimental one. Relative intensities of the three conformers are roughly estimated based on an energy disadvantage of 2–3 kJ mol−1 (Fig. 9, the zero-point corrected energy penalties are 3.0 and 3.2 kJ mol−1 for EEEN2 and EEEN3 monomers, respectively, the less relevant penalties for the monohydrates are somewhat lower) for the metastable conformers relative to the global minimum structure and a symmetry disadvantage of the non-chiral EEEN3 species (Fig. 9). Based on the assumption that EEEN1 does not profit from conformer relaxation in the jet due to the high interconversion barrier and assuming an isoenergetic situation for EEEN2 and EEEN3, this leads to a coarse 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4
0.4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.2 ratio which is combined with the relative intensity of the coupling partners based on average coupling constants. Depending on whether one interprets the highest energy xONn transition as b2ON2 (model C) or OHbON (model C′), slightly different spectra are expected despite the same nominal coupling matrix elements. This arises from the difference in empirical adjustment to the (unscaled) harmonic prediction of the xONn transition. As shown in Fig. 10, both models provide satisfactory predictions of the experimentally observed intensity pattern. The conformer spectral splitting for the dominant (OHb) transition is somewhat underestimated. A major difference in the prediction is expectedly found for the weak xONn state. While model C predicts the global minimum conformer to have a lower wavenumber, model C′ predicts the opposite. As long as we cannot unambiguously assign which of the two weak high wavenumber signals is due to EEEN1, the simulation does not provide strong evidence for either model C or model C′. However, it appears that model C′ achieves a slightly better match, with all simulated peaks being consistently higher in wavenumber than the experimental counterparts. Ultimately, anharmonic calculations will help to decide between the coupling models, whereas the present simulations are strictly limited to harmonic predictions in combination with training by the data set of 8 assigned amine hydrates. A detailed description of the simulations and the reasoning behind them is provided in the Tables S22 and S24 in the ESI.†
0.2 ratio which is combined with the relative intensity of the coupling partners based on average coupling constants. Depending on whether one interprets the highest energy xONn transition as b2ON2 (model C) or OHbON (model C′), slightly different spectra are expected despite the same nominal coupling matrix elements. This arises from the difference in empirical adjustment to the (unscaled) harmonic prediction of the xONn transition. As shown in Fig. 10, both models provide satisfactory predictions of the experimentally observed intensity pattern. The conformer spectral splitting for the dominant (OHb) transition is somewhat underestimated. A major difference in the prediction is expectedly found for the weak xONn state. While model C predicts the global minimum conformer to have a lower wavenumber, model C′ predicts the opposite. As long as we cannot unambiguously assign which of the two weak high wavenumber signals is due to EEEN1, the simulation does not provide strong evidence for either model C or model C′. However, it appears that model C′ achieves a slightly better match, with all simulated peaks being consistently higher in wavenumber than the experimental counterparts. Ultimately, anharmonic calculations will help to decide between the coupling models, whereas the present simulations are strictly limited to harmonic predictions in combination with training by the data set of 8 assigned amine hydrates. A detailed description of the simulations and the reasoning behind them is provided in the Tables S22 and S24 in the ESI.†
4.8 Methylation instead of deuteration
One way to empirically identify an intrinsic IR intensity of the OHbON transition, derived from vibrational Franck–Condon effects and free from resonance effects, is to switch from water to methanol (ESI,† Fig. S16). The HOC bending vibration in methanol is much lower than HOH bending in water and therefore any anharmonic resonance building on b2, including b2ON2, is minimised. If there is significant intensity in the region where the OHbON combination band is expected, it must be due to intensity redistribution through a vertical OH stretching excitation in the ON-stretching potential. Fig. 11 shows that this is not the case. In the upper two traces, a low methanol concentration was chosen such that no other strong bands interfere with the expected OHbON positions (spanned by two arrows due to the fact that the DFT calculations predict two intermolecular modes with significant ON stretching character, see Table S25 in the ESI†). In the lower two traces, the methanol concentration is higher to increase the visibility of any OHbON candidates. This increases the abundance of complexes with two solvent molecules (marked T). Note that the hydrogen bond conformation of monomethanolates typically differs from that of monohydrates (see Table S26 and Fig. S15 in the ESI†) in the torsion angle around the hydrogen bond, to optimise secondary dispersion and repulsion interactions of the methyl group with the amine ring. The preferred amine conformation is not affected by the solvent. OHbON intensity exceeding 10% of the OHb intensity can be safely ruled out. The chemical substitution of the free OH bond thus confirms the isotope substitution result that any substantial OHbON intensity in the parent monohydrate is more likely to derive from wave function mixing (resonance mediated by the b2 + ON manifold) rather than from Franck–Condon intensity redistribution (change in the preferred ON distance with OHb stretching excitation).4.9 Mono- and dihydrate contributions to the HyDRA database
The vibrational tertiary amine monohydrates and dihydrates reported in this work will be included in the database on hydrogen-bonded water OH stretching modes,34 because they provide anharmonic splitting patterns involving more than one resonance partner with substantial intensity sharing for monohydrates and also water stretching vibrations in dihydrates, for water units attached to monohydrates. The relevant parameters are summarised in Table 4. Wherever there is evidence for resonance, it is described by a purity factor P which denotes the spectral intensity fraction remaining on the vibrational transition closest to the centroid of the pattern (range provided in steps of 0.05). For the symmetric uncertainty of the deperturbed position, which is taken as the average of model predictions B and C, the larger of the individual integration uncertainties or one half of the difference between model B and C is used.| Amine | OHb-ra | P | OHb-db | OHb-ic |
|---|---|---|---|---|
| a Raw monohydrate wavenumber. b Deperturbed monohydrate wavenumber. c Raw dihydrate wavenumber for indirect solvation contact (T). | ||||
| MN4 | 3299(1) | 0.50–0.70 | 3289(5) | 3485(2) |
| MN5 | 3289(1) | 0.55–0.70 | 3278(5) | 3481(2) |
| MN5MMMM | 3257(1) | 0.30–0.45 | 3242(7) | 3499(2) |
| N555 | 3297(1) | 0.45–0.60 | 3281(4) | 3475(2) |
| MMEN | 3301(1) | 0.50–0.65 | 3293(4) | 3484(2) |
| MMIN | 3285(1) | 0.45–0.60 | 3267(3) | 3482(2) |
| MMCN | 3282(1) | 0.40–0.60 | 3271(4) | 3479(2) |
| MMTN | 3269(1) | 0.40–0.55 | 3250(4) | 3476(2) |
4.10 Towards an inaccessible nitrogen acceptor
Even the most bulky amine studied so far, MN5MMMM, still shows a progressive downshift of the coordinating water or methanol OH stretching vibration in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex, but the 2
1 complex, but the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (T) already starts to reverse its downshift due to poorer accessibility of the N acceptor. We tried to push this turn-over by investigating the very bulky IIIN species, where access along the last methyl substituent is blocked by double methylation. The spectrum (see ESI,† Fig. S21) is rather weak due to the weaker hydrogen bond, but one can distinguish two contributions scaling like a 1
1 complex (T) already starts to reverse its downshift due to poorer accessibility of the N acceptor. We tried to push this turn-over by investigating the very bulky IIIN species, where access along the last methyl substituent is blocked by double methylation. The spectrum (see ESI,† Fig. S21) is rather weak due to the weaker hydrogen bond, but one can distinguish two contributions scaling like a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex and one signal due to the 2
1 complex and one signal due to the 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex (T). Interestingly, the 1
1 complex (T). Interestingly, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex signals are located substantially higher in wavenumber than for MN5MMMM or MMCN (shown in ESI,† Fig. S22 and S23), whereas the T signal is more in line with these reference compounds. The latter observation does not agree well with harmonic predictions, but the 1
1 complex signals are located substantially higher in wavenumber than for MN5MMMM or MMCN (shown in ESI,† Fig. S22 and S23), whereas the T signal is more in line with these reference compounds. The latter observation does not agree well with harmonic predictions, but the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex shift is matched by harmonically predicted shifts, in particular when the larger of the two peaks is assigned to the OHb transition. It has to remain open whether the weaker of the two 1
1 complex shift is matched by harmonically predicted shifts, in particular when the larger of the two peaks is assigned to the OHb transition. It has to remain open whether the weaker of the two 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complex signals is due to a resonance or due to the OHb transition of some isomer. In any case, IIIN is the first tertiary amine which is inaccessible enough to water molecules to detune the OHb/b2 resonance.
1 complex signals is due to a resonance or due to the OHb transition of some isomer. In any case, IIIN is the first tertiary amine which is inaccessible enough to water molecules to detune the OHb/b2 resonance.
5 Conclusions
This work provides firm spectral OHb assignments for 8 mono- and 8 dihydrates of tertiary amines, summarized in Fig. 12, where they are ordered in the sequence of decreasing deperturbed monohydrate OHb wavenumber. The dominant monohydrate OHb signal follows more or less the same order. This order is compatible with the total number of substituents (nβ) at the three α carbons, if one unit is subtracted for every constraining ring unit (nr). The first four entries have nβ − nr = 1, whereas the following entries increase monotonically to nβ − nr = 5. Not shown is the IIIN case (ESI,† Fig. S21–S23) with nβ − nr = 6 because its assignment is not secured. In summary:• All amine monohydrates show a robust anharmonic band pattern of 3–4 signals, where a harmonic picture would predict just one signal
• Isotope substitution suggests that the deperturbed OHb band position (in the absence of anharmonic resonances) of the monohydrates must be close to the central, dominant OHb signal
• The two strongest or even all three satellite bands to the central OHb signal must be included in the intensity centroid to bring this centroid close to the dominant OHb signal
• Replacement of water by methanol reduces the spectrum to a single strong OHb signal, suggesting that any vibrational Franck–Condon intensity effects may be weak for the amine monohydrates as well
• For the weakest satellite band, most evidence points at a combination band of OHb with the intermolecular stretching mode ON (OHbON), likely with intensity contributions from wavefunction mixing, e.g. with b2ON as its Fermi resonance partner
• Against an alternative assignment of the weakest satellite as a four-quantum b2ON2 (water bending overtone combined with dimer ON stretching overtone) transition speak the steep mass dependence of the underlying ON overtone and the slightly poorer predictive power for the multiconformational EEEN case, but theory will probably be needed to firmly rule out this interpretation
For dihydrates as heterotrimers (T), only the OHb vibration of the indirectly solvating water is shown in Fig. 12, whereas the directly amine-solvating water is so much downshifted that it overlaps with the CH stretching manifold. The 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 trimer character of this signal can be easily differentiated from the 1
1 trimer character of this signal can be easily differentiated from the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 monohydrate signals by varying the water concentration (see also ESI,† Fig. S17–S20).9
1 monohydrate signals by varying the water concentration (see also ESI,† Fig. S17–S20).9
Our experimental findings are useful for theory at two levels. Methods which attempt to rigorously predict multi- or even full-dimensional anharmonic spectra37,39,40 can try to simulate the entire monohydrate resonance polyad which the softened OH bond creates around 3300 cm−1 and to resolve the residual ambiguities between b2ON2 and OHbON as well as between transition moment redistribution and wavefunction mixing. Methods which try to capture the softening of the OH bond as a function of the chemical environment can ignore the anharmonic coupling details and focus on the deperturbed centroid of the experimental spectrum.
An interesting challenge for the future is to find combinations of alkyl groups which lead to even stronger downshifts of the solvating water than observed in this work. In those cases, the OH stretching wavenumber may become the lowest among the interacting states, even lower than the water bending overtone, as in the case of H2S complexes with amines.41 In terms of chemical substitution strategy, bigger is not always better due to steric hindrance. In this context we note that the very bulky IIIN amine exhibits a weak hydrogen bond (ESI,† Fig. S21–S23). It may also be interesting to correlate the experimental spectra with the proton affinity of the amines, which is free of sterical constraints and of other secondary interactions of the solvent molecule.42
As reported here, the spectroscopic data provide a significant extension of the training database for future HyDRA challenges, roughly doubling the largest included hydrogen-bond downshifts from about 200 to 400 cm−1. This comes at the price of lighting up multiple anharmonic resonances, but the present work offers a path for coarse-grained predictions which average over the underlying wavefunction mixing events.
Author contributions
E. L.: data curation, formal analysis, investigation (IR), visualisation, writing – review & editing; N. O. B. L.: data curation, formal analysis, investigation (Raman), software, writing – review & editing; M. A. S.: conceptualisation, formal analysis, funding acquisition, methodology, supervision, writing – original draft.Data availability
The most important raw spectra for this work are made available in the GRO.Data repository at https://doi.org/10.25625/KRTNYQ. Extensive data supporting the claims are available as part of the ESI.† A compact summary of benchmarking-relevant quantities will be made available34 and linked to this publication.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Margarethe Bödecker, Beppo Hartwig, Casper Jensen and Henrik Kjaergaard for helpful discussions and Taija Fischer for initial experimental work and advice. This work was funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – 389479699/GRK2455.Notes and references
- E. T. J. Nibbering and T. Elsaesser, Chem. Rev., 2004, 104, 1887–1914 CrossRef CAS PubMed.
- L. C. Ch’ng, A. K. Samanta, G. Czakó, J. M. Bowman and H. Reisler, J. Am. Chem. Soc., 2012, 134, 15430–15435 CrossRef PubMed.
- K. Inoue, Y. Litman, D. M. Wilkins, Y. Nagata and M. Okuno, J. Phys. Chem. Lett., 2023, 14, 3063–3068 CrossRef CAS PubMed.
- M. Flór, D. M. Wilkins, M. de la Puente, D. Laage, G. Cassone, A. Hassanali and S. Roke, Science, 2024, 386, eads4369 CrossRef PubMed.
- E. L. Sibert, Annu. Rev. Phys. Chem., 2023, 74, 219–244 CrossRef CAS PubMed.
- I. León, P. F. Arnáiz, I. Usabiaga and J. A. Fernández, Phys. Chem. Chem. Phys., 2016, 18, 27336–27341 RSC.
- A. Potapov and P. Asselin, Int. Rev. Phys. Chem., 2014, 33, 275–300 Search PubMed.
- K. E. Otto, Z. Xue, P. Zielke and M. A. Suhm, Phys. Chem. Chem. Phys., 2014, 16, 9849–9858 RSC.
- E. Lwin, T. L. Fischer and M. A. Suhm, J. Phys. Chem. Lett., 2023, 14, 10194–10199 CrossRef CAS PubMed.
- M. Rozenberg, A. Loewenschuss and C. J. Nielsen, J. Phys. Chem. A, 2012, 116, 4089–4096 CrossRef CAS PubMed.
- S. Jiang, M. Su, S. Yang, C. Wang, Q.-R. Huang, G. Li, H. Xie, J. Yang, G. Wu, W. Zhang, Z. Zhang, J.-L. Kuo, Z.-F. Liu, D. H. Zhang, X. Yang and L. Jiang, J. Phys. Chem. Lett., 2021, 12, 2259–2265 CrossRef CAS PubMed.
- A. Kjaersgaard, E. Vogt, A. S. Hansen and H. G. Kjaergaard, J. Phys. Chem. A, 2020, 124, 7113–7122 CrossRef CAS PubMed.
- A. Iwasaki, A. Fujii, T. Watanabe, T. Ebata and N. Mikami, J. Phys. Chem., 1996, 100, 16053–16057 CrossRef CAS.
- O. J. Curnow and D. L. Crittenden, J. Phys. Chem. A, 2021, 125, 1355–1358 CrossRef CAS PubMed.
- H. C. Gottschalk, A. Poblotzki, M. Fatima, D. A. Obenchain, C. Pérez, J. Antony, A. A. Auer, L. Baptista, D. M. Benoit, G. Bistoni, F. Bohle, R. Dahmani, D. Firaha, S. Grimme, A. Hansen, M. E. Harding, M. Hochlaf, C. Holzer, G. Jansen, W. Klopper, W. A. Kopp, M. Krasowska, L. C. Kröger, K. Leonhard, M. M. Al-Mogren, H. Mouhib, F. Neese, M. N. Pereira, M. Prakash, I. S. Ulusoy, R. A. Mata, M. A. Suhm and M. Schnell, J. Chem. Phys., 2020, 152, 164303 CrossRef CAS PubMed.
- C. Emmeluth, M. A. Suhm and D. Luckhaus, J. Chem. Phys., 2003, 118, 2242–2255 CrossRef CAS.
- S. Horvath, A. B. McCoy, B. M. Elliott, G. H. Weddle, J. R. Roscioli and M. A. Johnson, J. Phys. Chem. A, 2010, 114, 1556–1568 CrossRef CAS PubMed.
- J. J. Talbot, N. Yang, M. Huang, C. H. Duong, A. B. McCoy, R. P. Steele and M. A. Johnson, J. Phys. Chem. A, 2020, 124, 2991–3001 CrossRef CAS PubMed.
- N. O. B. Lüttschwager, Phys. Chem. Chem. Phys., 2024, 26, 10120–10135 RSC.
- N. O. B. Lüttschwager, J. Open Source Software, 2021, 6, 3526 CrossRef.
- A. Nejad, A. F. Pérez Mellor, M. Lange, I. Alata, A. Zehnacker and M. A. Suhm, Phys. Chem. Chem. Phys., 2023, 25, 10427–10439 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- W. Sander, S. Roy, I. Polyak, J. M. Ramirez-Anguita and E. Sanchez-Garcia, J. Am. Chem. Soc., 2012, 134, 8222–8230 CrossRef CAS PubMed.
- D. Leicht, M. Kaufmann, R. Schwan, J. Schäfer, G. Schwaab and M. Havenith, J. Chem. Phys., 2016, 145, 204305 CrossRef PubMed.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- M. A. Marques, M. J. Oliveira and T. Burnus, Comput. Phys. Commun., 2012, 183, 2272–2281 CrossRef CAS.
- S. Lehtola, C. Steigemann, M. J. Oliveira and M. A. Marques, SoftwareX, 2018, 7, 1–5 CrossRef.
- T. L. Fischer, T. Wagner, H. C. Gottschalk, A. Nejad and M. A. Suhm, J. Phys. Chem. Lett., 2021, 12, 138–144 CrossRef CAS PubMed.
- E. M. Brás, C. Zimmermann, R. Fausto and M. A. Suhm, Phys. Chem. Chem. Phys., 2024, 26, 5822–5829 RSC.
- A. Gusach, Y. Lee, A. N. Khoshgrudi, E. Mukhaleva, N. Ma, E. J. Koers, Q. Chen, P. C. Edwards, F. Huang, J. Kim, F. Mancia, D. B. Veprintsev, N. Vaidehi, S. N. Weyand and C. G. Tate, Nat. Commun., 2024, 15, 7555 CrossRef CAS PubMed.
- Hydrate Donor Redshift Anticipation, a database maintained by the BENCh DFG research training group in Göttingen, 2024-2025, available under https://qmbench.net/databases/hydra.
- Q.-R. Huang, Y.-C. Li, T. Nishigori, M. Katada, A. Fujii and J.-L. Kuo, J. Phys. Chem. Lett., 2020, 11, 10067–10072 CrossRef CAS PubMed.
- N. O. B. Lüttschwager, Fermi4x4.jl - Extracting Anharmonic Coupling Constants from Vibrational Spectra, Zenodo, 2025, https://zenodo.org/records/14882836 Search PubMed.
- E. L. Sibert III, K. N. Blodgett and T. S. Zwier, J. Phys. Chem. A, 2021, 125, 7318–7330 CrossRef PubMed.
- E. R. Kjærgaard, K. H. Møller, T. Berndt and H. G. Kjaergaard, J. Phys. Chem. A, 2023, 127, 8623–8632 CrossRef PubMed.
- A. Nejad and E. L. Sibert III, J. Chem. Phys., 2021, 154, 064301 CrossRef CAS PubMed.
- X.-G. Wang and T. Carrington Jr., J. Chem. Phys., 2023, 158, 084107 CrossRef CAS PubMed.
- M. H. V. Graneri, D. Spagnoli, D. A. Wild and A. J. McKinley, J. Chem. Phys., 2024, 160, 124312 CrossRef CAS PubMed.
- O. Y. Ali, E. Jewer and T. D. Fridgen, Can. J. Chem., 2013, 91, 1292–1302 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Experimental, spectral, modeling and quantum-chemical details. See DOI: https://doi.org/10.1039/d5cp00332f |
| This journal is © the Owner Societies 2025 |


![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif)