Evaluating iron diimines: ion-pairing, lability and the reduced state

Abstract

Tris(diimine)iron(II) complexes are aspirational photosensitizers but their small ligand fields confer lability and distinct redox properties. We study these aspects in the gas phase using mass spectrometry and density-functional theory of [Fe(N^N)₃]²⁺ dications (N^N = 2,2′-bipyridine (bipy), 1,10-phenanthroline (phen), 4,4′-dibromo-2,2′-bipyridine (bipy^Br), 4,4′-di(tert-butyl)-2,2′-bipyridine (bipy^t-Bu)). Collision-induced dissociation of ion pairs {[Fe(N^N)₃]X}⁺ (X = BPh₄⁻ and BAr^F₄⁻; Ar^F = 3,5-bis(trifluoromethyl)phenyl) requires high energies, not because of strong ion pairing but because the tetraarylborates are poor ligands, such that the lowest-energy pathway requires ligand dissociation. Dissociation of dications reveals contrasting thermal stabilities ([Fe(bipy^t-Bu)₃]²⁺ > [Fe(phen)₃]²⁺ ≫ [Fe(bipy^Br)₃]²⁺ > [Fe(bipy)(phen)₂]²⁺ > [Fe(bipy)₂(phen)]²⁺ > [Fe(bipy)₃]²⁺), while ion-mobility spectrometry reveals their relative collision cross-sections ([Fe(bipy^t-Bu)₃]²⁺ > [Fe(bipy^Br)₃]²⁺ > [Fe(phen)₃]²⁺ > [Fe(bipy)(phen)₂]²⁺ > [Fe(bipy)₂(phen)]²⁺ > [Fe(bipy)₃]²⁺). Dications can be reduced to their respective monocations with [1,3-dicyanobenzene]⁻, and the extent of reaction increases with calculated redox potentials for [Fe(N^N)₃]^2+/+ couples. Despite the ligand-centered nature of the redox processes, the stabilities of the radical monocations ([Fe(bipy^t-Bu)₃]⁺ ≈ [Fe(phen)₃]⁺ > [Fe(bipy)(phen)₂]⁺ > [Fe(bipy)₂(phen)]⁺ > [Fe(bipy^Br)₃]⁺ > [Fe(bipy)₃]⁺) follow a similar order to the dications. This suggests that the π-donor and -acceptor properties of diimines are apt to stabilize both charge states, as would be present in photoredox catalysis.

---

Introduction

Tris(diimine)iron complexes¹ have enjoyed renewed attention because of their promise in photoredox catalysis.² For example, octahedral Fe complexes of 2,2′-bipyridine (bipy, Fig. 1a) or 1,10-phenanthroline (phen) derivatives are archetypes^3,4 from which one can develop first-row-transition-metal photosensitizers⁵ for the synthesis of solar fuels and fine chemicals.⁶ Although the small ligand fields of first-row-transition-metal complexes⁷ do not discount them from being useful photosensitizers, such complexes have lower thermal stabilities than do precious-metal d⁶ analogs like [Ru(bipy)₃]²⁺.⁸ The weak metal–ligand bonding in first-row-transition-metal complexes necessitates care but affords rich chemistry. For example, mixtures of [Fe(bipy)₃]²⁺ derivatives undergo rapid ligand redistribution (Fig. 1b),⁹ a process that is amenable to study by electrospray ionization mass spectrometry (ESI-MS). ESI affords gas-phase ions with similar internal energy distributions to those in solution,¹⁰ ensuring that the data are reflective of the diverse speciation in processes such as ligand exchange^11,12 and catalysis.¹³ This allows one to determine the relative thermal stabilities of labile species in terms of their propensity to undergo collision-induced dissociation (CID).

Fig. 1 (a) Fe and Ru diimines [M(N^N)₃]²⁺ have contrasting photochemistry. (b) [Fe(N^N)₃]²⁺ species undergo ligand exchange in solution, affording mixtures amenable to mass spectrometry. (c) Photoredox catalysis can involve reduced species like ligand-centered radicals [Fe(N^N)₂(N^N·)]⁺. (d) This paper describes homo- and heteroleptic [Fe(N^N)₃]²⁺ complexes in the gas phase: how they bind anions, undergo collision-induced dissociation (CID), get reduced and undergo electron-transfer dissociation (ETD).

Much like their Ru analogs, photoexcited Fe diimines [Fe(N^N)₃]²⁺* can, in principle, undergo oxidative or reductive quenching. The latter reaction affords the topical reduced species [Fe(N^N)₃]⁺, data for which are scarce. Solid salts of monocations [Fe(bipy)₃]⁺ and [Fe(bipy^t-Bu)₃]⁺ (bipy^t-Bu = 4,4′-di(tert-butyl)-2,2′-bipyridine, Fig. 1c) are known, and electrochemically- or chemically-generated [Fe(bipy)₃]⁺ gives rise to an almost isotropic EPR signal (g = 1.996 with temperature-dependent line-broadening),¹⁴ and a Mössbauer absorption (δ = 0.33 mms⁻¹; ΔE_Q = 0.37 mms⁻¹)¹⁵ that are consistent with bipy·⁻ binding Fe^II as part of a [Fe^II(bipy)₂(bipy·)]⁺ description with fast electron-hopping between ligands. In contrast, density functional theory (DFT) calculations suggest the radical to be fully delocalized.¹⁵ Despite the catalytic significance of such monocations, satisfactory analytical or structural data on them are not available,¹⁵ which suggested to us that alternative methods may be necessary to further understand these complexes.

Although we were inspired by the above and other^16–18 works, important unanswered questions remained. What are the atomic and electronic structures of ligand-exchange intermediates and fragments thereof? Do dications [Fe(N^N)₃]²⁺ interact appreciably with monoanions and what are the stabilities of the resulting ion pairs? What are the stabilities of the (homoleptic and heteroleptic) dications themselves? And, most crucially: how can we compare the propensities of different dications [Fe(N^N)₃]²⁺ to get reduced to monocations [Fe(N^N)₃]⁺, and what are the relative stabilities of the latter? Here, we answer these four important questions by studying [Fe(N^N)₃]²⁺ (N^N = bipy, phen, bipy^t-Bu, 4,4′-dibromo-2,2′-bipyridine (bipy^Br)) complexes in detail using MS, tandem MS (MS²) and ion-mobility spectrometry (IMS). Our annotations of mass spectra are aided by DFT and MD calculations, which further offer a detailed picture of atomic structure and redox potentials of Fe diimines (Fig. 1d).

Results and discussion

Diimine ligand redistribution

Tris(diimine)ruthenium complexes are kinetically inert, in contrast to their first-row Fe counterparts, for which ligand dissociation and redistribution are relatively rapid.¹² One study on [Fe(bipy)₃]²⁺ derivatives bearing amide hydrogen-bond donors (Fig. 1b) has described the catalytic effect that the basic anion Cl⁻ has on ligand redistribution.⁹ Being a hydrogen-bond acceptor, Cl⁻ ‘gathers’ bipy ligands together, making ligand exchange facile. Yet, we wondered if Cl⁻, aside from this hydrogen-bonding role, may have a catalytic role as a ligand for Fe intermediates. We considered equimolar [Fe(bipy)₃]²⁺ and [Fe(phen)₃]²⁺ (without amide substituents) and used ESI-MS to monitor ligand redistribution with: (i) no additive, (ii) 10 equivalents [ⁿBu₄N]Cl or (iii) 10 equivalents [ⁿBu₄N]PF₆ (we used [Ru(phen)₃]Cl₂ as a substitutionally-inert (and redox inert, under these conditions) internal standard), measuring intensities of [Fe(bipy)₃]²⁺ (m/z 262; Fig. 2a), [Fe(bipy)₂(phen)]²⁺ (m/z 274), [Fe(bipy)(phen)₂]²⁺ (m/z 286) and [Fe(phen)₃]²⁺ (m/z 298). The relative intensity of [Fe(bipy)₃]²⁺, for example, approximately follows first-order decay on the approach to equilibrium, which is slowest when no additive is present. It is faster with added [ⁿBu₄N]Cl but even faster with [ⁿBu₄N]PF₆ present (Fig. S43–S48, ESI†). Thus, ligand redistribution is faster in solutions of high ionic strength, particularly with the non-coordinating anion PF₆⁻. We posit that although Cl⁻ may help convert [Fe(bipy)₃]²⁺ into labile intermediates like cis-[Fe(bipy)₂Cl₂], excess Cl⁻ present may compete with phen for reaction with this intermediate, thereby slowing the subsequent formation of the ligand-exchange product [Fe(bipy)₂(phen)]²⁺. Given the possible intermediacy of cis-[Fe(bipy)₂Cl₂], we conducted DFT calculations on this complex in the gas phase. The ligand field for cis-[Fe(bipy)₂Cl₂] is weaker than that for [Fe(bipy)₃]²⁺, so the former certainly prefers a high-spin state (Fig. 2b), as it does in the solid state according to magnetic measurements.¹⁹ A high-spin state is also preferred for trigonal-bipyramidal [Fe(bipy)₂Cl]⁺. The solvated version of this complex cis-[Fe(bipy)₂Cl(MeOH)]⁺ is also a possible intermediate in ligand redistribution.⁹ One reason for the fast interconversion between diimine complexes [Fe(N^N)₃]²⁺, [Fe(N^N)₂Cl]⁺ and cis-[Fe(N^N)₂Cl₂] is that they all have the same ground-state spin (S = 2), such that the reactions are spin-allowed. Nevertheless, because our calculations are in the gas phase and the ligand-exchange processes happen in MeOH, we cannot rule out two-state reactivity (spin-crossover),^20–22 whereby the reactions also occur over other spin manifolds.

Fig. 2 (a) Example ESI-MS of a solution containing [Fe(bipy)₃]Cl₂ (2 μM) and [Fe(phen)₃]Cl₂ (2 μM) after 4 h at 26 °C in MeOH. (b) DFT-calculated structures of high-spin cis-[Fe(bipy)₂Cl₂] and trigonal-bipyramidal [Fe(bipy)₂Cl]⁺ at the PBE/DVZP level of theory.

For comparison, solid [Fe(bipy)₃]Cl₂·5H₂O is low-spin but extrudes bipy at 200 °C to give high-spin [Fe(bipy)₂Cl₂], which at 250 °C converts into [Fe(bipy)Cl₂], also a quintet.⁸ In that study, [Fe(bipy)₃]²⁺ might access a high-spin quintet state that undergoes rapid, spin-allowed pyrolysis into high-spin products.²³ We do not dwell on ligand redistribution here, and use it only as a route to heteroleptic complexes. We now describe homo- and heteroleptic complexes [Fe(N^N)₃]²⁺ in terms of the: (i) relative stabilities of ion pairs {[Fe(N^N)₃]X}⁺, (ii) relative stabilities of the complexes themselves, and (iii) nature of the reduced species [Fe(N^N)₃]⁺.

Anion binding

Metal diimine photosensitizers are usually deployed in solution, and the choice of anions can affect stability, solubility and reaction selectivity. Ion pairing is amenable to study by ESI because it is a gentle solution-phase process that affords charged droplets that are subsequently desolvated. Although ESI is a soft method, we must stress certain caveats in using ESI-MS data to make conclusions about ions pairs in solution. First, because we only observe charged species, we are blind to 2 : 1 ion clusters such as {[Fe(N^N)₃]X₂}. Second, desolvation of the droplets leads to high ionic strengths, and the observation of ion pairs that may only be very weakly associated, were they in solution.

ESI-MS of [Fe(N^N)₃]Cl₂ did not afford any detectable ion pairs {[Fe(N^N)₃]Cl}⁺, even when working at low RF energies, capillary voltages and cone voltages. These ion pairs were similarly not observed when switching to atmospheric-pressure chemical ionization. Addition of ⁿBu₄NOAc did not afford detectable {[Fe(N^N)₃]OAc}⁺, which contrasts previous detection by us²⁴ and others,^16,25 of {[Ru(N^N)₃]Cl}⁺ and {[Ru(N^N)₃]OAc}⁺. However, we do observe ion pairs {[Fe(N^N)₃]BPh₄}⁺ and {[Fe(N^N)₃]BAr^F₄}⁺ (Ar^F = 3,5-bis(trifluoromethyl)phenyl) on adding NaBPh₄ and NaBAr^F₄, respectively. If we consider the abundances of the ion pairs {[Fe(N^N)₃]BAr₄}⁺ relative to the dicationic complexes [Fe(N^N)₃]²⁺ (Table S2, ESI†), we see that [Fe(bipy)₃]²⁺ binds BPh₄⁻ more strongly than BAr^F₄⁻. In contrast, [Fe(phen)₃]²⁺ prefers BAr^F₄⁻ over BPh₄⁻. These intensities depend not only on the binding strength of the complexes with the tetraarylborates, but also on the relative binding strengths of other possible ions pairs and ionization efficiencies. Thus, the relative intensities cannot be taken to reflect the strength of the complex–tetraarylborate interaction. Although the tetraarylborates are weakly-coordinating in solution, they apparently experience strong interactions with the complex dications in the gas phase. We mass-select the ion pairs and plot the relative abundance (intensity divided by total intensity) of these parent ions and their daughter ions as a function of collision energy (CE). With respect to the parent ions, their relative abundances (‘survival yield’) typically follows a sigmoidal shape, fitting of which affords the energy required for 50% dissociation of the parent ion (CE_½, a measure of robustness).

CID of {[Fe(bipy)₃]BPh₄}⁺ (m/z 843; CE_½ = 1.7 eV; Fig. 3a, c and Fig. S15 and S16 (ESI†) and Table 1) in Ar gas does not afford [Fe(bipy)₂(BPh₄)]⁺ but instead gives [Fe(bipy)(BPh₄)]⁺ (m/z 531), which our DFT calculations suggest exists in a quintet ground state with two η¹-Ph rings binding Fe (Fig. 3b), rather than an arrangement with η⁶-Ph.²⁶ We find that BPh₄⁻ also undergoes B–C cleavage to give the aryl transmetallation products [Fe(bipy)₂(Ph)]⁺ (m/z 445) and [Fe(bipy)(Ph)]⁺ (m/z 289). Our calculations indicate that the quintet trigonal-bipyramidal complex [Fe(bipy)₂(Ph)]⁺ (Fig. S68, ESI†) is more thermodynamically stable than tetrahedral [Fe(bipy)(bipyPh)]⁺ (+0.18 eV, Fig. S65, ESI†), wherein the anionic ligand [bipyPh]⁻ results from Ph⁻ attacking a C6 site of bipy. The behavior of {[Fe(N^N)₃]X}⁺ ion pairs contrasts that of {[Ru(N^N)₃]X}⁺ analogs because the latter have such strong coordination bonds. Thus, the BPh₄⁻ anion falls apart before the Ru complex does, such that ligand-centered arylation of the intact complex affords [Ru(bipy)₂(bipyPh)]⁺ and BPh₃.²⁴

Fig. 3 (a) CID of {[Fe(bipy)₃]BPh₄}⁺ affords monocationic fragments. (b) DFT-calculated structure of high-spin [Fe(bipy)(BPh₄)]⁺ at the PBE/DVZP level of theory. Fe speciation during dissociation of (c) {[Fe(bipy)₃]BPh₄}⁺ and (d) {[Fe(bipy)₃]BAr^F₄}⁺.

Table 1 MS² and MS-IMS-MS data for [M(N^N)₃]²⁺ complexes and their derivatives

Ion	m/z	CE ½/eV	t d/ms
a Values obtained from ref. 24.N.D. not determined.
[Fe(bipy)2]^2+	184	26.2	7.45
[Fe(bipy)(phen)]^2+	196	30.0	7.87
[Fe(phen)2]^2+	208	37.3	8.24
[Fe(bipy)3]^2+	262	3.6	9.11
[Ru(bipy)3]^2+	285	26.4^a	9.36
[Fe(bipy)2(phen)]^2+	274	4.4	9.39
[Ru(bipy)2(phen)]^2+	297	28.5^a	9.74
[Fe(bipy)(phen)2]^2+	286	5.6	9.74
[Fe(phen)3]^2+	298	21.3	10.18
[Ru(phen)3]^2+	321	38.4^a	10.30
[Fe(bipy^Br)3]^2+	498	11.0	13.48
[Fe(bipy^t-Bu)3]^2+	430	24.7	16.85
{[Fe(bipy)3]BPh4}^+	843	1.7	33.14
{[Fe(phen)3]BPh4}^+	915	3.9	34.83
{[Fe(bipy)3]BAr^F4}^+	1387	27.4	N.D.
{[Fe(phen)3]BAr^F4}^+	1459	27.5	N.D.
[Co(bipy)3]^2+	263	2.3	9.58
[Co(bipy)2]^2+	185	23.8	7.87

---

The size of BPh₄⁻ prompted us to consider how much van der Waals forces contribute to the cation–anion binding energy. Our DFT calculations predict an energy change of −4.13 eV when BPh₄⁻ binds [Fe(bipy)₃]²⁺ to give {[Fe(bipy)₃]BPh₄}⁺. This decreases to −4.53 eV when D3 dispersion corrections are included, suggesting that dispersion forces account for ∼10% of the total interactions between the ions. As mentioned above, we did not observe the ion pair {[Fe(bipy)₃]Cl}⁺, but DFT calculations suggest that the ion interaction would be −6.15 eV, which is substantially stronger than that for the diffuse and large anion BPh₄⁻. Accounting for dispersion in the formation of {[Fe(bipy)₃]Cl}⁺ leads to an energy of −6.33 eV, suggesting that the interactions contribute only ∼2% in this case. That we do not see ion pairs involving Cl⁻ is likely more due to its strong solvation rather than Cl⁻ binding poorly to the dications in the gas phase.

In contrast to {[Fe(bipy)₃]BPh₄}⁺, the analog {[Fe(bipy)₃]BAr^F₄}⁺ (m/z 1387) does not cleanly lose bipy (CE_½ = 27.4 eV, Fig. 3d and Fig. S17–S19 (ESI†) and Table 1) because BAr^F₄⁻ cannot take its place by ligating Fe. However, the ion pair {[Fe(bipy)₃]BAr^F₄}⁺ does give the five-coordinate species [Fe(bipy)₂(Ar^F)]⁺ (m/z 581) as well as the F⁻ abstraction products [Fe(bipy)₂F]⁺ (m/z 387) and [Fe(bipy)F]⁺ (m/z 231). BAr^F₄⁻ is more weakly coordinating than BPh₄⁻ in solution, so dearylation of the former occurs only at higher CE_½ values. The analogous phen-containing ion pairs {[Fe(phen)₃]BPh₄}⁺ (m/z 915; Fig. S28–S30 (ESI†); CE_½ = 3.9 eV) and {[Fe(phen)₃]BAr^F₄}⁺ (m/z 1459; Fig. S31–S35 (ESI†); CE_½ = 27.5 eV) behave similarly to the bipy derivatives but have greater CE_½ values because phen binds Fe more strongly than does bipy. Although tetraarylborates are prized as weakly-coordinating anions in solution, it may at first seem strange that their ion pairs require high energies for dissociation in the gas phase. But it turns out that each ion pair {[Fe(N^N)₃]BAr₄}⁺ extrudes neutral species rather than relinquishing its ‘ionic’ bond to give [Fe(N^N)₃]²⁺, a process that would be prohibitive given the strength of the electrostatic interactions in the absence of solvent. Overall, MS is a powerful means to study the effects that counterions have on metal complexes.^27,28 We now describe our investigations of the homo- and heteroleptic [Fe(N^N)₃]²⁺ complexes in isolation using MS² and ion-mobility spectrometry (IMS).

Comparing stabilities and sizes of [Fe(N^N)₃]²⁺

The stabilities of cationic complexes [M(N^N)₃]ⁿ⁺ are often assessed in solution by methods such as potentiometry, spectrophotometry, NMR spectroscopy and calorimetry.²⁹ Though invaluable, these data are for mixtures that include anions and solvent, which may perturb the metal–ligand interactions we are concerned with. Here, we do away with anions and solvent by studying [Fe(N^N)₃]²⁺ species in the gas phase, comparing the stability against CID of the complexes [Fe(bipy)₃]²⁺, [Fe(bipy)₂(phen)]²⁺, [Fe(bipy)(phen)₂]²⁺, [Fe(phen)₃]²⁺, [Fe(bipy^Br)₃]²⁺ and [Fe(bipy^t-Bu)₃]²⁺. Each of these [Fe(N^N)₃]²⁺ species loses diimine N^N to give the unsaturated fragment [Fe(N^N)₂]²⁺. This reaction is clean because we have sigmoidal breakdown curves—plots of survival yield versus collision energy (Fig. 4a; see Fig. S10, S23, S37, S39, S52 and S56 (ESI†) for speciation plots).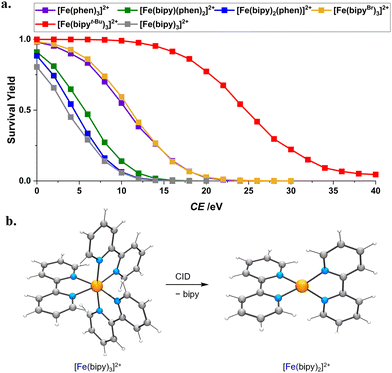

Fig. 4 (a) Breakdown curves of [Fe(N^N)₃]²⁺ as a function of collision energy. (b) DFT-calculated structures of quintet [Fe(bipy)₃]²⁺ and [Fe(bipy)₂]²⁺ at the PBE/DVZP level of theory.

Relative to [Fe(bipy)₃]²⁺ (CE_½ = 3.6 eV, Table 1), [Fe(bipy^t-Bu)₃]²⁺ (CE_½ = 24.7 eV) is more robust on account of the electron-donating t-Bu substituents making bipy^t-Bu more basic towards the Fe^II Lewis acid. We were curious whether intramolecular van der Waals forces also contribute to the greater robustness of the heavier complex, so we obtained energy-minimized DFT-calculated structures of [Fe(bipy^t-Bu)₃]²⁺ at the PBE/DVZP level of theory both with and without D3 dispersion corrections. The structures are virtually identical (for example, r(Fe–N) distances are within 0.01 Å), suggesting that van der Waals forces are not a significant contributor in this case. Given this, we might also infer that the greater stability of [Fe(bipy^Br)₃]²⁺ (CE_½ = 11.0 eV) relative to [Fe(bipy)₃]²⁺ cannot arise from dispersion interactions involving the heavy Br atoms. An alternative explanation may be that the electron-withdrawing Br substituents allow for stronger π-backbonding from Fe^II to bipy^Br. Replacing bipy with phen ligands gives more stable complexes, reflected in increased CE_½ values. That Fe²⁺ binds phen more strongly than it does bipy is also reflected in [Fe(bipy)₂(phen)]²⁺ (CE_½ = 4.4 eV) and [Fe(bipy)(phen)₂]²⁺ (CE_½ = 5.6 eV) preferentially losing bipy instead of phen. Yet, unlike [Ru(N^N)₃]²⁺ analogs, even without applying collision energy [Fe(N^N)₃]²⁺ affords ions for unsaturated [Fe(N^N)₂]²⁺ species, enabling us to select and study them. These species are very resistant to further dissociation (Table 1) because each Fe–N bond gets much stronger when there are only four of them. In terms of structure, DFT suggests that [Fe(bipy)₃]²⁺ favors a quintet state (Fig. 4b) over triplet (+0.55 eV) and singlet states (+0.56 eV). CID of [Fe(bipy)₃]²⁺ gives [Fe(bipy)₂]²⁺, which favors a high-spin tetrahedral structure (Fig. 4b) over low-spin distorted-square-planar (+1.09 eV, Fig. S66, ESI†) or high-spin distorted-square-planar (+0.62 eV) alternatives. As with the parent complex, the quintet for brominated derivative [Fe(bipy^Br)₃]²⁺ (Fig. S67, ESI†) is lower in energy than the triplet (+0.59 eV) and singlet (+0.64 eV) states.

We noted above that intramolecular van der Waals forces are not major contributors to the binding energy of a complex. The heavier complexes have greater CE_½ values likely because their mass also results in the complex and the Ar collision gas having a lower centre-of-mass kinetic energy. The multiple collisions experienced by the complex ions here preclude us from performing this coordinate transformation.³⁰ Although the Fe complexes discussed here are similar in structure, we cannot be certain that their kinetic energy distributions are similar. For this reason, we exercise caution when comparing our CE_½ values.

In addition to studying the robustness of complex dications, we also performed IMS, wherein we pass ions through N₂ gas and measure the arrival time (t_d, Table 1 and Fig. S62 and S63, ESI†) of each. For a given charge, ions with smaller collision cross-sections are more susceptible to a traveling voltage wave, affording smaller t_d values. Complexes with more phen ligands have larger t_d values, consistent with their larger size. The lability of some [Fe(N^N)₃]²⁺ species means that we also learn about the sizes of unsaturated fragments [Fe(N^N)₂]²⁺.

Along with [Fe(bipy)₃]²⁺, we also studied the analog [Co(bipy)₃]²⁺ (m/z 263), which forms on reductive quenching of photoexcited [Co(bipy)₃]³⁺*. Chromophores such as [Co(bipy)₃]³⁺ and [Co(bipy^Br)₃]³⁺ have found renewed interest because of the Marcus-inverted nature of their photochemistry, making them long-lived and amenable to electron-transfer with a catalyst.³¹ Relative to [Fe(bipy)₃]²⁺, we find that the 19e⁻ complex [Co(bipy)₃]²⁺ has a greater t_d, which reflects longer M–N bonds (Fig. S57 and S58, ESI†). Our measurements are consistent with related gas-phase measurements,^17,18 as well as crystallographic data for [Fe(bipy)₃](ClO₄)₂ (r(Fe–N)_average = 1.965 Å)³² and [Co(bipy)₃](ClO₄)₂ (r(Co–N)_average = 2.129 Å).³³

The reduced state: [Fe(N^N)₃]⁺

We now arrive at the final and most important part of our study. Oxidative quenching of photoexcited [M(N^N)₃]²⁺* (M = Fe, Ru) can afford trications [M(N^N)₃]³⁺, for which our ESI-MS data here for Fe (and earlier²⁴ for Ru) do not give any evidence ([Fe(bipy)₃]^3+/2+, E ≈ +0.61 V vs. Fc^+/0;³⁴ [Ru(bipy)₃]^3+/2+, E ≈ +0.80 V vs. Fc^+/0).³⁵ Conversely, reductive quenching of [Ru(N^N)₃]²⁺* affords monocations [Ru(N^N)₃]⁺ ([Ru(bipy)₃]^2+/+, E ≈ −1.65 V vs. Fc^+/0).³⁶ We recently found that solutions containing [Ru(bipy)₃]²⁺ and the weak reductant I⁻, when subjected to ESI, also give [Ru(bipy)₃]⁺, albeit in low relative abundance.²⁴ This is rather distinct from the gas-phase reduction of [Ru(bipy)₃]²⁺ with reductants such as Cs atoms³⁷ or [fluoranthene]⁻.³⁸ The role of the monocation in photocatalysis has seen its valence description attract great interest. The reduction is bipy-centered and gives [Ru^II(bipy)₂(bipy·)]⁺, which features the radical anionic ligand³⁹ bipy·⁻ and a metal ion that maintains its 18e⁻ valence count.

Reductive quenching of [Fe(bipy)₃]²⁺* gives the analogous monocation [Fe(bipy)₃]⁺, the thermal stability of which we probed in the gas phase. Thus, we mass-selected [Fe(bipy)₃]²⁺ (m/z 262, Fig. 5a and b) and reduced it with [1,3-dicyanobenzene]⁻ ([DCB]⁻) to give [Fe(bipy)₃]⁺ (m/z 524), albeit in low conversion. About 24% of the monocations lose bipy to give [Fe(bipy)₂]⁺ (m/z 368), indicating that [Fe(bipy)₃]⁺ is more fragile than the dication [Fe(bipy)₃]²⁺, which experiences less than 20% dissociation under the same conditions.

Fig. 5 (a) Reduction and dissociation of [Fe(bipy)₃]²⁺. Dissociation of the parent dication is negligible. Cationic reaction products of [DCB]⁻ with (b) [Fe(bipy)₃]²⁺, (c) [Fe(bipy)₂(phen)]²⁺, (d) [Fe(bipy)(phen)₂]²⁺, (e) [Fe(phen)₃]²⁺, (f) [Fe(bipy^Br)₃]²⁺ and (g) [Fe(bipy^t-Bu)₃]²⁺. Intensities in selected m/z regions are increased 15× for clarity.

For comparison, we reduced [Fe(bipy)₂(phen)]²⁺, [Fe(bipy)(phen)₂]²⁺ and [Fe(phen)₃]²⁺, as well as dibromo derivative [Fe(bipy^Br)₃]²⁺ and dialkyl derivative [Fe(bipy^t-Bu)₃]²⁺ to their respective monocations (Fig. 5c–g). The intensity of reductant anions [DCB]⁻ (∼2 × 10⁶) was consistent for each experiment and far greater than that of all Fe complex cations combined (∼10⁵). This ensures pseudo-first-order conditions,^40,41 such that the intensity of monocations—[Fe(N^N)₃]⁺ and fragments such as [Fe(N^N)₂]⁺—is proportional to the combined intensities of all Fe complex cations, which equals the starting [Fe(N^N)₃]²⁺ intensity because this is the parent ion. Thus, the intensity ratio {[Fe(N^N)₃]⁺ + [Fe(N^N)₂]⁺}/{[Fe(N^N)₃]⁺ + [Fe(N^N)₂]⁺ + [Fe(N^N)₃]²⁺} is the fraction of [Fe(N^N)₃]²⁺ that gets reduced. We find that the extent of reduction decreases in the order [Fe(bipy)₃]²⁺ > [Fe(bipy)₂(phen)]²⁺ > [Fe(bipy)(phen)₂]²⁺ > [Fe(phen)₃]²⁺ (Table 2). The complex [Fe(phen)₃]²⁺ is not readily reduced because the planar phen ligand does not accept an electron as well as bipy does. Likewise, the extent of reduction of the bulky, electron-rich derivative [Fe(bipy^t-Bu)₃]²⁺ is negligible. Curiously, we find [Fe(bipy^Br)₃]²⁺ to be an outlier—its electron-withdrawing groups suggest a strong driving force for reduction but the conversion to [Fe(bipy^Br)₃]⁺ was very low.

Table 2 DFT-calculated (gas-phase, E_calc) and measured (solution, E) potentials for [Fe(N^N)₃]^2+/+ couples correlate with intensity ratios for the gas-phase reduction [Fe(N^N)₃]²⁺ + [DCB]⁻ → [Fe(N^N)₃]⁺ + [DCB], and the dissociation reaction [Fe(N^N)₃]⁺ → [Fe(N^N)₂]⁺ + N^N

Precursor ion	E calc/V vs. DCB^0/−	E/V vs. Fc^+/0	%reduction	% [Fe(N^N)3]^+ intact
a Value from ref. 42. b Value from ref. 15.Fc = ferrocene.
[Fe(bipy)3]^2+	6.07	–1.66^a	11	76
[Fe(bipy)2(phen)]^2+	N.D.	N.D.	6	85
[Fe(bipy)(phen)2]^2+	N.D.	N.D.	4	89
[Fe(phen)3]^2+	5.90	N.D.	3	100
[Fe(bipy^Br)3]^2+	6.29	N.D.	2	84
[Fe(bipy^t-Bu)3]^2+	5.28	−1.85^b	1	100

---

If our electron transfers are outer-sphere, the rate of reduction should be related to the potential difference between the [Fe(N^N)₃]^2+/+ and [DCB]^0/− couples, as per the Marcus cross-relation. To learn about the driving force for reduction, we calculated potentials⁴³ (E_calc, Table 2) for gas-phase couples [Fe(N^N)₃]^2+/+ relative to [DCB]^0/− using the linear response approximation (LRA) as part of the thermodynamic integration method.⁴⁴ Briefly, we took snapshots from ab initio molecular dynamics (MD) trajectories, and used these to compute redox potentials at the DFT level of theory. E_calc values are qualitatively consistent with experimental solution-phase values for [Fe(bipy)₃]^2+/+ (E = −1.66 V vs. Fc^+/0)⁴² and [Fe(bipy^t-Bu)₃]^2+/+ (E = −1.85 V vs. Fc^+/0).¹⁵ Moreover, E_calc values are consistent with our MS data for the [Fe(bipy)_3−n(phen)_n]²⁺ series—complexes with more bipy ligands are more rapidly reduced. However, the high E_calc for [Fe(bipy^Br)₃]^2+/+ was not reflected in the observed extent of reduction, perhaps due to steric hindrance. Lastly, in addition to reducing the octahedral [Fe(N^N)₃]²⁺ species, we could generate, select and reduce the unsaturated fragments [Fe(N^N)₂]²⁺, with the reduction yields being high (40% for [Fe(bipy)₂]²⁺ and 57% for [Fe(phen)₂]²⁺; Fig. S14 and S27, ESI†) because these ions are more electron-poor than the octahedral dications.

Dissociation of [Fe(N^N)₃]²⁺ is slow under our conditions, so we only observe negligible [Fe(N^N)₂]²⁺. Thus, the reduced complex [Fe(N^N)₃]⁺ is the main precursor to [Fe(N^N)₂]⁺, whence the monocation intensity ratio [Fe(N^N)₃]⁺/([Fe(N^N)₃]⁺ + [Fe(N^N)₂]⁺) is the ‘survival yield’ of [Fe(N^N)₃]⁺—a measure of how stable it is to diimine loss (Table 2). Complexes in the [Fe(bipy)_3−n(phen)_n]⁺ series are more robust if they bear more phen ligands. Although this is to be expected for the dications [Fe(bipy)_3−n(phen)_n]²⁺, it is not a priori obvious for monocations because the bipy derivatives are better electron acceptors in view of their higher potentials. The substituted monocation [Fe(bipy^t-Bu)₃]⁺ is more robust than [Fe(bipy^Br)₃]⁺, which shows appreciable fragmentation due to the poor basicity of bipy^Br. The electron-withdrawing Br atoms stabilize the ligand in its radical anionic [bipy^Br]⁻· form, as would be present in a [Fe^II(bipy^Br)₂(bipy^Br·)]⁺ valence description for [Fe(bipy^Br)₃]⁺. Yet this stabilization is insufficient to overcome the low ligand basicity, such that the complex is somewhat labile, with 84% remaining intact (Table 2).

Our data reveal two distinct trends. First, the extent of reduction trends with redox potential—complexes with higher redox potentials experience a greater extent of reduction. The weakness of the trend is likely due to ligand substituents, which can perhaps attenuate reduction with [DCB]⁻ because of steric or other effects. Second, the robustness of the monocations follows the opposite trend, and mirrors the trend in measured stability of the dications (Table 1). Thus, ligands that best stabilize the dications also stabilize the monocations, perhaps because diimines (i) are intermediate between being hard and soft, and (ii) confer adaptability in the form of redox non-innocence. A theoretical study on [Fe(bipy)₃]²⁺ derivatives has described how diimines act not only as weak π-acceptors but also π-donors,⁴⁵ and this might explain how the ligands stabilize the different charge states.

The gas-phase reduction used here—referred to as electron transfer dissociation (ETD) or electron transfer with no dissociation (ETnoD)^46,47—is useful for inorganic chemistry because it can afford species that are challenging to generate in solution. ETD is a common feature even on low-resolution mass spectrometers, making it accessible to non-specialists. Whether used in this study to generate [Fe(N^N)₃]⁺, or elsewhere to make [Ru(bipy)₃]⁺,³⁸ [M(phen)₂]⁺ (M = Fe, Co, Ni, Cu, Zn),⁴⁸ [Cu(bipy)₂]⁺,⁴⁹ [M(cyclam)]⁺ (M = Ni, Cu)^49,50 or multinuclear complexes,⁵¹ the technique is a powerful way to generate low-valent species, not least those involved in photo- and electrocatalysis. Elegant research has shown how the nature of the reductant anion and charge density of the analyte cation affect the extent of the latter's dissociation,^46,52,53 which is desirable in the case of biomolecular sequencing using ETD. However, the influence of analyte redox potential is not well-explored, and our systematic study here shows how the extent of reduction—whether dissociative or non-dissociative—is indeed sensitive to redox potential.

Conclusion

The literature on [Fe(bipy)₃]²⁺ dates back to 1898,⁵⁴ yet Fe diimines continue to yield new knowledge in coordination chemistry and its application to catalysis. We tease out this knowledge using gas-phase experimental and theoretical methods to study a range of diimine complexes [M(N^N)₃]²⁺. ESI of MeOH solutions affords ion pairs {[Fe(N^N)₃]X}⁺ in the case of tetraarylborates. The lability of [Fe(N^N)₃]²⁺, which increases in solutions of high ionic strength, enables us to generate heteroleptic species, and the propensity of the complexes to undergo CID is related to the basicity, mass and rigidity of the ligands N^N. Although we do not have absolute stabilities or activation energies, the relative gas-phase stabilities gleaned here are relevant to solution chemistry because species in the two different phases can nevertheless have similar qualitatively similar energy distributions.¹⁰

The first report on [Fe(bipy)₃]²⁺ described its oxidation to [Fe(bipy)₃]³⁺,⁵⁴ yet the monocation [Fe(bipy)₃]⁺ has received much less attention, despite its role in photocatalysis. Here, we uncovered how redox potential and ligand substituents influence the extent to which [Fe(N^N)₃]²⁺ gets reduced to [Fe(N^N)₃]⁺. Moreover, the extent to which [Fe(N^N)₃]⁺ dissociates gives us clues on the robustness of these monocations. Overall, we have demonstrated a sensitive and rapid method to probe Fe diimines in the di- and monocationic forms, which are charge states relevant to catalysis. We hope that this methodology proves useful in developing sustainable photosensitizers that also maintain their integrity.

Methods

Experimental section

[Fe(bipy)₃]Cl₂·5H₂O and [Fe(phen)₃]Cl₂·5H₂O,⁸ [Fe(bipy)₃](PF₆)₂ and [Fe(phen)₃](PF₆)₂,⁵⁵ [Co(bipy)₃](PF₆)₂⁵⁶ were prepared according to literature procedures. [Fe(bipy^t-Bu)₃](PF₆)₂ has previously been described.¹⁵ [Fe(bipy^t-Bu)₃]Cl₂ and [Fe(bipy^Br)₃]Cl₂ were prepared in a N₂-filled MBraun LabStar glovebox equipped with an Al₂O₃-charged solvent purification system. NMR data were acquired at room temperature using a Bruker Avance 400. The solvent was CD₃OD, with residual CHD₂OD (δ(¹H)@3.31 ppm relative to SiMe₄) and (δ(¹³C)@49 ppm relative to SiMe₄) used as ref. 57.

[Fe(bipy^t-Bu)₃]Cl₂. FeCl₂ (41.2 mg, 0.325 mmol) and bipy^t-Bu (270.5 mg, 1.008 mmol, 3.1 equivalents) were suspended in MeCN (2 mL) and stirred for 3 days. The suspension was cooled to −30 °C, and the fine red precipitate isolated by filtration, washed with MeCN (2 mL) and dried to give the product as a red powder (245.9 mg, 0.2639 mmol, 81%).

¹H NMR: δ 8.73 (m, 6H, H3,3′), 7.54 (dd, ³J_HH = 6.0 Hz, ⁴J_HH = 2.0 Hz, 6H, H5,5′), 7.34 ppm (d, ³J_HH = 6.0 Hz, 6H, H6,6′). ¹³C{¹H} NMR: δ 165.25, 160.65, 154.41, 126.05, 122.49, 36.59, 30.60 ppm. ESI-MS: m/z calc. for C₅₄H₇₂FeN₆⁺: 430.2578. Found: 430.2572.

[Fe(bipy^Br)₃]Cl₂. FeCl₂ (17.9 mg, 0.141 mmol) and bipy^Br (137.5 mg, 0.438 mmol, 3.1 equivalents) were suspended in MeCN (2 mL) and stirred for 3 days. The suspension was cooled to −30 °C, and the blue-grey precipitate was isolated by filtration, washed with MeCN (2 mL) and dried to give the product as a blue-grey powder (138.9 mg, 0.1300 mmol, 92%).

¹H NMR: δ 9.08 (s, 6H, H3,3′), 7.75 (m, 6H, H6,6′), 7.37 ppm (m, 6H, H5,5′). ¹³C{¹H} NMR: δ 160.39, 156.01, 137.70, 132.71, 129.78 ppm. ESI-MS: m/z calc. for C₃₀H₁₈Br₆FeN₆⁺: 498.7989. Found: 498.8000.

Caution! [Fe(bipy^t-Bu)₃]Cl₂ and [Fe(bipy^Br)₃]Cl₂ are new compounds with unknown toxicities. The hazards associated with their handling are likely minor and comparable to those of [Fe(bipy)₃]SO₄ (NFPA: Health 1, Flammability 0, Instability 0, Physical Hazard 0).

Methods for ESI-MS sample preparation and measurement were similar to those in our previous study on Ru compounds²⁴ and are detailed in the ESI.† The collision energies reported here (eV) are the product of the transfer collision energy (principally voltage, V) used on our Synapt XS spectrometer, and the ion charge (1e or 2e). Electron transfers were performed using the Synapt XS ETD option, flowing DCB vapor in He (30 mLmin⁻¹) over a glow discharge source at 1.5 kV and selecting the generated [DCB]⁻ (m/z 128) with the quadrupole set at low-mass resolution of 4.7 in negative-ion mode. The same quadrupole periodically switches polarity to select the parent dications [Fe(N^N)₃]²⁺ for chemical reduction. Due to the different ionization efficiencies of the complex salts, we adjusted the concentration and low-mass resolution of the quadrupole in positive-ion mode (Table S1, ESI†) to obtain comparable ion intensities, which were much lower than the [DCB]⁻ intensity. In each case, the data presented are sums of 40 scans.

Computational methods

We calculated the redox potentials by the linear response approximation (LRA) within the thermodynamic integration method.⁴⁴ The redox potential E_calc for a reaction transferring n moles of electrons is related to the standard Gibbs free energy change ΔG by E_calc = −ΔG/nF, where F is the Faraday constant. In the LRA, ΔG is calculated by ΔG = ½ (〈ΔE〉_red + 〈ΔE〉_ox), where 〈ΔE〉_red and 〈ΔE〉_ox are the vertical energy gaps E_red − E_ox averaged over the configurations of the potential energy surface for reduced and oxidized species, respectively.^58,59 In this work, both 〈ΔE〉_red and 〈ΔE〉_ox were calculated at the DFT level, using configurations extracted from ab initio MD trajectories.

All atomistic simulations were performed within the CP2K package,⁶⁰ using the PBE functional,⁶¹ DZVP-MOLOPT basis set,⁶² and GTH pseudopotentials.⁶³ We did not set any periodicity and used a time step of 0.5 fs to integrate the equations of motion. All DFT optimizations relied on a limited memory algorithm (LBFGS)⁶⁴ with a force convergence criterion of 0.02 eV Å⁻¹. Systems were successfully equilibrated for 2 ps to converge the potential energy in the NVT ensemble at 300 K.⁶⁵ During the subsequent 2 ps production run, 100 evenly spaced snapshots were saved for the single-point calculations required for 〈ΔE〉_red and 〈ΔE〉_ox. The PBE functional is known to overestimate the stability of low-spin states relative to high-spin states of Fe complexes.⁶⁶ To address this, more expensive hybrid functionals are typically used.⁶⁷ Here, relative spin-state energies were assessed by single-point calculations with B3LYP*.⁶⁸

Author contributions

D. S. designed research; D. S., C. B. S. and R. R. R. performed the experiments and analyzed data; U. T. performed and analyzed the theoretical calculations; D. S. wrote the paper.

Data availability

NMR spectra, MS, MS² and MS-IMS-MS data, and DFT-calculated structures supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors are grateful for financial support from the National Institutes of Health (SuRE-First award 1R16GM150472-01), the National Science Foundation (CheMIE REU award 2150510) and Texas State University. The UK HEC Materials Chemistry Consortium, funded by EPSRC (EP/R029431, EP/X035859/1), enabled use of the ARCHER2 UK National Supercomputing Service.

Notes and references

1. E. C. Constable and C. E. Housecroft, The Early Years of 2,2′-Bipyridine—A Ligand in Its Own Lifetime, Molecules, 2019, 24, 3951,  DOI:10.3390/molecules24213951.
2. J. K. McCusker, Electronic Structure in the Transition Metal Block and Its Implications for Light Harvesting, Science, 2019, 363, 484–488,  DOI:10.1126/science.aav9104.
3. M. C. Carey, S. L. Adelman and J. K. McCusker, Insights into the Excited State Dynamics of Fe(II) Polypyridyl Complexes from Variable-Temperature Ultrafast Spectroscopy, Chem. Sci., 2019, 10, 134–144,  10.1039/C8SC04025G.
4. L. H. M. de Groot, A. Ilic, J. Schwarz and K. Wärnmark, Iron Photoredox Catalysis–Past, Present, and Future, J. Am. Chem. Soc., 2023, 145, 9369–9388,  DOI:10.1021/jacs.3c01000.
5. K. Heinze, C. Förster, P. Vöhringer and B. Sarkar, Licht Und Leuchten Bei 3d-Metallen, Nachr. Chem., 2019, 67, 54–59,  DOI:10.1002/nadc.20194089001.
6. S. B. Beil, S. Bonnet, C. Casadevall, R. J. Detz, F. Eisenreich, S. D. Glover, C. Kerzig, L. Næsborg, S. Pullen, G. Storch, N. Wei and C. Zeymer, Challenges and Future Perspectives in Photocatalysis: Conclusions from an Interdisciplinary Workshop, JACS Au, 2024, 4, 2746–2766,  DOI:10.1021/jacsau.4c00527.
7. A. Lee, M. Son, M. Deegbey, M. D. Woodhouse, S. M. Hart, H. F. Beissel, P. T. Cesana, E. Jakubikova, J. K. McCusker and G. S. Schlau-Cohen, Observation of Parallel Intersystem Crossing and Charge Transfer-State Dynamics in [Fe(Bpy)₃]²⁺ from Ultrafast 2D Electronic Spectroscopy, Chem. Sci., 2023, 14, 13140–13150,  10.1039/D3SC02613B.
8. H. Sato and T. Tominaga, Mössbauer Studies of the Thermal Decomposition of Tris(2,2′-Bipyridine)Iron(II) Chloride and the Structures of the Isomers of 2,2′-Bipyridineiron(II) Chloride, Bull. Chem. Soc. Jpn., 1976, 49, 697–700,  DOI:10.1246/bcsj.49.697.
9. H. I. A. Phillips, A. V. Chernikov, N. C. Fletcher, A. E. Ashcroft, J. R. Ault, M. H. Filby and A. J. Wilson, The Use of Electrospray Mass Spectrometry to Determine Speciation in a Dynamic Combinatorial Library for Anion Recognition, Chem. – Eur. J., 2012, 18, 13733–13742,  DOI:10.1002/chem.201201302.
10. C. Collette and E. De Pauw, Calibration of the Internal Energy Distribution of Ions Produced by Electrospray, Rapid Commun. Mass Spectrom., 1998, 12, 165–170,  DOI:10.1002/(SICI)1097-0231(19980227)12:4<165:AID-RCM140>3.0.CO;2-1.
11. Q. Duez, P. Tinnemans, J. A. A. W. Elemans and J. Roithová, Kinetics of Ligand Exchange in Solution: A Quantitative Mass Spectrometry Approach, Chem. Sci., 2023, 14, 9759–9769,  10.1039/D3SC03342B.
12. R. Kobetić, D. Gembarovski, G. Baranović and V. Gabelica, ESI-MS Studies of Mixed-ligand Fe(II) Complexes Containing 1,10-phenanthroline and 1,10-phenanthroline-5,6-dione as Ligands, J. Mass Spectrom., 2008, 43, 753–764,  DOI:10.1002/jms.1372.
13. J. Mehara and J. Roithová, Identifying Reactive Intermediates by Mass Spectrometry, Chem. Sci., 2020, 11, 11960–11972,  10.1039/D0SC04754F.
14. A. G. Motten, K. Hanck and M. K. DeArmound, ESR of the Reduction Products of [Fe(Bpy)₃]²⁺ and [Ru(Bpy)₃]²⁺, Chem. Phys. Lett., 1981, 79, 541–546,  DOI:10.1016/0009-2614(81)85032-4.
15. J. England, C. C. Scarborough, T. Weyhermüller, S. Sproules and K. Wieghardt, Electronic Structures of the Electron Transfer Series [M(Bpy)₃]ⁿ, [M(Tpy)₂]ⁿ, and [Fe(Tbpy)₃]ⁿ (M = Fe, Ru; n = 3+, 2+, 1+, 0, 1–): A Mössbauer Spectroscopic and DFT Study, Eur. J. Inorg. Chem., 2012, 4605–4621,  DOI:10.1002/ejic.201200232.
16. C. A. Bignozzi, O. Bortolini, O. Curcuruto and M. Hamdan, Investigation of Ruthenium(II) and Iron(II) Tris-Bipyridyl Complexes by Means of 10-30 keV Cs⁺ Ion Bombardment and Collision-Induced Dissociation, Rapid Commun. Mass Spectrom., 1994, 8, 706–710,  DOI:10.1002/rcm.1290080909.
17. H. Nose and M. T. Rodgers, Energy-Resolved Collision-Induced Dissociation Studies of 2,2′-Bipyridine Complexes of the Late First-Row Divalent Transition-Metal Cations: Determination of the Third-Sequential Binding Energies, ChemPlusChem, 2013, 78, 1109–1123,  DOI:10.1002/cplu.201300156.
18. H. Nose, Y. Chen and M. T. Rodgers, Energy-Resolved Collision-Induced Dissociation Studies of 1,10-Phenanthroline Complexes of the Late First-Row Divalent Transition Metal Cations: Determination of the Third Sequential Binding Energies, J. Phys. Chem. A, 2013, 117, 4316–4330,  DOI:10.1021/jp401711c.
19. F. Basolo and F. P. Dwyer, DICHLORO-BIS-(2,2′-DIPYRIDYL)-IRON(II) AND DICHLORO-BIS-(1,10-PHENANTHROLINE)-IRON(II), J. Am. Chem. Soc., 1954, 76, 1454–1455,  DOI:10.1021/ja01634a099.
20. L. M. Lawson Daku, Spin-State Dependence of the Structural and Vibrational Properties of Solvated Iron(II) Polypyridyl Complexes from AIMD Simulations: Aqueous [Fe(Bpy)₃]Cl₂, a Case Study, Phys. Chem. Chem. Phys., 2018, 20, 6236–6253,  10.1039/C7CP07862E.
21. L. M. Lawson Daku and A. Hauser, Ab Initio Molecular Dynamics Study of an Aqueous Solution of [Fe(Bpy)₃](Cl)₂ in the Low-Spin and in the High-Spin States, J. Phys. Chem. Lett., 2010, 1, 1830–1835,  DOI:10.1021/jz100548m.
22. D. Schröder, S. Shaik and H. Schwarz, Two-State Reactivity as a New Concept in Organometallic Chemistry, Acc. Chem. Res., 2000, 33, 139–145,  DOI:10.1021/ar990028j.
23. J. A. Broomhead, C. G. Young and P. Hood, Tris(2,2′-Bipyridine)Ruthenium(II) Dichloride Hexahydrate, Inorg. Synth., 2007, 28, 338–340,  DOI:10.1002/9780470132593.ch86.
24. D. Schilter, U. Terranova and R. R. Robinson, Ruthenium Diimines Exhibit Diverse Intra- and Intermolecular Dynamics, Cell Rep. Phys. Sci., 2024, 5, 102071,  DOI:10.1016/j.xcrp.2024.102071.
25. V. Katta, S. K. Chowdhury and B. T. Chait, Electrospray Ionization: A New Tool for the Analysis of Ionic Transition-Metal Complexes, J. Am. Chem. Soc., 1990, 112, 5348–5349,  DOI:10.1021/ja00169a051.
26. M. Aresta, E. Quaranta and A. Albinati, Tetraphenylborate Coordination Chemistry. Synthesis, Solid-State and Solution Characterization, and Properties of {[(C₂H₄)₂Rh(η^₆-Ph)]₂BPh₂}O₃SCF₃ and {[(C₂H₄)₂Rh(η^₆-Ph)]₃BPh}(O₃SCF₃)₂: The First Examples of a Tetraphenylborate Anion Acting as a 12- or 18-e Donor to Metal Centers, Organometallics, 1993, 12, 2032–2043,  DOI:10.1021/om00030a012.
27. A. Kondinski, N. Vankova, F. Schinle, P. Jäger, O. Hampe, U. Kortz and T. Heine, How Counterions Affect the Solution Structure of Polyoxoaurates: Insights from UV/Vis Spectral Simulations and Electrospray Mass Spectrometry, Eur. J. Inorg. Chem., 2014, 3771–3778,  DOI:10.1002/ejic.201402494.
28. J. S. Mathieson, G. J. T. Cooper, M. D. Symes and L. Cronin, Quantification of Ion Binding Using Electrospray Mass Spectrometry, Inorg. Chem. Front., 2014, 1, 49,  10.1039/c3qi00037k.
29. L. G. Sillén and A. E. Martell, Stability Constants of Metal-Ion Complexes, The Chemical Society, London, 1971.
30. P. B. Armentrout, Mass Spectrometry—Not Just a Structural Tool: The Use of Guided Ion Beam Tandem Mass Spectrometry to Determine Thermochemistry, J. Am. Soc. Mass Spectrom., 2002, 13, 419–434,  DOI:10.1016/S1044-0305(02)00347-1.
31. A. Y. Chan, A. Ghosh, J. T. Yarranton, J. Twilton, J. Jin, D. M. Arias-Rotondo, H. A. Sakai, J. K. McCusker and D. W. C. MacMillan, Exploiting the Marcus Inverted Region for First-Row Transition Metal–Based Photoredox Catalysis, Science, 2023, 382, 191–197,  DOI:10.1126/science.adj0612.
32. S. R. Batten, K. S. Murray and N. J. Sinclair, Tris(2,2′-Bipyridyl-N,N′)Iron(II) Diperchlorate, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 2000, 56, e320–e320,  DOI:10.1107/S0108270100009185.
33. J.-C. Yao, L.-F. Ma and F.-J. Yao, Crystal Structure of Tris(2,2′-Bipyridine)Cobalt(II) Diperchlorate, [Co(C₁₀H₈N₂)₃][ClO₄]₂, Z. Kristallogr. - New Cryst. Struct., 2005, 220, 483–484,  DOI:10.1524/ncrs.2005.220.3.483.
34. H. L. Chum, M. Rock, N. Y. Murakami, I. Jordan and T. Rabockai, Cyclic Voltammetry of Iron Dimine Complexes in Acetonitrile, J. Electroanal. Chem. Interfacial Electrochem., 1977, 76, 277–285,  DOI:10.1016/S0022-0728(77)80480-4.
35. T. Saji and S. Aoyagui, Polarographic Studies on Bipyridines Complexes, J. Electroanal. Chem. Interfacial Electrochem., 1975, 60, 1–10,  DOI:10.1016/S0022-0728(75)80196-3.
36. Y. Ohsawa, M. K. DeArmond, K. W. Hanck, D. E. Morris, D. G. Whitten and P. E. Neveux, Spatially Isolated Redox Orbitals: Evidence from Low-Temperature Voltammetry, J. Am. Chem. Soc., 1983, 105, 6522–6524,  DOI:10.1021/ja00359a045.
37. C. S. Byskov, J. M. Weber and S. B. Nielsen, Gas-Phase Spectroscopy of Singly Reduced Tris(Bipyridine)Ruthenium Ions, Ru(Bipy)₃⁺, Phys. Chem. Chem. Phys., 2015, 17, 5561–5564,  10.1039/C4CP05477F.
38. M. U. Munshi, J. Martens, G. Berden and J. Oomens, Vibrational Spectra of the Ruthenium–Tris-Bipyridine Dication and Its Reduced Form in Vacuo, J. Phys. Chem. A, 2020, 124, 2449–2459,  DOI:10.1021/acs.jpca.0c00888.
39. C. C. Scarborough, S. Sproules, T. Weyhermüller, S. DeBeer and K. Wieghardt, Electronic and Molecular Structures of the Members of the Electron Transfer Series [Cr(Tbpy)₃]ⁿ (n = 3 +, 2 +, 1 +, 0): An X-Ray Absorption Spectroscopic and Density Functional Theoretical Study, Inorg. Chem., 2011, 50, 12446–12462,  DOI:10.1021/ic201123x.
40. P. D. Compton, J. V. Strukl, D. L. Bai, J. Shabanowitz and D. F. Hunt, Optimization of Electron Transfer Dissociation via Informed Selection of Reagents and Operating Parameters, Anal. Chem., 2012, 84, 1781–1785,  DOI:10.1021/ac202807h.
41. S. A. McLuckey, J. L. Stephenson and K. G. Asano, Ion/Ion Proton-Transfer Kinetics: Implications for Analysis of Ions Derived from Electrospray of Protein Mixtures, Anal. Chem., 1998, 70, 1198–1202,  DOI:10.1021/ac9710137.
42. J. M. Rao, M. C. Hughes and D. J. Macero, Further Studies on the Stabilization of High and Low Oxidation States in Aromatic Imine Ligand Complexes of First Row Transition Metals. I. Substituted Bipyridine Complexes of Cobalt and Iron, Inorg. Chim. Acta, 1979, 35, L369–L373,  DOI:10.1016/S0020-1693(00)93402-9.
43. B. H. Solis and S. Hammes-Schiffer, Proton-Coupled Electron Transfer in Molecular Electrocatalysis: Theoretical Methods and Design Principles, Inorg. Chem., 2014, 53, 6427–6443,  DOI:10.1021/ic5002896.
44. J. Blumberger, I. Tavernelli, M. L. Klein and M. Sprik, Diabatic Free Energy Curves and Coordination Fluctuations for the Aqueous Ag⁺/Ag²⁺ Redox Couple: A Biased Born-Oppenheimer Molecular Dynamics Investigation, J. Chem. Phys., 2006, 124, 064507,  DOI:10.1063/1.2162881.
45. D. C. Ashley and E. Jakubikova, Tuning the Redox Potentials and Ligand Field Strength of Fe(II) Polypyridines: The Dual π-Donor and π-Acceptor Character of Bipyridine, Inorg. Chem., 2018, 57, 9907–9917,  DOI:10.1021/acs.inorgchem.8b01002.
46. S. J. Pitteri, P. A. Chrisman and S. A. McLuckey, Electron-Transfer Ion/Ion Reactions of Doubly Protonated Peptides: Effect of Elevated Bath Gas Temperature, Anal. Chem., 2005, 77, 5662–5669,  DOI:10.1021/ac050666h.
47. N. M. Riley and J. J. Coon, The Role of Electron Transfer Dissociation in Modern Proteomics, Anal. Chem., 2018, 90, 40–64,  DOI:10.1021/acs.analchem.7b04810.
48. M. L. Parker and S. Gronert, Investigating Reduced Metal Species via Sequential Ion/Ion and Ion/Molecule Reactions: The Reactions of Transition Metal Phenanthrolines with Allyl Iodide, Int. J. Mass Spectrom., 2017, 418, 73–78,  DOI:10.1016/j.ijms.2016.11.018.
49. M. U. Munshi, J. Martens, G. Berden and J. Oomens, Gas-Phase Infrared Ion Spectroscopy Characterization of Cu(II/I)Cyclam and Cu(II/I)2,2′-Bipyridine Redox Pairs, J. Phys. Chem. A, 2019, 123, 4149–4157,  DOI:10.1021/acs.jpca.9b00793.
50. M. U. Munshi, S. M. Craig, G. Berden, J. Martens, A. F. DeBlase, D. J. Foreman, S. A. McLuckey, J. Oomens and M. A. Johnson, Preparation of Labile Ni⁺(Cyclam) Cations in the Gas Phase Using Electron-Transfer Reduction through Ion–Ion Recombination in an Ion Trap and Structural Characterization with Vibrational Spectroscopy, J. Phys. Chem. Lett., 2017, 8, 5047–5052,  DOI:10.1021/acs.jpclett.7b02223.
51. M. C. Pfrunder, D. L. Marshall, B. L. J. Poad, E. G. Stovell, B. I. Loomans, J. P. Blinco, S. J. Blanksby, J. C. McMurtrie and K. M. Mullen, Exploring the Gas-Phase Formation and Chemical Reactivity of Highly Reduced M8L6 Coordination Cages, Angew. Chem., Int. Ed., 2022, 61, e202212710,  DOI:10.1002/anie.202212710.
52. D. M. Good, M. Wirtala, G. C. McAlister and J. J. Coon, Performance Characteristics of Electron Transfer Dissociation Mass Spectrometry, Mol. Cell. Proteomics, 2007, 6, 1942–1951,  DOI:10.1074/mcp.M700073-MCP200.
53. J. Liu and S. A. McLuckey, Electron Transfer Dissociation: Effects of Cation Charge State on Product Partitioning in Ion/Ion Electron Transfer to Multiply Protonated Polypeptides, Int. J. Mass Spectrom., 2012, 330–332, 174–181,  DOI:10.1016/j.ijms.2012.07.013.
54. F. Blau, Über Neue Organische Metallverbindungen, Monatsh. Chem., 1898, 19, 647–689,  DOI:10.1007/BF01517438.
55. J. T. Yarranton and J. K. McCusker, Ligand-Field Spectroscopy of Co(III) Complexes and the Development of a Spectrochemical Series for Low-Spin d⁶ Charge-Transfer Chromophores, J. Am. Chem. Soc., 2022, 144, 12488–12500,  DOI:10.1021/jacs.2c04945.
56. F. Bella, N. Vlachopoulos, K. Nonomura, S. M. Zakeeruddin, M. Grätzel, C. Gerbaldi and A. Hagfeldt, Direct Light-Induced Polymerization of Cobalt-Based Redox Shuttles: An Ultrafast Way towards Stable Dye-Sensitized Solar Cells, Chem. Commun., 2015, 51, 16308–16311,  10.1039/C5CC05533D.
57. G. R. Fulmer, A. J. M. Miller, N. H. Sherden, H. E. Gottlieb, A. Nudelman, B. M. Stoltz, J. E. Bercaw and K. I. Goldberg, NMR Chemical Shifts of Trace Impurities: Common Laboratory Solvents, Organics, and Gases in Deuterated Solvents Relevant to the Organometallic Chemist, Organometallics, 2010, 29, 2176–2179,  DOI:10.1021/om100106e.
58. M. Alfonso-Prieto, H. Oberhofer, M. L. Klein, C. Rovira and J. Blumberger, Proton Transfer Drives Protein Radical Formation in Helicobacter Pylori Catalase but Not in Penicillium Vitale Catalase, J. Am. Chem. Soc., 2011, 133, 4285–4298,  DOI:10.1021/ja1110706.
59. G. Hong, D. M. Ivnitski, G. R. Johnson, P. Atanassov and R. Pachter, Design Parameters for Tuning the Type 1 Cu Multicopper Oxidase Redox Potential: Insight from a Combination of First Principles and Empirical Molecular Dynamics Simulations, J. Am. Chem. Soc., 2011, 133, 4802–4809,  DOI:10.1021/ja105586q.
60. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An Electronic Structure and Molecular Dynamics Software Package - Quickstep: Efficient and Accurate Electronic Structure Calculations, J. Chem. Phys., 2020, 152, 194103,  DOI:10.1063/5.0007045.
61. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868,  DOI:10.1103/PhysRevLett.77.3865.
62. J. VandeVondele and J. Hutter, Gaussian Basis Sets for Accurate Calculations on Molecular Systems in Gas and Condensed Phases, J. Chem. Phys., 2007, 127, 114105,  DOI:10.1063/1.2770708.
63. S. Goedecker, M. Teter and J. Hutter, Separable Dual-Space Gaussian Pseudopotentials, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 1703–1710,  DOI:10.1103/PhysRevB.54.1703.
64. R. H. Byrd, P. Lu, J. Nocedal and C. Zhu, A Limited Memory Algorithm for Bound Constrained Optimization, SIAM J. Sci. Comput., 1995, 16, 1190–1208,  DOI:10.1137/0916069.
65. W. G. Hoover, Canonical Dynamics: Equilibrium Phase-Space Distributions, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697,  DOI:10.1103/PhysRevA.31.1695.
66. M. Swart, A. R. Groenhof, A. W. Ehlers and K. Lammertsma, Validation of Exchange−Correlation Functionals for Spin States of Iron Complexes, J. Phys. Chem. A, 2004, 108, 5479–5483,  DOI:10.1021/jp049043i.
67. D. N. Bowman and E. Jakubikova, Low-Spin versus High-Spin Ground State in Pseudo-Octahedral Iron Complexes, Inorg. Chem., 2012, 51, 6011–6019,  DOI:10.1021/ic202344w.
68. O. Salomon, M. Reiher and B. A. Hess, Assertion and validation of the performance of the B3LYP* functional for the first transition metal row and the G2 test set, J. Chem. Phys., 2002, 117, 4729–4737,  DOI:10.1063/1.1493179.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00199d

‡ Present address: Department of Biochemistry and Biophysics, Texas A&M University, College Station, TX 77843, USA.

---