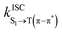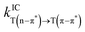An efficient reverse intersystem crossing process exploiting non-bonding states in an inverted singlet–triplet gap system

Abstract

Reverse intersystem crossing (rISC) is an essential process in organic light-emitting diodes to populate singlet excited states from non-emissive triplet states. A small or negative singlet–triplet energy gap and a large spin–orbit coupling between low-lying singlet and triplet states are key requirements to enhance the rISC rate. Here, we present a molecular design exploiting the n–π* excited state to maximize the efficacy of the rISC process for efficient light emitters using thermodynamic and kinetic calculations validated with high-level quantum chemical methods. Heptazine-based molecules with carbonyl groups attached are shown to possess a reasonable singlet energy gap for blue-light emission with the energy level of the n–π* triplet state modulated by addition of electron withdrawing or donating groups to achieve the optimal energy level ordering of T(π–π*) > T(n–π*) > S₁, leading to enhanced spin–orbit coupling between the lowest triplet and singlet states with an inverted energy gap.

---

1 Introduction

Reverse intersystem crossing (rISC) is a process involving transition from a state with higher spin multiplicity to a state with lower spin multiplicity.^1–4 This is the key process for organic light-emitting diodes (OLEDs) utilizing thermally activated delayed fluorescence (TADF)^5–7 due to the production of singlet states from non-emissive triplet states, increasing the electricity-to-light conversion efficiency. The rate of rISC is thus an important criterion in evaluating the efficacy of potential materials for optoelectronics.^8–13 The two main strategies that are in use to facilitate rISC are (i) lowering the singlet–triplet gap (ΔE_ST)^14–18 and (ii) aiming for S₁ and T₁ states with different characters^19–23 to allow strong spin–orbit coupling (SOC).

Finding molecules with small ΔE_ST that facilitates the rISC is non-trivial as the exchange energy puts the S₁ state above the T₁ state in the single reference description of the many-body electronic wavefunction. Molecules possessing the desired energy level usually show excited states with charge transfer (CT) character, with small overlap between the donor and acceptor orbitals resulting in low exchange energy. Recent works have also shed light on molecules with negative ΔE_ST,^17,24–34 which makes rISC thermodynamically favored and thus are recognized as promising candidates for OLED materials. From a kinetic point of view, the main challenge is the weak SOC between the lowest singlet and triplet states. As OLED materials usually lack heavy atoms that strengthen the SOC, the rISC rate is expected to be slow even when energetically feasible. Moreover, states with the same electronic configuration have vanishing SOC between them because the change in spin angular momentum without the change in orbital angular momentum violates the conservation of momentum, known as the El-Sayed rule.³⁵ Search for systems that have S₁ and T₁ states with different characters has thus been a popular means of achieving appreciable SOC, with locally excited (LE) configurations^19–23 mixing with CT type configurations in either the lowest excited singlet or triplet state.

A family of molecules derived from phenalene possessing negative ΔE_ST that emanates from the small overlap of orbitals and coupling of the doubly excited configuration with the lowest singlet excited state¹⁷ have emerged as prospective emitters, owing to the appeal of the thermodynamic stability of the S₁ state. The work conducted by De Silva¹⁷ demonstrated that using correlated electronic structure methods that take doubly excited states into consideration, such as equation of motion coupled cluster singles and doubles (EOM-CCSD) and algebraic diagrammatic correction (ADC(2)), is crucial for predicting the correct ΔE_ST, inspiring fruitful high-throughput computational studies in pursuit of discovering such inverted ΔE_ST (IST) emitters.^24,28,36 The experimental verification of the inverted gap²⁶ has also motivated further development and investigation of IST emitters. The computational studies to optimize the properties of IST molecules are mainly focused on finding IST molecules with appreciable oscillator strength,²⁴ as the symmetry of the IST molecules derived from phenalene leads to weak transition dipoles. Direct kinetic assessment^30,37 has also been performed to shed light on the importance of vibronic coupling in enhancing the transition dipole and the higher excited states that can become intermediates to enhance the spin–orbit coupling (SOC). Enhancing the weak SOC of singlet and triplet states sharing the same configuration is particularly not straightforward for the planar phenalene derivatives, as the mixing of LE and CT characters to increase the SOC is not an option without perpendicular moieties bonded to the molecule and adding branches to introduce low-lying excited states with CT character may bring the ΔE_ST to a positive value.^24,38 Moreover, molecules with perpendicular donor–acceptor geometry have a propensity to exhibit broad emission due to high reorganization energy, which is undesirable for optoelectronic devices.³⁹

Recently, molecules that bear carbonyl groups have been introduced as promising TADF emitters that show enhanced SOC from the non-bonding electrons.^40,41 Non-bonding electrons in the carbonyl group are naturally in a perpendicular orientation from the π electrons along the molecular plane and thus allow finite SOC.⁴² Even though attaching carbonyl groups to IST emitters has been tried in previous studies, the focus was mainly on their effect on the ΔE_ST and the oscillator strength, rather than on the nature of the excited states and the SOC strength.²⁴ The work of Pollice et al.²⁴ has shown that the ΔE_ST of IST emitters can be kept negative with reasonable robustness, and thus investigating the effect of non-bonding electrons on the SOC and the electronic state manifold of IST emitters is a worthwhile research topic to optimize the properties of IST molecules for optoelectronic applications.

In this work, we propose a molecular design that can satisfy both IST and appreciable SOC based on heptazine derivatives with the carbonyl group attached to give low-lying n–π* states. While the HOMO and LUMO show delocalized π and π* characters, respectively, the non-bonding orbital of the carbonyl group (HOMO−1) is perpendicular to the molecular plane of heptazine, as shown in Fig. 1a. The key strategy is to adjust the relative energy of the T(n–π*) state to S₁ and T(π–π*) states to maximize the efficacy of the T(n–π*) state by functional group engineering. We propose the desired energy level of the T(n–π*) state to be situated between those of the T(π–π*) state and the S₁ state, with the S₁ state as the state with the lower energy. As shown in Fig. 1b, having a lower-lying T(π–π*) state can result in internal conversion (IC) down to the T(π–π*) state from T(n–π*), thereby becoming unable to utilize the stronger SOC between the S₁ and T(n–π*) states and behaving in the same manner as the conventional IST emitters. The T(n–π*) state with a lower energy than S₁ means loss of the IST properties of the molecule, needing thermal activation (TA) to the S₁ state. To achieve the optimal energetic ordering S₁ < T(n–π*) < T(π–π*), the T(n–π*) energy can be tuned by attaching functional groups to the carbonyl branch, which modulates the energy of the non-bonding orbital and therefore the energy of the T(n–π*) state, as is suggested in Fig. 1c. As addition of an electron donating group (EDG) increases the energy of the n-orbital, the energy of the T(n–π*) state decreases, and vice versa upon addition of an electron withdrawing group (EWG).

Fig. 1 Schematic representation of utilizing n–π* states to facilitate rISC in IST molecules. (a) The non-bonding orbital and the π/π* orbitals of an IST molecule with the carbonyl group attached. (b) The outcome of rISC according to the energy of the T(n–π*) state, with the target energy of T(n–π*) between those of S₁ and T(π–π*). (c) Scheme showing the tuning of the energy of T(n–π*) through attachment of electron donating or electron withdrawing functional groups. The potential energy surface of the T(n–π*) state is twisted and displaced with respect to the π–π* states, which show Duschinsky rotation and shift of relaxed geometry.

2 Computational details

The molecules studied are shown in Fig. 2, with heptazine (1) and its derivatives having branches containing the carbonyl group attached (2 to 4). 2 has an acetyl group attached, 3 has a cyano group attached to 2 to tune the energy of the n–π* state by adding an electron-withdrawing group, and 4 has an amino group attached to 2 to tune the energy using an electron-donating group. Heptazine was chosen among IST molecules due to its small size that minimizes the computational cost and its S₁ energy that coincides with the blue light region (∼2.7 eV).

Fig. 2 Chemical structures of the molecules studied.

To analyze the capability of the molecules 2 to 4 to be used in OLEDs, the relaxed geometries of S₀, S₁, T(π–π*), and T(n–π*) states were obtained to examine the electronic state with the lowest adiabatic energy. The geometries of all four molecules in Fig. 2 were optimized using the B3LYP functional with the 6-31G(d) basis using Gaussian16 software.⁴³ The optimized geometires for S₁ states were obtained using time-depedent density functional theory (TDDFT) and Tamm–Dancoff approximation (TDA) methods. However, for triplet states, as previous studies report that TDDFT can have larger errors for triplet states compared to Tamm–Dancoff approximation (TDA) or unrestricted DFT (UDFT),^44,45 three geometries, one from each of the TDDFT, TDA, and UDFT methods, were obtained for the T(π–π*) and T(n–π*) states. We confirmed that the optimized geometries of all four molecules showed real frequencies for all modes for each state of interest.

As a highly correlated electronic structure method is desirable to predict accurate ΔE_ST, each of the optimized geometries was subject to single point calculation using EOM-CCSD in the cc-pVDZ basis set to calculate the energy of the low-lying electronic states including S(n–π*) at the relaxed geometries of each electronic state of interest. The geometry that gives the lowest energy from the single point calculations was considered as the best guess for the relaxed geometry of each excited state (see ESI† for the corresponding geometries). The energies of each geometry obtained with each level of theory are listed in Tables S1–S4 (ESI†). The oscillator strengths of molecules 1–4 were obtained at the respective relaxed S₁ geometries to examine the fluorescence intensity. To compare the rate of rISC and ISC involving the two triplet states, the SOC between the triplet states and the S₁ state was computed at the relaxed geometries of the respective states. The SOC and non-adiabatic coupling (NAC) were also calculated from the EOM-CCSD calculations, with mean-field treatment of the two-electron interaction part of the SOC. To analyze the effects of geometry fluctuation due to finite temperature on the oscillator strength and the SOC, the displaced S₁ geometries of the molecules 2–4 were obtained with Wigner sampling using the S₁ state normal modes at 300 K, sampling 80 geometries for each molecule, with the oscillator strength and SOC at each geometry obtained using the EOM-CCSD method. All EOM-CCSD calculations were performed using Q-Chem 6.0 software.⁴⁶

To assess the kinetics, the ISC and rISC rate between the singlet and the triplet excited states and the internal conversion (IC) rate between the T(π–π*) state and the T(n–π*) state were computed to compare the rate of rISC of two triplet states and verify that the internal conversion between the triplet states can effectively populate the state with stronger spin–orbit coupling. As previous works have shown that the difference in the relaxed geometry and normal modes of electronic states plays a pivotal role in determining the transition rate,^47–49 the effect of Duschinsky rotation and displacement of normal modes should be taken into account correctly. The rate of the ISC/rISC process was thus calculated using the equation based on the golden rule⁵⁰

in which the ρ factor carries the effects of geometric distortion. ΔE^ad_fi is the adiabatic energy gap between the final and initial states (E_f − E_i), in which the initial state is a triplet for rISC and a singlet for ISC. Z_i is the partition function of the vibrational states of initial electronic state at temperature T, β = 1/k_BT, and Ĥ^f/i_HO is the harmonic oscillator Hamiltonian in the final/initial state, respectively. For rISC, we assumed that the three sub-levels of the initial triplet state are evenly populated and thus the average of SOC can be computed as .⁵⁰ For ISC, the SOC is the sum of the SOC of the three levels:⁵¹. See computational details in the ESI† for more details regarding the computation of the integral in eqn (1).

The IC rate between the triplet states was also calculated based on the golden rule rate with consideration of the change in geometry and normal modes, according to the formalism of Miyazaki et al.,⁵² as

where k and l are indices of the N normal modes of the final electronic state and R_kl is the product of vibronic coupling elements 〈Φ_f| − iħ∂/∂Q_k|Φ_i〉·〈Φ_i| − iħ∂/∂Q_l|Φ_f〉, andwhere Q_k is the mass-weighted normal mode coordinate. The details of computing the integral are provided in the ESI.†

While the SOC strength of ISC and rISC between the S₁ and the T(n–π*) state was simply taken as the value computed at the relaxed geometries of the initial states, the SOC strength of transition between S₁ and the T(π–π*) was averaged according to the Boltzmann population of the initial state at its relaxed geometry and the relaxed geometry of the final state to take into account the low reorganization energy and considerable change in SOC upon reorganization. For example, the S₁ → T(π–π*) SOC was computed to be

where λ_S1 is the reorganization energy of the S₁ state from the T(π–π*) state geometry to the S₁ state geometry and |H^ISC_SO|^{S₁/T(π–π*) Geom} is the SOC strength computed at the relaxed geometry of the S₁/T(π–π*) state. The T(π–π*) → S₁ SOC was also computed in the same manner with the reorganization energy changed to that of the T(π–π*) state. The golden rule rates of the ISC/rISC were calculated using the correlation function formalism of Ianconescu et al., which is expressed in eqn (1).^50,53–55

3 Results and discussion

The energy diagrams of molecules 1–4 are shown in Fig. 3. The numerical values of the energies are listed in Tables S5–S8 (ESI†), showing agreement of the vertical excitation energies of the S₁ and T₁ states of molecule 1 with the theoretical best estimate using the CC3 approach⁵⁶ with the energies within ∼0.1 eV. The adiabatic energies show slightly larger errors with 0.16 eV for the S₁ state and 0.15 eV for the T₁ state compared to the CC3 approach. Fig. S1–S4 (ESI†) show the dominant excitations corresponding to S₁, T(π–π*), T(n–π*), and S(n–π*) states. The calculated energies show the promising prospects of utilizing the T(n–π*) state in rISC by showing that (i) T(n–π*) can be the lowest triplet excited state with energy close to the blue light region, (ii) the lowest singlet state is still the S(π–π*) state to achieve stronger spin–orbit coupling with the T(n–π*) state and (iii) the energy level of T(n–π*) can be tuned with functional groups with relatively little effects on (π–π*) state energies. In contrast to the negative energy gap of S₁ and T(π–π*) states, the S(n–π*) state lies considerably higher in energy than the T(n–π*) state due to higher exchange energy between the non-bonding orbital and the π* orbital. Inclusion of the S(n–π*) state into the dynamics would lead to a more complete picture of the kinetics of our molecules, but optimization of the geometry of the S(n–π*) state at the DFT level did not agree with the single point calculation at the EOM-CCSD level of theory as the energy of the S(n–π*) state at the optimized geometry was higher than the energy of the S(n–π*) state at the relaxed geometry of the T(n–π*) state. To obtain a guess about the transition rates involving the S(n–π*) state, we optimized the S(n–π*) state with the EOM-CCSD/6-31G* level of theory to compute the adiabatic energy of the S(n–π*) state and referenced to a work⁵⁵ that uses the theory we use to compute the ISC/rISC rate of systems. The adiabatic energies of the S(n–π*) states for molecules 2–4 are listed in Table S9 (ESI†).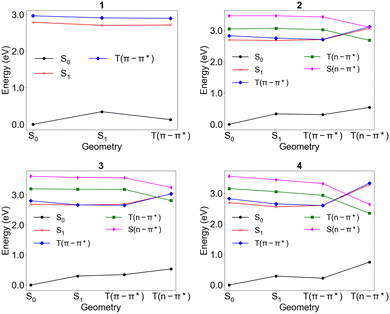

Fig. 3 Energies of the electronic states of interest plotted at each of the relaxed geometries calculated at the EOM-CCSD/cc-pVDZ level of theory.

The computed electronic energies give deeper insights into exploiting the n–π* state in rISC, showing that the addition of the carbonyl group does alter the π–π* state energies to an appreciable degree and may result in less negative ΔE_ST, as in the case of 3, and that reorganization to the T(n–π*) states’ minimum energy geometry incurs a significant change in the electronic state energies and thus the quantitative amount of reorganization is also a variable to be controlled to tune the relative adiabatic energies. The change in energy with respect to the geometry is especially prominent for 4, for which the energy of the T(n–π*) state stabilizes by ∼0.8 eV. The tuning of energy levels using functional groups is yet reliable, with 3 showing higher T(n–π*) energy and 4 showing lower T(n–π*) energy relative to 2 and exhibiting all three possibilities of energetic alignment shown in Fig. 1b. Molecules 2 and 4 have T(n–π*) as the triplet state with the lowest adiabatic energy, which means the T(n–π*) state is thermally more favored when the triplet excited state is produced upon electric excitation. The relative adiabatic energies of 2 resemble the desired energetic alignment with the adiabatic energy of T(n–π*) lying between those of S₁ and T(π–π*), thus making the transition from the lowest triplet state to the lowest singlet excited state both kinetically and thermodynamically favorable.

The oscillator strengths computed at the relaxed geometries are shown in Table S10 (ESI†) and the histograms of oscillator strengths at thermally excited geometry sampled from Wigner sampling are shown in Fig. S5 (ESI†). The oscillator strengths at the relaxed geometry show that due to the loss of symmetry upon addition of the carbonyl group, the oscillator strength of the S₁ → S₀ state transition also increases, albeit to an order of 0.0001. The oscillator strength can occasionally reach 0.01 with thermal excitation and thus the molecules can still be used as prototypes when designing IST emitters with an enhanced rISC rate. It should be noted that the sampling shows that 4 is prone to dissociation, thus calling for the need to design emitters with stability put into consideration.⁵⁷ The oscillator strength can be further improved by an additional modification of the molecule, as heptazine derivatives were shown to exhibit oscillator strength on the order of 0.01 in the work conducted by Aizawa et al.²⁶

The |H^ISC/rISC_SO| at the relaxed geometry of the initial states and ΔE^ad_ST between the S₁ state and the triplet states are shown in Table 1. The SOC with S₁ is shown to be at least an order of magnitude stronger for T(n–π*) than for T(π–π*), which results in a more than 100 times larger SOC factor for the rISC rate in eqn (1) after taking the square value. It is noteworthy that SOC strength between the S₁ and T(π–π*) states gets significantly altered according to the geometry with the SOC strength computed at the relaxed geometry of one state one to two orders of magnitude stronger than the SOC strength computed at the relaxed geometry of the other state. This change in SOC can be attributed to the rotation of the bond between the heptazine molecule and the carbonyl group, which breaks the planar symmetry and mixes the non-bonding orbitals of the oxygen with the HOMO and LUMO of pre-dominantly π character, thus indicating that the carbonyl group facilitates the ISC by lending its SOC strength to transition between states of π–π* character. The dihedral angles of the heptazine plane and the plane made by the carbonyl group for the relaxed S₁ and T(π–π*) geometries of each molecule are listed in Table S11 (ESI†), measured using the atoms shown in Fig. S6 (ESI†). The SOC strengths from Wigner sampled geometries also show that the SOC can vary appreciably with thermal fluctuation of the geometry, but the difference in the SOC between S₁ and T(π–π*) and the SOC between S₁ and T(n–π*) still remains significant. The histograms of the SOC of molecules 2–4 are shown in Fig. S7 (ESI†).

Table 1 The SOC strength, |H_SO| (in cm⁻¹) and the adiabatic singlet–triplet energy gap, ΔE^ad_ST, (in eV) calculated at the level of EOM-CCSD/cc-pVDZ

T(π–π*)
Molecule	|H^ISCSO|^a	|H^rISCSO|^b	|H^ISCSO|eff^c	|H^rISCSO|eff^c	ΔE^adST
a Calculated at the relaxed S1 state geometry, scaled down by a factor of for a direct comparison with |H^rISCSO|. b Calculated at the relaxed T(π–π*) state geometry. c Effective SOC from thermal average. See computational details. d Calculated at the relaxed T(n–π*) state geometry.
1	1.62 × 10^−4	1.40 × 10^−4	1.53 × 10^−4	1.49 × 10^−4	−1.92 × 10^−1
2	2.08 × 10^−1	5.19 × 10^−3	1.53 × 10^−1	3.67 × 10^−2	−3.05 × 10^−2
3	7.98 × 10^−3	1.41 × 10^−2	9.66 × 10^−3	1.18 × 10^−2	1.03 × 10^−2
4	3.14 × 10^−2	6.55 × 10^−3	2.81 × 10^−2	1.42 × 10^−2	−3.84 × 10^−2

---

T(n–π*)
Molecule	|H^ISCSO|^a	|H^rISCSO|^d	ΔE^adST
2	1.68	1.74	−4.99 × 10^−3
3	1.80	1.52	−1.47 × 10^−1
4	1.37	7.26 × 10^−1	2.11 × 10^−1

---

The ISC, rISC, and the IC rates are shown in Table 2. The rates show that the energetic alignment of the T(n–π*) state placed with the T(π–π*) above and the S₁ below is indeed advantageous for rISC, with IC transferring the population from T(π–π*) to T(n–π*) and large SOC facilitating the rISC from the T(n–π*) to the S₁. The theoretical rISC rate from the T(n–π*) state in 3 also benefits from the strong SOC, but it also relaxes rapidly to the T(π–π*) state, which has a relatively slow rISC rate. 4 shows virtually negligible IC and ISC both to and from the T(n–π*) state. The kinetics of 4 is heavily affected by the large difference in the geometry of the T(n–π*) state from those of the states of (π–π*) nature, which leads to a rapid decay of the ρ factor in eqn (1) and (2). The decay of the integrand of eqn (1) and the trace of the ρ_kl term in eqn (2) are shown in Fig. S8–S10 (ESI†). As the rate calculation is based on harmonic approximation, the extremely slow rate of transition to and from the T(n–π*) state of 4 is expected to be an underestimation stemming from the large difference in geometry. The ISC and rISC rates involving the T(n–π*) state in all molecules thus have smaller integral values compared to the transitions involving the T(π–π*) state, thereby not achieving transition rates proportional to the much stronger SOC. The dynamics between the S₁ and T(π–π*) states is also noteworthy in that despite the lower energy of the S₁ state of 2, the ISC from the singlet to the triplet state is faster by an order of magnitude, which can be attributed to the stronger SOC strength at the S₁ geometry given by the breaking of planar symmetry. The rates involving transition to S(n–π*) are not expected to be substantial enough to bring nontrivial changes to the overall kinetics, as for 2 and 3 the S(n–π*) state lies ∼0.4 eV higher in energy than either of the triplet states, which is an energy gap that resulted in the rISC rate on order of 10² s⁻¹ in a recent study.⁵⁵ The S(n–π*) state of 4 lies low enough for rISC from T(π–π*) to be energetically viable, but the large displacement between the states of (π–π*) character and the states of (n–π*) character is expected to hinder the transition, as how the transitions to and from T(n–π*) show negligible transition rates. The rISC from the T(n–π*) state to the S(n–π*) state is highly endothermic at ∼0.27 eV, which also results in the rISC rate on the order of 10³ s⁻¹.⁵⁵

Table 2 ISC, rISC, and IC rates in s⁻¹ calculated using effective SOC values in Table 1

	1	2	3	4
	6.37 × 10^−1	3.46 × 10^6	1.61 × 10^5	4.30 × 10^5
	6.50	4.78 × 10^5	2.62 × 10^4	3.59 × 10^4
	—	1.66 × 10^6	1.43 × 10^3	4.60 × 10^−3
	—	6.63 × 10^6	1.35 × 10^6	0.38
	—	1.32 × 10^9	8.27 × 10^4	0.54
	—	1.05 × 10^9	2.97 × 10^9	19.82

---

The difference in the geometry of the singlet and triplet states involved in ISC/rISC is shown in the plots of the Duschinsky matrices and displacement vectors involved in the ISC/rISC processes shown in Fig. 4a, and the rotation angles of the Duschinsky matrix are shown in Fig. 4b. The normal modes with the largest displacement vectors for each transition are shown in Fig. S11 (ESI†). The rotation angles are calculated as described in the ESI.† As expected from the different electronic structures, the T(n–π*) state has considerably larger relative displacements and more rotation angles are near the vicinity of π/4 with respect to S₁ compared to the T(π–π*) state for all molecules, with especially large displacements for 4. The Duschinsky matrix and the displacement vectors between the triplet states involved in IC are shown in Fig. S12 (ESI†), again showing that the large change in geometry inhibits transitions to and from the T(n–π*) state.

Fig. 4 (a) Plots of the absolute value of the Duschinsky matrix and displacement vectors between the S₁ state and the triplet states for the molecules studied. (b) Histogram of the angle of rotation of the Duschinsky matrix, grouped into eight bins within the range .

The steady state population for S₁, T(π–π*), and T(n–π*) of molecules 2–4 can be readily obtained using the rates calculated, and thus the propensity of each molecules to populate the emissive singlet state can be quantified. 2 shows the most promising prospect as expected, with 42% populating the S₁ at the steady state, and T(π–π*) and T(n–π*) taking 27% and 31%, respectively. Since T(π–π*) and T(n–π*) have similar energy levels, the IC rates between them are on the same order, which results in almost 1 : 1 population. The high population of the S₁ state can be attributed to it being the lowest in energy and active participation of the T(n–π*) state in drawing population from the T(π–π*) state that subsequently undergoes rISC, counteracting the rather rapid ISC back to the T(π–π*) state. 3 shows the case when T(n–π*) is too high in energy to participate in the dynamics and the ΔE_ST inversion is broken to favor population of the triplet state, with 11% of the population in the S₁ state and 89% in the T(π–π*) state and negligible population of the T(n–π*) state. The dynamics of 4 shows the situation when the T(n–π*) state is the lowest in energy but becomes inaccessible due to high reorganization energy and the SOC from the singlet state to the triplet state is stronger due to the breaking of planar symmetry, with 92% of the population in the T(π–π*) state and 8% in the S₁ state, with virtually no population of the T(n–π*) state.

4 Conclusion

In this work, we show a new design strategy of OLED emitters that not only have negative ΔE_ST but also utilize the change in orbital angular momentum between the n–π* state and the π–π* state to overcome the weak SOC of previously discussed IST emitters. The computations on both energetics and kinetics provide encouraging prospects for development of carbonyl attached IST emitters by showing that (i) the T(n–π*) state energy is comparable to the T(π–π*) energy and can be populated using electronic excitation, (ii) the energy can be tuned using a relatively intuitive method of attaching functional groups that either donate or withdraw electrons, and (iii) the SOC of T(n–π*) → S₁ transition is indeed stronger than that seen in conventional IST emitters. To make better use of the T(n–π*) state, means to control the geometric factors must be investigated, as the degree of displacement of relaxed geometry in the T(n–π*) state and the break of planar symmetry in either the S₁ or T(π–π*) state are found to be especially impactful on the ISC/rISC dynamics. The large difference in geometries of states with (n–π*) character and states with (π–π*) character can become a major roadblock by (i) inhibiting the IC from T(π–π*) even in the case of T(n–π*) being the lower energy triplet state and (ii) inhibiting the rISC to S₁. The break of planar symmetry can have synergistic effects with the non-bonding orbital as the contribution of non-bonding orbitals to the π and π* orbitals can also increase the rISC rate from the T(π–π*) to the S₁ state. To better take into account the dependence of electronic state energies and couplings on the geometries, a molecular dynamics simulation to monitor the change in geometry at finite temperature and confirm the stability of the compound can be a promising topic for future studies. As satisfying the criteria of negative ΔE_ST, the right energy level of the T(n–π*) state, and moderate reorganization are not straightforward, a high-throughput study may help in discovering optimal molecules for rISC. Further investigations into optimizing the change in geometry and normal modes may lead to the discovery of numerous emitters for which the rISC happens in a prompt timescale and is thermodynamically driven.

Author contributions

Conceptualization: Hwon Kim and Seung Kyu Min; data curation: Hwon Kim; formal analysis: Hwon Kim; funding acquisition: Seung Kyu Min; investigation: Hwon Kim and Seung Kyu Min; methodology: Hwon Kim and Seung Kyu Min; project administration: Hwon Kim and Seung Kyu Min; resources: Seung Kyu Min; software: Hwon Kim; supervision: Seung Kyu Min; validation: Hwon Kim; visualization: Hwon Kim and Seung Kyu Min; and writing – Hwon Kim and Seung Kyu Min.

Data availability

All data generated in this study are available from the corresponding author upon request. The codes used for the rate calculation are available at: https://github.com/hkimaf/Nonbonding_ISC_calculation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the National Research Foundation of Korea (NRF) funded by the Korean government (Ministry of Science and ICT(MSIT)) (NRF-2023M3K5A1094813, RS-2023-00257666, and RS-2024-00455131).

Notes and references

1. J. Larkin, W. Donaldson, T. Foster and R. Knox, Chem. Phys., 1999, 244, 319–330.
2. T. Huang, X. Song, M. Cai, D. Zhang and L. Duan, Mater. Today Energy, 2021, 21, 100705.
3. S. Gorgon, K. Lv, J. Grüne, B. H. Drummond, W. K. Myers, G. Londi, G. Ricci, D. Valverde, C. Tonnelé and P. Murto, et al. , Nature, 2023, 620, 538–544.
4. L. Lv, Y. Zhang and Z. Ning, RSC Adv., 2024, 14, 23987–23999.
5. H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238.
6. Q. Zhang, B. Li, S. Huang, H. Nomura, H. Tanaka and C. Adachi, Nat. Photonics, 2014, 8, 326–332.
7. Y. Wada, H. Nakagawa, S. Matsumoto, Y. Wakisaka and H. Kaji, Nat. Photonics, 2020, 14, 643–649.
8. R. J. Vázquez, J. H. Yun, A. K. Muthike, M. Howell, H. Kim, I. K. Madu, T. Kim, P. Zimmerman, J. Y. Lee and T. G. Iii, J. Am. Chem. Soc., 2020, 142, 8074–8079.
9. A. P. Monkman and T. J. Penfold, ChemPhysChem, 2016, 17, 2956–2961.
10. K. R. Naveen, P. Palanisamy, M. Y. Chae and J. H. Kwon, Chem. Commun., 2023, 59, 3685–3702.
11. H. S. Kim, J. Y. Lee, S. Shin, W. Jeong, S. H. Lee, S. Kim, J. Lee, M. C. Suh and S. Yoo, Adv. Funct. Mater., 2021, 31, 2104646.
12. Q. Ou, Y. Shao and Z. Shuai, J. Am. Chem. Soc., 2021, 143, 17786–17792.
13. J. Ochi, Y. Yamasaki, K. Tanaka, Y. Kondo, K. Isayama, S. Oda, M. Kondo and T. Hatakeyama, Nat. Commun., 2024, 15, 2361.
14. P. Rajamalli, N. Senthilkumar, P. Gandeepan, C.-C. Ren-Wu, H.-W. Lin and C.-H. Cheng, ACS Appl. Mater. Interfaces, 2016, 8, 27026–27034.
15. X. Chen, S. Bagnich, R. Pollice, B. Li, Y. Zhu, R. Saxena, Y. Yin, W. Zhu, A. Aspuru-Guzik and E. Zysman-Colman, et al. , Adv. Opt. Mater., 2024, 12, 2301784.
16. P. L. Santos, J. S. Ward, P. Data, A. S. Batsanov, M. R. Bryce, F. B. Dias and A. P. Monkman, J. Mater. Chem. C, 2016, 4, 3815–3824.
17. P. de Silva, J. Phys. Chem. Lett., 2019, 10, 5674–5679.
18. L. Sun, W. Hua, Y. Liu, G. Tian, M. Chen, M. Chen, F. Yang, S. Wang, X. Zhang and Y. Luo, et al. , Angew. Chem., 2019, 131, 11433–11438.
19. X.-K. Chen, D. Kim and J.-L. Brédas, Acc. Chem. Res., 2018, 51, 2215–2224.
20. P. de Silva, C. A. Kim, T. Zhu and T. Van Voorhis, Chem. Mater., 2019, 31, 6995–7006.
21. R. S. Nobuyasu, Z. Ren, G. C. Griffiths, A. S. Batsanov, P. Data, S. Yan, A. P. Monkman, M. R. Bryce and F. B. Dias, Adv. Opt. Mater., 2016, 4, 597–607.
22. F. B. Dias, J. Santos, D. R. Graves, P. Data, R. S. Nobuyasu, M. A. Fox, A. S. Batsanov, T. Palmeira, M. N. Berberan-Santos, M. R. B. Bryce and A. P. Monkman, Adv. Sci., 2016, 3, 1600080.
23. P. K. Samanta, D. Kim, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2017, 139, 4042–4051.
24. R. Pollice, P. Friederich, C. Lavigne, G. dos Passos Gomes and A. Aspuru-Guzik, Matter, 2021, 4, 1654–1682.
25. Y. Lee, J. Kim, S. Lee, E. Sim and J.-I. Hong, Chem. Eng. J., 2023, 476, 146659.
26. N. Aizawa, Y.-J. Pu, Y. Harabuchi, A. Nihonyanagi, R. Ibuka, H. Inuzuka, B. Dhara, Y. Koyama, K.-I. Nakayama, S. Maeda, F. Araoka and D. Miyajima, Nature, 2022, 609, 502–506.
27. J. Ehrmaier, E. J. Rabe, S. R. Pristash, K. L. Corp, C. W. Schlenker, A. L. Sobolewski and W. Domcke, J. Phys. Chem. A, 2019, 123, 8099–8108.
28. O. H. Omar, X. Xie, A. Troisi and D. Padula, J. Am. Chem. Soc., 2023, 145, 19790–19799.
29. M. Bedogni, D. Giavazzi, F. Di Maiolo and A. Painelli, J. Chem. Theory Comput., 2023, 20, 902–913.
30. D. Valverde, C. T. Ser, G. Ricci, K. Jorner, R. Pollice, A. Aspuru-Guzik and Y. Olivier, ACS Appl. Mater. Interfaces, 2024, 16, 66991–67001.
31. J. Terence Blaskovits, M. H. Garner and C. Corminboeuf, Angew. Chem., Int. Ed., 2023, 62, e202218156.
32. A. Actis, M. Melchionna, G. Filippini, P. Fornasiero, M. Prato, M. Chiesa and E. Salvadori, Angew. Chem., Int. Ed., 2023, 62, e202313540.
33. R. Pollice, B. Ding and A. Aspuru-Guzik, Matter, 2024, 7, 1161–1186.
34. G. Ricci, J.-C. Sancho-García and Y. Olivier, J. Mater. Chem. C, 2022, 10, 12680–12698.
35. M. A. El-Sayed, Acc. Chem. Res., 1968, 1, 8–16.
36. K. Jorner, R. Pollice, C. Lavigne and A. Aspuru-Guzik, J. Phys. Chem. A, 2024, 128, 2445–2456.
37. F. Dinkelbach, M. Bracker, M. Kleinschmidt and C. M. Marian, J. Phys. Chem. A, 2021, 125, 10044–10051.
38. H. Kim, G. D. Scholes and S. K. Min, Phys. Chem. Chem. Phys., 2024, 26, 5508–5516.
39. Y. Yu, F. Liu, X. Meng, L. Ding, L. Liao and Z. Jiang, Chem. – Eur. J., 2023, 29, e202202628.
40. S. Wu, L. Zhang, J. Wang, A. K. Gupta, I. D. Samuel and E. Zysman-Colman, Angew. Chem., Int. Ed., 2023, 62, e202305182.
41. Y.-C. Cheng, X. Tang, K. Wang, X. Xiong, X.-C. Fan, S. Luo, R. Walia, Y. Xie, T. Zhang and D. Zhang, et al. , Nat. Commun., 2024, 15, 731.
42. M. Baba, J. Phys. Chem. A, 2011, 115, 9514–9519.
43. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford, CT, 2016.
44. M. J. Peach, M. J. Williamson and D. J. Tozer, J. Chem. Theory Comput., 2011, 7, 3578–3585.
45. Y. Guo, L. Zhang and Z. Qu, Molecules, 2023, 28, 3257.
46. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al. , Mol. Phys., 2015, 113, 184–215.
47. P. Karak and S. Chakrabarti, Phys. Chem. Chem. Phys., 2020, 22, 24399–24409.
48. L. Paul, T. Moitra, K. Ruud and S. Chakrabarti, J. Phys. Chem. Lett., 2019, 10, 369–374.
49. P. Karak, P. Manna, A. Banerjee, K. Ruud and S. Chakrabarti, J. Phys. Chem. Lett., 2024, 15, 7603–7609.
50. I. Kim, S. O. Jeon, D. Jeong, H. Choi, W.-J. Son, D. Kim, Y. M. Rhee and H. S. Lee, J. Chem. Theory Comput., 2019, 16, 621–632.
51. C. M. Marian, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 187–203.
52. K. Miyazaki and N. Ananth, J. Chem. Phys., 2022, 156, 044111.
53. R. Ianconescu and E. Pollak, J. Phys. Chem. A, 2004, 108, 7778–7784.
54. Y. Niu, Q. Peng, C. Deng, X. Gao and Z. Shuai, J. Phys. Chem. A, 2010, 114, 7817–7831.
55. B. K. Min, D. Kim, D. Kim and Y. M. Rhee, Bull. Korean Chem. Soc., 2023, 44, 989–1003.
56. P.-F. Loos, F. Lipparini and D. Jacquemin, J. Phys. Chem. Lett., 2023, 14, 11069–11075.
57. N. Lin, J. Qiao, L. Duan, L. Wang and Y. Qiu, J. Phys. Chem. C, 2014, 118, 7569–7578.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5cp00166h

---