Oxygen exchange kinetics of BaGd_0.3La_0.7Co₂O_6−δ with exsolved Co₃O₄ nanoparticles in dry and humid atmospheres

Abstract

The oxygen exchange kinetics of BaGd_0.3La_0.7Co₂O_6−δ were investigated with pulsed isotope exchange (PIE) measurements in dry and humid atmospheres in the temperature range 400–600 °C in 0.005–0.21 bar O₂. Synchrotron X-ray diffraction and scanning transmission electron microscopy (STEM) revealed exsolved Co₃O₄ nanoparticles dispersed on the surfaces that may contribute to the catalytic activity of the material towards the oxygen exchange reactions. The obtained oxygen exchange rate was 4.45 × 10⁻³ mol m⁻² s⁻¹ at 600 °C in 0.21 bar O₂ with an activation energy of 0.76 eV. The rate determining step of the exchange reaction was determined to be dissociative adsorption of oxygen in both dry and humid atmospheres based on the individual rates of dissociative adsorption and incorporation, as well as pO₂ dependencies of the oxygen exchange rate of around 1. The effect of water on the oxygen exchange rate was found to be dependent on the oxygen partial pressure, decreasing the rate at 0.21 bar O₂ and 600 °C by a factor of approx. 2, while increasing the rate at 0.02 bar and 0.005 bar O₂ by a similar amount. In situ thermogravimetric analysis was used to characterise the oxygen non-stoichiometry of the material throughout the oxygen exchange measurements.

---

1. Introduction

Proton ceramic electrolysis cells (PCEs) are promising electrochemical devices for efficient and clean production of hydrogen from steam using renewable electricity.^1–4 Their operation at intermediate temperatures of 300–600 °C results in a lower thermodynamic cell voltage and enables utilization of waste heat for higher energy efficiency compared to water electrolysis cells, e.g., proton exchange membranes (PEM).^5,6 The intermediate operating temperatures of PCEs also lead to improved electrode kinetics and reduced reliance on noble metal catalysts.^7,8 Advantages of PCEs over solid oxide electrolysis cells (SOEC) – operating at higher temperatures – include their ability to produce dry pressurised hydrogen and presumably lower module costs and improved long-term stability.^8–12

The performance of PCEs is limited by the sluggish kinetics of the air/steam electrode (denoted positrode).¹¹ The rate limiting reactions at the positrode are the oxygen reduction and evolution reactions (ORR/OER).^13–15 These reactions involve several of the same steps as oxygen exchange, which thereby can be used to probe the catalytic activity towards the ORR and OER. Two main mechanisms for oxygen exchange have been defined. In the homoexchange mechanism, oxygen adsorbs dissociatively and exchange occurs between adsorbates on the surface.^16–20 This exchange mechanism is typical for materials that are primarily electronic conductors with negligible oxide ion conductivity such as Sr-doped LaMnO₃.^21–23 In the heteroexchange mechanism, one or two oxygen atoms are incorporated into the surface after dissociative adsorption and the exchange occurs with oxygen from the bulk of the material.^16–20 The heteroexchange mechanism is typical for mixed ionic electronic conductors such as La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ (LSCF).^21,24,25

Understanding the role of water on the oxygen exchange kinetics of positrodes in PCEs is essential as both species are involved in the electrochemical reaction under device operation. The presence of water and other co-adsorbates can lead to complex relationships with the oxygen exchange kinetics, depending on the type of exchange mechanism and the environmental conditions. On one hand, co-adsorbates such as H₂O and CO₂ may block catalytically active sites and reduce the exchange rate, unless the adsorption is not competitive (i.e., low surface coverage of adsorbates). A decrease in oxygen exchange rate in the presence of these co-adsorbates has been reported for LSCF, attributed to blocking of active sites.^21,26 On the other hand, oxygen containing adsorbates may take part in the exchange reaction and contribute to the overall oxygen exchange, as shown for homoexchange on LSM, and heteroexchange on LSCF.^26–28 In such cases, it is crucial to distinguish exchange from O₂ involving oxygen reduction/evolution from other exchange reactions that do not represent the electrode redox processes.²⁹ Notably, oxygen exchange between water and lattice oxygen proceeds at a faster rate and with lower activation energy compared to exchange from O₂, as shown for (La_0.8Sr_0.2)_0.95Cr_0.5Fe_0.5O_3−δ and SrTiO₃, since no electron transfer is required for chemisorption of water, i.e., oxygen reduction is only required for one of the molecules in the exchange reaction.^30,31 Similarly, oxygen exchange has been shown to be significantly faster between lattice oxygen and CO₂ compared to O₂ on acceptor doped ZrO₂ and Pd/Al₂O₃ catalysts.^32–34 The presence of water was shown to increase the measured oxygen exchange rate by almost one order of magnitude on dense La_0.6Sr_0.4CoO_3−δ (LSC) thin films at 400 °C,³⁵ although the contribution from exchange with H₂O was not quantified. A limited effect of humidity on the oxygen exchange coefficient was recently observed for SrTi_0.65Fe_0.35O_3−δ.³⁶ Finally, adsorbates can react to form secondary phases at the surface, induce cation segregation, or carry impurities such as silicon that are deposited on the surface, leading to degradation of the oxygen exchange rates as reported for LSC.^35,37

Isotope exchange techniques are powerful methods for obtaining information about the oxygen exchange kinetics of metal oxides. Among these methods, pulsed isotope exchange (PIE) provides a quick way to gauge the oxygen surface exchange rate under different atmospheric conditions and temperatures.³⁸ Parameters derived from isotope exchange experiments include the oxygen exchange rate and the contributions from dissociative adsorption and incorporation, as well as their activation energies.³⁸

Double perovskite rare earth cobaltites LnBaCo₂O_5+δ (Ln = La, Pr, Nd, Sm, Gd, and Y) have been extensively studied as air electrode materials for solid oxide fuel cells.³⁹ The oxygen exchange kinetics of PrBaCo₂O_5+δ and GdBaCo₂O_5+δ have been investigated with isotope exchange measurements. The obtained activation energies in 0.21 bar O₂ were 0.8–1.0 eV for PrBaCo₂O_5+δ^40–43 in the temperature range 300–850 °C and around 0.85 eV for GdBaCo₂O_5+δ⁴² in the temperature range 500–800 °C. Ba_1−yGd_0.8−xLa_0.2+x+yCo₂O_6−δ (BGLCs) represents a group of double perovskites considered among the state-of-the-art positrodes for steam/water electrolysis over a wide temperature range (25–700 °C).^44–46 Some compositions take up protons from water vapour and exhibit bulk protonic conductivity, making them particularly interesting for PCEs.⁴⁷

In the present work, the oxygen exchange kinetics of BaGd_0.3La_0.7Co₂O_6−δ (BGLC37) were studied using pulsed isotope exchange in dry and humid atmospheres to further elucidate the role of steam on the materials performance as steam electrode. The oxygen non-stoichiometry and crystal structure of the material were quantified using thermogravimetry and synchrotron X-ray diffraction (XRD), respectively, to track the evolution of the material under the same conditions as the oxygen exchange measurements. Scanning transmission electron microscopy (STEM) and XRD revealed that the material contains exsolved Co₃O₄ nanoparticles dispersed on the surfaces that may contribute to the catalytic activity of the material towards the oxygen exchange reactions.⁴⁸

2. Methods

2.1. Sample preparation

BaGd_0.3La_0.7Co₂O_6−δ (BGLC37) powder from spray pyrolysis (Marion Technologies, France) was uniaxially pressed into disks (25 mm diameter) and sintered at 1200 °C for 20 hours in ambient air to obtain dense samples (approx. 95% density). The sintered samples were crushed with a pestle and mortar, and sieved to acquire the particle size fractions 90–125 μm and 60–90 μm. A surface area of 0.10567 m² g⁻¹ for the 90–125 μm fraction was obtained with BET utilising a Belsorp mini II (Bel, Japan) with a pretreatment at 300 °C for three hours in vacuum.^49,50

2.2. Synchrotron X-ray diffraction

Synchrotron X-ray diffraction experiments were conducted at the Swiss-Norwegian Beamline (SNBL) BM01⁵¹ at the European Synchrotron Radiation Facility (ESRF). A 0.5 mm diameter capillary filled with BGLC37 powder was rotated during measurements as the temperature increased from room temperature to 900 °C in air. An X-ray energy of 17.42 keV (λ = 0.72173 Å) was applied during the experiment and diffraction patterns were measured on a PILATUS@SNBL diffractometer. The 2D detector image was calibrated with a LaB₆ standard and the in situ data were processed using the SNBL Toolbox and BUBBLE software.⁵¹ Rietveld refinements were performed using TOPAS v6 Academic software.⁵²

2.3. Scanning transmission electron microscopy

High-angle annular dark field (HAADF) imaging and elemental mapping were conducted using STEM in combination with energy dispersive spectroscopy (EDS) using a Super-X detector. These analyses were performed on a Thermo Fisher Scientific Cs-corrected Titan G2 60–300 kV microscope, operated at an accelerating voltage of 200 kV. The BGLC37 sample was prepared by dispersing the crushed powder in ethanol using ultrasonic bath sonication to ensure uniform dispersion. A small amount of the dispersion was drop-cast onto a lacey carbon copper grid and allowed to dry.

2.4. Electron probe microanalysis

Electron probe microanalysis (EPMA) was performed with a CAMECA SX100 electron microprobe on a sintered and polished BGLC37 disk sample. The microprobe was calibrated with cobalt metal, BaSO₄, GdPO₄ and LaPO₄. The characteristic X-rays chosen for each of the elements were Ba Lα, Co Kα, La Lα and Gd Lβ. A focused beam was utilized with an energy of 15 kV and a beam current of 15 nA. The background was measured on each side of the chosen signals followed by a measurement of 20 s for each element.

2.5. Pulsed isotope exchange

Pulsed isotope exchange measurements were performed in a custom setup with a gas supply line controlling both the carrier gas and the pulse, a packed bed reactor comprising a quartz tube inserted into a horizontal tube furnace, and a quadrupole mass spectrometer (Pfeiffer QME 220) connected to the exhaust line at the other end of the quartz tube. A powder sample of 43.7 mg of the 90–125 μm particle size fraction was placed in the quartz tube with an inner diameter of 2 mm. The powder bed (4 mm length) was held in place by quartz wool on both sides.

The sample was pre-treated at 950 °C for 5 hours in a carrier gas with the desired pO₂ and pH₂O balanced with nitrogen at a flow rate of 50 mL s⁻¹, before cooling to the first measurement temperature. Measurements were performed in 0.21, 0.02 and 0.005 bar O₂ upon cooling from 600 °C to 200 °C. Measurements were performed isothermally at 25–50 °C intervals after a 30-minute equilibration time at each temperature and the heating and cooling rates were 3 °C per minute.

A pulse containing ¹⁸O (97% from Sigma Aldrich or 99% from Isotec) at the same pO₂ as the carrier gas (balanced by 2% Ar and N₂) was passed over the sample (pulse time 0.60 s), and the composition of the pulse was monitored at the outlet with the mass spectrometer. Gas containing 97% ¹⁸O was used for oxygen partial pressures of 0.21 bar, and 0.02 bar in dry conditions. Gas containing 99% ¹⁸O was used for oxygen partial pressures of 0.005 bar, and 0.02 bar O₂ in humid conditions. The carrier gas was either bottle dry or bubbled through water to achieve a humidification of approximately 3% (0.03 bar), while the pulse was always bottle dry due to constraints in the setup. Thereby, the water content in the atmosphere while the pulse passes over the sample is not certain. Nevertheless, the measurements provide insight into the role of humidity on the oxygen exchange reactions. Blank measurements with only the quartz tube and quartz wool were performed to investigate possible exchange with the reaction chamber itself in a temperature range of 100–1100 °C. No exchange of oxygen with the reaction chamber was observed in the temperature range of interest (200–600 °C) with both dry and humid carrier gases (ESI†).

The PIE data was analysed according to a two-step model involving dissociative adsorption of O₂ and incorporation of adsorbed oxygen into oxygen vacancies.³⁸ The oxygen exchange reaction for heteroexchange can be written with Kröger–Vink notation as reversible adsorption, dissociation, and incorporation of oxygen into oxygen vacancies :

The oxygen exchange rate is calculated with the following equation:

where n is the total number of oxygen atoms in the gas phase, τ is the residence time in the reactor, S is the surface area of the oxide sample, f_i¹⁸ and f_o¹⁸ are the fractions of oxygen-18 at the inlet and outlet, respectively. The residence time τ was 15.1 ms based on a pulse length of 159 mm, flow rate of 50 mL min⁻¹, and 4 mm bed length.

The oxygen exchange reaction can be split into two different reaction steps – dissociative adsorption and incorporation – and it is here not explicitly described in which step the oxygen reduction occurs:^22,38

O* + v_O ⇌ O_O + * (4)

where * denotes a surface site and v_O is an oxygen vacancy. The oxygen exchange rate from eqn 2 can be deconvoluted into the rate of adsorption (ℜ_ads) and rate of incorporation (ℜ_inc):where p is the probability of incorporating an adsorbed oxygen into the bulk.

With this two-step model, the pO₂ dependency of the oxygen exchange rate becomes 1 when dissociative adsorption is the rate limiting step and 0.5 when incorporation is the rate limiting step,²² as long as the materials properties do not change with pO₂. Data analysis of the isotopologue fractions, extraction of reaction rates and activation energies were performed using a MATLAB script based on the aforementioned two-step model.⁵³

2.6. Thermogravimetry

Thermogravimetry (TG) was performed using a Jupiter STA 449 F3 thermogravimetric analyser (Netzsch, Germany) with a 3.1 mL Al₂O₃ crucible. The TG measurements were performed for the 90–125 μm and 60–90 μm powder fractions, following the same pre-treatment and temperature profiles, and similar atmospheres to the PIE measurements. Blank measurements were performed with an empty crucible and the same atmospheres and temperature program. The mass change from the blank measurements was subtracted from the BGLC37 data to account for any instrumental background. All mass change after the correction with the blank measurements was attributed to the loss or uptake of oxygen. The absolute oxygen non-stoichiometry at the end of the 5-hour pre-treatments was separately determined by decomposition of BGLC37 in an atmosphere of 5% H₂ in argon at 950 °C. The mass change was ascribed to oxygen loss due to reduction of cobalt to the metallic phase, i.e., assuming no change in oxidation states of the remaining cations.

3. Results

3.1. Structure and exsolved Co₃O₄ nanoparticles

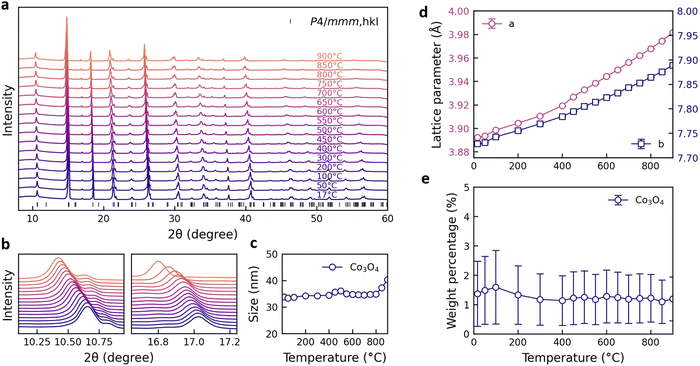
The structure of BaGd_0.3La_0.7Co₂O_6−δ has been reported to exhibit either tetragonal (P4/mmm)⁴⁶ or orthorhombic (Pmmm)⁵⁴ symmetry. The collected temperature dependent synchrotron X-ray diffraction patterns reveal no significant structural changes or phase transitions with increasing temperature (Fig. 1a and b). A minor Co₃O₄ phase (∼1 wt%) is identified at around 17° (Fig. 1b), with a crystallite size of about 35 nm that remained stable up to 800 °C (Fig. 1c). Rietveld refinements were first performed with the tetragonal P4/mmm space group for temperatures up to 900 °C. The lattice parameters increase linearly with increasing temperature, with a transition around 400 °C that may be ascribed to chemical expansion upon reduction (Fig. 1d).⁵⁵ The weight fraction of the Co₃O₄ phase is given in Fig. 1e. Notably, the amount of the secondary Co₃O₄ phase remains essentially unchanged within the temperature range of the oxygen exchange measurements. Therefore, any contributions from the Co₃O₄ particles to the oxygen exchange kinetics can be expected to remain constant throughout the measurements. No significant improvement in the refinement quality (R_w) was obtained using the lower symmetry orthorhombic Pmmm space group (ESI†). Additionally, the lattice parameters and the amount of Co₃O₄ show similar trends for both P4/mmm and Pmmm phases as temperature increases.

Fig. 1 (a) Temperature-dependent synchrotron X-ray diffraction patterns of BGLC37 from room temperature to 900 °C. (b) Individual peaks of BGLC37 (P4/mmm) phase at (100), (002) and secondary phase Co₃O₄ at (311). (c) Grain size of Co₃O₄ estimation from the (311) peak calculated with the Scherrer equation. (d) Temperature-dependent lattice parameters of the primary P4/mmm phase from Rietveld refinements of synchrotron X-ray diffraction data. (e) Co₃O₄ weight percentage obtained from Rietveld refinements using a two-phase model comprising P4/mmm and a minor Co₃O₄ content of ∼1 wt%.

To further investigate the nature of the Co₃O₄ phase, STEM analysis was performed on a sample from the crushed BGLC37 powder. STEM imaging revealed the presence of nanoparticles distributed across the surface of the sample, while some particles may also be embedded within the bulk (Fig. 2a and b). The size of the particles in these images appear to be somewhat smaller than the crystallite size of about 35 nm obtained from XRD (Fig. 1c). The elemental maps obtained through STEM-EDS confirmed the localized enrichment of cobalt in the particles protruding from the surface, consistent with Co₃O₄ (Fig. 2c–f).

Fig. 2 (a) and (b) high-angle annular dark field (HAADF) micrographs of the BGLC37 sample showing nanoparticles distributed over the surface. (c)–(f) Elemental maps of Ba (green), Gd (yellow), La (orange), and Co (pink), respectively, derived from micrograph (b), illustrating elemental distribution.

The chemical composition of an as-sintered sample was investigated by electron probe microanalysis and the results are summarized in Table 1. The analysis includes contributions from the exsolved Co₃O₄ nanoparticles due to the comparatively large beam size and interaction volume. The obtained composition indicates minor cobalt deficiency, consistent with exsolution of Co₃O₄ not originating from excess cobalt or A-site deficiency in the BGLC material.

Table 1 Elemental analysis from EPMA measurements at eleven locations on a sintered and polished BGLC37 sample

Element	Mol fraction
Ba	0.99 ± 0.12
Gd	0.32 ± 0.16
La	0.76 ± 0.08
Co	1.94 ± 0.12
O	5.51 ± 0.02

---

3.2. Oxygen exchange kinetics

3.2.1. Dry carrier gas. The measured oxygen isotopologue fractions as a function of temperature in 0.21 bar O₂ is shown in Fig. 3. The presence of ¹⁶O in the pulse (97% enriched ¹⁸O) results in a fixed background level of ¹⁶O¹⁸O at lower temperatures, while the background was negligible in the case of 99% enriched ¹⁸O (ESI†). Under these measurement conditions, oxygen exchange with BGLC37 is detectable at temperatures of approx. 400 °C and above, as seen from the increase in mass 32 (¹⁶O₂) and mass 34 (¹⁶O¹⁸O), along with the decrease in mass 36 (¹⁸O₂). The measured data can be fitted reasonably well to the two-step adsorption/incorporation model described in Section 2. Methods (solid lines in Fig. 3) from 450 °C to 600 °C. The uncertainty in the measured data increases with decreasing temperature as the amount of exchange is lower, which results in a weaker fit between 400 °C and 450 °C. Due to the negligible exchange at temperatures lower than 400 °C, these data were not included in the further analysis to extract exchange rates and activation energies.

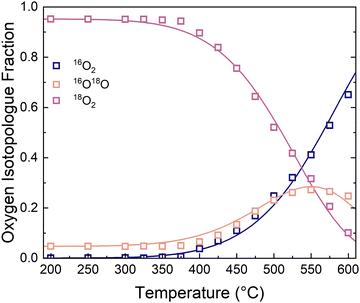Fig. 3 Oxygen isotopologue fractions as a function of temperature at 0.21 bar O₂. The solid lines are fitted according to the two-step adsorption/incorporation model.

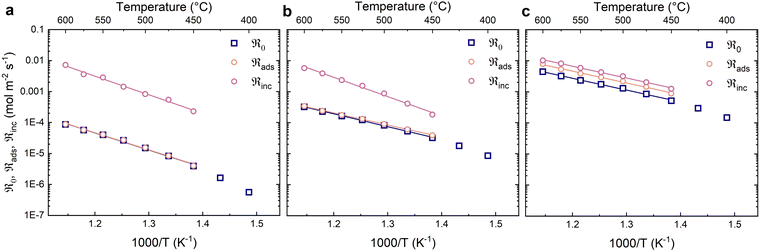
Fig. 4 shows the oxygen exchange rates as a function of inverse temperature at different partial pressures of oxygen. The oxygen exchange rates exhibit Arrhenius behaviour and increase with oxygen partial pressure. The contributions from dissociative adsorption (ℜ_ads) and incorporation (ℜ_inc) to the oxygen exchange rate (ℜ₀) were calculated for a narrower temperature range (450–600 °C) where the data showed less scatter and consistent Arrhenius type behaviour (Fig. 4). The fastest process – in this case incorporation – generally exhibits the largest uncertainty. The oxygen exchange rate is limited by the dissociative adsorption of oxygen at all oxygen partial pressures, although to a lesser extent at 0.21 bar O₂.

Fig. 4 Oxygen exchange rate (ℜ₀) and the contributions from dissociative adsorption (ℜ_ads) and incorporation (ℜ_inc) at different oxygen partial pressures (dry carrier gas): (a) 0.005 bar (b) 0.02 bar (c) 0.21 bar. The solid lines are linear fits.

The activation energies for the different reaction steps were obtained from the linear fits in Fig. 4 and are summarised in Table 2. The activation energies for dissociative adsorption (ℜ_ads) are essentially the same as for the oxygen exchange rate (ℜ₀). The activation energies of incorporation (ℜ_inc) are essentially the same as for the oxygen exchange at the highest oxygen partial pressure and slightly higher at the lower oxygen partial pressures.

Table 2 Activation energies for the oxygen exchange rate (ℜ₀), dissociative adsorption rate (ℜ_ads) and incorporation rate (ℜ_inc) at different oxygen partial pressures in dry and humid atmospheres. The uncertainties are based on the linear fitting of the rates

Atmosphere		Activation energies (eV)
pH2O (bar)	pO2 (bar)	ℜ 0	ℜ ads	ℜ inc
3E-5	0.005	1.10 ± 0.04	1.10 ± 0.04	1.20 ± 0.05
3E-5	0.02	0.82 ± 0.02	0.77 ± 0.01	1.24 ± 0.05
3E-5	0.21	0.76 ± 0.02	0.76 ± 0.02	0.76 ± 0.02
0.03	0.005	0.85 ± 0.02	0.87 ± 0.03	—
0.03	0.02	0.84 ± 0.02	0.90 ± 0.02	—
0.03	0.21	0.95 ± 0.04	1.10 ± 0.04	0.54 ± 0.05

---

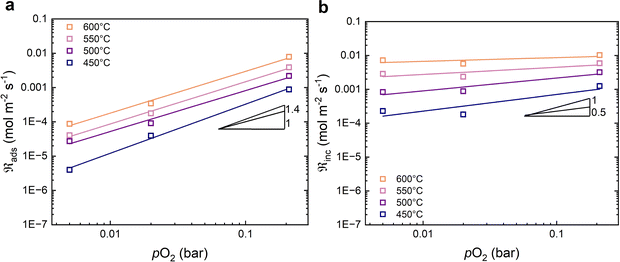
Fig. 5 shows the oxygen exchange rate as a function of pO₂ at 450–600 °C. The power-law dependence of the exchange rate is in the range of 1.0 to 1.3, decreasing slightly as the temperature increases. The pO₂ dependency of the dissociative adsorption and incorporation rates are shown in Fig. 6. The rate of dissociative adsorption shows a pO₂ dependency of around 1.2 to 1.4, and it increases with decreasing temperature. The incorporation rates show weaker dependencies on pO₂ which appear to decrease with increasing temperature, and it is essentially zero at 600 °C. Overall, the pO₂ dependencies are associated with some uncertainty as they are based on only three measurement points at each temperature.

Fig. 5 Oxygen exchange rate as a function of pO₂ at 400–600 °C in dry carrier gas. The solid lines are linear fits.

Fig. 6 Oxygen partial pressure dependencies in dry carrier gas of (a) the dissociative adsorption rate, and (b) the incorporation rate. The solid lines are linear fits.

3.2.2. Humid carrier gas. The role of humidified atmospheres on the oxygen exchange reactions was evaluated by humidifying the carrier gas only. Therefore, the precise amount of water in the gas stream as the pulse passes over the sample is not known. Fig. 7 shows the oxygen exchange rate as a function of inverse temperature with humidified carrier gas (0.03 bar H₂O) and a dry pulse at different oxygen partial pressures, and the rates of dissociative adsorption and incorporation. The rates exhibit the same trends as in dry atmosphere, i.e., the oxygen exchange rate increases with temperature and pO₂, and dissociative adsorption is rate limiting. Compared to the data in dry atmosphere, these data show a slightly larger uncertainty in the linear fits for the calculations of the activation energies.

Fig. 7 Oxygen exchange rate (ℜ₀) and the contributions from dissociative adsorption (ℜ_ads) and incorporation (ℜ_inc) at different oxygen partial pressures with humid carrier gas (0.03 bar H₂O): (a) 0.005 bar (b) 0.02 bar (c) 0.21 bar. The solid lines are linear fits.

The activation energies of the oxygen exchange processes are summarised in Table 2, showing a slight increase at 0.21 bar O₂. The activation energies for dissociative adsorption are similar to the oxygen exchange rate at all measured oxygen partial pressures. The activation energies of incorporation exhibit the largest uncertainties and could not be reliably extracted from the data at 0.02 bar and 0.005 bar O₂. The obtained activation energy for incorporation at 0.21 bar O₂ was 0.54 eV, which is notably smaller than in dry carrier gas (0.76 eV). The pO₂ dependencies of the oxygen exchange rate with a humid carrier gas exhibit a slight deviation from linearity as can be seen in Fig. 8. The pO₂ dependency at the lower partial pressures is close to unity while the dependency at the highest pO₂ is about 0.5.

Fig. 8 Oxygen exchange rate as a function of pO₂ with humid carrier gas (0.03 bar H₂O).

It is noted that the obtained oxygen exchange rate in nominally dry atmosphere decreased after the measurements in humid atmospheres, e.g., the exchange rate at 500 °C and 0.21 bar O₂ decreased from 1.30 × 10⁻³ mol m⁻² s⁻¹ to 1.06 × 10⁻³ mol m⁻² s⁻¹. This may be ascribed to changes to the material and/or experimental uncertainty between measurement series.

3.3. Oxygen non-stoichiometry

The oxygen non-stoichiometry of BGLC37 as measured by thermogravimetry is shown for the same temperature program as the PIE measurements in Fig. 9. The oxygen content of the material decreases with decreasing oxygen partial pressure and increasing temperature. The oxygen uptake is approximately proportional to the temperature from 600 °C to around 350 °C where it appears to start leveling off. The pO₂ dependency of the oxygen non-stoichiometry is close to linear in dry atmospheres (Fig. 9b). When the atmosphere is humidified, the oxygen non-stoichiometry is essentially the same as in dry conditions at 0.21 bar and 0.02 bar O₂, while it is slightly lower at 0.005 bar O₂. This deviation leads to a more pronounced non-linearity in the oxygen non-stoichiometry as a function of pO₂ in humid atmosphere (Fig. 9b).

Fig. 9 Oxygen non-stoichiometry of BGLC37 measured by TG with the same temperature program as for the PIE measurements as a function of (a) temperature and (b) pO₂ in dry (open symbols) and humidified (0.03 bar H₂O) atmospheres (filled symbols). The solid and dashed lines are guides to the eye.

The nominal oxidation state of cobalt can be evaluated from the oxygen non-stoichiometry by assigning formal oxidation states to the cations, i.e., Ba²⁺, La³⁺ and Gd³⁺. Accordingly, the oxidation state of cobalt approaches Co³⁺ as the oxygen non-stochiomtry δ approaches 0.5 at the highest temperatures in 0.005 bar O₂, while it is Co^3.35+ for δ = 0.15 at 200 °C in 0.21 bar and 0.02 bar O₂. The Co₃O₄ nanoparticles exhibit mixed valency of Co²⁺ and Co³⁺. Exsolution of the Co₃O₄ nanoparticles may therefore originate from partial reduction of cobalt at the higher temperatures during sintering in air at 1200 °C, similar to observations after mild reduction of PrBaCo₂O_6−δ in inert atmosphere at lower temperature.⁵⁶

4. Discussion

In dry atmosphere the rate determining step of the oxygen exchange reaction has been identified as the dissociative adsorption of oxygen. This has been determined through the calculation of dissociative adsorption and incorporation rates (Fig. 4) as well as through the pO₂ dependency of the oxygen exchange rates (Fig. 5). A rate determining step of dissociative adsorption has been reported for other mixed ionic electronic conducting materials such as LSCF.²² The activation energy of 0.76 eV for the oxygen exchange rate in 0.21 bar O₂ is similar to what has been reported for other double perovskite cobaltites, e.g., 0.85 eV for GdBaCo₂O_5+δ⁴² and 0.8–1.0 eV for PrBaCo₂O_5+δ^40–43 and other perovskite materials, e.g., SrTi_0.5Fe_0.5O_3−δ (0.85 eV),⁵⁷ and Sr_1.95Fe_1.4Ni_0.1Mo_0.5O_6−δ (0.82 eV).⁵⁸

When water is introduced into the carrier gas, additional exchange reactions involving ¹⁶O from water can take place. Notably, the data showed no sign of substantial exchange between water and lattice oxygen based on analysis of masses 17 (¹⁶OH), 18 (H₂¹⁶O), 19 (¹⁸OH), and 20 (H₂¹⁸O) under the pulse (ESI†). Therefore, all oxygen exchange was ascribed to exchange between gas phase and lattice oxygen. This contrasts the findings reported by Sha et al.³⁰ for (La_0.8Sr_0.2)_0.95Cr_0.5Fe_0.5O_3−δ where the activation energy decreased significantly when water (0.03 bar) was introduced into the oxygen gas (0.20 bar).

When comparing the oxygen exchange rates in dry and humid atmospheres, the effect of water in the carrier gas is pO₂ dependent (Fig. 10). With the addition of water in the carrier gas, the oxygen exchange rate decreases in high pO₂ and increases in low pO₂, e.g., at 600 °C the rate decreases from 4.45 × 10⁻³ mol m⁻² s⁻¹ by a factor of approx. 2 in 0.21 bar O₂, while it increases from 3.24 × 10⁻⁴ mol m⁻² s⁻¹ by the same amount in 0.02 bar O₂. Water can adsorb and block active sites for the rate limiting dissociative adsorption step and thereby cause a decrease in the oxygen exchange rate. Furthermore, blocking of active sites by water or hydroxide species may predominate at higher pO₂ (0.21 bar) due to the need for a larger number of adsorption sites. Blocking of active sites at 0.21 bar O₂ may also explain the decrease is the pO₂ dependency of the oxygen exchange rate towards 0.21 bar considering the non-linearity in the measured data (Fig. 8). The activation energy of the oxygen exchange rate in 0.21 bar O₂ increased in humid atmosphere from 0.76 eV to 0.95 eV. However, these activation energies appear to become similar at the highest temperatures where the effect of water or hydroxide adsorbates may be less prominent. Otherwise, these differences may indicate a change in the reaction mechanism that is not distinguishable here due to the limitations of the method.^22,59

Fig. 10 Comparison of the oxygen exchange rate of BGLC37 in dry and humid carrier gases (0.03 bar H₂O). The solid lines are linear fits.

The activation energies of the oxygen exchange rate were similar between dry and humid atmospheres in 0.02 bar O₂ (Fig. 10). At this oxygen partial pressure, the presence of water had a minor impact on the oxygen non-stoichiometry in the temperature range of interest (Fig. 9). In contrast, the presence of water appears to increase the amount of oxygen deficiency in the material at 0.005 bar O₂ (Fig. 9), which may be related to the increased oxygen exchange rate and the significant change in activation energy from 1.1 eV to 0.85 eV.

In comparison to other materials measured with PIE, BGLC37 shows a similar oxygen exchange rate in dry 0.21 bar O₂ (Fig. 11). In humid atmospheres, the oxygen exchange rate decreases slightly but remains quite similar to the other materials in dry atmospheres. When the oxygen exchange coefficient (k) is compared between different materials and methods, BGLC37 shows a slightly higher oxygen exchange coefficient at lower temperatures than other materials measured with PIE, but the values become more similar as the temperature increases (Fig. 11b). The surface exchange coefficient for BGLC37 was calculated by dividing the oxygen exchange rate at each temperature by the oxygen concentration in the oxide (8.8741 × 10⁴ m³ mol⁻¹).³⁸ The oxygen exchange coefficient for BSCF measured by chemical expansion relaxation is significantly higher than the other materials (2.9 × 10⁻³ cm s⁻¹ at 700 °C).^38,60

Fig. 11 (a) Comparison of oxygen exchange rate of BGLC37 (this work), SrTi_0.5Fe_0.5O_3−δ (STF50),⁵⁷ SrTi_0.65Fe_0.35O_3−δ (STF35),⁵⁷ PrBaCo₂O_5+δ (PBCO),⁴⁰ Sr_1.95Fe_1.4Ni_0.1Mo_0.5O_6−δ (SFNMO),⁵⁸ Ba_0.5Sr_0.5Co_0.8Fe_0.2O_3−δ (BSCF),³⁸ and La₂NiO_4+δ (LNO)³⁸ at 0.21 bar O₂ from PIE measurements. (b) Comparison of the oxygen exchange coefficient of BGLC37 (this work), PrBaCo₂O_5+δ (PBCO),⁴³ La_0.6Sr_0.4Co₂O_3−δ (LSCO),⁶¹ and La₂NiO_4+δ (LNO)³⁸ measured with varying methods. Squares: PIE, Circles: Isotope exchange depth profile.

5. Conclusions

The oxygen exchange rate of BGLC37 containing exsolved Co₃O₄ nanoparticles was measured with pulsed isotope exchange as a function of temperature and oxygen partial pressure in dry and humid atmospheres. The obtained oxygen exchange rate was 4.45 × 10⁻³ mol m⁻² s⁻¹ at 600 °C in 0.21 bar O₂. The activation energy of the exchange rate was 0.76 eV and 0.82 eV in 0.21 bar and 0.02 bar O₂, respectively, while it increased to 1.1 eV at 0.005 bar O₂. The rate determining step of the exchange reaction was determined to be dissociative adsorption of oxygen in both dry and humid atmospheres based on the individual rates of dissociative adsorption and incorporation, as well as a pO₂ dependencies of the oxygen exchange rate of around 1.

The effect of water on the oxygen exchange rate was found to be dependent on the oxygen partial pressure, decreasing the rate at 0.21 bar O₂ and 600 °C by a factor of approx. 2, while increasing the rate at 0.02 bar and 0.005 bar O₂ by a similar amount. These results were interpreted in terms of blocking of active sites on the surface by water or hydroxide species at 0.21 bar O₂, and changes to the material due to increased oxygen non-stoichiometry at 0.005 bar O₂. The presence of water led to an increased activation energy of 1.01 eV at 0.21 bar, while the activation energy remained similar at 0.02 bar O₂ and decreased to 0.85 eV in 0.005 bar O₂.

Data availability

Data from pulsed isotope exchange and thermogravimetry measurements are available at the figshare repository at https://doi.org/10.6084/m9.figshare.28061276. The synchrotron X-ray diffraction data is available at https://doi.org/10.15151/ESRF-ES-1550904430.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the Research Council of Norway (RCN) for financial support under the FRIPRO program (project no. 315058) and for support to the Norwegian Center for Transmission Electron Microscopy (NORTEM) national infrastructure (project no. 197405). The authors further acknowledge the European Synchrotron Radiation Facility (ESRF) for provision of synchrotron radiation facilities under proposal number ma6015 and we would like to thank Chloe Fuller for assistance and support in using beamline BM01.

References

1. C. Duan, R. Kee, H. Zhu, N. Sullivan, L. Zhu, L. Bian, D. Jennings and R. O’Hayre, Nat. Energy, 2019, 4, 230–240.
2. S. Choi, T. C. Davenport and S. M. Haile, Energy Environ. Sci., 2019, 12, 206–215.
3. D. Kim, K. T. Bae, K. J. Kim, H.-N. Im, S. Jang, S. Oh, S. W. Lee, T. H. Shin and K. T. Lee, ACS Energy Lett., 2022, 7, 2393–2400.
4. Y. Wang, Y. Ling, B. Wang, G. Zhai, G. Yang, Z. Shao, R. Xiao and T. Li, Energy Environ. Sci., 2023, 16, 5721–5770.
5. D. Medvedev, Int. J. Hydrogen Energy, 2019, 44, 26711–26740.
6. F. Liu, H. Deng, D. Diercks, P. Kumar, M. H. A. Jabbar, C. Gumeci, Y. Furuya, N. Dale, T. Oku, M. Usuda, P. Kazempoor, L. Fang, D. Chen, B. Liu and C. Duan, Nat. Energy, 2023, 8, 1145–1157.
7. M. M. Rashid, M. K. Al Mesfer, H. Naseem and M. Danish, Int. J. Eng. Adv. Technol., 2015, 4, 2249–8958.
8. L. Bi, S. Boulfrad and E. Traversa, Chem. Soc. Rev., 2014, 43, 8255–8270.
9. Y. Wang, Y. Ling, B. Wang, G. Zhai, G. Yang, Z. Shao, R. Xiao and T. Li, Energy Environ. Sci., 2023, 16, 5721–5770.
10. M. Choi, D. Kim, T. K. Lee, J. Lee, H. S. Yoo and W. Lee, Adv. Energy Mater., 2025, 15, 2400124.
11. H. Ding, W. Wu, C. Jiang, Y. Ding, W. Bian, B. Hu, P. Singh, C. J. Orme, L. Wang and Y. Zhang, Nat. Commun., 2020, 11, 1–11.
12. Z. Luo, Y. Zhou, X. Hu, N. Kane, T. Li, W. Zhang, Z. Liu, Y. Ding, Y. Liu and M. Liu, Energy Environ. Sci., 2022, 15, 2992–3003.
13. J. Jing, Z. Lei, Z. Zheng, H. Wang, P. Zhang, Z. Wang, H. Xu and Z. Yang, Int. J. Hydrogen Energy, 2023, 48, 9037–9045.
14. Y. Yi, R. Ran, W. Wang, W. Zhou and Z. Shao, Curr. Opin. Green Sustainable Chem., 2022, 38, 100711.
15. F. He, Y. Zhou, T. Hu, Y. Xu, M. Hou, F. Zhu, D. Liu, H. Zhang, K. Xu and M. Liu, Adv. Mater., 2023, 35, 2209469.
16. M. Den Otter, B. A. Boukamp and H. J. Bouwmeester, Solid State Ionics, 2001, 139, 89–94.
17. G. Boreskov and V. Muzykantov, Ann. N. Y. Acad. Sci., 1973, 213, 137–170.
18. K. Klier, J. Novakova and P. Jiru, J. Catal., 1963, 2, 479–484.
19. A. Ezin, V. Tsidilkovski and E. K. Kurumchin, Solid State Ionics, 1996, 84, 105–112.
20. V. Muzykantov, G. Boreskov and G. Panov, React. Kinet. Catal. Lett., 1974, 1, 315–319.
21. Y.-L. Huang, C. Pellegrinelli and E. D. Wachsman, ACS Catal., 2017, 7, 5766–5772.
22. C. Kan, H. Kan, F. Van Assche, E. Armstrong and E. Wachsman, J. Electrochem. Soc., 2008, 155, B985.
23. Y.-L. Huang, C. Pellegrinelli and E. D. Wachsman, ACS Catal., 2016, 6, 6025–6032.
24. Y. L. Huang, C. Pellegrinelli and E. D. Wachsman, Angew. Chem., Int. Ed., 2016, 55, 15268–15271.
25. Y.-L. Huang, C. Pellegrinelli, A. Geller, S.-C. Liou, A. Jarry, L. Wang, Y. Yu, H. Bluhm, E. J. Crumlin, K. J. Gaskell, B. W. Eichhorn and E. D. Wachsman, Energy Environ. Sci., 2017, 10, 919–923.
26. V. Thoreton, M. Niania and J. Kilner, Phys. Chem. Chem. Phys., 2021, 23, 2805–2811.
27. Y.-L. Huang, C. Pellegrinelli, A. Geller, S.-C. Liou, A. Jarry, L. Wang, Y. Yu, H. Bluhm, E. J. Crumlin and K. J. Gaskell, Energy Environ. Sci., 2017, 10, 919–923.
28. J. Yang, J. M. Polfus, Z. Li, H. L. Tuller and B. Yildiz, Chem. Mater., 2020, 32, 5483–5492.
29. A. Nenning, E. Navickas, H. Hutter and J. Fleig, J. Phys. Chem. Lett., 2016, 7, 2826–2831.
30. Z. Sha, E. Cali, Z. Shen, E. Ware, G. Kerherve and S. J. Skinner, Chem. Mater., 2021, 33, 8469–8476.
31. J. Kler and R. A. De Souza, J. Phys. Chem. Lett., 2022, 13, 4133–4138.
32. E. K. Kurumchin and M. V. Perfiliev, Solid State Ionics, 1990, 42, 129–133.
33. S. Ojala, N. Bion, S. Rijo Gomes, R. L. Keiski and D. Duprez, ChemCatChem, 2010, 2, 527–533.
34. A. Nau, R. Pointecouteau, M. Richard, T. Belin, F. Can, C. Comminges and N. Bion, Catal. Commun., 2023, 180, 106704.
35. J. H. Joo, R. Merkle and J. Maier, J. Power Sources, 2011, 196, 7495–7499.
36. D. M. Schwenkel, R. A. De Souza and G. F. Harrington, J. Mater. Chem. A, 2025, 13, 8541–8548.
37. E. Bucher, W. Sitte, F. Klauser and E. Bertel, Solid State Ionics, 2012, 208, 43–51.
38. H. J. Bouwmeester, C. Song, J. Zhu, J. Yi, M. van Sint Annaland and B. A. Boukamp, Phys. Chem. Chem. Phys., 2009, 11, 9640–9643.
39. J.-H. Kim and A. Manthiram, J. Mater. Chem. A, 2015, 3, 24195–24210.
40. C.-Y. Yoo, B. A. Boukamp and H. J. Bouwmeester, Solid State Ionics, 2014, 262, 668–671.
41. M. Ananyev, V. Eremin, D. Tsvetkov, N. Porotnikova, A. Farlenkov, A. Y. Zuev, A. Fetisov and E. K. Kurumchin, Solid State Ionics, 2017, 304, 96–106.
42. A. C. Tomkiewicz, M. Meloni and S. McIntosh, Solid State Ionics, 2014, 260, 55–59.
43. M. Burriel, J. Pena-Martinez, R. J. Chater, S. Fearn, A. V. Berenov, S. J. Skinner and J. A. Kilner, Chem. Mater., 2012, 24, 613–621.
44. R. Strandbakke, V. A. Cherepanov, A. Y. Zuev, D. S. Tsvetkov, C. Argirusis, G. Sourkouni, S. Prünte and T. Norby, Solid State Ionics, 2015, 278, 120–132.
45. E. Vøllestad, R. Strandbakke, M. Tarach, D. Catalán-Martínez, M.-L. Fontaine, D. Beeaff, D. R. Clark, J. M. Serra and T. Norby, Nat. Mater., 2019, 18, 752–759.
46. J. Zhu, J. B. Guđmundsdóttir, R. Strandbakke, K. G. Both, T. Aarholt, P. A. Carvalho, M. H. Sørby, I. J. Jensen, M. N. Guzik and T. Norby, ACS Appl. Mater. Interfaces, 2021, 13, 20313–20325.
47. T. Miruszewski, R. Strandbakke, K. Dzierzgowski, I. Szpunar, A. Mielewczyk-Gryń, S. Wachowski and M. Gazda, J. Mater. Chem. A, 2024, 12, 13488–13497.
48. C. Nicollet, C. Toparli, G. F. Harrington, T. Defferriere, B. Yildiz and H. L. Tuller, Nat. Catal., 2020, 3, 913–920.
49. S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319.
50. P. Llewellyn, F. R. Reinoso, J. Rouqerol and N. Seaton, Characterization of porous solids VII: proceedings of the 7th International Symposium on the Characterization of Porous Solids (COPS-VII), Aix-en-Provence, France, 26-28 May 2005, Elsevier, 2006.
51. V. Dyadkin, P. Pattison, V. Dmitriev and D. Chernyshov, J. Synchrotron Radiat., 2016, 23, 825–829.
52. A. A. Coelho, J. Appl. Crystallogr., 2018, 51, 210–218.
53. V. Thoreton, https://github.com/vthoreton/PIE_fit.
54. R. Strandbakke, D. S. Wragg, M. H. Sørby, M. N. Guzik, A. E. Gunnæs, I. Szpunar, S. L. Wachowski, M. Balaguer, P. A. Carvalho, A. Mielewczyk-Gryń, J. M. Serra and T. Norby, Dalton Trans., 2022, 51, 18667–18677.
55. I. Szpunar, R. Strandbakke, M. H. Sørby, S. L. Wachowski, M. Balaguer, M. Tarach, J. M. Serra, A. Witkowska, E. Dzik and T. Norby, Materials, 2020, 13, 4044.
56. A. J. Carrillo, M. Balaguer, C. Solís, A. López-García, S. Haas, M. Fabuel, B. Delgado-Galicia, I. Rodriguez, E. Vøllestad, S. Wachowski, R. Strandbakke, T. Norby and J. M. Serra, J. Phys.: Energy, 2025, 7, 025007.
57. C.-Y. Yoo and H. J. Bouwmeester, Phys. Chem. Chem. Phys., 2012, 14, 11759–11765.
58. N. Porotnikova, A. Khodimchuk, D. Zakharov, N. Bogdanovich and D. Osinkin, Appl. Surf. Sci., 2023, 613, 156015.
59. R. Merkle and J. Maier, Phys. Chem. Chem. Phys., 2002, 4, 4140–4148.
60. M.-B. Choi, S.-Y. Jeon, H.-N. Im, E. Wachsman and S.-J. Song, J. Electrochem. Soc., 2011, 159, P23.
61. A. Berenov, A. Atkinson, J. Kilner, E. Bucher and W. Sitte, Solid State Ionics, 2010, 181, 819–826.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04791e

---