Theoretical insights into aggregation-induced emission of bis(cyanostyryl)pyrrole derivatives

Abstract

The molecular architecture and the positioning of the cyano group in cyanostilbene derivatives give rise to intriguing variations in their photophysical properties. The present study provides theoretical insights into the contrasting photoluminescence behaviors of bis(cyanostyryl)pyrrole derivatives with different cyano group positions. Using quantum mechanics/molecular mechanics (QM/MM) free energy perturbation methods, we investigated o-DCSP and i-DCSP isomers, which exhibited markedly different fluorescence quantum yields in the solution (Φ_f = 0.0036 vs. 0.43) and aggregated states (Φ_f = 0.15 vs. 0.12). We identified the minimum energy conical intersection (MECI) structures for both isomers, characterized by substantial rotation and pyramidalization of one ethylenic C=C bond, and determined the minimum energy path (MEP) connecting the Franck–Condon point to the MECI using the string method. By calculating the free energy profiles along this MEP, we revealed significant differences in energy barriers: o-DCSP showed a low barrier in solution (0.57 eV), which dramatically increased upon aggregation (2.36 eV), explaining its aggregation-induced emission behavior, whereas i-DCSP maintains relatively high barriers in both states (1.40 eV and 1.67 eV), resulting in efficient emission regardless of the environment. These findings establish a quantitative molecular-level understanding of the structure–property relationships in fluorescent materials and provide design principles for developing high-performance luminescent compounds with tailored emission characteristics for specific applications.

---

Introduction

The exploration of organic π-conjugated materials has garnered substantial attention in recent years, owing to their ability to fine-tune their optical and electronic properties.^1–3 This versatility has led to significant advancements in their utilization in a wide range of optoelectronic devices including organic light emitting diodes (OLEDs), organic solar cells, and chemical sensors.^4,5 The use of these materials in various optoelectronic applications depends on their photophysical parameters, particularly fluorescence quantum yields.⁶ Fluorophores with high quantum yields emit strong fluorescence even at low concentrations and are suitable for lasers and OLEDs. Dyes with high quantum yields are also useful for the staining, labeling, and imaging of cells.

A few organic luminescent materials exhibit high quantum yields in both solid and liquid phases.^7,8 Typically, these materials suffer from low quantum yields in the condensed phase due to co-facial π–π stacking interactions, which lead to aggregation-caused quenching (ACQ).⁹ Another photophysical phenomenon observed in luminescent molecules is aggregation-induced emission (AIE), which is characterized by weak emission in dilute solutions but highly emissive properties upon aggregation or in the solid phase.¹⁰

Cyanostilbene derivatives are promising materials for the production of AIE-active compounds and have received significant attention because of their high emissivity, particularly in the solid phase.¹¹ While these fluorophores generally display weak emission in solution,^12,13 some reports have documented exceptions where certain cyanostilbene molecules exhibit highly emissive behavior in solution.^14,15 This variability illustrates that the fluorescence properties of cyanostilbene-based compounds are highly dependent on their molecular architecture and substitution patterns.

In this context, Yokoyama and Nishiwaki recently synthesized two structural isomers of bis(cyanostyryl)pyrrole derivatives, named o-DCSP and i-DCSP, which differ in the positioning of the cyano groups on the olefin units (Scheme 1). These compounds exhibit structure-dependent fluorescence emission, making them ideal systems for investigating the aggregation-induced emission (AIE) phenomenon.¹⁶o-DCSP exhibited AIE behavior, displaying minimal emission in solution (Φ_f = 0.0036) but enhanced luminescence in the single-crystal state (Φ_f = 0.15). In contrast, i-DCSP demonstrated different photophysical properties with a high fluorescence quantum yield in solution (Φ_f = 0.43), which slightly diminished upon aggregation to the single-crystal state (Φ_f = 0.12). This striking contrast in emission properties between positional isomers highlights the critical role of cyano group positioning in determining the photophysical behavior. The investigation of these structurally similar yet photophysically distinct molecules offers valuable insights into the molecular mechanisms underlying the AIE phenomenon and structure–function relationships in fluorescent materials.

Scheme 1 Chemical structures of bis(cyanostyryl)pyrrole derivatives o-DCSP and i-DCSP.

In this study, we focused on elucidating the molecular mechanism underlying the distinct photoluminescence behaviors of o-DCSP and i-DCSP through quantum mechanics/molecular mechanics (QM/MM) modeling. We employed QM/MM free energy perturbation methods to quantitatively analyze the excited-state relaxation processes in both solution and aggregated states. By determining the free-energy profiles along the minimum energy path for the relaxation process after photoexcitation, we reveal how subtle differences in cyano group positioning lead to dramatically different energy barriers that control the radiative and non-radiative decay pathways. This comprehensive analysis provides fundamental insights into the structure–property relationships in AIE-active materials and establishes design principles for developing high-performance luminescent compounds with tailored emission characteristics for specific applications.

Computational details

Quantum chemical calculations offer valuable insights into molecular-level photoexcitation processes by analyzing ground and excited-state potential energy surfaces (PESs).^17,18 Conical intersection (CI), the crossing point between PESs, is a theoretical tool for describing the photoexcitation process.^19–21 The lowest energy point within the CI hyperspace is referred to as the minimal energy conical intersection (MECI).^22–24 Identifying the location of the MECI between the ground and first electronic excited states (S₀/S₁) can provide valuable information on the radiative and non-radiative decay processes.^25,26 The fluorescence quantum yield of a molecule is primarily determined by the fraction of non-radiative transitions that occur near the S₀/S₁-MECI.^21,27

In this study, we employed QM/MM models to investigate the effects of molecular environments on these photophysical processes. Specifically, we determined the minimum energy path (MEP) from the Franck–Condon (FC) point to the MECI using the string method^28,29 and then calculated the free energy changes along this MEP using QM/MM free energy perturbation (FEP) methods.^30,31 This approach allows us to quantitatively analyze how the surrounding molecules in both solution and aggregated states influence the energetic barriers between the excited and ground states, providing a molecular-level explanation for the observed differences in fluorescence quantum yields.

Geometry optimizations

Density functional theory (DFT) calculations were performed to determine the minimum energy structures in the S₀ ground state. The optimized structure in the S₀ state obtained here is denoted as S₀-Min. The point at which S₀-Min is vertically excited to reach the S₁-state potential energy hypersurface is called the Franck–Condon (FC) point. The BHHLYP functional^32,33 was selected for its effectiveness in handling electron correlations in spin–flip (SF) time-dependent (TD) DFT scenarios,³⁴ which is particularly crucial for analyzing conical intersections in molecular systems.³⁵ For all DFT calculations, 6-31G(d) basis functions were utilized.

The minimum energy point on the CI hypersurface (MECI) is the critical point below which nonadiabatic transitions via CIs cannot occur. The MECI between the S₀ and S₁ states of o-DCSP and i-DCSP was determined using a branching-plane updating technique,³⁶ where the electronic structures of the molecule were determined using the spin–flip approach³⁷ within the time-dependent DFT (SF-TD-DFT) method.³⁵ The initial coordinates for the MECI searches were the rotated and pyramided conformations of one of the two ethylenic C=C bonds in each compound. The Q-Chem 6.2 program package³⁸ (Q-Chem, Inc., Pleasanton, CA) was used for the DFT calculations.

Path optimizations

An MEP can be defined as the reaction coordinate at which the potential energy is minimized for changes in the molecular geometry corresponding to the orthogonal motions. The MEPs for the excited-state relaxation process to reach the CIs were determined for both o-DCSP and i-DCSP using DFT calculations.

The MEPs connecting the FC points and MECI of both o-DCSP and i-DCSP were determined using the string method.^28,29 The basic idea of the string method is to find an MEP by evolving a sequence of images, called a string, in the direction of the force derived from the potential energy gradient. The potential energy gradients for the S₁ states of the molecules were calculated using SF-TD-DFT. Path optimization using the string method was performed using a program developed in-house. An initial path was prepared by linearly interpolating the molecular geometries of the FC point and the MECI in internal coordinates with ten discrete points. The update step size in path optimization was set to 1.0 Bohr. The convergence of the path optimization was examined using the average value of the potential energy change when updating the path, ΔV, and the average value of the energy gradient in the direction perpendicular to the path in each image, ∇_⊥V. The resultant MEPs for o-DCSP and i-DCSP were linearly interpolated with 60 discrete points in the internal coordinate space to improve the accuracy of the free energy calculations. The reaction coordinate parameter σ ∈ [0,1] was used to parameterize the MEPs.

Free energy calculations

The free-energy profiles along the MEPs of o-DCSP and i-DCSP embedded in their aggregates were computed using the QM/MM-FEP method.^30,31 In this study, a single molecule embedded in its aggregate formed a QM subsystem that changed its conformation along with the MEP, and the surrounding molecules formed an MM subsystem. The QM/MM-FEP method can be summarized as follows: the free energy difference between the two adjoining conformational states, A and B, in a QM/MM system can be defined as

ΔF^(A→B)_qm/mm = ΔE^(A→B)_qm + ΔF^(A→B)_int. (1)

The ΔE^(A→B)_qm term is expressed as follows:

ΔE^(A→B)_qm = 〈E_qm(r^(B),R^(B))_R^(B)〉 − 〈E_qm(r^(A),R^(A))_R^(A)〉, (2)

where 〈⋯〉_R^(B) represents an ensemble average over the MM subsystem in the Ath state. Here, the perturbation corresponds to the forward or backward movement of the QM atoms when all MM atoms are fixed. Canonical MD simulations were performed while fixing QM atoms to obtain the required ensembles. The ΔF^(A→B)_int term is related to an average of the function of the energy difference between the two states, as determined by sampling for the Ath state:where β is the reciprocal temperature, and

ΔE^(A→B)_int = E_int(r^(B),R^(A)) − E_int(r^(A),R^(A)) (4)

The first term represents the perturbation corresponding to the conformational change of the QM atoms from r^(A) to r^(B) when all the MM atoms are fixed at R^(A). The E_int term consists of additive contributions from van der Waals and electrostatic interactions between QM and MM atoms:

E_int(r^(B),R^(A)) = E_vdW(r^(B),R^(A)) + E_es(r^(B),R^(A)). (5)

QM/MM-FEP calculations were performed using an in-house program.

MD simulations

The QM/MM-FEP calculation requires ensemble averages over the MM subsystem, while fixing all QM atoms. Canonical MD simulations were performed to obtain the necessary ensembles. All MD simulations were performed using the AMBER 20 program package³⁹ (University of California, San Francisco, CA). The computational models for the aggregated structures of the o-DCSP and i-DCSP were taken from the crystal structures reported in the previous study.¹⁶ For the crystal structures, we extended the unit cell to construct a supercell encompassing a region with a radius of 20 Å from the central molecule. The MD simulations of the aggregated state were performed for the systems containing 192 o-DCSP and 180 i-DCSP molecules in the 8 × 3 × 2 and 3 × 3 × 5 supercells with sizes of 105.4 and 85.4 nm³, respectively, under periodic boundary conditions. Following the energy minimization and equilibration processes, 2 ns of production runs were performed under an isothermal–isobaric (NpT) ensemble. A time step of 2.0 fs was used in all MD simulations. Room temperature (300 K) and a constant pressure of 1 bar were maintained using the weak-coupling algorithm.⁴⁰ All bonds involving hydrogen were constrained using the SHAKE algorithm.⁴¹ The electrostatic interactions were computed using the particle mesh Ewald algorithm⁴² with a cut-off radius of 8 Å. The coordinates of the QM subsystem were frozen during the MD simulations, and the MM subsystem was modeled using the general AMBER force field (GAFF).⁴³ For the QM/MM calculations and QM/MM-FEP analysis, 50 and 1000 structures were sampled, respectively, from the 2-ns MD trajectory at each discrete point along the MEP.

Results

Fig. 1 displays the optimized structures of o-DCSP and i-DCSP in their ground state (S₀-Min) and at the S₀/S₁-MECI point. Scheme 2 shows the conformational parameters of the ethylenic C=C group, highlighting the significant structural changes at the MECI point using o-DCSP as an example. Table 1 provides detailed conformational data for both molecules, with a particular emphasis on the ethylenic C=C group.

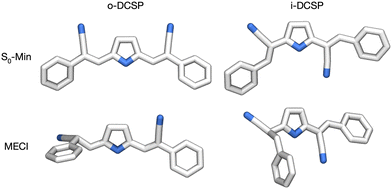Fig. 1 Optimized local stable structures of o-DCSP and i-DCSP in the (a) ground state (S₀-Min) and at the minimum-energy conical intersection points between the S₀ and S₁ states (MECI).

Scheme 2 Conformational parameters of the ethylenic C=C moiety, as exemplified by o-DCSP.

Table 1 Summary of conformational details for the ethylenic C=C moiety in o-DCSP and i-DCSP, comparing their ground state (S₀-Min) structures and minimum-energy conical intersection points between S₀ and S₁ states (MECI)

Compound	σ 2–4		θ 1–2–4–5		τ 1–2–3–4
	[Å]		[degree]		[degree]
	S0-Min	MECI	S0-Min	MECI	S0-Min	MECI
o-DCSP	1.349	1.439	178.7	114.8	178.8	117.1
i-DCSP	1.349	1.436	178.9	113.9	178.8	113.0

---

The S₀/S₁-MECI structure exhibited substantial variations from the S₀-Min structure, as illustrated in Fig. 1 and Table 1. At the MECI point, one of the two ethylenic C=C double-bond sites in each molecule rotates and forms a pyramidal shape. The ethylenic moiety parameters (including bond length, σ, and dihedral angles, θ and τ) displayed significant conformational changes from the S₀-Min to MECI structure. These changes indicated substantial molecular distortions at the MECI point. This transition from the S₀ → S₁ FC point (corresponding to the S₀-Min state) to the MECI state is characteristic of cyanostilbene derivatives, consistent with previous studies.^35,36

Previous studies have demonstrated that conical intersections, which are regions of energetic overlap between the ground and excited states, play a critical and intricate role in the AIE mechanism.^44–48 AIEgens, which are compounds that exhibit AIE, undergo spontaneous conformational changes in the excited state following photoexcitation, moving from a vertically excited FC point to CIs. At these CIs, non-radiative transitions occur from the excited state to the ground state, resulting in no emission. However, when AIEgens are in an aggregated state, the suppression of conformational changes along the relaxation pathway from the FC point to the CIs inhibits the non-radiative transition process, leading to emission.

Branching plane analysis is a helpful tool for characterizing conical intersections and is crucial for understanding photochemical reactions and non-radiative decay processes.^49–53 This analysis, which involves calculating the energy difference gradient vector (g) and nonadiabatic coupling vector (h) in the MECI geometry, defines a plane, the branching plane. This plane is the locus of the most significant geometric distortion, which leads to non-radiative decay. In the context of AIE, branching plane analysis provides profound insights into the structural factors that govern the accessibility of conical intersections, and thus, the efficiency of non-radiative decay in the aggregated state.

Branching plane analysis, as shown in Fig. 2, revealed that the main components of both the g and h vectors for all the compounds were localized around one of the cyano groups. This concentration suggests that the relaxation pathways from S₀/S₁-MECI primarily involve the rotational and pyramidalization motions of these groups. No significant differences in the vectors were found between o-DCSP and i-DCSP, implying that the AIE properties are influenced by other factors, such as the topology of the excited-state potential energy surface, and not solely by the MECI geometry. These findings suggest that intermolecular interactions and excited-state energy landscapes are crucial for determining the AIE behavior.

Fig. 2 Branching plane analysis of S₀/S₁-MECIs for o-DCSP and i-DCSP. The energy difference gradient vector (g) and nonadiabatic coupling vector (h) are indicated by orange arrows.

AIE is a significant photophysical phenomenon characterized by unique fluorescence properties in the aggregated molecular state. This complex phenomenon cannot be comprehensively understood through isolated gas-phase analysis alone, necessitating a detailed examination of molecular environmental effects. The two isomers, o-DCSP and i-DCSP, exhibited distinct fluorescence characteristics in THF solution versus aggregated states, suggesting differential relaxation processes following photoexcitation in each environment. To elucidate these differences at the molecular level, we constructed QM/MM models and conducted theoretical analyses, where we treated the central molecule as the QM region and the surrounding molecules as the MM region to examine the fluorescence properties in the aggregated state in detail.

Fig. 3 illustrates the three-dimensional structures of o-DCSP and i-DCSP in THF solution and their aggregated states. To quantitatively analyze the excited-state relaxation processes, we employed the QM/MM FEP method. This comprehensive analysis consisted of three sequential steps. First, the MEP from the FC point to the MECI was determined for o-DCSP and i-DCSP in the isolated gas phase using the string method.^28,29 Second, NpT ensemble MD simulations were performed for 4 ns at 60 discrete points along the MEP between the FC and MECI points under thermodynamic conditions of constant temperature (T = 300 K) and pressure (p = 1 atm), where only the central QM molecule was fixed, while the surrounding MM molecules were allowed to move. Finally, from the latter 2 ns of the MD trajectories, we extracted 50 structures for QM/MM calculations and 1000 structures for QM/MM FEP analysis to determine free energy changes along the MEP in both the THF solution and molecular aggregated states.

Fig. 3 Three-dimensional structures of o-DCSP and i-DCSP in THF solution and aggregated states.

Fig. 4 displays the free energy changes along the MEP from the FC to MECI points for both o-DCSP and i-DCSP in the THF solution. The graph shows the average potential energy values (E_qm) obtained from QM/MM calculations performed on 50 structures extracted from 2 ns NpT MD simulations at 60 discrete points along the MEP. The E_qm values reflect the influence of electrostatic interactions between the QM molecule and surrounding molecules, fluctuating with the thermal motion of the surrounding molecules. Additionally, we present values with free energy changes calculated using the QM/MM FEP method (F_qm/mm), which we define as the free energy profile along the MEP. For o-DCSP, the free-energy profile reveals that the MECI point is energetically more stable than the FC point. However, an energy barrier of approximately 0.57 eV (13 kcal mol⁻¹) exists along the pathway from the FC to the MECI points. Experimentally, o-DCSP exhibited a notably low fluorescence quantum yield in THF solution.¹⁶ This suggests that excess energy during photoexcitation readily overcomes this energy barrier, enabling an efficient radiationless transition through rapid access to CIs.

Fig. 4 Free energy profiles along the minimum energy path (MEP) from the Franck–Condon (FC) point to the minimum energy conical intersection (MECI) point for (a) o-DCSP and (b) i-DCSP in THF. The graphs show the average potential energy values (E_qm) from the QM/MM calculations, as well as the free energy profiles (F_qm/mm) calculated using the QM/MM FEP method.

In contrast, for i-DCSP, while the FC and MECI points are energetically comparable, a significant energy barrier of approximately 1.40 eV (32 kcal mol⁻¹) exists between them. Experimentally, i-DCSP demonstrated a relatively high fluorescence quantum yield even in a THF solution.¹⁶ This indicates that because of the substantial energy barrier, structural changes from the FC point to CIs after photoexcitation are energetically unfavorable, suppressing radiationless transitions and resulting in stronger emission compared to o-DCSP.

For both isomers, the contribution of the free energy changes obtained from FEP was relatively small, suggesting a limited impact of steric hindrance from the THF solvent molecules.

Fig. 5 illustrates the free energy changes along the MEP from the FC to the MECI points for o-DCSP and i-DCSP in the aggregated state. The free-energy profile of o-DCSP differed markedly from that of the THF solution. Specifically, the pathway from the FC to the MECI points becomes a steep uphill, with a maximum value of approximately 2.36 eV (54 kcal mol⁻¹) higher than the FC point. This reaction barrier is 1.79 eV (41 kcal mol⁻¹) greater than that in THF solution. Experimentally, the fluorescence quantum yield of o-DCSP in the aggregated state is significantly higher than that in a dilute solution.¹⁶ This suggests that in the aggregated state, steric hindrance from the surrounding molecules strongly inhibits structural changes from the FC point to CIs, making the radiationless transition pathway energetically highly unfavorable, thereby enhancing the emission intensity. This was proposed as the molecular mechanism by which o-DCSP induces AIE.

Fig. 5 Free energy profiles along the minimum energy path (MEP) from the Franck–Condon (FC) point to the minimum energy conical intersection (MECI) point for (a) o-DCSP and (b) i-DCSP in the aggregated state. The graphs show the average potential energy values (E_qm) from the QM/MM calculations, as well as the free energy profiles (F_qm/mm) calculated using the QM/MM FEP method.

Conversely, the free energy profile for i-DCSP in the aggregated state resembles that in THF solution, with a reaction barrier of approximately 1.67 eV (39 kcal mol⁻¹) along the pathway from the FC to the MECI points. This barrier height is only 0.27 eV (6 kcal mol⁻¹) greater than that in THF solution. Experimentally, the fluorescence quantum yield of i-DCSP in the aggregated state was slightly lower than that in the dilute solution.¹⁶ These results suggest that for i-DCSP, similar to that in THF solution, radiationless transitions are suppressed owing to relatively high energy barriers, making the pathway from the FC point to CIs energetically unfavorable.

Compared to o-DCSP in the aggregated state, the free energy barrier for i-DCSP in the aggregated state is 0.69 eV (16 kcal mol⁻¹) lower. Experimentally, the fluorescence quantum yield of i-DCSP in the aggregated state is lower than that of o-DCSP in the aggregated state.¹⁶ This indicates that steric hindrance in the aggregated state is less pronounced for i-DCSP than that for o-DCSP, resulting in weaker suppression of radiationless transitions. Consequently, some molecules undergo radiation-less transitions via the CI point, thereby reducing their emission intensity.

Discussion

The fluorescence quantum yield (Φ_f) depends on the balance between the radiative (k_r) and non-radiative (k_nr) decay rates, according to Φ_f = k_r/(k_r + k_nr). Although our calculations do not directly yield k_r or k_nr values, the computed energy barriers offer insights into k_nr through the Arrhenius relationship (k_nr ∝ exp(–ΔE/kT)). In solution, i-DCSP displays a higher quantum yield (Φ_f = 0.43) than o-DCSP (Φ_f = 0.0036),¹⁶ consistent with a larger computed barrier (1.40 eV vs. 0.57 eV) for the conformational change leading to non-radiative decay. This significant difference in barrier heights explains why i-DCSP maintains efficient emission in solution, whereas o-DCSP exhibits very weak fluorescence. The high energy barrier effectively suppresses the C=C torsion that governs the main non-radiative decay pathway in i-DCSP, despite both compounds having a similar potential for rotation in isolated molecules.

Our QM/MM-FEP analysis demonstrated that aggregation influences excited-state behavior by reshaping the overall energy landscape through specific intermolecular interactions. In o-DCSP, aggregation dramatically increases the barrier to the non-radiative pathway (from 0.57 eV in solution to 2.36 eV in the solid state), leading to a more pronounced solid-state emission. X-ray crystallographic analysis revealed that o-DCSP forms a hydrogen-bonding network between stacking columns with a π–π stacking distance of 3.395 Å,¹⁶ indicating strong intermolecular interactions that effectively restrict molecular motion. In contrast, i-DCSP experienced only a modest increase in barrier height (0.27 eV) upon aggregation, resulting in a smaller enhancement; indeed, its solid-state quantum yield decreased slightly compared to its solution value. The molecular packing of i-DCSP, characterized by dimeric structures with hydrogen bonding (2.230 Å) and weaker π–π interactions (a stacking distance of 3.611 Å),¹⁶ provides less restriction to the critical motion compared to o-DCSP. These observations reinforce the conclusion that subtle differences in molecular packing can significantly modulate excited-state processes rather than uniformly impeding all possible rotational motions.

While this study focused primarily on intramolecular photophysics, intermolecular processes may also contribute to non-radiative decay in the condensed phase. Recent reports have indicated the possibility of dimeric conical intersections in closely stacked aromatic systems,⁵⁴ which could provide alternative non-radiative pathways. In particular, for i-DCSP, such intermolecular channels may partially offset the high intramolecular barrier, contributing to its reduced solid-state quantum yield compared with that of the solution. This mechanism could explain why i-DCSP, despite its inherently high barrier to intramolecular conical intersection, shows a decrease in fluorescence efficiency upon aggregation. The present study provides a clear theoretical explanation of the impact of cyano group positioning on the photophysical properties in the solution state, along with the various factors that emerge in the aggregated state to modulate these properties.⁵⁵ Future investigations employing multi-chromophore QM regions within QM/MM frameworks could offer greater insight into these intermolecular mechanisms and their potential roles in fine-tuning the aggregation-induced emission phenomenon.

Conclusion

Through systematic QM/MM free energy perturbation analysis, we established a quantitative molecular-level understanding of the contrasting photoluminescence behaviors observed in o-DCSP and i-DCSP isomers. Our computational findings correlate with the experimental observations and provide mechanistic explanations for their divergent fluorescence properties.

The AIE phenomenon exhibited by o-DCSP can be directly attributed to the dramatic increase in the energy barrier from the FC to the MECI point when transitioning from the solution (0.57 eV) to the aggregated state (2.36 eV). This 1.79 eV increase results from steric hindrance imposed by the surrounding molecules in the aggregated state, effectively blocking the pathway to radiationless decay. As reported by Yokoyama et al.,¹⁶ this leads to a significant enhancement in emission efficiency, with the fluorescence quantum yield increasing from Φ_f = 0.0036 in solution to Φ_f = 0.15 in the aggregated state.

Conversely, the lack of significant AIE behavior of i-DCSP can be attributed to its substantial energy barrier in solution (1.40 eV), which increases only marginally (by 0.27 eV) upon aggregation. This molecular mechanism aligns with the experimental observations of Yokoyama et al.,¹⁶ who reported a high fluorescence quantum yield in solution (Φ_f = 0.43) and a slight decrease in the aggregated state (Φ_f = 0.12). The relatively lower barrier in the i-DCSP aggregated state compared to o-DCSP (by 0.69 eV) suggests weaker steric constraints, allowing some molecules to access radiation-less decay pathways.

These findings highlight the profound impact of cyano group positioning on the molecular conformation, excited-state dynamics, and photophysical properties. By employing QM/MM (and particularly QM/MM-FEP) calculations, we demonstrated a powerful approach for probing environment-dependent phenomena in complex molecular systems. Our results offer valuable design principles for next-generation AIE-active materials, indicating that molecular architectures that significantly increase the energy barriers upon aggregation hold the greatest promise for enhanced solid-state emission.

Moreover, by focusing our study on isomers with experimentally determined crystal structures, we established a reliable computational framework for quantifying and explaining intricate photophysical processes. This methodology not only captures the subtle interplay between molecular structure, electronic properties, and environmental effects but also provides predictive capabilities for designing luminescent compounds with tailored emission profiles. These insights will serve as a foundation for the rational design of innovative AIE-active materials for specific technological applications.

Data availability

The quantum chemical calculations in this study were performed using Q-Chem 6.2 software. The optimized molecular geometries and energies for the S₀-Min and S₀/S₁-MECI structures of o-DCSP and i-DCSP are available from the corresponding author upon reasonable request. No new experimental data were generated as part of this theoretical study.

Conflicts of interest

The authors declare no conflicts of interest.

Acknowledgements

This work was supported by JSPS KAKENHI (grant number 22K05025). The quantum chemical calculations were performed at the Research Center for Computational Science, Okazaki, Japan. CF acknowledges the Department of Science and Technology (DST) for funding research under Women Scientist Scheme-A (WOS-A), DST/WOS-A/CS-126/2021. PKS acknowledges the Science and Engineering Research Board (SERB), Govt. of India, for the ECRA grant ECR/2017/000524.

References

1. L. Luo, W. Huang, C. Yang, J. Zhang and Q. Zhang, Recent advances on π-conjugated polymers as active elements in high performance organic field-effect transistors, Front. Phys., 2021, 16, 33500.
2. S.-Y. Yang, Y.-K. Qu, L.-S. Liao, Z.-Q. Jiang and S.-T. Lee, Research Progress of Intramolecular π-Stacked Small Molecules for Device Applications, Adv. Mater., 2022, 34, 2104125.
3. D. Barman, K. Narang, R. Parui, N. Zehra, M. N. Khatun, L. R. Adil and P. K. Iyer, Review on recent trends and prospects in π-conjugated luminescent aggregates for biomedical applications, Aggregate, 2022, 3, e172.
4. J. Gierschner, J. Shi, B. Milián-Medina, D. Roca-Sanjuán, S. Varghese and S. Park, Luminescence in Crystalline Organic Materials: From Molecules to Molecular Solids, Adv. Opt. Mater., 2021, 9, 2002251.
5. X.-L. Hao, A.-M. Ren, L. Zhou and H. Zhang, Theoretical Research and Photodynamic Simulation of Aggregation-Induced Thermally Activated Delayed Fluorescence Materials for Organic Light-Emitting Diodes, J. Phys. Chem. A, 2023, 127, 9771–9780.
6. G. Díaz Mirón and M. C. González Lebrero, Fluorescence Quantum Yields in Complex Environments from QM-MM TDDFT Simulations: The Case of Indole in Different Solvents, J. Phys. Chem. A, 2020, 124, 9503–9512.
7. Y. Ni, L. Yang, L. Kong, C. Wang, Q. Zhang and J. Yang, Highly efficient dual-state emission and two-photon absorption of novel naphthalimide functionalized cyanostilbene derivatives with finely tuned terminal alkoxyl groups, Mater. Chem. Front., 2022, 6, 3522–3530.
8. Z. Huang, F. Tang, F. He, L. Kong, J. Huang, J. Yang and A. Ding, Pyrene and triphenylamine substituted cyanostyrene and cyanostilbene derivatives with dual-state emission for high-contrast mechanofluorochromism and cell imaging, Org. Chem. Front., 2022, 9, 5118–5124.
9. M. Huang, R. Yu, K. Xu, S. Ye, S. Kuang, X. Zhu and Y. Wan, An arch-bridge-type fluorophore for bridging the gap between aggregation-caused quenching (ACQ) and aggregation-induced emission (AIE), Chem. Sci., 2016, 7, 4485–4491.
10. J. Mei, N. L. C. Leung, R. T. K. Kwok, J. W. Y. Lam and B. Z. Tang, Aggregation-Induced Emission: Together We Shine, United We Soar!, Chem. Rev., 2015, 115, 11718–11940.
11. P. Mahalingavelar and S. Kanvah, α-Cyanostilbene: a multifunctional spectral engineering motif, Phys. Chem. Chem. Phys., 2022, 24, 23049–23075.
12. S. Guo, J. Pan, J. Huang, L. Kong and J. Yang, Two AIEE-active α-cyanostilbene derivatives containing BF2 unit for detecting explosive picric acid in aqueous medium, RSC Adv., 2019, 9, 26043–26050.
13. X. Wang, L. Wang, X. Mao, Q. Wang, Z. Mu, L. An, W. Zhang, X. Feng, C. Redshaw, C. Cao, A. Qin and B. Z. Tang, Pyrene-based aggregation-induced emission luminogens (AIEgens) with less colour migration for anti-counterfeiting applications, J. Mater. Chem. C, 2021, 9, 12828–12838.
14. H. Wu, Z. Chen, W. Chi, A. K. Bindra, L. Gu, C. Qian, B. Wu, B. Yue, G. Liu, G. Yang, L. Zhu and Y. Zhao, Structural Engineering of Luminogens with High Emission Efficiency Both in Solution and in the Solid State, Angew. Chem., Int. Ed., 2019, 58, 11419–11423.
15. C. Femina, M. Shanthil, P. K. Sajith and R. Thomas, Anthracene-incorporated cyanostilbene based donor–acceptor systems: intramolecular charge transfer and aggregation induced emission, New J. Chem., 2023, 47, 13810–13819.
16. S. Yokoyama and N. Nishiwaki, Fluorescence Behavior of Bis(cyanostyryl)pyrrole Derivatives Depending on the Substituent Position of Cyano Groups in Solution and in Solid State, J. Org. Chem., 2019, 84, 1192–1200.
17. D. Li, X. Song, J. Liu and S. Zhang, Photochemical mechanistic study of hexafluorobenzene involving the low-lying states, Phys. Chem. Chem. Phys., 2024, 26, 6638–6645.
18. M. T. do Casal, K. Veys, M. H. E. Bousquet, D. Escudero and D. Jacquemin, First-Principles Calculations of Excited-State Decay Rate Constants in Organic Fluorophores, J. Phys. Chem. A, 2023, 127, 10033–10053.
19. S. Nanbu, T. Ishida and H. Nakamura, Future perspectives of nonadiabatic chemical dynamics, Chem. Sci., 2010, 1, 663–674.
20. D. R. Yarkony, Conical Intersections:  Diabolical and Often Misunderstood, Acc. Chem. Res., 1998, 31, 511–518.
21. Y. Harabuchi, T. Taketsugu and S. Maeda, Exploration of minimum energy conical intersection structures of small polycyclic aromatic hydrocarbons: toward an understanding of the size dependence of fluorescence quantum yields, Phys. Chem. Chem. Phys., 2015, 17, 22561–22565.
22. N. Koga and K. Morokuma, Determination of the lowest energy point on the crossing seam between two potential surfaces using the energy gradient, Chem. Phys. Lett., 1985, 119, 371–374.
23. J. M. Anglada and J. M. Bofill, A reduced-restricted-quasi-Newton–Raphson method for locating and optimizing energy crossing points between two potential energy surfaces, J. Comput. Chem., 1997, 18, 992–1003.
24. K. Veys, M. H. E. Bousquet, D. Jacquemin and D. Escudero, Modeling the Fluorescence Quantum Yields of Aromatic Compounds: Benchmarking the Machinery to Compute Intersystem Crossing Rates, J. Chem. Theory Comput., 2023, 19, 9344–9357.
25. J. Hoche, A. Schulz, L. M. Dietrich, A. Humeniuk, M. Stolte, D. Schmidt, T. Brixner, F. Würthner and R. Mitric, The origin of the solvent dependence of fluorescence quantum yields in dipolar merocyanine dyes, Chem. Sci., 2019, 10, 11013–11022.
26. Q. Ou, Q. Peng and Z. Shuai, Toward Quantitative Prediction of Fluorescence Quantum Efficiency by Combining Direct Vibrational Conversion and Surface Crossing: BODIPYs as an Example, J. Phys. Chem. Lett., 2020, 11, 7790–7797.
27. S. Maeda, Y. Harabuchi, T. Taketsugu and K. Morokuma, Systematic Exploration of Minimum Energy Conical Intersection Structures near the Franck–Condon Region, J. Phys. Chem. A, 2014, 118, 12050–12058.
28. E. Weinan, W. Ren and E. Vanden-Eijnden, String method for the study of rare events, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 52301.
29. E. Weinan, W. Ren and E. Vanden-Eijnden, Simplified and improved string method for computing the minimum energy paths in barrier-crossing events, J. Chem. Phys., 2007, 126, 164103.
30. Y. Zhang, H. Liu and W. Yang, Free energy calculation on enzyme reactions with an efficient iterative procedure to determine minimum energy paths on a combined ab initio QM/MM potential energy surface, J. Chem. Phys., 2000, 112, 3483–3492.
31. J. Kästner, H. M. Senn, S. Thiel, N. Otte and W. Thiel, QM/MM Free-Energy Perturbation Compared to Thermodynamic Integration and Umbrella Sampling:  Application to an Enzymatic Reaction, J. Chem. Theory Comput., 2006, 2, 452–461.
32. A. D. Becke, Density-functional exchange-energy approximation with correct asymptotic behavior, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100.
33. C. Lee, W. Yang and R. G. Parr, Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789.
34. M. Huix-Rotllant, B. Natarajan, A. Ipatov, C. Muhavini Wawire, T. Deutsch and M. E. Casida, Assessment of noncollinear spin-flip Tamm–Dancoff approximation time-dependent density-functional theory for the photochemical ring-opening of oxirane, Phys. Chem. Chem. Phys., 2010, 12, 12811–12825.
35. Y. Shao, M. Head-Gordon and A. I. Krylov, The spin–flip approach within time-dependent density functional theory: Theory and applications to diradicals, J. Chem. Phys., 2003, 118, 4807–4818.
36. S. Maeda, K. Ohno and K. Morokuma, Updated Branching Plane for Finding Conical Intersections without Coupling Derivative Vectors, J. Chem. Theory Comput., 2010, 6, 1538–1545.
37. A. I. Krylov, Size-consistent wave functions for bond-breaking: the equation-of-motion spin-flip model, Chem. Phys. Lett., 2001, 338, 375–384.
38. E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons, A. L. Dempwolff, Z. Gan, D. Hait, P. R. Horn, L. D. Jacobson, I. Kaliman, J. Kussmann, A. W. Lange, K. U. Lao, D. S. Levine, J. Liu, S. C. McKenzie, A. F. Morrison, K. D. Nanda, F. Plasser, D. R. Rehn, M. L. Vidal, Z.-Q. You, Y. Zhu, B. Alam, B. J. Albrecht, A. Aldossary, E. Alguire, J. H. Andersen, V. Athavale, D. Barton, K. Begam, A. Behn, N. Bellonzi, Y. A. Bernard, E. J. Berquist, H. G. A. Burton, A. Carreras, K. Carter-Fenk, R. Chakraborty, A. D. Chien, K. D. Closser, V. Cofer-Shabica, S. Dasgupta, M. de Wergifosse, J. Deng, M. Diedenhofen, H. Do, S. Ehlert, P.-T. Fang, S. Fatehi, Q. Feng, T. Friedhoff, J. Gayvert, Q. Ge, G. Gidofalvi, M. Goldey, J. Gomes, C. E. González-Espinoza, S. Gulania, A. O. Gunina, M. W. D. Hanson-Heine, P. H. P. Harbach, A. Hauser, M. F. Herbst, M. Hernández Vera, M. Hodecker, Z. C. Holden, S. Houck, X. Huang, K. Hui, B. C. Huynh, M. Ivanov, Á. Jász, H. Ji, H. Jiang, B. Kaduk, S. Kähler, K. Khistyaev, J. Kim, G. Kis, P. Klunzinger, Z. Koczor-Benda, J. H. Koh, D. Kosenkov, L. Koulias, T. Kowalczyk, C. M. Krauter, K. Kue, A. Kunitsa, T. Kus, I. Ladjánszki, A. Landau, K. V. Lawler, D. Lefrancois, S. Lehtola, R. R. Li, Y.-P. Li, J. Liang, M. Liebenthal, H.-H. Lin, Y.-S. Lin, F. Liu, K.-Y. Liu, M. Loipersberger, A. Luenser, A. Manjanath, P. Manohar, E. Mansoor, S. F. Manzer, S.-P. Mao, A. V. Marenich, T. Markovich, S. Mason, S. A. Maurer, P. F. McLaughlin, M. F. S. J. Menger, J.-M. Mewes, S. A. Mewes, P. Morgante, J. W. Mullinax, K. J. Oosterbaan, G. Paran, A. C. Paul, S. K. Paul, F. Pavošević, Z. Pei, S. Prager, E. I. Proynov, Á. Rák, E. Ramos-Cordoba, B. Rana, A. E. Rask, A. Rettig, R. M. Richard, F. Rob, E. Rossomme, T. Scheele, M. Scheurer, M. Schneider, N. Sergueev, S. M. Sharada, W. Skomorowski, D. W. Small, C. J. Stein, Y.-C. Su, E. J. Sundstrom, Z. Tao, J. Thirman, G. J. Tornai, T. Tsuchimochi, N. M. Tubman, S. P. Veccham, O. Vydrov, J. Wenzel, J. Witte, A. Yamada, K. Yao, S. Yeganeh, S. R. Yost, A. Zech, I. Y. Zhang, X. Zhang, Y. Zhang, D. Zuev, A. Aspuru-Guzik, A. T. Bell, N. A. Besley, K. B. Bravaya, B. R. Brooks, D. Casanova, J.-D. Chai, S. Coriani, C. J. Cramer, G. Cserey, A. E. DePrince III, R. A. DiStasio Jr., A. Dreuw, B. D. Dunietz, T. R. Furlani, W. A. Goddard III, S. Hammes-Schiffer, T. Head-Gordon, W. J. Hehre, C.-P. Hsu, T.-C. Jagau, Y. Jung, A. Klamt, J. Kong, D. S. Lambrecht, W. Liang, N. J. Mayhall, C. W. McCurdy, J. B. Neaton, C. Ochsenfeld, J. A. Parkhill, R. Peverati, V. A. Rassolov, Y. Shao, L. V. Slipchenko, T. Stauch, R. P. Steele, J. E. Subotnik, A. J. W. Thom, A. Tkatchenko, D. G. Truhlar, T. Van Voorhis, T. A. Wesolowski, K. B. Whaley, H. L. Woodcock III, P. M. Zimmerman, S. Faraji, P. M. W. Gill, M. Head-Gordon, J. M. Herbert and A. I. Krylov, Software for the frontiers of quantum chemistry: An overview of developments in the Q-Chem 5 package, J. Chem. Phys., 2021, 155, 84801.
39. D. A. Case, H. M. Aktulga, K. Belfon, I. Y. Ben-Shalom, J. T. Berryman, S. R. Brozell, D. S. Cerutti, T. E. C. Iii, G. A. Cisneros, V. W. D. Cruzeiro, T. A. Darden, N. Forouzesh, M. Ghazimirsaeed, G. Giambaşu, T. Giese, M. K. Gilson, H. Gohlke, A. W. Goetz, J. Harris, Z. Huang, S. Izadi, S. A. Izmailov, K. Kasavajhala, M. C. Kaymak, A. Kovalenko, T. Kurtzman, T. S. Lee, P. Li, Z. Li, C. Lin, J. Liu, T. Luchko, R. Luo, M. Machado, M. Manathunga, K. M. Merz, Y. Miao, O. Mikhailovskii, G. Monard, H. Nguyen, K. A. O’Hearn, A. Onufriev, F. Pan, S. Pantano, A. Rahnamoun, D. R. Roe, A. Roitberg, C. Sagui, S. Schott-Verdugo, A. Shajan, J. Shen, C. L. Simmerling, N. R. Skrynnikov, J. Smith, J. Swails, R. C. Walker, J. Wang, J. Wang, X. Wu, Y. Wu, Y. Xiong, Y. Xue, D. M. York, C. Zhao, Q. Zhu and P. A. Kollman, Amber 2020, University of California, San Francisco, 2020.
40. H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, Molecular dynamics with coupling to an external bath, J. Chem. Phys., 1984, 81, 3684–3690.
41. J.-P. Ryckaert, G. Ciccotti and H. Berendsen, Numerical-Integration of Cartesian Equations of Motion of a System with Constraints – Molecular-Dynamics of N-Alkanes, J. Comput. Phys., 1977, 23, 327–341.
42. T. Darden, D. York and L. Pedersen, Particle mesh Ewald: An N·log(N) method for Ewald sums in large systems, J. Chem. Phys., 1993, 98, 10089–10092.
43. J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, Development and testing of a general amber force field, J. Comput. Chem., 2004, 25, 1157–1174.
44. N. Yamamoto, Mechanisms of Aggregation-Induced Emission and Photo/Thermal E/Z Isomerization of a Cyanostilbene Derivative: Theoretical Insights, J. Phys. Chem. C, 2018, 122, 12434–12440.
45. N. Yamamoto, Free Energy Profile Analysis for the Aggregation-Induced Emission of Diphenyldibenzofulvene, J. Phys. Chem. A, 2020, 124, 4939–4945.
46. N. Yamamoto, Free energy profile analysis to identify factors activating the aggregation-induced emission of a cyanostilbene derivative, Phys. Chem. Chem. Phys., 2021, 23, 1317–1324.
47. X.-L. Peng, S. Ruiz-Barragan, Z.-S. Li, Q.-S. Li and L. Blancafort, Restricted access to a conical intersection to explain aggregation induced emission in dimethyl tetraphenylsilole, J. Mater. Chem. C, 2016, 4, 2802–2810.
48. J. Peng, X. He, Y. Li, J. Guan, B. Wu, X. Li, Z. Yu, J. Liu and J. Zheng, Restriction of crossing conical intersections: the intrinsic mechanism of aggregation-induced emission, Phys. Chem. Chem. Phys., 2023, 25, 12342–12351.
49. Y. Shen and D. R. Yarkony, Unified Description of the Jahn–Teller Effect in Molecules with Only Cs Symmetry: Cyclohexoxy in Its Full 48-Dimensional Internal Coordinates, J. Phys. Chem. A, 2022, 126, 61–67.
50. Y. Shen and D. R. Yarkony, Construction of Quasi-diabatic Hamiltonians That Accurately Represent ab Initio Determined Adiabatic Electronic States Coupled by Conical Intersections for Systems on the Order of 15 Atoms. Application to Cyclopentoxide Photoelectron Detachment in the Full 39 Degrees of Freedom, J. Phys. Chem. A, 2020, 124, 4539–4548.
51. Y. Shen and D. R. Yarkony, Compact Bases for Vibronic Coupling in Spectral Simulations: The Photoelectron Spectrum of Cyclopentoxide in the Full 39 Internal Modes, J. Phys. Chem. Lett., 2020, 11, 7245–7252.
52. S. Matsika, Electronic Structure Methods for the Description of Nonadiabatic Effects and Conical Intersections, Chem. Rev., 2021, 121, 9407–9449.
53. X. Zhang and J. M. Herbert, Nonadiabatic dynamics with spin-flip vs linear-response time-dependent density functional theory: A case study for the protonated Schiff base C₅H₆NH₂⁺, J. Chem. Phys., 2021, 155, 124111.
54. A. Bende and A.-A. Farcaş, Intermolecular-Type Conical Intersections in Benzene Dimer, Int. J. Mol. Sci., 2023, 24, 2906.
55. C. Femina, P. K. Sajith, K. Remya, R. Thomas and R. V. Solomon, Theoretical Insights into the Structural and Optical Properties of D−π–A-based Cyanostilbene Systems of α and β Variants, ACS Omega, 2024, 9(21), 22764–22776.

---

Footnote

† Cherumannil Femina and Toshiya Yamagami contributed equally to the work.

---