Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mesoscopic theory for a double layer capacitance in concentrated ionic systems
A.
Ciach
 *a and
O.
Patsahan
*a and
O.
Patsahan
 b
b
aInstitute of Physical Chemistry, Polish Academy of Sciences, Warszawa, 01-224, Poland. E-mail: aciach@ichf.edu.pl
bInstitute for Condensed Matter Physics of the National Academy of Sciences of Ukraine, 1 Svientsitskii St., Lviv, 79011, Ukraine
First published on 3rd April 2025
Abstract
The effect of oscillatory decay in charge density in concentrated ionic solutions and ionic liquids on the double-layer capacitance is studied within the framework of a mesoscopic theory. Only Coulomb and steric forces between the ions that are present in all ionic systems are taken into account. We show that the charge oscillations lead to a rescaled distance between the electrode and the virtual monolayer of counterions in the Helmholtz capacitance, and the scaling factor depends on the period of the charge oscillations. Our very simple formula for large density of ions and small voltages can serve as a reference point for the double layer capacitance in concentrated ionic solutions and ionic liquids, and can help to disentangle the universal and specific contributions to the capacitance in particular systems.
I. Introduction
Understanding the fundamental properties of a double-layer in concentrated electrolytes and room temperature ionic liquids is of great importance for designing fuel cells, batteries, supercapacitors and energy storage devices. In the early model of the double layer, the counterions form a layer separated from the electrode by a distance L that was first approximated by the ionic diameter a. In this model, the Helmholtz capacitance is simply CH = ε/(4πa), where ε is the dielectric constant. In a more accurate model of the double layer,1 thermal motion of the ions is taken into account, and in the screening cloud of ions the charge density decays with the distance from the electrode with the Debye screening length λD.1,2 In the Debye capacitance, the diffuse layer of counterions is taken into account, and L = λD. The Debye capacitance CD = ε/(4πλD) is a reference point for dilute electrolytes at very small voltages.In concentrated electrolytes and ionic liquids (IL), however, the charge density decays with the distance from the electrode in an oscillatory way, and the decay length differs significantly from λD. The simple picture of dilute electrolytes where the average distance between the ions is much larger than their diameter is no longer valid, and the assumption of point-like ions is not justified.
A lot of effort has gone into experimental, theoretical and simulation studies of the structure of concentrated electrolytes and IL.3–22 On the one hand, universal behavior was observed by the Perkin group for the decay length λs of the force between charged objects immersed in concentrated electrolytes or IL.4–6,8λs determined in these experiments obeys the scaling λs/λD ∼ (a/λD)n with n = 3 for all ionic systems confined between crossed mica cylinders.4–6,8 This result indicates increasing charge–charge correlation length for increasing concentration of ions. In theoretical and simulation studies of concentrated ionic solutions as well as in recent SAXS experiments,10–23 the increasing λs for increasing concentration of ions was confirmed, but different values of n were obtained in different works. The underscreening observed in the above experimental, simulation and theoretical studies was not confirmed by the AFM experiments with ionic systems confined between silica surfaces,24 and the issue remains controversial.
On the other hand, specific effects play an important role in determining the capacitance, especially in the case of polar solvents, where ε may exhibit strong dependence on ρ and on the distance from the electrode.25–28 In general, the performance of the double layer capacitance is determined by a combination of many factors that include the concentration of ions in the electrolyte solution, size and nature of the ions, solvent polarity, electrode material, electrolyte–surface interactions, pore geometry, temperature, etc.28–41 In particular, electrode surface morphology modifies the structure of the electric double layer and can either break or enhance overscreening depending on the relationship of the surface roughness to the electrostatic correlation length and the ion size-asymmetry.42,43
It is not easy to disentangle different effects on the capacitance. In this work, we consider the simplest model of ionic systems with the size of the ions taken into account, namely the restricted primitive model (RPM) of charged hard spheres with equal diameter a and opposite charges in a structureless solvent characterized by the dielectric constant ε. In this model, the Coulomb and steric interactions lead to the oscillatory decay of the charge density with the distance from a charged boundary.44–46 We can thus determine the effect of the charge layering near the electrode on the capacitance that should be common for many concentrated ionic solutions. In particular cases, specific interactions and the dielectric constant dependence on the local environment can play important roles. Our purpose, however, is to find a reference point for the capacitance in concentrated ionic solutions at very small voltages, in analogy with the Debye capacitance for dilute electrolytes. To achieve this goal, we use the theoretical approach developed in our previous works for the description of systems with spontaneous inhomogeneity in the bulk, near a charged wall and in a slit geometry.17,22,45,47,48
In Section II, we briefly summarize the mesoscopic theory developed in ref. 17,22,45,47 and 48. In Section III.A, we present results for dilute electrolytes to test the mesoscopic theory predictions for the capacitance. In Section III.B, we derive our results for the capacitance of systems with large density of ions. We discuss our results in Section IV, and conclude in Section V.
II. The mesoscopic theory
In this section, we briefly summarize the key concepts, assumptions, approximations and results of the mesoscopic theory that can be applied to dilute as well as to concentrated electrolytes. The theory developed and described in detail in previous studies17,22,47,48 allows the determination of the differential capacitance of the double layer in terms of the structure of the ionic solution. In principle, different levels of approximation in this theory are possible, but in this work, we limit ourselves to the simplest approximation to highlight the underlying effect of the structure, i.e., the distribution of the ions, on the capacitance.In order to calculate the capacitance of the double layer, we consider the electrolyte in contact with a planar metallic electrode, and assume that the charge of the electrode is distributed over its flat surface. In the case of concentrated ionic solutions, for example water in the salt electrolyte, IL, or IL mixture with a neutral solvent, the assumption of point charges is not valid. The simplest model that takes the size of the ions into account is the restricted primitive model (RPM) of charged hard spheres with equal diameter a and opposite charges in a structureless solvent characterized by the dielectric constant ε. If the sizes of the positive and negative charge ions, a+ and a−, are somewhat different, we assume a = (a+ + a−)/2. We adopt this model, and assume in addition monovalent ions with the charge homogeneously distributed over the whole volume of the ion. For the same valency n of the cations and the anions, all our results apply when e is replaced by ne, where e is the elementary charge. For different valences of the anions and the cations, the theory becomes more difficult because of the lack of symmetry.49,50 We should mention that significantly different sizes of ionic cores together with specific interactions can lead to spontaneous formation of relatively large charged domains,51,52 as well as an asymmetric shape of the electric double layer capacitance.53–55 The cases of significant size disparity, different valences of the cations and the anions and strong specific interactions require separate study.
Our theory56 is based on the local mesoscopic volume fraction ζi of the ith component of the mixture. The mesoscopic volume fraction is defined by analogy with its macroscopic counterpart, namely, ζi(r) is equal to the fraction of a mesoscopic volume with the center at r that is occupied by the particles of the considered species. In general, it depends on the scale of the coarse graining.
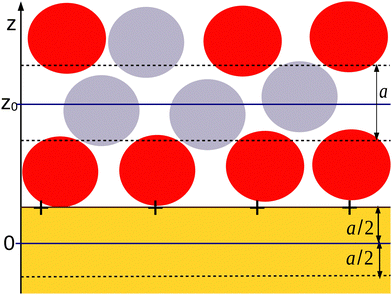
We assume that, near a flat electrode, ζi depends only on the distance z from the solid–liquid interface. As illustrated in Fig. 1, for the IL in contact with a flat solid surface, we identify the mesoscopic regions with layers of thickness a that are parallel to the solid surface. The mesoscopic volume fraction of the anions or the cations at the center of the layer is equal to the fraction of the volume of that layer that is occupied by the anions or the cations, respectively. With this definition, we obtain continuous functions of the distance from the electrode. Dimensionless mesoscopic densities are defined by ρi(z) = 6ζi(z)/π, and in the ionic system, i = +, −. It is convenient to introduce the local dimensionless number density of ions, ρ(z) = ρ+(z) + ρ−(z) and the local dimensionless charge, c(z) = ρ+(z) − ρ−(z). For monovalent ions, the local charge density is ec(z), where e is the elementary charge.
There are some ambiguities in defining the mathematical surface representing the solid–liquid interface at the microscopic and mesoscopic levels. We choose the origin of the coordinate frame, z = 0, inside the solid at the distance a/2 from the solid surface at which the electrode charge with the surface charge density eσ0 is homogeneously distributed (see Fig. 1). From Fig. 1, it can be clearly seen that in our mesoscopic approach, c(0) is equal to the dimensionless surface charge density  . For z < 0, we have c(z) = 0 when the charge of the electrode is confined to the surface of the solid, since this surface is now outside the layer with the center at z < 0. For 0 < z < a, both the electrode and the liquid contribute to c(z). Finally, for z > a, the only contribution to the charge density ec(z) comes from the electrolyte. The charge-neutrality condition of the whole system in this theory takes the simple form
. For z < 0, we have c(z) = 0 when the charge of the electrode is confined to the surface of the solid, since this surface is now outside the layer with the center at z < 0. For 0 < z < a, both the electrode and the liquid contribute to c(z). Finally, for z > a, the only contribution to the charge density ec(z) comes from the electrolyte. The charge-neutrality condition of the whole system in this theory takes the simple form
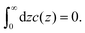 | (1) |
The electrostatic potential at z = 0 is given by the Poisson equation in the integral form,
 | (2) |
Determination of the equilibrium shape of c(z) is the main difficulty of the theory. From thermodynamics, we know that in a system with fixed volume and fixed temperature T that is in contact with a bulk reservoir of ions, the grand thermodynamic potential Ω takes a minimum. Thus, we should consider the grand potential for different forms of ρ(z) and c(z), and find the functions that minimize the functional
| Ω[c,ρ] = U[c] − TS[c,ρ] − μN, | (3) |
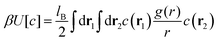 | (4) |
The exact expressions for Ω[c,ρ] (including the precise form of g(r) and S[c,ρ]) are not known, and different approximate theories were developed. In the bulk, the position independent ρ is a function of the chemical potential and temperature. The average charge density is c = 0 because it is equally probable to find an anion or a cation in a given microscopic volume in the absence of external fields. If an ion is kept at a given position, however, then it is more probable to find an oppositely charged ion in its vicinity than an ion of the same charge because the energy in the former case is lower. The charge–charge correlation function is a result of the competition between the energy favoring oppositely charged close neighbors and the entropy favoring the random distribution of the ions in the whole volume.
In our mesoscopic theory,17,56 we assume that the ions cannot overlap; therefore, g(r) = 0 for r<1 (r is in a units), and g(r) → 1 for r → ∞, since at very large distances the ions are not correlated. In the mean-field (MF) approximation, the correlations are neglected for r > 1, and g(r) ≈ θ(r − 1), where θ(r − 1) = 1 for r > 1 and θ(r − 1) = 0 for r < 1. In this approximation,
 | (5) |
 | (6) |
![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) C(k) < 0 and the energy decreases when the charge wave with k > π/2 is excited. It takes a minimum for k0 ≈ 2.46 (in 1/a units), consistent with energetically favorable oppositely charged close neighbors.
C(k) < 0 and the energy decreases when the charge wave with k > π/2 is excited. It takes a minimum for k0 ≈ 2.46 (in 1/a units), consistent with energetically favorable oppositely charged close neighbors.
The charge–charge correlation function in Fourier representation takes in this theory the form
 | (7) |
The charge–charge correlations in real space are obtained by the inverse Fourier transform of 〈ĉ(k)ĉ(−k)〉, and the decay lengths are obtained from simple poles of 〈ĉ(k)ĉ(−k)〉 extended to the complex q plane. In general, the imaginary pole q = iai gives a monotonic decay with the decay length 1/ai, and the complex poles q = iα0 ± α1 give an oscillatory decay with the decay length 1/α0 and the period 2π/α1.
In the presence of the electrode, the excess density over the bulk value, Δρ(z) = ρ(z) − ρb, and c(z) ≠ 0 minimizes the functional ΔΩ[c,Δρ] = Ω[c,ρb + Δρ] − Ωbulk[0,ρb]. When the bulk is in thermal equilibrium, the terms linear in Δρ and c in Taylor expanded ΔΩ[c,Δρ] vanish, and ΔΩ[c,Δρ] contains terms of the second and higher orders in the fields,
 | (8) |
 is defined through the Taylor expansion, and the last term in eqn (9) is given by
is defined through the Taylor expansion, and the last term in eqn (9) is given by | (9) |
 | (10) |
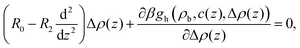 | (11) |
When the derivatives of βgh can be neglected, the EL equations for Δρ and c are linear and decoupled. The linearized EL equation for c(z) is
 | (12) |
A solution of a linear equation is a sum of exponential terms ∝ exp(λz). In our case, λ = −iq, where complex q is a solution of the equation  . For our purpose here, it is important that the linearized EL equation leads to c(z) decaying at large distances with the same decay lengths as the charge–charge correlation function (compare eqn (12) and (7)). The solution of eqn (12) must satisfy the charge neutrality condition (1).
. For our purpose here, it is important that the linearized EL equation leads to c(z) decaying at large distances with the same decay lengths as the charge–charge correlation function (compare eqn (12) and (7)). The solution of eqn (12) must satisfy the charge neutrality condition (1).
Eqn (12), (1), (2) and c(0) = a2σ0 allow for the calculation of the differential capacitance in the case of small voltages, and with the specific effects of the solvent neglected.
III. Results
III.A Capacitance of dilute electrolytes
In our mesoscopic theory, there are two inverse decay lengths, a1 > a2 for large T and small ρ, because there are two solutions of the equation (see eqn (7)) | (13) |
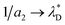 , where
, where 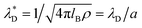 is the dimensionless Debye screening length (recall that lB and ρ are dimensionless), and a1 is of order of unity (in 1/a units). a1 and a2 merge at the so-called Kirkwood line on the (ρ,T) diagram,59 and at lower T they transform to a pair of complex inverse decay lengths that lead together to an oscillatory decay of the charge–charge correlations. This result agrees with previous theories and simulations,60–62 and is consistent with dominant roles of the entropy and energy at high and low T, respectively.
is the dimensionless Debye screening length (recall that lB and ρ are dimensionless), and a1 is of order of unity (in 1/a units). a1 and a2 merge at the so-called Kirkwood line on the (ρ,T) diagram,59 and at lower T they transform to a pair of complex inverse decay lengths that lead together to an oscillatory decay of the charge–charge correlations. This result agrees with previous theories and simulations,60–62 and is consistent with dominant roles of the entropy and energy at high and low T, respectively.
Because the decay lengths of the charge density are the same as the correlation lengths, the charge-density profile satisfying the charge-neutrality condition has on the high-T small ρ side of the Kirkwood line the form
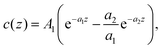 | (14) |
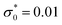 , lB = 2 and ρ = 0.01.
, lB = 2 and ρ = 0.01.
 | ||
Fig. 2 The dimensionless charge density in the case of dilute electrolytes with ρ = 0.01, lB = 2 and dimensionless surface charge density 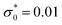 as obtained in the mesoscopic theory. The decay lengths satisfy the equation 4πlBρR as obtained in the mesoscopic theory. The decay lengths satisfy the equation 4πlBρR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosh cosh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ai = ai2, and ρR ≤ ρ satisfies the equations presented in ref. 17. z is in units of the ion diameter a. ai = ai2, and ρR ≤ ρ satisfies the equations presented in ref. 17. z is in units of the ion diameter a. | ||
The physical meaning of the two decay lengths in the context of the mesoscopic theory can be understood by comparing Fig. 2 for the representative charge density and Fig. 1 illustrating the construction of the theory. For large z, the decay of the charge is monotonic and the sign of c(z) is opposite to the sign of the electrode. The decay length is  for ρ → 0, as discussed above. By construction of the mesoscopic theory, however, for z increasing from z = 0 to z = 1, there is a contribution to c(z) from the charge of the electrode and an increasing contribution from the opposite charge of the ions in the electrolyte (see Fig. 1 for 0 < z < 1). Thus, c(z) must change sign for z < 1. The two terms in eqn (14), one with the same sign as the sign of the charge of the electrode and small decay length 1/a1 and the other one with the opposite sign and large decay length 1/a2, are consistent with the above physical picture.
for ρ → 0, as discussed above. By construction of the mesoscopic theory, however, for z increasing from z = 0 to z = 1, there is a contribution to c(z) from the charge of the electrode and an increasing contribution from the opposite charge of the ions in the electrolyte (see Fig. 1 for 0 < z < 1). Thus, c(z) must change sign for z < 1. The two terms in eqn (14), one with the same sign as the sign of the charge of the electrode and small decay length 1/a1 and the other one with the opposite sign and large decay length 1/a2, are consistent with the above physical picture.
The surface-charge density in the mesoscopic theory is
 | (15) |
For the potential at z = 0, we obtain from eqn (14) and (2)
 | (16) |
The capacitance C = d(eσ0)/dU is easily obtained from eqn (15) and (16) and is given by
 | (17) |
For dilute electrolytes, a2/a → 1/λD that can be easily seen from the equation lB![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) C(ia2) + 1/ρ = 0 for the imaginary simple pole and
C(ia2) + 1/ρ = 0 for the imaginary simple pole and ![[V with combining circumflex]](https://www.rsc.org/images/entities/i_char_0056_0302.gif) C(ia2) → −4π/a22 for ρ ≪ 1 (see eqn (7) and (6)), giving a22 = 4πlBρ. Thus, for dilute electrolytes, we obtain
C(ia2) → −4π/a22 for ρ ≪ 1 (see eqn (7) and (6)), giving a22 = 4πlBρ. Thus, for dilute electrolytes, we obtain
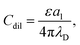 | (18) |
In order to understand the origin of the difference between eqn (18) and the Debye capacitance, recall that the Debye capacitance was obtained for point charges. The point charges can be at the distance z = 0 from the electrode surface, and c(z) is monotonic for the whole range of z > 0. If the size a of the ions is taken into account, microscopic details such as the charge distribution over the volume of the ion, the definition of the position of the electrode surface, etc. start to play a role, and some ambiguities in the definition of the capacitance in terms of the charge distribution appear. In our mesoscopic theory, the charge density c(z) is averaged over the layers of the thickness a (Fig. 1), and as discussed above, the charge profile is nonmonotonic and changes sign for z ∼ 1. This leads to a smaller value of Ψ(0) defined in eqn (2), and as a result to a larger value of the capacitance, with the coefficient a1 associated with the charge distribution in the close neighborhood of the electrode surface. To compare our predictions with the results of simulations or experiments on the quantitative level, we should take into account that formulas (17) and (18) contain the factor a1 that in the theory with the microscopic structure averaged over the region with the linear size a is 2 ≤ a1 ≤ 6 rather than a1 = 1 present in the Debye capacitance for point charges.
III.B Capacitance of concentrated electrolytes
The solution of the EL eqn (12) at the low-T side of the Kirkwood line has the formc(z) = Ace−α0z![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(α1z + θ). sin(α1z + θ). | (19) |
The above dimensionless charge density profile agrees with the fixed surface charge density σ0 and satisfies the charge-neutrality conditions (1) when
 | (20) |
A typical dimensionless charge density near a weakly charged electrode is shown in Fig. 3. Predictions of the mesoscopic theory for the charge profile45 agree with simulation results of the RPM model in the case of large density of ions.44 Namely, the electrostatic potential βΨ(z) was very similar in the simulations and in our mesoscopic theory for two values of the surface charge studied in the simulations and for the same thermodynamic states and parameters of the model. In addition, as shown for example in ref. 46, eqn (19) perfectly fits the charge density in atomistic simulations of IL – alcohol mixture for z > 2π/α1. The atomistic simulations give different shapes of c(z) for z < 2π/α1 because the microscopic charge density obtained in the simulations is compared with the charge density averaged over the layers of the thickness a in the mesoscopic theory.
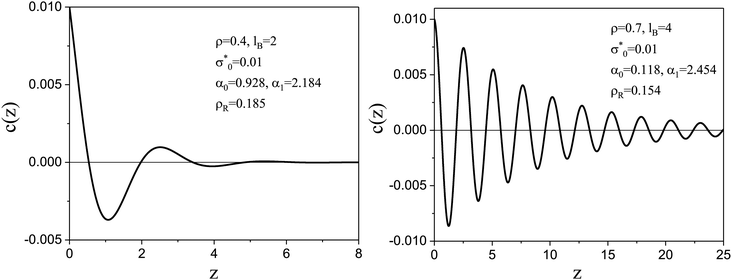 | ||
Fig. 3 The dimensionless charge density in the case of the concentrated electrolyte with ρ = 0.4, lB = 2 and ρR ≈ 0.185 (left) and ρ = 0.7, lB = 4 and ρR ≈ 0.154 (right) for dimensionless surface charge density  , as obtained in the mesoscopic theory. α0 and α1 satisfy the equations (α12 − α02) + 4πlBρR , as obtained in the mesoscopic theory. α0 and α1 satisfy the equations (α12 − α02) + 4πlBρR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cosh cosh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α0 α0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1 = 0 and α1α0 − 2πlBρR α1 = 0 and α1α0 − 2πlBρR![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sinh sinh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α0 α0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α1 = 0.17z is in units of the ion diameter a. α1 = 0.17z is in units of the ion diameter a. | ||
The electrostatic potential (2) at z = 0 for the charge density given by eqn (19) and (20) is
 | (21) |
The capacitance can be easily calculated using eσ0 = eAc![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/a2 with eqn (20) and (21), and the result is
θ/a2 with eqn (20) and (21), and the result is
 | (22) |
The dimensionless wavenumber α1 ≤ k0 ≈ 2.46 of the damped charge oscillations decreases slightly for increasing (lBρ)−1 in the concentrated electrolyte.59 As found recently4,6,56 in concentrated electrolytes, the dimensionless inverse decay length is α0 ≪ 1. In the lowest order approximation, we keep only the terms quadratic in Δρ and c, and follow the steps described in ref. 45 and 48. We can assume that in concentrated electrolytes and IL α02 ≪ α12, and
 | (23) |
Formulas (22) and (23) relating the capacitance with the period 2πa/α1 of the damped charge oscillations near the electrode are the main result of this work. We should emphasize, however, that the smoothed shape of the mesoscopic c(z) near the electrode leads to a smaller value of the electrostatic potential at z = 0, hence to a larger value of the capacitance, as already discussed in detail in Section III.A.
IV. Discussion
The expressions for the capacitance of dilute and concentrated electrolytes in the RPM near a flat metallic electrode, eqn (17) and (22), are significantly different. They become identical, however, at the Kirkwood line separating the monotonic and oscillatory asymptotic decays of the charge density because at the Kirkwood line a1 = a2 = α0 and α1 = 0. Thus, we obtained a continuous function for the whole range of the density of ions. Comparison of C with CH = εrε0/a and CD = ε/(4πλD) for the density of ions 0 < ρ < 0.7 and for fixed Bjerrum lengths lB = 2 and lB = 4 is shown in Fig. 4. | ||
| Fig. 4 The capacitance C/CH obtained from (17) and (22) (solid lines) and CD/CH (dashed lines) as a function of the dimensionless density of ions for the Bjerrum length lB = 2 and lB = 4 in a-units. | ||
Our general analytical formulas (17) and (22) were obtained from the linearized EL eqn (12); therefore, they are valid only for very small voltages. Nevertheless, they highlight the effect of the charge distribution on the capacitance for the whole range of the density of ions on a general qualitative level. For large voltages, the charge density is no longer small, and the coupled nonlinear EL equations for c and Δρ (see eqn (10) and (11) and ref. 56) have to be solved to determine C. This is possible only numerically for particular cases, and will be a subject of our future study.
The formulas for the capacitance become particularly simple for very dilute and very dense electrolytes. In the former case, we obtain the well-known Debye capacitance CD = ε/(4πλD) up to a dimensionless coefficient of order unity (see eqn (18)). For the very concentrated electrolyte or IL, we obtain formula (23) that is strikingly similar to the Helmholtz capacitance CH(L) = ε/(4πL) in the early model of the double layer, where L is the distance between the electrode and the surface occupied by the counterions. We take into account the whole oscillatory charge profile such as the ones shown in Fig. 3, and find that the alternating oppositely charged layers have the same effect as a single layer of counterions located at the distance L = a/α12 from the electrode. This shows that the simplest model of the double layer works well even in the case of a rather complex structure, but with the distance of the virtual monolayer of counterions from the electrode, L, depending on the dimensionless wavenumber α1 ≈ 2.46 of the charge oscillations.
As shown in Fig. 4, C/CH increases quickly for increasing ρ < 0.15, and slowly for ρ > 0.3, whereas CD/CH increases with ρ gradually, with almost constant slope. For the two considered values of lB, C/CH > 5 if ρ > 0.3. Moreover, C > CD, but C − CD decreases with increasing ρ, and for lB = 4, C ≈ CD for ρ ≈ 0.7. Let us compare predictions of the mesoscopic theory for the charge-density profiles shown in Fig. 3 with the classical Debye capacitance in more detail. For ρ = 0.4 and lB = 2, and the diameter of hydrated ions a ≈ 0.5 nm corresponding to ∼2.65 M NaClaq, we get α0 ≈ 0.93 and α1 ≈ 2.18, and obtain from eqn (22)
| C ≈ 10εr μF cm−2. | (24) |
From  , we get in this case λD ≈ 0.16 nm, and the formula valid for dilute electrolytes gives
, we get in this case λD ≈ 0.16 nm, and the formula valid for dilute electrolytes gives
| CD ≈ 5.6εr μF cm−2. | (25) |
The Debye length in this case differs from the physically relevant lengths a/α0 ≈ 0.54 nm and 2πa/α1 ≈ 1.44 nm, however. In another example shown in Fig. 3 with ρ = 0.7 and lB = 4, we obtain assuming a = 0.9 nm
| C ≈ 6εr μF cm−2. | (26) |
The Debye length is λD ≈ 0.15 nm, and
| CD ≈ 5.9εr μF cm−2. | (27) |
The values of C and CD are very similar in this case, but the interpretation is quite different. For the oscillatory decay of the charge density, the key factor is the period of the charge oscillations near the electrode, and the Debye length is not associated with characteristic lengths of the charge distribution. These examples show that care must be taken in interpreting experiments and simulations because correct numbers can follow from incorrect formulas.
In order to verify the accuracy of C given in eqn (22) and (23) on the quantitative level, we should compare the theoretical and simulation results for the same model. In ref. 44, C was obtained by simulations of the RPM with a = 1 nm, T = 450 K, εr = 2 and ρ ≈ 0.6 nm−3, and the result of simulations was C/CD ≈ 0.15. For the above parameters, we obtain λD ≈ 0.084 nm and eqn (23) gives C/CD = α12λD/a ≈ 0.5, where we used α1 = 2.45. Recall that the capacitance obtained in the mesoscopic theory for dilute electrolytes was overestimated by the factor 2 ≤ a1 ≤ 6. In the case of ρ = 0.6 nm−3 and large lB, the theoretical result is about three times larger than the simulation result, i.e. a systematic overestimation of the capacitance by a factor ∼3 is present in the mesoscopic theory for the whole density range.
Our results show the effect on the capacitance of the charge ordering in the region extending to large distances from the electrode. On the quantitative level, however, the capacitance also depends on the details of the microscopic structure in the vicinity of the electrode that should be determined within a more exact microscopic theory. In our mesoscopic theory, the effect of the microscopic structure can be taken into account by additional scaling factor that based on the comparison with simulations is about 1/3. As already discussed at the end of Section III.A, the larger value of the capacitance in our theory follows from the smaller value of the electrostatic potential at z = 0 that in turn is a result of the smoothed shape of the mesoscopic c(z) near the electrode.
Let us discuss consequences of eqn (23) on a general level. The capacitance decreases with increasing size of the ions, in agreement with experimental results for aqueous ionic solutions and IL.27,63 The dimensionless period of the charge wave in concentrated electrolytes depends rather weakly on density. According to our mesoscopic theory, in IL or highly concentrated electrolytes, the dimensionless α1 = 2πa/λc is 2 ≤ α1 ≤ 2.46, corresponding to the wavelength of the charge-density wave 2.55a ≤ λc ≤ 3.14a. Hence, in IL, we have for eqn (23) the approximation
 | (28) |
In the RPM, the dependence of εr (and in turn of lB) on the density of ions and on the distance from the electrode is neglected, whereas in different solvents, especially in water, this dependence can be quite strong. In aqueous solutions, εr decreases from about 80 in pure water to about 40 for 5 M solution of NaCl.4 In the Stern layer, the orientations of dipoles of water molecules in the hydration shells of ions are almost fixed, and the dielectric constant may decrease to εr ∼ 5 or even less.55,64–66 Thus, quantitative predictions for the capacitance in particular cases are not possible within the RPM, especially for polar solvents such as water. Our results show, however, the general relationship between the capacitance and the period of the damped charge oscillations. The complex charge distribution can be replaced by the simplest model of the double layer, provided that the virtual single layer of counterions is separated from the electrode by the distance equal to the diameter of the ions re-scaled by the coefficient proportional to α1−2, where α1 is the wavenumber of the damped charge oscillations in 1/a units and the proportionality constant is ∼3.
Detailed comparison of our prediction with results of simulations and experiments for particular systems goes beyond the scope of this work because it would be necessary to disentangle the universal properties captured by the RPM and the specific properties such as the size and nature of the ions, polarity of the solvent, the charge distribution and the roughness of the electrode's surface. Such an analysis should be done in future studies.
V. Conclusions
Our goal was to determine on a very general level the effect of charge ordering in concentrated electrolytes and IL on the capacitance of the double layer. We limited ourselves to the restricted primitive model, RPM, where spherical ions with equal diameters and opposite charges are dissolved in a structureless solvent characterized by the dielectric constant ε. This way we can determine the effect of the Coulomb and steric interactions in the absence of specific effects that differ from one system to the other. We obtained very simple expressions for the capacitance in dilute and concentrated electrolytes in the framework of the same mesoscopic theory. The main conclusion is that the simplest early model of the double layer works surprisingly well in the case of large density of ions, provided that the distance between the virtual single layer of counterions and the electrode is equal to the ion diameter re-scaled by a coefficient determined by the period of the damped charge oscillations. This conclusion agrees with recent simulation results.66 Our formulas (22) and (23) should play for concentrated ionic systems a similar role as the Debye capacitance plays for dilute electrolytes. These equations can serve as a reference point that allows to disentangle universal and specific features of the capacitance.Finally, it is worth mentioning that since our theory is suitable for describing the structural properties of concentrated electrolytes and their effect on capacitance, it is worthwhile to extend it to nonequilibrium properties, because in energy storage devices, the charging/discharging dynamics plays an important role.67,68 The extension can be performed by analogy with the DFT extension to the DDFT.69
Author contributions
Conceptualization: AC; formal analysis: OP and AC; investigation: OP and AC; methodology: OP and AC; visualization: OP and AC; writing – original draft: AC and OP; writing – review and editing: AC and OP.Data availability
All formulas derived in this work are included in the article. The figures were obtained from these formulas. No more data were used.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge the financial support from the European Union Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement no. 734276 (CONIN).References
- P. Debye and E. Hückel, Phys. Z., 1923, 24, 185–206 CAS.
- J. L. Barrat and J.-P. Hansen, Basic Concepts for Simple and Complex Liquids, Cambridge University Press, 2003 Search PubMed.
- M. A. Gebbie, M. Valtiner, X. Banquy, E. T. Fox, W. A. Henderson and J. N. Israelachvili, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 9674–9679 CrossRef CAS PubMed.
- A. M. Smith, A. A. Lee and S. Perkin, J. Phys. Chem. Lett., 2016, 7, 2157 CrossRef CAS PubMed.
- A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Phys. Rev. Lett., 2017, 119, 026002 CrossRef PubMed.
- A. A. Lee, C. S. Perez-Martinez, A. M. Smith and S. Perkin, Faraday Discuss., 2017, 199, 239–259 RSC.
- R. Kjellander, J. Chem. Phys., 2018, 148, 193701 CrossRef PubMed.
- T. Groves and S. Perkin, Faraday Discuss., 2024, 253, 193–211 RSC.
- F. Coupette, A. A. Lee and A. Härtel, Phys. Rev. Lett., 2018, 121, 075501 CrossRef CAS PubMed.
- B. Rotenberg, O. Bernard and J.-P. Hansen, J. Phys.: Condens. Matter, 2018, 30, 054005 CrossRef PubMed.
- R. M. Adar, S. A. Safran, H. Diamant and D. Andelman, Phys. Rev. E, 2019, 100, 042615 CrossRef CAS PubMed.
- S. W. Coles, C. Park, R. Nikam, M. Kanduč, J. Dzubiella and B. Rotenberg, J. Phys. Chem. B, 2020, 124, 1778–1786 CAS.
- J. Zeman, S. Kondrat and C. Holm, Chem. Commun., 2020, 56, 15635–15638 RSC.
- J. Zeman, S. Kondrat and C. Holm, J. Chem. Phys., 2021, 155, 204501 CrossRef CAS PubMed.
- P. Cats, R. Evans, A. Härtel and R. van Roij, J. Chem. Phys., 2021, 154, 124504 CrossRef CAS PubMed.
- S. Safran and P. Pincus, Soft Matter, 2023, 19, 7907–7911 RSC.
- A. Ciach and O. Patsahan, J. Mol. Liq., 2023, 377, 121453 CrossRef CAS.
- J. Yang, S. Kondrat, C. Lian, H. Liu, A. Schlaich and C. Holm, Phys. Rev. Lett., 2023, 131, 118201 CrossRef CAS PubMed.
- A. Härtel, M. Bültmann and F. Coupette, Phys. Rev. Lett., 2023, 130, 108202 CrossRef PubMed.
- S. Wang, H. Tao, J. Yang, J. Cheng, H. Liu and C. Lian, J. Phys. Chem. Lett., 2024, 33, 7147–7153 CrossRef PubMed.
- G. R. Elliott, K. P. Gregory, H. Robertson, V. S. Craig, G. B. Webber, E. J. Wanless and A. J. Page, Chem. Phys. Lett., 2024, 843, 141190 CrossRef CAS.
- A. Ciach and O. Patsahan, J. Phys.: Condens. Matter, 2021, 33, 37LT01 CrossRef CAS PubMed.
- M. Dinpajooh, E. Biasin, E. T. Nienhuis, S. T. Mergelsberg, C. J. Benmore, G. K. Schenter, J. L. Fulton, S. M. Kathmann and C. J. Mundy, J. Chem. Phys., 2024, 161, 151102 CrossRef CAS PubMed.
- S. Kumar, P. Cats, M. B. Alotaibi, S. C. Ayirala, A. A. Yousef, R. van Roij, I. Siretanu and F. Mugele, J. Colloid Interface Sci., 2022, 622, 819–827 CrossRef CAS PubMed.
- L. Fumagalli, A. Esfandiar, R. Fabregas, S. Hu, P. Ares, A. Janardanan, Q. Yang, B. Radha, T. Taniguchi, K. Watanabe, G. Gomila, K. S. Novoselov and A. K. Geim, Science, 2018, 360, 1339–1342 CrossRef CAS PubMed.
- M. H. Motevaselian and N. R. Aluru, ACS Nano, 2020, 14, 12761–12770 CrossRef PubMed.
- A. D’Alessandro, S. Bellani, A. Gamberini, V. Mastronardi, M. I. Zappia, M. Abruzzese, S. Thorat, E. Calcagno and F. Bonaccorso, Batteries Supercaps, 2024, 7, e202300458 CrossRef.
- E. Gongadze and A. Iglič, Electrochim. Acta, 2015, 178, 541–545 CrossRef CAS.
- O. K. Coskun, M. Muñoz, S. Dongare, W. Dean and B. E. Gurkan, Langmuir, 2024, 40, 3283–3300 CrossRef CAS PubMed.
- A. Kasina, E. Cocklin, S. Horswell, Y. Grunder and C. A. Lucas, J. Phys. Chem. C, 2024, 128, 13318–13332 CrossRef CAS.
- K. Wippermann, Y. Suo, C. Rodenbücher, C. Korte and A. A. Kornyshev, Electrochim. Acta, 2023, 469, 143207 CrossRef CAS.
- K. Zhang, C. Wei, M. Zheng, J. Huang and G. Zhou, Molecules, 2024, 29, 1246 CrossRef CAS PubMed.
- R. Costa, I. V. Voroshylova, M. N. D. Cordeiro, C. M. Pereira and A. F. Silva, Electrochim. Acta, 2018, 261, 214–220 CrossRef CAS.
- A. A. Kornyshev, J. Phys. Chem. B, 2007, 111, 5545–5557 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, Chem. Rev., 2014, 114, 2978–3036 CrossRef CAS PubMed.
- J. P. de Souza, Z. A. Goodwin, M. McEldrew, A. A. Kornyshev and M. Z. Bazant, Phys. Rev. Lett., 2020, 125, 116001 CrossRef CAS PubMed.
- J. Wu, Chem. Rev., 2022, 122, 10821–10859 CrossRef CAS PubMed.
- P. Cats, R. S. Sitlapersad, W. K. den Otter, A. R. Thornton and R. van Roij, J. Solution Chem., 2022, 51, 296–319 CrossRef CAS.
- G. Jeanmairet, B. Rotenberg and M. Salanne, Chem. Rev., 2022, 122, 10860–10898 CrossRef CAS PubMed.
- E. Gongadze and A. Iglič, Bioelectrochemistry, 2012, 87, 199–203 CrossRef CAS PubMed.
- C. Cruz, A. Ciach, E. Lomba and S. Kondrat, J. Phys. Chem. C, 2019, 123, 1596–1601 CrossRef CAS.
- A. Khlyupin, I. Nesterova and K. Gerke, Electrochim. Acta, 2023, 450, 142261 CrossRef CAS.
- I. Nesterova, N. M. Evstigneev, O. I. Ryabkov, K. M. Gerke and A. Khlyupin, J. Colloid Interface Sci., 2025, 677, 396–405 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, Electrochim. Acta, 2008, 53, 6835–6840 CrossRef CAS.
- A. Ciach, J. Mol. Liq., 2018, 270, 138–144 CrossRef CAS.
- J. M. Otero-Mato, H. Montes-Campos, O. Cabeza, D. Diddens, A. Ciach, L. J. Gallego and L. M. Varela, Phys. Chem. Chem. Phys., 2018, 20, 30412–30427 RSC.
- A. Ciach and O. Patsahan, Condens. Matter Phys., 2012, 15, 23604 CrossRef.
- O. Patsahan, A. Meyra and A. Ciach, J. Mol. Liq., 2022, 363, 119844 CrossRef CAS.
- A. Ciach, W. T. Góźdź and G. Stell, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 051505 CrossRef CAS PubMed.
- O. Patsahan and A. Ciach, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 031504 CrossRef CAS PubMed.
- O. Borodin, L. Suo, M. Gobet, X. Ren, F. Wang, A. Faraone, J. Peng, M. Olguin, M. Schroeder, M. S. Ding, E. Gobrogge, A. von Wald Cresce, S. Munoz, J. A. Dura, S. Greenbaum, C. Wang and K. Xu, ACS Nano, 2017, 11, 10462–10471 CrossRef CAS PubMed.
- O. Patsahan and A. Ciach, ACS Omega, 2022, 7, 6655–6664 CrossRef CAS PubMed.
- M. V. Fedorov and A. A. Kornyshev, J. Phys. Chem. B, 2008, 112, 11868–11872 CrossRef CAS PubMed.
- A. Velikonja, V. Kralj-Iglič and A. Iglič, Int. J. Electrochem. Sci., 2015, 10, 1–7 CrossRef.
- A. Iglič, E. Gongadze and V. Kralj-Iglič, Acta Chim. Slov., 2019, 66, 534–541 CrossRef.
- A. Ciach and O. Patsahan, J. Mol. Liq., 2023, 382, 121949 CrossRef CAS.
- Z. A. Goodwin and A. A. Kornyshev, Electrochem. Commun., 2017, 82, 129–133 CrossRef CAS.
- Z. A. M. Chen, Z. A. H. Goodwin, G. Feng and A. A. Kornyshev, J. Electroanal. Chem., 2018, 819, 347–358 CrossRef.
- A. Ciach, W. T. Góźdź and R. Evans, J. Chem. Phys., 2003, 118, 3702–3710 CrossRef CAS.
- P. Attard, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 1993, 48, 3604 CrossRef CAS PubMed.
- R. L. de Carvalho and R. Evans, Mol. Phys., 1994, 83, 619–654 CrossRef.
- G. M. Torrie and J. P. Valleau, J. Chem. Phys., 1980, 73, 5807–5816 CrossRef CAS.
- V. Lockett, M. Horne, R. Sedev, T. Rodopoulos and J. Ralston, Phys. Chem. Chem. Phys., 2010, 12, 12499–12512 RSC.
- A. Velikonja, E. Gongadze, V. Kralj-Iglič and A. Iglič, Int. J. Electrochem. Sci., 2014, 9, 5885–5894 CrossRef.
- A. V. Dubtsov, S. V. Pasechnik, D. V. Shmeliova, A. S. Saidgaziev, E. Gongadze, A. Iglič and S. Kralj, Soft Matter, 2018, 14, 9619–9630 RSC.
- S. Park and J. G. McDaniel, J. Chem. Phys., 2024, 160, 164709 CrossRef CAS PubMed.
- S. Kondrat, G. Feng, F. Bresme, M. Urbakh and A. A. Kornyshev, Chem. Rev., 2023, 123, 6668–6715 CrossRef CAS PubMed.
- C. Noh and Y. Jung, Phys. Chem. Chem. Phys., 2019, 21, 6790–6800 RSC.
- A. J. Archer, J. Chem. Phys., 2009, 130, 014509 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2025 |