Rotational (de-)excitation of CH₃CN in collisions with H₂ on an accurate potential energy surface

Abstract

Observations of molecules with C_3v symmetry, such as CH₃CN, are particularly valuable in molecular clouds as the rotational transition selection rules of these molecules allow them to serve as gas thermometers. Interpreting their spectra in non-local thermodynamic equilibrium (non-LTE) conditions requires accurate collisional rate coefficients, especially for interactions with common interstellar species like H₂. In this work, we present a five-dimensional potential energy surface for CH₃CN in van der Waals interaction with H₂ (¹Σ⁺), computed using the CCSD(T)/F12 method and the aug-cc-pVTZ basis set. This potential energy surface is fitted with analytical functions suited for scattering calculations. Cross sections for rotational transitions in collisions between ortho- and para-CH₃CN and para-H₂ (j₂ = 0) are computed using the close-coupling quantum scattering method, across energies from threshold up to 150 cm⁻¹. These data are essential for interpreting interstellar CH₃CN emission lines and advancing our understanding of diverse astronomical environments.

---

1. Introduction

Over the last few years, the dynamic range, the sensitivity and spectroscopic accuracy of millimeter and sub-millimeter observatories have increased significantly. It is now possible for astrophysicists to observe in detail many complex molecules, including large organic molecules with small rotational constants, in various astronomical environments with temperatures ranging from a few to several hundreds kelvin. Among these species, symmetric top molecules are of particular interest as they probe the physical conditions of the sources such as the temperature. The nitrogen bearing species methyl cyanide (or acetonitrile, CH₃CN) is the simplest of the alkyl nitriles that belongs to this category and it is commonly used as an effective gas thermometer in interstellar clouds.¹

CH₃CN was observed in a wide variety of astronomical environments, both in our Solar System and beyond. It has been first identified in the Sgr B and Sgr A molecular clouds.² Since then, several studies focused on CH₃CN, including in gas affected by the passage of a shock wave such in L1157-B1,³ in comets,⁴ in protoplanetary disks,⁵ in cold dense cores,^6,7 as well as in extra-galactic sources.⁸ Recently, CH₃CN was detected towards the circumstellar disk around V883 Ori⁹ and it is also a constituent of the atmosphere of Titan, Saturn's largest moon.^10,11 CH₃CN is likely to be formed on icy grains from reactions involving CH₃ and CN radicals and injected into the gas phase as the icy grain mantles desorbs CH₃CN at temperatures above 90 K,¹² or directly in the gas phase by electron recombination of CH₃CNH⁺.¹³

Due to its large abundance, its prolate character and its large permanent electric dipole moment (μ = 3.913 Debye),¹⁴ CH₃CN shows strong rotational lines in the millimeter and sub-millimeter bands, making this molecule a useful probe of temperature, density and physicochemical conditions of the environment where it is detected. Furthermore, methyl cyanide displays a large number of rotational lines with the same k and different j (Δj = 1 and Δk = 0, where j is the rotational quantum number of CH₃CN and k is the projection of j on the C₃ molecular symmetry axis) that can be observed simultaneously in the same frequency range.¹⁵ The intensities of such transitions are related to the excitation temperature, which can be estimated without being affected by calibration errors or apparatus functions.

Because of the low density of most astrophysical regions, the populations of the energy levels cannot always maintain local thermodynamical equilibrium (LTE) with the ambient gas. In such conditions, interpreting the CH₃CN emission spectra, in terms of temperature, density, and column density requires solving simultaneously the radiative transfer equation and a set of statistical equilibrium equations for the molecular energy levels. A knowledge of the collisional rate coefficients for the excitation of CH₃CN by the main background gas, usually H₂ molecules, He atoms, or in some cases H atoms, is then necessary. The set of rate coefficients for the excitation of CH₃CN used in non-LTE models is often based on the data computed by Green,¹⁶ which were obtained at what is today considered a low level of theory. The collisional excitation of CH₃CN by He atoms has been the object of recent studies,^17–19 which showed major differences with the data from Green.¹⁶ He is often considered as a proxy for the spherical para-H₂ (j = 0) due to their similarity. Although this approximation is useful to simplify the study of the collisional excitation, it is often found that collisions with H₂ display a different behaviour than with He, warranting separate investigations.^20,21

In the following, we present a study of the rotational (de-)excitation of CH₃CN induced by collisions with para-H₂ (j₂ = 0) at energies below 150 cm⁻¹. A detailed summary of the construction of the potential energy surface (PES) for the interaction of CH₃CN and H₂ considered as two rigid rotors along with the fitting procedure of the PES is reported in Section 2. Section 3 describes the low-energy dynamics of collision. We end with conclusions and future outlook in Section 4.

2. Potential energy surface

2.1. Benchmark calculations

In the present work the potential energy surface of interacting CH₃CN(¹A₁) and H₂ (¹Σ⁺_g) molecules is described within the approximation of rotating rigid bodies. The frequency of the lowest vibrational mode (ν₈, the CCN bending mode) of CH₃CN is measured at 365 cm⁻¹, which could limit the validity of the rigid rotor approximation to energies below this threshold. However, because of the small magnitude of vibrational rate coefficients (typically orders of magnitude lower than those for rotational excitation^22,23), it remains sensible to use the rigid-rotor approximation even for energies above the ν₈ threshold.

To define the collisional complex, it is customary^24,25 to employ a 5D Jacobi coordinate system (R, θ₁, ϕ₁, θ₂, ϕ₂) as shown in Fig. 1. The origin of the coordinate system is in the center-of-mass G of the CH₃CN and one of the hydrogen atoms of CH₃CN is located in the XGZ-plane. The GXYZ frame coincides with the main axes of inertia of CH₃CN, with the GZ axis defined along the C₃ symmetry axis. The position of the center of mass of H₂ is characterized by the coordinates (R, θ₁, ϕ₁), where R is the length of the intermolecular vector R that connects the center of mass of CH₃CN to the one of H₂ and the polar angles (θ₁, ϕ₁) are the spherical angles defining the orientations of H₂ with respect to CH₃CN. The H₂ orientation is set by the spherical angles (θ₂, ϕ₂) in the frame (parallel to the GXYZ frame).

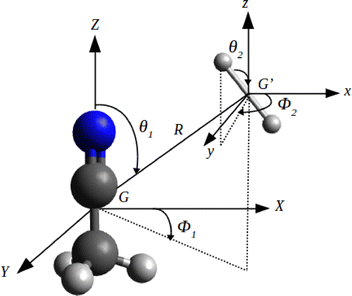Fig. 1 Jacobi coordinates system used to describe the interaction of CH₃CN–H₂ van der Waals complex. The origin of the reference frame is at the CH₃CN center-of-mass.

The geometry of the symmetric top molecule CH₃CN is defined by the following parameters, which correspond to the ground-state average values reported previously by Le Guennec et al.:²⁶r(N–C) = 1.156 Å, r(C–C) = 1.457 Å, r(C–H) = 1.087 Å, and ∠(HCC) = 110°. In the case of the H₂ molecule, a bond length r_H–H = 1.448 bohr was used, corresponding to the average value of the vibrationally ground-state geometry.

The ab initio calculations were performed with the MOLPRO (version 2019)²⁷ quantum chemistry software package. We first examined the mono-configurational behavior of CH₃CN–H₂ wave function by carrying out multiconfigurational computations with the CASSCF approach.²⁸ The electronic wave function is mainly described by only electron configuration with statistical weight around 0.95. Monoconfigurational coupled cluster methods are thus expected to be suitable to accurately describe the electronic correlation.

As a second test, we established a comparison of various methods and basis sets by computing the interaction potential for several molecular orientations. The computational method used as a reference for our closed shell system is the coupled cluster method with simple, double and perturbative triple excitations [CCSD(T)] with the complete basis set extrapolation (CBS)²⁹ limit technique. The basis extrapolation was performed using the aug-cc-pVXZ (X = D, T, Q) basis sets. At all selected geometries, the counterpoise scheme of Boys and Bernardi³⁰ was used for the description of interaction energies E(int) as follows:

E_X(int) = E_X(CH₃CN, H₂) − E_X(CH₃CN) − E_X(H₂), (1)

where the CH₃CN and H₂ energies are computed with the full bimolecular basis set, X, of the system.

One-dimensional cuts of the interaction energies as a function of R are presented in Fig. 2 at fixed angles corresponding to the global minimum of the PES (θ₁ = θ₂ = ϕ₁ = ϕ₂ = 0°, see below). We used both the standard CCSD(T) method³¹ and its explicitly correlated variant CCSD(T)-F12³² with basis sets aug-cc-pVXZ (aVXZ for short) of increasing size. The analysis of these benchmark calculations shows that the potential computed at the CCSD(T)-F12/aVDZ level is already of better quality than at the CCSD(T)/aVTZ level, despite the much smaller computational cost. While the explicitly correlated method overestimates slightly the depth of the well compared to the CBS results, Fig. 2 shows that the CCSD(T)-F12/AVTZ approach achieves an accuracy comparable to the reference CCSD(T)/CBS (D, T, Q) results.

Fig. 2 Potential energy (in cm⁻¹) of the CH₃CN–H₂ complex,computed at different levels of theory, as a function of the distance R for the fixed orientation θ₁ = θ₂ = ϕ₁ = ϕ₂ = 0° (for which the global minimum of the PES is found, see text and Fig. 3).

In addition, the use of the larger aVQZ basis set only leads to a minor improvement of the interaction energy at the cost of an important increase in computational time. Since the CCSD(T)-F12/aVTZ and CCSD(T)-F12/aVQZ are almost indistinguishable, we chose the former to compute the full PES of CH₃CN–H₂, an approach that is customarily employed to study weakly bound van der Waals complexes.

2.2. Description of the potential energy surface

Ab initio energies were computed in the C₁ symmetry group, on a grid of 37 intermolecular distances R ranging from 4 to 100 bohr with a variable step size along with a random sampling of the four angular coordinates of H₂ with respect to CH₃CN. This resulted in a total of 37 000 single-point ab initio energy points. A random grid of the four angles was chosen in order to be able to fit with efficiency the PES over the appropriate coordinates. Moreover, to account for the fact that the CCSD(T)-F12 method is not size consistent, the whole potential energy was shifted by subtracting the value of the residual interaction at large distance, V = 7.75 cm⁻¹, in order to force the PES to tend towards zero asymptotically.

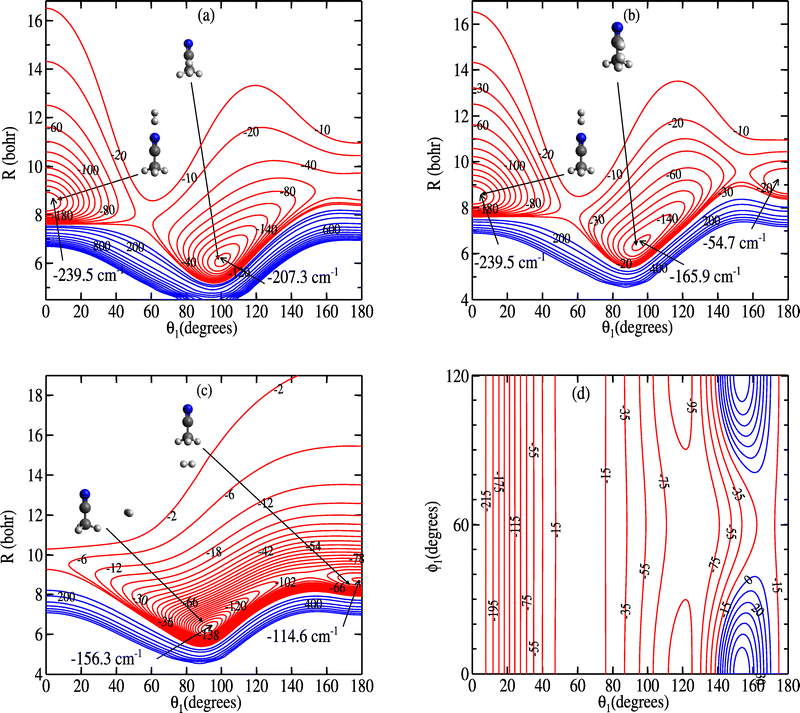
We present in Fig. 3 various contour plots of the 5D-PES of the CH₃CN–H₂ complex. Each contour plot allows a visualization of a slice of the PES depending on two variables, which are indicated by the axis labels. The three remaining coordinates were kept fixed.

Fig. 3 Two-dimensional contour plots of the interaction potential of CH₃CN–H₂ van der Waals complex. The 5D-PES is illustrated as a function of θ₁ and R at fixed ϕ₁ = 60°, ϕ₂ = 0°, θ₂ = 0° (panel a); θ₁ and R at fixed ϕ₁ = 0°, ϕ₂ = 0°, θ₂ = 0° (panel b); θ₁ and R at ϕ₁ = 0°, ϕ₂ = 90°, θ₂ = 90° (panel c); and ϕ₁ and θ₁ at fixed ϕ₂ = 0°, θ₂ = 0° and R = 8.5 bohr (panel d). For each panel, the blue (red) contours represent the positive (negative) parts of the potential (in units of cm⁻¹).

The global minimum (GM) of the PES is found at R = 8.5 bohr for the orientation θ₁ = θ₂ = 0° (where ϕ₁ and ϕ₂ are undefined) with a corresponding energy of 239.5 cm⁻¹ below the dissociation limit. This corresponds to H₂ co-linear with the C₃ axis of CH₃CN, on the side of the nitrogen atom. This is similar to results found for the interaction of symmetric tops with H₂, such as for ammonia.³³ The GM can be seen in the 2D contour plot shown in panels (a) and (b) of Fig. 3, which display two-dimensional cuts of the contour plot along (R, θ₁) for θ₂ = 0° and either ϕ₁ = 60° or ϕ₁ = 0°. When keeping the orientation of H₂ fixed to θ₂ = 0° and relaxing θ₁, the PES displays a local minimum with a well depth of 207.3 cm⁻¹ at θ₁ = 101° when ϕ₁ = 60°, that is, when H₂ is located between two of the three H atoms of CH₃CN (see panel (a) of Fig. 3). When ϕ₁ = 60° (H₂ in the plane formed by the C–C–H plane, panel (b) of Fig. 3), the local minimum is shallower, with an energy of 165.9 cm⁻¹. In both cases the local minimum is separated from the GM by a local maximum of about −17 cm⁻¹. For other orientations of H₂ the PES displays local minima again, as illustrated in panel (c) of Fig. 3. The interaction energies of the various minima and transition structures highlighted in the Fig. 3 are given in Table 1, along with the corresponding value of the coordinates. Fig. 3 shows that the interaction potential between CH₃CN and H₂ is attractive in the long-range, but that it is strongly anisotropic, especially along the θ₁ coordinate. This anisotropy will play an important role in the rotational energy transfer of methyl cyanide during the collision.

Table 1 Geometric parameters and potential energy for the global (GM) and local (LM) minima, as well as the transition structures (TS) of the CHCN–H₂ complex. Distances are in Bohr, angles are in degrees, and energies are in cm⁻¹

Geometries	R	θ 1	ϕ 1	θ 2	ϕ 2	V
GM	8.5	0	60	0	0	−239.5
LM	6.1	101	60	0	0	−207.3
TS	7.9	56	60	0	0	−17.2
LM	6.4	95	0	0	0	−165.9
TS	7.8	56	0	0	0	−16.5
GM	6.3	95	0	90	90	−156.3
LM	8.7	180	0	90	90	−114.6
TS	8.2	142	0	90	90	−86.1

---

2.3. Analytic fit

The ab initio energies are fitted onto the appropriate angular functions suitable for the subsequent dynamical calculation. Its form presented in eqn (2) was derived by Phillips et al.,³⁴ and employed previously for several asymmetric top molecules with C_2v symmetry such as H₂O–H₂²⁴ and C₃H₂–H₂.²⁵

In the rigid-rotor approximation, the C_3v symmetry of CH₃CN requires that m₁ be a multiple of 3, (m₁ = 3n, n integer). The C_∞h symmetry of H₂ requires that only even l₂ terms need to be included (l₂ = 2n).

For a given distance R, the 5D-PES was fitted according to the following expression:

with the following polyspheric representation of T:where Y_lr(θ, ϕ) are the spherical harmonics, δ_ij is a Kronecker symbol, l₁, l₂, and l are the tensor ranks describing the rotation of CH₃CN, H₂, and the collision vector orientation of H₂ with respect to CH₃CN (orbital angular momentum), respectively, and is a 3-j symbol with r + r₁ + r₂ = 0.

For each value of the intermolecular distance R, the values of the interaction energy computed on the grid of 1000 random orientations were fitted in a linear least squares procedure to determine the angular coefficients. We started the fit by minimizing the number of angular functions to T₀₀₀₀ function and we increased the number of function as long as the fit kept being more accurate (enough terms in the expansion) and reliable (enough ab initio energy points to define all terms). The best compromise between the number of ab initio energies per distance, accuracy of the fit, and number of fitting functions was found for values: m₁ ≤ l₁ ≤ 12 for CH₃CN and l₂ ≤ 2 for H₂. The final set was then composed of 181 angular functions. This set was used for all 37 intermolecular distances. In the long-range and minimum region of the PES (R ≥ 5.5 bohr), the fit is better than 1%. A somewhat larger error is found for smaller values of R, thereby limiting the precision of the fit at higher collisional energies. Finally, we performed a cubic spline interpolation of the coefficients throughout the intermolecular region (R ≤ 30 bohr) while at long range (R ≥ 30 bohr) the PES was extrapolated by a simple power-law behaviour V_l1m1l2l(R) = B/R^β, suitable for the dynamic calculations, where the value of the parameters B and β depends on l₁, m₁, l₂, and l. The long range extrapolations were finally smoothly connected to the cubic spline interpolation by an appropriate switch function given below:

whose first, second, and third derivatives are identically zero for x = 0 and 1.

We illustrate in Fig. 4 the variation of the first five radial coefficients (V_l1m1l2l) along the R Jacobi coordinate.

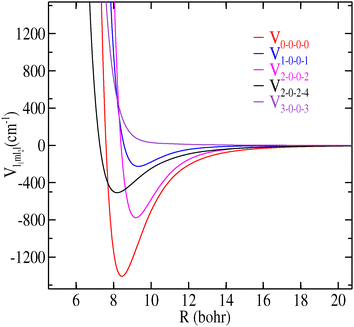Fig. 4 Dependence on R of the first V_l1m1l2l(R) expansion terms in eqn (2) for CH₃CN–H₂ with l ≤ 3.

3. Scattering calculations

The calculation of state-to-state collisional cross sections requires an accurate rotational spectroscopy for CH₃CN. Methyl cyanide is a prolate symmetric top molecule with the moments of inertia I_C = I_B > I_A. Rotational levels are characterized with the quantum numbers j, k where j is the angular momentum and k is a quantum number associated to the projection of j on the symmetry axis of the molecule. The rotational energy of CH₃CN is given, at fourth order, by the following expression:

E_J,K = BJ(J + 1) + (A − B)K² + D_JJ²(J + 1)² − D_JKJ(J + 1)K² − D_K⁴ (5)

The rotational constants and the centrifugal distortion constants of CH₃CN are given by B = C = 0.3068 and A = 5.2470, and D_J = 1.27 × 10⁻⁷, D_K = 5.90 × 10⁻⁶, and D_JK = 9.44 × 10⁻⁵ (all values in cm⁻¹).³⁵

The presence of three identical H atoms in CH₃CN results in two nuclear spin states, namely ortho-CH₃CN (total hydrogen nuclear spin 3/2) which correspond for k = 3n (n integer), including also k = 0, and para-CH₃CN (total hydrogen nuclear spin 1/2) with k ≠ 3n. Since ortho–para-transitions are forbidden in inelastic collisions as well as through radiative processes, the two spin modifications of CH₃CN can be considered as independent and separate scattering calculations can be carried out independently.

3.1. Cross sections

Time-independent quantum scattering computations were performed with the MOLSCAT³⁶ suite of programs. While the theory for the excitation of symmetric top molecule colliding with a closed-shell linear rotor within the fully quantum-mechanical close coupling approach is known,^37,38 it was not available in MOLSCAT and a subroutine has now been implemented for these systems.

Once the analytical PES was successfully integrated in the MOLSCAT computer code, the state-to-state rotational cross sections of both nuclear spin species, para- and ortho-CH₃CN, in collisions with para-H₂ (j₂ = 0) were computed using the exact time-independent close-coupling (CC) method.³⁹ The diabatic log derivative propagator⁴⁰ was employed to solve the coupled channels scattering equations. Total energies up to 150 cm⁻¹ were considered and the reduced collision mass was taken as μ = 1.92134 atomic mass units (isotopes ¹H, ¹²C and ¹⁴N). We do not take into consideration the hyperfine excitation in CH₃CN molecule because the component splitting is not resolved by the astrophysical observations.

We computed converged cross sections for transitions involving levels up to j_k = 13₃ for ortho-CH₃CN (rotational energy E_rot = 100.524 cm⁻¹) and j_k = 13₄ for para-CH₃CN (E_rot = 135.268 cm⁻¹). We started by testing the integrator parameters, which were adjusted to ensure convergence of the rotational cross sections over the entire energy range. The integration limits were set to R_min = 2.5 bohr and R_max = 30 bohr. Furthermore, the rotational basis was defined in order to include all open channels along with several closed channels to insure proper convergence of the cross sections with respect to the size of the rotational basis: For ortho-CH₃CN (resp. para-CH₃CN) convergence was achieved with j_max = 18(19) for E_tot ≤ 50 cm⁻¹, j_max = 19(20) for E_tot ≤ 100 cm⁻¹ and j_max = 24(25) for 100 ≤ E_tot ≤ 150 cm⁻¹, respectively. As the number of coupled equations and the computer time required for their solution increase quickly with the size of the rotational basis, we have used the cut-off parameter E_max = 1300 cm⁻¹ to eliminate some highly excited levels. By assigning values of 1 and 0.05 Ų to the diagonal and off-diagonal tolerances respectively, the convergence of the inelastic cross sections was ensured within better than 5 per cent for all inelastic transitions considered here. For example, for the total energy E_tot = 100 cm⁻¹, J_tot = 45 ensures the convergence. A proper description of resonances requires the accurate generation of cross sections especially at low energies. The density of the energy grid therefore varies with the total energy and cross sections were computed every 0.2 cm⁻¹ at low energy and every 1 cm⁻¹ at the highest energies.

As the ortho and para levels of CH₃CN cannot be converted in inelastic collisions, the cross sections were computed separately for each nuclear spin species. Fig. 5 highlights plots of the low energy dependence of state-to-state integral cross sections for dipolar (Δj = 1) and quadrupolar (Δj = 2) transitions with Δk = 0 for ortho-CH₃CN (panels (a) and (c)) and para-CH₃CN (panels (b) and (d)) in collisions with H₂(j₂ = 0).

Fig. 5 Rotational excitation cross section of ortho (left panels) and para (right panels) CH₃CN as a function of the collisional energy for |Δj| = 1 and |Δj| = 2 transitions while |Δk| = 0 (top panels) and |Δj| = 1 and 3 while |Δk| = 0,1 and 3 (bottom panels) as a function of the collisional energy (E_c).

All excitation cross sections exhibit a similar energy dependence: They increase in magnitude from their respective energy thresholds, achieve a maximum, and subsequently decrease with increasing collision energy in the range examined here. Moreover, as it is expected, due to the small values of the rotational constants and the comparatively large depth of the PES, all inelastic cross sections exhibit a dense resonance structure at low energies for collisions of both nuclear spin modifications of CH₃CN. These are a combination of both Feshbach and shape resonances resulting from the decay of quasibound states of the CH₃CN–H₂ complex, supported by the van der Waals well. As the kinetic energy increases, the resonances become smooth and less pronounced.

For both ortho and para-CH₃CN, we observe in Fig. 5 (panels (a) and (b)) that cross sections corresponding to transitions with Δj = 1 and Δk = 0 (e.g., 2₀–3₀ for ortho-CH₃CN and 2₁–3₁ for para-CH₃CN) are comparable in magnitude to transitions with Δj = 2 and Δk = 0 (e.g., 2₀–4₀ or 2₁–4₁) at low energy. However, the cross sections for Δj = 1 transitions decrease more quickly with increasing energy, and above collision energies of about 50 cm⁻¹ the Δj = 2 cross sections become significantly larger than those for the corresponding transitions involving Δj = 1. Transitions with Δj > 2 are comparatively much smaller (not shown). Such findings confirm that for the ortho- and para-CH₃CN–H₂ colliding system, a general propensity rule towards Δj = 2 transitions can be expected. In order to examine the dependence of cross sections on the variation of the quantum number k, we display in panels (c) and (d) of Fig. 5 the cross sections for rotational transitions corresponding to Δj = 1 and 3 with Δk = 0,1, and 3. A clear dominance of Δk = 0 transitions is noted, hence, a strong propensity rule on Δk = 0 component can be outlined. Such a result is not surprising since similar behaviors were also found for the related collisional system CH₃CN–He.¹⁷

We compare in Fig. 6 our results with the corresponding cross sections for CH₃CN–He collisions, which were calculated at a similar level of theory.¹⁷ We turn our focus to the case of para-CH₃CN excitation with initial level j_k = 3₁ and present cross sections for four transitions that correspond to Δj = 1 and Δk = 0, Δj = 2 and Δk = 0, Δj = 1 and Δk = 1, as well as Δj = 2 and Δk = 1. Significant differences can be observed between the present results and the cross sections of CH₃CN–He in the whole collision energy range considered. For the 3₁–5₁ transition (Δj = 2, Δk = 0) the shape of the cross section is similar for the excitation by H₂ and He, although the magnitude is larger for excitation by H₂. For all the other cases the cross sections for excitation by H₂ are much larger than the corresponding ones for He, especially for transitions with Δk ≠ 0 where the difference is more than an order of magnitude. Significantly, there is no constant linear scaling between the present cross sections and those for CH₃CN–He, which confirms the relevance of the new calculations. Furthermore, as one can also observe in Fig. 6, another important difference is that the inelastic cross sections for excitation by H₂ are characterized by a denser resonance structure than for excitation by He. This is likely due to the large difference between the well depth of the two interaction potentials: while for the CH₃CN–He system, it is about 55 cm⁻¹, the well depth of the PES in our calculation is more than four times larger (239.5 cm⁻¹), which allows the potential to support a much larger number of quasi-bound states.⁴¹

Fig. 6 Comparison of cross sections for the excitation of CH₃CN by para-H₂ (solid lines) and He atoms (dashed lines) for selected transitions with Δj = 1 or 2 and Δk = 0 or 1.

4. Conclusions

In this paper, we have presented the first five-dimensional PES for the interaction between CH₃CN and H₂ molecules. The 5D-PES was built based on ab initio calculations using the CCSD(T)-F12 method and the aug-cc-pVTZ basis set. Such an approach guarantees an accurate description at the van der Waals minimum of the interaction and of the asymptotic region. The interaction between methyl cyanide and molecular hydrogen is strongly anisotropic and presents a global minimum of −239.5 cm⁻¹ at θ₁ = θ₂ = 0° and R = 8.5 bohr, corresponding to H₂ co-linear with the axis of symmetry of CH₃CN, while several local minima of the PES were also found.

The PES was then used to investigate rotational energy transfer in CH₃CN–H₂ collisions, with H₂ in its j₂ = 0 state (para-H₂). Collisional excitation was investigated for energies ranging between the threshold and 150 cm⁻¹, and inelastic cross sections associated to rotational transitions in ortho- and para-CH₃CN were computed using the quantum close-coupling method. Propensity rules which favor transitions with Δj = 2 and Δk = 0 were found for both para- and ortho-symmetries of acetonitrile.

The accurate PES presented in this work and the associated scattering calculations are a first step towards obtaining a full data set of rate coefficients for the rotational excitation of CH₃CN, which should significantly help the interpretation of interstellar CH₃CN emission lines observed with current and future telescopes. In turn, this would allow to better constrain the abundance of CH₃CN in molecular clouds, which is crucial to understand the chemistry of cyanide species in the interstellar medium. In future work, we will extend the scattering calculations towards higher collisional energies, enabling the computation of the corresponding collisional rate coefficients. These rate coefficients can then be compared to those corresponding to the excitation induced by collisions by He atoms, but also by ortho-H₂, which cannot be inferred from the para-H₂ rate coefficients.^42,43 The impact of these new data in non-LTE radiative transfer models can subsequently be evaluated.

Data availability

The 5D-PES presented in this work and the associated scattering calculations are a first step towards obtaining a full data set of rate coefficients for the rotational excitation of CH₃CN. In future work, we aim to extend the scattering calculations towards to higher collisional energies, enabling the computation of the corresponding collisional rate coefficients up to T = 100 K. These future rate coefficients will be available online in both Lamda and EMAA databases.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank J. Hutson for help adapting MOLSCAT to meet the needs of the present project. M. B. K. thanks N.E. Jaidane and A. Faure for useful discussions. M. B. K. acknowledges support from the FWO through Project No. 12E6623N. J. L. acknowledges support from project no. C14/22/082 of KU Leuven. Scattering computations were carried out on the VSC clusters (Flemish Supercomputer Center), funded by the Research Foundation-Flanders (FWO) and the Flemish Government as well as LUMAT-MESOLUM computer center (Université Paris-Saclay).

References

1. S. Kalenskii, V. Promislov, A. Alakoz, A. Winnberg and L. E. Johansson, Astron. Astrophys., 2000, 354, 1036–1040.
2. P. Solomon, K. Jefferts, A. Penzias and R. Wilson, Astrophys. J., 1971, 168, L107.
3. H. G. Arce, J. Santiago-Garca, J. K. Jørgensen, M. Tafalla and R. Bachiller, Astrophys. J. Lett., 2008, 681, L21.
4. B. Ulich and E. Conklin, Nature, 1974, 248, 121–122.
5. K. I. Öberg, V. V. Guzmán, K. Furuya, C. Qi, Y. Aikawa, S. M. Andrews, R. Loomis and D. J. Wilner, Nature, 2015, 520, 198–201.
6. A. Potapov, Á. Sánchez-Monge, P. Schilke, U. Graf, T. Möller and S. Schlemmer, Astron. Astrophys., 2016, 594, A117.
7. S. Spezzano, P. Caselli, L. Bizzocchi, B. Giuliano and V. Lattanzi, Astron. Astrophys., 2017, 606, A82.
8. R. Mauersberger, C. Henkel, C. Walmsley, L. Sage and T. Wiklind, Astron. Astrophys., 1991, 247, 307–314.
9. J.-E. Lee, S. Lee, G. Baek, Y. Aikawa, L. Cieza, S.-Y. Yoon, G. Herczeg, D. Johnstone and S. Casassus, Nat. Astronomy, 2019, 3, 314–319.
10. J. Mitton, Lifting Titan's veil: exploring the giant moon of Saturn, Cambridge University Press, 2002.
11. A. Coustenis, R. K. Achterberg, B. J. Conrath, D. E. Jennings, A. Marten, D. Gautier, C. A. Nixon, F. M. Flasar, N. A. Teanby and B. Bézard, et al. , Icarus, 2007, 189, 35–62.
12. A. Belloche, R. Garrod, H. Müller, K. Menten, C. Comito and P. Schilke, Astron. Astrophys., 2009, 499, 215–232.
13. L. Giani, C. Ceccarelli, L. Mancini, E. Bianchi, F. Pirani, M. Rosi and N. Balucani, Mon. Not. R. Astron. Soc., 2023, 526, 4535–4556.
14. L. Olmi, R. Cesaroni, R. Neri and C. Walmsley, Astronomy Astrophys., 1996, 315, 565–577.
15. S. Pols, A. Schwörer, P. Schilke, A. Schmiedeke, Á. Sánchez-Monge and T. Möller, Astron. Astrophys., 2018, 614, A123.
16. S. Green, Astrophys. J., 1986, 309, 331–333 Part 1 (ISSN 0004-637X).
17. M. Ben Khalifa, P. J. Dagdigian and J. Loreau, J. Phys. Chem. A, 2022, 126, 9658–9666.
18. M. Ben Khalifa, P. J. Dagdigian and J. Loreau, Mon. Not. R. Astron. Soc., 2023, 523, 2577–2586.
19. M. B. Khalifa, E. Quintas-Sánchez, R. Dawes, K. Hammami and L. Wiesenfeld, Phys. Chem. Chem. Phys., 2020, 22, 17494–17502.
20. M. Ben Khalifa and J. Loreau, Mon. Not. R. Astron. Soc., 2021, 508, 1908–1914.
21. S. Demes, F. Lique, A. Faure and C. Rist, J. Chem. Phys., 2020, 153(9), 094301.
22. T. Stoecklin, O. Denis-Alpizar, A. Clergerie, P. Halvick, A. Faure and Y. Scribano, J. Phys. Chem. A, 2019, 123, 5704–5712.
23. J. Loreau and A. van der Avoird, Faraday Discuss., 2024, 251, 249–261.
24. P. Valiron, M. Wernli, A. Faure, L. Wiesenfeld, C. Rist, S. Kedžuch and J. Noga, J. Chem. Phys., 2008, 129, 134306.
25. M. B. Khalifa, L. Wiesenfeld and K. Hammami, Phys. Chem. Chem. Phys., 2019, 21, 9996–10002.
26. M. Le Guennec, G. Wlodarczak, J. Burie and J. Demaison, J. Mol. Spectrosc., 1992, 154, 305–323.
27. H. J. Werner, et al., MOLPRO, version 2015.1., A Package of ab initio Programs, 2015.
28. P. J. Knowles and H.-J. Werner, Chem. Phys. Lett., 1985, 115, 259–267.
29. K. A. Peterson, D. E. Woon and T. H. Dunning Jr, J. Chem. Phys., 1994, 100, 7410–7415.
30. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566.
31. P. J. Knowles, C. Hampel and H.-J. Werner, J. Chem. Phys., 2000, 112, 3106–3107.
32. G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104.
33. S. Maret, A. Faure, E. Scifoni and L. Wiesenfeld, Mon. Not. R. Astron. Soc., 2009, 399, 425.
34. T. R. Phillips, S. Maluendes and S. Green, J. Chem. Phys., 1995, 102, 6024–6031.
35. H. S. Müller, B. J. Drouin and J. C. Pearson, Astron. Astrophys., 2009, 506, 1487–1499.
36. J. M. Hutson and C. R. Le Sueur, Comput. Phys. Commun., 2019, 241, 9–18.
37. A. Offer and D. R. Flower, J. Phys. B: At., Mol. Opt. Phys., 1989, 22, L439.
38. C. Rist, M. H. Alexander and P. Valiron, J. Chem. Phys., 1993, 98, 4662–4671.
39. A. M. Arthurs and A. Dalgarno, Proc. R. Soc. London, Ser. A, 1960, 256, 540–551.
40. D. Manolopoulos, J. Chem. Phys., 1986, 85, 6425–6429.
41. Q. Ma, A. van der Avoird, J. Loreau, M. Alexander, S. Y. T. van de Meerakker and P. J. Dagdigian, J. Chem. Phys., 2015, 143, 044312.
42. P. J. Dagdigian, Mon. Not. R. Astron. Soc., 2023, 527, 2209–2213.
43. S. Demes, F. Lique, J. Loreau and A. Faure, Mon. Not. R. Astron. Soc., 2023, 524, 2368–2378.

---