Experimental unified pH scale in 1,2-dichloroethane

Abstract

Experimental potentiometric unified pH (pH_abs) scale is presented in 1,2-dichloroethane (1,2-DCE). The scale was compiled using differential potentiometric measurements, carried out by pair-wise comparisons between solutions. Aqueous standard buffer solutions were used as anchor points, so that the obtained pH values are linked to (i.e., are traceable to) the conventional aqueous pH scale and are expressed as values. They are directly comparable to pH values in water in terms of the chemical potential of the solvated proton. The “ladder” approach was used for data analysis and 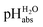values were assigned to 19 solutions in 1,2-DCE, leading to a scale spanning from −2.9 to 11.0. This is the first time that successful potentiometric measurements have been carried out in a solvent of as low polarity as 1,2-DCE. The whole set of measurements, comprising a total of 85 ΔpH_abs values, has a consistency standard deviation of 0.17 pH units. This is higher compared to the consistency standard deviations reported in the literature for similar measurements in other solvents and reflects the experimental difficulties with potentiometric measurements in a low-polarity solvent. This result means that potentiometric measurement of values is possible in low-polarity solvents, and it is thus expected that potentiometric measurement is possible in most organic solvents, opening the possibility of experimentally connecting many solvents into the unified scale.

---

1. Introduction

The quantity pH is defined in terms of the activity of hydrogen (H⁺) ions in aqueous solutions.¹ Because the measured potential is linked to the activity of ions of interest in the solution via the Nernst equation, pH measurement is usually performed using potentiometry. The primary measurement method of pH uses a hydrogen gas electrode that serves as the H⁺ ion indicator electrode to assign pH values to reference solutions (e.g., certified reference materials). Routine pH measurements performed in the laboratory are the secondary way of measuring pH by using glass electrodes that are highly sensitive to H⁺ ions against a reference electrode.¹

In dilute aqueous solutions pH measurement is typically straightforward. However it becomes challenging and less reliable, when the acid concentration increases and especially if non-aqueous solvents or solvent mixtures are employed.^2–4 The standard state of the conventional pH scale in a solvent is linked to the concentration of the H⁺ ions in that solvent. However, the H⁺ ions are solvated differently depending on the nature of the solvent.^5,6 This means that the thermodynamic activity (chemical potential) of the solvated H⁺ ions at the same concentration in different solvents can be very different. As a result, each solvent possesses its own unique pH scale,⁴ which means that it is impossible to compare the conventional pH values measured in different solvents. For example, measuring a pH 7.0 in water means the solution is neutral while, in acetonitrile, a pH 7.0 solution is (strongly) acidic.⁷

The recently introduced unified pH (pH_abs) scale solves the problem of non-comparability of pH values between different solvents. The pH_abs scale uses an ideal proton (hydrogen) gas at 1 bar and 298.15 K as a reference point for the absolute standard chemical potential of the proton for all media. Its value is arbitrarily set to zero, because “ideal” suggests that no interaction occur between protons and any other species.⁸ When immersed in a solution, the chemical potential of a proton changes (becomes negative) as it interacts with its environment.

Direct pH_abs measurements against the proton gas at standard state conditions is not possible. Thus, an experimentally accessible reference is needed. The most convenient reference is the conventional aqueous pH scale. When pH_abs measurements are referenced to the aqueous pH values they can be denoted as values. This means that the chemical potential of the solvated proton in any solution with a certain 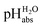value is equal to the chemical potential of the solvated proton in an aqueous solution with the same conventional pH value. Unified acidities can be measured by comparing the pH values of two solutions using differential potentiometry, a method in which the potential difference between two glass electrodes submerged in two different solutions is measured.⁹ Linking the measured values to the aqueous pH scale as the reference is achieved by comparing the pH_abs of unknown solutions to the pH of the aqueous standard buffer solutions.

Using 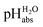for the comparison of solution acidity between different media will lead to a better understanding of how pH influences processes in catalysis, liquid chromatography, sustainable energetics, and the rationalization of acid–base processes in different solvents. These advantages would be especially evident in solvents with low polarity where pH scales have not been established. There are several reasons why it is valuable to study strong acids in solvents of low polarity. One of them is that it allows for the investigation of compounds’ behaviour in an environment that exerts less influence on their physical and chemical properties as compared to polar solvents. Moreover, it enables to mimic real processes in chemical and pharmaceutical industries, which are to a large extent carried out in non-polar media.^10–12 Low-polarity solvents have weak ability of solvating ions, including the H⁺ and therefore, the highest acidities should be achievable in such solvents.^13,14 1,2-dichloroethane (1,2-DCE) is an inert low-polarity solvent with negligible basicity. Despite its low polarity, 1,2-DCE has a high polarity for a chloroalkane (relative permittivity, ε_r = 10.36).¹⁵ This polarity, together with overall good solvating ability of 1,2-DCE is sufficient to dissolve many polar and ionic compounds at measurable concentrations, making it a suitable solvent for studying acids and superacids.¹⁴

In the past, pK_a (and linked to them also pH_abs) measurements of acids in 1,2-DCE were performed using UV-vis spectrophotometric titration.^13,14 The pK_a scale in 1,2-DCE is relative, meaning that the pK_a values have been measured against a reference acid (picric acid with pK_a arbitrarily taken as 0), not against the protonated solvent, and a direct experimental comparison of the actual acidities (in terms of H⁺ activity) of solutions using potentiometric approach has not been performed in 1,2-DCE or any other low-polarity solvents. Thus, this study aimed to measure the pH_abs of acidic buffer solutions prepared in 1,2-DCE using differential potentiometry and to establish a connection between the obtained pH_abs values and the conventional aqueous pH scale, allowing direct comparison in terms of the chemical potential of the solvated proton.

2. Experimental

2.1. Chemicals

1,2-Dichloroethane (1,2-DCE) was of analytical grade and was dried with 3 Å or 4 Å molecular sieves for at least 24 h to reduce the water content down to less than 5 ppm. Phosphazene base P1-t-Bu-tris(tetramethylene) (98%), triflic acid (TfOH, 99%), picric acid (≥98%), styphnic acid (≥98%), bromothymol blue (≥98%), bromocresol green (≥98%), tetraethylammonium chloride (Et₄NCl, ≥99%, dried under vacuum prior to usage), tetrabutylammonium nitrate (Bu₄NNO₃, ≥99%), tetrabutyl-ammonium hydrogen sulfate (Bu₄NHSO₄, ≥99%), ammonium formate (≥99%), ethanol (absolute, ≥99.8%), acetonitrile (≥99%) and the ionic liquid, triethylpentylammonium bis(trifluoromethanesulfonyl)imide ([N₂₂₂₅][NTf₂], 99%) were sourced commercially. The remaining compounds used in this study were the same as in previously published works.^13,16

2.2. Experimental setup

Two types of setups were used, differing by the configuration of the salt bridge (Fig. 1). The first setup included two half-cells connected at the bottom by a capillary tube which served as the salt bridge. The salt bridge electrolyte was first dispensed in the capillary tube before adding the solutions in the half-cells for the measurement. The second setup had its salt bridge separate from the half-cells. The salt bridge is made of glass with ends fitted with PEEK capillary tubes with internal diameter 0.13 mm to ensure slow release of the salt bridge ionic liquid to the half-cells. Both setups had large and small versions as shown in Fig. 2.

Fig. 1 Diagram of the salt bridge setups.

Fig. 2 Different salt bridge setups tested for the measurement of solutions in 1,2-DCE.

The differential potentiometry setup corresponds to electrochemical cell (1):

glass electrode 2|solution 2‖[N₂₂₂₅][NTf₂]‖solution 1|glass electrode 1 (1)

The ionic liquid, [N₂₂₂₅][NTf₂], serves as the salt bridge electrolyte in the setup. [N₂₂₂₅][NTf₂] has been found to be a suitable salt bridge electrolyte because it can cancel the liquid junction potentials at both ends of the salt bridge due to its near identical diffusion and solvation properties of the anion and cation.¹⁷

Metal solid contact glass electrodes were the same as used in ref. 18. Standard aqueous pH buffers (pH 4.01, 7.00, 10.01) with uncertainty of 0.02 pH unit from Mettler Toledo were used in the calibration of the glass electrodes. A Radiometer K401 saturated calomel reference electrode was used as a reference electrode in calibration measurements. Using aqueous solutions is in this case acceptable because the differential potentiometry measurements utilize only the slopes of the electrodes that are not expected to differ between different solvents.³ The potential difference between the glass electrodes immersed in the solutions was measured using an electrometer/high resistance meter (Keysight B2987A, California, USA) controlled by the Quick IV Measurement Software.

Preparation of solutions and all measurements involving 1,2-DCE solutions were carried out in an argon-filled glove box. The atmosphere inside the glove box was kept at a temperature of (25.0 ± 0.2) °C, with a moisture content of less than 0.1 ppm.

2.3. Preparation of equimolar buffer solutions in 1,2-DCE

The solutions prepared in 1,2-DCE were nearly equimolar buffer solutions, where the molarity of the acid and its anion are approximately the same. The compounds were selected based on their pK_a values in 1,2-DCE from a previous published data.^13,14

A 0.667 mM solution of each compound, the free acid (with most compounds) or its salt (with HCl, HNO₃ and H₂SO₄), was prepared with a total volume of 40 mL. The process began by accurately weighing the appropriate amount of each compound into a 4 mL glass vial. The compound was then dissolved by adding 3 mL of 1,2-DCE to the vial and transferred to a reagent bottle. The vial was rinsed four times with additional 3 mL of 1,2-DCE to achieve a cumulative volume of 15 mL. Then, 4.16 mg of phosphazene base P1-t-Bu-tris(tetramethylene) or 2.00 mg of triflic acid, depending on the compound used, was weighed and dissolved similarly with 3 mL of 1,2-DCE, repeated five times before transferring the solution to the reagent bottle containing the compound. Finally, an additional 10 mL 1,2-DCE was added to bring the total volume of the solution to 40 mL and the molar concentrations of the acid and its salt approximately 0.333 mM. The compounds used as free acids (most compounds) were mixed with the phosphazene base while the compounds used as salts of acids (Et₄NCl, Bu₄NNO₃ and Bu₄NHSO₄) were mixed with triflic acid to obtain solutions with nearly equal concentrations of the acid and its anion. The resulting buffer solutions were expected to be approximately equimolar and thus have pH values near the pK_a values of the acids. Solutions with remaining undissolved salts were left overnight in the glove box before being used to achieve complete dissolution.

2.4. Differential potentiometric measurements

In the case of setup 1, approximately 200 μL of the [N₂₂₂₅][NTf₂] ionic liquid was carefully transferred to the capillary tube. Care was taken to avoid bubbles inside the capillary, and the ionic liquid was safely secured by glass beads resting on each of the tube openings (see photo in Fig. 2). Bubbles in the capillary led to unstable potential readings. The glass beads prevented the ionic liquid from leaking into the solutions. In the case of setup 2, the ionic liquid was added when necessary. Around 6 mL to 10 mL of each solution was added to each half-cell depending on the setup used. In the case of setup 1, it was important to add the solutions to the half-cells simultaneously to prevent the ionic liquid from flowing out of the capillary. The electrochemical cell containing the solutions was then placed inside a Faraday cage to prevent electromagnetic interference during potential measurements. Thereafter, the glass electrodes were placed carefully in each cell.

The potential difference values were recorded at an interval of 10 seconds for at least an hour or as long as needed to observe stable readings. The selection of the time interval for data analysis was based on extended measurements, aiming to achieve a duration where the reading exhibited the best possible stability. The most stable 15-minute data was utilized, and the data points within this timeframe were averaged. The criteria of suitability were standard deviation of the readings less than 1 mV, and the slope or drift should be at most 4 mV h⁻¹.

2.5. Development of pH_abs scale in 1,2-DCE

The measured average potential difference is divided by the average slope of the glass electrodes to obtain the ΔpH_abs values between solutions and these values were used to build the ladder. The “ladder approach” was used to get the assigned pH_abs for the solutions from the directly measured ΔpH_abs values. Least-squares minimization was performed using Microsoft Excel's solver function to minimize the sum of squares of the difference between the assigned values and the experimental values.⁹

Directly measuring the pH of 1,2-DCE solutions against standard pH buffers is challenging because water contamination on the non-aqueous solutions could significantly change the pH of the solutions. Thus, “bridging solutions” were used to link the 1,2-DCE scale to the conventional pH scale. The two bridging solutions were 10 mM ammonium formate solution in absolute ethanol and acetonitrile/pH 4 formate (60 : 40) solution with reported values of 8.88⁷ and 5.98,¹⁸ respectively. These bridging solutions were selected based on their known 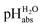values and their suitability for use inside the glove box. These solutions were then both measured against 1,2-DCE solutions inside the glove box and against standard pH buffer solutions (outside of the glove box). The assigned 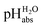values of the 1,2-DCE solutions were then obtained by performing the least-squares minimization and setting the standard pH buffers (4.01, 7.00 and 10.01) as anchor points, as explained in ref. 9.

3. Results and discussion

3.1. Optimization of cell setup

The electrochemical setup used for the measurement was previously used for polar organic solvents like ethanol, methanol and acetonitrile and their mixtures with water.^2,18 The 1,2-DCE solvent used in this work is characterized with very low water content and non-polar properties. It is the first time to measure the in a solvent of this low polarity using potentiometric method, thus, it required some changes to the setup to facilitate better measurement of pH in the new medium.

Two setups with altogether four different salt bridge (SB) configurations were investigated for measurement (Fig. 2). SB1 was the larger version of the first setup where the salt bridge is built-in with the half-cells. When performing measurements using this setup, no stable readings could be recorded. [N₂₂₂₅][NTf₂] was found to be highly miscible with 1,2-DCE and it was difficult to prevent the mixing of the ionic liquid and solutions while the measurement was on-going. This problem was also observed in the study of Heering et al.¹⁸ When solutions containing high amounts of organic solvent were measured, it was observed that: (1) no distinct liquid junction formed or (2) there were visible droplets in the junction region. Some of the measured 1,2-DCE solutions were yellowish in color and during the measurements, the salt bridge electrolyte also turned yellowish. High drift was observed in those measurements. As a result, setup SB1 was considered unsuitable for obtaining reliable results.

While measurements with setup SB1 encountered significant challenges, such as occasional absence of clear liquid junction and uncontrollable mixing of the ionic liquid with the solutions, SB2 employed an alternative approach. In this smaller version of the first setup, glass beads were placed at the bottom of the half-cells to slow the mixing process. As a result, stable results were obtained. However, careful handling of the electrochemical cell was still necessary. Even slight disturbance could dislodge the glass beads off from their positions at the bottom of the half cells and lead to unstable readings during the measurements. Moreover, even with extended measurement duration it was often impossible to obtain stable reading. Instead, the reading initially stabilized but then began to drift, indicating an interaction between the solution and the salt bridge electrolyte. SB2 was therefore also considered unsuitable for this work.

Given the challenges of getting stable measurements with setup 1, a second configuration, with SB3 and SB4, was introduced (Fig. 2). Unlike SB1 and SB2, where the built-in salt bridge connected the half-cells from the bottom, SB3 and SB4 employed a separate salt bridge with endings fitted with PEEK capillary tubes (0.13 mm internal diameter). The capillary tube endings are immersed in each half-cell ensuring an electrochemical connection during potentiometric analysis. The ionic liquid in this setup flows out very slowly, ensuring that the salt bridge always contains fresh ionic liquid.

SB3 featured an H-shaped salt bridge, similar to the one used in the study of ideal ionic liquid salt bridge electrolyte by Ermantraut et al. (2018).¹⁷ However, a drawback of this setup is that the salt bridge releases the ionic liquid too rapidly. Since it was originally designed for a system that uses larger volumes of solutions, the use of smaller volume of solution in this study leads to a relatively high rate of release of the salt bridge electrolyte into the half-cells. To address this, a similar smaller ∩-shaped salt bridge connection (SB4, Fig. 2) was implemented instead. Setup 2 with SB4 enabled faster switching between measurements, used less ionic liquid and yielded more stable measurement results, both in terms of standard deviation and drift. The measurements with this setup can be extended to five hours as demonstrated in this study to obtain stable reading without sudden drift changes. The majority of the measurements in this study were conducted using the SB4 setup. Some measurements were made with SB2 and SB3.

3.2. pH_abs measurement results in 1,2-DCE solutions

The values of 19 different acidic buffer solutions in 1,2-DCE were determined using differential potentiometry. Out of the 215 potentiometric measurement series, 96 met the predefined quality criteria: a standard deviation of less than 1 mV and a drift of less than 4 mV h⁻¹ during at least 15 minutes. In addition, ΔpH_abs values from 11 of the measurement series passing the standard deviation and drift criteria were additionally removed because they resulted in ΔpH_abs values that deviated by 0.4 or more pH units from the difference of the values of their respective solution pairs. The removal process was carried out one at a time after every least-squares minimization, starting with the largest deviations, to ensure that only true outliers were eliminated. These outliers might be due to a “potential locking” phenomenon that we have observed with our setup on different occasions, especially when measuring in non-aqueous solvents under the conditions of low conductivity. Under such conditions the measurement system occasionally “locks into” a potential difference that is seemingly stable but is in fact noise and does not correspond to the actual potential difference in the system. The situation is worsened in the case the glass electrodes have high impedance and if the connection cables (even though well shielded) are long. The best remedy against this that we have found is performing multiple overlapping ΔpH_abs measurements and setting he quality control criteria described above for eliminating such measurements that are likely to be incorrect.

Fig. 3 shows the 1,2-DCE pH_abs ladder and the assigned 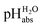values for the 19 acid compounds. After applying the least squares minimization, the consistency standard deviation of the pH ladder is used to evaluate the precision of the measured ΔpH_abs values and the assigned values. For the whole set of measurements, the overall consistency standard deviation is 0.17 pH units. This is higher compared to the values reported in literature for similar measurements. As an example, for the pH_abs measurements of mobile phases, the consistency standard deviations of 0.14 pH units³ and 0.09 pH units¹⁸ have been obtained. The higher consistency standard deviation is most likely due to the difficulty in getting stable and consistent measurement readings in 1,2-DCE.

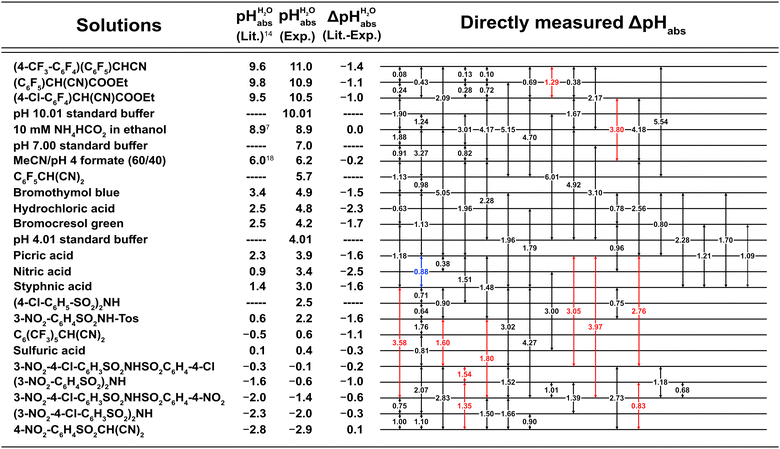Fig. 3 scale of solutions in 1,2-DCE and comparison against reported values in the literature.^7,14,18 Acid were used as equimolar buffer solutions of the acid and its salt at 0.333 mM concentration (see the Experimental). Black arrows were used for the 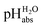assignment, red arrows were left out due to systematic deviations (see the text) and the blue arrow denotes the average of the picric acid-styphnic acid measurement series (altogether 14 series) as quality control system.

Altogether 14 ΔpH_abs measurement series were performed between the buffer solutions of picric acid and styphnic acid for quality control and validation. Both compounds were available in large quantities and are stable in 1,2-DCE solvent. The pH_abs difference of their buffer solutions 0.9 is neither too large nor too small, which makes them suitable for quality control solutions. The ΔpH_abs results from the measurement series of the picric acid-styphnic pair ranged from 0.68 to 1.21 pH units with a mean value of 0.88 and standard deviation 0.13. This result is significant and reflects the robustness and reliability of the data, as the measurements were conducted consistently over a period of more than a year.

3.3. Comparison with the previously obtained values

The assigned values from this study were compared to those previously published by Paenurk et al.,¹⁴ as illustrated in Fig. 3. The values from the current study are generally higher, on an average by 1.05 pH units, with a maximum difference of 2.47 pH units. Additionally, the differences between the values from this work and Paenurk et al.¹⁴ are not constant and no clear trend was identified in the discrepancies between the two sets of values. Several factors may account for the discrepancies.

The reported 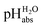values from literature¹⁴ were obtained from a spectrophotometrically measured pK_a ladder which thereafter was anchored to the computational 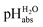value of the equimolar buffer solution of (CF₃SO₂)₂NH and its salt. The values of this work have been anchored to the experimental pH values of aqueous buffer solutions. Thus, the average systematic difference of 1.05 pH units can be considered a very good agreement, given how different are the origins of the values.

In contrast to the absolute values, the differences between the buffer solutions in this work and in the literature¹⁴ are expected to be similar, as in both cases the values are experimental. This is, however, not the case. The differences vary and occasionally even the order of compounds varies. We can think of three factors contributing to this situation.

First, among the challenges when working with very low polarity solvents is their weak ability to solvate ions. In 1,2-DCE, the acids do not simply dissociate. Instead, the effects of ion–ion interactions, such as ion-pairing and aggregation, are significant.¹⁴ Aggregation is especially favoured if small ions are involved. This is illustrated by the fact that HNO₃, H₂SO₄, and HCl buffer solutions in 1,2-DCE exhibit the highest relative discrepancies between this work and the literature.¹⁴

The second contributing factor, connected with the previous, is the use of varying compound concentrations. The previous study used concentrations in the range of n × 10⁻⁵ M, whereas this study employed concentrations 7 × 10⁻⁴ M, which makes the solutions in this study approximately 10 times more concentrated than those in Paenurk's work.¹⁴ Higher concentrations in solutions can lead to increase in ion–ion interactions, e.g. formation of higher aggregates than ion pairs, and certainly have influence on the acidity of the solution. Thus, the actual state of the ions in the solution is not necessarily the same in this work and in the work of Paenurk et al.¹⁴

Third, the ionic liquid [N₂₂₂₅][NTf₂] has been tested for its ability to eliminate the liquid junction potential in a number of solvents but only relatively polar ones, such as water, acetonitrile and methanol. We assume that when measuring potential difference between dilute solutions (7 × 10⁻⁴ M) in the same solution then, given that the ionic strength of [N₂₂₂₅][NTf₂] is 3.2 M and ionicity 0.95,¹⁹ the liquid junction potential should be largely eliminated. Nevertheless, the ability of [N₂₂₂₅][NTf₂] to eliminate the liquid junction potential in low-polarity solvents like 1,2-DCE has not been directly investigated.

Conclusions

Measurement of values of solutions in low-polarity solvent, 1,2-DCE, was successfully performed using differential potentiometry. Based on 85 relative potentiometric measurements, values were assigned to 19 solutions in 1,2-DCE ranging from −2.95 to 11.03. This research highlighted the importance of the design of the potentiometric setup to ensure stable and reliable results. The assigned values in this study were generally higher than those reported in the literature with no detectable trend in the discrepancies. These differences likely result from the weak ion solvating ability of 1,2-DCE, variations in solution concentrations, and the measurement method employed (as opposed to computations used in previous work). Moreover, the ionic liquid used in this study has not been investigated for its ability to eliminate the liquid junction potential in low-polarity solvents like 1,2-DCE. Despite these challenges, the results indicate that potentiometric pH measurement is feasible in low-polarity solvents, paving the way for experimentally integrating many other solvents into the unified pH_abs scale.

Author contributions

J. P. Samin: methodology, writing – original draft preparation, investigation, formal analysis, writing – review & editing; A. Heering: conceptualization, resources, supervision, formal analysis, writing – review & editing; J. Saame: methodology, investigation; A. Kütt: resources, writing – review & editing; I. Leito: conceptualization, resources, formal analysis, supervision, writing – review & editing, funding acquisition.

Data availability

Data for this article are available at DataDOI at https://doi.org/10.23673/re-493.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the Estonian Ministry of Education and Research (TK210) and by the Estonian Research Council grant PRG690. This work was carried out using the instrumentation at the Estonian Center of Analytical Chemistry (TT4, https://www.akki.ee).

Notes and references

1. R. P. Buck, S. Rondinini, A. K. Covington, F. G. K. Baucke, C. M. A. Brett, M. F. Camoes, M. J. T. Milton, T. Mussini, R. Naumann, K. W. Pratt, P. Spitzer and G. S. Wilson, Pure Appl. Chem., 2002, 74, 2169–2200.
2. L. Deleebeeck, A. Snedden, D. Nagy, Z. Szilágyi Nagyné, M. Roziková, M. Vičarová, A. Heering, F. Bastkowski, I. Leito, R. Quendera, V. Cabral and D. Stoica, Sensors, 2021, 21, 3935.
3. A. Suu, L. Jalukse, J. Liigand, A. Kruve, D. Himmel, I. Krossing, M. Rosés and I. Leito, Anal. Chem., 2015, 87, 2623–2630.
4. K. Izutsu, Electrochemistry in Nonaqueous Solutions, Wiley, 1st edn, 2002.
5. G. A. Olah, G. K. Surya Prakash, Á. Molnár and J. Sommer, Superacid Chemistry, Wiley, 1st edn, 2009.
6. Y. Marcus, M. J. Kamlet and R. W. Taft, J. Phys. Chem., 1988, 92, 3613–3622.
7. A. Heering, F. Bastkowski and S. Seitz, J. Sens. Sens. Syst., 2020, 9, 383–389.
8. D. Himmel, S. K. Goll, I. Leito and I. Krossing, Angew. Chem., Int. Ed., 2010, 49, 6885–6888.
9. A. Heering, D. Stoica, F. Camões, B. Anes, D. Nagy, Z. Nagyné Szilágyi, R. Quendera, L. Ribeiro, F. Bastkowski, R. Born, J. Nerut, J. Saame, S. Lainela, L. Liv, E. Uysal, M. Roziková, M. Vičarová, A. Snedden, L. Deleebeeck, V. Radtke, I. Krossing and I. Leito, Symmetry, 2020, 12, 1150.
10. C. Jimenez-Gonzalez, Curr. Opin. Green Sustainable Chem., 2019, 18, 66–71.
11. M. González-Miquel and I. Díaz, Curr. Opin. Green Sustainable Chem., 2021, 29, 100469.
12. European Environment Agency, 2023.
13. A. Kütt, T. Rodima, J. Saame, E. Raamat, V. Mäemets, I. Kaljurand, I. A. Koppel, R. Yu. Garlyauskayte, Y. L. Yagupolskii, L. M. Yagupolskii, E. Bernhardt, H. Willner and I. Leito, J. Org. Chem., 2011, 76, 391–395.
14. E. Paenurk, K. Kaupmees, D. Himmel, A. Kütt, I. Kaljurand, I. A. Koppel, I. Krossing and I. Leito, Chem. Sci., 2017, 8, 6964–6973.
15. C. Reichardt and T. Welton, Solvents and solvent effects in organic chemistry, Wiley-VCH, Weinheim, Germany, 4th edn, 2011.
16. I. Leito, E. Raamat, A. Kütt, J. Saame, K. Kipper, I. A. Koppel, I. Koppel, M. Zhang, M. Mishima, L. M. Yagupolskii, R. Y. Garlyauskayte and A. A. Filatov, J. Phys. Chem. A, 2009, 113, 8421–8424.
17. A. Ermantraut, V. Radtke, N. Gebel, D. Himmel, T. Koslowski, I. Leito and I. Krossing, Angew. Chem., Int. Ed., 2018, 57, 2348–2352.
18. A. Heering, M. Lahe, M. Vilbaste, J. Saame, J. P. Samin and I. Leito, Analyst, 2024, 149, 1481–1488.
19. A. Rupp, N. Roznyatovskaya, H. Scherer, W. Beichel, P. Klose, C. Sturm, A. Hoffmann, J. Tübke, T. Koslowski and I. Krossing, Chem. – Eur. J., 2014, 20, 9794–9804.

---