Open Access Article
Open Access ArticleDetermination of the rotational isomerization rate along carbon–carbon single bonds in solution†
Seongchul
Park
ab,
Hojeong
Yoon
b,
Juhyang
Shin
b and
Manho
Lim
 *b
*b
aKorea Institute for Future Earth, Pusan National University, Busan 46241, Korea
bDepartment of Chemistry and Chemistry Institute for Functional Materials, Pusan National University, Busan 46241, Korea. E-mail: mhlim@pusan.ac.kr; Tel: +82 51 510 2243
First published on 28th January 2025
Abstract
The temperature- and viscosity-dependent rotational isomerization time constant (τrot) along the C–C˙ bond of CF2BrCF2 radical in solution was measured using femtosecond infrared spectroscopy after photodissociating the I atom from CF2BrCF2I. Three density functional theory (DFT) functionals, ωB97XD, APFD, and B3LYP were used with the aug-cc-pVTZ basis set to calculate the required parameters in calculating τrot using Kramers’ theory of reaction rates. The measured τrot was consistent with the value calculated using the vibrational frequencies and rotational barriers of the related compounds calculated by DFT method with ωB97XD/aug-cc-pVTZ. Kramers’ theory calculation of τrot was further verified by an experimental measurement for CF3CF2CF2˙ in CCl4 at 293 K. The τrot along the C–C(˙) bond of ethyl radical and ethane derivatives in solution can be reliably estimated by Kramers’ theory combined with DFT calculations using the ωB97XD functional and aug-cc-pVTZ basis set.
Introduction
Rotation along the C–C bond of a 1,2-disubstituted ethane derivative exchanges between relatively stable gauche and anti (trans) conformations, resulting in rotational isomers.1,2 Rotational isomerization can influence the reactivity, dynamics, and biological activity of the related isomers.3,4 Although the isomerization rate is an important factor describing reactions involving the isomer, it is rarely measured at room temperature because the rotation is ultrafast and difficult to measure. The rotational isomerization of a reaction intermediate, which may be more important for reactions involving the intermediate, is even harder to measure due to its short lifetime and fast rotation.4The anti–gauche isomerization of n-butane is one of the simplest first-order chemical reactions and has thus been used as a model system for chemical reaction kinetics theory and molecular dynamics (MD) simulation studies of condensed phases.5–10 Extensive theoretical studies reported that the isomerization time of n-butane in liquid is tens of picoseconds at room temperature.5–10 However, no experimental confirmation of these theoretical results has been presented to date. Zheng et al. obtained the isomerization time of CH2FCH2NCO in CCl4 at room temperature using 2D infrared (IR) vibrational echo spectroscopy.3,4 Isomerization time constants of 40 (12) ps for n-butane (ethane) were estimated under the same conditions using the experimentally obtained values combined with the density functional theory (DFT) calculations of the barrier heights of the related compounds.3,4 However, it was concluded that CH2FCH2NCO is not a good reference compound for estimating the rotational time of other ethyl derivatives because the calculations could not reproduce even the equilibrium isomer population of CH2FCH2NCO.4
Recently we measured the rotational isomerization time constant (τrot) of the C–C˙ bond of CF2BrCF2 radical in CCl4 solution at 280 K.4 Excess gauche CF2BrCF2 radicals (g-CF2BrCF2˙) were produced upon ultrafast dissociation of I atoms from the excited CF2BrCF2I in CCl4 at 267 nm. The τrot was determined by probing that the excess g-CF2BrCF2˙ isomerizes into anti CF2BrCF2 radicals (a-CF2BrCF2˙) using the structure-specific femtosecond infrared spectroscopy. The barrier height of the rotation and the Gibbs free energies of two radical conformers, g-CF2BrCF2˙ and a-CF2BrCF2˙, were calculated using DFT. The calculated energies were then used to obtain the rotational time constants from gauche to anti (τGA) and anti to gauche (τAG), where 1/τrot = 1/τGA + 1/τAG. Based on the measured τrot and DFT calculations of ethyl radical derivatives and ethane derivatives (such as CF2BrCF2˙, CF2ICF2˙, CH3CH2CH˙CH3, CH3CH2˙, CF2BrCF2I, CH2FCH2NCO, CH3CH2CH2CH3, and CH3CH3), the rotation time constants along the C–C(˙) bond of these compounds were estimated under the same conditions. The time constant for the internal rotation was found to be similar to that calculated using transition state theory (TST) with a transmission coefficient (κ) of 0.75. However, it was not clear why κ = 0.75 was required and why the TST developed in the gas phase successfully estimated the rotational time in solution, where the compound is continuously perturbed by the interaction with solvent molecules.
The accuracy of the rotational energy barrier (Erot) is critical to the accurate calculation of the rotational rate because the latter is proportional to exp(−Erot/RT), where R and T are the gas constant and the absolute temperature, respectively. For example, the rotational rate changes by a factor of 2–0.5 at 298 K as Erot changes ±0.4 kcal mol−1. Therefore, calculating accurate energy values for each conformer and the rotational barrier for a compound of interest is one of the most important factors in accurately calculating the rotation rate along the C–C(˙) bond of the compound using the rate equation. As Erot can be experimentally estimated from the temperature-dependent rotational rates, the accuracy of the calculated Erot values can be confirmed experimentally.
TST was developed by H. Eyring to describe reactions in the gas phase11 based on the idea that the reaction proceeds at a rate at which an activated complex passes over the saddle point and assuming equilibrium between the reactants and activated complex.12–14 For reactions in solution, the reactants are continuously disturbed by collisions with solvent molecules. Often, the solvent affects the chemical reaction by changing its potential energy surface (PES).15 This effect is incorporated in TST by using the energies of the reactants and activated complex calculated in solution. Thus, solvent effects are incorporated to a certain degree in the rate constants estimated using the TST (kTST) with energies calculated assuming a solution environment.3,4 However, this approach excludes the dynamical solvent effects on the rate constant, which may impede or enhance molecular motion along the reaction coordinate.12,13 Kramers showed that, based on the Langevin equation with a time-independent frictional coefficient, the dynamical solvent effect is represented by a transmission coefficient that depends on the ratio of the solvent friction and the curvature of the PES at the transition state (i.e., Kramers’ transmission coefficient, κKR) and the rate constant in solution, ks = κKRkTST.13 The Kramers’ theory of reaction rates was further developed using the generalized Langevin equation with a time-dependent solvent friction (Grote–Hynes theory).16 Grote–Hynes theory is expressed as ks = κGHkTST, where κGH is a measure of the departure of the rate constant from kTST. The calculation of κGH requires an MD simulation.13
In energy calculations of a target compound in solution, solvent effects were incorporated using the dielectric constant of the solvent as a parameter.17 The polarity of the solvent, represented by the dielectric constant, is accounted for in the PES of the reaction in solution. Since the viscosity of the solvent represents the friction imposed on the reactant molecule along the reaction coordinate, it is a good parameter for the dynamical solvent effect. Measuring the reaction rates in solvents with various viscosities can reveal dynamical solvent effects that cannot be observed by measuring the rate in solvents with various dielectric constants. Thus, viscosity-dependent rotational time constants are considered useful in evaluating Kramer's theory of reaction rates to explicitly account for frictional forces imposed on the reaction coordinate by the solvent.
In this study, we measured the temperature- and the viscosity-dependent τrot of the C–C˙ bonds of CF2BrCF2 radicals produced by immediate photodissociation of I atoms from CF2BrCF2I in CCl4 solution using time-resolved IR (TRIR) spectroscopy. The energies of the reactants and activated complexes were calculated by DFT using three different functionals to identify a reliable and practical calculation method without using high-level calculations that require heavy computing power. The experimentally measured values were well reproduced by Kramers’ theory with energies calculated by DFT using the ωB97XD functional and aug-cc-pVTZ basis set. These findings were further tested by measuring the τrot of the C–C˙ bonds of CF3CF2CF2˙ after excitation of CF3CF2CF2I in CCl4 at 293 K. The measured τrot of 34 ps is similar to the value of 30 ps calculated using Kramers’ theory based on DFT calculations using ωB97XD/aug-cc-pVTZ.
Experimental details
Time-resolved mid-infrared spectroscopy
The femtosecond TRIR spectrometer used in this study was described in detail previously.4,18,19 Briefly, a femtosecond pulse (800 nm, 110 fs, and 2 kHz) from a Ti:sapphire oscillator/amplifier system was split to pump an optical parametric amplifier (OPA) and a third harmonic generator (THG). The near-IR signal and idler pulses from the OPA were difference-frequency mixed by a GaSe crystal to generate tunable mid-IR pulses (120 fs and spectral width of 160 cm−1). The THG produced a 120 fs, 267 nm pump pulse. A 1 μJ UV pulse was optically advanced relative to the mid-IR probe pulse and used to excite the sample, which was probed by the weak (∼10 nJ) mid-IR probe pulse. The isotropic absorbance was measured by setting the relative polarization of the pump pulse to that of the probe pulse magic angle (54.7°). The experiment was repeated with probe pulses centered at 920 or 940 cm−1 for CF2BrCF2 and 1050, 1130, 1210, 1270, or 1330 cm−1 for CF3CF2CF2˙. The data were combined for broader spectral regions than the spectral width of the probe pulses (160 cm−1). The probe pulses were sent through the sample and detected by 1 × 128 or 1 × 64 pixel MCT array detectors for wavenumbers of >1000 and <1000 cm−1, respectively, with a 320 mm monochromator with a grating of 50, 75, or 100-lines per mm. These settings resulted in a spectral resolution of 1 and 2.7 cm−1 for the spectral regions of >1000 and <1000 cm−1, respectively. The instrument response function was 0.2 ps. To avoid complication arising from the overlap of pump and probe pulses, data were collected starting from 0.3 ps.Sample preparation
CF2BrCF2I and n-hexane were purchased from Alfa Aesar and CF3CF2CF2I, CCl4, and DMF were purchased from Sigma-Aldrich and used without further purification. The flowing sample cell consisted of two 2-mm-thick BaF2 windows and a 100-μm-thick Teflon spacer. A peristaltic tubing pump was used to refresh 50 mM CF2BrCF2I or CF3CF2CF2I in the sample cell fast enough for each probe pulse at a repetition rate of 2 kHz. The sample volume was sufficiently large to maintain the sample concentration above 98% of the initial concentration, even after the photoreaction of the sample by 267-nm excitation. The temperature of the sample was adjusted by passing a coolant through the sample mount block, which maintained the temperature within ±2 K of the set value. Equilibrium UV-vis and FTIR spectra were collected throughout the experiment to ensure the integrity of the sample.Computational details
All quantum chemical calculations were performed using Gaussian 16 software.20,21 The DFT method with three different functionals (ωB97XD,22,23 APFD,24 and B3LYP25) and the aug-cc-pVTZ basis set was used for molecular geometry optimization and calculating the vibrational frequency and energies of the optimized compounds. The ωB97XD functional (the long-range corrected hybrid density functional with damped atom–atom dispersion corrections) has been reported to yield satisfactory accuracy for thermochemistry, kinetics, and non-covalent interactions.22–27 The APFD functional (the Austin–Frisch–Petersson functional with dispersion) was reported to reproduce the relative conformational energies of organic molecules and the accuracy of weak interactions is comparable to that of CCSD(T)/aug-cc-pVTZ.24 The B3LYP functional (the Becke, 3-parameter, Lee–Yang–Parr exchange–correlation functional) is one of the most commonly used hybrid functionals.25 The solvent effects were incorporated into the polarizable continuum model using the integral equation formalism variant. The calculated parameters were used to calculate the rotational rate constant of an interested compounds using Kramers’ theory of reaction rates.Results and discussion
Fig. 1 displays IR spectra of CF2BrCF2I, a-CF2BrCF2˙, and g-CF2BrCF2˙ in CCl4. The equilibrium FTIR spectrum of CF2BrCF2I was collected at room temperature. The spectra of the two radicals were obtained from the previous study on the photodissociation dynamics of CF2BrCF2I in CCl4 at 267 nm.4 Although most of the spectral features of three compounds overlap in the 1400–1050 cm−1 range, the absorption bands in the 1050–850 cm−1 range are significantly different for each compound, enabling these bands to be readily distinguished. Therefore, population changes of the three compounds over time can be easily monitored by observing changes in the 1050–850 cm−1 range of the TRIR spectra.TRIR spectra of CF2BrCF2I in CCl4 at 280, 300, and 310 K were collected in the spectral region of 1050–850 cm−1 from 0.3 to 1000 ps after excitation at 267 nm and representative TRIR spectra are shown in Fig. 2(a). The negative band at 993 cm−1 arises from the population depletion of CF2BrCF2I as I atoms are immediately dissociated upon excitation at 267 nm. The magnitude of this band remained stable over the measurement period, implying that no geminate recombination (GR) of the dissociated pairs within 1 ns. The magnitudes of the two absorption bands near 900 cm−1 changed over time, accompanied by peak narrowing and blue shifts. The blue-shifted and narrowed bands at 943 and 888 cm−1 arise from g-CF2BrCF2˙ and a-CF2BrCF2˙, respectively. The spectral narrowing and blue shifts result from the thermalization of the nascent radicals produced under excess energy with a time constant of 15 ± 3 ps.4 The decay of the 943 cm−1 band and simultaneous intensification of the 888 cm−1 band result from the equilibration of excess g-CF2BrCF2˙ produced during the photodissociation of CF2BrCF2I via the rotational isomerization of the nascent radicals.4 The population of each compound was obtained from the amplitude of the corresponding band once its extinction coefficient was determined. The relative integrated extinction coefficient of the band at 943 cm−1 compared with that at 888 cm−1, estimated from the spectra shown in Fig. 1, is 0.57 ± 0.03. Fig. 3(a) exhibits the changes in the mole fractions of a-CF2BrCF2˙ and g-CF2BrCF2˙ over time, which were determined from the changes in the integrated area of the corresponding bands and the ratio of the integrated extinction coefficients of the bands. As shown in Fig. 3(a), the changes in mole fractions at 280, 300, and 310 K were well described by the interconversion kinetics between two isomers, with time constants of 48, 34, and 30 ps, respectively. These values represent the τrot for the C–C˙ bond of CF2BrCF2˙ in CCl4 at the corresponding temperatures.
 | ||
| Fig. 3 (a) Changes of the mole fractions for g-CF2BrCF2˙ and a-CF2BrCF2˙ produced by the photoexcitation of CF2BrCF2I in CCl4 at 280, 300, and 310 K. Excess g-CF2BrCF2˙ was produced upon photoexcitation at 267 nm and relaxes to equilibrium mole fractions of 0.02–0.03, 0.02–0.04, and 0.03–0.05 at 280, 300, and 310 K, respectively. The equilibrium mole fraction was estimated from the calculated Gibbs free energy differences between two CF2BrCF2˙ isomers in CCl4 at 280, 300, and 310 K using DFT with the aug-cc-pVTZ basis set (Table 1). The changes in the mole fractions (symbols) were well described by the interconversion kinetics between two isomers (solid lines) with time constants of 48, 34, and 30 ps, which are attributed to the τrot values for the C–C˙ bond of CF2BrCF2˙ in CCl4 at 280, 300, and 310 K, respectively. (b) Changes in the mole fractions of g-CF2BrCF2˙ and a-CF2BrCF2˙ under the photoexcitation of CF2BrCF2I in n-hexane and DMF at 293 K. Excess g-CF2BrCF2˙ was produced upon photoexcitation at 267 nm, which relaxes to an equilibrium fraction of 0.02–0.04. This was estimated from the calculated Gibbs free energy differences between two CF2BrCF2˙ isomers in n-hexane and DMF at 293 K using DFT with the aug-cc-pVTZ basis set (Table 1). The changes in the mole fractions (symbols) were well described by the interconversion kinetics between two isomers (solid lines) with time constants of 24 and 35 ps, which are attributed to the τrot values of the C–C˙ bond of CF2BrCF2˙ in n-hexane and DMF at 293 K, respectively. The nascent photoproducts of CF2BrCF2I at 267 nm are ∼18% CF2ICF2˙ and ∼82% CF2BrCF2˙, but we considered only CF2BrCF2˙ in calculating the mole fractions for simplicity. | ||
The excess energy from the photodissociation of vicinal dihaloethanes has been reported to partition roughly equally between internal degrees of freedom and translation.28,29 Given that the excitation energy is 107 kcal mol−1 (267 nm) and the dissociation energy of the C–I bond is 52 kcal mol−1, the internal energy of the nascent CF2BrCF2˙ is approximately 28 kcal mol−1. The partitioning between rotational and vibrational energies remains unknown. Clearly, the dissociation of CF2BrCF2˙ would generate considerable rotational energy, but this excess energy is expected to relax into the surrounding solvent within a few picoseconds. Thus, the rotational isomerization process is unlikely to be significantly affected by the excess energy. The dissociated I atom may remain in the vicinity of CF2BrCF2˙. Due to its bulkiness and polarizability, the presence of the I atom could influence the dielectric environment and mechanical friction of the C–C isomerization process, as well as the Gibbs free energy of the nascent radical. If the I atom remains near the nascent CF2BrCF2 radical, it could geminately rebind with the radical, reverting it to the reactant. However, no GR was observed in the photodissociation of CF2BrCF2I at 267 nm,19 indicating that the dissociated I atom does not stay close enough to interact with CF2BrCF2˙. Therefore, the presence of the dissociated I atom was not considered in the analysis of the C–C isomerization process. While the excess rotational and translational energies of radicals produced from photodissociation dissipate within a few picoseconds, the excess vibrational energy relaxes on the same time scale as the observed rotational isomerization time constants. Although the impact of excess vibrational energy on rotational isomerization remains unclear, it may accelerate the process. Therefore, the experimentally observed rotational time constants represent the lower limit.
| Solvent | Method | Temp. (K) | ΔG (kcal mol−1) | x G (%) |
|---|---|---|---|---|
| CCl4 | ωB97XD | 280 | 2.258 | 3.3 |
| 293 | 2.253 | 4.0 | ||
| 300 | 2.251 | 4.4 | ||
| 310 | 2.247 | 5.0 | ||
| APFD | 280 | 2.586 | 1.9 | |
| 293 | 2.581 | 2.3 | ||
| 300 | 2.578 | 2.6 | ||
| 310 | 2.573 | 3.0 | ||
| B3LYP | 280 | 2.668 | 1.6 | |
| 293 | 2.664 | 2.0 | ||
| 300 | 2.663 | 2.3 | ||
| 310 | 2.659 | 2.6 | ||
| n-Hexane | ωB97XD | 293 | 2.257 | 4.0 |
| APFD | 2.583 | 2.3 | ||
| B3LYP | 2.668 | 2.0 | ||
| DMF | ωB97XD | 293 | 2.224 | 4.2 |
| APFD | 2.560 | 2.4 | ||
| B3LYP | 2.632 | 2.1 | ||
As mentioned above, a solvent can influence a chemical reaction by perturbing the reaction PES. The energies of the reactants and activated complex in solution were calculated by incorporating the dielectric constant of the solvent to represent its contribution.30 To explore the contribution of the solvent viscosity (dynamical solvent effect), comparative measurements of the reaction rates using solvents with different viscosities but the same dielectric constants or the same viscosities but different dielectric constants would be valuable. A good solvent for TRIR spectroscopy under 267-nm excitation should have negligible absorption at 267 nm, a good IR spectral window in the probed spectral region (here, 1050–850 cm−1), and reasonable solubility of the target reactant molecule. n-Hexane and dimethylformamide (DMF) are good solvents for the TRIR spectroscopy of CF2BrCF2I as they satisfy the above-mentioned conditions. In addition, the dielectric constant (ε) of n-hexane (ε = 1.882) is similar to that of CCl4 (ε = 2.228) but its viscosity (0.31 mPa s at 293 K) is about one-third that of CCl4 (0.91 mPa s at 293 K).31 In contrast, the viscosity of DMF (0.86 mPa s at 293 K) is similar to that of CCl4, but its dielectric constant (ε = 37.32) is about 17 times higher than that of CCl4. Therefore, the τrot values of CF2BrCF2˙ were also measured in n-hexane and DMF solutions for comparison.
TRIR spectra of CF2BrCF2I in n-hexane and DMF were collected at 293 K in the spectral region of 1050–850 cm−1 from 0.3 to 1000 ps after excitation at 267 nm. Representative TRIR spectra are shown in Fig. 2(b). The bleach bands arise from the population depletion of CF2BrCF2I and their magnitudes remain constant up to 1 ns, as is the case for the TRIR spectra of CF2BrCF2I in CCl4. Although the absorption bands in n-hexane and DMF are slightly shifted compared to those obtained in CCl4, the spectral evolution is similar to that observed in CCl4, namely the decay of the band near 940 cm−1 and simultaneous growth of the band near 890 cm−1, accompanied by blue shifts and peak narrowing. Therefore, the bands near 940 and 890 cm−1 were assigned to g-CF2BrCF2˙ and a-CF2BrCF2˙, respectively.
The changes in the mole fractions of g-CF2BrCF2˙ and a-CF2BrCF2˙ in n-hexane and DMF were obtained from the time-dependent amplitude changes of the corresponding bands by assuming that their integrated extinction coefficients are the same as those in CCl4. Inaccuracies in the extinction coefficients result in changes in the final equilibrated mole fractions but they do not influence the τrot values, which are the parameters of interest here. As shown in Fig. 3(b), the mole fractions of g-CF2BrCF2˙ and a-CF2BrCF2˙ in n-hexane and DMF at 293 K change simultaneously, and τrot values of 24 and 35 ps, respectively, were determined.
A τrot of 37 ps for CF2BrCF2˙ in CCl4 at 293 K was interpolated from data at 280, 300, and 310 K. Changing the solvent from CCl4 to n-hexane results in a decrease in the viscosity (by a factor of ∼3), and the corresponding τrot decreases by ∼1.5 times. In contrast, the significant difference in the dielectric constants (that of DMF is ∼17 times higher than that of CCl4) has a negligible effect on τrot. Therefore, the τrot of CF2BrCF2˙ is significantly affected by the solvent viscosity but not its dielectric constant. When the charge distribution of the reactant is similar to that in the transition state and/or the polarities of the reactant compounds are small, the PES along the reaction coordinate is not significantly influenced by the polarity of the solvent (i.e., the dielectric constant), and thus has little influence on the rate constant of the reaction.12,13
Kramers expressed the rate constant of a chemical reaction in solution, ks, as follows:12,13
 | (1) |
 ΔrE = ETS − ER.
ΔrE = ETS − ER.
Here, ωTS and ωR are the angular frequencies associated with the reactive mode in the transition state and reactant, respectively, γ is the friction constant of the solvent, M is the reactant mass, η is the viscosity of the solvent, Rh is the hydrodynamic radius of the compound, and ETS and ER are the energies of the transition state and reactant, respectively. Eqn (1) can be further expressed as follows:13
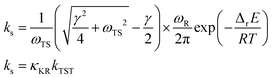 | (2) |
Kramers’ theory of reaction rates shows that ks is described simply as a product of the transmission coefficient, κKR, and the rate constant calculated by conventional TST, kTST. In Kramers’ theory, the dynamical solvent effect is represented by κKR. As ETS and ER are calculated in solution, the static solvent effect is incorporated in kTSTvia ΔrE.
The rotational interconversion rates for the anti-to-gauche (kAG) and gauche-to-anti (kGA) conversions of CF2BrCF2˙ were calculated using Kramers’ theory with the corresponding kTST (kTST,AG and kTST,GA, respectively) and κKR (κAKR, κGKR, respectively) values as follows.
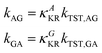 | (3) |
Here, ω and E have the same meanings as in eqn (1), and the subscripts or superscripts G and A indicate the gauche- and anti-states of the isomer, respectively. RAh and RGh represent the hydrodynamic radii of the anti and gauche compounds, respectively. Note that multiplication by the pre-factor of 2 is required in the calculation of kTST,AG as there are two gauche isomers in CF2BrCF2˙.4 The rotational isomerization rate, krot is obtained from the rotational interconversion rates:4
| krot = kAG + kGA | (4) |
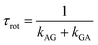 | (5) |
Three different DFT functionals were used to calculate the energies and vibrational frequencies of the target compounds using the aug-cc-pVTZ basis set. Namely, ωB97XD was reported to yield satisfactory accuracy in thermochemical studies,22,23 APFD is reliable for energy calculations,24,26 and B3LYP is one of the most widely used DFT methods.25,27Table 2 shows the τrot values of CF2BrCF2˙ dissolved in various solvents obtained using Kramers’ theory based on the energies and vibrational frequencies calculated using the three DFT functionals. Among the values calculated using the three DFT functionals, although the κKR values are similar and the rotational barriers are within a fraction of a kcal mol−1, the τrot values significantly differ. The ΔETG of CF2BrCF2˙ in CCl4 is smaller than ΔETA by 2.32–2.74 kcal mol−1, resulting in a kGA that is more than 18 times larger than kAG. Therefore, the τrot of CF2BrCF2˙ is dominated by the interconversion time of (kGA)−1, implying that ΔETG is the major influencing factor in the calculation of τrot. The ΔETG values calculated using the three DFT functionals differ marginally, by <0.36 kcal mol−1, which is within the accepted accuracy of energy calculations for general purposes. However, the calculated τrot values for CF2BrCF2˙ in CCl4 differ by up to 1.9 times (see Table 2). As stated earlier, accurate PES values are a prerequisite for accurately calculating rate constants. Although high-level calculations of the PES along the reaction coordinate would be beneficial for the accurate calculation of the rate constants, DFT calculations were used for the sake of practicality, as high-level methods such as CCSD(T) require more time and computing power.
| Solvent31 | Method | Temp. (K) | Viscosity32,33 (mPa s) | ΔETG (kcal mol−1) | ΔETA (kcal mol−1) | κ A KR, κGKR | τ (cal’d)rot (ps) | τ (exp)rot (ps) | |
|---|---|---|---|---|---|---|---|---|---|
| a Interpolated value from data at 280, 300, and 310 K. | |||||||||
| CCl4 (ε = 2.228) | ωB97XD | 280 | 1.13 | 65, 72, 59 | 2.06 | 4.40 | 0.42, 0.38 | 58 | 48 |
| 293 | 0.91 | 0.48, 0.44 | 42 | (37)a | |||||
| 300 | 0.83 | 0.51, 0.47 | 36 | 34 | |||||
| 310 | 0.72 | 0.55, 0.51 | 30 | 30 | |||||
| APFD | 280 | 1.13 | 63, 70, 57 | 1.70 | 4.38 | 0.36, 0.37 | 33 | 48 | |
| 293 | 0.91 | 0.42, 0.43 | 25 | — | |||||
| 300 | 0.83 | 0.45, 0.46 | 21 | 34 | |||||
| 310 | 0.72 | 0.49, 0.50 | 18 | 30 | |||||
| B3LYP | 280 | 1.13 | 64, 71, 57 | 1.87 | 4.61 | 0.41, 0.40 | 44 | 48 | |
| 293 | 0.91 | 0.47, 0.46 | 30 | — | |||||
| 300 | 0.83 | 0.50, 0.50 | 26 | 34 | |||||
| 310 | 0.72 | 0.54, 0.54 | 22 | 30 | |||||
| n-Hexane (ε = 1.882) | ωB97XD | 66, 72, 59 | 2.08 | 4.42 | 0.73, 0.74 | 26 | 23 | ||
| APFD | 293 | 0.31 | 64, 71, 57 | 1.73 | 4.40 | 0.74, 0.74 | 15 | 23 | |
| B3LYP | 64, 71, 56 | 1.89 | 4.63 | 0.74, 0.72 | 20 | 23 | |||
| DMF (ε = 37.22) | ωB97XD | 64, 72, 58 | 1.92 | 4.24 | 0.48, 0.46 | 32 | 35 | ||
| APFD | 293 | 0.86 | 60, 70, 55 | 1.57 | 4.23 | 0.44. 0.47 | 19 | 35 | |
| B3LYP | 61, 71, 56 | 1.72 | 4.43 | 0.45, 0.44 | 25 | 35 | |||
As expected, the κKR values were similar for solvents with similar viscosities, such as CCl4 and DMF. Although the dielectric constant of DMF is 17 times larger than that of CCl4, the rotational energy barriers of CF2BrCF2˙ in these two solvents differ by only 0.13–0.18 kcal mol−1, resulting in similar τrot values in these solvents, i.e., 42 (32), 25 (19), and 30 (25) ps in CCl4 (DMF) at 293 K were calculated using the ωB97XD, APFD, and B3LYP functionals, respectively. The κKR of CF2BrCF2˙ in n-hexane is 1.6–1.7 times larger than that in CCl4, but the rotational energy barriers are similar in n-hexane and CCl4, resulting in smaller τrot values in n-hexane (by a factor of 1.5–1.7). The rotational isomerization of CF2BrCF2˙ in n-hexane was ∼1.6 times faster than that in CCl4 due to the 3 times smaller viscosity of n-hexane than CCl4, resulting in 1.6–1.7 times larger κKR values. The influence of solvent viscosity on C–C˙ bond rotation is significant whereas that of the solvent dielectric constant is negligible, and Kramers’ theory successfully estimated τrot of the C–C˙ bond for CF2BrCF2˙ in solution.
Table 2 shows the temperature-dependent τrot values of the C–C˙ bond for CF2BrCF2˙ in CCl4 and the viscosity-dependent τrot values at 293 K calculated based on the energies and vibrational frequencies of the related compounds using three-different DFT functionals. The experimentally determined τrot values of CF2BrCF2˙ in CCl4 at 280, 300, and 310 K, as well as those in n-hexane and DMF, best match the values obtained based on the DFT calculation using ωB97XD/aug-cc-pVTZ. Although the ωB97XD functional provided the best match with the experimental values, the other functionals used (APFD and B3LYP) also resulted in a reasonable match.
To test the validity of the rate constants calculated by Kramers’ theory, we measured the τrot about the C–C˙ bond of ethyl derivatives other than CF2BrCF2˙ and compared the values with the calculated ones. The equilibrium UV-vis and FTIR spectra of CF3CF2CF2I are given in Fig. 4. This compound is known to dissociate I atoms upon UV excitation34 and the produced radicals are expected to have two rotational conformers, g-CF3CF2CF2˙ and a-CF3CF2CF2˙. TRIR spectra of CF3CF2CF2I in CCl4 at 293 K were collected from 0.3 to 1000 ps in the spectral region of 1400–1000 cm−1 after excitation at 267 nm and representative TRIR spectra are shown in the lower panel of Fig. 5. Although congested, the TRIR spectra were expected to include contributions from three compounds: the reactant (CF3CF2CF2I) and two photoproducts (g-CF3CF2CF2˙ and a-CF3CF2CF2˙). The TRIR spectra were globally fitted using three basis spectra: equilibrium CF3CF2CF2I spectrum, and spectra of g-CF3CF2CF2˙ and a-CF3CF2CF2˙. The negative peaks were reproduced by inverting the equilibrium spectrum of CF3CF2CF2I. New absorption features were recovered by summing the two spectra assigned to g-CF3CF2CF2˙ and a-CF3CF2CF2˙ with the help of the vibrational frequencies calculated by DFT using ωB97XD/aug-cc-pVTZ. The lower panel of Fig. 5 shows that the TRIR spectra are reproduced well by the sum of the three basis spectra shown in the upper panel of Fig. 5.
Time-dependent amplitude changes of the basis spectra for g-CF3CF2CF2˙ and a-CF3CF2CF2˙ were obtained from global fitting, as shown in Fig. 6. The amplitude changes demonstrate that the fraction of a-CF3CF2CF2˙ decreases while that of g-CF3CF2CF2˙ increases simultaneously, indicating that excess a-CF3CF2CF2˙ produced upon photodissociation of CF3CF2CF2I rotationally isomerizes into g-CF3CF2CF2˙. The relative Gibbs free energies of g-CF3CF2CF2I (g-CF3CF2CF2˙) compared to those of a-CF3CF2CF2I (a-CF3CF2CF2˙) were calculated to be 1.83 (0.21) kcal mol−1 at 293 K, resulting in equilibrium mole fractions of a-CF3CF2CF2I (a-CF3CF2CF2˙) of 0.92 (0.42). The mole fractions of the rotational isomers for the nascent photoproduct appear similar to those of the reactant, indicating that the rotational conformer of CF3CF2CF2I in CCl4 mostly dissociates I atoms before rotational isomerization occurs under excitation at 267 nm. In other words, ∼92% of the dissociated radicals are expected to be a-CF3CF2CF2˙ and, thus, they undergo rotational isomerization to reach the equilibrium mole fraction of 42%.
Time-dependent amplitude changes of the basis spectra for g-CF3CF2CF2˙ and a-CF3CF2CF2˙ were well reproduced by the kinetics of rotational isomerization of CF3CF2CF2˙ with a time constant of 34 ps. In other words, τrot = 34 ps around the C–C˙ bond of CF3CF2CF2˙ in CCl4 at 293 K. A τrot of 30 ps was calculated at 293 K using Kramers’ theory based on the energies and vibrational frequencies calculated by DFT with ωB97XD/aug-cc-pVTZ. The calculated and experimental τrot values are similar, confirming that Kramers’ theory is suitable for calculating τrot around the C–C bond of ethyl derivatives in solution. We also calculated the τrot for several ethyl derivatives and ethane derivatives (see Table 3). For example, τrot = 58 ps for CH3CH2CH2CH3 in CCl4 at 298 K, which is about 3 times slower than the values obtained by MD simulations of n-butane as a model liquid at 292 or 273 K, but slightly faster than the value of 81 ps estimated using κ = 0.75 and the value of the TST.4 Since all of the MD simulations referenced here used the Ryckaert–Bellemans dihedral angle potential, which has a lower barrier energy than that calculated by DFT,4,35 a faster rotational time is expected. It would be interesting to determine the τrot of CH3CH2CH2CH3 in CCl4 by performing MD simulations using the rotational barrier obtained by the DFT method used here.
| Compounds | ΔETG (kcal mol−1) | ΔETA (kcal mol−1) | κ A KR, κGKR | τ rot (ps) | τ GA, τAG (ps) | |
|---|---|---|---|---|---|---|
| a Obtained by MD simulation of a model liquid at 292 K.5 b Obtained by MD simulation of a model liquid at 292 K.7 c Obtained by MD simulation of a model liquid at 273 K.9 d Obtained by MD simulation of a pure liquid at <292 K.8 e Obtained by MD simulation of CH3CH2CH2CH3 in CCl4 at 300 K.9 f For CH3CH3 and CH3CH2˙, all conformers are the same, resulting in τAG = τGA and τrot = τGA/3. g Derived from a reported τAG of 43 ps, obtained from 2D IR vibrational echo chemical exchange spectra measured at room temperature, which was fit assuming τAG = τGA.3 h Experimentally determined at room temperature.3 | ||||||
| CF2BrCF2˙ | 65, 72, 59 | 2.06 | 4.40 | 0.50, 0.46 | 38 | 40, 777 |
| CF3CF2CF2˙ | 56, 38, 35 | 1.89 | 2.28 | 0.42, 0.40 | 26 | 58, 49 |
| CF2BrCF2I | 50, 54, 57 | 5.19 | 6.30 | 0.52, 0.52 | 5583 | 7202, 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 840 840 |
| CH3CH2CH2CH3 | 132, 59, 104 | 2.63 | 3.45 | 0.36, 0.37 | 58 | 74, 265 |
| 22a | 57a, 37a | |||||
| 21b | 53b, 34b | |||||
| 20c | 47c, 34c | |||||
| — | 61d, — | |||||
| — | 43e, — | |||||
| CH3CH2CH˙CH3 | 68, 60, 51 | 0.07 | 0.75 | 0.19, 0.21 | 3 | 10, 5 |
| CH3CH3 | 295, 305, 305 | 2.39 | 2.39 | 0.44 | 4.7f | 14, — |
| CH3CH2˙ | 99, 111, — | — | −0.11 | 0.17 | 0.5f | 1.5, — |
| CF2ICF2˙ | 65, 73, 57 | 1.95 | 5.04 | 0.57, 0.53 | 29 | 30, 2004 |
| CH2ClCF2Cl | 98, 105, 97 | 4.39 | 5.03 | 0.51, 0.51 | 645 | 1122, 1517 |
| CH2FCH2NCO | 132, 133, 85 | 3.77 | 2.68 | 0.49, 0.50 | 22 | 473, 23 |
| 22g | —, 43h | |||||
A τrot of 0.64 ns was calculated for CH2ClCF2Cl, which can be determined experimentally by 2D IR vibrational echo spectroscopy as the two gauche- and anti-conformations have distinct C–F stretching modes and the vibrational relaxation time is slow enough to determine τrot. In a future study, we plan to measure τrot around the C–C bond of CH2ClCF2Cl to compare the experimental value with the calculated one to confirm that the use of Kramers’ theory and DFT calculations with ωB97XD/aug-cc-pVTZ estimates τrot with sufficient accuracy. These findings could be relevant for analyzing the C–C(˙) bonds of ethane derivatives as well as ethyl radical derivatives.
Kramers’ theory, a classical approach in theoretical reaction dynamics, assumes diffusive barrier crossing and primarily relies on the harmonic approximation of the modes along the reaction coordinate. However, the nascent CF2BrCF2˙ may not be in a fully thermal equilibrium state during the rotation. Despite this, Kramer's theory appears sufficient for calculating a reliable rate constant of rotation along the C–C˙ bond of CF2BrCF2˙ in solution. The rotational time constant along the C–C(˙) bond in organic compounds can be estimated using Kramers’ theory combined with DFT calculations.
Conclusion
We measured the temperature- and viscosity-dependent τrot about the C–C˙ bond of CF2BrCF2˙ in solution and compared these values with those calculated using Kramers’ theory of reaction rates. The rotational energy barriers and vibrational frequencies of the related compounds required for the calculation of the rate constant using Kramers’ theory were calculated by DFT using three different functionals (ωB97XD, APFD, and B3LYP) with the aug-cc-pVTZ basis set to identify a reliable and practical computational method without the need for high-level calculations. The τrot values calculated using Kramers’ theory and the DFT results were similar to the experimental ones, and the ωB97XD/aug-cc-pVTZ DFT conditions gave the best results. The τrot values calculated using Kramers’ theory and ωB97XD/aug-cc-pVTZ DFT were further validated by experimentally measuring the τrot about the C–C˙ bond of CF3CF2CF2˙ in CCl4 at 293 K by photodissociating I atoms from CF3CF2CF2I at 267 nm. The findings confirm that reliable τrot values about the C–C(˙) bond of ethyl radical and ethane derivatives in solution can be readily obtained using Kramers’ theory and DFT.Author contributions
S. P. and M. L. designed the experiment; S. P. and J. S. collected time-resolved infrared spectra. S. P., H. Y., J. S., and M. L. analyzed the data. S. P. and M. L. wrote the manuscript. All authors approved the final version of the manuscript.Data availability
The data supporting the findings of this study are provided within the article and its ESI.†Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This work was supported by a National Research Foundation of Korea grant funded by the Korean government (NRF-2023R1A2C2004993). S. Park was supported by the LAMP program of the NRF grants funded by the Korean government (RS-2023-00301938). We acknowledge the usage of the Femtosecond Laser System in the PNU Core Research Facilities.References
- W. J. Orville-Thomas, Internal Rotation in Molecules, John Wiley & Sons, 1974 Search PubMed.
- M. B. Smith and J. March, March's Advanced Organic Chemistry: Reactions, Mechanisms, and Structure, John Wiley & Sons, Inc., 6th edn, 2006 Search PubMed.
- J. Zheng, K. Kwak, J. Xie and M. D. Fayer, Science, 2006, 313, 1951–1955 CrossRef CAS PubMed.
- S. Park, J. Shin, H. Yoon and M. Lim, J. Phys. Chem. Lett., 2022, 13, 11551–11557 CrossRef CAS.
- D. Brown and J. H. R. Clarke, J. Chem. Phys., 1990, 92, 3062–3073 CrossRef CAS.
- D. Chandler, J. Chem. Phys., 1978, 68, 2959–2970 CrossRef CAS.
- R. Edberg, D. J. Evans and G. P. Morriss, J. Chem. Phys., 1987, 87, 5700–5708 CrossRef CAS.
- J. Ramirez and M. Laso, J. Chem. Phys., 2001, 115, 7285–7292 CrossRef CAS.
- R. O. Rosenberg, B. J. Berne and D. Chandler, Chem. Phys. Lett., 1980, 75, 162–168 CrossRef CAS.
- T. A. Weber, J. Chem. Phys., 1978, 69, 2347–2354 CrossRef CAS.
- H. Eyring, J. Chem. Phys., 1935, 3, 107 CrossRef CAS.
- P. Haenggi, P. Talkner and M. Borkovec, Rev. Mod. Phys., 1990, 62, 251–341 CrossRef CAS.
- N. E. Henriksen and F. Y. Hansen, Theories of Molecular Reaction Dynamics: The Microscopic Foundation of Chemical Kinetics, Oxford University Press, 2008 Search PubMed.
- P. Atkins and J. de Paula, Atkins' Physical Chemistry, Oxford University Press, 9th edn, 2009 Search PubMed.
- J. Chandrasekhar, S. F. Smith and W. L. Jorgensen, J. Am. Chem. Soc., 1985, 107, 154–163 CrossRef CAS.
- R. F. Grote and J. T. Hynes, J. Chem. Phys., 1980, 73, 2715–2732 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS PubMed.
- P. Hamm, R. A. Kaindl and J. Stenger, Opt. Lett., 2000, 25, 1798–1800 CrossRef CAS PubMed.
- S. Park, J. Shin and M. Lim, Int. J. Mol. Sci., 2023, 24, 1319 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision B.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView, Version 6, Semichem Inc., Shawnee Mission, KS, 2016 Search PubMed.
- J.-D. Chai and M. Head-Gordon, J. Chem. Phys., 2008, 128, 084106 CrossRef PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- A. Austin, G. A. Petersson, M. J. Frisch, F. J. Dobek, G. Scalmani and K. Throssell, J. Chem. Theory Comput., 2012, 8, 4989–5007 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- F. Jensen, J. Chem. Theory Comput., 2014, 10, 1074–1085 CrossRef CAS PubMed.
- P. J. Wilson, T. J. Bradley and D. J. Tozer, J. Chem. Phys., 2001, 115, 9233–9242 CrossRef CAS.
- G. M. Nathanson, T. K. Minton, S. F. Shane and Y. T. Lee, J. Chem. Phys., 1989, 90, 6157–6170 CrossRef CAS.
- M. Rasmusson, A. N. Tarnovsky, T. Pascher, V. Sundstroem and E. Akesson, J. Phys. Chem. A, 2002, 106, 7090–7098 CrossRef CAS.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef.
- C. Wohlfahrt and M. D. Lechner, Static Dielectric Constants of Pure Liquids and Binary Liquid Mixtures, Springer-Verlag Berlin Heidelberg, 1st edn, 2015 Search PubMed.
- Chemical Engineering and Materials Research Information Center, Pure Component Properties, (https://www.cheric.org/research/kdb/hcprop/cmpsrch.php).
- J. M. Bernal-García, A. Guzmán-López, A. Cabrales-Torres, A. Estrada-Baltazar and G. A. Iglesias-Silva, J. Chem. Eng. Data, 2008, 53, 1024–1027 CrossRef.
- E. Gerck, J. Chem. Phys., 1983, 79, 311 CrossRef CAS.
- J. P. Ryckaert and A. Bellemans, Faraday Discuss. Chem. Soc., 1978, 66, 95–106 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04471a |
| This journal is © the Owner Societies 2025 |