 Open Access Article
Open Access ArticleField-dependent relaxation profiles of biomolecular systems
Adam
Kubrak
 abc,
Rajka
Pejanovic
abc,
Rajka
Pejanovic
 d,
Kahinga
Kamau
d,
Kahinga
Kamau
 e,
Danuta
Kruk
e,
Fabien
Ferrage
d and
Giacomo
Parigi
e,
Danuta
Kruk
e,
Fabien
Ferrage
d and
Giacomo
Parigi
 *abc
*abc
aMagnetic Resonance Center (CERM), University of Florence, via Luigi Sacconi 6, Sesto Fiorentino, 50019, Italy. E-mail: parigi@cerm.unifi.it
bDepartment of Chemistry “Ugo Schiff”, University of Florence, via della Lastruccia 3, Sesto Fiorentino, 50019, Italy
cConsorzio Interuniversitario Risonanze Magnetiche Metallo Proteine (CIRMMP), via Luigi Sacconi 6, Sesto Fiorentino, 50019, Italy
dLaboratoire des Biomolécules, LBM, Département de chimie, École normale supérieure, PSL University, Sorbonne Université, CNRS, 75005 Paris, France
eDepartment of Physics and Biophysics, University of Warmia & Mazury in Olsztyn, Oczapowskiego 4, Olsztyn, 10-719, Poland
First published on 3rd January 2025
Abstract
The function of biomolecular systems, including biological macromolecules, often crucially depends on their dynamics. Nuclear magnetic resonance (NMR) is one of the most informative methods used to study biomolecules and their internal mobility, with atomic resolution, in near-physiological conditions. NMR relaxation profiles, obtained from the field dependence of the nuclear relaxation rates, in particular, offer the possibility to probe dynamic processes over a wide range of time scales. Relaxation profiles are routinely acquired using field-cycling relaxometers operating at a maximum field of the order of 1 T. These measurements however suffer from a lack of resolution. On the other hand, relaxation rates measured at the high magnetic fields (>4 T) of high resolution NMR spectrometers contain poor information on motions on timescales longer than few nanoseconds. The possibility to acquire relaxation profiles extended to low fields but with high resolution, obtained by shuttling the sample back and forth in the stray field of a high-field spectrometer, is expected to dramatically improve the potentialities of NMR relaxometry. Here, we review investigations of relaxometry in a wide range of biomolecular systems, such as proteins, phospholipids, or biological fluids. Although multiple models of motions have been developed to describe the relaxation rates and their field dependence, most experimental investigations rely on the model-free approach. A variety of relaxation profiles of both diamagnetic and paramagnetic biomolecular systems are here reviewed and analysed using point dipole–point dipole interaction models.
Introduction
Nuclei in NMR samples possess spin magnetic moments, which are oriented isotropically in the absence of magnetic fields, so that no macroscopic magnetization arises. Conversely, in the presence of a magnetic field B0, the spin magnetic moments process around the magnetic field direction, with an energy which depends on the direction, either parallel or antiparallel, of the magnetic moments with respect to the magnetic field. This difference in energy is responsible for a different population of the spin states, and thus for a net magnetization. The larger the applied magnetic field, the larger the differences in energy and thus the resulting magnetization at equilibrium. If the magnetization is perturbed by a change in the applied magnetic field or by external radiofrequency pulses, it recovers its equilibrium value with a process called spin relaxation.1–3 The longitudinal relaxation rate R1 is the exponential rate constant for recovering the equilibrium magnetization along the direction of the external magnetic field.Relaxation rate values depend on the time-dependent interactions present between the observed nuclei and the surrounding. In fact, the fluctuations in the energy of these interactions can determine transitions between spin states and thus allow for the recovery of the equilibrium conditions. Therefore, the evaluation of the nuclear relaxation rates can permit to obtain information on the interactions occurring in the system and on their dynamics (like molecular reorientation, translational diffusion, chemical exchange…). Each type of interaction can be the source of a different relaxation mechanism and can be modulated by a different motional process. In many cases, the measured relaxation rates are the sums of the contributions arising from many mechanisms. Each relaxation mechanism has a specific dependence on the applied magnetic field and on the relevant time constants of fluctuations. In many cases the measurement of the relaxation rates at a single magnetic field does not provide enough information to recover the relaxation mechanisms and all parameters used to describe them. On the other hand, the availability of the nuclear relaxation profile as a function of the applied magnetic field can be very informative on the type of interaction and dynamic processes driving the spin relaxation mechanisms, and on their time constants.
In biomolecules, the time-dependent interactions responsible for spin relaxation are usually (i) the dipole–dipole interaction (i.e. the interaction between nuclear magnetic moments),4 (ii) the quadrupolar interaction (i.e. the interaction between the molecular electric field gradients and the electric quadrupole moment of the nucleus, due to the anisotropic distribution of the nuclear electric charge, for nuclear spin quantum numbers greater than ½), and (iii) the chemical shift anisotropy (i.e. the interaction between the nuclear magnetic moment and the magnetic field generated by the electronic distribution around the nucleus).2 In paramagnetic systems, i.e. in the presence of unpaired electrons, the interaction between the nuclear magnetic moment and the electron magnetic moment should also be considered, and is often the dominant relaxation mechanism. The dynamic processes modulating all these interactions, and thus causing relaxation, can be of different types, mainly molecular reorientation, internal mobility, chemical exchange, translational diffusion, diffusion on a surface, etc. The time constants describing the persistence of a correlation in the energy values during these dynamic processes are commonly called correlation times.
Field-dependent relaxation profiles are most often collected with field-cycling (FC) relaxometers.5–9 FC relaxometry can allows for the measurement of nuclear relaxation rates from fields as low as 0.01 MHz proton Larmor frequency (B0 ≈ 200 μT), up to tens or more than one hundred of MHz, i.e. over 3–4 orders of magnitude. No spectral resolution is however possible due to the low field strength and relatively poor field homogeneity, so that only the collective relaxation of all nuclei of a given isotope in the sample can be measured.101H relaxometry measurements on water solutions of biomolecules are thus typically dominated by the relaxation rates of bulk water protons, so that the relaxation profiles can report only the relaxation rates of these protons. Therefore, information on the dynamic processes occurring in the system can be retrieved by modelling the effect that the different time-dependent interactions between water molecules and biomolecules have on water proton relaxation and its field-dependence.
The effective magnetic field that is sensed by nuclear magnetic moments, although mainly dictated by the external field, is slightly affected also by the field generated by electrons. Therefore, in high-resolution spectrometers, with a high homogeneity of the external field, all nuclei experiencing a different chemical environment sense a slightly different magnetic field with respect to one another. This results in a different chemical shift of the nuclei with different chemical environment, i.e. in a resolved NMR spectrum. The relaxation rates of individual nuclei present in a macromolecule can thus be measured, as well as the rate of bulk solvent nuclei. In order to obtain the field dependence of these relaxation rates, measurements can be performed by shuttling the sample between different positions inside the NMR spectrometer, in such a way to cycle between different magnetic fields. Shuttling the sample back and forth in the stray field of a high-field spectrometer thus permits to polarize and detect the signals at the high-field position while letting polarizations relax at low field. Measurements performed in the high field position can thus report on the relaxation rates of individual nuclei at lower fields,11–13 so that high-resolution relaxometry can be performed.
Both FC relaxometry and high-resolution relaxometry performed with the use of sample shuttling have been applied for obtaining the field-dependent relaxation profiles of biomolecular systems. FC relaxometry measurements, performed by switching the magnetic field generated by an electromagnet, has the advantage of being able to measure relaxation rates from tenths to thousands s−1, but with no spectral resolution. This technique is therefore particularly informative if the large majority of the detected nuclei present in the sample have the same rate, as for instance in the case of solvent protons in diluted solutions. In this case, observing the signal of the solvent nuclei probes the dynamic of the solute molecules, which can be quantified by modelling the nature of the interactions between solute and solvent molecules. On the other hand, high-resolution relaxometry, which exploits the high sensitivity of high-field NMR spectrometers, provides access to the relaxation rates of the individual nuclei, thus allowing for the characterization of the local mobility of specific molecules or chemical groups and over time scales of nanoseconds or longer. The application of this technique is however still limited by the time needed to shuttle the sample between the positions corresponding to the different magnetic fields, which restricts the observable relaxation rates to maximum values of tens of s−1. In addition, the stray field in a region of ca. 1 m above the magnetic centre of a shielded high-field magnet decays to ca. 10 mT, two order of magnitude above the minimum magnetic field accessible to common FC relaxometry apparatus. This limits the access to dynamics with correlation times in the high nanosecond range.
High-resolution relaxometry can also take advantage of the possibility of easily detecting nuclei different from protons, thanks to the availability of NMR probes for heteronuclear detection. Due to the intrinsically different properties (magnetogyric ratios and chemical shift ranges) of heteronuclear spins compared to protons, 15N and 13C direct detection, for instance, can be very informative in biomolecular NMR applications. It can in fact provide alternative spectroscopic solutions when proton detection finds its limitations, such as in the case of too fast relaxation rates, as occurring in large proteins, or in the case of a small chemical shift dispersion, as in intrinsically disordered proteins.14
FC relaxometry
Diamagnetic macromolecules in solution
FC relaxometry measurements of water solutions provide the relaxation rates of solvent nuclei, which are enhanced by their intermolecular interactions with the macromolecules present in the solution. In diluted water solutions of diamagnetic macromolecules, the dynamics of the water molecules on the coordination surface of the macromolecules, or transiently trapped into their cavities, is slowed down. Therefore, the proton dipole–dipole interactions of these molecules are modulated with a correlation time given by the shortest between their lifetime onto the macromolecule surface and the reorientation time of the macromolecule. In the presence of internal (local) dynamics, the time constant of the occurring faster mobility can also act as a limit for the correlation time. Chemical exchange allows for the propagation of the relaxation enhancement of these surface water molecules to the bulk, as well as of the exchangeable protons of the macromolecules.5In the simple case that dipole–dipole interactions are modulated by stochastic fluctuations occurring with a correlation time τc, the relaxation rates are given by ref. 4
 | (1) |
 is a constant proportional to the squared interaction energy (fM is the molar fraction of water molecules modulated with correlation time τc) and α is the relaxation rate of solvent molecules in the absence of the macromolecule.
is a constant proportional to the squared interaction energy (fM is the molar fraction of water molecules modulated with correlation time τc) and α is the relaxation rate of solvent molecules in the absence of the macromolecule.
Fig. 1a shows the field dependences of R1 when the correlation time τc is 50 ns. This model accounts for the appearance of a “dispersion”, i.e. of relaxation rate values which are constant at low fields and then decrease with increasing the magnetic field. The dispersion is centered at the nuclear frequency ν = 1/(2πτc). It is thus apparent that longitudinal relaxation rates measured at the high fields of high-resolution NMR spectrometers are most informative about motions in the subnanosecond time scale, whereas information on dynamics occurring on timescales of nanoseconds or longer are more easily accessible at lower magnetic fields (below 100 MHz proton Larmor frequency).
 | ||
| Fig. 1 (a) Field dependence of the nuclear relaxation rate according to the dipole–dipole interaction model where stochastic fluctuations are modulated with a correlation time τc of 50 ns (eqn (1), with α = 0, β = 5 × 106 s−2); (b) field dependence of the nuclear relaxation rate according to the two-dimensional translational diffusion with τD = 50 ps and τres = 1 μs (last term in eqn (3), with βT = 5 × 108 s−2). | ||
Usually, the relaxometry profiles of water solutions of biomacromolecules cannot be well fitted with eqn (1), containing a single correlation time. An “extended” model-free approach is thus often used, where multiple correlation times are considered. Therefore, the water proton longitudinal relaxation rate can be empirically analyzed as the sum of Lorentzian dispersions,15–18
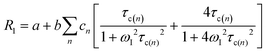 | (2) |
This approach can be justified considering that the very many interactions occurring between the many solvent molecules and the macromolecules are modulated with a variety of correlation times, due to the different time constants for the internal dynamics of the macromolecule, the anisotropy of its reorientation time (in case of non-spherical macromolecules) and the different solvent lifetimes. The correlation time for each interaction can be described by the relationship τc−1 = τR−1 + τf−1 + τM−1, where τR is the reorientation time of the macromolecule (assumed spherical), τf the internal local mobility experienced by that specific nuclear pair and τM its lifetime. In the presence of large macromolecular systems, the reorientation time is likely the largest of the τc(n) values, in the absence of fractional macromolecular aggregation.
In eqn (2), the parameter b depends on the squared energy of the dipole–dipole interactions and on the number of long-living (i.e. for a time >τc(n)) water molecules and exchanging macromolecular protons, and the parameter a on the contribution to the relaxation rate from interactions modulated with correlation times shorter than τc(n) (e.g. from very labile water molecules, with very short lifetime) and from non-dispersive terms.
The analysis of the FC relaxometry profiles using eqn (2) can thus inform on the time scales of the motions occurring in the system and on their relative importance in modulating the protons dipole–dipole interactions. Different values of the correlation times thus indicate the occurrence of different global reorientation times, internal fast dynamics and/or lifetimes of the water molecules interacting with the macromolecule.
Fig. 2 shows the water 1H relaxometry profiles of the catalytic subunit of the cAMP-dependent protein kinase A (PKA),19L-asparaginase II (ANSII),20,21 α7α7 proteasome solutions,18 and bovine serum albumin (BSA),22 at 298 K. The protein PKA, with a MW of 43.5 kDa, is expected to have a reorientation time of ca. 26 ns, as it can be estimated with HYDRONMR.23 The analysis of the relaxation profile actually shows contributions from correlation times of 28 ns (30%) and 5 ns (70%), with a very small contribution (0.4%) from a much longer correlation time of 240 ns which may point out to the presence of some aggregated form. The large contribution from the short correlation time indicates the relevance of the extensive fast local mobility for relaxation. The profiles of asparaginase can also be fitted with two correlation times, equal to 60 ns (42%) and 9 ns (58%). The former value confirms that the protein forms tetrameric assemblies, being close to what is expected for globular proteins with MW of ca. 140 kDa. In the case of α7α7 proteasome (360 kDa) in 40% v/v glycerol, four correlation times were needed to optimally fit the relaxation profile. Also in this case, the longest time, of 0.8 μs, is in nice agreement with HYDRONMR estimations of the overall reorientation time of the protein. In the case of BSA, three correlation times should be considered to achieve a good fit of the experimental data: the longest correlation time, equal to 270 ns and with a weight of 1.7%, may suggest the occurrence of partial aggregation; the protein (66 kDa) is in fact expected to have a reorientation time of about 45 ns. This value is actually in close agreement with the correlation time of 53 ns (42%), obtained together with a shorter time of 12 ns (56%). The fit performed with eqn (2) and the contributions from the different correlation times are shown in the left panels of Fig. 2.
 | ||
| Fig. 2 Water proton relaxometry profiles of the catalytic subunit of the cAMP-dependent protein kinase A (PKA, 0.5 mM, in the presence of the inhibitor peptide PKI),19L-asparaginase II (ANSII, 0.8 mM),20,21 α7α7 proteasome (3.6 mM) with 40% glycerol,18 and bovine serum albumin (BSA) (1.56 mM),22 at 298 K. The fit performed with eqn (2) and (3) are shown in left and right panels, respectively (solid lines). Dashed lines represent the contributions corresponding to the correlation time in agreement with the molecular reorientation time, dash-dot lines the contributions from additional correlation times, dotted lines the contributions from 2D translational diffusion. | ||
An alternative model that can be used to fit these profiles is considering the presence of solvent molecules that can be subjected to translational diffusion on the macromolecule surface.9,24 The contribution from the two-dimensional translational diffusion of these water molecules thus sums up to the contribution from water molecules rigidly reorienting by macromolecular tumbling (the contribution from three-dimensional translational diffusion of water molecules is expected to be negligible, due to its field dependence and the short diffusional correlation time, of the order of 30 ps). The profiles can thus be fitted using eqn (3)
 | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln[1 + (ωτD)−2]; then for ωτD ≪ 1 it reaches the linear dependence on logarithm of the resonance frequency.
ln[1 + (ωτD)−2]; then for ωτD ≪ 1 it reaches the linear dependence on logarithm of the resonance frequency.
The water 1H relaxometry profiles previously fitted with eqn (2) can actually be well reproduced also using eqn (3) (right panels of Fig. 2). In all these cases the best-fit value of τR is in nice agreement with the expectations (25 ns in PKA, 49 ns in ANSII, 0.7 μs in α7α7 proteasome, and 50 ns in BSA), whereas τD values from few tens of picoseconds to nanoseconds and τres of the order of microseconds or longer are found. Of note, the number of fitting parameters is reduced with respect to those used in eqn (2). The same model has been applied to analyze the relaxation profiles of concentrated BSA solutions.24
In general, a good fit of the relaxation profiles with the extended model-free approach is always possible, and this analysis may be informative on the spread and order of magnitude of the correlation times characteristic of the motional processes driving relaxation. Although in some cases these times may indeed report on different dynamical processes occurring at different time scales, such as reorientation of supramolecular adducts, global molecular reorientation, local mobility, or water exchange, it may also be possible that no physical meaning can be attributed to them. In fact, they may be just parameters allowing a good fit of the data under the assumption that the spectral density functions have a Lorentzian shape. It is however possible that the intervening mobility processes cause non-Lorentzian spectral density functions. Therefore, when fitting experimental data, it may be important to evaluate the presence of characteristic frequency dependences of the relaxation rates, in order to apply the correct model able to provide physically meaningful correlation times, which are really related to the motional mechanism.
Diamagnetic macromolecules in the solid state
FC relaxometry can also shed light on the dynamics of biological samples in the solid state, as for instance dry (lyophilized) proteins and frozen protein solutions, or in sedimented systems or low-level rehydrated lyophilized protein systems.8,22,25–27 In these cases, the relaxation profiles can be described by a power law in proton Larmor frequency (R1 = Aω−B with B = 0.76–0.78), resulting from rotationally immobilized protein protons with mobility restricted to geometries having lower dimensionality than the usual three dimensional diffusion, and considering an efficient magnetization transfer between protein and water protons.28 The low field relaxation rates can be as large as hundreds or thousands of s−1, and then the rates progressively decrease with increasing frequencies. These profiles have also been fitted using the model free approach (eqn (2)), with correlation times usually ranging between 10−6 and 10−9 s.22,29,30Nuclei with I > ½, like for instance 14N, are characterized by an anisotropic distribution of the nuclear electric charge, which gives rise to an electric quadrupole moment of the nucleus, interacting with the electric field gradients present in a molecular system. This interaction, independent of the magnetic field, should be considered together with the interaction of the nuclear magnetic moment with the external magnetic field (Zeeman interaction), which, on the other hand, is field dependent. Both these interactions contribute to the energy of the 14N states. In immobilized systems, a magnetization transfer arises when the transition energies between the states of the 14N nucleus match those between the states of a I = ½ nucleus (like for instance 1H) which is dipole–dipole coupled with the 14N nucleus. This process causes a fast decay of the 1H magnetization at specific frequencies, and thus the appearance of peaks with a high relaxation rate, called quadrupolar peaks. The contribution to the 1H relaxation rates due to the coupling with 14N nuclei can be described by eqn (4)31
 | (4) |
 ω0 = ω+ − ω−, aQ is the quadrupole coupling constant, η is the asymmetry parameter,
ω0 = ω+ − ω−, aQ is the quadrupole coupling constant, η is the asymmetry parameter,  and τQ is the correlation time characterizing the fluctuations of the 1H–14N dipole–dipole coupling. The angles θ and ϕ describe the orientation of the principal axis system of the electric field gradient tensor with respect to the 1H–14N dipole–dipole axis.
and τQ is the correlation time characterizing the fluctuations of the 1H–14N dipole–dipole coupling. The angles θ and ϕ describe the orientation of the principal axis system of the electric field gradient tensor with respect to the 1H–14N dipole–dipole axis.
The relaxation profile of 40% w/w of BSA in water at 263 K shows for instance the occurrence of three quadrupolar peaks (see Fig. 3),24 which can be nicely analyzed with eqn (4). These relaxation peaks are placed on the top of a relaxation decrease, which can be reproduced assuming contributions from dipole–dipole interactions modulated with a distribution of correlation times (eqn (2)).
 | ||
| Fig. 3 Water proton relaxometry profiles of 40% BSA at 263 K. The fit performed with eqn (2) and (4) to take into account both the contributions from the dipole–dipole interaction and the quadrupolar interaction are shown with dashed lines and dot-dashed line, respectively. Figure taken from ref. 24. | ||
Relaxation profiles have been measured also for healthy muscles and tumour tissues.32,33 In these cases, the water proton relaxation rates are of the order of few tens of s−1 at 0.01 MHz, due to the relatively large amount of water molecules present in the extracellular space and in exchange with those present in the intracellular compartment. The relaxation rates decrease with increasing the magnetic field, usually quite fast at low fields and more slowly at high fields (see Fig. 4). The overall shape of the relaxation profiles should be related to the dynamics of the water molecules in the two different compartments, where they are subjected to a restricted mobility. The relaxation profiles can be fitted with a sum of Lorentzian functions (eqn (2)) or with including contributions from two-dimensional translational diffusion (eqn (3)). Quadrupolar peaks are often visible. Interestingly, at low magnetic fields the relaxation rates of tumour tissues are often significantly smaller than those of healthy tissues, probably because of the shorter residence time of the water molecules in the intracellular compartment, where dynamics is slower.32
 | ||
| Fig. 4 Water proton relaxometry profiles of mouse leg tissue.32 | ||
Paramagnetic systems
In paramagnetic systems, characterized by the presence of unpaired electron(s) in molecular orbitals, a further interaction occurs, which is the dipole–dipole interaction between the electron magnetic moment and the nuclear magnetic moment. Since the magnetic moment of the free electron is 658.2 times larger than the magnetic moment of the proton, this interaction can contribute to the relaxation rate of a hydrogen nucleus at distance r from the unpaired electron(s), e.g. from a paramagnetic metal ion, much more than the dipole–dipole interaction between proton magnetic moments, even if the distance r is larger than the distance between hydrogen nuclei. In the presence of chemical exchange, this paramagnetic enhancement can be transferred to all water protons. The paramagnetic enhancement to the nuclear relaxation of bulk water protons (R1p) is often described by the Solomon–Bloembergen–Morgan (SBM) equations4,34| R1p = fM(R1M−1 + τM)−1 | (5) |
 | (6) |
| τc−1 = τR−1 + τe−1 + τM−1 | (7) |
 | (8) |
The field dependence of R1M and R1p, shown in Fig. 5, is thus characterized by two Lorentzian dispersions separated by a factor 658.2 and centred at the proton Larmor frequencies (2π658.2τc)−1 and (2πτc)−1. Depending on the value of the field dependent τe with respect to those of the field independent τr and τM, the correlation time τc can increase with increasing the magnetic field or can be field independent (for S = 1/2 systems, τc is always field independent). When τc is field dependent, a peak appears in the relaxation profile due to the increase in τe due to the ωSτv dispersion, and the subsequent decrease due to the ωIτc dispersion.
 | ||
| Fig. 5 Field dependence of the water proton relaxation rate (R1p) according to the SBM model (eqn (5)–(8)) for 1 water molecule coordinated to a Gd3+ ion (S = 7/2, in 1 mM concentration) at distance of 3.0 Å with τM = 20 ns, Δt = 0.02 cm−1, τv = 20 ps and τR of 100 ps (black line) or 3 ns (red line). | ||
Eqn (6)–(8) were derived under a number of approximations,35 among which the absence of static zero-field splitting and hyperfine coupling between the electron magnetic moment and the magnetic moment of the paramagnetic metal nucleus. These effects can drastically modify the values and the field dependence of the relaxation rates, especially at low fields.36,37
An additional contribution to the paramagnetic enhancement is provided by water molecules freely diffusing around the paramagnetic moiety up to a distance of closest approach d.38,39 According to the hard-sphere model,40,41 the modulation of the dipole–dipole interaction between the unpaired electron(s) and the diffusing water protons provides a translational diffusion contribution, given by
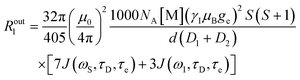 | (9) |
 | (10) |
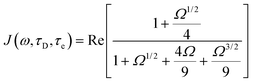 | (11) |
| Ω = iωτD + τD/τe |
 | ||
Fig. 6 Field dependence of the water proton relaxation rate according to the outer-sphere relaxation model (eqn (9) and (11)) for water molecules diffusing, up to a distance of closest approach of 3.6 Å, around spherical molecules containing a Gd3+ ion (S = 7/2, in 1 mM concentration), with diffusion coefficient D1 + D2 of 2.4 × 10−9 m2 s−1 and electron relaxation described by the parameters Δt = 3.77 × 109 s−1 (corresponding to 0.02 cm−1) and (i) τv = 20 ps (solid lines) or (ii) 0.2 ps (dotted lines). In the second case, the dipole–dipole interaction is modulated only by the diffusional time  . In the right panel, the rates are plotted against the square root of the frequency to show its linear dependence at low fields in the case that electron relaxation is negligible (red dotted line) and that the same does not hold when this is not the case (black solid line). . In the right panel, the rates are plotted against the square root of the frequency to show its linear dependence at low fields in the case that electron relaxation is negligible (red dotted line) and that the same does not hold when this is not the case (black solid line). | ||
Since the paramagnetic enhancements are linear with respect to the concentration of the paramagnetic centers, in the absence of concentration dependent changes in molecular structure and dynamics, it is common to define a quantity called relaxivity r1 as the enhancement due to 0.001 mol dm−3 (1 mM) of paramagnetic centers in solution.
Fig. 7 shows the relaxivity profile of the protein L-asparaginase II, where a gadolinium(III)-DOTA derivative has been attached via amide bond formation.21 The relaxivity of this paramagnetic macromolecule is much larger than that measured for the free gadolinium complex and the profile shows a peak in the high-field region. These effects are due to a reorientation time τR that is much longer for the macromolecule than for the Gd-DOTA complex, so that the correlation time for the electron–nucleus dipole–dipole interaction (eqn (7)), is largely determined by τR for the gadolinium(III) complex, and mostly given by the electron relaxation time for the biomolecule. Contributions from both the water molecule coordinated to the gadolinium(III) ion and from freely diffusing water molecules are considered. The SBM model appeared however insufficient for a satisfactory fit of the relaxivity profile, which required to consider the presence of static zero-field splitting, as done for instance in the Florence NMRD program.43–45 The temperature dependence of the relaxivity profiles also showed that the coordinated water molecule is in slow exchange.21
 | ||
| Fig. 7 1H relaxivity profiles of Gd-DOTA (empty symbols) and GdDOTA-conjugated ANSII (solid symbols) at 25 °C. Best fit profiles obtained with the Florence NMRD program are also shown.21 | ||
High-resolution relaxometry
FC relaxometry performed with electromagnets operating at a maximum field of the order of 1 T is a powerful method to probe molecular dynamics but the absence of high resolution prevents site-specific investigations as commonly performed in NMR spectroscopy. An alternative that preserves the high resolution and sensitivity of high-field NMR is to use the stray field of a high-field magnet (typically larger than 4 T) as the variable magnetic field. High-resolution (HR) relaxometry consists in polarizing a sample and detecting the NMR signals at high field. The sample experiences lower fields between polarization and detection times by shuttling in the stray field of an NMR spectrometer.11–13,46 A large range of magnetic fields is reached by simply varying the shuttling distance in the bore of the magnet. In this way, it is possible to measure longitudinal relaxation rates at low fields with the resolution and the sensitivity of high-field NMR. The availability of the relaxation profiles extended over 2–3 orders of magnitude of magnetic fields provides a sensitivity to longer correlation times, i.e. to much slower motions, than achievable with standard high field 15N relaxation measurements.47High-resolution relaxometry has been used to determine site-specific motions on pico- to nanosecond timescales in proteins. The first application was performed by the groups of Redfield and Kern and allowed them to detect rigid-body motions in the β-hairpin and adjacent loops of N-terminal domain of the SARS (Severe Acute Respiratory Syndrome) nucleocapsid protein (SARSN), with a timescale of approximately 0.8 nanoseconds.48 These HR relaxometry experiments utilized a stepper motor-driven shuttle system to move the sample between high and low magnetic fields, replacing the previous pneumatic system, both developed by Redfield.11 This setup allowed for controlled deceleration of the sample, avoiding issues like protein denaturation that occurred with the more abrupt deceleration of the pneumatic system. The inclusion of low-field data, more sensitive to slower mesodynamic fluctuations, provided a fuller picture of protein dynamics.
The ensemble of relaxation rates in the β-hairpin and adjacent loops were best described by an extended model-free spectral density function, with separate order parameters for fast and slow motions (Sf2, Ss2), confirming the presence of slower correlated motions within this structural unit. Despite the success of the combined high- and low-field approach, some discrepancies arose, particularly in the R1 values at lower fields. These deviations were attributed to cross-relaxation due to the cross correlation of chemical shift anisotropy (CSA) and dipolar relaxation mechanisms in the absence of control of relaxation pathways during the relaxation period. This problem was later addressed in different ways by Ferrage and coworkers (see below). Molecular dynamics simulations supported both the timescale and collective nature of motions of the β-hairpin.
This seminal study was followed by investigations by high-resolution relaxometry, combined with traditional high-field NMR, of the internal dynamics of proteins such as ubiquitin.13 To measure site-specific low-field relaxation rates, a pneumatic shuttling system was developed,13 enabling rapid transfer of samples between the magnetic center and the chosen position of the stray field. This system facilitated high-resolution measurements of longitudinal relaxation rates at low fields, although with reduced sensitivity compared to high-field experiments (about ten times less sensitivity) due to system design. This setup allowed the measurement of relaxation rates over a wide range of fields (0.5–14.1 T), correcting for systematic deviations of decay rates due to cross-relaxation using an iterative correction approach called ICARUS, which accounts for the effects of cross-relaxation pathways during shuttling.49 The ICARUS corrections for backbone nitrogen-15 decays varied between 4.5% and 13%, with greater corrections needed at fields below 3 T.
The analysis of low-field longitudinal relaxation rates revealed dynamics in the β1–β2 turn of ubiquitin on the nanosecond timescale, which exhibited nanosecond motions that were not identified with a similar amplitude in earlier studies at a single high magnetic field but highlighted by the analysis of residual dipolar couplings.50,51 These motions were best described by an extended model-free analysis, occurring with a timescale of ∼2 ns, suggesting a collective motion in this region.13 Relaxometry dispersion profiles (Fig. 8) highlight the differences between mobile and rigid residues, with nanosecond motions dominating at lower fields. While the experimental data mostly align with theoretical predictions, some discrepancies in the dispersion profiles, particularly for highly mobile residues like Gly75 and Gly76, suggested limitations in models of spectral density functions.
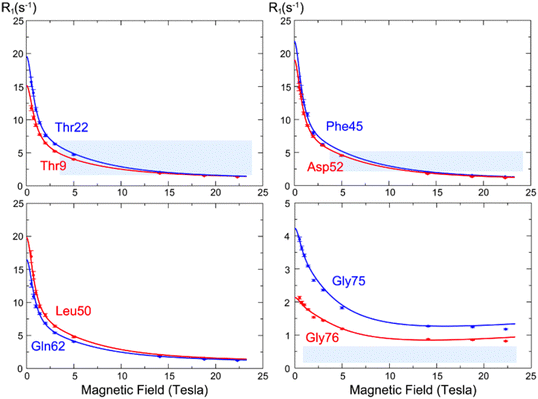 | ||
| Fig. 8 15N longitudinal relaxation rates as a function of the static field R1(B0) (so-called “relaxometry dispersion profiles”) for eight selected residues in ubiquitin. The blue and red dots show corrected longitudinal relaxation rates, adjusted to compensate for relaxation during shuttling, while the lines show dispersion profiles calculated from the microdynamic parameters obtained in our analysis. Figure taken from ref. 13. | ||
High-resolution relaxometry was also used to determine motions of protein sidechains. HR relaxometry was used to measure site-specific carbon-13 relaxation rates in protein methyl groups in the model protein ubiquitin.49 Specific isotopic labeling of methyl groups in isoleucine side chains was employed to obtain isolated 13C1H2H2 groups, for which carbon-13 relaxation is slow enough to minimize polarization losses during the transfer between high and low fields. Relaxation rates were measured over two orders of magnitude in magnetic field strength, down to 0.33 T. Heteronuclear nuclear Overhauser effects (NOEs) allowed to capture high-frequency motions, while parameters of slower motions were constrained by low-field longitudinal relaxation rates. It was possible to decompose motions of methyl group dynamics into three independent components: fast methyl group rotation, orientational motion of the CC bond, and global rotational diffusion of the protein. Fast methyl-group rotation was modeled using an order parameter set by the geometry of the methyl group and a single correlation time τmet, while the orientational motion of the CC bond was described with an extended model-free approach with two order parameters (Sf2 and Ss2) and their associated correlation times (τf and τs) for fast and slow motions, respectively.
Correlation times (τmet) for methyl group rotation ranged from 5.5 ps to 22 ps, with faster timescales observed for surface-exposed residues like Ile44 (τmet = 5.5 ps) and slower ones for core residues like Ile23 (τmet = 22 ps), possibly due to steric interactions.52 For residues without well-defined nanosecond-scale motions (Ile3, Ile23, Ile30, Ile61), relaxometry-derived fast-motion order parameters (Sf2) aligned well with those from high-field deuterium relaxation.53 However, for residues with defined nanosecond motions (Ile13, Ile36, Ile44), the analysis of relaxometry gave lower order parameters than those obtained from deuterium relaxation. Measurements of dipolar couplings in solids54 and nanoparticle assisted spin relaxation (NASR)55,56 in solution are in very good agreement with the lower order parameters obtained by relaxometry. Note that, of these three approaches, only relaxometry can determine the effective timescale for these motions.
In HR relaxometry, cross relaxation during the transfer between high and low magnetic fields is often not negligible, which leads to deviations of the decay rate from the longitudinal relaxation rate, as observed in the first investigation by Kern and Redfield. Several approaches have been implemented to take these effects into account.49 Alternatively, a two-field NMR spectrometer, with radiofrequency pulses at the low-field center, allows to select the proper nuclear spin operator at low field and suppress cross-relaxation pathways during the relaxation delay. In addition, both transverse and longitudinal relaxation rates can be measured.57 The combination of high-field relaxation rates and relaxation rates at a single low frequency provided more information than high-field relaxation alone when specifically labeled δ1 methyl groups of isoleucine residues in ubiquitin were considered57 as shown in Fig. 9.
 | ||
| Fig. 9 Distribution of parameters for internal dynamics of isoleucine-44 from Markov-Chain Monte-Carlo analysis of relaxation rates, showing order parameters (Sf2) and (Ss2) for fast and slow motions, with corresponding correlation times (τf, τs, τmet). Analysis was conducted under various conditions: (a) relaxation rates at 20 magnetic fields, with longitudinal relaxation measured at fields B0 < 9 T without any RF pulse at low field; (b) parameters derived from longitudinal, transverse relaxation, and dipolar cross-relaxation rates at high fields only (9.4 T, 14.1 T, 18.8 T, and 22.3 T); and (c) high-field relaxation rates from (b), supplemented by accurate longitudinal and transverse relaxation rates at 0.33 T using a two-field spectrometer. Reprinted (adapted) with permission from ref. 57. Copyright 2019 American Chemical Society. | ||
Accurate relaxation measurements at a single low magnetic field, coupled with high-field data can also be used to validate the procedure implemented to estimate longitudinal relaxation rates from the decay rates at low field. Such an approach was implemented both for carbon-13 relaxation in methyl groups in ubiquitin57 and backbone nitrogen-15 relaxation in a disordered protein region.58
Proteins are not the only type of biomolecule has been investigated by high-resolution relaxometry. For instance, Roberts and Redfield59 have investigated dynamics in a DNA octamer using 31P and 1H field-cycling NMR. Internal order parameters for CSA interactions were determined, as well as overall correlation times for rotational diffusion but a precise determination of internal dynamics was not possible based on the analysis of 31P relaxation alone.
The dynamics of lipids in membranes can span many orders of magnitude of timescales. Redfield and Roberts investigated the dynamics of phospholipids from 13C and 31P field-cycling relaxometry. Field-cycling 31P NMR of phospholipids in vesicles and micelles demonstrated that increased phospholipid motion of zwitterionic phosphatidylcholine (PC) contributed to enhance phosphatidylinositol-specific phospholipase C (PLC) activation.60 This insight underscores the importance of lipid–protein interactions in membrane function.
This approach was also used to investigate the reorientation of phospholipids at the lipid/water interface via HR relaxometry of 31P, highlighting how temperature and cholesterol impact lipid dynamics.61 This study showed that cholesterol reduced the energy barrier for phospholipid motion, thereby contributing to membrane fluidity and stability. Supporting this, Sivanandam et al.62 applied 13C high-resolution field-cycling NMR to assess the “wobble” of PC in vesicles, showing that cholesterol significantly increases lipid motion correlation times, further illustrating its role in modulating membrane properties. In addition, Roberts et al.63 investigated phospholipid dynamics in vesicles, revealing that 31P relaxation rates reflect varied lipid motion profiles in bilayers. They identified a residual dipolar interaction between phosphorus and nearby glycerol C3 protons, providing estimates of the P–H vector orientation relative to the membrane surface. This method was also used to monitor the interaction of micelles of PC with the peripheral membrane protein Bacillus thuringiensis phosphatidylinositol-specific phospholipase C (PI-PLC). This interaction helps anchor the enzyme to the membrane, highlighting the importance of lipid–protein interactions in regulating enzyme activity.
HR relaxometry can also allow for easily identifying weak interactions between ligands and macromolecules. The detection of the relaxation profiles of ligand nuclei permits to observe the occurrence of binding from the field dependence of their relaxation rates. In the absence of binding the rates are expected to be basically field independent, as a result of the short reorientation time of the ligand molecule, whereas in the presence of binding the reorientation time becomes that of the macromolecule, so that a dispersion in the relaxation profile must appear.
HR relaxometry of 31P was used by Pu et al.64 to determine the binding of inositol 1,2-(cyclic)-phosphate (cIP) to PLC (Fig. 10). The addition of about 0.03 equivalent of phosphatidylinositol-specific phospholipase C spin-labelled at residue H82C (H82C-SL), leads to a clear dispersion at low field, indicative of binding of cIP to PLC. This dispersion is more pronounced in the presence of diC7PC micelles, which is due to an increase of the size of the complex and thus of its rotational correlation time.64 Building on these observations, a series of investigations by Roberts, Redfield and coworkers exploited this method to further characterize interactions of small molecules with proteins. 31P NMR relaxometry was used to analyse enzyme–substrate dynamics in guanosine monophosphate reductase (GMPR), revealing distinct binding modes for guanosine monophosphate (GMP) and inosine monophosphate (IMP) during deamination and hydride transfer steps.65 Similarly, in phosphatase and tensin homolog (PTEN), this method identified a phosphatidylinositol 4,5-bisphosphate (PI(4,5)P2)-binding site distinct from the active site, providing new insights into PTEN's regulatory mechanisms.66
 | ||
| Fig. 10 Field dependence of the longitudinal relaxation rate of 31P in cIP (concentration 5 mM) without (+) or with (○) 14.4 μM phosphatidylinositol-specific phospholipase C spin-labelled at residue H82C (H82C-SL), as well as with H82C-SL and 5 mM diC7PC micelles (●). Reprinted (adapted) with permission from ref. 64. Copyright 2009 American Chemical Society. | ||
Redfield and Roberts also introduced the use of electron spin labels on proteins to identify the binding modes of small molecules thanks to paramagnetic relaxation enhancements at low field. Gradziel et al.67 demonstrated that spin labelling combined with 31P NMR high-resolution relaxometry could be used to study the binding of cytotoxic amphiphiles to the Akt1 PH domain. They identified two distinct binding sites, contributing to our understanding of how these molecules regulate protein activity, offering potential therapeutic targets. In addition, Pu et al.68 employed spin-labeled proteins to reveal discrete binding sites on PLC for PC and substrate analogs. Similarly, Roberts et al.69 identified specific phospholipid binding sites on PTEN and Akt1 PH domain, illustrating how phosphoinositides and alkylphospholipids anchor these proteins to membranes and modulate their activity.
It was shown that the analysis of the relaxation profile can also allow for determining the size of ligand–protein complexes as well as that of metabolite–protein complexes in human blood serum.70 In the case of a water solution of alanine, sodium 3-(trimethylsilyl)propionate-2,2,3,3-d4 (TSP) and bovine serum albumin, the relaxation profiles measured for the methyl protons of alanine and TSP are quite different as a result of the absence (for alanine) or of the presence (for TSP) of binding with albumin (Fig. 11). The position of the low field dispersion in the relaxation profile of TSP is consistent with a correlation time of ca. 40 ns, in good agreement with the reorientation time that has been estimated for albumin. On the other hand, a reorientation correlation time of 36 ps was obtained from the relaxation rates of alanine.70
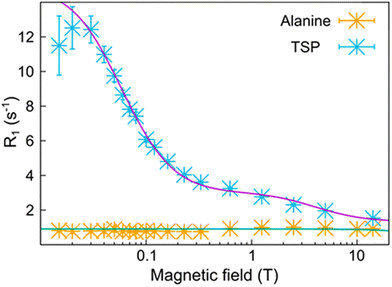 | ||
| Fig. 11 Relaxation profiles for the methyl protons of TSP (blue crosses) and alanine (orange crosses) in the presence of bovine serum albumin. Reprinted (adapted) with permission from ref. 70. Copyright 2021 American Chemical Society. | ||
This method was used to probe interactions of metabolites in human blood serum. The interactions of lactate and creatinine with serum albumin were clearly identified. Interestingly, the competition between lactate and TSP on serum albumin could be quantified in blood serum, opening the way for titrations and competition binding within biological fluids.
Conclusions and perspectives
NMR relaxometry has proven to be an invaluable tool for elucidating the dynamic processes occurring within biological macromolecules, both in solution and in the solid state. The application of FC and HR relaxometry enables the investigation of nuclear spin relaxation rates over a wide range of magnetic fields, revealing detailed information about molecular interactions and dynamics. For diamagnetic macromolecules in solution, FC and HR relaxometry have been instrumental in identifying the various correlation times associated with different dynamic processes, such as the global reorientation of the macromolecule, internal mobility, and the lifetimes of water molecules interacting with the macromolecule. For example, studies on proteins like the catalytic subunit of protein kinase A (PKA), L-asparaginase II (ANSII), and α7α7 proteasome have demonstrated the presence of multiple correlation times, reflecting complex internal and overall molecular dynamics. Similarly, in the solid state, FC relaxometry has provided insights into the restricted mobility and magnetization transfer mechanisms in lyophilized proteins.The extended model-free approach and the two-dimensional translational diffusion model have both been effective in fitting relaxometry profiles, offering complementary perspectives on the dynamic processes at play. The former, which uses a sum of Lorentzian dispersions, can accommodate the variety of correlation times present in complex systems, while the latter provides a specific framework for understanding the field dependence of relaxation rates in terms of two-dimensional diffusion dynamics.
In paramagnetic systems, the presence of unpaired electrons introduces additional complexity to the relaxation mechanisms. The Solomon–Bloembergen–Morgan (SBM) model has been successful in describing the paramagnetic enhancements to nuclear relaxation rates, accounting for the contributions from electron–nuclear dipole–dipole interactions. The ability of this model to characterize field-dependent relaxation rates highlights the importance of electron relaxation times and their interplay with nuclear relaxation mechanisms.
Looking forward, the continued development and refinement of relaxometry techniques will further enhance our understanding of molecular dynamics in biological systems. Advances in relaxometry instrumentation and data analysis methods will allow for even more precise measurements and more detailed interpretations of relaxation mechanisms. High-resolution relaxometry, in particular, holds great promise for studying individual nuclei in complex macromolecular assemblies, offering the potential to dissect the contributions of various interactions and dynamic processes at an unprecedented level of detail.
In conclusion, NMR relaxometry, through its ability to probe dynamic processes over a wide range of timescales and magnetic fields, remains a powerful tool in the study of biological macromolecules. Its applications in both solution and solid-state systems, as well as in paramagnetic and diamagnetic contexts, continue to provide valuable insights into the molecular mechanisms underlying biological function. Future developments in this field will undoubtedly expand its utility and impact, driving forward our understanding of molecular dynamics in increasingly complex biological environments.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the European Commission through HORIZON MSCA-DN project FC-RELAX (grant agreement no. 101072758) and H2020 FET-Open project HIRES-MULTIDYN (grant agreement no. 899683).References
- A. Abragam, The Principles of Nuclear Magnetism, Oxford University Press, Oxford, 1961 Search PubMed.
- J. Kowalewski and L. Maler, Nuclear Spin Relaxation in Liquids: Theory, Experiments, and Applications, Taylor & Francis, 2006 Search PubMed.
- I. Bertini, C. Luchinat, G. Parigi and E. Ravera, NMR of paramagnetic molecules: applications to metallobiomolecules and models, 2017 Search PubMed.
- I. Solomon, Relaxation Processes in a System of Two Spins, Phys. Rev., 1955, 99, 559–565 CrossRef CAS.
- G. Parigi, E. Ravera, M. Fragai and C. Luchinat, Unveiling protein dynamics in solution with field-cycling NMR relaxometry, Prog. Nucl. Magn. Reson. Spectrosc., 2021, 124–125, 85–98 CrossRef CAS PubMed.
- I. Bertini, C. Luchinat and G. Parigi, 1H NMRD profiles of paramagnetic complexes and metalloproteins, Adv. Inorg. Chem., 2005, 57, 105–172 CrossRef CAS.
- S. H. Koenig and R. D. Brown III, Field-Cycling Relaxometry of Protein Solutions and Tissue: Implications for MRI, Prog. Nucl. Magn. Reson. Spectrosc., 1990, 22, 487–567 CrossRef CAS.
- Y. A. Goddard, J.-P. Korb and R. G. Bryant, Water molecule contributions to proton spin–lattice relaxation in rotationally immobilized proteins, J. Magn. Reson., 2009, 199, 68–74 CrossRef CAS PubMed.
- J.-P. Korb, Multiscale nuclear magnetic relaxation dispersion of complex liquids in bulk and confinement, Prog. Nucl. Magn. Reson. Spectrosc., 2018, 104, 12–55 CrossRef CAS PubMed.
- C. Luchinat and G. Parigi, Collective relaxation of protein protons at very low magnetic field: a new window on protein dynamics and aggregation, J. Am. Chem. Soc., 2007, 129, 1055–1064 CrossRef CAS PubMed.
- A. G. Redfield, Shuttling device for high-resolution measurements of relaxation and related phenomena in solution at low field, using a shared commercial 500 MHz NMR instrument, Magn. Reson. Chem., 2003, 41, 753–768 CrossRef CAS.
- A. G. Redfield, High-resolution NMR field-cycling device for full-range relaxation and structural studies of biopolymers on a shared commercial instrument, J. Biomol. NMR, 2012, 52, 159–177 CrossRef CAS PubMed.
- C. Charlier, S. N. Khan, T. Marquardsen, P. Pelupessy, V. Reiss, D. Sakellariou, G. Bodenhausen, F. Engelke and F. Ferrage, Nanosecond Time Scale Motions in Proteins Revealed by High-Resolution NMR Relaxometry, J. Am. Chem. Soc., 2013, 135, 18665–18672 CrossRef CAS PubMed.
- I. C. Felli and R. Pierattelli, 13C Direct Detected NMR for Challenging Systems, Chem. Rev., 2022, 122, 9468–9496 CrossRef CAS PubMed.
- B. Halle, H. J¢hannesson and K. Venu, Model-Free Analysis of Stretched Relaxation Dispersions, J. Magn. Reson., 1998, 135, 1–13 CrossRef CAS PubMed.
- I. Bertini, M. Fragai, C. Luchinat and G. Parigi, 1H NMRD profiles of diamagnetic proteins: a model-free analysis, Magn. Reson. Chem., 2000, 38, 543–550 CrossRef CAS.
- E. Ravera, M. Fragai, G. Parigi and C. Luchinat, Differences in Dynamics between Crosslinked and Non-Crosslinked Hyaluronates Measured by using Fast Field-Cycling Relaxometry, ChemPhysChem, 2015, 16, 2803–2809 CrossRef CAS PubMed.
- E. Ravera, G. Parigi, A. Mainz, T. L. Religa, B. Reif and C. Luchinat, Experimental Determination of Microsecond Reorientation Correlation Times in Protein Solutions, J. Phys. Chem. B, 2013, 117, 3548–3553 CrossRef CAS PubMed.
- B. Wienen-Schmidt, H. R. A. Jonker, T. Wulsdorf, H.-D. Gerber, K. Saxena, D. Kudlinzki, S. Sreeramulu, G. Parigi, C. Luchinat, A. Heine, H. Schwalbe and G. Klebe, Paradoxically, Most Flexible Ligand Binds Most Entropy-Favored: Intriguing Impact of Ligand Flexibility and Solvation on Drug–Kinase Binding, J. Med. Chem., 2018, 61, 5922–5933 CrossRef CAS PubMed.
- L. Cerofolini, S. Giuntini, A. Carlon, E. Ravera, V. Calderone, M. Fragai, G. Parigi and C. Luchinat, Characterization of PEGylated Asparaginase: New Opportunities from NMR Analysis of Large PEGylated Therapeutics, Chem. – Eur. J., 2019, 25, 1984–1991 CrossRef CAS PubMed.
- G. Licciardi, D. Rizzo, M. Salobehaj, L. Massai, A. Geri, L. Messori, E. Ravera, M. Fragai and G. Parigi, Large Protein Assemblies for High-Relaxivity Contrast Agents: The Case of Gadolinium-Labeled Asparaginase, Bioconjugate Chem., 2022, 33, 2411–2419 CrossRef CAS PubMed.
- C. Luchinat, G. Parigi and E. Ravera, Water and Protein Dynamics in Sedimented Systems: A Relaxometric Investigation, ChemPhysChem, 2013, 14, 3156–3161 CrossRef CAS PubMed.
- J. G. de la Torre, M. L. Huertas and B. Carrasco, HYDRONMR: prediction of NMR relaxation of globular proteins from atomic-level structures and hydrodynamic calculations, J. Magn. Reson., 2000, 147, 138–146 CrossRef PubMed.
- D. Kruk, A. Kasparek, E. Masiewicz, K. Kolodziejski, R. Cybulski and B. Nowak, Water Dynamics in Highly Concentrated Protein Systems—Insight from Nuclear Magnetic Resonance Relaxometry, Int. J. Mol. Sci., 2023, 24, 4093 CrossRef CAS PubMed.
- R. G. Bryant, D. Mendelson and C. C. Lester, The Magnetic Field Dependence of Proton Spin Relaxation in Tissues, Magn. Reson. Med., 1991, 21, 117–126 CrossRef CAS PubMed.
- G. Diakova, Y. A. Goddard, J.-P. Korb and R. G. Bryant, Changes in protein structure and dynamics as a function of hydration from 1H second moments, J. Magn. Reson., 2007, 189, 166–172 CrossRef CAS PubMed.
- G. Diakova, Y. A. Goddard, J.-P. Korb and R. G. Bryant, Water and Backbone Dynamics in a Hydrated Protein, Biophys. J., 2010, 98, 138–146 CrossRef CAS PubMed.
- C. C. Lester and R. G. Bryant, Water–proton nuclear magnetic relaxation in heterogeneous systems: hydrated lysozyme results, Magn. Reson. Med., 1991, 22, 143–153 CrossRef CAS PubMed.
- D. Kruk, E. Masiewicz, A. M. Borkowska, P. Rochowski, P. H. Fries, L. M. Broche and D. J. Lurie, Dynamics of Solid Proteins by Means of Nuclear Magnetic Resonance Relaxometry, Biomolecules, 2019, 9, 652 CrossRef CAS PubMed.
- D. Kruk, E. Masiewicz, M. Wojciechowski, M. Florek-Wojciechowska, L. M. Broche and D. J. Lurie, Slow dynamics of solid proteins – Nuclear magnetic resonance relaxometry versus dielectric spectroscopy, J. Magn. Reson., 2020, 314, 106721 CrossRef CAS PubMed.
- P. H. Fries and E. Belorizky, Simple expressions of the nuclear relaxation rate enhancement due to quadrupole nuclei in slowly tumbling molecules, J. Chem. Phys., 2015, 143, 044202 CrossRef PubMed.
- M. R. Ruggiero, S. Baroni, S. Pezzana, G. Ferrante, S. Geninatti Crich and S. Aime, Evidence for the Role of Intracellular Water Lifetime as a Tumour Biomarker Obtained by In Vivo Field-Cycling Relaxometry, Angew. Chem., Int. Ed., 2018, 57, 7468–7472 CrossRef CAS PubMed.
- E. Masiewicz, G. P. Ashcroft, D. Boddie, S. R. Dundas, D. Kruk and L. M. Broche, Towards applying NMR relaxometry as a diagnostic tool for bone and soft tissue sarcomas: a pilot study, Sci. Rep., 2020, 10, 14207 CrossRef CAS PubMed.
- N. Bloembergen and L. O. Morgan, Proton relaxation times in paramagnetic solutions. Effects of electron spin relaxation, J. Chem. Phys., 1961, 34, 842–850 CrossRef CAS.
- G. Parigi, E. Ravera and C. Luchinat, Magnetic susceptibility and paramagnetism-based NMR, Prog. Nucl. Magn. Reson. Spectrosc., 2019, 114–115, 211–236 CrossRef CAS PubMed.
- F. Carniato, M. Ricci, L. Tei, F. Garello, C. Furlan, E. Terreno, E. Ravera, G. Parigi, C. Luchinat and M. Botta, Novel Nanogels Loaded with Mn(II) Chelates as Effective and Biologically Stable MRI Probes, Small, 2023, 19, 2302868 CrossRef CAS PubMed.
- M. A. Kaster, M. D. Levasseur, T. G. W. Edwardson, M. A. Caldwell, D. Hofmann, G. Licciardi, G. Parigi, C. Luchinat, D. Hilvert and T. J. Meade, Engineered Nonviral Protein Cages Modified for MR Imaging, ACS Appl. Bio Mater., 2023, 6, 591–602 CrossRef CAS PubMed.
- J.-H. Tang, H. Li, C. Yuan, G. Parigi, C. Luchinat and T. J. Meade, Molecular Engineering of Self-Immolative Bioresponsive MR Probes, J. Am. Chem. Soc., 2023, 145, 10045–10050 CrossRef CAS PubMed.
- M. Bennati, C. Luchinat, G. Parigi and M.-T. Türke, Water proton relaxation dispersion analysis on a nitroxide radical provides information on the maximal signal enhancement in Overhauser dynamic nuclear polarization experiments, Phys. Chem. Chem. Phys., 2010, 12, 5902–5910 RSC.
- L. P. Hwang and J. H. Freed, Dynamic Effects of Pair Correlation Functions on spin Relaxation by Transitional Diffusion in Liquids, J. Chem. Phys., 1975, 63, 4017–4025 CrossRef CAS.
- C. F. Polnaszek and R. G. Bryant, Nitroxide radical induced solvent proton relaxation: measurement of localized translational diffusion, J. Chem. Phys., 1984, 81, 4038–4045 CrossRef CAS.
- J. H. Freed, Dynamic effects of pair correlation functions on spin relaxation by translational diffusion in liquids. II. Finite jumps and independent T1 processes, J. Chem. Phys., 1978, 68, 4034–4037 CrossRef CAS.
- I. Bertini, O. Galas, C. Luchinat and G. Parigi, A computer program for the calculation of paramagnetic enhancements of nuclear relaxation rates in slowly rotating systems, J. Magn. Reson., Ser. A, 1995, 113, 151–158 CrossRef CAS.
- I. Bertini, J. Kowalewski, C. Luchinat, T. Nilsson and G. Parigi, Nuclear spin relaxation in paramagnetic complexes of S = 1: electron spin relaxation effects, J. Chem. Phys., 1999, 111, 5795–5807 CrossRef CAS.
- D. Kruk, T. Nilsson and J. Kowalewski, Nuclear spin relaxation in paramagnetic systems with zero-field splitting and arbitrary electron spin, Phys. Chem. Chem. Phys., 2001, 3, 4907–4917 RSC.
- C.-Y. Chou, M. Abdesselem, C. Bouzigues, M. Chu, A. Guiga, T.-H. Huang, F. Ferrage, T. Gacoin, A. Alexandrou and D. Sakellariou, Ultra-wide range field-dependent measurements of the relaxivity of Gd1−xEuxVO4 nanoparticle contrast agents using a mechanical sample-shuttling relaxometer, Sci. Rep., 2017, 7, 44770 CrossRef CAS PubMed.
- A. A. Smith, N. Bolik-Coulon, M. Ernst, B. H. Meier and F. Ferrage, How wide is the window opened by high-resolution relaxometry on the internal dynamics of proteins in solution?, J. Biomol. NMR, 2021, 75, 119–131 CrossRef CAS PubMed.
- M. W. Clarkson, M. Lei, E. Z. Eisenmesser, W. Labeikovsky, A. Redfield and D. Kern, Mesodynamics in the SARS nucleocapsid measured by NMR field cycling, J. Biomol. NMR, 2009, 45, 217–225 CrossRef CAS PubMed.
- S. F. Cousin, P. Kadeřávek, N. Bolik-Coulon, Y. Gu, C. Charlier, L. Carlier, L. Bruschweiler-Li, T. Marquardsen, J.-M. Tyburn, R. Brüschweiler and F. Ferrage, Time-Resolved Protein Side-Chain Motions Unraveled by High-Resolution Relaxometry and Molecular Dynamics Simulations, J. Am. Chem. Soc., 2018, 140, 13456–13465 CrossRef CAS PubMed.
- N.-A. Lakomek, K. F. A. Walter, C. Farès, O. F. Lange, B. L. Groot, H. Grubmüller, R. Brüschweiler, A. Munk, S. Becker, J. Meiler and C. Griesinger, Self-consistent residual dipolar coupling based model-free analysis for the robust determination of nanosecond to microsecond protein dynamics, J. Biomol. NMR, 2008, 41, 139–155 CrossRef CAS PubMed.
- L. Salmon, G. Bouvignies, P. Markwick and M. Blackledge, Nuclear Magnetic Resonance Provides a Quantitative Description of Protein Conformational Flexibility on Physiologically Important Time Scales, Biochemistry, 2011, 50, 2735–2747 CrossRef CAS PubMed.
- A. S. Maltsev, A. Grishaev, J. Roche, M. Zasloff and A. Bax, Improved Cross Validation of a Static Ubiquitin Structure Derived from High Precision Residual Dipolar Couplings Measured in a Drug-Based Liquid Crystalline Phase, J. Am. Chem. Soc., 2014, 136, 3752–3755 CrossRef CAS PubMed.
- A. L. Lee, P. F. Flynn and A. J. Wand, Comparison of 2H and 13C NMR Relaxation Techniques for the Study of Protein Methyl Group Dynamics in Solution, J. Am. Chem. Soc., 1999, 121, 2891–2902 CrossRef CAS.
- P. Schanda, M. Huber, J. Boisbouvier, B. H. Meier and M. Ernst, Solid-State NMR Measurements of Asymmetric Dipolar Couplings Provide Insight into Protein Side-Chain Motion, Angew. Chem., Int. Ed., 2011, 50, 11005–11009 CrossRef CAS PubMed.
- X. Xiang, A. L. Hansen, L. Yu, G. Jameson, L. Bruschweiler-Li, C. Yuan and R. Brüschweiler, Observation of Sub-Microsecond Protein Methyl-Side Chain Dynamics by Nanoparticle-Assisted NMR Spin Relaxation, J. Am. Chem. Soc., 2021, 143, 13593–13604 CrossRef CAS PubMed.
- C. Champion, M. Lehner, A. A. Smith, F. Ferrage, N. Bolik-Coulon and S. Riniker, Unraveling motion in proteins by combining NMR relaxometry and molecular dynamics simulations: a case study on ubiquitin, J. Chem. Phys., 2024, 160, 104105 CrossRef CAS PubMed.
- P. Kadeřávek, N. Bolik-Coulon, S. F. Cousin, T. Marquardsen, J.-M. Tyburn, J.-N. Dumez and F. Ferrage, Protein Dynamics from Accurate Low-Field Site-Specific Longitudinal and Transverse Nuclear Spin Relaxation, J. Phys. Chem. Lett., 2019, 10, 5917–5922 CrossRef PubMed.
- N. Salvi, V. Zapletal, Z. Jaseňáková, M. Zachrdla, P. Padrta, S. Narasimhan, T. Marquardsen, J.-M. Tyburn, L. Žídek, M. Blackledge, F. Ferrage and P. Kadeřávek, Convergent views on disordered protein dynamics from NMR and computational approaches, Biophys. J., 2022, 121, 3785–3794 CrossRef CAS PubMed.
- M. F. Roberts, Q. Cui, C. J. Turner, D. A. Case and A. G. Redfield, High-Resolution Field-Cycling NMR Studies of a DNA Octamer as a Probe of Phosphodiester Dynamics and Comparison with Computer Simulation, Biochemistry, 2004, 43, 3637–3650 CrossRef CAS PubMed.
- M. F. Roberts and A. G. Redfield, High-Resolution 31P Field Cycling NMR as a Probe of Phospholipid Dynamics, J. Am. Chem. Soc., 2004, 126, 13765–13777 CrossRef CAS PubMed.
- M. F. Roberts, A. G. Redfield and U. Mohanty, Phospholipid Reorientation at the Lipid/Water Interface Measured by High Resolution 31P Field Cycling NMR Spectroscopy, Biophys. J., 2009, 97, 132–141 CrossRef CAS PubMed.
- V. N. Sivanandam, J. Cai, A. G. Redfield and M. F. Roberts, Phosphatidylcholine “Wobble” in Vesicles Assessed by High-Resolution 13C Field Cycling NMR Spectroscopy, J. Am. Chem. Soc., 2009, 131, 3420–3421 CrossRef CAS PubMed.
- M. F. Roberts and A. G. Redfield, Phospholipid bilayer surface configuration probed quantitatively by 31P field-cycling NMR, Proc. Natl. Acad. Sci. U. S. A., 2004, 101, 17066–17071 CrossRef CAS PubMed.
- M. Pu, J. Feng, A. G. Redfield and M. F. Roberts, Enzymology with a Spin-Labeled Phospholipase C: Soluble Substrate Binding by 31P NMR from 0.005 to 11.7 T, Biochemistry, 2009, 48, 8282–8284 CrossRef CAS PubMed.
- M. M. Rosenberg, A. G. Redfield, M. F. Roberts and L. Hedstrom, Dynamic Characteristics of Guanosine-5′-monophosphate Reductase Complexes Revealed by High-Resolution 31P Field-Cycling NMR Relaxometry, Biochemistry, 2018, 57, 3146–3154 CrossRef CAS PubMed.
- Y. Wei, B. Stec, A. G. Redfield, E. Weerapana and M. F. Roberts, Phospholipid-binding Sites of Phosphatase and Tensin Homolog (PTEN): EXPLORING THE MECHANISM OF PHOSPHATIDYLINOSITOL 4,5-BISPHOSPHATE ACTIVATION, J. Biol. Chem., 2015, 290, 1592–1606 CrossRef PubMed.
- C. S. Gradziel, Y. Wang, B. Stec, A. G. Redfield and M. F. Roberts, Cytotoxic Amphiphiles and Phosphoinositides Bind to Two Discrete Sites on the Akt1 PH Domain, Biochemistry, 2014, 53, 462–472 CrossRef CAS PubMed.
- M. Pu, A. Orr, A. G. Redfield and M. F. Roberts, Defining Specific Lipid Binding Sites for a Peripheral Membrane Protein in Situ Using Subtesla Field-cycling NMR, J. Biol. Chem., 2010, 285, 26916–26922 CrossRef CAS PubMed.
- M. Roberts, B. Stec, C. Gradziel, Y. Wei and A. Redfield, High Resolution Field Cycling NMR Relaxometry Identifies Novel Phospholipid Binding Sites on PTEN and the Akt1 PH Domain, FASEB J., 2015, 29, 886.17 Search PubMed.
- Z. Wang, S. Pisano, V. Ghini, P. Kadeřávek, M. Zachrdla, P. Pelupessy, M. Kazmierczak, T. Marquardsen, J.-M. Tyburn, G. Bouvignies, G. Parigi, C. Luchinat and F. Ferrage, Detection of Metabolite–Protein Interactions in Complex Biological Samples by High-Resolution Relaxometry: Toward Interactomics by NMR, J. Am. Chem. Soc., 2021, 143, 9393–9404 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2025 |






