Kinetic processes of interfacial transport of reactive species across plasma–water interfaces: the effect of temperature

Abstract

This work quantifies, through use of molecular dynamics (MD) simulations, the kinetic rates of physical surface processes occurring at a plasma–water interface. The probabilities of adsorption, absorption, desorption and scattering were computed for O₃, N₂O, NO₂, NO, OH, H₂O₂, HNO₂, HNO₃, and N₂O₅ as they interact with the interface at three water temperatures: 298 K, 323 K, and 348 K. Species are categorised into the short-residence group (O₃, N₂O, NO₂, and NO) and the long-residence group (OH, H₂O₂, HNO₂, HNO₃, and N₂O₅) based on their mean surface residence time. It is reported that the most probable process for the short-residence group is desorption, which limits their characteristic residence time at the interface to less than 100 ps, while the long-residence species experience a mixture of absorption and desorption, with a characteristic residence time exceeding 200 ps for many species in this group. With increasing water temperature, a universal decline in characteristic surface residence time is observed. It is found that the short-residence group experience a reduction in probability of desorption in favour of scattering, whereas the long-residence group experience a reduction in probability of adsorption in favour of absorption and desorption. The data reported in this work facilitate the development of a basic surface kinetic model, which was used to find that tuning the plasma toward the production of HNO₃ will result in an increase in the rate of uptake of reactive nitrogen species by a factor of 250%.

---

1. Introduction

The question of how plasma-generated reactive species are transported across a plasma–water interface is crucial, with broad implications for various scientific and technological fields where plasma activates water.^1–4 Understanding the behaviour of these reactive species at a plasma–water interface holds significance for applications such as environmental remediation,^5,6 materials science⁷ and biomedicine.^3,8–10 Plasma-generated reactive species, particularly H₂O₂,^11,12 are known for their strong antimicrobial properties^13–15 and ability to treat toxic organic compounds in wastewater,^16,17 occupying key roles in plasma-based sterilization methods.^18–20

A key step to investigate the transport of plasma-generated reactive species across a plasma–water interface is to describe how a plasma–water interface differs from a gas–water interface. Since theory and measurements for the multiphase transport of reactive species across a gas–water interface are widely available,^21–24 it is reasonable to question how much of that knowledge is applicable to a plasma–water interface. The presence of plasma at the surface of water drives multiple processes that are unique to it; these include the application of an electric field, enhanced chemical reactivity due to the presence of reactive species, mechanical convection, and heat transfer. Multiple studies have investigated the electric field at such interfaces, reporting a typical strength in the order of 10⁴ to 10⁵ V m⁻¹.^25,26 Such values are much lower than 10⁹ V m⁻¹, the strength at which the electric field induces significant structural and behavioural changes in water.^27–29 Chemically, the typical plasma densities in atmospheric pressure plasmas, along with the densities of generated reactive species (assuming no significant accumulation) are on the order of 10²¹ m⁻³,³⁰ which is seven orders of magnitudes lower than the density of liquid water at ambient conditions (around 10²⁸ m⁻³). When converted to surface densities, this means that for every molecule of a reactive species at the interface, there are approximately 50,000 surface water molecules. This suggests that the characteristics of water at the interface are minimally impacted by the presence of reactive species as their influence is negligible. Mechanically, despite the very dilute nature of the plasma, it has been shown in multiple studies that the interaction at the interface is significant enough to drive a flow in the bulk of the water.^26,31–33 In addition to the observed macroscopic flow, smaller and faster perturbations exist, such as the Kelvin–Helmholtz instability.³¹ Thermally, most experiments where the plasma interacts directly with water report a significant increase in the temperature of the bulk water.^34–36 Based on this discussion, it is reasonable to describe the plasma–liquid interface as a special case of the gas–liquid interface where the water experiences a shear turbulent flow at an elevated temperature, as a first approximation.

Most studies on the transport of gaseous species across a gas–water interface were conducted under equilibrium conditions, under which the interfacial transport can be described by Henry's law.³⁷ Indeed, this assumption is often made even in explicit treatment of a plasma–water interface.¹⁷ Given that nonthermal plasmas are far from equilibrium, the applicability of Henry's law is questionable, and a kinetic description is needed. In such a description, a molecule of a reactive species arriving from the plasma phase to the interface may experience a chemical process such as a chemical reaction, or may experience a physical process such as thermal or mass accommodation. In this work, we take thermal accommodation to mean that the radical arriving to the interface has had enough time interacting with water molecules such that its kinetic energy is equilibrated with that of the water molecules,³⁸ and mass accommodation is defined as the probability that a molecule residing at the interface will be absorbed into the bulk phase.^39,40 Therefore, quantifying the characteristic timescales and probabilities of such processes is vital for constructing a detailed model of the surface in plasma liquid interactions.⁴¹ Indeed, in a comprehensive 2016 review of plasma–liquid interactions, Bruggeman et al. concluded that understanding the transport and chemistry of reactive species at the plasma–liquid interface is a key challenge in the field.⁴²

To build a kinetic description of the interfacial transport of reactive species at the gas–water interface, previous work has been undertaken focusing on the thermal and mass accommodation of a variety of reactive species in the context of atmospheric chemistry. One approach was to compute the free energy of solvation for a variety of reactive species (notably O₃, OH and H₂O₂) via molecular dynamics (MD) simulations, subsequently computing the probability of surface effects such as adsorption, absorption and desorption.^38,43 However, this approach has proven challenging as the calculated probabilities depend upon how they are derived from the solvation energy. An alternative, more intuitive approach has since emerged, which has been applied to a wider range of species including N₂O₅, NO₂, HO₂ and CH₃NH₂.^4,38,44–47 In this approach, a molecule is bombarded against a slab of water and its fate; namely whether it is scattered, absorbed, adsorbed or desorbed, is determined within a timeframe. By repeating this process over sufficiently many runs it is possible to quantify the probability of each individual process.⁴⁸ Notably, work by Vieceli et al.⁴ using this approach applies it to O₃ and OH, reporting that an O₃ molecule has an approximate desorption probability of 65% on the water surface, an adsorption probability of 20%, and an absorption probability of 4%. The corresponding figures for OH were found to be 5%, 57% and 33% respectively. This work aims to investigate and quantify the mass accommodation processes of reactive species typically generated in air plasmas, these are H₂O₂, O₃, OH, N₂O, N₂O₅, HNO₂, HNO₃, NO and NO₂, as the water temperature is varied. Processes investigated include absorption, adsorption, scattering and desorption, as well as quantifying the characteristic residence time of a given species on the interface as function of temperature. The data reported in this work paves the way for the construction of detailed surface kinetic models of the reactive species at the plasma–water interface, capable of capturing the non-equilibrium nature of the transport of reactive species across the plasma–water interface. Mathematically, the processes analysed in this work can be represented as processes 1 to 3, which are desorption, adsorption and absorption respectively.

where M_(g) is the species M in the gas phase, M_(s) is the species M on the interface, and M_(l) is the species M in the liquid phase.

2. Methods

The MD simulations in this work were conducted using LAMMPS (version 8 Feb 2023).⁴⁹ The reactive species investigated were H₂O₂, OH, O₃, N₂O, N₂O₅, HNO₂, HNO₃, NO and NO₂ as these are the most frequently reported-on species in the context of air plasmas. The molecular geometries used for the simulated molecules were obtained from the Automated Topology Builder (ATB) repository,⁵⁰ which uses the GROMOS 54A7 force field.⁵¹ The repository utilises GAMESS-US, wherein the first stage the molecule is optimised at HF/STO-3G level of theory, followed by refinement stage where it is further optimised at B3LYP/6-31G level of theory. This is done assuming an implicit polarisable continuum model (PCM). The optimization process yields the geometry as well as the partial charges assigned to each atom in the molecule.⁵⁰ For water, the SPC/E model was used as this combination of force field is widely used.^52–55 Both force fields are nonreactive force fields, which restricts the investigated surface processes to physical processes as chemical reactions cannot be directly captured. Despite the existence of reactive force fields such as ReaxFF⁵⁶ that explicitly model bond formation, the size of the timesteps required to resolve these dynamics appropriately is too small to capture the timescale of the physical processes studied in this article. The size of the simulation domain was 31 Å × 31 Å × 150 Å. A slab of water consisting of 1000 molecules was created in the region of 0 < Z < 31 Å, leaving enough space for the studied molecule to be introduced into the simulation domain far from the surface of the water slab. These parameters were chosen to obtain a water density of approximately 1 g cm⁻³. To further verify the density, a hyperbolic tangent function was fit to the Z axis profile of the water slab. Selecting a cutoff density threshold of one-half the bulk maximum, a value of 30.75 Å was obtained. Taking the X and Y axes to both equal 31 Å according to spatial restriction due to the application of a periodic boundary condition, we found that the density of the slab to be 1.01 g cm⁻³. The Ewald summation method was used to calculate long-range coulombic interactions.⁵⁷ The Nosé–Hoover thermostat was used to control the system temperature,⁵⁸ which was set to three values for each species, being 298 K, 323 K and 348 K. The SHAKE algorithm was employed to keep the water molecules rigid.⁵⁹ The simulation box as well as the procedure used for generating the results are summarised in Fig. 1. The procedure for generating the reported data consisted of 3 stages: the equilibration phase, production phase, and post-processing analysis.

Fig. 1 (Left) A snapshot of the simulation system at the beginning of the simulation including the water (blue) slab and studied species (red/yellow). (Right) A flow chart describing the procedure followed in this work to generate the results.

In the water equilibration phase, the water slab was equilibrated for 2 nanoseconds in the canonical (NVT) ensemble with a timestep of 2 femtoseconds, for the three investigated temperatures. To prevent the slab from drifting in the box, an invisible atom of large mass was attached to the bulk. A snapshot of the system at the end of equilibration for each temperature was then used as the starting point for the subsequent bombardment simulations to circumvent the need to equilibrate the system for every run. In the production phase, a molecule was introduced into the simulation box at a distance, calculated from the centres of mass of the molecules, of 30 Å above the surface and assigned an initial velocity that directed it toward the water slab. Its interaction with the slab was quantified by recording the Z coordinate of the centre of mass of the molecule as function of time, and outputting that into a trajectory file. Note that the positions of all molecules are recorded using the centre of mass of the molecule. For each trajectory, the file begins recording this data as soon as the molecule's distance from the surface is equal to or less than 9 Å as this is the cut off used for the force field, defining the threshold at which the molecule starts to interact with the surface. If the molecule's Z coordinate is higher than 75 Å, which corresponds to the molecule leaving the surface after having interacted with it, the simulation was terminated to prevent the molecule from crossing the periodic boundary condition. The orientation of the molecule with respect to the surface, and its X and Y coordinates in the plane where it is introduced, were randomly assigned for each trajectory. The molecule is assigned an initial thermal velocity in the negative Z direction, calculated using eqn (4), which moves it toward the surface of the water. The molecule at this stage is excluded from the NVT ensemble until it reaches the surface.

where ν_rms is the root mean square velocity, k_B is the Boltzmann constant, T is temperature of the gas (set to 298 K for all simulations), and m is the mass of the molecule bombarding the water. This gas temperature was chosen based on preliminary findings that varying the impact velocity of neutral species has a marginal effect on the surface processes studied, as long as the impact velocity is not far off from the thermal velocity of the gas. Therefore, maintaining a constant temperature is sufficient and does not influence the conclusions drawn from these simulations. At least 200 runs per molecule for each water temperature were simulated. This number was determined through preliminary testing to be the minimum required number of trajectories to ensure correct sampling. This was done by sampling 1000 trajectories of one molecule and reducing the number of runs systematically until the results deviated significantly. It was found that the statistics provided by 200 trajectories deviated 5.2% from those obtained at 1000 trajectories. Therefore the 200-trajectory threshold was considered the minimum number of trajectories to compute meaningful statistics. For all species investigated in this work, 400 trajectories were generated up to 100 ps. Given that some species such as H₂O₂ and OH appeared to reside on the surface for exceedingly long periods of time if allowed, 200 trajectories for such species were run for up to 200 ps to provide a better insight into their behaviour on longer timescales. After trajectory files were collected for all investigated species, analysis was conducted for each molecule at each of the three liquid temperatures. Specifically, this is the computation of the desorption, scattering, absorption and adsorption event counts at the end of each trajectory file. To calculate the event counts and the probability of the process subsequently, the state of the molecule is categorised into one of the 4 categories based on its Z coordinate. This process is repeated for each trajectory for each species at each liquid temperature, generating a classification histogram for each species at 100 ps and 200 ps (for species that required longer run times), where the amplitude of each column represents the probability of the corresponding process, as explained in Fig. 2. The criterion for the classification requires the surface to be defined by a range of values in the Z axis, from Z_Smin to Z_Smax. However, no universal definition for the interface region exists, as is evident by the array of the different methods used in previous works.^1,38,43,55 In this work, Z_Smax was defined to be equal to the coordinate of the water molecule with the highest Z coordinate plus half the cut-off distance of the force field, giving a typical value of 32 to 33 Å. While Z_Smin was defined to be equal to the coordinate of the water molecule with highest Z minus half the cutoff distance of the force field, yielding a typical value of approximately 26 Å. Surface roughness, defined as the condition under which the plane of the surface may at any given timestep not be perpendicular to the Z axis, is accounted for in our surface definition by time-averaging where the Z coordinate of the surface is determined by averaging the density profile over a million timesteps. The classification criteria were as follows:

Fig. 2 Illustration of the classification criteria used to quantify the probability of the individual surface processes and explaining the procedure followed for the quantification.

Scattering: a species is considered scattered if it resides on the water surface for less time than required to reach thermal equilibrium with the water slab. This definition renders scattering phenomenologically distinct from desorption, given that there is not sufficient contact with the surface to facilitate significant energy exchange. This value was chosen to be 2 picoseconds before being ejected back into the gas phase, based on previous work.^4,38,60 precisely, that is Z_Smin < Z_molecule < Z_Smax for less than 2 ps. Notably, there is some contention in the literature regarding the thermal equilibration time, with some works reporting that it can take an interval on the order of 10 ps or longer for the kinetic energy of some of the investigated molecules to equilibrate with that of the bulk.⁶¹ However, an analysis of time-dependent kinetic energy fluctuation with respect to ensemble average by Vieceli et al. yields the general result that 2 ps is sufficient time for a molecule to dissipate its excess kinetic energy.⁴

Desorption: if the species is not on or below the surface at the end of the simulation, but was not scattered, then it is considered desorbed, that is: Z_molecule > Z_Smax at the end of the trajectory file. Absorption: if the species is below the surface at the end of the simulation, then it is considered absorbed, that is: Z_molecule < Z_Smin. Adsorption: if the species is on the surface at the end of the simulation, then it is considered adsorbed, that is: Z_Smin < Z_molecule < Z_Smax. It is worth noting that the investigated species, during the simulation, may undergo one or several of these processes during its trajectory, but only its state at the end of the trajectory is recorded. For example, a molecule residing on the water surface may become absorbed by entering the bulk but return to the surface for the remaining duration of the simulation. In this case, it is considered absorbed while under the surface, but will cease to be considered absorbed after returning to the surface. Ultimately, the classification for that trajectory will be adsorption.

3. Results and discussion

3.1. Validation of the simulation procedure

To verify that the results obtained in this work are physical, two validation approaches were followed. First, a comparison of the data obtained in this work to that already reported for similar conditions, which validates the simulation procedure. Second, considering that the temperature variance is a novel aspect of this work, the suitability of the employed force field to capture temperature variation is discussed. Most of the previous works focused on the processes that O₃ and OH experience at ambient conditions on the surface of water,^4,38 as such conditions are the most common in the context of atmospheric chemistry. O₃ and OH are chosen as representatives for hydrophobic and hydrophilic species, respectively. Fig. 3 shows the normalised time-dependent surface population of both species for the 298 K case as computed in this work in comparison to those reported in the literature. It should be noted that t = 0 in this figure is the time of arrival of the molecule to the interface from the gas phase for all trajectories. As time progresses, some trajectories leave the surface by either desorption or absorption, therefore the fraction shown on the Y axis of this figure indicates the ratio of the resident molecules at a given time to the overall number of molecules at the surface. A clear qualitative agreement exists between the presented results in this work and the reported results in the literature, showing the tendency of O₃ to completely leave the surface within 100 ps, where it is mostly desorbed due to its hydrophobic nature. The figure shows a similar agreement for OH, which stays for an extended period on the surface and is mostly lost to absorption. This is a reflection of its solvation energy, which has a pronounced minimum at the surface.³⁸ Quantitively, there are noticeable differences between the results reported here and those reported in the literature, particularly for OH. These stem largely from differences in the method used to classify whether the molecule is in the gas, interfacial or bulk phase. Some work has employed the solvent accessible surface area (SASA) technique, where the surface area of a molecule that is available to a solvent is calculated, and its phase inferred.³⁸ This approach precludes the requirement for an interface region, though at increased computational cost. Another reason is the difference in some of the force field parameters used. In this work we opted for consistency by using the GROMOS force field for all molecules. In the referred works, the force field parameters were collected from diverse sources, potentially arbitrarily. Despite the differences, the overall behaviour is similar and therefore the method followed in this work is valid for generating a similar type of data. It is worth noting that while the classical force field effectively models hydrogen bonding and other non-reactive interactions, and allows for a direction comparison to the literature in this case, it does not capture potential reactive pathways, such as OH recombination or reaction with the water surface.

Fig. 3 The time-dependent surface populations of O₃ and OH as computed in this work in comparison to those reported by Roselová¹et al. and Vieceli et al.⁴

The validation of the temperature trend is more challenging, as data on surface processes as a function of temperature for different molecules is scarce. However, there are multiple works reporting on the GROMOS force field's ability to capture the effect of different temperatures in the solvent.^51,62,63 Furthermore, considering that the decrease of solubility of gases in water with increasing temperature is a well-established phenomenon in physical chemistry, a simple test was conducted, computing the radial distribution function (RDF) of O₃ and HNO₃ molecules at the three investigated temperatures in this work. The RDF was computed and averaged over a trajectory of 1 ns in the bulk of the water slab shown in Fig. 1. The RDFs of O₃ and HNO₃ are shown in Fig. 4, which demonstrates a reduction in the peak of the RDF as the temperature of the solvent is increased, representing a weaker hydration shell which indirectly corresponds to lower solubility. While the decrease in this peak seems marginal, it is consistent in its amplitude to that reported for the RDF of water at different temperatures.⁶⁴ Quantitively, the RDF and the solubility of gases are fundamentally correlated, but their correlation is complex and far beyond the scope of this work.

Fig. 4 Time-averaged RDFs for O₃ and HNO₃ at the three studied water temperatures.

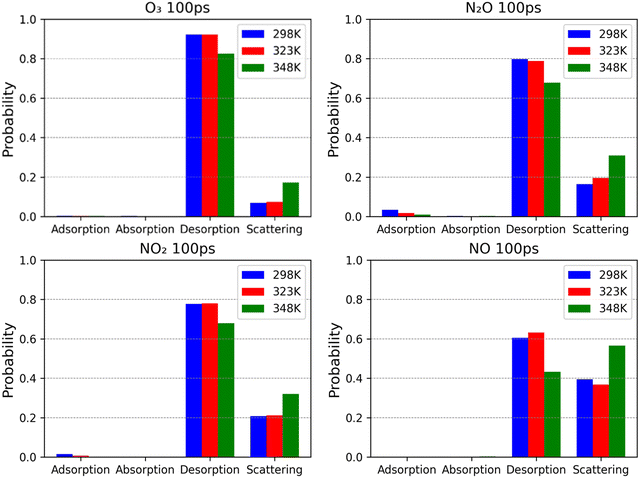
3.2. Probabilities of surface processes

As explained in Section 2, the outcome of each trajectory was categorised at two timeframes into adsorption, desorption, absorption and scattering, then the number of trajectories in each category was normalised by the overall number of trajectories to give the probability of a specific process. Based on the preliminary analysis of the results it was found that the species can be split into two groups with distinctive behaviours, differing mainly in surface residence time and absorption probability. The first group will be referred to as the short-residence group, that includes O₃, N₂O, NO and NO₂. The second is the long-residence group that consists of OH, H₂O₂, HNO₂, HNO₃, and N₂O₅. Fig. 5 shows the probability of these surface processes at 100 ps for the short-residence group at the three temperatures, while Fig. 6 shows the same figure for the long-residence group at two timeframes (100 ps and 200 ps). To give an example of how these figures can be interpreted; a species the probability of adsorption after 100 ps of arrival to the surface is 40%.

Fig. 5 The probabilities of four surface processes for the short-residence group over a duration of 100 ps, at each of the three investigated temperatures. Here, t = 0 indicates the time of arrival of the molecule to the surface. A total of 400 trajectories were used to generate each figure.

Fig. 6 The probabilities of four surface processes for the long-residence species group in periods of 100 ps (left hand column) and 200 ps (right hand column) at three temperatures of the water. In these figures t = 0 indicates the arrival time at the surface. A total of 200 trajectories were used to generate each 200 ps figure, whereas 400 were used for each 100 ps figure.

3.2.1. Relation to other descriptions of interfacial transport. To put the probabilities displayed in Fig. 5 and 6 into context, it is useful to discuss their meaning with respect to other descriptions of the interfacial transport of reactive species across a gas–water interface. The most widely used parameter in this context is Henry's coefficient H^cc, which describes the ratio of the solvated species concentration in water to that in the gas phase.⁶⁵ Based on their Henry's coefficient, the species analysed in this work can be categorised into poorly soluble (H^cc < 1) such as O₃, N₂O, NO and NO₂. Moderately soluble (1 < H^cc < 10³) including OH and N₂O₅, and highly soluble species (H^cc >10³) such as H₂O₂, HNO₂, and HNO₃.⁶⁵ Given that Henry's coefficient represents the tendency of a species to be solvated in water, it is expected to be correlated with the absorption probability in Fig. 5 and 6, anticipating that species with higher Henry's coefficients will have larger absorption probability. However, considering that Henry's coefficient describes a dynamic equilibrium between solvation and degassing,⁶⁶ it only gives an indication of the relative probability of absorption rather an absolute measure of it as Fig. 5 and 6 show. Furthermore, since this equilibrium requires a characteristic time to be reached, which is often much longer than 200 ps, Henry's coefficient describes the steady state behaviour rather than the transient behaviour shown in Fig. 5 and 6.

Another more general description of interfacial transport is given by the free energy of solvation or the potential of mean force (PMF) corresponding to the solvation process,⁴³ which can be computed using umbrella sampling.⁶⁷ This description encapsulates the same information contained in Henry's coefficient in addition to providing information on the likelihood of the species residing on the surface. Examining the PMF reported in the literature for most species analysed in this work, a common feature is the existence of a free energy minimum at the interface, indicating a preference for adsorption over immediate absorption (that is molecules residing on the surface for some time before being absorbed). This applies to O₃,⁴³ OH,⁴³ H₂O₂,⁴³ N₂O₅⁶⁸ and NO₂.⁶⁹ We could not find the PMF of NO, HNO₂ or HNO₃, however, a MD study has shown a strong preference for HNO₃ to reside on the surface as well,⁷⁰ indicating the presence of a minimum of the PMF there. Since the PMF describes the Gibbs free energy of solvation, it can be converted into a relative probability using the Boltzmann factor, providing information on the relative probability of adsorption and desorption, which makes a direct comparison between the PMF and the absolute probabilities presented in Fig. 5 and 6 impossible. Moreover, the relative probabilities described by the PMF represent steady state behaviour, providing further difficulty in making a direct comparison between the PMF and the probabilities reported in Fig. 5 and 6.

A third description of the interfacial transport of reactive species in water is given by the mass accommodation coefficient (α) which, unlike the earlier descriptions, provides kinetic information on the interfacial transport process; that is the fraction of the gaseous molecules being taken into the water bulk following thermal accommodation. Experimental determination of the mass accommodation coefficient of a species is challenging, and as a result their exact values vary widely.⁷¹ Even from the perspective of an atomistic simulation, inconsistency still exists due to the variety of the force fields used in the simulations. Nonetheless, the range of values reported for a given species is relatively consistent. For example, α of NO and NO₂ in water are reported to be less than 10⁻³,⁷² for O₃ and HNO₂ it is in the order of 10⁻²,^4,38,73,74 for OH, H₂O₂, and HNO₃ it is in the order of 10⁻¹.^38,40,73,75 The literature varies widely on the mass accommodation coefficient of N₂O₅, ranging from values close to 10⁻³ to values approaching 0.5.^73,76 We could not find α for N₂O reported anywhere in the literature. The mass accommodation coefficient is the closest parameter to be compared to the absorption probability of any species shown in Fig. 5 and 6. However, a small difference is that the mass accommodation coefficients describe the overall probability of absorption, which includes the direct absorption from the gas phase as well as the adsorption-mediated absorption,⁴³ which are dealt with as two separate processes in Fig. 5 and 6. Therefore, these figures paint the most comprehensive picture of the molecular processes occurring on the surface among all reported works in the literature.

3.2.2. Trends of surface processes at constant temperature (298 K). Once the molecule arrives to the surface, the most likely process to occur is adsorption, with an overwhelming probability of more than 95% across the two groups, reflecting the presence of the PMF minima on the surface as discussed earlier. The only alternative process upon arrival to the surface is scattering. This process has the highest probability for the short-residence group (that is O₃, N₂O, NO and NO₂), as Fig. 5 shows. As mentioned, our chosen timeframe for scattering is 2 ps. While scattering probabilities were observed to be small for most species, particularly in the long-residence group, it remains essential to treat scattering and desorption as distinct processes because they represent subtly but fundamentally different physical interactions. This distinction is particularly relevant for short-residence species, where scattering contributes significantly to their rapid departure from the surface.

As time progresses, the difference in the behaviour of the two groups becomes clearer. Within the first 100 ps, desorption has the highest probability among the short-residence group, with values ranging from 60% for NO to 92% for O₃. The absence of data for absorption in O₃ and NO may suggest that no absorption occurs. However, considering the finite number of trajectories used to generate these figures, the absence of a process merely indicates that its probability is less than the threshold detectable probability of 0.25%. Comparing this number to the values of α reported earlier for O₃ shows that this work slightly underestimates the probability of absorption. The probability of absorption as described in Fig. 5 for O₃ at a temperature of 298 K has already been reported for two other works.^4,38 Comparing our value to those, it is perfectly in line with O₃ behaviour reported by Roeselová et al.,³⁸ while it is underestimated in comparison to that reported by Vieceli et al.⁴ Since our values and those of Roeselová et al. are much closer to the experimental mass accommodation coefficient of O₃, we believe our estimate is closer to the real value than that reported by Vieceli et al. The behaviour of N₂O, NO₂ and NO is similar to that of O₃, as Fig. 5 shows. This demonstrates a perfect overlap between the short-residence group and the poorly soluble species as defined by Henry's coefficient. It is also quite consistent with the very low mass accommodation coefficient of NO₂ reported earlier. The long-residence group (OH, H₂O₂, HNO₂, HNO₃ and N₂O₅) is characterised by spending considerable periods of time on the surface compared to the short-residence group. Over time, their adsorption probabilities decline as the probabilities of absorption and desorption increase as Fig. 6 shows. A common feature among these 5 species is the non-negligible desorption probability, in the range of 5–10% in the 100 ps timeframe. This explains why highly soluble species such as H₂O₂, HNO₂, and HNO₃, with H^cc approaching 10⁶ have mass accommodation coefficients in the order of 10⁻² to 10⁻¹; desorption in this case works as a limiting process, setting the characteristic time needed for the solvated concentration to reach its steady state value. A distinctive feature among these species is how much of the absorbed species end up desorbing or absorbing. On one end there is N₂O₅, for which the desorption probability increases from 19% at 100 ps to 57% in 200 ps, while the absorption probability increases from 1% to 4% in the same time interval. This indicates that the reported results are more consistent with the lower estimate of the mass accommodation coefficient of N₂O₅ reported in the literature. On the other end there is HNO₃, for which there is an increase in the probability of absorption from 3% at 100 ps to 5% at 200 ps. For its probability of desorption, there is a decrease from 8% to 4% in the same interval. Other species such as OH, H₂O₂, and HNO₂, show an intermediate behaviour in which the increase in the desorption rate is more significant than that of absorption. However, the increase in the desorption rate of OH and H₂O₂, at ∼15% each remains higher than or roughly equal to that of adsorption. In general, the overall behaviour of the long-residence group is consistent with its solubility as described by Henry's coefficients and the reported mass accommodation coefficients.

3.2.3. Temperature effect. It is a well-established fact that the solubility of gases in water decreases as the water temperature is increased.⁷⁷ This is evident from the temperature dependence of Henry's coefficient. However, that does not directly correlate to the kinetic nature of these processes at the surface. As expected, examining the temperature trend observed in Fig. 5 and 6 shows a clear shift in the probabilities of adsorption and absorption toward desorption and scattering. Quantifying this variation however reveals a noticeable consistency with the sensitivity of Henry's coefficient to water, which depends on the energy of solvation of the species. For example, Fig. 6 shows that desorption competes with adsorption for the most probable process within 200 ps for a temperature of 348 K for H₂O₂ and HNO₂, while HNO₃ seems to be the least affected by the increase in the temperature. Considering that the energy of solvation of H₂O₂ and HNO₂ are approximately 10 kcal mol⁻¹ and 9.7 kcal mol⁻¹ respectively,^43,78 and that of HNO₃ is 1.4 kcal mol⁻¹,⁷⁰ it becomes clear why H₂O₂ and HNO₂ are so sensitive to the temperature of water. The same trend applies to OH, with a solvation energy of 4.5 kcal mol⁻¹.⁴³ The outlier here is N₂O₅, which despite its low energy of solvation of 2.3 kcal mol⁻¹,⁶⁸ shows a high sensitivity to the temperature of the water. We have no firm explanation for this observation, however we hypothesise that considering the large molecular structure of N₂O₅, it is reasonable to expect a steric factor to have a noticeable influence on its surface kinetics. The molecule needs to be aligned in a specific orientation with respect to the water molecules at the surface to most advantageously form hydrogen bonds with them. As the temperature increases, the likelihood of this alignment becomes smaller, adding a steric effect to its adsorption at the surface. In the context of transition state theory, the steric factor is not part of the exponential factor, hence this hypothesis is consistent with the low energy of solvation of N₂O₅.

The response to the increase in the temperature of the short-residence group, namely O₃, N₂O, NO and NO₂, is different from the long-residence group, as the competition here is between desorption and scattering. An increase in temperature shows a shift from desorption to scattering, with the exception of NO, which is discussed below. Fundamentally, the result of both processes is the same in that the molecule is ejected from the surface, while the core difference is the interaction time with the surface. In that sense, the shift toward scattering as the temperature increases is a result of a reduced average residence time on the surface.

The increase in the temperature of the water from 298 K to 323 K appears to affect NO differently, wherein scattering probability decreases slightly, with a complementary increase in desorption probability. From 323 K to 348 K however, there is a sharp increase in scattering probability. This is seemingly anomalous, but in fact is due to choice of scattering threshold. While our selection of 2 ps is supported by previous works, it is possible that it is not appropriate for all species given the range of factors, such as mass of the investigated species,⁷⁹ that may impact thermal equilibration time. Fig. 7 can be used to illustrate this point. The surface residence probabilities for each temperature for NO transiently form the expected temperature trend at around 20 ps. Therefore, a scattering threshold set at 20 ps would reflect this temperature trend, though would deviate from the consensus of previous works. However, it is still favourable to use this threshold rather than calculate such a threshold for each species in this work, given the large range of species included.

Fig. 7 The time-dependent surface population for all species investigated in this work at the three investigated water temperatures. Note that O₃, N₂O, NO₂ and NO have data up to 100 ps because they approach zero within this timeframe. The solid lines indicate simulation data, and the dashed lines indicate an exponential fit.

3.3. The time-dependent surface population

As discussed in Section 3.2, all species experience surface interaction, however briefly. Since adsorption is the most common and best statistically sampled process and, given also that adsorption quantifies the residence time on the surface, it defines a time window in which chemical reactions may occur. In this section the trajectories are analysed based on the time they spent on the surface. That is, the number of trajectories on the surface for each timestep is computed, omitting all scattered trajectories. When a trajectory leaves the surface at a given time, the value of the population of the surface is decreased by 1 at that time. All plots are normalised to 1 at t = 0 (the moment of arrival to the surface) such that scattered trajectories are omitted. Fig. 7 shows the time-dependent surface residence probabilities for all species at all temperatures. Clearly, surface populations decrease exponentially with time, indicating first order kinetics. It should be noted that the decay in these plots is a result of a combination of desorption and absorption. The relative contribution of each process can be inferred from Fig. 5 and 6. Fig. 7 is an illustration of the basis on which the species were split into the two groups; the short residence group (O₃, N₂O, NO₂, and NO) leaves the surface within the first 100 ps, while the long-residence group exhibits variable behaviour. For example, OH, HNO₂, N₂O₅ and H₂O₂ seem to leave the surface at comparable rates. HNO₃ is the slowest at leaving the surface, almost exhibiting zeroth-order kinetics, as it has a strong preference to stay on the surface as discussed in Section 3.2. To provide a better overview of the characteristic residence times, the data shown in Fig. 7 were fit to a single decaying exponential and presented in Table 1.

Table 1 The characteristic residence time of the species on the surface as the temperature is varied, obtained by fitting the curves shown in Fig. 6 to a single decaying exponential. The unit displayed in the table is ps

Group	Species	298 K	323 K	348 K
Short residence	O3	20.5	17.5	14.1
	N2O	40.8	27.6	21.6
	NO2	23.9	20.2	16.8
	NO	12.1	9.7	8.9
Long residence	OH	597.4	251.8	242.4
	H2O2	296.3	136.3	132.6
	HNO2	561.3	454	208.1
	HNO3	669.3	550.5	289.8
	N2O5	292.5	116.7	96.1

---

The main influence of temperature on the characteristic residence time of the species is to cause a decrease in the residence time for all species. The most interesting aspect of this behaviour is N₂O₅, which experiences a reduction in characteristic residence time from 292.5 ps at 298 K to 96.1 ps at 348 K. As such, it is possible to postulate that N₂O₅ at elevated temperature ‘switches groups’ and acts as a short-residence species. The remaining species appear to stay in their corresponding groups. The species least affected by the temperature increase is N₂O, which shows an average decrease in the characteristic residence time of 10% per 25 K increase. On the other end, HNO₃ shows a decrease of 36% per 25 K increase. The rate of the decrease is nonlinear in most of the long-residence group, while it is linear in the short-residence group. Species such as HNO₃ and N₂O₅ show a noticeable change in the rate of variation in the curve, particularly at 348 K.

An interesting feature observed in Fig. 7 is the presence of small-scale fluctuations in the time-dependent surface populations for long-residence species such as HNO₃ and H₂O₂, and its complete absence in short-residence species such as O₃ and N₂O. These small-scale fluctuations are a result of trajectories that switch between adsorbed and absorbed states during the simulation. Similarly, some trajectories switch between desorbed and adsorbed states, albeit this occurs to a smaller extent in comparison to adsorption–absorption fluctuations. While the existence of these fluctuations may introduce a source of noise to the probabilities depicted in Fig. 5 and 6, their small amplitude in comparison to the overall trend supports its validity. The origin of these fluctuations stems from the previously discussed solvation free energy minimum present at the interface for the investigated species. It follows from this that after absorption, assuming the molecule stays close to the surface for some time, there should be a greater probability of returning to the surface than remaining in the bulk, and that this should be more pronounced for species with a greater surface free energy minimum, which is reflected in the literature.⁴³ Considering that only a small fraction of trajectories experiences these rapid fluctuations, proper quantification for this phenomenon requires much larger statistical sampling to provide accurate quantitative measures of their importance, thus it is beyond the scope of this work.

3.4. Implications on the plasma–water interfacial transport processes

Considering that the aim of the work presented here is to build a detailed picture of processes occurring at the plasma–water interface, it is important to put the results into perspective. At the plasma–water interface, it is possible to describe the surface population of a reactive species by eqn (5), which assumes that the surface is far from saturation, which is a reasonable condition considering the dilute nature of low temperature plasmas:

In eqn (5), n_s is the surface density of the reactive species, γ is the sticking coefficient, which is defined from Fig. 5 and 6 as 1 minus the scattering probability. n_g is the density of the species in the plasma phase, v_th is its thermal velocity. The first term describes the flux from the plasma phase to the interface. In the second and the third terms, k_des is the rate constant of the desorption process as described by eqn (1) and k_abs is the rate constant of the absorption in the bulk as described by eqn (2). The second and the third term on the right-hand side of eqn (5) can be summed into one term that describes the departure of the surface species from the interface, that is k_dep = k_abs + k_des. The departure rate can be directly estimated as 1/τ where τ is the characteristic residence time given in Table 1. The split of k_dep into k_abs and k_des is done based on the probabilities of desorption and absorption shown in Fig. 5 and 6, according to eqn (6).

where P_des is the normalised probability of desorption. The normalisation is done such that P_des + P_abs = 1. Similarly, k_abs is obtained by substituting P_abs, the normalised probability of absorption, in eqn (6). These rate constants are used to obtain n_s from eqn (6).

The same procedure was applied to all species and processed, and the corresponding rate constants are reported in Table 2. It should be noted that eqn (5) only describes the physical processes, implicitly lacking a description of chemical kinetics at the interface, as well as the processes of resurfacing and hopping along the interface, for which work on extending the description of eqn (5) is ongoing. Table 3 reports the sticking coefficients of the different species as a function of temperature.

Table 2 The kinetic rate constants for adsorption and desorption processes reported for the short and the long-residence groups

Group	Species	k des (s^−1)			k abs (s^−1)
		298 K	323 K	348 K	298 K	323 K	348 K
Short residence	O3	4.9 × 10^10	5.7 × 10^10	7.1 × 10^10	<2.7 × 10^8	<3 × 10^8	<4.3 × 10^8
	N2O	2.5 × 10^10	3.6 × 10^10	4.6 × 10^10	<1.4 × 10^8	<1.9 × 10^8	<2.8 × 10^8
	NO2	4.2 × 10^10	5 × 10^10	6 × 10^10	<2.3 × 10^8	<2.6 × 10^8	<3.5 × 10^8
	NO	8.3 × 10^10	1.0 × 10^11	1.1 × 10^11	<4.9 × 10^8	<5.8 × 10^8	<8.6 × 10^8
Long residence	OH	7 × 10^8	2.0 × 10^9	2.1 × 10^9	9.8 × 10^8	1.9 × 10^9	2 × 10^9
	H2O2	1.5 × 10^9	3.8 × 10^9	5 × 10^9	1.9 × 10^9	3.6 × 10^9	2.5 × 10^9
	HNO2	1.7 × 10^9	2.0 × 10^9	4.2 × 10^9	4.6 × 10^7	1.8 × 10^8	6.2 × 10^8
	HNO3	3.9 × 10^8	3.2 × 10^8	1.3 × 10^9	1.1 × 10^9	1.5 × 10^9	2.1 × 10^9
	N2O5	3.3 × 10^9	8.4 × 10^9	1 × 10^10	1.5 × 10^8	1.7 × 10^8	<6 × 10^7

---

Table 3 Sticking coefficients for all species as a function of temperature

Group	Species	γ
		298 K	323 K	348 K
Short-residence	O3	0.915	0.95	0.815
	N2O	0.920	0.96	0.810
	NO2	0.935	0.96	0.855
	NO	0.845	0.885	0.760
Long-residence	OH	0.985	0.995	0.975
	H2O2	0.995	0.995	0.995
	HNO2	0.995	1	0.970
	HNO3	0.995	1	0.985
	N2O5	0.975	0.970	0.940

---

Using eqn (5) and the data presented in Tables 2 and 3, it becomes clear that the uptake of short-residence reactive species into the water is a slow process. Among the long residence group on the other hand there is a noticeable variation in the rate of the uptake of the different species. An apt comparison is between HNO₂ and HNO₃. Hydrolysis of these species leads to the formation of nitrates and nitrites in the water, which is vital for many emerging applications relying on plasma activation of water. At room temperature, and assuming an equal density of 10²¹ m⁻³ for both species in the gas phase, the rate of bulk uptake, defined as the third term in the right-hand side of eqn (5) of HNO₂ is 2.54 × 10²¹ m⁻² s⁻¹, while that of HNO₃ is 6.32 × 10²² m⁻² s⁻¹. This shows that the flux of HNO₃ into the bulk is 25 times larger than that of HNO₂ assuming the same temperature and densities in the gas phase. Combining that with the characteristic time of hydrolysis (dissociation into H⁺ and an anion) of HNO₃ being in the order of 3 ps and that of HNO₂ in the order of 10 ns,⁸⁰ shows that the rate of activation by the plasma can be faster by 4 to 5 orders of magnitude if the formation of HNO₃ is promoted in the plasma. Therefore, tuning the plasma chemistry to maximise the formation of HNO₃ will lead to significantly faster activation rate.

4. Conclusions

This work presents one of the most comprehensive studies on the physical processes occurring at a plasma–liquid interface for 9 of the most widely encountered reactive species in the context of air plasmas. The study investigated adsorption, desorption, absorption and scattering probabilities for the investigated species on a longer timescale than reported for any species for which similar studies were conducted, to the best of the authors’ knowledge. The results reported in this work were found to be consistent with experimentally reported mass accommodation coefficients, as well as with the findings of other studies. In comparison to widely reported parameters describing the interfacial transport processes of gaseous species such as Henry's coefficients, the probabilities presented in this work are absolute probabilities that describe the kinetic rate of these processes, paving the way for a new generation of plasma–water interaction models where the chemical kinetics of the surface can be explicitly modelled.

The 9 species investigated were O₃, N₂O, NO, NO₂, OH, H₂O₂, HNO₂, HNO₃, and N₂O₅. It was found that these species can be split into two groups based on their characteristic residence times on the surface; a short-residence group consisting of O₃, N₂O, NO, and NO₂, while the rest fall into the long-residence group. A discussion of surface process probability at a constant temperature of 298 K finds that the short-residence group has a probability of desorption in the order of 95% within the first 100 ps of residence on the surface, followed by scattering as the second most probable process. Absorption has a probability of less than 0.5%. The behaviour of this group is fully consistent with its Henry's coefficient being less than 1, reflecting their poor solubility in water. It is also consistent with their mass accommodation coefficients being in the order of 10⁻³ to 10⁻².

The long-residence group on the other hand, shows that the most probable surface process in the first 100 ps is adsorption, which ranges from a minimum of ∼78% for N₂O₅ and H₂O₂ to a maximum of 90% for HNO₃. Noticeably, all the species in this group have a relatively large desorption probability of around 10–20%, which explains the low values of the mass accommodation coefficients, in the range of 10⁻² to 10⁻¹ despite their high Henry's coefficients that exceed 1000 for the majority of them. This indicates that a molecule of these species experiences multiple absorption and adsorption events before ultimately being desorbed. On a longer timeframe of 200 ps, the probability of adsorption decreases, with the sharpest decrease occurring in N₂O₅, dropping from 78% at 100 ps to 37% at 200 ps. In contrast, HNO₃ experienced the lowest decrease, remaining at ∼90% for both timeframes. The decrease in the adsorption probability manifests foremost as an increase in the probability of desorption, followed by absorption.

The influence of the temperature of water was also investigated in this work, since the plasma–water interface was modelled as hot water as a first approximation. For the short-residence group, the increase in the temperature manifested as a reduction in the desorption probability and an increase in the scattering probability. For the long-residence group, the temperature increase shifted the probability from adsorption and absorption to desorption. The residence time of all species decreased as the temperature increased, the most notable behaviour is that of N₂O₅, which experiences a significant reduction in its residence time to the point that it can be counted as a short-residence species at elevated water temperature.

Given that the scope of this work lies within the study of strictly physical processes at the plasma–water interface, it follows that a major limitation is not accounting for the chemical reactions that many of these reactive species may experience at the surface. Our choice of the force field was made so that it provides a broad coverage of as many species that can be encountered in plasma conditions as possible. While this approach offers a flexible “recipe” extendable to other plasma types, fully capturing reactivity requires a reactive force field (such as ReaxFF) equipped with plasma-optimised parameters, which are not yet available. Addressing this limitation is a work in progress. Nonetheless, a basic kinetic model describing the uptake of HNO₂ and HNO₃ into the water was built using the data computed in this work. It was found that the uptake flux, the rate at which the species is solvated, of reactive nitrogen species at the plasma–liquid interface can be 250% times faster if the plasma chemistry is tuned to maximise the production of HNO₃.

Data availability

The data supporting this article has been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge support of Engineering and Physical Sciences Research Council (EPSRC) Grant No. EP/T000104/1. We would like to acknowledge Dr Martin Stroet from the University of Queensland for his assistance with open-shell molecular models.

References

1. M. Roeselová, J. Vieceli, L. X. Dang, B. C. Garrett and D. J. Tobias, J. Am. Chem. Soc., 2004, 126, 16308–16309.
2. P. Vanraes and A. Bogaerts, Appl. Phys. Rev., 2018, 5(3), 031103.
3. R. Zhou, R. Zhou, P. Wang, Y. Xian, A. Mai-Prochnow, X. Lu, P. J. Cullen, K. Ostrikov and K. Bazaka, J. Phys. D: Appl. Phys., 2020, 53, 303001.
4. J. Vieceli, M. Roeselová, N. Potter, L. X. Dang, B. C. Garrett and D. J. Tobias, J. Phys. Chem. B, 2005, 109, 15876–15892.
5. Y. Y. Zhao, T. Wang, M. P. Wilson, S. J. MacGregor, I. V. Timoshkin and Q. C. Ren, IEEE Trans. Plasma Sci., 2016, 44, 2084–2091.
6. D. Gimžauskaitė, A. Tamošiūnas, M. Aikas and R. Uscila, Environ. Res., 2023, 229, 115976.
7. K. Takenaka and Y. Setsuhara, Jpn. J. Appl. Phys., 2013, 52, 11NE04.
8. S. Kim and C.-H. Kim, Biomedicines, 2021, 9(11), 1700.
9. H.-R. Metelmann, T. Von Woedtke and K.-D. Weltmann, Comprehensive clinical plasma medicine: cold physical plasma for medical application, Springer, 2018.
10. N. K. Kaushik, B. Ghimire, Y. Li, M. Adhikari, M. Veerana, N. Kaushik, N. Jha, B. Adhikari, S.-J. Lee and K. Masur, Biol. Chem., 2019, 400, 39–62.
11. M. N. Bathina, S. Mickelsen, C. Brooks, J. Jaramillo, T. Hepton and F. M. Kusumoto, J. Am. Coll. Cardiol., 1998, 32, 1384–1388.
12. M. Krebs, P. Bécasse, D. Verjat and J. Darbord, Int. J. Pharm., 1998, 160, 75–81.
13. K. S. Wong, N. S. L. Chew, M. Low and M. K. Tan, Processes, 2023, 11(7), 2213.
14. B. J. Juven and M. D. Pierson, J. Food Prot., 1996, 59, 1233–1241.
15. E. Linley, S. P. Denyer, G. McDonnell, C. Simons and J.-Y. Maillard, J. Antimicrob. Chemother., 2012, 67, 1589–1596.
16. O. Lesage, L. Falk, M. Tatoulian, D. Mantovani and S. Ognier, Chem. Eng. Process., 2013, 72, 82–89.
17. J. Foster, Phys. Plasmas, 2017, 24(5), 055501.
18. A. Sakudo, Y. Yagyu and T. Onodera, Int. J. Mol. Sci., 2019, 20, 5216.
19. T. G. Klämpfl, G. Isbary, T. Shimizu, Y.-F. Li, J. L. Zimmermann, W. Stolz, J. Schlegel, G. E. Morfill and H.-U. Schmidt, Appl. Environ. Microbiol., 2012, 78, 5077–5082.
20. H. Rauscher, O. Kylián, J. Benedikt, A. von Keudell and F. Rossi, ChemPhysChem, 2010, 11, 1382–1389.
21. T. Kamidollayev and J. P. Trelles, J. Phys. D: Appl. Phys., 2023, 56, 505203.
22. G. Uchida, A. Nakajima, K. Takenaka, K. Koga, M. Shiratani and Y. Setsuhara, IEEE Trans. Plasma Sci., 2015, 43, 4081–4087.
23. T. Brubaker, K. Ishikawa, H. Kondo, T. Tsutsumi, H. Hashizume, H. Tanaka, S. Knecht, S. Bilén and M. Hori, J. Phys. D: Appl. Phys., 2018, 52, 075203.
24. B. C. Garrett, G. K. Schenter and A. Morita, Chem. Rev., 2006, 106, 1355–1374.
25. P. Rumbach, J. P. Clarke and D. B. Go, Phys. Rev. E, 2017, 95, 053203.
26. A. Dickenson, J. Walsh and M. Hasan, J. Appl. Phys., 2021, 129(21), 213301.
27. M. Prasad, N. J. English and S. N. Chakraborty, J. Chem. Phys., 2023, 159(5), 054504.
28. S. V. Shevkunov and A. Vegiri, J. Mol. Struct. THEOCHEM, 2002, 593, 19–32.
29. A. Vegiri, J. Chem. Phys., 2002, 116, 8786–8798.
30. A. A. Fridman, M. Keidar and E. H. Choi, Plasma Biosciences and Medicine, Springer, 2023, pp. 1–34.
31. J. Lai, V. Petrov and J. E. Foster, IEEE Trans. Plasma Sci., 2018, 46, 875–881.
32. F. Mitsugi, S. Kusumegi, K. Nishida and T. Kawasaki, IEEE Trans. Plasma Sci., 2020, 49, 9–14.
33. C. T. Ryan, A. A. Darhuber, R. P. Kunnen, H. Gelderblom and A. Sobota, Sci. Rep., 2024, 14, 17152.
34. W. Hoeben, P. Van Ooij, D. Schram, T. Huiskamp, A. Pemen and P. Lukeš, Plasma Chem. Plasma Process., 2019, 39, 597–626.
35. F. Judée, S. Simon, C. Bailly and T. Dufour, Water Res., 2018, 133, 47–59.
36. J. Silsby, A. Dickenson, J. Walsh and M. Hasan, Front. Phys., 2022, 10, 1045196.
37. R. Sander, Atmos. Chem. Phys., 2015, 15, 4399–4981.
38. M. Roeselová, P. Jungwirth, D. J. Tobias and R. B. Gerber, J. Phys. Chem. B, 2003, 107, 12690–12699.
39. C. Kolb, P. Davidovits, J. Jayne, Q. Shi and D. Worsnop, Prog. React. Kinet. Mech., 2002, 27, 1–46.
40. J. Ponche, C. George and P. Mirabel, J. Atmos. Chem., 1993, 16, 1–21.
41. P. Bruggeman, A. Bogaerts, J. Pouvesle, E. Robert and E. Szili, J. Appl. Phys., 2021, 130(20), 200401.
42. P. J. Bruggeman, M. J. Kushner, B. R. Locke, J. G. E. Gardeniers, W. G. Graham, D. B. Graves, R. C. H. M. Hofman-Caris, D. Maric, J. P. Reid, E. Ceriani, D. Fernandez Rivas, J. E. Foster, S. C. Garrick, Y. Gorbanev, S. Hamaguchi, F. Iza, H. Jablonowski, E. Klimova, J. Kolb, F. Krcma, P. Lukes, Z. Machala, I. Marinov, D. Mariotti, S. Mededovic Thagard, D. Minakata, E. C. Neyts, J. Pawlat, Z. L. Petrovic, R. Pflieger, S. Reuter, D. C. Schram, S. Schröter, M. Shiraiwa, B. Tarabová, P. A. Tsai, J. R. R. Verlet, T. von Woedtke, K. R. Wilson, K. Yasui and G. Zvereva, Plasma Sources Sci. Technol., 2016, 25, 053002.
43. P. S. Robert Vácha, Martin Mucha, Barbara J. Finlayson-Pitts and Pavel Jungwirth, J. Phys. Chem. A, 2004, 108, 11573–11579.
44. R. D. Hoehn, M. A. Carignano, S. Kais, C. Zhu, J. Zhong, X. C. Zeng, J. S. Francisco and I. Gladich, J. Chem. Phys., 2016, 144(21), 214701.
45. S. D. Belair, H. Hernandez and J. S. Francisco, J. Am. Chem. Soc., 2004, 126, 3024–3025.
46. B. Hirshberg, E. R. Molina, A. W. Götz, A. D. Hammerich, G. M. Nathanson, T. H. Bertram, M. A. Johnson and R. B. Gerber, Phys. Chem. Chem. Phys., 2018, 20, 17961–17976.
47. G. Murdachaew, M. E. Varner, L. F. Phillips, B. J. Finlayson-Pitts and R. B. Gerber, Phys. Chem. Chem. Phys., 2013, 15, 204–212.
48. R. J. Kee, M. E. Coltrin, P. Glarborg and H. Zhu, Chemically reacting flow: theory, modeling, and simulation, John Wiley & Sons, 2017.
49. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, Comput. Phys. Commun., 2022, 271, 108171.
50. A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, J. Chem. Theory Comput., 2011, 7, 4026–4037.
51. N. Schmid, A. P. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. E. Mark and W. F. van Gunsteren, Eur. Biophys. J., 2011, 40, 843–856.
52. G. D. Barbosa and C. H. Turner, J. Mol. Liq., 2023, 389, 122826.
53. V. Sundaram, A. V. Lyulin and B. R. Baumeier, J. Phys. Chem. B, 2020, 124, 11030–11039.
54. M. M. Reif, M. Winger and C. Oostenbrink, J. Chem. Theory Comput., 2013, 9, 1247–1264.
55. J. Razzokov, S. Fazliev, A. Kodirov, P. AttrI, Z. Chen and M. Shiratani, Int. J. Mol. Sci., 2022, 23, 6330.
56. T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik, H. M. Aktulga, T. Verstraelen, A. Grama and A. C. T. van Duin, npj Comput. Mater., 2016, 2(1), 1–14.
57. B. A. Wells and A. L. Chaffee, J. Chem. Theory Comput., 2015, 11, 3684–3695.
58. H. A. Posch, W. G. Hoover and F. J. Vesely, Phys. Rev. A:At., Mol., Opt. Phys., 1986, 33, 4253.
59. J.-P. Ryckaert, G. Ciccotti and H. J. Berendsen, J. Comput. Phys., 1977, 23, 327–341.
60. A. Rajabpour, R. Seif, S. Arabha, M. M. Heyhat, S. Merabia and A. Hassanali, J. Chem. Phys., 2019, 150(11), 114701.
61. M. A. Wilson and A. Pohorille, J. Phys. Chem. B, 1997, 101, 3130–3135.
62. M. Stroet, M. Setz, T. Lee, A. K. Malde, G. van den Bergen, P. Sykacek, C. Oostenbrink and A. E. Mark, J. Phys. Chem. B, 2024, 128, 4602–4620.
63. Z. Gattin, S. Riniker, P. J. Hore, K. H. Mok and W. F. van Gunsteren, Protein Sci., 2009, 18, 2090–2099.
64. A. Soper, Chem. Phys., 2000, 258, 121–137.
65. R. Sander, Atmos. Chem. Phys., 2023, 23, 10901–12440.
66. D. V. Schroeder, An introduction to thermal physics, Oxford University Press, 2020.
67. J. Kästner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 932–942.
68. V. W. D. Cruzeiro, M. Galib, D. T. Limmer and A. W. Götz, Nat. Commun., 2022, 13, 1266.
69. M. T. Martins-Costa, J. M. Anglada, J. S. Francisco and M. F. Ruiz-López, Chem. - Eur. J., 2019, 25, 13899–13904.
70. J. M. Anglada, M. T. Martins-Costa, J. S. Francisco and M. F. Ruiz-Lopez, J. Am. Chem. Soc., 2020, 143, 453–462.
71. M. J. Gleichweit, M. A. Mohajer, D. P. B. Dit Avocat, M. E. Divéky, G. David and R. Signorell, Phys. Chem. Chem. Phys., 2024, 26, 16296–16308.
72. J. Lee and I. Tang, Atmos. Environ., 1988, 22, 1147–1151.
73. M. Leriche, L. Deguillaume and N. Chaumerliac, J. Geophys. Res.:Atmos., 2003, 108(14), 4433.
74. S. Mertes and A. Wahner, J. Phys. Chem., 1995, 99, 14000–14006.
75. M. Barth, S. W. Kim, W. Skamarock, A. L. Stuart, K. Pickering and L. Ott, Atmos. Chem. Phys., 2007, 7(18), 4709–4731.
76. G. Gržinić, T. Bartels-Rausch, A. Türler and M. Ammann, Atmos. Chem. Phys., 2017, 17, 6493–6502.
77. D. R. Lide, CRC handbook of chemistry and physics, CRC Press, 2004.
78. J. Y. Park and Y. N. Lee, J. Phys. Chem., 1988, 92, 6294–6302.
79. Y. Sheng, Y. Hu, Z. Fan and H. Bao, Phys. Rev. B, 2022, 105, 075301.
80. J. Silsby, S. Simon, J. Walsh and M. Hasan, Plasma Chem. Plasma Process., 2021, 41, 1363–1380.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04272g

---