 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The influence of halogen-mediated interactions on halogen abstraction reactions by formyl radicals†
Matias O.
Miranda
 ab,
Darío J. R.
Duarte
ab,
Darío J. R.
Duarte
 *a and
Victor M.
Rayón
*a and
Victor M.
Rayón
 *b
*b
aLaboratorio de Estructura Molecular y Propiedades, Departamento de Química, Facultad de Ciencias Exactas y Naturales y Agrimensura, Universidad Nacional del Nordeste, Corrientes, Argentina. E-mail: djr_duarte@hotmail.com; Tel: +54-3794473931
bDepartamento de Química Física y Química Inorgánica, Facultad de Ciencias, Universidad de Valladolid, Valladolid, Spain. E-mail: victormanuel.rayon@uva.es; Tel: +34-983423000
First published on 22nd January 2025
Abstract
This article reports a theoretical study on the halogen exchange reactions YX + CHO → Y + XCHO (with Y = F, Cl, Br; X = Cl, Br, I) carried out at a high level of accuracy using coupled-cluster based methodologies including CCSD(T)-F12, CCSD(T)/CBS and CCSDT(Q)Λ. Most of the reactions are exothermic at room temperature, with the exception of the reactions FI + CHO → F + ICHO and ClI + CHO → Cl + ICHO. Exothermicity follows two concurrent trends established by the strength of the bonds being cleaved and formed: Y = F < Cl < Br (X–Y bond strength) and X = Cl > Br > I (C–X bond strength). Regarding the topology of the potential energy surfaces, we find that at the CCSD level of theory only some processes present the expected reaction profile: a pre-reactive complex (preRC) followed by a transition state (TS) and a post-reactive complex (postRC). However, when triple excitations are taken into account, all reactions become barrierless with no preRC/TS along the reaction profile. We propose that halogen-mediated interactions through the σ-hole, which represent the driving force in the early stages of the title reactions, are responsible for the absence of a tight transition state. We suggest that the strength of these interactions formed during these processes triggers the onset of the halogen atom exchange, before the preRC is formed. Therefore, this study aims to show the relevant role of halogen-mediated interactions in the mechanism of reactions in which a halogen atom is abstracted by the formyl radical (CHO).
1 Introduction
The formyl radical (CHO) is an essential intermediate in both HOx cycles and hydrocarbon combustion in the atmosphere,1,2 where it is mainly produced due to the photolysis of aldehydes (especially formaldehyde) by sunlight. The CHO radical is an important intermediate in most hydrocarbon combustion systems and it also participates in reactions in the lower and upper atmosphere.3,4While the reactivity of the CHO radical towards different species of atmospheric interest has already been studied in the past,5–9 reactions between CHO and halogenated compounds have not been investigated in depth, with some exceptions.10,11 Therefore, additional reaction mechanisms need to be studied for a quantitative modeling of gas-phase reactions involved in tropospheric and stratospheric processes.
Certain halogenated species are known for participating in processes of stratospheric ozone (O3) favoring its destruction. Reservoirs of halogen atoms (RXAs) have a major influence on these processes, as they temporarily sequester reactive halogens and photochemically dissociate releasing halogen atoms into the environment. These halogen atoms (X) react with O3 to form O2 and the corresponding halogen monoxides (XO). Examples of inorganic RXAs are X2, YX, HOX, XNO2 and HX, where X and Y = Cl, Br, and I.12
An experimental study carried out by Timonen et al. showed that Cl2 and Br2 can react with CHO to form ClCHO and BrCHO, respectively.10 Experimental data show that the reaction with Br2 has a slightly negative activation energy (Ea) of −4.0 kJ mol−1, while the reaction with Cl2 has an Ea close to 0.0 kJ mol−1. The latter is in agreement with a joint experimental and theoretical study carried out by Ninomiya et al. in which the reaction Cl2 + CHO → Cl + ClCHO is described to occur with a negligible energy barrier.11 Theoretical calculations carried out in this study do not find any transition structure along the reaction path, just a single reaction intermediate which results from the “attachment of Cl2 to the carbon atom of HCO”. Interestingly, the Cl⋯Cl bond distance in this complex is quite large, 2.846 Å, so the bond “is almost cleaved”. The authors therefore suggest that this reaction proceeds through two loose transition states, one located at the entrance channel that leads to the reaction intermediate and the other one located between the intermediate and the products of the reaction.
Radical-molecule reactions (RMRs) usually have low Eas due to the high reactivity of the radicals which, in many cases, yields negative Ea.13–16 This fact can be understood if we consider that reaction paths present a potential energy curve (PEC) over the potential energy surface (PES) in which the formation of a pre-reactive complex (preRC) is observed before reaching a transition state (TS), whose energy remains below the energy of the isolated reactants. Thus, preRCs play a key role in order to elucidate both the mechanism and outcome of a RMR. The formation of preRCs, in the particular case of the reactions studied in this work, should involve some sort of halogen-mediated interaction between a halogen atom in YX and the carbon atom in CHO. The nature of this interaction becomes therefore of utmost importance to understand these radical exchange reactions.
In this work we have carried out a theoretical study of the reaction paths of the halogen exchange reactions YX + CHO → Y + XCHO, with Y = F, Cl, and Br and X = Cl, Br, and I:
| FCl + CHO → F + ClCHO | (R1) |
| Cl2 + CHO → Cl + ClCHO | (R2) |
| BrCl + CHO → Br + ClCHO | (R3) |
| FBr + CHO → F + BrCHO | (R4) |
| ClBr + CHO → Cl + BrCHO | (R5) |
| Br2 + CHO → Br + BrCHO | (R6) |
| FI + CHO → F + ICHO | (R7) |
| ClI + CHO → Cl + ICHO | (R8) |
| BrI + CHO → Br + ICHO | (R9) |
To the best of our knowledge, and with the exception of reaction (R1) as commented above, there are no previous studies on the mechanisms of these reactions.
2 Computational methods
2.1 Geometry optimizations and energetics
Equilibrium geometries and vibrational frequencies were computed using the singles and doubles coupled cluster method (CCSD),17–19 in conjunction with the all-electron 6-311+G(d,p) basis set as implemented in Gaussian 16 (G16).20 The all-electron (AE) 6-311G basis for iodine21 was downloaded from the basis set exchange,22 since it is not implemented in G16. These basis sets were augmented with a single set of polarization functions both on hydrogen and heavy atoms and an additional set of diffuse functions on the heavy atoms. In order to verify the nature of the transition states, we have followed the intrinsic reaction coordinate (IRC)23,24 for all the reactions where a transition structure was located. Only valence electrons were correlated (“frozen core approximation”). We have nevertheless checked that inclusion of outer core-valence electron correlation does not affect the topology of the potential energy surfaces. Default thresholds in the G16 program were used throughout. We also point out that G16 uses an unrestricted Hartree–Fock (UHF) reference in the CCSD calculations for open-shell systems.Alongside the location of stationary points on PES obtained at CCSD/6-311+G(d,p) as described above, accurate CCSD(T)18,25–27 PECs were calculated varying the distance between the C of CHO radical and the transferred halogen atom, X, of the YX compound [d(X⋯C)] for the whole set of reactions considered in this study. These calculations were carried out in conjunction with the aug-cc-pVTZ basis set.28–33 In the case of iodine, this basis set is used in conjunction with the ECP28MDF pseudopotential.33 CCSD(T) calculations were carried out with molpro 202234,35 using default thresholds. We point out that these calculations used a ROHF reference.
We have also carried out CCSD(T)/cc-pVQZ and CCSD(T)/aug-cc-pVQZ single point calculations and the resulting energies are extrapolated to the complete basis set limit (CBS) using a two-points n−3 extrapolation:
| En = ECBS + A·n−3 |
An alternative procedure to approach the CBS limit is the explicitly correlated coupled cluster method, CCSD(T)-F12. These calculations converge faster than canonical ones with respect to the one-particle expansion and therefore a 3-ζ quality basis set may be sufficient to get close to the CBS limit. In this study we report CCSD(T)-F12a36 PECs computed in conjunction with the cc-pVTZ-F12 basis set37 as implemented in molpro. The cc-pVTZ-F12 basis includes pseudo-potentials (PP) for both Br and I atoms,38 In molpro there exists an augmented correlation consistent basis set for chlorine, aug-cc-pVTZ-F12.39 It is worth mentioning that the cc-pVTZ-F12 basis set already includes s and p diffuse functions. Thus, the only difference with the aug-cc-pVTZ-F12 basis is that the latter has higher angular momentum d and f diffuse functions. We have, nevertheless carried out calculations with this augmented basis set as well but we found no significant differences between this basis and the non-augmented one.
In order to check the effect of a more accurate electron correlation treatment we carried out CCSDT and CCSDT(Q)Λ40–43 calculations along the reaction path for reaction (R2). It is well known that the good performance of CCSD(T), denoted as the “gold standard” method of quantum-chemical calculations, is mainly due to error compensation between the neglect of connected T4 and iterative T3 contributions.44 A similar error compensation appears to operate as well in CCSDT(Q)45 and this is the reason why we chose this specific methodology. CCSDT(Q)Λ calculations are significantly more expensive since they scale as O(N9) (where N is a measure of the size of the system).46 We have therefore carried out these calculations in conjunction with the cc-pVDZ and 6-311G* basis sets. The MRCC code with default thresholds has been used to perform these calculations.47 Finally, we point out that an atomic density initial guess was used for the cc-pVDZ calculations and the resulting density matrices used in turn as the initial guess for the 6-311G* basis set.
We checked that reactions (R1)–(R9) do not have a strong multi-reference character. We have used the t1 diagnostic in the transition state region which shows values below or slightly larger than 0.02 (for reactions that did not exhibit a transition state, namely, (R4), (R7), (R8) and (R9), the t1 diagnostic was determined at d(X⋯C) = 2.6 Å). We nevertheless carried out complete active space self-consistent field calculations (CASSCF) followed by multireference Rayleigh Schrödinger perturbation theory (CASPT2) for the (R2) reaction, that we have taken as a model (as it is the one with the highest t1 = 0.025) to corroborate that the shape of the PEC does not change significantly. The molpro code was used for these calculations. Since the multi-reference character in this reactions is not large and we are focusing on the usage of single reference methods we provide CASPT2‖CASSCF results in the ESI,† with further details about the calculations.
Finally, full PECs for reactions (R1)–(R9) were also obtained with several density functional approximations (DFAs) with the aug-cc-pVTZ basis set (aug-cc-pVTZ-PP for Br and I). Arranged by their rung on the Jacobs ladder, these are the chosen functionals: B3LYP (hybrid),48 M06-2X (hybrid-meta-GGA),49 ωB97XD (range-separated hybrid),50 B2PLYP-D3BJ,51 B2T-PLYP-D2,52 and mPW2PLYP-D253 (perturbatively corrected double hybrids). All DFT calculations were performed using the ORCA software suite (version 5.0.4)54,55 using default thresholds and algorithms, including integral approximations (RI-JK and RI-MP2 which is the default for double-hybrids).
For more detailed information on the methodology used, please refer to the methodology section in the ESI.†
2.2 Characterization of halogen-mediated interactions
Halogen-mediated interactions along the reaction paths were studied by analyzing the maps of electrostatic potentials (MEPs) on isosurfaces of electron density [ρ(r)]. These MEPs were explored from the spatial distributions of the total electrostatic potential [ϕ(r)] and ρ(r), which were calculated from the wavefunctions obtained at the M06-2X/aug-cc-pVTZ level with G16 software.20 The spin density [ρs(r)] topology was also studied on the CHO radical. The real-space functions of ρ(r), ϕ(r) and ρs(r) were obtained with the Multiwfn program.56 MEPs and isosurfaces of ρs(r) were visualized with Jmol57 and GaussView,58 respectively.3 Results and discussion
3.1 Halogen-mediated interactions between dihalogens and CHO radicals
The CHO radical has a MEP with minima at both C and O atoms. These minima are the preferred sites for interaction with an electrophile, especially via the O atom, which shows the lowest potential value (Fig. 1, left). However, halogen abstraction reactions (such as (R1)–(R9)) take place through the C atom, where the highest ρs(r) is located, indicating the site where the unpaired electron is most likely to be found (Fig. 1, right). Thus, two possible intermolecular complexes can be formed between YX and CHO, depending on whether the interaction takes place via the oxygen or carbon atoms. However, only the second possibility forms a truly preRC since the former is clearly not located along the reaction path.On the other hand, dihalides show a charge-depleted area, the σ-hole, characterized by a positive value of the MEP which is prone to interact with electron rich partners. The interaction of the positively charged σ-hole with a nucleophilic region gives rise to the so-called halogen bond (XB) interaction. The capabilities of dihalides as XB donors depend on the nature of their σ-hole. Table 1 shows the values of the electrostatic potential (Vs,max) which has been widely used as a descriptor of the ability of a given system to form a σ-hole interaction, as in the case of XBs.59,60 For a given halogen, X in YX, it is observed that Vs,max increases from Cl to I (that is, FCl < FBr < FI, and so on). On the other hand, for a given Y in YX, Table 1 shows that Vs,max increases in the opposite order: from Br to F (BrCl < Cl2 < FCl, etc.). Thus, the values of the electrostatic potential suggest that both the polarizability of the interacting halogen (X in YX) and the electronegativity of the partner (Y) favor the formation of a halogen-mediated interaction between the reactant moieties at the entrance channel of these reactions, as is the case with conventional XBs.61
| Reaction | interaction | d(X⋯C) | ρ(BCP) | V s,max | E CPint | E int |
|---|---|---|---|---|---|---|
| R1 | FCl⋯CHO | 3.45 | 0.0053 | 9.8 | −6.2 | −7.2 |
| R2 | Cl2⋯CHO | 3.45 | 0.0057 | 6.0 | −5.4 | −6.5 |
| R3 | BrCl⋯CHO | 3.45 | 0.0058 | 4.7 | −4.0 | −4.7 |
| R4 | FBr⋯CHO | 3.55 | 0.0055 | 11.8 | −9.8 | −10.3 |
| R5 | ClBr⋯CHO | 3.55 | 0.0058 | 7.9 | −7.3 | −8.8 |
| R6 | Br2⋯CHO | 3.55 | 0.0059 | 6.6 | −5.9 | −6.9 |
| R7 | FI⋯CHO | 3.68 | 0.0054 | 14.8 | −10.7 | −13.4 |
| R8 | ClI⋯CHO | 3.68 | 0.0059 | 7.9 | −9.8 | −10.5 |
| R9 | BrI⋯CHO | 3.68 | 0.0059 | 6.6 | −8.6 | −9.0 |
3.2 Pre-reactive complexes
As a first step in the reaction profile for (R1)–(R9) reactions we therefore expect to find preRCs of the type YX⋯CHO. As commented above, these complexes are stabilized by halogen-mediated interactions which therefore represent the driving force at the entrance channel of these reactions. After formation of the preRCs the reaction will subsequently proceed through a TS structure to yield a post-reactive complex (postRC) which precedes the products of the reaction. In this section we therefore aim to analyze the nature of these halogen-mediated interactions formed between reactants. However, as described in more detail in the following section, we have found that at the highest level of theory, namely CCSD(T)/CBS, all of the studied reactions proceed with no preRC in the PEC, that is, reactions proceed directly from reactants all the way down to the formation of a postRC. Notice that this means that no transition structure is located along the PEC either. Therefore, the only barrier height for these processes would be a loose TS located in the entrance channel. Why do these reactions lack preRCs? Is this fact related to the nature of the potential halogen-mediated interactions formed between the reactant moieties?In order to shed light on these questions we now briefly analyze the nature of these interactions in the preRCs. Since for these processes a preRC does not exist on the PEC we will consider the interaction between the reactants at the d(X⋯C) = rvdW(X) + rvdW(C) distances instead, where rvdW(X) and rvdW(X) are the van der Waals radii of the interacting atoms X and C, respectively. All other degrees of freedom of the system have been relaxed. The presence of a halogen-mediated YX⋯CHO interaction is made manifest by the appearance of a bond critical point (BCP) in the electronic density distribution, ρ(r).
Fig. 2 shows the MEPs of the interacting reactants for reactions (R2), (R5) and (R8) that we take as an example. It can be seen how the maximum in the electrostatic potential, Vs,max, indicated with a white dot, is paired to the minimum in the potential located in the formyl radical, indicated with a black dot. These interactions between maxima and minima of ϕ(r) are a typical feature of non-covalent bonding,62 and represent the driving force for the orientation of interacting species at intermediate distances. The MEPs for all the reactions (R1)–(R9) are collected in Fig. S7 of the ESI.†
 | ||
| Fig. 2 MEPs on the ρ = 0.01 a.u. isosurface for (R2) (top), (R5) (middle) and (R8) (bottom) at d(X⋯C) = rvdW(X) + rvdW(C). Black and white dots indicate the maximum (values shown in eV) and the minimum of MEPs in the XB region, respectively. | ||
Table 1 collects some relevant information for the description of the halogen-mediated interactions formed between reactants in reactions (R1)–(R9), namely, the distance between the interacting moieties (which corresponds to the sum of the van der Waals radii), the value of the Vs,max for the dihalogens YX (measured on the ρ(r) = 0.001 a.u. isosurface), the electron density measured at the BCP [ρ(BCP)], and the interaction energy (Eint) as computed at the CCSD(T)/aug-cc-pVTZ level of theory. Since aug-cc-pVTZ interaction energies will be affected by the basis set superposition error, BSSE, we also provide corrected energies using the counterpoise, CP, procedure, ECPint.
Table 1 shows a clear correlation between the values of Vs,max and the interaction energy for the nine dimers. As a matter of fact, Eint shows the same trend previously described for the values of the electrostatic potential: it increases with the polarizability of X (Cl < Br < I) for a given Y in the dihalogen YX, and it also increases with the electronegativity of Y (Br < Cl < F) for a given X.63 This correlation nicely highlights the role of the halogen-mediated interaction in the intermediate region of the PECs where both moieties approach each other in an appropriate orientation along the reaction energy path.
3.3 Stationary points and thermochemistry
Energy profiles of the PECs obtained for reactions (R1)–(R9) are shown in Fig. 3: Cl transfer reactions ((R1), (R2) and (R3), left panels), Br transfer reactions ((R4), (R5) and (R6), middle panels) and I transfer reactions ((R7), (R8) and (R9), right panels). This figure collects CCSD(T)/CBS single point electronic energies computed on the CCSD/6-311+G(d,p) optimized geometries.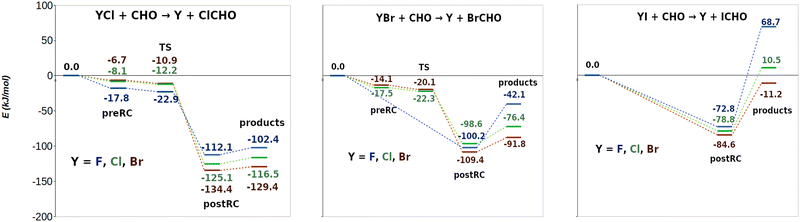 | ||
| Fig. 3 Energy profiles for stationary points obtained for reactions (R1)–(R9), at CCSD(T)/CBS//CCSD/6-311+G(d,p) (all the energies in kJ mol−1). Cl, Br and I transfer reactions are presented on the left, in the middle and on the right respectively. | ||
For reactions (R1), (R2), (R3), (R5) and (R6) a preRC between reactants followed by a TS was actually found at the optimization level, CCSD/6-311+G(d,p) (the structures and the most relevant geometrical parameters of preRCs and TSs are presented in Fig. S8 of the ESI†). However, at the CCSD(T)/CBS level of theory (single point energy calculations) TSs of the same set of reactions appear submerged with respect to preRCs, which is observed in Fig. 3. TSs energies with respect to the reactants are increasingly lower in the order of (R3) > (R2) > (R1) for Cl exchange reactions, and in the order of (R6) > (R5) for Br exchange reactions. On the other hand, for reactions (R4), (R7), (R8) and (R9) no preRCs (and thus, no TSs) were located at the optimization level CCSD/6-311+G(d,p). Notice that these reactions present the strongest halogen-mediated interactions right before the transfer of the X atom (see Table 1). Moreover, the decay of the TS energy (for the reactions that did show a TS) follow the same trend as the strength of these interactions. This correlation suggests a key influence of halogen-mediated interactions on the energy profile of these halogen exchange reactions: strong interactions allow us to convey reactants directly to the postRCs whereas weaker ones require an additional energy input and the concomitant pass through a transition state. Thus, CCSD(T)/CBS energies suggest, indeed, that for all these processes (R1)–(R9) halogen-mediated interactions are strong enough as to convey reactants directly to the formation of postRCs.
The equilibrium d(X⋯C) in preRCs ((R1), (R2), (R3), (R5), (R6)) collected in Fig. S8 (see the ESI†) provides additional evidence for this discussion. For chlorine exchange reactions ((R1), (R2) and (R3)) YX⋯CHO distances are clearly below the sum of the van der Waals radii (2.758 Å, 3.147 Å, 3.213 Å compared to 3.450 Å). The same occurs for bromine exchange reactions (R5) and (R6) (2.920 Å, 3.029 Å compared to 3.550 Å). Notice also the larger interaction energies when computed on the optimized geometries (Fig. 3) compared to those computed at the van der Waals radii distance (Table 1). All this information suggests that the strength of the halogen-mediated interactions is “pushing” the preRCs forward on the reaction coordinate. At a particular point, this strength is enough to “overcome” the TS structure allowing these reactions to evolve then directly from reactants all the way down towards the postRCs. This conclusion is also supported by the geometrical similarity between the preRCs and the corresponding TS structures (see Fig. S8 in the ESI†): for example, the difference between the halogen–halogen bond distance Y–X in the preRCs and the TS ranges a mere 1–4%. This is in agreement with the results obtained by Ninomiya et al.11 for reaction (R2) where it was found that the long Cl⋯Cl bond distance in the intermediate complex suggests that it “is almost cleaved”. In summary, we believe that the results discussed so far clearly suggest that halogen atoms have already begun to be transferred toward the CHO moiety in the preRC zone of the PECs. Moreover, we relate this fact to the existence of strong halogen-mediated interactions at the onset of the reaction. Further experimental work is desirable to validate this proposal.64
Table 2 collects the electronic reaction energies for the title reactions at the CCSD(T) level in conjunction with correlation-consistent basis sets ranging from cc-pVTZ to aug-cc-pVQZ. Complete basis set (CBS) extrapolated values are included as well as CCSD(T)-F12/cc-pVTZ-F12 results. The last column collects reaction enthalpies, (ΔHr), evaluated at the CCSD(T)/CBS level with thermal corrections obtained at the optimization level, CCSD/6-311+G**.
| Reaction | CCSD | CCSD(T) | CCSD(T) | CCSD(T) | CCSD(T) | CCSD(T) | CCSD(T)-F12a | ΔHr |
|---|---|---|---|---|---|---|---|---|
| aug-cc-pVTZ | cc-pVTZ | aug-cc-pVTZ | cc-pVQZ | aug-cc-pVQZ | CBS | cc-pVTZ-F12 | ||
| R1 | −114.2 | −114.4 | −105.7 | −107.2 | −103.6 | −103.8 | −101.5 | −92.7 |
| R2 | −129.1 | −126.0 | −124.4 | −120.4 | −119.7 | −117.7 | −114.7 | −106.8 |
| R3 | −134.6 | −133.5 | −130.6 | −132.4 | −131.8 | −130.0 | −128.8 | −131.7 |
| R4 | −56.1 | −59.5 | −48.6 | −46.1 | −42.1 | −42.2 | −41.2 | −33.4 |
| R5 | −89.5 | −86.0 | −86.4 | −77.0 | −76.4 | −73.6 | −72.1 | −65.3 |
| R6 | −98.3 | −95.7 | −96.2 | −91.9 | −91.8 | −88.9 | −88.8 | −92.8 |
| R7 | 47.4 | 38.1 | 49.7 | 59.7 | 63.9 | 65.4 | 65.8 | 71.9 |
| R8 | −11.2 | −10.1 | −13.0 | 3.7 | 3.7 | 8.4 | 7.0 | 12.8 |
| R9 | −25.8 | −24.7 | −28.7 | −16.8 | −17.8 | −12.7 | −15.3 | −20.4 |
We first point out that CCSD(T)/CBS and CCSD(T)-F12/cc-pVTZ-F12 reaction energies are very close to each other, as expected. The mean unsigned error (MUE) is 1.5 kJ mol−1 and the standard deviation (SD) is also small, 1.0 kJ mol−1 (the error is also relatively homogeneous among the whole set of reactions). CCSD(T)-F12 is closer to CCSD(T)/CBS than CCSD(T)/aug-cc-pVQZ which shows a slightly larger MUE, 2.3 kJ mol−1, and SD, 1.7 kJ mol−1. On the other hand, CCSD(T)/aug-cc-pVTZ energies exhibit larger errors, MUE 9.9 kJ mol−1, and standard deviations, 7.0 kJ mol−1. Here, errors increase with the size of the transferred halogen, MUE((R1)–(R3)) = 3.1 kJ mol−1, MUE((R4)–(R6)) = 8.8 kJ mol−1, MUE((R7)–(R9)) = 17.7 kJ mol−1 with standard deviations between 3.2 and 3.5 kJ mol−1. Thus, CCSD(T)/aug-cc-pVTZ still provides reasonably good energies for Cl and Br reactions although not so good for I.
Results collected in Table 2 also show that the effect of perturbative triple excitations is not large in the reaction energies: CCSD(T)/aug-cc-pVTZ MUE is 9.9 kJ mol−1, as stated above, only slightly smaller than that of CCSD/aug-cc-pVTZ, 12.9 kJ mol−1. We will see in the next section that inclusion of triple excitations has, in contrast, a much larger effect on the intermediate region of the PECs.
Finally, we collect in Table 2 the enthalpies of reactions (R1)–(R9). Values of ΔHr indicate that all reactions, with the exceptions of (R7) and (R8), are exothermic. The observed trend is the following: exothermicity decreases with the electronegativity of the substituent Y (Y = Br > Cl > F) and with the size of X (X = Cl > Br > I). Thus, chlorine exchange reactions are the most exothermic followed by bromine and iodine. This trend can be easily understood taking into account that for a particular halogen being transferred X, the Y–X bond strength follows the trend Br–X < Cl–X < F–X whilst the formed X–C bond strength decreases Cl–C > Br–C > I–C.
Fig. 3 also shows that all reactions present a postRC. For example, Fig. 4 illustrates the MEP (up) and the molecular graph (down) of the postRC found for the reaction (R2) (postRC2). Notice the existence of two stabilizing interactions: Cl⋯Cl–C and Cl⋯H–C. Fig. 4 nicely shows that maxima of the MEP in Cl and H (white dots) are oriented towards higher potential areas (yellow rings around chlorine atoms). PostRCs for the whole set of reactions are presented in Fig. S9 of the ESI.† In all cases, the released halogen atom Y maintains a double coordination with the XCHO species. In the particular case of (R2), we point out that postRC2 corresponds to the intermediate complex described by Ninomiya and coworkers, although the interactions that stabilize this complex were not analyzed in their work.11
3.4 Potential energy curves
We commented in Section 2.5 that, for those reactions with the weakest halogen-mediated interactions, both preRC and TS appear on the PES at the CCSD/6-311+G(d,p) level of theory. However, we also saw that at the higher CCSD(T)/CBS level no preRC/TS exists for any of the reactions, including those with the weakest halogen-mediated interactions. This shows a remarkable dependency of the topology of the PEC on the level of theory since CCSD in conjunction with the 6-311+G(d,p) basis set already represents a relatively high quality computational level. In this section we analyze how the profile of these halogen exchange reactions depends on both the treatment of electron correlation and the quality of the basis set.First, we point out that electronic reaction energies did not show a critical dependency on the inclusion of triple excitations since CCSD(T) and CCSD with the aug-cc-pVTZ basis set do not differ much (see Table 2) with an average deviation of 4.1 kJ mol−1 for (R1)–(R9) (the largest difference is 8.5 kJ mol−1 for (R1) and the smallest 1.8 kJ mol−1 for (R8)). The quality of the basis set was more relevant, since MUEs with respect to CBS for the series CCSD(T)/cc-pVTZ, aug-cc-pVTZ, cc-pVQZ and aug-cc-pVQZ (SD in parenthesis) are 13.0 kJ mol−1 (7.2), 9.9 kJ mol−1 (7.0), 3.7 kJ mol−1 (1.0) and 2.3 kJ mol−1 (1.7), respectively. As stated previously, the aug-cc-pVTZ basis set provides reasonable results for Cl and Br reactions (MUE: 3.1 kJ mol−1 and 8.8 kJ mol−1, respectively) but not for I (MUE: 17.7 kJ mol−1).
We turn now to the analysis of the whole set of reaction profiles, where we can examine how the topology of intermediate region of the PEC depends on the level of theory. Fig. 5 shows the PECs for (R1) (left pannel), (R2) (middle pannel) and (R3) (right pannel) obtained at the following levels of theory: CCSD/6-311+G(d,p) (blue line) CCSD/aug-cc-pVTZ (red), CCSD(T)/aug-cc-pVTZ (black) and CCSD(T)-F12a/cc-pVTZ-F12 (green). We recall that CCSD/6-311+G(d,p) is the level of theory we chose for the geometry optimizations. We clearly see from Fig. 5 that the height of the energy barrier is reduced as the level of theory increases showing a gradual vanishing of the local maximum and a flattening of the curves. The same behaviour is observed in (R5) and (R6) whose energy profiles are shown in Fig. S10 of the ESI,† together with the PECs of the rest of the reactions, which do not present neither preRC nor TS at the optimization level, as discussed before.
 | ||
| Fig. 5 PECs of reactions (R1) (left), (R2) (center) and (R3) (right) as obtained at the following levels of theory: CCSD/6-311+G(d,p) (in blue), CCSD/aug-cc-pVTZ (in red), CCSD(T)/aug-cc-pVTZ (in black) and CCSD(T)-F12a/aug-cc-pVTZ-F12 (in green). The corresponding TS structures are shown. | ||
The lowest energy barriers at the CCSD/6-311+G(d,p) level are found for reactions (R1), (R5), and (R6), those with the strongest halogen-mediated interactions within the group of reactions that present preRC/TS ((R1), (R2), (R3), (R5), (R6)). For (R1), increasing the quality of the basis set from 6-311+G(d,p) to aug-cc-pVTZ already changes the topology of the PEC and the energy barrier disappears (see Fig. 5, left panel). On the other hand, for (R2) and (R3) we observe that when moving from 6-311+G** to aug-cc-pVTZ (blue and red curves, respectively) both preRCs and TSs are still located in the PEC, although the profile is a little flatter. For these two reactions, what definitely changes the profile of the reaction is the inclusion of perturbative triple excitations. Thus, we see that both the electron correlation treatment and the quality of the basis set are key for a correct description of the reaction profile of these halogen exchange processes.
We have analyzed in further detail the role of electron correlation taking (R2) as a model reaction. Single point calculations have been performed at different d(X⋯C) distances along the reaction path with increasingly refined post-HF methods: MP2, CCSD, CCSD(T), CCSDT and CCSDT(Q)Λ. These energies have been obtained in conjunction with the cc-pVDZ and 6-311G* basis sets. We point out that our main goal at this point is to assess the contribution of higher electron excitations beyond perturbative triples in the correlation treatment, not to provide highly accurate energies (due to the limited basis sets we used). Thus, we have not tried to correct the CCSDT(Q)Λ energies as, for example, proposed by Boese et al. for CCSDTQ/cc-pVDZ.67
Table 3 presents the electronic energies obtained for (R2) at different points along the reaction path (first column) using the methods described above (columns 2–6). The last column shows the CCSD percentage error with respect to CCSDT(Q)Λ, E%(CCSD), for each structure i, that is:
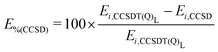 | (1) |
| d (Cl⋯C) | cc-pVDZ | 6-311G* | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MP2 | CCSD | CCSD(T) | CCSDT | CCSDT(Q)Λ | E %(CCSD) | MP2 | CCSD | CCSD(T) | CCSDT | CCSDT(Q)Λ | E %(CCSD) | |
| 3.850 | −3.9 | −3.2 | −3.5 | −3.5 | −3.5 | 9 | −4.5 | −3.9 | −4.3 | −4.2 | −4.3 | 10 |
| 3.250 | −7.9 | −6.1 | −7.1 | −7.1 | −7.2 | 14 | −7.9 | −6.3 | −7.5 | −7.4 | −7.6 | 16 |
| 2.850 | −8.6 | −5.7 | −8.0 | −8.0 | −8.2 | 31 | −8.1 | −5.5 | −8.1 | −8.1 | −8.4 | 35 |
| 2.466 | 2.0 | −1.0 | −7.0 | −7.7 | −8.4 | 88 | 2.1 | −1.3 | −8.2 | −9.1 | −10.0 | 87 |
| 2.040 | −77.1 | −66.0 | −72.7 | −73.2 | −74.0 | 11 | −82.5 | −70.2 | −77.7 | −78.5 | — | — |
| 1.761 | −139.8 | −131.1 | −130.6 | −129.9 | −129.6 | 1 | −150.5 | −140.9 | −140.2 | −139.8 | — | — |
| 1.759 | −148.2 | −140.0 | −138.9 | −138.1 | −137.8 | 2 | −160.1 | −150.8 | −149.5 | −149.1 | −149.0 | 1 |
3.5 DFT reaction profiles
Stimulated by the results discussed in the previous section we present, in the last part of our study, PECs obtained with several density functional approximations (DFAs), see Fig. 6. The DFAs employed include three hybrid functionals: ω-B97X-D2 (light blue line), M06-2X (orange), B3LYP (brown), and three double hybrids functionals: B2PLYP-D3BJ (purple), B2T-PLYP-D2 (green) and mPW2PLYP-D2 (magenta). All DFAs were used in conjunction with the aug-cc-pVTZ basis set. The PECs computed at the CCSD(T)/aug-cc-pVTZ level, taken as a reference, are also presented in black. | ||
| Fig. 6 PECs of reactions (R1)–(R9), obtained at different DFT functionals: ω-B97XD2 (in light blue), M06-2X (in orange), B3LYP (in brown), B2PLYPD3BJ (in purple), B2T-PLYPD2 (in green) and mPW2PLYPD2 (in magenta). All DFT functionals were used with the aug-cc-pVTZ basis set. PECs obtained at the CCSD(T)/aug-cc-pVTZ level are also presented in black. | ||
In order to provide a more quantitative analysis we show in Table 4 the root mean squared error (RMSE) and root mean squared percentage error (RMSPE) for each DFA as calculated using expressions (2) and (3), respectively:
 | (2) |
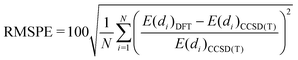 | (3) |
| Reaction | ω-B97XD2 | M06-2X | B3LYP | B2T-PLYPD2 | B2PLYPD3BJ | mPW2PLYPD2 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| RMSE | RMSPE | RMSE | RMSPE | RMSE | RMSPE | RMSE | RMSPE | RMSE | RMSPE | RMSE | RMSPE | |
| R1 | 7.9 | 38 | 7.4 | 37 | 13.6 | 63 | 5.6 | 27 | 8.1 | 38 | 8.3 | 39 |
| R2 | 2.6 | 24 | 4.7 | 43 | 8.3 | 72 | 2.5 | 21 | 4.2 | 36 | 4.6 | 40 |
| R3 | 0.5 | 4 | 5.2 | 47 | 11.4 | 101 | 3.0 | 27 | 5.7 | 50 | 5.7 | 51 |
| R4 | 7.9 | 24 | 7.6 | 23 | 12.6 | 36 | 5.9 | 17 | 8.2 | 24 | 8.4 | 25 |
| R5 | 2.7 | 12 | 4.8 | 19 | 10.0 | 38 | 3.4 | 13 | 5.8 | 22 | 5.9 | 23 |
| R6 | 1.0 | 5 | 4.3 | 18 | 8.4 | 34 | 2.2 | 9 | 4.5 | 18 | 4.6 | 19 |
| R7 | 6.1 | 14 | 5.6 | 13 | 9.2 | 21 | 5.9 | 13 | 7.6 | 17 | 7.9 | 18 |
| R8 | 1.6 | 5 | 2.9 | 8 | 7.4 | 21 | 3.5 | 10 | 5.7 | 16 | 5.5 | 16 |
| R9 | 1.7 | 6 | 3.7 | 12 | 6.4 | 21 | 3.6 | 12 | 5.5 | 18 | 5.5 | 18 |
| RMSEm | 3.5 | 5.1 | 9.7 | 4.0 | 6.1 | 6.3 | ||||||
| RMSESD | 2.9 | 1.6 | 2.4 | 1.4 | 1.5 | 1.5 | ||||||
Interestingly, DFT PECs do not present energy barriers for any of the reactions (R1)–(R9) which is in agreement with CCSD(T) predictions. This is a fortunate result since DFT is computationally much cheaper than CCSD(T). However, it is also worth pointing out that already in the TS region and more clearly at shorter X⋯C distances the PECs diverge in some cases significantly, reaching energy deviations of about 20.0 kJ mol−1. DFT PECs usually lie below the reference CCSD(T) and show the following trend: B3LYP < B2PLYPD3BJ ≈ mPW2PLYPD2 < M06-2X < B2T-PLYPD2 < ω-B97XD2. We note in passing the PECs in Fig. 6 should be affected by basis set superposition error (BSSE). However, as shown in previous sections, the topology of the PEC is clearly dependent on the electron correlation treatment and, thus, results collected in Fig. 6, should provide useful insights about the performance of the tested DFAs regardless of the magnitude of BSSE.
Results collected in Table 4 allow us to have a more quantitative picture. The average RMSE, RMSEm, shows that the ω-B97xD2 functional presents the lowest error (3.5 kJ mol−1), followed by B2T-PLYPD2 (4.0 kJ mol−1), M06-2X (5.1 kJ mol−1), B2PLYPD3BJ (6.1 kJ mol−1), mPW2PLYPD2 (6.3 kJ mol−1) and B3LYP (9.7 kJ mol−1). This means that in the intermediate region, where the transition structure is expected to be located, all DFAs perform reasonably well. Taking into account the larger computational cost of double hybrids it is pleasant to find out that both ω-B97xD2 and M06-2X provide a good agreement with CCSD(T).
4 Conclusions
The main conclusions of this study can be summarized as follows:(1) Halogen exchange reactions between dihalogens YX (Y = F, Cl, Br, X = Cl, Br, I) and formyl radical are generally exothermic, except for the reactions with FI and ClI which are endothermic. It is observed that exothermicity increases with the size of Y (F < Cl < Br) and decreases with the size of X (Cl > Br > I).
(2) Halogen-mediated interactions are the driving force in the onset of the reaction where reactants approach each other. The strength of this interaction increases with the size of X (Cl < Br < I) and with the electronegativity of Y (Br < Cl < F). For those reactions with weaker X⋯C interactions, namely reactions with FCl, Cl2, BrCl, ClBr, and Br2 a pre-reactive complex appears as a minimum on the CCSD/6-311+G(d,p) PEC followed by a local maximum corresponding to the transition structure that leads to the products of the reaction. Those reactions with stronger X⋯C interactions, namely FBr, FI, ClI, and BrI, do not show either preRC nor TS on the intermediate region of the reaction profile. However, at the higher CCSD(T)/CBS level of theory no reaction features preRC/TS. We derive two conclusions from these observations:
(1) Halogen exchange reactions between dihalogens and formyl radicals evolve directly from reactants to the post-reactive complexes without passing through a transition state.
(2) We relate the absence of transition structure in these reactions to the strength of the halogen bonding interactions between reactants.
(3) CCSD does not provide correct reaction energy profiles for reactions with weaker X⋯C interactions since CCSD shows a tight transition structure. Inclusion of perturbative triple corrections is mandatory in order to provide the correct barrierless potential energy curves. Inclusion of higher order excitations do not seem to noticeably improve CCSD(T) results. Thus, we conclude that CCSD(T) in conjunction with a 3-ζ basis set represents the lowest level of theory appropriate for the study of these reactions. We can also conclude that 6-311+G(d,p) provides qualitatively correct results but we recommend the usage of at least aug-cc-pVTZ for the study of these processes.
(4) The tested hybrid and double-hybrid DFAs provide fairly accurate predictions compared to CCSD(T). In particular, they correctly predict the absence of a transition structure for the whole set of reactions.
Data availability
The data supporting the findings of this study are available within the article or included as part of the ESI.† Raw data can be obtained from the authors upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET – Argentina) and from the Asociación Universitaria Iberoamericana de Postgrado (AUIP – Spain). D. J. R. D. thanks SEGCYT-UNNE for financial support (PI-22V002). Also, the joint collaboration of the National University of the Northeast (UNNE – Argentina) and the University of Valladolid (UVa – Spain) is appreciated. All the aforementioned support and collaboration has helped the doctoral training of Matias Miranda, who spent time at UVa on a co-tutelle basis. Financial support from the Spanish Ministerio de Ciencia e Innovación (PID2020-117742GB-I00) is gratefully acknowledged.References
- J. A. Barnard and J. N. Bradley, Flame and Combustion, Springer, US, 1984 Search PubMed.
- J. N. Pitts, Jr., R. Zellner and B. Finlayson-Pitts, Ber. Bunsen-Ges., 1986, 90, 1244 Search PubMed.
- G. Pietzka, Angew. Chem., 1958, 70, 613 CrossRef.
- H. Eyring, Science, 1962, 135, 427–428 CrossRef.
- N. Washida, R. I. Martinez and K. D. Bayes, Z. Naturforsch., A: Phys. Sci., 1974, 29, 251–255 CAS.
- D. J. Donaldson and J. J. Sloan, Can. J. Chem., 1983, 61, 906–911 CrossRef CAS.
- R. Lesclaux, P. Roussel, B. Veyret and C. Pouchan, J. Am. Chem. Soc., 1986, 108, 3872–3879 CrossRef CAS.
- K. Mondal and B. Rajakumar, J. Phys. Chem. A, 2022, 126, 6135–6147 CrossRef CAS PubMed.
- L. Krasnoperov, E. Chesnokov, H. Stark and A. Ravishankara, Proc. Combust. Inst., 2005, 30, 935–943 CrossRef.
- R. S. Timonen, E. Ratajczak and D. Gutman, J. Phys. Chem., 1988, 92, 651–655 CrossRef CAS.
- Y. Ninomiya, M. Goto, S. Hashimoto, Y. Kagawa, K. Yoshizawa, M. Kawasaki, T. J. Wallington and M. D. Hurley, J. Phys. Chem. A, 2000, 104, 7556–7564 CrossRef CAS.
- W. R. Simpson, S. S. Brown, A. Saiz-Lopez, J. A. Thornton and R. von Glasow, Chem. Rev., 2015, 115, 4035–4062 CrossRef CAS PubMed.
- F. Xiao, X. Sun, Z. Li and X. Li, ACS Omega, 2020, 5, 12777–12788 CrossRef CAS PubMed.
- S. W. Benson and O. Dobis, J. Phys. Chem. A, 1998, 102, 5175–5181 CrossRef CAS.
- M. J. Pilling, Pure Appl. Chem., 1992, 64, 1473–1480 CrossRef CAS.
- J. R. Alvarez-Idaboy, N. Mora-Diez and A. Vivier-Bunge, J. Am. Chem. Soc., 2000, 122, 3715–3720 CrossRef CAS.
- J. Cizek, Chem. Phys., 1969, 14, 35 CAS.
- G. D. Purvis and R. J. Bartlett, J. Chem. Phys., 1982, 76, 1910–1918 CrossRef CAS.
- G. E. Scuseria, C. L. Janssen and H. F. Schaefer III, J. Chem. Phys., 1988, 89, 7382–7387 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.03, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- M. N. Glukhovtsev, A. Pross, M. P. McGrath and L. Radom, J. Chem. Phys., 1995, 103, 1878–1885 CrossRef CAS.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS PubMed.
- H. P. Hratchian and H. B. Schlegel, Chapter 10 – Finding minima, transition states, and following reaction pathways on ab initio potential energy surfaces, Elsevier, Amsterdam, 2005, pp. 195–249 Search PubMed.
- K. Fukui, Acc. Chem. Res., 1981, 14, 363–368 CrossRef CAS.
- J. D. Watts and R. J. Bartlett, Int. J. Quantum Chem., 1993, 48, 51–66 CrossRef.
- J. A. Pople, M. Head-Gordon and K. Raghavachari, J. Chem. Phys., 1987, 87, 5968–5975 CrossRef CAS.
- K. Raghavachari, G. W. Trucks, J. A. Pople and M. Head-Gordon, Chem. Phys. Lett., 1989, 157, 479–483 CrossRef CAS.
- J. Dunning and H. Thom, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef.
- D. E. Woon, J. Dunning and H. Thom, J. Chem. Phys., 1993, 98, 1358–1371 CrossRef CAS.
- J. Dunning, H. Thom, K. A. Peterson and A. K. Wilson, J. Chem. Phys., 2001, 114, 9244–9253 CrossRef.
- R. A. Kendall, J. Dunning, H. Thom and R. J. Harrison, J. Chem. Phys., 1992, 96, 6796–6806 CrossRef CAS.
- A. K. Wilson, D. E. Woon, K. A. Peterson and T. H. Dunning, Jr., J. Chem. Phys., 1999, 110, 7667–7676 CrossRef CAS.
- K. A. Peterson, B. C. Shepler, D. Figgen and H. Stoll, J. Phys. Chem. A, 2006, 110, 13877–13883 CrossRef CAS PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2, 242–253 CAS.
- H.-J. Werner, P. J. Knowles, F. R. Manby, J. A. Black, K. Doll, A. Heßelmann, D. Kats, A. Köhn, T. Korona, D. A. Kreplin, Q. Ma, I. Miller, F. Thomas, A. Mitrushchenkov, K. A. Peterson, I. Polyak, G. Rauhut and M. Sibaev, J. Chem. Phys., 2020, 152, 144107 CrossRef CAS PubMed.
- G. Knizia, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2009, 130, 054104 CrossRef PubMed.
- K. A. Peterson, T. B. Adler and H.-J. Werner, J. Chem. Phys., 2008, 128, 084102 CrossRef PubMed.
- J. G. Hill and K. A. Peterson, J. Chem. Phys., 2014, 141, 094106 CrossRef PubMed.
- N. Sylvetsky, M. K. Kesharwani and J. M. L. Martin, J. Chem. Phys., 2017, 147, 134106 CrossRef PubMed.
- M. Kállay and P. R. Surján, J. Chem. Phys., 2001, 115, 2945–2954 CrossRef.
- M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123, 214105 CrossRef PubMed.
- M. Kállay and J. Gauss, J. Chem. Phys., 2008, 129, 144101 CrossRef PubMed.
- Y. J. Bomble, J. F. Stanton, M. Kállay and J. Gauss, J. Chem. Phys., 2005, 123(5), 054101 CrossRef PubMed.
- K. L. Bak, P. Jørgensen, J. Olsen, T. Helgaker and J. Gauss, Chem. Phys. Lett., 2000, 317, 116–122 CrossRef CAS.
- M. Spiegel, E. Semidalas, J. M. L. Martin, M. R. Bentley and J. F. Stanton, Mol. Phys., 2023, 122(7–8), e2252114 Search PubMed.
- J. J. Eriksen, D. A. Matthews, P. Jørgensen and J. Gauss, J. Chem. Phys., 2015, 143, 041101 CrossRef PubMed.
- M. Kállay, P. R. Nagy, D. Mester, Z. Rolik, G. Samu, J. Csontos, J. Csóka, P. B. Szabó, L. Gyevi-Nagy, B. Hégely, I. Ladjánszki, L. Szegedy, B. Ladóczki, K. Petrov, M. Farkas, P. D. Mezei and A. Ganyecz, J. Chem. Phys., 2020, 152, 074107 CrossRef PubMed.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241 Search PubMed.
- J.-D. Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620 RSC.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- A. Tarnopolsky, A. Karton, R. Sertchook, D. Vuzman and J. M. L. Martin, J. Phys. Chem. A, 2008, 112, 3–8 CrossRef CAS PubMed.
- T. Schwabe and S. Grimme, Phys. Chem. Chem. Phys., 2006, 8, 4398–4401 RSC.
- F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2022, 12, e1606 Search PubMed.
- F. Neese, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2012, 2, 73–78 CAS.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- Jmol development team, Jmol, 2016, https://jmol.sourceforge.net/.
- R. Dennington, T. A. Keith and J. M. Millam, GaussView Version 6, Semichem Inc., Shawnee Mission KS, 2019 Search PubMed.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2013, 15, 11178 RSC.
- L. Brammer, A. Peuronen and T. M. Roseveare, Acta Crystallogr., Sect. C: Struct. Chem., 2023, 79, 204–216 CrossRef CAS PubMed.
- D. J. R. Duarte, G. L. Sosa, N. M. Peruchena and I. Alkorta, Phys. Chem. Chem. Phys., 2016, 18, 7300–7309 RSC.
- J. S. Murray and P. Politzer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1326 Search PubMed.
- M. Domagała and M. Palusiak, Comput. Theor. Chem., 2014, 1027, 173–178 CrossRef.
- B. Dereka, Q. Yu, N. H. C. Lewis, W. B. Carpenter, J. M. Bowman and A. Tokmakoff, Science, 2021, 371, 160–164 CrossRef CAS PubMed.
- K. P. Huber and G. Herzberg, Constants of diatomic molecules, Springer, US, 1979, pp. 8–689 Search PubMed.
- C. E. Moore, Atomic energy levels as derived from the analyses of optical spectra, National Bureau of Standards, 1971 Search PubMed.
- A. D. Boese, M. Oren, O. Atasoylu, J. M. L. Martin, M. Kállay and J. Gauss, J. Chem. Phys., 2004, 120, 4129–4141 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03882g |
| This journal is © the Owner Societies 2025 |


