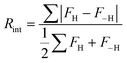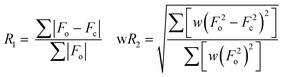Useful practices in single crystal diffraction analysis of reticular structures

Abstract

Single crystal diffraction analysis remains the gold standard for the three-dimensional atomic structure characterization of framework materials such as metal–organic frameworks, covalent organic frameworks, zeolites, and many others. Despite many leaps in automation and user-friendliness, crystal structure determination using X-ray and electron diffraction continues to require adequate education, expertise, and a critical mindset, which have not been replaceable by informatic tools. This contribution aims at overviewing useful practices and tips for dealing with recurring cases, where routine procedures fail and emerging structural scientists might feel lost or too reliant on pre-defined procedures. Each section is dedicated to a specific subject within the crystallographic practice and provides advice to avoid common practical and conceptual pitfalls, thereby making the crystallographic analysis more accurate and promoting the long-lasting value of its results.

---

Stefano Canossa

Stefano Canossa is a senior scientist with over a decade of experience in the crystallographic analysis of open-framework compounds using X-ray and electron diffraction. Trained as a coordination chemist, his crystallographic journey began during his MSc research on host–guest chemistry in metal–organic frameworks, and later expanded to include co-crystals, metal complexes, zeolites, and perovskites. Alongside crystal structure determination, his independent research explores the synthesis and characterization of correlated disorder in crystalline materials by leveraging on single crystal total scattering analysis in both real and reciprocal space.

---

Key learning points

I. Crystal structures are artificial simplifications of the non-periodic structure of real crystals. Nonetheless, these models are key enablers of scientific progress, if they maintain accuracy before precision in describing the average structure.

II. Steps such as sample preparation, data collection, data reduction, and structure modelling should be based on educated intentional choices. Default options provided by software or pre-made routines can be accepted only when their significance has been understood in the appropriate context.

III. Models can be only as reliable as the data allows for, and data can be only as good as the crystal allows for. Investing adequate care firstly on crystal selection, then on data collection and reduction, and ultimately on structure modelling, is a defining aspect of a crystallographer's work.

IV. The distinction between ‘data’, ‘information’ and ‘model’ — herewith provided — is necessary for a correct crystallographic practice and a scientifically rigorous representation of its results.

V. Standard diffraction data provide a wealth of information beyond the simple numerical values of integrated intensities. This information can be found in reciprocal space reconstructions and include aspects such as mosaicity, disorder, and defects.

1. Introduction

Across the many evolutions that transformed reticular materials† such as coordination polymers^1,2 and metal–organic frameworks (MOFs)³ from chemical curiosity to applied technology in just over two decades,^4,5 there is perhaps a single foundational concept that best withstood the test of time, remaining the cornerstone of their modular design: the ‘repeating unit’. Its earliest meaning was arguably linked to the concept of ‘unit cell’, which highlights the close intellectual relationship with crystallography. Over time, ‘repeating unit’ ceased to refer exclusively to atoms and molecules of a specific type but rather focused on their structural role within the framework architecture. This conceptual leap led to MOFs with non-repeating chemical compositions, also known as multivariate, to be conceptualized and synthesized.⁶ Structure ‘multivariation’ — the simultaneous presence of more than one kind of local structures in a crystal⁷ — is just one of many kinds of framework complexity that are being leveraged upon to create competitive materials for a remarkable variety of functions. These non-periodic aspects include chemical composition of the framework backbone, vacancy defects, displacive disorder, pore structure, functional groups, and presence of species in the cavities. Most importantly, their occurrence can be intentional or accidental, but it always affects the properties of interest unless proven otherwise, and regardless of whether its influence is deemed relevant or negligible.

While the structural complexity of MOFs evolved impressively since their early years, single crystal diffraction (SCD) analysis — traditionally using X-rays, more recently also electrons⁸ — remained the gold standard for their atomic structure characterization.⁹ Therefore, the field remained anchored to the concept of ‘crystal structure’: an atomic model created to fit the averaged projection of the crystal's entire structure into a hypothetical repeating volume known as unit cell. Even though it is widely known that crystal structures represent — as opposed to “are” — space- and time-averaged views of actual structures, it is possible to overlook that these are crafted models and not experimental data, and even more that these models exercise a steady bias on our minds due to their convenience and ready availability. For reducing these risks, it is critical for crystallographers to disclose models that are faithful to the available experimental information and to adopt considerate and transparent modelling choices, especially when experimental evidence is too weak to justify them alone. These cases are remarkably frequent in the crystallography of MOFs, since structural disorder is commonly found as a side effect of their characteristic conformational flexibility.¹⁰ In an increasing number of reported cases, disorder is also presented as gateway to properties otherwise unachievable, and as intrinsic identity trait of specific frameworks.^11–15

This contribution aims at assisting the delicate and important practice of SCD analysis of reticular structures to produce models that are as meaningful and informative as possible, depending on their research context. While valuable overviews with a more general scope and extensive coverage can be found in published literature, which readers are encouraged to consult,^16–21 this work focuses on common pitfalls and ambiguities for encouraging their appropriate handling and promoting integrity and long-lasting value of the crystallographic practice (Fig. 1). Although the considered examples revolve primarily around MOFs, readers will appreciate that most of the advice is also valid for SCD analysis of other porous framework compounds such as covalent organic frameworks (COFs), as well as many others.

Fig. 1 Schematic overview of the key aspects of single crystal diffraction analysis considered in this article. In its context, it is important to maintain awareness of the information left behind at every step of the process, most notably the unexamined crystals or solids, the discarded intensities, and the unmodelled information.

2. Data collection

2.1. Selection of experimental conditions

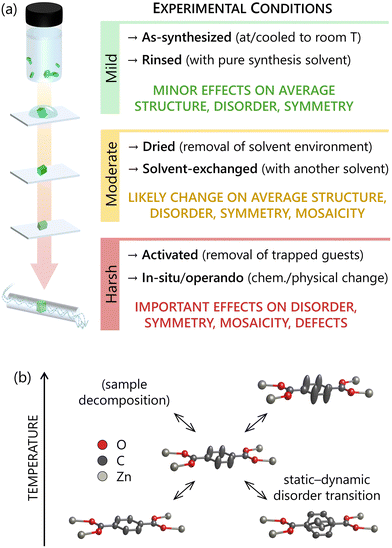
Perhaps the most sought-after concept in reticular chemistry is ‘rational design’, i.e. some degree of predictability linking the synthesis procedure and the structure of the self-assembled product.²² Hence, scientists are usually interested in characterizing what they synthesized and not what they unintentionally turned their product into, due to change in chemical or physical environment (Fig. 2). For example, crystals with a well-formed, faceted morphology might give only broad and low-angle Bragg peaks due to loss of crystallinity (long-range order) after solvent removal or exchange,²³ and such a poor crystal quality might be erroneously assumed also for the as-synthesized material. Loss of crystallinity due to de-solvation affects numerous classes of crystalline materials, but it is particularly relevant in reticular structures since solvent molecules can account for up to 90% of their volume.²⁴ Solvent extraction is commonplace in electron diffraction experiments, as these expose porous crystals to a vacuum of <10–5 Pa, enough to remove species from the pores²⁵ except when dedicated environmental cells are used to isolate the sample²⁶ or cryogenic conditions isolate it in amorphous ice. If on the one hand it is useful to know the structure of evacuated crystals used for gas adsorption or separation, on the other hand it is their as-synthesized form that provides the most reliable insights into their formation. In this context, one parameter to be carefully selected for SCD analysis is the temperature.

Fig. 2 Possible effects of sample treatment (a) and temperature conditions (b) on the samples for SCD analysis. In (b), a terephthalate linker with arbitrary ellipsoids is used to show different temperature-dependent behaviours due to, for example, functional groups and interactions with guests in the cavities.

2.2. Risks and benefits of cryogenic temperatures

A common practice is using cryogenic temperatures (e.g. 100 K), which offers both benefits and risks. On the positive side, lower temperatures can yield stronger high-resolution peaks due to decreased thermal motions and more localized average atomic positions. Secondly, extra-framework species such as solvent molecules become more ordered (less oscillating dangling moieties, favoured hydrogen bonding and other non-covalent interactions) Furthermore, decreased diffusion of moisture from the environment to the framework cavities protects sensitive metal–organic linkages such as Zn–carboxylates from hydrolysis. Lastly, cryogenic conditions also limit the extraction of solvent molecules from the pores, which is a common cause of partial collapse and loss of crystallinity during SCD data collections. This becomes critical for ED analysis due to the mentioned vacuum conditions,²⁷ along with the fact that cryogenic temperatures make organic and metal–organic structures remarkably more stable to the radiolysis damage induced by the electron beam illumination.^28,29

On the negative side, however, low temperatures are a well-documented cause of phase transitions,³⁰ possibly triggered by interactions of solvent molecules with the host framework.^23,30–32 Renowned examples are MOFs based on [Zn₄O] metal nodes such as MOF-5 and related structures, where trapped dimethylformamide molecules go from dynamic to stable binding on metal centres, thereby causing change of local symmetry and framework conformation.^33–35 Another possible disadvantage of using cryogenic conditions is a decrease of diffraction quality from crystals containing partly static structural disorder.³⁶ This somewhat counter-intuitive type of crystallinity loss can originate from dynamically disordered components that, below a certain temperature, settle in statically disordered conformations with identical or analogous energy — a phenomenon that is also influenced by the cooling rate. Three possible scenarios can be the following: (1) solvent molecules becoming locally ordered with various alternative arrangements; (2) solvent-induced distortions of the architecture turning it in alternative conformations; (3) disordered parts of the framework backbone, whose contribution to the average structure would be mostly smeared out by thermal motions, becoming locally ordered with various arrangements (Fig. 2b, bottom right). Such cases might be considered rare, but they are most certainly underreported, since one could simply conclude that a sample is poorly crystalline from the synthesis, instead of trying to obtain better data by increasing the temperature to room conditions, or even above.

While the selection of experimental conditions depends on the specifics of each case, conducting a first SCD analysis at room temperature and without removing the native content of the cavities provides a structure that better represents the as-synthesized product. Moreover, room-temperature structures allow for a more meaningful comparison between experimental powder XRD patterns (usually collected without temperature control) and those calculated from SCD models. Indeed, temperature change does not only shift peak positions due to thermal expansion or contraction of the structure, but it can also alter space group symmetry leading to more dramatic effects such as peak splitting or change in systematic absences. Special care is needed for structures that are moisture sensitive or damaged by de-solvation. For these cases, a solution that prevents excessive cooling can be conducting the analysis in protected environments. A common solution for XRD experiments is using sealed glass or Kapton capillaries, where crystals can be kept in a saturated atmosphere of their native solvent. For ED experiments, similar conditions can be achieved by using so-called ‘environmental’ sample holders, which protect the sample from vacuum while placing it in a gas or liquid solvent of interest.²⁶ Another solution is adopting sufficiently low temperatures to prevent de-solvation and protect sample integrity, but not low enough to induce changes in the structure. For example, collecting data from moisture sensitive frameworks at mildly cryogenic conditions (∼260 K) can be sufficient to disfavour water from travelling across the protective oil used for the crystal mounting, and reaching the cavities.

2.3. Twinning and multiple domains

Once a specimen is ready for the analysis, the determination of an adequate data collection strategy is commonly conducted by the software controlling the instrument. A workflow integrated in many programs starts with the acquisition of a pre-defined dataset for determining the unit cell metric (a, b, c, α, β, and γ), orientation, and Bravais lattice. Based on the outcome, the program autonomously defines a strategy for the final data collection that provides adequate completeness and redundancy (according to IUCr standards included in the CheckCIF validation test³⁷) in the shortest time possible. Although this approach is convenient for minimizing the duration of the measurement, it is not always successful. One frequent reason is the presence of twinning or multiple crystals, which is evidenced by two or more sets of Bragg peaks arrays in reciprocal space. Cases of ‘multi-crystal’ refers to experiments where more than one set of Bragg peaks carrying information on different phases are present in the same dataset. Differently, the term ‘twin’ is used in the more specific case when the domains at the origin of those peaks have (essentially) the same average structure. Among these, merohedral twins are those where the symmetry operation that brings one twin to coincide with the other (twin operation) belongs to the crystal system, but not to the point group of the crystal.^38,39 The Bragg peaks of these twins overlap exactly, and it is not possible to distinguish their presence upon simple inspection of reciprocal space or diffraction images. Similarly, pseudo-merohedral twins also have overlapped peaks (although not always perfectly),⁴⁰ but the symmetry of the crystal is lower than the symmetry of the lattice: the twin operation belongs to a higher crystal system than the structure. Finally, non-merohedral twinning describes cases where the Bragg peak arrays are misaligned and only partly overlapped.⁴¹ Here, the twin operation does not belong neither to the crystal system nor to the lattice system of the unit cell. Even though recognizing these cases from single diffraction images might be possible, a more reliable practice is to use a reciprocal space viewer (e.g. “Ewald Explorer” in CrysAlisPro or “View Reciprocal Lattice” in APEX) after harvesting the diffraction maxima measured in the initial scan. These viewers allow to inspect the 3D reconstruction of the positions of intensity maxima in reciprocal space, and to assess whether these belong to a single lattice or more than one. In the latter case, it is necessary to index these maxima by using more than one domain to obtain reliable unit cell parameters and Bravais lattice. A simpler and safer approach is to assume a triclinic non-centrosymmetric structure, which will lead the software to define a complete — and most time consuming — data collection for any possible case. Concerning conventional ED data collections, these make use of a single rotation axis with useful tilt range up to 140–150°, which implies that adequate data completeness is rarely obtained with a single dataset. Collecting datasets from different crystals and averaging them is therefore often necessary to obtain sufficient completeness, as well as to improve measurement redundancy, lower the uncertainty of integrated intensities (thus increasing the I/σ), and reducing the influence of multiple scattering.⁴²

2.4. Lattice symmetry vs. structure symmetry

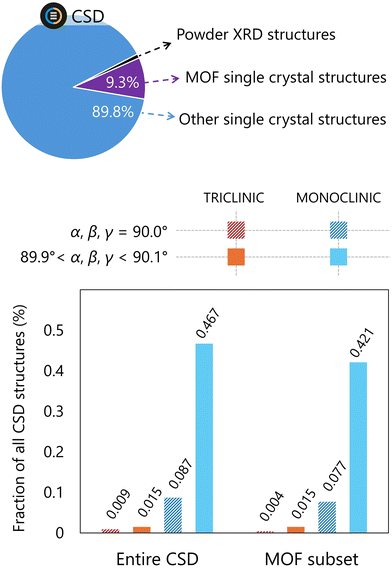
While a preliminary data collection provides enough peaks to determine a unit cell from the reciprocal lattice underlying the Bragg peaks, it is important to remember that a crystal structure can have a symmetry that is lower than its lattice. In other words, there is no connection — other than a mere correlation — between the unit cell parameters of a crystal structure and its symmetry. The associated risk is caused by the automatic unit cell determination procedures being programmed to assign to a unit cell the highest possible symmetry compatible with its cell parameters. For example, a monoclinic structure having unit cell parameters a ≈ b ≈ c and α ≈ β ≈ γ ≈ 90° will be assigned by default a cubic crystal system. Using this choice, the automatic data collection strategy calculation will lead to poor data completeness and, consequently, a less robust structure refinement. These cases are at least as common in reticular structures as in other classes of molecular compounds reported in the Cambridge Structural Database (CSD;⁴³Fig. 3). Subtle unbalance of lattice parameters from the ideal ratio (for example α = γ = 90.01° and β = 90.08°) might caution against this kind of pseudosymmetry, however these small deviations can also originate from extrinsic factors such as crystal misalignment or instrumental imperfections. In every case, it is fair to say that lattice symmetry generally correlates well with crystal symmetry, but the latter can be identified more reliably by inspecting the Bragg intensities in reciprocal space reconstructions, as explained in the next section.

Fig. 3 Statistics on cases of pseudosymmetric triclinic and monoclinic structures found in the CSD. Values for MOF structures align well with the general trend, with approximately one every 200 crystals (ca. 1% of all monoclinic MOFs) having a pseudosymmetric monoclinic unit cell compatible with higher lattice symmetries.

3. Crystal diagnosis in reciprocal space

After completion of SCD data collection, the usual workflow proceeds with automatic unit cell determination and refinement, therefore intensities integration, correction, and space group determination. Within a few minutes, the user leaves behind the data reduction software to focus on crystal structure solution and refinement. There is, however, a practice that despite being quick, accessible and at times critical, remains rarely used especially in XRD: the inspection of 2D reciprocal space reconstructions. These images contain a wealth of information on aspects ranging from space group symmetry to twinning, mosaicity, crystallinity, disorder, and defects (Fig. 4). Most importantly, all this information cannot be accessed by lattice viewers because these do not display all the intensities, but only a few values harvested from the SCD images and stored in their corresponding positions in reciprocal space. These values are of course derived from the intensities, but do not reliably represent the actual pixel-wise, continuous landscape of the sample's reciprocal space (Fig. 4a). Furthermore, in-projection views of a 3D reconstructed reciprocal space are also not convenient for assessing a specimen, since meaningful features might be overlapped and undistinguishable. Reciprocal space reconstructions, also known as ‘precession images’ although not collected with a precession camera,⁴⁴ are undistorted 2D cuts of the sample's diffraction space. Differently, in SCD images the diffraction space is intersected with the Ewald sphere, thus showing features belonging to a non-flat portion of reciprocal space. These reconstructions can be created by accessing the dedicated section of most SCD data reduction software and inputting a few parameters for their extraction from the data. Once the unit cell is determined and refined, a useful practice accompanying every experiment is to extract the hk0, h0l and 0kl planes. Their list can be extended to planes with higher indices (e.g. hkn, hnl and nkl with n = 0, 1, 2) to have a reliable assessment of Bravais lattice centring. Reconstructions should be created with the smallest possible plane thickness and deactivating any symmetry averaging, smoothing or convolution filters to ensure the resulting images reflect as faithfully as possible the experimental data. Once obtained, they serve five important purposes: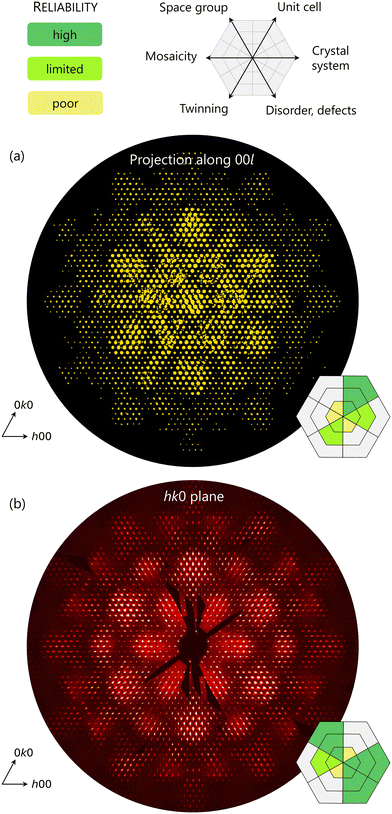

Fig. 4 Qualitative classification of reliability for different types of information obtained from reciprocal lattice viewer (a) and reciprocal space reconstructions (b). The earlier are better suited to identify aspects such as twinning or unit cell parameters, which do not make quantitative use of the intensities, but only of the positions of their maxima. Data used for the exemplary images are taken from literature.¹⁵

(1) Verifying whether Bragg peaks lie on the nodes of the reciprocal lattice based on the refined unit cell. The software used for making reconstructions typically allows to visualize the positions of reciprocal lattice nodes, reciprocal lattice grid, or the Miller indices of pixels in the image. If the mismatch between predicted and actual Bragg positions is significant, the unit cell has not been determined or refined adequately.

(2) Assessing the absence or presence of Bragg peaks belonging to secondary domains like non-merohedral twins, that partly overlap with the main peaks and are not noticeable from the reciprocal lattice viewer.

(3) Determining crystal system and space group by identifying whether specific groups of peaks have similar intensities, and which ones are systematically absent. In this regard, systematic absences can point to specific space groups with the assistance of convenient criteria (so-called ‘reflection conditions’) reported in the International Tables of Crystallography.⁴⁵ This use of reciprocal space reconstructions is essential when using ED data. Here, Bragg intensities are affected by various effects that are more prominent compared to XRD, most notably multiple scattering and high measurement uncertainty, which can alter intensity values and lead to violations of systematic absences. In these frequent cases, automated software can fail in guessing the correct space group or lattice centring, yet an experienced eye could recognize picked-up intensities that should be discarded, or those that should be considered, but fell below the software's cut-off limit.

(4) Assessing the sample's mosaicity (spread of orientations of the crystalline subdomains composing the crystal) and coherence (extension of the long-range order defining the size of said crystalline domains).⁴⁶ Both characteristics are also influenced by extrinsic factors such as crystal misalignment or movement, beam coherence (energy spread and divergence or convergence), and instrumental imperfections.

(5) Verifying the presence of extra-Bragg intensities such as streaks, superstructure peaks, or other forms of structured diffuse scattering. These intensities originate from local features in the real non-periodic structure of the crystal, which do not reach the same long-range order of those features that contribute to the main Bragg peaks. Albeit generally termed ‘diffuse’, such intensities can be sharper or broader depending on the range of local order in different crystallographic directions. Most importantly, diffuse intensities originate from any source of random or locally structured non-periodicity in a crystal such as vacancies, substitutional defects, static disorder, or thermal motions. Therefore, since crystals are never strictly periodic and perfectly ordered, SCD experiments always produce diffuse scattering, even though it might be insufficiently intense to be detected. Some additional information on how to assess crystal imperfections is provided in section 6, titled “Beyond average models”.

4. Data processing and quality assessment

4.1. Intensity integration

Transforming diffraction images into a simple list of numbers (Miller indices and intensity of each Bragg peak with associated error) is as critical as it should sound, since these define the limits of accuracy and precision of the final crystal structure. Ideally, intensity values should not be affected by anything that does not result from the average structure of the crystal. For example, the presence of disorder or merohedral twinning are intrinsic properties of the specimen and their contribution to Bragg intensities can be valuable. Differently, problems such as overlapping split peaks, saturated intensities, faulty absorption correction, or missing measurements (e.g. the intensities hidden by the beam stop) should normally be avoided or handled.

Cases of recurrently twinned crystals will require users to treat data containing multiple sets of Bragg peaks. Most crystallographic software allows for dedicated treatment of such cases, provided that all main domains are appropriately indexed, and their unit cells refined along with their orientation. The performance of this process can vary strongly, and in some cases more reliable integrated intensities are obtained by using a single domain and manually imposing, in the integration software, a systematic change of the default integration box size (increase for fully integrating nearly overlapped peaks or decrease to better integrate peaks that overlap to a limited extent).

When Bragg peaks are strong enough to saturate the detector, they are commonly recognized and excluded from the data, since their integrated values would be meaningless. Such cases of missing peaks can be a significant threat to structure solution and refinement. Particularly, low-order intensities have more dominant effects on the Fourier synthesis from their structure factors, and thus on the calculated densities used for structure modelling. For this reason, automatic data collection strategies include dedicated parts aimed at measuring strong, low-angle peaks using shorter exposure time per frame. Similarly, if some peaks are not recorded because they are hidden by the beamstop, a dedicated fraction of the data collection with longer sample–beamstop (or, in some cases, sample–detector) distance should be used to make sure their structural information is not left out from the data.⁴⁷ It is important to consider that some Bragg peaks that do not saturate photon-counting detectors might still be intense enough to exceed their counting linearity range. If these are integrated without any automated correction or exclusion, their unreliability will be transferred to the model refinement with possibly serious consequences for its value. Intensities affected by problematic issues can be omitted post-integration during structure modelling, by explicitly excluding them via the ShelX command OMIT. This possibility can be easily abused to exclude intensities that are poorly consistent with the model, therefore obtaining an artificially improved fit for low-accuracy models. It is therefore important to use OMIT only to exclude values that are intrinsically unreliable, for example having error/esd values above 10 or being partly shadowed by the beamstop.

4.2. Significance of the R_int

A routine quality indicator for integrated intensities is the ‘internal reliability factor’, expressed as:
Here, F_H and F_−H are the structure factor amplitudes (proportional to the square root of intensities) of Bragg peaks that are Friedel pairs (i.e. having respective Miller indices h, k, l and –h, −k, −l) and are therefore expected to have the same intensity when ignoring anomalous scattering. Since the accuracy of intensities benefit strongly from measurement redundancy, it is important that a given peak is measured several times during a data collection, to make sure that fluctuations in its value due to noise, multiple scattering or other sources of error in intensity values are reduced. For crystal systems more symmetric than triclinic, some intensities that are not Friedel pairs must be equal by symmetry, thus in these cases the R_int is calculated based on the relationship not only between Friedel pairs, but also between all pairs of peaks that should be symmetry equivalent. For this reason, R_int can indicate whether a selected crystal system is not compatible with the observed intensities, since normally R_int increases gradually when a higher symmetry is acceptable, and it jumps steeply if it is not.

When used as an indicator for SCD data quality, R_int does not necessarily signal whether integrated intensities are usable or not, but rather how reliable they are for the determination of a crystal structure.⁴⁸ The more R_int is close to 0, the higher their reliability, and vice versa. The meaning of a ‘good R value’ in the crystallography community gradually shifts to smaller numbers over time, thanks to improved methods and instrumentation, but it also depends on type of sample, instrument, and scientific context. Highly crystalline structures can yield values as low as 2–3%, whereas data from severely disordered ones can still be useful while having R_int in a more concerning range like 10–15%. Such indicative numbers increase to even double the values for ED data, particularly when intensities are strongly affected by multiple scattering. These can be used for so-called ‘dynamical refinements’,^49,50 which make use of the dynamical theory of diffraction to better describe multiple scattering phenomena occurring in single crystals and redistributing the intensities. As the calculation of R_int is only valid within the kinematical approximation, its value is less meaningful for data that are strongly affected by multiple scattering.

In any scenario where the kinematical approximation can be adopted, R_int should be viewed as a measure of reliability of the data used for formulating a model, not of the model itself: it is an indicator of precision, not accuracy. Although better data quality provides a stronger likelihood of a correct model and possibility of deriving finer details such as accurate atomic displacements and interatomic distances, lower-quality data might still afford structures with sensible molecular connectivity and geometry. It is therefore essential to be conscious of the reliability of SCD data and the information it does or does not contain, as discussed in the next section.

5. Data, information, model

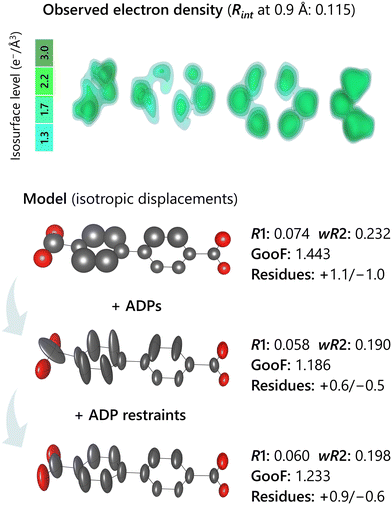
SCD experiments provide data, data processing provides information, and fitting of information provides a model. Knowing the difference between these three concepts is essential to understand the significance of each step in the crystallographic analysis.

In this regard, models can be mistaken for experimental information. This fallacy is particularly tempting for those who are not familiar with the crystallographic process and are more exposed to the biasing influence of pictures created from models and displayed in publications. Therefore, one should be aware that crystal structures are personally crafted by a crystallographer according to their criteria and scope. These creations must be the result of a fitting procedure targeting a three-dimensional map of values: electron densities from XRD, electrostatic potential from ED, nuclei densities from neutron diffraction. By using conventional software for structure refinement, these maps can be produced by a Fourier synthesis of the observed structure factors (Fig. 5). Further details on how to produce these maps with the program Vesta⁵¹ can be found in the supplementary information of a study where their inspection has been key for solving a complex case of structural disorder.¹¹ Even though automatic structure solution and refinement routines do not encourage the visualization of these maps, it is good practice to inspect them, particularly when poor data quality or problematic disorder produces questionable models.^11,12 These densities are the information that refinement programs try to fit during the optimization of a model by, for example, least square refinements of atomic coordinates and displacement parameters. As any kind of information derived from the processing of real data, Fourier maps contain intrinsic structural information as well as other effects. Generally, the most observed features are localised maxima, smeared densities, noise, and ripples due to faulty absorption correction and/or limited resolution. A localized maximum normally signals the presence of an atom, provided that its shape and extension is consistent with it. For example, a maximum with a diameter of 0.1 Å is most certainly a structurally meaningless spike of density. Smeared densities generally result from dynamic or static disorder distributing the otherwise localized average presence of atoms over a wider volume. Truncation ripples are the unavoidable consequence of limited data resolution (Fig. 5, lower part). These are always present but become particularly intrusive when data resolution is worse than ∼0.8 Å. Noise is also unavoidable and appears as chaotic oscillations of densities above and below zero. As refinement programs report maximum and minimum values of residual densities after a refinement, when these are approximately identical in magnitude but with opposite sign, and relatively weak (e.g. less than 0.5 e⁻ Å⁻³ when using XRD data) it is a common indication that the meaningful densities have been modelled, and what is left is noise.

Fig. 5 Effect of limited resolution of the available information from SCD data of ZIF-65, viewed on (111) as density isosurfaces (a) and sections (b). In (a), the loss of precision in structural information is evident as atomic positions can be localized more ambiguously for worse resolutions than 1.0 Å, and information on molecular structures is already lost at 1.5 Å. in (b), truncation ripples are visible in proximity of heavier atoms, increasing in magnitude and oscillation length for worse resolutions and creating, already at 1.0 Å, strong oscillations that cannot be described by an atomic model. Density maps were calculated by using intensities from a structure published with CSD identifier ‘foqpaf’.

6. Crystal structure modelling

6.1. General philosophy

Crystallographers face routinely what might be considered an overarching dilemma in crystal structure modelling: should one accept the risks of creating information unsupported by the data for the sake of chemical soundness, or should crystal structures strictly adhere to the available evidence even if this leads to chemically meaningless structures? This question might sound difficult for crystallographers taking their first steps; however, it is widely known that the latter choice bears significantly higher risks than the first one. A common example concerns the modelling of hydrogen atoms. Particularly in XRD data, their presence is only visible with high-resolution data, and their positions are not accurate, since X-rays only show where their electrons are located, somewhere between the hydrogen nucleus and the atom it is bound to — a shortcoming that can be circumvented by modern methods based on aspherical scattering factors.^52,53 While on the one hand the exact hydrogen positions are not observed directly in the electron densities from XRD data, a structure lacking one or more hydrogen atoms contributes false information in the form of incorrect valence, wrong chemical composition, lack of hydrogen bonding interactions, etc. Other cases are structures containing unrealistic geometries or bonding distances resulting from restraints-free refinements. The risks become important when these models deteriorate the statistical value of databases, require human or automated editing before usage in computational chemistry, or are simply trusted and used as-found by researchers who lack chemical expertise — especially since these structures are supposedly approved by expert reviewers. Furthermore, the increasing interest in training machine learning algorithms for materials discovery or properties prediction^54–56 brought the value of structure databases under an even stronger spotlight, along with the open challenge of automating ‘sanity checks’ on large numbers of experimental crystal structures.^57,58

6.2. Useful modelling practices

To bring a positive contribution in this context, crystallographers should strive to disclose models that represent as faithfully as possible the experimental information while being chemically meaningful, the latter aspect being of utmost priority. For example, a molecular fragment not clearly visible in the residues due to disorder should be modelled if its presence can be assumed or confirmed by complementary analysis. As chemical soundness is an essential aspect of the process, crystallographers should have sufficient knowledge of structural chemistry to recognize features that require particular attention. Regardless, the use of structural databases for statistical analysis of geometrical details such as bonding distances or angles should be a standard practice whenever there are doubts about their refined values. Their likelihood can be verified by setting up an optimized search in the CSD program ConQuest,⁵⁹ or by conducting a ‘Geometry Check’ using the dedicated feature in the program Mercury.⁶⁰ When the observed value is clearly an outlier, it can be either the result of a refinement that tries to fit weak densities, well-defined maxima belonging to split positions of a disordered species, or the discovery of a rare case. In the first two instances, refinements should be conducted with appropriate restraints, and disorder should be modelled by taking care of separating the alternative components in different parts (using the PART command of ShelXL^61–63). If the outlier is genuine, the rule ‘exceptional claims require exceptional evidence’ applies, hence the importance of verifying ambiguous or unusual structures with complementary techniques beyond diffraction. Overall, it is important to remain aware that SCD is not optimal for chemical analysis — especially quantitative — like, for example, mass spectrometry is not optimal for structural analysis.

6.3. Significance of R₁ and wR₂

In the context of model reliability, two dedicated parameters represent the ‘bread and butter’ of crystal structure modelling, namely R₁ and wR₂. These are defined by the following expressions:⁶²

Here, ‘o’ and ‘c’ indicate whether the structure factors are derived from the measured intensities or from the artificial model that is refined to describe them; ‘w’ is a weighting factor derived from the standard deviation of the F_o values. While R₁ (a mean deviation) remains of common use, wR₂ is more statistically meaningful since it is essentially a normalized standard deviation.⁶⁴ Both these parameters are indicators of reliability of a model to fit integrated intensities. As such, they can have satisfyingly low values even when working with problematic data, since poorly reliable data is not necessarily difficult to fit. Although minimizing these values affords models that describe better the observed densities, this practice should not coincide with overfitting. For example, isolated density maxima in cavities can be assigned to oxygen atoms of water molecules. This choice will produce lower R₁ and wR₂, regardless of whether water molecules are present or whether their position is compatible with realistic intermolecular interactions. On the opposite side, incomplete or incorrect modelling can provide satisfactory R factors that are fully compliant with IUCr publication standards. For example, heavy-metal MOF structures will exhibit subtle R factors improvement during final refinement cycles involving light-atom species, for example in modelling solvent molecules and refining their displacement parameters. In the crystallography of porous structures, these characteristics can be critical since solvent molecules affects both functional activity and flexibility of the host framework.^65–69 Some useful advice on their handling is provided as follows.

6.4. Handling solvent molecules

Solvent coordinating metal centres should be modelled when these species can be identified in the density residues, even if disordered. When they are weakly interacting with the framework, they can be included in the refinement if their presence can be unambiguously identified. Otherwise, overfitting of weak and smeared densities can be avoided by applying a solvent mask such as the one created by the ‘SQUEEZE’⁷⁰ command in the program Platon,⁷¹ or the analogous function in Olex2.⁷² In so doing, crystallographers should take the time of inserting sensible chemical information in the cif file to provide their best hypothesis of which species have been excluded from the refinement. Their amount should be specified consistently with the number of electrons present in the cavities, as reported by the solvent masking process — a procedure only valid for models refined against XRD intensities, since X-rays are scattered by electrons. This is currently a step requiring minimal manual input (molecules type and number), since software such as Olex2 inserts the resulting information in the crystal's formula appropriately, in the cif file. This step also allows to clarify charge balance in structures, where charge neutrality is achieved by the presence of ions that cannot be modelled because of disorder. Inserting these ions in the formula without modelling them in completely arbitrary positions is an appropriate solution to these cases.

6.5. Justified use of restraints

Crystallographers working on framework structures become rapidly familiar with ShelX restraint commands affording refinement-stable and chemically sound models from non-ideal data. Among the most common, we have those forcing bond distances and molecular geometries to user-specified values (e.g. DFIX and DANG), whose deviation from the actual — unknown — ones can be negligible or significant. As previously mentioned in the opening of section 6.1, both chemical soundness and adherence to experimental information are paramount, with the earlier taking precedence over the latter. It follows that the use of unnecessary or unnecessarily strict restraints should be avoided, since they limit the freedom of model optimisation towards a better fitting the average structure.

In some cases, redundant restraints can be safe for structural accuracy, and their avoidance is essentially a matter of crystallographic elegance or philosophy. For example, forcing the geometry of a benzene molecule to a regular hexagon even though this already results from unrestrained refinement can be considered safe in terms of safeguarding structural accuracy, since the final model will not be affected significantly. However, it is arguably more difficult to predict whether a restraint is redundant, than avoiding its use altogether when the refinement produces a chemically sound model that can be unequivocally recognized in the Fourier maps.

When restraints are necessary, on the other hand, they might be needed just for allowing the optimisation of a complete model to settle during the final steps of the refinement. Once this has occurred, ‘obsolete’ restraints can be eliminated to conduct final refinement cycles and reach a more accurate model.

If the use of restraints is justified, their target values (including standard deviation) should be chosen according to meaningful criteria. As an example, let us consider a case that requires restraining the C–O distance of an ethanol molecule, modelled from data collected at 200 K. A sensible value for the target distance can be obtained by using the program ConQuest for extracting, from the CCDC database, the C–O distance distribution for all ethanol molecules in structures analysed at 200 K. The restrained distance can be fixed according to the value that is most frequently found. To document the process appropriately, this statistical analysis and the resulting modelling choice should be described in the crystallographic section of the SI file.

A class of restraints that is particularly relevant for framework structures are those regulating the behaviour of anisotropic displacement parameters. The following section discusses key aspects related to their handling.

6.6. Anisotropic displacement parameters (ADPs)

Another essential modelling aspect concerns anisotropic displacement parameters, shortened as ADPs.⁷³ Often incorrectly referred to as ‘thermal parameters’ or ‘temperature factors’, these are ellipsoids used to model atoms, whose averaged density adopt a non-spherical shape due to both thermal vibrations and static disorder. Within the approximation, it is assumed that the average densities in an atomic structure can be appropriately described by a three-dimensional gaussian distribution of density centred on each average atomic position. The numerical values of ADPs along specific directions correspond to the fitted mean-square displacements of the atom from its coordinate. From a qualitative standpoint, there are two main distinguishing features of ADPs: the ratios between their components and the size of their spherical approximant (U_eq). The first defines whether the density of the modelled atom is distributed, on average, in a volume that is approximately isotropic like a sphere, elongated like a cigar, or flat like a pancake. In this regard, ADPs should not be left free to adopt physically non-meaningful shapes. For example, when the direction of the widest ADP component of a single atom in a molecule is roughly aligned with a covalent bond, such a model cannot be realistic since covalent bonds are the most rigid entities in the vibrational degrees of freedom of a molecule. Therefore, the largest ADP component(/-s) should point away from these bonds. A reasonable exception to this rule is when an entire molecular fragment exhibits similarly elongated ADPs, which represents a rigid displacive disorder — thermal or static — of the whole fragment. Another problematic behaviour that can be found during structure modelling is when atoms belonging to a rigid fragment have erratic ellipsoid orientations (Fig. 6). A typical example is a benzene ring, whose ADPs must be consistent with the collective rigid displacement of its six sp² carbon atoms.

Fig. 6 Example of a problematic average density requiring ADP restraints to prevent erratic behaviour during refinements. Intensities are taken from a deposited structure with CSD identifier piwvav, used with default weighting parameter value of 0.1 to avoid an artificial improvement of the goodness of fit (GoF). Note that worse figures of merit are more adequate than lower values linked to inappropriate modelling like, in the considered case, overfitting with unrestrained ADPs.

In the context of U_eq, it is important to be aware that partly vacant atoms and presence of displacive disorder have one common consequence on the average structure: both create lower densities associated to atomic positions. Thus, it is not sensible to freely refine parameters describing both ADPs and occupancy of atoms at the same time, since the effects of these variables are strongly correlated. When seeking a refined occupancy value, appropriate ADP restraints should be used when describing occupancy with a freely refined variable, and the final ADPs should be checked in terms of how they compare with those of the fully occupied component of the structure. Another key point concerning occupancy is that at least some structural components should be kept with unitary values, as reference points for the remaining ones. For example, it is not possible to determine whether, in a structure composed of two building blocks, vacancy defects are found for only one of them, or both. The occupancy related variable of one of the two components should be fixed, the other one refined. If the other refines to unrealistic values above 1, then it should be fixed to 1, and the other should be refined instead (resulting in a partial occupancy below 1). Therefore, the only information available from SCD refinement will be the ratio between the components, i.e. their stoichiometric amount in the crystal. It is worth mentioning that wrong atom type assignment can also result in change of ADP values, since, for example, a heavier atom having more density to be fitted will result in a shrinkage of ADPs. An indication of this issue is when U_eq of neighbouring atoms is homogeneous except for an isolated position. For example, modelling a chlorine as heteroatom in a fluorobenzene will result in suspiciously larger ADPs for chorine compared to the neighbouring carbon, because the chlorine density would need to be more spread in space to fit the density belonging to a fluorine.

6.7. Structure pseudosymmetry

Space group pseudosymmetry is another relevant topic when determining reticular structures. Generally, it is the crystallographic analogue of the phrase “almost but not quite”, that is when a structure can be approximately described by a certain space group but is more accurately described by using a less symmetric one. The reason for preferring the second choice should be an increase of structural information. If by using lower symmetry the refined structure remains essentially identical, using higher symmetry is the correct choice, since it allows for a more robust fitting (fewer parameters) of the same structure. Since framework structures frequently feature highly symmetric connectivity but quite complex molecules, pseudosymmetry is arguably more common than one might expect, and the number of overlooked cases in reticular structures is likely underestimated due to these being underreported. There are two common reasons for this to happen: (1) pseudosymmetry of structures is transferred also to their diffracted intensities, which are therefore mistaken for having a higher symmetry; (2) crystallographic software (as well as classical crystallographic education) is biased towards prioritizing the use of higher symmetries, thereby eliminating useful information in cases of lower-symmetry structures. When suspiciously high R₁/wR₂ values are found, which cannot be due to disorder or data quality, it can be useful to solve a structure by using a different space group. These cases can coincide with the presence of merohedral twinning (undistinguishable based on reciprocal space inspection), which creates average atomic densities having an apparently higher symmetry. These structures can be solved well once the correct space group and twin law are identified, and the twin fraction is refined along with the average model.

7. Beyond average models

Even though disorder structure determination is outside the scope of this article, there are some routines that every crystallographer is encouraged to follow for having better control over their analysis, and for providing useful structural information with minor additional effort. Crystallographic software dedicated to the analysis and integration of SCD data includes a section dedicated to the creation of reciprocal space reconstructions, as mentioned in an earlier section. Creating these images and adding them to the supplementary information file of a manuscript is as effortless as it is significant. Indeed, while serving as a quality check for your crystal or robust evidence for difficult-to-handle data, they might also reveal precious information to other scientists studying the real non-periodic complexity of crystals. A few indications for a qualitative interpretation of reciprocal space images are provided as follows.

Isotropic peak broadening (larger Bragg peaks) indicates a smaller crystallite size of the domains composing the singe crystal — when it is not originating from instrumental factors. Smearing of peaks into arc-shaped intensities (Fig. 7a) indicates that the sample is composed by a multitude of fragments, each one having slightly different orientation. Diffuse scattering in the form of broad clouds (Fig. 7b), streaks, or superstructure peaks with profiles different from that of the main Bragg peaks indicates the presence of structural disorder. Disorder is always present in crystals, but it frequently results in intensities around 4–5 orders of magnitude weaker than those of Bragg peaks. For this reason, this scattering component can be missing in diffraction patterns acquired with insufficient exposure or source intensity. In the reconstructed reciprocal space, the dimensionality of diffuse scattering (3D clouds, 2D planes or 1D streaks) indicates how many of the three related crystal directions are affected by disorder. One should remember that, in each reciprocal space cut, diffuse scattering planes might appear as streaks if the plane of diffuse intensities is not coplanar with the reconstructed slab. Furthermore, contrarily to a common misconception, not only correlated disorder creates recognizable diffuse scattering in the reconstructions, but also random disorder. It is only when random disorder involves isolated single-atom vacancies or substitutional defects, that the related diffuse scattering is isotropic and usually undistinguishable from the amorphous extrinsic background.

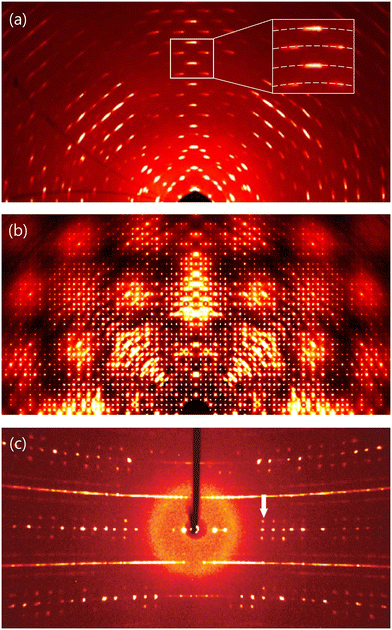Fig. 7 Published examples of scattering features that are best analysed using reciprocal space reconstructions: (a) crystal damage induced mosaicity resulting in arc-shaped intensities;⁸¹ (b) diffuse clouds from three-dimensional disorder;¹¹ (c) simultaneous presence of diffuse lines likely due to stacking faults, and satellite peaks from a modulated structure (marked with a white arrow; this last is an oriented SCD pattern and not a reconstruction).⁷⁹ Re-use of images (a) and (c) is compliant with the policies of the respective publishers; image (b) has been produced from raw data.

When using electron diffraction data, additional effects such as multiple inelastic scattering and beam coherence can introduce features such as streaks or bands that might be confused for diffuse scattering. However, since their origins are fundamentally different, they can be recognized and reduced or corrected.^74,75 Last, but not least, sharp satellite peaks with profiles analogous to those of the main Bragg peaks indicate the presence of so called ‘modulated’ structures (Fig. 7c). This phenomenon occurs when an ordered structure has repeating features that do not match its translational symmetry. One such example are frameworks, where molecules dispersed in the cavities form long-range ordered assemblies, whose repetition length differs from the length of the unit cell.^76–78 Another type of modulated structure is when the framework itself exhibits modulation due to symmetry frustration and/or so-called ‘charge density waves’.^79,80 In some cases, an integer multiple of the unit cell suffices to describe the periodicity of these features: these are classified as ‘commensurately modulated’ structures. Otherwise, the structure is aperiodic and is classified as ‘incommensurately modulated’. Their treatment requires specialized expertise, but the presence of these rare phases can be recognized in reciprocal space reconstructions and displayed in manuscripts for the awareness of the community.

8. Integrity of the crystallographic practice

8.1. Foundations of a meaningful model

One last defining aspect of SCD analysis is transparency and correctness in presenting results. In terms of transparency, by far the most important requirement is the disclosure of the intensities used for structure solution and refinement, which must be listed in the cif file in their values and uncertainty. This information is automatically inserted by the ShelXL keyword ‘ACTA’ when finalizing the structure. In the absence of these intensities, the cif file is fully falsifiable, thus should not be considered significant or acceptable for publication. Although most CSD structures deposited in recent years contain this information,⁸² publication of models without intensity information is still an existing practice allowed by some journals and possibly also overlooked by editors and reviewers. Moving a step further from integrated intensities, disclosure of raw experimental data (diffraction images and related metadata) should also be encouraged.⁸³ This initiative is ideally aligned with the F.A.I.R. (findable, accessible, interoperable, and reusable) principles of scientific research and allows other researchers to re-use the data for different purposes, or revisit models once their accuracy can be improved thanks to advancements that were unavailable at the time of first publication.⁸⁴ Concerning the significance of model description in the text, numerical values taken from structure refinement should be reported together with their standard uncertainty (s.u.). Most commonly, these values include bonding distances, angles, intermolecular contacts, unit cell parameters, and refined occupancies, whose precision and significance would only be known if their s.u. is disclosed.

8.2. Fourier density maps

Another choice that significantly elevates the transparency of the crystallographic work is displaying so-called “Fourier density” maps calculated from the observed structure factors (or, alternatively, difference density maps) to show the information that has been fitted with a model. These maps should be requested when disordered species are discussed, or weak data are used to make a relevant point in a study. When needed, peer-reviewers can independently produce them starting from submitted cif files that include (mandatory) intensity information. Good practice for an informative display of density maps is using multiple semi-transparent isosurfaces with gradually different colour and sensible levels (similarly to Fig. 5 and 6), depending on the context. When levels are too low, noisy surfaces can make the picture confusing. However, carefully lowering them without letting the noise dominate, it is possible to create pictures highlighting the finer details of density residues. These can be useful to study subtle features such as the effects of disordered framework species or guest molecules.^11,85,86 When, for the sake of clarity, only positive signals of a density or residual density map are shown, it is necessary to declare explicitly that the negative part has been hidden. As a rule of thumb, if positive densities are analogous in distribution and magnitude to the negative ones, these can be considered structurally irrelevant. As such, they should not lead to confirmation biases such as believing that a familiar-looking density distribution can be attributed to a desired molecule — a cognitive bias known as ‘pareidolia’. These cases are relatively common when dealing with the modelling of guest molecules in reticular structures. Particularly if data quality is poor (but not only in these cases), modelling ambiguous residual density as trapped H₂O or CO₂ molecules, for example, can be straightforward and without problematic consequences on the final R factors. By normalizing the scrutiny and display of the observed densities behind a model, the dangers of such incorrect uses of SCD data can be effectively reduced.

8.3. The value of terminology

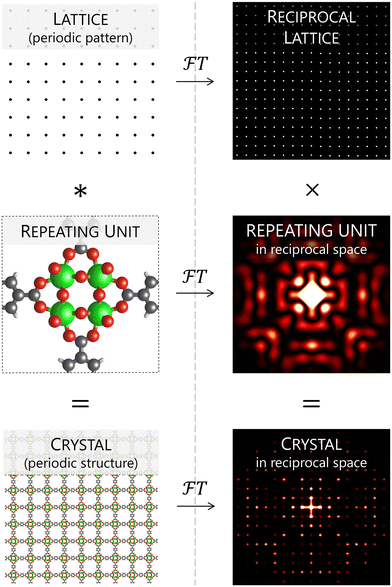
One last aspect with respect to correct reporting of structural data concerns the correct use of terminology. This is a delicate topic since terminology conventions set by IUCr for the rigor and benefit of the community can differ from how some terms are used in a more colloquial context.⁸⁷ A common case is the word ‘lattice’, whose meaning corresponds to an ideal, periodic collection of points in space, but is instead used with the meaning of ‘structure’ in various instances.^88,89 Expressions such as ‘atomic lattice’, ‘lattice energy’, ‘lattice vibration’ or ‘lattice defects’ are all common misuses of this word in a crystallographic context, whereas replacing ‘lattice’ with ‘structure’ results in perfectly functional and correct expressions. Dimensionality is another misused concept, as many studies describe 2D, 1D or even 0D structures, which are three-dimensional since even a single atom has a volume. Here, replacing ‘nD’ with ‘nD-connected’ (where n is the number of dimensions) is a more careful rephrasing. Although these might be considered irrelevant issues in the general context of materials science, those who pay attention to the correct use of terminology are less exposed to the bias that words impose on our scientific thinking. For instance, knowing the difference between ‘structure’ and ‘lattice’ allows to understand how pseudosymmetry can originate from the symmetry difference between lattice and crystal structure, and to fully capture the relationship between the latter and the observed Bragg peaks (Fig. 8). On a related note, using ‘Bragg peak’ instead of ‘reflection’ avoids a ubiquitous misnomer, since light reflection and diffraction are fundamentally different phenomena. Further, referring to a crystal structure as an ‘average model’ reminds us that these are artificial ball-and-stick constructs that do not fully display the actual complexity of crystals, not even on average. In fact, the closest picture we can have of an average structure is the density map calculated from the observed structure factors, which shows the real continuous complexity of the projected image of the crystal's structure along its three crystallographic directions. In a general perspective, striving to use correct terminology allows a crystallographer to maintain a rigorous scientific mindset, which can safeguard them from many unpredictable fallacies we are exposed to during our research.

Fig. 8 Schematic relationship between lattice, unit cell and crystal, which underlies Bragg intensities in SCD data (FT: Fourier transform). When ‘lattice’ is used with its meaning of ‘repetition motif’, the description of crystals as convolution (*) of lattice with the unit cell content is consistent with its consequences in reciprocal space, and therefore on diffraction patterns.

Conclusions

The crystallography of single crystals is a remarkably solid science with respect to average structure determination of essentially any type of materials. If, on the one hand, porous crystals can have more diverse structures compared to other classes of solids, the toolbox of modern crystallography is fully equipped to address every structure determination challenge. However, due to such a singular structural versatility, crystallographers working on MOFs, COFs, etc. should be experienced in dealing, sometimes simultaneously, with complex cases of disorder, host–guest modelling, pseudosymmetry, merohedral twinning, etc. This work surveyed several of such challenges to create awareness towards frequent pitfalls, which can lead to misleading or wrong models slipping through peer-review and becoming fragile strands in the fabric of published literature. By addressing the most common sources of struggle and error in SCD of reticular structures, the goal of this overview is not to make this analysis an unambiguous and straightforward technique, but to guide both newcomers and experienced crystallographers towards elevating the reliability of their work, nurturing their self-critical side, and ultimately discovering new questions and challenges in the art of single crystal structure determination.

Conflicts of interest

There are no conflicts of interest to declare.

Data availability

All data cited in the article are available as published in other sources, as reported in the main text. No experimental data has been produced in the context of this manuscript.

Acknowledgements

This article would not exist without the support and education I received from friends and collaborators over the past decade of interaction with the crystallographic community. Among them, I particularly thank Arianna Lanza and Peter Müller for their precious feedback on the working manuscript, as well as Martin Lutz, Volodymyr Bon, and Andrew K. Inge for their useful suggestions. I also thank Prof. Alessia Bacchi and other talented crystallographers at the University of Parma who accompanied my first defining steps as a researcher. I am grateful to the reviewers for their thoughtful assessment and requests, which elevated the value of this work. Lastly, I dedicate my most sincere gratitude to the many colleagues, most importantly students, who engaged in insightful discussions on the science and art of crystallography, challenging my knowledge and shaping my identity as a structural chemist up till now.

Notes and references

1. B. F. Hoskins and R. Robson, J. Am. Chem. Soc., 1989, 111, 5962–5964.
2. S. Kitagawa, T. Okubo, S. Kawata, M. Kondo, M. Katada and H. Kobayashi, Inorg. Chem., 1995, 34, 4790–4796.
3. O. M. Yaghi and H. Li, J. Am. Chem. Soc., 1995, 117, 10401–10402.
4. S. Kitagawa, R. Kitaura and S. I. Noro, Angew. Chem., Int. Ed., 2004, 43, 2334–2375.
5. R. Freund, S. Canossa, S. M. Cohen, W. Yan, H. Deng, V. Guillerm, M. Eddaoudi, D. G. Madden, D. Fairen-Jimenez, H. Lyu, L. K. Macreadie, Z. Ji, Y. Zhang, B. Wang, F. Haase, C. Wöll, O. Zaremba, J. Andreo, S. Wuttke and C. S. Diercks, Angew. Chem., Int. Ed., 2021, 60, 23946–23974.
6. H. Deng, C. J. Doonan, H. Furukawa, R. B. Ferreira, J. Towne, C. B. Knobler, B. Wang and O. M. Yaghi, Science, 2010, 327, 846–850.
7. S. Canossa, Z. Ji, C. Gropp, Z. Rong, E. Ploetz, S. Wuttke and O. M. Yaghi, Nat. Rev. Mater., 2023, 8, 331–340.
8. M. Gemmi, E. Mugnaioli, T. E. Gorelik, U. Kolb, L. Palatinus, P. Boullay, S. Hovmöller and J. P. Abrahams, ACS Cent. Sci., 2019, 5, 1315–1329.
9. C. Gropp, S. Canossa, S. Wuttke, F. Gándara, Q. Li, L. Gagliardi and O. M. Yaghi, ACS Cent. Sci., 2020, 6, 1255–1273.
10. T. D. Bennett, A. K. Cheetham, A. H. Fuchs and F. X. Coudert, Nat. Chem., 2016, 9, 11–16.
11. C. Koschnick, M. W. Terban, R. Frison, M. Etter, F. A. Böhm, D. M. Proserpio, S. Krause, R. E. Dinnebier, S. Canossa and B. V. Lotsch, J. Am. Chem. Soc., 2023, 145, 10051–10060.
12. C. Koschnick, R. Stäglich, T. Scholz, M. W. Terban, A. von Mankowski, G. Savasci, F. Binder, A. Schökel, M. Etter, J. Nuss, R. Siegel, L. S. Germann, C. Ochsenfeld, R. E. Dinnebier, J. Senker and B. V. Lotsch, Nat. Commun., 2021, 12, 1–9.
13. E. G. Meekel, E. M. Schmidt, L. J. Cameron, A. D. Dharma, H. J. Windsor, S. G. Duyker, A. Minelli, T. Pope, G. O. Lepore, B. Slater, C. J. Kepert and A. L. Goodwin, Science, 2023, 379, 357–361.
14. S. Ehrling, E. M. Reynolds, V. Bon, I. Senkovska, T. E. Gorelik, J. D. Evans, M. Rauche, M. Mendt, M. S. Weiss, A. Pöppl, E. Brunner, U. Kaiser, A. L. Goodwin and S. Kaskel, Nat. Chem., 2021, 13, 568–574.
15. S. L. Griffin, E. G. Meekel, J. M. Bulled, S. Canossa, A. Wahrhaftig-Lewis, E. M. Schmidt and N. R. Champness, Nat. Commun., 2025, 16, 1–9.
16. F. Gándara and T. D. Bennett, IUCrJ, 2014, 1, 563–570.
17. A. L. Thompson, Crystallogr. Rev., 2019, 25, 3–53.
18. P. Müller, Crystallogr. Rev., 2009, 15, 57–83.
19. S. Øien-ØDegaard, G. C. Shearer, D. S. Wragg and K. P. Lillerud, Chem. Soc. Rev., 2017, 46, 4867–4876.
20. B. Dittrich, IUCrJ, 2021, 8, 305–318.
21. A. J. Thompson, J. J. Whittaker, A. J. Brock, H. A. B. AL-Fayaad, K. S. A. Arachichage, M. C. Pfrunder, J. C. McMurtrie and J. K. Clegg, Cryst. Growth Des., 2024, 24, 5349–5354.
22. H. Jiang, D. Alezi and M. Eddaoudi, Nat. Rev. Mater., 2021, 6, 466–487.
23. R. Pallach, J. Keupp, K. Terlinden, L. Frentzel-Beyme, M. Kloß, A. Machalica, J. Kotschy, S. K. Vasa, P. A. Chater, C. Sternemann, M. T. Wharmby, R. Linser, R. Schmid and S. Henke, Nat. Commun., 2021, 12, 1–12.
24. H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428.
25. M. Quintelier, A. Hajizadeh, A. Zintler, B. F. Gonçalves, R. Fernández de Luis, L. Esrafili Dizaji, C. M. L. Vande Velde, S. Wuttke and J. Hadermann, Chem. Mater., 2024, 36, 7274–7282.
26. Y. Ling, T. Sun, L. Guo, X. Si, Y. Jiang, Q. Zhang, Z. Chen, O. Terasaki and Y. Ma, Nat. Commun., 2022, 13, 1–8.
27. Z. Huang, E. S. Grape, J. Li, A. K. Inge and X. Zou, Coord. Chem. Rev., 2021, 427, 213583.
28. F. Banihashemi, G. Bu, A. Thaker, D. Williams, J. Y. S. Lin and B. L. Nannenga, Ultramicroscopy, 2020, 216, 113048.
29. T. Sun, W. Lei, Y. Ma and Y. B. Zhang, Chin. J. Chem., 2020, 38, 1153–1166.
30. C. Castillo-Blas, A. M. Chester, D. A. Keen and T. D. Bennett, Chem. Soc. Rev., 2024, 53, 3606–3629.
31. C. Mariette, E. Trzop, J. Y. Mevellec, A. Boucekkine, A. Ghoufi, G. Maurin, E. Collet, M. C. Munõz, J. A. Real and B. Toudic, Phys. Rev. B, 2020, 101, 134103.
32. A. Schneemann, V. Bon, I. Schwedler, I. Senkovska, S. Kaskel and R. A. Fischer, Chem. Soc. Rev., 2014, 43, 6062–6096.
33. A. Lanza, L. S. Germann, M. Fisch, N. Casati and P. Macchi, J. Am. Chem. Soc., 2015, 137, 13072–13078.
34. S. Canossa, P. Pelagatti and A. Bacchi, Isr. J. Chem., 2018, 58, 1131–1137.
35. C. K. Brozek, V. K. Michaelis, T. C. Ong, L. Bellarosa, N. López, R. G. Griffin and M. Dincǎ, ACS Cent. Sci., 2015, 1, 252–260.
36. S. Lee, H. B. Bürgi, S. A. Alshmimri and O. M. Yaghi, J. Am. Chem. Soc., 2018, 140, 8958–8964.
37. I. U. of Crystallography, https://journals.iucr.org/services/cif/checking/checkfaq.html.
38. S. Parsons, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2003, 59, 1995–2003.
39. M. Nespolo, Cryst. Res. Technol., 2015, 50, 362–371.
40. S. R. Parkin, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2021, 77, 452–465.
41. M. Sevvana, M. Ruf, I. Uson, G. M. Sheldrick and R. Herbst-Irmer, Acta Crystallogr., Sect. D: Struct. Biol., 2019, 75, 1040–1050.
42. M. Ge, T. Yang, Y. Wang, F. Carraro, W. Liang, C. Doonan, P. Falcaro, H. Zheng, X. Zou and Z. Huang, Faraday Discuss., 2021, 231, 66–80.
43. C. R. Groom, I. J. Bruno, M. P. Lightfoot and S. C. Ward, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2016, 72, 171–179.
44. M. J. Buerger, The Photography of the Reciprocal Lattice, ASXRED Monograph No. 1, American Society for X-Ray and Electron Diffraction, 1944.
45. B. H. D. Flack, U. Shmueli and B. H. D. Flack, in International Tables for Crystallography, Vol. A, Section 1.6.5, 2016, pp. 114–128.
46. IUCr, dictionary.iucr.org/Mosaic_crystal, https://dictionary.iucr.org/Mosaic_crystal, (accessed 3 July, 2025).
47. H. I. Süss, M. Lutz and J. Hulliger, CrystEngComm, 2002, 4, 610–612.
48. P. A. Karplus and K. Diederichs, Science, 2012, 336, 1030–1033.
49. P. B. Klar, Y. Krysiak, H. Xu, G. Steciuk, J. Cho, X. Zou and L. Palatinus, Nat. Chem., 2023, 15, 848–855.
50. H. Bethe, Ann. Phys., 1928, 392, 55–129.
51. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.
52. S. C. Capelli, H. B. Bürgi, B. Dittrich, S. Grabowsky and D. Jayatilaka, IUCrJ, 2014, 1, 361–379.
53. F. Kleemiss, O. V. Dolomanov, M. Bodensteiner, N. Peyerimhoff, L. Midgley, L. J. Bourhis, A. Genoni, L. A. Malaspina, D. Jayatilaka, J. L. Spencer, F. White, B. Grundkötter-Stock, S. Steinhauer, D. Lentz, H. Puschmann and S. Grabowsky, Chem. Sci., 2021, 12, 1675–1692.
54. P. Nguyen, D. Loveland, J. T. Kim, P. Karande, A. M. Hiszpanski and Y.-J. Han, J. Chem. Inf. Model., 2021, 61, 2147–2158.
55. Y. A. Alghofaili, M. Alghadeer, A. A. Alsaui, S. M. Alqahtani and F. H. Alharbi, J. Phys. Chem. C, 2023, 127, 16645–16653.
56. Y. Luo, S. Bag, O. Zaremba, A. Cierpka, J. Andreo, S. Wuttke, P. Friederich and M. Tsotsalas, Angew. Chem., Int. Ed., 2022, 61, e202200242.
57. A. J. White, M. Gibaldi, J. Burner, R. A. Mayo and T. K. Woo, J. Am. Chem. Soc., 2025, 147, 17579–17583.
58. M. Gibaldi, A. Kapeliukha, A. White, J. Luo, R. A. Mayo, J. Burner and T. K. Woo, Chem. Sci., 2025, 16, 4085–4100.
59. I. J. Bruno, J. C. Cole, P. R. Edgington, M. Kessler, C. F. Macrae, P. McCabe, J. Pearson and R. Taylor, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2002, 58, 389–397.
60. C. F. MacRae, I. Sovago, S. J. Cottrell, P. T. A. Galek, P. McCabe, E. Pidcock, M. Platings, G. P. Shields, J. S. Stevens, M. Towler and P. A. Wood, J. Appl. Crystallogr., 2020, 53, 226–235.
61. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
62. G. Sheldrick, User guide to crystal structure refinement with SHELXL, (accessed 24 July, 2025).
63. P. Müller, R. Herbst-Irmer, A. L. Spek, T. R. Schneider and M. R. Sawaya, Crystal Structure Refinement: A Crystallographer's Guide to SHELXL, Oxford University Press, 2006.
64. W. C. Hamilton, Acta Crystallogr., 1965, 18, 502–510.
65. Y. Chen, W. Lu, M. Schröder and S. Yang, Acc. Chem. Res., 2023, 56, 2569–2581.
66. H. Woo, A. M. Devlin and A. J. Matzger, J. Am. Chem. Soc., 2023, 145, 18634–18641.
67. P. H. H. Duong, Y. K. Shin, V. A. Kuehl, M. M. Afroz, J. O. Hoberg, B. Parkinson, A. C. T. Van Duin and K. D. Li-Oakey, ACS Appl. Mater. Interfaces, 2021, 13, 42164–42175.
68. C. Y. Heo, M. L. Díaz-Ramírez, S. H. Park, M. Kang, C. S. Hong and N. C. Jeong, ACS Appl. Mater. Interfaces, 2024, 16, 9068–9077.
69. A. P. Katsoulidis, D. Antypov, G. F. S. Whitehead, E. J. Carrington, D. J. Adams, N. G. Berry, G. R. Darling, M. S. Dyer and M. J. Rosseinsky, Nature, 2019, 565, 213–217.
70. P. Van Der Sluis and A. L. Spek, Acta Crystallogr., Sect. A: Found. Crystallogr., 1990, 46, 194–201.
71. A. L. Spek, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 9–18.
72. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
73. K. N. Trueblood, H. B. Bürgi, H. Burzlaff, J. D. Dunitz, C. M. Gramaccioli, H. H. Schulz, U. Shmueli and S. C. Abrahams, Acta Crystallogr., Sect. A: Found. Crystallogr., 1996, 52, 770–781.
74. B. Mendis, Acta Crystallogr., Sect. A: Found. Adv., 2024, 80, 178–188.
75. R. Poppe and J. Hadermann, Ultramicroscopy, 2024, 265, 114023.
76. X. Wang and A. J. Jacobson, J. Solid State Chem., 2016, 236, 230–235.
77. J. Li, Z. Zhou, X. Han, X. Zhang, Y. Yan, W. Li, G. L. Smith, Y. Cheng, L. J. McCormick McPherson, S. J. Teat, M. D. Frogley, S. Rudić, A. J. Ramirez-Cuesta, A. J. Blake, J. Sun, M. Schröder and S. Yang, J. Am. Chem. Soc., 2020, 142, 19189–19197.
78. G. Chaplais, A. Simon-Masseron, F. Porcher, C. Lecomte, D. Bazer-Bachi, N. Bats and J. Patarin, Phys. Chem. Chem. Phys., 2009, 11, 5241–5245.
79. G. Skorupskii, K. N. Le, D. L. M. Cordova, L. Yang, T. Chen, C. H. Hendon, M. Q. Arguilla and M. Dincă, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2205127119.
80. K. J. Zhang, T. Chen, J. J. Oppenheim, L. Yang, L. Palatinus, P. Müller, T. Van Voorhis and M. Dincă, Chem. Sci., 2025, 16, 12416–12420.
81. S. Canossa, L. Fornasari, N. Demitri, M. Mattarozzi, D. Choquesillo-Lazarte, P. Pelagatti and A. Bacchi, CrystEngComm, 2019, 21, 827–834.
82. N. Johnson, https://www.ccdc.cam.ac.uk/discover/blog/10-years-of-structure-factors/.
83. J. R. Helliwell, J. R. Hester, L. M. J. Kroon-Batenburg, B. McMahon and S. L. S. Storm, IUCrJ, 2024, 11, 464–475.
84. M. D. Wilkinson, M. Dumontier, Ij. J. Aalbersberg, G. Appleton, M. Axton, A. Baak, N. Blomberg, J. W. Boiten, L. B. da Silva Santos, P. E. Bourne, J. Bouwman, A. J. Brookes, T. Clark, M. Crosas, I. Dillo, O. Dumon, S. Edmunds, C. T. Evelo, R. Finkers, A. Gonzalez-Beltran, A. J. G. Gray, P. Groth, C. Goble, J. S. Grethe, J. Heringa, P. A. C. t Hoen, R. Hooft, T. Kuhn, R. Kok, J. Kok, S. J. Lusher, M. E. Martone, A. Mons, A. L. Packer, B. Persson, P. Rocca-Serra, M. Roos, R. van Schaik, S. A. Sansone, E. Schultes, T. Sengstag, T. Slater, G. Strawn, M. A. Swertz, M. Thompson, J. Van Der Lei, E. Van Mulligen, J. Velterop, A. Waagmeester, P. Wittenburg, K. Wolstencroft, J. Zhao and B. Mons, Sci. Data, 2016, 3, 1–9.
85. S. Øien, D. Wragg, H. Reinsch, S. Svelle, S. Bordiga, C. Lamberti and K. P. Lillerud, Cryst. Growth Des., 2014, 14, 5370–5372.
86. X. Pei, H. B. Bürgi, E. A. Kapustin, Y. Liu and O. M. Yaghi, J. Am. Chem. Soc., 2019, 141, 18862–18869.
87. O. Anosova, V. Kurlin and M. Senechal, IUCrJ, 2024, 11, 453–463.
88. M. Nespolo, J. Appl. Crystallogr., 2019, 52, 451–456.
89. IUCr, https://dictionary.iucr.org/Lattice.

---

Footnote

† In the context of this article, the word ‘reticular’ (from Latin reticulum: small net) refers to any structure, where molecular and/or atomic building blocks form a network featuring cavities, which can accommodate guest atoms or molecules. In this sense, the class of “reticular structures” includes not only MOFs but also charged coordination networks, organic frameworks, and zeolites, to mention a few.

---