Advancements in mononuclear dysprosium-based single-molecule magnets via synthetic and molecular engineering

Abstract

Advancements towards improving the magnetic properties of mononuclear dysprosium-based single-molecule magnets, or as they are more commonly referred to as single-ion magnets, have been reaching their theoretical limits with slow magnetic relaxation in these molecules surpassing the liquid nitrogen barrier in recent years. The targeted design of axial crystal fields for the oblate Kramers ion of dysprosium(III) is responsible for these improvements with the strategies for these crystal fields discussed herein.

---

Introduction

The magnetic properties of materials have intrigued scientists for centuries, with the fundamentals of magnetism being developed as what we understand today as classical magnetism.¹ The word magnet derives from the district Magnesia (Mαγνησας), a region in Thessaly, Greece, where the first magnetic ores were discovered, referred to as either stone from magnesia or lodestones.¹ The ancient Greeks commented on the stones ability to attract one another and their ability to exert forces on iron.¹ It was not until the 11th century that lodestones' ‘magnetic’ behaviour was used in technology, that being in compasses for navigation by the Chinese.¹ Unlike traditional ferromagnets and/or paramagnets, an emerging type of magnetic behaviour is that displayed by single-molecule magnets (SMMs). SMMs are materials that display paramagnetism and belong to a class of magnetic materials called superparamagnets, whereby below a certain temperature, traditionally the magnetic blocking temperature (T_B), SMMs display slow relaxation of their magnetisation that is a consequence of overcoming an anisotropic barrier.²

Since the discovery of SMM behaviour, which was first observed in [Mn₁₂O₁₂(OAc)₁₆(H₂O)₄] (1, {OAc}⁻ = {CH₃COO}⁻, Fig. 1),³ many metrics have been used to describe the performance of SMMs. The metrics of importance for the implementation of SMMs are the effective anisotropic energy barrier (U_eff, the energy required to overcome the magnetic anisotropic barrier imposed by the crystal field), the hysteretic temperature (T_H, the highest temperature at which open-looped magnetic hysteresis is observed), and the newly defined 100-second magnetic blocking temperature (T_B100, the temperature at which the remnant magnetisation last for 100 seconds).^4,5

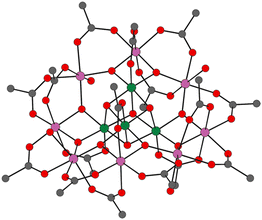Fig. 1 Solid-state structure of [Mn₁₂O₁₂(OAc)₁₆(H₂O)₄] (1). Mn(IV) = green, Mn(III) = pink, O = red, C = grey and H omitted for clarity.^3b

Long and Rinehart are known for generating a pivot to lanthanide-based SMMs over the traditional polymetallic transition metal clusters (e.g. 1).⁶ Their frontier article concludes that oblate lanthanide ions in axial crystal fields should be targeted, especially those that are Kramers ions (possess a half integer spin).⁶ It is for this reason that Dy(III) is chosen as the main source of single-ion anisotropy as it is a Kramers ion, is oblate and possesses a large J value (Dy(III), ⁶H_15/2). Dy(III) ions in axial crystal fields place the projection of the ground m_J (commonly referred to as the axis of magnetisation) along the molecular axis.^4–6 This produces a ground state where g_z is maximised (known as the Ising-limit, where g_x, g_y ca. 0), and thus the ion possesses axial magnetic anisotropy (easy axis type magnetisation).^4–6 Since 2011, literature has been flooded with Dy(III) complexes in axial crystal fields to induce large axial anisotropy, with the design of these crystal fields requiring rigorous synthetic methodologies which are discussed in this article.

There is a debate in the literature as to whether a subclass of SMMs, where one magnetic ion is used, i.e. a discrete mononuclear metal complex, should be referred to as single-ion magnets (SIMs) as the magnetic behaviour stems from the crystal field the said metal centre is exposed to. Within this article, the term ‘SIMs’ is used and refers to discrete complexes containing one metal centre which are the main focus throughout.

Discussion

Brief introduction to magnetic and electronic properties of lanthanide ions

The magnetic properties of lanthanide ions differ from transition metals in that they come from the coordination bond character and ligand field geometries, which arise from the radially contracted property of the 4f orbitals. In most transition metal complexes, especially first-row transition metals, ligand orbitals overlapping with the d-orbitals of the metal centre quenches the orbital angular momentum of valence electrons on the said centre. Quenching of orbital angular momentum is not as prominent in second- and third-row transition metals and leads to small spin–orbit coupling between the electron spin and its orbital motion. Having radially contracted 4f orbitals means that ligands in lanthanide complexes do not quench the orbital angular momentum of the valent 4f electrons, which gives rise to large spin–orbit coupling. The strength of spin–orbit coupling is what differentiates transition metal and lanthanide-based SMMs and is what Long and Rinehart concluded in 2011.⁶

The electronic states of lanthanide (Ln) ions are well described by the Russell–Saunders coupling scheme (or L–S coupling).⁷ L–S coupling is used when the interelectronic repulsion is large in comparison with the spin–orbit coupling, which is the case in lanthanide ions.⁸ L–S coupling sums the total spin angular momentum vector, S, and the total orbital angular momentum vector, L, to produce a new total angular momentum vector, J, which takes values of J = L + S, L + S − 1, …, |L–S|.^7,8 The term symbol used to describe these J multiplets is given by ^2S+1L_J, with its multiplicity given by 2J + 1. As mentioned, spin–orbit coupling is large in Ln ions and as a consequence, the ground J multiplet is the only thermally accessible state which describes the magnetic behaviour of Ln(III) ions with the exception of Sm(III) and Eu(III) which have low-lying excited states that are thermally accessible at room temperature.⁸

It was shown by Skomski that when using the quadrupolar approximations to the electrostatic potential model, where the second harmonic term dominates, free Ln(III) ions have aspherical electron distributions (except for La(III) Gd(III), Lu(III) and Eu(III)).⁹ The depiction of these ions showed that Ce(III), Pr(III), Nd(III), Tb(III), Dy(III) and Ho(III) take on an elliptical shape where the electron density is compressed axially, which is referred to as oblate electron density.⁹ Similarly, Pm(III), Sm(III), Er(III), Tm(III) and Yb(III) have axially elongated electron densities, referred to as prolate electron density.⁹ Ln(III) electron distributions are key to generating magnetic anisotropy as they show from free ion consideration that they possess axial magnetic anisotropy.^6,10 To go a step further, particular crystal fields can enhance the single-ion anisotropy of these ions.^6,10 In literature, large axial magnetic anisotropy is generally achieved with oblate lanthanide ions in axial crystal fields (axial with respect to the axis of compression for the oblate ion). Therefore, Dy(III) and Tb(III) are generally used in SMMs as they have oblate ground states and possess large J values.^6,10 The same can be said for prolate ions in equatorial fields but the resulting molecules are underused.^11,12 There are also examples of oblate Ln(III) that are Kramers ions (e.g. Ce(III)) that do not show the same trend when axial crystal fields are used, either newly designed or analogues of pre-existing Dy(III)-based SIMs.^13–15 However, the particular energy levels that are involved with slow magnetic relaxation must be discussed first.

Upon placing Ln(III) ions within a crystal field, the degeneracy of the ground J multiplet is broken into a series of either pure or superimposed magnetic states, m_J states, with values ranging from J to −J, in integer steps (Fig. 2).^4,6,10,16 However, to behave as a SMM, these m_J states must form pairs of doubly degenerate states or have the ground state be doubly degenerate, which can be enforced through Kramers degeneracy theorem. Kramers theorem states that for any atom with a half-integer spin, any two eigenstates with the same m_J magnitude must have the same eigenvalue (i.e., energy) when exposed to the same crystal field Hamiltonian.¹⁷ In other words, in pure electric fields (i.e., the electrostatic potential established by a crystal field) the energy of these so-called Kramers doublets will be equal.¹⁰ Thus, Kramers ions are sought after in Ln-based SMMs due to their property of establishing an energy profile that fulfills a crucial criterion for SMMs of possessing a doubly degenerate ground state (commonly referred to as bistability, Fig. 2). In non-Kramers ions (ions with integer spins), a high and strict symmetry at a local level must be used to enforce pairs of m_J states, forming pseudo-doublets.^4,18

Fig. 2 Splitting diagram of lanthanide ions exemplified with dysprosium(III). The electron repulsion term (left, ground state of ⁶H) is split by spin–orbit coupling (or L–S coupling) to produce Russel–Saunders terms (middle, ground state of ⁶H_15/2), and then when the ion is placed in a perfectly axial crystal field, the desired ground electronic profile for SMM behaviour is established (right, ground state of m_J = 15/2 within the ⁶H_15/2 J-manifold). The types of magnetic relaxation within this ground J-manifold are highlighted: Orbach relaxation (blue) – multiple direct processes that occur via single-phonon transitions between adjacent m_J states; Raman relaxation (green) – an indirect two phonon process that occurs via a virtually excited state; quantum tunnelling of magnetisation (QTM, red) – a temperature independent process that occurs by tunnelling under the anisotropic barrier via the ground doublet; thermally assisted quantum tunnelling of magnetisation (TA-QTM, purple) – follows an Orbach-like relaxation before tunnelling via an excited state. The separation of the ground state and the highest excited state via Orbach (or the highest state via TA-QTM) gives rise to the effective anisotropic energy barrier (U_eff).^4,8

The progression of splitting energy terms that is seen in Ln-based SMMs (Fig. 2) is what differentiates them from those containing transition metals. In transition metal cluster complexes, the crystal field breaks the degeneracy of the d-orbitals before the spin states of each ion couple, producing a m_S manifold that is responsible for the SMM energy profile.⁴ Meanwhile, Ln ions act as if they are free ions which create near degenerate 4f-orbitals and hence are well described by their L–S coupled terms, where a large splitting is caused by spin–orbit coupling before a crystal field then splits these into m_J states (Fig. 2).^4,6,10 Due to the nature of the electronic profile that is established by Ln ions, the remnant magnetisation comes purely from the single-ion anisotropy and not from the coupled spin ground state of a polymetallic molecule (as is for 1). Thus, the subclass of SMMs that is used to describe those containing one ion, where the magnetic behaviour derives from one ion within a discrete molecule, is known as SIMs (vide supra).

Magnetic relaxation in Ln-SMMs

To experimentally determine the magnitude of U_eff and the types of magnetic relaxation occurring in Ln-SMMs, ac magnetometry is used where the in-phase (χ′) and out-of-phase (χ′′) magnetic susceptibilities are modelled to the generalised Debye equation (eqn (1)) in order to determine the magnetic relaxation times (τ) per temperature.^19–21 For high performance Ln-SMMs, where the magnetic relaxation mechanism cannot be fully characterised by ac magnetometry, dc decay experiments are used to determine τ at lower temperatures by fitting to a stretched exponential (eqn (2)).²¹ Here, χ_ac is the total ac magnetic susceptibility, χ_T and χ_S are the isothermal and adiabatic magnetic susceptibilities, respectively, ω is the angular frequency of the oscillating magnetic field, i is the imaginary number , α describes the distribution of magnetic relaxation times (0 ≤ α ≤ 1), M(t) is the magnetisation at time t, M_∞ and M₀ are the magnetisation at t = ∞ and t = 0, respectively, and β is the stretch parameter that again describes the distributions of τ at a given temperature.

Once the magnetic relaxation times are known, they can be fitted to a relaxation rate equation. The typical equation used is shown in eqn (3), where each term represents magnetic relaxation via Orbach, Raman and quantum tunnelling of magnetisation (QTM), respectively.^4,19

These three types of magnetic relaxation most commonly describe the global magnetic relaxation in high performance Ln-based SIMs. Orbach relaxation is multiple direct transitions between ±m_J states to traverse the J-manifold (Fig. 2, right, blue) and follows an Arrhenius like equation represented by the first term in eqn (3), giving rise to U_eff. If Orbach relaxation is present, it generally occurs at the highest temperature where SIM behaviour is observable. Orbach relaxation is also defined by τ₀, which is considered an attempt factor for Orbach relaxation to occur. Raman relaxation is an indirect two-phonon process that occurs via a virtual excited state (Fig. 2, right, green) and conventionally follows a power law dependence (central term in eqn (3)) defined by a coefficient (C) and an exponent (n). The total energy change of the molecular system when relaxing via a Raman mechanism is the difference in phonons absorbed and emitted (hence the name Raman). Raman relaxation has previously been linked to molecular vibration with theoretical work being used to explain the requirements to mitigate or reduce the relaxation rate due to a Raman mechanism via reducing the number of the said vibrational modes.²² Raman relaxation occurs at an intermediate temperature usually between Orbach and QTM. QTM is a temperature independent process that occurs in the ground state (Fig. 2, right, red) at low temperatures. The magnetic relaxation rate caused by QTM (τ_QTM⁻¹) is therefore a horizontal line in rate plots due to its temperature independence. QTM will occur in SMMs when the ground state is not strictly pure, which may seem contradicting as the previous mention of the use of Kramers ions should ensure doubly degenerate crystal fields states. However, within a bulk sample, inclusion of neighbouring paramagnetic centres can cause the degeneracy of the said Kramers ions to be lost, thus increased intermolecular Ln⋯Ln distances should be targeted. Another cause of the loss of degeneracy is from hyperfine coupling which can be mitigated by isotopic labelling of the Ln ion, though this is generally underused and expensive.¹⁰ Tunnelling between two states of equal energy can also occur between any of the excited states, which is referred to as thermally assisted-QTM (TA-QTM, Fig. 2, right, purple), though this follows an Orbach type relaxation until the said excited state is reached and is generally labelled as Orbach relaxation. Thus, a key feature to high performance Ln-based SIMs is to ensure purity of both the ground and excited states to mitigate any tunnelling of magnetisation.

To determine the electronic profile of the ground J-manifold for a given SIM, ab initio calculations are generally employed. Complete-active space self-consistent field (CASSCF) calculations give insight into the energy of the crystal field states in the ground J-manifold, the m_J character of these states (i.e., the m_J purity), how anisotropic these states are and the possible magnetic transitions that give rise to the slow magnetic relaxation behaviour.²³ For Dy(III)-based SIMs, the Ising limit should be targeted, where the ground state is completely comprised of the m_J = ±15/2 state and is void of any transverse anisotropy (g_x = g_y = 0, g_z = 20). CASSCF calculations have become a routine theoretical technique for describing the above properties and are well-received by the community, especially since MOLCAS has become open source.²³ However, there are few experimental methods that have been used in the literature to determine the energy of the crystal field states. For cases where the total crystal field splitting is low, or if the instrumentation is available for high splitting fields, inelastic neutron scattering (INS) spectroscopy has been used.²⁴ An interesting example of this is for the Tb(III)-based SIM Na₉[Tb(W₅O₁₈)₂] (2) where INS spectroscopy was used to identify the crystal field splitting of two different polymorphs in a bulk crystalline sample.²⁴ Another common spectroscopic technique to experimentally determine the crystal field energies is via luminescence.²⁵ In most cases, the first excited states are accurately reflected by the ab initio calculations though the remaining states are typically off. A unique example of this is with [Dy(Tp^2-py)F(μ-diox)]_n(PF₆)_n (3, Tp^2-py = hydrotris(3-(2′-pyridyl)pyrazol-1-yl)borate, diox = 1,4-dioxane) where the previous case is true (luminescence: 318 cm⁻¹, ab initio: 297 cm⁻¹), and the total crystal field splitting is very close to the ab initio calculated splitting (luminescence: 770 cm⁻¹, ab initio: 778 cm⁻¹).²⁵

Oblate Ln ions in axial crystal fields

In recent years, the U_eff barrier has systematically been improved within the following classes of compounds discussed herein. Several other classes of lanthanide SMMs have emerged, i.e., radical bridged lanthanide SMMs,^26–28 mixed transition metal/lanthanide-based SMMs^29,30 or SIMs containing prolate ions in equatorial crystal fields,^11,12 but the main focus herein is SIMs containing one oblate lanthanide centre in axial (or near axial) crystal fields. A compound architecture of note that will not be discussed is dilanthanide complexes [{Ln(Cp^iPr₅)}₂(μ-I)₃] (4-Ln, Ln = Y, Gd, Tb, Dy, Ho, Er, Tm) which have shown record coercive fields (H_c), though in this case the magnetic behaviour is enhanced through f–f interactions.^31,32 Each class discussed herein raise important features that are essential for Ln-based SIMs, all of which have been mentioned previously.

All SIM behaviour discussed vide infra relates to data collected in the absence of applied magnetic fields. The use of applied magnetic fields are generally used to ‘turn on’ SIM behaviour or to mitigate relaxation caused by QTM.

From humble beginnings in pseudo-axial crystal fields

The first complexes identified as Ln-based SMMs were the double decker compounds (ⁿBu₄N)[Ln(Pc)₂] (5-Ln, {ⁿBu₄N}⁺ = tetra-n-butylammonium, H₂Pc = phthalocyanine, Ln = Dy, Tb, Fig. 3).¹⁸

Fig. 3 Structure of the anion from (ⁿBu₄N)[Ln(Pc)₂] (5-Ln).¹⁸

At the time, 5-Tb presented a record breaking energy barrier of U_eff = 230 cm⁻¹ and exhibited peaks in χ′′ up to 40 K (previous transition metal cluster showed peaks below 8 K).¹⁸ However, 5-Dy showed a much lower energy barrier of U_eff = 28 cm⁻¹,¹⁸ on par with that of polymetallic transition metal complexes but with a higher blocking temperature. The placement of charges is not axial in 5-Ln, being roughly 60° from the z-axis of the crystal field, therefore the limit of U_eff was not achieved with these molecules due to higher order harmonics dominating the crystal field Hamiltonian (hexadecapole and hexacontatetrapole moments).^10,18

The axial point charge approach

The first method to adopt charged ligands in an axial crystal field with no other charged ligands in the coordination sphere was the axial point charge approach in 2016.³³ Here, two monoanionic ligands, where the charge is localised to one atom, are coordinated in an axial (or near axial) fashion with neutral molecules, typically solvents, coordinated equatorially. The first three examples of axial point charge compounds were [Dy(O^tBu)₂(py)₅](BPh₄) (6, {O^tBu}⁻ = tert-butoxide, py = pyridine, {BPh₄}⁻ = tetraphenylborate),³³ [Dy(O^tBu)Cl(THF)₅](BPh₄) (7, THF = tetrahydrofuran)³⁴ and [DyCl₂(THF)₅](BPh₄) (8),³⁵ where 6 and 8 adopt pseudo-D_5h symmetry, and pseudo-C_5v for 7, as five solvent molecules are coordinated perpendicular to the point charge pseudo-axis (Fig. 4).

Fig. 4 Examples of bis-axial point charge complexes with the cations from [Dy(O^tBu)₂(py)₅](BPh₄) (6), [Dy(O^tBu)Cl(THF)₅](BPh₄) (7), [DyCl₂(THF)₅](BPh₄) (8), [Dy(OSiMe₃)Br(THF)₅](BPh₄) (11), [Dy(OPh)₂(py)₅](BPh₄) (13), [Dy(OSiMe₃)₂(py)₅](BPh₄) (15), [Dy(O^tBu)₂(4-Phpy)₄](BPh₄) (18), [Dy(OSiPh₃)₂(N₅-macro)](BPh₄) (21), [Dy(OPh^tBu₂)₂(N₆-macro)]PF₆ (23), [Dy(O^tBu)Cl(18-crown-6)](BPh₄) (32), [Dy(O^tBu)₂(18-crown-6)]I₃ (33) and [Dy(OAd)₂(18-crown-6)]I₃ (34). Dysprosium(III) = turquoise, bromine = brown, silicone = orange, chlorine = dark green, oxygen = red, nitrogen = blue, and carbon = grey; hydrogen atoms and counter ions have been omitted for clarity.^{33–36,38–41,46,47}

Electrostatically, compounds 6–8 are comparable with an axis of magnetisation along the point charge axis; however, all three compounds display different slow magnetic relaxation behaviour. The axial groups for these compounds have short coordination distances and present pseudo-linear point charges (Table 1).^33–35 Complex 8 shows only a slight improvement over the original SMM, 1, with an energy barrier of U_eff = 54(22) cm⁻¹,³⁵ which is also similar to that of 5-Dy. 6 and 7 show dramatic improvements over 5-Dy and 8, with energy barriers of U_eff = 652(104) cm⁻¹ and U_eff = 1261(1) cm⁻¹, respectively.^33,34 Based on these facts only, one could suggest that the improvement of magnetic behaviour comes from systematically changing the electron density, or hardness, of the point charge (i.e., diffuse chloride ion to harder alkoxide donor) and reducing the coordination distances of the said charged ligand.

Table 1 Structural and SIM properties of bis-axial point charge Dy(III) complexes^{33–44,46,47,49,53}

Compound	Local pseudo-symmetry	Axial ligands	Equatorial ligands	Dy–Xax/Å	Xax–Dy–Xax/°	Ueff/cm^−1	TB100/K	TH/K
a Multiple unique Dy(III) centres within the asymmetric unit.b Multiple Orbach relaxation processes experimentally determined.c Half-ion symmetry present in the solid state.d Molecules are chiral within the solid state, thus only the larger Ueff parameters are shown (which are within error of the enantiomer).e Disorder in the solid-state gives rise to two conformations.f No temperature at which the magnetisation last for 100 seconds.g Open looped hysteresis not observed at any temperature.h Manuscript not published and authors did not clearly state TH but instead detailed high cohesive fields above 100 K.i No errors provided by the original authors.
[Dy(O^tBu)2(py)5](BPh4) 6	D5h	O^tBu	py	2.110(2)	178.91(9)	1261(1)	10.9	25
				2.114(2)
[Dy(O^tBu)Cl(THF)5](BPh4) 7	C5v	O^tBu	THF	2.043(4)	178.26(9)	652(104)	—^f	11
				2.6619(12)
		Cl
[DyCl2(THF)5](BPh4)^a 8	D5h	Cl	THF	2.562(1)–2.587(1)	175.90(4)	54(22)	—^f	—^f
					179.68(3)
[Dy(OSiMe3)Cl(THF)5](BPh4) 9	C5v	OSiMe3	THF	2.074(2)	178.50(7)	557(11)	5.9	9
				2.6473(8)
		Cl
[Dy(O^tBu)Br(THF)5](BPh4) 10	C5v	O^tBu	THF	2.023(4)	178.0(1)	569(126)	3.2	9
		Br		2.8293(6)
[Dy(OSiMe3)Br(THF)5](BPh4) 11	C5v	OSiMe3	THF	2.092(2)	178.95(6)	509(49)	—^f	9
				2.7973(4)
		Br
[Dy(OPh)Cl(THF)5](BPh4) 12	C5v	OPh	THF	2.113(4)	178.47(11)	512(32)	5.1	9
				2.5872(12)
		Cl
[Dy(OPh)2(THF)5](BPh4) 13	D5h	OPh	THF	2.123(3)	176.34(10)	924(78)	10.0	18
				2.131(3)
[Dy(OPh)2(py)5](BPh4)^a^,^b 14	D5h	OPh	py	2.1222(41)–2.1226(40)	176.4(3)	905(31)	6.3	16
							13.1
					176.9(3)	832(18)
[Dy(OSiMe3)2(py)5](BPh4) 15	D5h	OSiMe3	py	2.152(2)	176.08(6)	1109(20)	12.9	22
				2.136(2)
[Dy(OSiMe3)2(4-Mepy)5](BPh4) 16	D5h	OSiMe3	4-Mepy	2.145(3)	177.7(1)	1041(68)	11.1	23
				2.148(3)
[Dy(OAd)2(py)5](BPh4) 17	D5h	OAd	py	2.1055(19)	173.77(7)	1276(5)	17	23
				2.1096(19)
[Dy(O^tBu)2(4-Phpy)4](BPh4)^c 18	D4h	O^tBu	4-Phpy	2.066(8)	180	1442(8)	—^f	—^g
[Dy(O^tBu)2(4-pipy)4](BPh4)^c 19	D4h	O^tBu	4-pipy	2.127(2)	178.90(15)	1311(6)	—^f	—^g
[Dy(O^tBu)2(4-pyrpy)4](BPh4)^c 20	D4h	O^tBu	4-pyrpy	2.138(3)	180.0(3)	1258(3)	—^f	—^g
[Dy(OSiPh3)2(N5-macro)](BPh4) 21	D5h	OSiPh3	N5-macro	2.139(4)	169.06(17)	406(22)	—^f	13
				2.143(4)
[Dy(OSiPh3)2(N6-macro)](BPh4)^a 22	D6h	OSiPh3	N6-macro	2.136(4)–2.161(4)	176.54(15)	770^i	—^f	14
					173.13(15)
[Dy(OPh^tBu2)2(N6-macro)]PF6 23	D6h	OPh^tBu2	N6-macro	2.1456(14)	176.54(5)	676^i	—^f	—^g
				2.1303(14)
[Dy(OSiPh3)2(N6-macro)](BPh4) 24	D6h	OSiPh3	N6-macro	2.1425(16)	176.13(6)	781^i	—^f	—^g
				2.1514(16)
[Dy(OSiPh3)2(N6-macro)]PF6 25	D6h	OSiPh3	N6-macro	2.153(7)	179.8(2)	751^i	—^f	—^g
				2.163(6)
[Dy(OSiPh3)2(N6-macro)]ClO4 26	D6h	OSiPh3	N6-macro	2.138(2)	175.53(8)	1204(30)	—^f	—^g
				2.141(2)
[Dy(OSiPh3)2(N6-macro)](CF3SO3) 27	D6h	OsiPh3	N6-macro	2.129(2)	177.05(15)	1168(6)	—^f	—^g
				2.142(4)
[Dy(OSiPh3)2(N6-macro)][BPh3(3-BrPh)]^d 28	D6h	OSiPh3	N6-macro	2.133(5)	175.0(3)	983(17)	—^f	—^g
				2.137(5)
[Dy(OSiPh3)2(N6-macro)][BPh3(4-BrPh)]^d 29	D6h	OSiPh3	N6-macro	2.140(6)	179.1(3)	997(20)	—^f	—^g
				2.141(5)
[Dy(OPh^4Me)2(N6-macro)](BPh4)^d 30	D6h	OPh^4Me	N6-macro	2.136(4)	170.45(17)	556(34)	—^f	—^g
				2.145(4)
[Dy(OSiPh3)2(N6-macro^F)]PF6^d 31	D6h	OSiPh3	N6-macro	2.124(6)	178.3(3)	1273(24)	5	20
				2.139(7)
[Dy(O^tBu)Cl(18-crown-6)](BPh4)^a 32	C6v	O^tBu	18-crown-6	2.043(5), 2.07(1)	166.6(2)	695(348)	—^f	—^g
		Cl		2.690(3), 2.689(8)	173.6(5)
[Dy(O^tBu)2(18-crown-6)]I3 33	D6h	O^tBu	18-crown-6	2.067(5)	177.5(2)	1635(15)	10	30
				2.069(5)
[Dy(OAd)2(18-crown-6)]I3 34	D6h	OAd	18-crown-6	2.058(6)	177.5(2)	1687(13)	11	30
				2.049(6)
[Dy{N(Si^iPr3)2}2][Al(OC(CF3)3)4] 37	C∞	Silyl amide	—	2.209(5)	128.7(2)	660(21)	—^f	—^g
				2.202(5)
[ChemTemp]^iPr3)(Si^iPr2Et)}{N(Si^iPr3) (Si^iPr2C(CH3)=CHCH3)}][Al(OC(CF3)3)4]^e 38	C∞	Silyl amide	—	2.205(9)–2.236(11)	150.1(5)–165.3(8)	1843(11)	—^f	—^h

---

To investigate the reasons for the said drastic changes between these axial point charge systems, Zheng in collaboration with Winpenny made a family of pentagonal-bipyramidal (PB) molecules.³⁶ The magnetic properties of this PB family are summarised in Table 1 (complexes 6–16). These point charge axial systems varied the axial ligands, that being a mixture of oxygen donors ({O^tBu}⁻, phenoxide {OPh}⁻ and trimethylsiloxide {OSiMe₃}⁻) and halides (Cl⁻ and Br⁻), and the solvent molecules coordinated in the equatorial environment, that being THF, pyridine and 4-methylpyridine (4-Mepy) (Fig. 4). Besides compound 8, all of Zheng's compounds have energy barriers of U_eff > 500 cm⁻¹.³⁶

All mono-halide complexes (7, 9–12) have intermediate energy barriers (509(49) cm⁻¹ < U_eff < 652(104) cm⁻¹), whereas the bis-oxide systems, compounds 6, 13–16, have larger barriers (832(18) cm⁻¹ < U_eff < 1261(1) cm⁻¹).³⁶ The difference between the two subclasses of PB compounds suggests that the harder the charged axial donors are, the greater the energy barrier of the system will be. The hardness of the axial ions and the linearity of these systems do have a consequence on the electronic structure of the lanthanide ion. Thus, the true reason as to why these energy barriers fall into nice categories is apparent when looking at the breakdown of the electronic structure for these systems.^33,34,36

The heavily mixed ground and second excited states of 8 lead to a small U_eff (ab initio calculated first excited state at 7 cm⁻¹).³⁶ This derives from two soft axial charges and longer coordination distances with respect to oxygen donor ligands (Table 1). These heavily mixed states are comprised of more than three m_J wavefunctions and include large transverse anisotropic g values (ground state of 8 has g_x = 1.16, g_y = 5.88; the second excited state of 8 has g_x = 3.83, g_y = 4.14).³⁶ The combination of mixed states and the transverse anisotropic character of the Kramers doublets in 8 causes fast relaxation to occur via these states. Complex 7 has pure ground and first excited states (m_J = ±15/2 and ±13/2, respectively) with negligible transverse anisotropy.³⁶ Unlike 8, the cation in 7 includes the harder donor ligand of {O^tBu}⁻ leading to a first excited state that is 397 cm⁻¹ above the ground state (cf. 7 cm⁻¹ in 8).^34,36 The second excited state of 7 is mixed with a highest wavefunction contribution of 59% m_J = ±1/2, therefore through barrier processes can occur from this state.³⁴ The ab initio calculated energy level in 7, where these through barrier processes have a high probability of occurring (654 cm⁻¹), is in good agreement with the experimentally determined energy barrier of U_eff = 652(104) cm⁻¹.³⁴

Complex 6 has several pure crystal field states, with the first four Kramers doublets being greater than 96% purity, emphasising the importance of hard single atom donors along an axis.³³ At the time of publishing, complex 6 had the largest energy barrier of the pseudo-D_5h systems, which is a reflection of the ligand geometry and charge density of the ligands. Zheng later improved on this energy barrier via the use of rigid axial ligands in [Dy(OAd)₂(py)₅](BPh₄) (17, {OAd}⁻ = adamantoxide), where these rigid adamantoxide ligands aid in lowering the number of low energy vibrations (Table 1).³⁷ With these low energy vibrations suppressed, 17 shows an increased T_B100 and T_H of 17 K and 23 K, respectively, with the symmetry and charge distribution producing a larger effective energy barrier of U_eff = 1276(5) cm⁻¹.³⁷

Further improvements to the point charge family were made with other geometries, namely D_4h, which favours strict local symmetries and linear point charge axes. Work by Zheng increased the effective energy barrier for point charge systems past that of 17 with [Dy(O^tBu)₂(py^R)₄](BPh₄) (18, py^R = 4-phenylpyride (4-Phpy); 19, py^R = (4-pieridin-1-yl)pyridine (4-pipy); 20, py^R = (4-pyrrolidin-1-yl)pyridine (4-pyrpy)) complexes (Table 1, Fig. 4).³⁸ Functionalisation of the equatorial pyridine ligands offers steric effects that resulted in four coordinated solvent molecules to generate pseudo-D_4h symmetry. The increased linearity and true symmetry increased the effective energy barrier to U_eff = 1442(8) cm⁻¹ with complex 18.³⁸

The symmetry seen in Zheng's work is not limited to his group with alternative strategies being adopted by others to obtain strict local symmetry. Additional work includes complexes from Murrie,^39,40 Li & Yin,⁴¹ and Tang^42–44 where synthetic design of nitrogen-based neutral macrocycles (N_x-macro, x = denticity) was used to enforce strict local symmetry (Table 1, Fig. 4). These polydentate macrocycles are easily synthesised in situ and coordinated to dysprosium(III) without the need for an inert atmosphere. To support these macrocycles, point charged axial ligands such as triphenylsiloxide ({OSiPh₃}⁻), 2,4-di-tert-butylphenoxide ({OPh^tBu₂}⁻) and 4-methylphenoxide ({OPh^4Me}⁻) are used to obtain the desired local geometries in the complexes of the general form [Dy(OSiPh₃)₂(N₅-macro)](BPh₄) (21); [Dy(OSiPh₃)₂(N₆-macro)]Y (22; 24, Y = {BPh₄}⁻; 23, Y = {PF₆}⁻; 26, Y = {ClO₄}⁻; 27, Y = {CF₃SO₃}⁻; 28, Y = {BPh₃(3-BrPh)}⁻; 29, Y = {BPh₃(4-BrPh)}⁻), [Dy(OPh^tBu₂)₂(N₆-macro)]PF₆ (25) and [Dy(OPh^4Me)₂(N₆-macro)](BPh₄) (30) (Fig. 4).^39–43 In general, the use of said macrocycles in Dy(III) complexes resulted in energy barriers below 1000 cm⁻¹ and complexes retaining low blocking temperatures.^39–45 An exception to this is with Tang's use of a fluorinated macrocycle (N₆-macro^F), giving rise to an exceptional high energy barrier of 1274(24) cm⁻¹ in [Dy(OSiPh₃)₂(N₆-macro^F)](BPh₄) (31).⁴⁴ Compound 31 also produced a relatively large and measurable T_B100 and T_H of ca. 5 K (stated as a relaxation time of 111 s at 5 K) and 20 K, respectively.⁴⁴ Regardless of their low blocking temperatures, these pseudo-D_5h and -D_6h complexes (i.e. complexes 21–31) were examples of some of the first air-stable, high effective anisotropic energy barrier lanthanide-based SIMs.

To further reduce the degrees of freedom, i.e., the number of vibrational modes, substitution of the equatorial solvent molecules and/or nitrogen-based macrocycles vide supra with crown ethers, namely 18-crown-6 (1,4,7,10,13,16-hexaoxacyclooctadecane), was achieved by Zheng and co-workers.^46,47 18-crown-6 not only reduces the number of vibrational modes around the equatorial plane of the bis-point charge complexes, but also changes the local symmetry as it is hexadentate, giving rise to complexes with pseudo-D_6h and -C_6v symmetries. The first of these complexes was the C_6v complex [Dy(O^tBu)Cl(18-crown-6)](BPh₄) (32), which takes the axial components of 7 and replaces the five THF molecules with 18-crown-6 (Table 1, Fig. 4).⁴⁶ Variable temperature single-crystal X-ray diffraction results for 32 showed that when cooling, the molecular structure heavily deviates from the desired symmetry and results in a 10% decrease in the calculated energy of the excited electronic states. Thus, further improvement in the molecular design was needed to raise the blocking temperature and energy barrier, as T_B100 could not be determined for 32 despite possessing an energy barrier of U_eff = 695(348) cm⁻¹.⁴⁶

Pseudo-D_6h SIMs employing crown ethers were first reported towards the end of 2024 by Zheng with [Dy(O^tBu)₂(18-crown-6)]I₃ (33) and [Dy(OAd)₂(18-crown-6)]I₃ (34) (Fig. 4).⁴⁷ Unlike 26, both 27 and 28 employ bulkier alkoxides in the axial positions, which resulted in marginal changes in the geometry when the same variable temperature studies were conducted. The coordination distances and bond angles of the axial ligands with the Dy(III) centres for 32 to 34 see an improvement in targeted symmetries and perturbation, which correlate well to their measured energy barriers (Table 1).^46,47 Not only did compound 34 set a record for the largest energy barrier observed in any SMM, but it was also reported to be air-stable at room temperature for several months (though the synthesis was conducted in an inert atmosphere) and therefore holds the record for the highest U_eff (1687(13) cm⁻¹) for an air-stable SIM.⁴⁷ The magnetic blocking and hysteresis temperatures are still relatively low for 33 and 34, which arise from the complexity of the ligands used, but are among the highest for air-stable SIMs (Table 1).

When designing point charge SIMs, certain molecular symmetries are targeted as they can minimize the amount of transverse anisotropy which can increase both T_B and T_H. To minimise the transverse anisotropy experienced by each of the m_J states of the ground J-manifold, the crystal field parameters must be ‘quenched’, that is, they must tend towards zero (B^k_q = 0, when q ≠ 0).¹⁰ Tong has analytically shown that there are some point groups that ensure that all of the desired crystal field parameters tend towards zero; C_n (n ≥ 7), C_5h/D_5h, S₈/D_4d, and S₁₂/D_6d.¹⁰ Whilst D_4h is not in this list, it still quenches most of the crystal field terms (|q| = 1, 2, 3, 5, 6), and since molecules, such as the cation of 18, are in strict local symmetry, they have better SIM behaviour.³⁸ There are examples of pseudo-D_4h complexes that do not perform well, such as [Dy(carbazolyl)₂(Solv)₄](BPh₄) (35, Solv = THF; 36, Solv = py), with effective energy barriers U_eff ≤ 50 cm⁻¹,⁴⁸ demonstrating the importance of strict local symmetry.

The higher excited states for axial point charge molecules are still mixed and limit the potential energy barrier that could be reached for point charge systems. Linking back to symmetry, the point axial charge family does not exhibit strict global symmetry which causes the higher states to be mixed, with the equatorial solvent and/or crown ether ligands inducing transverse anisotropy in the excited states of the central Dy(III) ion. To limit the amount of transverse anisotropy induced in excited states, bulkier axial ligands have been employed to stop any ligands, whether that be charged or neutral, coordinating in the equatorial plane of the crystal field. A recent example that employs point charge ligands in a two-coordinate complex (though achieved through rigorous drying and synthetic techniques) is with the isolation of the bent bis-amide complex [Dy{N(SiⁱPr₃)₂}₂][Al(OC(CF₃)₃)₄] (37, {N(SiⁱPr₃)₂}⁻ = bis(tri-iso-propylsilyl)amide, {Al(OC(CF₃)₃)₄}⁻ = tetrakis(perfluoro-tert-butoxide)aluminate, which uses functionalised amides to sterically hinder the Dy(III) centre from neutral coordinating molecules (Fig. 5).⁴⁹ The isolation of 37 is aided by the use of the weakly coordinating anion (WCA) {Al(OC(CF₃)₃)₄}⁻, known as Krossing's reagent.⁵⁰ Complex 37 has an average amide coordination distance of Dy–N = 2.206(7) Å, though presents deviation from linearity, with a N–Dy–N angle of 128.7(2)° (Table 1).⁴⁹ The large deviation from linearity limits the magnetic behaviour of 37, as it does not target point charges along the magnetisation axis, which results in the introduction of transverse anisotropy in excited states. The large transverse anisotropy in the excited states results in an experimentally determined energy barrier of U_eff = 660(21) cm⁻¹.⁴⁹ T_B100 could not be determined for 37 as there is no temperature at which the magnetisation lasts for 100 seconds.⁴⁹

Fig. 5 (left) Solid-state structure of the cation in [Dy{N(SiⁱPr₃)₂}₂][Al(OC(CF₃)₃)₄] (37). Dysprosium(III) = turquoise, silicone = orange, nitrogen = blue, and carbon = grey; hydrogen atoms have been omitted for clarity. (right) Structure of the cation in [Dy{N(SiⁱPr₃)(SiⁱPr₂Et)}{N(SiⁱPr₃)(SiⁱPr₂C(CH₃)=CHCH₃)}][Al(OC(CF₃)₃)₄] (38), showcasing the weak η²-alkene coordination.^49,53

There are multiple examples of bis-amide Dy(III) complexes in literature; however, these examples typically possess higher coordination numbers due to either extra coordinating atoms or weak aryl coordination.^51,52 However, an improvement to 37 has been reported, but not published, by Mills and co-workers with the isolation of the dehydrogenative C–C bond rearranged species [Dy{N(SiⁱPr₃)(SiⁱPr₂Et)}{N(SiⁱPr₃)(SiⁱPr₂C(CH₃)=CHCH₃)}][Al(OC(CF₃)₃)₄] (38, {N(SiⁱPr₃)(SiⁱPr₂Et)}⁻ = (tri-iso-propylsilyl)(ethyl-di-iso-propylsilyl)amide, {N(SiⁱPr₃)(SiⁱPr₂C(CH₃)=CHCH₃)}⁻ = (tri-iso-propylsilyl)(di-iso-propyl-sec-pent-3-enyl-silyl)amide), (Fig. 5).⁵³ The rearrangement results in the formation of an alkene on what was an original iso-propyl substituent and weak η²-coordination is observed between said alkene and the Dy(III) centre (shortest Dy–H_alkene distance of 2.519 Å). The cation in 38 is disordered over two sites and exhibits similar amide coordination distances to 37, being Dy–N = 2.205(9)–2.236(11) Å (Table 1).⁵³ However, the cation in 38 shows greater linearity over 37, having N–Dy–N angles of 150.1(5) and 165.3(8)°.⁵³ The dramatic change in the structure greatly influences the SIM properties when comparing these bis-amide complexes as 38 possesses a record-breaking energy barrier to magnetic reversal of U_eff = 1843(11) cm⁻¹, which is the highest reported U_eff to date.⁵³ As with most of the point charge complexes, a 100-second magnetic blocking temperature is not observable for 38 as the rate of magnetic relaxation caused by QTM, i.e. the limiting magnetic relaxation mechanism, is ca. 68 seconds.⁵³

The point charge family have low T_B100 and T_H for compounds that established high energy barriers, implying that U_eff and magnetic relaxation rates are not correlative. Due to the nature of how SMMs relax in the Orbach region, spin–phonon coupling must be irrespective of the energy barrier height. It has been stated that along with optical phonons (i.e. vibration from the lattice), molecular vibrations also cause spin–phonon coupling.⁴ Thus, the number of molecular vibrations a molecule that behaves as an SMM has, the greater the chance that some of those vibrational modes have the correspond energy for m_J = ±1 transitions. In particular, synthetic design should employ ligands that have high energy molecular vibrational modes, as low energy modes can cause the initial excitations to traverse the energy barrier, whilst also being large enough to sterically hinder equatorially coordinating ligands/solvent molecules. For the case of the bis-axial point charge family examples listed here (compounds 6–34), the axial ligands used have low energy vibrational modes, and the coordinated solvent molecules add to the complexity of the molecule.^33–48 For the case where equatorial ligands have been mitigated, as for compounds 37 and 38, the importance of ensuring linearity of point charges and rigidity of axial ligands is reinforced.^49,53

Whilst the point charge family was initially used to test the employment of axial crystal fields for oblate Ln ions, further synthetic strategies were needed to raise not only the U_eff but also the T_B (and T_B100). There have been countless other examples of axial point charges with other functionalised oxides,^54–56 or other Ln ions, e.g. Sm(II),⁵⁷ but all possess the same problems as discussed vide supra. Hypothetical Dy(III) systems are numerous with most of them showing large energy barriers. These hypothetical systems usually include the removal of coordinated solvent ligands in an equatorial fashion (e.g. the point charge family),⁵⁵ the point charge system of different Ln metals swapped out for Dy(III)^55,57 or simple systems such as {Dy=O}⁺ or {X–Ce–X}⁺ (X = any monoanionic point charge) for computational purposes.^10,54 All the said hypothetical systems show promising results, thus systems that minimise these equatorial dentations and use rigid ligands should be targeted.

The lanthanocenium approach

To overcome the issues of low energy vibrational modes in Ln complexes, solvent coordination and maintaining the desired uniaxiality, the isolation of lanthanocenium ions was sought out as a potential target. Initial reactions involving substituted cyclopentadienyl (Cp) ligands were met with the coordination of counter-ions, the first of which was [Ln(Cp*)₂(BPh₄)] (39-Ln, Cp* = 1,2,3,4,5-pentamethylcyclopentadienyl; Ln = Dy, Tb) which has similar problems to the pentagonal bipyramidal class of compounds where molecules (or in this case a counter-ion) coordinate equatorially with respect to the desired magnetisation axis (39-Tb, U_eff = 216 cm⁻¹; 39-Dy, U_eff = 331 cm⁻¹).⁵⁸ This counter-ion problem led to the use of WCAs, in particular the fluorinated counter-ions tetrakis(pentafluorophenyl)borate ({B(C₆F₅)₄}⁻) and Krossing's ({Al(OC(CF₃)₃)₄}⁻) which are generally non-coordinating unlike {BPh₄}⁻ in 39-Ln.⁵⁸ {B(C₆F₅)₄}⁻ was used to isolate the first lanthanocenium ion in [Dy(Cp^ttt)₂][B(C₆F₅)₄] (40-Dy, Cp^ttt = 1,2,4-tri-tert-butylcyclopentadienyl, Fig. 6) in 2017.⁵⁹ The successful synthesis of 40-Dy led to a family of dysprosocenium ions to be synthesised, namely the bis-Cp^R family [Dy(Cp^iPr₄R)₂][B(C₆F₅)₄] (41, R = H, Cp^iPr₄ = 1,2,3,4-tetra-iso-propylcyclopentadienyl; 42, R = Me, Cp^iPr₄Me = 1,2,3,4-tetra-iso-propyl-5-methylcyclopentadienyl; 43, R = Et, Cp^iPr₄Et = 1-ethyl-2,3,4,5-tetra-iso-propylcyclopentadienyl; 44-Dy, R = ⁱPr, Cp^iPr₅ = 1,2,3,4,5-penta-iso-propyl-cyclopentadienyl)⁶⁰ and the heteroleptic system [Dy(Cp^iPr₅)(Cp*)][B(C₆F₅)₄] (45)⁶¹ (Fig. 6), in 2018. A more recent example is the newly isolated heteroleptic system [Dy(Cp^ttt)(Cp*)][Al(OC(CF₃)₃)₄] (46) by Mills in 2023 employing rigorous synthetic techniques that have been refined over the last decade for the isolation of isolated dysprosocenium ions.⁶² The synthesis of dysprosocenium ions entails the use of reactive bis-Cp intermediates, namely borohydride or allyl intermediates, with selective cations that react with these ligands, i.e. trityl ({CPh₃}⁺), silylinium ({{Et₃Si}₂(μ-H)}⁺) or triethylammonium ({Et₃NH}⁺) ions, leaving behind the desired weakly coordinating anion with clean and easy to remove by-products. There are other examples throughout literature where the targeted synthesis of isolated dysprosocenium ions results in the isolation of bridged dimers via borohydrides,⁶³ coordinating counter-ions^58,64 or solvent molecules,^65,66 which results in relatively poor SIM behaviour due to the introduction of transverse anisotropy from these groups when compared to the aforementioned isolated dysprosocenium ions. Other notable examples include isolating bis-five-membered ring complexes where one carbon atom is substituted with other elements, such as in the two borolide complexes [K(18-crown-6)(THF)₂][Dy(BC₄Ph₅)₂] (47, {BC₄Ph₅}²⁻ = pentaphenylborolide)⁶⁷ and [K(2.2.2)][Dy(BC₄Ph₄Pip)₂] (48, 2.2.2 = 2,2,2-cryptand, {BC₄Ph₄Pip}²⁻ = 1-(piperidino)-2,3,4,5-tetraphenylborolide),⁶⁸ and the phosphorus containing complex, [Dy(PC₄^tBu₂Me₂)₂][Al(OC(CF₃)₃)₄] (49, {PC₄^tBu₂Me₂}⁻ = 2,5-di-tert-butyl-3,4-dimethylphospholyl)⁶⁹ (Fig. 6).

Fig. 6 Examples of the pseudo-linear dysprosocenium ions from [Dy(Cp^ttt)₂][B(C₆F₅)₄] (40-Dy), [Dy(Cp^iPr₄)₂][B(C₆F₅)₄] (41, R₁ = H), [Dy(Cp^iPr₄Me)₂][B(C₆F₅)₄] (42, R₁ = Me), [Dy(Cp^iPr₄Et)₂][B(C₆F₅)₄] (43, R₁ = Et), [Dy(Cp^iPr₅)₂][B(C₆F₅)₄] (44-Dy, R₁ = ⁱPr), [Dy(Cp^iPr₅)(Cp*)][B(C₆F₅)₄] (45), [Dy(Cp^ttt)(Cp*)][Al(OC(CF₃)₃)₄] (46), [K(18-crown-6)(THF)₂][Dy(BC₄Ph₅)₂] (47, R₂ = Ph), [K(2.2.2)][Dy(BC₄Ph₄Pip)₂] (48, R₂ = NC₅H₁₀) and [Dy(PC₄^tBu₂Me₂)₂][Al(OC(CF₃)₃)₄] (49).^{59–62,67–69}

The synthesis of compounds 41–49 was targeted due to the SIM behaviour of 40-Dy (Table 2). The solid-state structure of 40-Dy shows that two Cp^ttt ligands sit above and below the Dy(III) centre in a near axial orientation as the Cp^ttt_cent⋯Dy⋯Cp^ttt_cent angle is 152.56(7)° (Cp^ttt_cent = calculated centroid of the Cp^ttt ring).⁵⁹ The combination of both sterically hindering tert-butyl groups and the non-coordinating {B(C₆F₅)₄}⁻ counter-ion means that no ligands are coordinated equatorially (as the easy axis is along the Cp^ttt_cent⋯Dy⋯Cp^ttt pseudo-axis), with the closest Dy⋯F distance being 5.996(3) Å.⁵⁹ The geometry present in 40-Dy yields <96% purity of crystal field states for the first six pairs of Kramers doublets which are all quantised along the Cp^ttt_cent⋯Dy⋯Cp^ttt_cent pseudo-axis, with the fifth excited state reflecting axial anisotropy (g_x, g_y < g_z = 6.44).⁵⁹ The slow magnetic relaxation of 40-Dy predominantly goes via the fifth excited state which sits 1277 cm⁻¹ above the ground state (ab initio calculated).⁵⁹ The calculated energy of the fifth excited state is in good agreement with the experimentally determined effective energy barrier of U_eff = 1223 cm⁻¹.⁵⁹

Table 2 Magnetic and structural properties of dysprosocenium complexes^{59–62,67–69}

Complex	Ueff/cm^−1	TB100/K	TH/K	Cpcent⋯Dy⋯Cpcent^a/°	Cpcent⋯Dy^a/Å
a Cpcent = calculated centroid of the Cp ring.b No errors provided by original authors.c Magnetic behaviour is based on the conformation of the dysprosium centre, each with unique magnetic behaviour.d Relaxation rates were fitted to multiple regimes, when the Orbach regime is modelled independently, the energy barrier is Ueff = 1658(2) cm^−1.e Approximate value provided as authors did not quote TH but open loop hysteresis at 60 K and a closed loop at 70 K were given.
[Dy(Cp^ttt)2][B(C6F5)4] 40-Dy	1223^b	56	60	152.56(7)	2.316(3)
[Dy(Cp^iPr4)2][B(C6F5)4] 41	1285^b	17	32	147.2(8)	2.29(1)
[Dy(Cp^iPr4Me)2][B(C6F5)4] 42	1468^b	62	72	156.6(3)	2.298(5)
[Dy(Cp^iPr4Et)2][B(C6F5)4] 43	1380^b	59	66	161.1(2)	2.302(6)
[Dy(Cp^iPr5)2][B(C6F5)4] 44-Dy	1334^b	56	66	162.1(7)	2.340(7)
[Dy(Cp^iPr5)(Cp*)][B(C6F5)4] 45	1541(11)	67	80	162.507(1)	2.284(1), 2.296(1)
[Dy(Cp^ttt)(Cp*)][Al(OC(CF3)3)4] 46	1221(25)	28	52	149.15(9)	2.297(2), 2.314(3)
[K(18-crown-6)(THF)2][Dy(BC4Ph5)2] 47	1500(100)	65	66	156.5^b	2.326^b
[K(2.2.2)][Dy(BC4Ph4Pip)2]^c 48	1600(100)^d	66	~60^e	161.4(3)	2.274(6), 2.244(6)
	1300(300)	60		158.6(3)	2.258(6), 2.280(5)
[Dy(PC4^tBu2,Me2)2][Al(OC(CF3)3)4] 49	1220(50)	23	48	157.94(4)	2.354(3)

---

It is worth noting that Mills further extended the bis-Cp^ttt moiety to all the lanthanides in either the separated ion-pair [Ln(Cp^ttt)₂][B(C₆F₅)₄] (40-Ln, Ln = Y, Sm, Eu, Gd, Tb, Ho, Er, Tm, Yb, Lu), or the contact ion-pair [Ln(Cp^ttt)₂{B(C₆F₅)₄-μ-F}] (40-Ln, Ln = La, Ce, Pr, Nd).^15,70,71 Here, two different molecules are favoured due to the size of the Ln(III) ion used. The magnetic studies and ab initio calculations performed on 40-Ln highlighted the importance of axial crystal-fields in low coordination environments for Ln ions that possess an oblate ground state⁷⁰ and the influence that coordinating anions have on the electronic structure.¹⁵ 40-Dy outperforms the other lanthanide complexes 40-Ln in regard to their magnetic behaviour due to reasons outlined vide supra.

The remaining family of dysprosocenium ions employ other weakly coordinating anions, or captured potassium ions, and bis-Cp moieties reflecting large Cp_cent⋯Dy⋯Cp_cent angles and short Dy⋯Cp_cent distances (Table 2).^{59–62,67–69} As outlined by Goodwin,⁴ there should be a trend between a SIM's performance and increased linearity/proximity of Cp ligands. Long⁶⁰ explored the said relationships with compounds 41–44-Dy, before Layfield⁶¹ synthesised the first heteroleptic dysprosocenium ion 45 that showed the largest Cp_cent⋯Dy⋯Cp_cent angle and shortest Dy⋯Cp_cent distances for Cp-based dysprosocenium ions (Table 2). Complex 45 presents the highest T_B100 and T_H for Ln-based SIMs of 67 K and 80 K, respectively.⁶¹ Not only is there a correlation between the structural properties and U_eff in dysprosocenium ions, but there is also a correlation between the linearity and proximity of the Cp ligands with both T_B100 and T_H that are observed among complexes 40-Dy to 49 (Table 2).^{59–62,67–69}

Bis-Cp complexes remained uncontested for several years as the best performing SIMs before Nippe opted to bis-cap Dy(III) with the dianionic borolide ligand {BC₄Ph₄Pip}²⁻ in 47.⁶⁸ Interestingly, Nippe showed that 47 has two different conformations for the coordination geometry, where each has unique and measurable magnetic relaxation rates, producing a fast and slow Orbach type relaxation with energy barriers of 1600(100) cm⁻¹ and 1300(300) cm⁻¹, respectively.⁶⁸ Modelling the Orbach irrespective of any other relaxation mechanism occurring in 47 for the fast process produces the highest reported energy barrier for lanthanocenium-type SIMs of U_eff = 1658(2) cm⁻¹.⁶⁸

Mono-capped strong field ligated complexes

The two sections vide supra rely on the bis-axial environment for generating large axial magnetic anisotropy in Dy(III) complexes, though there are few examples where the same anisotropy can be achieved with “mono-axial” crystal fields. An example from each class is exemplified vide infra.

Though the following Ln moiety was introduced in the early 1990s by McCleverty and Ward,⁷² three Dy(III) analogues of the mono-fluoride complexes [Dy(Tp^2-py)F(Solv)₂]PF₆ (3, Solv = diox; 50, Solv = py; 51, Solv = THF) have recently been reported.^25,73 Initially targeted by Norel and Long, the two solvated adducts 3 and 44 were targeted based on the idea that the short Dy–F bond would generate large axial anisotropy (Table 3).²⁵ Both magnetometry and ab initio calculations revealed that the hard fluoride ion and relatively weak crystal field produced by the scorpionate ligand were successful in generating axial anisotropy, with the easy axis aligning with the Dy–F bond resulting in zero-field SIM behaviour being recorded up to 54 K for 3 via ac magnetometry.⁷³ The SIM behaviour of the mono-fluoride moiety was improved by Sulway and Giansiracusa with the THF adduct 51 (Fig. 7), which produced a record energy barrier for high-coordinate (coordination number larger than 8), air-stable Ln-SIMs of U_eff = 661(6) cm⁻¹ (Table 3).⁷³ However, like the remaining point-charge approach molecules, vide supra, the magnetic blocking temperatures for 3, 50 and 51 are low (magnetic relaxation does not last for 100 seconds at any temperature, i.e. no T_B100) and do not show open-looped magnetic hysteresis at 2 K.

Table 3 Coordination distances of the highest perturbing ligand and energy barriers of mono-capped SIMs^25,73,74

Complex	Dominating ligand	Dy–Xax/Å	Ueff/cm^−1
a Multiple Orbach processes.b No errors presented by original authors.c Multiple energy barriers fitted to the same Orbach mechanism.d Coordination distance of Cp* is .
[Dy(Tp^2-py)F(μ-diox)]n(PF6)n^a 3	F^−	2.094(4)	432^b528^b
[Dy(Tp^2-py)F(py)2]PF6 50	F^−	2.1007(11)	336(12)^c
[Dy(Tp^2-py)F(THF)2]PF6 51	F^−	2.110(2)	661(6)
[Dy(Cp*)(κ^1-FC6H5)6] [{Al(OC(CF3)3)3}2(μ-F)]2 52	Cp*^−	2.2737(4)^d	545(30)

---

Fig. 7 Solid-state structures of the cations from [Dy(Tp^2-py)F(THF)₂]PF₆ (51) and [Dy(Cp*)(κ¹-FC₆H₅)₆][{Al(OC(CF₃)₃)₃}₂(μ-F)]₂ (52). Dysprosium(III) = turquoise, fluorine = fluoro-green, oxygen = red, nitrogen = blue, carbon = grey, and boron = orange; hydrogen atoms have been omitted clarity.^73,74

Using the lanthanocenium approach, the half-sandwich Dy(III) complex [Dy(Cp*)(κ¹-FC₆H₅)₆][{Al(OC(CF₃)₃)₃}₂(μ-F)]₂ (52, FC₆H₅ = fluorobenzene) has been recently synthesised by Mills and Chilton (Fig. 7).⁷⁴ Complex 52 exhibits six weakly coordinated solvent molecules of FC₆H₅, where one is axial with respect to the hard Cp* ligand and the remaining five are coordinated equatorially. The easy axis for 52 is along the axis and the ground state is highly axial and completely comprised of the m_J = ±15/2 state, as is for 3, 50 and 51.^25,73,74 Magnetometry placed the effective energy barrier at U_eff = 545(30) cm⁻¹ (Table 3) for 52, which is in good agreement with the ab initio calculated 5th excited state (589 cm⁻¹) which is where significant transverse g_x and g_y components are observed.⁷⁴ Unlike the mono-capped point charge approach, 52 exhibits open-looped hysteresis up to T_H = 14 K which originates from the rigidity of the {Dy(Cp*)(μ-FC₆H₅)₆}²⁺ ion.⁷⁴

All ‘mono-capped’ examples (3, 50–52) highlight that only one hard ligand is required to generate axial magnetic anisotropy in Dy(III) complexes though the resultant energy barriers are less than half that of the bis-axial examples. Ab initio calculations reveal that for 3 and 50–52 the total crystal field splitting in the ground ⁶H_15/2 multiplet for Dy(III) centres is less than 800 cm⁻¹, thus reinforcing the need for a bis-axial crystal field for better SIM performance in Dy(III) complexes. These mono-capped complexes also reiterate the need for rigidity in ligands to not only increase U_eff, but also T_B100 and T_H.

The importance of (non)-Kramers ions and the crystal field geometry

The final methodology highlights the importance of the use of Kramers and non-Kramers ions in low coordination environments and strict symmetries with rigid ligands. In 2019, a series of previously synthesised lanthanocenium ions, compounds 44-Ln (Ln = Dy(III), Tb(III)),⁶⁰ were compared to that of newly synthesised lanthanocene molecules [Ln(Cp^iPr₅)₂], compounds 53-Ln (Ln = Dy(II), Tb(II)), prepared via a reduction of the halide precursor [Ln(Cp^iPr₅)₂I] by Long (Fig. 8).⁷⁵ The divalent 53-Ln complexes have half-molecule symmetry with angles of 180°, generated by symmetry, and the Cp^iPr₅ ligands being further from the Ln(II) centres then in analogous trivalent 53-Ln complexes by 0.1–0.2 Å due to an increase in ionic radii.^60,75 Analogous chemistry was used in a similar study to compare the difference in magnetic behaviours of the two bis-amidinate complexes [Ln(Piso)₂][B(C₆F₅)₄] (54-Ln, Piso = {(NDipp)₂C^tBu}-, Dipp = 2,6-di-iso-propylphenyl, Ln = Tb(III), Dy(III)) and [Ln(Piso)₂] (55-Ln, Ln = Tb(II), Dy(II)) (Fig. 8).⁷⁶ The same linearity is observed in divalent 55-Ln complexes which has been attributed to the ground state electronic configurations of 4fⁿ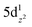 (Ln = Tb(II), n = 8; Ln = Dy(II), n = 9) in both divalent cases.^75,76 With an electron occupying the 5d_z² orbital, axially symmetric and linear architectures are supported due to the linear shapes of the said orbital.

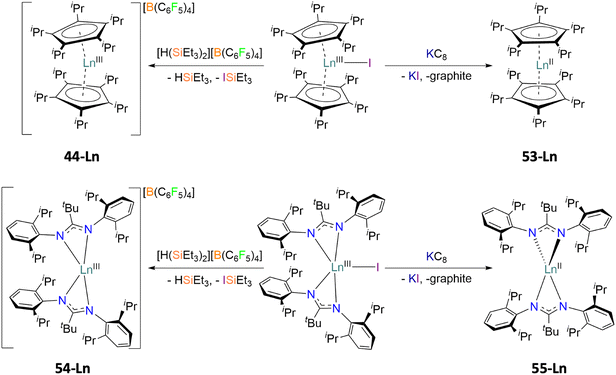Fig. 8 Synthetic routes and structural differences of the cationic lanthanocenium ion [Ln(Cp^iPr₅)₂][B(C₆F₅)₄] 44-Ln versus the neutral lanthanocene molecule [Ln(Cp^iPr₅)₂] 53-Ln (top), and the bis-amidinate complexes [Ln(Piso)₂][B(C₆F₅)₄] 54-Ln and [Ln(Piso)₂] 55-Ln (bottom), Ln = Dy, Tb.^75,76

The magnetic performance between 44-Dy and 53-Dy shows that upon reduction of the Kramers Dy(III) ion to a non-Kramers Dy(II) ion, the magnetic behaviour is ‘lost’ as Orbach relaxation is not observed in 53-Dy (Table 4).⁷⁵ The additional SIM parameters of 53-Dy present a dramatic drop in magnitude, where T_B100 = 5 K and T_H = 10 K (cf. 56 K and 66 K in 44-Dy, respectively).^60,75 The opposing argument is true between the non-Kramers 44-Tb and Kramers 53-Tb; there is no observable Orbach relaxation mechanism for 44-Tb (or T_B100 and T_H); however 53-Tb possessed the highest energy barrier observed in a Tb-based SIM upon publishing (U_eff = 1205 cm⁻¹).⁷⁵ Ab initio calculations were never performed on these molecules but the main reason for the difference in energy barriers between 44-Dy and 53-Tb is likely due to the proximity of the Cp^iPr₅ ligands ( = 2.340(7)Å in 44-Dy and = 2.417(1) Å in 53-Tb), as the pseudo-environment in 44-Dy and the D_5d symmetry in 53-Tb are not dissimilar enough to cause a large amount of transverse anisotropy in excited states.⁷⁵ The strict symmetry environment in 53-Dy results in higher hysteresis and magnetic blocking temperatures relative to 44-Tb (Table 4), highlighting the importance of strict axial symmetry to enhance the SIM behaviour in non-Kramers ions.

Table 4 Magnetic and electronic properties of bis-capped lanthanide complexes with trivalent and divalent lanthanide centres^60,75,76

Complex	Ln (OS)^a	Ueff/cm^−1	TB100/K	TH/K			CPiso⋯Ln⋯CPiso^b/°	NPiso-Ln^c/Å
a Ln (OS) = lanthanide (oxidation state).b CPiso = carbon atom of the CN2 backbone of the Piso ligand.c NPiso = coordinating nitrogen atom of the Piso ligand; no errors presented by original authors.d No observable Orbach relaxation in zero-applied fields.e Magnetic relaxation does not last for 100 seconds.f TH recorded as a dilute solution of 53-Dy in toluene (28 mM).g Only butterfly and/or closed loop hysteresis is observed at 2 K.
[Dy(Cp^iPr5)2]^+ 44-Dy	Dy(III)	1334 d	56	66	162.1(7)	2.340(7)	—	—
[Dy(Cp^iPr5)2] 53-Dy	Dy(II)	—^d	5	10^f	180.0	2.385(1)	—	—
[Tb(Cp^iPr5)2]^+ 44-Tb	Tb(III)	—^d	—^e	—^g	159.8(4)	2.356(6)	—	—
[Tb(Cp^iPr5)2] 53-Tb	Tb(II)	1205	52	55	180.0	2.417(1)	—	—
[Dy(Piso)2]^+ 54-Dy	Dy(III)	—^d	—^e	4.5	—	—	148.80(9)	2.258(3)–2.332(2)
[Dy(Piso)2] 55-Dy	Dy(II)	1365(33)	—^e	—^g	—	—	174.82(8)	2.314(2)–2.365(2)
[Tb(Piso)2]^+ 54-Tb	Tb(III)	—^d	—^e	—^g	—	—	150.01(7)	2.257(2)–2.352(2)
[Tb(Piso)2] 55-Tb	Tb(II)	1334(63)	—^e	—^g	—	—	174.58(9)	2.312(3)–2.367(2)

---

Contrary to previous discussion, both trivalent bis-amidinate complexes 54-Ln show poor SIM behaviour, which the authors have attributed to the introduction of transverse fields from the multidentate and off-axis nitrogen-donor amidinate ligands, resulting in considerable mixing of m_J states in the ground J-manifold.⁷⁶ However in the divalent 55-Ln, these nitrogen donors sit relatively linear due to the pseudo-linear C⋯Ln⋯C arrangement (55-Tb, 174.58(9)°; 55-Dy, 174.82(8)°) established by the CN₂ backbone (Fig. 8).⁷⁶ The bis-amidinate complexes show fast magnetic relaxation as only 54-Dy presents an attainable SIM metric of T_H (4.5 K), much lower than what is observed within the bis-Cp analogues (Table 4).⁷⁶ One hundred-second magnetic blocking temperatures were determined for the divalent species 55-Ln (T_B100 > 25 K), though they were measured by dc decay experiments where the resting field is non-zero.⁷⁶ Although 54-Tb and 55-Dy present fast magnetic relaxation, their energy barriers are the highest yet reported for divalent lanthanide-based SIMs of 1365(33) cm⁻¹ for 54-Dy and 1334(63) cm⁻¹ for 55-Tb.⁷⁶ Post exploring these bis-amidinate complexes, the authors conclude that divalent lanthanide complexes as SIMs, where the ground electronic configurations reflect 4fⁿ , are not as straightforward as ensuring the use of Kramers ions or strict geometries but emphasise that the bond character of the coordination bonds play a crucial role in the magnetic properties of these complexes.⁷⁶ The relatively slower magnetic relaxation seen in bis-Cp complexes has been linked to the use of the rigid Cp^R moieties, which are not captured in amidinate ligands. Thus, these studies reiterate the use of rigid ligands, in axial crystal fields to ensure extinction of low energy vibrations and a large separation in m_J states, respectively.

Future prospects and conclusions

The introduction of Ln-SIMs has slowly led to the increased performance and metrics of SMMs via systematic changes in molecular design and the physical understanding of exploiting the single-ion anisotropy of lanthanide ions. Though they were the first molecules synthesised and measured, bis-axial point charge molecules are intrinsically more vibrationally complex. The magnetic blocking and hysteretic temperatures for these point charge systems are limited due to the introduction of transverse anisotropy by neutral molecules coordinated equatorially with respect to the magnetisation axis. The omission of these neutral molecules, as is for the cations in 37 and 38,^49,53 reiterates the need for the charged ligands to be linear to increase both the anisotropy and effective energy barrier. Meanwhile, the systemic change of the axial ligands within the cations in 6, 7 and 8, for example,^33–35 highlights the need for hard coordinating atoms and short coordination distances to stabilise the largest m_J state, increase the purity of the ground and excited crystal field states and increase crystal field splitting. The latter is again reiterated by the cations in 51 and 52 where the use of only one hard axial ligand results in a lower total crystal field splitting.^73,74

To overcome the low temperature at which point charge systems operate as SIMs, the use of more rigid Cp^R ligands increased the said temperatures. The dysprosocenium ions discussed vide supra show that the increased linearity (Cp_cent⋯Dy⋯Cp_cent) and short proximity of the Cp ring (Dy⋯Cp_cent) are approximately proportional to the slow magnetic relaxation behaviour of the ions.^59–62 The synthesis of lanthanocenium ions in general, along with low coordinate lanthanide complexes, was facilitated by the use of WCAs in sensitive synthetic procedures, where few research groups are experts in. WCAs allow for the synthesis of isolated cations that possess unsaturated coordination environments, though the steric bulk of the cation must be fined tuned to achieve the said isolation. The isolated dysprosocenium ions not only boast high energy barriers to magnetic relaxation but also present some of the highest magnetic blocking and hysteretic temperatures for SMMs, which again is due to the increased rigidity of the ions that shift molecular vibrations off resonances with magnetic transitions (i.e. reduces spin-phonon coupling).²²

Using the dysprosocenium ion architecture of 44-Dy, the synthesis of 44-Tb lastly validates the use of/need for Kramers ions when designing Ln-SIMs,^60,75 although the plethora of high performance Dy(III)-based SIMs highlights their importance in the field. The reduction of 44-Ln to 53-Ln (Ln = Dy, Tb) further emphasises the (non)-Kramers nature of the central lanthanide ion, where the swap of ‘Kramersness’ sees the inverse magnetic behaviour.⁷⁵ Meanwhile, molecules such as 55-Ln (Ln = Dy, Tb) that include divalent centres show the importance of symmetry and linearity which are enforced by the geometry of the occupied atomic orbitals when compared to their trivalent counterparts 54-Ln.⁷⁶

Implementing the technique/strategies discussed here, the humble beginnings of Ln-SIMs with 5-Ln seem to be reaching a point where improvements are being made at a much slower rate. It may be that a ‘U_eff’ ceiling is being reached, which one may approximate to be 2000 cm⁻¹ as the best performing Ln-SIMs are currently sitting at just above 1800 cm⁻¹. Although, a more interesting feat is the dramatic increase in operating temperatures, i.e. T_B100 and T_H, within the last decade, with some molecules surpassing the liquid nitrogen barrier (77 K), making SIMs more viable for their possible implantation into devices. Improvements in these metrics may arise from the use of other substituted Cp ligands, or other cyclic aromatics such as substituted cyclobutadienyl ({Cb^R}²⁻) either as molecular mixed Cp^R/Cb^R complexes or bis-Cb^R anions (possible molecular designs are shown in Fig. 9). This postulation is not new to the SIM field (e.g. Goodwin⁴ suggested this in 2020) as Cb ligands offer the same steric demands as and possess the same rigidity as Cp ligands but are more charge dense (i.e. Cb ligands are dianionic and are smaller cyclic molecules). Some work has been done to try and achieve the latter, alas a completely isolated {Dy(Cb^R)₂}⁻ ion has not been realised.^77,78 The attempts to access {Dy(Cb^R)₂}⁻ complexes are generally met with group I metals coordinating to the opposing side of the Cb ring when they have not been trapped appropriately, as is for the bis-borolide complexes 41 and 42.^67,68

Fig. 9 Future molecular design of high performance Dy-based SIMs of the general formula [Dy(Cp^R)(Cb^R)] (right) and {Dy(Cb^R)₂}⁻ (left), where R is any alkyl, aryl, silyl, etc. group.

Data availability

All data from the article are taken from other sources and are cited accordingly.

Conflicts of interest

There are no conflicts to declare.

References

1. A. A. Mills, Ann. Sci., 2004, 61, 273–319.
2. D. Gatteschi, J. Alloys Compd., 2001, 317–318, 8–12.
3. (a) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143; (b) T. Lis, Acta Crystallogr., Sect. B, 1980, 36, 2042–2046.
4. C. A. P. Goodwin, Dalton Trans., 2020, 49, 14320–14337.
5. D. N. Woodruff and R. E. P. Winpenny, Chem. Rev., 2013, 113, 5110–5148.
6. J. D. Rinehart and J. R. Long, Chem. Sci., 2011, 2, 2078–2085.
7. H. N. Russell and F. A. Saunders, Astrophys. J., 1925, 61, 38–69.
8. N. Kaltsoyannis and P. Scott, The f elements, Oxford University Press, Oxford, 1999.
9. R. Skomski, Simple Models of Magnetism, Oxford University Press, Oxford, 2008.
10. J. Liu, Y. Chen and M. Tong, Chem. Soc. Rev., 2018, 47, 2431–2453.
11. P. Zhang, L. Zhang, C. Wang, S. Xue, S. Lin and J. Tang, J. Am. Chem. Soc., 2014, 135(12), 4484–4487.
12. S. Jiang, B. Wang, H. Sun, Z. Wang and S. Gao, J. Am. Chem. Soc., 2011, 133(13), 4730–4733.
13. H. Wada, S. Ooka, T. Yamamura and T. Kajiwara, Inorg. Chem., 2017, 56, 147–155.
14. J. R. Thomas, K. A. Sarma, M. J. Giansiracusa and S. A. Sulway, Acta Crystallogr., Sect. C:Struct. Chem., 2024, 80, 761–765.
15. L. Liu, D. Reta, J. A. Cleghorn, Y. X. Yeoh, F. Ortu, C. A. P. Goodwin, N. F. Chilton and D. P. Mills, Chem. – Eur. J., 2019, 25, 7749–7758.
16. (a) D. Gatteschi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, 2006; (b) J. Tang and P. Zhang, Lanthanide Single Molecule Magnets, Springer-Verlag, Berlin, Heidelberg, 2015.
17. H. A. Kramers, Proc. K. Ned. Akad. Wet., 1930, 33, 959–972.
18. N. Ishikawa, M. Sugita, T. Ishikawa, S. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695.
19. D. Reta and N. F. Chilton, Phys. Chem. Chem. Phys., 2021, 21, 23567–23575.
20. K. S. Cole and R. H. Cole, J. Chem. Phys., 1941, 9, 341–351.
21. J. D. Hilgar, A. K. Butts and J. D. Rinehart, Phys. Chem. Chem. Phys., 2019, 21, 22302–22307.
22. E. Garlatti, A. Chiesa, P. Bonfà, E. Macaluso, I. J. Onuorah, V. S. Parmar, Y. Ding, Y. Zheng, M. J. Giansiracusa, D. Reta, E. Pavarini, T. Guidi, D. P. Mills, N. F. Chilton, R. E. P. Winpenny, P. Santini and S. Carretta, J. Phys. Chem. Lett., 2021, 12, 8826–8832.
23. I. Fdez Galván, M. Vacher, A. Alavi, C. Angeli, F. Aquilante, J. Autschbach, J. J. Bao, S. I. Bokarev, N. A. Bogdanov, R. K. Carlson, L. F. Chibotaru, J. Creutzberg, N. Dattani, M. G. Delcey, S. S. Dong, A. Dreuw, L. Freitag, L. M. Frutos, L. Gagliardi, F. Gendron, A. Giussani, L. Gonzalez, G. Grell, M. Guo, C. E. Hoyer, M. Johansson, S. Keller, S. Knecht, G. Kovacevic, E. Kaellman, G. Li Manni, M. Lundberg, Y. Ma, S. Mai, J. P. Malhado, P. A. Malmqvist, P. Marquetand, S. A. Mewes, J. Norell, M. Olivucci, M. Oppel, Q. M. Phung, K. Pierloot, F. Plasser, M. Reiher, A. M. Sand, I. Schapiro, P. Sharma, C. J. Stein, L. K. Soerensen, D. G. Truhlar, M. Ugandi, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, O. Weser, T. A. Wesolowski, P. Widmark, S. Wouters, A. Zech, J. P. Zobel and R. Lindh, J. Chem. Theory Comput., 2019, 15, 5925–5964.
24. M. Vonci, M. J. Giansiracusa, R. W. Gable, W. V. Heuvel, K. Latham, B. Moubaraki, K. S. Murray, D. Yu, R. A. Mole, A. Sonicini and C. Boskovic, Chem. Commun., 2016, 52, 2091–2094.
25. L. Norel, L. E. Darago, B. Le Guennic, K. Chakarawet, M. I. Gonzalez, J. H. Olshansky, S. Rigaut and J. R. Long, Angew. Chem., 2018, 130, 1951–1956.
26. (a) J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, J. Am. Chem. Soc., 2011, 133, 14236–14239; (b) S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Coummun., 2017, 8, 2144–2147.
27. S. Demir, J. M. Zadrozny, M. Nippe and J. R. Long, J. Am. Chem. Soc., 2012, 134, 18546–18549.
28. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202.
29. H. L. C. Feltham, Y. Lan, F. Klower, L. Ungur, L. F. Chibotaru, A. K. Powell and S. Brooker, Chem. – Eur. J., 2011, 17, 4362–4365.
30. C. Papatriantafyllopoulou, W. Wernsdorfer, K. A. Abboud and G. Christou, Inorg. Chem., 2010, 50, 421–423.
31. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202.
32. H. Kwon, K. R. McClain, J. G. C. Kragskow, J. K. Staab, M. Ozerov, K. R. Meihaus, B. G. Harvey, E. Choi, N. F. Chilton and J. R. Long, J. Am. Chem. Soc., 2024, 146, 18714–18721.
33. Y. Ding, N. F. Chilton, R. E. P. Winpenny and Y. Zheng, Angew. Chem., Int. Ed., 2016, 55, 16071–16074.
34. Y. Ding, K. Yu, D. Reta, F. Ortu, R. E. P. Winpenny, Y. Zheng and N. F. Chilton, Nat. Commun., 2018, 5, 3134.
35. J. Long, A. N. Selikhov, E. Mamontova, K. A. Lyssenko, Y. Guari, J. Larionova and A. A. Trifonov, Dalton Trans., 2019, 48, 35–39.
36. Y. Ding, T. Han, Y. Zhai, D. Reta, N. F. Chilton, R. E. P. Winpenny and Y. Zheng, Chem. – Eur. J., 2020, 26, 5893–5902.
37. X. Ding, Q. Luo, Y. Zhai, X. Zhang, Y. Lv, X. Zhang, C. Ke, C. Wu and Y. Zheng, Chin. J. Chem., 2022, 40, 562–570.
38. X. Ding, Y. Zhai, T. Han, W. Chen, Y. Ding and Y. Zheng, Chem. – Eur. J., 2021, 27, 2623–2627.
39. A. B. Canaj, S. Dey, E. R. Marti, C. Wilson, G. Rajaraman and M. Murrie, Angew. Chem., Int. Ed., 2019, 58, 14146–14151.
40. A. B. Canaj, S. Dey, C. Wilson, O. Cespedes, G. Rajaraman and M. Murrie, Chem. Commun., 2020, 80, 12037–12040.
41. S. Jia, X. Zhu, B. Yin, Y. Dong, A. Sun and D. Li, Cryst. Growth Des., 2023, 23, 6967–6973.
42. S. Liu, Y. Gil, C. Zhao, J. Wu, Z. Zhu, Z. Li, D. Aravena and J. Tang, Inorg. Chem. Front., 2022, 9, 4982–4989.
43. C. Zhao, Z. Zhu, X. Li and J. Tang, Inorg. Chem. Front., 2022, 9, 4049–4055.
44. Z. Zhu, C. Zhao, T. Feng, X. Liu, X. Ying, X. Li, Y. Zhang and J. Tang, J. Am. Chem. Soc., 2021, 143, 10077–10082.
45. Z. Li, Y. Zhai, W. Chan, S. Ding and Y. Zheng, Chem. – Eur. J., 2019, 25, 16219–16224.
46. Y. Ding, W. J. A. Blackmore, Y. Zhai, M. J. Giansiracusa, D. Reta, I. Vitorica-Yrezabal, R. E. P. Winpenny, N. F. Chilton and Y. Zheng, Inorg. Chem., 2021, 61, 227–235.
47. W. Xu, Q. Luo, Z. Li, Y. Zhai and Y. Zheng, Adv. Sci., 2024, 11, 2308548.
48. J. Long, A. N. Selikhov, E. Mamontova, K. A. Lyssenko, Y. Guari, J. Larionova and A. A. Trifonov, Dalton Trans., 2020, 49, 4039–4043.
49. J. Emerson-King, G. K. Gransbury, G. F. S. Whitehead, I. J. Vitorica-Yrezabal, M. Rouzieres, R. Clerac, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2024, 146, 3331–3342.
50. I. Krossing, Chem. – Eur. J., 2001, 7, 490–502.
51. K. L. M. Harriman, J. Murillo, E. A. Suturina, S. Fortier and M. Murugesu, Inorg. Chem. Front., 2020, 7, 4805–4812.
52. F. Benner, R. Jena, A. L. Odom and S. Demir, J. Am. Chem. Soc., 2025, 147, 8156–8167.
53. J. Emerson-King, G. K. Gransbury, B. Atkinson, W. Blackmore, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, ChemRxiv, 2024, preprint,  DOI:10.26434/chemrxiv-2024-36vjp.
54. L. Ungur and L. F. Chibotaru, Inorg. Chem., 2016, 55(20), 10043–10056.
55. Y. Chen, J. Liu, L. Ungur, J. Liu, Q. Li, Z. Ni, L. F. Chibotaru, X. Chen and M. Tong, J. Am. Chem. Soc., 2016, 138(8), 2829–2837.
56. V. S. Parmar, D. P. Mills and R. E. P. Winpenny, Chem. – Eur. J., 2021, 27, 7625–7645.
57. (a) N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, Chem. Commun., 2015, 51, 101–103; (b) N. F. Chilton, Inorg. Chem., 2015, 54(5), 2097–2099.
58. S. Demir, J. M. Zadrozny and J. R. Long, Chem. – Eur. J., 2014, 20, 9524–9529.
59. (a) F. Guo, B. M. Day, Y. Chen, M. Tong, A. Manskkamaki and R. Layfield, Angew. Chem., 2017, 129, 11603–11607; (b) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Nature, 2017, 548, 439–442.
60. K. R. McClain, C. A. Gould, K. Chakarawet, S. J. Teat, T. J. Groshens, J. R. Long and B. G. Harvey, Chem. Sci., 2018, 9, 8492–8503.
61. F. Guo, B. M. Day, Y. Chen, M. Tong, A. Manskkamaki and R. Layfield, Science, 2018, 362, 1400–1403.
62. G. K. Gransbury, S. C. Corner, J. G. C. Kragskow, P. Evans, H. M. Yeung, W. J. A. Blackmore, G. F. S. Whitehead, I. J. Vitorica-Yrezabal, M. S. Oakley, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2023, 145, 22814–22825.
63. C. G. T. Price, A. Mondal, J. P. Durrant, J. Tang and R. A. Layfield, Inorg. Chem., 2023, 62, 9924–9933.
64. D. Errulat, B. Gabidullin, A. Mansikkamaki and M. Murugesu, Chem. Commun., 2020, 56, 5937–5940.
65. S. C. Corner, G. K. Gransbury, I. J. Vitorica-Yrezabal, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2024, 63, 9552–9561.
66. S. C. Corner, G. K. Gransbury, I. J. Vitorica-Yrezabal, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2024, 63, 9562–9571.
67. A. H. Vincent, Y. L. Whyatt, N. F. Chilton and J. R. Long, J. Am. Chem. Soc., 2023, 145, 1572–1579.
68. J. C. Vanjak, B. O. Wilkins, V. Vieru, N. S. Bhuvanesh, J. H. Reibenspies, C. D. Martin, L. F. Chibotaru and M. Nippe, J. Am. Chem. Soc., 2022, 144, 17743–17747.
69. P. Evans, D. Reta, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2019, 141, 19935–19940.
70. C. A. P. Goodwin, D. Reta, F. Ortu, N. F. Chilton and D. P. Mills, J. Am. Chem. Soc., 2017, 139, 18714–18724.
71. C. A. P. Goodwin, D. Reta, F. Ortu, J. Liu, N. F. Chilton and D. P. Mills, Chem. Commun., 2018, 54, 9182–9185.
72. (a) A. J. Amoroso, A. M. C. Thompson, J. C. Jeffery, P. J. Jones, J. A. McCleverty and M. D. Ward, J. Chem. Soc., Chem. Commun., 1994, 2751–2752; (b) P. L. Jones, A. J. Amoroso, J. C. Jeffery, J. C. McCleverty, E. Psillakis, L. H. Rees and M. D. Ward, Inorg. Chem., 1997, 36, 10–18.
73. J. R. Thomas, M. J. Giansiracusa and S. A. Sulway, Dalton Trans., 2024, 53, 9252–9256.
74. S. C. Corner, W. J. A. Blackmore, G. K. Gransbury, A. Mattioni, G. F. S. Whitehead, N. F. Chilton and D. P. Mills, Chem. Sci., 2025, 16, 610–620.
75. C. A. Gould, K. R. McClain, J. M. Yu, T. J. Groshens, F. Furche, B. G. Harvey and J. R. Long, J. Am. Chem. Soc., 2019, 141, 12967–12973.
76. P. Jin, Q. Luo, G. K. Gransbury, I. J. Vitorica-Yrezabal, T. Hajdu, I. Strashnov, E. J. L. McInnes, R. E. P. Winpenny, N. F. Chilton, D. P. Mills and Y. Zheng, J. Am. Chem. Soc., 2023, 145, 27993–28009.
77. A. Chakraborty, B. M. Day, J. P. Durrant, M. He, J. Tang and R. A. Layfield, Organometallics, 2020, 39, 8–12.
78. J. P. Durrant, J. Tang, A. Mansikkamaki and R. A. Layfield, Chem. Commun., 2020, 56, 4708–4711.

---