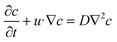DOI:
10.1039/D4CE00931B
(Paper)
CrystEngComm, 2025,
27, 90-101
Optimization of carbon transport and growth rates in top-seeded solution growth of Al-doped SiC
Received
12th September 2024
, Accepted 20th November 2024
First published on 21st November 2024
Abstract
The top-seeded solution growth (TSSG) method is an emerging technique for the production of silicon carbide (SiC). Due to its advantage of lower growth temperature compared to the physical vapor transport method, it holds significant potential in the preparation of Al-doped SiC. In this study, a global numerical model calculating heat and mass transfer was established to investigate the impact of solution radius and height, coil position, and rotational speed of the seed crystal on the flow pattern and carbon transport. The results indicated that a meticulous determination of these growth parameters could enhance both carbon transport and growth rate. Furthermore, abundant transient calculation results were utilized to train back-propagation (BP) neural networks to extract the correlation between growth parameters, growth rate, and Al concentration. The optimal parameters were ultimately obtained using the non-dominated sorting genetic algorithm (NSGA-II). The Al concentration calculated in the solution under the optimal growth conditions demonstrated that the evaporation of Al was sufficiently low to satisfy the p-type doping requirement. This study provides valuable insights for the future development of a TSSG system tailored for the rapid growth of Al-doped SiC.
1 Introduction
Silicon carbide (SiC), as a wide bandgap semiconductor material, possesses the advantages of a large bandgap, high thermal conductivity, high saturation electron drift mobility, strong radiation resistance, and excellent thermal stability and chemical stability, which exhibits outstanding potential for applications in high-temperature, high-frequency, and high-power electronic devices.1–4
The top-seeded solution growth (TSSG) method is a promising technique for the growth of large-size and high-quality SiC crystals with a low dislocation density under conditions approaching thermal equilibrium.5–7 Compared with the physical vapor transport method, the lower growth temperature in the TSSG technique offers enhanced potential for p-type doping.8,9 However, the solubility of carbon (C) in silicon melt (less than 1%) is insufficient to meet the demand for efficient crystal growth, therefore improving the C solubility is pivotal in TSSG research. Researchers have discovered that the C solubility can be significantly enhanced by introducing transition metal elements or rare earth elements into the silicon melt as a fluxing agent.10,11 For instance, Kawanishi et al.12 reported that using Si–Cr solvent could achieve the highest growth rate among the three solvent systems of Si–Ti, Si–Fe, and Si–Cr at the same temperature. Hyun et al.13 investigated the C solubility in Si0.56Cr0.4M0.04 (M = Al, Sc, Ti, V, Cr, etc.) solvents and found that the highest C solubility can reach 8.37 at% in Si0.56Cr0.4Co0.04 solvent.
The optimization of crucible design and process parameters can significantly enhance both the growth rate and uniformity.14,15 Recent advancements in computational fluid dynamics (CFD) have facilitated the achievement of this objective. For example, Li et al.16 employed numerical simulations to investigate the effect of crystal rotation on SiC crystal growth in TSSG technology and discovered that maintaining an intermediate rotational speed was advantageous for achieving a uniform and enhanced growth rate. The simulation conducted by Liu et al.17 suggests that a well-designed crucible could facilitate stable growth of 4-inch SiC ingots. The advent of machine learning technology has greatly facilitated the determination of optimal conditions for material processing. Numerous researchers have employed this technology in CFD simulations of the TSSG method, resulting in a significant reduction in calculation time.18 For instance, Takehara et al.19 utilized Bayesian optimization to determine the optimal state of magnetic field and seed rotation.
In the present study, a TSSG furnace was designed for 4-inch Al-doped SiC crystal growth. Numerical studies of the impact of solution radius and height, coil position, and rotational speed of the seed crystal on the flow structure and crystal growth rate were conducted. The concentration distribution of Al at the seed crystal surface and the evaporation of Al during growth were also investigated. Subsequently, the optimal growth conditions was explored through the back-propagation (BP) neural network and the double-objective non-dominated sorting genetic algorithm (NSGA-II).
2 Methods
2.1 Geometric model
The numerical simulation of TSSG growth is performed in COMSOL Multiphysics using the finite element method. The schematic diagram of the designed TSSG furnace is depicted in Fig. 1(a). A graphite crucible serves as both a container for the melt and a source of carbon, which is heated in a radio-frequency heating system with a frequency of 30 kHz and a heating current of 270 A. The initial position of the coil is set to “0 mm” in subsequent simulations, which is 40 mm above the bottom insulation. The solution with the chemical composition of Si0.58Cr0.4Al0.02 is chosen for the growth of Al-doped SiC. A 4-inch seed crystal is mounted on a rotating graphite rod and immersed into the solution with an approximate depth of 2 mm. The meshed TSSG model used in this study can be seen in Fig. 1(b). In the fluid domain, an extremely refined mesh has been employed to improve the accuracy of the fluid calculation. The fluid domain has a total of 79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 grids and the most refined grid-scale of 50 μm is set at the crystal–solution interface.
823 grids and the most refined grid-scale of 50 μm is set at the crystal–solution interface.
 |
| | Fig. 1 (a) Configuration of the designed TSSG furnace and (b) global mesh for the simulations. | |
2.2 Governing equation
The electromagnetic equation and heat transfer equation refer to the reported literature.20 The Si0.58Cr0.4Al0.02 solution is assumed to be an incompressible Newtonian liquid and the Boussinesq approximation is adopted. Besides, solute convection is disregarded due to the low C concentration within the solution.21 Free surface deformation caused by melt flow and meniscus effects is not considered in our model. The physical parameters of the Si0.58Cr0.4Al0.02 solution used in the simulation are derived from a previous study and given in Table 1.22 Under these assumptions, the governing equations for the fluid flow and mass transport in the solution are given as follows:| |  | (2) |
| | 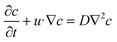 | (3) |
where u is the solution flow velocity, ρ is the density, p is the pressure, ν is the dynamic viscosity, FE represents the Lorentz force density, g is the gravitational acceleration, β is the thermal expansion coefficient, T is the temperature and Tref is the reference temperature. Finally, D and c are the diffusion coefficient and the concentration of C or Al in the solution, respectively. The diffusion coefficient of C and Al in the Si0.58Cr0.4Al0.02 solution can be calculated through the Stokes–Einstein equation:23| |  | (4) |
where kB is Boltzmann's constant and rsol is the radius of the solute atom.
Table 1 Parameters of the Si0.58Cr0.4Al0.02 solution used in the calculation22
| Parameter |
Value |
Units |
| Thermal conductivity |
−68.28 + 5.40 × 10−2 T |
W m−1 K−1 |
| Electrical conductivity |
2.21 × 106–2.80 × 109 T−1 |
S m−1 |
| Viscosity |
1.266 × 10−3 exp(1982 T−1) |
Pa s |
| Density |
5199–0.552 T |
kg m−3 |
| Surface tension |
1.195–1.23 × 10−4 T |
N m−1 |
| Heat capacity |
1196 |
J kg−1 K−1 |
| Emissivity |
0.28 |
|
The boundary conditions of the fluid domain are consistent with our previous work24 and can be briefly described as follows: the gas–liquid interface is simplified as a horizontal plane and Marangoni convection is applied to it; no-slip conditions are applied to all solid–liquid interfaces. The force convection induced by crystal rotation is achieved through the boundary condition of rotation speed at the seed–liquid interface:
where
vφ is the rotation speed,
ωseed is the angular velocity and
r is the rotation radius. In the solution growth of SiC, the carbon in the solution was supplied from the graphite crucible by dissolution. Therefore, C equilibrium concentration was used as the boundary condition for the solid–liquid interfaces:
25| |  | (6) |
where
ceq is the C equilibrium concentration,
xeq is the C molar fraction, which is the temperature dependence of C solubility derived from phase diagrams of the Si–Cr–C systems,
26 and
Msol and
ρsol are the molar mass and density of Si
0.58Cr
0.4Al
0.02 solution, respectively.
The dissolved C is transported to the surface of the seed crystal via convection and diffusion. The growth rate can be calculated from the diffusive flux of the C atom normal to the seed surface:27
| |  | (7) |
where
MSiC and
ρSiC are the molar mass and the density of 4H-SiC, and
n is the unit vector normal to the seed surface. To clarify the dissolution and crystallization of C in the solution, the supersaturation is defined as follows:
28| |  | (8) |
2.3 Optimization algorithm
To rapidly optimize the 4-inch TSSG conditions, a machine learning model was constructed. The parameters included the rotation speed of the graphite rod (ωs), the position of the coil (Z), the radius (R), and the height (H) of the solution. The BP neural network was applied to map the complex relationships between these parameters (ωs, Z, R, and H) and the target (average growth rate “Vag” and residual Al concentration after 10 h growth “RAl”). Subsequently, the NSGA-II was employed to determine the optimal process parameters for the 4-inch TSSG.29 A total of 1200 datasets were collected for training, validation, and testing, with parameter ranges detailed in Table 2. The number of hidden layers is two, with each hidden layer containing 15 neurons.
Table 2 Range of parameters for optimization
| Parameter |
Lower limit |
Upper limit |
Units |
| Rotation speed of seed crystal (ωs) |
0 |
30 |
rpm |
| Position of induction coil (Z) |
−40 |
30 |
mm |
| Radius of solution (R) |
70 |
115 |
mm |
| Height of solution (H) |
65 |
105 |
mm |
The BP neural network consists of two parts: signal propagation and error backpropagation. During signal propagation, the input layer receives and processes the input before transmitting it to the next layer for further processing until reaching the output layer. For error backpropagation, the difference between the output and target values is propagated backward, adjusting weights or thresholds to minimize errors and accurately representing the relationship between the input and target. The hidden layer is located between the input and output layers, transmitting information through weights and activation functions without direct interaction with inputs or outputs. The complexity of the model can be enhanced by incorporating additional hidden layers and neurons, albeit potentially leading to overfitting issues. Therefore, neural network design should be adjusted based on the specific task and dataset characteristics. The NSGA-II is a computational model that emulates the mechanisms of natural selection and genetic evolution, making it particularly effective in efficiently optimizing complex combinatorial problems.
3 Results and discussion
3.1 Effect of crystal rotation speed
The results presented in Fig. 2(a) and (b) indicate that, in the absence of seed rotation, the thermal buoyancy force significantly outweighs the electromagnetic force due to the utilization of a high frequency of 30 kHz. Therefore, a typical counterclockwise convective vortex caused by buoyancy and Marangoni convection can be observed in Fig. 2(c). It can be seen from Fig. 2(d) and (e) that the carbon dissolved from the walls of the graphite crucible is transported to the surface of the seed crystal (exhibiting a positive C supersaturation) and subsequently undergoes precipitation. The concentration of C in the solution exceeds 3300 mol m−3, significantly surpassing that found in a pure silicon solution. However, the crystal growth rate is low because the downward flow below the seed crystal hinders the transport of C. It should be noted that the growth rate around the seed edge is significantly higher in comparison to the central position (Fig. 2(f)) due to the intense Marangoni convection near the seed edge, resulting in a reduction in the thickness of the concentration layer and an increase in the concentration gradient.30 Consequently, the growth rate at the periphery of the seed is not taken into account in subsequent calculations.
 |
| | Fig. 2 In the case of no seed rotation: distribution of the (a) thermal buoyancy force and (b) electromagnetic force in solution; (c) velocity field in the solution; distribution of the (d) C concentration and (e) supersaturation in solution; (f) crystal growth rate along the growth interface. | |
The seed crystal rotation was employed to investigate the impact of forced convection on the growth rate and flow field. As depicted in Fig. 3(a), the highest temperature and the lowest temperature appear on the side wall of the crucible and the seed crystal respectively. The implementation of a crystal rotation speed of 5 rpm results in the generation of an upward flow beneath the seed crystal due to the influence of centrifugal force. As the rotational speed increases, the upward flow expands outward while the initial counterclockwise vortex gradually shrinks, as shown in Fig. 3(b)–(e). However, at a rotational speed of 30 rpm, the flow pattern changes due to the excessive forced convection (Fig. 3(f)). Consequently, the temperature of the free surface approaches that of the seed crystal, potentially leading to spontaneous nucleation on the free surface. The average growth rate and average C supersaturation at the free surface at different rotation speeds are summarized in Fig. 4. The implementation of crystal rotation significantly improves the growth rate by reducing the boundary layer thickness and increasing the carbon concentration gradient. At a low rotational speed of 5 rpm, the growth rate is low and the uniformity is poor, which is not conducive to stabilizing the crystal type. As the crystal rotation speed gradually increased to 30 rpm, the growth rate reduced instead. Because the seed temperature rise caused by the higher rotational speed hinders the crystallization of C. In addition, it is evident that an increase in rotational speed from 25 rpm to 30 rpm results in excessive C supersaturation at the free surface, potentially leading to the precipitation of SiC polycrystals and the deterioration of crystal quality.31,32 Consequently, too high a crystal rotational speed is not beneficial to the crystal growth.
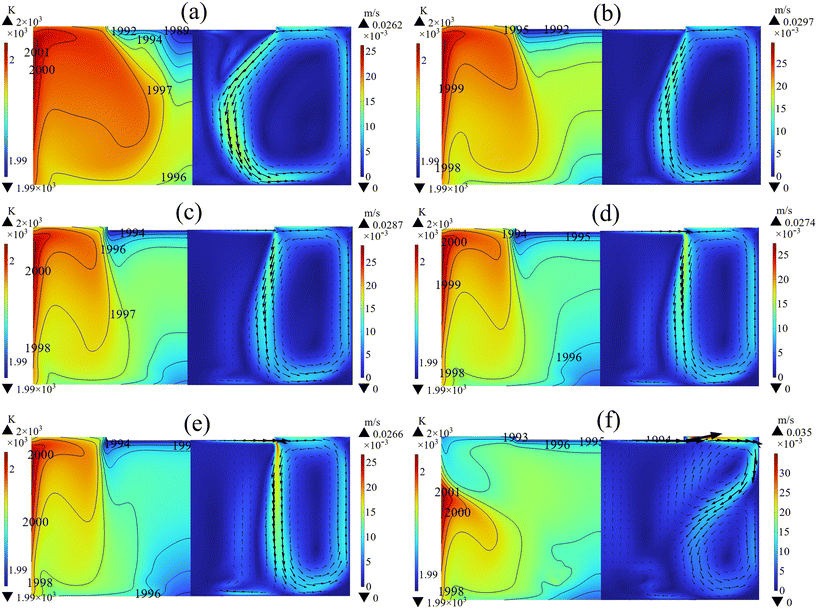 |
| | Fig. 3 Temperature distribution (left) and velocity field (right) in the solution with different crystal rotational speeds: (a) 5 rpm, (b) 10 rpm, (c) 15 rpm, (d) 20 rpm, (e) 25 rpm, and (f) 30 rpm. | |
 |
| | Fig. 4 Average growth rate and average C supersaturation at the free surface at different rotational speeds. The insets are crystal growth rate along the growth interface at 5 rpm (left) and supersaturation at 30 rpm (right), respectively. | |
3.2 Effect of coil height
The influence of coil position on the temperature field distribution in the solution is significant due to the variation of magnetic field density. As illustrated in Fig. 5, the solution temperature decreases as the coil descends, while the temperature difference increases. A small clockwise vortex emerges and gradually expands in the upper right corner of the solution. At a coil position of −15 mm (Fig. 5(d)), the small vortex merges with the forced convective vortex, resulting in a final flow pattern characterized by a double-vortex structure. Analysis of the free surface temperature in Fig. 5(e) reveals that the radial temperature profile follows a parabolic distribution and the emergence of the small clockwise vortex can be attributed to the intensified Marangoni effect.33 Based on the findings depicted in Fig. 5(f), it can be inferred that an excessively low coil position results in an excessive C supersaturation at the free surface, which ultimately leads to the precipitation of SiC polycrystals.
 |
| | Fig. 5 Distribution of supersaturation (left), temperature and solution flow velocity (right) at different coil relative heights with the rotation speed of 25 rpm: (a) 30 mm, (b) 15 mm, (c) 0 mm, and (d) −15 mm. The numbers above and below the color legend are the maximum and minimum values of the data; (e) temperature distribution along the free surface and (f) average growth rate and average C supersaturation at the free surface at different coil relative heights. | |
3.3 Effect of solution height and radius
In addition to the coil position, the radius and height of the solution also affect the internal temperature distribution and flow field structure. As depicted in Fig. 6, a smaller radius results in an elevated solution temperature and reduced supersaturation below the seed crystal. In the case of the 85 mm solution radius (Fig. 6(d)), forced convection plays a dominant role in the flow field, resulting in a diminished buoyancy convection vortex and an inappropriate flow pattern for crystal growth. It can be seen from Fig. 8(a) that an increase in the solution radius leads to a higher crystal growth rate. However, the expansion of the solution radius necessitates a larger graphite crucible, leading to elevated expenses. The solution height can be easily adjusted by manipulating the quantity of raw material added. As shown in Fig. 7, too low and too high solution height are both adverse to crystal growth. At the height of 55 mm, the small temperature difference results in a limited growth rate (Fig. 8(b)). Meanwhile, at the height of 145 mm, the clockwise convective vortex expands outward due to the intensification of Marangoni convection, leading to an excessive C supersaturation at the free surface. In conclusion, it is imperative to ensure that the radius and height of the solution are maintained within an appropriate range.
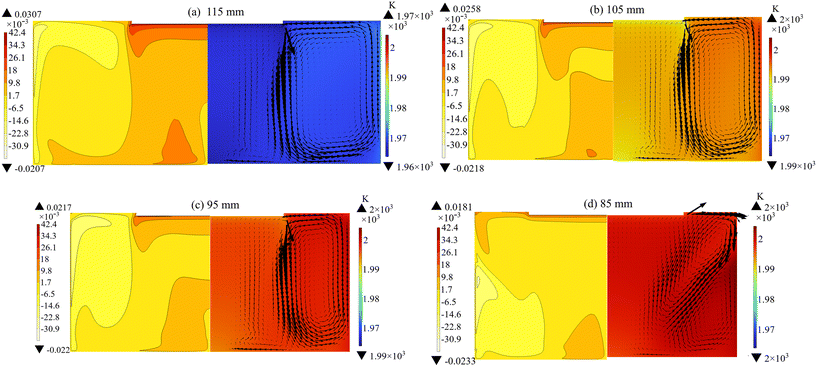 |
| | Fig. 6 Distribution of supersaturation (left), temperature, and solution flow velocity (right) at different solution radii with the rotation speed of 25 rpm: (a) 115 mm, (b) 105 mm, (c) 95 mm, and (d) 85 mm. | |
 |
| | Fig. 7 Distribution of supersaturation (left), temperature, and solution flow velocity (right) at different solution heights with the rotation speed of 25 rpm: (a) 145 mm, (b) 115 mm, (c) 85 mm, and (d) 55 mm. | |
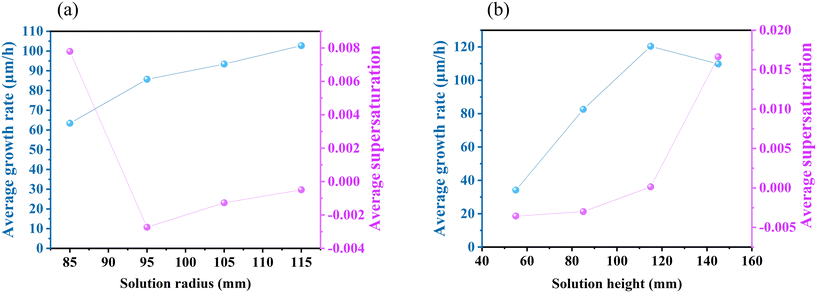 |
| | Fig. 8 Average growth rate and average C supersaturation at the free surface at different solution (a) radii and (b) heights with the rotation speed of 25 rpm. | |
3.4 Al concentration calculation
Compared to the physical vapor transport (PVT) method, the TSSG technique exhibits higher growth pressure and relatively lower temperature, thereby reducing Al volatilization during SiC crystal growth and facilitating the preparation of p-type SiC crystals.34 Al can significantly improve the crystal surface morphology and polytype stability in addition to acting as a dopant.35,36 The incorporation of Al into the crystal during growth and the evaporation of Al on the free surface are taken into account in our model, with an initial Al concentration set at 2000 mol m−3. Details of the boundary conditions are given below:
(1) Since this model does not consider the volume change of the crystal during growth, the solution volume is constant. To calculate the concentration of Al in the solution, the dynamic segregation process can be equivalent to the inward flux of Al on the seed-solution surface, which can be obtained as:37
where
k0 is the segregation coefficient of Al. Experimental results indicate that the segregation coefficient of Al in SiC is significantly low, so the term 1 −
k0 can be approximated to 1.
(2) The evaporation of Al at the free surface can be expressed by the Hertz–Knudsen flux equation, in which the saturated vapor pressure of Al in the solution and evaporation coefficient can be referenced from the literature.38
As depicted in Fig. 9, compared with its initial state, the Al concentration on the seed crystal surface decreases to approximately 1820 mol m−3 after 10 h. The Al concentration on the seed crystal surface exhibits a slight increase with the rise in rotational speed. Fig. 10 investigates variations in crystal growth rate and average Al concentration in solution with growth time by altering the applied heating currents from 240 A to 300 A. From Fig. 10(a), it can be inferred that the evaporation of Al is influenced by the temperature since the saturated vapor pressure of Al is inherently reliant on the temperature. The reduction of the heating current can effectively mitigate Al evaporation; however, it may also result in a decline in the growth rate (Fig. 10(b)).
 |
| | Fig. 9 (a) The distribution of Al concentration on the seed crystal surface after 10 h growth and (b) the change of average Al concentration in solution with growth time at different rotational speeds. | |
 |
| | Fig. 10 (a) The change of average Al concentration in solution with the growth time and (b) the crystal growth rate at different heating currents. The corresponding growth temperature is shown in parentheses. | |
3.5 Parameter optimization
To meet the requirements of p-type growth, it is crucial to attain a high crystal growth rate and ensure a low Al volatilization rate. Undoubtedly, exploring appropriate growth conditions solely through the CFD simulation poses a formidable challenge. The utilization of machine learning can streamline this procedure and reduce the time required. Given the complex non-linear relationships between the growth parameters (ωs, Z, R, and H) and the targets (Vag and RAl), the BP neural network and NSGA-II were applied to determine the optimal variable parameters for the 4-inch TSSG conditions. Given that the NSGA-II is designed for solving minimum value problems, we define the objective function as y(x1) = −Vag and y(x2) = −RAl. The final objective is to identify a solution that fulfills all the requirements while minimizing deviations from the minimum values of each goal, thereby maximizing both Vag and RAl. As shown in Fig. 11(a) and (b), the plot points are almost concentrated on the straight red line (correlation coefficient = 1), indicating that the trained neural network model is sufficiently precise to explore optimal crystal growth conditions. Subsequently, the model obtained the relationship between the parameters and the targets, as shown in Fig. 11(c)–(f).
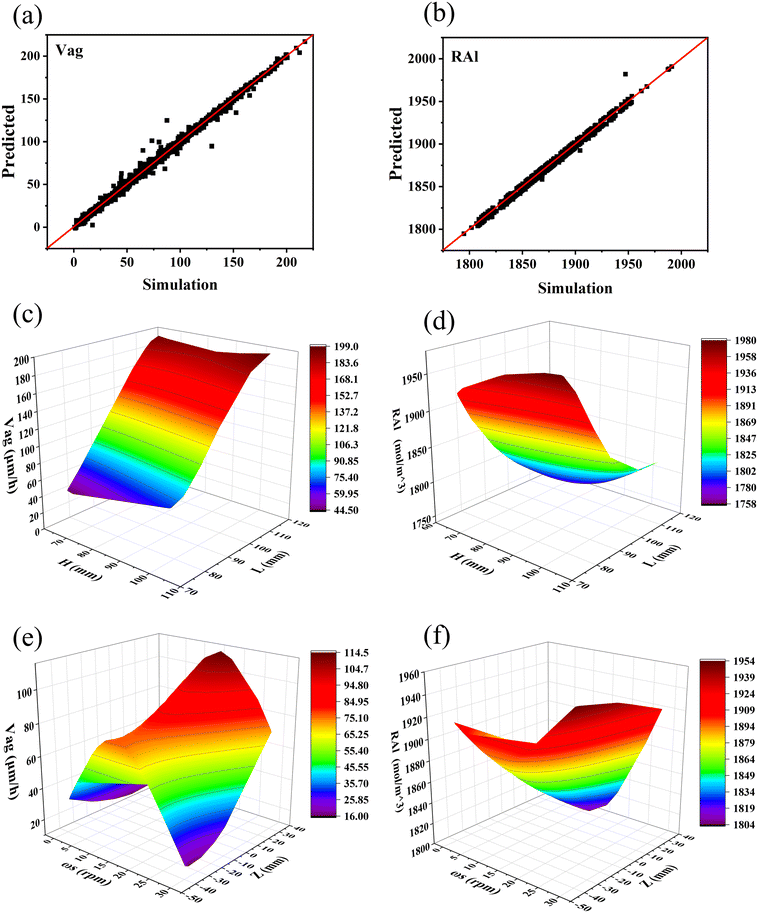 |
| | Fig. 11 Parity plots of (a) Vag and (b) RAl for the test data; the H and L dependence of (c) Vag and (d) RAl; the ωs and Z dependence of (e) Vag and (f) RAl. | |
The objectives in a multi-objective optimization problem constrain each other, potentially sacrificing the performance of one objective for the improvement of another. It is impossible to find a solution that optimizes all objectives simultaneously. Therefore, the solution typically consists of a set of non-inferior solutions known as the Pareto front solutions (a solution set that is not dominated by any other solution). In double objective optimization, if the two objective values of solution A are better than solution B, it is defined that solution A dominates solution B; otherwise, A and B are not dominated by each other. The Pareto front solutions are situated at the periphery of the solution set, thus rendering them the optimal solutions.39
After hundreds of iterations, the Pareto front solutions for the ultimate generation are illustrated in Fig. 12(a). The optimized RAl value demonstrates a significantly high level (1750–1980 mol m−3), which indicates a low Al loss, while the growth rate varies from 0 to 255 μm h−1. As shown by the intersection of two dashed lines in the figure, a candidate of RAl = 1800 mol m−3 was selected to ensure that the growth rate meets the production requirements. The average growth rate under these growth conditions (ωs = 20 rpm, Z = −37 mm, R = 115 mm, and H = 78 mm) can reach 236 μm h−1. It can be seen in Fig. 12(b) that the flow pattern under the optimal parameters is appropriate. The temperature and supersaturation of the solution adjacent to the crucible wall exhibit the highest values, whereas those beneath the seed crystal demonstrate the lowest values, thereby satisfying the requirements of TSSG. As depicted in the three-dimensional Al concentration distribution diagram (Fig. 13(a)), under the optimal growth conditions, Al concentration dropped to approximately 1800 mol m−3 after 10 hours of growth, a decrease of only 10 percent compared to the initial concentration. It can be seen in Fig. 13(b) that less Al evaporation is achieved due to the low growth temperature without compromising the growth rate at the optimal growth parameters, which facilitates p-type doping.
 |
| | Fig. 12 (a) The Pareto front solutions for the final generation (the point of intersection between two perpendicular dotted lines represents the selected candidate solution); (b) distribution of supersaturation (left), temperature, and solution flow velocity (right) under the optimal parameters. | |
 |
| | Fig. 13 (a) The distribution of Al concentration in solution after 10 h growth; (b) comparison of the optimal growth parameters with initial parameters. | |
4 Conclusions
This paper established a global numerical model of heat and mass transfer for the TSSG system. The effects of growth parameters on the flow pattern, carbon transport, and crystal growth rate were investigated. The findings indicate that elevated rotation speeds, increased solution heights, reduced solution radii, and lower coil positions may facilitate the precipitation of SiC polycrystals on the free surface; conversely, diminished rotation speeds, decreased solution heights, and higher coil positions are associated with a reduced growth rate. The Al concentration in the solution was calculated considering the evaporation of Al on the free surface. To further optimize the growth conditions, abundant transient calculations were conducted to prepare the dataset for the BP neural network to extract the relationship between growth parameters and targets, and then the double objective NSGA-II was applied to predict the maximum targets and determine the optimal parameters. The results demonstrate that following 10 hours of growth, the concentration of Al in the solution decreased by a mere 10%. Compared with the initial condition, the Al evaporation under the optimized conditions was significantly inhibited without compromising the growth rate. It is concluded that machine learning and genetic algorithms can be effectively utilized in the development of a TSSG system for the rapid growth of Al-doped SiC in future applications.
Data availability
Data for this article are available at zenodo at https://doi.org/10.5281/zenodo.13756050.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is supported by the “Pioneer” and “Leading Goose” R&D Program of Zhejiang Province (Grant No. 2022C01021, 2023C01010), the National Natural Science Foundation of China (Grant No. 52202189, 61721005), the Hangzhou Joint Funds of the Zhejiang Provincial Natural Science Foundation of China (LHZSD24E020001), the Leading Innovative and Entrepreneur Team Introduction Program of Hangzhou (Grant No. TD2022012), and the Qianjiang Distinguished Experts Program of Hangzhou.
References
- C. E. Weitzel, J. W. Palmour, C. H. Carter, K. Moore, K. K. Nordquist, S. Allen, C. Thero and M. Bhatnagar, IEEE Trans. Electron Devices, 1996, 43, 1732–1741 CrossRef CAS.
- J. B. Casady and R. W. Johnson, Solid-State Electron., 1996, 39, 1409–1422 CrossRef.
- S. Yang, X. Liang, J. Cui, Q. Zheng, J. Sun, M. Liu, D. Zhang, H. Feng, X. Yu, C. Xiang, Y. Li and Q. Guo, J. Semicond., 2021, 42, 082802 CrossRef CAS.
- R. Tian, C. Ma, J. Wu, Z. Guo, X. Yang and Z. Fan, J. Semicond., 2021, 42, 061801 CrossRef CAS.
- Y. Yamamoto, S. Harada, K. Seki, A. Horio, T. Mitsuhashi, D. Koike, M. Tagawa and T. Ujihara, Appl. Phys. Express, 2014, 7, 065501 CrossRef CAS.
- K. Murayama, T. Hori, S. Harada, S. Xiao, M. Tagawa and T. Ujihara, J. Cryst. Growth, 2017, 468, 874–878 CrossRef CAS.
- D. H. Hofmann and M. H. Müller, Mater. Sci. Eng., B, 1999, 61–62, 29–39 CrossRef.
- T. Shirai, K. Danno, A. Seki, H. Sakamoto and T. Bessho, Mater. Sci. Forum, 2014, 778–780, 75–78 CAS.
- T. Mitani, N. Komatsu, T. Takahashi, T. Kato, S. Harada, T. Ujihara, Y. Matsumoto, K. Kurashige and H. Okumura, J. Cryst. Growth, 2015, 423, 45–49 CrossRef CAS.
- K. Kamei, K. Kusunoki, N. Yashiro, N. Okada, T. Tanaka and A. Yauchi, J. Cryst. Growth, 2009, 311, 855–858 CrossRef CAS.
- K. Kusunoki, Y. Kishida and K. Seki, Mater. Sci. Forum, 2019, 963, 85–88 Search PubMed.
- S. Kawanishi, Y. Nagamatsu, T. Yoshikawa and H. Shibata, J. Cryst. Growth, 2020, 549, 125877 CrossRef CAS.
- K. Y. Hyun, T. Taishi, K. Suzuki and K. Teshima, Mater. Sci. Forum, 2018, 924, 43–46 Search PubMed.
- K. Kusunoki, N. Okada, K. Kamei, K. Moriguchi, H. Daikoku, M. Kado, H. Sakamoto, T. Bessho and T. Ujihara, J. Cryst. Growth, 2014, 395, 68–73 CrossRef CAS.
- T. Horiuchi, L. Wang, A. Sekimoto, Y. Okano, T. Yamamoto, T. Ujihara and S. Dost, Cryst. Res. Technol., 2019, 54, 1900014 CrossRef.
- F. Li, L. He, Z. Yan, X. Qi, W. Ma, J. Chen, Y. Xu and Z. Hu, J. Cryst. Growth, 2023, 607, 127112 CrossRef CAS.
- B. Liu, Y. Yu, X. Tang and B. Gao, J. Cryst. Growth, 2020, 533, 125406 CrossRef CAS.
- Y. Dang, C. Zhu, M. Ikumi, M. Takaishi, W. Yu, W. Huang, X. Liu, K. Kutsukake, S. Harada, M. Tagawa and T. Ujihara, CrystEngComm, 2021, 23, 1982–1990 RSC.
- Y. Takehara, A. Sekimoto, Y. Okano, T. Ujihara and S. Dost, J. Cryst. Growth, 2020, 532, 125437 CrossRef CAS.
- M. T. Ha, Y. J. Yu, Y. J. Shin, S. Y. Bae, M. H. Lee, C. J. Kim and S. M. Jeong, RSC Adv., 2019, 9, 26327–26337 RSC.
- T. Umezaki, D. Koike, S. Harada and T. Ujihara, Jpn. J. Appl. Phys., 2016, 55, 125601 CrossRef.
- H. Daikoku, S. Kawanishi, T. Ishikawa and T. Yoshikawa, J. Chem. Thermodyn., 2021, 160, 106476 CrossRef CAS.
- C. C. Miller, Proc. R. Soc. Lond. Ser. A-Contain. Pap. Math. Phys. Character, 1924, 106, 724–749 CAS.
- Z. R. Sui, L. B. Xu, C. Cui, R. Wang, X. D. Pi, D. R. Yang and X. F. Han, CrystEngComm, 2024, 26, 1022–1031 RSC.
- T. Horiuchi, L. Wang, A. Sekimoto, Y. Okano, T. Ujihara and S. Dost, J. Cryst. Growth, 2019, 517, 59–63 CrossRef CAS.
- K. Hyun, S. J. Kim and T. Taishi, Acta Phys. Pol., A, 2019, 135, 1012–1017 CrossRef CAS.
- L. Wang, A. Sekimoto, Y. Takehara, Y. Okano, T. Ujihara and S. Dost, Crystals, 2020, 10, 791 CrossRef CAS.
- B. Liu, Y. Yu, X. Tang and B. Gao, J. Cryst. Growth, 2019, 527, 125248 CrossRef CAS.
- B. Xu, X. Han, S. Xu, D. Yang and X. Pi, J. Cryst. Growth, 2023, 614, 127238 CrossRef CAS.
- T. Yamamoto, Y. Okano, T. Ujihara and S. Dost, J. Cryst. Growth, 2017, 470, 75–88 CrossRef CAS.
- Y. Shin, T. Park, S. Bae and S. Jeong, J. Korean Cryst. Growth Cryst. Technol., 2019, 29, 294–297 Search PubMed.
- Y. Tsunooka, N. Kokubo, G. Hatasa, S. Harada, M. Tagawa and T. Ujihara, CrystEngComm, 2018, 20, 6546–6550 RSC.
- F. Mercier, J.-M. Dedulle, D. Chaussende and M. Pons, J. Cryst. Growth, 2010, 312, 155–163 CrossRef CAS.
- G. Wang, D. Sheng, Y. Yang, Z. Zhang, W. Wang and H. Li, Cryst. Growth Des., 2024, 24, 5686–5692 CrossRef CAS.
- K. Suzuki and T. Taishi, Jpn. J. Appl. Phys., 2020, 59, 025504 CrossRef CAS.
- N. Komatsu, T. Mitani, Y. Hayashi, T. Kato, S. Harada, T. Ujihara and H. Okumura, J. Cryst. Growth, 2017, 458, 37–43 CrossRef CAS.
- X. Han, X. Liu, S. Nakano and K. Kakimoto, J. Cryst. Growth, 2020, 545, 125752 CrossRef CAS.
- Y. Dang, C. Zhu, X. Liu, W. Yu, X. Liu, K. Suzuki, T. Furusho, S. Harada, M. Tagawa and T. Ujihara, J. Cryst. Growth, 2022, 579, 126448 CrossRef CAS.
- K. Deb, A. Pratap, S. Agarwal and T. Meyarivan, IEEE Trans. Evol. Comput., 2002, 6, 182–197 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  a,
Xuefeng
Han
a,
Xuefeng
Han
 *ab,
Yuanchao
Huang
ab,
Binjie
Xu
*ab,
Yuanchao
Huang
ab,
Binjie
Xu
 ab,
Yanwei
Yang
ab,
Deren
Yang
ab,
Yanwei
Yang
ab,
Deren
Yang
 ab and
Xiaodong
Pi
ab and
Xiaodong
Pi
 *ab
*ab
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 823 grids and the most refined grid-scale of 50 μm is set at the crystal–solution interface.
823 grids and the most refined grid-scale of 50 μm is set at the crystal–solution interface.