Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Topological sorting of magnetic colloidal bipeds†
Aneena Rinu
Perayil
 a,
Piotr
Kuświk
a,
Piotr
Kuświk
 b,
Maciej
Urbaniak
b,
Maciej
Urbaniak
 b,
Feliks
Stobiecki
b,
Feliks
Stobiecki
 b,
Sapida
Akhundzada
c,
Arno
Ehresmann
b,
Sapida
Akhundzada
c,
Arno
Ehresmann
 c,
Daniel
de las Heras
c,
Daniel
de las Heras
 d and
Thomas M.
Fischer
d and
Thomas M.
Fischer
 *a
*a
aExperimentalphysik X, Physikalisches Institut, Universität Bayreuth, D-95440 Bayreuth, Germany. E-mail: thomas.fischer@uni-bayreuth.de
bInstitute of Molecular Physics, Polish Academy of Sciences, 60-179 Poznań, Poland
cInstitute of Physics and Center for Interdisciplinary Nanostructure Science and Technology (CINSaT), Universität Kassel, D-34132 Kassel, Germany
dTheoretische Physik II, Physikalisches Institut, Universität Bayreuth, D-95440 Bayreuth, Germany
First published on 10th March 2025
Abstract
Topologically nontrivial adiabatic loops of the orientation of a homogeneous external magnetic field drive the walking of paramagnetic colloidal bipeds above a deformed quasi-periodic magnetic square pattern. Depending on the topological properties of the loop we can simultaneously control the walking directions of colloidal bipeds as a function of their size and as a function of the size of a deformed unit cell of the pattern. The bipeds walk performing steps with their two feet alternatingly grounding one foot and lifting the other. The step width of the bipeds is given by a set of winding numbers (wx, wy) ∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 2 – a set of topological invariants – that can only change by integers as we continuously increase the length of the bipeds. We experimentally use this discrete size dependence for the robust sorting of bipeds according to their length.
2 – a set of topological invariants – that can only change by integers as we continuously increase the length of the bipeds. We experimentally use this discrete size dependence for the robust sorting of bipeds according to their length.
1. Introduction
In a first step, sorting classifies a set of objects into disjunct categories that are determined by the properties of the objects. In a second step, subsets of objects falling into one category are transported to a region in space reserved for one category thereby being separated in space from objects belonging to other categories. The properties of the objects can be discrete. For example, in the Golgi apparatus different proteins are sorted and packed into vesicles for transport to various destinations within the cell.1 On the cellular scale, during the embryo genesis the cells differentiate and move toward their correct location.2,3 The objects properties can also be continuous such as the length,4 the width,5 and the size6–11 among others.11–14 In the continuous case, categories are intervals and the interval boundaries are bifurcation points between different discrete categories. Sorting objects with a computer algorithm is a serial or weakly parallel process, while the separation of chemicals via electrophoresis is a massive parallel process. Massive parallel processes allow for high-throughput sorting.15 Active sorting16–19 occurs when self propelled objects sort themselves. Active sorting is usually more robust than passive sorting.20,21 Microfluidic sorting devices often rely on optical,22 steric23 patterns that guide specific particles along different conduits. In biology one tries to understand sorting mechanisms – originally developed via evolution – by analyzing whether the sorting persists or not after applying all kinds of perturbations.24–27Analytical24–27 as well as machine learning28,29 approaches try to identify and exploit how a preexisting sorting mechanism works. Synthetic approaches are used to construct a sorting process by having understood a priori how it works. Here we follow a synthetic path to generate a sorting device for colloidal bipeds of different length from first principles. Knowing the mathematical laws that govern the transport of colloidal bipeds30–32 we design a magnetic pattern and a modulation that forces the sorting of colloidal bipeds according to their length using external commands.
The mathematical principles that govern the transport are of topological nature, that is, the transport is fully controlled by a set of topological invariants. We have used those topological laws to robustly transport paramagnetic and diamagnetic colloids on periodic patterns,33–35 to independently transport them into different directions,33,34 to simultaneously write different letters,30 or to walk in a time reversal or non-time reversal way.36 We have induced skipping orbits at the edge of topologically distinct37 and topologically equivalent38 lattices. We have generalized this topological concept to non-periodic metamorphic patterns that are locally but not globally periodic39 and used the concept to synthesize colloidal assemblies called bipeds of a desired length on a hexagonal pattern with constant lattice constant but varying symmetry phase32 and to cloak certain regions against colloidal trespassers.40 In this work we show that a metamorphic square pattern with varying lattice constant and a magnetic driving loop with a mirror symmetry different from ref. 32 can force the colloids to automatically fulfill a new task compared to those reported in ref. 30–40: different length colloidal bipeds sort themselves. This requires them not only to separate but additionally to walk to predefined attractor locations differing for each different biped length.
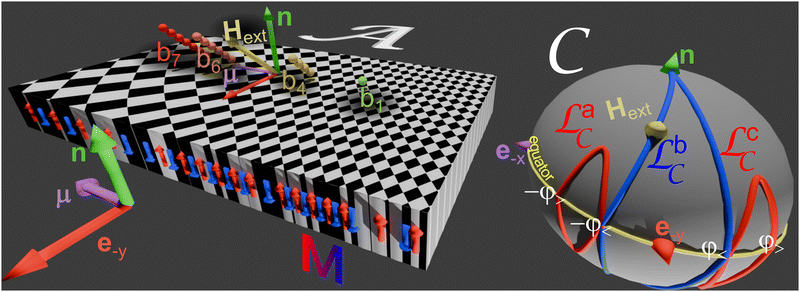
2. Setup
Paramagnetic colloidal particles (diameter d = 2.8 μm) immersed in water are placed on top of a two-dimensional magnetic pattern. The pattern is a deformed square lattice of alternating regions with positive and negative magnetization relative to the direction normal to the pattern, see Fig. 1. For our thin film we choose a pattern with magnetization | (1) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) is the two dimensional vector in action space
is the two dimensional vector in action space ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) , which is the plane parallel to the pattern where the colloids move. The modulus of the saturation magnetization is denoted by Ms, h is the thickness of the film, n is the vector normal to the film, the z coordinate runs in direction of n. The vectors qi = qRiπ/2·ex, (i = 0, 1), are two coplanar primitive reciprocal unit vectors of common modulus q, and Rπ/2 is an anticlockwise rotation matrix around the normal vector n by π/2. In previous work30,34–36 we have fixed the modulus (∇
, which is the plane parallel to the pattern where the colloids move. The modulus of the saturation magnetization is denoted by Ms, h is the thickness of the film, n is the vector normal to the film, the z coordinate runs in direction of n. The vectors qi = qRiπ/2·ex, (i = 0, 1), are two coplanar primitive reciprocal unit vectors of common modulus q, and Rπ/2 is an anticlockwise rotation matrix around the normal vector n by π/2. In previous work30,34–36 we have fixed the modulus (∇![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) q = 0) and the pattern was a periodic square pattern of fixed period a = 2π/q.
q = 0) and the pattern was a periodic square pattern of fixed period a = 2π/q.
Rendering the modulus, q(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ), a function of action space (r
), a function of action space (r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ∈
∈ ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) breaks the discrete translational symmetry. Here we use a modulus
) breaks the discrete translational symmetry. Here we use a modulus
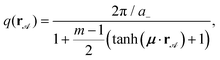 | (2) |
 | ||
| Fig. 2 Magnetic pattern (top view). The magnetization of the pattern follows eqn (1) with the modulus given by eqn (2). The larger lattice constant is a+ = 21 μm, the magnification factor is m = 3 (a− = 7 μm), and the transition length is ξ = 75 μm. | ||
A uniform time-dependent external field Hext of constant magnitude Hext = 3.5 kA m−1 is superimposed to the non-uniform time-independent magnetic field generated by the pattern. The strong external field induces strong dipolar interactions between the colloidal particles which respond by self-assembling into rods of n = 2–10 particles with length bn = nd. The two ends of the rod are called the feet and when the rods start to walk we call them bipeds.
The orientation of the external field changes adiabatically along a closed loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) sort
sort![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) (Fig. 1). We call the set of possible external field orientations the control space
(Fig. 1). We call the set of possible external field orientations the control space ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) , represented by a sphere in Fig. 1.
, represented by a sphere in Fig. 1.
3. Periodic pattern
On top of a periodic pattern, where ∇![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) q = 0, despite the field returning to its initial direction, single colloidal particles and bipeds can be topologically transported by one unit cell after completion of one loop.30,33,35 The current section summarizes our previous work on the transport on periodic patterns30,33,35 that already allowed us to separate bipeds by moving them into different directions but did not allow us to sort them to a final destination.
q = 0, despite the field returning to its initial direction, single colloidal particles and bipeds can be topologically transported by one unit cell after completion of one loop.30,33,35 The current section summarizes our previous work on the transport on periodic patterns30,33,35 that already allowed us to separate bipeds by moving them into different directions but did not allow us to sort them to a final destination.
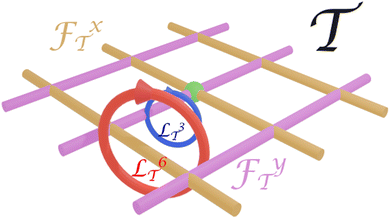
The orientation of the biped is locked to that of the external field with the northern foot being a magnetic north pole and the southern foot being a south pole. Let bn denote the vector from the northern foot to the southern foot of a biped of length bn. We call the three-dimensional vector space spanned by the end to end vectors bn of the bipeds the transcription space ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) . While the control space
. While the control space ![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) has units of a magnetic field, transcription space
has units of a magnetic field, transcription space ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) has units of a length. The loop
has units of a length. The loop  is a transcription of the control loop
is a transcription of the control loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) onto a sphere of radius bn in transcription space
onto a sphere of radius bn in transcription space ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) . The transport occurs provided that the transcribed loop
. The transport occurs provided that the transcribed loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) n
n![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) winds around specific fences
winds around specific fences ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) x
x![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and
and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) y
y![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) in transcription space.30 These fences are parallel lines along the ey and ex directions equally spaced in
in transcription space.30 These fences are parallel lines along the ey and ex directions equally spaced in ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) by the lattice period a of the periodic pattern in action space
by the lattice period a of the periodic pattern in action space ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) . The central fence lines pass through the origin of transcription space
. The central fence lines pass through the origin of transcription space ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) . If the transcribed loop
. If the transcribed loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) n
n![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) winds around the
winds around the ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) x
x![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and
and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) y
y![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) lines with winding numbers wnx(
lines with winding numbers wnx(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) n
n![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) ∈
) ∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) and wny(
and wny(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) n
n![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) ∈
) ∈ ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) the biped is topologically transported by
the biped is topologically transported by
Δr![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = a(wnxex + wnyey). = a(wnxex + wnyey). | (3) |
Fig. 3 shows two transcriptions ![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 3 and
3 and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) 6 of the same loop
6 of the same loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) with different winding numbers around the fences
with different winding numbers around the fences ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) x
x![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) and
and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) y
y![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) in transcription space
in transcription space ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) . The winding number wx3 = 0 and hence a biped of length b3 will not be transported by the loop
. The winding number wx3 = 0 and hence a biped of length b3 will not be transported by the loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) , while the winding number wx6 = 1 and therefore a biped of length b6 will be transported by the displacement Δr
, while the winding number wx6 = 1 and therefore a biped of length b6 will be transported by the displacement Δr![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = aex.
= aex.
4. Non-periodic pattern
Due to the topological nature of the transport, eqn (3) remains valid for small deformations of the periodic pattern. We have shown that eqn (3) is invariant under rotations39 and under conformal transformations40 of the pattern and invariant under modulations of the symmetry phase of patterns with three fold symmetry.32 We therefore expect the displacement on top of a deformed non-periodic four fold pattern with varying lattice constant ∇![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) q ≠ 0 to be expressed by the same eqn (3), provided that the deformation is locally small. That is:
q ≠ 0 to be expressed by the same eqn (3), provided that the deformation is locally small. That is:Δr![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) = a(r = a(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) )(wnx(r )(wnx(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) )ex + wny(r )ex + wny(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) )ey), )ey), | (4) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) the local value of the lattice constant at the position r
) the local value of the lattice constant at the position r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) , and with local fences lines in transcription space
, and with local fences lines in transcription space ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) x
x![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (r
(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) and
) and ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) y
y![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) (r
(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) now being parallel lines along the ey and ex direction equally spaced by the local lattice constant a(r
) now being parallel lines along the ey and ex direction equally spaced by the local lattice constant a(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) of the non-periodic pattern in action space
) of the non-periodic pattern in action space ![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) . The loop
. The loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) n
n![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) is independent of the location r
is independent of the location r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) of the biped on the pattern. However the fences change with the biped location r
of the biped on the pattern. However the fences change with the biped location r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) and so do the winding numbers of the fixed loop around the varying fences. It is for this reason that the winding numbers and thus the displacement of a fixed loop
and so do the winding numbers of the fixed loop around the varying fences. It is for this reason that the winding numbers and thus the displacement of a fixed loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif)
![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) causes different transport for different biped length bn as well as for different locations r
causes different transport for different biped length bn as well as for different locations r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) .
.
5. Sorting loop
We test the validity of eqn (4) using a sorting loop![[script L]](https://www.rsc.org/images/entities/char_e144.gif) sort
sort![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) =
= ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) a
a![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ×
× ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) b
b![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ×
× ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) c
c![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) being the concatenation of three fundamental loops
being the concatenation of three fundamental loops ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) a
a![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ,
, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) b
b![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) , and
, and ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) c
c![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) . We present
. We present ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) sort
sort![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) in Fig. 1. We call a fundamental loop a loop that crosses the equator of control space twice: once at time t↑ up from the southern hemisphere to the northern hemisphere at an external field Hext(t↑) and once at time t↓ down from the northern hemisphere to the southern hemisphere at an external field Hext(t↓). The angle of the crossing field direction to the reciprocal unit vector q1 is given by qHext
in Fig. 1. We call a fundamental loop a loop that crosses the equator of control space twice: once at time t↑ up from the southern hemisphere to the northern hemisphere at an external field Hext(t↑) and once at time t↓ down from the northern hemisphere to the southern hemisphere at an external field Hext(t↓). The angle of the crossing field direction to the reciprocal unit vector q1 is given by qHext![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin(ψ↑↓) = (q1 × Hext(t↑↓))·n. We choose a loop
sin(ψ↑↓) = (q1 × Hext(t↑↓))·n. We choose a loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) sort
sort![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) with the three pairs of equator crossing angles ψa↑,ψa↓,ψb↓,ψb↑,ψc↑, and ψc↓ that may be described by the two angles φ< and φ> as indicated in Table 1 (see also Fig. 1). Due to the symmetric choice of the angles, the winding number around the
with the three pairs of equator crossing angles ψa↑,ψa↓,ψb↓,ψb↑,ψc↑, and ψc↓ that may be described by the two angles φ< and φ> as indicated in Table 1 (see also Fig. 1). Due to the symmetric choice of the angles, the winding number around the ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) y
y![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) -fences vanishes irrespective of the length of the biped wny(
-fences vanishes irrespective of the length of the biped wny(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) sort
sort![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ) = 0 and we expect no topological transport along the y-direction.
) = 0 and we expect no topological transport along the y-direction.
6. Experimental results
We define a parameter λ to characterize the sorting loop as λ(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) sort
sort![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) ) = sin
) = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ>/(2
φ>/(2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ<). Due to the symmetric choice of the sorting loop, λ is the only relevant loop parameter determining the winding numbers. We have performed experiments using sorting loops with λ = 0.67, 0.76, 0.84, and 1.17 that sort bipeds of size b3−b8 with single particle diameter d = 2.8 μm on top of the pattern depicted in Fig. 2. Fig. 4 shows an overlay of microscopy images of the pattern covered with bipeds subject to a sorting loop with λ = 0.84 at different times together with trajectories of those bipeds obtained via particle tracking. Single particles, n = 1 (red), and doublets n = 2, are traveling one unit cell per loop in the positive x-direction, i.e., toward the unit cells of smaller size a−. The travel direction of larger bipeds (n > 2) depends on the location on the pattern. For each biped size bn there is a set of attractor lines
φ<). Due to the symmetric choice of the sorting loop, λ is the only relevant loop parameter determining the winding numbers. We have performed experiments using sorting loops with λ = 0.67, 0.76, 0.84, and 1.17 that sort bipeds of size b3−b8 with single particle diameter d = 2.8 μm on top of the pattern depicted in Fig. 2. Fig. 4 shows an overlay of microscopy images of the pattern covered with bipeds subject to a sorting loop with λ = 0.84 at different times together with trajectories of those bipeds obtained via particle tracking. Single particles, n = 1 (red), and doublets n = 2, are traveling one unit cell per loop in the positive x-direction, i.e., toward the unit cells of smaller size a−. The travel direction of larger bipeds (n > 2) depends on the location on the pattern. For each biped size bn there is a set of attractor lines  along the y-direction separated by separatrixes rs,n
along the y-direction separated by separatrixes rs,n![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) . For initial positions r
. For initial positions r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) in the region between two adjacent separatrixes all bipeds of size bn are attracted toward the attractor line
in the region between two adjacent separatrixes all bipeds of size bn are attracted toward the attractor line  between both seperatrixes. On either side of the attractor line after each application of the sorting loop the bipeds perform a step by one, two or more unit cells closer to the attractor line. At the attractor line after each application of the sorting loop, bipeds step from one side of the attractor line toward the other side of the line. This essentially makes the bipeds stop to move after reaching the attractor line.
between both seperatrixes. On either side of the attractor line after each application of the sorting loop the bipeds perform a step by one, two or more unit cells closer to the attractor line. At the attractor line after each application of the sorting loop, bipeds step from one side of the attractor line toward the other side of the line. This essentially makes the bipeds stop to move after reaching the attractor line.
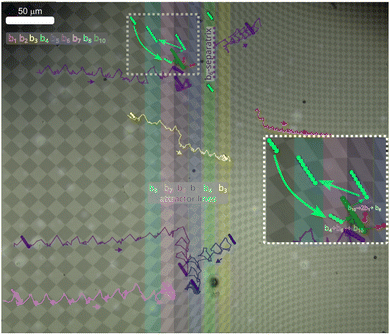 | ||
| Fig. 4 Sorting experiments. Overlay of several microscopy images of bipeds at different times above the sorting pattern, together with trajectories of bipeds of different length bn subject to the repeated sorting loop with sorting parameter λ = 0.84. The trajectories are colored according to the biped length as indicated in the image. The magnified dotted square region shows a biped reaction b4 + b6 → b10 → b8 + 2b1 and the resorting of the resulting b8-biped. Supplementary movie 1 (ESI†) provides a dynamic impression of the sorting process. Supplementary movie 2 (ESI†) shows the sorting of a b7-biped that is missing in the experiment shown in this figure. | ||
Far away from the symmetry line, y = 0, the unit cells of the pattern are sheared. A shear is a superposition of an extension and a rotation. The rotation of cells in action space also rotates the direction of the fence lines in transcription space. This also causes transport into the y-direction, of bipeds residing in the transition region further away from the symmetry line (see e.g. the b5- and the b6-trajectories in the lower part of Fig. 4).
Because the attractor line depends on the length bn of the biped, all bipeds are essentially sorted to their individual attractor line. In Fig. 4 we also see a non-sorted b6-biped to the right of the b6-separatrix walking away from the separatrix toward a second b6-attractor line, with  , that does not exist on the current pattern since the lattice constant does not shrink below the minimum lattice constant of a−.
, that does not exist on the current pattern since the lattice constant does not shrink below the minimum lattice constant of a−.
Eventually a walking biped of length bm, can collide with a sorted and therefore no longer walking biped of larger length bn with n > m to form a longer biped of length bn+m. The attractor line for the bn+m-biped is different from both attractor lengths of the bipeds prior to the collision. Hence, they are sorted to their new attractor line after the collision. The inset of Fig. 4 is a magnification of the dotted squared region of the main figure. There we see a b6-biped already sorted to its attractor line. A not yet sorted b4-biped while walking to its attractor line collides with the sorted b6 biped an initiates an addition reaction b4 + b6 → b10. The resulting b10-biped loses two single colloidal particles, i.e. b10 → b8 + 2b1 leaving a non-sorted b8 behind that is then sorted toward its attractor line by moving into the −x direction. Supplementary movie 1 (ESI†) shows the sorting of bipeds of length b3, b4, b5, b6 and b8 and the resorting after a biped addition reaction of Fig. 4. Supplementary movie 2 (ESI†) shows the sorting of bipeds of length b7 toward its attractor line. Note that Supplementary movie 1 and 2 (ESI†) are speeded up by a factor of 50 and 70, respectively.
7. Winding number
The winding number around the family of![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) x
x![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) fence lines depends on the sorting loop parameter λ and the biped length measured in units of the local lattice constant β(r
fence lines depends on the sorting loop parameter λ and the biped length measured in units of the local lattice constant β(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) = bn
) = bn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ</a(r
φ</a(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ). The winding number can be computed using the construction of Fig. 3 to our sorting loop
). The winding number can be computed using the construction of Fig. 3 to our sorting loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) sort and it reads:
sort and it reads:wnx(λ, β) = 1 + 4[β(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) )] − 2[2λβ(r )] − 2[2λβ(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) )] )] | (5) |
 . The winding number wnx(λ, β) around the
. The winding number wnx(λ, β) around the ![[scr F, script letter F]](https://www.rsc.org/images/entities/char_e141.gif) x
x![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) fence lines is an odd integer that can be smaller or larger than zero. In Fig. 5 we plot the signum of the winding number as a function of β(r
fence lines is an odd integer that can be smaller or larger than zero. In Fig. 5 we plot the signum of the winding number as a function of β(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) and λ. The border between positive (wnx = 1) and negative (wnx = −1) winding number is a line given by
) and λ. The border between positive (wnx = 1) and negative (wnx = −1) winding number is a line given by | (6) |
![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) a(r
a(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) )·ex<0, as in our pattern, the parameter β(r
)·ex<0, as in our pattern, the parameter β(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) will increase with each walking step to the right. The walking direction changes at the position
) will increase with each walking step to the right. The walking direction changes at the position  when the bipeds cross from the bright gray (wx < 0) to the line between the dark (wx > 0) and the bright gray region at a negative slope of the line λc(β). Negative slopes of the line λc(β) between positive and negative winding numbers are attractors of bipeds that are classified by the integer [β]. Sections with positive slopes are separatrices between regions where bipeds are attracted toward different sections with negative slope. For λ = 1 there are an infinite number of attractor sections while for λ ≠ 1 the number of attractor sections is finite.
when the bipeds cross from the bright gray (wx < 0) to the line between the dark (wx > 0) and the bright gray region at a negative slope of the line λc(β). Negative slopes of the line λc(β) between positive and negative winding numbers are attractors of bipeds that are classified by the integer [β]. Sections with positive slopes are separatrices between regions where bipeds are attracted toward different sections with negative slope. For λ = 1 there are an infinite number of attractor sections while for λ ≠ 1 the number of attractor sections is finite.
 | ||
Fig. 5 The winding number wnx, eqn (5), as a function of β(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) = bn ) = bn![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ</a(r φ</a(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ) and λ. If the gradient of the lattice constant points in the negative x-direction ∇ ) and λ. If the gradient of the lattice constant points in the negative x-direction ∇![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) a(r a(r![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) )·ex<0 negative slopes of the line, eqn (6), between positive and negative winding numbers are attractors for bipeds, while sections with positive slopes are separatrices between regions where bipeds are attracted toward different sections with negative slope. The star symbols correspond to final experimental positions of the bipeds, the circles are initial experimental positions beyond the first separatrix with bipeds walking toward the [β] = 1 attractor line. The solid circle is most left initial position observed among all those initial positions. )·ex<0 negative slopes of the line, eqn (6), between positive and negative winding numbers are attractors for bipeds, while sections with positive slopes are separatrices between regions where bipeds are attracted toward different sections with negative slope. The star symbols correspond to final experimental positions of the bipeds, the circles are initial experimental positions beyond the first separatrix with bipeds walking toward the [β] = 1 attractor line. The solid circle is most left initial position observed among all those initial positions. | ||
We check our sorting experiments by measuring the biped length bn, the attractor positions  and the local unit cell size
and the local unit cell size 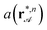 of the attractor line for all different biped sizes and loop parameters λ. From these measurements we compute
of the attractor line for all different biped sizes and loop parameters λ. From these measurements we compute  . Experimental pairs of
. Experimental pairs of  and λ are then plotted as star symbols into Fig. 5. For all different lengths of bipeds bn, n = 3,…,8 the experimental attractor points fit well on the theoretical prediction of eqn (6). Bipeds attracted to the second attractor line with [β] = 1 start walking from initial locations ri,n
and λ are then plotted as star symbols into Fig. 5. For all different lengths of bipeds bn, n = 3,…,8 the experimental attractor points fit well on the theoretical prediction of eqn (6). Bipeds attracted to the second attractor line with [β] = 1 start walking from initial locations ri,n![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) , i = 1,…,k in the direction opposite to the separatrix location rs,n
, i = 1,…,k in the direction opposite to the separatrix location rs,n![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) . In Fig. 5 we plot the corresponding pairs λ, and minki=1β(ri,n
. In Fig. 5 we plot the corresponding pairs λ, and minki=1β(ri,n![[scr A, script letter A]](https://www.rsc.org/images/entities/char_e520.gif) ), that lie closest to the separatrix for each value of λ (solid circle). These points are upper bounds for the separatrix location. All initial locations of bipeds approaching the [β] = 1 attractor line (open circles) lie in the bright gray region of negative winding number wnx<0 consistent with the theoretical prediction. Their very different separations from the theoretical separatrix is due to the random initial placements of the set of bipeds on the pattern.
), that lie closest to the separatrix for each value of λ (solid circle). These points are upper bounds for the separatrix location. All initial locations of bipeds approaching the [β] = 1 attractor line (open circles) lie in the bright gray region of negative winding number wnx<0 consistent with the theoretical prediction. Their very different separations from the theoretical separatrix is due to the random initial placements of the set of bipeds on the pattern.
8. Discussion and conclusion
Our experimental data is in good agreement with the predictions of eqn (6). Therefore by choosing a specific sorting loop, bipeds walk to their attractor position without any need to enforce their proper walk using a feedback mechanism. The decision to walk to the proper place under the periodic external driving is made internally by the bipeds. This is particularly prominent when an addition reaction bn + bm → bn+m changes the length of two colliding bipeds toward a third length and the longer length biped is automatically resorted. For an attractor line family with the same integer classification [β], the attractor line position evolves continuously with the length bn of the bipeds. Using attractor lines with family classification [β] > 0 it is possible to separate larger length bipeds from shorter biped attractor destinations even further, when choosing a driving loop with parameter λ ≠ 1 such that the larger biped is part of the family with classification [β] > 0, while the shorter is not.We have sorted bipeds of length b3–b8. One may ask what happens to bipeds of shorter and longer length. Single colloidal particles and b2 bipeds are both shorter than the smallest unit cell on the pattern. Therefore the transcription of control space into transcription space for these two biped lengths are spheres of radius 2.8 μm and 5.6 μm. Both transcription spheres are smaller than the smallest unit cell (the spacing of the fences in Fig. 3). The winding number of the transcribed side loops wx(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) na
na![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) = 0 = wx(
) = 0 = wx(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) nc
nc![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) vanish anywhere on the pattern, and the winding number of the transcribed central loops wx(
) vanish anywhere on the pattern, and the winding number of the transcribed central loops wx(![[script L]](https://www.rsc.org/images/entities/char_e144.gif) nb
nb![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) ) = 1 is constant and positive anywhere on the pattern. Single colloidal particles and b2 bipeds therefore walk toward the right searching for putative attractor lines smaller than the smallest unit cell size a−, which they can never find on this pattern. Single colloidal particles and b2 bipeds are thus never sorted.
) = 1 is constant and positive anywhere on the pattern. Single colloidal particles and b2 bipeds therefore walk toward the right searching for putative attractor lines smaller than the smallest unit cell size a−, which they can never find on this pattern. Single colloidal particles and b2 bipeds are thus never sorted.
In the experiments there are no bipeds of size b10 or larger before starting the loops. Such long bipeds only occur due to irreversible additions of smaller bipeds to the longer biped. For an addition reaction to occur, smaller bipeds must collide with each other. This happens predominantly in the attractor regions of the b3–b8 bipeds because it is in this region that smaller bipeds of different length counter propagate. Long bipeds are therefore found mostly on the right half of the pattern, which is a location already to the right of the first separatrices of these bipeds. Like the single colloidal particles and b2 bipeds, they start to search for an attractor line smaller than 7 μm that does not exist on the pattern. Ultimately they are not sorted for the very same reason as the single colloidal particles and b2 bipeds.
The probability of collisions in the attractor regions of the b3–b8 bipeds is also the reason one cannot increase the concentration of colloids. Colloids will collide in this region to form large bipeds that leave the pattern and only a small amount of sorted bipeds similar to what we see in our experiments presented remain sorted on the pattern.
We define the efficiency of sorting as the probability that a biped bn is transported to the correct attractor line λc(β) without colliding with another biped to form a biped of a different length prior to the sorting. At our low concentration of particles the efficiency of the sorting is roughly 90%. Note that sorting is not the same as separation. Attractor lines for bipeds of different lengths bn and bn+dn are separated by a distance that is the larger the smaller is the morphing reciprocal vector μ. If we define the efficiency of separation as the differential of separation of attractor lines with respect to the variation biped length  , then the efficiency of separation is proportional to the correlation length ξ of the pattern. A third efficiency is the time efficiency, i.e. the time we need to sort the bipeds. The deeper the colloidal potential, the faster we can modulate and still be in the adiabatic regime. The colloidal potential is deeper the farther we are separated with the loop in transcription space from the fence lines. This is best done amongst the family of topologically equivalent loops by choosing loops that avoid spending significant arclength of their path near the equator. In our experiments we use a period of T = 20 s per fundamental loop. The pattern and the loop are optimized with respect to the task of sorting bipeds to different predefined locations given the constraints of also being able to simultaneously observe all bipeds.
, then the efficiency of separation is proportional to the correlation length ξ of the pattern. A third efficiency is the time efficiency, i.e. the time we need to sort the bipeds. The deeper the colloidal potential, the faster we can modulate and still be in the adiabatic regime. The colloidal potential is deeper the farther we are separated with the loop in transcription space from the fence lines. This is best done amongst the family of topologically equivalent loops by choosing loops that avoid spending significant arclength of their path near the equator. In our experiments we use a period of T = 20 s per fundamental loop. The pattern and the loop are optimized with respect to the task of sorting bipeds to different predefined locations given the constraints of also being able to simultaneously observe all bipeds.
In conclusion we placed paramagnetic colloidal particles on top of a square-like magnetization pattern with alternating domains of magnetization with a locally varying unit cell size and apply a sorting loop ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) sort
sort![[capital script C]](https://www.rsc.org/images/entities/char_e522.gif) that lets bipeds assembled via dipolar attraction automatically sort themselves to attractor lines that depend on the length of the bipeds. In contrast to separation techniques like electrophoresis, the biped length do not separate as a function of time but all bipeds walk simultaneously to their attractor final destination that varies with the length of the bipeds.
that lets bipeds assembled via dipolar attraction automatically sort themselves to attractor lines that depend on the length of the bipeds. In contrast to separation techniques like electrophoresis, the biped length do not separate as a function of time but all bipeds walk simultaneously to their attractor final destination that varies with the length of the bipeds.
Author contributions
ARP, DdlH, & TMF designed and performed the experiment and wrote the manuscript with input from all the other authors. PK, MU & FS produced the magnetic film. SA, & ArE performed the fabrication of the micromagnetic patterns within the magnetic thin film.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under project number 531559581. DdlH acknowledges support via the Heisenberg program of the DFG via project number HE 7360/7-1. P. K., F. S., and M. U. acknowledge financial support from the National Science Centre Poland through the OPUS funding (Grant No. 2019/33/B/ST5/02013). S. A. acknowledges funding by a PhD scholarship of Kassel University. A. E., S. A. acknowledges support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under project numbers 514858524, INST 159/139-1 FUGG, INST 159/94-1 FUGG, and INST 159/95-1 FUGG.Notes and references
- E. Rodriguez-Boulan and A. Müsch, Biochim. Biophys. Acta, Mol. Cell Res., 2005, 1744, 455–464 CrossRef PubMed.
- P. Haffter, M. Granato, M. Brand, M. C. Mullins, M. Hammerschmidt, D. A. Kane, J. Odenthal, F. J. M. van Eeden, Y.-J. Jiang, C.-P. Heisenberg, R. N. Kelsh, M. Furutani-Seiki, E. Vogelsang, D. Beuchle, U. Schach, C. Fabian and C. Nüsslein-Volhard, Development, 1996, 123, 1–36 CAS.
- S. F. Krens and C.-P. Heisenberg, in Forces and Tension in Development, ed. M. Labouesse, Current Topics in Developmental Biology, Academic Press, 2011, pp. 189–213, vol. 95 Search PubMed.
- Y. Zhang, Y. Li, H. Wen, L. Cao, W. Xiao, J. Zhao, Z. Nan, S. Zhang, S. Qiu and Q. Li, Carbon, 2023, 215, 118468 CAS.
- M. S. Arnold, A. A. Green, J. F. Hulvat, S. I. Stupp and M. C. Hersam, Nat. Nanotechnol., 2006, 1, 60–65 CAS.
- L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Science, 2004, 304, 987–990 CAS.
- P. Zhou, J. He, Y.-M. Zha, G.-P. Zhang, G.-Y. Jiang and Y.-X. Huang, Chem. Eng. Sci., 2023, 282, 119319 CAS.
- X. Wang and I. Papautsky, Lab Chip, 2015, 15, 1350–1359 CAS.
- F. Nan and Z. Yan, Nano Lett., 2018, 18, 4500–4505 CAS.
- Y.-C. Tan, Y. L. Ho and A. P. Lee, Microfluid. Nanofluid., 2008, 4, 343–348 CrossRef CAS.
- M. P. MacDonald, G. C. Spalding and K. Dholakia, Nature, 2003, 426, 421–424 CrossRef CAS PubMed.
- H. Jung, M.-S. Chun and M.-S. Chang, Analyst, 2015, 140, 1265–1274 RSC.
- A. Dalili, E. Samiei and M. Hoorfar, Analyst, 2019, 144, 87–113 RSC.
- H.-D. Xi, H. Zheng, W. Guo, A. M. Gañán-Calvo, Y. Ai, C.-W. Tsao, J. Zhou, W. Li, Y. Huang, N.-T. Nguyen and S. H. Tan, Lab Chip, 2017, 17, 751–771 RSC.
- P. Sajeesh and A. K. Sen, Microfluid. Nanofluid., 2014, 17, 1–52 CrossRef.
- S. Goh, R. G. Winkler and G. Gompper, New J. Phys., 2022, 24, 093039 CrossRef.
- J. Rozman and J. M. Yeomans, Phys. Rev. Lett., 2024, 133, 248401 CrossRef CAS PubMed.
- S. Bhattacharyya and J. M. Yeomans, Phys. Rev. Lett., 2023, 130, 238201 CrossRef CAS PubMed.
- J. N. Graham, G. Zhang and J. M. Yeomans, Soft Matter, 2024, 20, 2955–2960 CAS.
- C. Dobson, C. Zielke, C. W. Pan, C. Feit and P. Abbyad, Micromachines, 2020, 11, 964 Search PubMed.
- Y. Zhang, T. Zheng, L. Wang, L. Feng, M. Wang, Z. Zhang and H. Feng, Rev. Adv. Mater. Sci., 2021, 60, 313–324 Search PubMed.
- R. L. Smith, G. C. Spalding, K. Dholakia and M. P. MacDonald, J. Opt. A: Pure Appl. Opt., 2007, 9, S134 Search PubMed.
- N. P. Vizarim, C. Reichhardt, C. J. O. Reichhardt and P. A. Venegas, New J. Phys., 2020, 22, 053025 CAS.
- P. L. Townes and J. Holtfreter, J. Exp. Zool., 1955, 128, 53–120 Search PubMed.
- C. Carlberg and F. Molnár, Embryogenesis and Cellular Differentiation, Springer Singapore, Singapore, 2018, pp. 123–140 Search PubMed.
- M. E. Rula, K. Q. Cai, R. Moore, D.-H. Yang, C. M. Staub, C. D. Capo-chichi, S. A. Jablonski, P. H. Howe, E. R. Smith and X.-X. Xu, Genesis, 2007, 45, 327–338 CAS.
- O. Cochet-Escartin, T. T. Locke, W. H. Shi, R. E. Steele and E.-M. S. Collins, Biophys. J., 2017, 113, 2827–2841 CAS.
- A. Torrik and M. Zarif, J. Chem. Phys., 2024, 161, 094907 CAS.
- Z. Zhou, J. Shang and Y. Li, Electronics, 2023, 12, 3700 Search PubMed.
- M. Mirzaee-Kakhki, A. Ernst, D. de las Heras, M. Urbaniak, F. Stobiecki, J. Gördes, M. Reginka, A. Ehresmann and T. M. Fischer, Nat. Commun., 2020, 11, 4670 CAS.
- M. Mirzaee-Kakhki, A. Ernst, D. de las Heras, M. Urbaniak, F. Stobiecki, A. Tomita, R. Huhnstock, I. Koch, A. Ehresmann, D. Holzinger and T. M. Fischer, Soft Matter, 2021, 17, 1663–1674 CAS.
- J. Elschner, F. Farrokhzad, P. Kuświk, M. Urbaniak, F. Stobiecki, S. Akhundzada, A. Ehresmann, D. de las Heras and T. M. Fischer, Nat. Commun., 2024, 15, 5735 CAS.
- J. Loehr, M. Loenne, A. Ernst, D. de las Heras and T. M. Fischer, Nat. Commun., 2016, 7, 11745 CAS.
- J. Loehr, D. de las Heras, M. Loenne, J. Bugase, A. Jarosz, M. Urbaniak, F. Stobiecki, A. Tomita, R. Huhnstock, I. Koch, A. Ehresmann, D. Holzinger and T. M. Fischer, Soft Matter, 2017, 13, 5044–5075 RSC.
- D. de las Heras, J. Loehr, M. Loenne and T. M. Fischer, New. J. Phys., 2016, 18, 105009 Search PubMed.
- M. Mirzaee-Kakhki, A. Ernst, D. de las Heras, M. Urbaniak, F. Stobiecki, A. Tomita, R. Huhnstock, I. Koch, J. Gördes, A. Ehresmann, D. Holzinger, M. Reginka and T. M. Fischer, Soft Matter, 2020, 16, 1594–1598 RSC.
- J. Loehr, D. de las Heras, A. Jarosz, M. Urbaniak, F. Stobiecki, A. Tomita, R. Huhnstock, I. Koch, A. Ehresmann, D. Holzinger and T. M. Fischer, Commun. Phys., 2018, 1, 4 CrossRef.
- H. Massana-Cid, A. Ernst, D. de las Heras, A. Jarosz, M. Urbaniak, F. Stobiecki, A. Tomita, R. Huhnstock, I. Koch, A. Ehresmann, D. Holzinger and T. M. Fischer, Soft Matter, 2019, 15, 1539–1550 RSC.
- N. C. X. Stuhlmüller, F. Farrokhzad, P. Kuświk, F. Stobiecki, M. Urbaniak, S. Akhundzada, A. Ehresmann, T. M. Fischer and D. de las Heras, Nat. Commun., 2023, 14, 7517 CrossRef PubMed.
- A. M. E. B. Rossi, T. Märker, N. C. X. Stuhlmüller, P. Kuświk, F. Stobiecki, M. Urbaniak, S. Akhundzada, A. J. Vereijken, A. Ehresmann, D. de las Heras and T. M. Fischer, Nat. Commun., 2025, 16, 1828 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01480d |
| This journal is © The Royal Society of Chemistry 2025 |