Open Access Article
Open Access ArticleBaTa0.5Li0.5O2.5: a new highly oxygen deficient perovskite oxide-ion conductor†
Jungu
Xu
 *a,
Qin
Cao
a,
Lin
Wang
b,
Bin
Ouyang
*b,
Tianjie
Wei
a,
Jiazheng
Hao
cd,
Jie
Chen
cd,
Lunhua
He
*a,
Qin
Cao
a,
Lin
Wang
b,
Bin
Ouyang
*b,
Tianjie
Wei
a,
Jiazheng
Hao
cd,
Jie
Chen
cd,
Lunhua
He
 *cef,
Laijun
Liu
*cef,
Laijun
Liu
 a and
Kevin
Huang
a and
Kevin
Huang
 *g
*g
aMOE Key Laboratory of New Processing Technology for Nonferrous Metals and Materials, Guangxi Universities Key Laboratory of Non-ferrous Metal Oxide Electronic Functional Materials and Devices, College of Materials Science and Engineering, Guilin University of Technology, Guilin 541004, China. E-mail: xujungu@glut.edu.cn
bDepartment of Chemistry and Biochemistry, Florida State University, Tallahassee, FL 32304, USA. E-mail: bouyang@fsu.edu
cSpallation Neutron Source Science Center, Dongguan 523803, China. E-mail: lhhe@ihep.ac.cn
dInstitute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China
eBeijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academic of Sciences, Beijing 100190, China
fSongshan Lake Materials Laboratory, Dongguan 523808, China
gDepartment of Mechanical Engineering, University of South Carolina, Columbia, South Carolina 29201, USA. E-mail: huang46@cec.sc.edu
First published on 20th November 2023
Abstract
High oxide-ion and proton conductivity in perovskite oxides has been well documented in the literature. Herein, we report a highly oxygen deficient perovskite oxide BaTa0.5Li0.5O2.5 (BTLO) as a new oxide-ion conductor. The material exhibits a simple primitive cubic perovskite structure (S.G.: Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) with lattice parameter a = 4.1024(1) Å and completely disordered Ta and Li cations on the B-site. The ionic conduction is predominated by oxide-ion over a wide range of oxygen partial pressure and temperature, with an ionic conductivity comparable to the state-of-the-art yttria-stabilized zirconia. Ab initio molecular dynamics (AIMD) simulations reveal that oxide-ion diffusion follows three-dimensional pathways, involving oxygen vacancy hopping along the edges of (Ta/Li)O4 tetrahedra and (Ta/Li)O6 octahedra. This work may inspire future work to discover new oxide-ion conductors in similar systems.
m) with lattice parameter a = 4.1024(1) Å and completely disordered Ta and Li cations on the B-site. The ionic conduction is predominated by oxide-ion over a wide range of oxygen partial pressure and temperature, with an ionic conductivity comparable to the state-of-the-art yttria-stabilized zirconia. Ab initio molecular dynamics (AIMD) simulations reveal that oxide-ion diffusion follows three-dimensional pathways, involving oxygen vacancy hopping along the edges of (Ta/Li)O4 tetrahedra and (Ta/Li)O6 octahedra. This work may inspire future work to discover new oxide-ion conductors in similar systems.
1. Introduction
The oxide-ion electrolyte is a core functional component in solid oxide cells (SOCs) for high-efficiency and low-emission power/chemical production.1–5 They not only define the chemistry of SOCs, but also determine the working temperature. The latter is of paramount importance to the commercialization of SOC technology because too high a working temperature would invoke unwanted chemical reactions with the adjacent components, causing performance degradation. The current benchmark SOCs based on 8 mol% Y2O3-stabilized ZrO2 (YSZ) oxide-ion electrolyte must have a thickness <10 μm in order to achieve reasonable performance even at ≥700 °C. However, ≥700 °C is still considered too high to reach commercially meaningful 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000+ hours of operation for SOCs. Therefore, new oxide-ion electrolytes that can further lower SOC's working temperature are of high interest.
000+ hours of operation for SOCs. Therefore, new oxide-ion electrolytes that can further lower SOC's working temperature are of high interest.
The magnitude, purity, and stability of oxide-ion conductivity in both oxidizing and reducing atmospheres are the top three criteria for the discovery of new oxide-ion conductors. In this regard, the early oxide-ion conductors were primarily found in solid oxides with cubic fluorite structures.6 Examples include stabilized ZrO2 and CeO2. In recent decades, the search for new oxide-ion conductors has been expanded to perovskite or perovskite-related oxides.7,8 The well-known examples are Sr and Mg doped LaGaO3 (LSGM),9,10 Na0.5Bi0.5TiO3,11 hexagonal perovskites Ba3NbMO8.5 (M = Mo, W) and Ba7Nb4MoO20,12,13 Ruddlesden–Popper-type La2−xMxBaIn2O7−0.5x (M = Ca, Sr, Ba),14 Dion-Jacobson-type CsBi2Ti2NbO10−δ,15 Aurivillius-type Bi4Ti3O12,16 and pyrochlore Sr2Nb2O7.17 Besides these perovskite or perovskite-related oxides with relatively low oxygen vacancy concentrations, is the brownmillerite structure with the general formula A2B2O5, including the well-known Ba2In2O5-based materials18,19 and Sr2ScGaO5-based materials,20,21 which can be viewed as highly oxygen-deficient perovskites with one-sixth of the oxygen sites vacant and ordered in the tetrahedral layers, which also show good oxide ion conduction properties, especially at temperatures above the oxygen vacancy order–disorder transition or when the disordered oxygen vacancies are stabilized at a low temperature by cation doping. While high oxide-ion conductivity is generally observed, these materials (except LSGM) do not have sufficient ionic purity and chemical stability in SOC operating environments. Therefore, direct use of these materials in SOCs still presents a challenge.
Herein, we report on a primitive cubic structured perovskite BaTa0.5Li0.5O2.5 (BTLO) as a new oxide-ion conductor, the nominal chemical composition of which can be viewed as the same as the general formula of brownmillerite. We show that Ta and Li ions are in a complete disordered state on the B-site in BTLO and oxide-ion conductivity is nearly purely ionic under SOC operating conditions. We also discuss oxide-ion conduction mechanisms using ab initio molecular dynamic (AIMD) simulations.
2. Experimental procedure
2.1 Material synthesis
A traditional solid-state reaction method was employed to prepare BTLO samples with BaCO3 (99.0%, Aladdin), Ta2O5 (99.99%, Macklin), and Li2CO3 (99.0%, Aladdin) as starting materials. After stoichiometric amounts of the starting materials were intimately mixed and pressed into pellets, they were first calcined at 800 °C for 12 h, then ground, pelletized, and sintered again at 1100 °C for 48 h. To compensate for the loss of lithium during high-temperature sintering, excess Li2CO3 (10 mol%) was added into the samples, and the pressed pellets were buried in the original powders.2.2 Characterization
X-ray powder diffraction (XRD) was performed using a Panalytical X’pert Pro X-ray diffractometer with Cu Kα radiation. Topas-Academic software22 was used for Rietveld refinements. Atomic absorption analysis was performed using a PinAAcle 900T atomic absorption spectrometer to check the stoichiometry of the samples. Electron diffraction (ED) was performed on a JEOL JEM-2100F field-emission transmission electron microscope with an accelerating voltage of 200 kV. Time-of-flight (TOF) powder neutron diffraction (NPD) data were collected from a general-purpose powder diffractometer (GPPD) (90° bank) at the China spallation neutron source (CSNS).23The electrical properties such as ionic conductivity and ionic transport number determined from an oxygen concentration cell were investigated using a Bio-Logic VSP electrochemical system. For electrochemical impedance spectroscopy (EIS) measurements, the frequency was swept from 106 to 10−1 Hz with an AC amplitude of 10 mV. For all the cells subject to electrical characterization, electrodes were prepared by coating Pt paste on opposite sides of the pellets and cured at 750 °C for 1 hour to remove any organic components. Before the impedance measurements, the temperature was equilibrated at each setpoint for an hour. The measurements were conducted from 300 to 800 °C in various atmospheres.
2.3 Ab initio molecular dynamics (AIMD) simulations
To study the oxide-ion conduction mechanism, first-principles calculations are carried out within the density functional theory (DFT) framework as implemented in the Vienna Ab Initio Simulation Package (VASP),24 with the generalized gradient approximation (GGA-PBE)25 and a projector-augmented wave (PAW) approach.26 The cutoff energy was set to 520 eV with a force criterion of 1.0 × 10−2 eV Å−1 for the lattice optimization and an energy tolerance criterion of 10−4 eV. For modelling the targeted composition of BaTa0.5Li0.5O3, a supercell 2 √2 × 2√2 × 4 (144 atoms) is constructed. Moreover, we used a special quasi randoms structure to represent the cation ordering in the current structure by assuming all ions are randomly distributed.27 For all calculations, a reciprocal space discretization of 25 K-points per Å−1 was applied, and the convergence criteria were set as 10−6 eV for electronic loops and 0.02 eV Å−1 for ionic loops. All the AIMD calculations are performed in an NVT ensemble with a time step of 2 fs and using a Nose–Hoover thermostat28 for a period of 500 ps. To perform extrapolation following the Arrhenius relationship, three temperatures, e.g., 2000 K, 1800 K and 1600 K were used, at which the conductivity at 1073 K (800 °C) was extrapolated.3. Results and discussion
3.1 Phase and structure analysis
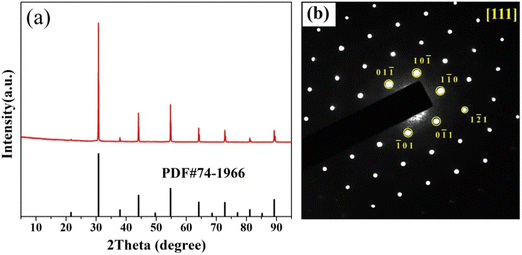
Since there is a possibility of Li-loss during sintering, the chemical stoichiometry in the as-made BTLO sample was first chemically analyzed using an atomic absorption technique. The result indicates a Li content of 1.18 ± 0.1 wt% vs. nominal 1.279 wt% in the sample, suggesting ∼8% percent Li-deficiency in the sample. After confirming the composition, the XRD pattern of Fig. 1(a) further suggests that BTLO possesses a primitive perovskite unit cell with space group Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; the latter is further verified by the SAED analysis shown in Fig. 1(b).
m; the latter is further verified by the SAED analysis shown in Fig. 1(b).
To further investigate the defect structure of BTLO, especially the exact Li content and oxygen vacancy concentration in the crystal structure, Rietveld structural refinements were carried out against the NPD data using a typical simple cubic perovskite structure as the model, in which Ba atoms were placed at the A site (1a), while Ta and Li were first mixed on the B site (1b), and O on the 3c site. For an initial refinement, the occupancies of both Ta and Li were simply set to be 0.5 and fixed without being refined according to the nominal composition and based on the experimental chemical analysis. This resulted in a poor fitting result with the reliability of Rwp ∼ 8.23% and Rp ∼ 6.12%, see Fig. 2(a). To address this issue, we allow the sum of Ta and Li occupancies to be the unit, instead of a fixed value of 0.5. This significantly improves Rwp to ∼2.26% and Rp to ∼2.20. The resultant occupancies are 0.592(1) and 0.408(1) for Ta and Li, respectively. In addition, the refinement yields O-occupancy of 0.858(4), implying a high concentration of oxygen vacancy, and Ba-occupancy of 1.013(4), implying a nearly full occupation on the A site. The final refined composition of BTLO is BaTa0.592(1)Li0.408(1)O2.574(5), slightly deviated from the nominal BaTa0.5Li0.5O2.5. The Li concentration of 0.982 wt% by the refinement is a little bit lower than the chemically analyzed result of 1.18 ± 0.1 wt%. The final refinement is shown in Fig. 2(b) and the corresponding structural parameters are summarized in Table 1.
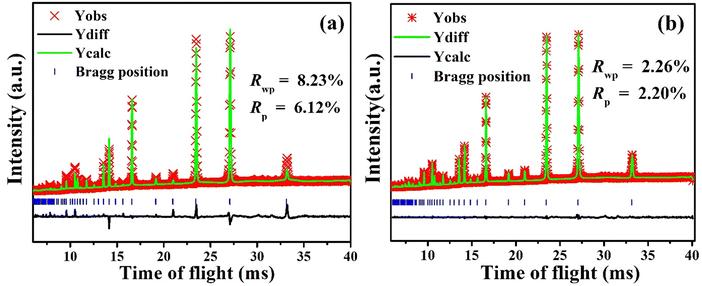 | ||
| Fig. 2 (a) Refinement plots with Li and Ta occupancies fixed at 0.5; (b) the final refinement plots with the sum of Li and Ta occupancies fixed at the unit. | ||
| Atoms | x | y | z | Occupancy | Beq (Å2) | BVS |
|---|---|---|---|---|---|---|
Lattice parameters: a = 4.0910(3) Å; space group, Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m; interatomic distances (Ta/Li)–O (×6): 2.0455(2) Å; Ba–O (×12): 2.8928(2) Å. The refined composition: BaTa0.592(1)Li0.408(1)O2.574(5). m; interatomic distances (Ta/Li)–O (×6): 2.0455(2) Å; Ba–O (×12): 2.8928(2) Å. The refined composition: BaTa0.592(1)Li0.408(1)O2.574(5). |
||||||
| Ba | 0 | 0 | 0 | 1.0 | 1.36(3) | 2.32 |
| Ta/Li | 0.5 | 0.5 | 0.5 | 0.5978(3)/0.4022(3) | 0.46(2) | 4.27/1.25 |
| O | 0.5 | 0.5 | 0 | 0.858(4) | 1.75(3) | 1.94 |
There have been several reports in the literature on perovskite oxides ABO3 with B-site containing Ta/Nb and alkaline metals, which crystalize into a simple cubic perovskite or hexagonal eight-layered perovskite structure. Examples include Ba4(Ta/Nb)3LiO12, Ba4(Ta/Nb)3NaO12, Sr4(Ta/Nb)3LiO12, and Sr4Ta3NaO12.29 For Ba4(Ta/Nb)3LiO12, it forms a hexagonal eight-layered perovskite structure with 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ordering of tantalum or niobium with lithium. However, the molar fractions of Li/Na on the B site (25 mol%) in these compounds are determined by the stoichiometry of oxygen. A higher molar fraction of Li/Na on the Ta/Nb-site would lead to oxygen deficiency in the structure, which has not been reported to the best of our knowledge. The BTLO perovskite reported in this work is thus the first example of simple cubic perovskite oxides with random/disordered occupancy of Ta and Li and high oxygen deficiency. Usually, for an A(B′B′′)O3-type perovskite compound, the B cation centered octahedron is distorted if the B′′ cation is substituted by a B′ cation. If there is an insignificant difference in the shape and size between two stable B′O6 and B′′O6, the distribution of B′ and B′′ cations may be random. If the distortion of BO6 is large enough after substituting B′ for B′′, then B′ and B′′ will prefer to be in a certain way in order to stabilize the perovskite structure. The distortion of BO6 caused by substitution depends not only on the differences in ionic radii and charges of B′ and B′′, but also on their polarizabilities, because the polarizability of an ion represents the deformability of the ion under the action of the neighboring ions.
1 ordering of tantalum or niobium with lithium. However, the molar fractions of Li/Na on the B site (25 mol%) in these compounds are determined by the stoichiometry of oxygen. A higher molar fraction of Li/Na on the Ta/Nb-site would lead to oxygen deficiency in the structure, which has not been reported to the best of our knowledge. The BTLO perovskite reported in this work is thus the first example of simple cubic perovskite oxides with random/disordered occupancy of Ta and Li and high oxygen deficiency. Usually, for an A(B′B′′)O3-type perovskite compound, the B cation centered octahedron is distorted if the B′′ cation is substituted by a B′ cation. If there is an insignificant difference in the shape and size between two stable B′O6 and B′′O6, the distribution of B′ and B′′ cations may be random. If the distortion of BO6 is large enough after substituting B′ for B′′, then B′ and B′′ will prefer to be in a certain way in order to stabilize the perovskite structure. The distortion of BO6 caused by substitution depends not only on the differences in ionic radii and charges of B′ and B′′, but also on their polarizabilities, because the polarizability of an ion represents the deformability of the ion under the action of the neighboring ions.
To predict the order or disorder of the distribution of B′ and B′′ in A(B′B′′)O3-type perovskite compounds, some rules and methods have been proposed.30–33 Among which, a simple method proposed by Liu et al.30 has been proven to work well for the compounds with the ratio of B′/B′′ = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (or 2
2 (or 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1). In this method, an order–disorder phase diagram is drawn into three regions corresponding to ordered, disordered, and order–disorder transition regions. For this diagram, the coordinate Y is defined as Y = ln(100 × |Δα|/(NA × nA)), where Δα is the difference in the polarizabilities of B′ and B′′ cations in A(B′B′′)O3 compounds, NA and nA are the largest principal quantum number and the number of total electrons in the outer electronic shells of the A atom, respectively. For the abscissa X, it is defined as
1). In this method, an order–disorder phase diagram is drawn into three regions corresponding to ordered, disordered, and order–disorder transition regions. For this diagram, the coordinate Y is defined as Y = ln(100 × |Δα|/(NA × nA)), where Δα is the difference in the polarizabilities of B′ and B′′ cations in A(B′B′′)O3 compounds, NA and nA are the largest principal quantum number and the number of total electrons in the outer electronic shells of the A atom, respectively. For the abscissa X, it is defined as 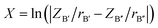 where
where 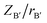 and
and 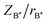 are the ratios of charges to ionic radii of B′ and B′′ cations, respectively. According to this diagram, a compound with X >1.8 would be located in the ordered region regardless of the Y value. Here in our work, the calculated X value for BaTa0.5Li0.5O2.5 is 1.87, greater than 1.8, and thus expected to result in an ordered distribution of Ta and Li ions in the structure, which is contrary to our experimental results. This might be caused by the high concentration of oxygen vacancy in the structure; as pointed out by Liu et al.30 their method could lead to a contradictory conclusion if there is significant change in oxygen stoichiometry.
are the ratios of charges to ionic radii of B′ and B′′ cations, respectively. According to this diagram, a compound with X >1.8 would be located in the ordered region regardless of the Y value. Here in our work, the calculated X value for BaTa0.5Li0.5O2.5 is 1.87, greater than 1.8, and thus expected to result in an ordered distribution of Ta and Li ions in the structure, which is contrary to our experimental results. This might be caused by the high concentration of oxygen vacancy in the structure; as pointed out by Liu et al.30 their method could lead to a contradictory conclusion if there is significant change in oxygen stoichiometry.
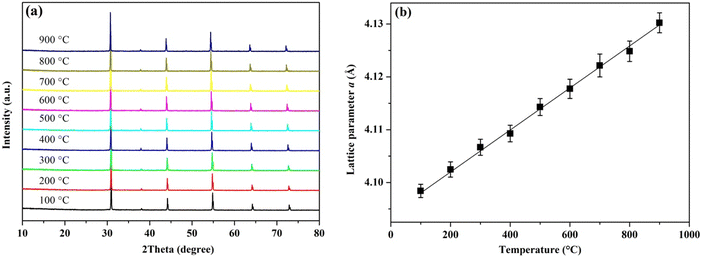
In addition, it is important to highlight that BTLO should be perceived as a cubic perovskite not Brownmillerite Ba2TaLiO5 due to the fact that Ta and Li are randomly distributed, and oxygen vacancies are disordered; the latter is the key for oxide-ion conduction. It is well known that highly acceptor-doped ABO3 can transform into an orthorhombic A2B2O5 brownmillerite structure, in which the two B cations have distinct positions and 1/6 of the O-site becomes vacant and ordered at lower temperatures. Above the characteristic temperature, the highly ordered orthorhombic brownmillerite structure can transform into a cubic perovskite structure by oxygen vacancies disordering, which is accompanied by an order of magnitude increase in oxide-ion conductivity such as that observed in Sr2Fe2O534 and Ba2In2O5,35,36 just to name a few. Interestingly, a cubic oxygen disordered single crystal was reported to be synthesized for the Sr2ScGaO5 material,20 although the polycrystalline sample for this material also showed an orthorhombic ordered phase at ambient temperature. The cubic phase of this single crystal Sr2ScGaO5 material can be maintained until 1400 °C where it then transforms into an orthorhombic phase and is then transferred to the cubic phase again at 1600 °C. Here for our BTLO material, the VT-XRD study revealed that the pure cubic phase of BTLO can be maintained at least to 900 °C (higher temperatures were not investigated due to the limitation for the instrument in our lab), as shown in Fig. 3(a). As can be seen, within the studied temperature region, no peaks from the secondary phase were detected, and the refined lattice parameters showed a linear increase with temperature (Fig. 3(b)), from which the thermal expansion coefficient was estimated to be ∼9.71 × 10−6 K−1. Therefore, it is expected that simple cubic perovskite BaTa0.5Li0.5O2.5 with disordered oxygen vacancies exhibits good oxide-ion conductivity over a broad temperature range.
3.2 Electrical properties
The conductivity of BTLO was measured using AC impedance spectroscopy. Fig. 4(a) shows an example of a Nyquist plot at 300 °C, which features a semicircle that can be modeled by a parallel R–C circuit in the high frequency range and Warburg impedance with characteristic capacitance higher than 10−7 F cm−1 that can be modeled by semi-infinite ionic diffusion at the electrolyte/electrode interface in the low frequency range.37 The intercept of the semicircular arc at low frequency represents the sum of resistance contributed from the grain and grain boundary (Rg + Rgb), from which the total conductivity of the material can be calculated out. At higher temperatures, e.g. 700 °C, the R–C semicircular arc becomes less pronounced due to reduced Rg + Rgb and increased double layer capacitance, which makes the electrode response (Re) to frequency dominate the spectrum, see Fig. 4(b). To preliminarily determine the nature of charge carriers responsible for the ionic conduction, impedance spectra were also measured under N2, air and O2 atmospheres with different oxygen partial pressures (pO2) at 750 °C; the results are shown in Fig. 4(b). Two observations are noted: (1) the electrode response is very sensitive to pO2, i.e., the higher the pO2, the lower the electrode resistance (Re). The strong dependence of Re on pO2 infers the nature of active oxygen electrocatalysis (O2 + 4e− ↔ 2O2−) at the BTLO/Pt interface, which is commonly observed in the oxide-ion conductors;11,38 (2) Rg + Rgb is insensitive to pO2, implying pure ionic conduction.11,38 Furthermore, Fig. 4(c) shows that the independence of Rg + Rgb occurs over a wide pO2 range from highly reducing to highly oxidizing atmospheres and a temperature range of 600–800 °C. It is evident that the total conductivity is invariable over pO2 = 1 to 10−25 atm from 600 to 800 °C, showing no sign of n-type electronic conduction even at low pO2. It should be stressed here that the three low pO2 at the 600 °C studied temperature were achieved by bubbling the 10%H2–90Ar% gas, 5%H2–95Ar% gas, and 1%H2–99% Ar gas through room temperature water, respectively. This also means that the conductivities under wet atmospheres did not show obvious enhancements compared to that measured under dry gas (four different gases were used in this work: pure Ar with pO2 of ∼10−4 atm; 1%O2–99%Ar gas with pO2 of 10−2 atm; air gas with pO2 of 0.21 atm; pure O2 with pO2 of 1.0 atm). Therefore, this strongly indicates that the proton conduction in the BTLO material, if any, is small. For the low pO2 at 700 and 800 °C, they were achieved by mixing the dry CO and CO2 gases. Moreover, the conductivities of BTLO under both dry and wet air atmospheres from 300 to 800 °C were also closed to each other at a given temperature, as shown in Fig. 4(d), which again supported the conclusion that the proton conduction in BTLO can be negligible. This is unlike in many other oxygen deficient perovskite materials where both oxide ion conduction and proton conduction are usually observed under wet atmospheres, such as in typical proton conducting Ba(Zr/Ce)O3-based materials39 and recently reported SrSc0.5−xZnxGa0.5O2.5−0.5-based materials.21 As reported in Kreuer et al.'s work,40 for the Y- and Sc-doped BaZrO3 materials, the former (Y-doped) have a lower activation energy and higher proton conductivity than that of the latter (Sc-doped), which was ascribed to the difference in the basicity of the oxygen ions coordinated to Y and Sc: the electron densities on the oxygen ions coordinated to Y are almost the same with the electron densities of oxygen coordinated to Zr, whereas the oxygen ions coordinated to Sc had significantly higher electron densities and therefore higher basicities. The more basic oxygen ions coordinated to Sc have therefore more strong bonds with protons, leading to lower proton mobility and higher activation energy. In the present work for the BaTa0.5Li0.5O2.5 material, almost half of the B-sites were occupied by the Li ions, and the oxygen ions coordinated to these Li ions were supposed to have much higher electron densities and basicity. Therefore, the protons bonding to these oxygen ions would have much lower mobility and higher activation energy. This may be a possible reason for the negligible proton conduction in the BaTa0.5Li0.5O2.5 material.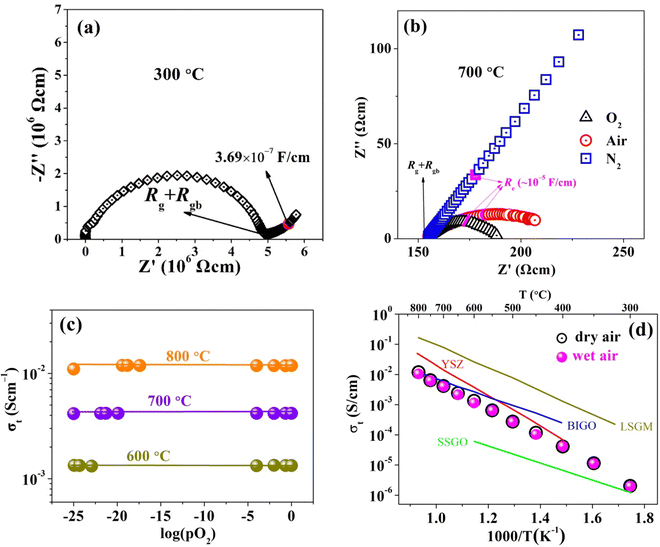 | ||
| Fig. 4 (a) Nyquist impedance plot of BTLO at 300 °C; (b) impedance spectra under oxygen, air and nitrogen atmospheres at 750 °C; (c) pO2 dependence of the total conductivity for BTLO; (d) Arrhenius plot of the total conductivity of BTLO in both dry and wet air, compared with yttria-stabilized zirconia (YSZ),44 gallium-doped cubic Ba2In1.5Ga0.5O5 (BIGO),43 cubic single crystal SrSc0.5Ga0.5O2.5 (SSGO),38 and Sr- and Mg-doped cubic La0.8Sr0.2Ga0.83Mg0.17O2.815 (LSGM).10 | ||
Fig. 4(d) also compares BTLO's total conductivity with YSZ, Ba2In1.5Ga0.5O5 (BIGO), and SrSc0.5Ga0.5O2.5 in an Arrhenius plot. As shown, the conductivities of BTLO are comparable to YSZ at temperatures below 400 °C and close to BIGO at temperatures above 700 °C. However, the conductivities of BTLO here are apparently higher than that of the SrSc0.5Ga0.5O2.5 material which has the same oxygen defect level and cubic perovskite structure. As Sammells et al.41,42 suggested, the activation energies of oxide ions in perovskite oxides have a strong relationship with the radius of the saddle point (bottleneck) which was formed by two A-site cations and one B-site cation in the perovskite structure. The radius of this kind of saddle point (rcritical) can be calculated according to the following equation
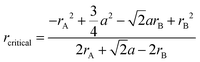 | (1) |
In addition, we can see in Fig. 4(d) that the conductivity of BTLO is more than one order of magnitude lower than that of the Sr and Mg co-doped LaGaO3 (LSGM) with the composition of La0.8Sr0.2Ga0.83Mg0.17. As has been reported for LSGM materials,10 that their conductivities increase with the increase of Sr/Mg concentration at first, after reaching a maximum, and the oxide ion conductivities of LSGM decrease with the increase of Sr/Mg concentration (or oxygen vacancy concentration). The composition of La0.8Sr0.2Ga0.83Mg0.17O2.815 was reported to exhibit the highest conductivity of 0.166 S cm−1 at 800 °C. Moreover, the activation energy of oxide ion conduction in LSGM was reported to increase with the oxygen vacancy concentration. Here for the BTLO, although it has apparently higher oxygen vacancy concentration than that in LSGM, the oxide ion conduction was significantly lower than that of LSGM. Here, as the radius of the saddle point for oxide ion migration in La0.8Sr0.2Ga0.83Mg0.17O2.815 was calculated to be ∼0.948, which is apparently higher than that of BTLO (0.872), and thus was expected from this point of view to have a much higher conductivity than BTLO.
Based on the above results, we can draw a general conclusion that the oxide-ion conduction is likely dominating in BTLO with negligible electronic conductivity, although the possibility for lithium-ion conduction could not be ruled out yet. The dominant oxide-ion conduction is further verified by the electromotive force (EMF) measurement using an oxygen concentration cell consisting of air|BTLO|O2, which shows an EMF value of ∼33.5 mV at 750 °C, which is 97% of the theoretical EMF calculated from the Nernst equation. To further obtain partial oxide-ion conductivity, we employed a modified four-probe Hebb–Wagner cell, with which the Li+ ion conductivity, if any, can be obtained by subtracting the partial oxide-ion conductivity from the total conductivity. In this modified four-probe Hebb–Wagner cell, the La1.54Sr0.46Ga3O7.27 (denoted as LSGO in the following) material, which has been well-documented to be a pure oxide ion conductor,38 was used as an electron as well as a Li+ blocking layer. Besides two reversible porous Pt electrodes, there is an additional porous Pt layer situated between BTLO and LSGO. The cell configuration in this work can thus be described as (+) Pt‖LSGO/Pt/BTLO‖Pt (−); a schematic of this cell is shown in Fig. 5(a). The additional porous Pt layer between BTLO and LSGO was applied to mainly overcome the high BTLO/LSGO interfacial resistance, which is usually observed in a traditional Hebb–Wagner cell. The cell was placed in a quartz tube furnace filled with pure O2. The measurements were carried out at 800 °C to ensure a sufficient rate of the oxygen redox reactions (oxidation/reduction) on the porous Pt electrodes. Under a constant current (I), the voltage drop (V) across a given distance of the specimen was measured. Oxide-ion conductivity (σo) is then calculated by Ohm's law with the known sample dimensions. It is important to mention that the electrical measurements by the Hebb–Wagner polarization method should be carried out under steady-state conditions, see Fig. 5(b), where only the oxide-ion current should be observed in BTLO. The constant current I was kept in a range of 0.3–2.0 mA in the present study to ensure a steady-state voltage. The results are summarized in Table 2 and compared with the total conductivities obtained using an AC impedance technique. The results reveal clearly that the oxide-ion conduction dominates the conductivities of BTLO, with an average oxide-ion transport number (to) of ∼0.965, suggesting almost negligible electronic and lithium-ion conductions.
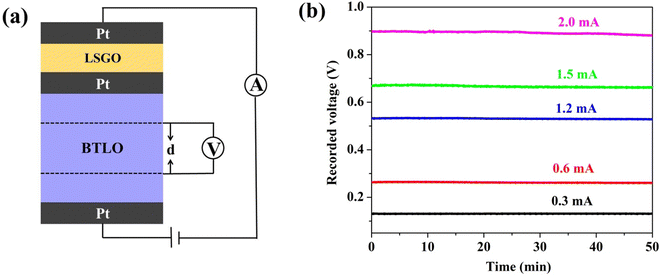 | ||
| Fig. 5 (a) Schematic of the four-probe Hebb–Wagner cell configuration in this work; (b) the recorded voltages as a function of time using various currents. | ||
| I (mA) | σ o | σ t | t o |
|---|---|---|---|
| 0.3 | 0.01172 | 0.01195 | 0.981 |
| 0.6 | 0.01168 | 0.01195 | 0.977 |
| 1.2 | 0.01151 | 0.01195 | 0.963 |
| 1.5 | 0.01144 | 0.01195 | 0.957 |
| 2.0 | 0.01132 | 0.01195 | 0.947 |
Thus, it is safe to say that the measured total conductivity of BTLO under air conditions shown in Fig. 4(d) is largely attributed to oxide-ion conduction. The same magnitude of ionic conductivity in BTLO as that of the conventional YSZ and BIGO implies the same level of mobile oxygen vacancy concentration. Given the fact that the oxide-ion conductivity is independent of pO2, BTLO is a new electrolyte candidate for SOFCs. Like LSGM or other perovskite oxide-ion conductors, one distinct advantage of BTLO is the direct use of highly active perovskite cathodes without a barrier layer such as Gd-doped CeO2 that must be used in ZrO2-based SOFCs.
3.3 Discussion on the oxide-ion conduction mechanism
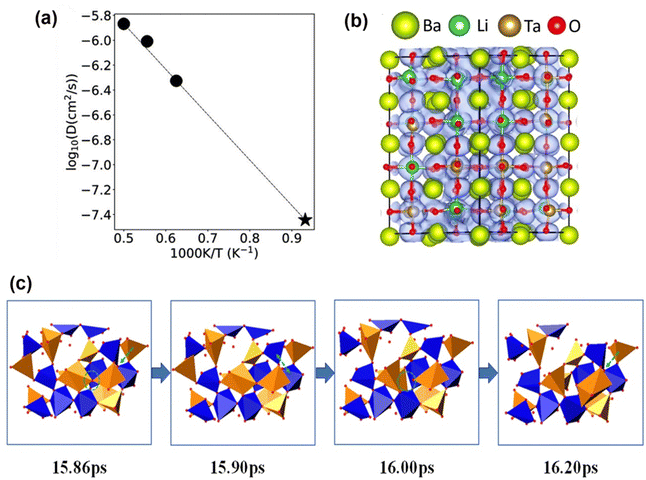
As have been reported for other perovskite materials, such as LaBO3 (B = Cr, Mn, Fe, Co),45 La0.6Sr0.4CoO3−δ,46 (La0.8Sr0.2)(Ga0.8Mg0.15Co0.05)O2.8,47 and so on, the oxygen mobility is mainly mediated by hopping of oxygen vacancies along the octahedral edge of BO6. In the present work, we performed AIMD simulations on ionic diffusion. The diffusivities at three selected temperatures (2000 K, 1800 K and 1600 K) are obtained from the mean square displacements (MSD) as shown in Fig. S1a (ESI†). Fig. S1b–d (ESI†) present the MSD for Ba, Ta, and Li ions, respectively. One can clearly see that the Ta and Ba ions are not mobile at all the simulated temperatures (1600 K, 1800 K, and 2000 K). While for the Li ions, the MSD values (below 1 Å2 at 300 ps) at 1600 and 1800 K are significantly lower than that of the oxygen ions (∼14 Å2 and ∼27 Å2 at 1600 and 1800 K, respectively) at 300 ps. However, at a higher simulated temperature of 2000 K, the Li ions seem to have an even larger MSD value than that of oxygen ions at the same temperature. This may suggest that at a sufficiently high temperature, the Li ions in the BTLO would have a long-range displacement and then contribute to the ionic conductivity. However, in our work the experimentally investigated temperatures are believed to be lower than this trigger temperature for Li ions’ long-range migration.Furthermore, the simulation data at these three temperatures fit the Arrhenius relationship well as shown in Fig. 6(a). Extrapolated to 800 °C, the ionic conductivity at 800 °C is 3.014 × 10−2 S cm−1 with an activation energy of 0.734 eV, which are close to our experimental data. Fig. 6(b) clearly displays three-dimensional migrating pathways, while Fig. 6(c) shows some selected snapshots for demonstrating the role of the (Ta/Li)On polyhedral for oxygen transport, which is akin to that observed in other simple cubic perovskite oxide-ion conductors.48 More specifically, the simulations revealed that Ta ions are mainly coordinated by 5 or 6 oxygen atoms. Whereas the Li ions are coordinated by 3 or 4 oxygen atoms within most of the simulated time, sporadically 5, 6 and even 2 oxygen coordinated Li ions were also observed.
4. Conclusion
In this work, we report a new simple cubic perovskite material BaTa0.5Li0.5O2.5 with disordered oxygen vacancies. A high and pure oxide ion conductivity of ∼1.2 × 10−2 S cm−1 at 800 °C is observed, which is comparable to that of the widely used YSZ material. In addition, the oxide-ion conduction mechanism in BaTa0.5Li0.5O2.5 is supported by ab initio molecular dynamic simulations, revealing 3D migration pathways for oxygen vacancies. This work may inspire future work to discover new oxide-ion conductors in similar systems.Author contributions
Jungu Xu, conceptualization, data curation, funding acquisition, writing – review & editing; Qin Cao, investigation, data curation; writing – original draft; Lin Wang, formal analysis; Bin Ouyang, formal analysis, funding acquisition, writing – review & editing; Tianjie Wei, investigation, data curation; Jiazheng Hao, investigation, data curation; funding acquisition; Jie Chen, investigation, data curation; Lunhua He, supervision, funding acquisition, writing – review & editing; Laijun Liu, resources, writing – review & editing; Kevin Huang, supervision, writing – review & editing.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The National Natural Science Foundation of China (no. 21965008, U2032220, 2019B1515120028), Guangxi Natural Science Foundation (no. 2021GXNSFFA220002 and 2019GXNSFGA245006), Guangxi BaGui Scholars Special Funding, CAS Project for Young Scientists in Basic Research under Grant (no. YSBR-024), Open Fund of Key Laboratory of New Processing Technology for Nonferrous Metal & Materials, Ministry of Education/Guangxi Key Laboratory of Optical and Electronic Materials and Devices (no. 20AA-4) are acknowledged for the financial support. The computations carried out by Bin Ouyang and Lin Wang were supported by startup funding at Florida State University. The computing resources were supported by the FSU Research Computing Center.References
- A. Boudghene Stambouli and E. Traversa, Solid oxide fuel cells (SOFCs): a review of an environmentally clean and efficient source of energy, Renewable Sustainable Energy Rev., 2002, 6, 433–455 CrossRef.
- Y. Zhang, R. Knibbe, J. Sunarso, Y. Zhong, W. Zhou, Z. Shao and Z. Zhu, Recent Progress on Advanced Materials for Solid-Oxide Fuel Cells Operating Below 500 °C, Adv. Mater., 2017, 29, 1700132 CrossRef PubMed.
- S. Suthirakun, G. Xiao, S. C. Ammal, F. Chen, H.-C. zur Loye and A. Heyden, Rational design of mixed ionic and electronic conducting perovskite oxides for solid oxide fuel cell anode materials: A case study for doped SrTiO3, J. Power Sources, 2014, 245, 875–885 CrossRef CAS.
- H. Su and Y. H. Hu, Progress in low-temperature solid oxide fuel cells with hydrocarbon fuels, Chem. Eng. J., 2020, 402, 126235 CrossRef CAS.
- Y. Zhang, M. Han and Z. Sun, High performance and stability of nanocomposite oxygen electrode for solid oxide cells, Int. J. Hydrogen Energy, 2020, 45, 5554–5564 CrossRef CAS.
- B. C. H. Steele, Oxygen transport and exchange in oxide ceramics, J. Power Sources, 1994, 49, 1–14 CrossRef CAS.
- A. S. Bhalla, R. Guo and R. Roy, The perovskite structure—a review of its role in ceramic science and technology, Mater. Res. Innovations, 2016, 4, 3–26 CrossRef.
- T. Wan, L. Zhang, H. Du, X. Lin, B. Qu, H. Xu, S. Li and D. Chu, Recent Developments in Oxide-Based Ionic Conductors: Bulk Materials, Nanoionics, and Their Memory Applications, Crit. Rev. Solid State Mater. Sci., 2016, 43, 47–82 CrossRef.
- C. Cristiani, L. Zampori, S. Latorrata, R. Pelosato, G. Dotelli and R. Ruffo, Carbonate coprecipitation synthesis of Sr- and Mg-doped LaGaO3, Mater. Lett., 2009, 63, 1892–1894 CrossRef CAS.
- K. Huang, R. S. Tichy and J. B. Goodenough, Superior Perovskite Oxide-Ion Conductor; strontium- and Magnesium-Doped LaGaO3: I, Phase Relationships and Electrical Properties, J. Am. Ceram. Soc., 1998, 81, 2565–2575 CrossRef CAS.
- M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, A family of oxide ion conductors based on the ferroelectric perovskite Na0.5Bi0.5TiO3, Nat. Mater., 2014, 13, 31–35 CrossRef CAS.
- J. E. Auckett, K. L. Milton and I. R. Evans, Cation Distributions and Anion Disorder in Ba3NbMO8.5 (M = Mo, W) Materials: Implications for Oxide Ion Conductivity, Chem. Mater., 2019, 31, 1715–1719 CrossRef CAS.
- M. Yashima, T. Tsujiguchi, Y. Sakuda, Y. Yasui, Y. Zhou, K. Fujii, S. Torii, T. Kamiyama and S. J. Skinner, High oxide-ion conductivity through the interstitial oxygen site in Ba7Nb4MoO20-based hexagonal perovskite related oxides, Nat. Commun., 2021, 12, 556 CrossRef CAS.
- Q. Cao, R. Qiu, L. Lei, W. Zhang, S. Deng, J. Chen, L. He and J. Xu, Oxide Ion Conduction, Defect Chemistry and Conducting Mechanism in Ruddlesden–Popper La2−xMxBaIn2O7−0.5x (M = Ca, Sr, Ba), ACS Appl. Energy Mater., 2022, 5, 11213–11222 CrossRef CAS.
- W. Zhang, K. Fujii, E. Niwa, M. Hagihala, T. Kamiyama and M. Yashima, Oxide-ion conduction in the Dion-Jacobson phase CsBi2Ti2NbO10−δ, Nat. Commun., 2020, 11, 1224 CrossRef CAS PubMed.
- C. Long, W. Ren, Y. Li, L. Liu, Y. Xia and H. Fan, High oxide ion conductivity in the layer-structured Bi4Ti3O12-based ferroelectric ceramics, J. Mater. Chem. C, 2019, 7, 8825–8835 RSC.
- Y. Guo, W. Guo, L. Lei and J. Xu, Oxide ion conduction and transporting mechanism in the layered perovskite-related material Sr2Nb2O7, Scr. Mater., 2022, 221, 114962 CrossRef CAS.
- J. B. Goodenough, J. E. Ruiz-Diaz and Y. S. Zhen, Oxide-ion conduction in Ba2In2O5 and Ba3In2MO8 (M = Ce, Hf, or Zr), Solid State Ionics, 1990, 44, 21–31 CrossRef CAS.
- G. B. Zhang and D. M. Smyth, Defects and transport of the brownmillerite oxides with high oxygen ion conductivity—Ba2In2O5, Solid State Ionics, 1995, 82, 161–172 CrossRef CAS.
- S. Corallini, M. Ceretti, A. Cousson, C. Ritter and W. Paulus, Cubic Sr2ScGaO5 Perovskite: Structural Stability, Oxygen Defect Structure, and Ion Conductivity Explored on Single Crystals, Inorg. Chem., 2017, 56, 2977–2984 CrossRef CAS PubMed.
- C. A. Fuller, Q. Berrod, B. Frick, M. R. Johnson, M. Avdeev, J. S. O. Evans and I. R. Evans, Oxide Ion and Proton Conductivity in Highly Oxygen-Deficient Cubic Perovskite SrSc0.3Zn0.2Ga0.5O2.4, Chem. Mater., 2020, 32, 4347–4357 CrossRef CAS.
- A. Coelho, TOPAS Academic Version 4.1, Coelho Software, Brisbane, Australia. 2007 Search PubMed.
- J. Chen, L. Kang, H. Lu, P. Luo, F. Wang and L. He, The general purpose powder diffractometer at CSNS, Phys. B, 2018, 551, 370–372 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- A. Zunger, S.-H. Wei, L. G. Ferreira and J. E. Bernard, Special Quasirandom Structures, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed.
- S. Nose, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef CAS.
- B. M. Collins, A. J. Jacbson and B. E. F. Fender, Preparation of the Ordered Perovskite-Like Compounds Ba4M3LiO12 (M = Ta,Nb): A Powder Neutron Diffraction Determination Structure of Ba4Ta3LiO12, J. Solid State Chem., 1974, 10, 29–35 CrossRef CAS.
- R. Liu, Y. Xuan and Y. Q. Jia, A Simple Method for Judging Order or Disorder in A(B′B′′)O3 Perovskite Compound, J. Solid State Chem., 1997, 134, 420–422 CrossRef CAS.
- N. Setter and L. E. Cross, The contribution of structural disorder to diffuse phase transitions in ferroelectrics, J. Mater. Sci., 1980, 15, 2478–2482 CrossRef CAS.
- X. Zhang and Q. Wang, Study of the Order–Disorder Transition in A(B′Br′)O3 Perovskite Type Ceramics, J. Am. Ceram. Soc., 1991, 74, 2846–2850 CrossRef CAS.
- H. Gui and B. Gu, Order–Disorder Transition in (A′A′′)BO3 and A(B′B′′)O3 Complex Perovskite Crystals, J. Am. Ceram. Soc., 1996, 79, 381–384 CrossRef CAS.
- J. C. Grenier, N. Ea, M. Pouchard and P. Hagenmuller, Structural Transitions at High Temperature in Sr2Fe2O5, J. Solid State Chem., 1985, 58, 243–252 CrossRef CAS.
- G. B. Zhang and D. M. Smyth, Defects and transport of the brownmillerite oxides with high oxygen ion conductivity-Ba2In2O5, Solid State Ionics, 1995, 82, 161–172 CrossRef CAS.
- S. A. Speakman, J. W. Richardson, B. J. Mitchell and S. T. Misture, In situ diffraction study of Ba2In2O5, Solid State Ionics, 2002, 149, 247–259 CrossRef CAS.
- J. T. S. Irvine, D. C. Sinclair and A. R. West, Electroceramics: Characterization by Impedance Spectroscopy, Adv. Mater., 1990, 2, 132–138 CrossRef CAS.
- X. Kuang, M. A. Green, H. Niu, P. Zajdel, C. Dickinson, J. B. Claridge, L. Jantsky and M. J. Rosseinsky, Interstitial oxide ion conductivity in the layered tetrahedral network melilite structure, Nat. Mater., 2008, 7, 498–504 CrossRef CAS PubMed.
- D. Han, X. Liu, T. S. Bjrheim and T. Uda, Yttrium-Doped Barium Zirconate-Cerate Solid Solution as Proton Conducting Electrolyte: Why Higher Cerium Concentration Leads to Better Performance for Fuel Cells and Electrolysis Cells, Adv. Energy Mater., 2021, 11, 2003149 CrossRef CAS.
- K. D. Kreuer, S. Adams, W. Münch, A. Fuchs, U. Klock and J. Maier, Proton conducting alkaline earth zirconates and titanates for high drain electrochemical applications, Solid State Ionics, 2001, 145, 295–306 CrossRef CAS.
- R. L. Cook and A. F. Sammells, On the systematic selection of perovskite solid electrolytes for intermediate temperature fuel cells, Solid State Ionics, 1991, 45, 311–321 CrossRef CAS.
- A. F. Sammells, R. L. Cook, J. H. White, J. J. Osborne and R. C. MacDuff, Rational selection of advanced solid electrolytes for intermediate temperature fuel cells, Solid State Ionics, 1992, 52, 111–123 CrossRef CAS.
- T. Yao, Y. Uchimoto, M. Kinuhata, T. Inagaki and H. Yoshida, Crystal structure of Ga-doped Ba2In2O5 and its oxide ion conductivity, Solid State Ionics, 2000, 132, 189–198 CrossRef CAS.
- S. P. S. Badwal, Electrical conductivity of single crystal and polycrystalline yttria-stabilized zirconia, J. Mater. Sci., 1984, 19, 1767–1776 CrossRef CAS.
- M. Cherry, M. S. Islam and C. R. A. Catlow, Oxygen ion migration in perovskte-type oxides, J. Solid State Chem., 1995, 118, 125–132 CrossRef CAS.
- M. Yashima and T. Tsuji, Structural investigation of the cubic perovskite-type doped lanthanum cobaltite La0.6Sr0.4CoO3 d at 1531 K: possible diffusion path of oxygen ions in an electrode material, J. Appl. Crystallogr., 2007, 40, 1166–1168 CrossRef CAS.
- M. Yashima, K. Nomura, H. Kageyama, Y. Miyazaki, N. Chitose and K. Adachi, Conduction path and disorder in the fast oxide-ion conductor (La0.8Sr0.2)(Ga0.8Mg0.15Co0.05)O2.8, Chem. Phys. Lett., 2003, 380, 391–396 CrossRef CAS.
- R. A. D. Souza, Oxygen Diffusion in SrTiO3 and Related Perovskite Oxides, Adv. Funct. Mater., 2015, 25, 6326–6342 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: The mean square displacements (MSD) for Ba, Ta, Li, and O ions. See DOI: https://doi.org/10.1039/d3ya00268c |
| This journal is © The Royal Society of Chemistry 2024 |