Marcus inverted region in organic long-persistent luminescence host–guest systems designed from thermally activated delayed fluorescence molecules: a mechanistic study

Abstract

Organic long-persistent luminescence (OLPL) systems have long been experimentally investigated. First reported by Ifor D. W. Samuel et al., OLPL can be observed upon doping thermally activated delayed fluorescence (TADF) molecules in host materials of PPT, TPBi and PMMA and is proposed to proceed via a two-photon mechanism. In this work, OLPL that occurs upon doping CzPhAP in PPT/TPBi systems with charge-separation features was theoretically investigated to understand the essence of transformation from TADF to OLPL and to provide insights for further research. Theoretical results of this study revealed that OLPL emission from CzPhAP:PPT/TPBi systems proceeded via a double-luminescence mechanism. The main S₃ state emission peak (observed at 608 nm) was a mixture of TADF and OLPL. Moreover, large reorganization energy associated with converting S₁ into a low-lying charge-separation S₃ state enabled S₃ fluorescence with a larger emission rate (7.92 × 10⁷ s⁻¹) compared to that of S₁ fluorescence (3.94 × 10⁷ s⁻¹, shoulder peak observed at 584 nm). Thermodynamic equilibria between S₁ and low-lying charge-separation states of S₃ and T₃ were constructed, which stimulated fast conversion among the S₁, S₃ and T₃ states. Furthermore, our investigations indicated that when the reorganization energy of the ISC process is smaller than that of rISC, a larger ΔE_ST value is required to obtain k_rISC > k_ISC. Although a larger ΔE_ST value will make the ISC process deeply rooted in the Marcus inverted region, the ISC process will be strongly hindered and TADF emission could not be observed. Meanwhile, OLPL emission was enhanced with a larger ΔE_ST owing to frustrated charge recombination to the neutral T₁ state and electron–hole dissociation could occur. More importantly, our study indicated that the essence of conversion of TADF into OLPL in CzPhAP:PPT/TPBi systems is due to a low-lying neutral T₁ state.

---

1. Introduction

In ancient times, natural night-luminescent pearls were viewed as a precious heirloom and people believed that these pearls can keep corpses from decaying. However, in modern times, night-luminescent materials are no longer a noble secret and have gradually come into daily use. For example, the coat of paint on the hands of watches is one of the most common applications. Commercialized as glow-in-the-dark paints, long-persistent luminescence (LPL) materials have long been investigated and universally applied, stimulating the extensive research interests of materials scientists, chemists, physicists and biologists.^1–8 Among them, doped metallic oxides,^9–11 metal–organic frameworks^12–16 and host–guest systems^5,17–19 are three typical LPL materials. There are two major methods used to achieve the longer persistence of luminescence: doping with radioactive elements (such as radium) for continuous excitation in the dark and using materials with long-lived emission. As a typical example, MAl₂O₄ (M = Ca, Sr^20,21 or Ba^11,22,23) doped with europium and dysprosium was developed as a highly efficient LPL system. However, considering the requirement for RE elements and energy-consuming manufacturing processes, most pure inorganic LPL materials cannot meet the current principles of green chemistry and sustainable development.⁴ Organic compounds with a long-lived emission property have attracted considerable attention as alternatives to pure inorganic systems. In 1997, Ohkita et al. reported the first solid-state OLPL system of perylene:PnBMA (poly(n-butyl methacrylate)) with an after-glow reaching 200 s.²¹ In recent years, long-persistence has reached the thousand-second level for OLPL materials with an exciplex emission process, such as TMB (tetramethylbenzidine):PPT (2,8-bis(diphenyl-phosphoryl)dibenzo[b,d]thiophene), which was the first to reach the hour level,²⁴m-MTDATA (4,4′,4′′-tris[phenyl(m-tolyl)amino]-triphenylamine):PPT,²⁵ TMB:PBPO (poly(arylene ether phosphine oxide)),²⁶ and carbazolyl units doped poly(vinyl alcohol) (PVA) films.²⁷

It is well known that the TADF process increases the fluorescence quantum yields via re-converting the T₁ state to the S₁ state, yet there is no clear evidence showing that molecular TADF emission may produce LPL. Inspired by TADF's breakthrough in efficiency, Ifor D. W. Samuel et al. designed a new TADF molecule CzPhAP and doped it into the conventional hosts PPT and TPBi and the polymer host PMMA.²⁸ As reported, OLPL with a thousand-second level was observed with the three systems. Detailed spectroscopic research revealed that a combination of TADF small molecules and suitable hosts could bring great flexibility in the design of OLPL materials, making it possible to further decrease their cost and increase their efficiency. The OLPL mechanism of this novel system was reported to proceed via a two-photon mechanism, and experimental evidence showed that the OLPL duration increased with the application of a higher excitation density. However, the previous studies on OLPL were mainly based on spectroscopy and a theoretical study has not yet been carried out.

In this work, we studied CzPhAP-doped PPT and TPBi (CzPhAP:PPT, TPBi) (shown in Scheme 1) through density functional theory. According to our study, a different insight into the photophysical process is proposed to account for the experimental results, which is in contrast to the previous proposal discussed in the original work. First, our results revealed that the host material PPT plays the role of donor in this host–guest system, instead of the acceptor role mentioned in previous literatures, according to the inter-fragment charge-transfer (IFCT) analysis. Second, based on the non-radiative rates calculation proposed by Marcus–Levich–Jortner in their equation, out results showed that “OLPL” in this novel system (CzPhAP:PPT, TPBi) majorly resulted from a new kind of quasi-TADF process; whereas, traditional OLPL occurs via an electron–hole dissociation mechanism and charge-transfer excitation plays a negligible role. Through this work, a general computational scheme was constructed for investigating host–guest systems formed by the coupling of donor and acceptor molecules with OLPL or TADF properties.

Scheme 1 Guest molecule CzPhAP, where the AP moiety acts as an acceptor in intermolecular charge transfer, and the host molecules PPT and TPBi, where the DBT and PBi moieties act as donors in intermolecular charge transfer.

2. Methodology

2.1. MD simulations

In order to obtain the reasonable stacking patterns of CzPhAP and PPT, six initial models were built by the Packmol program, corresponding to CzPhAP : PPT ratios of 3 : 100, 1 : 100, 1 : 200, 1 : 300, 1 : 400, and 1 : 500, respectively. This ratio considers the high concentration of PPT in the experiment. The restrained electrostatic potential (RESP) atomic charges of CzPhAP and PPT were fitted by Multiwfn (development version 3.8).²⁹

Molecular dynamics (MD) simulations were performed using the GROMACS (version 2022.5) package³⁰ and the topology file and forcefield parameters were created by Sobtop.³¹ The long-range electrostatic interactions were handled by the particle-mesh Ewald (PME) method and the cut-off value of the van der Waals (vdWs) interactions was set to 10 Å.³² After energy minimization, the six systems were heated from 0 K to 500 K in 1 ns simulations and then maintained for 3 ns at the NPT ensemble. Subsequently, the temperature of the six systems was dropped to 300 K and another 100 ns unrestrained MD simulations were performed at the NPT ensemble to analyze the stacking patterns of PPT and CzPhAP. Based on the MD results, the favoured stacking conformation was selected as AP and DBT moieties, and then used for the following quantum mechanical (QM) investigations.

2.2. QM computational details

All the geometric structures were optimized with the Gaussian16 program (Revision C.01),³³ with the Minnesota hybrid functional with the M06-2X form³⁴ and def2-SVP basis sets developed by Ahlrich and co-workers used.³⁵ Grimme's third dispersion correction (D3) was adopted for better consideration of the intermolecular weak interactions.³⁶ Frequency calculations at the same level were performed for all structures on steady points to ensure no imaginary frequency existed. Excited states were calculated under the framework of time-independent density functional theory (TD-DFT) except for the T₁ states, which were calculated by the unrestricted Kohn–Sham method.

The electronic coupling integrals (V) in non-adiabatic processes were calculated by the fragment charge-difference (FCD) method^37,38 according to eqn (1), where ΔE_FC stands for the vertical energy gap between the studied states. Elements of the donor–acceptor 2 × 2 charge-difference matrix Δq were defined using eqn (2), where ρ_mn stands for the transition density matrix between states m and n. For the diagonal elements Δq₁₁ and Δq₂₂, ρ_mn refers to the transition electronic density for the excited states. For the off-diagonal elements Δq₁₂ and Δq₂₁, eqn (3) was applied for symmetrizing. The integrals involved in the FCD calculation can be calculated as summations on the introduced basis set according to Slater–Condon's rule, and an approach for this can be found in the ESI.†

The spin–orbit coupling integrals (H) were calculated using the Dalton2020 program,^39,40 with both single- and double-electron spin–orbit integrals precisely calculated under the CAM-B3LYP/def2-SVP level of theory.⁴¹ Wavefunction analysis was carried out using Multiwfn (development version 3.8),²⁹ and visual molecular dynamics (VMD, version 1.9.3) was applied for better visualization of our results.⁴² More details and full results of the calculation works are available in the ESI.†

2.3. Theoretical backgrounds

Charge-separation states exist in many chemical systems.⁴³ Consider an arbitrary donor–acceptor system D–A, where D refers to the donor and A refers to the acceptor. As pointed out by the electroneutrality principle,^44,45 it is impossible to observe D⁺A⁻, where exactly one electron is transferred from D to A. Theoretically, we use the population number, which is commonly not an integer, to evaluate the fuzzy concept of the “number of electrons” evolved in a charge-transfer process.

In an OLPL system, the charge-separation state is a key metastable intermediate.²⁴ Generally, such a charge-separation state is a special charge-transfer state in which the obviously separation of electrons and holes can be observed. Conceptually, the population number change should be close to 1. Fig. 1 shows a potential energy surfaces diagram of the neutral state and charge-separation state with a conical intersection point. The charge-separation state can be reached via photoinduced or thermally activated charge transfer. On the opposite, charge recombination is usually realized by a non-radiative process. These concepts have been commonly acknowledged in the research on OLPL materials.²⁴ Therefore, the charge-separation state is an excited state, if the neutral state is selected as the reference state. The main difficulty with this idea is that the charge-separation state of complicated systems is not the lowest excited state, especially for host–guest or highly conjugated systems. Moreover, ideal charge-separation states usually include a singlet state and a triplet state with a quite small energy gap. Therefore, in investigating OLPL systems, it is essential to refer to proper excited states as the charge-separation states.

Fig. 1 Charge transfer in the donor–acceptor system.

In this framework, the rates of non-radiative processes are calculated by the Marcus–Levich–Jortner equation under the classical situation (eqn (4)), which gives a semi-empirical prediction of the rate of charge transfer between the donor and acceptor.

where λ stands for the reorganization energy and ΔE stands for the energy change of the process. For the internal conversion (IC) type of charge transfer, H_ij is replaced by the electronic coupling integral (V) between states i and j. For the intersystem crossing (ISC) type of charge transfer, H_ij corresponds to the spin–orbit coupling integral. The reorganization energy is decomposed into contributions of each vibrational normal mode under a harmonic oscillator model, as shown in eqn (5), where k_i refers to the vibrational force constant and ΔQ_i refers to an element of the shift vector. The shift vector is defined by Duschinsky's relation (eqn (6)), which points out the linear transformation relation between the vibrational normal modes of two states. Here, J is Duschinsky's matrix and ΔQ is the shift vector.

Q₂ = J·Q₁ + ΔQ (6)

The Huang–Rhys factor S_i is defined by eqn (7).

The Huang–Rhys factor reveals the strength of vibronic coupling.^46–48 Non-radiative processes with large Huang–Rhys factors tend to occur easier. Apart from this, we may also gain insight into which normal vibrational mode makes a crucial contribution to the process.

Einstein's spontaneous emission rate formula (eqn (8)) was used to calculate the rates of the radiative processes including fluorescence and phosphorescence,^49,50 where f_ij stands for the transition oscillator strength and ν stands for the transition energy in the form of a wavenumber (cm⁻¹). Since phosphorescence is spin forbidden, spin–orbit coupling was considered to calculate the oscillator strength between the T₁ state and S₀ state.

3. Results and discussion

3.1. Stacking conformation

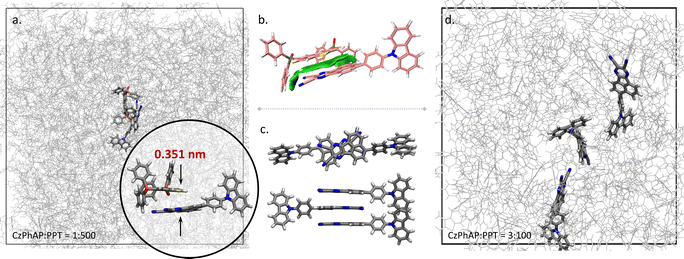
Annealing MD simulations showed that the stacking conformation was favoured between the AP moiety of CzPhAP and the DBT moiety of PPT (see abbreviations in Scheme 1). Taking the MD system with 501 molecules (CzPhAP : PPT = 1 : 500) as an example (Fig. 2a), though the initial position and orientation of molecules were randomly generated, after annealing, the stacking conformation between the AP and DBT moieties was always observed, with a minimum distance of 3.51 Å between the mass centres of the AP and DBT moieties. Changing the concentration of the dopant did not affect obtaining such a conformation (Fig. S1–S5, ESI†). The statistics of the distance between the mass centres showed that such a conformation could be maintained during a notable length of simulation time. The mass centre distance led by the PPT molecule possessed the longest binding period with CzPhAP during the 100 ns MD simulation after annealing, as plotted in Fig. S1–S5 (ESI†). The minimum distance ranged between 2.8–5.1 Å, which is a suitable distance for π–π stacking interactions. This was also demonstrated by the reduced density gradient (RDG) analysis (Fig. 2b). At the same time, it has also been acknowledged in experimental designation that the AP moiety in CzPhAP usually acts as an electron acceptor while the DBT moiety in PPT acts as an electron donor. A D–A pair close in space is generally reasonable. Therefore, the following investigation based on quantum chemical calculations adopted the structure optimized from a stacking conformation between AP and DBT.

Fig. 2 (a) MD simulation showing π–π stacking conformation between the DBT moiety of PPT and AP moiety of CzPhAP; (b) non-covalent interactions between DBT and AP revealed by reduced density gradient analysis (isovalue: 0.60); (c) Initial stacking conformation with multiple dopant molecules and (d) separated by host molecules after MD simulation.

Considering that dopant clusters with more than one dopant molecule may influence performance, i.e. in this system, π–π stacking between AP and AP moieties may prevent that between AP and DBT moieties, the stacking behaviour in the model system with a high dopant concentration (CzPhAP : PPT = 3 : 100) was investigated as well. The AP–AP stacking conformation shown in Fig. 2c was used as the initial structure for the MD simulation, while after 100 ns MD simulations, these dopant molecules were largely separated by host molecules (Fig. 2d). These results demonstrated that the binding affinity between CzPhAP and PPT brought about by AP–DBT π–π stacking interactions plays a crucial role in the host–guest system investigated.

3.2. Charge-separation state

The electron–hole analysis and inter-fragment charge-transfer (IFCT) method^51,52 were adopted to reveal the character of electron transfer in the excited states in the studied host–guest system. The distributions of electrons and holes in the CzPhAP:PPT host–guest system are shown in Fig. 3, where the electron area is coloured with green and the hole area is coloured with magenta. The lowest S₁ state, which was reached via single photon excitation, showed charge transfer by a population number of 0.4575 from PPT to CzPhAP, as evaluated by the IFCT method. Thus, PPT molecules can be regarded as donors in this single photon excitation process. In contrast, the T₁ state was associated with a negligible charge transfer by only the 0.0380 population number involved. Besides, the electron and hole areas were all distributed on the AP moiety of the CzPhAP molecule in the T₁ state. Moreover, among the lowest 10 singlet excited states studied, only the S₃ state showed the feature of charge separation. The IFCT population number of the S₃ state reached the highest as 0.8418, being close to the ideal value of 1.0. Similarly, among the lowest 10 triplet excited states studied, the IFCT population number of the T₃ state ranked the highest, with a calculated IFCT population number of 0.5634. Therefore, the T₃ state can be viewed as a triplet charge-separation state. According to the isosurface distribution displayed in Fig. 3, the electron areas of both the S₁ and S₃ states were distributed mainly on AP moiety; however, the hole area of the S₁ state was distributed on both the CzPhAP and PPT molecules, indicating that the S₁ state was a mixture of through-space charge transfer (TSCT, PPT → CzPhAP) and through-bridge charge transfer (TBCT, within CzPhAP).

Fig. 3 Isosurface (isovalue: 0.0030 a.u.) of the electron–hole distribution and IFCT population change for different excited states of the CzPhAP:PPT host–guest system. Electron refers to the area in the excited state where electron density is increased compared with that of the ground state, while hole is the opposite, as evaluated by the population number. The detailed electron–hole distributions and IFCT results are listed in Tables S3 and S4 (ESI†).

A similar conclusion was also reached for the host–guest system CzPhAP:TPBi. As shown in Fig. S6 (ESI†), both the higher S₃ and T₁₀ states showed a notable charge-transfer feature, with calculated IFCT population changes of 0.9253 and 0.7901, respectively. Whereas, the lowest excited states S₁ and T₁ did not show a charge-transfer character, with the calculated IFCT population change nearly zero. Moreover, it should also be pointed out that TPBi also acts as a donor molecule and the designed CzPhAP molecule plays the acceptor role in this host–guest system. Our conclusion is in contrast to the viewpoints in previous references, where PPT and TPBi molecules were claimed to be acceptors,^24,25,53,54 which was based on HOMO–LUMO levels simply calculated by DFT, or wrongly took from redox potentials measured by cyclic voltammetry. The excited states reached by single photon excitation do not necessarily correspond to HOMO → LUMO excitation. Therefore, the optical gap and donor–acceptor roles cannot be determined via simply comparing the HOMO–LUMO levels of different molecules.⁵⁵ As demonstrated by previous electron–hole analysis and inter-fragment charge-transfer (IFCT) analysis, the host–guest molecules should be viewed as a whole as the influence of the host–guest effect on the molecular optical or electronic properties cannot be ignored. However, in heterojunction structure systems, the properties of one bulk phase are not strongly influenced by another, which thus ensures materials can retain their major electronic–structural features. Therefore, the HOMO–LUMO levels of different materials determined in the bulk phase can be applied to predict their photochemical or electrochemical performance.

In the following, the transition density matrix (TDM) was calculated to analyze the transition feature in the host–guest systems CzPhAP:PPT and CzPhAP:TPBi. For a many-electron system, the real space function form of TDM is expressed as eqn (9.1), where, Φ⁰ and Ψ^exc represent the ground-state and excited-state wavefunctions, respectively. It can be further written as a three-dimensional real function in eqn (9.2) under the TDDFT framework, where ϕ_i and ϕ_a stand for occupied and unoccupied orbitals involved in a specific single excitation configuration function with the coefficient of w^a_i.

By introducing a set of basis functions, the orbitals in eqn (9.2) can be expanded to eqn (10.1) and the TDM element is defined as eqn (10.2). Here, C_μi represents the coefficient of the basis function χ_μ in orbital ϕ_i and the double summation runs over every single excitation configuration function i → a.

The above definition extracts excitation information into each couple of basis functions. A more chemically meaningful expression is to condense the basis function TDM into atomic TDM, whose element corresponding to atoms A and B is given in eqn (11).

Fig. 4 shows the atomic TDMs of the S₁, S₃, T₁, and T₃ states in the CzPhAP:PPT system, where the atom range is marked with PPT or CzPhAP. Elements in the diagonal area from the lower left to the upper right show a local-excitation (LE) character while elements in the non-diagonal area show a charge-transfer (CT) character. The S₁ state of the CzPhAP:PPT system showed a strong PPT → CzPhAP CT character, while the CzPhAP → CzPhAP LE character also made a notable contribution. While in the S₃ state, the bright area was majorly distributed within the PPT → CzPhAP CT area, indicating a stronger CT character in the S₃ state, and thus it acts as a charge-separation state. This is consistent with the previous discussion. This also holds for other key excited states and moreover, the LE and CT characters showed an even starker contrast in the other three pairs of excited states. Therefore, in the studied system, the higher excited states acting as charge-separation states was confirmed, which is theoretically most relevant to OLPL. A similar conclusion also holds for the S₃ and T₁₀ states in the CzPhAP:TPBi system (as discussed in Fig. S7, ESI†). In the following sections, the photochemical mechanism in the CzPhAP:PPT system is discussed.

Fig. 4 Atomic transition density matrices of key excited states in the form of heat maps for the CzPhAP:PPT host–guest system.

3.3. Geometry and vibration

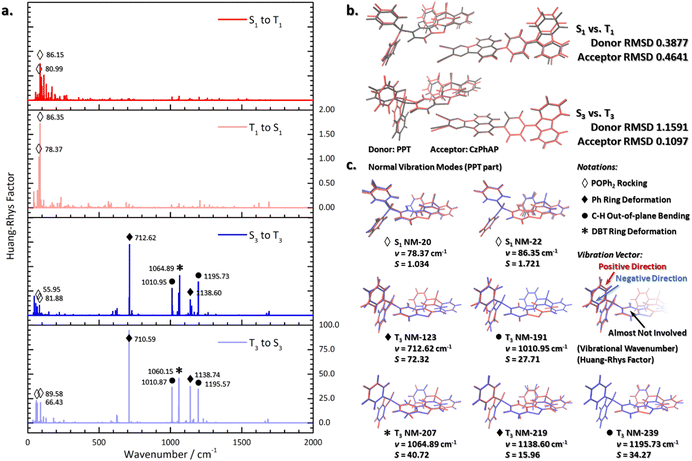
Previous theoretical works have pointed out that the geometric structure plays a significant role in non-radiative processes. As revealed by the Huang–Rhys factors calculated according to eqn (5)–(7), geometric reorganization during the (r)ISC process can be decomposed into the normal vibration modes, shown in Fig. 5a. Larger Huang–Rhys factors reveal a stronger vibronic coupling effect and indicate a faster non-radiative process.^56–60 For S₁–T₁ processes, low-frequency normal vibration modes have larger Huang–Rhys factors, which are subjected to the rocking vibration modes of POPh₂ groups in the PPT part (marked with white diamond in Fig. 5). This could also be revealed by the overlapping minimum points of both structures with the root-mean-square deviation (RMSD) minimized. Since the donor and acceptor molecules are not bound with chemical bonds, they are separated when evaluating the geometric change with the RMSD in order to avoid disturbing each other.

Fig. 5 (a) Huang–Rhys factor diagrams for S₁–T₁ and S₃–T₃ (r)ISC processes. (b) Root-mean-square deviation between S₁–T₁ and S₃–T₃ minimum structures. (c) Normal vibration modes with significant contributions to (r)ISC processes.

As shown in Fig. 5b, the structural deformation of PPT was majorly contributed by the POPh₂ groups. Thus, the RMSD value of the rigid central thiophene ring of PPT was first minimized, and then the total RMSD value was calculated to evaluate the structural deformation of PPT. The black framework (singlet state structure) overlapped with the red framework (triplet state structure) at the central aromatic rings in the PPT part, while showed a deviation at the lateral groups. In comparison of the S₁ and T₁ states for the CzPhAP part, the major deviation came from the Cz group. However, due to the micro Huang–Rhys factors associated with the related normal vibration modes, the non-radiative processes between the S₁ and T₁ state were not enhanced. In comparison between the structures of the S₃ and T₃ states, the deviation in the POPh₂ group of the PPT part was much stronger, while the deviation in the CzPhAP part was negligible. This was the same with the two couples of structures where the structural deviation majorly originated from the lateral groups. Both the donor and acceptor parts contributed to structural deviation, notably in the S₁–T₁ couple; however, in great contrast, for the S₃–T₃ couple, the donor molecule accounted for most of the structural deviation, as revealed by the RMSD in Fig. 5b. Since both POPh₂ and Cz groups are exposed to the surrounding environment, S₁–T₁ processes will be strongly affected by solvent molecules. A strong interaction with solvent molecules or a rigid environment (thin-layer for instance) make related processes harder to occur by hindering reorganization of the lateral groups.

Moreover, the deformation and bending modes of the PPT part (marked with black notations) had a greater impact in the S₃–T₃ related non-radiative processes. As shown in Fig. 5a, the deformation and bending modes of the PPT part were distributed in a wider region of wavenumber (700–1200 cm⁻¹, but narrower in energy indeed), which was in contrast to the low-frequency region (50–100 cm⁻¹) associated with the rocking modes. This is the most important feature that distinguishes the S₁–T₁ and S₃–T₃ processes. Although the rocking modes of the S₃–T₃ series had even larger Huang–Rhys factors compared with those of the S₁–T₁ series, they did not dominant the S₃–T₃ related non-radiative processes since the deformation and bending modes of the PPT part had comparatively larger Huang–Rhys factors, acting as the decisive strengths.

It is well known that the surrounding environment has a more important impact on the rocking mode compared with deformation and bending modes due to the steric hindrance. Hence, the S₃–T₃ related non-radiative processes are reliably ensured by normal vibration modes with higher Huang–Rhys factors. This is important since S₃–T₃ related non-radiative processes are crucial to thermochemical equilibrium between singlet and triplet charge-separation states (S₃ and T₃) and we discuss this further in the next section. Nevertheless, it is worth noting that for the normal vibration modes in the region of 700–1200 cm⁻¹, although the large Huang–Rhys factors and reorganization energies indicated remarkable structure distortion in the related processes, they were not reliable for calculating the total reorganization energies of non-radiative processes. This is because in the calculation of the reorganization energies contributed by each normal vibration mode, harmonic oscillator approximation is applied to evaluate the vibration potential energy. It was obvious that the potential energy surfaces (PESs) of S₃ and T₃ presented notable differences and so eqn (5) is no longer applicable. Moreover, the reorganization energy decomposition and Huang–Rhys factors calculated under the harmonic oscillator approximation can still reveal the key normal vibration mode contribution to the non-radiative processes. But when calculating the total reorganization energy for rates prediction (Section 3.4), and to account for the reorganization energy induced by electronic structure change, the four-point method should be adopted instead of eqn (5).

Besides, the unchanged parts of the structures also play an important role in ensuring charge transfer and the photochemical properties. In the host–guest system CzPhAP:PPT, the donor and acceptor molecules are bound by intermolecular π–π stacking interactions, involving the dibenzothiophene (DBT) part of PPT and AP part of CzPhAP (Fig. 2b). The rigid aromatic ring structures ensure the π–π stacking structure act as a reliable TSCT tunnel. The related key normal vibration mode is a DBT ring deformation mode (1060.15 cm⁻¹ in the S₃ state and 1064.89 cm⁻¹ in the T₃ state, marked with “*”). Thus, the distance between π-conjugate systems does not increase obviously due to the within-plane deformation mode, and it can hardly influence the π–π stacking structure. As aforementioned, both S₁–T₁ and S₃–T₃ processes showed charge-transfer characters, and so an effective π–π stacking structure acting as a TSCT tunnel is crucial for good photochemical properties.

3.4. Photochemical mechanism

In the following sections, the detailed photochemical relaxation pathways and mechanism why the TADF molecule CzPhAP can display the OLPL property when doped in the host material PPT were studied based on Marcus’ theory.‡

3.4.1. Primary processes. The theoretically predicted steady-state UV-vis absorption spectra of related species are shown in Fig. 6. The full spectra (200–800 nm) can be found in Fig. S8 (ESI†). Both the CzPhAP molecule and CzPhAP:PPT host–guest system have the first absorption peak at around 375 nm. However, the excitation features are different. As can be seen from the electron–hole distributions, the molecular absorption of CzPhAP resulted in TBCT from the AP moiety to the CzPh moiety. In the host–guest system, the acceptor moiety (where the isosurface of the electrons is majorly distributed) remains the AP group; however, the main donor moiety is PPT, behaving as TSCT. This is consistent with the experimental results showing that when CzPhAP was doped in different host materials, it displayed similar steady-state absorption spectra. This phenomenon can be misleading, since the commonly used host materials should be insensitive to the visible or near-UV region, and thus the observation of similar spectra may hide the truth that interactions between the host and guest molecules may have an influence on the absorption feature. Here, the electron–hole distributions again demonstrated that the host materials participate in the photochemical mechanism in the very first step.

Fig. 6 Calculated UV-vis absorption spectra and electron (grey)–hole (white) distributions for CzPhAP and CzPhAP:PPT.

3.4.2. Secondary processes. The rates of all the non-radiative processes, including the intersystem crossings and internal conversions, were calculated using the Marcus–Levich–Jortner equation and the results are listed in Tables 1 and 2, respectively. Total reorganization energies were calculated by the four-points method. Below we use the notations in Table 1 and 2 to discuss these for clarity. From the S₁ state obtained via a one-photon absorption process, two non-radiative processes towards the T₃ state and S₃ state were accessible dynamically, with rates of r₂ = 4.95 × 10⁸ and k₁ = 3.02 × 10¹¹, respectively. ISC from S₁ to T₁ is an exothermic process and has advantages thermochemically. However, the rate constant of ISC from S₁ to T₁ (r₁ = 1.36 × 10⁻²⁹) is too small to take place. By comparing the reorganization energy and electronic energy difference, it can be seen that this process lies in the Marcus inverted region, as ΔE ≪ −λ (−0.724 eV vs. −0.050 eV) for ISC from S₁ to T₁. The neutral triplet state was lower in energy than the charge-separated triplet state (T₃), nevertheless, such energy stability brings dynamical disadvantage in charge recombination from the S₁ state. Conversely, converting the S₁ state to T₃ (ΔE = −0.015 eV) and S₃ (ΔE = −0.018 eV) states have notable non-radiative rates owing to the narrow energy gaps between the initial and final states.

Table 1 Intersystem crossing rates

Process	Notation	λ/eV	ΔE/eV	H/cm^−1^a	k/s^−1
a Spin–orbit coupling matrices elements are listed in Table S5 (ESI).
S1 → T1	r 1	0.050	−0.724	2.245	1.36 × 10^−29
S1 → T3	r 2	0.107	−0.015	1.165	4.95 × 10^8
S3 → T1	r 3	0.193	−0.706	0.654	4.53 × 10^2
S3 → T3	r 4	0.162	0.003	1.774	3.91 × 10^8
T1 → S1	r −1	0.899	0.724	4.237	2.01 × 10^−3
T1 → S3	r −3	0.104	0.706	4.171	2.66 × 10^−17
T3 → S1	r −2	0.553	0.015	1.072	1.36 × 10^6
T3 → S3	r −4	0.095	−0.003	1.110	4.36 × 10^8

---

Table 2 Internal conversion rates

Process	Notation	λ/eV	ΔE/eV	V/cm^−1^a	k/s^−1
a Detailed FCD results are listed in Table S6 (ESI).
S1 → S3	k 1	0.659	−0.018	636.7	3.02 × 10^11
S3 → S1	k −1	0.419	0.018	1655.7	1.30 × 10^13
T1 → T3	k 2	0.100	0.709	158.7	5.39 × 10^−15
T3 → T1	k −2	0.213	−0.709	145.5	1.52 × 10^8

---

We should also notice that since the potential energy surfaces (PESs) of the S₁ and S₃ states interact with each other, the minimum point reached by state-tracking the PES of the S₃ state was even slightly lower in energy compared with the S₁ state minima. This shows that partial charge recombination and relaxation bring extra stability for the charge-separation state. Since r_±2 and k_±1 were much larger than the rates for the following processes, we can consider both processes as fast equilibria reached between 1–1 order opposing reactions, with equilibrium constants of K_ISC2 = r₂/r₋₂ = 2.75 × 10⁻³ and K_IC1 = k₁/k₋₁ = 2.32 × 10⁻², respectively. Both equilibria hold the concentration of systems in the S₁ state. With the T₃ and S₃ states being converted in the following processes and the S₁ state produced by continuous excitation (since the excitation time was much longer than that needed for reaching fast equilibria, it could be viewed as continuous), the equilibria were pushed towards the direction of the products, within which S₃ was the major product since k₁ > r₂.

Another equilibrium was then reached between S₃ and T₃ states (K_ISC4 = r₄/r₋₄ = 0.897). The small energy gap (0.003 eV) between charge-separation states with different spin multiplicity enabled the Marcus inverted region to be impossible to be reached for both the ISC and rISC processes. This is different from (r)ISC processes between the S₁ and T₁ states. Such a difference was also consistent with the non-radiative coupling strength qualitatively revealed by the Huang–Rhys factors in Fig. 5a. Generally, the three fast equilibria discussed above ensure the concentration of excited systems as S₁ > S₃ > T₃.

3.4.3. Luminescence. We next focus on fluorescence emission. Since the S₃ minimum was lower in energy than the S₁ minimum, it is important to consider fluorescence emission at the S₃ minimum. There was a peak emission at 608 nm and a shoulder emission at 584 nm based on the experimental steady-state photoluminescence spectrum. Moreover, there was only a peak at 584 nm observed in 1–100 ns under the same condition based on the time-resolved photoluminescence (TRPL) spectrum. The major peak red-shift from 584 nm to 608 nm was experimentally explained as the structural reorganization or relaxation of excited molecules. Whereas, based on our computations, the 608 nm peak was generated via emission at the S₃ minimum, which contributed most to the observed OLPL emission. Therefore, we can conclude that the long-persistent luminescence in the CzPhAP:PPT host–guest system was not conventional OLPL.

Previously, three OLPL mechanism have been reported: (1) two-photon mechanism proposed by Ohkita et al.,^21,61,62 (2) charge-separation model based on CT excitation dissociation proposed by Kabe et al.,^24,53 and (3) CT excitation dissociation based on spontaneous orientation polarization (SOP) proposed by Yamanaka et al.⁶³ In previous charge-separation systems, the high-lying charge-separation state can be reconverted into a neutral state (usually the S₁ state), and thus delayed luminescence emission at the S₁ minimum would be observed, which is referred to as the OLPL mechanism (charge-separation model based on CT excitation dissociation). In those reported charge-separation OLPL mechanisms, the minimum points of the available charge-separation states are higher in energy than the neutral S₁ state. Thus, charge-separation states can be continuously reconverted via non-radiative charge recombination processes, which obeys Kasha's rule and emits at the lowest singlet state. Vibronic coupling is significant for non-radiative processes in such a situation. From a more non-radiative viewpoint, the minimum energy crossing point (MECP)^64,65 of neutral and charge-separation states is too high in energy to be reached. However, in the studied CzPhAP:PPT host–guest system, luminescence can also be emitted by the charge-separation state (S₃).

In the studied CzPhAP:PPT host–guest system, for the S₃ and T₃ states, the RMSD calculation values of the donor molecule and DBT part of the acceptor molecule that acts as the hole were both very small (Fig. 5b). Hence, the two minimum points were quite close in nuclear coordinates. Therefore, MECP was strictly limited within the two minimum points and only a small energy barrier was needed to overcome this. Therefore, the related non-radiative processes could be forwarded by the thermal-driven force. This is why the harmonic oscillator approximation failed to give reasonable reorganization energies and Huang–Rhys factors. Meanwhile, a thermodynamic equilibrium was built between the two minimum points of the neutral and charge-separation states, as discussed in previous sections. The charge-separation state could be close to or even lower than that of the neutral S₁ state. Furthermore, it resulted in double fluorescence emissions, which is anti-Kasha's rule. This new double-luminescence mechanism originated from the energy gap of the neutral and charge-separation states and is in great contrast to the previously reported mechanism.

As shown above, the CzPhAP:PPT host–guest system induced double luminescence. The S₁ emission (observed at 584 nm) displayed a conventional OLPL peak generated by a charge-separation–recombination mechanism. This is because both the S₃ and T₃ states were charge-separation states. The S₃ emission (observed at 608 nm) is more complicated. Since the S₃ state can be reached from both the S₁ and T₃ states, a mixture of emissions from the two mechanisms can be generated. First, the new OLPL mechanism discussed above could be constructed via the S₁ → S₃ IC process, emitting directly via radiative charge recombination. Second, a quasi-TADF pathway could be constructed via the T₃ → S₃ ISC process. The difference between the “quasi-TADF” and TADF pathway is that the minimum point of the S₃ state was slightly lower than that of the T₃ state in this system. This photochemical mechanism also explains the influence of the quasi-TADF effort in the OLPL system.

However, in both mechanisms, the thermal barrier cannot be avoided and it still behaves as a thermally activated process. Moreover, the quasi-TADF mechanism demonstrated that TADF emission can not only be generated by the lowest couple of excited states (S₁ and T₁), but also can be generated from higher ones with a different excitation character. Table 3 also shows that the S₃ emission had a larger oscillator strength and emission rate compared with the S₁ emission, which well corresponded to the experimental spectrum showing that the main peak was longer in wavelength.

Table 3 Fluorescence and phosphorescence rates

Process	Notation	f/a.u.	λ/nm^a	k/s^−1
a Fluorescence wavelengths were taken from experimental results. b Calculated via the Dalton2020 program using quadratic response theory.
S1 → S0	k F1	0.2016	584	3.94 × 10^7
S3 → S0	k F3	0.4391	608	7.92 × 10^7
T1 → S0	k P1	2.21 × 10^−9^b	667	3.32 × 10^−1

---

Apart from the fluorescence emission, phosphorescence emission also existed on the T₁ state, albeit the emission strength was much weaker than fluorescence (Table 3). Compared with the neutral T₁ state, the charge-separation T₃ state was a high-lying excited state, with a calculated T₃ → T₁ IC rate of k₋₂ = 1.52 × 10⁸. Therefore, the phosphorescence emission in the CzPhAP:PPT host–guest system still obeys Kasha's rule, which indicated that the high-lying state converted to the lowest triplet state via an IC process. These results were consistent with the experimental findings.

3.4.4. Marcus inverted region and reorganization energy. Theoretical studies have shown that the energy gap between the lowest singlet and triplet states (ΔE_ST) is an important parameter in designing various kinds of photochemical properties. The ΔE_ST value of the CzPhAP:PPT system was calculated as the difference in the on-set values of the fluorescence and phosphorescence spectra, which was reported to be 0.24 eV. However, as discussed above, the main peak of the fluorescence spectrum originated from S₃ emission. The measured ΔE_ST value experimentally was thus calculated as the energy difference between the S₃ and T₁ states. It is not reliable to take the emission energies difference as the energy gap of the excited states due to the corresponding Franck–Condon structures of the two emissions on the ground-state PES usually possess different energies. The ΔE_ST (0.724 eV) was theoretically predicted to be larger than the true value, since only one host molecule was included in the studied system.

Fig. 7a gives the ln k–ΔE_ST curve of processes related to T₁ state, where reorganization energies and coupling integrals are viewed as constants. With the experimental ΔE_ST value, ISC processes from both S₁ and S₃ states to T₁ state will have notable rate constants, resulting in obvious phosphorescence emission. However, the theoretical ΔE_ST value (0.724 eV) reveals that the above two ISC processes are remarkably limited by Marcus inverted region (monotonic decreasing part of the curve). Only IC process from T₃ state to T₁ state is not strictly limited, with a rate constant k₋₂ = 1.52 × 10⁸; however, ISC process from T₃ state to S₁ state (r₋₄ = 4.36 × 10⁸) and low concentration of T₃ state are extra limitations. This result indicates that that no obvious phosphorescence emission is observed in long-persistent luminescence, which is in consistence with the experiments.

Fig. 7 (a) The ln k–ΔE_ST curves of non-radiative processes related to the T₁ state, with reorganization energies and coupling integrals viewed as constants. Energy of the S₁ state was taken as the zero point. (b) Three conditions of possible crossing.

As discussed above, the Marcus inverted region plays a significant role in non-radiative processes. Taking the CzPhAP:PPT host–guest system as an example, a larger ΔE_ST value is an advantage for OLPL; however, a smaller ΔE_ST value does not have a similar influence on TADF. In previous research, TADF systems were believed to have a small ΔE_ST value (usually < 0.10 eV) in order to enhance the rISC process from the T₁ state to the S₁ state. As shown in Fig. 7a, TADF emission induced by the rISC process from the T₁ state to the S₁ state could only be observed when the black dot line was higher than the black solid line (r₁ < r₋₁). This condition can be satisfied within two regions.

First, when ΔE_ST > 0.36 eV, although the TADF condition is satisfied, TADF emission will be limited by the small ISC rate constant deeply located in the Marcus inverted region. In other words, the pre-process for rISC in the TADF mechanism is limited and a singlet system cannot be efficiently converted to a triplet system. Another region is where the T₁ state is higher than the S₁ state (ΔE_ST < 0), which is not displayed in Fig. 7a since it is unlikely to be realized in organic systems. Therefore, it is worth noting that a small ΔE_ST value is not always advantageous for TADF emission. Such a result is different from the viewpoint of previous research, where a small ΔE_ST value was always considered an advantage for TADF emission. Based on the above discussion, we can expand the old viewpoint for the better by taking the first-derivative of the ln k–ΔE_ST curve into consideration. According to the Marcus–Levich–Jortner equation (eqn (1)), this curve is a parabolic curve with a negative quadratic term coefficient (−1/4λkT, eqn (12)) and its first-derivative is eqn (13).

The absolute value of the quadratic term coefficient (1/4λkT) of the solid line is smaller than that of the dotted line for both the red and blue couples in Fig. 7a. The non-radiative process corresponding to the solid line has a larger reorganization energy compared with its reverse process. In such a circumstance, a larger ΔE_ST value will be beneficial for the TADF behaviour since the TADF region where the dotted line is higher than the solid line lies in the left side of the crossing point of two curves. This scheme can explain the observation in previous literature. Nevertheless, the crossing of two parabolic curves has three conditions (Fig. 7b). Only Condition III is allowed for relation eqn (12) (Fig. 7a can be an example) and we provide a simple proof for this conclusion in the appendix section (eqn (A1)–(A3)).

However, if the reorganization energy of the ISC process from the S₁ to T₁ process (0.050 eV) is smaller than that of the corresponding rISC process (0.899 eV), the smaller ΔE_ST value will not benefit the TADF behaviour and the T₁ state cannot be effectively reconverted to the S₁ state through the rISC process. When ΔE_ST value increases, although the rISC rate increases to be higher than the ISC rate, the Marcus inverted region limits both processes and conversion between the S₁ and T₁ states is almost banned, which also has no benefit for TADF emission. Conversely, this phenomenon may enhance OLPL emission by avoiding the loss of excited molecules on the neutral triplet state T₁. This is because in the CzPhAP:PPT host–guest system, all non-radiative processes starting from the T₁ state had quite low rates due to the low energy level of the T₁ state and only phosphorescence emission or non-radiative decay to the ground state were possible pathways, which should be avoided in designing OLPL systems. Therefore, we suggest that a low-lying neutral T₁ state is the key point for observation of the OLPL property upon a TADF molecule being doped in to host materials like PPT or TPBi.

Now we have noticed that the reorganization energy is an important influencing factor in OLPL emission, for a further step considering two minimum points connected by a couple of non-radiative processes, since the shift vector ΔQ is the same for both processes, the reorganization energies depend on the force constants of the normal vibration modes (k). Larger force constants correspond to larger gradients of PES, graphically behaving as a steeper PES. Therefore, the reorganization energies depend on whether the specific PES is steep or not. In experimental studies, reorganization energy can be examined by measuring Stokes shifts of absorption and the PL spectra, which provides a possible direction to adjust and improve the host–guest system. We may focus on the rational design of these two kinds of systems and relationship between them therefore.

4. Conclusions

In this work, we present a theoretical scheme for investigating the photochemical properties and mechanism of OLPL host–guest systems with charge-separation features. A recently reported OLPL system designed from the TADF molecule (CzPhAP:PPT/TPBi) was taken as an example. The rates of non-radiative processes and influence of the Marcus inverted region were analysed in detail. New insights into the rational design and adjustment of OLPL and TADF systems were provided.

The host materials PPT and TPBi acted as donors in these novel systems, which is different from previous viewpoints reached by simply comparing the HOMO–LUMO gaps of the materials measured by cyclic voltammetry. The S₁ and T₁ states of both systems (CzPhAP:PPT and CzPhAP:TPBi) majorly showed local excitation, while the higher excited states S₃, T₃ for CzPhAP:PPT and S₃, T₁₀ for CzPhAP:TPBi displayed charge-transfer states. Based on this, the detailed photochemical mechanism of the example system CzPhAP:PPT demonstrated that the observed OLPL emission was a mixture of two emissions, corresponding to the steady-state PL spectrum with a main peak at 608 nm and a shoulder peak at 584 nm. This double-luminescence mechanism is different from the previously known three OLPL mechanisms.

In this double-luminescence mechanism, the singlet charge-separation state has a minimum point lower in energy and can directly luminate, which is an anti-Kasha's rule emission, corresponding to the main peak at 608 nm in the steady-state PL spectrum. Considering that the singlet and triplet charge-separation states form a thermodynamic equilibrium, the quasi-TADF emission resulting from the T₃ → S₃ rISC also contributed to this main peak notably. Emission at the shoulder peak was related to the traditional OLPL mechanism, in which the charge-separation state was reached by a further electron–hole dissociation of the charge-transfer excitation. With a lower emission rate (S₁, k_F1 = 3.94 × 10⁷ s⁻¹vs. S₃, k_F3 = 7.92 × 10⁷ s⁻¹), it behaved as a shoulder peak in the steady-state PL spectrum. These mechanisms can explain why the emission duration time did not display quadratic growth with respect to the increase I the excitation intensities. It also indicated that the CzPhAP:PPT system can be excited and show the OLPL property with a simple excitation source, where laser light is not necessary.

Moreover, it is worth noting that the traditional viewpoint that a smaller ΔE_ST value benefits TADF emission should be carefully examined. When the reorganization energy of the ISC process is larger than that of rISC, this conclusion can be accepted. However, when the reorganization energy of the ISC process is smaller than that of rISC, a larger ΔE_ST value is needed in order to get k_rISC > k_ISC. This will have the ISC process deeply rooted in the Marcus inverted region, which will hinder singlet-to-triplet conversion, resulting in no TADF emission. Conversely, for OLPL systems designed from TADF molecules like CzPhAP:PPT, OLPL emission will be enhanced since charge recombination of the charge-transfer excited-state S₁ is hindered and further dissociation into charge-separation states can be enhanced. We believe this is the essence why TADF molecules can display an OLPL property when doped in host materials like PPT or TPBi. We also hope further experimental research can improve such novel systems based on our tentative mechanism study.

Author contributions

Yajie Meng and Xi Chen: data curation and investigation; Yingqi Li, Yunlong Shang and Yulin Guo: visualization and formal analysis; Yong Wu and Haiyan Wei: supervision and resources; Jiawei Xu: writing – original draft, review & editing.

Data availability

Necessary data has been provided in supplemental information. Further details are available upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

Appendix

For non-radiative process with reorganization energy λ₁, coupling integral V₁ and energy difference ΔE, eqn (12) is written as eqn (A1). The corresponding reverse process (λ₂, V₂ and −ΔE) will be eqn 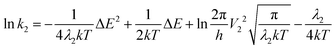(A2).

To have crossing point, let ln k₁ = ln k₂ and apply the approximation that a couple of reverse processes have V₁ ≈ V₂ to get eqn (A3):

Assume that λ₁ < λ₂, coefficients and constant term of eqn (A3) have determined signs and eqn (A3) has one negative root and one positive root, which corresponds to Condition III. It is also the same case for λ₁ > λ₂.

Acknowledgements

We would like to acknowledge a project funded by Jiangsu Key Laboratory of Biofunctional Materials, and Ministry-of-Education Key Laboratory of Numerical Simulation of Large-Scale Complex System (NSLSCS) for their technical support.

References

1. G. Che, C. Liu, Q. Wang and Z. Xu, Chem. Lett., 2008, 37(2), 136–137.
2. C. E. Cui, G. Jiang, P. Huang, L. Wang and D. Liu, J. Lumin., 2014, 145, 665–668.
3. Y. Gong, G. Chen, Q. Peng, W. Z. Yuan, Y. Xie, S. Li, Y. Zhang and B. Z. Tang, Adv. Mater., 2015, 27(40), 6195–6201.
4. Y. Li, M. Gecevicius and J. Qiu, Chem. Soc. Rev., 2016, 45(8), 2090–2136.
5. Y. Hu, Y. Yuan, Y.-L. Shi, D. Li, Z.-Q. Jiang and L.-S. Liao, Adv. Funct. Mater., 2018, 28(32), 1802597.
6. W. Jia, Q. Wang, H. Shi, Z. An and W. Huang, Chem. – Eur. J., 2020, 26(20), 4437–4448.
7. G. X. Xu, S. W. Zeng, B. T. Zhang, M. T. Swihart, K. T. Yong and P. N. Prasad, Chem. Rev., 2016, 116(19), 12234–12327.
8. K. Y. Zhang, Q. Yu, H. J. Wei, S. J. Liu, Q. Zhao and W. Huang, Chem. Rev., 2018, 118(4), 1770–1839.
9. P. F. Feng, Y. D. Wei, Y. N. Wang, J. C. Zhang, H. H. Li and Z. P. Ci, J. Am. Ceram. Soc., 2016, 99(7), 2368–2375.
10. X. Liu, X. X. Zhang and Z. F. Zhou, Mater. Res. Bull., 2016, 79, 84–89.
11. S. Das, J. Manam and S. K. Sharma, New J. Chem., 2017, 41(13), 5934–5941.
12. X. G. Yang, X. Q. Lin, Y. B. Zhao, Y. S. Zhao and D. P. Yan, Angew. Chem., Int. Ed., 2017, 56(27), 7853–7857.
13. S. Yuan, Y. K. Deng and D. Sun, Chem. – Eur. J., 2014, 20(32), 10093–10098.
14. X. G. Yang and D. P. Yan, Chem. Sci., 2016, 7(7), 4519–4526.
15. Y. Zhao, Y. J. Wang, N. Wang, P. Zheng, H. R. Fu, M. L. Han, L. F. Ma and L. Y. Wang, Inorg. Chem., 2019, 58(19), 12700–12706.
16. Z. Wang, C. Y. Zhu, Z. W. Wei, Y. N. Fan and M. Pan, Chem. Mater., 2020, 32(2), 841–848.
17. D. F. Li, F. F. Lu, J. Wang, W. D. Hu, X. M. Cao, X. Ma and H. Tian, J. Am. Chem. Soc., 2018, 140(5), 1916–1923.
18. T. Chatterjee and K. T. Wong, Adv. Opt. Mater., 2019, 7(1), 1800565.
19. L. X. Xiao, Z. W. Wang, C. F. Zhang, X. Y. Xie, H. B. Ma, Q. Peng, Z. F. An, X. Y. Wang, Z. G. Shuai and M. Xiao, J. Phys. Chem. Lett., 2020, 11(9), 3582–3588.
20. T. Matsuzawa, Y. Aoki, N. Takeuchi and Y. Murayama, J. Electrochem. Soc., 1996, 143, 2670–2673.
21. H. Ohkita, W. Sakai, A. Tsuchida and M. Yamamoto, Bull. Chem. Soc. Jpn., 1997, 70, 2665–2670.
22. B. Cheng, L. Fang, Z. Zhang, Y. Xiao and S. Lei, J. Phys. Chem. C, 2011, 115(5), 1708–1713.
23. H. F. Brito, M. C. F. C. Felinto, J. Holsa, T. Laamanen, M. Lastusaari, M. Malkamaki, P. Novak, L. C. V. Rodrigues and R. Stefani, Opt. Mater. Express, 2012, 2(4), 420–431.
24. R. Kabe and C. Adachi, Nature, 2017, 550(7676), 384–387.
25. K. Jinnai, N. Nishimura, R. Kabe and C. Adachi, Chem. Lett., 2019, 48(3), 270–273.
26. Z. Lin, R. Kabe, N. Nishimura, K. Jinnai and C. Adachi, Adv. Mater., 2018, 30(45), 1803713.
27. C. Y. Zhu, Z. Wang, J. T. Mo, Y. N. Fan and M. Pan, J. Mater. Chem. C, 2020, 8(29), 9916–9922.
28. W. Li, Z. Li, C. Si, M. Y. Wong, K. Jinnai, A. K. Gupta, R. Kabe, C. Adachi, W. Huang, E. Zysman-Colman and I. D. W. Samuel, Adv. Mater., 2020, 32(45), e2003911.
29. T. Lu and F. Chen, J. Comput. Chem., 2012, 33(5), 580–592.
30. B. Hess, C. Kutzner, D. Van Der Spoel and E. Lindahl, J. Chem. Theory Comput., 2008, 4(3), 435–447.
31. T. Lu, Sobtop, (accessed 2024-01-01, 2024).
32. T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98(12), 10089–10092.
33. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, Williams, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16, Gaussian Inc., 2016.
34. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 119(5), 525.
35. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305.
36. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132(15), 154104.
37. A. A. Voityuk and N. Rösch, J. Chem. Phys., 2002, 117(12), 5607–5616.
38. Z. Q. You, Y. C. Hung and C. P. Hsu, J. Phys. Chem. B, 2015, 119(24), 7480–7490.
39. K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I.-M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4(3), 269–284.
40. J. M. H. Olsen, S. Reine, O. Vahtras, E. Kjellgren, P. Reinholdt, K. O. Hjorth Dundas, X. Li, J. Cukras, M. Ringholm, E. D. Hedegård, R. Di Remigio, N. H. List, R. Faber, B. N. Cabral Tenorio, R. Bast, T. B. Pedersen, Z. Rinkevicius, S. P. A. Sauer, K. V. Mikkelsen, J. Kongsted, S. Coriani, K. Ruud, T. Helgaker, H. J. A. Jensen and P. Norman, J. Chem. Phys., 2020, 152(21), 214115.
41. T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393(1–3), 51–57.
42. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14(1), 33–38.
43. Y. Q. Hou, X. Zhang, K. P. Chen, D. Y. Liu, Z. J. Wang, Q. Y. Liu, J. Z. Zhao and A. Barbon, J. Mater. Chem. C, 2019, 7(39), 12048–12074.
44. J. Xu, L. Deng, H. Zhang, H. Zhang, Y. Luo, X. Yan, J. Bao, M. Fang and Y. Wu, Chin. J. Inorg. Chem., 2020, 36(22), 2157–2168.
45. R. G. Pearson, J. Am. Chem. Soc., 1963, 85(22), 3533–3539.
46. M. F. Gelin, L. Chen, R. Borrelli and E. Thyrhaug, Chem. Phys., 2020, 528, 110495.
47. Y. Zhang, K. Wang, G. Jia, J. Li, H. Wang and Y. Tian, J. Alloys Compd., 2021, 860, 157914.
48. N. Christensson, H. F. Kauffmann, T. Pullerits and T. Mancal, J. Phys. Chem. B, 2012, 116(25), 7449–7454.
49. R. C. Hilborn, Am. J. Phys., 1982, 50(11), 982–986.
50. K. Schmidt, S. Brovelli, V. Coropceanu, D. Beljonne, J. Cornil, C. Bazzini, T. Caronna, R. Tubino, F. Meinardi, Z. Shuai and J.-L. Bredas, J. Phys. Chem. A, 2007, 111(42), 10490–10499.
51. T. Lu and F. Chen, J. Comput. Chem., 2012, 33(5), 580–592.
52. Z. Liu, T. Lu and Q. Chen, Carbon, 2020, 165, 461–467.
53. N. Nishimura, Z. S. Lin, K. Jinnai, R. Kabe and C. Adachi, Adv. Funct. Mater., 2020, 30(22), 2000795.
54. W. Li, Z. Li, C. Si, M. Y. Wong, K. Jinnai, A. K. Gupta, R. Kabe, C. Adachi, W. Huang, E. Zysman-Colman and I. D. W. Samuel, Adv. Mater., 2020, 32(45), e2003911.
55. J.-L. Bredas, Mater. Horiz., 2014, 1(1), 17–19.
56. N. Christensson, H. F. Kauffmann, T. Pullerits and T. Mančal, J. Phys. Chem. B, 2012, 116(25), 7449–7454.
57. M. F. Gelin, L. Chen, R. Borrelli and E. Thyrhaug, Chem. Phys., 2020, 528, 110495.
58. Y. Zhang, K. Wang, G. Jia, J. Li, H. Wang and Y. Tian, J. Alloys Compd., 2021, 860, 157914.
59. R. Zhu, X. Chen, N. Shu, Y. Shang, Y. Wang, P. Yang, Y. Tang, F. Wang and J. Xu, J. Phys. Chem. A, 2021, 125(47), 10144–10154.
60. Y. Shang, Z. Zhang, M. Huang, N. Shu, H. Luo, Q. Cao, B. Fan, Y. Han, M. Fang, Y. Wu and J. Xu, Phys. Chem. Chem. Phys., 2023, 25(47), 32666–32674.
61. M. Yamamoto, H. Ohkita and S. Ito, Chin. J. Polym. Sci., 2001, 19(2), 129–134.
62. M. Yamamoto, H. Ohkita, W. Sakai and A. Tsuchida, Synth. Met., 1996, 81, 301–304.
63. T. Yamanaka, H. Nakanotani and C. Adachi, Nat. Commun., 2019, 10, 5748.
64. J. Xu, J. Hao, C. Bu, Y. Meng, H. Xiao, M. Zhang and C. Li, J. Chem. Theory Comput., 2024, 20(9), 3590–3600.
65. C. M. Marian, Annu. Rev. Phys. Chem., 2021, 72, 617–640.

---

Footnotes

† Electronic supplementary information (ESI) available: supplemental figures and tables, molecular structures in xyz format and other computational results. See DOI: https://doi.org/10.1039/d4tc00805g

‡ Note for non-theoretical readers: In the article, excited states S₁, S₃, T₁ and T₃ are all labelled according to the state energy at the ground state minima. However, as structure relaxing on the PES, states may go across conical intersections (CI), for example, going across the S₁–S₃ CI may lead to inversion of energy level (before: S₁ < S₃; after S₃ < S₁). In brief words, we use diabatic state notation for excited states in the article.

---