A mixed Weyl semimetal in a two-dimensional ferromagnetic BaCrSe₂ monolayer

Abstract

Weyl semimetals (WSMs) are of significant fundamental and technological importance in topotronics. Despite the fact that numerous WSMs in three dimensions are achieved, the emergence of WSMs in two-dimensional (2D) ferromagnets remains elusive. Here, we put forward the 2D BaCrSe₂ monolayer with intrinsic ferromagnetic order and full spin polarization as a specific representative of WSMs via including the magnetization direction θ into the topological analysis. Remarkably, the mixed Weyl points pinned exactly at the Fermi level, and the nonzero topological charge Q = ±1 is indeed achieved through a closed surface that encompasses a distinct mixed Weyl point in phase space (k_x, k_y, θ). The presented results not only advance the general understanding of WSMs in 2D ferromagnets but also put forward potential applications in topotronics.

---

Introduction

Weyl semimetals (WSMs), obtained usually in three-dimensional (3D) systems with breaking time-reversal or spatial-inversion symmetries, have garnered significant attention in the field of emerging topotronics.^1–5 With linear electronic dispersions, the Weyl points (WPs) of WSMs must appear in pairs according to the no-go theorem,⁶ and show positive and/or negative chirality that can be regarded as the respective source and/or drain of the Berry curvatures in momentum space.^7–11 In particular, a pair of WPs with opposite chiralities is connected by non-closed Fermi arcs.^8,12 When a two-dimensional (2D) k-plane intersects with a Fermi arc, the integral of the Berry curvatures along this plane is none-zero, defining the Chern number [capital script C].^13–15 Consequently, a 2D plane behaves as a Chern insulator with a dissipationless channel determined by the Chern number [capital script C], otherwise it is deemed to be a trivial insulator. These unique properties of WSMs have found extensive theoretical and experimental applications, such as in topological phase transition,¹⁶ surface Fermi arcs,¹⁷ high-mobility carriers,^18,19 anisotropic nonlinear optical response,²⁰ negative magnetoresistive,^21–23 and giant intrinsic spin/anomalous Hall effects.^24,25

On the other hand, while 2D ferromagnets are a focus of intensive research,^26,27 the combining of 2D magnetism and nontrivial topology holds great opportunities for exploring fundamental quantum physics and innovative design of topotronic devices.^28–32 Remarkably, including the magnetization direction θ into the topological analysis allows for a natural classification of the topologically nontrivial semimetallic states, i.e., the emergence of mixed WSMs (MWSMs), as a result of the interplay between spin–orbit and exchange interactions.^33,34 Indeed, the MWSMs in 2D ferromagnets have been observed experimentally.³⁵ Moreover, in MWSMs, the strength of the spin–orbit torques and Dzyaloshinskii–Moriya interaction can exceed by far that of trivial metals,³³ and the shape and location of the Fermi arcs can be controlled by tuning the magnetization direction.³⁵ However, the mixed WPs (MWPs) are usually buried in the bulk states and there are trivial Fermi pockets around the Fermi level in addition to the Weyl nodes. It is therefore essential to search for ideal MWSMs with MWPs not buried in the bulk states and exactly residing at the Fermi level.

In the present paper, we theoretically demonstrate the emergence of long-awaited ideal MWSMs in a 2D BaCrSe₂ monolayer, which is an intrinsic and dynamically stable ferromagnet according to our calculations of total energies and phonon spectra. Unlike previous MWSMs, the bands of BaCrSe₂ monolayer are completely spin-polarized in a large range near the Fermi level, yielding 100% spin polarization that is endowed with intriguing quantum phenomena and potential applications in spin Hall effect devices. Remarkably, we find four pairs of MWPs exactly at the Fermi level in the whole mixed phase space (k_x, k_y, θ) with linear dispersion for the cones, where θ is the polar angle that the direction of magnetism makes with the z axis. With nonzero topological charge Q = ±1, the MWPs are robust against perturbations that preserve the protective in-plane mirror symmetry as the magnetization direction is fixed. Moreover, non-zero Chern numbers [capital script C] = ±2 with two chiral edge states are obtained for planes with different θ, further explicitly confirming the topologically nontrivial MWSM nature of the BaCrSe₂ monolayer. Our results suggest that the BaCrSe₂ monolayer is an intriguing candidate for both the research of magnetic topological phases and innovative topotronics applications.

Methods

Density functional calculations were performed for structural relaxations and electronic structure calculations as implemented in the Vienna ab initio simulation package (VASP).³⁶ The generalized gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) is used for the exchange correlation potential.³⁷ A vacuum layer of 20 Å is used to avoid interactions between the nearest layers. The energy cutoff of the wave functions is set to be 500 eV. All structures are relaxed until the convergence threshold of the maximum force per atom is less than 0.01 eV Å⁻¹, and the criterion of total energy convergence is set to 10⁻⁶ eV. The GGA+U method with a value of U = 3 eV is employed to correct the Coulomb repulsive interaction of Cr-3 d orbitals. The phonon calculation is carried out by using the PHONOPY code.³⁸ The maximally localized Wannier functions (MLWFs) are constructed using the WANNIER90 code.³⁹

Results and discussion

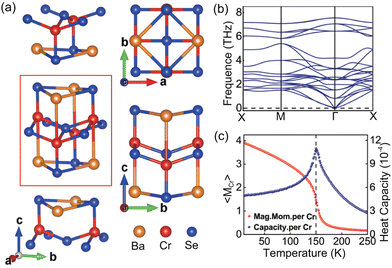
Bulk BaCrSe₂ has a tetragonal crystal structure with the space group P4/nmm, that is of interest owing to the exotic magnetic and topological properties.⁴⁰ As illustrated in Fig. 1(a), each unit cell consists of eight atoms with two Cr atoms located in the Wyckoff 2c position, two Ba atoms in the 2c position, and four Se atoms in the 2c and 2b positions.^28,41 The crystal structure can be visualized as a stacking of the BaCrSe₂ monolayer, marked with dashed red lines, along the z axis. The optimized lattice constant of the BaCrSe₂ monolayer is a = b = 4.87 Å. To confirm the structural stability, we utilize the binding energy given by E_b = E(BaCrSe₂) − E(Ba) − E(Cr) − 2E(Se), where E(BaCrSe₂), E(Ba), E(Cr), and E(Se) represent the total energies of the BaCrSe₂ monolayer, Ba crystal, Cr crystal, and Se crystal, respectively. The calculation result shows that E_b = −1.1552 eV indicating that the formation is an exothermic reaction. Moreover, the dynamic stability is investigated through the phonon spectrum calculations. There is no imaginary frequency in the entire Brillouin zone, as displayed in Fig. 1(b), which indicates that the BaCrSe₂ monolayer is dynamically stable once formed.

Fig. 1 (a) Crystal structures of the BaCrSe₂ in space group P4/nmm with the two-dimensional (2D) monolayer highlighted by solid red lines. The adjacent images depict the top and side views of the 2D BaCrSe₂ monolayer. (b) Phonon dispersion of the BaCrSe₂ monolayer, indicating that the structure is dynamically stable. (c) Evolutions of specific heat capacity and ionic magnetic moments per Cr with temperature.

The ground state of the BaCrSe₂ monolayer is spin polarized with the calculated net magnetic moments of 4 μ_B per Cr, and it leads to an intrinsic ferromagnetic (FM) coupling based on the foundational Goodenough–Kanamori rules because of the Cr–Se–Cr bond angle approaching 90°.^42,43 This is further verified by the calculations of magnetization energy with E_mag = E_FM − E_AFM, where E_FM and E_AFM are the total energies of the BaCrSe₂ monolayer under FM and antiferromagnetic (AFM) configurations, respectively. As expected, our total energy calculations reveal that the FM state is energetically preferred over the AFM state by 140 meV. After including SOC, the magnetic anisotropy energy E_MAE, defined as the total-energy difference between the spin orientations aligned in the out-of-plane and in-plane x directions, is carefully checked. The results suggest that the in-plane magnetization is energetically preferred with a tiny magnitude of 0.04 meV, which is indistinguishable and thus the magnetic directions can be effectively tuned. Furthermore, as a crucial factor for practical applications, the Curie temperature is estimated via the Monte Carlo simulations based on Heisenberg Hamiltonian 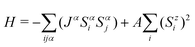.^19,44,45 Here, we focus solely on the nearest neighbor interactions, and S_i represents the spin of the Cr atom in the ith site. J and A are the exchange and anisotropy constants. By employing first-principles calculations, we obtained J^z = −51.295 K, J^x = −51.383 K, J^y = −52.383 K, A^z = 0.051 K and A^x = A^y = 0 K, and the evolutions of specific heat capacity and ionic magnetic moments are plotted in Fig. 1(c). It is obtained that the Curie temperature of the BaCrSe₂ monolayer reaches as large as 150 K, implying the possibility of potential applications at high temperature and the magnetism can be maintained over a wide temperature range.

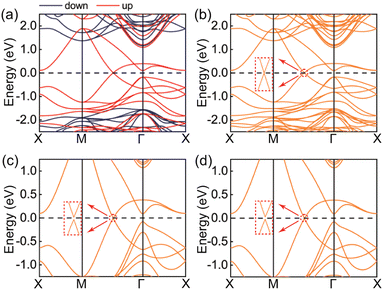
To get preliminary insight into the topological properties of the BaCrSe₂ monolayer, we present in Fig. 2(a) the spin-resolved band structures in the absence of SOC. The conduction and valence bands around the Fermi level are completely composed of the spin-up bands, while that of the spin-down bands are far away from the Fermi level, indicating a good half-metallic characteristic near the Fermi energy with the exotic band crossings emerging in the spin-up bands along the Γ–M path. Taking into account the SOC, the band structures around the Fermi level do not change significantly. Remarkably, as shown in Fig. 2(b), one notes that the band crossings along the Γ–M path remain intact for the BaCrSe₂ monolayer with in-plane magnetization. This is observable under a condition of unbroken in-plane mirror symmetries, such as [scr M, script letter M]_x. When the magnetization directions rotate towards the out-of-plane one, all of the four in-plane mirror symmetries, as schematically plotted in Fig. 3(a), are disrupted. As a result, the degenerate points near the Fermi level disappear with the band gap opening, as shown in Fig. 2(c) and (d). It therefore suggests that the topological phase transition accompanied by a closing of the band gap occurs as the magnetization direction is varied, and moreover the mixed Weyl semimetals (MWSMs) are obtained in the mixed phase space of the crystal momentum k = (k_x, k_y) and the magnetization direction θ, i.e., (k_x, k_y, θ). It belongs to the type-I MWSM, for which the mixed Weyl points are robust against perturbations that preserve the protective mirror symmetry, as long as the magnetization direction is fixed.^34,46

Fig. 2 (a) Spin-resolved band structures of the BaCrSe₂ monolayer without SOC. The spin-up bands are gapless while a gap appears in the spin-down ones. Band structures for the BaCrSe₂ monolayer after including SOC with different magnetization directions of (b) θ = 90°, (c) θ = 0°, and (d) θ = 180°. The bands for θ = 90° are gapless while there are small gaps for that of θ = 0° and θ = 180° as shown in the locally enlarged views, suggesting the emergence of mixed topological semimetallic states.

Fig. 3 (a) The Brillouin zone for the BaCrSe₂ monolayer with marked high symmetry points, in which the mirror symmetries depend sensitively on the magnetization directions. Topological edge states for semi-infinite BaCrSe₂ nanoribbons with different magnetization directions of (b) θ = 90°, (c) θ = 0°, and (d) θ = 180°. Evolution of the sum of Wannier charge centers (WCC) for the BaCrSe₂ monolayer associated with (e) θ = 0° and (f) θ = 180°, showing the discrete jumps of Chern number from [capital script C] = 2 to [capital script C] = −2.

One of the most important properties for MWSMs, in mixed phase space (k_x, k_y, θ), is the discrete jumps of the momentum Chern number 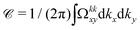with respect to the magnetization direction θ. Here, Ω^kk_xy is the momentum Berry curvature for all occupied states 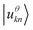, namely the states below the Fermi level, given by where θ represents the angle that the magnetization m̂ = (sin θ, 0, cos θ) makes with the z-axis. We thus calculate the Chern number [capital script C] via MLWFs of a BaCrSe₂ unit cell, and analyze the chiral edge states that are the hallmark of nonzero [capital script C]. Ba-p, Se-p, and Cr-d orbitals are considered in constructing the MLWFs, and band dispersions of the BaCrSe₂ unit cell are reproduced very accurately.

As expected, for the out-of-plane magnetization with θ = 0°, the Chern number [capital script C] indeed acquires an integer value of [capital script C] = 2, demonstrating the quantum anomalous Hall effect (QAHE) in the BaCrSe₂ monolayer with the out-of-plane ferromagnetization. 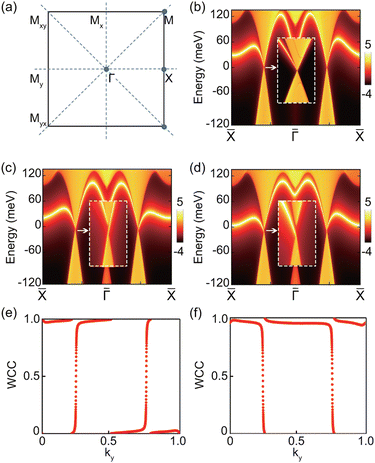As a further confirmation of the topologically nontrivial phase, the edge states are calculated using the MLWFs, and the nonzero value of [capital script C] = 2 suggests that there are two chiral edge states in the nontrivial insulating regions. Fig. 3(c) displays the results for the semi-infinite BaCrSe₂ monolayer, where two chiral edge states are clearly visible. This is in direct agreement with the calculated Chern number [capital script C] = 2. We then rotate the magnetic direction, which provides an intriguing way to control both the symmetry and topology. Indeed, as discussed above, switching the angle θ can lead to a gap closure and give rise to the nontrivial semimetallic state for the in-plane magnetization with θ = 90°. As illustrated in Fig. 3(b), there is no band gap observed in the edge-projected bulk energy bands, and the exotic nodal points project onto two distinct points that are connected by emergent edge states.

Fig. 4(a) and (b) indicate that there are four isolated band crossing points in the Brillouin zone when the in-plane mirror symmetry survives at θ = 90°, and remarkably the four nodal points mediate the topological phase transitions from the nontrivial Chern numbers [capital script C] = 2 to [capital script C] = −2. To elucidate this transition more clearly, we carry out the calculations of edge states using the MLWFs of the BaCrSe₂ monolayer with θ = 180°, and the result for the corresponding semi-infinite nanoribbon is plotted in Fig. 3(d). Clearly, two chiral edge states emerge at the nontrivial gap. However, the chiralities of the edge states at θ = 0° and 180° are opposite to each other. This is further explicitly confirmed by the WCC calculations on both sides of the θ = 90°, as illustrated in Fig. 3(e) and (f), where their propagation directions are reversed, suggesting the emergence of mixed Weyl points (MWPs) at θ = 90°.

Fig. 4 (a) Phase diagram of the BaCrSe₂ monolayer in the mixed phase space (k_x, k_y, θ). The color maps indicate the presence of four mixed Weyl points (MWPs) located at θ = 90° and 270°. Opposite jumps of Chern number [capital script C] = ±2 are seen when the planes move across the MWPs, indicating that the chiralities of MWPs are related to the magnetization directions. (b) The three-dimensional band structure of the BaCrSe₂ monolayer with θ = 90° around the four MWPs. (c) Berry curvature distribution around an MWP with θ = 90°.

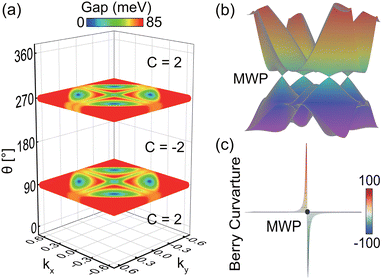
We then turn to the in-plane magnetization with θ = 270°, as illustrated in Fig. 4(a), where the gap closing with four isolated MWPs occurs again. However, in contrast to θ = 90°, the topological phase transition is mediated with the nontrivial Chern numbers from [capital script C] = −2 to [capital script C] = 2. In analogy to the Berry curvature Ω^kk_xy in conventional momentum space, we can describe the field of these MWPs by extra adopting the mixed Berry curvature 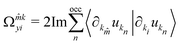.^33,34 Furthermore, by integrating the flux of the mixed Berry curvature Ω^m̂k_yi through a closed surface S that contains an MWP, we can define the integer topological charge as 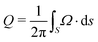.^33,34 This allows us to determine the chirality of MWPs by examining whether the topological charge acts as a source or a sink. Indeed, our calculations, as shown in Fig. 4(c), verify that the chiralities of MWPs at θ = 90° and θ = 270° are opposite with topological charges of Q = −1 and Q = +1, respectively, further explicitly confirming the topological nontrivial nature of MWPs.

Conclusion

In conclusion, we demonstrated that the 2D BaCrSe₂ monolayer in the FM order exhibits the distinctive features of the MWSMs, characterized by the presence of four pairs of highly symmetric MWPs at the Fermi level protected by [scr M, script letter M]_x symmetry. Moreover, we explored the connection between the QAH effect and MWPs through Berry curvature analysis in the mixed phase space. Our study not only offers insights into the intricate relationship between topological properties and magnetic orientations but also paves the way for practical applications of spintronic devices.

Data availability

The data that support the findings of this study are available within the article.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grants No. 12174220 and No. 12074217), the Shandong Provincial Key Research and Development Program (Major Scientific and Technological Innovation Project) (Grant No. 2019JZZY010302), and the Qilu Young Scholar Program of Shandong University.

References

1. B. Q. Lv, T. Qian and H. Ding, Rev. Mod. Phys., 2021, 93, 025002.
2. N. P. Armitage, E. J. Mele and A. Vishwanath, Rev. Mod. Phys., 2018, 90, 015001.
3. B. Yan and C. Felser, Annu. Rev. Condens. Matter Phys., 2017, 8, 337.
4. C.-K. Chiu, J. C. Y. Teo, A. P. Schnyder and S. Ryu, Rev. Mod. Phys., 2016, 88, 035005.
5. A. Bansil, H. Lin and T. Das, Rev. Mod. Phys., 2016, 88, 021004.
6. H. Nielsen and M. Ninomiya, Phys. Lett. B, 1983, 130, 389.
7. Z. Fang, N. Nagaosa, K. S. Takahashi, A. Asamitsu, R. Mathieu, T. Ogasawara, H. Yamada, M. Kawasaki, Y. Tokura and K. Terakura, Science, 2003, 302, 92.
8. X. Wan, A. M. Turner, A. Vishwanath and S. Y. Savrasov, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 205101.
9. H. Weng, C. Fang, Z. Fang, B. A. Bernevig and X. Dai, Phys. Rev. X, 2015, 5, 011029.
10. S.-M. Huang, S.-Y. Xu, I. Belopolski, C.-C. Lee, G. Chang, B. Wang, N. Alidoust, G. Bian, M. Neupane, C. Zhang, S. Jia, A. Bansil, H. Lin and M. Z. Hasan, Nat. Commun., 2015, 6, 7373.
11. A. A. Soluyanov, D. Gresch, Z. Wang, Q. Wu, M. Troyer, X. Dai and B. A. Bernevig, Nature, 2015, 527, 495.
12. D. Xiao, M.-C. Chang and Q. Niu, Rev. Mod. Phys., 2010, 82, 1959.
13. R. Yu, W. Zhang, H.-J. Zhang, S.-C. Zhang, X. Dai and Z. Fang, Science, 2010, 329, 61.
14. C. Z. Chang, J. Zhang, X. Feng, J. Shen, Z. Zhang, M. Guo, K. Li, Y. Ou, P. Wei, L. L. Wang, Z. Q. Ji, Y. Feng, S. Ji, X. Chen, J. Jia, X. Dai, Z. Fang, S. C. Zhang, K. He, Y. Wang, L. Lu, X. C. Ma and Q. K. Xue, Science, 2013, 340, 167.
15. L. Muechler, E. Liu, J. Gayles, Q. Xu, C. Felser and Y. Sun, Phys. Rev. B, 2020, 101, 115106.
16. Y. J. Jin, R. Wang, Z. J. Chen, J. Z. Zhao, Y. J. Zhao and H. Xu, Phys. Rev. B, 2017, 96, 201102.
17. B. W. Xia, Y. J. Jin, J. Z. Zhao, Z. J. Chen, B. B. Zheng, Y. J. Zhao, R. Wang and H. Xu, Phys. Rev. Lett., 2019, 122, 057205.
18. K. Takiguchi, Y. K. Wakabayashi, H. Irie, Y. Krockenberger, T. Otsuka, H. Sawada, S. A. Nikolaev, H. Das, M. Tanaka, Y. Taniyasu and H. Yamamoto, Nat. Commun., 2020, 11, 4969.
19. Y.-Q. Ma and W. Figueiredo, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 5604.
20. L. Wu, S. Patankar, T. Morimoto, N. L. Nair, E. Thewalt, A. Little, J. G. Analytis, J. E. Moore and J. Orenstein, Nat. Phys., 2017, 13, 350.
21. X. Huang, L. Zhao, Y. Long, P. Wang, D. Chen, Z. Yang, H. Liang, M. Xue, H. Weng, Z. Fang, X. Dai and G. Chen, Phys. Rev. X, 2015, 5, 031023.
22. F. Arnold, C. Shekhar, S.-C. Wu, Y. Sun, R. D. dos Reis, N. Kumar, M. Naumann, M. O. Ajeesh, M. Schmidt, A. G. Grushin, J. H. Bardarson, M. Baenitz, D. Sokolov, H. Borrmann, M. Nicklas, C. Felser, E. Hassinger and B. Yan, Nat. Commun., 2016, 7, 11615.
23. C.-L. Zhang, S.-Y. Xu, I. Belopolski, Z. Yuan, Z. Lin, B. Tong, G. Bian, N. Alidoust, C.-C. Lee, S.-M. Huang, T.-R. Chang, G. Chang, C.-H. Hsu, H.-T. Jeng, M. Neupane, D. S. Sanchez, C. Zhang, J. Wang, H. Lin, C. Zhang, H.-Z. Lu, S.-Q. Shen, T. Neupert, M. Z. Hasan and S. Jia, Nat. Commun., 2016, 7, 10735.
24. Y. Sun, Y. Zhang, C. Felser and B. Yan, Phys. Rev. Lett., 2016, 117, 146403.
25. E. Liu, Y. Sun, N. Kumar, L. Muechler, A. Sun, L. Jiao, S.-Y. Yang, D. Liu, A. Liang, Q. Xu, J. Kroder, V. Süβ, H. Borrmann, C. Shekhar, Z. Wang, C. Xi, W. Wang, W. Schnelle, S. Wirth, Y. Chen, S. T. B. Goennenwein and C. Felser, Nat. Phys., 2018, 14, 1125.
26. V. D. Waals, C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, Z. Q. Qiu, R. J. Cava, S. G. Louie, J. Xia and X. Zhang, Nature, 2017, 546, 265.
27. B. Huang, G. Clark, E. Navarro-moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. Mcguire, D. H. Cobden, W. Yao, D. Xiao, P. Jarillo-herrero and X. Xu, Nature, 2017, 546, 270.
28. C. Niu, H. Wang, N. Mao, B. Huang, Y. Mokrousov and Y. Dai, Phys. Rev. Lett., 2020, 124, 066401.
29. Y. Ren, Z. Qiao and Q. Niu, Phys. Rev. Lett., 2020, 124, 166804.
30. C. Chen, Z. Song, J.-Z. Zhao, Z. Chen, Z.-M. Yu, X.-L. Sheng and S. A. Yang, Phys. Rev. Lett., 2020, 125, 056402.
31. R.-X. Zhang, F. Wu and S. Das Sarma, Phys. Rev. Lett., 2020, 124, 136407.
32. R. Li, N. Mao, X. Wu, B. Huang, Y. Dai and C. Niu, Nano Lett., 2023, 23, 91.
33. J.-P. Hanke, F. Freimuth, C. Niu, S. Blügel and Y. Mokrousov, Nat. Commun., 2017, 8, 1479.
34. C. Niu, J.-P. Hanke, P. M. Buhl, H. Zhang, L. Plucinski, D. Wortmann, S. Blügel, G. Bihlmayer and Y. Mokrousov, Nat. Commun., 2019, 10, 3179.
35. Y.-J. Chen, J.-P. Hanke, M. Hoffmann, G. Bihlmayer, Y. Mokrousov, S. Blügel, C. M. Schneider and C. Tusche, Nat. Commun., 2022, 13, 5309.
36. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
38. A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1.
39. A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685.
40. W. Sun, B. Li, X. Zou, R. Li, B. Huang, Y. Dai and C. Niu, Adv. Sci., 2023, 10, 2301474.
41. X. Li, N. Mao, R. Li, Y. Dai, B. Huang and C. Niu, J. Mater. Chem. C, 2021, 9, 16952.
42. J. B. Goodenough, Phys. Rev., 1955, 100, 564.
43. J. Kanamori, J. Appl. Phys., 1960, 31, S14.
44. L. Liu, S. Chen, Z. Lin and X. Zhang, J. Phys. Chem. Lett., 2020, 11, 7893.
45. B. V. Costa, A. R. Pereira and A. S. T. Pires, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 3019.
46. Z. Liu, G. Zhao, B. Liu, Z. F. Wang, J. Yang and F. Liu, Phys. Rev. Lett., 2018, 121, 246401.

---