Open Access Article
Open Access ArticleThe interplay of chemical bonding and thermoelectric properties in doped cubic GeTe†
Sree Sourav
Das
 a,
Safoura Nayeb
Sadeghi
a,
Safoura Nayeb
Sadeghi
 b,
Keivan
Esfarjani
bcd and
Mona
Zebarjadi
*ac
b,
Keivan
Esfarjani
bcd and
Mona
Zebarjadi
*ac
aDepartment of Electrical and Computer Engineering, University of Virginia, Charlottesville, VA 22904, USA. E-mail: m.zebarjadi@virginia.edu
bDepartment of Mechanical and Aerospace Engineering, University of Virginia, Charlottesville, VA 22904, USA
cDepartment of Materials Science and Engineering, University of Virginia, Charlottesville, VA 22904, USA
dDepartment of Physics, University of Virginia, Charlottesville, VA 22904, USA
First published on 13th May 2024
Abstract
GeTe-based alloys hold great promise for thermoelectric applications. Our comprehensive study investigates the intricate interplay between chemical bonding and transport properties in cubic GeTe. We demonstrate a balance between minimizing thermal conductivity and maximizing power factor, guided by the mediating influence of chemical bonding. Our primary findings reveal that Pb-doped GeTe exhibits low lattice thermal conductivity due to weak p–p orbital interactions, whereas In-doping boosts lattice thermal conductivity by reinforcing the chemical bonds, as elucidated by crystal orbital hamilton population (COHP) analysis. Further investigation reveals weak s–p interactions in Bi-, Sb-, and Pb-doped GeTe, and strong s–p interactions in In-doped GeTe compared to the pure GeTe, as probed by projected density of state (PDOS). These dual effects explain the experimentally observed high power factor and enhanced zT in Bi-, Sb-, and Pb- doping in contrast to In-doping. In our study, we find that weak s–p interactions improves electronic performance by modifying DOS whereas weak p–p interactions reduce thermal transport by diminishing the strength of chemical bonding. These findings underscore the correlation between doping-induced modifications in chemical bonding and resulting thermoelectric properties. Utilizing a first-principles framework, we systematically explore the temperature and carrier concentration-dependent transport properties of pure GeTe under relaxation time approximation. Optimization strategies yield a maximum peak power factor times temperature of 2.2 Wm−1 K−1 and a maximum zT value of ∼0.83 at 800 K, showcasing the potential for tailored thermoelectric performance. Finally, this research presents a systematic approach to improve thermoelectric performance by modifying chemical bonds through doping.
Introduction
Thermoelectric materials hold remarkable potential to harness heat, transforming it into clean electricity. They offer a sustainable solution for both efficient refrigeration and the recovery of wasted heat.1–4 For example, over 60% of the energy generated from household heating, automotive engines, and industrial processes is lost as heat. This lost heat can be exploited by readily available thermoelectric devices (TEDs).5,6 Furthermore, TEDs are employed for stabilizing the working temperature of semiconductor lasers, infrared detectors, and microchips.7 In the field of space exploration and unmanned systems,8,9 radioisotope thermoelectric generators serve as the primary power source,10,11 enabling missions that were once deemed impossible. Even more intriguingly, flexible TEDs seamlessly integrated into clothing act as wearable air conditioning systems,11–16 providing comfort in extreme environmental conditions. The potential of materials for thermoelectric applications is evaluated by their thermoelectric figure of merit, zT, defined as, where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity, and T is the absolute temperature. Thermal conductivity has two components: lattice thermal conductivity (κl) and electronic thermal conductivity (κe = LσT), where L is the Lorentz number. The term S2σ is called the power factor and affects the output power of TEDs. To achieve a high zT, a material needs to have a high-power factor and a low thermal conductivity (κ = κl + LσT). However, due to the complex interrelationship among S, σ, and κ, the improvement of zT has proven to be a challenging task. To ensure a high power factor, significant efforts including band structure engineering,17–20 carrier optimization,21 and resonant doping22 have been widely employed. On the other hand, to obtain low κ, specially κl, intrinsic anharmonicity,18,23 nano structuring,24,25 introducing lattice defects26–28 and nanoscale grain boundaries29,30 are the generally-adopted strategies.
where S is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity, and T is the absolute temperature. Thermal conductivity has two components: lattice thermal conductivity (κl) and electronic thermal conductivity (κe = LσT), where L is the Lorentz number. The term S2σ is called the power factor and affects the output power of TEDs. To achieve a high zT, a material needs to have a high-power factor and a low thermal conductivity (κ = κl + LσT). However, due to the complex interrelationship among S, σ, and κ, the improvement of zT has proven to be a challenging task. To ensure a high power factor, significant efforts including band structure engineering,17–20 carrier optimization,21 and resonant doping22 have been widely employed. On the other hand, to obtain low κ, specially κl, intrinsic anharmonicity,18,23 nano structuring,24,25 introducing lattice defects26–28 and nanoscale grain boundaries29,30 are the generally-adopted strategies.
Bi2Te3-related compounds find applications in room temperature thermoelectric devices, with commercialization for cooling purposes.31–33 Other materials such as SiGe34,35 and half-Heusler36,37 compounds are good for high-temperature applications. Meanwhile, semiconducting group IV–VI chalcogenides, with a focus on PbTe, SnTe, and GeTe, have long been celebrated for their remarkable thermoelectric performance in the mid-temperature range (500–800 K).17 However, GeTe-based materials, while holding promise since the 1960s,17 are now experiencing a resurgence of interest, sparking noteworthy advancements in their thermoelectric performance. The tremendous interest in GeTe, particularly in its cubic form, arises from its unique properties. It has a special type of bonding mixture of dominant covalent and weak ionic character. This special bonding is called metavalent bonding. Due to the metavalency, GeTe possesses high bond polarizability and high electronic polarizability as evidenced by anomalously large Born effective charge, Z* and optical dielectric constant, respectively.38 GeTe also shows a high value of the Grüneisen parameter ϒTO, a measure of lattice anharmonicity, which leads to an intrinsically low lattice thermal conductivity despite having a simple and high-symmetry crystal structure.39 Additionally, GeTe is harboring multiple sub-valence bands as well as low density of state and conductivity effective masses (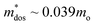 and
and  )40 that significantly impact electronic transport. Doping provides an exciting avenue for manipulating electronic bands in GeTe, resulting in a higher degree of band degeneracy and, consequently, remarkable enhancements in electronic performance.39 In addition to superior thermoelectric performance, GeTe-alloys have shown better mechanical properties compared to other conventional Bi2Te3 and IV–VI thermoelectrics,17 showing a great potential as p-types legs for efficient thermoelectric devices. The combination of these unique properties in GeTe makes it an exceptionally promising candidate for high-performance thermoelectric applications at both mid-temperatures and near room temperatures with possible further advancements. In this work, we adopt a strategy of enhancing the thermoelectric properties of GeTe by tuning its metavalency using doping or chemical pressure. Fine-tuning of metavalency can optimize the power factor further and lower thermal conductivity at the same time by weakening the bonds and increasing anharmonicity.
)40 that significantly impact electronic transport. Doping provides an exciting avenue for manipulating electronic bands in GeTe, resulting in a higher degree of band degeneracy and, consequently, remarkable enhancements in electronic performance.39 In addition to superior thermoelectric performance, GeTe-alloys have shown better mechanical properties compared to other conventional Bi2Te3 and IV–VI thermoelectrics,17 showing a great potential as p-types legs for efficient thermoelectric devices. The combination of these unique properties in GeTe makes it an exceptionally promising candidate for high-performance thermoelectric applications at both mid-temperatures and near room temperatures with possible further advancements. In this work, we adopt a strategy of enhancing the thermoelectric properties of GeTe by tuning its metavalency using doping or chemical pressure. Fine-tuning of metavalency can optimize the power factor further and lower thermal conductivity at the same time by weakening the bonds and increasing anharmonicity.
As-grown GeTe is predominantly a highly p-doped degenerate narrow gap semiconductor due to a high level of Ge vacancies. The introduction of additional dopants in GeTe lowers the high hole concentration by effective suppression of intrinsic Ge vacancies and concurrently modifies the electronic structure.41–43 In the pursuit of enhancing performance, various elements have been explored as dopants to date. Fig. S1 in the ESI† illustrates a map of elements introduced as dopants in GeTe, showcasing a figure of merit (zT) exceeding 1.0 in the mid-temperature range (500–800 K). Aliovalent dopants like Sb and Bi which have higher valence states than Ge and occupy vacant Ge sites, serve as electron donors and effectively reduce the hole concentration.44 Doping by Pb or Sc induces nanostructures within the GeTe matrix,45 elevating the formation energy of Ge vacancies39,46 and consequently reducing carrier concentration. Isoelectronic dopants like Al and Ba were found to be a poor choice for GeTe as they inflate hole concentration and drastically increase the gap between light and heavy hole bands in GeTe, resulting in a reduced thermoelectric power factor.47 On the other hand, In doping introduced a resonant energy state in the density of states (DOS) near the Fermi level (Ef).43 This resonant state significantly augments the Seebeck coefficient, S, without compromising electrical conductivity, σ, leading to an overall improvement in the power factor (S2σ). Dopants like Mg,48 Mn,49,50 and Y51 tend to reduce the first valence band effective mass near VBM without altering sub-valence bands, which may facilitate the transport of charge carriers. The valence band of GeTe is dominated by Ge(s) and Te(p) orbitals and dopants with s-orbital in the outer shell such as Cr,42 Zn,52 Cd,41,53 V,54 and Ag51 were used to decrease the s-contribution in the valence band. This lowers the valence band and increases the band degeneracy as well as increases DOS effective mass and subsequently the Seebeck coefficient.
Another advantage of substitutional doping is to lower the lattice thermal conductivity. Substitutional doping on the Ge sites e.g. Pb, Bi, Sb introduces large mass fluctuations and surrounding local strain-field fluctuations due to the difference in atomic mass and radius between dopant and Ge atoms which enables a reduction in lattice thermal conductivity.55 Due to the inherent presence of native Ge vacancies, using aliovalent dopants on the Ge lattice sites46 not only reduces the lattice thermal conductivity but also influences the carrier concentration. Fig. 1(a) summarizes literature data on various dopants usage and the corresponding TE properties, spanning the past decade where most of the cases Sb and Bi were used as dopants in GeTe. The violin plot depicted in Fig. 1(b) depicts a comprehensive overview of the distribution of measured zT values across various dopants. It combines the characteristics of both a box plot and a density plot. Within the violin plot, the black lines represent a box plot, outlining the data range. The white dot at the center signifies the mean value, while the thick bar denotes the interquartile range. Additionally, the violin plot incorporates a density plot, illustrating the frequency distribution of the data. The zT can have a large range from 0.75 to 2.5 depending on the type of dopants and their concentration. The average zT utilizing Sb or Bi alone or co-doped with X/Y elements as dopants in GeTe is notably 35–50% higher compared to other configurations. Pb has not been extensively employed due to its toxicity; however, its promising potential has also been demonstrated, with an average zT of 1.75–1.95. Extensive investigation reveals that lattice thermal conductivity is the key determinant for achieving high performance with dopants like Pb, Sb, and Bi. Notably, Pb, Sb, and Bi doping exhibit a significant reduction in lattice thermal conductivity considering the same level of doping when compared to other dopant elements (e.g., Cd,56 Sn,57 Al,58 Cu,59 Mn,50 Y,51 Sc46). Interestingly, the lattice thermal conductivity even increases with doping in some cases, e.g. In,43 Mg,48 Ti,60,61 and Al.47 For instance, although indium doping enhances the Seebeck coefficient by introducing resonant levels near the Fermi level, it also leads to an increase in lattice thermal conductivity. Consequently, the overall performance does not show a noticeable improvement in In-doped GeTe. However, this is not the case for Pb, Sb, and Bi. These three elements play a pivotal role in optimizing carrier concentrations while simultaneously decreasing lattice thermal conductivity. As a result, the overall thermoelectric performance is substantially enhanced upon the introduction of these doping elements. Nevertheless, the question of what attributes make these elements so promising for reducing lattice thermal conductivity, and why other elements do not achieve the same effect, remains unanswered.
 | ||
| Fig. 1 (a) Frequently used dopant materials in GeTe,41–62,80 (b) figure of merit zT of GeTe considering different dopants, and (c) lattice thermal conductivity trend with Pb,88 Sb,60 Bi,50 and In43 doping. Interpolated or extrapolated the doping-dependent lattice thermal conductivity data for comparison purposes. Zero doping data are from various sources and have therefore some spread. | ||
Recent studies suggest that the nature of the chemical bonds plays an important role in getting ultralow thermal conductivities in a range of materials, explaining the lower thermal conductivity in materials with dominant ionic or van der Waals than those with dominant covalent bonds.62–64 In this paper, we study the effects of Pb, Sb, Bi, and In doping in GeTe from the chemical bonding perspective and establish a relation with thermoelectric properties in the material.
Additionally, we employed a first-principles approach to solve the Boltzmann Transport equation and studied the impacts of doping as well as temperature-dependent TE properties of GeTe. To date, numerous theoretical investigations have been conducted on GeTe; however, these studies have some limitations. They rely on simplifying assumptions, such as employing the constant relaxation time approximation, as seen in the use of the BoltzTrap code,40,65–68 or adopting the single parabolic band model,69,70 effective mass modeling,39,71 3-band model72 with tuning parameters to predict the thermoelectric properties of GeTe. The utilization of a constant relaxation time or a single parabolic model expedites total transport calculations, rendering them fast and straightforward. However, these approaches lack predictive power and are not correct. For instance, the relaxation time (τ) is not a constant; rather, it is a function of electronic and phononic band structure, energy, temperature, and doping concentration.69–71 Employing a fixed τ can yield misleading results, as it fails to capture the dynamic and multifaceted nature of the relaxation time. These simplifications hinder the ability of phenomenological formalisms to accurately describe and predict the experimental TE properties. Here, we have adopted an energy-dependent relaxation time approximation including electron–phonon scattering and ionized impurity scattering. This first-principles-based framework combining electron–phonon scattering and ionized impurity scattering has proven successful in previous studies of materials such as SnSe2,73 MoSe2,74 and MoTe2.75 Through this approach, we aim to enhance the accuracy of our predictions and provide a more comprehensive understanding of the thermoelectric behavior of GeTe.
Herein, we have organized our discussion into two parts. First, we'll delve into the chemical bonding analysis of GeTe with various dopants—Pb, Bi, Sb, and In. We explore how these elements influence chemical bonding strength and establish a link with transport properties in GeTe. Next, we use our first principles-based method to assess the thermoelectric properties of GeTe across different carrier concentrations and temperatures, comparing and validating our findings with experimental results.
Methods
GeTe exhibits a stable distorted rhombohedral structure (rhombohedral angle < 60°) with R3m space group at low temperatures, transitioning to cubic structures (rhombohedral angle = 60°) with Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group above 700 K.69,76 Despite the stability of GeTe in the rhombohedral phase, historical research on GeTe-based thermoelectric materials mainly focused on the performance of the cubic phase as it has high valley degeneracy due to its high symmetry.77 Therefore, in our study, we have limited our calculation to the high-temperature cubic phase of GeTe.
m space group above 700 K.69,76 Despite the stability of GeTe in the rhombohedral phase, historical research on GeTe-based thermoelectric materials mainly focused on the performance of the cubic phase as it has high valley degeneracy due to its high symmetry.77 Therefore, in our study, we have limited our calculation to the high-temperature cubic phase of GeTe.
Chemical bonding analysis
To understand chemical bonding (bonding, non-bonding, and anti-bonding) and the strengths of it, we utilized crystal orbital Hamilton population (COHP) analysis.78 COHP has been a tool for studying various compounds, including phase change materials,79 intermetallics,80 and magnetic materials,81 for about three decades. Nowadays, these analyses can be performed through density functional theory (DFT) calculations using the projector augmented wave method.82 In this process, the original delocalized basis, based on plane waves, is projected onto atomic orbitals (e.g., Slater orbitals), as implemented in computer programs like LOBSTER.83–85 LOBSTER not only performs these projections but also calculates COHPs, crystal orbital overlap population (COOPs), crystal orbital bond index (COBIs), and other similar properties based on the information resulting from the projection. This method involves the partitioning of one-particle band energies of a solid into pairs of orbital interactions, allowing the identification of different chemical bonds and their associated strengths, measured through integrated COHP (ICOHP). It has also been shown that this quantity is directly correlated with bond strength characterized by the interatomic force constants.86 Besides ICOHP, the integrated crystal orbital bond index (ICOBI) is also calculated which denotes the bond order of a compound and gives an idea about the effective coordination number (ECoN) of the compound. A decrease in ICOBI suggests a reduced sharing of electrons (high ECoN), potentially indicating a weaker bond, while an increase suggests a stronger bond (low ECoN).87We used a 3 × 3 × 3 supercell comprised of 54 atoms as the initial GeTe cell and the Pb, Bi, Sb, and In doping are studied by replacing 2 Ge atoms with Pb, Bi, Sb, and In atoms respectively, representing 8% doping concentration. This doping level falls within the solubility limits of the dopants in GeTe, as supported by previous research GeTe.43,50,61,88–93 Additionally, because of the low formation energy of VGe (Eform = 0.5 eV) compared to VTe (Eform = 2.4 eV), Ge deficiency commonly exists in the GeTe matrix.39,94 As a result, external dopants dissolve into Ge precipitates, thereby mitigating the intrinsic high hole concentration, as evidenced by the previous studies.55,95,96 We also note due to the cubic structure of GeTe, all Ge sites are equivalent and the effects of dopants remain the same regardless of their occupancy sites. The calculations are performed using plane-wave self-consistent field code utilizing DFT as implemented in Quantum ESPRESSO package.97 The generalized gradient approximation (GGA)98 with Perdew–Bruke–Ernzerhof (PBE) parameters for the exchange–correlation functional is adopted. In this analysis, we have considered 4s24p23d10, 5s25p44d10, 6s26p25d10, 6s26p35d10, 5s25p3, 5s25p14d10 as valence electrons of Ge, Te, Pb, Bi, Sb, and In, respectively. The plane-wave energy cutoff and charge density cutoff are set at 80 Ry and 800 Ry, respectively. During structural relaxation of the supercells, atomic positions, as well as lattice constant, are relaxed until the force on each atom was less than 10−5 Ry/Bohr using the conjugate-gradient method99 and BFGS quasi-newton algorithm.100 A uniform mesh of 4 × 4 × 4 is used in sampling integrations over the Brillouin zone for self-consistent calculations. The current version of LOBSTER code does not support spin–orbit coupling (SOC), with the rationale that SOC is considered relatively unimportant for chemical bonding. Therefore, SOC is not included in the COHP analysis to simplify our calculations. To determine the required number of wavefunctions for the projection from plane waves to atomic orbitals, the DFT calculations must include enough bands in the self-consistent calculations. The number of bands depends on the structure and the basis used for the projection in LOBSTER.101 The calculation of the minimum number of bands for different supercells is discussed in ESI.† Based on the calculations, we included 405 bands for GeTe and Pb: GeTe, 406 bands for Bi: GeTe, 396 bands for Sb: GeTe, and 404 bands for In: GeTe in supercell DFT calculations. Gaussian smearing width of 0.2 eV is used during projections in LOBSTER calculation. Importantly, in this study, the sign of the COHP distinguishes bonds with either bonding or anti-bonding nature: a positive sign corresponds to anti-bonding interactions, while a negative sign corresponds to bonding interactions. Following convention, COHP diagrams represent the negative value (–COHP), facilitating the visualization of bonding (anti-bonding) states on the right (left) of the axis. To quantify the extent of anti-bonding/bonding strength, we computed the ICOHP and ICOBI with respect to the electron band energy.
To further confirm the bonding strength and anharmonicity, bulk modulus 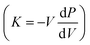 is also computed for different compounds where V is the volume and P is the pressure. This involves modifying the volume of the supercell by ±1% of its equilibrium volume, determining the corresponding pressures at these altered volumes, and subsequently calculating the bulk modulus using the finite-difference method. A higher bulk modulus generally indicates stronger interatomic or intermolecular forces and thus stronger bonding within the material.
is also computed for different compounds where V is the volume and P is the pressure. This involves modifying the volume of the supercell by ±1% of its equilibrium volume, determining the corresponding pressures at these altered volumes, and subsequently calculating the bulk modulus using the finite-difference method. A higher bulk modulus generally indicates stronger interatomic or intermolecular forces and thus stronger bonding within the material.
Transport properties of GeTe
Transport calculation is performed considering the primitive cell of cubic GeTe. The primitive cell of the cubic phase comprises two atoms: 1 Ge and 1 Te. Structural relaxation is performed with a force convergence criterion of 10−5 Ry/Bohr and obtained lattice parameters (a = b = c = 6.008 Å) closely match the neutron diffraction results.76 A kinetic energy cutoff of 60 Ry and Monkhorst–Pack k-point mesh of 16 × 16 × 16 is employed in the atomic and electronic structure calculations. Fully relativistic pseudopotentials within Perdew–Bruke–Ernzerhof generalized gradient approximation are employed to include SOC effects. The dynamical matrix is computed on a 4 × 4 × 4 q-point mesh in the phonon calculations. The phonon modes and frequencies at other general k-points are then computed by Fourier transformation of the dynamical matrix in reciprocal space. As cubic-GeTe shows strong lattice anharmonicity, density functional perturbation theory (DFPT) calculation exhibits unstable soft phonon modes with negative frequency in the phonon dispersion (Fig. S2 in the ESI†). To account for finite temperature lattice dynamics, we have utilized the temperature-dependent effective potentials (TDEP) method,102–104 effectively stabilizing the phonon modes. TDEP extracts the effective interatomic force constants (IFCs) that best describe the anharmonic Born–Oppenheimer potential surface at a given temperature. Later, the electron–phonon (e–ph) matrix elements are computed, using both harmonic (DFPT) and anharmonic (TDEP) phonons, in the PERTURBO package,105 which is also employed to efficiently compute the e–ph scattering rates.106 PERTURBO interpolates the electron–phonon matrices, obtained from DFT and DFPT + TDEP calculations, from a coarse grid to fine k-mesh (60 × 60 × 60) and q-mesh (5 × 106) using Wannier interpolation scheme.107,108 In Wannier interpolation, automatic projection scheme109 is employed for the Wannierization of the 12 bands. Details of electron–phonon matrix calculations in PERTURBO are discussed elsewhere106 and convergence study of the k-mesh and q-mesh for e–ph scattering rates is available in Fig. S3 in the ESI.†The ionized impurity scattering rates are essential in the calculations because of the high concentration of native Ge vacancies. We have used a modified Brooks-Herring approach for strongly screened coulomb potential.110 The impurity scattering rate is given by,
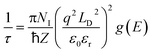 | (1) |
 | (2) |
The electrical conductivities, electronic thermal conductivities, and the Seebeck coefficients are calculated using the PERTURBO code by solving the linearized Boltzmann transport equation (BTE) under energy-dependent relaxation time approximation.
The lattice thermal conductivity was then computed by using TDEP. The first principles calculations were performed using density functional theory (DFT) with a projector augmented wave method and the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation by employing the Vienna ab initio simulation (VASP) package.111,112 The harmonic and anharmonic interatomic force constants (IFCs) were obtained using a 4 × 4 × 4 supercell with a 5 × 5 × 5 Γ-centered Monkhorst–Pack k mesh. The converged cutoff for harmonic and cubic IFCs were considered up to 7 Å and 10 Å, respectively. The convergence of the forces with respect to number of configurations was obtained by iteratively generating a set of displacements, computing forces, and fitting IFCs. The lattice thermal conductivity of natural GeTe with 8% Ge vacancies was calculated on a converged q-space grid 20 × 20 × 20 by iteratively solving the phonon Boltzmann transport equation as implemented in TDEP. The effect of vacancy scattering rates were considered the same as isotopic scattering rates with zero mass.
Results and discussion
Chemical bonding analysis
GeTe is known to have a special type of bonding with signatures in between covalent and metallic bonding and with a small degree of ionicity in the bonding, called metavalent bonding. The impact of substituting Ge with Pb, Bi, Sb, and In has been carefully examined in the supercell model through COHP analysis with the aid of electronic projected density of states (PDOS) calculations. The electronic PDOS using DFT reveals that the valence band in GeTe is dominated by Te(p) orbital and Ge(p) orbital with a small contribution from Ge(s) orbital as shown in Fig. 2(a). This indicates the dominant orbital interaction in Ge–Te bonding is Ge(p)–Te(p) interaction. Fig. S4 in the ESI† visually depicts the Ge–Te orbital interaction using isosurfaces of electronic wavefunctions at the valence band maxima of GeTe. | ||
| Fig. 2 (a) Projected density of state (PDOS) of pure GeTe, (b) average COHP curves for different bonding configurations. | ||
Similar to Ge–Te, bonding, X–Te (X: Pb, Sb, Bi, In) bonding interactions are also coming from X(p)–Te(p) orbital in Pb, Bi, Sb, and In-doped GeTe as evidenced by PDOS calculations (Fig. S5 in the ESI†). However, in the case of In-doped GeTe, strong In(s)–Te(p) orbital interaction is also present in the bonding. The nature of these interactions is illustrated by COHP analysis as shown in Fig. 2(b) which shows antibonding states near the Fermi level in all cases. To assess the strength of the X–Te bonding, ICOHPs are evaluated using,
 | (3) |
| Compounds | Bonding interactions | Bond length (Å) | ICOHP (eV) |
|---|---|---|---|
| Pure GeTe | Ge–Te (average) | 3.01 | −1.68 |
| Ge(p)–Te(p) | −1.18 | ||
| Pb doped GeTe | Ge–Te (average) | 2.93 | −1.94 |
| Ge(p)–Te(p) | −1.34 | ||
| Pb–Te (average) | 3.16 | −1.49 | |
| Pb(p)–Te(p) | −1.08 | ||
| Bi doped GeTe | Ge–Te (average) | 2.95 | −1.79 |
| Ge(p)–Te(p) | −1.24 | ||
| Bi–Te (average) | 3.12 | −1.53 | |
| Bi(p)–Te(p) | −1.23 | ||
| Sb doped GeTe | Ge–Te (average) | 2.97 | −1.72 |
| Ge(p)–Te(p) | −1.20 | ||
| Sb–Te (average) | 3.07 | −1.59 | |
| Sb(p)–Te(p) | −1.25 | ||
| In doped GeTe | Ge–Te (average) | 2.94 | −1.86 |
| Ge(p)–Te(p) | −1.32 | ||
| In–Te (average) | 3.09 | −2.04 | |
| In(p)–Te(p) | −0.97 | ||
| In(p)–Te(s) | −0.35 | ||
| In(s)–Te(p) | −0.69 |
We found that average ICOHPs for Pb–Te, Bi–Te, and Sb–Te bonds are higher than the Ge–Te bond corresponding to weaker interatomic bonds. On the other hand, In–Te bonding is stronger than Ge–Te as shown by the lower value of ICOHP. The same trend is also found in the dominant orbital interactions in different compounds.62,113,114
As shown before by many i.e. Schlohmann,115 Slack,116 Klemens,117 and Toberer,118 the lattice thermal conductivity strongly depends on the sound velocity (κ1 ∼ vs3 where vs is the sound velocity). And sound velocity is correlated with chemical bond strength ( where k denotes the bond strength). A weaker bond leads to lower sound velocity as well as lower lattice thermal conductivity. Based on ICOHP, bond becomes weaker in the case of Pb, Bi, and Sb doped GeTe which lowers the sound velocity and corresponds to a lower experimentally measured thermal conductivity. On the other hand, stronger bonding in In-doped GeTe results in larger thermal conductivity values compared to pure GeTe as depicted in Fig. 1(c). Within Pb, Bi, and Sb-doped GeTe, compounds with Sb doping demonstrate the highest bonding interactions (total and p–p), while those with Pb doping exhibit the lowest, aligning with the observed the lowest lattice thermal conductivity in Pb-doped compounds compared to others. The length of the corresponding bonds obtained after relaxing the lattice structure is also in agreement with ICOHPs results: i.e. the higher the bond length, the weaker the bonds. A shorter bond involves a greater degree of orbital overlap between the atomic orbitals, leading to a more stable configuration.
where k denotes the bond strength). A weaker bond leads to lower sound velocity as well as lower lattice thermal conductivity. Based on ICOHP, bond becomes weaker in the case of Pb, Bi, and Sb doped GeTe which lowers the sound velocity and corresponds to a lower experimentally measured thermal conductivity. On the other hand, stronger bonding in In-doped GeTe results in larger thermal conductivity values compared to pure GeTe as depicted in Fig. 1(c). Within Pb, Bi, and Sb-doped GeTe, compounds with Sb doping demonstrate the highest bonding interactions (total and p–p), while those with Pb doping exhibit the lowest, aligning with the observed the lowest lattice thermal conductivity in Pb-doped compounds compared to others. The length of the corresponding bonds obtained after relaxing the lattice structure is also in agreement with ICOHPs results: i.e. the higher the bond length, the weaker the bonds. A shorter bond involves a greater degree of orbital overlap between the atomic orbitals, leading to a more stable configuration.
The calculated bond index by ICOBI for pure GeTe is close to 0.4, which corresponds to a sharing of 0.8 electrons as depicted in Fig. 3. This is in reasonable agreement with metavalent bonding where two atoms are held together by a single electron (bond order ∼0.5).119 The observed lower ICOBI in Pb-doped GeTe indicates less electron localization as well as less bonding interactions compared to pure GeTe. This reduction in bonding interactions may result in a weaker bond strength. Conversely, the higher ICOBI in In-doped GeTe suggests more localized electrons clouds, implying a stronger bond. Bond order can also be visualized by electron localization function (ELF) which denotes the localization and delocalization of electron clouds. An ELF value of 0.5 corresponds to a free electron gas (metal), 1 corresponds to totally localized electrons while small values correspond to a lack of electrons. The evolution of ELF isosurfaces for Pb and In doping is shown in Fig. 4 where red color denotes perfect localization and blue color denotes absence of electrons. One can see that the electrons are more localized at the dopant sites with In-doping compared to Pb-doping and electron sharing is higher around Pb sites. Increased electron sharing corresponds to a greater extent of electron delocalization in Pb-doped GeTe (high ECoN). Due to the delocalized electrons in Pb-doped GeTe, the bond order is relatively low.
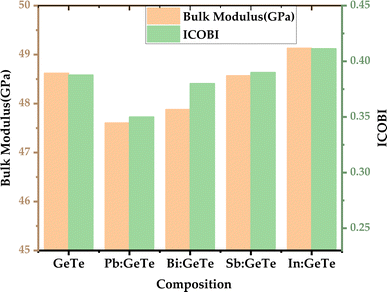 | ||
| Fig. 3 (Left) bulk modulus of different compounds, (right) integrated crystal orbital bond indices (ICOBI) for different bonding. | ||
 | ||
| Fig. 4 Electron localization function plot (a) Pb-doped (b) In-doped GeTe. Electrons around Pb seems more delocalized compared to In. | ||
The observed trend in bulk modulus is also consistent with the bonding strength insights obtained from ICOHP and ICOBI analysis. In Pb-doped GeTe, weaker bonds correspond to a lower bulk modulus, while in In-doped GeTe, stronger bonds align with a higher bulk modulus. Thus, this explains the reason behind the more substantial reduction in lattice thermal conductivity with Pb doping (87% reduced at 8 at%) compared to other dopants and increased lattice thermal conductivity with In-doping as it makes the bond stronger and more stable. These findings underscore the intricate relationship between bonding characteristics and thermal properties in doped GeTe systems, emphasizing the notably higher decrement observed in lattice thermal conductivity with Pb doping.
Next, we explored the effect of chemical bonding on electronic transport via projected density of state calculations. As mentioned earlier, in cubic-GeTe, the chemical bonding orbitals are mainly from p-orbitals in σ-bonding configuration with weak s–p hybridization.120 According to Wuttig,120 small cation(s)–anion(p) orbital hybridization together with small ionicity results in a strong anisotropic band valley. A highly anisotropic band structure has a large difference in  and
and  (
( where,
where, 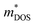 is the DOS effective mass and
is the DOS effective mass and  is the conductivity effective mass). According to Pisarenko and Drude equations,33
is the conductivity effective mass). According to Pisarenko and Drude equations,33 can be considered as a figure of merit of the band structure indicating a potentially high power factor where a heavy
can be considered as a figure of merit of the band structure indicating a potentially high power factor where a heavy 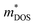 and a larger mass ratio (
and a larger mass ratio ( 〉〉 1) leads to superior thermoelectric power factors.39,121 Therefore, the reported maximal S2σ of cubic-GeTe is higher than those of SnTe122 and PbTe123 at optimized carrier concentration. Here, Pb, Bi, Sb, and In all have S2 lone pairs of electrons in their outer shells like Ge. The contribution from the s and p orbital of dopants compared with Ge(s) and Ge(p) is shown in Fig. S6 in the ESI.† It is evident that the In(s) contribution is higher than Ge(s) near the valence band. Therefore, the substitution of Ge with In strengthens In(s)–Te(p) hybridization and charge transfer. This results in a reduction of the anisotropy of the band valley (lower
〉〉 1) leads to superior thermoelectric power factors.39,121 Therefore, the reported maximal S2σ of cubic-GeTe is higher than those of SnTe122 and PbTe123 at optimized carrier concentration. Here, Pb, Bi, Sb, and In all have S2 lone pairs of electrons in their outer shells like Ge. The contribution from the s and p orbital of dopants compared with Ge(s) and Ge(p) is shown in Fig. S6 in the ESI.† It is evident that the In(s) contribution is higher than Ge(s) near the valence band. Therefore, the substitution of Ge with In strengthens In(s)–Te(p) hybridization and charge transfer. This results in a reduction of the anisotropy of the band valley (lower  than GeTe). With the reduction of
than GeTe). With the reduction of  overall power factor reduces. On the other hand, substituting Ge with Pb, Sb, or Bi reduces the s contribution near the valence band, resulting in s–p interactions reduction. This increases
overall power factor reduces. On the other hand, substituting Ge with Pb, Sb, or Bi reduces the s contribution near the valence band, resulting in s–p interactions reduction. This increases  and boosts the power factor. For reference, the bonding strength from s–p interactions derived from COHP calculations is tabulated in Table S1.† The relation between s–p hybridization and thermoelectric power factor explained here is also consistent with experimental observations.88,124
and boosts the power factor. For reference, the bonding strength from s–p interactions derived from COHP calculations is tabulated in Table S1.† The relation between s–p hybridization and thermoelectric power factor explained here is also consistent with experimental observations.88,124
In summary, in this section, we have identified and explained a link between chemical bonding and thermoelectric properties of doped GeTe. Except for Indium, Pb, Bi, and Sb, do not have significant effect in the total DOS rather than modifying the Fermi level as shown in Fig. S6 in the ESI.† Thus, in the next section, we have limited our calculations to intrinsic GeTe as simulating and solving transport coefficients for doped GeTe with doping inclusion from first principles requires supercell calculations which are not possible due to limitations in computational resources. So, the doping effect has been modeled by a shift in the Fermi level in the pure GeTe.
Thermoelectric transport properties of GeTe
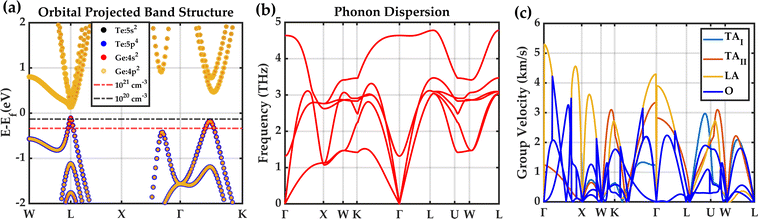
The orbital projected electronic band structure with SOC and phonon dispersion of cubic GeTe are shown in Fig. 5. The electronic band structure is plotted along the high symmetry points W(0.500,0.250,0.750) → L(0.500,0.500,0.500) → X(0.500,0.000,0.500) → Γ(0.000,0.000,0.000) → K(0.375,0.375,0.375) in Fig. 5(a). The inclusion of SOC has minimal effects on band structure near the band maxima which is shown in Fig. S7 in the ESI.† The conduction band minimum (CBM) and valence band maximum (VBM) lie at the L-point (with band degeneracy Nv of 4), denoting a direct bandgap of 0.21 eV. The data on the fundamental energy gap in GeTe is controversial125 and it varies from 0.1 to 0.24 eV. However, our obtained bandgap matches with some experimental values126–128 as well as prior theoretical calculations.40,129–133 A secondary valence band is located along Γ → K path (∑ band with band degeneracy Nv of 12) and the third valence band maximum is along X → Γ path that are 0.07 eV and 0.30 eV below the VBM, respectively. This suggests that the L and Σ bands are more likely to converge for charge carrier transport in cubic-GeTe, providing a partial explanation for the large thermoelectric zTs in cubic-GeTe at elevated temperatures. The obtained DFT band structure was further interpolated using maximally localized Wannier functions, and the resulting Wannier interpolated band structure aligns well with the DFT band structure (Fig. S7 in the ESI†).As mentioned earlier cubic-GeTe is thermodynamically unstable at room temperature, vibrational modes are stabilized by a finite temperature of 800 K in TDEP calculations. The phonon dispersion agrees with the previously theoretical reports.134,135 The phonon dispersion of cubic-GeTe reveals the presence of six vibrational modes, consisting of three acoustic modes, two transverse optical modes, and one longitudinal optical mode. The group velocities for each phonon mode are shown along high symmetry points in Fig. 5(c). From the value of acoustic group velocities along [110] direction, it is possible to also extract the elastic constants. These values are summarized in Table 2.
| Group velocity (km s−1) | 1.24 | 3.34 | 4.29 |
| ρv 2 (GPa) | 9.4 | 68.2 | 112.6 |
| Elastic constants (GPa) | C 44 = 9.4 | C 12 = 35 | C 11 = 171.4 |
After successfully obtaining harmonic phonon from DFPT and anharmonic part from TDEP, e–ph scattering rates at different temperatures are computed by the PERTURBO package. As cubic-GeTe is a highly p-doped degenerate semiconductor, we have studied the e–ph interaction within the valence band.
Fig. 6(a) shows the calculated e–ph rates obtained from PERTURBO codes with respect to the valence band. In the case of doped semiconductors, it is important to include ionized impurity scattering in addition to e–ph interactions. The ionized impurity scattering at different carrier concentrations calculated using modified Brook's Herring approach is shown in Fig. 6(b). Both scattering rates versus band energy show a similar trend to that of the electronic DOS, consistent with the fact that DOS regulates the phase space for scattering. As expected, the e–ph scattering rate increases with the temperature. The ionized impurity scattering decreases with increasing carrier concentration. This is because of the assumption of the strongly screened coulomb potential as formulated in eqn (1). Within strong screening approximation, while the number of vacancy/impurity concentrations (NI) increases at higher carrier concentrations, the electrons screen the background ionic charges, resulting in a lowering of the ionized impurity scattering potential. At very large concentrations, electron-impurity screening length is short resulting in lower scattering rates (see eqn (2) and Fig. S8 in the ESI†).
Utilizing computed e–ph and ionized impurity scattering rates, the thermoelectric transport properties including electrical conductivity (σ), Seebeck coefficient (S), and electronic thermal conductivity (κe) within the temperature range of 650–800 K are computed by solving the linearized BTEs at different carrier concentrations. Fig. 7 illustrates the electrical conductivity and Seebeck coefficient at different temperatures and carrier concentrations. Our calculated values are compared with experimental results, revealing a generally strong agreement, except for a few data points representing GeTe low carrier concentration. This is because of the use of intrinsic GeTe structure for electronic structure calculation and changing the carrier concentration to include the effects of doping. In reality, as-grown GeTe contains a significant number of Ge-vacancies, contributing to its highly p-type carrier concentration. To mitigate these vacancies and decrease the overall carrier concentration, a significant amount of doping is used. External doping can modify the electronic band structure that was discussed in DOS calculations as well as prior theoretical calculations.39,43,133 Specifically, the introduction of In and Bi create defect states near the Fermi level as in Fig. S6 in the ESI,† reducing Seebeck at higher Bi & In doping concentrations while showing slightly improved electrical conductivity compared to our predictions.43,136 These defect states directly affect the effective mass according to Pisarenko and Drude equations. Overall, our first principles-based framework demonstrates successful predictions of experimental results. Any observed discrepancies are attributed to nuanced variations in the electronic band structure as a result of doping, a factor not explicitly considered in our calculations.
 | ||
| Fig. 7 Calculated (a–c) electrical conductivity, (d–f) Seebeck coefficient at different temperatures w.r.t carrier concentration solving RTA-based BTE equations and compared with experimentally obtained results.50,60,61,131 | ||
In Fig. 8, the computed thermal conductivity of GeTe, encompassing both electronic and lattice components, is presented alongside experimental results for as-grown GeTe. The calculated thermal conductivity values tend to overestimate the experimental results, primarily resulting from the inaccuracies in modeling the lattice part of thermal conductivity. Fig. S9 in the ESI† illustrates the distinct contributions of the electronic and lattice components. As can be seen in both Fig. 8 and S9,† the lattice thermal conductivity reduces with increasing temperature throughout the range of carrier concentrations due to stronger phonon–phonon scattering rates at higher temperatures. Notably, the total thermal conductivity is predominantly influenced by the lattice part at low carrier concentrations, while the electronic part becomes dominant at higher carrier concentrations. The overestimation observed in our calculations is attributed to the neglect of various factors affecting lattice thermal conductivity, such as grain sizes, structural dislocations, nano precipitates, and microstructure variations arising from different sample preparation methods. These aspects were not accounted for in the theoretical model, leading to the commonly observed overestimation in calculated values. Recognizing the impact of these factors on lattice thermal conductivity is crucial for refining theoretical models and achieving better agreement with experimental observations.
 | ||
| Fig. 8 Calculated total thermal conductivity (solid lines) and lattice thermal conductivity (dashed lines) at different temperatures (blue: 650 K, purple: 700 K, yellow: 750 K, and red: 800 K) compared with experimental results (+ symbols).21,45,50,57,58,60,132 | ||
Subsequently, we proceed to compute the power factor times temperature (PFT) and the dimensionless figure of merit (zT) across varying carrier concentrations and temperatures. It is evident from Fig. 9 that the optimum operating point shifts towards a high carrier concentration region with increasing temperature. Finally, a maximum PFT of 2.2 Wm−1 K−1 is achieved at around 4.8 × 1020 cm−3 at 800 K which is comparable to experimentally measured value for as-grown GeTe (2.0–2.5 Wm−1 K−1).49,61,72,129,137 Experimental evidence indicates that this PFT value can range up to 4.0 Wm−1 K−1 with the presence of doping21,50,137 or excessive Ge vacancies133 which alters the electronic structure significantly.39 The discrepancy arises from the fact that we used intrinsic GeTe bandstructure in our transport calculations. We assumed dopants to only change the carrier concentration and the scattering rates without modifying the electronic band structure. This is the reason behind underestimation of PFT in our model compared to experimentally derived state of art doped GeTe.
 | ||
| Fig. 9 (a) Optimized power factor time temperature (PFT), (b) figure of merit (zT) versus carrier concentrations at different temperatures. | ||
Regarding thermal conductivity as mentioned earlier, we only consider isotropic scattering to account for Ge vacancies, resulting in an overestimation attributed to neglecting factors affecting lattice thermal conductivity, such as grain sizes, structural dislocations, nano precipitates, microstructure and strain variations from sample preparation methods. These aspects were not accounted for in the theoretical model. Overall, underestimation in power factor and overestimation in thermal conductivity calculation leads to lower zT compared to experimental findings. The highest zT of 0.83 is obtained at 3.4 × 1020 cm−3 and our calculated zT is still comparable to experimental average values for as-grown GeTe (zTavg = 1.0 at 800 K).21,45,50,57,61,138,139
Conclusions
In summary, this study illustrates that tuning chemical bonding through doping offers in metavalent materials a degree of freedom for optimizing thermoelectric properties, not only through changing the Fermi level, but also by modifying softness of the bonds, thereby affecting anharmonicity and the lattice thermal conductivity. The observed low lattice thermal conductivity in Pb-doped GeTe is attributed to weak p–p interactions. In contrast, the thermal conductivity increases in In-doped GeTe, where the chemical bonds are strengthened by In-doping as verified by COHP analysis. Simultaneously, weak s–p interactions in Bi, Sb, and Pb-doped GeTe, in contrast to strong s–p interactions in In-doped GeTe, contribute to the strong anisotropic band which explains experimentally observed high power factor and elevated zT values in the former group. The utilization of a first-principles framework allows for a detailed exploration of transport properties in pure GeTe, considering factors such as electron-phonon and ionized impurity scattering. The optimization of thermoelectric performance, as illustrated by the power factor times temperature and zT values, highlights specific carrier concentrations and temperatures that yield optimal results. The comprehensive analysis presented here enhances our understanding of the intricate interplay between chemical bonding and transport properties in GeTe, providing valuable insights for the quest to discover new material systems with superior thermoelectric capabilities.Author contributions
M. Z. and K. E. supervised the project. S. S. D. performed the chemical bonding analysis and the electronic first-principles calculation. S. N. S. performed the TDEP and lattice thermal conductivity calculations. S. S. D., K. E., and M. Z. drafted the manuscript. All authors reviewed the manuscript prior to submission.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge discussions with Professor Jin-Jian Zhou from Beijing Institute of Technology on the TDEP to PERTURBO calculations. This work is supported by National Science Foundation grant number 2230352. The Rihanna cluster of UVA was used for these computations.Notes and references
- H. Goldsmid, Thermoelectric Refrigeration, Springer, 2013 Search PubMed.
- B. C. Sales, Smaller is cooler, Science, 2002, 295(5558), 1248–1249, DOI:10.1126/science.1069895.
- B. Poudel, Q. Hao, Y. Ma, Y. Lan, A. Minnich, B. Yu, X. Yan, D. Wang, A. Muto, D. Vashaee, X. Chen, J. Liu, M. S. Dresselhaus, G. Chen and Z. Ren, High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys, Science, 2008, 320(5876), 634–638, DOI:10.1126/science.1156446.
- D. M. Rowe, CRC Handbook of Thermoelectrics, CRC Press, 2018 Search PubMed.
- G. Tan, L.-D. Zhao and M. G. Kanatzidis, Rationally designing high-performance bulk thermoelectric materials, Chem. Rev., 2016, 116(19), 12123–12149, DOI:10.1021/acs.chemrev.6b00255.
- T. Zhu, Y. Liu, C. Fu, J. P. Heremans, J. G. Snyder and X. Zhao, Compromise and synergy in high-efficiency thermoelectric materials, Adv. Mater., 2017, 29(14), 1605884, DOI:10.1002/adma.201605884.
- I. Chowdhury, R. Prasher, K. Lofgreen, G. Chrysler, S. Narasimhan, R. Mahajan, D. Koester, R. Alley and R. Venkatasubramanian, On-chip cooling by superlattice-based thin-film thermoelectrics, Nat. Nanotechnol., 2009, 4(4), 235–238, DOI:10.1038/nnano.2008.417.
- J. H. Yang and T. Caillat, Thermoelectric materials for space and automotive power generation, MRS Bull., 2006, 31(3), 224–229, DOI:10.1557/mrs2006.49.
- Q. Yan and M. G. Kanatzidis, High-performance thermoelectrics and challenges for practical devices, Nat. Mater., 2022, 21(5), 503–513, DOI:10.1038/s41563-021-01109-w.
- A. Witze, Desperately seeking plutonium, Nature, 2014, 515(7528), 484–486, DOI:10.1038/515484a.
- R. He, G. Schierning and K. Nielsch, Thermoelectric devices: a review of devices, architectures, and contact optimization, Adv. Mater. Technol., 2018, 3(4), 1700256, DOI:10.1002/admt.201700256.
- M. Hong, J. Zou and Z. G. Chen, Thermoelectric GeTe with diverse degrees of freedom having secured superhigh performance, Adv. Mater., 2019, 31(14), 1–23, DOI:10.1002/adma.201807071.
- C. Wang, K. Xia, H. Wang, X. Liang, Z. Yin and Y. Zhang, Advanced carbon for flexible and wearable electronics, Adv. Mater., 2019, 31(9), e1801072, DOI:10.1002/adma.201801072.
- S. Xu, X.-L. Shi, M. Dargusch, C. Di, J. Zou and Z.-G. Chen, Conducting polymer-based flexible thermoelectric materials and devices: from mechanisms to applications, Prog. Mater. Sci., 2021, 121, 100840, DOI:10.1016/j.pmatsci.2021.100840.
- S. Dongmin Kang and G. Jeffrey Snyder, Charge-transport model for conducting polymers, Nat. Mater., 2017, 16(2), 252–257, DOI:10.1038/nmat4784.
- T. Cao, X.-L. Shi, J. Zou and Z.-G. Chen, Advances in conducting polymer-based thermoelectric materials and devices, Microstructures, 2021, 1(1), 2021007, DOI:10.20517/microstructures.2021.06.
- X. Zhang, Z. Bu, S. Lin, Z. Chen, W. Li and Y. Pei, GeTe thermoelectrics, Joule, 2020, 4(5), 986–1003, DOI:10.1016/j.joule.2020.03.004.
- S. Perumal, S. Roychowdhury, D. S. Negi, R. Datta and K. Biswas, High thermoelectric performance and enhanced mechanical stability of P-type Ge1-XSbxTe, Chem. Mater., 2015, 27(20), 7171–7178, DOI:10.1021/acs.chemmater.5b03434.
- Y. Tang, Z. M. Gibbs, L. A. Agapito, G. Li, H.-S. Kim, M. B. Nardelli, S. Curtarolo and G. J. Snyder, Convergence of multi-valley bands as the electronic origin of high thermoelectric performance in CoSb3 skutterudites, Nat. Mater., 2015, 14(12), 1223–1228, DOI:10.1038/nmat4430.
- K. Imasato, S. D. Kang, S. Ohno and G. J. Snyder, Band engineering in Mg3Sb2 by alloying with Mg3Bi2 for enhanced thermoelectric performance, Mater. Horiz., 2018, 5(1), 59–64, 10.1039/C7MH00865A.
- M. Hong, Z. G. Chen, L. Yang, Y. C. Zou, M. S. Dargusch, H. Wang and J. Zou, Realizing zT of 2.3 in Ge1−x−ySbxInyTe via reducing the phase-transition temperature and introducing resonant energy doping, Adv. Mater., 2018, 30(11), 1–8, DOI:10.1002/adma.201705942.
- J. P. Heremans, V. Jovovic, E. S. Toberer, A. Saramat, K. Kurosaki, A. Charoenphakdee, S. Yamanaka and G. J. Snyder, Enhancement of thermoelectric efficiency in PbTe by distortion of the electronic density of states, Science, 2008, 321(5888), 554–557, DOI:10.1126/science.1159725.
- L.-D. Zhao, S.-H. Lo, Y. Zhang, H. Sun, G. Tan, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals, Nature, 2014, 508(7496), 373–377, DOI:10.1038/nature13184.
- M. G. Kanatzidis, Nanostructured thermoelectrics: the new paradigm?, Chem. Mater., 2010, 22(3), 648–659, DOI:10.1021/cm902195j.
- G. Zhang, B. Kirk, L. A. Jauregui, H. Yang, X. Xu, Y. P. Chen and Y. Wu, Rational synthesis of ultrathin N-Type Bi2Te3 nanowires with enhanced thermoelectric properties, Nano Lett., 2012, 12(1), 56–60, DOI:10.1021/nl202935k.
- T. Zhu, L. Hu, X. Zhao and J. He, New insights into intrinsic point defects in V2VI3 thermoelectric materials, Adv. Sci., 2016, 3(7), 270, DOI:10.1002/advs.201600004.
- H. Zhu, J. Mao, Y. Li, J. Sun, Y. Wang, Q. Zhu, G. Li, Q. Song, J. Zhou, Y. Fu, R. He, T. Tong, Z. Liu, W. Ren, L. You, Z. Wang, J. Luo, A. Sotnikov, J. Bao, K. Nielsch, G. Chen, D. J. Singh and Z. Ren, Discovery of TaFeSb-based half-heuslers with high thermoelectric performance, Nat. Commun., 2019, 10(1), 270, DOI:10.1038/s41467-018-08223-5.
- G. Tan, F. Shi, J. W. Doak, H. Sun, L.-D. Zhao, P. Wang, C. Uher, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Extraordinary role of hg in enhancing the thermoelectric performance of P-type SnTe, Energy Environ. Sci., 2015, 8(1), 267–277, 10.1039/c4ee01463d.
- H. Fang, T. Feng, H. Yang, X. Ruan and Y. Wu, Synthesis and thermoelectric properties of compositional-modulated lead telluride-bismuth telluride nanowire heterostructures, Nano Lett., 2013, 13(5), 2058–2063, DOI:10.1021/nl400319u.
- H. Fang, H. Yang and Y. Wu, Thermoelectric properties of silver telluride-bismuth telluride nanowire heterostructure synthesized by site-selective conversion, Chem. Mater., 2014, 26(10), 3322–3327, DOI:10.1021/cm501188c.
- L.-P. Hu, T.-J. Zhu, Y.-G. Wang, H.-H. Xie, Z.-J. Xu and X.-B. Zhao, Shifting up the optimum figure of merit of P-type bismuth telluride-based thermoelectric materials for power generation by suppressing intrinsic conduction, NPG Asia Mater., 2014, 6(2), e88, DOI:10.1038/am.2013.86.
- S. Wang, Y. Sun, J. Yang, B. Duan, L. Wu, W. Zhang and J. Yang, High thermoelectric performance in Te-free (Bi,Sb)2Se3via structural transition induced band convergence and chemical bond softening, Energy Environ. Sci., 2016, 9(11), 3436–3447, 10.1039/C6EE02674E.
- W.-D. Liu, L.-C. Yin, L. Li, Q. Yang, D.-Z. Wang, M. Li, X.-L. Shi, Q. Liu, Y. Bai, I. Gentle, L. Wang and Z.-G. Chen, Grain boundary Re-crystallization and sub-nano regions leading to high plateau figure of merit for Bi2Te3 nanoflakes, Energy Environ. Sci., 2023, 16(11), 5123–5135, 10.1039/D3EE02370B.
- G. Joshi, H. Lee, Y. Lan, X. Wang, G. Zhu, D. Wang, R. W. Gould, D. C. Cuff, M. Y. Tang, M. S. Dresselhaus, G. Chen and Z. Ren, Enhanced thermoelectric figure-of-merit in nanostructured p-type silicon germanium bulk alloys, Nano Lett., 2008, 8(12), 4670–4674, DOI:10.1021/nl8026795.
- M. Zebarjadi, K. Esfarjani, M. S. Dresselhaus, Z. F. Ren and G. Chen, Perspectives on thermoelectrics: from fundamentals to device applications, Energy Environ. Sci., 2012, 5(1), 5147–5162, 10.1039/C1EE02497C.
- C. Fu, S. Bai, Y. Liu, Y. Tang, L. Chen, X. Zhao and T. Zhu, Realizing high figure of merit in heavy-band p-type half-heusler thermoelectric materials, Nat. Commun., 2015, 6(1), 8144, DOI:10.1038/ncomms9144.
- S. Anand, K. Xia, V. I. Hegde, U. Aydemir, V. Kocevski, T. Zhu, C. Wolverton and G. J. Snyder, A valence balanced rule for discovery of 18-electron half-heuslers with defects, Energy Environ. Sci., 2018, 11(6), 1480–1488, 10.1039/C8EE00306H.
- Y. Cheng, S. Wahl and M. Wuttig, Metavalent bonding in solids: characteristic representatives, their properties, and design options, Phys. Status Solidi RRL, 2021, 15(3), 2000482, DOI:10.1002/pssr.202000482.
- M. Hong, M. Li, Y. Wang, X. L. Shi and Z. G. Chen, Advances in versatile GeTe thermoelectrics from materials to devices, Adv. Mater., 2023, 35(2), 2208272, DOI:10.1002/adma.202208272.
- G. Xing, J. Sun, Y. Li, X. Fan, W. Zheng and D. J. Singh, Thermoelectric properties of p-type cubic and rhombohedral GeTe, J. Appl. Phys., 2018, 123(19), 1–6, DOI:10.1063/1.5025070.
- M. Hong, Y. Wang, W. Liu, S. Matsumura, H. Wang, J. Zou and Z.-G. Chen, Arrays of planar vacancies in superior thermoelectric Ge1−x−yCdxBiyTe with band convergence, Adv. Energy Mater., 2018, 8(30), 1801837, DOI:10.1002/aenm.201801837.
- M. Hong, K. Zheng, W. Lyv, M. Li, X. Qu, Q. Sun, S. Xu, J. Zou and Z.-G. Chen, Computer-aided design of high-efficiency GeTe-based thermoelectric devices, Energy Environ. Sci., 2020, 13(6), 1856–1864, 10.1039/D0EE01004A.
- L. Wu, X. Li, S. Wang, T. Zhang, J. Yang, W. Zhang, L. Chen and J. Yang, Resonant level-induced high thermoelectric response in indium-doped GeTe, NPG Asia Mater., 2017, 9(1), e343, DOI:10.1038/am.2016.203.
- S. Perumal, P. Bellare, U. S. Shenoy, U. V. Waghmare and K. Biswas, Low thermal conductivity and high thermoelectric performance in Sb and Bi codoped GeTe: complementary effect of band convergence and nanostructuring, Chem. Mater., 2017, 29(24), 10426–10435, DOI:10.1021/acs.chemmater.7b04023.
- L. Xu, H.-Q. Wang and J.-C. Zheng, Thermoelectric properties of PbTe, SnTe, and GeTe at high pressure: an ab initio study, J. Electron. Mater., 2011, 40(5), 641–647, DOI:10.1007/s11664-010-1491-y.
- Z. Liu, W. Gao, W. Zhang, N. Sato, Q. Guo and T. Mori, High power factor and enhanced thermoelectric performance in Sc and Bi codoped GeTe: insights into the hidden role of rhombohedral distortion degree, Adv. Energy Mater., 2020, 10(42), 2002588, DOI:10.1002/aenm.202002588.
- B. Srinivasan, A. Gellé, J.-F. Halet, C. Boussard-Pledel and B. Bureau, Detrimental effects of doping Al and Ba on the thermoelectric performance of GeTe, Materials, 2018, 11(11), 2237, DOI:10.3390/ma11112237.
- L. Wang, J. Li, Y. Xie, L. Hu, F. Liu, W. Ao, J. Luo and C. Zhang, Tailoring the chemical bonding of GeTe-based alloys by MgB2 alloying to simultaneously enhance their mechanical and thermoelectric performance, Mater. Today Phys., 2021, 16, 100308, DOI:10.1016/j.mtphys.2020.100308.
- J. K. Lee, M. W. Oh, B. S. Kim, B. K. Min, H. W. Lee and S. D. Park, Influence of Mn on crystal structure and thermoelectric properties of GeTe compounds, Electron. Mater. Lett., 2014, 10(4), 813–817, DOI:10.1007/s13391-014-4149-8.
- Z. Liu, J. Sun, J. Mao, H. Zhu, W. Ren, J. Zhou, Z. Wang, D. J. Singh, J. Sui, C.-W. Chu and Z. Ren, Phase-transition temperature suppression to achieve cubic GeTe and high thermoelectric performance by Bi and Mn codoping, Proc. Natl. Acad. Sci. U. S. A., 2018, 115(21), 5332–5337, DOI:10.1073/pnas.1802020115.
- C. Liu, Z. Zhang, Y. Peng, F. Li, L. Miao, E. Nishibori, R. Chetty, X. Bai, R. Si, J. Gao, X. Wang, Y. Zhu, N. Wang, H. Wei and T. Mori, Charge transfer engineering to achieve extraordinary power generation in GeTe-based thermoelectric materials, Sci. Adv., 2023, 9(17), eadh0713, DOI:10.1126/sciadv.adh0713.
- M. Hong, Y. Wang, T. Feng, Q. Sun, S. Xu, S. Matsumura, S. T. Pantelides, J. Zou and Z. G. Chen, Strong phonon–phonon interactions securing extraordinary thermoelectric Ge1−xSbxTe with Zn-alloying-induced band alignment, J. Am. Chem. Soc., 2019, 141(4), 1742–1748, DOI:10.1021/jacs.8b12624.
- E. Nshimyimana, S. Hao, X. Su, C. Zhang, W. Liu, Y. Yan, C. Uher, C. Wolverton, M. G. Kanatzidis and X. Tang, Discordant nature of Cd in GeTe enhances phonon scattering and improves band convergence for high thermoelectric performance, J. Mater. Chem. A, 2020, 8(3), 1193–1204, 10.1039/c9ta10436d.
- Q. Sun, M. Li, X.-L. Shi, S.-D. Xu, W.-D. Liu, M. Hong, W. Lyu, Y. Yin, M. Dargusch, J. Zou and Z.-G. Chen, Versatile vanadium doping induces high thermoelectric performance in GeTe via band alignment and structural modulation, Adv. Energy Mater., 2021, 11(20), 2100544, DOI:10.1002/aenm.202100544.
- X. Zhang, J. Li, X. Wang, Z. Chen, J. Mao, Y. Chen and Y. Pei, Vacancy manipulation for thermoelectric enhancements in GeTe alloys, J. Am. Chem. Soc., 2018, 140(46), 15883–15888, DOI:10.1021/jacs.8b09375.
- J. Li, W. Li, Z. Bu, X. Wang, B. Gao, F. Xiong, Y. Chen and Y. Pei, Thermoelectric transport properties of CdxBiyGe1−x−yTe Alloys, ACS Appl. Mater. Interfaces, 2018, 10(46), 39904–39911, DOI:10.1021/acsami.8b15080.
- M. Hong, W. Lyv, M. Li, S. Xu, Q. Sun, J. Zou and Z.-G. Chen, Rashba effect maximizes thermoelectric performance of GeTe derivatives, Joule, 2020, 4(9), 2030–2043, DOI:10.1016/j.joule.2020.07.021.
- X. Wang, W. Xue, Z. Zhang, X. Li, L. Yin, C. Chen, B. Yu, J. Sui, F. Cao, X. Liu, J. Mao, Y. Wang, X. Lin and Q. Zhang, Stabilizing the optimal carrier concentration in Al/Sb-codoped GeTe for high thermoelectric performance, ACS Appl. Mater. Interfaces, 2021, 13(38), 45717–45725, DOI:10.1021/acsami.1c12282.
- L. Xie, Y. Chen, R. Liu, E. Song, T. Xing, T. Deng, Q. Song, J. Liu, R. Zheng, X. Gao, S. Bai and L. Chen, Stacking faults modulation for scattering optimization in GeTe-based thermoelectric materials, Nano Energy, 2020, 68, 104347, DOI:10.1016/j.nanoen.2019.104347.
- M. Li, M. Hong, X. Tang, Q. Sun, W. Y. Lyu, S. D. Xu, L. Z. Kou, M. Dargusch, J. Zou and Z. G. Chen, Crystal symmetry induced structure and bonding manipulation boosting thermoelectric performance of GeTe, Nano Energy, 2020, 73, 104740, DOI:10.1016/j.nanoen.2020.104740.
- J. Li, X. Zhang, S. Lin, Z. Chen and Y. Pei, Realizing the high thermoelectric performance of GeTe by Sb-doping and Se-alloying, Chem. Mater., 2017, 29(2), 605–611, DOI:10.1021/acs.chemmater.6b04066.
- A. Das, K. Pal, P. Acharyya, S. Das, K. Maji and K. Biswas, Strong antibonding I(p)–Cu(d) states lead to intrinsically low thermal conductivity in CuBiI(4), J. Am. Chem. Soc., 2023, 145(2), 1349–1358, DOI:10.1021/jacs.2c11908.
- K. Yuan, X. Zhang, Z. Chang, D. Tang and M. Hu, Antibonding induced anharmonicity leading to ultralow lattice thermal conductivity and extraordinary thermoelectric performance in CsK2X (X = Sb, Bi), J. Mater. Chem. C, 2022, 10(42), 15822–15832, 10.1039/D2TC03356A.
- J. Zhang, H. Jiang, X. Xia, Y. Gao and Z. Huang, Antibonding p–d and s–p hybridization induce the optimization of thermal and thermoelectric performance of MGeTe3 (M = In and Sb), ACS Appl. Energy Mater., 2022, 5(12), 15566–15577, DOI:10.1021/acsaem.2c03138.
- A. Shafique and Y.-H. Shin, Thermoelectric and phonon transport properties of two-dimensional IV–VI compounds, Sci. Rep., 2017, 7(1), 506, DOI:10.1038/s41598-017-00598-7.
- W. Namhongsa, M. Rittiruam, K. Singsoog, P. Pilasuta, S. Paengson, S. Ruamruk and T. Seetawan, Thermoelectric properties of GeTe and Sb2Te3 calculated by density functional theory, Mater. Today Proc., 2018, 5(6, Part 1), 14131–14134, DOI:10.1016/j.matpr.2018.02.077.
- H. L. Kagdada, P. K. Jha, P. Śpiewak and K. J. Kurzydłowski, Structural stability, dynamical stability, thermoelectric properties, and elastic properties of GeTe at high pressure, Phys. Rev. B, 2018, 97(13), 134105, DOI:10.1103/PhysRevB.97.134105.
- U. S. Shenoy, G. K. D and D. K. Bhat, Probing of Bi doped GeTe thermoelectrics leads to revelation of resonant states, J. Alloys Compd., 2022, 921, 165965, DOI:10.1016/j.jallcom.2022.165965.
- D. Guo, C. Li, K. Qiu, Q. Yang, K. Li, B. Shao, D. Chen, Y. Ma, J. Sun, X. Cao, W. Zeng, Z. Wang and R. Xie, The N- and p-type thermoelectricity property of GeTe by first-principles study, J. Alloys Compd., 2019, 810, 151838, DOI:10.1016/j.jallcom.2019.151838.
- B. Zhou, W. Li, X. Wang, J. Li, L. Zheng, B. Gao, X. Zhang and Y. Pei, Promising cubic MnGeTe2 thermoelectrics, Sci. China Mater., 2019, 62(3), 379–388, DOI:10.1007/s40843-018-9328-5.
- C. Wood, Materials for thermoelectric energy conversion, Rep. Prog. Phys., 1988, 51(4), 459, DOI:10.1088/0034-4885/51/4/001.
- D. Wu, L. D. Zhao, S. Hao, Q. Jiang, F. Zheng, J. W. Doak, H. Wu, H. Chi, Y. Gelbstein, C. Uher, C. Wolverton, M. Kanatzidis and J. He, Origin of the high performance in GeTe-based thermoelectric materials upon Bi2Te3 doping, J. Am. Chem. Soc., 2014, 136(32), 11412–11419, DOI:10.1021/ja504896a.
- S. S. Das, M. G. Rosul and M. Zebarjadi, Optimization of the thermoelectric properties of SnSe2 using first-principles calculations, J. Phys. Chem. C, 2023, 127(14), 6916–6924, DOI:10.1021/acs.jpcc.2c09137.
- M. G. Rosul and M. Zebarjadi, Effect of electron–phonon interaction and ionized impurity scattering on the room-temperature thermoelectric properties of bulk MoSe2, J. Phys. Chem. C, 2022, 126(35), 15011–15018, DOI:10.1021/acs.jpcc.2c03782.
- T. Zhu, S. S. Das, S. Nayeb Sadeghi, F. F. Tonni, S. Krylyuk, C. Constantin, K. Esfarjani, A. V. Davydov and M. Zebarjadi, Electrostatic modulation of thermoelectric transport properties of 2H-MoTe2, Energy Adv., 2023, 2(11), 1882–1892, 10.1039/D3YA00316G.
- T. Chattopadhyay, J. X. Boucherle and H. G. von Schnering, Neutron diffraction study on the structural phase transition in gete, J. Phys. C Solid State Phys., 1987, 20(10), 1431–1440, DOI:10.1088/0022-3719/20/10/012.
- J. Li, X. Zhang, Z. Chen, S. Lin, W. Li, J. Shen, I. T. Witting, A. Faghaninia, Y. Chen, A. Jain, L. Chen, G. J. Snyder and Y. Pei, Low-symmetry rhombohedral GeTe thermoelectrics, Joule, 2018, 2(5), 976–987, DOI:10.1016/j.joule.2018.02.016.
- M.-H. Whangbo and R. Hoffmann, The band structure of the tetracyanoplatinate chain, J. Am. Chem. Soc., 1978, 100(19), 6093–6098, DOI:10.1021/ja00487a020.
- P. M. Konze, R. Dronskowski and V. L. Deringer, Exploring chemical bonding in phase-change materials with orbital-based, Phys. Status Solidi RRL, 2019, 13(4), 1800579, DOI:10.1002/pssr.201800579.
- S. Steinberg and R. Dronskowski, The crystal orbital hamilton population (COHP) method as a tool to visualize and analyze chemical bonding in intermetallic compounds, Crystals, 2018, 8(5), 225, DOI:10.3390/cryst8050225.
- G. A. Landrum and R. Dronskowski, The orbital origins of magnetism: from atoms to molecules toferromagnetic alloys, Angew. Chem., Int. Ed., 2000, 39(9), 1560–1585, DOI:10.1002/(SICI)1521-3773(20000502)39:9<1560::AID-ANIE1560>3.0.CO;2-T.
- R. Dronskowski, From Plane Waves via Atomic Orbitals, De Gruyter, Berlin, Boston, 2023, DOI:10.1515/9783111167213.
- S. Maintz, V. L. Deringer, A. L. Tchougréeff and R. Dronskowski, LOBSTER: a tool to extract chemical bonding from plane-wave based DFT, J. Comput. Chem., 2016, 37(11), 1030–1035, DOI:10.1002/jcc.24300.
- S. Maintz, V. L. Deringer, A. L. Tchougreeff and R. Dronskowski, Analytic projection from plane-wave and PAW wavefunctions and application to chemical-bonding analysis in solids, J. Comput. Chem., 2013, 34(29), 2557–2567, DOI:10.1002/jcc.23424.
- R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, LOBSTER: local orbital projections, atomic charges, and chemical-bonding fromprojector-augmented-wave-baseddensity-functional theory, J. Comput. Chem., 2020, 41(21), 1931–1940, DOI:10.1002/jcc.26353.
- M. Khazaei, A. Ranjbar, K. Esfarjani, D. Bogdanovski, R. Dronskowski and S. Yunoki, Insights into exfoliation possibility of MAX phases to MXenes, Phys. Chem. Chem. Phys., 2018, 20(13), 8579–8592, 10.1039/C7CP08645H.
- P. C. Müller, C. Ertural, J. Hempelmann and R. Dronskowski, Crystal orbital bond index: covalent bond orders in solids, J. Phys. Chem. C, 2021, 7959–7970, DOI:10.1021/acs.jpcc.1c00718.
- Y. Jin, D. Ren, Y. Qiu and L.-D. Zhao, Electrical and thermal transport properties of Ge1–xPbxCuySbyTeSe2y, Adv. Funct. Mater., 2023, 33(45), 2304512, DOI:10.1002/adfm.202304512.
- Z. Chen, B. Ge, W. Li, S. Lin, J. Shen, Y. Chang, R. Hanus, G. J. Snyder and Y. Pei, Vacancy-induced dislocations within grains for high-performance PbSe thermoelectrics, Nat. Commun., 2017, 8(1), 13828, DOI:10.1038/ncomms13828.
- Z. Guo, Q. Zhang, H. Wang, X. Tan, F. Shi, C. Xiong, N. Man, H. Hu, G. Liu and J. Jiang, Bi–Zn codoping in GeTe synergistically enhances band convergence and phonon scattering for high thermoelectric performance, J. Mater. Chem. A, 2020, 8(41), 21642–21648, 10.1039/D0TA08700A.
- J. Li, Q. Hu, S. He, X. Tan, Q. Deng, Y. Zhong, F. Zhang and R. Ang, Enhancing near-room-temperature GeTe thermoelectrics through In/Pb Co-doping, ACS Appl. Mater. Interfaces, 2021, 13(31), 37273–37279 CrossRef CAS PubMed.
- T. M. Alakbarova, E. N. O. Hans-Jürgen Meyer, I. R. Amiraslanov and M. B. Babanly, Phase equilibria of the GeTe−Bi2Te3 quasi-binary system in the range 0–50 Mol\% Bi2Te3, Phase Transitions, 2021, 94(5), 366–375, DOI:10.1080/01411594.2021.1937625.
- Y. Jiang, T.-R. Wei and X. Shi, Beyond phase-change materials: pseudo-binary (GeTe)n(Sb2Te3)m alloys as promising thermoelectric materials, Mater. Today Phys., 2023, 36, 101167, DOI:10.1016/j.mtphys.2023.101167.
- H. Huo, Y. Wang, L. Xi, J. Yang and W. Zhang, The variation of intrinsic defects in XTe (X = Ge, Sn, and Pb) induced by the energy positions of valence band maxima, J. Mater. Chem. C, 2021, 9(17), 5765–5770, 10.1039/D1TC00513H.
- J. Li, Z. Chen, X. Zhang, H. Yu, Z. Wu, H. Xie, Y. Chen and Y. Pei, Simultaneous optimization of carrier concentration and alloy scattering for ultrahigh performance GeTe thermoelectrics, Adv. Sci., 2017, 4(12), 1700341, DOI:10.1002/advs.201700341.
- Q. Chen, C. Yang, T. Xing, J. Xi, W. Zhang, J. Yang and L. Xi, Defect engineering and alloying strategies for tailoring thermoelectric behavior in GeTe and its alloys, J. Mater., 2024 DOI:10.1016/j.jmat.2024.01.007.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys. Condens. Matter, 2009, 21(39), 395502, DOI:10.1088/0953-8984/21/39/395502.
- D. Vanderbilt, Soft self-consistent pseudopotentials in a generalized eigenvalue formalism, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892–7895, DOI:10.1103/PhysRevB.41.7892.
- H. Jiang and W. Yang, Conjugate-gradient optimization method for orbital-free density functional calculations, J. Chem. Phys., 2004, 121(5), 2030–2036, DOI:10.1063/1.1768163.
- R. H. Byrd, J. Nocedal and Y.-X. Yuan, Global convergence of a class of quasi-newton methods on convex problems, SIAM J. Numer. Anal., 1987, 24(5), 1171–1190 CrossRef.
- J. George, G. Petretto, A. Naik, M. Esters, A. J. Jackson, R. Nelson, R. Dronskowski, G.-M. Rignanese and G. Hautier, Automated bonding analysis with crystal orbital hamilton populations, ChemPlusChem, 2022, 87(11), e202200123, DOI:10.1002/cplu.202200123.
- O. Hellman, P. Steneteg, I. A. Abrikosov and S. I. Simak, Temperature dependent effective potential method for accurate free energy calculations of solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87(10), 104111, DOI:10.1103/PhysRevB.87.104111.
- O. Hellman and I. A. Abrikosov, Temperature-dependent effective third-order interatomic force constants from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88(14), 144301, DOI:10.1103/PhysRevB.88.144301.
- O. Hellman, I. A. Abrikosov and S. I. Simak, Lattice dynamics of anharmonic solids from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84(18), 180301, DOI:10.1103/PhysRevB.84.180301.
- J. J. Zhou, J. Park, I. T. Lu, I. Maliyov, X. Tong and M. Bernardi, PERTURBO: a software package for ab initio electron–phonon interactions, charge transport and ultrafast dynamics, Comput. Phys. Commun., 2021, 264, 107970, DOI:10.1016/j.cpc.2021.107970.
- J.-J. Zhou and M. Bernardi, Ab initio electron mobility and polar phonon scattering in GaAs, Phys. Rev. B, 2016, 94(20), 201201, DOI:10.1103/PhysRevB.94.201201.
- F. Giustino, M. L. Cohen and S. G. Louie, Electron–phonon interaction using wannier functions, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76(16), 165108, DOI:10.1103/PhysRevB.76.165108.
- N. Marzari, A. A. Mostofi, J. R. Yates, I. Souza and D. Vanderbilt, Maximally localized wannier functions: theory and applications, Rev. Mod. Phys., 2012, 84(4), 1419–1475, DOI:10.1103/RevModPhys.84.1419.
- J. I. Mustafa, S. Coh, M. L. Cohen and S. G. Louie, Automated construction of maximally localized wannier functions: optimized projection functions method, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(16), 165134, DOI:10.1103/PhysRevB.92.165134.
- M. Lundstrom, Fundamentals of carrier transport, 2nd edn, Meas. Sci. Technol., 2002,(2), 230, DOI:10.1088/0957-0233/13/2/703.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50, DOI:10.1016/0927-0256(96)00008-0.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186, DOI:10.1103/PhysRevB.54.11169.
- K. Hirata, H. Yamada, M. Uehara, S. A. Anggraini and M. Akiyama, First-principles study of piezoelectric properties and bonding analysis in (Mg, X, Al)N solid solutions (X = Nb, Ti, Zr, Hf), ACS Omega, 2019, 4(12), 15081–15086, DOI:10.1021/acsomega.9b01912.
- J. Yuan, Y. Chen and B. Liao, Lattice dynamics and thermal transport in semiconductors with anti-bonding valence bands, J. Am. Chem. Soc., 2023, 145(33), 18506–18515, DOI:10.1021/jacs.3c05091.
- G. Liebfried and E. Schlömann, Nachr. Akad. Wiss. Göttingen Math. Phys. Kl., 1954, 4, 71 Search PubMed.
- G. A. Slack, Nonmetallic Crystals With High Thermal-Conductivity, J. Phys. Chem. Solids, 1973, 34(2), 321–335, DOI:10.1016/0022-3697(73)90092-9.
- P. G. Klemens, Thermal Conductivity, Acdemic Press, 1969 Search PubMed.
- E. S. Toberer, A. Zevalkink and G. J. Snyder, Phonon engineering through crystal chemistry, J. Mater. Chem., 2011, 21(40), 15843–15852, 10.1039/c1jm11754h.
- M. L. Du, V. Baru, F. K. Guo, C. Hanhart, U. G. Meißner, J. A. Oller and Q. Wang, Revisiting the nature of the Pc pentaquarks, J. High Energy Phys., 2021, 8, 1–50 Search PubMed.
- M. Cagnoni, D. Führen and M. Wuttig, Thermoelectric performance of IV–VI compounds with octahedral-like coordination: a chemical-bonding perspective, Adv. Mater., 2018, 30(33), 1801787, DOI:10.1002/adma.201801787.
- U. V. Waghmare, N. A. Spaldin, H. C. Kandpal and R. Seshadri, First-principles indicators of metallicity and cation off-centricity in the IV–VI rocksalt chalcogenides of divalent Ge, Sn, and Pb, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67(12), 10, DOI:10.1103/PhysRevB.67.125111.
- G. Tan, L.-D. Zhao, F. Shi, J. W. Doak, S.-H. Lo, H. Sun, C. Wolverton, V. P. Dravid, C. Uher and M. G. Kanatzidis, High thermoelectric performance of P-Type SnTe via a synergistic band engineering and nanostructuring approach, J. Am. Chem. Soc., 2014, 136(19), 7006–7017, DOI:10.1021/ja500860m.
- Y. Pei, A. LaLonde, S. Iwanaga and G. J. Snyder, High thermoelectric figure of merit in heavy hole dominated PbTe, Energy Environ. Sci., 2011, 4(6), 2085–2089, 10.1039/C0EE00456A.
- Y. Jin, D. Wang, Y. Zhu, L. Su, T. Hong, Z. Wang, Z.-H. Ge, Y. Qiu and L.-D. Zhao, Contrasting roles of trivalent dopants M (M = In, Sb, Bi) in enhancing the thermoelectric performance of Ge0.94M0.06Te, Acta Mater., 2023, 252, 118926, DOI:10.1016/j.actamat.2023.118926.
- M. A. Korzhuev, On the fundamental energy gap in GeTe, Phys. Status Solidi, 1982, 112(1), 39–41, DOI:10.1002/pssb.2221120149.
- R. Tsu, W. E. Howard and L. Esaki, Optical properties of GeTe, Solid State Commun., 1967, 5(3), 167–171, DOI:10.1016/0038-1098(67)90511-X.
- S. K. Bahl and K. L. Chopra, Amorphous versus crystalline GeTe films. III. Electrical properties and band structure, J. Appl. Phys., 2003, 41(5), 2196–2212, DOI:10.1063/1.1659189.
- J. E. Lewis, Optical properties and energy gap of GeTe from reflectance studies, Phys. Status Solidi, 1973, 59(1), 367–377, DOI:10.1002/pssb.2220590138.
- J. Li, Z. Chen, X. Zhang, Y. Sun, J. Yang and Y. Pei, Electronic origin of the high thermoelectric performance of GeTe among the P-type group IV monotellurides, NPG Asia Mater., 2017, 9(3), e353, DOI:10.1038/am.2017.8.
- D. J. Singh, Optical properties of cubic and rhombohedral GeTe, J. Appl. Phys., 2013, 113(20), 203101, DOI:10.1063/1.4807638.
- R. Tsu, W. E. Howard and L. Esaki, Optical and electrical properties and band structure of GeTe and SnTe, Phys. Rev., 1968, 172(3), 779–788, DOI:10.1103/PhysRev.172.779.
- K. Hoang, S. D. Mahanti and M. G. Kanatzidis, Impurity clustering and impurity-induced bands in PbTe-, SnTe-, and GeTe-based bulk thermoelectrics, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81(11), 1–15, DOI:10.1103/PhysRevB.81.115106.
- P. Li, T. Ding, J. Li, C. Zhang, Y. Dou, Y. Li, L. Hu, F. Liu and C. Zhang, Positive effect of Ge vacancies on facilitating band convergence and suppressing bipolar transport in GeTe-based alloys for high thermoelectric performance, Adv. Funct. Mater., 2020, 30(15), 1910059, DOI:10.1002/adfm.201910059.
- M. Ghim, Y.-J. Choi and S.-H. Jhi, Lattice thermal conductivity of cubic GeTe with vacancy defects, Phys. Rev. B, 2023, 107(18), 184301, DOI:10.1103/PhysRevB.107.184301.
- S. A. J. Kimber, J. Zhang, C. H. Liang, G. G. Guzmán-Verri, P. B. Littlewood, Y. Cheng, D. L. Abernathy, J. M. Hudspeth, Z.-Z. Luo, M. G. Kanatzidis, T. Chatterji, A. J. Ramirez-Cuesta and S. J. L. Billinge, Dynamic crystallography reveals spontaneous anisotropy in cubic GeTe, Nat. Mater., 2023, 22(3), 311–315, DOI:10.1038/s41563-023-01483-7.
- U. S. Shenoy, G. K. D and D. K. Bhat, Probing of Bi doped GeTe thermoelectrics leads to revelation of resonant states, J. Alloys Compd., 2022, 921, 165965, DOI:10.1016/j.jallcom.2022.165965.
- J. Li, X. Zhang, S. Lin, Z. Chen and Y. Pei, Realizing the high thermoelectric performance of GeTe by Sb-doping and Se-alloying, Chem. Mater., 2017, 29(2), 605–611, DOI:10.1021/acs.chemmater.6b04066.
- Y. Feng, J. Li, Y. Li, T. Ding, C. Zhang, L. Hu, F. Liu, W. Ao and C. Zhang, Band convergence and carrier-density fine-tuning as the electronic origin of high-average thermoelectric performance in Pb-doped GeTe-based alloys, J. Mater. Chem. A, 2020, 8(22), 11370–11380, 10.1039/D0TA02758H.
- H. Jeong, S. K. Kihoi, H. Kim and H. S. Lee, High seebeck coefficient and low thermal conductivity in bi and in Co-doped GeTe thermoelectric material, J. Mater. Res. Technol., 2021, 15, 6312–6318, DOI:10.1016/j.jmrt.2021.11.065.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta01088d |
| This journal is © The Royal Society of Chemistry 2024 |