Inverse design for materials discovery from the multidimensional electronic density of states

Abstract

To accelerate materials discovery, an inverse design scheme to find materials with desired properties has been recently introduced. Despite successful efforts, previous inverse design methods have focused on problems in which the desired properties are described by a single number (one-dimensional vector), such as the formation energy and bandgap. The limitation becomes apparent when dealing with material properties that require representation with multidimensional vectors, such as the electronic density of states (DOS) pattern. Here, we develop a deep learning method for inverse design from multidimensional DOS properties. In particular, we introduce a composition vector (CV) to describe the composition of predicted materials, which serves as an invertible representation for the DOS pattern. Our inverse design model exhibits exceptional prediction performance, with a composition accuracy of 99% and a DOS pattern accuracy of 85%, greatly surpassing the capabilities of existing CVs. Furthermore, we have successfully applied the inverse design model to find promising candidates for catalysis and hydrogen storage. Notably, our model suggests a hydrogen storage material, Mo₃Co, that has not yet been reported. This readily reveals that our model can greatly expand the space of inverse design for materials discovery.

---

Introduction

Historically, materials discovery has been carried out mostly by the Edisonian approach based on trial-and-error,^1,2 such as high-throughput screening, in which numerous materials are tested until the desired target properties are found. The Edisonian approach is, however, regarded as an inefficient strategy because the chemical spaces to explore are typically vast, which thus leads to a very large amount of time and high costs for the discovery. Although the efficiency of materials discovery can be improved by theoretically or experimentally combining this approach with an automation technique, which is called high-throughput screening, many tests are still necessary to search for a material with the target property. For example, high-throughput density functional theory (DFT) calculations have recently been widely used for materials design and have shown various success for materials discovery;^3–6 however, these methods only allow us to predict the properties of materials from their chemical information (e.g., atomic structure and composition).

As a strategy for further accelerating materials discovery, an inverse design scheme has been introduced, in which a user defines the target properties of materials and an algorithm then suggests materials that meet the target properties. State-of-the-art computer simulation techniques (e.g., DFT calculations) only allow a forward prediction from material information to the properties. However, deep learning (DL) algorithms make inverse design of materials possible not only for organic materials⁷ but also for inorganic materials,⁸ in which DL methods such as generative adversarial networks (GANs)⁹ or variational autoencoders (VAEs)¹⁰ have usually been used.^7,8,11–19 For example, Noh et al.¹⁴ found new metastable vanadium oxide (V–O) compounds using the VAE algorithm. Ren et al.⁸ also used a VAE to generate materials with the desired formation energies, bandgaps, or thermoelectric power factors. Xie et al.¹⁸ developed a chemical diffusion variational autoencoder (CDVAE) model and Wines et al.¹⁹ utilized the CDVAE to design superconductors with a high critical temperature. In contrast, Kim et al.¹¹ generated various porous zeolites with the desired heat of adsorption of methane via a GAN. Despite these efforts, these inverse design methods are limitedly applicable to problems for which the target properties are described by a single scalar value, such as a formation energy of 1.0 eV per atom or a bandgap energy of 3.2 eV. In some cases, the material properties and performance can be well represented by a single number, but in many other cases, the properties need to be represented by multidimensional vectors (a series of numbers). Recently, various inverse design models dealing with multidimensional properties have been developed. Li et al.²⁰ developed forward and inverse design models capable of handling multiple structural and property features of nanoparticles. Expanding on their efforts, the same research group applied their methodologies to predict multiple target electrochemical properties of MXene-type materials.²¹ And Dong et al.¹⁵ specifically addressed the light absorption spectrum, developing an inverse design framework for predicting a material's formula. These advancements demonstrate the importance and potential for the development of an inverse design model to target multidimensional properties.

A representative example of such multidimensional properties, which is the focus of this study, is the electronic density of states (DOS) pattern. The electronic DOS pattern can often be represented by the number of electronic states at each energy level (typically represented by approximately a few hundred values). The DOS properties determine not only the electrical properties of materials but also their chemical properties. It is well known that catalytic properties are also significantly affected by the DOS pattern.^22,23 Although the d-band center value (single number) has been widely used as a simplified but effective descriptor in catalyst design,^22–24 this value is not sufficient to fully represent and understand the whole electronic structure of catalyst materials. Recent DL studies^25,26 show that the d-band center is not sufficient to fully describe adsorption energies. In this regard, the DOS pattern itself or its derivative, although much more complex than the d-band center, has served as an improved and complementary descriptor in catalyst design.^27–31 Fung et al.²⁹ developed an ML model designed to accurately predict adsorption energies from DOS patterns. Similarly, Hong et al.³⁰ predicted adsorption energies from DOS patterns and interpreted the correlation between DOSs and chemisorption properties. Knøsgaard et al.³¹ successfully estimated quasiparticle band structures from DOS fingerprints using standard DFT calculations. Despite the ML model's success in utilizing DOS patterns as input, there have been no efforts thus far to directly predict material information (compositions of inorganic material) from DOS patterns, which is the key inverse design strategy in this work. Therefore, it is necessary and timely to develop a machine-learning-based inverse design strategy applicable to multidimensional properties such as DOS patterns, which should suggest material information (e.g., atomic structure or composition) from an input of desired DOS patterns.

For the development of such an inverse design technique, it is critical to develop a machine-readable representation to reflect the electronic DOS pattern information that is invertible, allowing conversion back to material information. Among the types of material information, the atomic structure and the chemical composition both affect the properties of materials. Consequently, various inverse design studies have employed representations which include both structure and chemical details.^8,19 Nevertheless, the vastness of possible variations in chemical composition and atomic structure makes it challenging to navigate the landscape. Hence, there is still a need to limit the information used in inverse design strategies. For instance, Fung et al.³² examined the atomic structure of MoS₂ composition, while Lyngby et al.³³ explored the composition in the 2D-type structure. Likewise, a restriction would be needed in the atomic structure or chemical composition for manageability. Interestingly, our previous DL studies showed that in predicting material's properties, feature vectors derived from chemical compositions hold more weight than those from X-ray diffraction patterns representing atomic structures.³⁴ The result provides a meaningful guideline for inverse design, i.e., it would be more efficient to specify the chemical compositions of materials for a given atomic structure. This guideline calls for the development of a representation for the chemical composition that is invertible to the electronic DOS pattern information. In fact, there have been several efforts to develop a representation for mapping the chemical compositions of materials, in which one-hot encoding methods have been used.^35–37 For example, Zhou et al.³⁵ generated one-hot encoded datasets consisting of elements in the material formulae and their chemical environments and embeddings of elements through singular value decomposition and a probability model. Tshitoyan et al.³⁶ extracted elemental information through natural language processing of published papers to generate a one-hot encoded dataset and embeddings of elements through word2vec.^38,39 However, these previously reported representations do not include electronic DOS information and have not been tested for inverse design.

In this work, we develop and report a convolutional neural network (CNN)-based DL model that is effective for inverse design of inorganic materials from multidimensional DOS patterns. This model can suggest the chemical composition for a given atomic structure and consequently several candidate materials with ranks. The composition vector (CV) created from the DOS patterns of each element is used as a representation vector for the inverse design, which greatly enhances the performance of the inverse design model, as evidenced by the composition prediction accuracy of 99% and the DOS pattern accuracy of 85%. To demonstrate the effectiveness of our model, we apply the model to two exemplary applications, namely, oxygen reduction reaction catalysis and hydrogen storage, where the inputs are DOS patterns for Pt₃Ni and Pd, respectively, since these materials are regarded as prototypical materials in each field. The model successfully proposes novel binary alloys that have DOS patterns similar to those of the input materials in both applications. The workflow presented herein is not limited to DOS patterns but can be readily expanded to many other properties described by multidimensional vectors, such as spectrum data in materials science.

Results and discussion

Workflow of our inverse design model

Fig. 1 shows a schematic diagram of our inverse design model, where the multidimensional DOS pattern is used as an input and the output is a vector called the composition vector (CV) which represents the compositions of materials. To make it invertible, the CVs were defined as a concatenation of element vectors (EVs), which represent element information. The CV for the binary material A_mB_n, CV_AmBn, is defined as follows:

CV_AmBn = mEV_A ⊕ nEV_B (1)

where ⊕ denotes a concatenation operation and EV_A and EV_B denote the EVs of elements A and B, respectively. If an EV for each element is unique and element A is selected to have a lower atomic number than element B, the CV_AmBn is also unique according to its composition A_mB_n. Therefore, CVs are one-to-one correspondences to all available compositions and are invertible to composition. From the predicted CVs with an input of the DOS pattern, the model finally enables suggesting several candidate materials with ranks. The detailed process is described in the following sections.

Fig. 1 Schematic diagrams of DL models. Inverse design model to predict compositions from the target DOS. The input is the target DOS pattern, and the output is the CV that is invertible to the material composition.

Generation of DOS-based EVs with chemical information

Since a CV is composed of predefined EVs as described above, how EVs are produced is one of the key components of our model. In Fig. 2a, we explained how the EV representation is generated. To construct compatible composition vectors with our model using DOSs as inputs, we developed EVs based on DOS patterns which include chemical and electronic structural information about elements. We collected 32 659 total DOS patterns for unary, binary, and ternary materials from the Materials Project library^40,41 and created a DOS database, as shown in Fig. S1.† Each DOS pattern is converted into a DOS vector with an energy range of −7.5 to 7.5 eV and 151 energy levels for standardization, i.e., the DOS pattern is represented by a 151-dimensional vector. Since an element could be in a variety of environments (interacting with various elements or placed in various types of structures), we used centroid DOSs to construct EVs. The centroid DOS of element A is defined as the average DOS of all materials containing element A in the collected database. The centroid DOS can readily represent not only the physical and chemical information of element A but also various environments where an element A could be placed. To enable machines to learn their own knowledge for a particular element, we passed the centroid DOSs of elements (H to Bi in this work) to the autoencoder and then used latent space vectors as EVs (Fig. 2a). As a result, the centroid DOS vector of each element is compressively encoded into a 30-dimensional latent vector that can be finally used as an EV.

Fig. 2 Generation of EVs and its analysis. (a) Autoencoder model for generating EVs. In the autoencoder model, the centroid DOSs are passed to the input and output layers, and the latent space vector for each element is acquired as an EV. (b) Projection of the EV map obtained with the t-SNE algorithm. Each dot denotes an EV of an element. Seven groups of elements (alkali metals, alkaline earth metals, lanthanides, 3d transition metals, noble metals, post-transition metals, and halogens) are highlighted. Elements in the same group are grouped into circles.

To validate whether the DOS-based EVs contain chemical information about elements and materials, t-distributed stochastic neighbor embedding (t-SNE)⁴² analysis is applied to the EVs (Fig. 2b). This algorithm is known to show good performance in visualizing high-dimensional vectors compared to other algorithms, such as principal component analysis (PCA).⁴³ Interestingly, the t-SNE analysis reveals that elements in the same group of the periodic table are distributed at similar positions, indicating that each group is distinguished by the position. Additionally, the distances between groups reflect the chemical relations of the periodic table. For example, because the alkali metal group and alkaline metal group differ by only one valence electron, they are located close to each other in the t-SNE plot. Here, we highlight that the EV readily reflects the chemical information of elements, although we have not trained on the element information such as the atomic number or period number and only used the centroid DOS in constructing the EVs with the autoencoder. We also tested the performance of the DOS-based CV by training an artificial neural network (ANN) model, in which the CV for a given material was used as an input and classifying the bandgap energy of the input material into three categories: small gap (E_g < 0.2 eV), medium gap (0.2 eV < E_g ≤ 3.6 eV), and large gap (E_g > 3.6 eV). The results showed a high accuracy of 92% with DOS-based CVs (Table S1†). If we use the element embedding with normalized composition matrix (EENCM) method to create CVs, which is trained on the chemical formula of materials,³⁴ then the accuracy approaches 93%, which is similar to that obtained with our DOS-based CVs, although our case is trained with a much lower amount of data (32 659 DOS patterns) compared to the EENCM case (118 176 chemical formulas). These results show that our DOS-based CVs well represent the chemical composition information of materials.

Model structure to predict the material composition from target DOS patterns

Using our DOS-based CVs, we are now ready to develop an inverse design model that predicts the compositions of materials from multidimensional DOS patterns. The model is schematized in Fig. 3a, where one can observe the CNN model with DOS vectors as an input and CVs as an output. For the training, the DOS pattern data were collected from the Materials Project library,⁴⁰ where binary composition materials were considered. In the composition database, over 80% of binary materials exhibit a composition of A_mB_n, where m and n ≤ 3 (7763 out of 9622). It is noteworthy that the majority of prototypical materials usually maintain a stoichiometry below four. To concentrate on the bulk of the dataset in this work, the composition ratio of A_mB_n binary materials was restricted such that both m and n are equal to or less than 3, i.e., m and n ≤ 3 (Fig. S1†). Additionally, the DL model was trained with materials with cubic (2112 materials) or hexagonal (1239 materials) crystal structures, which indicates that the model is designed to predict the CVs of materials with the trained crystal structures. Several candidate materials can be suggested based on CV similarity by comparing the predicted CV and the CVs of all available compositions (Fig. 3b). Given that the EV is defined for each element, CVs for all viable compositions (A_mB_n where m, n < 3) can be formulated by merging EVs and then saved in the CV table. For the CVs predicted by the DL model, we calculate the Euclidean distance between the predicted CV and each CV in the CV table. Then, the top 5 materials with the shortest distance (with ranks) are suggested as candidate materials by the inverse design model from a given DOS pattern.

Fig. 3 Detailed structure of the DL inverse design model. (a) Representation of each layer in the model. The input is a DOS pattern vector with a size of 151, and the output is a CV with a size of 60. The DL model is composed of CNN and FCNN layers. (b) Schematics of the generation of candidates from the predicted CVs. For the predicted CVs, the Euclidean distances from every CV of possible compositions are calculated, and then, the top 5 closest candidates are suggested as the candidate compositions.

The performance of the inverse design model is shown in Fig. 4a. We tested the performance with 100 randomly selected DOS patterns in the DOS DB. Two metrics for the performance are considered: the composition accuracy and DOS pattern accuracy. The composition accuracy is defined as the proportion of test samples for which the composition of an input DOS is included in the five candidate materials predicted by the inverse design model. In contrast, the DOS pattern accuracy is measured based on the comparison of the DOS patterns of the input material and the five candidate materials. First, if the DOS pattern of the candidate material exists in the DOS DB, then the DOS similarity between the input material (A) and the candidate (B) is calculated using a cosine similarity as follows:

where DOS_A and DOS_B are the DOS pattern vectors of materials A and B, respectively. Then, the DOS pattern accuracy is defined as the proportion of test samples for which the average of the DOS similarity values is greater than a threshold, which is set to 0.7 in this work. If the DOS pattern of the candidate material doesn't exist in the DOS DB, it is not counted in calculating the average. By using the DOS-based CV proposed in this work, the composition accuracy is very high at 0.98, which indicates that this method can readily discriminate compositions of materials only from the DOS information with a high accuracy. Moreover, the DOS pattern accuracy is measured to be 0.85. In Fig. 4b and c, two examples are shown with the DOS pattern inputs of Al₃Zr and Sn₃Bi with a cubic Bravais lattice. Our inverse design model predicts that the composition of the topmost candidate is identical to the original composition, which supports the high composition accuracy of our model. The 2nd-rank candidate materials in the two examples are Al₃Hf and Sn₃Sb. Because their DOS patterns are included in the DOS DB, the DOS pattern similarity between the given DOS and the pattern of the candidates can be calculated, and they have very high values of 0.96 for Al₃Hf and 0.98 for Sn₃Sb, as shown in Fig. 4b and c. These results indicate that our inverse design model could find candidate materials that possess similar DOS patterns to the input DOS.

Fig. 4 Performance of our inverse design model. (a) Performance comparison with different CVs. The composition accuracy (solid bar) and DOS pattern accuracy (dashed bar) are shown. (b) and (c) DOS patterns of the input (red line) and predicted (cyan area) compositions. The inset atomic structure shows a unit cell of the material with the predicted composition.

We also compare the DOS-based CVs with other types of CVs (formula-based CVs³⁴ and one-hot encoding-based CVs) previously reported as an output of the inverse design in Fig. 4a. Although one-hot encoding can be used as a representation of an element or composition, it does not include chemical information. Thus, the accuracy of the inverse design model is lower than that when using the DOS-based CVs. If the inverse model is based on the formula-based CVs, then the composition accuracy is approximately 0.77, which is higher than that in the one-hot encoding case but is still much lower than that in our DOS-based CV case. Since our DOS-based CVs include the DOS information itself, the DOS pattern accuracy is also much higher than those obtained with formula-based or one-hot encoding-based CVs.

Application of our inverse design model into the fields of catalysts and hydrogen storage materials

After examining the performance of our inverse design model, we now apply it to materials design in two exemplary applications to confirm its effectiveness, namely, catalyst materials and hydrogen storage materials. For optimal performance, materials should possess ideal chemical bond strengths that are neither excessively strong nor excessively weak with reactants and intermediates for catalysts and with hydrogen for hydrogen storage. The DOS characterizes the electronic structure of a material,⁴⁴ establishing a significant correlation between the DOS and chemical bonds, which ultimately influence material performance. Consequently, our inverse design model is applied to find promising candidates for catalysis and hydrogen storage with the DOS patterns of prototypical materials.

First, for catalysis applications, Pt₃Ni has been regarded as one of the prototypical and best-performing catalyst materials for the oxygen reduction reaction (ORR) in a proton exchange membrane fuel cell (PEMFC).^45,46 By using the inverse design model, we intend to design ORR catalysts with catalytic performance as high as that of Pt₃Ni, and therefore, the DOS pattern of Pt₃Ni was used as an input in our inverse design model. The model predicts the following five candidates: Pt₃Ni (1st rank), Pt₃Co (2nd rank), Pt₃Rh (3rd rank), Pt₃Fe (4th rank), and Pt₃Mn (5th rank) (Fig. 5a). The fact that the 1st-rank candidate is Pt₃Ni (identical to the input material) once again supports that the inverse design model has a high composition accuracy. In addition, it is noteworthy that the Pt₃Co, Pt₃Rh, Pt₃Fe, and Pt₃Mn candidates have all been previously reported as potential ORR catalysts, and all of them show higher activity than Pt.^46–50 In particular, Pt₃Co⁴⁷ and Pt₃Fe⁴⁹ have very similar mass activity to Pt₃Ni.⁴⁶ We also compare the DOS patterns of Pt₃Co and Pt₃Ni (Fig. 5b) and find that the DOS similarity is as high as 0.94. Although these candidates are previously reported catalysts for the ORR, our inverse design model successfully finds candidate materials without training based on prior knowledge of the catalytic properties of the materials. These facts definitely reveal the effectiveness of our DL model for catalyst design. Moreover, we need to note that Pt₃Co, Pt₃Rh, and Pt₃Mn are not included in the DOS DB used for the training of our inverse design model. This indicates that our model can readily identify candidate materials not only within the DB but also outside of the training dataset. This reveals that our inverse design can be more powerful for materials design than high-throughput screening. If we employ high-throughput screening of the DOS patterns in the DB, then we would never find candidates outside of the DB.

Fig. 5 Inverse design for the prediction of ORR catalysts with an input of the Pt₃Ni DOS. (a) ORR mass activity of candidates predicted via our inverse design model. The materials shown in dashed bars are out-of-the-training-dataset samples. All mass activity values are gathered from ref. 46–50. (b) DOS patterns of the input Pt₃Ni (red line) and predicted Pt₃Co (cyan area). The inset atomic structure shows a unit cell of Pt₃Co.

We further investigated the expandability of our model. For this, we applied the model to binary systems with a hexagonal crystal structure. The space groups of predicted materials were assigned to the most common space group (P6₃/mmc) in the Materials Project database. When provided with the Pt₃Ni DOS as the target, our model recommends three materials as candidates with a DOS similarity of approximately 0.9: AuCo₂, PtMn₂, and PtFe₂ (Fig. S2†). In particular, the DOS similarity of AuCo₂ exceeds 0.9, indicating that our model is readily applicable to hexagonal structure systems. To investigate the thermodynamic stability of the candidate materials, we also calculated their formation energies using DFT calculations. PtMn₂ and PtFe₂ have negative formation energies. Although AuCo₂ has a positive formation energy, the value is very close to zero, indicating that AuCo₂ could be stable at temperatures well above 0 K.

Additionally, we expanded our model to ternary systems with a tetragonal crystal system, where the target DOS was maintained as that of Pt₃Ni (Fig. S3†). The space groups of predicted materials were assigned to the most common space group (P4/mmm) in the Materials Project database. Similar to the binary hexagonal structure case, our model readily recommends a ternary tetragonal material (CoRh₂Pd) with a high DOS similarity of 0.9, in which the formation energy of the candidate material is close to zero. As the 2nd tier candidate, our model recommends ZrRh₂Ir and ScRh₂Ir with a DOS similarity of 0.8, in which their formation energies are negative. Based on the two additional tests, it is confirmed that our inverse design model is not only limited to a cubic structure but also works for various crystal structures. Moreover, it is applicable to not only binary systems but also ternary systems.

As a second application example, we apply the inverse design model to find a novel hydrogen storage material as an alternative to the prototypical Pd.^51,52 As a descriptor to evaluate the hydrogen storage properties of a material, the formation energy of interstitial hydrogen is well known to be very useful.^53,54 To have high hydrogen uptake and release properties, the formation energy value should be small but negative. Because the formation energy of an interstitial defect is related to the DOS pattern,^55,56 we tried to find a bimetallic hydrogen storage material whose DOS pattern is similar to that of pristine Pd by using the inverse design model.

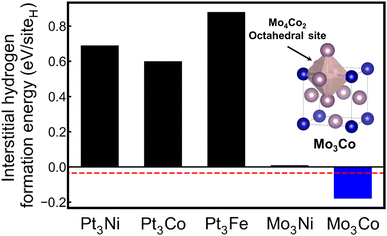
As shown in Fig. 6, the inverse design model proposes five candidates by using the DOS pattern of Pd as an input: Pt₃Ni, Pt₃Co, Pt₃Fe, Mo₃Ni, and Mo₃Co. To investigate the formation energies of interstitial hydrogen, we first determined the structure of candidate compositions. As Pd, the input material has a cubic structure, and all candidates are assumed to have cubic Bravais lattices. Among the crystal structures with the A₃B composition in the cubic Bravais lattice, the L1₂ structure was selected as a prototype. DFT calculations were conducted for the candidate material with the L1₂ crystal structure in which octahedral and tetrahedral sites for the interstitial hydrogen were considered. Here, several Pt alloys are predicted as candidate materials, which results from the fact that Pt and Pd are in the same group and have similar electronic structures, as shown in Fig. 2. However, bulk Pt is known to have no hydrogen storage properties;⁵⁷ thus, the Pt alloy candidates have positive formation energies for interstitial hydrogen, likely indicating low hydrogen storage properties. In contrast, additional DFT calculations reveal that among the candidates, Mo₃Co has a negative formation energy of −0.18 eV per site_H, implying that Mo₃Co can show hydrogen storage properties. The preferential site for the interstitial hydrogen in Mo₃Co is an octahedral site, identical to the Pd case. In fact, pristine Mo and Co are not promising hydrogen storage materials under ambient conditions.^58,59 However, homogeneous mixing of Mo and Co elements in the Mo₃Co lattice creates a different electronic structure from those of pristine Mo and Co but similar to that of Pd, readily leading to high hydrogen storage properties. To the best of our knowledge, this work is the first report on the hydrogen storage properties of Mo₃Co.

Fig. 6 Inverse design for the prediction of hydrogen storage materials with an input of the Pd DOS. The interstitial hydrogen formation energies of the candidates are presented. The red dotted line represents the formation energy of interstitial hydrogen in Pd. The inset shows the crystal structure of Mo₃Co, and the most stable site of interstitial hydrogen is the Mo₄Co₂ octahedral site.

Lastly, since the training database also includes DOSs for non-metallic materials, our model has the potential to be applied to oxide materials. To evaluate its applicability to oxide systems, we tested our model using the target DOS of BaTiO₃ a material known for its high dielectric constant and common usage in multi-layer ceramic capacitors. Recognizing the perovskite structure of BaTiO₃, we hypothesized that the predicted material would also exhibit a cubic perovskite structure. As shown in Fig. S4,† our model predicts SrTiO₃, BaMnO₃, and BaZrO₃ as candidate materials with high DOS similarity. While the DOS of SrTiO₃ shows a high cosine similarity of 0.85, BaMnO₃ and BaZrO₃ show DOS similarities of approximately 0.8. However, all three candidates exhibit negative formation energies. Here, it is noteworthy that, as the DOS in the database were calculated using the typical PBE functional, inherent errors may exist in the DOSs for oxide materials. This result demonstrates that our model can extend to non-metallic systems.

Conclusion

In conclusion, we have developed an inverse design model to find the compositions of candidate materials from a DOS pattern of a target material. By using the DOS-based CV as an output vector of our DL model, the chemical information and electronic structural information of materials can all be learned by the model. Thus, the prediction performance (composition accuracy and DOS pattern accuracy) is greatly enhanced compared to the existing CVs. Moreover, we have successfully applied the inverse design model to find materials as alternatives to Pt₃Ni for ORR catalysis and Pd for hydrogen storage. In contrast to other ML-based inverse design methods that are limited to problems in which one specific property (e.g., the formation energy or bandgap) is described by a one-dimensional vector (a single number), our inverse design scheme can readily handle a multidimensional DOS pattern as a material property. Although the current scheme is limited to designing binary cubic materials in this work, it can be expanded into ternary systems with different kinds of crystal structure if we prepare CVs for those in a similar manner. Moreover, the workflow presented herein is not limited to DOS patterns but can be readily expanded to many other properties described by multidimensional vectors, such as spectrum data in materials science. Accordingly, our model is expected to be used to greatly expand the range of the design space for inverse design.

Methods

DOS dataset generation

We employed the MPRester.get_dos_by_material_id function of the Materials Project API to collect DOS data in September 2020. For standardization, all DOS data were cropped in the energy range from −7.5 to 7.5 eV with 151 energy levels. DOS values were normalized to have the same area.

Architecture of the autoencoder model for generating DOS-based EVs

The neural network of the autoencoder model was a fully connected neural network (FCNN) model with 3 hidden layers. The input and output vectors were the same with 151 nodes, corresponding to the size of the centroid DOS of the elements. Several numbers of hidden nodes were tested, and 30 were selected considering the efficiency. A latent vector of the 2nd hidden layer was used as the EV. The hyperparameters of the neural network were as follows: activation function – hyperbolic tangent, optimizer – Adam, and learning rate – 0.001.

Architecture of the inverse design model

The inverse design model was composed of a 1-dimensional convolutional neural network (CNN) connected to one fully connected layer. The input vector was a DOS pattern vector with 151 nodes, and the output vector was a CV with 60 nodes. The CNN block included 4 iterations of convolution and pooling layers. In the convolution layers, 32 kernels with a size of 13 were used. The stride number was set to 1, and zero-padding was used to maintain the number of dimensions. In the pooling layer, max pooling with a filter of size 2 and a stride of 2 was applied. The output vector of the 4th pooling layer was flattened and passed to the fully connected layers with 60 output nodes, identical to the size of the CV. The hyperparameters of the model were as follows: activation function – ReLU, optimizer – Adam, and learning rate – 0.001.

DFT calculations

DFT calculations were carried out using the plane-wave-basis Vienna ab initio simulation package (VASP) code with an energy cutoff of 520 eV. Projector-augmented wave method pseudopotentials were adopted to treat core and valence electrons. The generalized gradient approximation Perdew–Burke–Ernzerhof functional was used for the exchange-correlational functional. The geometry was fully relaxed until the maximum Hellmann–Feynman forces were less than 0.01 eV Å⁻¹, and the electronic structures were relaxed with a convergence criterion of 10⁻⁴ eV. Brillouin-zone integrations were performed using Monkhorst–Pack k-point samplings of 10 × 10 × 10 and 24 × 24 × 24 for the geometry optimization and DOS calculation, respectively.

Data availability

All the code and the data that support the findings of this study are available from the corresponding authors upon reasonable request.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This work was supported by the Samsung Research Funding & Incubation Center of Samsung Electronics under Project Number SRFC-MA1801-03 and the National Center for Materials Research Data (NCMRD) through the National Research Foundation of Korea funded by the Ministry of Science and ICT (Project Number 2021M3A7C2089739).

References

1. E. W. McFarland and W. H. Weinberg, Trends Biotechnol., 1999, 17, 107–115.
2. B. Jandeleit, D. J. Schaefer, T. S. Powers, H. W. Turner and W. H. Weinberg, Angew. Chem., Int. Ed., 1999, 38, 2494–2532.
3. W. F. Maier, K. Stöwe and S. Sieg, Angew. Chem., Int. Ed., 2007, 46, 6016–6067.
4. Y. Wu, P. Lazic, G. Hautier, K. Persson and G. Ceder, Energy Environ. Sci., 2013, 6, 157–168.
5. B. C. Yeo, D. Kim, H. Kim and S. S. Han, J. Phys. Chem. C, 2016, 120, 24224–24230.
6. B. C. Yeo, H. Nam, H. Nam, M.-C. Kim, H. W. Lee, S.-C. Kim, S. O. Won, D. Kim, K.-Y. Lee, S. Y. Lee and S. S. Han, npj Comput. Mater., 2021, 7, 137.
7. N. W. A. Gebauer, M. Gastegger, S. S. P. Hessmann, K.-R. Müller and K. T. Schütt, Nat. Commun., 2022, 13, 973.
8. Z. Ren, S. I. P. Tian, J. Noh, F. Oviedo, G. Xing, J. Li, Q. Liang, R. Zhu, A. G. Aberle, S. Sun, X. Wang, Y. Liu, Q. Li, S. Jayavelu, K. Hippalgaonkar, Y. Jung and T. Buonassisi, Matter, 2022, 5, 314–335.
9. I. J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville and Y. Bengio, Presented in Part at the Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, Canada, 2014, vol. 2.
10. D. P. Kingma and M. Welling, Auto-Encoding Variational Bayes, arXiv, 2013, preprint, arXiv:1312.6114,  DOI:10.48550/arXiv.1312.6114.
11. B. Kim, S. Lee and J. Kim, Sci. Adv., 2020, 6, eaax9324.
12. T. Long, N. M. Fortunato, I. Opahle, Y. Zhang, I. Samathrakis, C. Shen, O. Gutfleisch and H. Zhang, npj Comput. Mater., 2021, 7, 66.
13. J. Noh, G. H. Gu, S. Kim and Y. Jung, Chem. Sci., 2020, 11, 4871–4881.
14. J. Noh, J. Kim, H. S. Stein, B. Sanchez-Lengeling, J. M. Gregoire, A. Aspuru-Guzik and Y. Jung, Matter, 2019, 1, 1370–1384.
15. R. Dong, Y. Dan, X. Li and J. Hu, Comput. Mater. Sci., 2021, 188, 110166.
16. L. Chen, W. Zhang, Z. Nie, S. Li and F. Pan, J. Mater. Inf., 2021, 1, 4.
17. J. Wang, Y. Wang and Y. Chen, Materials, 2022, 15, 1811.
18. T. Xie, X. Fu, O.-E. Ganea, R. Barzilay and T. Jaakkola, 2021, preprint, arXiv:2110.06197,  DOI:10.48550/arXiv.2110.06197.
19. D. Wines, T. Xie and K. Choudhary, J. Phys. Chem. Lett., 2023, 14, 6630–6638.
20. S. Li and A. S. Barnard, Adv. Theory Simul., 2022, 5, 2100414.
21. S. Li and A. S. Barnard, Chem. Mater., 2022, 34, 4964–4974.
22. B. Hammer and J. K. Nørskov, Advances in Catalysis, Academic Press, 2000, vol. 45, pp. 71–129.
23. J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Nat. Chem., 2009, 1, 37–46.
24. M. J. Banisalman, M.-C. Kim and S. S. Han, ACS Catal., 2022, 12, 1090–1097.
25. M. Andersen, S. V. Levchenko, M. Scheffler and K. Reuter, ACS Catal., 2019, 9, 2752–2759.
26. L. Foppa and L. M. Ghiringhelli, Top. Catal., 2022, 65, 196–206.
27. M. T. Gorzkowski and A. Lewera, J. Phys. Chem. C, 2015, 119, 18389–18395.
28. S. Bhattacharjee, U. V. Waghmare and S.-C. Lee, Sci. Rep., 2016, 6, 35916.
29. V. Fung, G. Hu, P. Ganesh and B. G. Sumpter, Nat. Commun., 2021, 12, 88.
30. D. Hong, J. Oh, K. Bang, S. Kwon, S.-Y. Yun and H. M. Lee, J. Phys. Chem. Lett., 2022, 13, 8628–8634.
31. N. R. Knøsgaard and K. S. Thygesen, Nat. Commun., 2022, 13, 468.
32. V. Fung, J. Zhang, G. Hu, P. Ganesh and B. G. Sumpter, npj Comput. Mater., 2021, 7, 200.
33. P. Lyngby and K. S. Thygesen, npj Comput. Mater., 2022, 8, 232.
34. J. Kim, L. C. O. Tiong, D. Kim and S. S. Han, J. Phys. Chem. Lett., 2021, 12, 8376–8383.
35. Q. Zhou, P. Tang, S. Liu, J. Pan, Q. Yan and S.-C. Zhang, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E6411–E6417.
36. V. Tshitoyan, J. Dagdelen, L. Weston, A. Dunn, Z. Rong, O. Kononova, K. A. Persson, G. Ceder and A. Jain, Nature, 2019, 571, 95–98.
37. Y. Dan, Y. Zhao, X. Li, S. Li, M. Hu and J. Hu, npj Comput. Mater., 2020, 6, 84.
38. T. Mikolov, I. Sutskever, K. Chen, G. Corrado and J. Dean, 2013, preprint, arXiv:1310.4546,  DOI:10.48550/arXiv.1310.4546.
39. T. Mikolov, K. Chen, G. Corrado and J. Dean, 2013, preprint, arXiv:1301.3781,  DOI:10.48550/arXiv.1301.3781.
40. A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002.
41. J. M. Munro, K. Latimer, M. K. Horton, S. Dwaraknath and K. A. Persson, npj Comput. Mater., 2020, 6, 112.
42. L. van der Maaten and G. Hinton, J. Mach. Learn. Res., 2008, 9, 2579–2605.
43. K. Pearson, Lond. Edinb. Dublin philos. mag. j. sci., 1901, 2, 559–572.
44. M. Y. Toriyama, A. M. Ganose, M. Dylla, S. Anand, J. Park, M. K. Brod, J. M. Munro, K. A. Persson, A. Jain and G. J. Snyder, Mater. Today Electron., 2022, 1, 100002.
45. V. R. Stamenkovic, B. Fowler, B. S. Mun, G. Wang, P. N. Ross, C. A. Lucas and N. M. Marković, Science, 2007, 315, 493–497.
46. J. Wu, J. Zhang, Z. Peng, S. Yang, F. T. Wagner and H. Yang, J. Am. Chem. Soc., 2010, 132, 4984–4985.
47. Y. Xiong, L. Xiao, Y. Yang, F. J. DiSalvo and H. D. Abruña, Chem. Mater., 2018, 30, 1532–1539.
48. B. Narayanamoorthy, K. K. R. Datta, M. Eswaramoorthy and S. Balaji, RSC Adv., 2014, 4, 55571–55579.
49. C. Jung, C. Lee, K. Bang, J. Lim, H. Lee, H. J. Ryu, E. Cho and H. M. Lee, ACS Appl. Mater. Interfaces, 2017, 9, 31806–31815.
50. J. Lim, C. Jung, D. Hong, J. Bak, J. Shin, M. Kim, D. Song, C. Lee, J. Lim, H. Lee, H. M. Lee and E. Cho, J. Mater. Chem. A, 2022, 10, 7399–7408.
51. B. D. Adams and A. Chen, Mater. Today, 2011, 14, 282–289.
52. S. K. Konda and A. Chen, Mater. Today, 2016, 19, 100–108.
53. J. Bellosta von Colbe, J.-R. Ares, J. Barale, M. Baricco, C. Buckley, G. Capurso, N. Gallandat, D. M. Grant, M. N. Guzik, I. Jacob, E. H. Jensen, T. Jensen, J. Jepsen, T. Klassen, M. V. Lototskyy, K. Manickam, A. Montone, J. Puszkiel, S. Sartori, D. A. Sheppard, A. Stuart, G. Walker, C. J. Webb, H. Yang, V. Yartys, A. Züttel and M. Dornheim, Int. J. Hydrogen Energy, 2019, 44, 7780–7808.
54. P. Modi and K.-F. Aguey-Zinsou, Front. Energy Res., 2021, 9, 616115.
55. Y. Cui, B. Liu, L. Chen, H. Luo and Y. Gao, AIP Adv., 2016, 6, 105301.
56. X. Xiang, W. Zhu, T. Lu, T. Gao, Y. Shi, M. Yang, Y. Gong, X. Yu, L. Feng, Y. Wei and Z. Lu, AIP Adv., 2015, 5, 107136.
57. L. S. R. Kumara, O. Sakata, H. Kobayashi, C. Song, S. Kohara, T. Ina, T. Yoshimoto, S. Yoshioka, S. Matsumura and H. Kitagawa, Sci. Rep., 2017, 7, 14606.
58. M. Wang, J. Binns, M.-E. Donnelly, M. Peña-Alvarez, P. Dalladay-Simpson and R. T. Howie, J. Chem. Phys., 2018, 148, 144310.
59. S. N. Abramov, V. E. Antonov, B. M. Bulychev, V. K. Fedotov, V. I. Kulakov, D. V. Matveev, I. A. Sholin and M. Tkacz, J. Alloys Compd., 2016, 672, 623–629.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta06491c

‡ These authors contributed equally.

---