 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Revisiting the density profile of the fuzzy sphere model for microgel colloids
Frank
Scheffold

Department of Physics, University of Fribourg, Chemin du Musée 3, 1700, Fribourg, Switzerland. E-mail: Frank.Scheffold@unifr.ch
First published on 7th October 2024
Abstract
Common neutral polymer microgels exhibit an inhomogeneous density profile with a gradual decay that is commonly described using the fuzzy sphere model. The model is based on the idea of convolving the collapsed solid sphere profile with a Gaussian to describe inhomogeneous swelling of the microgel in a good solvent. Here we show that the corresponding density profile in real space used in several recent works – such as in super-resolution microscopy – is different from the fuzzy sphere model, and we explain how to correctly transition between reciprocal space modelling to real space. Our work aims to clarify the application of the model so that errors can be avoided in the future. Our discussion is also crucial when comparing alternative real-space models for the density profile with the established fuzzy sphere model.
Polymer microgels, also called hydrogels or nanogels, are cross-linked polymer gels where the polymer chain and cross-linking reaction are deliberately stopped to obtain small polymeric beads that can be highly swollen in a solvent medium.1–6 Microgels are among the most studied colloidal systems. Some microgels respond to external stimuli, allowing their size and porosity to automatically adapt to environmental changes, which has led to these systems being referred to as ‘intelligent’ or ‘smart’.7 Stimuli-responsive behavior can be observed when the polymer's solubility reacts to temperature, pH, ionic strength, or other external triggers. If the solvent quality changes from good to bad, a volume phase transition (VPT) occurs, where the microgel shifts from a highly swollen to a collapsed state.
Among the many microgels that have been studied, those made from thermoresponsive poly(N-isopropylacrylamide), or pNIPAM, are probably the most well-known example. The homopolymer poly(N-isopropylacrylamide), when dissolved in water, exhibits a lower critical solution temperature (LCST) at around 33 °C.8 Above this temperature, the solvent changes from good to bad, causing the polymer to undergo a coil-to-globule transition. For submicron-sized pNIPAM microgels, this transition leads to a rapid shrinking of the colloids by a factor of two or three in size.9 While far below the LCST the microgel is composed of more than ninety percent water, after collapse, almost all of the water is expelled.10
An important characteristic of pNIPAM microgels is that they acquire a radially inhomogeneous density profile once they are swollen. Instead of a sharp cutoff at the outer perimeter, it has long been known that the density decays more gradually at the interface.1 This is generally attributed to the fact that during the synthesis, the cross-linker is consumed more rapidly compared to the NIPAM monomer.11 However, even if this were not the case, there must be an interfacial layer, comparable in thickness to the mesh size of the gel,6,12 where the polymer chains are dangling and forming brush-like structures, leading to a gradually decaying density profile on several nanometer length scales.13 Since many properties of microgels and microgel suspensions are controlled by their interfacial characteristics, it is of prime importance to understand the microgel structure and morphology, particularly at the interface.14 In the present work, we will discuss the widely employed fuzzy-sphere model for the microgel density profile and its representations in both real space and reciprocal space. Notably, we will demonstrate that a description of the real space density profile used in several recent papers,15–19 including our own,15 is not identical to the fuzzy sphere density profile. This work aims to clarify the application of the model so that such inconsistencies can be avoided in the future. This discussion is also important if alternative real-space models for the density profile are proposed16,20,21 and compared to the established fuzzy-sphere model.
Early pioneering work by Stieger and co-workers introduced the fuzzy-sphere model for pNIPAM microgels10 based on a similar approach by Svaneborg and Pedersen to model the scattering of block copolymer micelles.22 The idea is to model the microgels density profile by convolving the profile of a solid sphere with radius R with a Gaussian function, where σ is the ‘fuzzyness’ parameter given by the standard deviation of the Gaussian.10,22,23 They obtain an expression for the microgel scattering form factor:
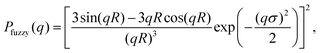 | (1) |
 | (2) |
The normalized scattering amplitude can be expressed by the microgel radial density profile as follows:
 | (3) |
The fuzzy-sphere model has been applied in numerous studies over the last 20 years in order to establish swelling curves, characterize microgel core–shell architecture, and relate quantities to microgel softness, the rheology of microgel suspensions25–27 or their optical properties.28 Ratios of the fuzzy shell to the core radius, σ/R, well above 20% have been reported for highly swollen microgels.10 Until not long ago, scattering techniques were the only methods that allowed the nanoscale characterization of microgels in solution, particularly for monitoring the volume phase transition.29,30 Direct and indirect inversion methods for scattering has been discussed in the literature, however these inversion algorithms are either ill-posed,31,32 and thus very sensitive to experimental noise, or they provide only the pair distance distribution function, which is a measure of spatial density–density correlations.33 With the advent of powerful numerical modeling32,34,35 and modern fluorescent super-resolution microscopy,15,36,37 real-space access to the internal structure and density profile of microgels in solution has become possible,15 even allowing for the distinction of different constituents of the microgel at the nanoscale.36 These new capabilities have also necessitated the direct modeling of the radially averaged internal density profile of individual microgel beads or density profiles derived from particle ensembles.
Since the fuzzy sphere model proposes to convolve the profile of a solid sphere with a Gaussian, several studies have suggested using the complementary error function as a basis for modeling the radial density profile:15–19
 | (4) |
This discrepancy becomes evident when integrating the density profile. For constant R the integral  should be independent of σ, but this is not the case when using eqn (4). As σ increases, mass is redistributed from the inside to the outside of the sphere perimeter R and the redistributed mass ρ(r) is weighted by r2. Consequently, the total mass would ‘magically’ increase as the microgel's interface becomes fuzzier. Moreover, in eqn (1), the position of the first minimum remains unchanged as long as R is the same, while the minimum shifts to smaller values when using the complementary error function, eqn (4), with eqn (3).
should be independent of σ, but this is not the case when using eqn (4). As σ increases, mass is redistributed from the inside to the outside of the sphere perimeter R and the redistributed mass ρ(r) is weighted by r2. Consequently, the total mass would ‘magically’ increase as the microgel's interface becomes fuzzier. Moreover, in eqn (1), the position of the first minimum remains unchanged as long as R is the same, while the minimum shifts to smaller values when using the complementary error function, eqn (4), with eqn (3).
To illustrate the discrepancy between the correct and incorrect model assumptions for fuzzy-spheres in real space, we plot in Fig. 1 different density profiles ρ(σ/R) and form factors P(qR) for increasing values of σ/R. In addition, we plot the dependence of the apparent mass of the microgels as a function of σ/R in Fig. 2. For small values of σ/R the differences are minor, but increase when σ/R exceeds 10–15%. In the superresolution work of Conley et al., the largest σ/R value reported was 13%, meaning the impact of using the complementary error function did not substantially affect the comparison with light scattering data15 since the first minimum of P(qR) would be shifted from qR = 4.49 (hard spheres) to qR = 4.42 only. However, other scattering studies have reported σ/R values of 25% and more for more weakly cross-linked microgels,10 where the effect would be significant. From Fig. 1(e), we can see that for σ/R = 0.25, the first minimum is shifted to qR = 4.25, corresponding to a more than 5% difference. This value has to be compared to the typical swelling of the core by 20–30%.10,30
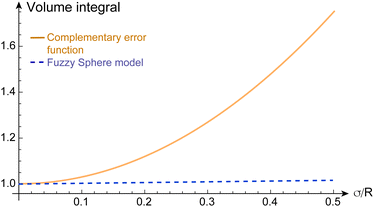 | ||
Fig. 2 The volume integral  of the radial density profile, corresponding to the microgel's mass, divided by (4πR3)/3, as a function of σ/R. Dashed line: for the fuzzy sphere model, the integral is one in all cases. Solid line: for the case of the complementary error function, the apparent mass increases with σ/R. For the cases shown in Fig. 1, we find values of 1.0675 for σ/R = 0.15, 1.1875 for σ/R = 0.25, and 1.36751 for σ/R = 0.35. of the radial density profile, corresponding to the microgel's mass, divided by (4πR3)/3, as a function of σ/R. Dashed line: for the fuzzy sphere model, the integral is one in all cases. Solid line: for the case of the complementary error function, the apparent mass increases with σ/R. For the cases shown in Fig. 1, we find values of 1.0675 for σ/R = 0.15, 1.1875 for σ/R = 0.25, and 1.36751 for σ/R = 0.35. | ||
It is important to emphasize that we make no claim here as to which model, eqn (2) or (4), better describes the real-space properties of the microgels. The complementary error function can certainly be used for this effect if the amplitude of ρ(r) or the core radius R is adjusted such that polymer mass is conserved upon swelling. However, it is important to note that the values of R and σ obtained from a fit with the complementary error function cannot (!) be compared one-to-one with the values obtained from scattering and the fuzzy sphere model.
In summary, we find that although the fuzzy sphere model provides a convenient and simple analytical description of scattering data, the model does not provide such a simple result in real space. Similarly, although the complementary error function can be easily fitted to experimental or numerical real-space data, there is no corresponding simple solution in reciprocal space. For comparison with scattering data, the density profile predicted by a theoretical model, or determined by a real-space characterization method or simulations, must therefore, in most cases, be numerically integrated using eqn (3).
Data availability
The data sets shown in Fig. 1 and 2 have been uploaded to the Zenodo repository and are available at https://doi.org/10.5281/zenodo.13895420.Conflicts of interest
There are no conflicts to declare.Acknowledgements
I would like to thank Jan Skov Pedersen, James Harden, Joseph Brader, and Chi Zhang for stimulating discussions, and Matthias Karg for useful comments that helped improve the manuscript. This research was financially supported by the Swiss National Science Foundation through grant no. 182881, as well as projects no. 149867 and 197146. This work work also benefited from support provided by the National Centre of Competence in Research (NCCR) ‘Bio-Inspired Materials’ and the European Union's Horizon 2020 research and innovation program under the Marie Sklodowska-Curie program (ITN SUPERCOL, Grant Agreement 860914).Notes and references
- B. R. Saunders and B. Vincent, Adv. Colloid Interface Sci., 1999, 80, 1–25 CrossRef CAS.
- A. Fernandez-Nieves, H. Wyss, J. Mattsson and D. A. Weitz, Microgel suspensions: fundamentals and applications, John Wiley & Sons, 2011 Search PubMed.
- Y. Jiang, J. Chen, C. Deng, E. J. Suuronen and Z. Zhong, Biomaterials, 2014, 35, 4969–4985 CrossRef CAS PubMed.
- M. Karg, A. Pich, T. Hellweg, T. Hoare, L. A. Lyon, J. Crassous, D. Suzuki, R. A. Gumerov, S. Schneider and I. I. Potemkin, et al. , Langmuir, 2019, 35, 6231–6255 CrossRef CAS PubMed.
- F. Scheffold, Nat. Commun., 2020, 11, 4315 CrossRef CAS PubMed.
- F. A. Plamper and W. Richtering, Acc. Chem. Res., 2017, 50, 131–140 CrossRef CAS PubMed.
- M. Karg and T. Hellweg, Curr. Opin. Colloid Interface Sci., 2009, 14, 438–450 CrossRef CAS.
- C. Wu and X. Wang, Phys. Rev. Lett., 1998, 80, 4092 CrossRef CAS.
- F. Scheffold, P. Daz-Leyva, M. Reufer, N. Ben Braham, I. Lynch and J. L. Harden, Phys. Rev. Lett., 2010, 104, 128304 CrossRef PubMed.
- M. Stieger, W. Richtering, J. S. Pedersen and P. Lindner, J. Chem. Phys., 2004, 120, 6197–6206 CrossRef CAS PubMed.
- X. Wu, R. Pelton, A. Hamielec, D. Woods and W. McPhee, Colloid Polym. Sci., 1994, 272, 467–477 CrossRef CAS.
- A. Fernández-Barbero, A. Fernández-Nieves, I. Grillo and E. López-Cabarcos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051803 CrossRef PubMed.
- S. Meyer and W. Richtering, Macromolecules, 2005, 38, 1517–1519 CrossRef CAS.
- M. J. Bergman, N. Gnan, M. Obiols-Rabasa, J.-M. Meijer, L. Rovigatti, E. Zaccarelli and P. Schurtenberger, Nat. Commun., 2018, 9, 5039 CrossRef PubMed.
- G. M. Conley, S. Nöjd, M. Braibanti, P. Schurtenberger and F. Scheffold, Colloids Surf., A, 2016, 499, 18–23 CrossRef CAS.
- S. Bergmann, O. Wrede, T. Huser and T. Hellweg, Phys. Chem. Chem. Phys., 2018, 20, 5074–5083 RSC.
- M. Ledesma-Motolina, M. Braibanti, L. F. Rojas-Ochoa and C. Haro-Pérez, Colloids Surf., A, 2015, 482, 724–727 CrossRef.
- A. Ninarello, J. J. Crassous, D. Paloli, F. Camerin, N. Gnan, L. Rovigatti, P. Schurtenberger and E. Zaccarelli, Macromolecules, 2019, 52, 7584–7592 CrossRef CAS PubMed.
- C. Balderas-Cabrera and R. Castillo, J. Chem. Phys., 2024, 161, 084903 CrossRef CAS PubMed.
- T. Mason and M. Lin, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2005, 71, 040801 CrossRef CAS PubMed.
- N. Boon and P. Schurtenberger, Phys. Chem. Chem. Phys., 2017, 19, 23740–23746 RSC.
- C. Svaneborg and J. S. Pedersen, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2001, 64, 010802 CrossRef CAS PubMed.
- I. Berndt, J. S. Pedersen and W. Richtering, J. Am. Chem. Soc., 2005, 127, 9372–9373 CrossRef CAS PubMed.
- Neutrons, X-rays, and Light: Scattering Methods Applied to Soft Condensed Matter, ed. P. Lindner and T. Zemb, Elsevier Science, Amsterdam, 2002 Search PubMed.
- G. M. Conley, C. Zhang, P. Aebischer, J. L. Harden and F. Scheffold, Nat. Commun., 2019, 10, 2436 CrossRef PubMed.
- J. R. Seth, M. Cloitre and R. T. Bonnecaze, J. Rheol., 2006, 50, 353–376 CrossRef CAS.
- A. Le Grand and G. Petekidis, Rheol. Acta, 2008, 47, 579–590 CrossRef CAS.
- M. Otten, M. Hildebrandt, B. Pfeffing, V. C. Voigt, F. Scheffold, T. Hellweg and M. Karg, Langmuir, 2024, 40, 14515–14526 CrossRef CAS PubMed.
- B. Zhou, U. Gasser and A. Fernandez-Nieves, Phys. Rev. E, 2023, 108, 054604 CrossRef CAS PubMed.
- M. Reufer, P. Daz-Leyva, I. Lynch and F. Scheffold, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 28, 165–171 CrossRef CAS PubMed.
- O. Virtanen, A. Mourran, P. Pinard and W. Richtering, Soft Matter, 2016, 12, 3919–3928 RSC.
- N. Hazra, A. Ninarello, A. Scotti, J. E. Houston, P. Mota-Santiago, E. Zaccarelli and J. J. Crassous, Macromolecules, 2023, 57, 339–355 CrossRef.
- O. Glatter, J. Appl. Crystallogr., 1977, 10, 415–421 CrossRef.
- N. Gnan, L. Rovigatti, M. Bergman and E. Zaccarelli, Macromolecules, 2017, 50, 8777–8786 CrossRef CAS PubMed.
- A. J. Moreno and F. L. Verso, Soft Matter, 2018, 14, 7083–7096 RSC.
- A. P. Gelissen, A. Oppermann, T. Caumanns, P. Hebbeker, S. K. Turnhoff, R. Tiwari, S. Eisold, U. Simon, Y. Lu and J. Mayer, et al. , Nano Lett., 2016, 16, 7295–7301 CrossRef CAS PubMed.
- A. A. Karanastasis, Y. Zhang, G. S. Kenath, M. D. Lessard, J. Bewersdorf and C. K. Ullal, Mater. Horiz., 2018, 5, 1130–1136 RSC.
| This journal is © The Royal Society of Chemistry 2024 |

