Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Accessing the free expansion of a crystalline colloidal drop by optical experiments†
Marcus U.
Witt
 a,
G. H. Philipp
Nguyen
a,
G. H. Philipp
Nguyen
 b,
Josefine R.
von Puttkamer-Luerssen
a,
Can H.
Yilderim
a,
Johannes A. B.
Wagner
a,
Ebrahim
Malek
ac,
Sabrina
Juretzka
a,
Jorge L.
Meyrelles
Jr.
ad,
Maximilan
Hofmann
a,
Hartmut
Löwen
b,
Josefine R.
von Puttkamer-Luerssen
a,
Can H.
Yilderim
a,
Johannes A. B.
Wagner
a,
Ebrahim
Malek
ac,
Sabrina
Juretzka
a,
Jorge L.
Meyrelles
Jr.
ad,
Maximilan
Hofmann
a,
Hartmut
Löwen
 b and
Thomas
Palberg
b and
Thomas
Palberg
 *a
*a
aInstitute of Physics, Johannes Gutenberg University, Mainz, Germany. E-mail: palberg@uni-mainz.de
bInstitute of Theoretical Physics II: Soft Matter, Heinrich-Heine-Universität, Düsseldorf, Germany
cInstitute for Biophysics, Goethe University, Frankfurt, Germany
dPontifícia Universidade Católica, Rio de Janeiro, Brazil
First published on 27th August 2024
Abstract
We study poly-crystalline spherical drops of an aqueous suspension of highly charged colloidal spheres exposed to a colloid-free aqueous environment. Crystal contours were obtained from standard optical imaging. The crystal spheres first expand to nearly four times their initial volume before slowly shrinking due to dilution-induced melting. Exploiting coherent multiple-scattering by (110) Bragg reflecting crystals, time-dependent density profiles were recorded within the drop interior. These show a continuously flattening radial density gradient and a decreasing central density. Expansion curves and density profiles are qualitatively consistent with theoretical expectations based on dynamical density functional theory for the expansion of a spherical crystallite made of charged Brownian spheres. We anticipate that our study opens novel experimental access to density determination in turbid crystals.
1 Introduction
A block of solid composed of repulsive individual particles will immediately explode when exposed to a particle-free, vacuum-like environment. The reason is the strong interparticle forces or – in thermodynamic terms – the positive pressure of the solid, which needs to be counterbalanced to keep a solid stable. The resulting expansion process has been addressed, numerically and in experiments employing various model systems. In particular, charged plasmas and colloidal spheres are well suited for these investigations. Here, the repulsion type, range and strength are conveniently adjusted between the theoretical limits of hard spheres and the one component plasma.1,2 Moreover, the low shear rigidity of colloidal crystals allows their facile manipulation by external fields, like shear, gravity or gradients of chemical potential.3–5 Starting with the pioneering work of Tang et al.,6 the majority of investigations studied expansion in two-dimensional systems.7–13 Many of these studies were motivated by and thus focussed on the 2D-specific two-step melting process induced by changes in density.14 This is different in 3D, where expansion experiments have rarely been used to induce melting, which is a fascinating topic on its own15–17 and can be conveniently induced by tuning the interaction strength18,19 or using temperature to induce particle size variations.20,21In 2D, both density and refractive index mismatch between particles and suspending solvent allow for the facile preparation of experimental colloid systems, which are readily accessible by high resolution optical methods like confocal microscopy or light scattering.22,23 Moreover, for small two-dimensional samples, solvent currents arising during the initial placement or release process are typically too weak to affect the crystal evolution. By contrast, 3D expansion experiments in general require to start at elevated densities, where optical access is hampered by multiple scattering effects and sample turbidity. Further, isotropic expansion may be difficult to realize. The few reports available on the expansion of 3D crystals concentrated on unidirectional expansion after unidirectional compression.24 Kanai et al.25,26 studied the expansion of centrifuged charged sphere crystals. They reported an approximately linearly decreasing density profile with discontinuity at the melting transition at values closely matching the equilibrium melting and freezing densities.
Isotropic expansion in three dimensions so far has been studied only for small plasma systems, which are still optically accessible.27 Here, electrostatically driven collective effects dominate the expansion. Plasma systems come in two main variants, differing by repulsion type. Dusty plasmas in μg environments or thermophoretic levitation can form crystalline Yukawa balls (YBs). Laser-cooled ion plasmas released from harmonic trap potentials form expanding Coulomb balls (CBs). The density profiles of CBs are strictly flat at continuously decreasing densities and feature sharp boundaries, while those of YBs peak in the centre and have smeared boundaries.28,29 Presumably due to the challenges involved preparing well-defined starting conditions and the difficulties in optical access, experiments on the isotropic 3D expansion of colloidal solids have not been reported yet and experimental density profiles are missing.
The present study aims at closing this gap. We conduct expansion experiments on crystalline drops of highly concentrated crystalline colloidal suspensions in contact with a particle-free environment. The drops initially expand and later shrink by melting outward-in. They are overall turbid but show a brilliant colour display, which leaves their outer region and their contour accessible to various optical methods. The large central density, however, inhibits direct observation of the drop interior. We therefore developed an imaging method drawing contrast from the pronounced wavelength-dependent multiple scattering occurring within thin concentric shells of constant density, and matching the Bragg condition for (110) scattering. The approach allowed to deduce a considerable section of the radial density profiles as a function of time and yields density-dependent expansion curves.
To check the consistency of our heuristic concepts and to compare our data to theoretical expectations, we model the expansion by calculations based on dynamical density functional theory.30 There, we consider particles interacting by DLVO-like Yukawa pair potentials. As starting configuration, we assume an isotropic expanding, spherical crystallite of body centred cubic crystal structure as well as a large and homogeneous initial density. Our results show a generally good qualitative agreement of the experimental data and this theoretical model. Few remaining discrepancies indicate room for further experimental and theoretical improvement. Overall, we successfully demonstrate a novel approach to time-dependent density profiling in expanding turbid media. We anticipate that multiple scattering based density determination will be useful in many future investigations on concentrated crystalline colloidal materials.
In what follows, we first introduce the materials and experimental techniques employed for drop fabrication and optical analysis. The following results section presents the experimental data. A short theoretical chapter presents our simple model and compares its expectations to the experimental data. In the discussion section, we address open points and remaining challenges. We conclude with some prospects for future applications of the demonstrated approach for improved expansion experiments.
2 Materials and experimental methods
2.1 Sample and sample characterization
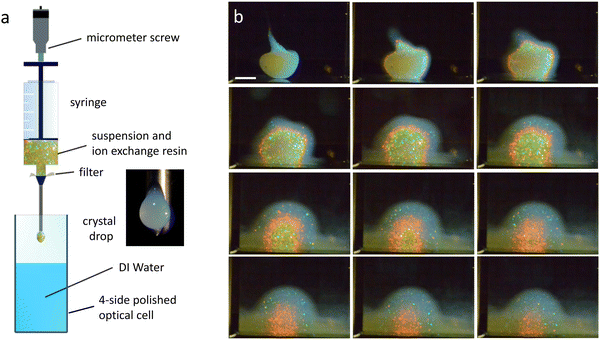
Crystalline drops were prepared from highly charged polymer spheres in aqueous suspension. Our particles were a kind gift from BASF, Ludwigshafen (Batch no. GK2876 4542, Lab code PnBAPS80). From SAXS-measurements, their diameter and their polydispersity-index are d = 87.5 nm and PI = 0.08, respectively. Conductivity measurements31 yielded a conductivity charge of Zσ = 513 ± 3, torsional resonance spectroscopy gave an interaction effective charge of ZG = 365.1 ± 2.332,33 (see also Fig. S1 in the ESI†). The particle mass density was ρmass = 1.005 g cm−3. Deionized and decarbonized suspensions were prepared using standard procedures.34,35 In this state the systems are fluid at low and crystalline at large number densities, ρ, respectively. From reflection spectroscopy,36 their crystal structure is body centred cubic (bcc) up to the largest densities probed (Fig. S2 in the ESI†). From crystal growth measurements,37 the melting density is ρm = (1 ± 0.2) μm−3 under deionized, decarbonized conditions and ρm ≈ 15 μm−3, after equilibration against ambient air.38 Model calculations on deionized and decarbonized systems show little variation of the interaction strength over the density-range of interest (Fig. S3 in the ESI†).2.2 Drop fabrication
For the expansion experiments, we prepared a stock of deionized and decarbonized suspension at ρ = 110 μm−3 ≫ ρm. A small amount of it was filled with some ion exchange resin [AmberjetTM Nr. K306.2, Carl Roth, Germany] into a syringe featuring an extrusion needle of inner diameter of 1.0 mm [Needle blunt 1.2 × 40 mm, Braun, Germany]. After extruding a sacrifice-drop (not shown), we place the syringe tip some mm above the surface of deionized water contained in a four-side-polished optical cell with a square cross-section of 10 × 10 mm2. Then we extrude another drop into the water and start the observation. A scheme of our experimental set-up is shown in Fig. 1a.Due to the low shear modulus, the drop is shear-molten during the extrusion process, but it starts to recrystallize immediately after leaving the needle tip, i.e., within t ≈ 0.3 s. Shape stabilization, however, take somewhat longer. For spherical drops, this occurs on average around t ≈ 5 s. Since the initial placement history strongly influences the drop shape, it may take some manual skill and practice to obtain compact, spherical drops (cf. Fig. S5 of the ESI†). Due to the slight density mismatch with the environment, drops settle to the cell bottom. They initially expand and later shrink due to outward-in melting. Throughout, they show a brilliant colour display. The characteristic sequence of visual appearance is depicted in the unprocessed Bragg images shown in Fig. 1b (see also Video 1. For processed images, see below Fig. 3 and Fig. S9 in the ESI†).
2.3 Optical properties of drops and observation schemes
Our approach to density profiling in turbid systems relies on both light scattering and microscopic imaging.39,40 Scattering simply provides the colour and intensity contrast for different microscopic regions (e.g., crystallites) which are then imaged. Regarding the contrast mechanism, we consider that the expanding drops are ensembles of non-adsorbing, dielectric spheres. In general, their scattering properties depend on the magnitude of the scattering vector q = (4πn/λ0)sin(Θ/2), where λ0 is the wavelength in vacuum, n is the index of refraction of the solvent (nH2O = 1.333), and Θ is the scattering angle. Images capture both coherent and incoherent, single and multiple scattering contributions (CS, IS, SS and MS, respectively).41 These vary with density and wavelength, and further depend on suspension structure. Additional experiments were conducted to carefully characterize the effects of a density-gradient and the melting transition on the optical properties (see Fig. S2a, S7 and S8 of the ESI†). From these, we deduce our drops to feature concentric layers of different scattering properties. Most prominent is a narrow, sheet of suitable density perpendicular to the radial gradient. Within and from it, we see very intense coherent MS caused by the 110-Bragg reflection and by incoherent scattering (Fig. S7a and b of the ESI†). Under monochromatic illumination, MS provides excellent imaging contrast, while the density dependence of the Bragg reflection allows precise localization of isopycnic-surfaces. At the same time, the increased reflectivity results in a drastic reduction of transmission42 (Fig. S8b, ESI†). The MS-sheets will hinder light from penetrating into the core underneath, which, despite increasing incoherent MS, is actually more transparent again. Outside the sheets, the suspension is fairly transparent and SS dominates, allowing for imaging of individual (200) and occasionally (211)-Bragg reflecting crystals (Fig. S6c and Video 1 in the ESI†). For the (110) reflection of the MS-sheet and the (200) reflections in the enveloping region, the local density is calculated as: | (1) |
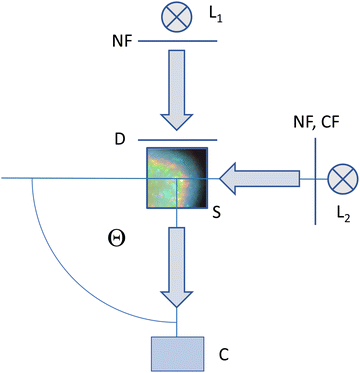
Regarding imaging, a combination of different illumination and observation arrangements was employed. A sketch of the optical set-up is given in Fig. 2. A more detailed drawing can be found in Fig. S4 of the ESI.† The setup allows for flexible switching between different imaging modes, which are presented by example images in Fig. 3a–c. We first consider the two alternative illumination paths.
Both in transmission and in the 90° scattering geometry, the sample (S) is illuminated by commercial white light sources (L1, L2) of 5000 K [L, Avalight-DH-S; LS-0610025, Avantes B.V. Apeldoorn, NL]. These instruments deliver the light via a fibre-optic transmission line terminating in a collimation unit. Backside-illumination by L1 is used for transmission imaging (TR). Here, we set the collimating unit to slightly divergent. The light impinges on a diffusor screen (Optolite™ HSR, Knight Optical, GB) to provide homogeneous diffuse background illumination at a width of 3 cm. To adjust image brightness at constant colour temperature, we inserted an attenuating neutral filter (NF; D1.0-D2.3, Edmund Optics, DE).
The illumination path coming from L2 on the right side is used for imaging at Θ = 90° scattering angle. Here the collimation unit is set to deliver parallel white light at a beam width of ≈1.5 cm. A wheel with a neutral filter and several monochromatic band-pass filters ranging from deep blue to deep red (Edmund Optics, DE) allows flexible switching of the imaging mode. In white light Bragg-imaging (WB) we use the NF to adjust brightness. In monochromatic Bragg-imaging (MB) the selected λ correspond to the following densities: λ = 633 nm: ρ = 31.54 μm−3; λ = 611 nm: ρ = 35.07 μm−3 orange; λ = 590 nm: ρ = 38.95 μm−3; λ = 547 nm: ρ = 48.88 μm−3; λ = 514 nm: ρ = 58.91 μm−3; λ = 488 nm: ρ = 68.83 μm−3). In several experiments reported here, we combined monochromatic illumination under 90° with transmission illumination (mixed mode, MM) to minimize overexposure effects. For drop shape checking, a sample illuminated by L2 can alternatively be observed in transmission under Θ = 0° with the camera placed to the right side (not shown in Fig. 2).
2.4 Imaging, image processing and analysis
All drops were observed in portrait mode with a 46Mpix consumer CMOS camera (C; Nikon D850) equipped with a belly and an inversely mounted f1.4, 50 mm lens. This resulted in an approximately 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 image on the sensor screen. ISO was set to 400 and exposure times were in the range of 1/50–1/400 s. In MB image series with six colours, we have a minimum time resolution of Δtmin = 10 s between subseries due to the time needed for filter switching. In each subseries, we switched colours from long to short wavelengths to counteract any timing-bias due to intermediate expansion. For a series of 6 colours, one white light and one transmission image, Δtmin = 30 s. The 14-bit raw images were saved to a computer in .nef-format. Examples of unprocessed images were shown in Fig. 1b. Subsequent image processing (centring, alignment, cropping, size calibration and colour temperature correction) was performed with ViewNX2 and/or NX Studio software (Nikon, JP) and the results stored as 16-bit.tiff-images. In each mode, the crystal spheres display a characteristic appearance and different quantities can be determined. Processed examples of images taken in TR, MM and WB mode are displayed in Fig. 3a–c, respectively. A set of characteristic observable extractable from the images is shown in Fig. 3d.
1 image on the sensor screen. ISO was set to 400 and exposure times were in the range of 1/50–1/400 s. In MB image series with six colours, we have a minimum time resolution of Δtmin = 10 s between subseries due to the time needed for filter switching. In each subseries, we switched colours from long to short wavelengths to counteract any timing-bias due to intermediate expansion. For a series of 6 colours, one white light and one transmission image, Δtmin = 30 s. The 14-bit raw images were saved to a computer in .nef-format. Examples of unprocessed images were shown in Fig. 1b. Subsequent image processing (centring, alignment, cropping, size calibration and colour temperature correction) was performed with ViewNX2 and/or NX Studio software (Nikon, JP) and the results stored as 16-bit.tiff-images. In each mode, the crystal spheres display a characteristic appearance and different quantities can be determined. Processed examples of images taken in TR, MM and WB mode are displayed in Fig. 3a–c, respectively. A set of characteristic observable extractable from the images is shown in Fig. 3d.
In the TR image, one notes a gradual increase of extinction towards the centre. This projection effect results from the spherical contour of the MS-layers. Additional smoothing is provided by their wavelength-dependent location and the overall strong extinction by incoherent MS. Fig. 3b shows a typical MM-image. Here, the drop-core appears as a compact, uniformly coloured sphere. Its fine surface-texture originates from individual reflections of small crystallites embedded in a uniform MS-background. This (110)-MS sphere shows an excellent contrast to the surrounding, crystalline region. It can be precisely localized and followed in time (cf. Video 2, ESI†). Remarkably, under variation of the illumination wavelength, we observe different locations for differently coloured MS-shells relating to different isopycnic surfaces. This allows using eqn (1) to infer the corresponding density profile. These MS-shells are embedded in a more transparent outer region with only few reflections, in which individual crystallites can be distinguished.
In the early-stage WB image of Fig. 3c, the overall impression is a turbid, milky-white core dotted with individual, coloured reflections. We attribute this to strong incoherent MS at all illuminating wavelengths. Note that initially, differently coloured reflections are observable over the whole drop (cf. Video 1, ESI†), which can be attributed to additional Bragg scattering of individual crystallites. After about a minute, however, a concentric colour banding appears, presenting a characteristic radial sequence of dominant colour, which relates to the MS-core (see also in Fig. 1b). As the MS-core retreats at later stages, it gets surrounded by an extended transparent crystalline region. This region shows much weaker IS and (200) Bragg reflections become nicely visible (Fig. 5b, below). In principle, eqn (1) should be applicable to these reflections, given that the scattered wavelength can be identified. We tried to extract the latter from the corresponding RGB readings in WB images using a recently proposed protocol.43 Yet, this approach failed for the monochromatic (200) Bragg reflections of individual crystals. The scattered wavelengths are lying outside the RGB-triangle in the C.I.E. 1931 colour chart.44,45 This leads to hue-dependent calibration issues and the RGB readings cannot be unequivocally assigned to individual scattered wavelengths (see Fig. S9 in the ESI†). This prevented density profiling in the transparent outer regions.
General shape fitting, determination of the centre of mass, object tracking for drifting crystals and brightness analysis for the TR and MM images used standard Image-j routines [ImageJ; https://imagej.nih.gov/ij] as well as home-written algorithms. Specifically, we fitted ellipses of horizontal and vertical semi-axes, a and b, respectively, to the projections of the crystal-fluid boundary for all three modes. The boundary is shown in Fig. 3a–c as a dashed line. In TR, we located it from the change in radial slope of the transmission signal, in WB and MM, we used the scattering contrast provided by the outer border of Bragg reflections and the simultaneous increase of CS in the fluid phase. In MM, we further fitted an ellipse to the outline of the central MS core in dependence on wavelength using brightness contrast. Its contour is shown in Fig. 3b as the inner dashed ellipse. From the semi-axes of fitted ellipses, we calculated the radii of equivalent spheres as: Ri = (a2b)(1/3). Note that for sufficiently small eccentricities, a ≈ b, and the centre-to-rim distances approaches the radius Ri of the equivalent sphere. Irrespective of imaging mode, the outermost ellipse yields the equivalent radius of the crystalline region, i.e., the melting radius, Rm. In MM mode, we additionally determine the wavelength-dependent equivalent radius of the 1st order Bragg multiple-scattering shell, RMScore. Further, the centres of the ellipses yielded the heights, Hcenter, of the drop centre-of-mass above ground. Fig. 3d shows the evolution of these observables for the example drop shown in Fig. 3a–c. The error bars are estimates based on deviation from rotation symmetry, contrast issues and interfacial smoothness. Since the crystallite number decreases while the crystal sphere size increases, the assignment of an outer boundary from WB gets somewhat less certain toward late stages. The same applies to the monochrome MM images, albeit at generally smaller uncertainties. Irrespective of imaging mode, however, data on Rm, RMScore and Hcenter agree well within experimental uncertainty. This agreement worsens only slightly for the two shortest wavelengths used in MM. There, incoherent MS emerging from the corresponding blue and cyan (110) Bragg scattering shell is pronounced enough to slightly blur its contour.
3 Results
3.1 General scenario
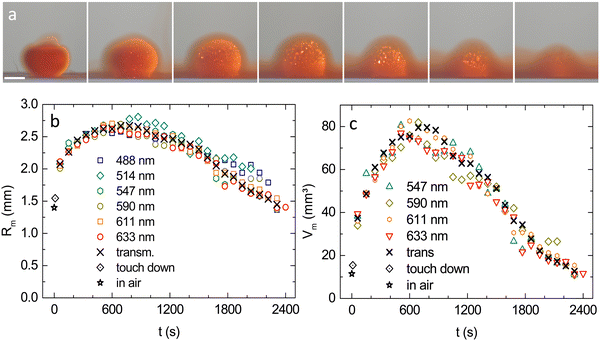
In air, the drop has an equivalent radius of about Rair = 1400 μm. Immediately after entering the water, it starts expanding and re-crystallizing. Mechanical stabilization starts upon contact between individual crystallites. On average, the shape became stable at t ≈ 5 s with a corresponding average radius of 〈Rm(t ≈ 5 s)〉 = (1550 ± 150) μm. After some ten minutes, the crystalline part of the drop reaches its maximum radial extension of about Rm ≈ 2500 μm. Thus, drops expand while they are diluting simultaneously. The broadening of the inward shifting coloured banding in the WB images indicates a decreasing slope of the density profile as well as an ever decreasing values for the central density. Thus, we observe two continuous but counterpropagating modes of motion for the observables. Initially, expansion dominates the location of a certain density or lattice constant, later on dilution takes over but no stationary state is reached.A measurement focusing on the short-time crystal sphere expansion is shown in Fig. 4, where we display the expansion-curves for Rm and for the outer rim of the reddish band Rred![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) stripe seen in Fig. 1b and 3c. (The shown equivalent radii were derived from fitted ellipses as described above) In this double logarithmic plot, the initial increase is seen to follow a power law, with a significant exception for the very first data point. While at this time (t = 5 s) the crystal shape has already stabilized to a sphere, the optical appearance is misleading, in that it suggests completed solidification. In fact, despite their optically compact appearance, polycrystalline materials may remain semi-solid for some further time until full rigidity is obtained after t ≈ 5–8 s.46 Therefore in Fig. 4, we can safely assume completed crystallization only for the power-law increase seen between 10 s and 200 s. After reaching a maximum, the crystalline region shrinks due to inward melting, as does the core region due to ongoing dilution. The latter disappears after some 25–30 min, the last outer crystals melt after some 30–45 min slightly depending on drop history and shape.
stripe seen in Fig. 1b and 3c. (The shown equivalent radii were derived from fitted ellipses as described above) In this double logarithmic plot, the initial increase is seen to follow a power law, with a significant exception for the very first data point. While at this time (t = 5 s) the crystal shape has already stabilized to a sphere, the optical appearance is misleading, in that it suggests completed solidification. In fact, despite their optically compact appearance, polycrystalline materials may remain semi-solid for some further time until full rigidity is obtained after t ≈ 5–8 s.46 Therefore in Fig. 4, we can safely assume completed crystallization only for the power-law increase seen between 10 s and 200 s. After reaching a maximum, the crystalline region shrinks due to inward melting, as does the core region due to ongoing dilution. The latter disappears after some 25–30 min, the last outer crystals melt after some 30–45 min slightly depending on drop history and shape.
3.2 Expansion and dilution on the level of individual crystallites
Immediately after solidification, we observe a fine-grained polycrystalline solid encapsulated by a thin fluid layer (Fig. 3c). Throughout drop evolution, individual crystals show an outward drift and an increase in size, while their persistent and directed colour-changes demonstrate their ongoing dilution. This is illustrated in Fig. 5 for two runs starting at t0 = 150 s and t0 = 2820 s.Individual crystallites could be followed over 30 s to 120 s, during which they typically showed constant radial velocities ranging between 0.2 μm s−1 in the central region to 15 μm s−1 close to the drop rim. This spatial variation is shown in Fig. 5a. The observed correlation of drift velocities to crystal location is attributed to projection effects, as centrally seen crystallites move preferentially towards the camera, while rim crystallites drift preferentially perpendicular to that direction. In Fig. 5b, we show an evolved drop with a shrunken core. In Fig. 5c, we display a series of cropped images focusing on the evolution of an individual crystal close to the core-rim. As it drifts slowly outward, the initially small dark blue crystal expands considerable and continuously changes its Bragg-reflected colour. The crystallite to its immediate right even shows colour banding within its interior. Both directly visualize the ongoing interplay of drop expansion and dilution.
3.3 Size evolution of the crystalline part of the drop
A typical MM time series for λ = 611 nm is shown in Fig. 6a. (For large images and the λ = 590 nm series, see Fig. S9 in the ESI†). Results for Rm from MM at different illumination wavelengths are compared in Fig. 6b to results from TR. The overall agreement is very good, except for the shortest wavelengths, which at later stages show a slight systematic deviation towards larger values. This is attributed to blurring caused by incoherent MS. In Fig. 6c, we omit these two data sets for small λ and display the volume of the crystalline part of the drop, calculated as: Vm = (4π/3)Rm3. Data from both observation modes coincide nicely within experimental scatter. The initially fast volume increase gradually slows and past the maximum expansion at t ≈ 700 s, the crystal sphere volume decreases. The straight, dashed line is a guide to the eye. Over more than 1000 s, the decrease is nearly linear. The observed late stage slowing may relate to the crystalline region being meanwhile immersed in a rather concentrated fluid environment (see last images in Fig. 6a).3.4 Density profiling
A colour series of MM images taken at t = 480 s is displayed in Fig. 7a. Most strikingly, we observe a concentric nesting of the thin, isopycnic MS-shells, vividly Bragg scattering a certain wavelength but obviously transparent to all others. The derived RMScore(t) are shown in Fig. 7b. As the core regions expand and shrink again, the wavelength dependent shell-radii keep their sequence, i.e. the largest densities are consistently found in the innermost shell. This nesting qualitatively confirms the intuitively expected radial gradient in density and allows for density profiling. Fig. 7c shows the derived radial density profiles for different times. At all times, we see a radially decreasing density profile. Initially, the profile follows the general expansion and shifts rightward. This trend is later reversed due to core shrinkage. Most importantly, the initial density profiles are rather steep, but flatten continuously with time. | ||
| Fig. 7 Evolution of the crystal sphere core–density profiles. (a) Processed MM images recorded at t = 480 s for different wavelengths as indicated in the key, ranging from dark blue to dark red and corresponding to densities from ρm = 31.54 μm−3 to ρ = 68.83 μm−3, respectively. Note the nested structure of shells with different densities, i.e. R488 < R633< Rm. Scale bars 2 mm. (b) Equivalent MS-core radii obtained in MM. Note the increase in uncertainty for the shortest wavelengths due to blurring by incoherent MS. (c) Density profiles as obtained from the radial positions of MS-core scattering using eqn (1) for different times indicated in the key. Note the initial right shift and the gradual decrease in profile steepness. | ||
4 Modelling
4.1 Dynamical density functional theory for the isothermal expansion of a spherical crystallite
We now turn to a theoretical description of the crystal expansion process. We use the framework of classical dynamical density functional theory (DDFT) which provides an ideal microscopic framework for expanding solids.30,47 We apply it here in a simple way to describe the isothermal expansion of a three-dimensional spherical colloidal crystallite in the bulk in the absence of any boundary and solvent flow. The crystal sphere dilutes by expansion and simultaneously melts at its contour. The remaining crystalline portion decreases. We consider a coarse-grained inhomogeneous time-dependent density field with radial symmetry, ρ(r, t), where r > 0 denotes the distance from the centre of the crystallite.The initial density distribution is modelled as a steep tanh-profile:
| ρ(r, t = 0) = ρ0(1 − tanh((r − r0)/ξ)), | (2) |
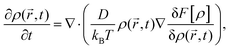 | (3) |
 | (4) |
 | (5) |
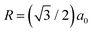 for the nearest neighbours and accordingly for the next nearest neighbours. Zσ is the effective macroion charge, ε0 the dielectric permittivity of vacuum, εr = 80 the dielectric constant of the solvent, and κ the inverse Debye–Hückel screening length.49 We express the excess free energy approximately as
for the nearest neighbours and accordingly for the next nearest neighbours. Zσ is the effective macroion charge, ε0 the dielectric permittivity of vacuum, εr = 80 the dielectric constant of the solvent, and κ the inverse Debye–Hückel screening length.49 We express the excess free energy approximately as | (6) |
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) N of the three-dimensional bcc-lattice. In radial symmetry, eqn (3) reads:
N of the three-dimensional bcc-lattice. In radial symmetry, eqn (3) reads: | (7) |
 | (8) |
| ρ(rm(t),t) ≡ ρm. | (9) |
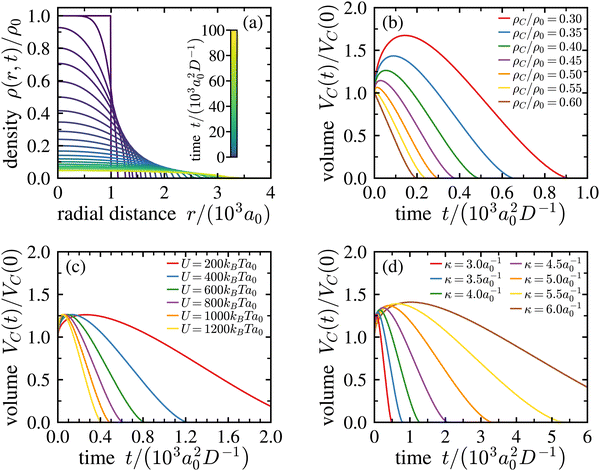 | ||
| Fig. 8 Numerical solution of the dynamical density functional theory equation. (a) Density evolution of the crystallite. During the crystal expansion, the local density decreases, which leads to melting. The initial size of the crystallite is r0 = 103a0, the inverse Debye–Hückel screening length is κ = 3a0−1 and the strength of the Yukawa pair potential is U = 103kBTa0, where a0 is the initial bcc-lattice constant given by a0 = (2/ρ0)1/3. The sum of eqn (6) is approximated by truncating after the fourth nearest neighbours. (b) Time dependence of the crystalline volume VC(t) (i.e., the crystalline volume enclosed by an isopycnic shell of density ρC) for various densities ρC as indicated in the key. Here, κ = 3a0−1 and U = 103kBTa0. For ρC ≤ 0.55 ρ0, the crystallite initially expands before its volume decreases linearly in time over an extended period. (c) The same for ρC/ρ0 = 0.40, κ = 3a0−1, and different Yukawa repulsion strengths, U, as indicated in the key. U has little influence on the functional form of the curve but leads to a stretching of the time scale of expansion. (d) The same for ρC/ρ0 = 0.40, U = 103kBTa0, and different κ as indicated in the key. An increased κ leads to a slight increase of the curve maximum and a stretching of time scales. | ||
Suitable start-parameters were chosen close to those in the experiment and are provided in the legend and in the captions. We find a continuously flattening density profile in Fig. 8a. Simultaneously, the central density decreases (cf. Fig. S11 of the ESI†). Note that at large times, the crystal core has developed a near constant density, and a significant slope is observable only at an increasing radial distance. For the core region, this implies a homogeneous and isotropic expansion at late times. While the decrease in central density with time, as well as the radial decrease of density can be intuited, this specific prediction for the screened Yukawa interaction cannot and further differs markedly from the results obtained for plasma crystals.27
Each numerical run at given start parameters yields a set of density profiles, from which the characteristic expansion curves for any chosen ρC/ρ0 can be derived. Curves for different ρC generated from the run shown in Fig. 8a are shown in Fig. 8b. For small ρC, we have only expansion. For density ratios ρC ≤ 0.55ρ0, an initial expansion precedes the dynamical decrease of the crystalline volume VC(t). There, the volume evolution features a pronounced maximum followed by a stretched, almost linear decrease as a function of time t. Note the pronounced increase of the maximum volume for decreasing density ratios ρC/ρ0. Performing repeated calculations under systematic variation of parameters then shows the dependence of expansion curve shape and extension on these. Fig. 1c and d demonstrate that the strength of the Yukawa potential U = Zσ2e2/4πε0ε has practically none, and the inverse screening length has only moderate influence on the maximal expansion, but both influence the temporal evolution of the volume for a given density ρm.
Finally, we remark that the theory is simple in the sense, that it involves only the density as a dynamical order parameter and basically uses a local density approximation for the density functional. Nonlocal extensions with a full density field which is strongly peaked on the colloidal length scale would imply much larger numerical effort. The zero-temperature lattice sum for the Yukawa system is another approximation that may lead to deviations from the behaviour of an actual Brownian Yukawa system. Moreover, we assumed that the mobility of the particles is the same in both the crystal and the fluid phase. This is clearly an approximation that induces a smearing of the density profiles.54 However, our simpler version already yields a specific prediction for the expansion of colloidal crystals as well as valuable information on the influence of important experimental parameters on the expansion, which cannot be controlled well in plasma experiments. By contrast, they are readily adjusted in the present study via CO2 content and salt concentration.35
5 Discussion
Thus far, we reported the fabrication of initially highly concentrated drops of suspensions made of strongly repulsive spheres in a sphere-free environment. This allowed for the first time to study the isotropic expansion of a polycrystalline solid in three dimensions. In the transparent parts of the drops, we used white light Bragg imaging to monitor the drift motion and expansion of individual, Bragg reflecting crystallites. Bragg imaging and complementary transmission imaging gave consistent results for the crystal sphere radii with high spatial resolution. We could overcome the limitations of white light Bragg imaging using monochromatic illumination Bragg imaging. Exploiting the peculiarities of coherent multiple scattering at Bragg reflections then allowed probing the locations of certain densities within the turbid drop core as well as density profiling.Fig. 9 compares the measured expansion curves to our theoretical expectations. To obtain the best overall least squares fits, we here varied the ratios ρC/ρ0 as indicated in the key. The other input parameters were fixed to values corresponding to the experimental ones: Z = 365; κ = 3.5; D = 4D0 (except for Vm, where D = 7.6D0); ρ0 = 110 μm−3; and R0 = 1.40 mm. The fits capture the general curve shape very well. On the one hand, this demonstrates that our novel experimental approach can provide successful and reproducible access to density profiling in turbid crystalline media. Moreover, the remaining statistical and systematic uncertainties (cf.Fig. 3d, 6c and 7b) are small enough allowing for a quantitative comparison to theoretical predictions. On the other hand, Fig. 9 clearly shows that, in spite of the simplicity of the theoretically considered situation, our modelling approach is sufficiently sophisticated to yield an excellent and nearly quantitative description.
As compared to previous studies on isotropic, three-dimensional expansion, polycrystalline aqueous charged sphere suspensions show a behaviour midway between that of Coulomb balls and Yukawa balls.27–29 The former revealed a strictly flat density profile, while the latter produced strongly peaked profiles. Concerning two-dimensional experiments, our findings bear resemblance to those of Tanaka et al., who studied short range repulsive spheres in slit confinement. They found a continuously decreasing core density, albeit with only a weak density gradient within the crystal. They also reported the crystalline core embedded in a widening interfacial boundary region towards the fluid phase. In the present experiments, the innermost density profile was not (yet) accessible, but the density profiles observed roughly halfway remained for extended times while flattening continuously. Further, in the outer, transparent region, we could show clear evidence of a persistent radial density gradient. Crystal spheres made of charged colloidal spheres therefore provide a valuable platform for future systematic experiments. Particles of different sizes and charge densities are at hand, which will facilitate tuning of the time-scales and the repulsive strength. Using a polymer solution as solvent for the suspension and/or the receiving bath may further allow investigations of the effects of (depletion-) attraction and/or facilitate damping of the expansion by introducing an outer osmotic pressure. Experiments with drops of lower start density are under way, which should yield better access to the innermost drop regions. Experiments using X-ray tomography appear to be a possible alternative approach to monitor the density evolution throughout the complete drop.
Fig. 9 also shows a few systematic deviations between experiment and theoretical model. There appears to be a mismatch between the density ratios, ρC/ρ0 probed in the experiments starting at t = 60 s and the densities used in obtaining the overall best fits. Interestingly, also the other two discrepancies are restricted to certain time intervals. In these, the corresponding statistical and systematic errors considered in Fig. 3d and 6c are rather small. The observed deviations are thus both characteristic and significant. Further, in both cases, these discrepancies occur at characteristic times. In particular, at early times and for the largest densities probed, the measured and expected core–volume expansion curves appear flatter than expected, showing only weak maxima, while at late times experiment and theory are in very good agreement. Conversely, the measured crystal sphere volume, Vm, follows the expectations closely at early times, while from some 800 s onward, it deviates towards smaller than expected volumes. None of these disparities can be attributed to the level of sophistication used in our model. In fact, modelling the expanding drops as isotropically expanding crystals made of electrostatically repulsive Brownian spheres and considering melting as only due to density reduction at otherwise constant interaction parameters performs well enough to yield an overall excellent description of the experimental observations. Rather, the following discussion traces the mismatch back to violations of the required constant boundary conditions, which occur on the experimental side.
First, at the start of the expansion experiments the basic condition of an overall crystalline drop is only given for the model. On the experimental side, the drops are shear-molten by their extrusion and the impact on/in the water. Start of re-crystallization occurs at t ≈ 0.3 s, but complete solidification takes considerably longer. Therefore, the drops initially are in a highly mobile fluid, respectively semi-solid state, and the expansion proceeds significantly faster in at this initial stage than later under fully crystalline conditions. This was demonstrated Fig. 4 by the switch in expansion behaviour occurring for t = 5–10 s. We believe that as a consequence, the initially faster expansion shifts the observable isopycnic shells further out to locations actually expected for much smaller densities. This explains the overall mismatch between probed and fitted densities. The stage of initial rapid expansion fastens the dilution, in particular for the densest core regions. Since the measurements in MM mode start only after complete solidification, this stage is completely missed in the experimental curves probing the largest densities. The mismatch becomes smaller at smaller probed densities. There is a well-developed maximum for λ = 633 nm, and the effect appears to be absent for Vm. The initial rapid expansion of the molten or partially solidified drop also readily explains the overall larger than expected dilution of the experimental drops.
To avoid shear melting, the extrusion process should be improved. We followed this challenge to minimize mechanical impact in additional experiments, but thus far could not obtain satisfactory results. Alternatively, future modelling could implement a time dependent effective diffusion constant during the first instances of calculation. This could be implemented without extensive numerical effort, albeit at the introduction of further free parameters and additional assumptions to be made about the crystallization kinetics far off mechanical equilibrium.55
Second, at long times, we violate the condition of spatially homogeneous and constant particle charge and amount of screening electrolyte. This results from a slight difference in conditioning procedure for the drops and the receiving solvent. In fact, the suspension had been deionized and decarbonized, while the receiving water was merely deionized but equilibrated against ambient air. According to recent literature, dissolved CO2 and its reaction products will significantly reduce the particle charge due to a combination of screening effects with pH-driven and dielectric charge regulation.35,56 In the present situation, CO2 diffusing from the surrounding water towards the drop cores will significantly lower the particle charge in the contaminated regions and there increase ρm. After traversing the outer fluid layer, the inward migrating CO2 and its dissociation product carbonic acid reach the crystalline part of the drop. In Fig. 9, this happens shortly past the maximum of Vm(t). From thereon, the remaining crystalline volume shrinks much faster by CO2-related melting than predicted for dilution related melting at constant deionized and decarbonized conditions. The idea of an advancing CO2-front is corroborated by the very early disappearance of the blueish 221 Bragg reflections at the drop rim (cf. Video 1, ESI†) and the simultaneous unaffectedness of the core volume curves. Future experiments could therefore attempt to use a gas-tight container filled with decarbonized water as receiving fluid.
An additional experimental improvement would be a buoyancy match between particles, suspending medium and receiving solvent. Under the present conditions, all drops settled to the cell bottom. There, additional influences of gravity may become operative. While for the small drops used in the present experiments, no evidence of a height dependent lattice constant was detected, there were several indirect effects observable. For instance, we observed a systematic deviation from a strictly spherical drop shape at late stages. Specifically, the presence of a well-observable particle enriched environment causes the lower drop half to expand slower than the upper. We believe that the bottom layer of sedimented particles creates an increased osmotic pressure counteracting the expansion of the crystal sphere. To exclude an influence on our measurements, drop size analysis was solely based on data taken from the upper drop halve. To fully circumvent this effect, one may try to buoyancy-match the particles, by using low molecular weight sugar-solutions for both the drop and the environment. Preliminary efforts in that direction indeed indicate a way to prepare freely suspended drops residing in the cell centre (Fig. S6 in the ESI†).
Finally, we like to stress that the here employed, scattering-based microscopic imaging technique is not restricted to experiments on the expansion of crystalline drops. Rather, we anticipate that there are a number of interesting non-equilibrium experiments, which could profit from it ref. 3–5, 55 and 57. This concerns, in particular, experiments at large particle concentrations, which so far were only accessible for hard sphere systems and a few other well-index-matched systems. Possible applications comprise a straight forward extension of the range of accessible densities in studies of crystallization, coarsening and melting kinetics, both with and without applied shear, as well as compression experiments using gravity, centrifugation or other suitable experimental techniques.
6 Conclusion
We developed and successfully demonstrated a novel approach to determine the density profiles in freely expanding turbid crystalline drops. We observed a promising agreement between our experiments and theoretical modelling based on dynamical density functional theory. Using highly charged spheres in an aqueous environment, we reproducibly observed an expansion scenario reminiscent, but not exactly identical to previous findings. The characteristic development should serve as a reliable starting point for systematic investigations of expansion and profiling in dependence on interaction type, shape, and strength as well as on environmental boundary conditions including their theoretical modelling. Further, our method should be readily transferable to unidirectional expansion experiments between confining surfaces or to free-standing extruded colloidal wires. We thus anticipate, that our novel approach can pave the way to density profiling also in many other situations of fundamental and/or practical interest.Author's contributions
This study was conceptualized by T. P. Funding was acquired and administered by T. P. and H. L. Experimental methodology was developed by J. L. M. Jr., J. A. B. W., C. H. Y, and S. J. Analysis software was developed by E. M. and M. W. Experiments were performed and analysed by M. W., J. R. vP.-L.; J. A. B. W., C. H. Y., S. J., and M. H. Experiments were supervised by M. W. and T. P. The theory part of this study was conceptualized and supervised by H. L. Theoretical modelling and its analysis were developed and performed by G. H. P. N. The manuscript was written by T. P., G. H. P. N., and H. L., M. W. and G. H. P. N. contributed equally to this study.Data availability
Original data and artwork is available from the corresponding author upon reasonable request.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
We thank Ramsia Sreij for the X-ray characterization. We thank Daniela Kronmüller for the documentation of fully buoyant drops. We thank P. Leiderer, to whom we dedicate this paper on occasion of his 80th birthday, for many inspiring discussions on charged sphere phase transitions. Financial support from the DFG (Projects PA459/19 and LO418/25) and from the Inneruniversitäre Forschungsförderung der Johannes Gutenberg-Universität, Mainz, is gratefully acknowledged. G. M. Jr. was trainee within the IAESTE program and received a fellowship by the Deutsche Akademische Austauschdienst (DAAD).References
- A. Ivlev, H. Löwen, G. E. Morfill and C. P. Royall, Complex Plasmas and Colloidal Dispersions: Particle-Resolved Studies of Classical Liquids and Solids, World Scientific, Singapore, 2012 Search PubMed.
- C. P. Royall, P. Charbonneau, M. Dijkstra, J. Russo, F. Smallenburg, T. Speck and C. Valeriani, Rev. Mod. Phys., 2024 Search PubMed , Colloidal hard spheres: Triumphs, challenges, and mysteries, Rev. Mod. Phys., Accepted Submitted, https://journals.aps.org/rmp/accepted/fe079E7cP7b1b60921a5179849e480df424635cf1.
- R. Piazza, Rep. Prog. Phys., 2014, 77, 056602 CrossRef PubMed.
- H. Löwen, J. Phys.: Condens. Matter, 2001, 13, R415–R432 CrossRef.
- H. Zhou, W. Ouyang, S. Zou and S. Xu, Nanomaterials, 2004, 14, 355 CrossRef PubMed.
- Y. Tang, A. J. Armstrong, R. C. Mockler and W. J. O'Sullivan, Phys. Rev. Lett., 1989, 62, 2401–2404 CrossRef PubMed.
- K. Zahn, R. Lenke and G. Maret, Phys. Rev. Lett., 1999, 82, 2721–2724 CrossRef CAS.
- W. J. He, T. Cui, Y. M. Ma, Z. M. Liu and G. T. Zou, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 195104 CrossRef.
- A. V. Straube, A. A. Louis, J. Baumgartl, C. Bechinger and R. P. A. Dullens, Europhys. Lett., 2011, 94, 48008 CrossRef.
- J. R. Savage, D. W. Blair, A. J. Levine, R. A. Guyer and A. D. Dinsmore, Science, 2006, 314, 795–798 CrossRef CAS PubMed.
- A. V. Straube, A. A. Louis, J. Baumgartl, C. Bechinger and R. P. A. Dullens, Europhys. Lett., 2011, 94, 48008 CrossRef.
- A. E. Larsen and D. G. Grier, Phys. Rev. Lett., 1996, 76, 3862–3865 CrossRef CAS PubMed.
- S. Tanaka, Y. Oki and Y. Kimura, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 052305 CrossRef PubMed.
- K. J. Strandburg, Rev. Mod. Phys., 1988, 60, 161–207 CrossRef CAS.
- B. J. Ackerson and N. A. Clark, Phys. A, 1983, 128, 221–249 CrossRef.
- A. Samanta, M. E. Tuckerman, T.-Q. Yu and E. Weinan, Science, 2014, 346, 729–732 CrossRef CAS.
- F. Wang, D. Zhou and Y. Han, Adv. Funct. Mater., 2016, 26, 8903–8919 CrossRef CAS.
- H. Thomas and G. E. Morfill, Nature, 1996, 379, 806–809 CrossRef CAS.
- N. J. Lorenz, I. Gupta and T. Palberg, J. Chem. Phys., 2023, 158, 114902 CrossRef CAS PubMed.
- Z. Wang, F. Wang, Y. Peng and Y. Han, Nat. Commun., 2015, 6, 9642 Search PubMed.
- A. M. Alsayed, M. F. Islam, J. Zhang, P. J. Collings and A. G. Yodh, Science, 2005, 309, 1207–1210 CrossRef CAS.
- M. D. Elliot and W. C. K. Poon, Adv. Colloid Interface Sci., 2001, 92, 133–194 CrossRef CAS.
- T. Palberg, J. Phys.: Condens. Matter, 1999, 11, R323–R360 CrossRef CAS.
- J. S. van Duijneveldt, J. K. G. Dhont and H. N. W. Lekkerkerker, J. Chem. Phys., 1993, 99, 6941–6949 CrossRef CAS.
- T. Kanai, T. Sawada, J. Yamanaka and K. Kitamura, J. Am. Chem. Soc., 2004, 126, 132010–132011 CrossRef.
- T. Kanai, T. Sawada, J. Yamanaka and K. Kitamura, Langmuir, 2005, 21, 7633–7637 CrossRef CAS.
- A. Piel, Plasma Phys. Controlled Fusion, 2017, 59, 014001 CrossRef.
- T. Antonova, C. R. Du, A. V. Ivlev, B. M. Annaratone, L.-J. Hou, R. Kompaneets, H. M. Thomas and G. M. Morfill, Phys. Plasmas, 2012, 19, 93709 CrossRef.
- A. Piel and J. Goree, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 88, 063103 CrossRef PubMed.
- S. van Teeffelen, C. N. Likos and H. Löwen, Phys. Rev. Lett., 2008, 100, 108302 CrossRef PubMed.
- D. Hessinger, M. Evers and T. Palberg, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 61, 5493–5506 CrossRef CAS.
- T. Palberg, H. Hecht, E. Simnacher, T. Loga, F. Falcoz, J. Kottal and P. Leiderer, J. Phys. III, 1994, 4, 457–471 CrossRef CAS.
- L. Shapran, H. J. Schöpe and T. Palberg, J. Chem. Phys., 2006, 125, 194714 CrossRef PubMed.
- P. Wette, H.-J. Schöpe, R. Biehl and T. Palberg, J. Chem. Phys., 2001, 114, 7556–7562 CrossRef CAS.
- P. Vogel, N. Möller, M. N. Qaisrani, B. Pravash, S. Weber, H.-J. Butt, B. Liebchen, M. Sulpizi and T. Palberg, J. Am. Chem. Soc., 2022, 144, 21080–21087 CrossRef CAS.
- T. Okubo and H. Ishiki, J. Colloid Interface Sci., 1999, 211, 151–159 CrossRef CAS PubMed.
- T. Palberg, J. Phys.: Condens. Matter, 1999, 11, R323–R360 CrossRef CAS.
- S. Heidt, private communication.
- P. Schall, Rep. Prog. Phys., 2009, 72, 076601 CrossRef.
- H. J. Schöpe, A. Barreira Fontecha, H. König, J. Marques Hueso and R. Biehl, Langmuir, 2006, 22, 1828–1838 CrossRef.
- G. R. Untracht, M. Chen, P. Wijesinghe, J. Mas, H. T. Tura, D. Marti, P. E. Andersen and K. Dholakia, Sci. Adv., 2023, 9, eadh543 Search PubMed.
- R. J. Spry and D. J. Kosan, Appl. Spectrosc., 1986, 40, 782–784 CrossRef.
- J. Teyssier, S. V. Saenko, D. van der Marel and M. C. Milinkovitch, Nat. Commun., 2015, 6, 6368 CrossRef CAS PubMed.
- T. Smith and J. Gould, Trans. Opt. Soc., London, 1931, 33, 73–134 CrossRef.
- J. Schanda, Colorimetry: Understanding the CIE System, John Wiley & Sons, Hoboken, 2007 Search PubMed.
- N. Lorenz, H. J. Schöpe and T. Palberg, J. Chem. Phys., 2007, 131, 134501 CrossRef PubMed.
- M. te Vrugt, H. Löwen and R. Wittkowski, Adv. Phys., 2020, 69, 121–247 CrossRef.
- H. Löwen and E. Allahyarov, J. Phys.: Condens. Matter, 1998, 10, 4147–4160 CrossRef.
- J.-P. Hansen and H. Löwen, Annu. Rev. Phys. Chem., 2000, 51, 209–242 CrossRef CAS PubMed.
- M. O. Robbins, K. Kremer and G. S. Grest, J. Chem. Phys., 1988, 88, 3286–3312 CrossRef CAS.
- E. J. Meijer and D. Frenkel, J. Chem. Phys., 1991, 94, 2269–2271 CrossRef CAS.
- S. Hamaguchi, R. T. Farouki and D. H. E. Dubin, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 56, 4671–4682 CrossRef CAS.
- F. Bitzer, T. Palberg, H. Löwen, R. Simon and P. Leiderer, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 2821–2826 CrossRef CAS.
- H. E. Hermes, C. E. Sitta, B. Schillinger, H. Löwen and S. U. Egelhaaf, Phys. Chem. Chem. Phys., 2015, 17, 15781–15787 RSC.
- H. Löwen, A. van Blaaderen, J. K. G. Dhont, P. Nielaba and T. Palberg, Eur. Phys. J.: Spec. Top., 2013, 222(11), 2723–3087 Search PubMed.
- P. Vogel and T. Palberg, J. Colloid Interface Sci., 2023, 656, 280–288 CrossRef.
- M. E. Leunissen and A. van Blaaderen, J. Chem. Phys., 2008, 128, 164509 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm00413b |
| This journal is © The Royal Society of Chemistry 2024 |